(Boratabenzene)(cyclooctatetraenyl) lanthanide complexes: a new type of organometallic single-ion magnet†
Yin-Shan
Meng‡
a,
Chun-Hong
Wang‡
b,
Yi-Quan
Zhang
c,
Xue-Bing
Leng
b,
Bing-Wu
Wang
 *a,
Yao-Feng
Chen
*b and
Song
Gao
*a
*a,
Yao-Feng
Chen
*b and
Song
Gao
*a
aBeijing National Laboratory of Molecular Science, State Key Laboratory of Rare Earth Materials Chemistry and Applications, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, P. R. China. E-mail: wangbw@pku.edu.cn; gaosong@pku.edu.cn
bState Key Laboratory of Organometallic Chemistry, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, 345 Lingling Road, Shanghai 200032, P. R. China. E-mail: yaofchen@mail.sioc.ac.cn
cJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, P. R. China
First published on 4th March 2016
Abstract
A series of new sandwich type lanthanide complexes containing both boratabenzene and cyclooctatetraenyl ligands, [(C5H5BR)Ln(COT)] (1Er: R = H, Ln = Er; 2Er: R = Me, Ln = Er; 3Er: R = NEt2, Ln = Er; 4Dy: R = H, Ln = Dy; 5Dy: R = Me, Ln = Dy; 6Dy: R = NEt2, Ln = Dy; 7Y: R = NEt2, Ln = Y), were synthesized. The structures of 1Er–7Y were all characterized by single crystal X-ray diffraction. Dynamic susceptibility experiments showed that the erbium complexes 1Er–3Er exhibited slow magnetic relaxation under zero dc field while the dysprosium complexes 4Dy–6Dy did not. For the erbium complexes, the magnetic properties were influenced by the substituent on the boron atom. 1Er exhibited hysteresis up to 8 K, and 2Er featured the highest energy barrier (300 cm−1) among all the reported erbium single-ion magnets (SIMs). The influence of the boron substituent on the magnetic properties was highlighted by ab initio calculations.
Introduction
Since the discovery of the Mn12 molecule which exhibits magnet-like behaviour at liquid helium temperature,1 many efforts have been made to the design and synthesis of single-molecule magnets (SMMs).2 This fascinating magnetic property originates from a combination of a large spin ground state and uniaxial magnetic anisotropy, and makes SMMs potential candidates for the next generation high-density data storage materials, quantum computing and spintronic devices.3 Later, single-ion magnets (SIMs) which contain only a single spin carrier have been developed.4 Recently, several reports disclosed that carbon-based ligands, such as Cp* and COT (Cp* = pentamethylcyclopentadienyl, COT = cyclooctatetraenyl), supporting erbium complexes show interesting SIM properties.5Boratabenzenes are a type of heterocyclic, 6π-electron aromatic anion. The first boratabenzene derivative [CpCoC5H5BPh]+ was reported by Herberich and co-workers in 1970.6 One year later, Ashe III described the synthesis of lithium 1-phenylboratabenzene.7 Their pioneering research opened up the fascinating area of boratabenzene chemistry. In the last four decades, a large number of metal complexes bearing boratabenzenes have been reported.8,9 However, the properties and applications of these complexes were mostly limited to their reactivity and catalytic applications in organic and polymer synthesis.10 Considering the similarity between boratabenzene and cyclopentadienyl, it is possible to construct new erbium SIMs by using boratabenzene ligands. On the other hand, boratabenzene is a poorer electron donor in comparison with Cp*, promoting the 4f electrons stretching along the uniaxial direction. Therefore, the uniaxial magnetic anisotropy of (boratabenzene)(cyclooctatetraenyl) lanthanide might be enhanced, which may bring a new opportunity in the design of erbium SIMs with high Ueff and/or TB. Furthermore, the specific electrostatic contribution of boratabenzene and electronic structure modulation on SIMs can be tuned by the choice of the exocyclic substituent on boron. Herein, we report the synthesis, characterization and magnetic properties of (boratabenzene)(cyclooctatetraenyl) lanthanide complexes. The ab initio calculations were also performed to provide further insight into the magnetic properties of these complexes.
Results and discussion
Synthesis and structural characterization of (boratabenzene)(cyclooctatetraenyl) lanthanide complexes
Salt elimination reactions of Li(C5H5BR) (R = H, Me, NEt2) with [(COT)LnCl(THF)] (Ln = Er, Dy, Y) in THF gave crude products, which recrystallized in toluene or hexane to provide the desired (boratabenzene)(cyclooctatetraenyl) lanthanide complexes [(C5H5BR)Ln(COT)] (1Er: R = H, Ln = Er; 2Er: R = Me, Ln = Er; 3Er: R = NEt2, Ln = Er; 4Dy: R = H, Ln = Dy; 5Dy: R = Me, Ln = Dy; 6Dy: R = NEt2, Ln = Dy; 7Y: R = NEt2, Ln = Y) in moderate yields (Scheme 1). Complexes 1Er–7Y were characterized by single crystal X-ray diffraction. 1Er–7Y all crystallize in the monoclinic space group P21/c. The molecular structures of 1Er–3Er are shown in Fig. 1, while those of 4Dy–6Dy and 7Y are presented in the ESI.† The structural features of 1Er–3Er and 4Dy–6Dy are very similar and 1Er–3Er were taken as the examples to analyze the structural features. 1Er–3Er are sandwich type organometallic complexes, and the erbium ion is much closer to the centroid of the cyclooctatetraenyl ring (1.674–1.679 Å) than to that of the boratabenzene ring (2.245–2.257 Å). The average Er–C(COT) bond lengths in 1Er, 2Er and 3Er are 2.495(8), 2.491(2) and 2.493(5) Å, respectively, which are close to that in [(Cp*)Er(COT)] (Cp* = pentamethylcyclopentadienyl) (2.513 Å).5a On the other hand, the average Er–C(boratabenzene) bond lengths in 1Er, 2Er and 3Er (2.661(8), 2.657(3) and 2.647(4) Å) are much longer than the average Er–C(Cp*) bond length in [(Cp*)Er(COT)] (2.573 Å) as boratabenzene is a poorer electron donor in comparison with Cp*. The Er–C(boratabenzene) bond lengths in 1Er, 2Er and 3Er are in the ranges of 2.618(9)–2.694(9), 2.629(3)–2.678(3) and 2.603(8)–2.698(8) Å, respectively; the erbium ion is far away from the ortho carbon atoms and closer to the para carbon atom. The Er–B distances (2.76(1) Å (1Er), 2.779(3) Å (2Er) and 2.83(1) Å (3Er)) are longer than the Er–C(boratabenzene) distances. These observations revealed a slippage of the erbium ion away from boron and toward the para carbon. Due to the strong π-interaction between boron and the amino-substituent, the Er–B distance in 3Er is longer than those in 1Er and 2Er and the deviation of the boron atom from the boratabenzene plane in 3Er (0.097 Å) is larger than those in 1Er and 2Er (0.028 and 0.059 Å, respectively). Dihedral angles between the cyclooctatetraenyl ring and the boratabenzene ring in 1Er, 2Er and 3Er are 10.6°, 5.5° and 9.3°, respectively. The nearest neighboring molecules are nearly perpendicular to each other through the C–H⋯B interaction and edge to face π⋯π stacking between the two aromatic rings. The nearest Er⋯Er distances in 1Er, 2Er and 3Er are 6.1, 6.8 and 6.3 Å, respectively (see the ESI†).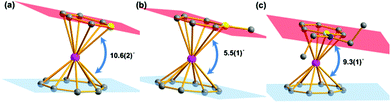 | ||
| Fig. 1 Molecular structures of 1Er–3Er. (a), (b) and (c) Represent 1Er, 2Er and 3Er, respectively. Color code: pink, Er, dark grey, C, yellow, B, blue, N. Hydrogen atoms are omitted for clarity. | ||
Magnetic properties
Dc magnetic measurements were conducted under 1 kOe dc field with the temperature ranging from 300 to 2 K (Fig. 2 and S4 in the ESI†). At room temperature, the χmT values of 1Er, 2Er, 3Er, 4Dy, 5Dy and 6Dy are 11.01, 11.04, 11.08, 13.92, 13.94 and 14.06 emu mol−1 K, respectively, which are in good agreement with the theoretical values of ErIII (4I15/2, S = 3/2, L = 6, g = 6/5) and DyIII (6H15/2, S = 5/2, L = 5, g = 4/3). The χmT value of 1Er decreases very slightly with decreasing temperature, but when the temperature decreases to 12 K, the χmT value jumps to 11.32 cm3 mol−1, and then decreases sharply upon further cooling. The χmT value of 2Er also slightly upturns at about 6 K, and then drops precipitously. Similar to other reported ErIII SIMs, upon a decrease of the temperature, the χmT value of 3Er decreases slightly, until about 3 K where it drops drastically. The sudden drop in χmT observed for 1Er, 2Er and 3Er indicated that their magnetizations are blocked. The sudden drop in χmT observed for 1Er, 2Er and 3Er may arise from antiferromagnetic coupling, saturation of the magnetization, the Zeeman effect, and the spin–orbit coupling effect, which led to a change of spin population or magnetization blocking. This phenomenon is not uncommon in previously reported SMMs.4f,5 The variable field dc measurements showed that the unusual χmT rising observed for 1Er at 12 K is not due to the polycrystalline samples’ reorientation along the magnetic field, but is related to the SIM properties (Fig. S5†). Further discussions on this χmT rising at low temperatures are provided vide infra. For DyIII complexes, upon cooling, the χmT values are nearly constant until 100 K, and then slowly decrease. Below 25 K, the χmT values drop steeply upon further cooling. At 2 K, the values are 9.52, 10.00, and 10.00 emu mol−1 K, respectively (Fig. S4†). These static properties could be attributed to the typical stark sublevel depopulation.11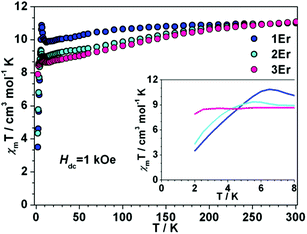 | ||
| Fig. 2 Temperature dependence of the dc magnetic susceptibility time temperature χmT for 1Er–3Er under 1 kOe applied magnetic field. (Inset) Expanded view of χmT vs. T plots below 8 K. | ||
The out-of-phase ac susceptibility of 1Er and 2Er exhibited strong frequency-dependent behaviour between 15 K and 24 K or 16 K and 25 K under zero dc field (Fig. 3(a), (b) and S7, S8†), while below 10 K, no χ′′m peaks could be observed since the magnetic relaxation rate is so slow that it is beyond the lowest limit of our equipment (Fig. S9†). The relaxation time extracted from the temperature-dependent and frequency-dependent out-of-phase susceptibilities gave the same results (Fig. S10(a) and S10(b)†). The effective energy barrier of 1Er is 371 K (259 cm−1) with τ0 of 5.3 × 10−12 s (Fig. 3(d)). The χ′′m peak of the 1 Hz plot for 2Er is 17.4 K, which is higher than that for 1Er (15.8 K) (Fig. 3(a), (b) and S7, S8†). As a consequence, the effective energy barrier and τ0 of 2Er are 421 K (300 cm−1) and 5.5 × 10−12 s, respectively (Fig. 3(e)), whereas the τ vs. T−1 plot for 2Er at low temperature showed an evident curvature, indicating a faster QTM process than that of 1Er. The energy barriers of 1Er and 2Er are higher than those of the previously reported erbium based SIMs (ranging from 15 cm−1 to 225 cm−1),4k,l,5 revealing the advantage of introducing poorer electron donating boratabenzene as the ligand. Utilizing a poorer electron donor decreases the electronic interaction between the 4f electrons and the aromatic electrons of ligands along the uniaxial direction, and enhances the uniaxial magnetic anisotropy. This experimental result is in line with the theoretical study of Rajaraman et al.12 It is also noteworthy that 2Er has the highest effective energy barrier among all reported ErIII SIMs. The out-of-phase ac susceptibility of 3Er also showed strong frequency-dependent magnetic behaviour, which is significantly different from those observed for 1Er and 2Er. When the temperature is below 10 K, the intensity of the out-of-phase component of 3Er is distinctly larger than those of 1Er and 2Er, implying a much stronger and faster QTM process. The peaks of the corresponding frequency plots are nearly unchanged until the temperature rises to 10 K, confirming the existence of a temperature independent QTM process (Fig. 3(c) and S11†). The effective energy barrier of 3Er is 250 K (174 cm−1 under zero dc field) (Fig. 3(f) and S10(c)†). When an optimized field 2 kOe was applied, the Ueff increased slightly (Fig. 3(f) and S12†). The lower energy barrier of 3Er compared to those of 1Er and 2Er can be attributed to two facts: (a) aminoboratabenzene is a better electron donor than the hydrogen (or methyl)-substituted one; (b) the deviation of the boron atom from the boratabenzene plane in 3Er is larger than those in 1Er and 2Er, which may cause more transverse components (see ab initio calculations below). Dynamic studies showed that 4Dy–6Dy only exhibited slow magnetic relaxation under an applied dc field with small effective energy barriers (Fig. S13–S15†). Combined with the previous reports, the sandwich type geometry utilizing cyclomultiene ligands seems not suitable for dysprosium to be a good SIM.
The hysteresis measurements showed that all ErIII complexes exhibited butterfly-type hysteresis loops (Fig. 4). Interestingly, 1Er and 2Er have the hysteresis loops up to 8 and 6 K, respectively, which are higher than that of [(Cp*)Er(COT)] (5 K).5a So far, only two ErIII complexes, [K(18-crown-6)(THF)2][Er(COT)2] (10 K),5b–d and [Li(DME)3][Er(COT′′)2] (8 K),5c have blocking temperatures (TB) up to 8 K, and both of them are ion pairs. For 3Er, hysteresis could not be observed until the temperature was decreased to 2 K. To see whether thermal relaxation or QTM is predominant in TB, we extrapolated the Arrhenius fitting and found that the blocking temperatures of 1Er–3Er (defined as the relaxation time of 100 s) were similar, which were 12.8, 13.7 and 10.3 K, respectively. Therefore, hysteresis is mostly determined by the QTM rate and strength at low temperatures. The differences in their hysteresis we believe are due to the QTM, which could be caused by the following reasons: 1. the differences in their local structures. 2Er has a smaller bending angle than 1Er, which may be responsible for the observed higher Ueff, but the introduction of the electron-donating methyl group in 2Er enhances the electronic interaction between the ErIII ion and the boratabenzene ligand along the uniaxial direction, leading to a more obvious QTM than that of 1Er. For 3Er, aminoboratabenzene is a better electron donor than the hydrogen (or methyl)-substituted one due to the strong π-interaction between boron and nitrogen. The π-interaction between boron and nitrogen also causes a deviation of the boron atom out from the 5 Cs plane of 0.097 Å, which is apparently larger than those in 1Er and 2Er (0.028 and 0.059 Å, respectively). The unchanged maximum of the out-of-phase ac susceptibility below 10 K for 3Er implies a much stronger and faster QTM process compared to QTM of 1Er and 2Er. 2. As the dipole–dipole interaction is anisotropic, the different arrangement of molecules in the lattice may also give different QTM rates for 1Er, 2Er and 3Er. Their different magnetic behaviors at low temperatures may also be caused by the different relaxation processes like the Direct/Raman process. Since QTM is more obvious in 3Er, the dilution experiment was subsequently carried out to study the role of the dipole–dipole interaction. A diluted sample of 3Er was prepared by the co-crystallization of 3Er with the isostructural [(COT)Y(C5H5BNEt2)] in a Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y molar ratio of 1
Y molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19. The co-crystallization method has been used for the magnetic dilution studies of the analogues, such as [(Cp*)Er(COT)]5a and [K(18-crown-6)(THF)2][Er(COT)2],5b by us and others. The ICP analysis indicated that the Er
19. The co-crystallization method has been used for the magnetic dilution studies of the analogues, such as [(Cp*)Er(COT)]5a and [K(18-crown-6)(THF)2][Er(COT)2],5b by us and others. The ICP analysis indicated that the Er![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y molar ratio in the diluted sample is 4.2
Y molar ratio in the diluted sample is 4.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95.8. The ac measurement indicated that the χ′′m peaks occur in the range of 18 to 26 K, with a Ueff of 239 cm−1, which is higher than that of the pure 3Er (174 cm−1) under zero dc field (Fig. S16 and S17†). The variable-field magnetization plots displayed a hysteresis loop up to 3 K (Fig. 4(c)), which is still lower than those observed for 1Er and 2Er. The sudden magnetization loss near zero field still occurred and the coercive field was not observed. The above results indicated that the differences in the QTM of 1Er–3Er are mainly due to their local structures.
95.8. The ac measurement indicated that the χ′′m peaks occur in the range of 18 to 26 K, with a Ueff of 239 cm−1, which is higher than that of the pure 3Er (174 cm−1) under zero dc field (Fig. S16 and S17†). The variable-field magnetization plots displayed a hysteresis loop up to 3 K (Fig. 4(c)), which is still lower than those observed for 1Er and 2Er. The sudden magnetization loss near zero field still occurred and the coercive field was not observed. The above results indicated that the differences in the QTM of 1Er–3Er are mainly due to their local structures.
Ab initio calculations
To further elucidate the differences in their dynamic relaxations, ab initio CASSCF/RASSI/SINGLE_ANISO calculations with the MOLCAS 7.8 package were performed to determine the low-lying energy levels and magnetic properties of molecules.13The calculated results showed that the ground Kramer's doublets of ErIII complexes are well separated from the excited states (Table S3†). The effective gz values of 1Er–3Er are 17.87, 17.89 and 17.81, respectively, indicating their magnetically uniaxial anisotropic ground states. Correspondingly, the gx,y value is almost negligible (gx,y ≈ 1 × 10−4), except for 3Er (gx = 0.0025, gy = 0.0028). Even for the first excited Kramer's doublets, the transversal components still show small values for 1Er and 2Er (gx,y ≈ 2 × 10−2). A relatively opposite case happens for 3Er, the gx,y value of the higher excited states increases obviously. These relatively large transverse components may promote a more pronounced QTM process, which is consistent with the hysteresis measurements. The calculations also revealed that all DyIII complexes have small magnetic anisotropic ground Kramer's doublets and low energy first excited states (Table S4†). The gx,y values are not negligible, giving a significantly large transversal magnetic moment to DyIII complexes. The energy gap between the ground state and the first excited state is also small. Fig. 5 indicates that the transversal diagonal magnetic moments (ca. 10−1μB) in the ground state arising from internal magnetic fields of 4Dy–6Dy are much larger than those (ca. 10−3–10−4μB) of 1Er–3Er, therefore allowing a fast QTM. According to a recent proposal by Ungur and co-workers,14 the relaxation path can be related to the tunneling gaps. Thus, according to the relaxation path indicated in Fig. 5, the blocking barriers of 1Er–6Dy were deduced, which are 201.0 cm−1 (15/2− → 13/2− → 5/2+), 223.5 cm−1 (15/2− → 13/2− → 9/2− → 9/2+), 158.8 cm−1 (15/2− → 13/2− → 13/2+), 56.2 cm−1 (15/2− → 13/2− → 13/2+), 33.6 cm−1 (15/2− → 13/2+) and 39.7 cm−1 (15/2− → 11/2+), respectively. These calculated blocking barriers are in the same sequence of the experimental ones, although deviations in particular values are observed, due to the exclusion of electron dynamic correlation in the calculations. The tunneling gaps of the diagonal and off-diagonal in the ground and the first excited states of 3Er are much larger than those of 1Er and 2Er, therefore 3Er has the fastest QTM among the three ErIII complexes. This is also consistent with the ac susceptibility and hysteresis measurements. Moreover, only the magnetic relaxation in the complexes 1Er and 2Er can occur by the second excited state.5d,15 The calculated magnetic easy axis of ErIII complexes further confirmed that the sandwich type geometry is preferable for the prolate type ErIII ion possessing SIM properties (Fig. S18†). On the contrary, the easy axis of DyIII complexes is not perpendicular to the COT ring as in the case of the ErIII complexes (Fig. S18†), as the equatorial ligand field is not suitable to stabilize the Ising type oblate ground state of the DyIII ion.
Unprecedented frozen magnetization
The χmT rising observed for 1Er and 2Er at 12 or 6 K has no precedent. As the rising occurs around their TB, the magnetization may be “frozen” below a certain temperature. Two independent measurements were carried out: (a) the magnetization of 1Er was measured upon cooling; (b) the sample was firstly cooled to 2 K under 1 kOe dc field, and then the magnetization was measured upon warming. At each data point, the measurement was delayed for a certain time before the data were recorded. During the cooling down experiment, the χmT value decreases smoothly and no peak was observed (Fig. S19†), while in the warming up experiment, the χmT rising was observed (Fig. 6). When the delay time is 2 s, a distinct peak was observed at about 6.3 K. The χmT rising becomes less pronounced when increasing the delay time. When the delay time is up to 7200 s, the χmT rising can be ignored (Fig. 6). These results indicate that a long delay time is needed to let the system relax to equilibrium. Indeed, the magnetization equilibrium at 2 K can only be reached by delaying as long as 10 hours (Fig. S20†). This is probably due to the poor coupling of the spin system and the phonon bath.16 These results indicate that the observed χmT rising is not due to the long range ordering, but the non-equilibrium of magnetization.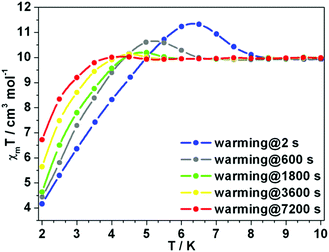 | ||
| Fig. 6 Variable-temperature dc susceptibility data of 1Er. Changing the interval time can make the unexpected rising disappear. | ||
Conclusions
In summary, sandwich type lanthanide organometallic complexes [(C5H5BR)Ln(COT)] were successfully synthesized, the erbium complexes are SIMs while the dysprosium ones are not, and the magnetic properties of the erbium complexes are strongly influenced by the substituent on the boron atom. Using poorer electron donating boratabenzene [C5H5BR]− (R = H or Me) instead of carbon aromatic anions, such as Cp* and COT, results in erbium SIMs with a higher effective energy barrier. It is also noteworthy that the blocking temperature of [(C5H5BH)Er(COT)] is higher than that of [(Cp*)Er(COT)]. This study experimentally demonstrated that utilizing poorer electron donors—boratabenzenes—decreases the electronic interaction between the 4f electrons and aromatic electrons of ligands along the uniaxial direction, and enhances the uniaxial magnetic anisotropy. Therefore, this study not only disclosed a new application of the boratabenzene metal complexes but also provided a practical guideline for the design and synthesis of erbium SIMs with better performance. Further studies following this guideline are actually ongoing.Experimental
General methods
The synthesis of air and/or moisture sensitive compounds was carried out under an atmosphere of argon using Schlenk techniques or in a nitrogen filled glovebox. Toluene, hexane, and THF were dried over a Na/K alloy, transferred under vacuum, and stored in the glovebox. [(COT)LnCl(THF)](Ln = Er, Dy, Y),17 Li(C5H5BH),10e and Li(C5H5BNEt2)10d were prepared according to literature procedures. 1H NMR and 13C NMR spectra were recorded on a VARIAN Mercury 400 MHz spectrometer at 400 MHz and 100 MHz, respectively. 11B NMR spectra were recorded on an Agilent 600 MHz spectrometer at 193 MHz. All chemical shifts were reported in δ units with reference to the residual solvent resonance of the deuterated solvents for proton and carbon chemical shifts, and to external BF3·OEt2 for boron chemical shifts. Elemental analysis was performed by the Analytical Laboratory of Shanghai Institute of Organic Chemistry. ICP analysis was performed by the Analytical Instrumentation Center of Peking University.X-ray crystallography
Suitable single crystals of 1Er–7Y (CCDC 1416019–1416025) were mounted under a nitrogen atmosphere on a glass fiber at low temperature, and data collection was performed on a Bruker APEX2 diffractometer with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). The SMART program package was used to determine the unit cell parameters. The absorption correction was applied using SADABS. The structures were solved by direct methods and refined on F2 by full-matrix least-squares techniques with anisotropic thermal parameters for nonhydrogen atoms. The hydrogen atoms were placed at calculated positions and were included in the structure calculation. All calculations were carried out using the SHELXL-97 program. The software used is listed in ref. 20. Crystallographic data and refinement for 1Er–7Y are listed in Table S1.†Magnetic measurements
Samples were fixed with eicosane to avoid moving during the measurement and sealed in the glass tube to avoid reaction with moisture and oxygen. Direct current susceptibility and alternative current susceptibility with frequencies ranging from 1 to 997 Hz were performed on a Quantum Design MPMS XL-5 SQUID magnetometer on polycrystalline samples. The alternative current susceptibility measurement with frequencies ranging from 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz was performed on Quantum Design PPMS on polycrystalline samples. All dc susceptibilities were corrected for diamagnetic contribution from the sample holder, and eicosane and diamagnetic contributions from the molecule using Pascal's constants.
000 Hz was performed on Quantum Design PPMS on polycrystalline samples. All dc susceptibilities were corrected for diamagnetic contribution from the sample holder, and eicosane and diamagnetic contributions from the molecule using Pascal's constants.
Ab initio calculations
All calculations were done with CASSCF/RASSI/SINGLE_ANISO implanted in the MOLCAS 7.8 package. All calculations used the complete structures of 1Er–6Dy. Using the SINGLE_ANISO program we obtained their magnetic properties. Complete-active-space self-consistent field (CASSCF) calculations on the complete structures of complexes 1Er–6Dy on the basis of X-ray determined geometry have been carried out with the MOLCAS 7.8 program package. For CASSCF calculations, the basis sets for all atoms are atomic natural orbitals from the MOLCAS ANO-RCC library: ANO-RCC-VTZP for the ErIII or DyIII ion, VTZ for close C and B, VDZ for the distant atoms. The calculations employed the second order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set and the spin–orbit coupling was handled separately in the restricted active space state interaction (RASSI-SO) procedure. The active electrons in 7 active spaces include all the f electrons (CAS(11 in 7) for complexes 1Er–3Er and CAS(9 in 7) for complexes 4Dy–6Dy) in the CASSCF calculation. To exclude all the doubts we calculated all the roots in the active space. We have mixed the maximum number of spin-free states which was possible with our hardware (all from 35 quadruplets and all from 112 doublets for three ErIII fragments, all from 21 sextets, 128 from 224 quadruplets and 130 from 490 doublets for three DyIII fragments).Acknowledgements
We thank the National Basic Research Program of China (2013CB933401, 2011CB808705), the National Science Foundation of China (21321001, 91422302, 21272256, 21325210) and the Chinese Academy of Sciences for support.Notes and references
- (a) A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873 CrossRef CAS; (b) R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804 CrossRef CAS; (c) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (d) D. Gatteschi, A. Caneschi, L. Pardi and R. Sessoli, Science, 1994, 265, 1054 CAS.
- (a) A. J. Tasiopoulos, A. Vinslava, W. Wernsdorfer, K. A. Abboud and G. Christou, Angew. Chem., Int. Ed., 2004, 43, 2117 CrossRef CAS PubMed; (b) A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926 CrossRef CAS PubMed; (c) C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754 CrossRef CAS PubMed.
- (a) J. A. Jones, Science, 1998, 280, 229 CrossRef CAS; (b) W. Wernsdorfer, C. R. Chim., 2008, 11, 1086 CrossRef CAS; (c) W. Wernsdorfer and R. Sessoli, Science, 1999, 284, 133 CrossRef CAS PubMed; (d) Y. F. Zhang, N. Lorente, K. Katoh, Y. Yoshida, M. Yamashita and B. K. Breedlove, Nat. Commun., 2011, 2, 217 CrossRef CAS PubMed; (e) L. E. Rosaleny and A. Gaita-Arino, Inorg. Chem. Front., 2016, 3, 61 RSC.
- (a) N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed; (b) N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Phys. Chem. B, 2004, 108, 11265 CrossRef CAS; (c) N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931 CrossRef CAS PubMed; (d) S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448 CrossRef CAS PubMed; (e) M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874 CrossRef CAS PubMed; (f) J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310 RSC; (g) Y. Bi, Y.-N. Guo, L. Zhao, Y. Guo, S.-Y. Lin, S.-D. Jiang, J. Tang, B.-W. Wang and S. Gao, Chem. – Eur. J., 2011, 17, 12476 CrossRef CAS PubMed; (h) M. Jeletic, P.-H. Lin, J. J. Le Roy, I. Korobkov, S. I. Gorelsky and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 19286 CrossRef CAS PubMed; (i) S. Demir, J. M. Zadrozny and J. R. Long, Chem. – Eur. J., 2014, 20, 9524 CrossRef CAS PubMed; (j) W.-B. Sun, B. Yan, Y.-Q. Zhang, B.-W. Wang, Z.-M. Wang, J.-H. Jia and S. Gao, Inorg. Chem. Front., 2014, 1, 503 RSC; (k) P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484 CrossRef CAS PubMed; (l) P. Martín-Ramos, M. Ramos Silva, J. T. Coutinho, L. C. J. Pereira, P. Chamorro-Posada and J. Martín-Gil, Eur. J. Inorg. Chem., 2014, 2014, 511 CrossRef; (m) W.-B. Sun, B. Yan, Y.-Q. Zhang, B.-W. Wang, Z.-M. Wang, J.-H. Jia and S. Gao, Inorg. Chem. Front., 2014, 1, 503 RSC; (n) K. Soussi, J. Jung, F. Pointillart, B. Le Guennic, B. Lefeuvre, S. Golhen, O. Cador, Y. Guyot, O. Maury and L. Ouahab, Inorg. Chem. Front, 2015, 2, 1105 RSC.
- (a) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef CAS PubMed; (b) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952 CrossRef CAS PubMed; (c) J. J. Le Roy, I. Korobkov and M. Murugesu, Chem. Commun., 2014, 50, 1602 RSC; (d) L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413 CrossRef CAS PubMed.
- G. E. Herberich, G. Greiss and H. F. Heil, Angew. Chem., Int. Ed. Engl., 1970, 9, 805 CrossRef CAS.
- A. J. Ashe III and P. Shu, J. Am. Chem. Soc., 1971, 93, 1804 CrossRef.
- For reviews, see: (a) G. E. Herberich and H. Ohst, Adv. Organomet. Chem., 1986, 25, 199 CrossRef CAS; (b) A. J. Ashe III, S. Al-Ahmad and X. G. Fang, J. Organomet. Chem., 1999, 581, 92 CrossRef; (c) G. C. Fu, Adv. Organomet. Chem., 2001, 47, 101 CrossRef CAS; (d) P. Cui and Y. F. Chen, Coord. Chem. Rev. DOI:10.1016/j.ccr.2015.07.014.
- (a) G. E. Herberich, U. Englert, A. Fischer, J. H. Ni and A. Schmitz, Organometallics, 1999, 18, 5496 CrossRef CAS; (b) M. A. Putzer, J. S. Rogers and G. C. Bazan, J. Am. Chem. Soc., 1999, 121, 8112 CrossRef CAS; (c) A. J. Ashe III, S. Al-Ahmad, X. D. Fang and J. W. Kampf, Organometallics, 2001, 20, 468 CrossRef; (d) N. Auvray, T. S. Basu Baul, P. Braunstein, P. Croizat, U. Englert, G. E. Herberich and R. Welter, Dalton Trans., 2006, 2950 RSC; (e) A. Languérand, S. S. Barnes, G. Bélanger-Chabot, L. Maron, P. Berrouard, P. Audet and F. G. Fontaine, Angew. Chem., Int. Ed., 2009, 48, 6695 CrossRef PubMed; (f) G. Bélanger-Chabot, P. Rioux, L. Maron and F. G. Fontaine, Chem. Commun., 2010, 46, 6816 RSC; (g) P. Frank, R. A. Lalancette and F. Jäkle, Chem. – Eur. J., 2011, 17, 11280 CrossRef PubMed; (h) A. Glöckner, P. Cui, Y. F. Chen, C. G. Daniliuc, P. G. Jones and M. Tamm, New J. Chem., 2012, 36, 1392 RSC; (i) B. B. Macha, J. Boudreau, L. Maron, T. Maris and F. Fontaine, Organometallics, 2012, 31, 6428 CrossRef CAS; (j) A. Mushtaq, W. Bi, M.-A. Légaré and F.-G. Fontaine, Organometallics, 2014, 33, 3173 CrossRef CAS.
- (a) G. C. Bazan, G. Rodriguez, A. J. Ashe III, S. Al-Ahmad and C. Müller, J. Am. Chem. Soc., 1996, 118, 2291 CrossRef CAS; (b) G. C. Bazan, G. Rodriguez, A. J. Ashe III, S. Al-Ahmad and J. W. Kampf, Organometallics, 1997, 16, 2492 CrossRef CAS; (c) J. S. Rogers, X. H. Bu and G. C. Bazan, J. Am. Chem. Soc., 2000, 122, 730 CrossRef CAS; (d) Y. Y. Yuan, Y. F. Chen, G. Y. Li and W. Xia, Organometallics, 2008, 27, 6307 CrossRef CAS; (e) Y. Y. Yuan, X. F. Wang, Y. X. Li, L. Y. Fan, X. Xu, Y. F. Chen, G. Y. Li and W. Xia, Organometallics, 2011, 30, 4330 CrossRef CAS; (f) X. F. Wang, W. J. Peng, P. Cui, X. B. Leng, W. Xia and Y. F. Chen, Organometallics, 2013, 32, 6166 CrossRef CAS; (g) E. L. Lu, Y. Y. Yuan, Y. F. Chen and W. Xia, ACS Catal., 2013, 3, 521 CrossRef CAS.
- O. Kahn, Molecular Magnetism, VCH Publishers, New York, Weinheim, 1993 Search PubMed.
- S. K. Singh, T. Gupta and G. Rajaraman, Inorg. Chem., 2014, 53, 10835 CrossRef CAS PubMed.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P.-å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673 CrossRef CAS PubMed.
- (a) R. Orbach, Spin-Lattice Relaxation in Rare-Earth Salts, 1961, vol. 264 Search PubMed; (b) P. L. Scott and C. D. Jeffries, Phys. Rev., 1962, 127, 32 CrossRef CAS; (c) M.-E. Boulon, G. Cucinotta, S.-S. Liu, S.-D. Jiang, L. Ungur, L. F. Chibotaru, S. Gao and R. Sessoli, Chem. – Eur. J., 2013, 19, 13726 CrossRef CAS PubMed.
- (a) K. O. Hodgson, F. Mares, D. F. Starks and A. Streitwieser, J. Am. Chem. Soc., 1973, 95, 8650 CrossRef CAS; (b) A. L. Wayda, Organometallics, 1983, 2, 565 CrossRef CAS.
- G. E. Herberich, B. Schmidt and U. Englert, Organometallics, 1995, 14, 471 CrossRef CAS.
- S. Qiao, D. A. Hoic and G. C. Fu, J. Am. Chem. Soc., 1996, 118, 6329 CrossRef CAS.
- (a) G. M. Sheldrick, SADABS, An Empirical Absorption Correction Program for Area Detector Data, University of Göttingen, Göttingen, Germany, 1996 Search PubMed; (b) G. M. Sheldrick, SHELXS-97 and SHELXL-97, University of Göttingen, Göttingen, Germany, 1997 Search PubMed; (c) SMART Version 5.628, Bruker AXS Inc., Madison, WI, 2002 Search PubMed; (d) SAINT+ Version 6.22a, Bruker AXS Inc., Madison, WI, 2002 Search PubMed; (e) SHELXTL NT/2000, Version 6.1, Bruker AXS Inc., Madison, WI, 2002 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1416019–1416025. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6qi00028b |
| ‡ These authors contributed equally to this work. |
| This journal is © the Partner Organisations 2016 |