Open Access Article
Open Access ArticleImportance of the curvature in electronic, structural and charge transport properties: oligomers of N-pyridine carbazole†
Clément
Brouillac
 a,
Ari
Serez
b,
Nemo
McIntosh
b,
Joëlle
Rault-Berthelot
a,
Olivier
Jeannin
a,
Benoît
Heinrich
a,
Ari
Serez
b,
Nemo
McIntosh
b,
Joëlle
Rault-Berthelot
a,
Olivier
Jeannin
a,
Benoît
Heinrich
 c,
Cassandre
Quinton
c,
Cassandre
Quinton
 a,
Olivier
De Sagazan
d,
Emmanuel
Jacques
d,
Jérôme
Cornil
a,
Olivier
De Sagazan
d,
Emmanuel
Jacques
d,
Jérôme
Cornil
 b and
Cyril
Poriel
b and
Cyril
Poriel
 *a
*a
aUniv Rennes, CNRS, ISCR-UMR 6226, F-35000 Rennes, France. E-mail: cyril.poriel@univ-rennes.fr
bLaboratory for Chemistry of Novel Materials, University of Mons, Mons, Belgium
cInstitut de Physique et Chimie des Matériaux de Strasbourg, UMR 7504, CNRS-Université de Strasbourg, 67034 Strasbourg Cedex 2, France
dUniv Rennes, CNRS, IETR-UMR 6164, F-35000 Rennes, France
First published on 8th July 2024
Abstract
The recent development of π-conjugated nanohoops in organic electronics has opened new perspectives for this family of curved materials. Addressing the difference arising from curved vs. non-curved materials is an important concern in order to highlight the specific properties of curved materials. Herein, we discuss the significant differences arising between [4]-cyclo-N-pyridine-2,7-carbazole [4]C-Py-Cbz and its linear counterpart, N-pyridine-2,7-tetracarbazole [4]L-Py-Cbz. This study gathers optical, electrochemical, structural, morphological and charge transport properties and highlights the key role played by the curvature. We notably show how the electronic effects of the pending pyridines differently affect the molecular orbitals energies. We have also shown how structural rearrangements between ground and first excited states can be at the origin of the peculiar emission of nanohoops. Finally, the huge difference in terms of charge transport properties was discussed. Nanohoop [4]C-Py-Cbz displays a field-effect mobility in the saturated regime μFEsat of 3.4 × 10−6 cm2 V−1 s−1, six times higher than that of its linear analogue [4]L-Py-Cbz (5.7 × 10−7 cm2 V−1 s−1). However, the detailed study of the charge transport properties shows that the linear analogue forms a semi-conducting layer with a lower trap density, more favourable to the charge hopping processes. Theoretical calculations have provided clues on the origin of these differences, revealing that despite the intensity of electronic couplings is significantly in favor of [4]L-Py-Cbz, their highly anisotropic character renders them more sensitive to defects and disorder. This is consistent with the fact that [4]C-Py-Cbz displays experimentally better charge transport properties than [4]L-Py-Cbz. Such a type of structure–property relationship study provides fundamental findings of interest for the future design of high-performance nanohoops.
Nanohoops represent nowadays an important research field worldwide.1,2 Constituted by the assembly of π-conjugated fragments forming a macrocycle with a cylindrical shape, nanohoops have fascinated chemists since the first example reported in 2008.3 Their curved and radially oriented π-system induce uncommon electronic properties4–12 and starts now to interest researchers involved in organic semiconductors for electronics. Indeed, curved materials represent a new generation of π-systems, which possess very specific properties and can be advantageously used in electronic devices. The first examples of incorporation in organic electronic devices,13 either organic light-emitting diodes (OLED),14–16 organic field-effect transistors (OFET),17–19 solar cells20,21 or photodetectors21,22 have been reported in recent years and some finding have appeared highly promising. For example, a high performance red emitting phosphorescent OLED using a nanohoop as host material has been reported very recently (external quantum efficiency EQE of 17%),15 revealing the potential of nanohoops in organic electronics. These performances are particularly promising as they are significantly higher than those obtained with its acyclic analogue (EQE = 11%). However, there is still plenty of room for improvement in terms of fundamental knowledge and practical electronic applications of nanohoops. In 2022, Stępień has discussed, through different examples, the properties arising from molecular curvature and how they can be specifically used in applications.23 In other words, what can do a curved material that a linear material could not? Thus, one of the most important targets in the field of nanohoops consists to well understand the difference between nanohoops and their linear counterparts in order to highlight the impact of the shape on the electronic and physical properties (HOMO/LUMO energy levels, absorption/emission spectra, decomposition and glass transition temperatures, etc). Such a type of study has been developed in nanohoop literature with different π-systems5,14,24–28 but very rarely includes device incorporation and materials properties. Thus, only a few data on the charge transport of nanohoops have been reported to date.17–19,29–32 However, as nanohoops have recently shown their potential in electronic devices,15,19,22 studying the experimental behaviour of such unusual structures in devices appears as a relevant direction of research. Doing so, contorting aromatic motifs could lead to high organic electronic performance, as recently shown by Nuckolls and coworkers.33 In the present work, through a combination of experiments and theoretical calculations, we discuss the difference arising between the nanohoop [4]-cyclo-N-pyridine-2,7-carbazole ([4]C-Py-Cbz) and its linear counterpart, N-pyridine-2,7-tetracarbazole [4]L-Py-Cbz. The [4]cyclo-2,7-carbazole backbone has been investigated due to the recent advances showing the high efficiency of cyclocarbazoles in organic electronics.15,18 We particularly discuss the significant difference observed in structural (supramolecular arrangement), electrochemical (HOMO/LUMO levels) and photophysical properties. The study of the charge transport properties has revealed that nanohoop [4]C-Py-Cbz displays a p-type field-effect mobility in the saturated regime μFEsat of 3.4 × 10−6 cm2 V−1 s−1, six times higher than that of its linear analogue [4]L-Py-Cbz (5.7 × 10−7 cm2 V−1 s−1) demonstrating the strength of the hoop shape in term of charge transport. However, the detailed studies of these charge transport and surface properties have highlighted that the linear analogue forms a semi-conducting layer with a lower density of traps, more favourable to the charge hopping processes. To shed light on these significant differences between the linear and hoop shapes, we have computed, for both molecules, the electronic couplings and the reorganization energies at the DFT level in the single crystal structures. Despite significantly higher electronic couplings are obtained for [4]L-Py-Cbz (vs.[4]C-Py-Cbz), their anisotropic character renders them more sensitive to defects and disorder. Thus, the homogeneity of the transfer integrals, which appears as an advantage of the hoop shape vs. classical linear structures has been proposed as a credible origin of the different performance.
The synthesis of [4]C-Py-Cbz is previously described in literature,32 and the one of [4]L-Py-Cbz is presented in ESI† (Scheme S1). Both cyclic [4]C-Py-Cbz and acyclic [4]L-Py-Cbz are built on four carbazole units attached by their C2 and C7 positions (Fig. 1). These linkages are in para position of the biphenyl linkage and in meta position of the nitrogen atom.
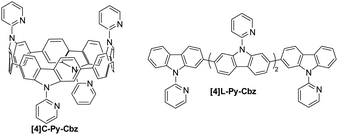 | ||
| Fig. 1 Molecular structures of tetracarbazole oligomers: cyclic [4]C-Py-Cbz (left) and acyclic [4]L-Py-Cbz (right). | ||
The structural analysis is particularly important in the understanding of the electronic properties. Single crystals of [4]C-Py-Cbz (CCDC no. 2265379) and [4]L-Py-Cbz (CCDC no. 2325120) were obtained by vapor diffusion of methanol in concentrated solutions of dichloromethane with several drops of THF (Fig. 2). [4]C-Py-Cbz and [4]L-Py-Cbz crystallize in the Cc and P212121 space groups, respectively (see X-ray diffraction Tables in the ESI†). The first difference in term of structural arrangement is related to the relative orientation of the pyridine rings (Fig. 2(A)). For [4]L-Py-Cbz, two adjacent pyridines are directed upwards and the two others downwards of the carbazole mean plane. This topology can be called ααββ. [4]C-Py-Cbz displays a different behaviour as an αβαβ topology is obtained. Indeed, this conformer is usually favoured during the synthesis of nanohoops and observed in many other examples.17,18,24,34
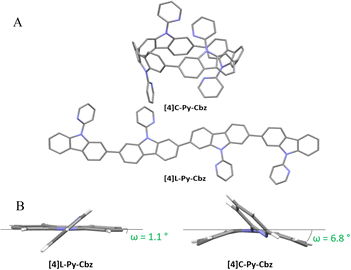 | ||
| Fig. 2 (A) Single-crystal structures of [4]C-Py-Cbz (top, CCDC no. 2265379) and [4]L-Py-Cbz (bottom, CCDC no. 2325120). (B) Representation of the displacement angle ω showing the deformation of the carbazole unit. | ||
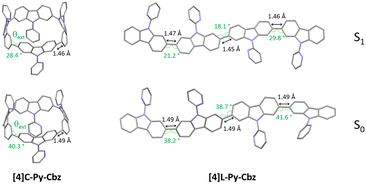
Since the main features governing the specific electronic properties of the nanohoops are the deformation of the constituting units and their relative arrangement, two structural parameters are determined: the mean displacement angle ω, and the mean torsion angle θ (see definitions Fig S13, S14 and values Tables S12, S13, ESI†). In π-conjugated systems, the torsion angle θ is an important parameter, which drives the electronic properties such as the HOMO and LUMO energy levels (see below). In nanohoop chemistry, two torsion angles should be determined, θint, which is the torsion angle between two phenyl rings of a carbazole, and θext, which is the torsion angle between two phenyl rings of two neighbouring carbazoles. Herein, θint is very similar for both molecules, showing that the hoop shape does not induce a higher torsion within the carbazole fragment. The situation is different for θext, which is measured as high as 46.4° for [4]C-Py-Cbz, this value being significantly higher than that measured for [4]L-Py-Cbz, 13.1°. The average torsion angles θ of [4]C-Py-Cbz and [4]L-Py-Cbz are measured at 24.4° and 8.1°, respectively. The torsion is therefore much greater in the nanohoop than in the linear oligomer, which in turn induces a better delocalization of π-electrons in the latter. This is a central notion in understanding electronic properties, see below. The average displacement angle ω corresponds to the curvature of the phenyl units and is also an important parameter in the structural characteristics of nanohoops. Indeed, unlike linear oligocarbazoles, the hoop shape induces a strong constraint, which disturbs the electronic delocalization. Thus, due to the nanohoop curvature, the average displacement angle ω of [4]C-Py-Cbz is measured as high as 6.8° whereas that of [4]L-Py-Cbz is measured at 1.1° (Fig. 2(B)). Finally, it should be mentioned that the angle formed by the pyridine and the carbazole γ (42.3 vs. 36.7°) is similar for both compounds and should not induce a significant difference between them.
The supramolecular self-assembly of the two N-pyridine tetracarbazoles is governed by their different molecular shape (Fig. 3 and Table 2). While the lath-like linear [4]L-Py-Cbz pack side by side into layers superposing in a lamellar structure, the loop-like cyclic analogues of [4]C-Py-Cbz stack on top each other by forming a supramolecular arrangement of hollow columns (Fig. 3). For the linear system [4]L-Py-Cbz, the in-plane structure of the layers is rectangular with two molecules per lattice, based on staggered rows of aligned molecules that are tilted from layer normal. The high tilt angle ϕ close to 54° (Table 2) allows the compact interlocking of the rows, since molecules are in fact not straight but S-shaped with protruding pyridine substituents. Along rows, the molecules stack in a face to face arrangement with a compact π-stacking distance hπ of 3.42 Å and a chevron angle ψ of nearly 50°. The lamellar sequence involves two layers with reversed in-plane orientations, leading to an orthorhombic structure with four molecules per cell. For [4]C-Py-Cbz, the in-plane-arrangement of the hollow columns is rectangular with two columns per lattice, following a staggered row arrangement very close to the hexagonal cylinder packing geometry (the lattice parameter ratio deviates from √3 by only 2%).32 The columns are segmented in carbazole loops and intermingled pyridine substituents; the molecules are tilted by ϕ ≈ 27° out of the lattice plane. This tilting leads to intercalation of the carbazole and pyridine segments of neighboring columns, which compensates their different bulkiness and ultimately optimizes the compacity of the supramolecular organization. Two molecular orientations alternate along columns, resulting in a monoclinic structure with four molecules per cell.
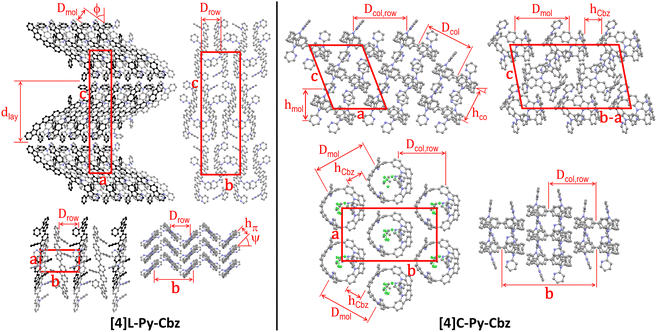 | ||
| Fig. 3 Left part: Views of the single-crystal structure of [4]L-Py-Cbz, from left to right and top to bottom, views along the b-axis (molecular slices in the foreground at y = 0.0, in the background and drawn in black at y = 0.5), the a-axis and the c-axis (molecular slice at z = 0; molecules in the foreground at x = 0.0, in the midground and drawn in dark grey at x = 0.5, in the background and drawn in black at x = 1.0), and view along the molecular axes (molecular slice at z = 0). Right part: Views of the single-crystal structure of [4]C-Py-Cbz, from left to right and top to bottom, views along the b-axis (molecular slices with centroids at y = 0.0 and y = 0.2), along the normal to the (b − a) × c diagonal plane (molecular slice at y = x) and along the normal to a × b plane (molecular slice at z = 0.0), and view in the molecular loop plane (molecular slice at z = 0.0). For sake of clarity, hydrogens are not shown and the solvent molecules co-crystallized with [4]C-Py-Cbz are only displayed for one view. The definition and value of the characteristic distances are given in Table 2. | ||
At the end, although the oligomer organizations are characterized by different self-assemblies and cell geometries, the building principles of the structures are nevertheless analogue, with in particular equal numbers of rows and molecular strata and molecules per cell. Both molecular organizations are compact, but the cell volume is 16% larger for [4]C-Py-Cbz due to the cavity inside the loop. However, co-crystallizing solvent molecules partly fill out the voids of this structure, reducing to 2% the excess of molecular volume of the (dry) cyclic oligomer. Conversely, the fact that voids are left by the self-assembly of [4]C-Py-Cbz but not of [4]L-Py-Cbz is consistent with the growing of lattice solvent-containing crystals for the former and of solvent-free crystals for the latter. Regarding the self-assembly features, there is a major impact of shape on molecular interactions: cohesive π-stacking assemblies with short stacking distance for the linear tetracarbazole vs. reduced contact zones at hoop circumferences for the cyclic analogue. As a matter of fact, the intercalation of carbazole and pyridine segments prevents the carbazole interactions in the direction of hollow column rows. There are carbazole contacts along diagonal rows but the average distance between proximal rings is as high as hCbz ≈ 4.35 Å, which exceeds the π-stacking distance of [4]L-Py-Cbz by 27%. As the supramolecular assembly drives the charge transport, one may expect, at this stage, higher mobilities for [4]L-Py-Cbzvs.[4]C-Py-Cbz. We will show below that it will not be the case.
Thanks to cyclic voltammetries (Fig. S9, ESI†), LUMO of [4]C-Py-Cbz and [4]L-Py-Cbz are evaluated at −2.38 and −2.30 eV, respectively (Table 3). In a nanohoop, the LUMO energy level is usually influenced by geometric parameters induced by the hoop shape. This is one important characteristic of nanohoops, which has been rationalized by Itami and co-workers in 20129 (the evolution of HOMO/LUMO energy levels and resulting gap in nanohoops has been the subject of several studies14,25,26,35). This usually provides a LUMO energy level significantly lowered compared to that of its linear analogue.15,20,36 For example, when the nitrogen atom of a cyclocarbazole is substituted with an electron donating butyl chain as in [4]C-Bu-Cbz, its LUMO energy level is recorded at −2.40 eV and that of its linear analogue [4]L-Bu-Cbz is measured at −2.17 eV (see structures in Fig. S1 and values in Table S1, ESI†).15 Herein, the LUMO of [4]C-Py-Cbz (−2.38 eV) is almost identical to that of its analogue bearing a butyl chain [4]C-Bu-Cbz (−2.40 eV), highlighting that the effect of the electron accepting pyridine does not impact the LUMO, which is mainly driven by geometric parameters and particularly by the torsion angle θ as detailed in Itami's works.9 Since θ of [4]C-Bu-Cbz (19°) is lower than that of [4]C-Py-Cbz (θ = 24.4°, Table 1), the LUMO of [4]C-Bu-Cbz is expected to be lower compared to that of [4]C-Py-Cbz. This is a counterintuitive result as [4]C-Py-Cbz possesses four electron-accepting units, which should decrease the LUMO energy. Herein, the electronic and geometric parameters compensate each others to give similar LUMO energy levels. This is a specificity of nanohoops and shows the importance of geometric parameters vs. electronic parameters in this peculiar family of materials. This result is strengthened by the different trend obtained for linear derivatives. Indeed, in [4]L-Py-Cbz, the electron-withdrawing effect of the pyridine classically decreases the LUMO energy level compared to that of its butyl analogue [4]L-Bu-Cbz (−2.30 vs. −2.17 eV). Thus, the electron-donating/accepting effects of the carbazole substituents differ from linear to hoop structures, providing different rules of molecular design. Similarly, the cyclic voltammetry of [4]C-Py-Cbz provides a HOMO level of −5.38 eV, significantly lower than that of [4]C-Bu-Cbz: −5.18 eV. In this case, both geometrical and electronic parameters induce similar effects on the HOMO energy levels. Indeed, the higher torsional angle θ (24.4 vs. 19.1°) and lower displacement angle ω (6.8 vs. 7.1°) of [4]C-Py-Cbzvs.[4]C-Bu-Cbz (geometric parameters) coupled to the electron-accepting effect of the pyridine (electronic parameter) all induce a decrease of the HOMO level ([4]C-Py-Cbz: −5.38 eV/[4]C-Bu-Cbz: −5.18 eV). Note that quantum chemical calculations show nevertheless that the pyridine is not involved in the HOMO delocalization (Fig. 4).
| [4]L-Py-Cbz | [4]C-Py-Cbz | |
|---|---|---|
| θ int (°) [min–max] | 3.0 [0.5–9.0] | 2.3 [0.0–5.8] |
| θ ext (°) [min–max] | 13.1 [5.6–17.8] | 46.4 [39.1–51.3] |
| θ (°) [min–max] | 8.1 [0.5–17.8] | 24.4 [0.0–51.3] |
| ω int (°) [min–max] | 1.1 [0.3–4.0] | 6.4 [3.0–8.9] |
| ω ext (°) [min–max] | 1.2 [0.7–2.3] | 7.2 [6.3–9.3] |
| ω (°) [min–max] | 1.1 [0.3–4.0] | 6.8 [3.0–9.3] |
| γ (°) [min–max] | 42.3 [33.7–48.1] | 36.7 [30.9–42.0] |
| [4]L-Py-Cbz | a = 7.8187 Å, b = 13.8355 Å, c = 43.716 Å, V = 4728.9 (Z = 4)b | |||||||
|---|---|---|---|---|---|---|---|---|
| a Composition, temperature of measurement and crystal symmetry. b Lattice parameters. c d lay: molecular layer periodicity. d ϕ: tilt angle of molecular rod axis from layer normal. e D row: spacing of the molecular rows. f D mol: molecular spacing along the rows. g h π: π-stacking distance. h ψ: chevron angle of the rows. i h mol: molecular slice height. j ϕ: tilt angle of the molecular loops out of the lattice plane. k h col: stacking distance into hollow columns. l D col: distance between hollow columns. m D col,row: spacing along the rows of hollow columns. n D mol: molecular spacing along the diagonal rows of the lattice. o h Cbz: carbazole nanohoop spacing along the diagonal rows of the lattice. p V/Z: cell volume per molecule. q V mol = V/Z – n·VS: molecular volume after subtraction of the contribution of co-crystallized solvent molecules ([4]C-Py-Cbz: n = 2; VS ≈ 82.06 Å3: volume of CH2Cl2 from crystal structure CSD-DCLMET10).37 | ||||||||
| T = −123 °C | d lay (Å) | ϕ (°) | D row (Å) | D mol (Å) | h π (Å) | ψ (°) | V/Zp (Å3) | V mol (Å3) |
| Orthorhombic P212121 | 21.86 | 53.7 ± 0.2 | 6.918 | 4.63 | 3.42 ± 0.02 | 49.4 ± 0.2 | 1182.2 | 1182.2 |
| [4]C-Py-Cbz | [4]L-Py-Cbz | |
|---|---|---|
| a In CH2Cl2. b In thin solid film prepared from a THF solution (1 mg mL−1). c Measured with quinine sulfate in 1 N H2SO4 as reference. d Measured with an integrated sphere using [4]cyclo-N-butyl-2,7-carbazole [4]C-Bu-Cbz as reference. e In CH2Cl2. f In DMF. g From electrochemical data. h By Ultraviolet photoelectronic spectroscopy in thin solid film prepared from a CHCl3 solution. i From TD-DFT B3LYP/6-311+G(d,p). j |HOMO–LUMO|. | ||
λ
solabs
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [nm]
[nm] |
335, 305, 256 | 361, 301, 258 |
λ
filmabs
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [nm]
[nm] |
339, 264 | 379, 310, 260 |
λ
solem![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fluo fluo
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [nm] (λexc)
[nm] (λexc) |
490 (340) | 403, 425 (310) |
λ
filmem![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fluo fluo
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [nm] (λexc)
[nm] (λexc) |
484 (350) | 445 (350) |
QYsol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
0.18 | 0.57 |
QYfilm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.11 | 0.32 |
| τ s [ns] (λem) | 7.1 (490) | <1 (403) |
| k r (× 108) [s−1] | 0.25 | >5.7 |
| k rnr (× 108) [s−1] | 1.2 | >4.3 |
| E ox (eV) | 1.08, 1.5, 1.7, 2.28 | 0.78, 0.89, 1.22, 1.77 |
| E red (eV) | −2.17, −2.62 | −2.34, −2.60, −2.85 |
| HOMOg (eV) | −5.38 | — |
| LUMOg (eV) | −2.38 | −2.30 |
| HOMOh (eV) | −5.56 | −5.71 |
| HOMOi (eV) | −5.15 | −5.41 |
| LUMOi (eV) | −1.87 | −1.77 |
| ΔEELj (eV) | 3.00 | — |
| ΔEtheoij (eV) | 3.28 | 3.64 |
If the cyclic voltammetry of [4]C-Py-Cbz was in accordance with those of other cyclocarbazoles,18 that of [4]L-Py-Cbz was unusual signing adsorption processes (Fig. S10, ESI†). Ultraviolet photoelectronic spectroscopy (UPS) has then been carried out to measure the HOMO energy levels of both compounds. In the solid state, [4]C-Py-Cbz and [4]L-Py-Cbz respectively present a HOMO level of −5.56 eV and −5.71 eV (see Fig. S12, ESI†). The HOMO of [4]L-Py-Cbz is therefore lower than that of [4]C-Py-Cbz in accordance with the theoretical study of Itami on CPPs9 and other previous works.18 This is also in accordance with the results obtained by theoretical calculations (−5.15 and −5.41 eV for [4]C-Py-Cbz and [4]L-Py-Cbz).
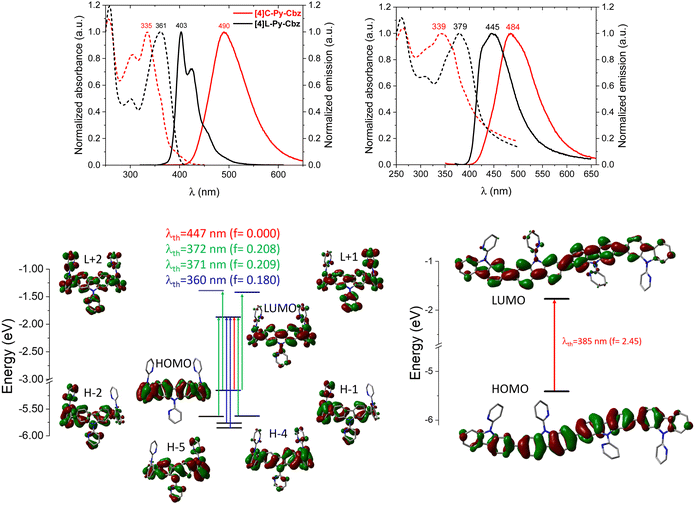
The optical characteristics of [4]C-Py-Cbz and [4]L-Py-Cbz are detailed in Fig. 4. In solution, [4]C-Py-Cbz displays a classical UV-vis absorption profile with three maxima at 256, 305 and 335 nm. The theoretically forbidden HOMO → LUMO transition, signature of nanohoops, is also observed between 375 and 425 nm (Fig. 4, top) and theoretically estimated at 447 nm. The main band is predicted at 360 nm (H−4→LUMO and H−5 → LUMO, see time-dependent density-functional theory, TD-DFT, analysis in Fig. 4, bottom). The shoulder experimentally detected at 361 and simulated at 371–372 nm is assigned to two transitions each involving two main contributions: H−1 → LUMO, HOMO → L+1, H−2 → LUMO, and HOMO → L+2. The linear counterpart [4]L-Py-Cbz displays a very different profile with a red shifted spectrum displaying three main bands at 258, 301 and 361 nm. The principal difference with the nanohoop arises from the main band, which is assigned to a HOMO → LUMO transition with a very high oscillator strength of 2.45, as classically observed in linear π-conjugated systems. Thus, the HOMO → LUMO transition of [4]L-Py-Cbz is detected at a lower wavelength than that of [4]C-Py-Cbz, implying a shorter HOMO/LUMO gap for the later, in accordance with electrochemical measurements.
In emission spectroscopy, the curvature effect leads to an impressive red shift of 87 nm, [4]L-Py-Cbz being a blue emitter (λ = 403 nm) whereas [4]C-Py-Cbz is a green emitter (λ = 490 nm). The different shape of the two spectra, structured for [4]L-Py-Cbz as classically observed for bridged oligophenyls,38 and unresolved for [4]C-Py-Cbz, as classically observed for nanohoops, can be tentatively related to structural features. Indeed, in the case of [4]L-Py-Cbz, in the first excited state S1, the bonds linking the carbazoles are shortened compared to ground state S0 and the torsion angles between them are reduced as well (Fig. 5, right) according to theoretical calculations, leading hence to a more planar conformation and a structured spectrum.39,40 However, the reduction of the dihedral angles is less pronounced in the case of [4]C-Py-Cbz potentially due to the hoop strain (Fig. 5, left). This is an interesting characteristic, which can be at the origin of the peculiar emission of nanohoops. The fluorescence decay curve provides a single lifetime of 7.1 ns for [4]C-Py-Cbz (Fig. S1, ESI†), which is noticeably longer than the corresponding lifetime, below 1 ns, estimated for [4]L-Py-Cbz (Fig. S2, ESI†). Thus, the radiative rate constant (kr) of [4]C-Py-Cbz was calculated to be 0.25 × 10−8 s−1, which is significantly lower than that evaluated for [4]L-Py-Cbz (>5.7 × 10−8 s−1). As kr is related to the oscillator strength and the energy of the transition,41 this difference can be correlated to these two parameters. The strong difference observed in term of oscillator strength appears particularly significant and also explain the different quantum yield values, around 3 times higher for [4]L-Py-Cbz (0.57 vs. 0.18).
Thin films have been prepared from a THF solution (1 mg mL−1) and spin-coated on quartz. [4]C-Py-Cbz presents a similar absorption spectrum as that recorded in solution with only a very short bathochromic shift of 4 nm. In emission, the difference between solution and film is also small (6 nm). This is the consequence of isolated chromophores displaying weak intermolecular interactions in the solid state as revealed in the structural analysis presented above. For linear derivative [4]L-Py-Cbz, in which stronger intermolecular interactions were detected, both absorption and emission spectra were broader and red shifted (ca. 20 nm in absorption and 40 in emission) compared to their solution spectra. For both molecules, the absolute quantum yield is divided by ca. 1.7 (0.32 for [4]L-Py-Cbz and 0.11 for [4]C-Py-Cbz). Thus, the different supramolecular arrangements have strong implications for the thin film optical properties.
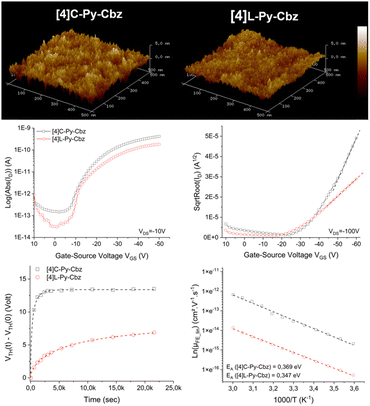
Finally, the charge transport properties were studied thanks to the electrical characterization of OFET devices fabricated with [4]L-Py-Cbz and [4]C-Py-Cbz as semi-conducting layer. Despite some theoretical works have predicted high mobilities for nanohoops, showing the importance, for example, of reorganization energies42–44 the number of experimental works remain very scarce in the field.17–19,29–32
The architecture of the OFET is provided in Fig. S14 (ESI†) and has been previously reported.45 Tetracarbazoles [4]C-Py-Cbz and [4]L-Py-Cbz present field effect (FE) mobilities in the saturated regime μFEsat (VDS = −100 V) of 3.4 × 10−6 cm2 V−1 s−1 and 5.7 × 10−7 cm2 V−1 s−1 respectively (Fig. 6, middle-right). Thus, the hoop shape found in [4]C-Py-Cbz appears to favor the charge transport and leads to a μFEsat 6 times higher than that of its linear analogue. As far as we know, such difference between a nanohoop and its linear analogue has never been discussed. This concept of ‘cyclic vs. acyclic’ molecular structures in organic electronics has been the subject of several studies in recent years as it can be an important feature in the development of curved molecules.15 Nuckolls and coworkers have shown, for example, that macrocycles based on perylenediimide fragment can be more efficient than their corresponding linear structures in organic solar cells.20,21
In the light of these promising results, other characteristics of the OFET were investigated. FE mobilities in the linear regime, μFElin, is an important data, which oppositely to μFESat, provides information on the trap density in the semi-conducting layer. μFELin was measured at 7 × 10−7 cm2 V−1 s−1 for [4]C-Py-Cbz and at 2.8 × 10−7 cm2 V−1 s−1 for [4]L-Py-Cbz (Fig. 6, middle-left). Thus, even in the linear regime, the mobility of [4]C-Py-Cbz remains higher than that of [4]L-Py-Cbz. However, μFElin appears to be less affected by the traps in the case of [4]L-Py-Cbz, highlighting a higher trap density for [4]C-Py-Cbz. To evaluate the capability of the materials to accumulate charges at the semi-conducting/insulator interface, subthreshold slope (SS) is an interesting data as it reflects notably the organization of the layer. The SS obtained confirm the values of μFElin discussed above as [4]C-Py-Cbz possesses a SS of 3.4 V dec−1, twice that measured for [4]L-Py-Cbz 1.7 V dec−1.
AFM studies have also been performed directly on the OFET device (Fig. 6, top). The root mean square roughness Rq of the surface is respectively measured at 0.65 and 0.98 nm for [4]L-Py-Cbz and [4]C-Py-Cbz, thus translating a smooth morphology (Table S17, ESI†). The difference observed is in accordance with the SS presented above and also with the smaller difference measured between μFElin and μFEsat in the case of [4]L-Py-Cbz. All these differences are the consequences of the different molecular arrangements of the two tetracarbazoles.
Electrical stress, using the gate bias stress protocol, has been finally carried out. A stretched exponential model has been applied to evaluate the structural trap effect on the electrical stability of OFETs (Fig. 6, bottom-left). ΔVTHmax, maximum threshold voltage shift under unlimited stress, β, average deepness of level energy of traps and t0, time for a carrier to be trapped, have been measured. These three parameters are in favor of a better layer organization for [4]L-Py-Cbz than for [4]C-Py-Cbz. For [4]C-Py-Cbz (t0 = 0.32 × 103 s), the carriers are significantly more quickly trapped than for [4]L-Py-Cbz (t0 = 7.9 × 103 s). The maximum threshold voltage shift is also higher for [4]C-Py-Cbz (ΔVTHmax = 13.4 V) than for [4]L-Py-Cbz (ΔVTHmax = 8.2 V). The energy level of traps into the [4]C-Py-Cbz layer (β = 0.63) is also deeper than for [4]L-Py-Cbz (β = 0.58). It has been proposed, since the development of nanohoops, that the lack of ends in such cyclic molecules, as opposed to the linear materials, may be beneficial for charge carrier as it may eliminate structural defects that can cause charge traps.20,22,43 We show herein that this statement should be tempered. If [4]C-Py-Cbz displays indeed a higher saturated mobility than its linear analogue [4]L-Py-Cbz, it also possesses more traps. The origin of the higher mobility should then be unraveled.
Measurements of μFElin as a function of temperature lead to an evaluation of the activation energy (Ea), Fig. 6, bottom-right. In the hopping regime, the conduction takes place via carrier jumps between localized states and the Marcus theory describes the transfer rate.46 For a hopping process, Ea is given by Ea = (ΔE + λ)2/4λ, with ΔE = Ef − Ei the difference between the final and initial site energies (energetic disorder) and λ the internal reorganization energy (driven by the geometric changes in the molecule when going from the neutral to the charged state and vice versa, see below).47 For both molecules, μFElin evolves linearly with the inverse of the temperature (1000/T). The activation energy calculated for [4]C-Py-Cbz appears to be higher than that of [4]L-Py-Cbz (369 vs. 347 meV) indicating that the linear shape of [4]L-Py-Cbz favours the hopping process. In term of stability, it is important to mention that both OFETs constructed either with [4]L-Py-Cbz or [4]C-Py-Cbz display an excellent stability with no modification of the mobility after 6 months (Fig. S16, ESI†). This is particularly interesting in the case of [4]C-Py-Cbz, as there is almost no study reported to date regarding the stability of nanohoops in electronic devices.
At this stage, the contribution of theoretical calculations appeared essential to unravel the origin of the different charge transport properties. Two key molecular parameters are decisive to gain a good understanding of the charge transport: the internal reorganization energy λ and the electronic coupling between adjacent molecules.48
The internal reorganization energy has been calculated here with the traditional four-point method47 from gas-phase geometries at the DFT level using the M06-2X functional (used herein in accordance with our previous work),19 and a 6-31G** basis set. Doing so, we obtain λ values of 338 and 370 meV for [4]L-Py-Cbz and [4]C-Py-Cbz respectively. Thus, the reorganization energy calculated for [4]C-Py-Cbz appears to be higher than that of [4]L-Py-Cbz. For [4]C-Py-Cbz, the torsion angle θext between the carbazole units is changing from 41° to 33° approximately when going from the neutral to the cation form respectively, while the angle between the carbazole and the pyridine (γ) is not changing significantly. For [4]L-Py-Cbz, θext is shifting from 35° (neutral form) to 28° (cation form) on average. Despite the fact that the variation of the torsion angle is very similar in absolute value, the difference in the reorganization energies primarily demonstrates that the energy costs are higher when dealing with larger torsion angle values. Note, however, that the value of 35° for [4]L-Py-Cbz corresponds to the dihedral angle of the neutral molecule in gas phase, which is reduced down to 13° in the crystal, i.e., closer to the value characteristic of the charged state. If we repeat the calculations by freezing the torsion angle to this value of 13°, the reorganization energy is then lowered to 281 meV. It seems then that [4]L-Py-Cbz is more influenced by packing effects than its cyclic counterpart [4]C-Py-Cbz. Hole transport is thus clearly favored in linear [4]L-Py-Cbz based on this parameter.
We now turn to the transfer integrals reflecting the strength of the electronic coupling between the HOMO of adjacent molecules. They are computed from the crystalline structures at the DFT Theory level within a fragment approach49 using the B3LYP function and a DZ basis set, as implemented in the ADF (Amsterdam density functional) package. In the case of [4]C-Py-Cbz, the largest transfer integrals on the order of 19 meV are found along one-dimensional columns highlighted in Fig. 7-top; smaller transfer integrals around 7–8 meV are also computed between adjacent columns. For [4]L-Py-Cbz, there is one favored stacking direction promoting a huge transfer integral (141 meV, Fig. 7-bottom) and much less efficient transport pathways between adjacent stacks with electronic couplings around 7–8 meV.
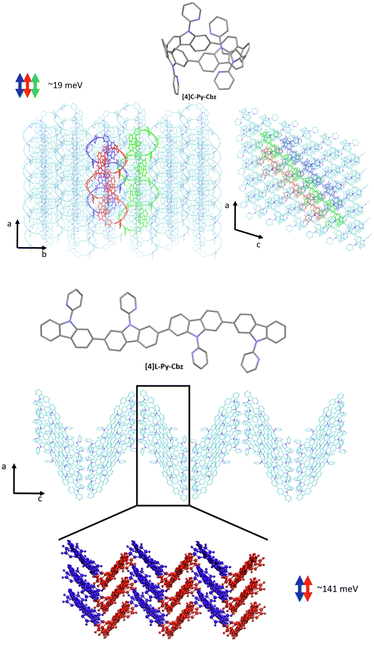 | ||
| Fig. 7 Transport direction yielding the highest transfer integrals in the crystalline structure of [4]C-Py-Cbz (top) and [4]L-Py-Cbz (bottom). | ||
Based on these results, we can now reach some relevant conclusions about the hole transport properties in the two compounds. For [4]C-Py-Cbz, the amplitude of the hole transfer integrals is much smaller than the reorganization energy, implying that the transport will mostly operate within the hopping regime. On the basis of the experimentally estimated activation energies Ea (see above) and the calculated reorganization energies λ, the Marcus expression for the activation barrier allows us to estimate the average energetic disorder ΔE = 363 meV in [4]C-Py-Cbz. For the linear analogue [4]L-Py-Cbz, the transport does not operate most likely in a pure hopping regime since the transfer integral is not much smaller than the reorganization energy along the main transport direction, which suggests that the charges are likely delocalized over several molecules in the stacks.
In [4]C-Py-Cbz, the key feature for an efficient transport is the rather isotropic character of the electronic couplings when comparing the values within the columns and between columns.50 This implies that there is an almost similar probability to move in different directions, which is very useful to cope with energetic disorder or the presence of defects. In contrast, in [4]L-Py-Cbz, the high spatial anisotropy of the electronic couplings is highly detrimental since it makes the transport between stacks much less probable; this imparts a strong one-dimensional character to the transport which becomes much more sensitive to defects and disorder. This analysis is fully consistent with the fact that [4]C-Py-Cbz displays experimentally better charge transport properties than [4]L-Py-Cbz.
Conclusion
To conclude, we report in this work the key effect played by the molecular curvature on the electronic, structural and charge transport properties of two tetracarbazoles, one with a hoop shape ([4]C-Py-Cbz), the other with a linear shape ([4]L-Py-Cbz). These different shapes lead to crystalline structures based on self-assembly into hollow columns and compact layers, respectively. Despite the substantially higher density and shorter distance between carbazole units in the [4]L-Py-Cbz structure, the charge transport was better for [4]C-Py-Cbz, in relation with the impact of the hoop shape on molecular properties. Cyclic voltammetries have notably revealed how the electronic effects of substituents differently affect the molecular orbitals energies. This is particularly relevant for further design rules. We have also shown how structural rearangements between ground and first excited states can be at the origin of the peculiar emission spectra of nanohoops. Finally, the different charge transport characteristics were particularly highlighted. The FE mobility in the saturated regime μFEsat of [4]C-Py-Cbz was measured at 3.4 × 10−6 cm2 V−1 s−1, six times higher than that of its linear analogue [4]L-Py-Cbz (5.7 × 10−7 cm2 V−1 s−1). However, studying in details the charge transport reveals that the linear analogue displays a lower trap density, which is a priori more favourable to the charge transport. Despite the fact that the intensity of electronic couplings is significantly in favor of the linear analogue [4]L-Py-Cbz, their anisotropic character renders them more sensitive to defects and disorder. This not only explains the higher mobilities measured for [4]C-Py-Cbzvs.[4]L-Py-Cbz but may also appear as an interesting characteristic, which can be further used in the future. The rational design of nanohoops for electronic applications is indeed now the next barrier to lift in this field in order to reach specific properties, which will translate in high performance devices. In this context, as presented in this study, we are convinced that the structures, the properties, the theoretical data and the device performance should be all connected in order to gain insights in the understanding of nanohoop performance.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work has been supported by the CNRS (International Emerging Action-2022). CB thanks the ANR (no. 19-CE05-0024-SpiroQuest Project) and the ADEME (Ecoelec Project, Dr Bruno Lafitte) for PhD grant. EJ and CP thank the Université de Rennes for the allocation of a Défi Scientifique 2023-Recherche transdisciplinaire interpoles. CQ thanks the Université de Rennes for the allocation of a Défi Scientifique 2021. We also thank the CRMPO (Rennes) for mass analyses. This work was granted access to the HPC resources of TGCC/CEA/CINES/IDRIS under the allocation 2024 AD010814136R1 awarded by GENCI. Dr Fabrice Mathevet (Paris) is also warmly acknowledge for the HOMO measurements by UPS. The authors acknowledged NanoRennes for the technological support, a platform affiliated to RENATECH+ (the French national facilities network for micro-nanotechnology). The work in Mons has been supported by the Marie Curie ITN project UHMob (GA-811284) and the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under grant #2.5020.11. J. C. is a FNRS research director.References
- E. J. Leonhardt and R. Jasti, Emerging applications of carbon nanohoops, Nat. Rev. Chem., 2019, 3, 672 CrossRef CAS.
- R. Zhang, D. An, J. Zhu, X. Lu and Y. Liu, Carbon Nanorings and Nanobelts: Material Syntheses, Molecular Architectures, and Applications, Adv. Funct. Mater., 2023, 33, 2305249 CrossRef CAS.
- R. Jasti, J. Bhattacharjee, J. Neaton and C. R. Bertozzi, Synthesis, Characterization, and Theory of [9]-, [12]-, and [18]Cycloparaphenylene: Carbon Nanohoop Structures, J. Am. Chem. Soc., 2008, 130, 17646 CrossRef CAS PubMed.
- H. Omachi, Y. Segawa and K. Itami, Synthesis of cycloparaphenylenes and related carbon nanorings: A step towards the controlled synthesis of carbon nanotubes, Acc. Chem. Res., 2012, 45, 1378 CrossRef CAS PubMed.
- E. R. Darzi and R. Jasti, The dynamic, size-dependent properties of [5]-[12]cycloparaphenylenes, Chem. Soc. Rev., 2015, 44, 6401 CAS.
- M. R. Golder and R. Jasti, Syntheses of the smallest carbon nanohoops and the emergence of unique physical phenomena, Acc. Chem. Res., 2015, 48, 557 CAS.
- S. E. Lewis, Cycloparaphenylenes and related nanohoops, Chem. Soc. Rev., 2015, 44, 2221 RSC.
- S. Yamago, E. Kayahara and T. Iwamoto, Organoplatinum-Mediated Synthesis of Cyclic π-Conjugated Molecules: Towards a New Era of Three-Dimensional Aromatic Compounds, Chem. Rec., 2014, 14, 84 CrossRef CAS PubMed.
- Y. Segawa, A. Kukazawa, S. Matsuura, H. Omachi, S. Yamaguchi, S. Irle and K. Itami, Combined experimental and theoretical studies on the photophysical properties of cycloparaphenylenes, Org. Biomol. Chem., 2012, 10, 5979 RSC.
- S. Wang, F. Chen, G. Zhuang, K. Wei, T. Chen, X. Zhang, C. Chen and P. Du, Synthesis of an all-carbon conjugated polymeric segment of carbon nanotubes and its application for lithium-ion batteries, Nano Res., 2023, 16, 10342 CrossRef CAS.
- J. S. Wössner, D. Wassy, A. Weber, M. Bovenkerk, M. Hermann, M. Schmidt and B. Esser, [n]Cyclodibenzopentalenes as Antiaromatic Curved Nanocarbons with High Strain and Strong Fullerene Binding, J. Am. Chem. Soc., 2021, 143, 12244 CrossRef PubMed.
- S. Hitosugi, K. Ohkubo, R. Iizuka, Y. Kawashima, K. Nakamura, S. Sato, H. Kono, S. Fukuzumi and H. Isobe, Photoinduced Electron Transfer in a Dynamic Supramolecular System with Curved π-Structures, Org. Lett., 2014, 16, 3352 CrossRef CAS PubMed.
- R. Roy, C. Brouillac, E. Jacques, C. Quinton and C. Poriel, π-Conjugated Nanohoops: A new generation of curved materials for organic electronics, Angew. Chem., Int. Ed., 2024, e202402608 CAS.
- Y.-Y. Liu, J.-Y. Lin, Y.-F. Bo, L.-H. Xie, M.-D. Yi, X.-W. Zhang, H.-M. Zhang, T.-P. Loh and W. Huang, Synthesis and Crystal Structure of Highly Strained [4]Cyclofluorene: Green-Emitting Fluorophore, Org. Lett., 2016, 18, 172 CrossRef CAS PubMed.
- C. Brouillac, F. Lucas, D. Tondelier, J. Rault-Berthelot, C. Lebreton, E. Jacques, C. Quinton and C. Poriel, [4]-Cyclo-2,7-Carbazole as Host Material in High-Efficiency Phosphorescent OLEDs: A New Perspective for Nanohoops in Organic Electronics, Adv. Opt. Mater., 2023, 11, 2202191 CrossRef CAS.
- D. Chen, Y. Wada, Y. Kusakabe, L. Sun, E. Kayahara, K. Suzuki, H. Tanaka, S. Yamago, H. Kaji and E. Zysman-Colman, A Donor–Acceptor 10-Cycloparaphenylene and Its Use as an Emitter in an Organic Light-Emitting Diode, Org. Lett., 2023, 25, 1523 Search PubMed.
- F. Lucas, L. Sicard, O. Jeannin, J. Rault-Berthelot, E. Jacques, C. Quinton and C. Poriel, [4]Cyclo-N-ethyl-2,7-carbazole: Synthesis, Structural, Electronic and Charge Transport Properties, Chem. – Eur. J., 2019, 25, 7740 CrossRef CAS PubMed.
- F. Lucas, N. McIntosh, E. Jacques, C. Lebreton, B. Heinrich, B. Donnio, O. Jeannin, J. Rault-Berthelot, C. Quinton, J. Cornil and C. Poriel, [4]Cyclo-N-alkyl-2,7-carbazoles: Influence of the Alkyl Chain Length on the Structural, Electronic, and Charge Transport Properties, J. Am. Chem. Soc., 2021, 143, 8804 CAS.
- F. Lucas, C. Brouillac, N. McIntosh, S. Giannini, J. Rault-Berthelot, C. Lebreton, D. Beljonne, J. Cornil, E. Jacques, C. Quinton and C. Poriel, Electronic and Charge Transport Properties in Bridged versus Unbridged Nanohoops: Role of the Nanohoop Size, Chem. – Eur. J., 2023, e202300934 CrossRef CAS.
- M. Ball, Y. Zhong, B. Fowler, B. Zhang, P. Li, G. Etkin, D. W. Paley, J. Decatur, A. K. Dalsania, H. Li, S. Xiao, F. Ng, M. L. Steigerwald and C. Nuckolls, Macrocyclization in the Design of Organic n-Type Electronic Materials, J. Am. Chem. Soc., 2016, 138, 12861 CrossRef CAS PubMed.
- M. Ball, B. Zhang, Y. Zhong, B. Fowler, S. Xiao, F. Ng, M. Steigerwald and C. Nuckolls, Conjugated Macrocycles in Organic Electronics, Acc. Chem. Res., 2019, 52, 1068 CrossRef CAS.
- B. Zhang, M. T. Trinh, B. Fowler, M. Ball, Q. Xu, F. Ng, M. L. Steigerwald, X. Y. Zhu, C. Nuckolls and Y. Zhong, Rigid, Conjugated Macrocycles for High Performance Organic Photodetectors, J. Am. Chem. Soc., 2016, 138, 16426 CAS.
- W.-S. Wong and M. Stępień, Emerging applications of curved aromatic compounds, Trends Chem., 2022, 4, 573 CAS.
- L. Sicard, F. Lucas, O. Jeannin, P. A. Bouit, J. Rault-Berthelot, C. Quinton and C. Poriel, [n]-Cyclo-9,9-dibutyl-2,7-fluorene (n = 4, 5): Nanoring Size Influence in Carbon-Bridged Cyclo-para-phenylenes, Angew. Chem., Int. Ed., 2020, 59, 11066 CAS.
- P. Li, T. J. Sisto, E. R. Darzi and R. Jasti, The Effects of Cyclic Conjugation and Bending on the Optoelectronic Properties of Paraphenylenes, Org. Lett., 2014, 16, 182 CrossRef CAS PubMed.
- M. Peña-Alvarez, L. Qiu, M. Taravillo, V. G. Baonza, M. C. R. Delgado, S. Yamago, R. Jasti, J. T. L. Navarrete, J. Casado and M. Kertesz, From linear to cyclic oligoparaphenylenes: electronic and molecular changes traced in the vibrational Raman spectra and reformulation of the bond length alternation pattern, Phys. Chem. Chem. Phys., 2016, 18, 11683 Search PubMed.
- P. Seitz, M. Bhosale, L. Rzesny, A. Uhlmann, J. S. Wössner, R. Wessling and B. Esser, Conjugated Nanohoop Polymers based on Antiaromatic Dibenzopentalenes for Charge Storage in Organic Batteries, Angew. Chem., Int. Ed., 2023, 62, e202306184 CAS.
- B. M. Wong, Optoelectronic Properties of Carbon Nanorings: Excitonic Effects from Time-Dependent Density Functional Theory, J. Phys. Chem. C, 2009, 113, 21921 CAS.
- E. Kayahara, L. Sun, H. Onishi, K. Suzuki, T. Fukushima, A. Sawada, H. Kaji and S. Yamago, Gram-Scale Syntheses and Conductivities of [10]Cycloparaphenylene and Its Tetraalkoxy Derivatives, J. Am. Chem. Soc., 2017, 139, 18480 CAS.
- S. Wang, X. Li, K. Wei, X. Zhang, S. Yang, G. Zhuang and P. Du, Facile Synthesis of a Conjugated Macrocyclic Nanoring with Graphenic Hexabenzocoronene Sidewall as the Segment of [12,12] Carbon Nanotubes, Eur. J. Org. Chem., 2022, e202101493 CrossRef CAS.
- S. Wang, X. Li, G. Zhuang, M. Chen, P. Huang, S. Yang and P. Du, Synthesis and properties of a nanographene-embedded conjugated macrocyclic nanoring via the Scholl reaction, Chem. Commun., 2021, 57, 9104 CAS.
- C. Brouillac, N. McIntosh, B. Heinrich, O. Jeannin, O. De Sagazan, N. Coulon, J. Rault-Berthelot, J. Cornil, E. Jacques, C. Quinton and C. Poriel, Grafting Electron-Accepting Fragments on [4]cyclo-2,7-carbazole Scaffold: Tuning the Structural and Electronic Properties of Nanohoops, Adv. Sci., 2024, 11, 2309115 CrossRef CAS.
- C. Schaack, A. M. Evans, F. Ng, M. L. Steigerwald and C. Nuckolls, High-Performance Organic Electronic Materials by Contorting Perylene Diimides, J. Am. Chem. Soc., 2022, 144, 42 CrossRef CAS.
- L. Sicard, O. Jeannin, J. Rault-Berthelot, C. Quinton and C. Poriel, [4]Cyclofluorene: Unexpected Influence of Alkyl Chain Length, ChemPlusChem, 2018, 83, 874 CrossRef CAS.
- M. R. Talipov, R. Jasti and R. Rathore, A Circle Has No End: Role of Cyclic Topology and Accompanying Structural Reorganization on the Hole Distribution in Cyclic and Linear Poly-p-phenylene Molecular Wires, J. Am. Chem. Soc., 2015, 137, 14999 CAS.
- J. Lin, S. Wang, F. Zhang, B. Yang, P. Du, C. Chen, Y. Zang and D. Zhu, Highly efficient charge transport across carbon nanobelts, Sci. Adv., 2022, 8, eade4692 CrossRef CAS.
- T. Kawaguchi, K. Tanaka, T. Takeuchi and T. Watanabé, The Crystal Structure of Methylene Bichloride, CH2Cl2, Bull. Chem. Soc. Jpn., 1973, 46, 62 CrossRef CAS.
- C. Poriel, C. Quinton, F. Lucas, J. Rault-Berthelot, Z. Q. Jiang and O. Jeannin, Spirobifluorene Dimers: Understanding How The Molecular Assemblies Drive The Electronic Properties, Adv. Funct. Mater., 2021, 2104980 CAS.
- J.-F. Wang, J.-K. Feng, A.-M. Ren and L. Yang, Theoretical Studies of the Structure, Absorption and Emission Properties of Terfluorene and Ter(9,9-diarylfluorene) Derivatives, Chin. J. Chem., 2005, 23, 1618 CAS.
- G. Heimel, M. Daghofer, J. Gierschner, E. J. W. List, A. C. Grimsdale, K. Müllen, D. Beljonne, J. L. Brédas and E. Zojer, Breakdown of the mirror image symmetry in the optical absorption/emission spectra of oligo(para-phenylene)s, J. Chem. Phys., 2005, 122, 054501 CrossRef.
- N. J. Turro, Modern Molecular Photochemistry, University science books, Sausalito, 1991 Search PubMed.
- S. Canola, C. Graham, Á. J. Pérez-Jiménez, J.-C. Sancho-García and F. Negri, Charge transport parameters for carbon based nanohoops and donor–acceptor derivatives, Phys. Chem. Chem. Phys., 2019, 21, 2057 RSC.
- J. B. Lin, E. R. Darzi, R. Jasti, I. Yavuz and K. N. Houk, Solid-State Order and Charge Mobility in [5]- to [12]Cycloparaphenylenes, J. Am. Chem. Soc., 2019, 141, 952 CAS.
- J. C. Sancho-García, M. Moral and A. J. Pérez-Jiménez, Effect of Cyclic Topology on Charge-Transfer Properties of Organic Molecular Semiconductors: The Case of Cycloparaphenylene Molecules, J. Phys. Chem. C, 2016, 120, 9104 Search PubMed.
- J.-D. Peltier, B. Heinrich, B. Donnio, O. Jeannin, J. Rault-Berthelot, E. Jacques and C. Poriel, N-Cyanoimine as an electron-withdrawing functional group for organic semiconductors: example of dihydroindacenodithiophene positional isomers, J. Mater. Chem. C, 2018, 6, 13197 RSC.
- R. A. Marcus, Electron transfer reactions in chemistry. Theory and experiment, Rev. Mod. Phys., 1993, 65, 599 CAS.
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Brédas, Charge transport in organic semi-conductors, Chem. Rev., 2007, 107, 926 CrossRef CAS PubMed.
- J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Organic semiconductors: a theoretical characterization of the basic parameters governing charge transport, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804 Search PubMed.
- K. Senthilkumar, F. C. Grozema, F. M. Bickelhaupt and L. D. A. Siebbeles, Charge transport in columnar stacked triphenylenes: Effects of conformational fluctuations on charge transfer integrals and site energies, J. Chem. Phys., 2003, 119, 9809 CAS.
- S. Fratini, S. Ciuchi, D. Mayou, G. T. de Laissardière and A. Troisi, A map of high-mobility molecular semiconductors, Nat. Mater., 2017, 16, 998 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2325120 ([4]L-Py-Cbz). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc02304h |
| This journal is © The Royal Society of Chemistry 2024 |