Three decades of unveiling the complex chemistry of C-nitroso species with computational chemistry
Pauline
Bianchi
and
Jean-Christophe M.
Monbaliu
 *
*
Center for Integrated Technology and Organic Synthesis, MolSys Research Unit, University of Liège, B-4000 Liège (Sart Tilman), Belgium. E-mail: jc.monbaliu@uliege.be; Web: http://www.citos.uliege.be
First published on 9th November 2021
Abstract
C-Nitroso species are characterized by a unique nitrogen–oxygen combination located next to a carbon backbone, which confers them a unique ambiphilic and high reactivity towards nucleophilic, electrophilic but also radical species. Although this ambivalence can be seen as a strong asset for developing versatile synthetic aminohydroxylation and/or hydroxylamination processes mainly through nitroso Diels–Alder, nitroso ene, and nitrosoaldol reactions, it also contributes to complex optimization and rationalization arising from the many competitive pathways, that is, the occurrence of regioisomers and stereoisomers, as well as dimerization and tautomerization side-reactions. Complex reactivity profiles are usually seen by synthetic organic chemists as major hurdles to overcome, despite the armada of analytical and purification methods available to them, and hence to achieve selective and exploitable developments of such reactions. The rise of computational chemistry and resources has certainly changed their perspectives, since it provides a very different angle to gather insights on intrinsic properties, reactivity, and mechanisms. In silico chemistry also provides a robust alternative to time and resource-consuming synthetic work and can therefore contribute to alleviate wasteful preparations by guiding the chemist toward the best combination of reagents to achieve high selectivity and yield. The synergistic combination of synthetic organic chemistry and computational chemistry, within the specific context of the complex chemistry of C-nitroso species, is discussed in this work. This review aims at giving an overview of the molecular and chemical properties obtained through computational chemistry as an enabling support for the rationalization and optimization of reactions relying on ambiphilic C-nitroso species over the 3 last decades. It provides clear, concise, and illustrated guidelines for the synthetic chemist in search of inspiration through computations.
Introduction
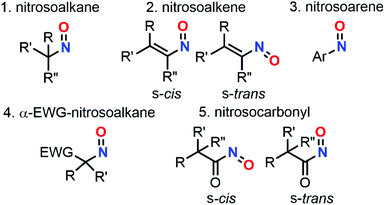
Nitroso compounds are reactive molecules known to bear an ambiphilic N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functional group that can be divided into various classes depending on the N
O functional group that can be divided into various classes depending on the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O neighboring atom: S-, O-, C- or N.1 Among these classes, C-nitroso species are widely used in synthetic organic chemistry for the integration of a broad range of moieties containing nitrogen, and/or oxygen-based functional groups.2–5 Nitrosoalkanes, nitrosoalkenes, nitrosoarenes, α-EWG-nitrosoalkanes, and nitrosocarbonyls are the main subclasses of C-nitroso species and possess different reactivity profiles that are strongly dependent on the presence of a specific secondary carbon-based scaffold (Fig. 1).6–10
O neighboring atom: S-, O-, C- or N.1 Among these classes, C-nitroso species are widely used in synthetic organic chemistry for the integration of a broad range of moieties containing nitrogen, and/or oxygen-based functional groups.2–5 Nitrosoalkanes, nitrosoalkenes, nitrosoarenes, α-EWG-nitrosoalkanes, and nitrosocarbonyls are the main subclasses of C-nitroso species and possess different reactivity profiles that are strongly dependent on the presence of a specific secondary carbon-based scaffold (Fig. 1).6–10
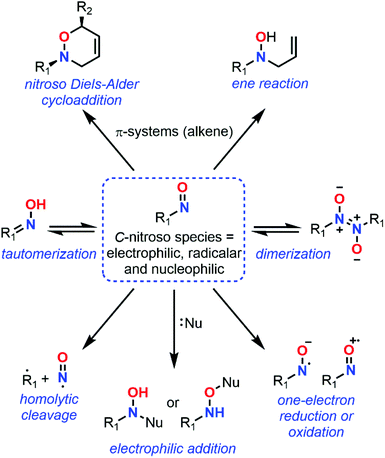
Despite major differences in terms of stability and reactivity, as well as a complex reaction profile, C-nitroso species can be involved in a series of well-defined reactions (Fig. 2). On the one hand, nitroso compounds are typically associated with a low-lying Lowest Unoccupied Molecular Orbital (LUMO) associated with the π*N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O antibonding orbital, which entitles them as good candidates for electrophilic addition such as in nitrosoaldol reactions.11,12 On the other hand, nitroso compounds have also a highly energetic Highest Occupied Molecular Orbital (HOMO) associated with the lone pairs nO and nN, which confers them a strong nucleophilic character. This ambiphilic behavior is not only responsible for their complex reactivity profile and their potential involvement in tautomerization, dimerization,13 and pseudocyclic reactions (previously so-called “pericyclic reactions” before the demonstration of the non-symmetrical pattern of electron delocalization in the transition structure)14,15 including nitroso Diels–Alder (NDA)16–20 and ene reactions,21,22 but also for their unique spectroscopic properties. In addition to heterolytic processes, C-nitroso species are also able to undergo radicalar processes such as C–NO homolytic bond cleavage and one-electron reduction or oxidation reactions into radical anions and cations respectively.23
O antibonding orbital, which entitles them as good candidates for electrophilic addition such as in nitrosoaldol reactions.11,12 On the other hand, nitroso compounds have also a highly energetic Highest Occupied Molecular Orbital (HOMO) associated with the lone pairs nO and nN, which confers them a strong nucleophilic character. This ambiphilic behavior is not only responsible for their complex reactivity profile and their potential involvement in tautomerization, dimerization,13 and pseudocyclic reactions (previously so-called “pericyclic reactions” before the demonstration of the non-symmetrical pattern of electron delocalization in the transition structure)14,15 including nitroso Diels–Alder (NDA)16–20 and ene reactions,21,22 but also for their unique spectroscopic properties. In addition to heterolytic processes, C-nitroso species are also able to undergo radicalar processes such as C–NO homolytic bond cleavage and one-electron reduction or oxidation reactions into radical anions and cations respectively.23
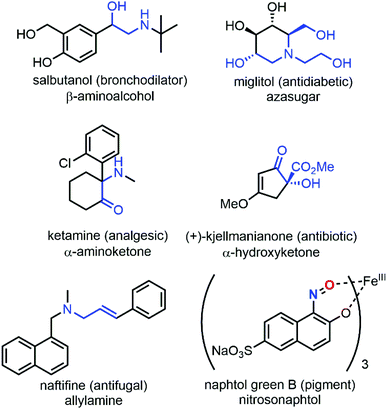
While NDA cycloadditions enable the synthesis of 1,2-oxazine scaffolds that can be derivatized into useful building blocks for the total synthesis of bioactive natural products such as β-aminoalcohols or azasugars, nitroso ene reactions afford allylamines that are other highly valuable scaffolds in synthetic organic and medicinal chemistry. Other high value-added moieties such as α-aminoketones or α-hydroxyketones can be obtained through nitrosoaldol reactions and derivatized into other useful functionalities such as β-aminoalcohols. Finally, some C-nitroso species such as nitrosonaphtol derivatives are used after tautomerization and metal complexation as dyes or pigments for their characteristic colors (Fig. 3).24,25
Although C-nitroso species have a solid track-record of utility as synthetic tools in organic chemistry, their toxicity and often instability prevent them to be exploited at the maximum of their inherent chemical potentiality. For some instances, their stability strongly depends on their ability to dimerize and the stability of the corresponding dimeric form. The dimerization of C-nitroso derivatives leading to a polar azoxy compound is quite a general feature and remains a reversible step for most compounds, although the extent and the outcome differ according to the nitroso subclasses. Nitrosocarbonyls are so reactive that they are considered as transient species (extremely short lifetime). In the absence of a suitable reaction partner, nitrosocarbonyls readily dimerize, and then undergo a fast and irreversible decomposition process according to Kirby's mechanism.2,26 By contrast, nitrosoarenes, that are considered as less reactive also dimerize, while the dimer does not trigger a decomposition pathway, but rather behaves as an inactive reservoir of nitroso species.27 Reactive α-EWG-nitrosoalkanes such as α-chloro-derivatives28 decompose more readily than nitrosoalkanes29 through thermal or photo homolytic cleavage of the C–NO to release gaseous nitric oxide (NO),5,30,31 which renders the former highly explosive and difficult to handle.32 The stability of nitrosoalkenes also depends on their inclination to tautomerize, nitrosoethylene derivatives being found to be highly unstable.6 The cytotoxicity of nitrosoarenes has been also related to deleterious nitroso-ene reactions.21 Moreover, the strong binding affinity between iron and nitroso compounds in heme moiety is responsible for the inhibition of the enzymatic activity of P450 or cyclooxygenase due to hydroxylamine-metabolite oxidation or nitro-metabolite reduction.1
The ability to gather a priori information on structure and reactivity is a very strong asset for synthetic organic chemists, not only to tune and design better reagents, but also to impact the selectivity or to support mechanistic or structure/relationship studies. While the palette of complex analytical and structural technologies that is now available to the chemist keeps increasing, the access to local and global reactivity indexes, as well as the structure and energy of transition states remains difficult to access experimentally. Besides, increasing safety and environmental regulations progressively hamper the handling of reactive or toxic species.
Using a theoretical approach has been already proved as being a strong asset to better understand the intrinsic reactivity of toxic or reactive species without requiring careful handling of dangerous chemicals and restrictive safety protocols.33 This branch of chemistry, whose fundamentals will be developed in the next paragraphs, gives insights into specific chemical questions such as reaction mechanisms, stereo- and regioselectivities, solvent effects, or intrinsic properties (conformational, spectroscopic, electronic, to name a few) without needing many costly resources.
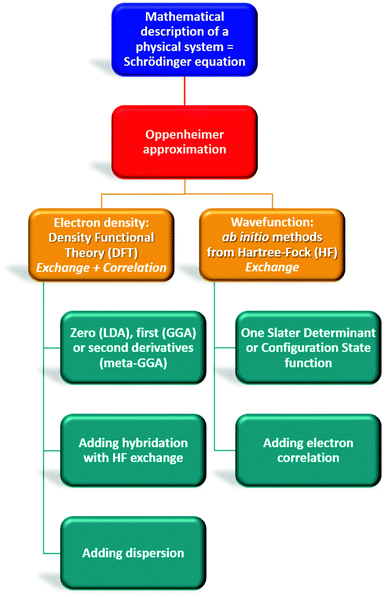
Computational chemistry combines theoretical chemistry with computer programming to mathematically determine the molecular structural, electronic, and energy properties. This branch of chemistry, born during the early 50s with the emergence of modern computing resources and the development of quantum mechanics (QM), aims at solving the non-relativistic time-independent Schrödinger equation (eqn (1)),34 the resolution of which gives the total energy of an isolated physical system. All internal forces arising within this system (nuclei and electron motions, electron–electron repulsions, electron–nuclei attractions, and nuclei–nuclei repulsions) are gathered in a mathematical Hamiltonian operator 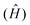 that is applied to the wavefunction (Ψ) that describes the system at a stationary state.
that is applied to the wavefunction (Ψ) that describes the system at a stationary state.
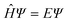 | (1) |
Since this equation cannot be solved analytically, a common approach consists in applying the variational method. The underlying idea is to determine a trial wavefunction based on orthonormal functions, which depend on variational parameters that can be adjusted until convergence. After optimization, the corresponding energy will be always higher than or equal to the exact unknown energy of the system. This principle allows determining the accuracy of the employed methods, which rely on specific approximations. Several workable and accurate approximations have emerged over the years to reduce the complexity and time required for calculations. However, these approximations inexorably give an inherent error to the final result. Larger molecular systems come with a significant computation time and are very resource-intensive, which can be alleviated with low-quality approximations, hence impacting the accuracy of the output. It is therefore the chemist's responsibility to find an acceptable compromise between computational cost/resources and accuracy.
Most of the computational methods are based on the Born–Oppenheimer approximation where the motion of the n electrons is decoupled from the N nuclei.35 The foundation of this approximation relies on the important mass difference between nuclei and electrons, allowing to consider nuclei as fixed with regards to the electrons. Consequently, the total wavefunction can be separated into an electronic and a nuclear part, while the Hamiltonian depends only on electronic variables in which electrons feel an average nuclear–nuclear repulsion potential (eqn (2)).
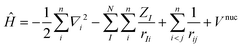 | (2) |
 | ||
| Fig. 4 Overview of theoretical chemistry highlighting differences between Density Functional Theory (DFT) and Hartree–Fock methods. | ||
By contrast, the Density Functional Theory (DFT)45,46 only considers 3 variables (x, y, z) to reduce the computational cost of ab initio methods that depend on 3N coordinates for N electrons (Fig. 4). The description of the system is not the electronic wavefunction anymore but the one-electron density ρ(r). In this method, the functional that relates ρ(r) to the energy includes an exchange–correlation term (different from ab initio methods), the approximation of which depends on the selected DFT subclass method.47 Functionals using the local density approximation (LDA), the generalized gradient approximation (GGA), or meta-GGA are respectively based on the zero, first and second derivative of ρ(r).48–50 Some functionals even add an empirical percentage of HF exchange which renders them extremely popular. They are named hybrid functionals (in this review: B3LYP, B3PW91, PBE0, CAMB3LYP, ωB97X, TPSSh, M06-2X, B2PLYP, DSD-PBEB86). Most of the time, these functionals can be upgraded by adding a dispersion correction term (D1, D2, D3 terms proposed by Grimme, or D3BJ by Becke and Jonhson) that considers long-range interactions (London dispersion).51
In 1984, Runge and Gross stated that the functional electron density could be extended to the time-dependent domain and developed the Time-Dependent Density Functional Theory (TD-DTF).52 This technique allowed the determination of the energies, structures, and properties of any excited state (ES) that is reached upon perturbation of the molecule at its GS in the presence of an external field (time-dependent potential).
The case of neutral, cationic, or anionic species represents closed-shell systems where the number of electrons is even, meaning that each electron is paired with another electron of opposite spin. This kind of system does not need to split the spatial orbital for each kind of spin electron, on the contrary to systems with an odd number of electrons such as radicals. This requires the use of unrestricted methods (U) which can be applied for each functional (such as UHF, UMP2, or UB3LYP), where a set of equations is created for each kind of electron (α or β) and then implemented in the same algorithms as used for restricted methods, hence enabling a separated spatial description for each electron.
The description of molecules to be computed depends on the basis set of atomic orbitals (AO) chosen by the chemist. As computational resources are limited, it is necessary to truncate the possibility of AOs per atom. These AOs are then linearly combined (LCAO method) to form the molecular orbitals (MO) of the system. The way these AOs are mathematically described also impacts the final result. Slater-type orbitals (STO) are based on the exact mathematic solution of the Schrödinger equation for the hydrogen atom while Gaussian-type orbitals (GTO) relate to mathematical Gaussian functions. These ones are easier to evaluate but require to be employed as a linear combination to adequately mimic STOs orbitals. The minimal basis set involves only totally or partially filled orbitals for each atom but can be multiple and split between core and valence electrons for a more accurate description of the molecules, as proposed by Pople.53 Moreover, polarization and diffuse functions, labeled * (or the type of polarization functions employed: d, p, f) and +, can be added for a better description of the electron density polarization and the orbital extension of atoms with lone pairs or anions, respectively. For example, one of the well-known Pople basis sets 6-31+G**/6-31+G(d,p) relates to 6 GTO orbitals for describing the core electrons, 3 for the valence electrons near the nuclei, 1 for the valence electrons far from the nuclei, an additional set for diffuse functions, a set of d functions for non-hydrogen atoms and a set of p functions for hydrogens. Other basis sets were also developed to better consider the electron correlation, such as the ones from Dunning (cc-pVNZ where N is the degree of splitting + aug-for diffuse functions).54
Since most of the time, organic reactions take place in condensed (liquid) systems where solute–solvent interactions are paramount, solvent integration is usually highly recommended. Explicit integration of solvent molecules within the system highlights strong interactions such as hydrogen bonding but suffers from an increased computational cost and complexity, whereas implicit solvation approximates the solvent only through its dielectric constant. This method considers electrostatic, cavitation, and dispersion interactions between the polarizable medium and a cavity that contains the system. The resolution of the Schrödinger equation with this kind of method needs to be done iteratively to finally give a solvation potential that is self-consistent, leading to a self-consistent reaction field (SCRF). Different models have been developed depending on the form of the cavity and the electrostatic treatment, the most known in organic chemistry being the Onsager reaction field method,55 polarizable continuum model (PCM),56 and the Solvation Model based on Density (SMD).57
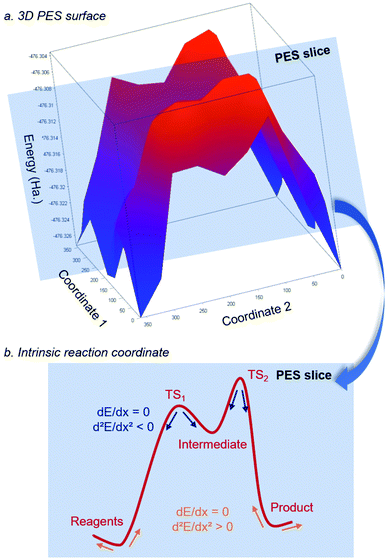
Computing a Potential Energy Surface (PES) describing the variation of the energy of a system based on the position of the atoms is typically achieved through geometry optimization (Fig. 5).58,59 Even for simple molecular systems, computing the PES can be extremely resource- and time-consuming. A conventional approach relies on “slicing” the PES to access a more reasonable 2D energy profile that connects stationary points. During this process, the zeros of the Slater determinant matrix are found through calculations of its first and second derivatives along the direction of the reaction coordinate. While the first derivatives give an idea about internal residual forces and, hence, the increase or decrease of energy within the system based on structural changes, the second derivatives aim at confirming the identity of a given stationary point along the reaction coordinate. If all frequencies (related to second derivatives) are positive, a local minimum is found along the reaction coordinate. Such local minimum relates to a reagent, a product, or an intermediate. If only one frequency is negative and the others are positive, the stationary point relates to a transition state. The steepest path liking the transition structure to reagents/products is called the intrinsic reaction coordinate (IRC) and draws the intrinsic reaction energy profile.60 From that steps, valuable information can be obtained from the system, such as its thermodynamic and kinetic properties, structural features, and electronic population, the last one being useful to determine atomic charges (number of electrons on a specific atom). These ones can derive either from the analysis of orbital populations, such as with the Mulliken61 and the natural population analysis62 (NPA, leading to natural bond orbital, NBO), or from the topology of the electron density with the Atoms in molecules (AIM) method.63 Finally, for thermochemistry data, electronic energies obtained during the optimization can be corrected with the zero-point energy (vibrational energy remaining at 0 K, ZPE) and a thermal factor (correction either to the energy, the Enthalpy, or the Gibbs Free energy).
All these features made computational chemistry a powerful tool to rationalize and predict experimental data, which explains its intensive use in various branches of chemistry,64–68 and the field of C-nitroso species has certainly not been ignored. Despite the availability of numerous reviews dealing with the various aspects of synthetic organic chemistry of C-nitroso species, ranging from their preparation to their use in nitroso Diels–Alder reactions or for the asymmetrical syntheses of natural products,11–23 the current literature is clearly lacking a review on the use of computational chemistry to understand their reactivity and properties. This review not only aims at gathering all the electronic, structural, and reactivity data computed for C-nitroso species during these past three decades, but also to provide clear and accessible guidelines to the synthetic chemist for efficiently employing computational chemistry. The review is articulated around two main subsections: (a) the computation of molecular properties – including electronic, spectroscopic, dimerization, tautomerization, and radicalar properties of C-nitroso species and (b) the computation of the reactivity of C-nitroso species involved in nitroso Diels–Alder (NDA), nitroso ene, nitrosoaldol, and other pseudocyclic or addition reactions.
Computational studies of the inherent properties of nitroso species
Intrinsic (electronic) properties
C-Nitroso species are known to bear a unique ambiphilic behavior towards nucleophilic and electrophilic centers. Understanding their intrinsic electronic properties has therefore been paramount to rationalize experimental results, including regioselectivity and reactivity. The introduction of descriptors for the stability and reactivity of C-nitroso species followed the rapid development and breakthroughs arising in the field of conceptual DFT (CDFT)69,70 and have provided answers regarding the intrinsic electronic properties of C-nitroso compounds.An early description of molecular reactivity was elaborated by Tomasi et al. in 1973 through the introduction of the molecular electrostatic potential (MEP, eqn (3)).71 The physical interpretation of this potential is defined as the energy required to bring a single positive charge from infinity to a specific point related to an atom. In this way, the MEP is a useful tool for identifying nucleophilic and electrophilic centers, characterized respectively by negative and positive potentials:
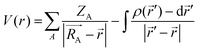 | (3) |
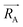 , and
, and 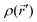 is the electronic density function of the molecule that can be computed from the molecular wave function.
is the electronic density function of the molecule that can be computed from the molecular wave function.
One of the first computational analyses using MEP that is relevant for studying nitroso species was written in 1987 when Politzer and Bar-Adon investigated the electronic impact of the nitroso moiety on an aromatic ring at the HF/STO-5G level (Fig. 6).72 Determination of the bond lengths and angles after geometry optimization supported the emergence of mesomers through the electron-withdrawing of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety on nitrosobenzene (1) and nitrosoaniline (2).
O moiety on nitrosobenzene (1) and nitrosoaniline (2).
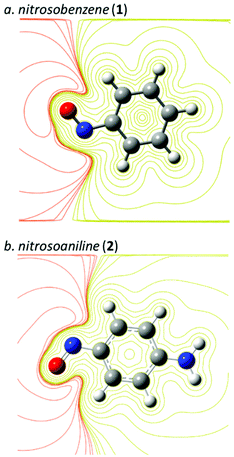 | ||
| Fig. 6 Molecular electrostatic potential contour of (a) nitrosobenzene (1) and (b) nitrosoaniline (2) at the B3LYP/6-31+G* level (isovalue = 0.02, in yellow: positive, in orange: negative). | ||
Calculation of the MEP emphasized a milder deactivation of the aromatic ring by the nitroso group than by a more conventional nitro (NO2) group, as expected by the lack of an additional oxygen atom. By contrast, nucleophilic centers around the lone pairs of nitrogen and oxygen atoms were determined due to strong negative potentials, especially for the nitrogen atom, which has no equivalent in nitrobenzene-related derivatives. The electrophilic center was also located at the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. The addition of an ortho or para NH2 substituent relative to the N
O moiety. The addition of an ortho or para NH2 substituent relative to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety somewhat counterbalanced the EWG contribution of N
O moiety somewhat counterbalanced the EWG contribution of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, hence resulting in an activation of the nucleophilic strength of the aromatic cycle at the ortho and para positions, while slightly deactivating the electrophilic nature of the nitroso group.
O, hence resulting in an activation of the nucleophilic strength of the aromatic cycle at the ortho and para positions, while slightly deactivating the electrophilic nature of the nitroso group.
Another concept for describing electronic changes upon reactions was developed by Parr and Yang in 1984 through the formulation of Fukui's function (PY).73 This concept showed the changes in electron density at a point r during a variation of the number of electrons N at a fixed external potential v(r). This expression could be expressed with the Frontier Molecular Orbitals (FMO) HOMO and LUMO, or with the differences felt by the molecular system by applying the finite difference approximation (eqn (4)–(6)).
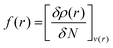 | (4) |
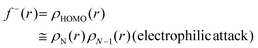 | (5) |
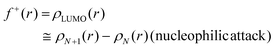 | (6) |
This function was later simplified by Yang and Mortier using the Mulliken gross charges q for a specific atom k (eqn (7) and (8), YM).74 With this in mind, the highest change in electron density would determine the most reactive center of a given molecule.
| f−(r) ≅ qN(r) − qN−1(r) | (7) |
| f+(r) ≅ qN+1(r) − qN(r) | (8) |
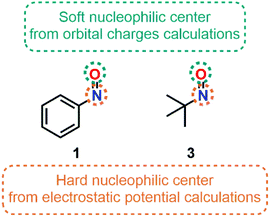
In 2001, Pilepić and Uršić supported their experimental observations relative to the nucleophilic character of nitroso species 1 and tert-nitrosobutane (3) with the use of Fukui function f− (Fig. 7).75 Using a high basis set (6-311++G**) to minimize errors related to a poor atomic description, they plotted the isodensity of f− for 1 and 3. Both N and O atoms were highlighted as nucleophilic centers in the gas phase. However, the extended resonance in 1 reduced the nucleophilic character of the nitrogen atom. Minor changes of the f− indices were observed when considering the solvation of the nitroso species with water. Correcting both Fukui indices (f− and f+) by the softness S of a molecule and comparing the new indices obtained (s−k/s+k, seen as the relative nucleophilicity of an atom k, as introduced by Roy in 1998)76 gave insights about the most nucleophilic site. The s−k/s+k indices calculated from electrostatic potential charges suggested a higher nucleophilic center located at the nitrogen atom, and which was defined accordingly as a hard center. On the contrary, orbital charge calculation methods, describing soft–soft interactions, emphasized the higher nucleophilicity of the oxygen atom. The introduction of implicit solvation within the SCRF (PCM model) led to an increase of the local reactivity indices but did not change the overall trend. The calculations of the MEP minima points with implicit solvation confirmed the position of the hard and soft nucleophilic centers on N and O, respectively.
The chemical hardness of a molecule (η) can be used to compare not only the reactivity but also the relative stability of chemical species. Defined as the resistance of a molecule towards electronic exchange within its environment, η can be expressed in terms of ionization potential (I) and electron affinity (A), or even with the respective energies of the HOMO and LUMO (eqn (9), usually factor ½ is neglected).69 The expression of the chemical potential μ, which translates the tendency of a molecule to receive electron density, follows a similar idea (eqn (10)). The concept of chemical hardness was introduced in 1993 by Pearson as a support to a new principle, namely, the maximum hardness principle (MHP), where the most stable molecules have the highest hardness for a constant value of μ.
 | (9) |
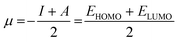 | (10) |
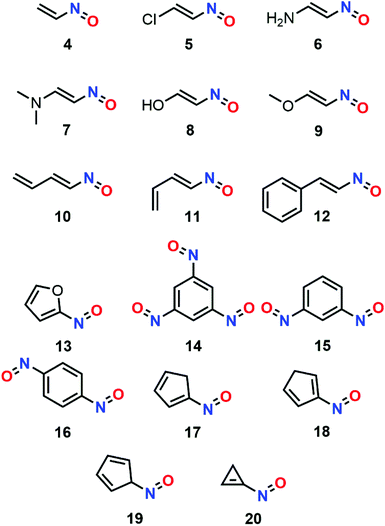
From 2002 to 2006, Kolandaivel et al. proposed a conformational study of various C-nitroso species that followed a similar methodology (Fig. 8). The structural aspects of various conformers were usually studied with DFT functionals (B3LYP and B3PW91) for a better description of the bond lengths and angles, especially around lone pairs, while the energy aspects were computed with ab initio methods (HF and MP2). The nature of each species was confirmed with a vibrational study. The trends in terms of stability were then compared with the MHP and μ data. The studies included various vinylnitroso derivatives, including compounds nitrosoethylene (4), 1-chloro-2-nitrosoethylene (5), 2-nitrosoethen-1-amine (6), N,N-dimethyl-2-nitrosoethen-1-amine (7), 2-nitrosoethen-1-ol (8), and 1-methoxy-2-nitrosoethylene (9).77 The geometry optimization showed an increase of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (from 1.23 to 1.25 Å) and C
O (from 1.23 to 1.25 Å) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths (from 1.33 to 1.38 Å) when π-electron donor substituents were conjugated to the vinyl moiety by weakening the conjugation effect, with the strongest impact attributed to NH2. For some amino and hydroxy derivatives 6–8, the emergence of an intramolecular hydrogen bond with the oxygen or nitrogen lone pair (≈ 25 kcal mol−1) of the N
C bond lengths (from 1.33 to 1.38 Å) when π-electron donor substituents were conjugated to the vinyl moiety by weakening the conjugation effect, with the strongest impact attributed to NH2. For some amino and hydroxy derivatives 6–8, the emergence of an intramolecular hydrogen bond with the oxygen or nitrogen lone pair (≈ 25 kcal mol−1) of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety decreased the C–N bond length and stabilized the cis–cis conformation between the hydroxyl/amino and nitroso moieties, which became more stable than the trans–trans form for 6 and 8. The MHP was applied successfully, yet it did not take such H-bonding interaction into account. Nitrosobutadienes (10 and 11) and nitrosostyrene (12)78 were also analyzed likewise, and the s-trans isomer was confirmed as the most stable one (Fig. 1).
O moiety decreased the C–N bond length and stabilized the cis–cis conformation between the hydroxyl/amino and nitroso moieties, which became more stable than the trans–trans form for 6 and 8. The MHP was applied successfully, yet it did not take such H-bonding interaction into account. Nitrosobutadienes (10 and 11) and nitrosostyrene (12)78 were also analyzed likewise, and the s-trans isomer was confirmed as the most stable one (Fig. 1).
Correction of the basis set superposition error was applied and the computational analyzes of 12 showed a lower chemical hardness and higher dipole moment after dimerization. The conformational study was even more sophisticated for the comparison between 2-nitrosofuran (13) and its nitro analog.79 This time, the most stable conformer was found to be the cis one (OC–NO). The nitroso derivative was also determined to be less stable than its nitro analogous. However, its dimeric structure showed a higher energy interaction. This statement was left unchanged with the inclusion of SCRF for water in the calculation. The authors also reported the calculation of Fukui's indices through Mulliken population analysis. The results spotlighted the carbon atom as the preferred site for interactions with nucleophiles, while the nitrogen of the nitroso moiety was found to be the most reactive towards electrophiles. Another study made by the same team was focused on nitroso substituted benzenes (1,3,5-trinitrosobenzene 14, 1,3-dinitrosobenzene 15, 1,4-dinitrosobenzene 16).80 The comparison between their relative energies enabled to predict an overall order of stability for the corresponding isomers of dinitrosotoluene: 14 > 15 > 16. These molecules were all less stable than their nitro analogs. Three nitroso 1,3-cyclopentadienes (1-nitrosocyclopenta-1,3-diene 17, 2-nitrosocyclopenta-1,3-diene 18, 5-nitrosocyclopenta-1,3-diene 19) were also compared likewise. However, MHP gave unreliable outputs due to high variations of the chemical potential μ between 17–19. The same team similarly considered nitrosocyclopropene (20) and all its positional isomers.81 This time, the corresponding computations relied on a larger basis set with the ab initio MP2 and HF functionals, namely, the 6-311++G** basis set. The potential energy surface (PES) of the eleven stable isomers was constructed but the drastic structural differences between them led to drastic changes in terms of dipolar moments, which precluded the use of the MHP principle. The thermochemistry of these systems was calculated as well, yet the data could not confirm the overall energy trends in terms of stability.
In 1999, Parr et al. developed another reactivity index that correlates μ to η through the electrophilicity index (ω).82ω reflects the stabilization of a given molecule when acquiring electron density (eqn (11)). In this way, compounds could be ranked according to their overall ω as strong (ω > 1.5 eV), moderate (1.5 > ω > 0.8 eV), and weak (ω < 0.8 eV) electrophiles.83 Besides, Parr et al. also defined the overall nucleophilicity (N) as the inverse of ω in such a way that the selection of the best-matching electrophile/nucleophile couples for a specific reaction could be easily determined. However, this assumption was proved to only be accurate for species bearing only one type of substituents, either EWG or EDG.
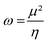 | (11) |
In 2011, Domingo et al. proposed a novel nucleophilicity index N based on the energy of the HOMO and relative to a poor reference nucleophile, tetracyanoethylene (TCE), to better describe captodative ethylenes bearing both EWG and EDG substituents (eqn (12)).84
| N = EHOMO(Nu) − EHOMO(TCE) | (12) |
The calculation at the B3LYP/6-31+G* level of ω indexes for nitrosoethylene derivatives showed that the addition of EDG substituent such as –Ph (12), –MeOPh (21), and –NMe2 (7) do not substantially impact the electrophilic behavior of the molecule compared to 4, ranging from 2.89 for 7 to 3.30 eV for 4 (Fig. 9). However, 7 acts as a better nucleophile than 4, making this species able to efficiently react with both electronic demands. This observation was confirmed by looking at the transition states between this molecule and 2-methylene, 1,3-dioxolane, which is considered as a strongly activated nucleophile, and 1,1-dicyanoethyne, which is at the antipode of reactivity and strongly activated as an electrophile. The activation barriers of these two reactions were found to be low, and the global electron density transfer (GEDT)85 associated to be large, showing a high reactivity of 7. Electron localization function (ELF) analysis based on analysis of electron density pinpointed domains (called basins) with a high probability for electron pairing, supported the GEDT of this polar process and showed the charge stabilization of the TS by the nitroso moiety.
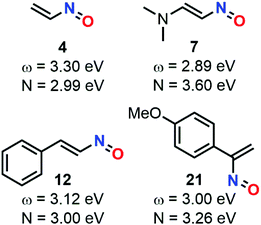 | ||
| Fig. 9 Global reactivity indexes derived from conceptual DFT (electrophilicity ω and nucleophilicity N) for various nitrosoalkenes. | ||
The case of the parent vinyl nitroso 4 was investigated in 2013 by Domingo that proposed a novel localized function i.e. Parr's function (P(r)), to better characterize the most electrophilic and nucleophilic centers of a molecule involved in polar cycloadditions, where bond formation takes place with two zwitterionic pseudoradical species.86 This time, the properties of the radicals (rc for radical cation, ra for radical anion), in terms of atomic spin density (ASD), were used (eqn (13) and (14)).
| P−(r) ≅ ρrcS(r) | (13) |
| P+(r) ≅ ρraS(r) | (14) |
Three localized functions were compared at the B3LYP/6-31+G* level, the Parr function (P), the Fukui function proposed by Parr and Yang (FPY), and the Fukui function implemented by Yang and Mortier (FYM). All functions led to a consensus for the most nucleophilic center which was seen as the oxygen atom whereas, for the most electrophilic one, the results diverged: the P function pinpointed the terminal carbon, while the FPY function and the FYM both concluded that N and O atoms were the most electrophilic centers. However, experimental evidence showed the terminal carbon as the most electrophilic center upon cycloaddition, which was, therefore, better described with Domingo's P descriptor. Using this new descriptor, comparing nitroso 4 to its nitro analog revealed a stronger electrophilicity and nucleophilicity character localized on the nitrogen atom in the nitroso moiety (Table 1).
| Molecule | Atom | P + k | P − k |
|---|---|---|---|
| Nitroethylene | C1 | 0.44 | −0.01 |
| C2 | 0.01 | 0.01 | |
| N 3 | 0.23 | −0.05 | |
| O4 | 0.22 | 0.83 | |
| O5 | 0.16 | 0.20 | |
| Nitrosoethylene (4) | C1 | 0.41 | −0.09 |
| C2 | −0.06 | 0.08 | |
| N 3 | 0.31 | 0.30 | |
| O4 | 0.38 | 0.68 |
From these studies, it can be seen that the unique combination of nitrogen and oxygen in C-nitroso species leads to an intrinsic ambiphilic nature that balances an electrophilic character through the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond but also nucleophilic properties with the lone pairs located both at the oxygen and nitrogen atoms. This shows a marked reactivity profile that differs from their closest nitro (NO2) analogs. The combination of a nitroso moiety with another electronically activating or deactivating substituent (EDG or EWG) does not interfere with its intrinsic reactivity. Depending on the reaction involved, localized functions and indexes can help to determine the most reactive center of this ambiphilic moiety in terms of nucleophilic or electrophilic attack. The use of global indexes is, therefore, less recommended. However, these indexes do not consider the propensity of the C–NO bond to be cleaved in a homolytic way, which opens new perspectives in synthetic organic chemistry.
O bond but also nucleophilic properties with the lone pairs located both at the oxygen and nitrogen atoms. This shows a marked reactivity profile that differs from their closest nitro (NO2) analogs. The combination of a nitroso moiety with another electronically activating or deactivating substituent (EDG or EWG) does not interfere with its intrinsic reactivity. Depending on the reaction involved, localized functions and indexes can help to determine the most reactive center of this ambiphilic moiety in terms of nucleophilic or electrophilic attack. The use of global indexes is, therefore, less recommended. However, these indexes do not consider the propensity of the C–NO bond to be cleaved in a homolytic way, which opens new perspectives in synthetic organic chemistry.
Spectroscopic properties
The presence of n(O) → π*(NO) chromophores gives C-nitroso species unique spectroscopic properties in the visible-light range (Fig. 10). | ||
| Fig. 10 Solid (top) and condensed (bottom) phases of nitrosotoluene (a and b); nitrosobenzene (c and d); N,N-dimethyl-4-nitrosoaniline (e and f). | ||
These colorful compounds can be used as organic dyes, especially nitrosonaphthol derivatives whose change of color after tautomerization is useful for molecular switches. These derivatives can also act as potent ligands with various metals, and the corresponding complexes can be used as pigments, such as Naphthol Green B, an iron(II) complex with 6-hydroxy-5-nitrosonaphthalene-2-sulfonate (22).25,87 The prediction of spectroscopic features, which can be easily implemented with computational chemistry, is, therefore, a strong asset for making tunable dyes.
While vibrational analysis can be performed considering only the GS of molecules, absorption phenomena require computations of the available ES. Despite TD-DFT method was widely used for the computations of UV spectra, Lacombe et al. used a multiconfigurational approach for estimating the spectra of the transition energies of nitrosomethane (23) and trichloro(nitroso)methane (24).88 Using the B3LYP/6-31G* level only for geometry optimization, a weak transition was estimated in the visible range at 2.11 eV for 23 and 2.10 eV for 24, attributed to a 1A′′ state (n(O) → π*(NO)) (Fig. 11). Other absorption peaks have been found but in the UV and far UV ranges.
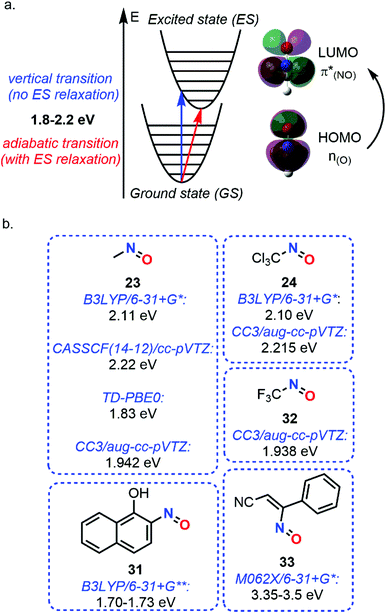 | ||
| Fig. 11 Absorption phenomenon of C-nitroso species. (a) theoretical principle. (b) n(O) → π*(NO) transition energies of various nitroso species. | ||
The use of a single reference was shown to give poorer results compared to multireference approaches since electronic excitation usually involves states mixing or conical/PES intersection, but the last methods are much more demanding. This conclusion was drawn by Godunov et al. when the low-exciting states, including the S1, responsible for the n → π* transition, and the T1 of 23, not visible experimentally, were studied with different ab initio descriptions.89 Electronic excitations to all the excited states of this study (up to T3 and S3 states) were shown to be localized on the nitroso moiety, highlighting the unique optical properties of C-nitroso species. A vertical transition of 2.22 eV (CASSCF(14-12)/cc-pVTZ level) and an adiabatic one of 1.82 eV (average of different multireference approaches) were estimated with relatively large basis sets (Fig. 11). A similar value of 1.76 eV was determined by Soto et al. with the CASPT2 method.29
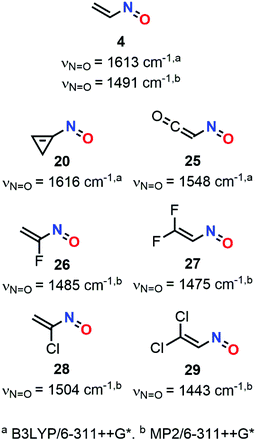
From 2001 to 2005, Badawi and Förner published some papers about the computational elaboration of infrared (IR) and Raman spectra for various nitroso species (Fig. 12).90–94 Based upon computations of vibrational frequencies and relative peak intensities, spectra were constructed considering the natural distribution of the different isomers (depending on their relative thermodynamic stability). Assignments of the peaks could be easily performed through the calculation of the potential energy distribution (PED), except when normal modes were mixed with other ones.
The first studies were carried out at the B3LYP/6-311++G* level. However, MP2 was then found more suitable since MP2 frequencies were known to be overestimated and therefore could be easily scaled while DFT calculations gave over- but also underestimations. Nitrosoketene (25), nitrosocyclopropene (20), nitrosoethylene (4) and its fluoro-(1-fluoro-1-nitrosoethylene 26 and 2,2-difluoro-1-nitrosoethylene 27) and chloro-derivatives (1-chloro-1-nitrosoethylene 28 and 2,2-dichloro-1-nitrosoethylene 29) were studied accordingly. IR spectra were characterized by an intense peak related to N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching centered at 1548, 1616, 1613 cm−1 for 25, 20, and 4 respectively at the B3LYP/6-311++G* level while scaled wavenumbers at the MP2/6-311++G* level for this vibration were located at 1491, 1485, 1475, 1504 and 1443 cm−1 for 4, 26, 27, 28, and 29, respectively. These vibrations were however less visible in Raman spectroscopy compared to C–H or C–X stretchings.
O stretching centered at 1548, 1616, 1613 cm−1 for 25, 20, and 4 respectively at the B3LYP/6-311++G* level while scaled wavenumbers at the MP2/6-311++G* level for this vibration were located at 1491, 1485, 1475, 1504 and 1443 cm−1 for 4, 26, 27, 28, and 29, respectively. These vibrations were however less visible in Raman spectroscopy compared to C–H or C–X stretchings.
In 2006, Jacquemin et al. considered the use of TD-DFT for determining the n → π* transition (λmax) of nitroso species.95 A screening of different basis sets was performed: 6-311G** for geometry optimization (PBE0 functional) and 6-311++G(3d,3p) for the UV spectrum. The λmax calculation (TD-PBE0, 1.83 eV, Fig. 11) showed a really good agreement with the experimental value of 23 (1.82 eV). Therefore, the λmax of 22 NO-bearing compounds including C-, N- and S-nitroso species were analyzed and compared to experimental data when available. The accuracy and small mean absolute error (MAE, 0.05 eV) were attributed to the use of a high basis set and solvent integration in the computation (PCM model). The following trend in terms of transition energy was first attributed to the differences in electronegativity between nitrogen and its neighboring atom and to the LUMO shape: O > N > S > Se > C > P > B > Si.
In 2012, Redi-Abshiro et al. used computational chemistry to confirm the dual fluorescence behavior of N,N-diethyl-4-nitrosoaniline (30).96 The bathochromic shift observed with the solvent polarity was studied by absorption, excitation, and emission spectroscopies and showed two emission bands, one for the locally excited and one for the charge transfer emission. Study at the B3LYP/6-31+G level confirmed the presence of two conformers at the ground state and their relative stability depending on the solvent, explaining the presence of two fluorescence bands.
Janeba, Dračínsky and coworkers published in 2016 a thorough study about the tunable push–pull interaction, also named intra-molecular charge transfer (ICT), arising from the simultaneous presence of the EWG nitroso substituent and the EDG amino substituent on pyrimidine derivatives.97 DFT calculations (B3LYP/6-31+G** including PCM for implicit DMSO consideration) were used to confirm the NMR chemical shifts of various 5-nitrosopyrimidines, but also to determine the high rotational barriers of these two kinds of substituents after ICT, explained also by the formation of stable intramolecular hydrogen bonds with the oxygen atom of the nitroso moiety. The authors stated that the overestimation of the computational data was due to a poor hydrogen-bonding description in the PCM model. TD-DFT helped to assign the two absorptions seen in the UV (π → π*) and visible range (n → π*). The oxidation of the nitroso moiety was also theoretically studied (M06L/cc-pVTZ). Spin densities and EPR parameters calculations with the EPR-II and -III basis sets agree with the high oxidation potential into nitroso radical cations that can be stabilized through the ICT.
The same year, calculations of IR, Raman, and UV spectra of 2-nitroso-1-naphthol (31) were performed by Ragavendran and Muthunatesan.98 Scaling the B3LYP/6-31G** vibrational wavenumbers gave results comparable with the experimental data, with a root mean square error of 9.69 cm−1. N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching was determined theoretically at 1545 cm−1 in Raman and 1572 cm−1 in IR spectra. TD-DFT method at the B3LYP/6-31G** level with PCM integration was used for evaluating a (n → π*) transition of 1.70–1.73 eV depending on the solvent considered (Fig. 11). NBO analyses showed reciprocal interactions π(C
O stretching was determined theoretically at 1545 cm−1 in Raman and 1572 cm−1 in IR spectra. TD-DFT method at the B3LYP/6-31G** level with PCM integration was used for evaluating a (n → π*) transition of 1.70–1.73 eV depending on the solvent considered (Fig. 11). NBO analyses showed reciprocal interactions π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)–π*(N
C)–π*(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and π*(N
O) and π*(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–π*(C
O)–π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) of 36.62 and 24.99 kcal mol−1, respectively.
C) of 36.62 and 24.99 kcal mol−1, respectively.
The description of n → π* transition energies remains a complex task. Several methods were assessed by Jacquemin et al. in 2017 (Fig. 11).99 Among the 16 small selected molecules, three C-nitroso species were included, namely, 23, 24, and trifluo(nitroso)methane (32). The case of these nitroso species was more complex to evaluate than the other classes of compounds and relied on experimental data found in the literature. The determination of the theoretical best estimates with multireference approaches was obtained with the CC3/aug-cc-pVTZ technique, giving vertical transition energies of 1.942 (23), 2.215 (24), and 1.938 eV (32). For single-determinant approaches, comparison between TD-DFT and BSE/evGW methods showed a higher dependency on the exchange–correlation functional for the former technique, especially with the M06 series, but closer results with the CC3 data.
A last example about the computation study of spectroscopic properties of C-nitroso species concerned the characterization of a nitrosoethylene derivative ((Z)-3-nitroso-3-phenylacrylonitrile 33), presumably formed during the photolysis of 5-azido-3-phenylisoxazole.100 Computational IR spectra calculated at the B3LYP/6-31+G* level confirmed the final formation of 33 instead of the corresponding singlet and triplet nitrene intermediates by comparing the frequencies obtained after scaling with the experimental ones determined during photolysis. The same protocol was done for UV-Vis absorption spectroscopy. However, another functional had to be chosen since B3LYP led to wavelength overestimation due to a poor description of weak noncovalent interactions. The CAMB3LYP functional gave the same effect while M062X presented a value close to the experimental one, namely a transition at 356–369 nm (3.35–3.5 eV, Fig. 11). The process leading to the formation of compound 33 was thought to proceed in one step.
This summary about spectroscopic studies of C-nitroso species highlights the complexity related to the description of their characteristic n(O) → π*(NO) transitions (vertical or adiabatic), which requires accurate functionals and basis sets for the TD-DFT analysis, or even a multireference approach. Usually, the energy transitions are in the range of 1.8–2.2 eV and relate to a low-lying excited state. However, vibrational frequencies can be easily computed and enable a simple understanding of the IR and Raman spectra of nitroso species, characterized by a strong N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching located around 1500 cm−1. These spectroscopic features suggest high reactivity from C-nitroso species towards visible light during photochemical reactions.
O stretching located around 1500 cm−1. These spectroscopic features suggest high reactivity from C-nitroso species towards visible light during photochemical reactions.
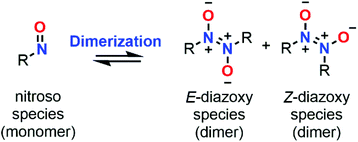
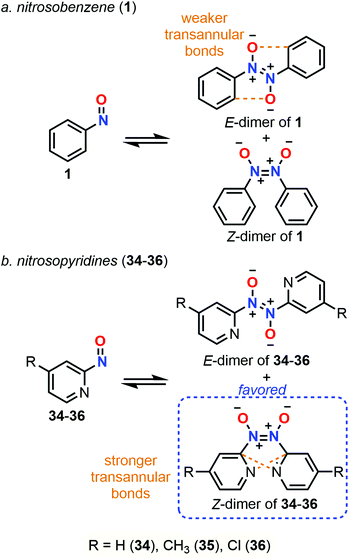
Dimerization properties
C-Nitroso species are known to be involved in a dimerization equilibrium with azodioxy compounds that exist as two E- and Z-structures (Fig. 13).13 This dimerization process strongly influences the likelihood of synthetic organic reactions employing C-nitroso species since it leads to an “inactive” reservoir of dimers, the intrinsic properties of which strongly differ from the monomers (Fig. 13). Dimerization is sensitive to complexation with a variety of metals, where it can form stable bidentate metal complexes.1 Moreover, the instability of the dimeric form of nitrosocarbonyls can lead to irreversible decomposition into the corresponding anhydride with the concomitant release of N2O, according to Kirby's mechanism.2 The dimerization process was mainly studied by structural analysis, especially with low-temperature dynamic NMR spectroscopy13 for thermodynamic and kinetic studies, and focused on nitrosoarenes. However, such analyses turned out to be cumbersome when dealing with additional equilibria such as C–NO rotation, which is known to be fast, leading to peak coalescence or broadening.101–103 Computational chemistry could help to predict or confirm dimerization trends by looking at energy differences between both forms.In 1996, Glaser et al. used computational chemistry to provide insights on why nitroxyl (HNO) and 23 dimerize while their oxime tautomers do not.104 Results showed a strong dependency of the theoretical model, however clear trends emerged: the dimerization is exothermic (ΔH° = −9.99 kcal mol−1 at the QCISD(T)/66-311G** level), slightly endergonic due to a negative entropy (ΔS° = −46.39 cal mol−1 K−1 at the QCISD(T)/66-311G** level) and characterized by a short N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond relative to a marked double character, which is even more pronounced in the Z isomer. The NBO analysis highlighted an increase of the N
N bond relative to a marked double character, which is even more pronounced in the Z isomer. The NBO analysis highlighted an increase of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O polarity during the course of the reaction, which is sensible to substituents since adding a methyl substituent in 23 increased even more the negative charge located at the oxygen atom. This observation was confirmed by showing that dimeric forms have a higher dipole moment than the monomeric ones. This charge transfer was considered the driving force of this reaction. Therefore, the authors stated that, while azodioxy compounds can easily accommodate the excess of charge on the oxygen atom, the oxime tautomers are less efficient in such accommodation due to the presence of the diol moiety, which explains why their dimers cannot be formed.
O polarity during the course of the reaction, which is sensible to substituents since adding a methyl substituent in 23 increased even more the negative charge located at the oxygen atom. This observation was confirmed by showing that dimeric forms have a higher dipole moment than the monomeric ones. This charge transfer was considered the driving force of this reaction. Therefore, the authors stated that, while azodioxy compounds can easily accommodate the excess of charge on the oxygen atom, the oxime tautomers are less efficient in such accommodation due to the presence of the diol moiety, which explains why their dimers cannot be formed.
The preliminary explanations about the natural dimerization of 23 was later extended to 40 other C-nitroso species in 2016 by Novak.27 Three subclasses were identified depending on the interactions between molecules, namely no interactions (most of all alkylated nitroso compounds), intramolecular interactions (polyarylated nitroso compounds), and intermolecular interactions (1 and its derivatives). Using the G4MP2 method, thermochemistry data were obtained in the gas phase and compared with experimental data from the condensed or solid-states. Dimerization was generally found to be thermodynamically unfavorable due to reduced entropy, especially for nitrosoarenes, while the E-dimer was favored over the Z form. The first statement did not agree with the dimer/monomer ratio determined in the solid phase for 1 and its derivatives, where the dimeric form is predominant. Structural changes in terms of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N
O and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N lengths as well as CCNO angles, and variations of the N
N lengths as well as CCNO angles, and variations of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond polarization between solid and gas phases emphasized the importance of π-stacking and direct electrostatic interactions between polarized atoms, such as π-delocalization, for stabilizing the dimeric species at the solid or condensed phased. These observations helped also to rationalize factors impacting the relative stability of the Z-form in solution.
O bond polarization between solid and gas phases emphasized the importance of π-stacking and direct electrostatic interactions between polarized atoms, such as π-delocalization, for stabilizing the dimeric species at the solid or condensed phased. These observations helped also to rationalize factors impacting the relative stability of the Z-form in solution.
Vančik et al. showed however in 2018 the poor accuracy of the G4MP2 method used previously during a study of the monomer-dimer equilibria of 1 and three nitrosopyridines (2-nitrosopyridine 34, 4-methyl-2-nitrosopyridine 35, and 4-chloro-2-nitrosopyridine 36).103 Comparison of various computational data obtained with different methods with experimental data showed large MAE values for the post-HF methods and the composite ones that include these ab initio methods. The authors specifically pointed out the great difficulty to obtain reliable potential energies. Accurate results with DFT were however only accessible with dispersion correction, especially for double-hybrid functionals (B2PLYP-D3, PBE0DH, and DSD-PBEB86) with MAE < 1 kcal mol−1. The hybrid PBE0 functional offered also accurate results (MAE = 0.5 kcal mol−1) in a much faster way than its double-hybrid counterparts. Calculations highlighted a highly exothermic process with a large negative entropy but different trends could be determined for 1 and 34–36 at the gas and condensed phase (use of SMD for CHCl3 and DCE integration). On the one hand, the E-conformer of 1 dimer is favored only in the gas phase (ΔG‡E = 4.2 kcal mol−1 and ΔG‡Z = 7.5 kcal mol−1), the weak stabilizing transannular bond (order of magnitude of a weak hydrogen bond) of the E-conformer being counterbalanced by the solvent interactions at the condensed phase (ΔG‡E = 2.7 kcal mol−1 and ΔG‡Z = 2.3 kcal mol−1). On the other hand, three conformers of both Z- and E-form can be determined for 34–36 (Fig. 14). One of the Z-conformer is found to be the most stable in both phases due to two transannular bonding interactions. The bonds formed between two nitrosopyridines are much stronger than between two nitrosobenzene molecules, resulting in a favorable dimer formation even at room temperature (ΔG‡Z = −1.5 and −3.3 kcal mol−1 in the gas and condensed phase, respectively).
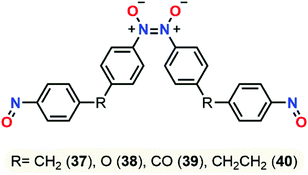
The same year, this group published a study about dimerization and polymerization of 4 dinitroso compounds (bis(4-nitrosophenyl)methane 37, 4,4′-oxybis(nitrosobenzene) 38, bis(4-nitrosophenyl)methanone 39, 1,2-bis(4-nitrosophenyl)ethane 40).105 NMR chemical shifts of monomeric and dimeric forms were calculated and compared with the data from comparative experiments. B3LYP-D3/6-311+G(2d,p) was found to be the best model compared to wB97X-D and TPSSH functionals, especially for the chemical shifts of the Z-dimer that were best described in chloroform using the SMD model. Energies and enthalpies pointed out the Z-dimer as the most stable conformer, yet they failed to give an accurate population representation between the Z and E dimeric forms due to exclusion of entropic factors in this study (Fig. 15). Experimental and computational negative enthalpy data were closed and explained the higher predisposition of dimerization at low temperatures.
Since stabilization of dimeric forms of C-nitroso species is influenced by intra- and intermolecular interactions, solvation and DFT dispersion integration is necessary to accurately predict and understand nitroso organic reactions. Solvent interactions can explain why some Z-dimers are the major forms in solution despite their inherent repulsions while strong N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds such as with the dimers of nitrosopyridine derivatives could also always lead to dimerization. Due to an exothermic but ordering process, favored dimerization at low temperatures can be avoided at higher temperatures, which also requires to consider the temperature during the computational analysis.
N bonds such as with the dimers of nitrosopyridine derivatives could also always lead to dimerization. Due to an exothermic but ordering process, favored dimerization at low temperatures can be avoided at higher temperatures, which also requires to consider the temperature during the computational analysis.
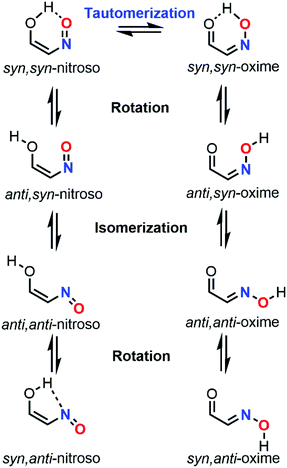
Tautomerization properties
When a nitroso moiety is near to a hydroxyl group, a tautomerization process can occur to give the corresponding oxime derivative through a 1,5-H shift (Fig. 16). As for the dimerization process, the formation of an oxime tautomer deeply influences the reactivity and selectivity of the outcome of the reaction. In addition to this equilibrium, the rotation of the O–H bond, as well as the C–N or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, leads to various rotamers for both species. Eight related species can be therefore considered during a nitroso tautomeric equilibrium. NMR spectroscopy was often relied on for studying this process, yet the presence of multiple equilibria with different kinetics makes the study cumbersome, especially when fast equilibria are involved, hence leading to peak coalescence.106 Such complexity explains the reason why NMR data are always supported with computations within this specific context. Computational chemistry can be a useful tool to predict or confirm the identity of the tautomers present in solution through the determination of their energy differences, as well as their corresponding activation energies (tautomerization, isomerization, and rotation barriers).
N bond, leads to various rotamers for both species. Eight related species can be therefore considered during a nitroso tautomeric equilibrium. NMR spectroscopy was often relied on for studying this process, yet the presence of multiple equilibria with different kinetics makes the study cumbersome, especially when fast equilibria are involved, hence leading to peak coalescence.106 Such complexity explains the reason why NMR data are always supported with computations within this specific context. Computational chemistry can be a useful tool to predict or confirm the identity of the tautomers present in solution through the determination of their energy differences, as well as their corresponding activation energies (tautomerization, isomerization, and rotation barriers).
The first computational investigations of the nitroso tautomerization process were performed by Enchev and coworkers by looking at polycyclic aromatic hydroxynitroso species. On the one hand, 3-hydroxy-2-nitroso-1-phenalenone (41) and 2-nitroso-1,3-indandione (42) were studied in 1998 with the ab initio method HF and two basis sets (3-21G* and 6-31G**, Fig. 17).107 A zero potential energy (ZPE) correction scaled by a factor of 0.893 was added to the energies obtained with the 6-31G** basis set for a better description. The syn,syn-oxime of 41 was found to be the most stable tautomer compared to the syn,syn-nitroso, and anti,syn-oxime forms respectively by 7.14 kcal mol−1 and 4.23 kcal mol−1. The same conclusion was obtained for 42, with stabilization energies of 14.22 kcal mol−1 and 1.02 kcal mol−1 compared to the syn,syn-nitroso, and anti,syn-oxime forms, respectively. The barrier of rotation (ΔE) between the syn,syn and anti,syn forms was calculated to be 10.56 kcal mol−1 for 41 and 9.70 kcal mol−1 for 42. The higher barrier for 41 was explained by the presence of an intramolecular bond, which was not found in 42 when looking at the optimized geometries. When DMSO was implicitly included in the computations through the Onsager reaction field method (SCRF model), the barrier energies increased slightly. On the other hand, 2-nitroso-1-acenaphthylenol (43) was investigated with the same methodology in 1999 (Fig. 17).108 The syn,syn-oxime was 18.4 kcal mol−1 more stable than the syn,syn-nitroso with a barrier of 2.4 kcal mol−1 leading to the first tautomer. The anti,anti-oxime was found to be slightly more stable than its isomeric syn,syn form. However, the isomerization barrier was found to be rather high (12.5 kcal mol−1), explaining the presence of two peaks in the 1H NMR spectra. The anti,syn-oxime rotamer had, however, a smaller barrier to overcome, namely, 8.0 kcal mol−1, but was found to be 2.0 kcal mol−1 higher in energy than its syn,syn rotamer. The rotation barrier of the nitroso bond was determined to be 17.4 kcal mol−1. Tautomerization, isomerization, and rotation barriers increased when the polarity of the solvent increased.
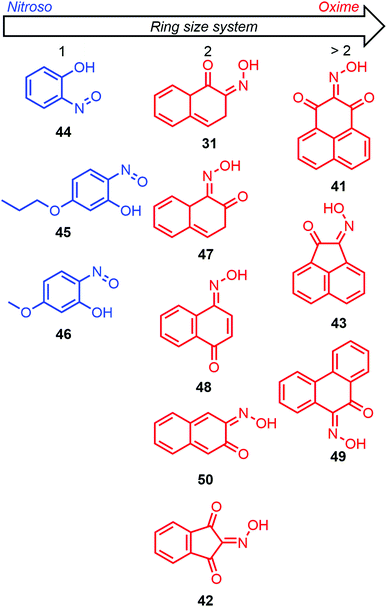 | ||
| Fig. 17 Representation of the most stable tautomer for various hydroxynitroso species depending on their ring size system. In blue: nitroso tautomer. In red: oxime tautomer. | ||
A report on the tautomerization of nitrosophenols (2-nitrosophenol 44, 2-nitroso-5-propoxyphenol 45, and 5-methoxy-2-nitrosophenol 46), nitrosonaphtols (2-nitroso-1-naphthol 31, 1-nitroso-2-naphthol 47, and 4-nitroso-1-naphthol 48) and 9-nitroso-10-phenanthrol (49) was detailed in 2000 by Kržan and coworkers (Fig. 17).109 The data obtained at the HF/6-31G level were systematically compared with experimental structural analysis (X-Ray, NMR and IR) data from the literature. The calculated properties were better described when polarization functions were added (6-31G*). The results showed that the syn,syn-oxime form was more favored when the ring size system increased. However, while computations gave good estimations for nitrosophenols 44–46 and 49, where the syn,syn-nitroso and the syn,syn-oxime were the most stable forms respectively, the case of nitrosonaphtols 31, 47, and 48 was less in adequation with experimental evidence, which emphasized the syn,syn-oxime form as the most stabilized tautomer. The authors rationalized this discrepancy by a poor computational description of intramolecular H-bonding that was underestimated with this method, especially for the syn,syn-oxime form. In the absence of any intramolecular H-bonding, higher energies were computed for the anti,syn-oxime rotamer compared to the syn,syn form.
The same team tried later to demonstrate that the tautomeric equilibrium of 31 was not responsible for the peak splitting visible by NMR spectroscopy.106 The energy barrier between the syn,syn-nitroso, and syn,syn-oxime was calculated to be only 1.47 kcal mol−1 in favor of the last one, which was more stable by 2.68 kcal mol−1 at the B3LYP/6-31+G* level (or 2.64 kcal mol−1 with the MP2 method). The authors assumed that such a low barrier was responsible for the appearance of a single peak on the experimental spectra. They calculated an experimental activation energy leading to a splitting of minimum 12.7 kcal mol−1. C–N internal bond rotation leading to the anti,anti-oxime was stated as the pathway giving the second visible peak since the anti,anti-form was more stable by 7.5 kcal mol−1 compared to the syn,syn form. The HF, MP2, and B3LYP/6-31G* calculated barriers were 70.8, 51.8, and 49.4 kcal mol−1, respectively, which confirmed the presence of two peaks. When both implicit (SCRF model) and explicit (one molecule of DMSO) solvations were included, the barrier was reduced to 44.9 kcal mol−1.
In 2001, Enchev et al. investigated the tautomeric equilibrium of o-nitrosonaphtols, namely, 47 and 31.110 Calculations at the HF/6-31G** level for optimizations and at the MP4(SDQT)/6-31G** level for energies calculations, including electron correlation in condensed state (PCM model), confirmed the trends determined in this study by NMR spectroscopy. The syn,syn-oxime of 47 was determined as the most stable form in the gas, solution, and solid states while for 31, the anti,syn-oxime was as stable as the syn,syn-tautomer in solution and even became the predominant form in the solid-state. The tautomerization process from the nitroso form arises from an intramolecular proton transfer, which explains the strong impact of adding electron correlation during computation on the calculated energies. Rotamers (syn–anti) of the corresponding oximes have been also included in the computational study. In the gas phase, the rotation barrier is larger than the one related to tautomerization, though, in solution, the trend is inverted, with a smaller energy gap between the various rotamers when the solvent polarity increased.
For a better description of H-bonding in the condensed phase, Lammertsma et al. decided not only to include implicit solvation through the SCIPC model (SCRF), but also to explicitly add two molecules of water to the system for studying the tautomerism process of 23.111 They first evaluated the equilibrium at the gas phase using the MP2/6-311+G**, HF/6-31+G*, and B3LYP/6-311+G** models. The results with the first model gave geometrical features close to the experimental data from the literature. The anti-oxime was found to be stabilized by 5.0 kcal mol−1 compared to its syn-conformer, which is characterized by a lone-pair-lone-pair repulsion, and by 12 kcal mol−1 compared the nitroso tautomer. The explicit addition of two molecules of water increased the energy difference (ΔE) between the two tautomers (17.16 kcal mol−1) due to stronger hydrogen bonds for the anti-oxime, and increased even more (17.44 kcal mol−1) when the SCIPCM model was utilized for the computations.
The results from Kržan et al. about the tautomerization of 31 and 49 were confirmed at the MP4/6-311G* + ZPE level by Enchev et al. in 2003.112 On the one hand, the calculations showed that the syn,syn-nitroso of 31 was more stable by 4.2 kcal mol−1 compared to its syn,syn-oxime tautomer. The rotamer syn,anti-nitroso was also found to be nearly isoenergonic (ΔE = 0.26 kcal mol−1). Its isomer anti,anti-oxime could also coexist since it was more energetic by only 0.75 kcal mol−1. On the other hand, the syn,syn-oxime tautomer of 49 was preferred by 8.56 kcal mol−1. Its isomer anti,syn-oxime was less stable by 1.64 kcal mol−1 and the anti,anti rotamer also increased by 0.69 kcal mol−1. The tautomerization barrier from the nitroso to the oxime form was calculated to be 10.24 kcal mol−1 for 31 and 2.4 kcal mol−1 for 49. Rotational barriers were also calculated and decreased with the solvent polarity when implicit and explicit solvations were included. A stable complex with DMSO led the anti–anti oxime of 49 to be the most stable tautomer in this medium instead of the syn,syn-oxime.
In 2005, Raczyńska et al. analyzed the relation between π-electron delocalization and stability in the tautomeric equilibrium of 44.113 Calculations of the HOMA (harmonic oscillator model of aromaticity) and NICS (nucleus independent chemical shift) indexes that reflect π-electron delocalization were performed at the B3LYP/6-311+G(2d f, 2p) and HF/6-31+G* levels, respectively. The pull-push effect between the EDG OH substituent and the EWG N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety was found to destabilize the tautomeric species while the aromaticity was responsible for an increased stabilization. The presence of an intramolecular H-bonding for some forms of the equilibrium weakened this pull-push interaction, which explained the increased stability of the syn,syn-nitroso, followed by the syn,anti-nitroso (2.8 kcal mol−1), and the syn,syn-oxime (3.2 kcal mol−1). The other species were however much more destabilized (>9 kcal mol−1) due to a more pronounced localization of the π-electron structure.
O moiety was found to destabilize the tautomeric species while the aromaticity was responsible for an increased stabilization. The presence of an intramolecular H-bonding for some forms of the equilibrium weakened this pull-push interaction, which explained the increased stability of the syn,syn-nitroso, followed by the syn,anti-nitroso (2.8 kcal mol−1), and the syn,syn-oxime (3.2 kcal mol−1). The other species were however much more destabilized (>9 kcal mol−1) due to a more pronounced localization of the π-electron structure.
2-Nitrosophenol (44) and nitrosonaphtols (1-nitroso-2-naphthol (47), 2-nitroso-1-naphthol (31), and 2-nitroso-3-naphthol (50)) were again studied by Enchev et al. in 2007 mainly at the B3LYP/6-311++G** level to evaluate the nature of intramolecular hydrogen bonding in the tautomeric equilibrium (Fig. 17).114 The syn,syn-nitroso of 44 was found to be the most stable conformer while the syn,syn-oxime form was preferred for 31, 47, and 50. In each case, the energy demand for a proton transfer in the tautomeric equilibrium was higher than for bond rotation. The change of bond length, electron density, and charge distribution when water was included in the computation (PCM model) showed a weakening of the hydrogen bonding strength in polar solvents. The energy to form this bond was larger for the nitroso form than for the oxime one. NBO, AIM and MO studies confirmed the stronger hydrogen bonding in oxime forms due to a greater electron redistribution and density as well as a strong second-order interaction (nO(π) → σ*O–H; 4.19 kcal mol−1). The drawing of MO showed that the proton-transfer process was less favored for 44 than for 31, 47, and 50. The AIM analysis at bond critical points (BCP) revealed that hydrogen bonds were all considered as strong.
A computational study by the same team was published in 2009 about the tautomerization process of 4-nitroso-pyrazolones (3-methyl-4-nitroso-5-pyrazolone (51) and 1-ethyl-3-methyl-4-nitroso-5-pyrazolone (52), Fig. 18).115 Energetics with different functionals (B3LYP, HF, MP2, and MP4 with the 6-31+G** and 6-311+G** basis sets) showed that these two species could be found with their most stable syn,syn-oxime form. Solvent incorporation with the PCM model highlighted also the anti,anti-oxime to be nearly isoenergetic with the first tautomer but only for 51, meaning that these two isomers could be detected in solution. The theoretical results were in accordance with the corresponding experimental NMR results.
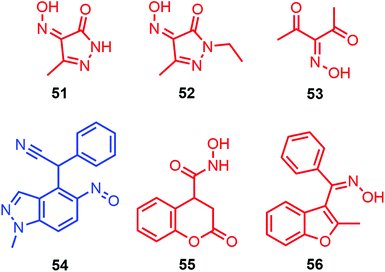 | ||
| Fig. 18 Representation of the most stable tautomer for various nitroso species. In blue: nitroso tautomer. In red: oxime tautomer. | ||
A recent computational study about nitroso tautomerization was reported in 2020 by Eshghi et al. when considering 3-nitroso-2,4-pentanedione (53).116 Calculations at the B3LYP/6-311++G** level including implicit solvent consideration (PCM model) revealed the syn,syn-oxime of 53 to be more stable than its syn,syn-nitroso tautomer (Fig. 18). The hydrogen bonding in such a conformation was determined to be 21.0 kcal mol−1, thus 4–6 kcal mol−1 lower than the ones found in its nitro analogs. The weakening of this intramolecular bonding was confirmed experimentally and computationally by analyzing geometry changes, hydrogen bond strengths, proton chemical shifts, and vibrational modes. NBO calculations highlighted that a difference in conjugation effect, where π-electron delocalization was determined in the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NOH fragment (oxime form) instead of HO–C
NOH fragment (oxime form) instead of HO–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–NO as found in the nitro analogs, was responsible for the reduction of the bonding strength.
C–NO as found in the nitro analogs, was responsible for the reduction of the bonding strength.
Recently, theoretical energetics concerning tautomerization were also included in papers that described the mechanism elucidation of multi-step processes (Fig. 18). In 2016, the combination of DFT and TD-DFT helped to understand the natural color change of the medium (green → blue in two days at r.t.) resulting from the oxime → nitroso process leading to the stable dye 2-(1-methyl-5-nitroso-1H-indazol-4-yl)-2-phenylacetonitrile (54).117 Two years later, a report about the 3-step synthesis of pyrrolidinedione derivatives showed that the nitroso coumarin derivative (4-(hydroxy(nitroso)methyl)chroman-2-one 55) synthesized through a Nef-type rearrangement was found to be less stable than its oxime tautomer, leading to a tautomerization process with a barrier height of 42.6 kcal mol−1 (MP2/6-311+G* level) when a molecule of water, acting as a proton shuttle, was explicitly included in the calculations.118 In 2021, an article related to a 4-step process for the synthesis of ketoximes revealed that the model nitroso alkene intermediate (Z)-2-methyl-3-(nitroso(phenyl)methylene)-2,3-dihydrobenzofuran (56) favorably led to its oxime tautomer with a barrier height of 11.8 kcal mol−1 (with the incorporation of the SMD model for implicit solvation in THF).119 This fast 1,5-H shift was triggered by aromatization to access the ketoxime and avoided product degradation.
Since nitroso tautomerization process is triggered by intramolecular hydrogen bonding, the incorporation of electron correlation and polarized functions is necessary to determine the most stable tautomer. A good computational description of aromaticity or second-order interactions through the NBO analysis is useful for predicting the extent and the nature of the equilibria. Usually, the syn,syn-oxime form is preferred over the syn,syn-nitroso tautomer due to a stronger hydrogen bonding, except for small aromatic systems such as 2-nitrosophenol where aromaticity prevails over hydrogen bonding strength (while for polyaromatic systems, at least one cycle of the oxime tautomer keeps this aromaticity). The presence of rotamers or isomers has to be considered for each case, especially in polar solvents where stable complexes can be formed. Implicit solvation is therefore usually not sufficient and explicit addition of a few solvent molecules is recommended during computation.
Radicalar properties
C-Nitroso species have unique radicalar properties. On the one hand, these species are known to potentially act as nitric oxide (NO) donors (Fig. 19). On the other hand, they can also abstract an electron or can accept the addition of radicalar species to give nitroxyl radicals. Some examples have illustrated their use for the synthesis of secondary amines and N-heterocycles.23 While the second topic has not been explored computationally, the first one led chemists to calculate the likelihood of such C-nitroso species to undergo homolytic cleavage. Such a line of research is useful for biological applications aiming at a controllable, “on-demand” release of NO, but also for understanding the unwanted thermal decomposition that occurs during organic reactions.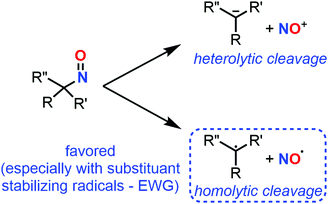 | ||
| Fig. 19 Competitive heterolytic and homolytic cleavages of C-nitroso species, releasing nitrosonium ion and radical nitric oxide respectively. | ||
The unimolecular decomposition of 1 into nitroxide (NO) and phenyl radicals was studied in 1997 by Lin et coworkers, both experimentally and computationally.120 According to the authors, the G2 M(rcc,MP2*) and G2 M(RCC,MP2) methods gave the most reliable results of the C–N bond dissociation energy (BDE), namely 53.8 and 55.4 kcal mol−1, respectively (Fig. 20). These values were similar to the experimental result (54.2 kcal mol−1) obtained by FTIR spectrometry (experiments at 553 and 648 K). The energies obtained with the (U)MP2 functional were overestimated due to a high spin contamination where mixture between high spin states with the singlet state is feasible. The corresponding equilibrium constant was determined to be 2.93 × 10−5 × exp(56 093/RT) cm3 mol−1.
In 2002, Guo, Liu and coworkers investigated with a high level of theory the homolytic dissociation energies for various nitroso species including alkylated nitroso compounds (Fig. 20).121 Composite G3 and CBS-Q methods afforded reliable BDEs values with an error ranging to 1–2 kcal mol−1, while RMP2 and composite CBS-4 M functionals led respectively to under- and overestimation. The low-computational cost UB3LYP method was found to underestimate the values for highly conjugated systems such as for (nitrosomethyl)benzene (56) and 1-nitrosopropan-2-one (57). Such systems witnessed a decrease in the BDE value due to a higher radical stabilization. A trend emerged from the study of various nitroso compounds: BDES–NO (≈ 30 kcal mol−1) < BDECH2–NO (≈ 40 kcal mol−1) < BDEO–NO (≈ 43 kcal mol−1) < BDENH–NO (≈ 48 kcal mol−1). The solvent effect had a higher impact for C- and N- than for O- and S-nitroso species. The substituent effects on the BDE value for C–NO systems clearly differed from C–H ones (ρ+C–H = 0.4 vs. ρ+C–NO = −0.9).
A similar conclusion was drawn in 2009 by Cheng et al. where computational results confirmed the experimental BDEs obtained in acetonitrile, which were found to be around 30 kcal mol−1 smaller than energies associated with heterolytic dissociation (Fig. 19).122 Results at the MP2/6-311+G** level led to BDEs from 26.8 to 34.2 kcal mol−1, while the BP86/6-31G* method gave values ranging from 23.8 to 28.3 kcal mol−1 for the eight alkylated nitroso species considered. These methods gave deviation of +2.4 and −3.0 kcal mol−1 respectively, showing a good agreement with the experimental results.
The release of neutral nitric oxide was also reported by Toone et al. in 2009, where α-cyanonitroso species were found to deliver selectively single redox form of NO through radicalar decomposition.123 Computations at the (U)B3LYP/6-31G* energy (open-shell species) and with the CBS-QB3 method showed that EWG substituents or substituents (such as CN and CHO) leading to radical stabilization through delocalization could decrease the C–N homolytic BDEs to 26–29 kcal mol−1, compared to nitrosomethane (23) or tert-nitrosobutane (3) that have BDEs or 36.0 and 40.8 kcal mol−1, respectively (Fig. 20). The stability of the cyanoalkyl radical decreased the rate of trapping with another α-cyanonitroso molecule which limited the yield of NO. Moreover, due to their weak acidic character, α-cyanonitroso compounds, it was clearly demonstrated that they could not generate nitrosonium (NO+) ions instead of NO (Fig. 19). Dimerization was also considered in the computational study and was shown to be endergonic and therefore disfavored in solution. All these results were confirmed experimentally through the quantification for the release of NO. In these experiments, the rate of NO release was found to be rather independent of solvent polarity. Further attempts to detect NO+ ions failed and additional biological activity assays led the authors to conclude that NO was solely released. The experimental BDEs were found to be similar to the computed values (23.0–23.3 kcal mol−1).
From these studies, it became clear that most C-nitroso compounds bearing a variety of radical stabilizing substituents could potentially be considered as NO-donors. A few years later, Katritzky et al. reported the synthesis of a new kind of geminally functionalized nitroso compounds bearing a 2-benzotriazoyl moiety (Fig. 20).124 By combining lead tetraacetate and 1H-benzotriazole with cyclohexanone oxime, a monomeric nitroso derivative 58 was obtained, and its structure was confirmed by single-crystal X-ray diffraction and computational (B3LYP/6-31+G*) analysis. Despite a theoretical global electrophilicity, ω, similar to its chloro- and acetoxy-analogs, 58 however suffered from a lack of reactivity towards dienes, which the authors could explain this lack of reactivity through a competitive oxidation into its nitro analog, which was less prone to be involved in NDA reactions. Kinetics experiments revealed a moderate sensitivity to solvent polarity for the disappearance of 58. The computation of one-electron redox potentials, homolytic BDEs, isodesmic heat, and radical stabilization energies supported a two-step mechanism. A preliminary homolytic rupture of the C–NO bond (characterized by a BDE close to the ones reported for α-cyanonitroso species) released NO and a tertiary [2-benzotriazoyl]cyclohexane radical species was subsequently followed by the oxidation of NO into a NO2 radical and its recombination with the stabilized 2-benzotriazolalkyl radical to give the corresponding α-[2-benzotriazoyl]alkyl nitro derivative.
Computational chemistry revealed that C–NO bonds are much likely to be cleaved according to a homolytic process. Calculations of bond dissociation energies require a high level of theory and the use of unrestricted methods for an accurate description of radicals. However, this can lead to spin contamination and impacts the computed energies; this can however be solved by spin projection. Since C-nitroso species are characterized by homolytic bond dissociation energies lower than other nitroso species, this radical pathway becomes competitive upon their utilization as electrophiles such in a variety of reactions. Therefore, the calculation of BDEs is recommended to evaluate the impact of such radical side-reaction on the expected reaction outcome and selectivity. The predominance of this radicalar process mostly depends on the ability of the vicinal carbon-based backbone to stabilize radicals. This stabilization is favored with EWG substituents and through delocalization.
Computational studies of the nitroso reactivity
Nitroso Diels–Alder reactions
The nitroso Diels–Alder (NDA) reaction is a versatile synthetic tool affording 1,2-oxazine scaffolds that can be easily functionalized into a wide range of aminated or oxygenated derivatives. This category of hetero- or Polar Diels–Alder (PDA) reactions follows a similar outcome than the classical Diels–Alder reaction, which can be defined by a one-step, asynchronous, [4 + 2] cycloaddition (Fig. 21a). The asynchronicity of the mechanism is mostly related to the nature of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Due to their electrophilic properties, most of the C-nitroso are involved as heterodienophiles in normal electron demand NDA reactions (Fig. 21b). The only exception stands for nitrosoalkenes, where the unique combination of the N
O bond. Due to their electrophilic properties, most of the C-nitroso are involved as heterodienophiles in normal electron demand NDA reactions (Fig. 21b). The only exception stands for nitrosoalkenes, where the unique combination of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety vicinal to a C
O moiety vicinal to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond confers an ability to act as an electron-poor heterodiene, hence leading to inverse electron demand (Fig. 21c) with electron-rich dienophiles. Usually, NDA reactions are highly regioselective and can be enantio- or diastereoselective in rigid molecules where the nitrogen atom of the oxazine pattern becomes stereogenically stable. The use of NDA reactions in synthetic organic chemistry has been already widely reviewed.16–20 This specific area of research for C-nitroso compounds was widely documented with dual experimental/computational studies. Computations were very supportive for collecting insights on the reaction mechanism, solvents effect, regio- and stereoselectivity, hence helping rationalization of the experimental observations or at least stimulating the chemist's imagination. This section emphasizes how computation chemistry was utilized to provide cost and time-saving insights through accurate predictions.
C bond confers an ability to act as an electron-poor heterodiene, hence leading to inverse electron demand (Fig. 21c) with electron-rich dienophiles. Usually, NDA reactions are highly regioselective and can be enantio- or diastereoselective in rigid molecules where the nitrogen atom of the oxazine pattern becomes stereogenically stable. The use of NDA reactions in synthetic organic chemistry has been already widely reviewed.16–20 This specific area of research for C-nitroso compounds was widely documented with dual experimental/computational studies. Computations were very supportive for collecting insights on the reaction mechanism, solvents effect, regio- and stereoselectivity, hence helping rationalization of the experimental observations or at least stimulating the chemist's imagination. This section emphasizes how computation chemistry was utilized to provide cost and time-saving insights through accurate predictions.
An early report about NDA reaction was written by Jursic in 1995 where the theoretical study of the BH3-catalyzed reaction between ethylene and 4 was reported.125 The most stable complex featured chelation between boron and the nitrogen atom of 4 in its s-cis conformation (Fig. 1). The authors reported an inverse electron demand for the reaction where the HOMO of the dienophile, namely ethylene, reacted with the LUMO of diene 4. The catalytic effect of borane arose from a decreased LUMO energy. The NDA was also characterized by a one-step asynchronous mechanism. Energies computed at the MP3/6-31G* level showed a lower activation barrier with 4 in its s-cis conformation and with B–N complexation.
One year later, Fabian and coworkers aimed at understanding the competitive pathways in electrocyclic reactions and cycloadditions by considering the simplest model reaction between 4 and ethylene (inverse electron-demand NDA).126 Energies and geometries were computed at the RMP2/6-31G* level for electron correlation which were built upon preliminary findings with the PM3 semi-empirical method and restricted HF ab initio method. The s-trans conformation of 4 was determined as the most stable (Fig. 22). Ring closure to 4-membered rings was found to be more favored than to 3-membered rings, while one-step cycloaddition leading to 6-membered rings (C–O bond formation) led to a smaller activation energy than for 5-membered rings (C–N bond formation). These reactions were not highly sensitive to solvent effects (SCRF model), and both MPA and NPA charges (only on the reagents) confirmed this observation by showing low dipole moments.
The conformational switches in transition states of inverse electron demand NDA reactions between enol ethers with different dienes, among which compound 4, were investigated by Houk et al. in 1998 at the RHF/3-21G and B3LYP/6-31G* levels.127 The s-trans endo structure for the one-step asynchronous transition state was favored for the reaction between 4 and methyl vinyl ether due to a stabilizing orbital interaction (nO → σ*CO from 4 to the enol ether) for the endo selectivity and to a smaller steric hindrance for the s-trans conformation. This selectivity showed the strength of these electrostatic interactions that were able to change the conformation of the enol ethers from s-cis in the ground state to s-trans in the transition state. On the contrary, the steric hindrance characterized by the silyl moiety in silyl vinyl ether changed the selectivity towards the s-trans exo transition state. However, the selectivity between the s-trans and s-cis conformations was less pronounced in the condensed state (SCRF model for solvation). These effects were less pronounced with a less polar diene (such as butadiene) due to a higher dipole moment of the s-cis conformation. The selectivity towards the s-trans conformation was confirmed experimentally with conformationally frozen enol ethers. This selectivity also rationalized the π-facial stereoselectivity in cycloadditions involving chiral enol ethers.
Due to an ever-increasing interest in NDA reactions, Houk et al. studied the nature of the mechanism, as well as the regioselectivity for nitroso species involved in normal electron demand processes.128 Computations with the B3LYP and MP2 functionals of different reactional pathways highlighted a favorable asynchronous one-step mechanism with a higher asynchronicity for the endo transition state. The presence of a diradical or zwitterionic pathway was however not rejected when nitroso species bearing smaller substituents that allow reaction with substituted dienes. The endo path was favored due to minimization of electrostatic repulsions between the nitrogen lone pair (nN) and the π electrons of the diene (πC); in contrast, in the exo transition state, the presence of these electrostatic interactions had a deleterious impact on the activation barrier (Fig. 23).
 | ||
| Fig. 23 Comparison between an endo (left) and an exo (right) approach during a normal electron demand nitroso Diels–Alder reaction. | ||
These repulsive interactions are usually referred to as the “exo lone pair effect” and were actually reported earlier with nitrosyl hydride, HNO. HNO is considered as the simplest model of nitroso species and was studied in two papers from the same team,129,130 where a comparison with other dienophiles highlighted the high reactivity of nitroso species due to a high electrophilic character. An alternative explanation of the selectivity toward the endo product was proposed by the authors and relied on FMO interactions. The authors argued that the minimization of the symmetry forbidden interaction between the HOMO of both reagents (antibonding combination of N and O lone pairs for nitroso species and πC for the diene) was likely responsible for the endo selectivity. In addition, a lower ΔH‡ and a higher ΔH° were calculated for reactions involving formylnitroso due to the formation of a highly stabilized amide rather than an amine, as expected for other C-nitroso species. Concerning the regioselectivity, a comparison between experimental and computational data enabled the generalization of some trends: (a) the selectivity with 2-substituted diene was less pronounced than with 1-substituted ones, (b) the presence of the largest orbital coefficient at the fourth position for 1-substituted dienes enabled an ortho preference, with a stronger selectivity when the substituent is electron-withdrawing, (c) the weaker directing effect for the meta isomer of 2-substituted isomers dictated the selectivity as a function of the structure of the nitroso species and (d) substituent effects are usually additive.
These results were summarized in a short review article from the same team published one year later that emphasized the dual behavior of a nitroso moiety that acts both as electrophile and nucleophile, highlighting the 1,1 bond formation (formation of two bonds in one atom, either N or O) that favors asynchronous one-step TS for NDA reactions and stepwise processes involving polarized diradicals for nitroso ene reactions.131
In 2003, Yu and Wu investigated the reaction of 5-alkoyoxazole with various dienophiles such as nitroso compounds.132 The computational study was carried out at the B3LYP/6-31G* level and relied on 23 as a simple nitroso model. A three-step process was determined to form the final product 1,2,4-oxadiazoline, namely, a NDA reaction followed by ring-opening (RO) then ring-closing (RC) steps (Fig. 24). Preliminary investigations at the HF/3-21G* level showed a preference for the path involving C–C–O and N–C–N bond formations during the rate-determining DA step. This regioselectivity was against the precepts of CDFT, yet the authors argued that it originates from the electron-donating effect of the methoxy substituent on the oxazole and the minimization of electronic repulsions. NBO analysis showed the normal electron demand of the cycloaddition, which was also characterized by an asynchronous one-step, exothermic, and endergonic reaction path. Both TS and NDA adducts favored the endo approach to minimize electrostatic repulsions. RO and RC became stepwise as a consequence of the strong stabilization of the zwitterionic intermediate arising from conjugation effects through the nitrogen lone pair. Compared to the other dienophiles, such as thioacetaldehyde (CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S) and acetaldehyde (CH3CH
S) and acetaldehyde (CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), the rate of the NDA was found to follow the decreasing order of LUMO orbital energy: CH3CH
O), the rate of the NDA was found to follow the decreasing order of LUMO orbital energy: CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S > 23 > CH3CH
S > 23 > CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O. RO and RC were rather one-step mechanisms for CH3CH
O. RO and RC were rather one-step mechanisms for CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S and CH3CH
S and CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O due to poor stabilization of the zwitterionic intermediate (absence of conjugation).
O due to poor stabilization of the zwitterionic intermediate (absence of conjugation).
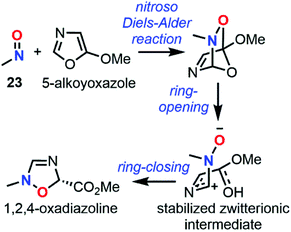 | ||
| Fig. 24 Reaction pathway between nitrosomethane (23) and 5-alkoyoxazole to give 1,2,4-oxadiazolines. | ||
The case of PDA cycloadditions between nitrosoalkenes and enamines species was thoroughly investigated by Domingo in 2006.133 The model reaction involving 4 and the enamine derived from pyrrolidine and propionaldehyde was studied at the B3LYP/6-31G* level. Calculations of the global electrophilicity index and Δω explained the polar nature and high rate of the NDA reactions due to strong electrophilic (ω4 = 3.30 eV) and nucleophilic candidates (ωenamine = 0.20 eV so Δω = 3.10 eV). The NDA reaction was highly exothermic and considered as irreversible. Its mechanism involved a highly asynchronous one-step process, considered as a one-step two-stage highly asynchronous process where the C–C bond formation (first stage) occurred before the formation of the C–O bond (second stage), which led to ring closure (Fig. 25). NBO and ELF analyses supported this mechanism and highlighted the large GEDT from the enamine to the nitroso species (inverse electron demand). This phenomenon led to a marked zwitterionic nature for the TS of this PDA reaction. However, an alternative pathway also emerged from the computations, namely, a stepwise process involving a zwitterionic intermediate. Despite this process was found to be uncompetitive with the selection of species at hand, it could become competitive in the presence of more electrophilic nitrosoalkenes and/or in more polar solvents that could stabilize this intermediate. The reaction was also found to be highly regio- and stereoselective, with a strong preference for the ortho product due to stronger coulombic interactions and for the endo conformation for minimizing electrostatic repulsions. The same conclusions were obtained with another nitrosoalkene candidate selected from an experimental case, namely, 1-nitrosovinylbenzene (59).134 Including dichloromethane (PCM model) in the computations did not change the trends observed.
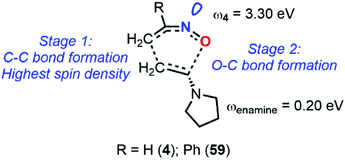 | ||
| Fig. 25 Endo asynchronous transition state between an enamine and nitrosoethylene (4) or 1-nitrosovinylbenzene (59). | ||
Another paper written by the same team gave an even deeper look at the regioselectivity for the same model reaction.135 Local electrophilic and nucleophilic indexes, ωk and Nk, respectively, based on both Parr and Yang or Yang and Mortier Fukui functions revealed the oxygen of 4 as the most electrophilic center and the terminal carbon of the enamine as the most nucleophilic center. These conclusions were not in agreement with the experimental ortho regioselectivity due to bond formation at the first stage between the terminal carbons of both species. Moreover, this selectivity was not as high as excepted by looking at the difference in global electrophilicity. The ELF analysis not only emphasized the one-step two-stage highly asynchronous process mechanism where the TS is formed early during the cycloaddition, but also gave a thorough understanding of both reaction pathways (involving 11 phases for the endo path, while only 3 phases were determined for the meta paths). The TS leading to the meta product was found to be more advanced (late stage, in the sense of Hammond's postulate) than the one for the endo product due to a larger GEDT. This led the authors to conclude that GEDT had to be seen in a global way instead of local approach to avoid misassumptions towards regioselectivity. The ELF study finally showed that the reaction was characterized by the coupling of zwitterionic pseudoradicals species due to electron-reorganization. This led the authors to state that ASD analysis could be suitable to understand this PDA. In contrast to the local reactivity indexes based on CDFT, ASD calculated in the radical cation of the enamine and in the radical anion of 4 correctly indicated the most reactive center leading to the ortho selectivity. These two centers bore the highest spin density after the GEDT process, and were, in this case, the two terminal carbons.
It is noteworthy that some NDA reactions are reversible and could thus act as a temporary trap for transient C-nitroso species such as nitrosocarbonyl reagents. Thermal treatment of the corresponding cycloadducts could therefore release the nitroso fragment, which then becomes available for reaction with other species at higher temperatures. Such a scenario is typically deployed to avoid the competitive and destructive dimerization of transient nitrosocarbonyl reagents, especially when a NDA reaction is attempted with unconstrained dienes (thus with a higher transoid population at low temperatures). A typical cycloadduct reservoir of nitrosocarbonyl reagents is their corresponding 9,10-dimethylanthracenyl cycloadducts. The capture of nitrosocarbonyl reagents by 9,10-dimethylanthracene and its release under thermal conditions was studied by Monbaliu et al. in 2009 (Fig. 26).136 In this study at the B3LYP/6-31G** level, two plausible pathways involving the thermolysis of such 9,10-dimethylanthracenyl cycloadducts for the release of 23 or (nitrosocarbonyl)methane (60) in the presence of butadiene as a model secondary diene were detailed. The thermal retro reaction (retro NDA) where anthracene was considered as a spectator showed a smaller activation barrier than the exchange process promoted by 9,10-dimethylanthracene (21.3 kcal mol−1 and 42.0 kcal mol−1 respectively for 23 and 27.6 kcal mol−1 and 40.8 kcal mol−1 for 60). The relatively high activation barrier for the release of 23 and its anthracenyl cycloadduct correlated nicely to the experimental conditions (thermolysis at ∼90 °C). The authors concluded that the slow release of 23 under thermolysis would favorably compete with its rapid destructive dimerization. Indeed, these thermal conditions enable a larger cisoid population of unconstrained dienes, which is a sine qua non requirement for a DA reaction to occur.
In the following years, DFT calculations were very supportive to predict and understand the regioselectivities of specific NDA reactions. In 2009, Studer et al. could rationalize the regioselectivity obtained between 33 and various dienes when the NDA reaction was catalyzed by a mixture of copper and iron complexes bearing bulky ligands.137 One year later, Marchand-Brynaert et al. studied at the B3LYP/6-31G** level the asymmetric NDA between 23 and nitrosotoluene (61) with chiral 1-phosphono-1,3-butadienes.138 As excepted, the PDA reaction was characterized by a highly asynchronous one-step mechanism with a preference for the ortho and endo approaches. However, computational data could not predict the poor experimental stereoselectivity obtained between these candidates. The authors argued such discrepancy as a consequence of a low energetic discrimination between the cisoid conformers of the diene and the high asynchronicity of the bond formation. Nevertheless, theoretical results showed a higher stereoselectivity upon increasing the steric hindrance for both the chiral auxiliary on the diene and of the ancillary substituents on the dienophiles. These results led to the synthesis of a new chiral diene and the use of bulky azodicarboxylates instead of nitroso species, which this time led to the formation of only one diastereoisomer.
To continue with the NDA of 1-phosphono-1,3-butadiene, its cycloadditions with various C-nitroso species were studied at the B3LYP/6-31G** level by the same team.139 The addition of a phosphonate moiety on the diene dictated an ortho regioselectivity. Again, a one-step asynchronous mechanism towards the endo adduct was determined for the PDA reactions. Calculations with the implicit addition of solvents (SCRF model) showed a low sensitivity towards solvent polarity. Kinetic NMR experiments and data obtained through an Arrhenius plot matched the computed thermochemistry data and further emphasized the one-step nature of the mechanism. A computational structure-(re)activity relationship showed an increased reactivity from 61 to α-chloro-2-nitrosopropane (62) then to nitrosocarbonyl species (methyl nitrosoformate 63, 1-nitrosoethan-1-one 64, 1-nitroso-2-phenylethan-1-one 65, nitroso(phenyl)methanone 66) towards the diene, with their respective regioselectivity essentially depending on the hindrance around the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety (Fig. 27). Reactivity indexes such as chemical potential μ and global electrophilicity ω emphasized the normal electronic demand of this DA reaction and the strong electrophile character of the C-nitroso species, respectively. This last parameter also demonstrated a slight increase of the global electrophilicity of the butadienyl moiety when attached to a phosphonate moiety. The computation of a large Δω confirmed the PDA character of this reaction.
O moiety (Fig. 27). Reactivity indexes such as chemical potential μ and global electrophilicity ω emphasized the normal electronic demand of this DA reaction and the strong electrophile character of the C-nitroso species, respectively. This last parameter also demonstrated a slight increase of the global electrophilicity of the butadienyl moiety when attached to a phosphonate moiety. The computation of a large Δω confirmed the PDA character of this reaction.
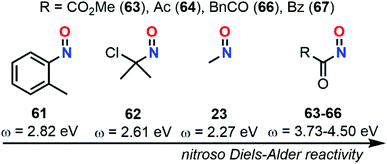 | ||
| Fig. 27 Trends in terms of reactivity towards dienes in nitroso Diels–Alder reactions between various subclasses of C-nitroso species. | ||
The presence of phosphonyl or phosphinyl moiety has also an impact on nitroso compounds as reported by Palacios et al. In their computational study, the authors reported on the behavior of phosphonyl and phosphinyl nitroso alkenes and their reaction with cyclic conjugated dienes (Fig. 28).140 Due to the ambivalence of both reagents, calculations at the B3LYP/6-31G* and M062X/6-31G* levels first confirmed nitroso alkenes to be the partner acting as an electron-poor heterodienophile. They would therefore be engaged in reaction with electron-rich cyclic dienes according to a normal electron demand NDA process. These conclusions were based on global electrophilicity indexes and energies comparison between the eight possible cycloadducts. The s-cis (Fig. 1) and endo conformations for the nitroso alkene and its corresponding TS, respectively, were preferred, especially when the solvent was included implicitly (PCM). From the endo-cycloadduct, it was possible to isolate a TS related to a [3,3]-shift, yielding a 1,2-oxazine that could undergo an imine–enamine tautomeric process and then eventually lead to the observed product. This one-step rearrangement was, as for the NDA reaction, exothermic, and asynchronous. However, such a rearrangement was only favored for cyclopentadiene since both a higher activation energy and a greater stability of the cycloadduct were computed with cyclohexadiene instead. When TMS was added to cyclopentadiene, a different result was obtained. An inverse electron demand NDA between both reagents was this time both kinetically and thermodynamically favored, leading directly to a bicyclic oxazine.
 | ||
| Fig. 28 Overview of the ambivalent reactivity of phosphonyl and phosphinyl nitroso alkenes during nitroso Diels–Alder reactions. | ||
A few years later, the same team focused on other types of dienes, namely indole, pyrrole, and 2,5-dimethylpyrrole.141 The study at the M062X/6-31G* level shed light on the mechanistic pathway involved with each diene. Each time, the one-step NDA reaction was more favored than the electrophilic aromatic substitution (EAS) alternative process. The subsequent ring-opening and rearomatization of the endo-cycloadduct enabled the formation of the experimental product, namely the E-oxime. When an EWG substituent such as a carboxylic acid moiety was added to the nitroso species, the EAS became rather competitive (ΔETS = 0.4 kcal mol−1), while not thermodynamically favored. It is worth mentioning that it would anyway lead to the same product after a 1,5-H shift. Concerning 2,5-dimethylpyrrole, the stability of the cycloadduct precluded ring-opening and only the bicyclic 1,2-oxazine was obtained.
In 2012, Mahajan et al. used a theoretical approach at the HF/6-31G* and B3LYP/6-31G* levels to explain their experimental observations associated with the NDA reaction of 3-dienyl-2-azetidinones bearing bulky stereocenters and nitrosoarenes (1 and 61).142 Only one regioisomer, namely the meta/endo, was detected when the diene was in its transoid conformation due to the minimization of steric hindrance. A mixture of both regioisomers was obtained with the cisoid conformation where the steric repulsions were less pronounced. The trends were not affected when implicit solvation was included (DCM with PCM model).
In 2013, the origin of the regio- and stereochemistry in an intramolecular N-acylnitroso Diels–Alder reaction was studied by Shea, Rychnovsky, and coworkers at the B3LYP/6-31+G* level.143 The reaction was found to be an exothermic process with a late TS characterized by a high asynchronicity. As observed experimentally, the 1,3-regioisomer was obtained for small chains (nC < 5) between the diene and nitroso fragment due to strain minimization, while the 1,4-regioisomer was calculated to become predominant for larger chains (nC > 5, Fig. 29). A methyl substituent placed in α to the nitrosocarbonyl fragment led to an anti-conformation, while alkoxy α-substituents favored the syn product but with a small ΔΔE. The flexibility of ether and silyl ether substituents compared to alkylated ones reduced the steric hindrance for the syn-diastereoisomer. Using cyclic diene fragments did not affect the trends, yet it lowered the energy difference between diastereoisomers by limiting torsional freedom. The accuracy of the computational method was confirmed by comparing geometrical values with data obtained from single crystal X-Ray diffraction (variations of about 4–5°).
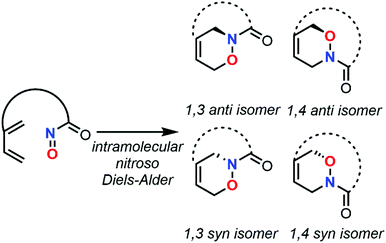 | ||
| Fig. 29 Overview of the different regio- and stereoisomers of an intramolecular N-acylnitroso Diels–Alder reaction. | ||
In 2015, Masson et al. used a theoretical approach to understand the high enantio- and diastereoselectivity, as well as the inversion of regioselectivity for the NDA reaction between nitrosoarenes, such as 1, and 1,3-diene-1-carbamates in the presence of a chiral phosphoric acid.144 Computations at the B3LYP/6-31G* level revealed that in the absence of a catalyst, the excepted ortho selectivity was maintained, while the use of a chiral phosphoric acid catalyst reverted the selectivity towards the meta cycloadduct due to proton transfer to the nitrogen atom of 1. This result was confirmed both experimentally and theoretically when the NDA reaction was studied without catalyst but under acidic conditions to protonate the nitrogen atom. The hydrogen-bonding network between both reagents and the catalyst was also responsible for the enantio- and diastereoselectivity. As expected, the IRC path showed a highly asynchronous one-step mechanism.
The in situ formation of nitroso species before trapping them during NDA reactions is another example where computational chemistry can advantageously be exploited to understand the formation of short-living nitroso intermediates. An experimental and computational study of NDA reactions from nitrosocarbonyl generated in situ from hydroxamic acid precursors and an oxidant was performed by Whiting et al. in 2015.145 The authors performed a computational study at the B3LYP/6-31G* level for accessing the geometries of the cycloadducts in the gas phase. The results were very similar to those obtained from X-ray diffraction on single crystals. The study revealed that a few adducts had access to two conformations, namely, syn and anti-conformations between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–O bonds in the bicycle (Fig. 30). The computation of the reaction pathway confirmed the predominance of the endo-NDA pathway over the exo-NDA and nitroso-ene ones. Usually, the TS for the s-trans to s-cis conversion of the nitrosocarbonyl (Fig. 1) was higher in energy than the one for the NDA reaction, emphasizing the high electrophilic reactivity of nitroso species. The low yields obtained for some adducts could be explained computationally by a favorable cyclo-reversion connecting the products to the starting reagents. Moreover, the presence of both meta and ortho isomers was comforted by a rather small transition state energy (<1 kcal mol−1). Finally, the authors related the appearance of a competitive ene product to the use of a copper complex that can trigger this pathway.
O and N–O bonds in the bicycle (Fig. 30). The computation of the reaction pathway confirmed the predominance of the endo-NDA pathway over the exo-NDA and nitroso-ene ones. Usually, the TS for the s-trans to s-cis conversion of the nitrosocarbonyl (Fig. 1) was higher in energy than the one for the NDA reaction, emphasizing the high electrophilic reactivity of nitroso species. The low yields obtained for some adducts could be explained computationally by a favorable cyclo-reversion connecting the products to the starting reagents. Moreover, the presence of both meta and ortho isomers was comforted by a rather small transition state energy (<1 kcal mol−1). Finally, the authors related the appearance of a competitive ene product to the use of a copper complex that can trigger this pathway.
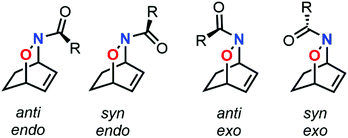 | ||
| Fig. 30 Overview of the different conformers during a nitroso Diels–Alder reaction between nitrosocarbonyls and dienes. | ||
In 2014, Pinho e Melo et al. compared the behaviors of 1-(p-bromophenyl)nitrosoethylene (67), generated in situ from the dehydrobromination of the corresponding bromooxime, and ethyl 2-nitrosoacrylate (68) towards pyrroles (Fig. 31).146 Computations at the B3LYP/6-31G** level confirmed the experimental results that differed between the two nitrosoalkenes. On the one hand, only one stereoisomer, namely the E-oxime, was obtained for 67 during an inverse electron-demand NDA reaction. The reaction involved a one-step mechanism where the endo approach of the asynchronous TS was favored. On the other hand, the presence of both isomeric forms of the oxime (E and Z) with 60 were supported by a high energy demand NDA reaction for both approaches (endo and exo), with an activation energy at least 30 kcal mol−1 higher than for 68. Instead, a conjugate addition followed by a 1,5-H shift led to both oximes, initially from two distinct conformations of 67 that could coexist, namely, the s-cis- and s-trans-conformations (Ecis − Etrans = 1.3 kcal mol−1, Fig. 1). When 2,5-dimethylpyrrole reacted with 67 instead of pyrrole, the initial conjugate addition was followed by an O- or N-nucleophilic addition to afford the corresponding bicyclic oxazine and a five-membered cyclic nitrone, respectively.
The same methodology was employed by the same team two years later for studying the reaction between 1-arylnitrosoethylenes and indoles. The computation at the B3LYP/6-31G** level was clearly in favor of an inverse electron-demand NDA mechanism for reactions with indoles but not with pyrroles, as already mentioned.147 Compound 67 was used as a model with two specific indole derivatives, 1-methylindole and 3-methylindole. The final product was either the cycloadduct from 3-methylindole or the E-oxime obtained after a subsequent ring-opening of the cycloadduct, as observed for 1-methylindole. The exo approach with the regioselectivity observed experimentally, that is, the formation of the final E-oxime, was calculated to be the most favored.
A few years later, Liao, Yu, and coworkers also implemented an in situ generation of zwitterionic nitrosoalkenes relying on the dehydrohalogenation of α-halo-N-alkylhydroxamic acids. The zwitterionic nitrosoalkenes reacted next with various olefins through an inverse electron demand NDA reaction.148 Energies computed at the B3LYP/6-311+G** level with the explicit addition of solvent showed that two molecules of the solvent 2,2,2-trifluoroethanol interacted with the hydroxamic acid through intermolecular hydrogen bonding during the generation of the heterodiene (dehydrohalogenation triggered by triethylamine). This step was found to be rate-determining compared to the NDA reaction. The regioisomer involving the bond formation between the terminal olefinic carbons was found to be the most stable. The regioselectivity could also be rationalized by looking at the coefficients of the FMOs. Again, the explicit addition of a protic solvent led to an interaction with the nitroso species and lowered its LUMO, and thus contributed to a significant acceleration of the reaction.
In 2020, the high regioselectivity of the NDA reaction between nitrosostyrene (12) and thiochalcones, a 4π-system, led Reissig et al. to rationalize their experimental results with computations.149 The calculations at the PBE0-GD3BJ/def2-TZVP level (PCM model for DCM) of both activation barriers and stability energies for the eight possible cycloadducts revealed that the one-step reaction was kinetically controlled. The reaction led to the product involving the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond of the thiochalcone, seen as an electron-rich dienophile, and both C
S bond of the thiochalcone, seen as an electron-rich dienophile, and both C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and N
C and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds of 12 that acted as the electron-deficient diene partner through an inverse electron demand (Fig. 32). The cycloadduct thermodynamically favored was obtained when the C
O bonds of 12 that acted as the electron-deficient diene partner through an inverse electron demand (Fig. 32). The cycloadduct thermodynamically favored was obtained when the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of the thiochalcone was involved, but it led to higher activation barriers. The regioisomers with three contiguous heteroatoms were the least stable due to destabilizing lone pairs repulsions. The nature of the NDA product was dictated by the monomer-dimer equilibrium of the thiochalcone, since both species could act as an heterodienophile and, hence, was substituent-dependent.
C bond of the thiochalcone was involved, but it led to higher activation barriers. The regioisomers with three contiguous heteroatoms were the least stable due to destabilizing lone pairs repulsions. The nature of the NDA product was dictated by the monomer-dimer equilibrium of the thiochalcone, since both species could act as an heterodienophile and, hence, was substituent-dependent.
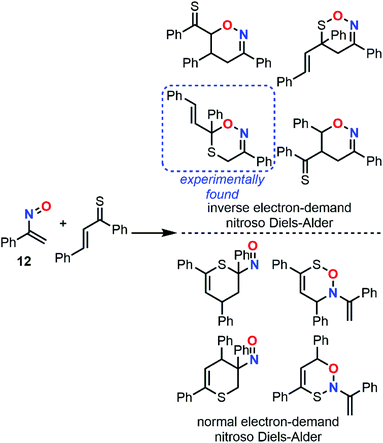 | ||
| Fig. 32 Overview of the ambiphilic reactivity between nitrosostyrene (12) and thiochalcones during nitroso Diels–Alder reactions. | ||
The same year, computational chemistry helped to understand the regio- and stereoselectivity of the NDA reaction between a nitrosocarbonyl compound bearing a camphorsultam chiral auxiliary, and a chiral cyclopentadiene, enabling the formation of a strategic intermediate for the total synthesis of the antibiotic pactamycin.150 Four possible reaction pathways (diastereotopic face-discrimination) were studied at the M06-2X/6-31G* level. Two transition states appeared to be less hindered and differed by their regioselectivity (N or O). Some of their conformers were then optimized and enabled the identification of the most stable form for each TS. An IRC analysis showed a fast and exothermic pathway that gave a N/O regioselectivity on the less crowed face with a 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio according to the Boltzmann distribution. These results were consistent with the observations obtained during the total synthesis.
2 ratio according to the Boltzmann distribution. These results were consistent with the observations obtained during the total synthesis.
Computational studies contribute to refining the specific inherent features of the NDA mechanism, which is characterized by a highly asynchronous one-step mechanism with zwitterionic pseudoradicals centers in the transition state. A two-step process involving polarized diradical intermediates could even be obtained for highly reactive nitroso species. The polarized and radical nature of such a transition state or intermediate has two direct consequences. On the one hand, the nature of the solvent has a higher impact on the activation barrier than in classical Diels–Alder reactions and must therefore be considered in the computations, at least implicitly. On the other hand, even though the electron demand nature is usually based on CDFT, local indexes are not able to accurately predict the regioselectivity, by contrast with functions related to atomic spin density. Theoretical chemistry also shows that the endo approach is most of the time favored due to the exo lone pair effect that leads to repulsions when the nitrogen lone pair is placed near the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of the diene partner. The ortho regioselectivity is also typically favored due to stronger coulombic interactions between the (pseudo)radicals. All these theoretical results are valid for each electron demand (inverse or normal) that can be predicted through reactivity indexes calculations. Most of the time, the electron demand is inverse for nitrosoalkenes and normal for the other C-nitroso species.
C bond of the diene partner. The ortho regioselectivity is also typically favored due to stronger coulombic interactions between the (pseudo)radicals. All these theoretical results are valid for each electron demand (inverse or normal) that can be predicted through reactivity indexes calculations. Most of the time, the electron demand is inverse for nitrosoalkenes and normal for the other C-nitroso species.
Nitroso ene reactions
Another pseudocyclic reaction, which is comparatively less explored than NDA cycloadditions yet it also involves C-nitroso species, is the ene reaction (Fig. 33).21,22 Due to the ambivalence of nitroso moiety, the nitroso ene reaction can potentially be centered on oxygen to give a C–O bond or on nitrogen to form a C–N bond, respectively. Yet to date only the latter was experimentally observed so far, yielding allylamines as final adducts. Such species are fundamental building blocks in organic and medicinal chemistry.151 Despite the appealing aspect of this mild and valuable synthetic methodology, the reactivity, mechanism, and regioselectivity are known to be challenging and can therefore benefit from computational chemistry.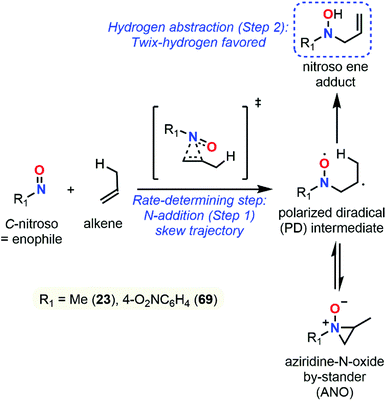 | ||
| Fig. 33 Mechanism of reaction during a nitroso ene reaction for nitrosomethane (23) and p-nitronitrosobenzene (69). | ||
A first dual experimental and computational study concerning nitroso ene reactions was published in 2001 by Bottke et al.152 The mechanism was investigated at the B3LYP/6-31+G* level using p-nitronitrosobenzene (69) and 3-substituted alkenes, such as 2-methyl-2-butene, as model compounds. The ene reaction was determined to proceed according to a two-step process governed by steric and conformational constraints. The first step, leading to an aziridine-N-oxide (ANO) intermediate, was found to be rate-determining. The following step involved hydrogen abstraction to give the corresponding allylhydroxylamine product. The hydrogen at the lone position was less easily removed due to high steric hindrance with the aromatic ring, while with such an unsymmetrical alkene, two diastereomeric hydrogens at the other sp2 carbon could be abstracted (twix and twin), hence leading to two competitive pathways (Fig. 34). A smaller activation barrier was calculated for the abstraction of the twix hydrogen, along a skew trajectory. To minimize steric hindrance, the bulky aryl group was determined to be located on the less crowded side with the twin substituent, while oxygen was in the direction of the twix and lone substituents. This reaction was known to be irreversible, except when the twix position was hindered by substituents leading to an increased energy barrier for the second step. In this case, the twin position which was less prone to conformational strain could be favored, which therefore reduced the regioselectivity.
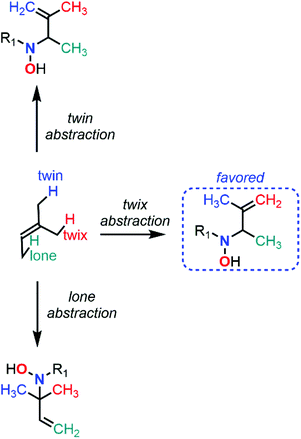 | ||
| Fig. 34 Overview of the regioselectivity during hydrogen abstraction step from nitroso ene reactions. | ||
Nevertheless, Houk et al. proved that the nature of the intermediate involved in nitroso ene reactions was rather an open-chain polarized diradical (PD) intermediate than an ANO.153 Restricted and unrestricted (with spin projection) calculations at the B3LYP/6-31G* level showed a closed-shell polar structure combined with a radical behavior that was sensitive to solvent effects (computed with the PCM model). CCSD(T), QCISD(T), and CASPT2 single-point calculations confirmed the nature of the intermediate. The authors also considered a one-step mechanism, but this led to much higher activation energies. The formation of such an intermediate was determined as rate-determining and endothermic, and then reversibly led to either ANO, seen therefore as an inactive reservoir and not an intermediate, or irreversibly to the excepted ene product. However, hydrogen abstraction was more favorable than cyclization into ANO. The PD intermediate has geometrical properties similar to ANO, namely a high rotational barrier that is larger than the one leading to the formation of the desired product. This restriction of rotation was stated to arise from bonding interactions between the nitrogen atom and the radicalar carbon, as well as by intramolecular hydrogen bonding between radicalar oxygen and terminal olefinic hydrogen. A comparison between HNO, 23, and 69 with propene revealed the same mechanism, although the ANO derivative of 69 was calculated to be isoenergetic with its TS. HNO was determined to be more similar to singlet oxygen in terms of regioselectivity than the two C-nitroso species 23 and 69. The regioselectivity towards twix hydrogen abstraction was rationalized through the formation of two favorable hydrogen bonds and one steric repulsion. By contrast in the twin approach, only one hydrogen bonding but two steric repulsions were identified. The lone approach appeared as too energetically demanding and the lone diradical easily led to cyclization into ANO before its opening into the twix diradical.
While the first theoretical studies gave evidence for a stepwise path during nitroso ene reactions, Lu showed that aromatic stabilization could change the reaction mechanism towards a one-step process (Fig. 35).154 For instance, the ene reaction between 23 and o-isotoluene was studied at the (U)B3LYP/6-31G* level and showed a much smaller activation barrier when the reaction involved a one-step pseudocyclic pathway instead of a stepwise pathway with diradical or zwitterionic intermediates. Similar to the NDA reaction, the endo approach was preferred to the exo one. Aromatic stabilization was not only responsible for the small activation barrier but also the high exothermicity of the reaction. Comparison with 69 also confirmed this hypothesis.
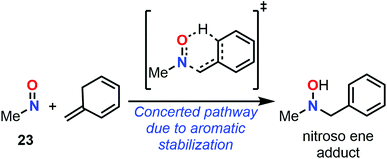 | ||
| Fig. 35 One-step pathway between nitrosomethane (23) and aromatic olefins during nitroso ene reactions. | ||
Up to now, the regioselectivity of the ene reaction with the selected C-nitroso species (HNO, 23 and 69) was determined to be favored towards the twix hydrogen abstraction. However, Caramella et al. showed another trend for nitrosocarbonyl compounds where both lone and twix hydrogens were removed, hence leading to a “cis effect”.155 Computations at the (U)B3LYP/6-31G* level between nitrosocarbonyl benzene (70) or nitrosocarbonyl mesitylene (71) with tetramethylethylene confirmed these experimental observations: 70 led exclusively to the twix approach, while bulkier nitrosocarbonyl species such as 71 afforded a mixture of lone and twix hydrogen abstractions (Fig. 36). This change in regioselectivity was explained through a stronger steric hindrance at the twix position with bulkier nitrosocarbonyl substituents, hence leading the lone hydrogen abstraction to become competitive. Comparison with nitrosoarenes such as 69 highlighted the higher reactivity of nitrosocarbonyl species by reducing the activation barrier of the addition step while keeping the same kinetics trends as the ones previously reported.
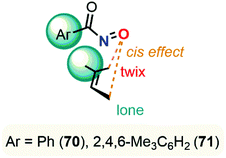 | ||
| Fig. 36 Regioselectivity of nitrosocarbonyl compounds (nitrosocarbonyl benzene (70) or nitrosocarbonyl mesitylene (71)) characterized by a “cis effect” during a nitroso ene reaction. | ||
In 2017, Hong and coworkers reported an intramolecular ene reaction from nitrosocarbonyl derivatives leading to a morphan skeleton.156 The methodology was applied for the total synthesis of (±)-Kopsone, a morphan-type monoterpene alkaloid. The study was also supported with computations at the (U)B3LYP/6-31G* level, which confirmed the presence of a stepwise mechanism involving zwitterionic or diradical intermediates. The first step was found to be rate-determining and irreversible. When a cyclopropyl ring was attached to the nitrosocarbonyl species, the PD intermediate could lead to ring-opening but this pathway was more energetically demanding than the hydrogen abstraction. The absence of the ene product for nitrosocarbonyl compounds bearing a phenyl substituent was related to a difficult hydrogen transfer, hence to a high activation energy (28.0 kcal mol−1).
Computational and mechanistic studies on the nitroso ene reaction emphasized that the reaction proceeds through a two-step process involving a polarized diradical intermediate. The presence of such diradicals can be better described with the use of unrestricted theoretical methods. A deeper look at the mechanism showed the presence of aziridine-N-oxide as a reversible inactive reservoir connected to the PD intermediate. The first step of the reaction, namely the addition between both reagents, is rate-determining and endothermic, while the second step related to hydrogen abstraction is a much faster, exothermic, and sterically-determined reaction. The experimental results can therefore be rationalized through the computation of reaction energy profiles: while regioselectivity is usually governed by the abstraction of the twix hydrogen, the presence of bulkier substituents increases the corresponding activation barrier hence enabling competition of the abstraction of the lone or twin hydrogens.
Nitrosoaldol reactions
The integration of aminated (or aminohydroxylated) moieties into readily available organic compounds, with high regioselectivity and ideally in an enantioselective way, is a significant area of research interest in methodology. Aminated functions are among the most privileged scaffolds in active pharmaceutical ingredients. The nitrosoaldol reaction, involving the addition of a carbon-centered nucleophile to an electrophilic C-nitroso species was first reported in the early eighties157,158 and provides a convenient and efficient integration of aminated (or aminohydroxylated) functions on enolizable carbonyls.11,12 The electrophilic ambivalence of the nitroso group can be seen as an advantage in this scenario, since the diversity of useful products reachable from the same starting material increases through either C–N or C–O bond formation through α-(hydr)oxyamination and α-aminoxylation respectively (Fig. 37). The synthetic utility of such a potentially tunable step critically depends on the factors governing the regioselectivity of the reaction. A deep understanding of these processes with computations can therefore help to tune the regioselectivity and to orientate the outcome of the reaction. The aspects of stereochemistry can also be studied through computations, as illustrated below.Based on experimental and theoretical studies about C-nitroso species, the nitrogen atom is undoubtedly more electrophilic than the oxygen, hence the addition of the C-based nucleophilic enolate during the nitrosoaldol reaction will primarily target the former. However, when the reaction with 1 is catalyzed by (L)-proline (or (S)-proline), the α-aminoxylation (i.e. the addition of the nucleophile onto the oxygen of the nitroso group) is favored. To shed light on this unexpected result, Houk et al. published in 2004 a computational study at the B3LYP/6-31G* level that provided mechanistic insights (Fig. 38).159 In the first stage of the reaction, the ketone substrate, here propionaldehyde, reacts with (L)-proline to give the corresponding (E)- or (Z)-enamine conformers. Transition states for the addition on the oxygen of 1 without intermolecular proton transfer or involving the (Z)-enamine were high in energy compared to the one involving an (E)-anti enamin. The phenyl and carboxylic groups were anti to each other during the addition (Si face). The addition on the nitrogen atom was disfavored by 2.6 kcal mol−1, which could be rationalized by a simultaneous proton transfer on the nitrogen atom, thus increasing the electrophilicity of its neighboring oxygen atom. This proton transfer was only triggered by the carboxylic moiety of (L)-proline. For reactions without proton transfers during catalysis such as with N,N-dimethylethenamine (the dimethyl enamine of propionaldehyde), calculations clearly emphasized the expected (R)-α-oxyamination product (i.e. the product from the addition onto the nitrogen of the nitroso group) as the most favorable. Finally, the aldol reaction involving the dimeric form of 1 was rejected due to the entropic cost for dimerization and low electrophilicity of the negative oxygen atom, the transition state lying 24.4 kcal mol−1 above the one with the monomeric species.
The same year, Córdova et al. also implemented a chemo-, regio- and stereoselective method for a proline-catalyzed α-aminoxylation reaction.160 (L)-Proline ( (S)-proline) led to the (R)-nitrosoaldol compounds derived from 1 and a broad range of aldehydes and ketones, while (D)-proline ((R)-proline) gave the (S)-corresponding product. Computations at the B3LYP/6-311+G** level confirmed that the stereoselectivity arose from a better TS stabilization through hydrogen bonding between the nitrogen atom and the carboxylic acid moiety.
This very potent reaction was thoroughly studied two years later by Han et al. at the B3LYP/6-31G** level.161 The reaction between (L)-proline and propionaldehyde led to an (E)-enamine that exists in two conformations characterized by a syn or an anti-arrangement between the methyl group and carboxylic moiety, respectively. The authors argued that the coexistence of the syn and anti-conformers was due to a large rotation barrier around the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond. These two enamines can add onto the oxygen atom of 1 either on its si or the re face, leading to four TSs, each related to a specific zwitterionic intermediate (Fig. 39).
N bond. These two enamines can add onto the oxygen atom of 1 either on its si or the re face, leading to four TSs, each related to a specific zwitterionic intermediate (Fig. 39).
 | ||
| Fig. 39 Zwitterionic intermediates obtained during the addition between nitrosobenzene (1) and an enamine derived from (L)-proline. | ||
By contrast to the paper reported by Houk et al.,153 the four TSs adopted a six-membered ring chair conformation where both the carboxylic acid and the proline amine participate in the hydrogen bonding network. Again, the most favorable pathway (more stable by 5–7 kcal mol−1) was found to be related to an anti conformation of the enamine that added onto the Si face of 1, thus explaining the high experimental stereoselectivity. Frequency analysis revealed the C–O bond formation to be the principal molecular motion at the TS, while the hydrogen bonding was established earlier, hence increasing the electrophilicity of the oxygen. Increasing the polarity of the solvent decreased significantly the activation barrier (PCM model). These computational results agreed with the Hughes-Ingold rules, since the TS was more polar, thus more stabilized than the reagents, in the presence of a polar solvent. The hydrolysis of the nitrosoaldol product was finally computed with explicit solvation of one molecule of water and proceeded to the elimination of (L)-proline to give the (R)-α-oxyaldehyde product through a four-step process.
The same year, Jemmis et al. gave insights on the diastereoselectivity of nitrosoaldol reactions catalyzed by (L)-proline between 1 and substituted meso-cyclohexanones.162 The computational study at the B3LYP/6-31G* level first excluded the selective formation of one conformation of the enamine formed between (L)-proline and the ketone, since the activation barrier between anti- and syn-conformations was only of 0.23 kcal mol−1. The diastereoselectivity, therefore, arose during the addition step, especially through the substituents at the 4th position of the ketones. Based on the previous theoretical studies, only the addition leading to an anti-conformation between the carboxylic acid of the enamine and the phenyl moiety of 1 was considered. While rigid spiroketo centers prevented the syn-conformation between 1 (added at the 2nd position so in α) and the substituents at the 3rd position due to electrostatic repulsions between the oxygens of the carbonyl and 1, hence only giving the anti-nitrosoaldol product, substituents enabling twisting between oxygens reduced the selectivity (Fig. 40). The authors also stated that electrostatic repulsions could play a role in diastereoselectivity, hence emphasizing the importance of dipole–dipole interactions.
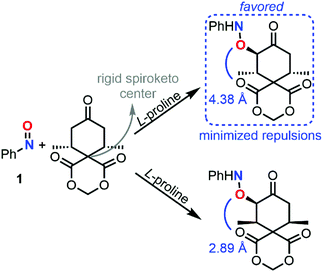 | ||
| Fig. 40 Origin of the diastereoselectivity during a nitrosoaldol reaction between nitrosobenzene (1) and substituted meso-cyclohexanones. | ||
A similar approach was adopted by Liu et al. to study at the B3LYP/6-311++G** the aldol reaction catalyzed with another cyclic amine, namely, L-pyrrolidine-2-yl-1H-tetrazole. A tandem nitrosoaldol/Michael reaction was studied between cyclohexanone and 1.163 This time, the two conformational forms of the enamine were related to the syn and anti-positions between the enamine double bond and the tetrazole ring, with a slight preference for the anti-arrangement due to the feasible C–N rotation. The nucleophilic addition was more favorable on the Re face and with the anti-conformation of the enamine. The activation barrier for the α-aminoxylation was again smaller than for the α-oxyamination due to an easier proton transfer from the tetrazole moiety on the nitrogen than on the oxygen atom of the nitroso group. The following Michael reaction from the O-nitrosoaldol product was then both thermodynamically and kinetically favorable.
Yamamoto et al. described the switch of regioselectivity when the nitrosoaldol reaction between 1 and enamines was catalyzed by Brønsted acids.164 Calculations at the B3LYP/6-311++G** level showed that at least two molecules of acid had to be involved to lower the activation barrier and enable mild conditions. In this way, three hydrogen bond-type of interactions were identified accounting for the regioselectivity through modulation of the electrophilicity of the neighboring atom: (a) between the most acidic hydrogen atom of the acid and the nitrogen of the nitroso moiety (hence rationalizing the O-selective nitrosoaldol reaction in the presence of acetic acid), (b) between the hydrogen ortho to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety and the oxygen atom of the acid (hence rationalizing the selective N-addition in presence of less acidic compounds such as MeOH) and (c) between the hydrogen atom of NCH3 from the enamine and the oxygen atom of the acid. Likewise, the enantioselectivity towards the (S)-nitrosoaldol product in the presence of chiral acids such as (S,S)-TADDOL or (S)-1-naphthylglycolic acid was also attributed to strong hydrogen bonding between the reagents and the catalyst.
O moiety and the oxygen atom of the acid (hence rationalizing the selective N-addition in presence of less acidic compounds such as MeOH) and (c) between the hydrogen atom of NCH3 from the enamine and the oxygen atom of the acid. Likewise, the enantioselectivity towards the (S)-nitrosoaldol product in the presence of chiral acids such as (S,S)-TADDOL or (S)-1-naphthylglycolic acid was also attributed to strong hydrogen bonding between the reagents and the catalyst.
The same strategy was adopted by Zhong for the implementation of an exclusive α-aminoxylation of enecarbamates by nitrosoarene species catalyzed by a BINOL-derived phosphoric acid.165 The regioselectivity was triggered by the high acidity of the chiral Brønsted acid, leading to strong hydrogen bonds with the nitrogen atom and enhanced electrophilicity of the oxygen atom.
In 2009, Wong showed at the MP2/6-311G** level that modifying the backbone of the proline catalyst with a silyl ether moiety had a profound impact on the outcome of the reaction.166 For instance, α,α-diphenylprolinol trimethylsilyl ether reacted with butanal to form a trans enol derivative instead of an enamine as a consequence of two favorable and simultaneous hydrogen bonds. The complex enol/catalyst then underwent aldol addition to 1 exclusively via its Si face to give the (S)-N-nitrosoaldol product. The corresponding transition state involved a C–N bond formation simultaneously with two hydrogen transfers with the nitrogen atom of the prolinol, one from the oxygen of the enol, the other with the oxygen of 1. The regioselectivity was rationalized through NBO charge analysis between nitrogen (+0.085) and oxygen (−0.313) of 1 with the carbon of the enol (−0.368).
One year later, Palomo et al. showed that adding p-nitrobenzoic acid as an additive for the nitrosoaldol reaction catalyzed by α,α-diphenylprolinol trimethylsilyl ether switched the selectivity from the N-(hydroxyamination) to the O-addition (aminoxylation).167 While their previous research at the B3LYP3/6-31G* level confirmed the exclusive α-hydroxyamination obtained with this catalyst alone,168 the addition of two molecules of p-nitrobenzoic acid led to two hydrogen bonds with the nitrogen atom, enabling the formation of the α-aminoxylation product. This time, the authors assumed the intermediate between the catalyst and aldehyde to be the E-enamine derivative where the double bond was anti to the silyl group instead of the trans enol species proposed by Wong.166 The stereoselectivity towards the (S)-nitrosoaldol product however remained unchanged.
The role of p-nitrobenzoic acid in the nitrosolaldol reactions was also investigated at the M06-2X/631+G** level (with the SMD model for implicit solvation with MeCN) by Luo, Mi et al. in 2014.169 The reaction focused on the reaction of nitrosocarbonyl species formed in situ by oxidation of N-hydroxycarbamates in the presence of enamines obtained from 1,3-dicarbonyl compounds and a tert-leucine-derived chiral primary amine. The addition of p-nitrobenzoic acid led to the protonation of the amine, hence resulting in a H-bond donor site on the catalyst. The (Z)-anti enamine was found to be the most stable conformer due to two favorable hydrogen bonds (Fig. 41). Compared to nitrosoarenes, nitrosocarbonyls compounds can be engaged in a bidentate hydrogen bonding network due to the carbonyl moiety. However, only monodentate hydrogen bonds could be located for the TS related to the O-addition (aminoxylation). The N-addition enabled the formation of two hydrogen bonds, hence explaining the regioselectivity towards the N-addition (α-oxyamination). This bidentate network was also responsible for the facial selectivity (Re face) upon addition of the enamine, thus leading exclusively to the (R)-nitrosoaldol product.
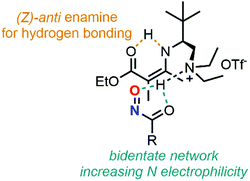 | ||
| Fig. 41 Origin of regio and enantioselectivity during a nitrosoaldol reaction between nitrosocarbonyls and an enamine derived from tert-leucine. | ||
In 2012, Nelson et al. rationalized the regioselectivity of nitrosoaldol reactions using the HSAB theory.170 One of the previous hypotheses could be ruled out through Mulliken charge calculations at the HF/6-31G* level: activation of the oxygen through Lewis acid (L.A.) complexation of the nitroso dimeric form is not sufficient to increase its electrophilicity and favor the O-addition (aminoxylation). Moreover, energy calculations showed that protonation on the oxygen atom led to more stable species than on the nitrogen of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety, hence ruling out previous explanations relying solely on the formation of a more stabilizing H-bonding with the nitrogen atom. Finally, their computations highlighted an increase of the Mulliken charge difference between the nitrogen and the oxygen when the strength of the complexation at the oxygen atom of the monomer increased. These results contributed to rationalize the mechanism based on the HSAB theory. On the one hand, nonexistent or weak (with MeOH) interactions with the oxygen atom leave the nitrogen atom as a soft electrophilic center, thus favoring the reaction with a soft nucleophilic center. In the specific case of the nitrosoaldol reaction with an enolate, the soft nucleophile center would be the α-carbon atom (enolizable position) of the enolate, hence leading to α-oxyamination (N-addition). On the other hand, strong complexation via a strong Lewis or Brønsted acid changes the nitrogen atom to a hard electrophilic center, thus favoring the reaction with a hard nucleophile. In the specific case of the nitrosoaldol reaction with an enolate, that would be the oxygen of the enolate, hence leading to the aminoxylation product. In the case of an enamine, that would be the nitrogen of the enamine. Next, the intermediate leading to O–N or N–N bond formation is then deprotonated to release the acidic catalyst (Fig. 42). Anion-type [2,3]-sigmatropic rearrangement eventually led to the zwitterionic intermediate of the α-aminoxylation product with the formation of a C–O bond.
O moiety, hence ruling out previous explanations relying solely on the formation of a more stabilizing H-bonding with the nitrogen atom. Finally, their computations highlighted an increase of the Mulliken charge difference between the nitrogen and the oxygen when the strength of the complexation at the oxygen atom of the monomer increased. These results contributed to rationalize the mechanism based on the HSAB theory. On the one hand, nonexistent or weak (with MeOH) interactions with the oxygen atom leave the nitrogen atom as a soft electrophilic center, thus favoring the reaction with a soft nucleophilic center. In the specific case of the nitrosoaldol reaction with an enolate, the soft nucleophile center would be the α-carbon atom (enolizable position) of the enolate, hence leading to α-oxyamination (N-addition). On the other hand, strong complexation via a strong Lewis or Brønsted acid changes the nitrogen atom to a hard electrophilic center, thus favoring the reaction with a hard nucleophile. In the specific case of the nitrosoaldol reaction with an enolate, that would be the oxygen of the enolate, hence leading to the aminoxylation product. In the case of an enamine, that would be the nitrogen of the enamine. Next, the intermediate leading to O–N or N–N bond formation is then deprotonated to release the acidic catalyst (Fig. 42). Anion-type [2,3]-sigmatropic rearrangement eventually led to the zwitterionic intermediate of the α-aminoxylation product with the formation of a C–O bond.
In 2020, the use of computational chemistry contributed to rationalize the switch of selectivity between nitrones and imines that was observed upon base-catalyzed aldol reaction between aryl acetic acid esters and nitrosoarenes. Lattanzi, Mazzanti and coworkers described at the M06-2X/6-311+G** level with DCM as solvent (IEFPCM model) the reaction between 1 and methyl phenylacetate catalyzed by a phosphazene base (2-tert-butylimino-2-diethylamino-1,3-dimethylperhydro-1,3,2-diazaphosphorine, BEMP).171 The deprotonation of the ester was determined as the rate-determining step due to the weak acidity of the α-proton and led to an enolate/BEMPH+ complex that rapidly underwent addition onto 1 (Fig. 43). Computation of the global electrophilicity index ω revealed that the nucleophilic addition was much more favored towards the monomeric form of 1 than its dimer (ω1,monomer = 1.99 eV, ω1,dimer = 1.55 eV). The intermediate obtained could exist as a nitrosoaldolate/BEMPH+ ionic pair or as a nitrosoaldol/BEMP complex obtained via tautomerization assisted by BEMPH+OH− for α-proton transfer. The authors found that this equilibrium depended on the stabilization of the enolate negative charge (and therefore on the thermodynamic acidity of the α-proton) and was responsible for the selectivity towards the corresponding nitrone or imine derivative. On the one hand, the nitrone product was obtained through an oxidative pathway (hydride transfer) of the nitrosoaldolate to the dimeric form of 1, which also resulted in the formation of azoxybenzene as a byproduct (1 equiv.). Calculations confirmed the dimer as a stronger oxidant than the monomer. On the other hand, an E1CB elimination of the neutral nitrosoaldol product led to an imine. With this in mind, the authors rationalized their experimental results by drawing a linear relationship between the computed ΔpKa and the content in nitrone. The decreased acidity of the α-proton increased the preference towards the nitrone derivative and vice versa, which explained why nitrosoarenes bearing EDG and EWG substituents led to the formation of either a nitrone or an imine, respectively.
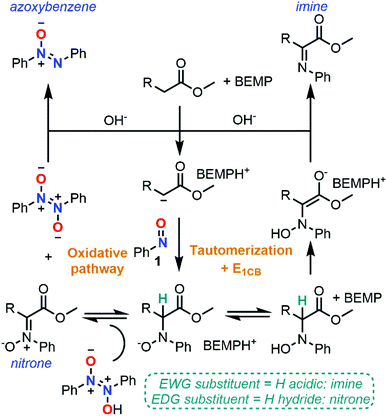 | ||
| Fig. 43 Mechanisms of reaction during catalytic pathways leading to either nitrone or imine formation from nitrosobenzene (1) and aryl acetic esters. | ||
In 2021, Monbaliu, Robiette et al. relied on computational chemistry to rationalize the better selectivity obtained using a continuous flow process instead of a batch one for an oxyamination process. The protocol aimed at the preparation of various α-aminohydroxylated compounds from enolizable ketones (e.g. acetophenone and propriophenone derivatives) and α-chloronitroso species (e.g. 1-chloro-1-nitrosocyclopentane (72) and 1-chloro-1-nitrosocyclohexane (73)).28 While the authors were after developing selective protocols for the preparation of mono α-aminohydroxylated ketones from a range of primary, secondary and tertiary ketones, the emergence of a bis amination side-product was observed for primary enolizable ketones (e.g. acetophenone). Calculations at the B3LYP-D3/6-311+G** level for electronic energies and B3LYP-D3/6-31+G* level for solvation by MTBE (PCM model) showed that the N-nitrosoaldol (oxyamination) reaction was diffusion-controlled since no activation barrier could be determined (Fig. 44). Deprotonation of the nitrone obtained could lead to another amination to give a bisnitrone compound that could be finally hydrolyzed. The second amination was found to be rate-determining while the deprotonation of the intermediate nitrone was characterized by a small activation barrier. The addition of a methyl substituent at the α-position of the ketone substrate (e.g. propiophenone instead of acetophenone) increased significantly both activations barriers and made the second amination unlikely to occur for propiophenone, and generally speaking for secondary and tertiary enolizable ketones. The computations, as well as the experimental continuous flow conditions, emphasized the paramount importance of ensuring an accurate control of the local stoichiometry to suppress the competitive bis amination on primary enolizable ketones. The issues related to poor mixing characterized in batch could therefore be overcome using continuous flow technology, hence leading to a better selectivity towards the mono nitrosoaldol product.
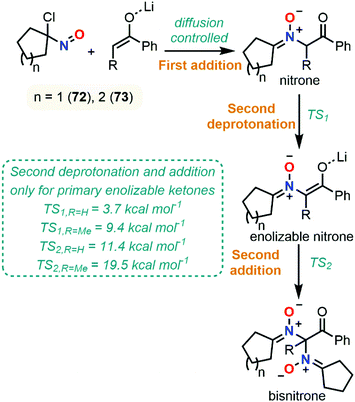 | ||
| Fig. 44 Selectivity of nitrosoaldol reactions between 1-chloro-1-nitrosocyclopentane (72) and enolizable ketones. | ||
Computational chemistry provided invaluable insights on the regioselectivity of the nitrosoaldol reaction, and in particular for understanding the origins of α-aminoxylation (O-addition) during acid catalysis. There is a general consensus in the literature towards the preferential hydrogen bonding or electrostatic interaction between a strong acid (Brønsted or Lewis) and the nitrogen atom of the nitroso species. This hydrogen bond is not only responsible for the increased electrophilicity of the oxygen and therefore the favorable attack on this atom (α-aminoxylation), but also for the experimental enantioselectivity. Additional hydrogen bonds can contribute to switch the regioselectivity for the α-hydroxyamination (N-addition). There is also a contribution of theoretical chemistry for understanding substituent effects from both reagents on selectivity and activation barrier of the rate-determining addition step. The TS involved in this step is highly sensitive to solvent effects that are therefore recommended to be included in the computations (at least implicitly).
Miscellaneous
While the NDA, nitroso ene, and nitrosoaldol reactions are the main classes involving C-nitroso species, other less popular reactions involving nitroso species relied on theoretical chemistry to refine the understanding of their mechanism. Examples from the literature include pseudocyclic and addition reactions, both relying on the electrophilic nature of nitroso species.Among pseudocyclic reactions, the [3 + 2] cycloaddition of nitrosoallenes or nitrosoketenes was investigated by computational means (Fig. 45). The trend for nitrosoketenes to undergo [3 + 2] instead of [4 + 2] cycloadditions with ketones and aldehydes was demonstrated by Birney et al. in the 90s at the RHF and MP4/6-31G* levels.172,173 The mechanism was characterized by a planar pseudopseudocyclic transition state. The choice of the carbonyl model was however important to reflect the experimental results obtained for acetophenone derivatives. While the results associated with formaldehyde and acetone were found to be inconsistent, 2-propenal, a conjugated carbonyl compound, was associated with an asynchronous TS that helped the authors to rationalize experimental substituent effects. The difference of reactivity and regioselectivity between nitrosoallenes, nitrosoketenes, and nitrosoalkenes was supported by theoretical chemistry in 2016 by Tanimoto et al.174 The LUMO coefficients computed at the B3LYP/6-31G** level highlighted not only the higher reactivity of nitroso compounds compared to conjugated carbonyls, but also the larger coefficient at the nitrogen than at the sp-carbon atom for nitrosoallenes. The opposite trend was determined for nitrosoalkenes (sp2 carbon instead of sp). The global reactivity for [3 + 2] cycloadditions was established accordingly: nitrosoketenes < nitrosoallenes < nitrosoalkenes.
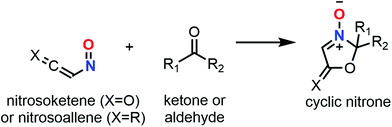 | ||
| Fig. 45 [3 + 2] cycloaddition of nitrosoallenes or nitrosoketenes leading to cyclic nitrones formation. | ||
In 2006, Houk et al. studied at the B3LYP level/6-31G* level the thermal and acid-catalyzed hetero-Cope rearrangement of nitrosobutenes (Fig. 46).175 Different pathways were considered for nitrosobutene (74), included diradical, radical pair, or ion pair formation but energies showed a favored one-step mechanism. The TS adopting a chair structure was 6 kcal mol−1 lower than the one involving a boat conformation. Although only the boat conformation could be allowed for cyclic species, cyclic nitrosobutenes had a lower activation barrier than acyclic ones. Adding an EWG substituent such as methoxycarbonyl on the nitroso compound lowered the activation barrier. The addition of a Lewis acid drastically accelerated the reaction (<5 kcal mol−1 instead of 25–30 kcal mol−1) through charge separation and stabilization in the TS via the coordination on the nitrogen atom.
Three years later, the same group investigated both experimentally and computationally the mechanism involved in the nitrosoarene-alkyne cycloaddition leading to 3-substituted indoles formation (Fig. 47).176 The study at the (U)B3LYP/6-31+G* level rapidly excluded the presence of a one-step pathway. The addition between the nitrosoarene and the alkyne was found to be rate-determining and leading to a diradical intermediate. The latter intermediate featured the smallest and largest unpaired electron density on the nitroso and vinyl moiety, respectively. The formation of such a stable vinyl radical was responsible for the regioselectivity towards the substitution at position 3. Spin contamination was determined for the transition state (S2 = 0.47) due to the use of an unrestricted method such as UB3LYP, but it was eliminated by using the spin projection method. The corresponding calculations highlighted the decrease of the activation barrier in the presence of EWG and EDG substituents on the nitroso and the alkyne, respectively. Moreover, the computations showed that a carbonyl substituent could also stabilize the vinyl radical and reduce the activation barrier. After the C–N bond formation, the intermediate underwent cyclization and tautomerization to give the final product.
Another report on using computational chemistry for a pseudocyclic reaction involving C-nitroso species was published one year later by Studer, Grimme et coworker (Fig. 48).177 The [2 + 2] cycloaddition between ketenes and nitrosopyridines (34 and 2-methyl-6-nitrosopyridine (75)) was demonstrated to be highly regio- and enantioselective upon catalysis with a Cu(I)/Walphos-CF3 complex. Computations at the B2PLYP-D/QZVPP level confirmed the lack of regioselectivity in the absence of the copper catalyst since the barrier leading to C(O)–O bond formation was calculated to be only 1.4 kcal mol−1 lower than for the C(O)–N bond formation. On the contrary, an energy difference of 6.6 kcal mol−1 in favor of the C(O)–N addition was determined in the presence of the Cu(I)/Walphos-CF3 complex. The cost for calculating such a large system (complex with copper) was reduced by applying the resolution of identity approximation (RI-JK) where the first calculations for the Coulomb and Exchange energies used a reduced auxiliary basis set until convergence was reached, then the last computation was made with a full auxiliary basis set.178 Their theoretical study also emphasized the one-step but asynchronous mechanism involved in this reaction, with the presence of a C(O)–N bond shorter than the C–O bond.
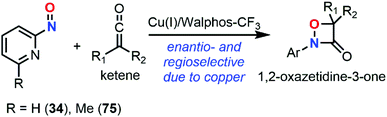 | ||
| Fig. 48 [2 + 2] Cycloaddition between ketenes and 2-nitrosopyridine (34) or 2-methyl-6-nitrosopyridine (75) leading to 1,2-oxazetidine-3-one. | ||
In 2007, Srivastava et al. used DFT to confirm the roles of complexes involved in a copper(I)-catalyzed allylic amination between 1 and alkenes (Fig. 49).179 Despite no transition state was considered in the study, computing the energies of each intermediate at the B3LYP/6-31G level excluded a thermodynamic control on the reaction. Indeed, only small differences in energy were calculated between the various regioisomers, which could not explain the high experimental regioselectivity for the C–N bond formation towards the less substituted olefinic carbon. The computational results suggested a plausible stepwise mechanism: (a) reduction of the Cu(II) complex into Cu(I), then (b) coordination to 1 that was obtained by oxidation of the corresponding hydroxylamine, followed by (c) alkene association before (d) an allyl-H transfer and finally (e) a reductive elimination to give the allyl hydroxylamine derivative. This mechanism was also supported with experimental data, which supported that 1 alone was not able to conduct the amination.
In 2017, Magdesieva et al. explored the synthetic utility of a copper-assisted amination of boronic acids with nitrosoarenes to synthesize bulky diarylamines (Fig. 50).180 The use of computational chemistry at the PBE/Λ22 level helped the authors to rationalize the observations and to propose a mechanism. The activation of 1 by the copper(I) complex was not associated with an enthalpy barrier and was determined to be exothermic. The second step, a transmetalation with the boronic acid involving a five-membered cyclic transition state, appeared as rate-determining (ΔE‡ = 24.0 kcal mol−1) and highly endergonic due to the decrease of entropy. An alternative pathway for this step was also considered. Calculations of the activation barrier showed a much stronger effect when a bulky group was placed on the boronic acid instead of on the nitroso compound. The implementation of either EWG or EDG substituents on both reagents had no impact on the activation barrier. An elimination of HBO2, which is thermodynamically and kinetically favored, was then considered, followed by a reductive elimination process to give the diaryl moiety. The latter step was found to be sensitive to electronic substituent effects. The best results were obtained with the presence of EDG and EWG substituents on the boronic acid and 1, respectively. The final steps leading to the free diarylamine appeared as an isomerization before a thermodynamically favorable oxidative addition of copper(I) to the N–O bond. All these results helped to determine the best reagents for the minimization of side-products.
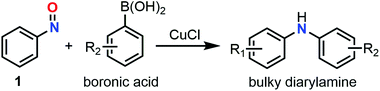 | ||
| Fig. 50 Copper-assisted amination of boronic acids with nitrosoarenes leading to bulky diarylamines formation. | ||
In 2019, Cibulka et al. gave mechanistic insights via computational chemistry about the mechanism of a Mitsunobu esterification reaction where 1 replaced the usual dialkyl azodicarboxylates (Fig. 51).181 The enantioselectivity of the protocol was sensitive to the nature of the nitroso electrophile, with a reduced yield towards the desired ester when aliphatic nitroso compounds or nitrosoarenes bearing EWG or EDG substituents were used. Indeed, an undesired formation of azoxybenzene through dimeric reduction of 1 was competitive to the Mitsunobu reaction. The two mechanisms were therefore studied at the B3PW91/def2-SVPD level using PCM to implicitly include acetonitrile in the calculations. Transition states were not considered due to the requirement of explicit solvation for accurate results. Based on the results of a report about interactions between trimethylphosphine and 2-nitrosostyrene (76),182 the authors reported 3 possible oxazaphophiridine intermediates resulting from the addition of 1 to triphenylphosphine, that were highly sensitive to solvation. On the one hand, an alkyphosphonium ion could be formed after the addition of an alcohol and the release of a phenylhydroxylamine fragment. On the other hand, the formation of a nitrene intermediate after the release of triphenylphosphine oxide is likely to compete with the first path, since the computed energy profiles were similar. While an alkyphosphonium ion was responsible for the ester formation, a nitrene led to azoxybenzene synthesis, hence emphasizing the importance of the nitroso substituents to tune the selectivity towards the Mitsunobu reaction.
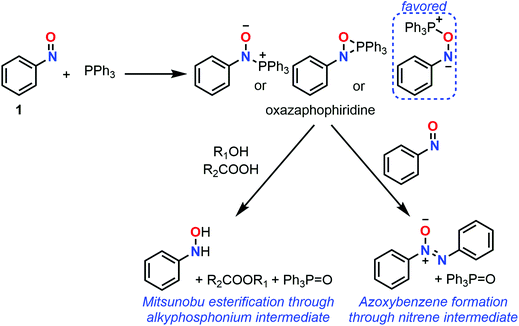 | ||
| Fig. 51 Mitsunobu esterification reaction with nitrosobenzene (1) replacing the usual dialkyl azodicarboxylates. | ||
Computations are strongly supportive to determine the mechanism involved in less common pseudocyclic reactions, which can proceed either through a one-step asynchronous pathway or a stepwise process involving diradical species, as previously determined for NDA and ene reactions. This similarity emphasizes the radicalar behavior of C-nitroso species during pseudocyclic reactions that involve TS with zwitterionic pseudoradicals centers or diradical intermediates and requires adequate theoretical methods for considering unpaired electrons. For addition reactions, computations emphasize that the mechanisms usually involve multi-step processes and can be catalyzed by metals. Energies calculations of the plausible intermediates and TS enable the determination of the rate-determining step, and therefore the parameters (steric hindrance, electronic, etc.) that can tune the rate and selectivity of the reaction. It can also determine whether the reaction is kinetically or thermodynamically controlled.
Conclusions
During these past 3 decades, computational chemistry has been increasingly relied on as a strong asset for demystifying the complex behavior of C-nitroso species. Different aspects of these species, including their molecular properties and complex reactivity profiles, have been thoroughly studied with various computational methods differing by their accuracy and their cost-efficiency.Computational chemistry helped the chemists to predict and tune the unique spectroscopic properties of C-nitroso species (UV, IR, and Raman), characterized by a small absorption energy (1.8–2.2 eV, making them colorful compounds) and a strong N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching around 1500 cm−1. In addition, the central C-nitroso dimerization equilibrium was determined as an exothermic but ordering process that could be tuned with temperature (ΔG‡ = ΔH‡ − T*ΔS‡). Computations also were essential for the identification of the main species experimentally observed during tautomerization, namely rotamers or isomers of the syn,syn-oxime form characterized by a strong intramolecular hydrogen bond. The computation of bond dissociation energies highlighted the likelihood of homolytic cleavage of the C–NO bond to be a competitive pathway to pseudocyclic or addition reactions, especially for C-nitroso compounds bearing a neighboring EWG substituent. It was also demonstrated that NDA cycloadditions have a strong preference for the endo approach and the ortho regioselectivity due to minimization of the “exo lone pair effect” and favorable coulombic interactions, respectively. By contrast with other nitroso species that are only seen as electron-deficient candidates, the intrinsic properties of nitrosoalkenes make them good candidates for both normal and reverse electron demand NDA reactions. Regarding the ene reactions, theoretical studies concluded that aziridine-N-oxide is not an intermediate leading to the ene product, as well as that regioselectivity is under steric control. In addition, computations provided valuable models and explanations about the origin of the stereoselectivity in nitrosoaldol reactions and the switch of regioselectivity from α-oxyamination (N-addition) to α-aminoxylation (O-addition) upon the addition of an acid. Central to these explanations is the formation of specific hydrogen bonds between the acid catalyst and the nitrogen atom of the C-nitroso species, which locks the enolate attack and increases the electrophilicity of the oxygen atom. Finally, computations offer an invaluable option to better tune the rate and selectivity of addition reactions by studying in silico each step of complex multistep processes and evaluating the effect of metal catalysis.
O stretching around 1500 cm−1. In addition, the central C-nitroso dimerization equilibrium was determined as an exothermic but ordering process that could be tuned with temperature (ΔG‡ = ΔH‡ − T*ΔS‡). Computations also were essential for the identification of the main species experimentally observed during tautomerization, namely rotamers or isomers of the syn,syn-oxime form characterized by a strong intramolecular hydrogen bond. The computation of bond dissociation energies highlighted the likelihood of homolytic cleavage of the C–NO bond to be a competitive pathway to pseudocyclic or addition reactions, especially for C-nitroso compounds bearing a neighboring EWG substituent. It was also demonstrated that NDA cycloadditions have a strong preference for the endo approach and the ortho regioselectivity due to minimization of the “exo lone pair effect” and favorable coulombic interactions, respectively. By contrast with other nitroso species that are only seen as electron-deficient candidates, the intrinsic properties of nitrosoalkenes make them good candidates for both normal and reverse electron demand NDA reactions. Regarding the ene reactions, theoretical studies concluded that aziridine-N-oxide is not an intermediate leading to the ene product, as well as that regioselectivity is under steric control. In addition, computations provided valuable models and explanations about the origin of the stereoselectivity in nitrosoaldol reactions and the switch of regioselectivity from α-oxyamination (N-addition) to α-aminoxylation (O-addition) upon the addition of an acid. Central to these explanations is the formation of specific hydrogen bonds between the acid catalyst and the nitrogen atom of the C-nitroso species, which locks the enolate attack and increases the electrophilicity of the oxygen atom. Finally, computations offer an invaluable option to better tune the rate and selectivity of addition reactions by studying in silico each step of complex multistep processes and evaluating the effect of metal catalysis.
The quality of a computational result is obviously inherently related to the appropriate selection of the computational method and resources to avoid misinterpretations. A consensus through the literature spotlights DFT with the B3LYP/6-31G* as a good compromise between accuracy and computational time. Adding diffuse functions to the basis set enables better results for describing long-range interactions with the lone pairs of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. However, the description of spectroscopic properties requires a higher level of accuracy, namely, the use of a larger basis set and a multi-reference approach or a least the integration of the time factor with the use of TD-DFT for instance in absorption studies.
O moiety. However, the description of spectroscopic properties requires a higher level of accuracy, namely, the use of a larger basis set and a multi-reference approach or a least the integration of the time factor with the use of TD-DFT for instance in absorption studies.
Local indexes from the CDFT reflect more accurately the intrinsic behavior of each nitroso species towards nucleophilic or electrophilic targets than global indexes. Both local and global reactivity indexes are relatively accessible to the chemist, and provide invaluable information regarding the regioselectivity by identifying the most electrophilic and nucleophilic centers on each reaction partner. In the case of the catalyzed nitrosoaldol reaction, the calculation of reactivity indexes must consider the complexes formed between the catalyst and all intermediates to take hydrogen bonding into account, knowing that these electrostatic interactions are pivotal in modifying the local electrophilic character of the C-nitroso species alone. The description of such complexes and the appropriate selection of computational methods is therefore critical, even more, when stereoselectivity is at stake.
In contrast to addition reactions where the reactivity is usually under control by the CDFT, pseudocyclic reactions involving C-nitroso species such as the NDA and the nitroso ene reactions are related to the inherent radical properties of C-nitroso species. Whether a radical intermediate is concerned or not during a C-nitroso pseudocyclic reaction strongly depends on the emergence of radical stabilizing factors. Most of the time, NDA reactions are characterized by a highly asynchronous one-step transition state with a zwitterionic pseudoradical character, while ene reactions proceed through a two-step process with a polarized diradical intermediate. The computation of these radical mechanisms, as well as calculating homolytic bond dissociation energies, require the use of unrestricted methods to adequately account for unpaired electrons. Moreover, the regioselectivity for NDA reactions can be better described with atomic spin density instead of CDFT indexes.
The presence of lone pairs on both the nitrogen and oxygen atoms in the nitroso moiety is responsible for strong intra- or intermolecular hydrogen bonds, besides other repulsive electrostatic interactions. Such H-bonding ability is for instance a fundamental property to unlock possible tautomerization in C-nitroso species bearing a hydroxyl group. Such a long-range interaction has to be properly described by incorporating electron correlation, dispersion forces, and diffuse functions in the computational method.
The polar nature of C-nitroso compounds and their related transitions states or intermediates during pseudocyclic or addition reactions typically required the incorporation of solvent in the computation, since their reactivity is strongly modulated by specific solute–solvent interactions. Results computed in the gas phase solely are therefore not considered as reliable. Implicit solvent integration with the PCM or SMD model is therefore necessary. The rate during nitrosoaldol reactions can be accelerated with polar solvents by stabilizing the polarized transition structure. The difference of polarity with the diazoxy species is also sensitive to solvent dielectric constant and therefore the monomer–dimer equilibria becomes tunable on demand. Sometimes, strong interactive forces with a polar solvent can lead to the formation of a donor–acceptor complex, as it is the case during the tautomerization or dimerization processes. In this scenario, implicit solvation is not sufficient and it requires the explicit integration of a cluster of a few solvent molecules (1–5).
Despite this considerable amount of information collected during 3 decades, one can pinpoint the lack of a general reactivity scale towards nucleophilic and/or radicalar species that is localized either on nitrogen or oxygen. Decomposition of these unstable species or complexation with metals in their monomeric or dimeric form was also not thoroughly investigated computationally so far. Moreover, the nucleophilic character as well as the photoreactivity revealed during theoretical studies have not been exploited and experimentally demonstrate yet, hence opening new windows of reactivity to the synthetic chemist. Finally, despite numerous experimental examples, radical processes involving C-nitroso species (outside the field of pseudocyclic reactions) are still lacking systematic and thorough computational studies.
This review clearly shows that computational chemistry is a powerful tool to the synthetic chemist when dealing with species that are toxic, transient, and that come with an ambiguous reactivity, such as C-nitroso compounds. By enabling fast and cost-effective predictions or avenues towards potential rationalization, computational chemistry will most likely enter the daily life of the synthetic chemist with the emergence of cheaper but more powerful computers to stimulate its imagination and help giving insights about reaction mechanisms, solvents effects, regio- and stereoselectivities. Besides the potential to support a more refined understanding, it is also foreseen that in silico chemistry will become increasingly relied on in the current general context of sustainability that hampers the reckless use of toxic, unstable intermediates or wasteful optimizations. Both the potential to the computation of toxic, unstable, or transient species that does not raise safety or environmental hazards, and the ability to screen (in silico) conditions or to generate large libraries of compounds and perform structure (re)activity relationships without the cost associated with experimental work are truly enabling. One can also foresee that the combination of in silico methods with new process technologies that come with a refined reaction control (e.g. continuous flow technology, including microfluidics) and/or that minimize human intervention and operator-dependent experimental variations (e.g. advanced automation, AI) will shortly contribute to the development of the next generation of chemists.
Author contributions
PB prepared and wrote the manuscript. JCMM advised for the overall structure and corrected the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the F.R.S.-FNRS (Incentive grant for scientific research MIS F453020F, JCMM). PB is a F.R.S.-FNRS PhD fellow (PhD fellowship 1.A.054.21F).Notes and references
- J. Lee, L. Chen, A. H. West and G. B. Richter-Addo, Interactions of organic nitroso compounds with metals, Chem. Rev., 2002, 102, 1019 CrossRef CAS.
- G. W. Kirby, Electrophilic C-nitroso-compounds, Chem. Soc. Rev., 1977, 6, 1 Search PubMed.
- B. G. Gowenlock and G. B. Richter-Addo, Preparations of C-nitroso compounds, Chem. Rev., 2004, 104, 3315 CrossRef CAS.
- H. Yamamoto and N. Momiyama, Rich chemistry of nitroso compounds, Chem. Commun., 2005, 3514 RSC.
- D. Gooden, H. Chakrapani and E. Toone, C-Nitroso Compounds: Synthesis, Physicochemical Properties and Biological Activities, Curr. Top. Med. Chem., 2005, 5, 687 CrossRef CAS PubMed.
- I. M. Lyapkalo and S. L. Ioffe, Conjugated nitrosoalkenes, Russ. Chem. Rev., 1998, 67, 467 CrossRef.
- I. Biljan and H. Vančik, Aromatic C-nitroso compounds and their dimers: A model for probing the reaction mechanisms in crystalline molecular solids, Crystals, 2017, 7, 376 CrossRef.
- S. Iwasa, A. Fakhruddin and H. Nishiyama, Synthesis of Acylnitroso Intermediates and Their Synthetic Applications, Mini-Rev. Org. Chem., 2005, 2, 157 CrossRef CAS.
- L. I. Palmer, C. P. Frazier and J. R. de Alaniz, Developments in nitrosocarbonyl chemistry: Mild oxidation of N-substituted hydroxylamines leads to new discoveries, Synthesis, 2014, 269 Search PubMed.
- M. G. Memeo and P. Quadrelli, Generation and Trapping of Nitrosocarbonyl Intermediates, Chem. Rev., 2017, 117, 2108 CrossRef CAS.
- P. Merino, T. Tejero, I. Delso and R. Matute, Recent Advances on Asymmetric Nitroso Aldol Reaction, Synthesis, 2016, 653 CrossRef CAS.
- S. Dana, I. Ramakrishna and M. Baidya, Ambident Reactivity of Nitroso Compounds for Direct Amination and Hydroxylation of Carbonyls, Synthesis, 2017, 3281 CAS.
- D. Beaudoin and J. D. Wuest, Dimerization of Aromatic C-Nitroso Compounds, Chem. Rev., 2016, 116, 258 CrossRef CAS.
- L. R. Domingo, M. Ríos-Gutiérrez, E. Chamorro and P. Pérez, Aromaticity in Pseudocyclic Transition State Structures? A Critical Rationalisation Based on the Topological Analysis of Electron Density, ChemistrySelect, 2016, 1, 6026 CrossRef CAS.
- L. R. Domingo, M. Ríos-Gutiérrez, B. Silvi and P. Pérez, The Mysticism of Pseudocyclic Reactions: A Contemporary Rationalisation of Organic Reactivity Based on Electron Density Analysis, Eur. J. Org. Chem., 2018, 1107 CrossRef CAS.
- Y. Yamamoto and H. Yamamoto, Recent advances in asymmetric nitroso Diels-Alder reactions, Eur. J. Org. Chem., 2006, 2031 CrossRef CAS.
- B. S. Bodnar and M. J. Miller, The nitrosocarbonyl hetero-Diels-Alder reaction as a useful tool for organic syntheses, Angew. Chem., Int. Ed., 2011, 50, 5630 CrossRef CAS.
- S. Carosso and M. J. Miller, Nitroso Diels-Alder (NDA) reaction as an efficient tool for the functionalization of diene-containing natural products, Org. Biomol. Chem., 2014, 12, 7445 RSC.
- L. Brulíková, A. Harrison, M. J. Miller and J. Hlaváč, Stereo- and regioselectivity of the hetero-Diels-Alder reaction of nitroso derivatives with conjugated dienes, Beilstein J. Org. Chem., 2016, 12, 1949 CrossRef PubMed.
- A. Menichetti, F. Berti and M. Pineschi, Nitroso Diels-Alder Cycloadducts Derived From N-Acyl-1,2-dihydropyridines as a New Platform to Molecular Diversity, Molecules, 2020, 25, 563 CrossRef PubMed.
- W. Adam and O. Krebs, The Nitroso Ene Reaction: A Regioselective and Stereoselective Allylic Nitrogen Functionalization of Mechanistic Delight and Synthetic Potential, Chem. Rev., 2003, 103, 4131 CrossRef CAS PubMed.
- M. Baidya and H. Yamamoto, Advancements in the nascent nitroso-ene reaction, Synthesis, 2013, 1931 CrossRef CAS.
- Y. Gao, S. Yang, W. Xiao, J. Nie and X. Q. Hu, Radical chemistry of nitrosoarenes: Concepts, synthetic applications and directions, Chem. Commun., 2020, 56, 13719 RSC.
- L. D. Ardila-Leal, R. A. Poutou-Piñales, A. M. Pedroza-Rodríguez and B. E. Quevedo-Hidalgo, A brief history of colour, the environmental impact of synthetic dyes and removal by using laccases, Molecules, 2021, 26, 3813 CrossRef CAS PubMed.
- R. Raue and J. F. Corbett, Nitro and nitroso dyes, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2000 Search PubMed.
- J. E. T. Corrie, G. W. Kirby and J. W. M. Mackinnon, Reactions of Transient C-Nitrosocarbonyl Compounds with Dienes, Mono- olefins, and Nucleophiles, J. Chem. Soc., Perkin Trans. 1, 1985, 883 RSC.
- I. Novak, Computational thermochemistry of C-nitroso compounds, Struct. Chem., 2016, 27, 1395 CrossRef CAS.
- V. E. H. Kassin, R. Morodo, T. Toupy, I. Jacquemin, K. Van Hecke, R. Robiette and J. C. M. Monbaliu, A modular, low footprint and scalable flow platform for the expedient α-aminohydroxylation of enolizable ketones, Green Chem., 2021, 23, 2336 RSC.
- J. F. Arenas, J. C. Otero, D. Peláez and J. Soto, CASPT2 study of the decomposition of nitrosomethane and its tautomerization reactions in the ground and low-lying excited states, J. Org. Chem., 2006, 71, 983 CrossRef CAS.
- S. Pou, D. E. Anderson, W. Surichamorn, L. L. Keaton and M. L. Tod, Biological studies of a nitroso compound that releases nitric oxide upon illumination, Mol. Pharmacol., 1994, 46, 709 CAS.
- A. Di Stilo, C. Medana, B. Ferrarotti, A. L. Gasco, D. Ghigo, A. Bosia, P. A. Martorana and A. Gasco, In vitro and in vivo vasodilating activity of nitroso derivatives gem-substituted with electron-withdrawing groups, Pharmacol. Res., 2000, 41, 469 CrossRef CAS PubMed.
- N. A. Magnus, S. Campagna, P. N. Confalone, S. Savage, D. J. Meloni, R. E. Waltermire, R. G. Wethman and M. Yates, Quaternary chiral center via diastereoselective enolate amination enables the synthesis of an anti-inflammatory agent, Org. Process Res. Dev., 2010, 14, 159 CrossRef CAS.
- N. Emmanuel, P. Bianchi, J. Legros and J. C. M. Monbaliu, A safe and compact flow platform for the neutralization of a mustard gas simulant with air and light, Green Chem., 2020, 22, 4105 RSC.
- E. Schrödinger, An undulatory theory of the mechanics of atoms and molecules, Phys. Rev., 1926, 28, 1049 CrossRef.
- M. Born and R. J. Oppenheimer, Zur Quamtentheorie der Molekeln, Ann. Phys., 1927, 20, 457 CrossRef.
- D. R. Hartree, The Wave Mechanics of an Atom with a Non-Coulomb Central Field Part I Theory and Methods, Math. Proc. Cambridge Philos. Soc., 1928, 24, 89 CrossRef CAS.
- J. C. Slater, The self consistent field and the structure of atoms, Phys. Rev., 1928, 32, 339 CrossRef.
- C. C. J. Roothaan, New developments in molecular orbital theory, Rev. Mod. Phys., 1951, 23, 69 CrossRef CAS.
- B. O. Roos, The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations, Adv. Chem. Phys., 1987, 69, 399 CAS.
- J. Čížek, On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods, J. Chem. Phys., 1966, 45, 4256 CrossRef.
- M. S. Plesset and C. Møller, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46, 618 CrossRef.
- K. Andersson, P. Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a complete active space self-consistent field reference function, J. Chem. Phys., 1992, 96, 1218 CrossRef CAS.
- J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, Gaussian-1 theory: A general procedure for prediction of molecular energies, J. Chem. Phys., 1989, 90, 5622 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 1999, 110, 2822 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, 864 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, 1133 CrossRef.
- J. P. Perdew and K. Schmidt, Jacob's ladder of density functional approximations for the exchange-correlation energy, AIP Conf. Proc., 2001, 577, 1 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, How Accurate Are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Composed of Main-Group Elements?, J. Chem. Theory Comput., 2016, 12, 4303 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC.
- S. Grimme, Accurate description of van der Waals complexes by density functional theory including empirical corrections, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS.
- E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-consistent molecular-orbital methods. IX. An extended gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 724 CrossRef CAS.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- L. Onsager, Electric Moments of Molecules in Liquids, J. Am. Chem. Soc., 1936, 58, 1486 CrossRef CAS.
- S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55, 117 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS.
- H. B. Schlegel, Optimization of Equilibrium Geometries and Transition Structures, J. Comput. Chem., 1982, 3, 214 CrossRef CAS.
- H. B. Schlegel, Exploring potential energy surfaces for chemical reactions: An overview of some practical methods, J. Comput. Chem., 2003, 24, 1514 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, Reaction path following in mass-weighted internal coordinates, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS.
- R. S. Mulliken, Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I, J. Chem. Phys., 1955, 23, 1833 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- R. F. W. Bader and C. F. Matta, Atoms in molecules as non-overlapping, bounded, space-filling open quantum systems, Found. Chem., 2013, 15, 253 CrossRef CAS.
- G. J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y. D. Wu, Computational organic chemistry: Bridging theory and experiment in establishing the mechanisms of chemical reactions, J. Am. Chem. Soc., 2015, 137, 1706 CrossRef CAS.
- P. Nakliang, S. Yoon and S. Choi, Emerging Computational Approaches for the Study of Regio- and Stereoselectivity in Organic Synthesis, Org. Chem. Front., 2021, 8, 5165–5181 RSC.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121, 9816 CrossRef CAS PubMed.
- Z. Lin, Interplay between theory and experiment: Computational organometallic and transition metal chemistry, Acc. Chem. Res., 2010, 43, 602 CrossRef CAS PubMed.
- D. Chen, Q. Xie and J. Zhu, Unconventional Aromaticity in Organometallics: The Power of Transition Metals, Acc. Chem. Res., 2019, 52, 1449 CrossRef CAS.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity, Molecules, 2016, 21, 748 CrossRef.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Conceptual density functional theory: status, prospects, issues, Theor. Chem. Acc., 2020, 139, 1 Search PubMed.
- E. Scrocco and J. Tomasi, The electrostatic molecular potential as a tool for the interpretation of molecular properties, Fortschr. Chem. Forsch., 1973, 42, 95 Search PubMed.
- P. Politzer and R. Bar-Adon, Computational Analysis of the Reactive Properties of Some Nitrosoaromatic Molecules, J. Phys. Chem., 1987, 91, 2069 CrossRef CAS.
- R. G. Parr and W. Yang, Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity, J. Am. Chem. Soc., 1984, 106, 4049 CrossRef CAS.
- W. Yang and W. J. Mortier, The Use of Global and Local Molecular Parameters for the Analysis of the Gas-Phase Basicity of Amines, J. Am. Chem. Soc., 1986, 108, 5708 CrossRef CAS PubMed.
- V. Pilepić and S. Uršić, Nucleophilic reactivity of the nitroso group. Fukui function DFT calculations for nitrosobenzene and 2-methyl-2-nitrosopropane, J. Mol. Struct.: THEOCHEM, 2001, 538, 41 CrossRef.
- R. K. Roy, S. Krishnamurti, P. Geerlings and S. Pal, Local softness and hardness based reactivity descriptors for predicting intra- and intermolecular reactivity sequences: Carbonyl compounds, J. Phys. Chem. A, 1998, 102, 3746 CrossRef CAS.
- K. Senthilkumar and P. Kolandaivel, Post Hartree-Fock and density functional theory studies on structure and conformational stability of nitrosoethylene and substituted compounds of nitrosoethylene, Comput. Chem., 2002, 26, 207 CrossRef CAS.
- R. Kanakaraju, P. Kolandaivel and B. G. Gowenlock, Quantum chemical studies of nitrosobuta-1,3-diene and nitrosostyrene molecules, J. Mol. Struct.: THEOCHEM, 2002, 577, 121 CrossRef CAS.
- K. Anandan, P. Kolandaivel, R. Kumaresan and B. G. Gowenlock, Ab initio and DFT studies on structure and stability of nitroso and nitro substituted furan molecules, J. Mol. Struct.: THEOCHEM, 2003, 639, 213 CrossRef CAS.
- K. Anandan, P. Kolandaivel, R. Kumaresan and B. G. Gowenlock, Quantum chemical studies on structure, conformation and isomerization of nitroso, nitro substituted benzene and 1,3-cyclopentadiene, J. Mol. Struct.: THEOCHEM, 2004, 680, 149 CrossRef CAS.
- S. Vijayakumar and P. Kolandaivel, Isomerization of C3H3NO isomers: Ab initio study, Mol. Phys., 2006, 104, 1401 CrossRef CAS.
- L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels-Alder reactions, Tetrahedron, 2002, 58, 4417 CrossRef CAS.
- L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels-Alder reactions, Tetrahedron, 2002, 58, 4417 CrossRef CAS.
- L. R. Domingo, E. Chamorro and P. Pérez, Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study, J. Org. Chem., 2008, 73, 4615 CrossRef CAS.
- L. R. Domingo, A new C-C bond formation model based on the quantum chemical topology of electron density, RSC Adv., 2014, 4, 32415 RSC.
- L. R. Domingo, P. Pérez and J. A. Sáez, Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions, RSC Adv., 2013, 3, 1486 RSC.
- W. Neugebauer, C. Sessa, C. Steuer, T. Allscher and H. Stege, Naphthol Green – a forgotten artists’ pigment of the early 20th century. History, chemistry and analytical identification, J. Cult. Herit., 2019, 36, 153 CrossRef.
- S. Lacombe, M. Loudet, A. Dargelos and J. M. Camou, Calculation of the electronic and photoelectronic spectra of nitroso compounds: A reinvestigation by use of configuration interaction methods, Chem. Phys., 2000, 258, 1 CrossRef CAS.
- E. K. Dolgov, V. A. Bataev, V. I. Pupyshev and I. A. Godunov, Ab initio description of the structure and dynamics of the nitrosomethane molecule in the first excited singlet and triplet electronic states, Int. J. Quantum Chem., 2004, 96, 589 CrossRef CAS.
- H. M. Badawi and W. Förner, Study of structural stability and vibrational spectra of nitroso and nitroketenes, J. Mol. Struct.: THEOCHEM, 2001, 542, 7 CrossRef CAS.
- H. M. Badawi and A. A. El-Rayyes, Vibrational spectra and potential energy distributions of normal modes of 3-nitroso- and 3-nitrocyclopropenes, J. Mol. Struct.: THEOCHEM, 2002, 588, 17 CrossRef CAS.
- H. M. Badawi and W. Förner, Analyses of vibrational spectra of nitroso- and nitroethylenes, J. Mol. Struct.: THEOCHEM, 2004, 677, 153 CrossRef CAS.
- W. Förner and H. M. Badawi, Infrared and Raman spectra and vibrational analyses calculated with Moeller-Plesset perturbation theory of second order of nitrosoethylene and its chloro-derivatives, J. Mol. Model., 2005, 11, 542 CrossRef.
- H. M. Badawi and W. Förner, Influence of fluorine substitution in nitrosoethylene and their vibrational spectra, calculated with Møller-Plesset perturbation theory of second order, J. Mol. Struct.: THEOCHEM, 2005, 725, 183 CrossRef CAS.
- D. Jacquemin and E. A. Perpète, The n → π* transition in nitroso compounds: A TD-DFT study, Chem. Phys. Lett., 2006, 420, 529 CrossRef CAS.
- N. A. Hussien, A. M. Mohammed, M. Tessema, F. B. Dejene and M. Redi-Abshiro, Solvent polarity and excitation wavelength dependence of the dual fluorescence in N,N-diethyl-4-nitrosoaniline, J. Fluoresc., 2012, 22, 451 CrossRef CAS.
- E. Procházková, L. Čechová, J. Tarábek, Z. Janeba and M. Dračínský, Tunable Push-Pull Interactions in 5-Nitrosopyrimidines, J. Org. Chem., 2016, 81, 3780 CrossRef.
- V. Ragavendran and S. Muthunatesan, An insight into the conformal flexibility and vibrational behavior of 2-nitroso-1-naphthol: A density functional theory approach, Spectrosc. Lett., 2016, 49, 294 CrossRef CAS.
- C. Azarias, C. Habert, Š. Budzák, X. Blase, I. Duchemin and D. Jacquemin, Calculations of n→π* Transition Energies: Comparisons between TD-DFT, ADC, CC, CASPT2, and BSE/GW Descriptions, J. Phys. Chem. A, 2017, 121, 6122 CrossRef CAS PubMed.
- U. Banerjee, W. L. Karney, B. S. Ault and A. D. Gudmundsdottir, Photolysis of 5-azido-3-phenylisoxazole at cryogenic temperature: Formation and direct detection of a nitrosoalkene, Molecules, 2020, 25, 543 CrossRef.
- R. H. Cox and M. Hamada, A 13C NMR investigation of restricted rotation and dimerization in p–substituted nitrosobenzenes, Org. Magn. Reson., 1979, 12, 322 CrossRef CAS.
- M. Azoulay and E. Fischer, Low-temperature Proton Nuclear Magnetic Resonance and Ultraviolet Absorption Spectra and Photochemistry of the System Nitrosobenzene- Azodioxybenzene and its Methyl Derivatives, J. Chem. Soc., Perkin Trans. 2, 1982, 637 RSC.
- K. Varga, I. Biljan, V. Tomišić, Z. Mihalić and H. Vančik, Quantum Chemical Calculations of Monomer-Dimer Equilibria of Aromatic C -Nitroso Compounds, J. Phys. Chem. A, 2018, 122, 2542 CrossRef CAS PubMed.
- R. Glaser, R. K. Murmann and C. L. Barnes, Why do nitroso compounds dimerize while their oxime tautomers do not? A structural study of the trans-dimer of 2-chloro-2-methyl-3-nitrosobutane and higher level ab initio study of thermodynamic stabilities and electronic structures of isomers of diazene, J. Org. Chem., 1996, 61, 1047 CrossRef CAS.
- I. Rončević, P. Bibulić, H. Vančik and I. Biljan, Solution equilibria of aromatic dinitroso compounds: a combined NMR and DFT study, Struct. Chem., 2018, 29, 1489 CrossRef.
- A. Kržan and J. Mavri, Nitroso-naphthol quinone-monooxime tautomeric equilibrium revisited: Evidence for oximo group isomerization, Chem. Phys., 2002, 277, 71 CrossRef.
- V. Enchev, G. Ivanova, A. Ugrinov, G. D. Neykov, S. Minchev and N. Stoyanov, Ab initio quantum chemical and NMR study of the symmetric monooximes of 1,2,3-phenalenetrione and 1,2,3-indantrione, J. Mol. Struct., 1998, 440, 227 CrossRef CAS.
- V. Enchev, G. Ivanova, A. Ugrinov and G. D. Neykov, Tautomeric and conformational equilibrium of acenaphthenequinonemonooxime, J. Mol. Struct., 1999, 508, 149 CrossRef CAS.
- A. Kržan, D. R. Crist and V. Horák, An ab initio molecular orbital study of nitrosophenol/quinone monooxime equilibria, J. Mol. Struct.: THEOCHEM, 2000, 528, 237 CrossRef.
- G. Ivanova and V. Enchev, Does tautomeric equilibrium exist in ortho-nitrosonaphthols?, Chem. Phys., 2001, 264, 235 CrossRef CAS.
- J. A. Long, N. J. Harris and K. Lammertsma, Formaldehyde oxime ⇌ nitrosomethane tautomerism, J. Org. Chem., 2001, 66, 6762 CrossRef CAS PubMed.
- V. Enchev, G. Ivanova and N. Stoyanov, Tautomeric and conformational equilibrium of 2-nitrosophenol and 9,10-phenanthrenequinonemonooxime: Ab initio and NMR study, J. Mol. Struct.: THEOCHEM, 2003, 640, 149 CrossRef CAS.
- E. D. Raczyńska, T. M. Krygowski, J. E. Zachara, B. Ośmiałowski and R. Gawinecki, Tautomeric equilibria, H-bonding and π-electron delocalization in o-nitrosophenol. A B3LYP/6–311+G(2df,2p) study, J. Phys. Org. Chem., 2005, 18, 892 CrossRef.
- A. E. Shchavlev, A. N. Pankratov and V. Enchev, Intramolecular hydrogen-bonding interactions in 2-nitrosophenol and nitrosonaphthols: Ab initio, density functional, and nuclear magnetic resonance theoretical study, J. Phys. Chem. A, 2007, 111, 7112 CrossRef CAS PubMed.
- V. Enchev and S. Angelova, Does tautomeric equilibrium exist in 4-nitroso-5-pyrazolones?, J. Mol. Struct.: THEOCHEM, 2009, 897, 55 CrossRef CAS.
- M. Rakhshanipour, H. Jalali, V. Darugar, H. Eshghi and M. Vakili, Synthesis, structure, tautomerism, intramolecular hydrogen bond, and vibrational assignment of 3-nitroso-2,4-pentanedione: A theoretical and experimental approach, Vib. Spectrosc., 2020, 107, 103036 CrossRef.
- S. Poorhaji, M. Pordel and S. Ramezani, New heterocyclic green, blue and orange dyes from indazole: Synthesis, tautomerism, alkylation studies, spectroscopic characterization and DFT/TD-DFT calculations, J. Mol. Struct., 2016, 1119, 151 CrossRef CAS.
- E. D. Ilieva, G. P. Petrova, R. D. Nikolova and G. N. Vayssilov, Computational elucidation of the reaction mechanism for synthesis of pyrrolidinedione derivatives: Via Nef-Type rearrangement-cyclization reaction, RSC Adv., 2018, 8, 3178 RSC.
- M. Zhao, W. He, L. H. Zou, D. Wang, T. Y. Sun and X. F. Xia, Iron-catalyzed hydrogen atom transfer induced cyclization of 1,6-enynes for the synthesis of ketoximes: A combined experimental and computational study, Org. Chem. Front., 2021, 8, 643 RSC.
- J. Park, I. V. Dyakov, A. M. Mebel and M. C. Lin, Experimental and theoretical studies of the unimolecular decomposition of nitrosobenzene: High-pressure rate constants and the C-N bond strength, J. Phys. Chem. A, 1997, 101, 6043 CrossRef CAS.
- Y. Fu, Y. Mou, B. L. Lin, L. Liu and Q. X. Guo, Structures of the X - Y - NO Molecules and Homolytic Dissociation Energies of the Y - NO Bonds (Y) C, N, O, (S), J. Phys. Chem. A, 2002, 106, 12386 CrossRef CAS.
- X. Li, H. Deng, X. Q. Zhu, X. Wang, H. Liang and J. P. Cheng, Establishment of the C-NO bond dissociation energy scale in solution and its application in analyzing the trend of NO transfer from C-nitroso compound to thiols, J. Org. Chem., 2009, 74, 4472 CrossRef CAS PubMed.
- H. Chakrapani, M. D. Bartberger and E. J. Toone, C-nitroso donors of nitric oxide, J. Org. Chem., 2009, 74, 1450 CrossRef CAS.
- J. C. M. Monbaliu, L. K. Beagle, J. Kovacs, M. Zeller, C. V. Stevens and A. R. Katritzky, En route towards α-benzotriazoyl nitroso derivatives, RSC Adv., 2012, 2, 8941 RSC.
- B. S. Jursic and Z. Zdravkovski, Theoretical Study of the BH3-Catalyzed Hetero Diels–Alder Reaction between Ethylene and Nitrosoethylene, J. Org. Chem., 1995, 60, 3163 CrossRef CAS.
- D. Sperling, A. Mehlhorn, H. U. Reißig and J. Fabian, Theoretical study of pericyclic reactions of nitrosoethylene and (thionitroso)ethylene, Liebigs Ann., 1996, 1615 CrossRef CAS.
- J. Liu, S. Niwayama, Y. You and K. N. Houk, Theoretical Prediction and Experimental Tests of Conformational Switches in Transition States of Diels-Alder and 1,3-Dipolar Cycloadditions to Enol Ethers, J. Org. Chem., 1998, 63, 1064 CrossRef CAS.
- A. G. Leach and K. N. Houk, Transition states and mechanisms of the hetero-Diels-Alder reactions of hyponitrous acid, nitrosoalkanes, nitrosoarenes, and nitrosocarbonyl compounds, J. Org. Chem., 2001, 66, 5192 CrossRef CAS PubMed.
- M. A. McCarrick, Y. D. Wu and K. N. Houk, Exo-Lone-Pair Effect on Hetero-Diels-Alder Cycloaddition Stereochemistry, J. Am. Chem. Soc., 1992, 114, 1499 CrossRef CAS.
- M. A. McCarrick, Y. D. Wu and K. N. Houk, Hetero-Diels-Alder Reaction Transition Structures: Reactivity, Stereoselectivity, Catalysis, Solvent Effects, and the exo-Lone-Pair Effect, J. Org. Chem., 1993, 58, 3330 CrossRef CAS.
- A. G. Leach and K. N. Houk, Diels-Alder and ene reactions of singlet oxygen, nitroso compounds and triazolinediones: Transition states and mechanisms from contemporary theory, Chem. Commun., 2002, 1243 RSC.
- Z. X. Yu and Y. D. Wu, A theoretical study of the mechanisms and regiochemistry of the reactions of 5-alkoxyoxazole with thioaldehydes, nitroso compounds, and aldehydes, J. Org. Chem., 2003, 68, 412 CrossRef CAS PubMed.
- L. R. Domingo, M. T. Picher and P. Arroyo, Towards an understanding of the polar Diels-Alder reactions of nitrosoalkenes with enamines: A theoretical study, Eur. J. Org. Chem., 2006, 2570 CrossRef CAS.
- T. C. Wabnitz, S. Saaby and K. A. Jørgensen, The first catalytic inverse-electron demand hetero-Diels-Alder reaction of nitroso alkenes using pyrrolidine as an organocatalyst, Org. Biomol. Chem., 2004, 2, 828 RSC.
- L. R. Domingo, P. Pérez and J. A. Sáez, Understanding the regioselectivity in hetero Diels-Alder reactions. An ELF analysis of the reaction between nitrosoethylene and 1-vinylpyrrolidine, Tetrahedron, 2013, 69, 107 CrossRef CAS.
- J. C. Monbaliu, J. Marchand-Brynaert and D. Peeters, Is anthracene cofactor or spectator for the thermolysis of anthracenyl acylnitroso cycloadducts in the presence of a diene?, Tetrahedron Lett., 2009, 50, 2555 CrossRef CAS.
- C. K. Jana, S. Grimme and A. Studer, Enantioselective nitroso-Diels-Alder reaction and its application for the synthesis of (-)-peracetylated conduramine A-I, Chem. – Eur. J., 2009, 15, 9078 CrossRef CAS PubMed.
- J. C. Monbaliu, B. Tinant, D. Peeters and J. Marchand-Brynaert, Novel chiral 1-phosphono-1,3-butadiene for asymmetric hetero Diels-Alder cycloadditions with nitroso and azodicarboxylate dienophiles, Tetrahedron Lett., 2010, 51, 1052 CrossRef CAS.
- J. C. Monbaliu, G. Dive, J. Marchand-Brynaert and D. Peeters, HDA cycloadditions of 1-diethoxyphosphonyl-1,3-butadiene with nitroso heterodienophiles: A computational investigation, J. Mol. Struct.: THEOCHEM, 2010, 959, 49 CrossRef CAS.
- J. M. De Los Santos, R. Ignacio, G. Rubiales, D. Aparicio and F. Palacios, Hetero-Diels-Alder reaction of phosphinyl and phosphonyl nitroso alkenes with conjugated dienes: An aza-Cope rearrangement, J. Org. Chem., 2011, 76, 6715 CrossRef CAS PubMed.
- J. M. De Los Santos, G. Rubiales, Z. E. Sbai, A. M. Ochoa de Retana and F. Palacios, Reaction of phosphinylated nitrosoalkenes with electron-rich heterocycles. Electrophilic aromatic substitution vs. cycloaddition, Org. Biomol. Chem., 2017, 15, 662 RSC.
- A. Anand, G. Bhargava, P. Singh, S. Mehra, V. Kumar, M. P. Mahajan, P. Singh and K. Bisetty, Regio- and Diastereoselective Nitroso Diels-Alder Cycloaddition Reactions of 3-dienyl-2-azetidinones with Nitrosoarenes, Lett. Org. Chem., 2012, 9, 411 CrossRef CAS.
- L. Cleary, V. W. Mak, S. D. Rychnovsky, K. J. Shea and N. Sizemore, Origins of regio- and stereochemistry in type 2 intramolecular N-acylnitroso diels-alder reactions: A computational study of tether length and substituent effects, J. Org. Chem., 2013, 78, 4090 CrossRef CAS PubMed.
- J. Pous, T. Courant, G. Bernadat, B. I. Iorga, F. Blanchard and G. Masson, Regio-, Diastereo-, and Enantioselective Nitroso-Diels-Alder Reaction of 1,3-Diene-1-carbamates Catalyzed by Chiral Phosphoric Acids, J. Am. Chem. Soc., 2015, 137, 11950 CrossRef CAS PubMed.
- D. Chaiyaveij, A. S. Batsanov, M. A. Fox, T. B. Marder and A. Whiting, An Experimental and Computational Approach to Understanding the Reactions of Acyl Nitroso Compounds in [4+2] Cycloadditions, J. Org. Chem., 2015, 80, 9518 CrossRef CAS PubMed.
- S. C. C. Nunes, S. M. M. Lopes, C. S. B. Gomes, A. A. C. C. Pais and T. M. V. D. Pinho e Melo, Reactions of Nitrosoalkenes with Dipyrromethanes and Pyrroles: Insight into the Mechanistic Pathway Sandra, J. Org. Chem., 2014, 79, 10456 CrossRef CAS PubMed.
- S. M. M. Lopes, S. C. C. Nunes, C. C. Caratão, A. A. C. C. Pais and T. M. V. D. Pinho e Melo, Reactivity of 1-arylnitrosoethylenes towards indole derivatives, Monatsh. Chem., 2016, 147, 1565 CrossRef CAS.
- W. Ji, C. L. Li, H. Chen, Z. X. Yu and X. Liao, A newly designed heterodiene and its application to construct six-membered heterocycles containing an N-O bond, Chem. Commun., 2019, 55, 12012 RSC.
- G. Mlostoń, K. Urbaniak, M. Jasiński, E. U. Würthwein, H. Heimgartner, R. Zimmer and H. U. Reissig, The [4+2]-Cycloaddition of α-Nitrosoalkenes with Thiochalcones as a Prototype of Periselective Hetero-Diels–Alder Reactions—Experimental and Computational Studies, Chem. – Eur. J., 2020, 26, 237 CrossRef PubMed.
- Y. Miura, H. Ouchi, M. Inai, T. Osawa, F. Yoshimura, J. Kanazawa, M. Uchiyama, M. Kondo and T. Kan, Synthetic Studies on Pactamycin: A Synthesis of Johnson's Intermediate, Org. Lett., 2020, 22, 3515 CrossRef CAS PubMed.
- P. A. Nocquet, S. Henrion, A. Macé, B. Carboni, J. M. Villalgordo and F. Carreaux, The Allyl Cyanate/Isocyanate Rearrangement: An Efficient Tool for the Stereocontrolled Formation of Allylic C–N Bonds, Eur. J. Org. Chem., 2017, 1295 CrossRef CAS.
- W. Adam, N. Bottke, B. Engels and O. Krebs, An experimental and computational study on the reactivity and regioselectivity for the nitrosoarene ene reaction: Comparison with triazolinedione and singlet oxygen, J. Am. Chem. Soc., 2001, 123, 5542 CrossRef CAS PubMed.
- A. G. Leach and K. N. Houk, The ene reactions of nitroso compounds involve polarized diradical intermediates, J. Am. Chem. Soc., 2002, 124, 14820 CrossRef CAS PubMed.
- X. Lu, Can the nitroso ene reaction proceed concertedly?, Org. Lett., 2004, 6, 2813 CrossRef CAS PubMed.
- P. Quadrelli, M. Mella, A. Piccanello, S. Romano and P. Caramella, Variable Markovnikov orientation and “cis effect” in ene reactions of nitrosocarbonyl intermediates, J. Org. Chem., 2007, 72, 1807 CrossRef CAS PubMed.
- L. Zhai, X. Tian, C. Wang, Q. Cui, W. Li, S. H. Huang, Z. X. Yu and R. Hong, Construction of Morphan Derivatives by Nitroso–Ene Cyclization: Mechanistic Insight and Total Synthesis of (±)-Kopsone, Angew. Chem., Int. Ed., 2017, 56, 11599 CrossRef CAS PubMed.
- T. Sasaki, Y. Ishibashi and M. Ohno, Unequivocal Synthesis Of Phenacylideneaniline From Silyl Enol Ethers And Nitrosobenzene And One-Pot Cycloaddition Reactions Of The Related Anils, Chem. Lett., 1983, 12, 863 CrossRef.
- T. Sasaki, K. Mori and M. Ohno, Synthesis of β-N-Phenylamino Alcohols and α-N-Phenylamino Acids via Reduction of the Adducts of Silyl Enol Ethers and Bis-silyl Ketene Acetals with Nitrosobenzene, Synthesis, 1985, 280 CrossRef CAS.
- P. H. Y. Cheong and K. N. Houk, Origins of selectivities in proline-catalyzed α-aminoxylations, J. Am. Chem. Soc., 2004, 126, 13912 CrossRef CAS PubMed.
- A. Córdova, H. Sundén, A. Bøgevig, M. Johansson and F. Himo, The direct catalytic asymmetric α-aminooxylation reaction: Development of stereoselective routes to 1,2-diols and 1,2-amino alcohols and density functional calculations, Chem. – Eur. J., 2004, 10, 3673 CrossRef PubMed.
- H. Wang, C. Yang and K. Han, Density functional study of the L-proline-catalyzed α-aminoxylation of aldehydes reaction: The reaction mechanism and selectivity, Struct. Chem., 2006, 17, 97 CrossRef CAS.
- J. Joseph, D. B. Ramachary and E. D. Jemmis, Electrostatic repulsion as an additional selectivity factor in asymmetric proline catalysis, Org. Biomol. Chem., 2006, 4, 2685 RSC.
- R. Zhu, D. Zhang, J. Wu and C. Liu, A DFT study on the mechanism and regioselectivity of the tandem O-nitroso aldol/Michael reaction of nitrosobenzene and cyclohexanone, J. Mol. Struct.: THEOCHEM, 2007, 815, 105 CrossRef CAS.
- M. Akakura, M. Kawasaki and H. Yamamoto, DFT study of brønsted acid catalyzed nitroso aldol reaction between achiral enamines and nitrosobenzene: The reason for regio- and enantioselectivity, Eur. J. Org. Chem., 2008, 4245 CrossRef CAS.
- M. Lu, Y. Lu, D. Zhu, X. Zeng, X. Li and G. Zhong, Chiral brønsted acid catalyzed enantioselective α- aminoxylation of enecarbamates, Angew. Chem., Int. Ed., 2010, 49, 8588 CrossRef CAS PubMed.
- C. T. Wong, A theoretical investigation on the mechanism of the α,α-diphenylprolinol trimethylsilyl ether-catalyzed oxyamination reaction, Tetrahedron Lett., 2009, 50, 811 CrossRef CAS.
- A. Mielgo, I. Velilla, E. Gómez-Bengoa and C. Palomo, Brønsted acid assisted regio- and enantioselective direct o-nitroso aldol reaction catalysed by α,α-diphenylprolinol trimethylsilyl ether, Chem. – Eur. J., 2010, 16, 7496 CrossRef CAS PubMed.
- C. Palomo, S. Vera, I. Velilla, A. Mielgo and E. Gómez-Bengoa, Regio- and Enantioselective Direct Oxyamination Reaction of Aldehydes Catalyzed by α,α-Diphenylprolinol Trimethylsilyl Ether, Angew. Chem., 2007, 119, 8200 CrossRef.
- L. Zhang, C. Xu, X. Mi and S. Luo, Origins of the enantio-and N/O selectivity in the primary-amine-catalyzed hydroxyamination of 1,3-dicarbonyl compounds with in situ-formed nitrosocarbonyl compounds: A theoretical study, Chem. – Asian J., 2014, 9, 3565 CrossRef CAS PubMed.
- D. J. Nelson, R. Kumar and Shagufta, Regiochemical reversals in nitrosobenzene reactions with carbonyl compounds-α-aminooxy ketone versus α-hydroxyamino ketone products, Eur. J. Org. Chem., 2012, 6013 CrossRef CAS PubMed.
- C. Volpe, S. Meninno, A. Roselli, M. Mancinelli, A. Mazzanti and A. Lattanzi, Nitrone/Imine Selectivity Switch in Base-Catalysed Reaction of Aryl Acetic Acid Esters with Nitrosoarenes: Joint Experimental and Computational Study, Adv. Synth. Catal., 2020, 362, 5457 CrossRef CAS.
- S. Ham and D. M. Bimey, An ab fnitio Study of the Reactivity of Nitrosoketene with Formaldehyde, Tetrahedron Lett., 1994, 35, 8113 CrossRef CAS.
- S. Ham and D. M. Birney, Further Ab initio studies on the reactivity of nitrosoketene, Tetrahedron Lett., 1997, 38, 5925 CrossRef CAS.
- H. Tanimoto, T. Shitaoka, K. Yokoyama, T. Morimoto, Y. Nishiyama and K. Kakiuchi, Formal [3+2] Cycloaddition of Nitrosoallenes with Carbonyl and Nitrile Compounds to Form Functional Cyclic Nitrones, J. Org. Chem., 2016, 81, 8722 CrossRef CAS PubMed.
- A. Jabbari and K. N. Houk, Hetero-Cope rearrangements of nitrosobutenes. DFT studies of thermal and acid-catalyzed reactions, Org. Lett., 2006, 8, 5975 CrossRef CAS PubMed.
- A. Penoni, G. Palmisano, Y. L. Zhao, K. N. Houk, J. Volkman and K. M. Nicholas, On the Mechanism of Nitrosoarene - Alkyne Cycloaddition, J. Am. Chem. Soc., 2009, 131, 653 CrossRef CAS PubMed.
- I. Chatterjee, C. K. Jana, M. Steinmetz, S. Grimme and A. Studer, Copper-catalyzed enantioselective [2.+2] cycloadditions of 2-nitrosopyridine with ketenes, Adv. Synth. Catal., 2010, 352, 945 CrossRef CAS.
- F. Weigend, A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency, Phys. Chem. Chem. Phys., 2002, 4, 4285 RSC.
- R. S. Srivastava, N. R. Tarver and K. M. Nicholas, Mechanistic studies of copper(I)-catalyzed allylic amination, J. Am. Chem. Soc., 2007, 129, 15250 CrossRef CAS PubMed.
- O. A. Levitskiy, Y. K. Grishin, V. V. Sentyurin and T. V. Magdesieva, Copper-Assisted Amination of Boronic Acids for Synthesis of Bulky Diarylamines: Experimental and DFT Study, Chem. – Eur. J., 2017, 23, 12575 CrossRef CAS PubMed.
- A. Pokluda, M. Kohout, J. Chudoba, M. Krupička and R. Cibulka, Nitrosobenzene: Reagent for the Mitsunobu Esterification Reaction, ACS Omega, 2019, 4, 5012 CrossRef CAS PubMed.
- M. Castiñeira Reis, M. Marín-Luna, C. Silva López and O. N. Faza, Mechanism of the Molybdenum-Mediated Cadogan Reaction, ACS Omega, 2018, 3, 7019 CrossRef PubMed.
| This journal is © the Partner Organisations 2022 |