Open Access Article
Open Access ArticleAnion ordering and vacancy defects in niobium perovskite oxynitrides†
Joshua J.
Brown
a,
Youxiang
Shao
b,
Zhuofeng
Ke
 b and
Alister J.
Page
b and
Alister J.
Page
 *a
*a
aSchool of Environmental & Life Sciences, The University of Newcastle, Callaghan 2308, NSW, Australia. E-mail: alister.page@newcastle.edu.au
bSchool of Materials Science & Engineering, PCFM Lab, Sun Yat-sen University, Guangzhou, 510275, P. R. China
First published on 22nd February 2021
Abstract
Niobium perovskite oxynitrides are emerging as promising semiconductor materials for solar energy conversion processes, due to their physical properties and amenability to defect engineering. However, defect engineering in mixed-anion semiconductors such as perovskite oxynitrides is generally hindered by the absence of long-range order in the crystal lattice, a phenomenon known as anion-ordering. We demonstrate how anion ordering influences the stability and mobility of point defects in two exemplar perovskite oxynitrides, BaNbO2N and LaNbON2. Accurate first-principles calculations show that fully cis-anion orderings in BaNbO2N are more stable than fully trans-anion orderings, whereas anion orderings with mixed dimensionality may be more prevalent in the lower-symmetry LaNbON2. Anion ordering in LaNbON2 is also influenced by a pronounced A-site coordination sphere effect not observed in BaNbO2N, whereby local La-(O,N)12 coordination environments give rise to alternating LaO and LaN layers in the bulk material. Anion order was predicted to effect the redistribution of electrons upon anion vacancy creation to the cation sublattice. Diffusion barriers for O2− vacancies in trans-ordered BaNbO2N were found to be lower than those for N3− vacancies, suggesting that stabilising trans-ordered phases of BaNbO2N will yield more effective retention of nitrogen content in this material. The reverse is the case for LaNbON2, with N3− vacancy defects exhibiting more facile diffusion than O2− vacancy defects. We believe these insights will aid the emergent understanding of defect engineering in mixed-anion perovskite oxynitride semiconductors, and specifically help facilitate strategies for stabilising their nitrogen content.
Introduction
Oxynitride materials have attracted recent interest for use in applications such as pigments, dielectrics, and optoelectronic materials.1 The overlap between the band gaps of many oxynitride materials and the solar spectrum also makes them potential water splitting photocatalysts that can operate in the visible-light region.2 Several niobium oxynitride perovskites, for instance, are promising candidate semiconductors for solar energy conversion owing to their wide visible light absorption.3–6However, niobium oxynitrides are known to be more prone to defect formation during their synthesis via nitridation, compared to other perovskite oxynitrides (e.g. tantalum oxynitrides). This is a feature, rather than a flaw. Structural defects, such as zero-dimensional defects (e.g. vacancy, interstitial and anti-site defects) and higher-dimensional defects (dislocations, grain boundaries, and volumetric defects) provide design parameters for modulating surface active sites, charge carrier mobilities, and band edge positions.7,8 Of these, zero-dimensional point defects have the strongest link to material non-stoichiometry.7 Niobium oxynitrides are therefore ideal candidates for defect engineering. For instance, the enhanced conductivity of BaNbO2N compared to BaTaO2N is suspected to arise from defect concentration in the former.9 Niobium oxynitrides also have larger absorption tails extending in the visible region of the spectrum, which is indicative of nitrogen vacancies and reduced B-site cations, compared to their tantalum counterparts.9
However, engineering structural defects in perovskite oxynitride photocatalysts, such as AM(O,N)3 (M = Ti, Zr, Hf, Ta, Nb), in a controlled manner is complicated by the lack of long-range structural order in their crystal lattices. Such disorder is otherwise known as ‘anion ordering’; despite exhibiting local ordering of anions within individual MO6−xNx octahedra, long-range structural order is lost due to the similarity between the Mn+–O2− and Mn+–N3− orbital overlaps, and hence bond lengths. The slightly larger Mn+–N3− bond length drives a predominantly cis-ordering in individual octahedra, giving rise to N3−-Mn+–N3− chains (or O2−–Mn+–O2− in the case of LaTaON2 and LaNbON2).10 Anion ordering induces local distortions11 in the crystal structure, influencing the ferroelectricity,12,13 bandgap14,15 and effective charge carrier mobility of these materials.16–18
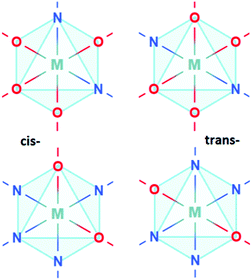
Anion ordering in oxynitride perovskites can be categorised into by the regimes of cis- or trans-ordering as illustrated in Fig. 1, as well as by the dimensionality the ordering travels in i.e. 2D/3D for cis-ordering or 1D/2D for trans-ordering. Recent research has focused on characterising the relative stabilities of these different regimes. While cis-ordering is the more stable for d0 oxynitrides, both regimes are sensitive to stoichiometry, strain, and interfacial effects. For instance, synthetic conditions and A-site cation substitution can yield fully 2D or 3D trans-orderings.16–20 For instance, increased Sr2+ doping in CaTaO2N induces partial trans-ordering, with cis-ordering becoming energetically prohibitive due to lattice strain.21 Similarly, Vonruti et al.22 have shown that >4% compressive strain stabilizes trans-ordering in bulk LaTiO2N. Ninova et al.23 have predicted that, for LaTiO2N, surface layers can favour trans-ordering due to the charge neutral stacking afforded by (LaN)-(TiO2) layers.
However, the impact of anion ordering on anion vacancy defect formation and anion vacancy diffusion remains largely unexplored in perovskite oxynitride photocatalysts.
Understanding this relationship is the first step towards controlling their defect engineering for enhanced photocatalysis. Here we address this issue by demonstrating how the stability and mobility of O2− and N3− vacancy point defects are influenced by local anion ordering in two representative niobium perovskite oxynitrides, BaNbO2N and LaNbON2. Vacancy defect formation energies and migration barriers are investigated systematically as a function of both cis- and trans-ordering of N3−-Mn+–N3− (BaNbO2N) and O2−–Mn+–O2− (LaNbON2) chains using accurate first-principles calculations. Cis-anion orderings are in general more energetically favourable than trans-orderings in these materials. However, there are secondary ordering effects that arise from the stoichiometric distribution of anions in the A-site cation coordination sphere, most prevalent for LaNbON2. We show below how both the stability and mobility of O2− and N3− vacancy defects are influenced by these two ordering effects.
Computational methodology
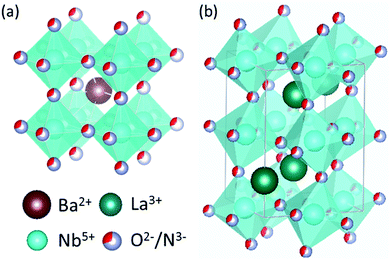
All calculations reported here employ the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) exchange–correlation functional, revised for solids (PBEsol),24 as implemented in the Vienna Ab initio Simulation Package (VASP) code25,26 using the projector augmented wave (PAW) method.27 A Hubbard-U correction28 has not been employed in this work, due to the non-trivial choice of selecting a +U potential that is independent of the anion ordering and vacancy defect type. All calculations employ (core)/valence configurations of Nb: ([Ne]3s)/3p3d4s; O: ([He])/2s2p N: ([He])/2s2p and a plane wave energy cutoff of 450 eV. Crystal structures of BaNbO2N and LaNbON2 at standard conditions were obtained from the International Crystal Structure Database (ICSD crystal IDs 434770 and 247261, respectively29), see Fig. 2. These structures are, respectively, of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and Pnma symmetry. However, these symmetries are only nominal; we show below that local anion orderings within each extended supercell induce differing degrees of three-dimensional anisotropy in these ideal lattice structures when they are fully relaxed. Monkhorst–Pack meshes consisting of 6 × 6 × 6 k-points were used for the 40 atom 2 × 2 × 2 BaNbO2N supercell, while 4 × 6 × 4 k-point meshes were used for 80 atom 2 × 1 × 2 LaNbON2 supercell. Vacancy migration barriers were pre-optimised using the nudged elastic band (NEB) algorithm30 to a force criterion of 0.1 eV Å−1, before being re-optimised the Climbing Image (CI-NEB) algorithm31 to a 0.05 eV Å−1 criterion. Five images were used in both cases.31
m and Pnma symmetry. However, these symmetries are only nominal; we show below that local anion orderings within each extended supercell induce differing degrees of three-dimensional anisotropy in these ideal lattice structures when they are fully relaxed. Monkhorst–Pack meshes consisting of 6 × 6 × 6 k-points were used for the 40 atom 2 × 2 × 2 BaNbO2N supercell, while 4 × 6 × 4 k-point meshes were used for 80 atom 2 × 1 × 2 LaNbON2 supercell. Vacancy migration barriers were pre-optimised using the nudged elastic band (NEB) algorithm30 to a force criterion of 0.1 eV Å−1, before being re-optimised the Climbing Image (CI-NEB) algorithm31 to a 0.05 eV Å−1 criterion. Five images were used in both cases.31
The formation of a neutral oxygen vacancy in BaNbO2N and LaNbON2 can be expressed in Kröger–Vink notation as,
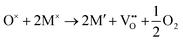 | (1) |
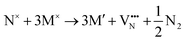 | (2) |
The oxidation state of the M cations in the vicinity of the defect will be determined by the localization of the electron density, which may vary between 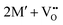 and
and 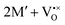 for a neutral oxygen vacancy, and
for a neutral oxygen vacancy, and 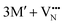 and
and 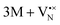 for a neutral nitrogen vacancy. As Nb is capable of exhibiting a range of oxidation states (+5 to −1), we reason that it will likely favour charged vacancies and reduced Nb cations in anion-deficient BaNbO2N and LaNbON2. To this end we investigate the effect of anion ordering effect on electron localization and Nb oxidation via a DDEC6 charge decomposition analysis.32–34
for a neutral nitrogen vacancy. As Nb is capable of exhibiting a range of oxidation states (+5 to −1), we reason that it will likely favour charged vacancies and reduced Nb cations in anion-deficient BaNbO2N and LaNbON2. To this end we investigate the effect of anion ordering effect on electron localization and Nb oxidation via a DDEC6 charge decomposition analysis.32–34
For a neutral supercell, the anion vacancy formation energy, Ef,vac, can be obtained from the simplified expression:35
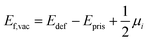 | (3) |
Results and discussion
Anion ordering in Nb perovskite oxynitrides
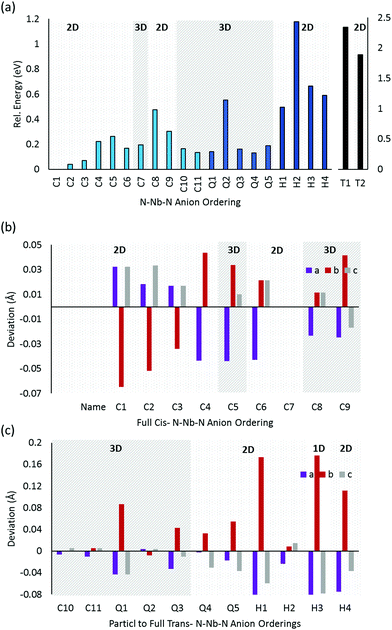
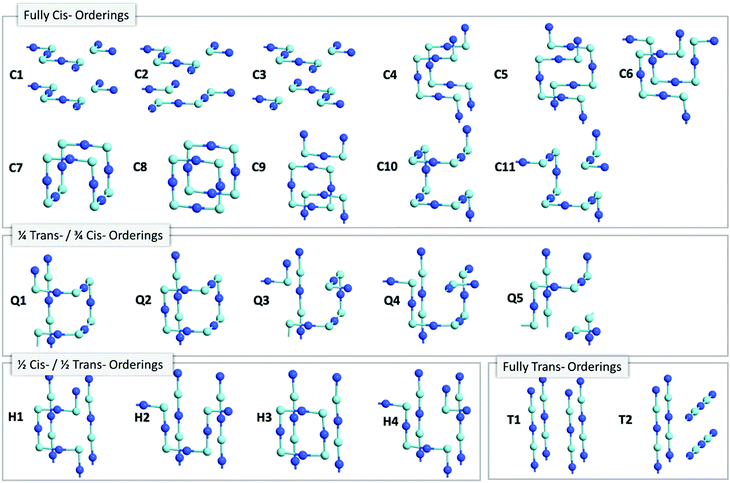
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group) enables an extensive search of anion orderings, including those that possess completely cis- or trans-ordered N3−–Nb5+–N3− chains, as well as those that possess a mixture of both cis- and trans-orderings. Fig. 4a depicts the relative energies of these distinct anion orderings, compared to the lowest energy structure of BaNbO2N. The latter is the fully cis-C1 ordering, which has previously been found to be the most stable ordering in LaTiO2N,14 CaTaO2N17 and SrTaO2N.15Fig. 4a shows that several fully cis-orderings considered here lie within 0.3 eV of C1, with the parallel ring structure C8 being the only exception. By comparison, local structures with fully trans-orderings (T1 and T2) are >2 eV less stable than the C1 ordering. Of these, the lowest energy fully trans configuration is T2, a 2D ordering comprised of stacked orthogonal layers of trans-N3−–Nb5+–N3− chains. Interestingly, Fig. 4a shows that the partial trans-anion orderings considered here (Q and H, which denote quarter and half trans-orderings, respectively) are all significantly lower in energy than the fully trans-configurations. Indeed, several quarter trans-orderings, such as Q1 and Q4, are predicted to be within 0.2 eV of the lowest energy C1 ordering. This suggests that distortion caused by trans-chains can be stabilized to a point by adjacent cis-chains. These results suggest that stabilizing the formation of a fully trans-ordered phase in BaNbO2N will be significantly more challenging than conversion from cis- to partially/fully trans-ordered phases, or forming mixed-phases comprising both cis- and trans-ordered regions. Of the ring & loop configurations considered here (i.e.C7, C8, C9, Q2, H2), Fig. 4a indicates that these orderings generally have higher energies than their counterparts. This suggests potentially unfavourable strain is produced when the N3−–Nb5+–N3− chains ‘loop back’ upon themselves too tightly.
m space group) enables an extensive search of anion orderings, including those that possess completely cis- or trans-ordered N3−–Nb5+–N3− chains, as well as those that possess a mixture of both cis- and trans-orderings. Fig. 4a depicts the relative energies of these distinct anion orderings, compared to the lowest energy structure of BaNbO2N. The latter is the fully cis-C1 ordering, which has previously been found to be the most stable ordering in LaTiO2N,14 CaTaO2N17 and SrTaO2N.15Fig. 4a shows that several fully cis-orderings considered here lie within 0.3 eV of C1, with the parallel ring structure C8 being the only exception. By comparison, local structures with fully trans-orderings (T1 and T2) are >2 eV less stable than the C1 ordering. Of these, the lowest energy fully trans configuration is T2, a 2D ordering comprised of stacked orthogonal layers of trans-N3−–Nb5+–N3− chains. Interestingly, Fig. 4a shows that the partial trans-anion orderings considered here (Q and H, which denote quarter and half trans-orderings, respectively) are all significantly lower in energy than the fully trans-configurations. Indeed, several quarter trans-orderings, such as Q1 and Q4, are predicted to be within 0.2 eV of the lowest energy C1 ordering. This suggests that distortion caused by trans-chains can be stabilized to a point by adjacent cis-chains. These results suggest that stabilizing the formation of a fully trans-ordered phase in BaNbO2N will be significantly more challenging than conversion from cis- to partially/fully trans-ordered phases, or forming mixed-phases comprising both cis- and trans-ordered regions. Of the ring & loop configurations considered here (i.e.C7, C8, C9, Q2, H2), Fig. 4a indicates that these orderings generally have higher energies than their counterparts. This suggests potentially unfavourable strain is produced when the N3−–Nb5+–N3− chains ‘loop back’ upon themselves too tightly.
 | ||
| Fig. 3 N3−Nb5+–N3− anion orderings in a 2 × 2 × 2 BaNbO2N supercell (Ba2+ and O2− atoms not shown for clarity). N3− and Nb5+ are dark and light blue atoms, respectively. | ||
Fig. 4 also considers the relative stability of anion orderings in BaNbO2N from the point of view of dimensionality, by highlighting which orderings are 2D and which are 3D. In general, cis-orderings are considered to be 2D, in that they consist predominantly of N3−–Nb5+–N3− chains aligned parallel with each other. Introducing locally trans-ordered N3−–Nb5+–N3− chains, either partially (Q configurations) or completely (T configurations) naturally increases the dimensionality of the ordering when ‘twists’ and ‘loops’ are present in the N3−–Nb5+–N3− sublattice (see Fig. 3). Nevertheless, Fig. 4a shows that there is no clear relationship between dimensionality and stability here. For instance, the 2D fully cis-ordered structures are lowest in energy (e.g.C1, C2, C3) whereas the 2D half-trans-ordered structures (H1, H2, H3, H4) are less stable by up to ∼1.2 eV. Similarly, of the 3D orderings studied, the fully cis-C7, C10 and C11 and the quarter trans-Q1 and Q4 orderings have mostly very similar energies. Notably, the C10, Q1 and Q4 orderings are only ∼0.13 eV higher in energy than the most stable C1 configuration. On the other hand, the dimensionality of the ordering has a clear relationship with the degree of lattice anisotropy, measured here via the deviation of each lattice constant from its value for a pristine Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m unit cell for each ordering (i.e. we define this value as the average of the a, b and c lattice constants in each case). Fig. 4b and c show that the 2D orderings considered here clearly induce greater anisotropy in the crystal lattice compared to 3D orderings, as anticipated. Indeed, lattice constant deviations correlate with the predominant alignment of N3−–Nb5+–N3− chains in the 2 × 2 × 2 supercell. For instance, for the most stable C1 ordering, the N3−–Nb5+–N3− chains are aligned along the a and c lattice vectors (Fig. 3). This alignment causes equivalent expansion in a and c of ∼0.03 Å, while the lattice is compressed in b approximately twofold, by ∼−0.07 Å (Fig. 4b). On the other hand, C7 yields an essentially isotropic Pm
m unit cell for each ordering (i.e. we define this value as the average of the a, b and c lattice constants in each case). Fig. 4b and c show that the 2D orderings considered here clearly induce greater anisotropy in the crystal lattice compared to 3D orderings, as anticipated. Indeed, lattice constant deviations correlate with the predominant alignment of N3−–Nb5+–N3− chains in the 2 × 2 × 2 supercell. For instance, for the most stable C1 ordering, the N3−–Nb5+–N3− chains are aligned along the a and c lattice vectors (Fig. 3). This alignment causes equivalent expansion in a and c of ∼0.03 Å, while the lattice is compressed in b approximately twofold, by ∼−0.07 Å (Fig. 4b). On the other hand, C7 yields an essentially isotropic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure, and Fig. 3 shows that alignment of the N3−–Nb5+–N3− chains are balanced exactly in all three directions. These results suggest that inducing lattice strain in BaNbO2N will yield selectivity over anion ordering which is in line with recent studies for other oxynitride perovskites.16,21,22 We return to a discussion of how these orderings influence thermokinetic parameters of vacancy defects below.
m structure, and Fig. 3 shows that alignment of the N3−–Nb5+–N3− chains are balanced exactly in all three directions. These results suggest that inducing lattice strain in BaNbO2N will yield selectivity over anion ordering which is in line with recent studies for other oxynitride perovskites.16,21,22 We return to a discussion of how these orderings influence thermokinetic parameters of vacancy defects below.
Beyond dimensionality, Fig. 4b and c show that these BaNbO2N anion orderings fall into three distinct groups. The first of these comprise orderings that minimally distort the cubic symmetry of the ideal BaNbO2N lattice, i.e. a ≈ b ≈ c. This isotropic group includes both high energy fully trans-orderings, as well as relatively stable C7 and Q2 orderings, and feature motifs in which N3−–Nb5+–N3− chains form a closed loop within a 2 × 2 × 2 extension of the BaNbO2N lattice. The second group consists of orderings that yield anisotropic compression/expansion in a single dimension (i.e. two lattice constants essentially equal but distinct from the third), such as C1, C2, C3, H1, H3, and H4. The third group are those orderings that yield complete anisotropy in the sense that all three BaNbO2N lattice constants are unique (e.g.C3, C4Q3, Q4, Q5). In the second group, the C1, C2 & C3 orderings (the three most stable orderings overall) are compressed in one axis and expanded in the other two. Interestingly, the half trans-orderings in this group (H1, H3, H4) all show the opposite trend, i.e. compression along two axes, and expansion in the third. These results suggest that cis-orderings in perovskite oxynitrides may be stabilised generally via in-plane lattice expansion, while trans-ordering may be stabilised via in-plane lattice compression. Indeed, Oka et al.21 demonstrated the formation of a metastable trans-type anion orderings in CaTaO2N via Sr2+ A-site doping, in which N3− preferentially resided in axial sites in TaO4N2 octahedra due to lattice strain induced by the A-site dopant. Similarly, Vonruti et al.22 predicted the stabilization of parallel trans-ordering of N3− anions (akin to T2) in LaTiO2N when in-plane compressive strains greater than 4% were applied to the lattice. While an exhaustive strain engineering study is beyond the scope of this work, results presented here indicate that intermediate partial trans-orderings potentially impede the stabilization of fully trans-orderings via compressive in-plane strain, and so are likely an important consideration in strain engineering of perovskite oxynitrides more generally.
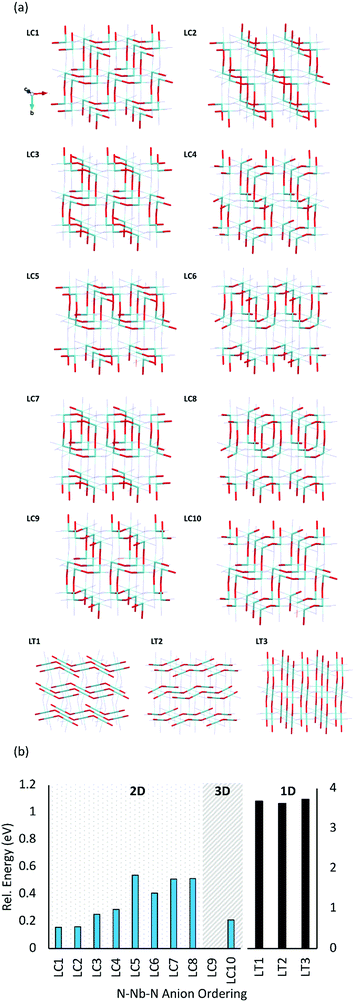
Fig. 5b displays the relative energies of the different anion orderings for the 2 × 1 × 2 LaNbON2 cell. It is clear that cis-orderings are preferred over trans-orderings, consistent with results for BaNbO2N presented in Fig. 4a. For LaNbON2 all trans-orderings considered here (LT1, LT2 & LT3) are >2 eV less stable than the most stable cis-ordering, LC9. The latter ordering features ‘zigzag’ O2−–Nb5+–O2− chains running through the 2 × 1 × 2 supercell alternating between the (101) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) planes and perpendicular to the (011) and (0
01) planes and perpendicular to the (011) and (0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1) directions. This zigzag motif is shared with the other stable anion orderings, LC1, LC2, and LC10, the only difference being the alignment of the motif within the crystal structure. For instance, in the LC10 ordering, the same zigzag O2−–Nb5+–O2− chains are present in the 2 × 1 × 2 supercell as those observed in the LC9 ordering. However, they are perpendicular to the (110) and (
1) directions. This zigzag motif is shared with the other stable anion orderings, LC1, LC2, and LC10, the only difference being the alignment of the motif within the crystal structure. For instance, in the LC10 ordering, the same zigzag O2−–Nb5+–O2− chains are present in the 2 × 1 × 2 supercell as those observed in the LC9 ordering. However, they are perpendicular to the (110) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10) lattice directions, and as a result are ∼0.2 eV higher in energy. Similarly, the LC1 and LC2 orderings also feature the zigzag O2−–Nb5+–O2− chain motif, but perpendicular to the (101) and (
10) lattice directions, and as a result are ∼0.2 eV higher in energy. Similarly, the LC1 and LC2 orderings also feature the zigzag O2−–Nb5+–O2− chain motif, but perpendicular to the (101) and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) lattice directions, respectively. Both orderings are only ∼0.15 eV less stable than the most favourable ordering, LC9. The other cis-orderings considered here consist of different structural motifs and are less stable than the zigzag motif. These include the LC3, LC4, LC5 and LC6 orderings, all of which consist of O2−Nb5+–O2− chains that create a repeating square-tooth pattern in the 2 × 1 × 2 LaNbON2 supercell and are ∼0.3–0.6 eV less stable than LC9, and the ring-like LC7 and LC8 motifs, which are both ∼0.5 eV less stable than LC9.
01) lattice directions, respectively. Both orderings are only ∼0.15 eV less stable than the most favourable ordering, LC9. The other cis-orderings considered here consist of different structural motifs and are less stable than the zigzag motif. These include the LC3, LC4, LC5 and LC6 orderings, all of which consist of O2−Nb5+–O2− chains that create a repeating square-tooth pattern in the 2 × 1 × 2 LaNbON2 supercell and are ∼0.3–0.6 eV less stable than LC9, and the ring-like LC7 and LC8 motifs, which are both ∼0.5 eV less stable than LC9.
Fig. 5b shows that the dimensionality of the ordering is also apparently unrelated to its stability. For instance, LC9 and LC10 are both 3D orderings, whereas all their cis-orderings of O2−–Nb5+–O2− chains in LaNbON2 are 2D. This is different from what was found in Fig. 4 for BaNbO2N, and suggests that controlling for 2D or 3D more ordering may not be possible in LaNbON2. Though we note that 2D–3D ordering transition temperatures have been observed in the comparable structure LaTaON2.20
Further, comparison of Fig. 5b with equivalent results for BaNbO2N (Fig. 3 and 4a), shows striking similarities between the relative stabilities of comparable O2−–Nb5+–O2− orderings in LaNbON2 and N3−–Nb5+–N3− orderings in BaNbO2N. For instance, cis-orderings featuring zigzag chain motifs are the most stable in both materials, and fully trans-anion orderings are significantly higher in energy (by ∼1 eV). Further, the ring-like and loop-like motifs are also energetically similar in both cases. For instance, LC3, LC4, LC5 and LC6 in LaNbON2 and C4, C5 and C6 in BaNbO2N both feature repeating square tooth O2−–Nb5+–O2− and N3−–Nb5+–N3− motifs and have comparable relative energies (∼0.3–0.4 eV). Similarly, the loop motifs in LC7 and LC8 for LaNbON2 and C8 and C9 in BaNbO2N are structurally similar and ∼0.5–0.6 eV higher in energy than the most favourable ordering.
Nevertheless, the La3+ and Ba2+ A-site cations also drive secondary ordering effects that differ between BaNbO2N and LaNbON2. Comparing the La-(O,N)12 coordination spheres between different orderings for LaNbON2, the lowest energy orderings (LC1–LC4 and LC9–10) all possess stoichiometric La-O4N8 coordination spheres, whereas the LC5–LC8 orderings feature a mix of La-O6N6 and La-O2N10 coordination spheres. This mix creates alternating LaO and LaN layers between NbON3− sheets aligned perpendicular to the b-axis in the 2 × 1 × 2 LaNbON2 supercell. There is a clear energetic difference between these two groups, with LC5–LC8 being ∼0.3 eV higher on average than LC1–LC4 and LC9–10. This A-site effect is notably absent in the BaNbO2N orderings, shown in Fig. 4. While the most stable zigzag orderings in BaNbO2N do indeed create an even distribution of Ba-O8N4 coordination spheres, other orderings like C6 & C8 have energies 0.15–0.30 eV higher than orderings with comparable Ba-(O,N)12 coordination sphere distributions. Thus, the N3−–Nb5+–N3− chain ordering in the more densely packed BaNbO2N supercell effectively masks the effect of the Ba-(O,N)12 coordination sphere on the stability of the material.
Vacancy defect formation energies in Nb perovskite oxynitrides
We now consider the impact of anion order in BaNbO2N and LaNbON2 on the stability of vacancy defects in both O2− and N3− lattice positions. This is achieved via predicting the vacancy defect formation energies, Ef,Vo and Ef,VN (eqn (3)) at the 12 distinct anion positions in the respective supercells of these materials, for each specific anion ordering considered in the preceding discussion. These distinct positions 1–12 for the 2 × 2 × 2 BaNbO2N and 2 × 1 × 2 LaNbON2 supercells are depicted in Fig. 6a and b.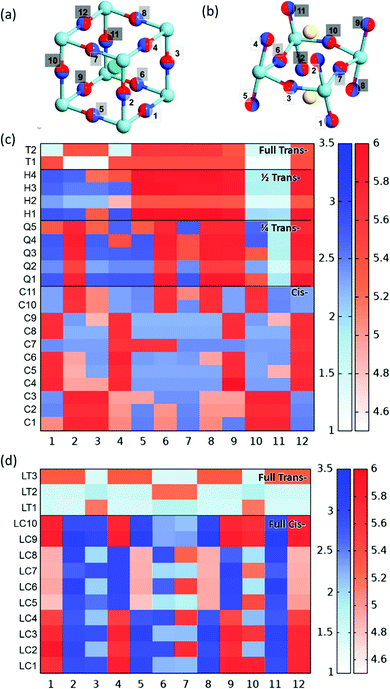 | ||
| Fig. 6 (a and b) Depiction of the 12 unique anion positions in the centroid of the (a) 2 × 2 × 2 BaNbO2N and (b) 2 × 1 × 2 LaNbON2 supercells. Light and dark blue spheres as in Fig. 3, red, green and yellow spheres represent oxygen, barium and lanthanum atoms respectively. (c and d) PBEsol vacancy formation energies VN and VO in positions 1–12 as a function of anion ordering for the (c) 2 × 2 × 2 BaNbO2N and (d) 2 × 1 × 2 LaNbON2 supercells; red indicates an O2− vacancy defect and blue indicates an N3− vacancy defect at that position. The colour depth indicates the magnitude of the formation energies VN and VO (blue and red, respectively) in eV, as indicated by the scale bar. | ||
The Ef,Vo formation energies vary quite significantly across the fully cis- (4.87–6.08 eV) and partial trans- (4.87–5.98 eV) orderings, compared to fully trans- (5.37–5.60 eV). This indicating that neutral oxygen vacancy formation energies are more sensitive to N3−–Nb5+–N3− chain disorder, whereas nitrogen vacancy formation energies depend simply on whether the site is in a cis- or trans-chain. N3− anions in trans-N3−–Nb5+–N3− chains, whether they be partially or fully trans-, have a reduced Ef,VN formation energy.
The question as to whether anion vacancies have the potential to affect local anion order in BaNbO2N is considered in Fig. S1 (ESI†), which shows the relative energies of these anion orderings in the presence of VO and VN defects. Compared to the defect-free relative energies in Fig. 4a, it can be seen in Fig. S1a (ESI†) that in several cases anion vacancies likely influence the anion ordering. For instance, the quarter-trans orderings (Q1–5) become energetically indistinguishable from the cis (C1-11) orderings in the presence of a neutral oxygen vacancy defect. Additionally, the relative orderings in the presence of a neutral nitrogen vacancy defect (Fig. S1b, ESI†) are significantly different from the defect-free orderings. While the cisC1-11 orderings are effectively equivalent in energy with and without a VN defect, the Q1–5 orderings are lowered by ∼0.5 eV, as the defect disrupts an N3−–Nb5+–N3− chain, thus making them the most favourable ordering.
Finally, we consider whether or not VO and VN defects in LaNbON2 have the potential to influence the relative stabilities of these anion orderings. Fig. S2 (ESI†) shows the relative energies of the anion orderings in the defective LaNbON2 structures. Compared to the defect-free relative energies in Fig. 5a and Fig. S2a (ESI†) the presence of VO does not appreciably influence the relative stability of many of the orderings. However, the LC5–9 orderings become the most stable orderings, as they can be lowered by up to ∼0.2 eV. Fig. S2b (ESI†) shows that, by comparison, VN defects are much more influential on the stabilities of these anion orderings, with all LC orderings being lowered by up to ∼0.5 eV. Nevertheless, the relative stabilities for all LC orderings become virtually indistinguishable in the presence of a VN defect.
Vacancy defects and charge redistribution
Nb is capable of exhibiting multiple low oxidation states. While our calculations enforce charge neutrality on the entire supercell, the region surrounding a vacancy defect is itself not necessarily guaranteed to be charge neutral due to electron density delocalisation. In turn, the oxidation states of Nb cations are not necessarily uniform throughout the supercell, since, despite the formal vacancy charge (i.e.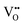 and
and 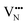 ) electron density delocalisation around the vacancy may lead to charge redistribution on neighbouring atoms. We examine this possibility in BaNbO2N and LaNbON2via the DDEC6 charge decomposition analysis presented in Table 1, which summarizes the partial atomic charges and charge redistribution in these materials following the formation of VO and VN defects. We limit our discussion to only the most thermodynamically stable cis/trans anion orderings for each material, established in the preceding discussion (i.e.C1 and T2 in BaNbO2N, and LC9 and LT2 for LaNbON2). Due to the size of the supercells used in this work, we have not verified these PBEsol results with higher-level exchange correlation functionals, such as HSE06.37 We point out, however, that charges based on PBEsol have been shown to be in close agreement with higher level functionals for closely related transition metal oxide perovskites.38,39
) electron density delocalisation around the vacancy may lead to charge redistribution on neighbouring atoms. We examine this possibility in BaNbO2N and LaNbON2via the DDEC6 charge decomposition analysis presented in Table 1, which summarizes the partial atomic charges and charge redistribution in these materials following the formation of VO and VN defects. We limit our discussion to only the most thermodynamically stable cis/trans anion orderings for each material, established in the preceding discussion (i.e.C1 and T2 in BaNbO2N, and LC9 and LT2 for LaNbON2). Due to the size of the supercells used in this work, we have not verified these PBEsol results with higher-level exchange correlation functionals, such as HSE06.37 We point out, however, that charges based on PBEsol have been shown to be in close agreement with higher level functionals for closely related transition metal oxide perovskites.38,39
| BaNbO2N | LaNbON2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | T2 | LC9 | LT2 | ||||||
| VO | VN | VO | VN | VO | VN | VO | VN | ||
| Partial Charge | Adjacent Nb | 1.89 | 1.73 | 1.93 | 1.84 | 1.78 | 1.64 | 1.64 | 1.89 |
| Other Nb | 2.21 | 2.20 | 2.20 | 2.17 | 2.08 | 2.08 | 2.09 | 2.08 | |
| Charge Redistribution | Ba/La | −0.25 | −0.30 | −0.28 | −0.32 | −0.27 | −0.35 | −0.46 | −0.34 |
| Nb | −1.26 | −1.65 | −1.15 | −1.47 | −0.79 | −1.11 | −1.71 | −1.36 | |
| Total | −1.51 | −1.95 | −1.43 | −1.79 | −1.06 | −1.46 | −2.17 | −1.70 | |
For BaNbO2N, Table 1 shows that charge redistribution, due to delocalisation of the electron density around the defect site, leads to the ‘true’ charge of 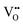 and
and 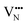 defects being only 65–75% of the expected formal values. For instance, for the C1 ordering the total charge redistribution in the BaNbO2N lattice around a VO defect is −1.51 e (rather than exactly −2), while for a VN defect this figure is −1.95 e (rather than exactly −3 e). Charge redistribution is slightly smaller for the T2 ordering (1.43 and 1.79 e, respectively), indicating that anion vacancies near trans-N3−–Nb5+–N3− anion configurations in BaNbO2N lead to less charge redistribution away from the vacancy site in the cation sublattice. Table 1 also shows that, following the formation of a neutral oxygen or nitrogen vacancy defect in BaNbO2N, the oxidation state of a Nb cation depends on its vicinity to the defect. For instance, the average partial charge of adjacent Nb cations is ∼0.5 e lower than those not coordinated to the vacancy. This is true for both the C1 and T2 anion orderings, although the effect is again marginally smaller for the latter (∼0.3 e), likely for the same reason noted above.
defects being only 65–75% of the expected formal values. For instance, for the C1 ordering the total charge redistribution in the BaNbO2N lattice around a VO defect is −1.51 e (rather than exactly −2), while for a VN defect this figure is −1.95 e (rather than exactly −3 e). Charge redistribution is slightly smaller for the T2 ordering (1.43 and 1.79 e, respectively), indicating that anion vacancies near trans-N3−–Nb5+–N3− anion configurations in BaNbO2N lead to less charge redistribution away from the vacancy site in the cation sublattice. Table 1 also shows that, following the formation of a neutral oxygen or nitrogen vacancy defect in BaNbO2N, the oxidation state of a Nb cation depends on its vicinity to the defect. For instance, the average partial charge of adjacent Nb cations is ∼0.5 e lower than those not coordinated to the vacancy. This is true for both the C1 and T2 anion orderings, although the effect is again marginally smaller for the latter (∼0.3 e), likely for the same reason noted above.
Very similar trends are observed in Table 1 regarding partial charges of adjacent and uncoordinated Nb cations in LaNbON2. For instance, for the lowest energy LC9 ordering, Nb cations adjacent to a VO defect are more reduced by ∼0.3 e, compared to Nb cations further away. Similarly, for a VN defect, the difference is ∼0.4 e (adjacent Nb cations being more reduced). Nb partial charges in the LT2 ordering are analogous by comparison. As for BaNbO2N, Table 1 shows that the DDEC6 charges obtained using PBEsol are notably lower than the expected formal values. For instance, in the LC9 ordering, the LaNbON2 lattice is reduced by only 1.06 e (VO) and 1.46 e (VN), respectively. However, a marked increase in charge distribution is observed for an oxygen vacancy defect in the LT2 ordering. Here, the LaNbON2 lattice is reduced by 2.17 e, which is comparable to the expected formal charge (i.e. −2). This is attributed to the effect of the ordering itself. While the pristine LT2 and LC9 structures exhibit essentially equivalent average Nb partial charges (2.14 compared to 2.10, not shown in Table 1), the introduction of the VO defect disrupts a trans-O2−–Nb5+–O2− chain in the LT2 structure, but leaves the chain in the cisLC9 ordering unperturbed. This reduces the Nb sublattice by ∼1 e (−1.71 e) more in LT2, compared to LC9 ordering (−1.06 e).
Vacancy diffusion barriers in Nb perovskite oxynitrides
With the thermochemical stability of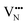 and
and 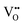 vacancy defects in BaNbO2N and LaNbON2 now established, we conclude our discussion by considering the impact of anion ordering on vacancy diffusion kinetics in these materials. Fig. 7 presents diffusion pathways of
vacancy defects in BaNbO2N and LaNbON2 now established, we conclude our discussion by considering the impact of anion ordering on vacancy diffusion kinetics in these materials. Fig. 7 presents diffusion pathways of 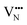 and
and 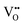 vacancy defects in BaNbO2N and LaNbON2 elucidated using the CI-NEB method. Due to the expense of this approach, we consider defect diffusion in only the most stable cis- and trans-anion orderings (i.e. the most relevant), and only those diffusion pathways corresponding to vacancies moving between adjacent positions in the crystal lattice (i.e. the distinct positions defined in Fig. 6a and b). For BaNbO2N we assess the accuracy of diffusion barriers obtained with the 2 × 2 × 2 supercell by comparing them with barriers obtained with a 3 × 3 × 3 supercell in Fig. S3 and Table S3 (ESI†). This comparison indicates that shorter diffusion pathways (rotation about a Nb ion) are significantly less sensitive to supercell size than longer pathways (shifting to other Nb ion coordination spheres), as anticipated. Importantly, Table S3 (ESI†) indicates that the trends in vacancy diffusion barriers found using the 2 × 2 × 2 supercell are reproduced with the 3 × 3 × 3 supercell. The longer diffusion pathways in LaNbON2 are orientated to the a/c plane in the 2 × 1 × 2 orthorhombic supercell, and so it is likely they are already converged with respect to the a/c dimensions of the supercell.
vacancy defects in BaNbO2N and LaNbON2 elucidated using the CI-NEB method. Due to the expense of this approach, we consider defect diffusion in only the most stable cis- and trans-anion orderings (i.e. the most relevant), and only those diffusion pathways corresponding to vacancies moving between adjacent positions in the crystal lattice (i.e. the distinct positions defined in Fig. 6a and b). For BaNbO2N we assess the accuracy of diffusion barriers obtained with the 2 × 2 × 2 supercell by comparing them with barriers obtained with a 3 × 3 × 3 supercell in Fig. S3 and Table S3 (ESI†). This comparison indicates that shorter diffusion pathways (rotation about a Nb ion) are significantly less sensitive to supercell size than longer pathways (shifting to other Nb ion coordination spheres), as anticipated. Importantly, Table S3 (ESI†) indicates that the trends in vacancy diffusion barriers found using the 2 × 2 × 2 supercell are reproduced with the 3 × 3 × 3 supercell. The longer diffusion pathways in LaNbON2 are orientated to the a/c plane in the 2 × 1 × 2 orthorhombic supercell, and so it is likely they are already converged with respect to the a/c dimensions of the supercell.
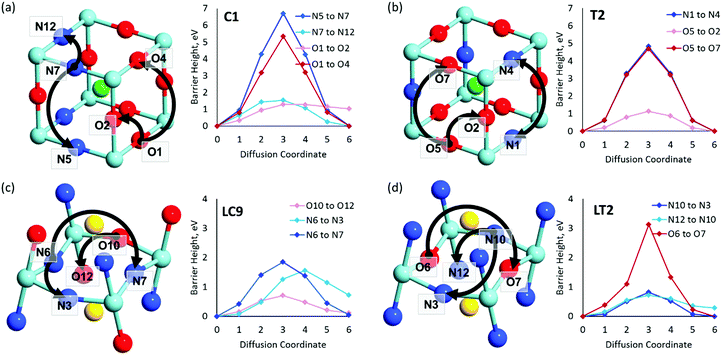 | ||
| Fig. 7 VN & VO diffusion pathways and associated PBEsol diffusion barriers (eV) for the most stable cis- and trans-anion orderings in (a and b) BaNbO2N and (c and d) LaNbON2. (a) BaNbO2N, C1 ordering, (b) BaNbO2N, T2 ordering, (c) LaNbON2, LC9 ordering, (d) LaNbON2, LT1 ordering. All diffusion pathways were calculated in the complete 3 × 3 × 3 and 2 × 1 × 2 supercells, respectively, however only the core region is depicted here for clarity. Anion positions are defined in Fig. 5a and b for BaNbO2N and LaNbON2, respectively. | ||
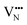 and
and 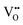 vacancies in the most stable C1 and T2 orderings of BaNbO2N and the corresponding energy barriers are presented in Fig. 7a and b. There are two distinct pathways for each vacancy type; the defect can rotate positions about a Nb5+ cation (O1 → O2, N7 → N12 in C1 (Fig. 7a); O5 → O2 in T2 (Fig. 7b)) or the defect can migrate to a non-adjacent position, shifting to a different Ta5+ cation but rotating about the Ba2+ cation (O1 → O4, N7 → N5 in C1 (Fig. 7a); O5 → O7, N1 → N4 in T2 (Fig. 7b)). The latter of these pathways is obviously the longest and so is anticipated to correlate with the highest diffusion barrier. Fig. 7a and b show that this is the case;
vacancies in the most stable C1 and T2 orderings of BaNbO2N and the corresponding energy barriers are presented in Fig. 7a and b. There are two distinct pathways for each vacancy type; the defect can rotate positions about a Nb5+ cation (O1 → O2, N7 → N12 in C1 (Fig. 7a); O5 → O2 in T2 (Fig. 7b)) or the defect can migrate to a non-adjacent position, shifting to a different Ta5+ cation but rotating about the Ba2+ cation (O1 → O4, N7 → N5 in C1 (Fig. 7a); O5 → O7, N1 → N4 in T2 (Fig. 7b)). The latter of these pathways is obviously the longest and so is anticipated to correlate with the highest diffusion barrier. Fig. 7a and b show that this is the case; 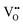 and
and 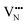 migration between non-adjacent sites is impeded by barriers ranging from 5.33 eV to 6.70 eV while rotation of the defect to adjacent positions around the Nb5+ cation corresponds to a barrier of only 1.13 eV to 1.53 eV. Fig. 7a and b also shows that, in general,
migration between non-adjacent sites is impeded by barriers ranging from 5.33 eV to 6.70 eV while rotation of the defect to adjacent positions around the Nb5+ cation corresponds to a barrier of only 1.13 eV to 1.53 eV. Fig. 7a and b also shows that, in general, 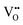 diffusion are barriers around ∼25% lower than the analogous diffusion pathways for
diffusion are barriers around ∼25% lower than the analogous diffusion pathways for 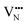 .
. 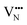 diffusion in the less stable T2 ordering is further impeded by the fact that it can only occur between adjacent NbO4N2 octahedra, and not via rotation around an individual Nb5+ cation, which would correspond to a lower barrier. Thus, despite being more stable in BaNbO2N, O2− vacancy defects are expected to undergo more facile diffusion, most notably in trans-ordered phases, impeding control over long range ordering in this material. We note also that these findings are consistent with our recent study of TaON, in which it was shown that diffusion barriers for
diffusion in the less stable T2 ordering is further impeded by the fact that it can only occur between adjacent NbO4N2 octahedra, and not via rotation around an individual Nb5+ cation, which would correspond to a lower barrier. Thus, despite being more stable in BaNbO2N, O2− vacancy defects are expected to undergo more facile diffusion, most notably in trans-ordered phases, impeding control over long range ordering in this material. We note also that these findings are consistent with our recent study of TaON, in which it was shown that diffusion barriers for 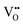 migration are potentially low enough to displace nitrogen content from the oxynitride.40 Thus, it is suggested that stabilising trans-ordered phases of BaNbO2N is likely to yield more effective retention of nitrogen content in this material, even if long-range order cannot be controlled.
migration are potentially low enough to displace nitrogen content from the oxynitride.40 Thus, it is suggested that stabilising trans-ordered phases of BaNbO2N is likely to yield more effective retention of nitrogen content in this material, even if long-range order cannot be controlled.
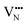 and
and 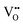 vacancies in the lowest energy cis- and trans-ordered structures of LaNbON2, LC9, and LT1, and the corresponding energy barriers are presented in Fig. 7c and d. In the LC9cis-ordering, Fig. 7c, O2− vacancies can only diffuse via the O10 → O12 pathway, while N3− vacancies have two possibilities for migration via rotation around a Nb5+ cation (N6 → N3) and between non-adjacent (N6 → N7) sites that cross the cavity between La3+ ions. In the latter case the defect is shifting to a separate NbO2N4 octahedron while rotating is coordinating about the local La-(O,N)12 coordinate sphere. In the less stable LT1trans-ordering, Fig. 7d, again O2− vacancies can only migrate via a single long pathway (O6 → O7) since rotation about an individual Nb5+ cation to another O2− site isn’t possible, whereas N3− vacancies can migrate via the N12 → N10 pathway and along the longer non-adjacent N10 → N3 pathway.
vacancies in the lowest energy cis- and trans-ordered structures of LaNbON2, LC9, and LT1, and the corresponding energy barriers are presented in Fig. 7c and d. In the LC9cis-ordering, Fig. 7c, O2− vacancies can only diffuse via the O10 → O12 pathway, while N3− vacancies have two possibilities for migration via rotation around a Nb5+ cation (N6 → N3) and between non-adjacent (N6 → N7) sites that cross the cavity between La3+ ions. In the latter case the defect is shifting to a separate NbO2N4 octahedron while rotating is coordinating about the local La-(O,N)12 coordinate sphere. In the less stable LT1trans-ordering, Fig. 7d, again O2− vacancies can only migrate via a single long pathway (O6 → O7) since rotation about an individual Nb5+ cation to another O2− site isn’t possible, whereas N3− vacancies can migrate via the N12 → N10 pathway and along the longer non-adjacent N10 → N3 pathway.
Consistent with BaNbO2N, the 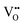 diffusion barriers are seen to be sensitive to whether the diffusion path is between adjacent anion positions or non-adjacent positions with O10 → O12 in LC9 predicted to have a barrier height of 0.71 eV, while O6 → O7 in LT2 is 3.12 eV. However, the difference in the
diffusion barriers are seen to be sensitive to whether the diffusion path is between adjacent anion positions or non-adjacent positions with O10 → O12 in LC9 predicted to have a barrier height of 0.71 eV, while O6 → O7 in LT2 is 3.12 eV. However, the difference in the 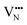 diffusion barriers for adjacent and non-adjacent paths is greatly reduced compared to BaNbO2N. In LC9 the adjacent pathway height is 1.56 eV with the non-adjacent path barrier only 0.29 eV higher, while in LT2 the adjacent
diffusion barriers for adjacent and non-adjacent paths is greatly reduced compared to BaNbO2N. In LC9 the adjacent pathway height is 1.56 eV with the non-adjacent path barrier only 0.29 eV higher, while in LT2 the adjacent 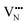 diffusion is now 0.72, with the non-adjacent barrier merely 0.82 eV. Interestingly, the kinetic stability of N3− vacancy defects in LaNbON2 is significantly reduced from that observed in BaNbO2N. In particular, in the less stable LT1trans-ordering, N3− vacancies diffuse more easily than O2− vacancies. The origin of this reduction is a cooperative effect in which the migrating
diffusion is now 0.72, with the non-adjacent barrier merely 0.82 eV. Interestingly, the kinetic stability of N3− vacancy defects in LaNbON2 is significantly reduced from that observed in BaNbO2N. In particular, in the less stable LT1trans-ordering, N3− vacancies diffuse more easily than O2− vacancies. The origin of this reduction is a cooperative effect in which the migrating 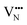 vacancy partially displaces an adjacent O2− anion. The additional space created by this displacement gives rise to an asymmetric path, in which the
vacancy partially displaces an adjacent O2− anion. The additional space created by this displacement gives rise to an asymmetric path, in which the 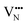 vacancy does not pass directly between adjacent La3+ cations along the diffusion pathway. In doing so, the migrating
vacancy does not pass directly between adjacent La3+ cations along the diffusion pathway. In doing so, the migrating 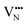 vacancy partially displaces an adjacent O2− anion and so reduces the diffusion barrier.
vacancy partially displaces an adjacent O2− anion and so reduces the diffusion barrier.
Conclusions
The impact of anion ordering on defect engineering in perovskite oxynitride photocatalysts remains largely unexplored, despite it being the necessary first step towards controlling defects in these materials for improved photocatalytic performance. Using accurate first-principles calculations, we have presented an extensive investigation of cis- and trans-anion orderings in two exemplar perovskite oxynitrides, BaNbO2N and LaNbON2, and examined how these orderings influence (1) overall stability, (2) the stability of N3− and O2− point defects and (3) the mobility of these defects through the bulk material. Analysis of partial charges with DDEC6 confirmed that the anion ordering influenced the degree of e− redistribution to adjacent and outer Nb cations from the creation of an anion vacancy.For BaNbO2N, our results show clearly that fully cis-anion orderings are more stable than fully trans-anion orderings. The influence of these orderings on the cubic lattice vectors however demonstrates differing degrees of anisotropy. This ultimately has implications for strain engineering in this oxynitride; specifically, it may be difficult to stabilize the fully trans-orderings in BaNbO2N, over half-trans or fully-cis orderings, via in-plane compression of the crystal lattice. In LaNbON2, 2D & 3D orderings have comparable energies, meaning that mixed dimensionality in anion ordering may be more prevalent in this material. However, our results show the presence of a secondary ‘A-site coordination sphere effect’ influencing the stability of different orderings in LaNbON2, where the stoichiometric distribution of O2− and N3− in La-(O,N)12 gives rise to obvious differences in the relative energies of different fully cis-anion orderings. This effect is less obvious in BaNbO2N, which we contend is due to the more densely packed lattice having a higher degree of symmetry, which masks any Ba-(O,N)12 coordination sphere on the overall stability of the material. Vacancy defect formation energies for BaNbO2N indicate that domains rich in cis-anion orderings (the most favourable) may preferentially stabilise O2− anion vacancies less uniformly in their structure, whereas N3− anion vacancies are less likely. On the other hand, O2− defect formation energies in LaNbON2 are more sensitive to the local anion ordering, than its overall cis- or trans-character. This is attributed to the effect of the La3+ A-site cation, which for particular orderings considered here gives rise to alternating layers of LaO and LaN that reduce significantly O2− vacancy defect formation energy.
For BaNbO2N, 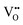 diffusion barriers were found to be lower than
diffusion barriers were found to be lower than 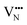 , most notably in trans-ordered phases. It is predicted that this will impede control over long range ordering in BaNbO2N. Stabilising trans-ordered phases of this material is thus predicted to yield more effective retention of nitrogen content in its structure, irrespective of long-range anion order. In this sense, BaNbO2N bears some resemblance to TaON, for which
, most notably in trans-ordered phases. It is predicted that this will impede control over long range ordering in BaNbO2N. Stabilising trans-ordered phases of this material is thus predicted to yield more effective retention of nitrogen content in its structure, irrespective of long-range anion order. In this sense, BaNbO2N bears some resemblance to TaON, for which 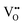 migration barriers are potentially low enough to displace nitrogen content from the oxynitride.40 The reverse is observed true for
migration barriers are potentially low enough to displace nitrogen content from the oxynitride.40 The reverse is observed true for 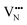 in LaNbON2, i.e. N3− vacancy defects exhibit lower diffusion barriers than O2− vacancy defects. VN diffusion via both adjacent and non-adjacent pathways in LaNbON2 benefits from the lower orthorhombic symmetry. In part this is due to the disruption the migrating N3− defect has on the local coordination environment; when rotating around a local La3+ cation the N3− anion vacancy partially displaces an adjacent O2− ion to lower the diffusion barrier.
in LaNbON2, i.e. N3− vacancy defects exhibit lower diffusion barriers than O2− vacancy defects. VN diffusion via both adjacent and non-adjacent pathways in LaNbON2 benefits from the lower orthorhombic symmetry. In part this is due to the disruption the migrating N3− defect has on the local coordination environment; when rotating around a local La3+ cation the N3− anion vacancy partially displaces an adjacent O2− ion to lower the diffusion barrier.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was undertaken with the assistance of resources provided at the NCI National Facility systems at the Australian National University, through the National Computational Merit Allocation Scheme supported by the Australian Government. AJP acknowledges support from the Australian Research Council (INTERSECT, LE170100032). JJB acknowledges support from an Australian Government RTP Scholarship.Notes and references
- T. Takata and K. Domen, Dalton Trans., 2017, 46, 10529–10544 RSC
.
- M. Ahmed and G. Xinxin, Inorg. Chem. Front., 2016, 3, 578–590 RSC
.
- B. Siritanaratkul, K. Maeda, T. Hisatomi and K. Domen, ChemSusChem, 2011, 4, 74–78 CrossRef CAS PubMed
.
- D. Y. Wan, Y. L. Zhao, Y. Cai, T. C. Asmara, Z. Huang, J. Q. Chen, J. Hong, S. M. Yin, C. T. Nelson, M. R. Motapothula, B. X. Yan, D. Xiang, X. Chi, H. Zheng, W. Chen, R. Xu, Ariando, A. Rusydi, A. M. Minor, M. B. H. Breese, M. Sherburne, M. Asta, Q. H. Xu and T. Venkatesan, Nat. Commun., 2017, 8, 15070 CrossRef CAS PubMed
.
- X. Xu, C. Randorn, P. Efstathiou and J. T. S. Irvine, Nat. Mater., 2012, 11, 595–598 CrossRef CAS PubMed
.
- K. Maeda, M. Higashi, B. Siritanaratkul, R. Abe and K. Domen, J. Am. Chem. Soc., 2011, 133, 12334–12337 CrossRef CAS PubMed
.
- J. Liu, Z. Wei and W. Shangguan, ChemCatChem, 2019, 11, 6177–6189 CrossRef CAS
.
- S. Bai, N. Zhang, C. Gao and Y. Xiong, Nano Energy, 2018, 53, 296–336 CrossRef CAS
.
- Y.-I. Kim, P. M. Woodward, K. Z. Baba-Kishi and C. W. Tai, Chem. Mater., 2004, 16, 1267–1276 CrossRef CAS
.
- M. Yang, J. Oró-Solé, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Nat. Chem., 2010, 3, 47 CrossRef PubMed
.
- A. Fuertes, J. Mater. Chem., 2012, 22, 3293–3299 RSC
.
- D. Oka, Y. Hirose, H. Kamisaka, T. Fukumura, K. Sasa, S. Ishii, H. Matsuzaki, Y. Sato, Y. Ikuhara and T. Hasegawa, Sci. Rep., 2014, 4, 4987 CrossRef CAS
.
- Y. Hinuma, H. Moriwake, Y.-R. Zhang, T. Motohashi, S. Kikkawa and I. Tanaka, Chem. Mater., 2012, 24, 4343–4349 CrossRef CAS
.
- N. Vonrüti and U. Aschauer, Phys. Rev. Mater., 2018, 2, 105401 CrossRef
.
- A. Ziani, C. Le Paven, L. Le Gendre, F. Marlec, R. Benzerga, F. Tessier, F. Cheviré, M. N. Hedhili, A. T. Garcia-Esparza, S. Melissen, P. Sautet, T. Le Bahers and K. Takanabe, Chem. Mater., 2017, 29, 3989–3998 CrossRef CAS
.
- H. Johnston, A. P. Black, P. Kayser, J. Oró-Solé, D. A. Keen, A. Fuertes and J. P. Attfield, Chem. Commun., 2018, 54, 5245–5247 RSC
.
- A. Kubo, G. Giorgi and K. Yamashita, Chem. Mater., 2017, 29, 539–545 CrossRef CAS
.
- P. J. Camp, A. Fuertes and J. P. Attfield, J. Am. Chem. Soc., 2012, 134, 6762–6766 CrossRef CAS PubMed
.
- S. G. Ebbinghaus, H.-P. Abicht, R. Dronskowski, T. Müller, A. Reller and A. Weidenkaff, Prog. Solid State
Chem., 2009, 37, 173–205 CrossRef CAS
.
- L. Clark, J. Oró-Solé, K. S. Knight, A. Fuertes and J. P. Attfield, Chem. Mater., 2013, 25, 5004–5011 CrossRef CAS
.
- D. Oka, Y. Hirose, F. Matsui, H. Kamisaka, T. Oguchi, N. Maejima, H. Nishikawa, T. Muro, K. Hayashi and T. Hasegawa, ACS Nano, 2017, 11, 3860–3866 CrossRef CAS PubMed
.
- N. Vonrüti and U. Aschauer, Phys. Rev. Lett., 2018, 120, 046001 CrossRef PubMed
.
- S. Ninova and U. Aschauer, J. Mater. Chem. A, 2017, 5, 11040–11046 RSC
.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS
.
- M. Hellenbrandt, Cryst. Rev., 2004, 10, 17–22 CrossRef CAS
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- N. G. Limas and T. A. Manz, RSC Adv., 2018, 8, 2678–2707 RSC
.
- T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801 RSC
.
- N. G. Limas and T. A. Manz, RSC Adv., 2016, 6, 45727–45747 RSC
.
- M. Pavone, A. M. Ritzmann and E. A. Carter, Energy Environ. Sci., 2011, 4, 4933–4937 RSC
.
- V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104 CrossRef
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- R. Wahl, D. Vogtenhuber and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104116 CrossRef
.
- K. K. Ghose, A. Bayon and A. J. Page, J. Phys. Chem. C, 2020, 124, 27055–27063 CrossRef CAS
.
- J. J. Bown and A. J. Page, J. Mater. Chem. A, 2019, 7, 13029–13035 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Relative energies of LaNbO2N, BaNbON2 anion orderings in the presence of vacancy defects, comparison of vacancy diffusion barrier heights as a function of supercell size. See DOI: 10.1039/d1ma00122a |
| This journal is © The Royal Society of Chemistry 2021 |