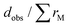Open Access Article
Open Access ArticleCrystal structure, magnetic and magnetocaloric properties of the new orthorhombic Y3Co2-type Gd3Co1+xNi1−x solid solution†
Aritz
Herrero
 *a,
Alessia
Provino
bcd,
Ivan R.
Aseguinolaza
a,
Serena
De Negri
*a,
Alessia
Provino
bcd,
Ivan R.
Aseguinolaza
a,
Serena
De Negri
 b,
Davide
Peddis
b,
Davide
Peddis
 be,
Pietro
Manfrinetti
bc and
Alberto
Oleaga
a
be,
Pietro
Manfrinetti
bc and
Alberto
Oleaga
a
aDepartamento de Física Aplicada, Escuela de Ingeniería de Bilbao, Universidad del País Vasco UPV/EHU, Plaza Torres Quevedo 1, 48013 Bilbao, Spain. E-mail: aritz.herrero@ehu.eus
bDepartment of Chemistry, University of Genova, Via Dodecaneso 31, 16146 Genova, Italy
cCNR, Institute SPIN, Corso Perrone 24, 16152 Genova, Italy
dDepartment of Material Sciences and Engineering, Alfred University, Alfred, New York 14802, USA
eCNR, Institute of Structure of Matter, nM2-lab, Monterotondo Scalo (RM), 00015, Italy
First published on 8th April 2025
Abstract
This work reports the existence of the new rare-earth intermetallic compound Gd3Co1+xNi1−x (with x = 0.1, 0.2, 0.3, and 0.4) and the investigation of its crystallographic, magnetic, and magnetocaloric properties. Gd3Co1+xNi1−x is a novel solid solution phase that crystallizes in the orthorhombic Y3Co2-type structure [oP20, Pnmm (no. 58)]. It constitutes the first representative of a compound crystallizing in this structural prototype. The research also includes an analysis of the critical behavior associated with the second-order phase transition from a paramagnetic to a ferromagnetic state (PM–FM) detected in the compound. This analysis indicates that short-range order isotropic magnetic interactions are present, consistent with the 3D Heisenberg model. Increasing the Co content leads to a higher Curie temperature (TC), thus, shifting the peak of the magnetic entropy change, while maintaining the overall physical properties. This demonstrates the potential of tuning the working temperature region by modifying the Co/Ni concentration without negatively affecting the magnetocaloric properties. For μ0ΔH = 5 T, the magnetic entropy change peaks range between 7.81 and 8.40 J kg−1 K−1, while the refrigerant capacity values are around 600 J kg−1. These results place this family among the top performing ones in their working temperature region. The scaling relations and the universal curve confirm the second-order nature of the phase transition and validate the calculated critical exponents.
1. Introduction
Reducing energy consumption, increasing the efficiency of heating and cooling devices, implementing new renewable energy sources and moving towards a greener economy and society are on the core of the current international scientific programs and research plans.1–4 The effort towards the achievement of these goals is increasing year by year, with the research on new, more efficient and environmentally friendly refrigeration devices as one of the most active research lines. To this end, magnetocaloric refrigeration has emerged as a promising candidate to fulfill the requirements of future energy demands. Besides the necessity of designing, building and testing the current refrigeration devices, the discovery of new magnetocaloric materials, the study of their crystallographic, thermal, magnetic and magnetocaloric properties, as well as the understanding of the physics ruling those properties, are the key to find the perfect magnetic refrigerant. To that end, many researchers are focusing their efforts on rare-earth based intermetallic compounds.5,6 The interplay between rare-earth elements and the rest of the constituents usually gives rise to relevant magnetocaloric effects in a wide range of temperatures. This phenomenon is behind the growing interest in the synthesis and study of new intermetallic compounds. In particular, the ability to tune the physical properties of these compounds by slightly varying their composition, i.e. mixing rare-earth elements,7–13 or substituting transition metals and/or p-block elements,11,14–18 is of great interest. This allows a better understanding of the role of each constituent element in the final properties.The present study aims to broaden the knowledge about a particular family of intermetallic compounds, R3CoNi (R = rare earth element), for which few studies have been performed so far.19–22 More specifically, this research is focused on the study of the effect of Co/Ni substitution on the crystallographic, magnetic and magnetocaloric properties of the Gd3Co1+xNi1−x family, with x = 0.1, 0.2, 0.3 and 0.4. Aiming to better understand the underlying physics of the system, the work will also include a critical behavior study of the second-order phase transition of the system from the paramagnetic state to the ferromagnetic state (PM–FM), which will provide insights into the range of magnetic interactions as well as the symmetry of the system. Unlike Ni, Co does not form a binary ‘R3Co2’ compound. Substitution of Ni by Co in the binary R3Ni2 phase, leading to the formation of R3CoyNi2−y phase, has been studied for R = Tb21 and Gd,22 with Co content y ≤ 1 (lower than that of Ni and up to R3CoNi composition). In contrast, the present investigation focuses on the opposite case, when Co content exceeds that of Ni. These previous studies have shown that in both Gd3CoyNi2−y and Tb3CoyNi2−y series,21,22 an increase in the Co content consistently results in a higher Curie temperature (TC). Therefore, we aimed to study the phase formation for Co rich compositions, to determine whether further tuning of the working temperature of these materials was possible while maintaining good magnetocaloric properties.
The new Gd3Co1+xNi1−x compound was recently identified during a previous investigation of the binary Gd3Ni2 and its solid solution Gd3CoyNi2−y series (for y ≤ 1).22 Gd3Ni2 is a high temperature compound existing between 650 °C and 715 °C; this phase can be retained at room temperature by quenching (as a metastable phase). Interestingly, the partial substitution of Ni by Co to form Gd3CoyNi2−y stabilizes this solid-solution phase down to room temperature. Both Gd3Ni2 and the pseudo-binary Gd3CoyNi2−y series crystallize in the monoclinic Dy3Ni2-type structure {Pearson symbol mS20, space group C2/m (no. 12), Z = 423}. This monoclinic structure is maintained up to Gd3CoNi (for the Co content y = 1.0). Furthermore, it was ascertained that the crystal structure of Gd3CoNi is a ternary ordered derivative of the monoclinic Dy3Ni2-type, where Co atoms preferentially occupy only one of the two 4i Wyckoff sites available for the transition metal.22 Upon a further increase of the Co content beyond Gd3CoNi (i.e. for y > 1), the crystal structure changes from the monoclinic Dy3Ni2-type to the orthorhombic Y3Co2-type [oP20, Pnnm (no. 58), Z = 4]24 forming the new Gd3Co1+xNi1−x compound. Notably, while the monoclinic Dy3Ni2-type structure is commonly adopted by several R3Ni2 and R3CoNi intermetallic compounds,19–21 the orthorhombic Y3Co2-type structure had only been reported for the prototype itself; no other binary or ternary compound has ever been reported to adopt this structure.25 Gd3Co1+xNi1−x is thus the first compound found to crystallize in the Y3Co2-type structure.1 A crystallographic phase transition was also observed in the Tb3CoyNi2−y series; however, in this case, increasing the Co content beyond y ≈ 0.34 induces a structural change from the monoclinic Dy3Ni2-type to the rhombohedral Er3Ni2-type.21
In this work we report on the crystal structure of the new solid-solution Gd3Co1+xNi1−x compound, present and discuss the magnetic and magnetocaloric properties along this series as a function of Co content (for x = 0.1, 0.2, 0.3, 0.4), and compare its physical properties with those observed in the monoclinic Gd3CoyNi2−y series (y ≤ 1). Finally, we analyze the critical behavior associated with the second-order phase transition detected in this series, occurring from a paramagnetic to a ferromagnetic state.
2. Experimental section
2.1. Synthesis
Polycrystalline samples (each approximately 4 g in total mass), with the nominal composition Gd3Co1+xNi1−x, with x = 0.1, 0.2, 0.3, 0.4, were synthesized by arc melting the elements, weighed in stoichiometric proportion and under a pure Ar atmosphere. The starting constituents were high-purity commercial elements (Gd >99.9 wt% purity, Co and Ni, both 99.99 wt% purity); a slight excess of Gd (2 wt%) was added to prevent the possible formation of the equiatomic phase GdCoxNi1−x, which is ferromagnetic.26 The buttons were melted three times, flipping them over between each melting to ensure homogeneity. Weight loss after melting was lower than 0.5% (about 0.2%). To maintain a clean atmosphere within the arc furnace, a TiZr getter was melted before melting each sample. The ingots were then wrapped in Ta foil, sealed under vacuum in quartz tubes, and annealed at 650 °C for 8 days (based on differential thermal analysis data). After annealing, the samples were slowly cooled to room temperature inside the furnace by simply switching off the power. The final samples exhibited typical metallic luster and brittle consistency.2.2. Phase analysis
Phase analysis was conducted using scanning electron microscopy (SEM) coupled with energy dispersive X-ray spectroscopy (EDX) for semi-quantitative analysis, as well as X-ray diffraction (XRD) on both powder (PXRD) and single crystal (SCXRD) samples. The microstructure and homogeneity of the alloys were examined by SEM-EDX using a Leica Cambridge 360 microscope, equipped with an Oxford X-Max 20 analyzer. The operating parameters included an electron high tension (EHT) of 20.0 kV and a probe current of 220 pA, controlled through Oxford Aztec software; Co was used as an internal standard. Micrographic specimens were prepared by a standard polishing technique on a representative vertical section of each sample, cut from top to bottom. Since the weight loss of each sample during melting was negligible, the EDX analysis over the entire area of each specimen (15–20 mm2) was used as a reference standard of known composition to ensure the accuracy of the compositional analysis. This approach allowed for an estimated measurement accuracy within 0.5 at% for all elements.2.3. Crystal structure determination
The crystal structure was determined by means of both powder and single-crystal X-ray diffraction. Powder diffraction patterns were collected with a Philips diffractometer (Cu Kα radiation, λ = 1.54184 Å) equipped with a line-detector. The powders were prepared by grinding polycrystalline pieces of each alloy and placing them on a zero-background Si-single-crystal sample holder. Data were collected over a 2θ range of 6–96°, with a step size of 0.02° and a counting time of 4–6 seconds per step. Pure Si [a = 5.4308(1) Å] was used as an internal standard. The X-ray powder patterns were indexed using Lazy Pulverix27 and accurate lattice parameters were calculated using home-made least squares methods. The Rietveld refinement was performed for all four samples using the FullProf software.28Single-crystal X-ray diffraction analysis was performed on a high-quality crystal selected from a crushed fragment of the sample with the nominal composition Gd3Co1.1Ni0.9. The crystal was affixed to a glass fiber using grease and then loaded into the diffractometer. A complete dataset was collected under ambient conditions using a three-circle Bruker D8 QUEST diffractometer equipped with a PHOTON III detector (graphite monochromatized Mo Kα radiation, λ = 0.71073 Å) operating in ω-scan mode. Intensity data were collected over the reciprocal space up to ≈36.3° in θ (resolution of ≈0.6 Å), with exposures of 30 s per frame. The data were reduced and corrected for Lorentz, polarization, and absorption effects using APEX5.29 The structure was solved and refined using the Bruker SHELXTL Software package.30,31
2.4. Magnetic measurements
Magnetization measurements were performed using a vibrating sample magnetometer (VSM) module installed in a physical properties measurement system (PPMS, Quantum Design). Various datasets were collected to thoroughly characterize the magnetism of the investigated compounds. The isofield magnetization, M(T), was measured at a small applied magnetic field of 0.01 T between 2 K and 300 K and under zero-field-cooled (ZFC), field-cooled (FC) and field-warmed (FW) conditions. To study the magnetic behavior under varying applied magnetic field, isothermal magnetization curves, M(H), were measured at temperatures ranging from 80 K to well above the Curie temperature. These measurements were performed under an externally applied magnetic field up to 7 T, using a step size of μ0ΔH = 0.1 T. Isotherms were collected at 5 K intervals, except near the magnetic phase transition at TC where a finer temperature step of ΔT = 1 K was used to ensure accurate critical behavior analysis. For the purpose of correctly evaluating the magnetic entropy change, the demagnetization effect has been considered.32 To this purpose, ac magnetic susceptibility measurements have been performed, from where the demagnetization factor (N) can be obtained using the Hopkinson maximum criteria.33,34 After this, the internal magnetic field (Hi) is calculated following Hi = Ha − NM (N being the demagnetization factor and Ha the applied magnetic field). To simplify the notation, H will be used from now on to denote the internal field Hi. The demagnetization factors obtained by this method for our compounds are 44.16 gOe emu−1 for x = 1.1, 39.06 gOe emu−1 for x = 1.2, 39.15 gOe emu−1 for x = 1.3 and 49.82 for x = 1.4.Finally, in order to rule out the possibility of any kind of magnetic hysteresis, hysteresis loops at 2 K, 165 K and 225 K have been measured for every compound.
2.5. Resistivity measurements
The zero-field electrical resistivity was measured for Gd3Co1.1Ni0.9 and Gd3Co1.4No0.6 using the commercially available physical properties measurement system (PPMS, Quantum Design) on a home-made sample holder. The data were collected in a standard four-probe configuration, experimentally realised with Cu lids glued to the sample by silver paint, in a temperature range between 5 and 310 K.3. Results and discussion
3.1. Crystal structure of Gd3Co1+xNi1−x
The crystal structure of Gd3Co1+xNi1−x was initially identified from the powder X-ray diffraction pattern of an as-cast sample prepared with the nominal composition Gd3CoNi, intended to synthesize the monoclinic Dy3Ni2-type Gd3CoNi phase. In the X-ray powder pattern of this sample, together with the diffraction peaks of the monoclinic and primary phase, additional peaks were observed; these extra peaks were indexed to the primitive orthorhombic unit-cell of the Y3Co2 prototype structure.22 The subsequent annealing process led to a sample with homogeneous composition, stabilizing the monoclinic phase as the unique equilibrium phase. Further investigation carried out in the present work revealed that the orthorhombic Y3Co2-type phase forms just as the Co content in the monoclinic Dy3Ni2-type Gd3CoyNi2−y exceeds y = 1.0. For this reason, we refer to the orthorhombic phase as Gd3Co1+xNi1−x.The crystal structure of Gd3Co1+xNi1−x was also confirmed by single-crystal X-ray diffraction on an annealed sample having the nominal composition Gd3Co1.1Ni0.9. The structure was solved with the aid of the intrinsic phasing algorithm and refined using the Bruker SHELXTL Software package30,31 in the space group Pnnm (with Z = 4 for the formula unit Gd3Co1.10Ni0.90). The crystal data and structure refinement details are presented in Table S1 (ESI†). The corresponding CIF file, available as ESI,† has been deposited in the Cambridge Structural Database under deposition code CSD-2401455.
This structure features five inequivalent Wyckoff sites with 4g symmetry: three occupied by Gd atoms (occupied by Y in the prototype) and two occupied by Co or Co/Ni atoms (occupied by Co atoms in the prototype). Interestingly, the monoclinic structure of Gd3Ni2 and Gd3CoyNi2−y compounds, despite belonging to a different crystalline system, exhibits similar atomic arrangement with five inequivalent Wyckoff sites with 4i symmetry [three occupied by Gd atoms (Dy in the prototype) and two occupied by Co/Ni atoms (Ni in the prototype)].22 Previous results from single-crystal X-ray diffraction and first-principles total energy calculations for the monoclinic Dy3Ni2-type Gd3CoNi revealed crystallographic ordering, with a preferential occupation of Co atoms at the 4i site with coordinates (0.2378, 0, 0.2371) and Ni atoms at the 4i site with coordinates (0.0354, 0, 0.1425).22 Based on these findings, the two 4g Wyckoff sites assigned to Co and Ni in the new orthorhombic Gd3Co1.1Ni0.9 structure were carefully analyzed for possible Co/Ni preferential occupancy. Consistent with expectations, a statistical analysis of multiple crystals revealed that the structural refinement converged with reasonably low and acceptable agreement factors only when the 4g site at coordinates (0.13735, 0.23394, 0) was fully occupied by Co atoms, and the 4g site at (0.12498, 0.03278, 0) was statistically filled by both Co and Ni with a 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9 occupancy ratio, consistent with the nominal phase composition (confirmed by the EDX data) (Table 1).
0.9 occupancy ratio, consistent with the nominal phase composition (confirmed by the EDX data) (Table 1).
| Atom | Wyckoff site | x/a | y/b | z/c | Occ. | U eq [Å2] |
|---|---|---|---|---|---|---|
| a Co/Ni occupancy was not refined. | ||||||
| Gd1 | 4g | 0.43573(3) | 0.36406(2) | 0 | 1 | 0.01282(6) |
| Gd2 | 4g | 0.19030(3) | 0.63045(2) | 0 | 1 | 0.01402(7) |
| Gd3 | 4g | 0.62744(3) | 0.10880(2) | 0 | 1 | 0.01393(6) |
| Co | 4g | 0.13735(10) | 0.23394(7) | 0 | 1 | 0.01882(17) |
| Co/Ni | 4g | 0.12498(9) | 0.03278(6) | 0 | 0.1/0.9a | 0.01806(15) |
| Atom | Wyckoff site | U 11 [Å2] | U 22 [Å2] | U 33 [Å2] | U 23 [Å2] | U 13 [Å2] | U 12 [Å2] |
|---|---|---|---|---|---|---|---|
| Gd1 | 4g | 0.01311(12) | 0.01321(12) | 0.01215(14) | 0 | 0 | −0.00029(9) |
| Gd2 | 4g | 0.01390(12) | 0.01527(13) | 0.01291(14) | 0 | 0 | −0.00081(9) |
| Gd3 | 4g | 0.01343(11) | 0.01379(12) | 0.01457(13) | 0 | 0 | −0.00039(10) |
| Co | 4g | 0.0297(4) | 0.0148(3) | 0.0120(4) | 0 | 0 | 0.0004(3) |
| Co/Ni | 4g | 0.0198(3) | 0.0170(3) | 0.0174(4) | 0 | 0 | 0.0003(3) |
The microstructure and the phase composition of the four samples were analyzed using SEM-EDX. The analyses revealed all samples to predominantly contain the orthorhombic Gd3Co1+xNi1−x phase as the main phase, with small amounts of Gd3Co1−xNix (Fe3Co-type, oP16, Pnma, no. 62) as the secondary phase. The SEM image showing the microstructure of the sample Gd3Co1.1Ni0.9, chosen as a representative, is depicted in Fig. 1. Rietveld refinement was performed for all four samples adopting the occupancies suggested by single-crystal data for the 4g sites assigned to Co and Ni, and accounting for the Co/Ni ratios measured by EDX [with Co occupying the 4g site at (0.13735, 0.23394, 0) and both Co and Ni occupying the 4g site at (0.12498, 0.03278, 0) in ratios 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.9, 0.2
0.9, 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8, 0.3
0.8, 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 and 0.4
0.7 and 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6]. The Co and Ni composition of both phases was kept constant and not refined during the Rietveld refinements.
0.6]. The Co and Ni composition of both phases was kept constant and not refined during the Rietveld refinements.
By combining SEM-EDX with Rietveld refinement data, it was determined that the sample with nominal composition Gd3Co1.1Ni0.9 contains ≈96 vol% Gd3Co1.10Ni0.90 and ≈4 vol% Gd3Co1−xNix with x ≈ 0.3, the sample Gd3Co1.2Ni0.8 contains ≈97 vol% Gd3Co1.20Ni0.80 and ≈3 vol% Gd3Co1−xNix with x ≈ 0.3, the sample Gd3Co1.3Ni0.7 contains ≈98.5 vol% Gd3Co1.30Ni0.70 and ≈2.5 vol% Gd3Co1−xNix with x ≈ 0.2, and the sample Gd3Co1.40Ni0.60 contains ≈98.2 vol% Gd3Co1.40Ni0.60 and ≈1.8 vol% Gd3Co1−xNix with x ≈ 0.2. The Rietveld refinement profile for Gd3Co1.4Ni0.6 is shown in Fig. 2, as an example. The corresponding profiles for the other three compounds are shown in Fig. S1–S3 (ESI†), while the relative atomic coordinates are reported in Tables S2–S5 (ESI†), respectively. Projections of the crystal structure along the three crystallographic axes are shown in Fig. 3. The coordination polyhedra in Gd3Co1.1Ni0.9, pertaining to the first coordination sphere [this defined for  , where dobs is the observed interatomic distance between two next-neighbor atoms and
, where dobs is the observed interatomic distance between two next-neighbor atoms and  is the sum of the two metallic radii (where rM = 1.802 Å, 1.252 Å and 1.246 Å for Gd, Co and Ni, respectively35)], are shown in Fig. 4. The corresponding distances are provided in Table 2. Both the crystal structure and coordination polyhedra were drawn using VESTA software.36 The coordination polyhedra surrounding Gd1, Gd2 and Gd3 atoms are a 7-capped pentagonal prism, a 16-vertex Frank–Kasper polyhedron and a 14-vertex Frank–Kasper polyhedron, respectively, while the coordination polyhedra around Co and Co/Ni atoms are both tricapped trigonal prisms. The shortest interatomic distances in Gd3Co1.1Ni0.9, as well as in the other members of the series Gd3Co1+xNi1−x (up to x = 0.4), are those between Gd and Co (Gd−Co) and Co/Ni [Gd−(Co/Ni)] atoms (Table 2). As indicated by Rietveld refinement, these distances vary non-uniformly with increasing Co content. While all the Gd−(Co/Ni) distances decrease as the Co content increases, some Gd1−Co and Gd3−Co distances increase, and other Gd1−Co, Gd2−Co and Gd3−Co distances decrease along the series. The specific values of interatomic distances obtained by Rietveld refinement for the four compounds are not reported to emphasize the qualitative analysis of the trends rather than numerical details.
is the sum of the two metallic radii (where rM = 1.802 Å, 1.252 Å and 1.246 Å for Gd, Co and Ni, respectively35)], are shown in Fig. 4. The corresponding distances are provided in Table 2. Both the crystal structure and coordination polyhedra were drawn using VESTA software.36 The coordination polyhedra surrounding Gd1, Gd2 and Gd3 atoms are a 7-capped pentagonal prism, a 16-vertex Frank–Kasper polyhedron and a 14-vertex Frank–Kasper polyhedron, respectively, while the coordination polyhedra around Co and Co/Ni atoms are both tricapped trigonal prisms. The shortest interatomic distances in Gd3Co1.1Ni0.9, as well as in the other members of the series Gd3Co1+xNi1−x (up to x = 0.4), are those between Gd and Co (Gd−Co) and Co/Ni [Gd−(Co/Ni)] atoms (Table 2). As indicated by Rietveld refinement, these distances vary non-uniformly with increasing Co content. While all the Gd−(Co/Ni) distances decrease as the Co content increases, some Gd1−Co and Gd3−Co distances increase, and other Gd1−Co, Gd2−Co and Gd3−Co distances decrease along the series. The specific values of interatomic distances obtained by Rietveld refinement for the four compounds are not reported to emphasize the qualitative analysis of the trends rather than numerical details.
 | ||
| Fig. 3 Projections of the crystal structure of the orthorhombic Y3Co2-type Gd3Co1.1Ni0.9 compound along the three crystallographic axes. | ||
 | ||
Fig. 4 Coordination polyhedra around Gd1, Gd2, Gd3, Co/Ni and Co atoms corresponding to the first coordination sphere for  in Gd3Co1.1Ni0.9. in Gd3Co1.1Ni0.9. | ||
 in Gd3Co1.1Ni0.9, as obtained from single crystal analysis
in Gd3Co1.1Ni0.9, as obtained from single crystal analysis
| Central atom | Ligands | d [Å] | Polyhedron | |
|---|---|---|---|---|
| Gd1 | 2 Co/Ni | 2.9195(6) | 0.957 | 7-Capped pentagonal prism Gd[Gd10Co3(Co,Ni)4] |
| CN = 17 | 2 Co/Ni | 2.9398(7) | 0.964 | |
| 2 Co | 2.9866(7) | 0.978 | ||
| 1 Co | 3.2837(10) | 0.911 | ||
| 2 Gd3 | 3.5326(3) | 0.980 | ||
| 1 Gd2 | 3.5708(4) | 0.991 | ||
| 1 Gd1 | 3.6271(4) | 1.004 | ||
| 1 Gd3 | 3.6904(4) | 1.024 | ||
| 2 Gd2 | 3.7081(3) | 1.029 | ||
| 2 Gd1 | 3.8477(1) | 1.068 | ||
| 1 Gd2 | 4.0834(4) | 1.133 | ||
| Gd2 | 2 Co | 2.8454(7) | 0.932 | 16-Vertex Frank–Kasper Gd[Gd11Co3(CoNi)2] |
| CN = 16 | 2 Co/Ni | 2.8835(7) | 0.945 | |
| 1 Co | 3.5613(10) | 1.166 | ||
| 1 Gd1 | 3.5708(4) | 0.991 | ||
| 2 Gd3 | 3.6023(4) | 1.000 | ||
| 2 Gd3 | 3.6170(3) | 1.004 | ||
| 1 Gd3 | 3.7072(4) | 1.029 | ||
| 2 Gd1 | 3.7081(3) | 1.029 | ||
| 2 Gd2 | 3.8477(1) | 1.067 | ||
| 1 Gd1 | 4.0834(4) | 1.133 | ||
| Gd3 | 2 Co | 2.7583(7) | 0.903 | 14-Vertex Frank–Kasper Gd[Gd11Co2(Co,Ni)1] |
| CN = 14 | 1 Co/Ni | 2.9573(9) | 0.969 | |
| 2 Gd1 | 3.5326(3) | 0.980 | ||
| 2 Gd2 | 3.6023(4) | 1.000 | ||
| 2 Gd2 | 3.6170(3) | 1.004 | ||
| 1 Gd3 | 3.6584(4) | 1.015 | ||
| 1 Gd1 | 3.6904(4) | 1.024 | ||
| 1 Gd2 | 3.7072(4) | 1.029 | ||
| 2 Gd3 | 3.8477(1) | 1.068 | ||
| Co | 1 Co/Ni | 2.5282(12) | 1.011 | Tricapped trigonal prism Co[Gd8(Co,Ni)1] |
| CN = 9 | 2 Gd3 | 2.7583(7) | 0.903 | |
| 2 Gd2 | 2.8454(7) | 0.932 | ||
| 2 Gd1 | 2.9866(7) | 0.978 | ||
| 1 Gd1 | 3.2837(10) | 1.075 | ||
| 1 Gd2 | 3.5613(10) | 1.166 | ||
| Co/Ni | 1 Co/Ni | 2.5242(12) | 1.010 | Tricapped trigonal prism (Co,Ni)[Gd7(Co,Ni)1Co1] |
| CN = 9 | 1 Co | 2.5282(12) | 1.011 | |
| 2 Gd2 | 2.8835(7) | 0.945 | ||
| 2 Gd1 | 2.9195(6) | 0.957 | ||
| 2 Gd1 | 2.9398(7) | 0.964 | ||
| 1 Gd3 | 2.9573(9) | 0.969 | ||
The refined values of the lattice parameters (a, b, c) for the four Gd3Co1+xNi1−x compounds are listed in Table 3, along with the unit cell volume (Vobs), mean atomic volume (Vat), and volume of formation (−ΔV%), as well as the elemental composition measured by EDX for the orthorhombic phase and the one obtained considering a broad area (global area) of the sample, the so called global analysis. While the lattice parameters a and b decrease, the parameter c increases with increasing Co content (Fig. 5a). Consequently, both the unit cell volume and mean atomic volume decrease along the Gd3Co1+xNi1−x series (Table 3). The trend of the unit cell volume as a function of x (Fig. 5b) is noteworthy. While the lattice parameters vary linearly with x, the unit cell volume follows a quadratic trend, decreasing and reaching a plateau at x = 0.4. This suggests that the Gd3Co1+xNi1−x compound may not form for Co content exceeding ≈1.4/formula. Given that the atomic volume of elemental Co is slightly larger than that of Ni (11.08 Å3 and 10.93 Å3, respectively37), one would expect the opposite trend, i.e., an increase of the unit cell volume with increasing Co content. A similar trend was observed in the monoclinic Dy3Ni2-type Gd3CoxNi1−x series,22 further supporting the hypothesis of preferential site occupation by Co atoms in the Y3Co2-type Gd3Co1+xNi1−x series.
| Sample | Nominal composition | Global analysis from EDX | EDX composition of Gd3Co1+xNi1−x | Lattice parameters (Rietveld) | V obs [Å3] | V at [Å3] | −ΔV% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gd [at%] | Co [at%] | Ni [at%] | Gd [at%] | Co [at%] | Ni [at%] | Gd [at%] | Co [at%] | Ni [at%] | a [Å] | b [Å] | c [Å] | ||||
| Gd3Co1.1Ni0.9 | 60.00 | 22.00 | 18.00 | 60.97 | 22.20 | 16.83 | 60.65 | 22.03 | 17.32 | 9.54636(7) | 12.5543(9) | 3.85078(3) | 461.510(6) | 23.075 | 4.9026 |
| Gd3Co1.2Ni0.8 | 60.00 | 24.00 | 16.00 | 60.38 | 24.40 | 15.22 | 59.80 | 24.75 | 15.46 | 9.53984(5) | 12.52853(7) | 3.85994(2) | 461.341(4) | 23.067 | 4.9488 |
| Gd3Co1.3Ni0.7 | 60.00 | 26.00 | 14.00 | 60.81 | 25.35 | 13.83 | 59.96 | 26.01 | 14.04 | 9.53396(4) | 12.50502(5) | 3.86908(2) | 461.280(3) | 23.064 | 4.9728 |
| Gd3Co1.4Ni0.6 | 60.00 | 28.00 | 12.00 | 60.68 | 27.52 | 11.81 | 60.09 | 27.86 | 12.04 | 9.52957(7) | 12.49058(8) | 3.87524(2) | 461.269(5) | 23.063 | 4.9870 |
 | ||
| Fig. 5 Trend of the lattice parameters (a, b, c) (a) and unit cell volume (Vcell) (b) as a function of the Co content x in the orthorhombic Y3Co2-type Gd3Co1+xNi1−x (x = 0.1, 0.2, 0.3, 0.4) series. | ||
By plotting both the unit cell volume and the volume of formation for both Dy3Ni2-type Gd3CoxNi1−x and Y3Co2-type Gd3Co1+xNi1−x as a function of the Co content, x, two interesting trends are observed (Fig. 6a and b). The two trends indicate a common composition point [which is a maximum for Vobsversus x (Fig. 6a) and a minimum for −ΔV versus x (Fig. 6b)] occurring between x = 0 and x = 1.1, which is where the structural change occurs. The absolute values of the volume of formation (|ΔV|%) for the Y3Co2-type Gd3Co1+xNi1−x phase range from 4.9% to 5.0%, while those for the Dy3Ni2-type Gd3CoyNi2−y compounds range from 4.7% to 5.1%. Although these two sets of values do not differ significantly from each other, their trend as a function of Co concentration is noteworthy for both phases. The new orthorhombic Y3Co2-type (oP20, Pnnm, no. 58, Z = 4) solid solution Gd3Co1+xNi1−x represents a continuation of the monoclinic Dy3Ni2-type (mS20, C2/m, no. 12, Z = 4) solid solution Gd3CoyNi2−y. The Dy3Ni2 and Y3Co2 prototypes are closely related to one another via displacements of slabs common to both structures, which is similar to the structural relationship between CrB-, FeB-, and TbNi-type structures.24
3.2. Physical properties
| MS(T) ∼ |t|β (T < TC) | (1) |
| χ0−1(T) ∼ |t|γ (T > TC) | (2) |
| M(H) ∼ H1/δ (T = TC) | (3) |
Criticality can only be studied in second-order phase transitions; therefore, the first step is to confirm that the PM-to-FM transition is second order in all compounds. This has been verified by analysing the slopes of the magnetization isotherms represented in the so called Arrott plots, where M2 is plotted as a function of H/M. According to the Banerjee criterion, if the slopes of all isotherms are positive, the transition corresponds to a second order, while if the slopes are negative, the transition is of first order.42 As an example, Fig. 9a shows the Arrott plot representation for Gd3Co1.2Ni0.8, where it can be clearly seen that the slopes are positive, thus, confirming the second-order nature of the phase transition and the applicability of the critical behavior analysis. The same behavior is observed in every compound (see Fig. S5a, S6a and S7a in the ESI†). Once the order of the phase transition has been confirmed to be second order, a rigorous step-by-step iterative procedure is used in order to obtain the critical exponent. The process begins by representing the modified Arrott plots (MAPs), which consist in plotting M1/β as a function of (H/M)1/γ. For the correct values of β and γ, the MAP should yield straight, parallel lines. Therefore, different universality models are tested in order to determine the best starting point. In this representation, the MF model corresponds with the Arrott plot, which clearly does not show the desired straight and parallel lines (see Fig. 9a). For every compound, the 3D Heisenberg model resulted in the best starting model. Once the starting model is chosen, MS and χ0−1 values are extracted from the interception of the straight lines in the MAP with the Y and X axes. These values are then fitted to eqn (1) and (2) to retrieve new values for β and γ. The critical exponents obtained through the previous fitting are then used to represent a new MAP, from where the process starts again until a convergence is reached. The final MAP for Gd3Co1.2Ni0.8 can be seen in Fig. 9b as an example, and the corresponding final MS and χ0−1 fittings are shown in Fig. 9c. The β and γ critical exponent values obtained from the iterative method are listed in Table 4.
 | ||
| Fig. 9 Critical behavior analysis for Gd3Co1.2Ni0.8. Arrott plot representation (a); modified Arrott plot representation using the correct critical exponents (b); fitting of MS and χ0−1 to eqn (1) and (2) respectively (c); magnetic equation of state, with the inset showing the fitting of the critical isotherm to eqn (3) (d). | ||
| β | γ | δ | δ* | |
|---|---|---|---|---|
| Universality class | ||||
| Mean field | 0.5 | 1 | 3 | |
| 3D Heisenberg | 0.3689(3) | 1.3960(9) | 4.78 | |
| 3D Ising | 0.32653(10) | 1.2373(2) | 4.79 | |
| Compound | ||||
| Gd3Co1.1Ni0.9 | 0.374 ± 0.005 | 1.34 ± 0.16 | 4.62 ± 0.01 | 4.58 ± 0.49 |
| Gd3Co1.2Ni0.8 | 0.372 ± 0.003 | 1.33 ± 0.02 | 4.643 ± 0.004 | 4.58 ± 0.07 |
| Gd3Co1.3Ni0.7 | 0.376 ± 0.003 | 1.29 ± 0.02 | 4.49 ± 0.008 | 4.44 ± 0.08 |
| Gd3Co1.4Ni0.6 | 0.387 ± 0.008 | 1.27 ± 0.05 | 4.302 ± 0.009 | 4.27 ± 0.21 |
In order to assess the robustness of the critical exponents obtained from the previous iterative method, two further procedures are performed. The last critical exponent, δ, can be obtained from β and γ values using the Widom scaling equation:
| δ = 1 + γ/β | (4) |
The values of δ obtained from eqn (4) are listed in Table 4 as δ*, and can be compared to the values of δ directly obtained from fitting the magnetization isotherm at the critical temperature to eqn (3), listed in the same table as δ. The values of δ obtained from both methods agree, supporting the results. The fitting of the critical isotherm for Gd3Co1.2Ni0.8 is shown in the inset of Fig. 9d.
Finally, the reliability of the critical exponent values obtained has been confirmed by means of the magnetic equation of state, according to which the reduced magnetization (M(H,t)|t|−β) should be a function of the reduced magnetic field (f±(H(t)|t|−(β+γ)):38
| M(H,t)|t|−β = f±(H(t)|t|−(β+γ)) | (5) |
Here β and γ are the critical exponents and ± indicates a different function for isotherms above the critical temperature and below it. Therefore, if the correct critical exponents are used to represent the reduced magnetization as a function of the reduced magnetic field, the resulting graph should yield two distinct branches, one for each temperature region. An example of the magnetic equation of state can be seen for Gd3Co1.2Ni0.8 in Fig. 9d, where the collapse of the isotherms into two branches is a clear indication of the reliability of the obtained values for the critical exponents. The plots for the other materials show exactly the same good agreement and they are shown in Fig. S5–S7 in the ESI.†
The critical exponents for the four compounds are close to the 3D Heisenberg model (βHeis = 0.3689(3), γHeis = 1.3960(9), δHeis = 4.78), which points to short-range order isotropic magnetic interactions. The β values of the two compounds with lower Co content (Gd3Co1.1Ni0.9 and Gd3Co1.2Ni0.8) agree, within the error, with the theoretical value corresponding to the 3D Heisenberg model. However, as the Co content increases, β slightly increases. A similar situation is found with the γ critical exponent. The γ values for the compounds with the lowest Co content are close to the value corresponding to the 3D Heisenberg universality class, but, in this case, the value decreases as Co content increases. These deviations are common in Gd-based intermetallic compounds, for which the critical behavior studies of their PM–FM phase transitions also point to the 3D Heisenberg model.43–45 This indicates that magnetism in these compounds mainly arises from Gd atoms; however, Co has been suggested to have a small magnetic moment in the Gd3CoNi compound.22 This magnetic moment may introduce magnetocrystalline anisotropy as the Co/Ni content increases, causing deviations of the critical exponents from the 3D Heisenberg universality class. A similar effect was observed in other members of this family when Gd was substituted by Nd in NdxGd3−xCoNi.20
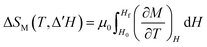 | (6) |
As an example, Fig. S8 (ESI†) shows the magnetization isotherms from which the magnetic entropy change has been calculated, along with the magnetization isofields for Gd3Co1.3Ni0.7. The results obtained from using eqn (6) are shown in Fig. 10, where the magnetic entropy change for different applied magnetic field changes (ΔH) is represented as a function of temperature for the four compounds. As expected, each sample shows a peak at its corresponding Curie temperature, where the magnetization change is most pronounced. The peak values of the magnetic entropy change (|ΔSpkM|), for applied fields of μ0ΔH = 2, 5 and 6.9 T (selected for comparison with the literature), are listed in Table 5. This table also contains further valuable information for assessing the applicability of these materials as magnetic refrigerants, such as the refrigerant capacity (RC), calculated using the two most common methods. The refrigerant capacity at full width at half maximum (RCFWHM):
| RCFWHM = |ΔSpkM|δTFWHM | (7) |
 | (8) |
 | ||
| Fig. 10 Magnetic entropy change values for the different compounds at different μ0ΔH as a function of temperature. The legend is the same for all the graphs. | ||
| Gd3Co1.1Ni0.9 | Gd3Co1.2Ni0.8 | Gd3Co1.3Ni0.7 | Gd3Co1.4Ni0.6 | ||
|---|---|---|---|---|---|
| T C = 177 K | T C = 181 K | T C = 184 K | T C = 186 K | ||
| 2 T | |ΔSpkM| (J kg−1 K−1) | 4.15 | 4.10 | 4.01 | 3.51 |
| RCFWHM (J kg−1) | 154 | 166 | 157 | 150 | |
| RCArea (J kg−1) | 114 | 125 | 119 | 110 | |
| TEC10 (J kg−1 K−1) | 3.76 | 3.80 | 3.71 | 3.25 | |
| 5 T | |ΔSpkM| (J kg−1 K−1) | 8.40 | 8.25 | 8.34 | 7.81 |
| RCFWHM (J kg−1) | 618 | 640 | 572 | 628 | |
| RCArea (J kg−1) | 443 | 468 | 423 | 437 | |
| TEC10 (J kg−1 K−1) | 7.88 | 8.03 | 7.98 | 7.37 | |
| 6.9 T | |ΔSpkM| (J kg−1 K−1) | 10.55 | 10.44 | 10.58 | 10.20 |
| RCFWHM (J kg−1) | 994 | 976 | 913 | 931 | |
| RCArea (J kg−1) | 704 | 710 | 662 | 646 | |
| TEC10 (J kg−1 K−1) | 9.89 | 10.17 | 10.16 | 9.59 |
Finally, the temperature averaged entropy change TEC10 defined as46,47
 | (9) |
The data in Table 5 show that the increase of Co content over Ni shifts the peak to higher temperatures. However, the magnetocaloric properties remain well preserved across all four compounds. This is interesting as it opens the possibility of tuning the transition temperature within a 10 K range without compromising the magnetocaloric properties. These values can be compared to those in ref. 22, where members of the same family with lower Co content [Gd3CoyNi2−y (0≤ y ≤ 1)] were studied. In this latter study, |ΔSpkM(μ0ΔH = 5T)| slightly increases with Co content from 8.0 J kg−1 K−1 for Gd3Ni2 to 8.3 J kg−1 K−1 for Gd3CoNi, while RCFWHM(μ0ΔH = 5T) values are approximately on the order of 540 J kg−1. These values are similar to those obtained in this study, suggesting the possibility of further tuning the working temperature region from 147 K (TC of Gd3Ni) to 186 K (TC of Gd3Co1.4Ni0.6), a shift of almost 40 K, solely by changing the Co/Ni concentration while preserving the good magnetocaloric properties. This contrasts with the behavior observed in Gd3CoNi when Gd was partially substituted by Nd,20 where an equal amount of Gd and Nd resulted in a drastic reduction of the magnetic entropy change peak at μ0ΔH = 5 T to 4.1 J kg−1 K−1 (half the value of the parent compound Gd3CoNi) and a drop of RCFWHM to one fifth of the values obtained in this work.
The magnetocaloric properties of these materials are outstanding when compared to other rare-earth containing compounds in the same working temperature region. In particular, the |ΔSpkM| values obtained in this work are higher than any other value (within the same temperature region) presented in Fig. 25 of ref. 48, an extensive review covering hundreds of magnetocaloric materials. This comparison can be extended to the equiatomic GdCoyNi1−y,26 with a slightly lower working temperature region ranging from 150 K for y = 0.5 to 171 K for y = 0.7. In GdCoyNi1−y, the values of the magnetic entropy change peak at 5 T are very similar to those obtained in this work, with the lowest value, |ΔSpkM| = 8.2 J kg−1 K−1, corresponding to the composition with y = 0.7 and the highest one, |ΔSpkM| = 9.7 J kg−1 K−1, to y = 0.5. The RCFWHM values at 5 T obtained for the aforementioned compounds are also similar, though lower (between 508 and 574 J kg−1) than those of the compositions presented in this work.
Some magnetocaloric properties, such as the magnetic entropy change peak |ΔSpkM| and the RC, are known to scale with the applied magnetic field according to the following relations:49,50
 | (10) |
| RC ∼ H1+1/δ | (11) |
 | ||
| Fig. 11 Field dependence of the magnetic entropy change peak for Gd3Co1.3Ni0.7 (a) and RCFWHM for Gd3Co1.2Ni0.8 (b); the red line is a linear fit to be used as a visual guide. | ||
The temperature dependence of the exponent n(T) defined in eqn (10) also provides valuable information about the system. In second-order phase transitions, n(T) should vary monotonically, tending to a value of 2 in the paramagnetic phase as temperature increases and to n(T)1 in the ferromagnetic phase, with a minimum at TC. However, an overshoot of the n parameter well above n > 2 would indicate a first-order transition.47,51 As an example, the n(T) curve at 7 T for Gd3Co1.4Ni0.6 is presented in Fig. 12, where the usual behavior for second order phase transition is observed, with the absence of any overshoot. The same behavior is found for the other three compounds (see Fig. S11 in the ESI†).
Another useful tool coming from the universality nature of second-order phase transitions is the so-called universal curve. Universality implies that all the magnetic entropy change curves corresponding to a certain compound should collapse into a single one after normalizing to the peak value of each curve (ΔSM/ΔSpkM) and rescaling the temperature axis according to ref. 50 and 52:
| θ = (T − TC)/(Tr − TC) | (12) |
Here TC is the Curie temperature and Tr is the reference temperature corresponding to a particular fraction of |ΔSpkM|, which is usually chosen as ΔSM(Tr) = 0.5ΔSpkM. Fig. 13 shows an example of the overlapping of the different isofields onto a single curve in the case of Gd3Co1.1Ni0.9. The universal curves for the other compounds can be seen in Fig. S12 (ESI†). The existence of this universality curve is a demonstration of the second-order nature of the phase transition. Furthermore, this curve, together with the scaling relation of ΔSpkM, enables the extrapolation of the magnetocaloric properties to applied magnetic fields and temperatures beyond instrumental limitations.53
4. Conclusions
The present investigation provides a comprehensive analysis of the interplay between chemical composition, structural rearrangement and the resulting physical properties in the new orthorhombic Gd3(Co,Ni)2 (Y3Co2-type Gd3Co1+xNi1−x) compared with the monoclinic Gd3(Co,Ni)2 (Dy3Ni2-type Gd3CoyNi2−y).22 We observe that the structural change from the monoclinic Dy3Ni2-type to the orthorhombic Y3Co2-type, occurring when the Co/Ni content per formula unit exceeds >1, has significant implications for the material's magnetic and electronic behavior. X-ray diffraction confirms the orthorhombic Y3Co2-type structure for the Gd3Co1+xNi1−x compounds to form when x > 1 and remain stable up to x = 1.4. It was also found that, between the two 4g Wyckoff sites occupied by the transition metal, one is exclusively occupied by Co atoms, while the other exhibits mixed occupancy of Co and Ni. This ordered arrangement aligns well with and follows the progressive preferential ordered Co/Ni distribution previously observed in the monoclinic Dy3Ni2-type Gd3CoyNi2−y compounds. Additionally, the unexpected decrease in the unit-cell volume with increasing Co content, accompanied by a non-uniform variation of the interatomic distances, suggests a complex interplay between the atomic properties (atomic size, valence and electronegativity) and site occupation. The study also analyses the evolution of the lattice parameters and unit-cell volume across the Gd3Co1+xNi1−x series. It reveals that while the a and b lattice parameters decrease linearly with increasing Co content, parameter c increases. This trend leads to a quadratic decrease in the unit-cell volume, which reaches a plateau at x = 0.4 (Gd3Co1.4Ni0.6), suggesting this Co concentration as the solubility limit of the orthorhombic phase.The critical exponents for the Gd3Co1+xNi1−x compounds (x = 0.1, 0.2, 0.3, and 0.4) suggest short-range order isotropic magnetic interactions, aligning with the 3D Heisenberg model. As Co concentration increases, slight deviations from the 3D Heisenberg universality class emerge. These deviations may be due to the magnetocrystalline anisotropy induced by the possible Co magnetic moment. A similar effect has been observed in other compounds within this family when Nd partially substitutes Gd.20
Increasing the Co content over Ni leads to a higher Curie temperature, consistent with previous observations in the Gd3CoxNi2−x and Tb3CoxNi2−x series.21,22 This results in a shift of the peak of the magnetic entropy change to higher temperatures with the increase of Co content, without negatively affecting the magnetocaloric properties. Comparing the results of this work to previous studies on the same family (with lower Co content)22 reveals the possibility of precisely tuning the working temperature region from 147 K to 186 K by modifying the Co/Ni concentration.
The analysis of scaling relations and the universal curve confirms the second-order nature of the phase transition in the studied compounds and validates the accuracy of the calculated critical exponents.
The results demonstrate that tuning the Co/Ni concentration allows for precise control of the working temperature range for magnetocaloric applications, potentially making these materials suitable for efficient and sustainable cooling technologies.
Data availability
The data supporting this article have been included and discussed as part of the manuscript. The data obtained from the relative measurements performed in this study, and the data from which the resulting results were derived/extracted, are original and already provided in the several different tables in the manuscript. Further, the crystal data and structure refinement details of the compound Gd3Co1.1Ni0.9 (which are presented in Table 1) are fully available as a CIF file deposited in the Cambridge Structural Database center by citing the deposition code CSD-2401455. Complementary information mentioned in the manuscript is available in the ESI.† For other datasets associated with previous studies, data citations in the proper format are included in the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Departamento de Educación del Gobierno Vasco (project IT1430-22). The authors are thankful for the technical and human support provided by the Advanced Research Facilities (SGIker) of UPV/EHU, especially for the fruitful discussions with Dr I. Orue.References
- Agenda 21: programme of action for sustainable development, Rio declaration on environment and development, statement of forest principles: the final text of agreements negotiated by Governments at the United Nations Conference on Environment and Development (UNCED), 3–14 June 1992, Rio de Janeiro, Brazil, 1993, 294, https://sustainabledevelopment.un.org/outcomedocuments/agenda21.
- Enerdata, Global Energy Trends – 2021 Edition ( 2021), https://www.enerdata.net/publications/reports-presentations/2021-energy-climate-trends.html.
- U. S. Environmental Protection Agency, Climate Change Indicators: Residential Energy Use (EPA, 2021), https://www.epa.gov/climate-indicators/climate-change-indicators-residential-energy-use.
- IEA, The Future of Cooling (IEA, Paris, 2018), https://www.iea.org/reports/the-future-of-cooling.
- W. Liu, T. Gottschall, F. Scheibel, E. Bykov, A. Aubert, N. Fortunato, B. Beckmann, A. M. Doring, H. Zhang, K. Skokov and O. Gutfleisch, A matter of performance and criticality: A review of rare-earth-based magnetocaloric intermetallic compounds for hydrogen liquefaction, J. Alloys Compd., 2024, 995, 174612 CrossRef CAS.
- J. Y. Law and V. Franco, Modern rare-earth-containing magnetocaloric materials: Standing on the shoulders of giant Gd5Si2Ge2, Handbook on the Physics and Chemistry of Rare Earths, 2023, ch. 332, vol. 64, pp. 175–246 Search PubMed.
- B. Hilliard, V. S. R. de Sousa, K. Dixon-Anderson, Y. Mudryk and J. Cui, Magnetocaloric effect in Gd1−xCexNi (x = 0–0.6): A cost-effective approach to tuning Curie temperature from 70 K to 30 K, J. Alloys Compd., 2024, 989, 174186 CAS.
- D. Guo, L. M. Moreno-Ramírez, J. Y. Law, Y. Zhang and V. Franco, Excellent cryogenic magnetocaloric properties in heavy rare-earth based HRENiGa2 (HRE = Dy, Ho, or Er) compounds, Sci. China Mater., 2023, 66, 249–256 CrossRef CAS.
- Y. Zeng, F. Tian, T. Chang, K. Chen, S. Yang, K. Cao, C. Zhou and X. Song, Large magnetocaloric effect and near-zero thermal hysteresis in the rare earth intermetallic Tb1−xDyxCo2 compounds, J. Phys.: Condens. Matter, 2017, 29, 055804 CrossRef PubMed.
- A. Elouafi, S. Ezairi, F. Lmai and A. Tizliouine, Excellent magnetocaloric effect at cryogenic temperature in amorphous (Fe35RE65) (RE = Er, Dy and Gd) alloys, J. Magn. Magn. Mater., 2023, 588, 171381 CrossRef CAS.
- A. Herrero, I. R. Aseguinolaza, A. Oleaga, A. Garcia-Adeva, E. Apiñaniz, A. V. Garshev, V. O. Yapaskurt and A. V. Morozkin, Selecting optimal R6TX2 intermetallics (R = Gd, Tb, Dy; T = Mn, Fe, Co, Ni; X = Sb, Te) for magnetic refrigeration, Dalton Trans., 2023, 52, 5780–5797 RSC.
- Y. Zhang, Y. Xie, J. Wei and W. Hao, Experimental and theoretical insights into the structural, magnetic, and low-temperature magnetocaloric properties of RE2CoTiO6 (RE = Gd, Dy, and Er) double perovskite oxides, J. Mater. Chem. A, 2024, 12, 32396–32407 RSC.
- F. Chen, Y. Na, Y. Xie and Y. Zhang, Insight into the Structural and Magnetic Properties of PrZnSi and NdZnSi Compounds Featuring Large Low-Temperature Magnetocaloric Effects, ACS Appl. Mater. Interfaces, 2024, 16, 52719–52726 CrossRef CAS PubMed.
- A. Biswas, T. Del Rose, Y. Mudryk, P. O. Ribeiro, B. P. Alho, V. S. R. de Sousa, E. P. Nóbrega, P. J. von Rankc and V. K. Pecharsky, Hidden first-order phase transitions and large magnetocaloric effects in GdNi1−xCox, J. Alloys Compd., 2022, 897, 163186 CrossRef CAS.
- I. R. Aseguinolaza, A. Herrero, A. J. Garcia-Adeva, E. Apiñaniz, A. V. Garshev, A. V. Morozkin and A. Oleaga, Broad table-like magnetocaloric effect in the full hydrogen liquefaction range in Gd3Ni6XY, J. Alloys Compd., 2025, 1010, 177154 CrossRef CAS.
- S. Sharma and P. Kumar, Modifications in the magnetocaloric effect owing to composition changes in Gd2In1−xGex (0 ≤ x ≤ 0.2) system of compounds, AIP Adv., 2022, 12, 035127 CrossRef CAS.
- S. Ghosh and S. Ghosh, Understanding the origin of the magnetocaloric effects in substitutional Ni-Mn-Sb-Z (Z = Fe, Co, Cu) compounds: Insights from first-principles calculations, Phys. Rev. B, 2020, 101, 024109 CrossRef CAS.
- A. J. Garcia-Adeva, E. Apiñaniz, A. Herrero, I. R. Aseguinolaza and A. Oleaga, First-principle calculations of magnetic properties of Ho6(Fe, Mn)Bi2 compounds, Rare Met., 2024, 43, 6034–6047 CrossRef CAS.
- A. Herrero, A. Oleaga, A. Provino, I. R. Aseguinolaza, A. Salazar, D. Peddis and P. Manfrinetti, Crystallographic, magnetic and magnetocaloric properties in novel intermetallic materials R3CoNi (R = Tb, Dy, Ho, Er, Tm, Lu), J. Alloys Compd., 2021, 865, 158948 CrossRef CAS.
- A. Oleaga, A. Erkoreka, A. Herrero, A. Provino, D. Peddis and P. Manfrinetti, Effect of Nd doping on the crystallographic, magnetic, and magnetocaloric properties of NdxGd3−xCoNi, APL Mater., 2023, 11, 061112 CrossRef CAS.
- C. Ritter, A. Provino, F. Fauth, S. K. Dhar, V. K. Pecharsky and P. Manfrinetti, From Tb3Ni2 to Tb3CoNi: The interplay between chemistry, structure, and magnetism, Phys. Rev. Mater., 2019, 3, 024406 CrossRef CAS.
- A. Provino, V. Smetana, D. Paudyal, K. A. Gschneidner, Jr., A.-V. Mudring, V. K. Pecharsky, P. Manfrinetti and M. Putti, Gd3Ni2 and Gd3CoxNi2−x: Magnetism and unexpected Co/Ni crystallographic ordering, J. Mater. Chem. C, 2016, 4, 6078–6089 RSC.
- J. M. Moreau, D. Paccard and E. Parthé, The monoclinic, CrB-related, crystal structure of Tb3Ni2, Dy3Ni2 and Ho3Ni2, Acta Crystallogr., Sect. B, 1974, 30, 2583–2586 CrossRef.
- J. M. Moreau, E. Parthé and D. Paccard, The orthorhombic structure of Y3Co2, a shift structure variation of the monoclinic Dy3Ni2 type, Acta Crystallogr., Sect. B, 1975, 31, 747–749 CrossRef.
- P. Villars and K. Cenzual, Pearson's Crystal Data: Crystal Structure Database for Inorganic Compounds (on DVD), Release 2022/23, ASM International, Materials Park, Ohio, USA Search PubMed.
- A. Provino, V. K. Pecharsky, C. Bernini, V. Smetana, A.-V. Mudring and P. Manfrinetti, Solubility limits, magnetic and magnetocaloric properties of MoB-type GdCoxNi1−x (0.47 ≤ x ≤ 0.72)”, J. Alloys Compd., 2023, 948, 169605 CrossRef CAS.
- K. Yvon, W. Jeitschko and E. Parthé, LAZY PULVERIX, a computer program, for calculating X-ray and neutron diffraction powder patterns, J. Appl. Crystallogr., 1977, 10, 73–74 CrossRef.
- J. Rodriguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192, 55–69 CrossRef CAS.
- Bruker, APEX5, V2023.9-2, Bruker AXS Inc., Madison, WI, USA, 2023 Search PubMed.
- G. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A:Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. Sheldrick, “Crystal structure refinement with SHELXL”, Acta Crystallogr., Sect. C:Struct. Chem., 2015, 71, 3–8 Search PubMed.
- H. Neves Bez, H. Yibole, A. Pathak, Y. Mudryk and V. K. Pecharsky, “Best practices in evaluation of the magnetocaloric effect from bulk magnetization measurements”, J. Magn. Magn. Mater., 2018, 458, 301–309 CrossRef CAS.
- W. Jiang, X. Z. Zhou, G. Williams, Y. Mukovskii and K. Glazyrin, Griffiths phase and critical behavior in single-crystal La0.7Ba0.3MnO3: Phase diagram for La1−xBaxMnO3 (x ≤ 0.33), Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 064424 CrossRef.
- W. Jiang, X. Z. Zhou, G. Williams, Y. Mukovskii and K. Glazyrin, Critical behavior and transport properties of single crystal Pr1−xCaxMnO3 (x = 0.27, and 0.29), Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 144409 CrossRef.
- E. Teatum, K. A. Gschneidner Jr. and J. Waber, Compilation of calculated data useful in predicting metallurgical behavior of the elements in binary alloy systems, Rep LA-4003, NTIS, Springfield, VA, 1968.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- P. Villars and J. L. C. Daams, Atomic-environment classification of the chemical elements, J. Alloys Compd., 1993, 197, 177–196 CrossRef CAS.
- H. E. Stanley, Introduction to Phase Transitions and Critical Phenomena, Oxford University Press, 1971 Search PubMed.
- J. M. Yeomans, Statistical Mechanics of Phase Transitions, Oxford Science Publications, 1992 Search PubMed.
- M. Campostrini, M. Hasenbusch, A. Pelissetto, P. Rossi and E. Vicari, Critical exponents and equation of state of the three-dimensional Heisenberg universality class, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 65, 144520 CrossRef.
- M. Campostrini, A. Pelissetto, P. Rossi and E. Vicari, “25-th order high-temperature expansion results for three-dimensional Ising-like systems on the simple-cubic lattice”, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2002, 65, 066127 CrossRef PubMed.
- B. K. Banerjee, “On a generalized approach to first and second-order magnetic transitions”, Phys. Lett., 1964, 12, 16–17 CrossRef.
- A. R. Chowdhury, G. S. Collins and C. Hohenemser, “Static universality class implied by the critical exponents of Gd”, Phys. Rev., 1986, 33, 6231 CAS.
- A. Herrero, A. Oleaga, P. Manfrinetti, A. Provino and A. Salazar, “Critical behavior of the ferromagnetic transition in GdSc(Si,Ge) intermetallic compounds”, Intermetallics, 2018, 101, 64–71 CrossRef CAS.
- A. Oleaga, A. Herrero, A. Salazar, A. V. Garshev, V. O. Yapaskurt and A. V. Morozkin, “Magnetocaloric properties and unconventional critical behavior in (Gd,Tb)6(Fe,Mn)Bi2 intermetallics”, J. Alloys Compd., 2020, 843, 155937 CrossRef CAS.
- J. Y. Law, A. Diaz-Garcia, L. M. Moreno-Ramirez and V. Franco, “Increased magnetocaloric response of FeMnNiGeSi high-entropy alloys”, Acta Mater., 2021, 212, 116931 CrossRef CAS.
- J. Y. Law and V. Franco, “Review on magnetocaloric high-entropy alloys: Design and analysis methods”, J. Mater. Res., 2023, 38, 37–51 CrossRef CAS.
- V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, “Magnetocaloric effect: From materials research to refrigeration devices”, Prog. Mater. Sci., 2018, 93, 112–232 CrossRef.
- C. Romero-Muñiz, R. Tamura, S. Tanaka and V. Franco, “Applicability of scaling behavior and power laws in the analysis of the magnetocaloric effect in second-order phase transition materials”, Phys. Rev. B, 2016, 94, 134401 CrossRef.
- V. Franco, A. Conde, J. M. Romero-Enrique and J. S. Blázquez, “A universal curve for the magnetocaloric effect: an analysis based on scaling relations”, J. Phys.: Condens. Matter, 2008, 20, 285207 CrossRef.
- J. Y. Law, V. Franco, L. M. Moreno-Ramirez, A. Conde, D. Y. Karpenkov, I. Radulov, K. P. Skokov and O. Gutfleisch, “A quantitative criterion for determining the order of magnetic phase transitions using the magnetocaloric effect”, Nat. Commun., 2018, 9, 2680 CrossRef PubMed.
- V. Franco, J. S. Blázquez and A. Conde, “Field dependence of the magnetocaloric effect in materials with a second-order phase transition: A master curve for the magnetic entropy change”, Appl. Phys. Lett., 2006, 89, 222512 CrossRef.
- V. Franco and A. Conde, “Scaling laws for the magnetocaloric effect in second-order phase transitions: from physics to applications for the characterization of materials”, Int. J. Refrig., 2010, 33, 465–473 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary information to this article containing X-ray powder patterns, isothermal magnetization loops, critical behavior analysis, magnetocaloric scaling relations, universal curves and additional crystallographic data can be found online at the end of the document (DOC). See DOI: https://doi.org/10.1039/d5tc00423c |
| This journal is © The Royal Society of Chemistry 2025 |