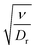Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling active turbulence by activity patterns†
Arghavan
Partovifard
 *,
Josua
Grawitter
*,
Josua
Grawitter
 and
Holger
Stark
and
Holger
Stark

Institut für Theoretische Physik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: arghavan.partovifard@tu-berlin.de
First published on 4th January 2024
Abstract
By patterning activity in space, one can control active turbulence. To show this, we use Doi's hydrodynamic equations of a semidilute solution of active rods. A linear stability analysis reveals the resting isotropic fluid to be unstable above an absolute pusher activity. The emergent activity-induced paranematic state displays active turbulence, which we characterize by different quantities including the energy spectrum, which shows the typical power-law decay with exponent −4. Then, we control the active turbulence by a square lattice of circular spots where activity is switched off. In the parameter space lattice constant versus surface-to-surface distance of the spots, we identify different flow states. Most interestingly, for lattice constants below the vorticity correlation length and for spot distances smaller than the nematic coherence length, we observe a multi-lane flow state, where flow lanes with alternating flow directions are separated by a street of vortices. The flow pattern displays pronounced multistability and also appears transiently at the transition to the isotropic active-turbulence state. At larger lattice constants a trapped vortex state is identified with a non-Gaussian vorticity distribution due to the low flow vorticity at the spots. It transitions to conventional active turbulence for increasing spot distance.
1 Introduction
Active matter refers to a collection of individual entities capable of converting free energy from their surroundings into directed motion.1–5 These systems are driven out of equilibrium by the continuous injection of energy and thereby exhibit interesting collective behaviors through the interactions of their constituents. Examples are motility-induced phase separation,6–9 dynamic clustering,10–12 various forms of cluster formation,13–17 flocking,18–21 swirling22,23 and swarming.24–26 Most prominently, active fluids can display self-driven spontaneous and complex flow patterns that are correlated on lengths larger than the size of individual active particles. These flow patterns display chaotic-like spatiotemporal behavior that, despite occurring at low Reynolds numbers, resemble classical turbulence and are therefore known as active turbulence.27–35 This phenomenon has been observed in experiments with different realizations of active fluids such as bacterial suspensions,27,28,36 cytoskeletal motor-protein suspensions,37–39 and cell colonies.40–42 In this article we show how active turbulence can be controlled by spatially patterning activity.The individual active units often have an elongated shape, which allows the active fluid to be treated as a collection of rod-shaped particles with head–tail symmetry. At sufficiently large density, they develop long-range orientational order and in the simplest case a nematic phase forms, where also topological defects are observable.43,44 One widely used continuum model for investigating active turbulence is the active-nematics model.31,32,35,38,45,46 It employs the hydrodynamic equations of a passive nematic liquid crystal supplemented by active stresses,47 which are generated by the self-propelling particles. Activity destroys the long-range orientational order and active turbulence occurs. It is characterized by a flow pattern with high vorticity, which displays chaotic dynamics in both space and time and where topological defects continuously emerge and annihilate.1,45,48,49 The described active-nematics model allows for nematic order even in the absence of activity. It is governed by the Landau-de Gennes free energy, an expansion in the nematic order parameter, where specific parameters determine the degree of nematic ordering.
Nematic order in an isotropic liquid crystal can also be induced by external fields or bounding surfaces, which then results in a paranematic phase.44,50,51 Likewise, several articles mention observations that some experimental systems do not exhibit nematic order in the absence of activity.52,53 Therefore, in our modeling we consider the active fluid to be in an isotropic state when activity is switched off. To model the dynamics of such a fluid, we utilize Doi's hydrodynamic equations for a semidilute solution of rods54 and add an active-stress term to account for their activity.47 In agreement with previous research works,52,53,55–57 we will demonstrate that initially isotropic pusher solutions can generate local nematic order solely due to activity. We refer to this state as the active paranematic state and show that it gives rise to active turbulence above a threshold value for the absolute pusher activity.
We characterize the observed state by its energy spectrum, along with the mean scalar order parameter, the enstrophy, the number of and distance between topological defects, as well as vorticity and nematic-order correlation functions.
In recent years, there has been a growing interest in directing the flow and dynamics of active matter with the ultimate goal of harnessing energy58–62 to power small-scale machines or design functional materials.35,63 So far, geometrical confinement has been the primary focus for controlling active matter. For example, when an active fluid is confined to a narrow rectangular channel, first a laminar flow is generated and then with increasing channel width a range of distinct regular flow patterns emerges such as oscillating and dancing flows.53,64–66 Other studies have explored weaker geometrical constraints. By introducing a square lattice of thin pillars into a turbulent bacterial solution, flow vorticity orders in an antiferromagnetic lattice.67,68 Another approach to regularizing turbulent flow is to interface the active fluid with a passive liquid crystal. Using a passive lamellar smectic phase as a substrate for the active nematic phase, experimental and theoretical studies showed that the turbulent flow transforms into a regular flow pattern consisting of lanes of alternating flow directions parallel to the smectic layers.69,70
One very appealing approach for controlling flow patterns in active fluids is to spatially pattern activity using photosensitive materials. For example, genetically modified E. coli bacteria can be activated by light and their swimming speed adjusted by varying the light intensity.71,72 Another approach utilizes cytoskeletal polymers powered by engineered motor proteins, where the gliding velocities and directions of the motors are controlled with light.73–75 Recent theoretical76–82 and experimental80 studies have highlighted the capability of using a spatially varying activity for controlling the speed and orientation of topological defects. Given the close relationship between the dynamics of defects and the generated flow field in active turbulence,1,45,48,49 spatially varying activity provides a powerful tool for manipulating flow patterns in active fluids.
In this article, we introduce a square lattice of inactivity spots, i.e., spots in which activity is turned off, to control the turbulent flow patterns of active paranematics. By systematically varying the surface-to-surface distance of the inactivity spots and the lattice constant we present a state diagram which reveals distinct flow states including trapped flow vortices. Most prominently, for lattice constants below the vorticity correlation length or an appropriately defined active length and for surface-to-surface distances smaller than the nematic coherence length, we observe a multi-lane flow state, where flow lanes with alternating flow directions are separated by a street of vortices. The flow pattern displays pronounced multistability and at the transition to the isotropic active-turbulence state transient multi-lane flow occurs.
The article is structured as follows. In Section 2 we introduce the theoretical modeling of the active fluid based on Doi's hydrodynamic equations for a semidilute solution of rods, which we supplement by an active stress tensor. Section 3 discusses turbulence in the active paranematic state and Section 4 presents the state diagram as well as the different flow states that emerge in the presence of a lattice of inactivity spots. We end with a summary and conclusions in Section 5.
2 Theoretical modeling
We introduce the continuum equations for describing the active fluid as a semidilute solution of self-propelling rods, write them in a nondimensional form, and shortly explain the pseudo-spectral method to numerically solve the equations as well as the relevant parameters.2.1 Continuum model
In contrast to standard models of active nematics, we consider a continuum model for a solution of rigid rodlike particles with activity and head–tail symmetry in two dimensions, which does not show nematic ordering in the passive case. Thereby, it allows us to study activity-induced nematic ordering. The equations of motion describing the hydrodynamics of such a liquid crystalline fluid are formulated in terms of a tensorial order parameter also called alignment tensor and the velocity field. The alignment tensor Q quantifies the local orientational or nematic ordering of the rodlike particles. It corresponds to the second moment of the orientational distribution function of the rods:54,83Q(x,t) = 〈![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) ⊗
⊗ ![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) − 1/d〉. Here, the average goes over all rods with orientational unit vector
− 1/d〉. Here, the average goes over all rods with orientational unit vector ![[q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0071_0302.gif) contained in a volume element at position x and at time t and d is the spatial dimension. Thus, the alignment tensor Q is symmetric and has zero trace.
contained in a volume element at position x and at time t and d is the spatial dimension. Thus, the alignment tensor Q is symmetric and has zero trace.
We consider a system in two dimensions. Then, the eigenvector n (with |n| = 1) corresponding to the largest eigenvalue S is called director. It indicates the mean direction of the rods and the scalar order parameter S quantifies how well the rods are aligned along n. Since Q is traceless, we can immediately write in two dimensions:
 | (1) |
For the dynamics of the Q tensor, we follow the approach proposed by Doi for a semidilute solution of rodlike particles.54 Doi's theory is based on the Smoluchowski equation for the orientational distribution of rods, from which one derives
 | (2) |
We consider an incompressible active fluid with constant density ρ. Then, the velocity field of the fluid obeys the continuity and the Navier–Stokes equations,
| ∇·u = 0 and ∂tu + u·∇u = −∇p + ∇Σ, | (3) |
| Σv = ν(L + LT), | (4) |
 | (5) |
| Σa = WQ. | (6) |
2.2 Nondimensional equations
We nondimensionalize our equations by introducing a characteristic length x0 and time t0 defined, respectively, as | (7) |
 | (8) |
| ∇·u = 0 | (9) |
 | (10) |
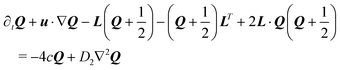 | (11) |
2.3 Numerical method and simulation parameters
The set of nondimensional dynamic eqn (9)–(11) are solved numerically using the pseudo-spectral method for spatial discretization84,85 and the 4th order Exponential Time Differencing Runge–Kutta scheme “HochOst4” for integration in time.86 The projection method is used to implement the incompressibility condition for the velocity field.87The simulations are performed on a square domain with edge length L and N × N grid points, which will be specified for each simulation. Due to the pseudo-spectral method periodic boundary conditions are fulfilled and N also is the number of wave vectors in one spatial direction.
For all simulations, grid size control is performed to ensure the independence of the results on the number of grid points. All simulations are initiated with u = 0 and Q = 0 corresponding to the isotropic distribution of rodlike particles and no flow.
In all our simulations, we fix the following parameters to ηp = 3 and c = 0.1, which corresponds to a semidilute solution of rodlike particles according to Doi's theory. We also use D2 = 10−3 and a wide range of activity parameters W. More details about the parameters that are used in this paper can be found in Appendix A.
3 Turbulence in an active paranematic state
For zero activity W the ground state described by our hydrodynamic equations is simply the isotropic state. Using a stability analysis, we show that for a sufficiently negative activity, the isotropic state becomes unstable. It develops into active turbulence, which we then characterize by different quantities. Since the nematic order is purely due to activity, we call it an active paranematic state similar to paranematic order generated by external fields or bounding surfaces.44,50,513.1 Linear stability analysis of the isotropic resting state
The nondimensional hydrodynamic eqn (9)–(11) for the active fluid have a steady-state solution with u0 = 0 and Q0 = 0, which corresponds to the isotropic state of the resting fluid. We perform a linear stability analysis of this state with respect to small perturbations, δQ and δu. More details of the stability analysis can be found in Appendix B. We use a plane-wave ansatz for the perturbations, δu = δû(k,ξ)eξt−ik·r and δQ = δ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) (k,ξ)eξt−ik·r, with the wave vector along the x direction, k = (k,0). The stability analysis reveals only one unstable mode, where the growth rate, the real part Re
(k,ξ)eξt−ik·r, with the wave vector along the x direction, k = (k,0). The stability analysis reveals only one unstable mode, where the growth rate, the real part Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ, can be become positive. For the complex growth rate, we find the dispersion relation
ξ, can be become positive. For the complex growth rate, we find the dispersion relation | (12) |
In Fig. 1(a) the growth rate Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ is plotted versus wave number k for different activities W. For activities below a threshold, W < Wc = −8c, the growth rate becomes positive in a range of wave numbers, which for our chosen parameter, c = 0.1, gives Wc = −0.8. The region of unstable wave numbers for different activities are illustrated in the diagram of Fig. 1(b). Thus, the isotropic state of a semidilute solution of pusher rods becomes unstable for W < −0.8 and as a consequence a spatially varying nematic order and flow field emerge. It develops in what is called active turbulence, which we characterize in the following Section 3.2.
ξ is plotted versus wave number k for different activities W. For activities below a threshold, W < Wc = −8c, the growth rate becomes positive in a range of wave numbers, which for our chosen parameter, c = 0.1, gives Wc = −0.8. The region of unstable wave numbers for different activities are illustrated in the diagram of Fig. 1(b). Thus, the isotropic state of a semidilute solution of pusher rods becomes unstable for W < −0.8 and as a consequence a spatially varying nematic order and flow field emerge. It develops in what is called active turbulence, which we characterize in the following Section 3.2.
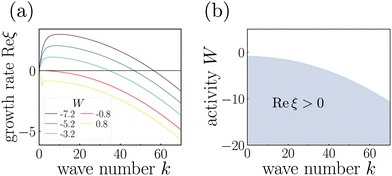 | ||
Fig. 1 (a) Growth rate Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ versus wave number k for different activities W. (b) The shaded region in the k − W plane indicates unstable modes with Re ξ versus wave number k for different activities W. (b) The shaded region in the k − W plane indicates unstable modes with Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ > 0. ξ > 0. | ||
To explain the physical mechanism of the instability, we follow the arguments of ref. 52, which are readily quantified by eqn (10) and (11). Once a local order of the active rods develops spontaneously, it drives a shear flow, which in turn aligns the rods along the extensional axis of the shear flow. Now, pushers support the shear flow in such an alignment, while pullers weaken it and, therefore, they cannot sustain it.88 This explains the instability for pushers. In contrast to ref. 52, we include the relaxation term −4cQ in eqn (11), which acts against alignment. So the instability does not start at W = 0 but at Wc = −8c.
3.2 Characterization of active turbulence
We numerically solved the governing eqn (9)–(11) for a range of activities W. In Fig. 2(c) we present the nematic scalar order parameter S averaged over space and time as a function of W. For W < Wc = −0.8, S develops a nonzero value indicating the emergent nematic order in the initially isotropic solution of active rods. Note that the nematic order is solely due to activity since in thermal equilibrium the free energy used by us would just give S = 0. The averaged scalar order parameter as a function of W can be fitted by a power law with exponent 0.33. A snapshot of the director field in Fig. 2(a) for W = −3.25 shows domains with uniform director orientation while in the regions between the domains the director field is strongly distorted. It shows walls and and
and  topological defects,89,90 indicated by red and cyan dots, respectiveley that develop and annihilate each other over time. This is illustrated in video 1 in the ESI,†
topological defects,89,90 indicated by red and cyan dots, respectiveley that develop and annihilate each other over time. This is illustrated in video 1 in the ESI,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 which shows the temporal evolution of director and scalar order parameter fields. The coexistence of walls and defects is in agreement with other studies, including systems without a prescribed ordering free energy92 as well as conventional active nematic models.45,93–95Fig. 2(d) plots the defect densities versus W. In particular, the density increases with absolute activity meaning the mean distance between defects decreases. We also note that the densities of +1/2 and −1/2 defects remain equal across all activity levels.
91 which shows the temporal evolution of director and scalar order parameter fields. The coexistence of walls and defects is in agreement with other studies, including systems without a prescribed ordering free energy92 as well as conventional active nematic models.45,93–95Fig. 2(d) plots the defect densities versus W. In particular, the density increases with absolute activity meaning the mean distance between defects decreases. We also note that the densities of +1/2 and −1/2 defects remain equal across all activity levels.
The distorted director field and its continuous reconfiguration, which looks chaotic, drives the fluid flow. A snapshot of the velocity field lines together with the color-coded vorticity ω = |∇ × u| are illustrated in Fig. 2(b). The chaotic flow pattern consists of vortices of different sizes and shapes. Video S2 in the ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 illustrates the temporal evolution of velocity and vorticity fields.
91 illustrates the temporal evolution of velocity and vorticity fields.
In order to gain more insights and quantify the flow field and the orientational order, we define the normalized spatial correlation functions for vorticity,
 | (13) |
 | (14) |
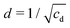 nicely aligns with ζ as Fig. 3(b) demonstrates.
nicely aligns with ζ as Fig. 3(b) demonstrates.
The correlation length roughly follows the activity dependence of the wave length λm = 2π/kmax of the most unstable mode, which we calculated in our linear-stability analysis [see eqn (27) in Appendix B]. This suggests that already λm provides the relevant length scale for active turbulence and we also call it active length in the following. Accordingly, the divergence of λm at Wc = −0.8 should also be observed for the correlation length ζ. Another important characteristic length of the system is the nematic coherence length.44,46,96 In our reduced units it amounts to  . This length, irrespective of the origin of the nematic order, for example, due to activity in our system, gives the distance over which order is maintained.
. This length, irrespective of the origin of the nematic order, for example, due to activity in our system, gives the distance over which order is maintained.
Additionally, we quantify the strength of the generated vortices by the enstrophy  , where the integral goes over the whole simulation box with area A. In Fig. 2(c) we plot the enstrophy with purple triangles versus W and fit it by a power law with exponent 1.64. For larger activities |W| stronger vortices are created, while for W > Wc vortices do not exist, of course. In summary, an increase in the absolute activity leads to the formation of stronger yet smaller vortices. Concurrently, the number of defects increases and their mean distance d decreases in nice agreement with the behavior of the vorticity and orientational correlation length ζ.
, where the integral goes over the whole simulation box with area A. In Fig. 2(c) we plot the enstrophy with purple triangles versus W and fit it by a power law with exponent 1.64. For larger activities |W| stronger vortices are created, while for W > Wc vortices do not exist, of course. In summary, an increase in the absolute activity leads to the formation of stronger yet smaller vortices. Concurrently, the number of defects increases and their mean distance d decreases in nice agreement with the behavior of the vorticity and orientational correlation length ζ.
Finally, in Fig. 4 we plot the energy spectrum E(k) ∝ k〈|u(k)|2〉 for different activity values, where the wave number is rescaled by kmin = 2π/L, with L the size of the simulation box. For all values of activity, the energy spectrum E(k) shows the typical power-law decay ∝k−4 for larger k values, in accordance with literature.32,96–98 However, to observe the scaling at small k values with a positive exponent, the box size in our simulations is not sufficiently large.32,96
4 Controlling active-fluid flow by an activity pattern
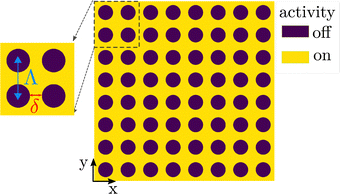
Aiming to control the flow field in an active fluid, we pattern the activity with a square lattice of circular spots, where activity is switched off and which we refer to as inactivity spots. In the region between the spots, activity has a constant value W = −3.25, which creates a sharp boundary between active and inactive regions. The lattice is characterized by two parameters: the lattice constant Λ and the surface-to-surface distance between spots δ.Specifically, we study a periodic square lattice consisting of 8 × 8 inactivity spots as depicted in Fig. 5. In the following we review the state diagram resulting from variations in Λ and δ and then introduce the different flow states in more detail.
The activity W = −3.25 is chosen since with an average order parameter of 0.55 the system displays well established orientational order. Furthermore, the lattice of 8 × 8 inactivity spots shows all the relevant states and features of such lattices, while maintaining computational efficiency.
4.1 State diagram in the presence of the activity pattern
We perform numerical simulations over ranges of lattice constant Λ and surface-to-surface distance δ and construct the resulting state diagram, as illustrated in Fig. 6. Our parameter scan reveals four distinct states. | ||
| Fig. 6 State diagram of the active fluid at activity W = −3.25, controlled by a square lattice of inactivity spots, in terms of lattice constant Λ and surface-to-surface distance δ. Four distinct states exist: multi-lane, trapped vortex, isotropic, and transition. The curve Λ = δ corresponds to bulk turbulence without any spots. The red dashed lines indicate the parameter scan of Fig. 11 and 14, respectively. | ||
First, the state that we refer to as multi-lane flow is the most interesting state. It arises for lattice constants Λ less than a critical value of Λ* ≈ 0.9 and surface-to-surface distances δ below a critical value δ* = 0.09. Note that all lengths are given in units of  and we will comment on them below. The velocity field in this state exhibits an interesting pattern of unidirectional flow lanes with adjacent lanes flowing in opposite directions. They are separated by a series of corotating vortices known as vortex street [see Fig. 7(a)].99,100 We will discuss this state in more detail in the next section. To get more insight and for later discussions, we note that the critical lattice constant Λ* = 0.9 is below but close to the active length λm, which for the specific parameters amounts to λm = 0.97. It is also close to the correlation length ζ = 1.2. Furthermore, the critical spot separation δ* = 0.09 is approximately the same as the nematic coherence length λn = 0.1, which we introduced in Section 3.2.
and we will comment on them below. The velocity field in this state exhibits an interesting pattern of unidirectional flow lanes with adjacent lanes flowing in opposite directions. They are separated by a series of corotating vortices known as vortex street [see Fig. 7(a)].99,100 We will discuss this state in more detail in the next section. To get more insight and for later discussions, we note that the critical lattice constant Λ* = 0.9 is below but close to the active length λm, which for the specific parameters amounts to λm = 0.97. It is also close to the correlation length ζ = 1.2. Furthermore, the critical spot separation δ* = 0.09 is approximately the same as the nematic coherence length λn = 0.1, which we introduced in Section 3.2.
 | ||
| Fig. 7 The multi-lane flow state for Λ = 0.6 and δ = 0.04. (a) Flow lines (in black) and normalized vorticity (background color) of the velocity field. Large arrows indicate the flow direction within the lanes and ωmax is the maximum vorticity. (b) Schematic of the flow field with four vortex streets using the analytic expression of eqn (28). (c) The y component of the velocity field, uy(x), plotted along a horizontal cut in x direction as indicated by the green line in (a). (d) Probability density function (PDF) of the vorticity P(ω). | ||
The second state, which we refer to as trapped vortex state (see Section 4.3), occurs for large lattice constants Λ > Λ* = 0.9 and small spot distances δ ≤ 0.4. In this state vortices are trapped in the active regions between the spots. They act like barriers, which vortices cannot easily cross. Adjacent to the multi-lane and trapped vortex states for increasing spot distance δ, the system exhibits an isotropic turbulent state equivalent to bulk active turbulence, i.e., in the absence of spots for δ = Λ. Only the extension of the vortices generated in the turbulent flow are smaller. Finally, between the isotropic and multi-lane flow states, a highly dynamic state emerges characterized by frequent transitions between isotropic and imperfect multi-lane configurations. We refer to this state as the transition state and will discuss its properties in Section 4.2.2.
4.2 Multi-lane flow state
The velocity field in the multi-lane flow state, as illustrated in Fig. 7(a), develops a pattern of unidirectional flow lanes with alternating directions. To invert the flow direction, a series of corotating vortices, known as vortex street and situated between neighboring lanes, is needed. The velocity field of the multi-lane flow is sketched in Fig. 7(b), where we show the streamlines of four vortex streets using the analytic expression in Appendix C. Vortices in two neighboring streets are counter-rotating.Of course, the lanes in the simulations can either be oriented along the x or y direction. Fig. 7(c) displays the y component of the velocity profile along a horizontal cut of the flow field in (a) as indicated by the green line. The centers of the vortex streets are situated at uy = 0 and regions of shear flow are separated by small plateaus indicating uniform flow. We will come back to the shear flow when discussing the director field associated with the multi-lane flow in Section 4.2.1. Of course, the probability density function (PDF) of the vorticity, P(ω), as shown in Fig. 7(d), deviates strongly from a normal distribution, which occurs for the isotropic active turbulence state.
The system in the multi-lane flow state exhibits multistability. Depending on the small random initialization of the velocity and Q tensor field, different realizations of this state exists. They differ in the number and widths of the unidirectional flow lanes and the location of the vortex streets. In Fig. 8 we show two realizations with two flow lanes of opposite direction. However, in (a) the vortex streets sit on the activity spots, while in (b) they are situated in between.
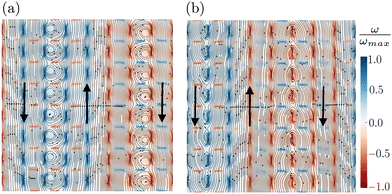 | ||
| Fig. 8 Two alternative configurations of the multi-lane state with two flow lanes compared to the one in Fig. 7(a). Vortex streets either sit on the activity spots (a) or in between (b). | ||
In passive nematics at large Ericken numbers,101,102 where elastic deformation forces are negligible against viscous forces, the nematic director field is primarily determined by the velocity profile. In particular, when subjected to shear flow the director exhibits shear alignment with the Leslie angle101,102
 | (15) |
To rationalize this observation, we note that at large Ericksen numbers flow and director field are connected by the hydrodynamic equation:103
| (λA + Ω)n = λn·Ann | (16) |
 . For linear shear flow one readily derives the Leslie angle from this equation. However, from Fig. 7(a) we notice that the vorticity in the regions between the four spots is nearly zero. In this case (Ω = 0), the nematic director aligned along the two eigenvectors of A solves eqn (16) and the stable orientation is the extensional direction belonging to the positive eigenvalue or extension rate A.104 In Fig. 9(d) we show the extensional directions scaled by the extension rate. Indeed, in areas between the four inactivity spots, their orientations with respect to the mean flow direction are ±45°. This is in close agreement with the nematic angles θ = ±41° obtained for these regions.
. For linear shear flow one readily derives the Leslie angle from this equation. However, from Fig. 7(a) we notice that the vorticity in the regions between the four spots is nearly zero. In this case (Ω = 0), the nematic director aligned along the two eigenvectors of A solves eqn (16) and the stable orientation is the extensional direction belonging to the positive eigenvalue or extension rate A.104 In Fig. 9(d) we show the extensional directions scaled by the extension rate. Indeed, in areas between the four inactivity spots, their orientations with respect to the mean flow direction are ±45°. This is in close agreement with the nematic angles θ = ±41° obtained for these regions.
We are now in a position to give a qualitative explanation for the observed multi-lane flow state. The vertical rows of inactivity spots are able to align the local activity-induced nematic order such that the regular structure visible in Fig. 9(a) occurs. The structure is stable once the spacing between the spot surfaces is below the nematic coherence length. The nematic order between the spots then drives a shear flow, which extends into the vertical rows of spots. Here the flow becomes roughly uniform since in the inactivity spots nematic order is zero. This reasoning is further supported by considering the multi-lane flow field in Fig. 8(a), where only two vortex streets exist, and by plotting the corresponding nematic order in Fig. 10(a) as well as the vertical velocity component uy along the dashed green line in Fig. 10(b). The vortex streets are located at uy = 0. From here, a steep increase of uy indicates the shear flow between the vertical rows of spots. Then, the velocity uy enters a plateau of uniform flow, which is followed again by a steep increase and a further plateau. Since the strength of the flow field cannot increase ever further, the trend has to be reversed as in Fig. 10(b). Ultimately, the flow direction reverses, for which a vortex street is needed.
 | ||
| Fig. 10 Director field in the multi-lane flow state corresponding to Fig. 8(a). (a) Scalar order parameter S quantified by the background color and the director field shown by black lines. (b) The y component of the velocity field, uy(x), plotted along a horizontal cut in x direction as indicated by the white dashed line in (a). | ||
| Γ = 2〈û ⊗ û − 1/2〉, | (17) |
In Fig. 11 we plot γ versus the spot distance δ for lattice constant Λ = 0.6 along the red dashed line in the state diagram of Fig. 6. For each value of δ, we performed eight simulation runs starting from the isotropic state Q = 0 and small random disturbances of the resting fluid u = 0. For δ > 0.12 including bulk active turbulence at δ = Λ = 0.6, the order parameter γ takes on values less than 0.1 indicating that there is no preferred direction for the velocity. So the flow state is isotropic as expected for active turbulence. Then, in the range δ ∈ [0.08,0.12] we observe a highly dynamic transition state with medium values of the flow order parameter between 0.1 and 0.3, which we will characterize further below. Finally, for δ < 0.08 the multi-lane flow state with γ > 0.5 is predominantly observed indicating the unidirectional flow throughout the system.
Before we address the transition state, we remark that similar to the multi-lane flow state, which shows multi-stability, we also observe different states in the eight simulation runs for the same δ, as Fig. 11 shows. For example, in the parameter region, where the majority of the simulations end up in the transition state, we also find isotropic active turbulence and multi-lane flow. More concrete, at δ = 0.1 five simulation runs exhibit the transition state, one the multi-lane flow state, and two the active turbulence state. Similarly, also in the multi-lane flow state one simulation out of eight ends up in the isotropic turbulent state. Thus, at small δ our system is characterized by a high degree of metastability.
The transition state shows intermittent switching between an imperfect multi-lane and a strongly disordered flow state as indicated in video 3 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 To quantify this, we calculate the tensorial flow order parameter of eqn (17) for each time snapshot by only averaging over space and then take its positive eigenvalue γs as the order parameter. The time evolution of γs for δ = 0.12 is depicted in Fig. 12 and shows strong fluctuations with peaks going up to γs = 0.4. Here, the flow field is disordered but locally flow lanes and larger vortices are observable as illustrated by the left inset of Fig. 12. Most pronounced is the large peak in the center where the multi-lane flow appears transiently and then vanishes again (right inset). In contrast, the time course of γs in the isotropic state only shows mild fluctuations around a mean value close to zero, while in the multi-lane flow state, it is fixed at a high value. This is quantified by the standard deviation Δγs determined for the time-varying order parameter and plotted versus δ in the inset of Fig. 11. While in the transition state values for Δγs up to 0.14 are observed, it is zero in the multi-lane flow state and below 0.6 in the isotropic and active-turbulence state. The time evolution of velocity and vorticity fields for the isotropic and multi-lane states can be observed in videos 4 and 5 in the ESI,†
91 To quantify this, we calculate the tensorial flow order parameter of eqn (17) for each time snapshot by only averaging over space and then take its positive eigenvalue γs as the order parameter. The time evolution of γs for δ = 0.12 is depicted in Fig. 12 and shows strong fluctuations with peaks going up to γs = 0.4. Here, the flow field is disordered but locally flow lanes and larger vortices are observable as illustrated by the left inset of Fig. 12. Most pronounced is the large peak in the center where the multi-lane flow appears transiently and then vanishes again (right inset). In contrast, the time course of γs in the isotropic state only shows mild fluctuations around a mean value close to zero, while in the multi-lane flow state, it is fixed at a high value. This is quantified by the standard deviation Δγs determined for the time-varying order parameter and plotted versus δ in the inset of Fig. 11. While in the transition state values for Δγs up to 0.14 are observed, it is zero in the multi-lane flow state and below 0.6 in the isotropic and active-turbulence state. The time evolution of velocity and vorticity fields for the isotropic and multi-lane states can be observed in videos 4 and 5 in the ESI,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 respectively.
91 respectively.
4.3 The trapped vortex state
As depicted in Fig. 6, the system is in the trapped vortex state for Λ ≤ 0.9 and for sufficiently small surface-to-surface distances of the spots, δ ≤ 0.4, while for δ > 0.4 it assumes the isotropic turbulent state. Typical snapshots in Fig. 13 illustrate the flow/vorticity fields (a) as well as the scalar order parameter and director field (b) of the trapped vortex state. One clearly notices vortices in the active region between the inactivity spots, while within the spots vorticity is weak. Thus, vortices are trapped in the active region between the spots and hardly enter them. Interestingly, the vortices are accompanied by a very dynamic director field, as video 6 in the ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 91 illustrates. It contains some defect structure, which, however, is hard to classify.
91 illustrates. It contains some defect structure, which, however, is hard to classify.
 | ||
| Fig. 13 The trapped vortex state for Λ = 1.0 and δ = 0.04. (a) Velocity (lines) and vorticity (color-coded) fields. (b) Scalar order parameter (color-coded) and director (lines) fields. | ||
To quantify this observation more thoroughly, we determined the probability distribution of the vorticity, P(ω), (insets of Fig. 14) and plotted the kurtosis of P(ω) versus δ in Fig. 14. The kurtosis
 | (18) |
 | ||
| Fig. 14 The kurtosis Kurt[P(ω)] of the vorticity distribution plotted versus the spot distance δ for Λ = 1.0. (along the red dashed line in Fig. 6) Insets show the probability density function (PDF) of the vorticity, P(ω), for the trapped vortex and isotropic turbulence states. | ||
5 Conclusions
In this article we have studied an active fluid in two dimensions using Doi's hydrodynamic equations for a semidilute solution of self-propelled rods and an additional active stress tensor. In contrast to the widely used active-nematics model, the ground state of our equations in the absence of activity does not show any nematic order. A linear stability analysis reveals that pusher solutions become unstable below an absolute threshold activity |Wc|. The range of unstable wave numbers, their growth rate, and the wave number of the most unstable mode increase for more negative activities.To determine the resulting paranematic state induced by activity, we solve the full hydrodynamic equations using the pseudospectral method. The emerging nematic order is accompanied by fluid flow with chaotic spatiotemporal behavior and high vorticity, which are characteristic features of the active-turbulence state. In particular, the energy power spectrum shows the typical power-law decay of active turbulence with exponent −4. The mean scalar order parameter and the enstrophy, quantifying the strength of the generated vortices, grow according to power laws beyond the absolute threshold value |Wc|. Furthermore, the vorticity and nematic correlation lengths, along with the mean distance between topological defects, which are all nearly identical, approximately follow the wavelength of the most unstable mode and decrease as the magnitude of activity increases. We call the wavelength of the most unstable mode as the active length, which together with the nematic coherence length provides two important length scales of the system.
In order to control active turbulence, we investigated the active fluid in the presence of a square lattice of inactivity spots for a specific activity value. The resulting state diagram in the parameter space, lattice constant versus surface-to-surface distance of the inactivity spots, is presented in Fig. 6. Most interestingly, for lattice constants below the active length and for distances between spots smaller than the nematic coherence length, we observe the multi-lane flow state. The fluid flows in parallel lanes, where the flow directions in neighboring lanes is reversed by a street of corotating vortices situated between the lanes (see Fig. 7). This flow state exhibits multistability, as the width and position of the lanes and vortex streets vary with the random initial conditions. We speculate that by “shaking'' the lattice of inactivity spots or single spots, one is able to control which of the states is realized. The nematic director in the active regions shows shear alignment along the mean flow direction at two characteristic angles, which can be explained by conventional nematodynamics. Increasing the surface-to-surface distance of the spots, isotropic active turbulence is recovered. However, a transition region exists with a strongly fluctuating flow order parameter and where imperfect multi-lane flow appears transiently.
Finally, for lattice constants larger than the active length, we observed the trapped vortex state, where vortices are confined to the active regions between the inactivity spots that strongly restrict the vortices' motion, while in the spot region vorticity is very low. This results in a pronounced peak of the vorticity distribution at zero vorticity, which therefore deviates from a Gaussian shape. With increasing spot distance the peak vanishes and isotropic active turbulence with a Gaussian vorticity distribution is recovered.
Doi's theory treats the nematic liquid crystal in the flow aligning regime assuming needlelike molecules, where the so-called flow aligning parameter assumes its maximum value one. However, it is known that nematics, depending on the molecule size and aspect ratio, can also exhibit flow tumbling behavior for a sufficiently small flow aligning parameter, as noted in ref. 45, 53, 70 and 101. So, the question arises about potential changes in the different flow states reported in this paper, when the active nematics is in the flow tumbling regime. We expect that tumbling of the director disrupts the formation of stable lanes, a phenomenon also observed in ref. 70, such that the multi-lane flow state will be replaced by either turbulent or zero flow depending on how deep the system is in this regime. We do not foresee any significant alterations to the trapped vortex state, as the formation of this state primarily depends on the vortices being trapped in the active regions, which should remain unaffected by variations in the flow aligning parameter.
Thus our work provides insight into the emergence of orientational order and active flow in dilute pusher-rod solutions and presents a novel approach for controlling active turbulence by employing a cubic lattice of inactivity spots. In future research we plan to implement different lattice patterns of inactivity spots, such as a checkerboard square lattice with alternating spot sizes, a hexagonal lattice, or a Kagome lattice but also to make the spots active instead of the regions in between and to investigate the emergent flow states. These are just a few promising examples for creating novel and programmable flow patterns out of active turbulence with the help of spatio-temporal activity patterns. We hope our work stimulates further experimental and theoretical exploration in this direction also using spatially controlled activity using photosensitive materials.
Conflicts of interest
There are no conflicts to declare.Appendices
A. Parameters
In Table 1 we explain the parameters used in this paper and state specific values. One of the advantages of Doi's approach for deriving the dynamic equations for a semidilute rod solution is that phenomenological coefficients are related to molecular parameters as summarized in Table 1 following ref. 54. For example, the coefficient of the relaxation term in eqn (2) is given as cDr. Here, Dr is the rotational diffusion coefficient of a single rod of length l and aspect ratio α diffusing in a fluid of dynamic viscosity μ. The correction factor c = β/ϕ2 takes into account the reduced rotational diffusion in the semidilute regime. It contains the factor ϕ = nrl3 with the number density nr. Thus, ϕ quantifies the fraction of excluded volume occupied by a rotating rod, while β is a numerical factor. Furthermore, ηp = πϕ/24 controls the contribution of the passive rods to the viscous stress tensor in eqn (5). Finally, we note to occupy the semidilute regime, the rod concentration should fall into the range .
.
B. Linear stability analysis
We consider the basic solution of eqn (9)–(11), u0 = 0 and Q0 = 0, which corresponds to the isotropic state of the rod solution with no flow. The velocity and alignment tensor fields are perturbed around the basic solution such that: u(x,t) = δu(x,t) and Q(x,t) = δQ(x,t). By substituting the perturbed fields into eqn (9)–(11) and only taking into account terms linear in the perturbations, the dynamic equations become| ∂tδu = −∇p + ∇2δu +∇(WδQ) | (19) |
 | (20) |
We transform the dynamic equations into Fourier space by making the plane-wave ansatz, δu = δû(k,ξ)eξt−ik·r and δQ = δ![[Q with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0051_0302.gif) (k,ξ)eξt−ik·r. Furthermore, applying the divergence operator on both sides of eqn (19) and using the incompressibility condition one obtains ∇2p = ∇·(∇(WδQ)). Converting this expression into Fourier space gives,
(k,ξ)eξt−ik·r. Furthermore, applying the divergence operator on both sides of eqn (19) and using the incompressibility condition one obtains ∇2p = ∇·(∇(WδQ)). Converting this expression into Fourier space gives,
 | (21) |
 | (22) |
 | (23) |
![[L with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_004c_0302.gif) = δû ⊗ k. These equations can be written in a compact form as, ξv = Av, where v is defined as
= δû ⊗ k. These equations can be written in a compact form as, ξv = Av, where v is defined as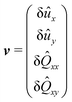 | (24) |
Note since Q is a symmetric and traceless tensor, one has Qyy = Qxx and Qyx = Qxy. Without loss of generality, we consider a wave vector along the x direction, k = (k,0), and the matrix A becomes
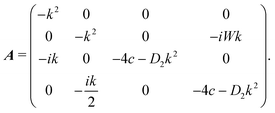 | (25) |
As evident from Fig. 1(a) and (b) in the main text, there is a critical wave number kc below which Re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ becomes positive,
ξ becomes positive,
 | (26) |
 | (27) |
Both kc and kmax increase with the magnitude of W indicating that smaller wavelengths become unstable for larger activity.
C. Velocity streamlines generated by a vortex street
In the context of incompressible irrotational flow in 2D, one can express the velocity components as vx = ∂yψ and uy = −∂xψ, where the velocity stream function ψ satisfies the Laplace equation ∇2ψ = 0. A simplest model for a irrotational vortex in 2D is described by the velocity components vr = 0 and . Here, r0 is the center position of the vortex, and K is a constant that determines the strength of the vortex. The stream function associated with this flow field is given by ψ = −K
. Here, r0 is the center position of the vortex, and K is a constant that determines the strength of the vortex. The stream function associated with this flow field is given by ψ = −K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln|r − r0|.
ln|r − r0|.
Now, consider an infinite row of such vortices arranged along the y-axis with equal spacing a. The superimposed stream function for this vortex street is  , where i indicates the ith vortex in the row. This summation can be written in closed form as99
, where i indicates the ith vortex in the row. This summation can be written in closed form as99
 | (28) |
To generate the streamlines depicted in Fig. 7(b), we superimpose the stream functions of four vortex streets ψ oriented along the y axis and with a distance of 2Λ. Adjacent vortex streets should have an alternating sign of K indicating that they rotate in opposite directions.
D. Vorticity analysis in trapped vortex state
To determine if a specific order in the vorticity pattern of the trapped vortex state exists, such as ferro or anti-ferromagnetic order similar to those reported in confined active systems,67,68 we focus on the vorticity in the regions between four inactivity spots, which we call Regions of Interest (ROIs). In Fig. 15 we show the mean value of vorticity within each ROI, 〈ω(r)〉r∈ROI, for two snapshots of a system in the trapped vortex state at Λ = 1.0 and δ = 0.04. The results indicate no specific order, also when we average each 〈ω(r)〉r∈ROI value over time. Furthermore, correlating each ROI with its four nearest neighbors, we see a tendency towards the same sign of vorticity but a regular pattern does not exist.The vorticity of a single vortex switches in time between positive and negative. To examine whether the switching occurs gradually or abruptly and also to assess the potential for synchronized vorticity switches between neighboring ROIs, we analyzed the time course of 〈ω(r)〉r∈ROI for three ROIs in one line. The results of this analysis, presented in Fig. 16, indicate that the switching behavior of vorticity is gradual and no synchronization is observed between adjacent ROIs.
Acknowledgements
We thank Cristina Marchetti, Amin Doostmohammadi, and Markus Bär for helpful discussions. We acknowledge support from Technische Universität Berlin, the Deutsche Forschungsgemeinschaft in the framework of the Collaborative Research Center SFB 910, and by a grant under STA352/11.References
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- W. C. K. Poon, Physics of Complex Colloids, IOS Press, 2013, pp. 317–386 Search PubMed.
- A. Zöttl and H. Stark, J. Phys.: Condens. Matter, 2016, 28, 253001 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- A. Zöttl and H. Stark, Annu. Rev. Condens. Matter Phys., 2023, 14, 109–127 CrossRef.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- O. Pohl and H. Stark, Phys. Rev. Lett., 2014, 112, 238303 CrossRef PubMed.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef PubMed.
- P. Digregorio, D. Levis, A. Suma, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Phys. Rev. Lett., 2018, 121, 098003 CrossRef CAS PubMed.
- M. Theers, E. Westphal, K. Qi, R. G. Winkler and G. Gompper, Soft Matter, 2018, 14, 8590–8603 RSC.
- F. Rühle and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2020, 43, 26 CrossRef PubMed.
- F. Rühle, A. W. Zantop and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 26 CrossRef PubMed.
- J. Toner and Y. Tu, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 4828–4858 CrossRef CAS.
- J. Toner, Y. Tu and S. Ramaswamy, Ann. Phys., 2005, 318, 170–244 CAS.
- A. Bricard, J.-B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- M. Knežević, T. Welker and H. Stark, Sci. Rep., 2022, 12, 19437 CrossRef PubMed.
- A. Bricard, J.-B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 7470 CrossRef CAS PubMed.
- T. Bäuerle, R. C. Löffler and C. Bechinger, Nat. Commun., 2020, 11, 2547 CrossRef PubMed.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef.
- J.-T. Kuhr, F. Rühle and H. Stark, Soft Matter, 2019, 15, 5685–5694 RSC.
- A. Beer, B. Ilkanaiv, R. Gross, D. B. Kearns, S. Heidenreich, M. Bär and G. Ariel, Commun. Phys., 2020, 3, 1–8 CrossRef.
- C. Dombrowski, L. Cisneros, S. Chatkaew, R. E. Goldstein and J. O. Kessler, Phys. Rev. Lett., 2004, 93, 098103 CrossRef PubMed.
- H. H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- J. Dunkel, S. Heidenreich, K. Drescher, H. H. Wensink, M. Bär and R. E. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 CrossRef PubMed.
- A. Doostmohammadi, T. N. Shendruk, K. Thijssen and J. M. Yeomans, Nat. Commun., 2017, 8, 15326 CrossRef CAS PubMed.
- M. James, W. J. T. Bos and M. Wilczek, Phys. Rev. Fluids, 2018, 3, 061101 CrossRef.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 CrossRef.
- A. W. Zantop and H. Stark, Soft Matter, 2022, 18, 6179–6191 RSC.
- K. Qi, E. Westphal, G. Gompper and R. G. Winkler, Commun. Phys., 2022, 5, 49 CrossRef.
- M. J. Bowick, N. Fakhri, M. C. Marchetti and S. Ramaswamy, Phys. Rev. X, 2022, 12, 010501 CAS.
- T. Ishikawa, N. Yoshida, H. Ueno, M. Wiedeman, Y. Imai and T. Yamaguchi, Phys. Rev. Lett., 2011, 107, 028102 CrossRef CAS PubMed.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- B. Martínez-Prat, R. Alert, F. Meng, J. Ignés-Mullol, J.-F. M. C. Joanny, J. Casademunt, R. Golestanian and F. Sagués, Phys. Rev. X, 2021, 11, 031065 Search PubMed.
- L. M. Lemma, S. J. DeCamp, Z. You, L. Giomi and Z. Dogic, Soft Matter, 2019, 15, 3264–3272 RSC.
- A. Doostmohammadi, S. P. Thampi, T. B. Saw, C. T. Lim, B. Ladoux and J. M. Yeomans, Soft Matter, 2015, 11, 7328–7336 RSC.
- T. B. Saw, W. Xi, B. Ladoux and C. T. Lim, Adv. Mater., 2018, 30, 1802579 CrossRef PubMed.
- S.-Z. Lin, W.-Y. Zhang, D. Bi, B. Li and X.-Q. Feng, Commun. Phys., 2021, 4, 21 CrossRef.
- P. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, 1993 Search PubMed.
- H. Stark, Phys. Rep., 2001, 351, 387–474 CrossRef CAS.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- E. J. Hemingway, P. Mishra, M. C. Marchetti and S. M. Fielding, Soft Matter, 2016, 12, 7943–7952 RSC.
- R. Aditi Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef CAS PubMed.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. C. Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
- S. Shankar, S. Ramaswamy, M. C. Marchetti and M. J. Bowick, Phys. Rev. Lett., 2018, 121, 108002 CrossRef CAS PubMed.
- P. Sheng, Phys. Rev. Lett., 1976, 37, 1059–1062 CrossRef CAS.
- P. Sheng, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 1610–1617 CrossRef CAS.
- S. Santhosh, M. R. Nejad, A. Doostmohammadi, J. M. Yeomans and S. P. Thampi, J. Stat. Phys., 2020, 180, 699–709 CrossRef CAS.
- S. Chandragiri, A. Doostmohammadi, J. M. Yeomans and S. P. Thampi, Soft Matter, 2019, 15, 1597–1604 RSC.
- M. Doi, S. F. Edwards and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988 Search PubMed.
- D. Saintillan and M. J. Shelley, Phys. Rev. Lett., 2008, 100, 178103 CrossRef PubMed.
- B. Ezhilan, M. J. Shelley and D. Saintillan, Phys. Fluids, 2013, 25, 070607 CrossRef.
- P. Srivastava, P. Mishra and M. C. Marchetti, Soft Matter, 2016, 12, 8214–8225 RSC.
- T. Ekeh, M. E. Cates and E. Fodor, Phys. Rev. E, 2020, 102, 010101 CrossRef CAS PubMed.
- P. Malgaretti, P. Nowakowski and H. Stark, EPL, 2021, 134, 20002 CrossRef CAS.
- P. Malgaretti and H. Stark, Phys. Rev. Lett., 2022, 129, 228005 CrossRef CAS PubMed.
- A. Pena-Francesch, J. Giltinan and M. Sitti, Nat. Commun., 2019, 10, 3188 CrossRef PubMed.
- S. Song, A. F. Mason, R. A. J. Post, M. De Corato, R. Mestre, N. A. Yewdall, S. Cao, R. W. van der Hofstad, S. Sanchez, L. K. E. A. Abdelmohsen and J. C. M. van Hest, Nat. Commun., 2021, 12, 6897 CrossRef CAS PubMed.
- G. Vizsnyiczai, G. Frangipane, C. Maggi, F. Saglimbeni, S. Bianchi and R. Di Leonardo, Nat. Commun., 2017, 8, 15974 CrossRef CAS PubMed.
- G. Duclos, C. Blanch-Mercader, V. Yashunsky, G. Salbreux, J.-F. Joanny, J. Prost and P. Silberzan, Nat. Phys., 2018, 14, 728–732 Search PubMed.
- A. Samui, J. M. Yeomans and S. P. Thampi, Soft Matter, 2021, 17, 10640–10648 RSC.
- J. Hardoüin, R. Hughes, A. Doostmohammadi, J. Laurent, T. Lopez-Leon, J. M. Yeomans, J. Ignés-Mullol and F. Sagués, Commun. Phys., 2019, 2, 121 CrossRef.
- D. Nishiguchi, I. S. Aranson, A. Snezhko and A. Sokolov, Nat. Commun., 2018, 9, 4486 CrossRef PubMed.
- H. Reinken, D. Nishiguchi, S. Heidenreich, A. Sokolov, M. Bär, S. H. L. Klapp and I. S. Aranson, Commun. Phys., 2020, 3, 76 CrossRef.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5498–5502 CrossRef CAS PubMed.
- K. Thijssen, L. Metselaar, J. M. Yeomans and A. Doostmohammadi, Soft Matter, 2020, 16, 2065–2074 RSC.
- J. Arlt, V. A. Martinez, A. Dawson, T. Pilizota and W. C. K. Poon, Nat. Commun., 2018, 9, 768 CrossRef PubMed.
- H. Massana-Cid, C. Maggi, G. Frangipane and R. Di Leonardo, Nat. Commun., 2022, 13, 2740 CrossRef CAS PubMed.
- M. Nakamura, L. Chen, S. C. Howes, T. D. Schindler, E. Nogales and Z. Bryant, Nat. Nanotechnol., 2014, 9, 693–697 CrossRef CAS PubMed.
- P. V. Ruijgrok, R. P. Ghosh, S. Zemsky, M. Nakamura, R. Gong, L. Ning, R. Chen, V. T. Vachharajani, A. E. Chu, N. Anand, R. R. Eguchi, P.-S. Huang, M. Z. Lin, G. M. Alushin, J. T. Liphardt and Z. Bryant, Nat. Chem. Biol., 2021, 17, 540–548 CrossRef CAS PubMed.
- L. M. Lemma, M. Varghese, T. D. Ross, M. Thomson, A. Baskaran and Z. Dogic, PNAS Nexus, 2023, 2, pgad130 CrossRef PubMed.
- S. Shankar and M. C. Marchetti, Phys. Rev. X, 2019, 9, 041047 CAS.
- S. Shankar, L. V. Scharrer, M. J. Bowick and M. C. Marchetti, arXiv, 2022, preprint, arXiv:2212.00666 DOI:10.48550/arXiv.2212.00666.
- J. Rønning, M. C. Marchetti and L. Angheluta, R. Soc. Open Sci., 2023, 10, 221229 CrossRef PubMed.
- A. Mozaffari, R. Zhang, N. Atzin and J. J. de Pablo, Phys. Rev. Lett., 2021, 126, 227801 CrossRef CAS PubMed.
- R. Zhang, S. A. Redford, P. V. Ruijgrok, N. Kumar, A. Mozaffari, S. Zemsky, A. R. Dinner, V. Vitelli, Z. Bryant, M. L. Gardel and J. J. de Pablo, Nat. Mater., 2021, 20, 875–882 CrossRef CAS PubMed.
- L. J. Ruske and J. M. Yeomans, Soft Matter, 2022, 18, 5654–5661 RSC.
- X. Tang and J. V. Selinger, Phys. Rev. E, 2021, 103, 022703 CrossRef CAS PubMed.
- H. Stark and T. C. Lubensky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061709 CrossRef CAS PubMed.
- H. Isliker, A tutorial on the pseudo-spectral method, 2004 Search PubMed.
- L. N. Trefethen, Spectral Methods in MATLAB, Society for Industrial and Applied Mathematics, 2000 Search PubMed.
- M. Hochbruck and A. Ostermann, SIAM J. Numer. Anal., 2005, 43, 1069–1090 CrossRef.
- J. E. M. Alexandre and J. Chorin, A Mathematical Introduction to Fluid Mechanics, Springer, New York, NY, 1993 Search PubMed.
- D. Saintillan, Annu. Rev. Fluid Mech., 2018, 50, 563–592 CrossRef.
- A. Doostmohammadi, S. P. Thampi and J. M. Yeomans, Phys. Rev. Lett., 2016, 117, 048102 CrossRef PubMed.
- A. U. Oza and J. Dunkel, New J. Phys., 2016, 18, 093006 CrossRef.
- See ESI† at [URL will be inserted by publisher] for videos.
- S. P. Thampi, A. Doostmohammadi, R. Golestanian and J. M. Yeomans, Europhys. Lett., 2015, 112, 28004 CrossRef.
- S. P. Thampi, R. Golestanian and J. M. Yeomans, Philos. Trans. R. Soc., A, 2014, 372, 20130366 CrossRef PubMed.
- S. Thampi and J. Yeomans, Eur. Phys. J.-Spec. Top., 2016, 225, 651–662 CrossRef.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. Cristina Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
- L. Giomi, Phys. Rev. X, 2015, 5, 1–11 Search PubMed.
- R. Alert, J.-F. Joanny and J. Casademunt, Nat. Phys., 2020, 16, 682–688 Search PubMed.
- J. Urzay, A. Doostmohammadi and J. Yeomans, J. Fluid Mech., 2017, 822, 762–773 Search PubMed.
- F. M. White, Fluid mechanics, McGraw-Hill, 2009 Search PubMed.
- P. K. Kundu, I. M. Cohen and D. R. Dowling, Fluid Mechanics (Sixth Edition), Academic Press, 2016, pp. 195–226 Search PubMed.
- A. N. Beris and B. J. Edwards, Thermodynamics of Flowing Systems: with Internal Microstructure, Oxford University Press, 1994 Search PubMed.
- Z. Kos, J. Aplinc, U. Mur and M. Ravnik, Flowing Matter, Springer, Cham, 2019 Search PubMed.
- J. Ericksen, Kolloid-Z., 1960, 173, 117–122 CrossRef.
- S. Kim and S. J. Karrila, Microhydrodynamics, Butterworth-Heinemann, 1991, pp. 107–145 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01050c |
| This journal is © The Royal Society of Chemistry 2024 |














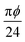

![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)