Efficient prediction of the local electronic structure of ionic liquids from low-cost calculations

Abstract

Understanding and predicting ionic liquid (IL) electronic structure is crucial for their development, as local, atomic-scale electrostatic interactions control both the ion–ion and ion–dipole interactions that underpin all applications of ILs. Core-level binding energies, E_B(core), from X-ray photoelectron spectroscopy (XPS) experiments capture the electrostatic potentials at nuclei, thus offering significant insight into IL local electronic structure. However, our ability to measure XPS for the many thousands of possible ILs is limited. Here we use an extensive experimental XPS dataset comprised of 44 ILs to comprehensively validate the ability of a very low-cost and technically accessible calculation method, lone-ion-SMD (solvation model based on density) density functional theory (DFT), to produce high quality E_B(core) for 14 cations and 30 anions. Our method removes the need for expensive and technically challenging calculation methods to obtain E_B(core), thus giving the possibility to efficiently predict local electronic structure and understand electrostatic interactions at the atomic scale. We demonstrate the ability of the lone-ion SMD method to predict the speciation of halometallate anions in ILs.

---

1. Introduction

Knowledge of local electronic structure within ionic liquids (ILs) is vital to understand and predict electrostatic interactions, which control both the ion–ion and ion–dipole interactions that underpin all applications of ILs.^1–7 Electrostatic interactions are of vital importance in ILs for e.g. anion–metal cation interactions in potential battery electrolytes,⁸ and cation–substrate interactions in cellulose processing.⁹

As it is not possible to experimentally test the very large number of possible ILs due to cost, computational screening offers an attractive option for identifying anions and cations with the optimum local electronic structure. However, validation against experimental data is required to demonstrate that the computational screening method captures IL local electronic structure properties and give confidence in predictions.

Element-specific core-level binding energy of an electron, E_B(core), from core-level X-ray photoelectron spectroscopy (XPS)^10–12 is a local, atomic-level electronic structure descriptor that quantifies non-covalent electrostatic interaction strengths in ILs, e.g. the overall anion basicity/electron donor ability.^10–12 Furthermore, differences in E_B(core) correlate very well with the electrostatic potential at a nucleus (V_n);^12–14V_n is used in the organic chemistry community as a descriptor for non-covalent electrostatic interaction strengths.^15–17 Experimental E_B(core,exp.) values are available for many elements for ILs from a diverse selection of anions (e.g., [NTf₂]⁻ = bis[(trifluoromethane)sulfonyl]imide and halometallate anions) and cations (mainly organic imidazolium and onium cations),^{10–12,18–25} and give consistent E_B(core,exp.) values across different experimental apparatus and research groups.^{10,11,18–23,25}

E _B(core,exp.) can be used for validation of computational screening methods for IL local electronic structure properties because differences in E_B(core,exp.) are driven mainly by local bonding/interactions. Contributions to E_B(core,exp.) can potentially come from: (i) ground-state effects (in XPS called initial-state effects) which are determined by the local bonding/interactions, and (ii) the influence of the core-hole created during the photoemission event (in XPS called final-state effects) which is controlled by the relaxation of other core and valence electrons. It is often assumed that final-state contributions are vital,²⁶ but there is increasing evidence that ground-state contributions dominate differences in E_B(core,exp.).^12,14,27 For 17 small organic molecules, a good correlation found between gas-phase E_B(N 1s,exp.) and ground-state calculated E_B(N 1s, calc.) (i.e., no core-hole included in the calculations) from density functional theory (DFT).²⁷ We recently demonstrated that E_B(core,exp.) and E_B(core,calc.) (with no core-hole included in the calculations) from ab initio molecular dynamics (AIMD) correlate very well for three [C₈C₁Im][A] ILs; structures of ILs from AIMD are expected to reflect very well the IL solvation structure.^12,14 These findings show that E_B(core,exp.) can be used to validate differences in E_B(core,calc.) (when no core-hole is included in the calculations), as differences in E_B(core,exp.) are driven mainly by differences in local bonding/interactions, with final-state effect contributions being far less important. Any significant difference between E_B(core,exp.) and E_B(core,calc.) would be due to an inability of the calculation to capture the IL solvation structure and therefore the local electronic structure; any final-state contributions to E_B(core,exp.) would be expected to be relatively small.

Screening ILs using E_B(core) as a descriptor requires a method to calculate E_B(core,calc.) with a good level of accuracy while still being relatively low-cost and technically undemanding. Using AIMD will give high quality IL solvation structures as noted above, but is very expensive and technically demanding, meaning that AIMD is not suitable to obtain E_B(core) for screening purposes. Classical molecular dynamics (MD) simulations are lower cost than AIMD to obtain structures, and links between calculated atomic charges from structures derived from MD simulations and XPS E_B(core) have been found,²⁸ but MD simulations are not ideal for screening ILs as they are still technically demanding and can be expensive, especially if polarisable force-fields are used to improve inter-ion interactions. Ion-pairs computed using (gas phase) density functional theory (DFT) show a good (qualitative) visual match to experimental E_B(core), however, the number of reported comparisons is very small,^20,29 and ion-pair calculations require knowledge of the IL anion–cation structure.^30–32

Using a lone-ion, an ion with no other explicit ions solvated to it, computed within a generalised solvation environment, such as SMD (solvation model based on density)³³ offers a potential solution to the problem of balancing cost and accuracy. Lone-ion-SMD calculations are very small-scale, relatively inexpensive and technically undemanding calculations. We recently found using lone-ion-SMD calculations that 39 ILs gave excellent linear correlations between calculated and experimental E_B(valence); but no data was given for E_B(core).³⁴ Moreover, preliminary results for onium cations and halozincate anions in ILs gave a good (qualitative) visual match between experimental and calculated XP spectra, but no quantitative comparisons of E_B(core) were made.^25,35

In this article we validate E_B(core,calc.) using both quantitative and qualitative (visual) methods for lone-ion-SMD DFT calculations against benchmark XPS. We collate and publish, mostly for the first time here, a significant quantity of largely our own E_B(core) data for 44 ILs. Seven elements (C, N, O, F, P, S, Cl) across 14 cations and 27 anions are examined, leading to XPS for 44 ILs being validated. This allows us to demonstrate that small-scale calculations using SMD capture the solvation environment of ILs and therefore give good quality E_B(core,calc.), which are descriptors of local electronic structure.

We present a case study to demonstrate the ability of lone-ion-SMD DFT calculations to identify speciation in a chlorobismuthate IL by comparison to experimental XPS data, a challenging undertaking given that Bi is a heavy metal that can expand its coordination sphere and a lone pair that could be either stereochemically active or inactive. Speciation is not easy to determine for closed shell, spectroscopically quiet metals, e.g. Bi³⁺; standard spectroscopic methods (e.g. UV-vis, NMR) cannot supply sufficient insight. Furthermore, the femtosecond timescale for a single X-ray photoemission event means XPS provides a snapshot of the chlorobismuthate anions present in the liquid-phase without having to consider dynamics of the nuclei during the timescale of the X-ray photoemission event, which is a significant positive for speciation studies. We have previously demonstrated that this approach works well for halozincate-based ILs where halide atoms bridge between two zinc atoms but no lone pairs are present.²⁵

2. Experimental

2.1. Experimental methods

2.1.1. IL drop XPS. IL drop XPS was recorded for five ILs ([C₄C₁Im][CH₃CO₂], [C₂C₁Im][NTf₂], [C₄C₁Im][NPf₂], [C₄Py][NTf₂], [C₂C₁Im][FAP]) at the University of Reading on a Thermo Scientific ESCALAB 250 monochromated Al Kα source (hν = 1486.6 eV) spectrometer. A thin drop of IL (∼0.5 mm height) was placed directly onto a stainless steel sample plate. This sample was placed in a loadlock and the pressure reduced to 10⁻⁷ mbar by pumping down for >6 hours. After attaining the required pressure, the IL was transferred to the analysis chamber. Acquisition parameters were matched to give comparable energy resolution with data already published; a pass energy of 20 eV was used for core-levels.

XPS for 39 ILs (Table S1, ESI†) have previously been published, where the focus was mainly on valence XPS, as well as one aqueous solution (Table S2, ESI†).^12,13,36,37 Core-level XP spectra were published mainly to demonstrate IL purity so most E_B(core) values are published here for the first time for these 39 ILs.

2.2. Computational methods: small-scale DFT

DFT calculations were carried out for 14 cations (Table S3, ESI†) and 30 anions (Table S4, ESI†) at the B3LYP-D3(BJ) level, using Becke's three-parameter exchange functional in combination with the Lee, Yang and Parr correlation functional (B3LYP) as implemented in the Gaussian 09 and Gaussian 16 suite of programs.^38–41 Grimme's D3 dispersion correction with Becke–Johnson damping was used to account for dispersion.^42–45 The 6-311+G(d,p) basis set was employed for lighter atoms (H, C, N, O, F, P, S, Cl, Fe, Co, Ni, Zn), except for calculations undertaken to test the effects of varying the basis set which are discussed further below.^46–49 LANL2DZ and LANL2DZdp pseudo potentials and the associated basis sets were employed for the heavier atoms In and Sn respectively.⁵⁰ Data for the chlorobismuthate anions was taken from calculations reported in ref. 51; cc-pVDZ-pp (scalar relativistic) pseudopotentials and aug-cc-pVDZ associated basis sets were employed for the heavy Bi atoms,^52,53 and the aug-cc-pVDZ basis set was employed for Cl in these calculations.

Optimisations were carried out without symmetry constraints. The self-consistent field (SCF) convergence criteria were 10⁻⁹ on the density matrix and 10⁻⁷ on the energy matrix (scf = conver = 9). The numerical integration grid was a pruned grid with 99 radial shells and 590 angular points per shell (int = ultrafine). Frequency analysis was carried out for all optimised structures, which are confirmed as minima by the absence of imaginary modes.

[C₄C₁Im][PF₆] parameters were used for calculations for all ions. The SMD parameters employed are shown in Table S5 (ESI†).

Structures were optimised as individual, isolated ions (referred to as lone-ion). Structures optimised in the gas phase are identified as GP structures while those optimised using SMD are referred to as SMD structures.

2.3. Computational methods: producing calculated XP spectra

To produce calculated XP spectra for core-levels that have spin–orbit coupling (Cl 2p, S 2p, P 2p), each calculated E_B(core) was adjusted using E_B separation and area factors given in Table S6 (ESI†). Once the adjusted calculated E_B(core) were obtained, a Gaussian–Lorentzian product (GLP) function was applied to each calculated E_B(core) data point using eqn (1) and then summed to produce calculated XPS data. The mixing parameter, m, and function width, F, were set to the values given in Table S6 (ESI†).

To produce calculated XP spectra for core-levels that do not have spin–orbit coupling (F 1s, O 1s, N 1s, C 1s), a GLP function was applied to each calculated E_B data point for each core-level using eqn (1) and then summed to produce calculated XPS data. E is the calculated E_B for each core-level and x is E_B at which the intensity is calculated. The mixing parameter, m, and function width, F, were set to the values given in Table S6 (ESI†).

2.4. Data analysis

All experimental XP spectra were fitted using CasaXPS™ software.⁵⁴ Fitting was carried out using a Shirley background and GL30 line shapes (70% Gaussian, 30% Lorentzian). Peak constraints used are outlined in the ESI,† Section S4.

In ESI,† Table S8, the core-level used for charge referencing is given. The experimental uncertainty in E_B(core,exp.) is ±0.10 eV.¹⁹

To align calculated XP spectra to experimental XP spectra, for each core-level the average difference between the E_B(core,exp.) and E_B(core,calc.) were used (average E_B values are given in ESI,† Tables S10–S16 and S18). The average difference for each core-level represents the average final-state contribution for that core-level (along with other systematic errors from DFT). The calculated uncertainty in lone-ion-SMD E_B(core,calc.) is ±0.20 eV (based on a combination of the experimental uncertainty in E_B(core,exp.) and the standard error of the sample mean for different lone-ion-SMD E_B(core,calc.), ESI,† Table S18).

3. Results and discussion

3.1. Validation of lone-ion-SMD for calculating IL core-level XPS

The excellent ability of lone-ion-SMD core-level calculations to capture core-level electronic structure is demonstrated here for both cations and anions (Fig. 1–3).

Fig. 1 Calculated binding energy, E_B(calc.) from lone-ion-SMD against experimental XPS binding energy, E_B(exp.) for: (a) C 1s, (b) N 1s, (c) S 2p_3/2, (d) O 1s, (e) F 1s, (f) Cl 2p_3/2, (g) P 2p_3/2. m is the gradient of each line-of-best fit. The experimental uncertainty is ±0.10 eV; the calculated uncertainty is ±0.20 eV.

Fig. 2 Experimental and calculated Cl 2p XPS for [C₈C₁Im][A] where A = Cl⁻, [ZnCl₄]²⁻, [SnCl₃]⁻ and [InCl₄]⁻: (top) experimental Cl 2p XPS (vertically offset for clarity); (middle) calculated Cl 2p XPS for lone-ion-SMD of the anions (E_B(correction) = +5.18 eV, vertically offset for clarity); (bottom) calculated Cl 2p XPS for lone-ion-gas-phase (GP) of the anions (E_B(correction) = +10.20 eV, vertically offset for clarity). Experimental XP spectra are area normalised and charge referenced using methods given in ESI,† Section S5.

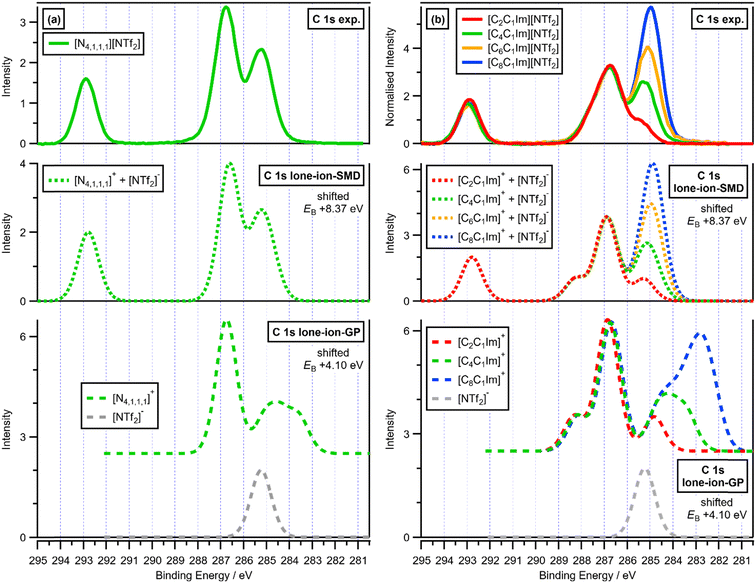Fig. 3 Experimental and calculated C 1s XPS: (a) (top) experimental C 1s XPS for [N_4,1,1,1][NTf₂]; (middle) calculated C 1s XPS for lone-ion-SMD of [N_4,1,1,1]⁺ and [NTf₂]⁻ (E_B(correction) = +8.37 eV); (bottom) calculated C 1s XPS for lone-ion-gas-phase (GP) of [N_4,1,1,1]⁺ and [NTf₂]⁻ (E_B(correction) = +4.10 eV), with the cation contribution vertically offset for clarity; (b) (top) experimental C 1s XPS for four [C_nC₁Im][NTf₂] ILs (where n = 2, 4, 6, 8); (middle) calculated C 1s XPS for lone-ion-SMD of four [C_nC₁Im]⁺ cations (where n = 2, 4, 6, 8) and the [NTf₂]⁻ anion (E_B(correction) = +8.37 eV); (bottom) calculated C 1s XPS for lone-ion-gas-phase (GP) of [C_nC₁Im]⁺ (where n = 2, 4, 8) and [NTf₂]⁻ (E_B(correction) = +4.10 eV), with the cation contributions vertically offset for clarity. Experimental XP spectra are area normalised and charge referenced using methods given in ESI,† Section S5.

3.1.1. Linear correlations between experimental core-level XPS and lone-ion-SMD calculated core-level XPS. For all seven elements considered here, excellent linear correlations are found between experimental E_B(core,exp.) and lone-ion-SMD E_B(core,calc.); furthermore, R² are near 1 for all seven elements (Fig. 1). The data for E_B(C 1s), E_B(N 1s) and E_B(S 2p_3/2) provide particularly strong evidence for linear correlations given the large E_B ranges and both cations and anions being included in the correlations (Fig. 1a, b and c respectively). These observations provide very strong validation of the ability of lone-ion-SMD calculations to capture the local electronic structure of ILs.

3.1.2. Visual matches between experimental core-level XPS and lone-ion-SMD calculated core-level XPS. Visual demonstrations of the excellent matches of the experimental and calculated XP spectra are shown for all seven elements reported here: Cl 2p (Fig. 2 and Fig. S15, ESI†), C 1s (Fig. 3 and Fig. S8–S10, ESI†), N 1s (Fig. S11, ESI†), S 2p (Fig. S12, ESI†), O 1s (Fig. S13, ESI†), F 1s (Fig. S14, ESI†), P 2p (Fig. 4). For example, in both experimental and calculated data the E_B(Cl 2p) order, [InCl₄]⁻ > [SnCl₃]⁻ > [ZnCl₄]²⁻ > Cl⁻, and the E_B(Cl 2p) differences from Cl⁻ to [ZnCl₄]²⁻ to [SnCl₃]⁻ to [InCl₄]⁻ are the same (Fig. 2). Important examples include elements with a large E_B range and contributions from both cations and anions, e.g., C 1s (Fig. 3).

Fig. 4 Experimental and calculated P 2p XPS for four P-containing ILs and four lone P-containing lone ions: (top) experimental P 2p XPS for and [C₄C₁Im][PF₆], [C₂C₁Im][FAP], [C₄C₁Im][Me₂PO₄] and [P_6,6,6,14][NTf₂] (vertically offset for clarity); (bottom) calculated P 2p XPS for lone-ion-SMD of the ions [PF₆]⁻, [FAP]⁻, [Me₂PO₄]⁻ and [P_6,6,6,14]⁺ (E_B(correction) = +3.23 eV, vertically offset for clarity). Experimental XP spectra are area normalised and charge referenced using methods given in ESI,† Section S5.

Calculated XP spectra from lone-ion-SMD for anions give very good visual matches to experimental XP spectra for anions, including when 1- and 2-anions are considered, with the same single E_B(correction) = +5.18 eV. A lone-ion-SMD Cl 2p calculation for the 2-anion [ZnCl₄]²⁻ matches almost perfectly to the experimental XP spectra both visually relative to other anions (Fig. 2, top and middle).

Calculated XP spectra from lone-ion-SMD for cations versus anions give very good matches to experimental XP spectra, showing that lone-ion-SMD calculations capture the electronic structure of the cation versus the anion very well in most cases. Lone-ion-SMD C 1s core-level calculations for [N_4,1,1,1][NTf₂] and [C_nC₁Im][NTf₂] match visually, with the same single E_B(correction) = +8.37 eV, almost perfectly to the experimental XP spectra for [N_4,1,1,1][NTf₂] and [C_nC₁Im][NTf₂] respectively (Fig. 3 top and middle). Furthermore, lone-ion-SMD P 2p core-level calculations for [PF₆]⁻, [FAP]⁻, [Me₂PO₄]⁻ and [P_6,6,6,14]⁺ match visually almost perfectly to the appropriate experimental XP spectra, all with the same single E_B(correction) = +3.23 eV (Fig. 4).

We now compare E_B(C 1s) in different cationic environments in more detail. A lone-ion-SMD C 1s calculation for the cation [N_4,1,1,1]⁺ matches visually almost perfectly to the shape of the experimental XP spectrum for [N_4,1,1,1]⁺ (with the anion [NTf₂]⁻, Fig. 3a top and middle respectively), with E_B(C_C–N 1s) larger than E_B(C_alkyl 1s) for both experimental and calculated data. For [C_nC₁Im]⁺, the visual match is excellent for the E_B(C 1s) order: E_B(C² 1s) > E_B(C_hetero 1s) > E_B(C_alkyl 1s) (Fig. S6 and S7, ESI†), which matches to all C 1s fitting models used for IL XPS.^18,37,55 However, for [C_nC₁Im]⁺ the E_B(C 1s) differences are slightly larger for E_B(C 1s,calc.) than E_B(C 1s,exp.) (Fig. S6 and S7, ESI†). Similar results were obtained from AIMD-DFT calculations for three [C₈C₁Im][A] ILs (see Fig. S7 for a visual comparison of lone-ion-SMD and AIMD C 1s data, ESI†),¹² demonstrating that these differences are likely due to a combination of the SMD method not quite capturing the effect of the solvation environment on the cations and final-state effect contributions not accounted for in the ground-state calculations of E_B(C_cation 1s).

Lone-ion-GP calculations perform very poorly compared to lone-ion-SMD calculations, demonstrating the importance of using an SMD in lone-ion calculations. The lone-ion-GP C 1s calculations for [N_4,1,1,1][NTf₂] and [C_nC₁Im][NTf₂] provide very poor matches to the corresponding experimental C 1s XP spectra (Fig. 3a top and bottom). ΔE_B for E_B(C_CF 1s) from the anion relative to E_B(C_hetero 1s) from the cation was ∼+6 eV from experiments and ∼−2 eV from lone-ion-GP calculations, a huge mismatch (Fig. 3a, top and bottom). Furthermore, lone-ion-GP C 1s calculations for the cationic alkyls give very poor visual matches to the experimental C 1s XP spectra for both [N_4,1,1,1]⁺ and [C_nC₁Im]⁺ (Fig. 3a and b, top and bottom). Lone-ion-GP calculations perform terribly at capturing the overall ion electronic structure. The lone-ion-GP calculations gave E_B(Cl 2p) differences that are clearly far too large compared to the experimental E_B(Cl 2p) differences, and also get the E_B order completely wrong compared to the experimental E_B data, e.g. E_B(Cl 2p_3/2,calc.) for [ZnCl₄]²⁻ smaller than Cl⁻, (Fig. 2, top and bottom).

We have found excellent matches for experimental and calculated XPS using a relatively modest basis set – 6-311+G(d,p) for the light atoms; the basis set choice had an impact on absolute E_B(core,calc.) but little impact on differences in E_B(core,calc.). Comparisons of tetraalkylammonium cations ([N_4,1,1,1]⁺, [C₄C₁Pyrr]⁺, [C₈C₁Pyrr]⁺) for the 6-311+G(d,p) data published here and def2-QZVPP employed in ref. 35 show the differences in E_B(N 1s,calc.) are very similar irrespective of the basis set identity, and very similar to the experimental differences in E_B(N 1s,exp.) (Fig. S17, ESI†). Note that for E_B(N 1s) the E_B(correction) = +9.76 eV for the 6-311+G(d,p) basis set and E_B(correction) = +6.37 eV for the def2-QZVPP basis set (data taken from ref. 35), demonstrating that the impact on absolute E_B(core,calc.) is relatively strong but the impact on relative E_B(core,calc.) is very little. Furthermore, comparisons of larger basis sets, def2-QZVPP and def2-TZVPP, against each other for the calculated Cl 2p XPS of chlorozincate anions showed minimal impact, with small absolute E_B differences of less than 1 eV and much smaller relative E_B differences than 1 eV.²⁵

Our calculation method allows easy and efficient prediction of E_B(core,exp.) for the seven core-levels for which E_B(correction) has been determined. A constant E_B(correction) = E_B(core,exp.) − E_B(core,calc.) for each core-level is required to align the experimental and calculated XP spectra (Fig. 2–4 and Fig. S6–S15, ESI†). For each core-level the E_B(correction) needed is calculated from the average of individual E_B(correction); the average E_B(correction) values are given in ESI,† Table S18, which are calculated using the individual E_B(correction) values given ESI,† Tables S10–S16. For example, a single E_B(correction) = +15.84 eV is needed for the calculated XPS to give excellent visual matches to experimental XPS (Fig. S14, ESI†). The effectiveness of a single E_B(correction) for each core-level across different chemical systems, including both cations and anions, indicates a high transferability for the E_B(correction) parameter to a wide range of ions. Our results for calculations with different basis sets demonstrate that an E_B(correction) value is needed for each core-level for each different basis set/functional combination (Fig. S17, ESI†). This situation is analogous to the calculations performed to aid interpretation of NMR spectroscopy data, where standard corrections in ppm are available for different basis set/functional combinations.⁵⁶ The order of the average E_B(correction), which is F 1s > O 1s > N 1s > C 1s > Cl 2p > S 2p > P 2p, matches the order of average E_B(core,exp.) for each element (Table S18, ESI†). This increasing average E_B(correction) with increasing average E_B(core,exp.) is likely due to a deficiency in the DFT calculations, but could also be due to the increasing importance of final-state effects for core-levels with larger average E_B(core,exp.).

3.2. Using calculated E_B(core) to determine halometallate anion speciation

One use of the combination of calculated and experimental XPS is to investigate halometallate anion speciation; here we demonstrate this approach for the very challenging case of an equimolar 1 × BiCl₃ + 1 × [C₈C₁Im]Cl mixture (Fig. 5), i.e., a mole fraction of x = 0.50 for BiCl₃. In this case, plausible anion structures include [BiCl₄]⁻ (tetrahedral or sawhorse), [Bi₂Cl₈]²⁻ and [Bi₃Cl₁₂]³⁻.⁵¹

Fig. 5 Experimental Cl 2p XPS for x = 0.5 BiCl₃ dissolved in [C₈C₁Im]Cl (top, middle and bottom) and calculated Cl 2p XPS for lone-ion-SMD of the anions (E_B(correction) = +4.74 eV): (top) [Bi₂Cl₈]²⁻; (middle) [Bi₃Cl₁₂]³⁻; (bottom) [BiCl₄]⁻. The experimental XP spectrum is charge referenced using methods given in ESI,† Section S5. The structures are given on the right-hand side.

Our experimental XPS results conclusively rule out the presence of free Cl⁻ anion. A Cl 2p_3/2 peak due to Cl⁻ would occur at E_B(Cl 2p_3/2,exp.) ≈ 197 eV,¹⁹ and no such contribution is evident (Fig. 5). Therefore, our experimental XPS results conclusively rule out [Bi₂Cl₇]⁻ as the chlorobismuthate species, as for 1 × BiCl₃ + 1 × [C₈C₁Im]Cl the presence of [Bi₂Cl₇]⁻ would also give Cl⁻, and there is clearly no Cl⁻ present in XPS of 1 × BiCl₃ + 1 × [C₈C₁Im]Cl (Fig. 5). Furthermore, the calculated XP spectrum for 1 × [Bi₂Cl₇]⁻ + 1 × Cl⁻ gives a poor visual match to the experimental XPS for 1 × BiCl₃ + 1 × [C₈C₁Im]Cl (Fig. S16, ESI†).

Contrary to a “first glance” visual interpretation of the experimental XPS (Fig. 5), it has been determined that more than one Cl electronic environment is present. The experimental Cl 2p spectrum for 1 × BiCl₃ + 1 × [C₈C₁Im]Cl appears to give a single Cl electronic environment. A single Cl electronic environment on standard lab XPS apparatus gives a 2 : 1 peak area ratio for Cl 2p with a E_B peak separation of 1.60 ± 0.02 eV and a full width at half maximum (FWHM) of ∼0.9 eV, as found for Cl⁻, [ZnCl₄]²⁻, [SnCl₃]⁻etc. (ref. 25). For 1 × BiCl₃ + 1 × [C₈C₁Im]Cl, the FWHM when fitted with two components with the appropriate spin–orbit coupling constraints (2 : 1 peak area ratio and E_B peak separation = 1.60 eV, Table S6, ESI†), i.e. potentially a single Cl electronic environment, gave FWHM for the two components of 1.1 eV, significantly larger than the 0.9 eV FWHM that we have observed for one Cl environment.²⁵ We were unable to produce a peak fitting model with two Cl electronic environments (i.e. four components); this observation does not rule out the presence of two different Cl electronic environments, it means that the two different Cl electronic environments have relatively similar E_B(Cl 2p).

Our experimental XPS results conclusively rule out [BiCl₄]⁻. Firstly, the most stable structure for [BiCl₄]⁻ (determined using differences in calculated total energies⁵¹), a seesaw/sawhorse structure, gives a poor visual match to the experimental Cl 2p XPS (Fig. 5 bottom) as seesaw/sawhorse [BiCl₄]⁻ gives two very different Cl electronic environments, with a substantial E_B difference of 0.9 eV (Table S17, ESI†). Secondly, tetrahedral [BiCl₄]⁻ with a stereochemically inactive lone pair (found to be unfavourable by calculated differences in total energies⁵¹) is not present, as only one Cl electronic environment would be observed for such a highly symmetric structure.

We assign the speciation for 1 × BiCl₃ + 1 × [C₈C₁Im]Cl as [Bi₂Cl₈]²⁻, as the best visual match of experimental and calculated Cl 2p XP spectra is for [Bi₂Cl₈]²⁻ (Fig. 5 top). There is a good visual match between experimental and calculated Cl 2p XPS for [Bi₃Cl₁₂]³⁻ (Fig. 5 middle), suggesting that [Bi₂Cl₈]²⁻ is the primary anion present but a small quantity of [Bi₃Cl₁₂]³⁻ may also be present. [Bi₂Cl₈]²⁻ gives two relatively similar Cl electronic environments, with a small E_B difference of 0.4 eV (Table S15, ESI†), which matches to our unsuccessful attempts to fit two Cl electronic environments in the Cl 2p XP spectrum. The E_B(correction) needed to obtain a very good visual match for both [Bi₂Cl₈]²⁻ and [Bi₃Cl₁₂]³⁻, +4.74 eV (Fig. 5 top and middle), is very similar to the E_B(correction) needed for a good visual match for all Cl-containing anions, +5.18 eV (Fig. 2 middle).

The total energies for the lone-ion-SMD calculations of [Bi₂Cl₈]²⁻ and [Bi₃Cl₁₂]³⁻ were both 8 kJ mol⁻¹ more stable than of [BiCl₄]⁻,⁵¹ matching well to our XPS finding of no [BiCl₄]⁻ present. However, such relatively small total energy differences, especially for [Bi₂Cl₈]²⁻versus [Bi₃Cl₁₂]³⁻, highlight the challenges of using total energies from small-scale calculations to determine halometallate speciation.

4. Summary and conclusions

We have presented small-scale calculations that can efficiently predict IL local electronic structure to a good level of accuracy without the need for experimental data. E_B(core) calculated using inexpensive and technically accessible DFT calculations employing an SMD on lone-ions to capture solvation for 14 cations and 27 anions are successfully validated against an extensive experimental XPS dataset of 44 ILs using quantitative and qualitative comparisons. E_B(core) values represent a descriptor for the ability of an atom to form electrostatic interactions. E_B(core) has great potential as a molecular-level local descriptor for non-covalent electrostatic interaction strengths in ILs, especially given the dearth of molecular-level descriptors available for ILs. This demonstration opens significant opportunities.

The experimental dataset published here is ideal for validation of IL calculations of E_B(core). The experimental dataset given here includes seven elements, and E_B(core,exp) data is available for other elements, e.g., Zn 2p and Br 3d for halometallate anions in ILs,²⁵ giving multiple opportunities to validate calculations. If calculations are validated, then the user can have high confidence that the local electronic structure is captured in their calculations, and it is highly likely that the calculations capture the liquid-phase solvation environment of ILs.

Our findings give the potential for screening ILs for specific desired electronic properties. For example, calculating E_B(core) can allow screening for atoms in ions that will give strong electrostatic interactions.

Our combination of experimental XPS data and lone-ion-SMD calculations shows great promise for determining the speciation of relatively complex metal-containing anions in ionic liquids. Through a combination of calculated and experimental spectra we find strong evidence that [Bi₂Cl₈]²⁻ is the dominant species; a finding which would be difficult to determine without both the experimental and computational results.

Our dataset of E_B(core) values can be used as input data for quantitative structure–property relationships (QSPR)⁵⁷ of ILs, a field that is expected to grow significantly in the coming years; the strong links of E_B(core) and the electrostatic potential at a nucleus (V_n)¹⁴ make E_B(core) values particularly attractive in this area. Both (or just one or the other) experimental and calculated E_B(core) can be used. Using just experiments or just calculations is simple; no E_B(correction) is needed for the calculations. If obtaining E_B(core) from a mixture of experiments and calculations, option one is use our calculation method (same basis set, functional and SMD parameters) for the ion or ions in question and use the appropriate E_B(correction) value for the core-level in question, option two is to use a different calculation method which would require a range of reference ions to be calculated to allow E_B(correction) to be obtained for the core-level in question.

Data availability

Data for this article, including X-ray photoelectron spectroscopy experimental data and log files for all calculated structures, are available at University of Reading Research Data Archive, DOI: 10.17864/1947.001411. Analysed data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

KRJL acknowledges support from a Royal Society University Research Fellowship (URF\R\150353, URF\R\211005, RGF\EA\180089, RGF\R1\180053, RF\ERE\210061 and RF\ERE\231015). RPM acknowledges support from the Royal Society of Chemistry through the RSC Research Fund grant (R21-4762139998).

References

1. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250.
2. D. R. MacFarlane, M. Forsyth, P. C. Howlett, M. Kar, S. Passerini, J. M. Pringle, H. Ohno, M. Watanabe, F. Yan, W. J. Zheng, S. G. Zhang and J. Zhang, Nat. Rev. Mater., 2016, 1, 15005.
3. T. Zhou, C. M. Gui, L. G. Sun, Y. X. Hu, H. Lyu, Z. H. Wang, Z. Song and G. Q. Yu, Chem. Rev., 2023, 123, 12170–12253.
4. Z. Y. Zhao, H. Li and X. Gao, Chem. Rev., 2023, 124, 2651–2698.
5. J. L. Shamshina and R. D. Rogers, Chem. Rev., 2023, 123, 11894–11953.
6. X. Q. Li, K. Chen, R. L. Guo and Z. Wei, Chem. Rev., 2023, 123, 10432–10467.
7. G. X. Li, K. Chen, Z. G. Lei and Z. Wei, Chem. Rev., 2023, 123, 10258–10301.
8. N. Takenaka, S. Ko, A. Kitada and A. Yamada, Nat. Commun., 2024, 15, 1319.
9. B. L. Lu, A. R. Xu and J. J. Wang, Green Chem., 2014, 16, 1326–1335.
10. T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem. – Eur. J., 2010, 16, 9018–9033.
11. B. B. Hurisso, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 17737–17748.
12. E. Gousseva, F. K. Towers Tompkins, J. M. Seymour, L. G. Parker, C. J. Clarke, R. G. Palgrave, R. A. Bennett, R. Grau-Crespo and K. R. J. Lovelock, J. Phys. Chem. B, 2024, 128, 5030–5043.
13. E. Gousseva, S. D. Midgley, J. M. Seymour, R. Seidel, R. Grau-Crespo and K. R. J. Lovelock, J. Phys. Chem. B, 2022, 126, 10500–10509.
14. F. K. Towers Tompkins, E. Gousseva, R. A. Bennett, R. Grau-Crespo and K. R. J. Lovelock, 2025, in preparation.
15. C. H. Suresh, G. S. Remya and P. K. Anjalikrishna, Wiley Interdiscip. Rev.-Comput. Mol. Sci., 2022, 12, e1601.
16. C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56, 1884–1895.
17. B. Galabov, S. Ilieva, G. Koleva, W. D. Allen, H. F. Schaefer and P. V. Schleyer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 37–55.
18. K. R. J. Lovelock, I. J. Villar-Garcia, F. Maier, H. P. Steinrück and P. Licence, Chem. Rev., 2010, 110, 5158–5190.
19. I. J. Villar-Garcia, E. F. Smith, A. W. Taylor, F. L. Qiu, K. R. J. Lovelock, R. G. Jones and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 2797–2808.
20. M. Reinmöller, A. Ulbrich, T. Ikari, J. Preiss, O. Höfft, F. Endres, S. Krischok and W. J. D. Beenken, Phys. Chem. Chem. Phys., 2011, 13, 19526–19533.
21. A. W. Taylor, S. Men, C. J. Clarke and P. Licence, RSC Adv., 2013, 3, 9436–9445.
22. R. M. Fogarty, R. P. Matthews, C. R. Ashworth, A. Brandt-Talbot, R. G. Palgrave, R. A. Bourne, T. V. Hoogerstraete, P. A. Hunt and K. R. J. Lovelock, J. Chem. Phys., 2018, 148, 193817.
23. R. M. Fogarty, R. Rowe, R. P. Matthews, M. T. Clough, C. R. Ashworth, A. Brandt, P. J. Corbett, R. G. Palgrave, E. F. Smith, R. A. Bourne, T. W. Chamberlain, P. B. J. Thompson, P. A. Hunt and K. R. J. Lovelock, Faraday Discuss., 2018, 206, 183–201.
24. F. K. T. Tompkins, L. G. Parker, R. M. Fogarty, J. M. Seymour, E. Gousseva, D. C. Grinter, R. G. Palgrave, C. D. Smith, R. A. Bennett, R. P. Matthews and K. R. J. Lovelock, Chem. Commun., 2024, 60, 10756–10759.
25. J. M. Seymour, E. Gousseva, F. K. T. Tompkins, L. G. Parker, N. O. Alblewi, C. J. Clarke, S. Hayama, R. G. Palgrave, R. A. Bennett, R. P. Matthews and K. R. J. Lovelock, Faraday Discuss., 2024, 253, 251–272.
26. W. F. Egelhoff, Surf. Sci. Rep., 1987, 6, 253–415.
27. N. P. Bellafont, F. Illas and P. S. Bagus, Phys. Chem. Chem. Phys., 2015, 17, 4015–4019.
28. N. V. S. Avula, A. Mondal and S. Balasubramanian, J. Phys. Chem. Lett., 2018, 9, 3511–3516.
29. M. Lembinen, E. Nommiste, H. Ers, B. Docampo-Alvarez, J. Kruusma, E. Lust and V. B. Ivanistsev, Int. J. Quantum Chem., 2020, 120, e26247.
30. P. A. Hunt and I. R. Gould, J. Phys. Chem. A, 2006, 110, 2269–2282.
31. R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3238–3253.
32. R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2015, 17, 14437–14453.
33. V. S. Bernales, A. V. Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122–9129.
34. R. M. Fogarty, R. P. Matthews, P. A. Hunt and K. R. J. Lovelock, 2025 10.1039/D5CP00214A.
35. F. K. Towers Tompkins, L. G. Parker, R. M. Fogarty, J. M. Seymour, E. Gousseva, D. C. Grinter, R. G. Palgrave, C. D. Smith, R. A. Bennett, R. P. Matthews and K. R. J. Lovelock, Chem. Commun., 2024, 60, 10756–10759.
36. R. M. Fogarty, R. G. Palgrave, R. A. Bourne, K. Handrup, I. J. Villar-Garcia, D. J. Payne, P. A. Hunt and K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2019, 21, 18893–18910.
37. J. M. Seymour, E. Gousseva, A. I. Large, C. J. Clarke, P. Licence, R. M. Fogarty, D. A. Duncan, P. Ferrer, F. Venturini, R. A. Bennett, R. G. Palgrave and K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2021, 23, 20957–20973.
38. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
39. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2009.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
42. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
43. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
44. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 014104.
45. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
46. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
47. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
48. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
49. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
50. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
51. R. Rowe, K. R. J. Lovelock and P. A. Hunt, J. Chem. Phys., 2021, 155, 014501.
52. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
53. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
54. N. Fairley, V. Fernandez, M. Richard-Plouet, C. Guillot-Deudon, J. Walton, E. Smith, D. Flahaut, M. Greiner, M. Biesinger, S. Tougaard, D. Morgan and J. Baltrusaitis, Appl. Surf. Sci. Adv., 2021, 5, 100112.
55. C. J. Clarke, S. Maxwell-Hogg, E. F. Smith, R. R. Hawker, J. B. Harper and P. Licence, Phys. Chem. Chem. Phys., 2019, 21, 114–123.
56. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
57. S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00892a

---