Subtle hydrogen bonds: benchmarking with OH stretching fundamentals of vicinal diols in the gas phase

Abstract

The theoretical description of spectral signatures for weakly bound hydrogen contacts between alcohol groups is challenging and remains poorly characterised. By combining Raman jet spectroscopy with appropriately scaled harmonic DFT predictions and relaxation path analyses for 16 vicinal diols (ethylene glycol (ethane-1,2-diol), propane-1,2-diol, 3,3,3-trifluoro-propane-1,2-diol, rac-butane-2,3-diol, 2-methyl-propane-1,2-diol, 2-methyl-butane-2,3-diol, pinacol (2,3-dimethyl-butane-2,3-diol), 3-butene-1,2-diol, 1-phenyl-ethane-1,2-diol, trans-cyclobutane-1,2-diol, trans-cyclopentane-1,2-diol, trans-cyclohexane-1,2-diol, trans-cycloheptane-1,2-diol, cis-cyclohexane-1,2-diol, 1-(1-hydroxy-1-methylethyl)-cyclopentanol and [1,1′-bicyclopentyl]-1,1′-diol), 69 conformational assignments become possible in a two-tier approach with a 5 diol training and an 11 diol test set. The latter reveals systematic deviations for ring strain and secondary π interactions, but otherwise a remarkably robust correction and correlation model based on hybrid DFT with a minimally augmented triple-zeta basis set is obtained, whereas GGA functionals perform significantly worse. Raw experimental data in the 3560–3700 cm⁻¹ wavenumber range as well as computed geometries of all conformations invite further vibrational and structural benchmarking at the onset of hydrogen bonding. Beyond this diol-probed threshold, the accurate prediction of hydrogen bond induced shifts of different magnitudes remains one of the challenges for DFT functionals.

---

1 Introduction

The predictability of OH stretching vibrations is of substantial importance in the field of carbohydrate research, perhaps most prominently for glycans.^1,2 This is particularly true for weakly hydrogen-bonded situations and low temperatures, where the spectroscopic signals remain narrow and characteristic. In the related case of silanols, it has even been postulated that such weakly connected neighbouring OH groups are a cause for toxicity.³ For isolated OH groups in alcohols, a recent systematic study⁴ has been successful in predicting the conformational and substitution trends based on harmonic quantum-chemical calculations within a couple of cm⁻¹, but it was noted that specific intramolecular interactions between the OH group and some other part of the molecule represent a challenge for accurate modeling, even if they are weak. This has further encouraged the present benchmark study, in which 16 vicinal diols with a total number of 98 low energy conformations are experimentally investigated and 69 of them are assigned in terms of their OH stretching fundamental transitions. These diols cover a multitude of constrained neighbourhood situations and substitution patterns for two OH oscillators, far from unconstrained strong hydrogen bonds such as in methanol dimer⁵ or tert-butyl alcohol dimer,⁶ which lead to 100–150 cm⁻¹ downshifts from the respective monomers. Still, they will be seen to span a wavenumber range of up to 120 cm⁻¹ and are therefore quite suitable for the benchmarking of weak hydrogen bond models. Note that it is debatable whether the weakest of these interactions in vicinal diols should be given a bond attribute,^7,8 but for simplicity, we use the term in the phenomenological sense of causing observable downshifts relative to free OH groups, independent on the presence or absence of a bond critical point or more continuous concepts. Of course, an important prerequisite for benchmarking is the correct spectroscopic assignment, which represents the most important task of this contribution and requires an understanding of interconversion barriers between conformations. This is because the non-equilibrium techniques used to prepare the cold molecules can only relax higher conformations if they differ sufficiently in energy and are connected via low barriers. Although most spectroscopic and correlation studies of alcohols and carbohydrates involve infrared spectroscopy,^1,2,9–11 we choose Raman jet spectroscopy for this purpose,^12,13 because it reduces rovibrational substructure in a particularly effective way and enables a high signal-to-noise ratio even for the less volatile species.

Several vicinal diols have been structurally characterised by microwave spectroscopy. Examples include ethane-1,2-diol,^14,15 propane-1,2-diol,^16,17 butane-1,2-diol,¹⁸rac-butane-2,3-diol,¹⁹meso-butane-2,3-diol¹⁹ and catechol (benzene-1,2-diol).^20,21 However, large amplitude motions which result in a tunneling splitting sometimes make the analysis of the symmetrically substituted aliphatic systems difficult.^19,22–24 Vibrational spectroscopy provides a lower resolution and thus initially simpler perspective, once a systematic comparison between experiment and theory is established. This also extends to the calculation of zero point vibrational energies to properly predict the energetic ranking of conformers.

Most of the systems presented here have been previously investigated in solution^10,25–44 or matrices^{32,35,45–47}via IR spectroscopy. However, the resulting vibrational frequencies are less suited as reference data for quantum chemistry. Although the simulation of environmental effects is of much interest by itself, the isolated gas phase provides a better entry point for theory. This is particularly true for the low rotational temperatures accessible by jet spectroscopy. In contrast to low temperature matrix isolation studies,^35,47 the jet expansion conserves more population of higher conformations and therefore provides richer access to the conformational landscape of these diols, besides avoiding matrix shifts.

Two diols, ethane-1,2-diol and trans-cyclohexane-1,2-diol, have already been vibrationally characterized by us in detail and lend themselves to an initial exploration, because they consist of only two conformations separated by a low barrier.¹³ They are complemented by the more heavily substituted pinacol (2,3-dimethyl-butane-2,3-diol) in the same conformational complexity class, such that primary, secondary and tertiary alcohol environments are represented. Mixed substitution patterns are provided by propanediol and a methyl-butanediol. After its characterization by experiment and theory and unambiguous assignment, this set of 5 training systems is used to establish linear reference correlations between theory and experiment. These correlations are tested step-by-step by investigating 11 less symmetric, unsaturated, cyclic and fluorinated vicinal diols, thus introducing secondary interactions and environments which conserve or affect the systematic correlation between theoretical (harmonic) and experimental (anharmonic) OH stretching wavenumbers.

In this work, we show that different density functionals can be used in the harmonic approximation to assign and correlate experimentally observed OH stretching fingerprints across a number of populated conformations from a database of vicinal diols. Only one of these functionals yields fitting parameters which look physically reasonable, but even in that case, it remains to be explored by higher level electronic structure and vibrational dynamics calculations whether the description of these weakly hydrogen-bonded and loosely coupled OH groups is accurate for the right reason or whether different errors cancel in a systematic way. For this purpose, the present benchmark database is made available to the theoretical chemistry community. In our opinion, only theoretical models which are able to describe this comprehensive dataset of vicinal diols sufficiently well should be considered for a reliable future modelling of carbohydrate vibrational spectra.

2 Methodology

2.1 Compounds and their nomenclature

Depending on the number of C–H substituents n_D = 0–4 on the HO–CH₂–CH₂–OH scaffold, the 16 investigated vicinal diols fall in five classes and are abbreviated with a compact nomenclature which encodes the substitution pattern at the two neighbouring carbon atoms carrying the OH groups, separated by a dash and complemented by a stereochemical prefix, where needed. 0 stands for an unsubstituted CH₂ group, so 0-0 is ethanediol. M represents a methyl group, F stands for a CF₃ group, V for a vinyl and Ph for a phenyl group. Thus, MM-MM represents pinacol and 0-Ph stands for phenyl-ethanediol, whose chirality is not relevant for a monomer study. When the two alcohol carbons are connected in a ring of size n, this is denoted n–n (with a prefix t(rans) or c(is) specifying the stereochemical orientation of the OH groups). If the methylene unit is replaced by a cyclopentane ring, this is encoded CP. In the case of butanediol, the r(acemic) form rM-M was investigated, not the meso form. The abbreviations are introduced in Fig. 1 together with full names and chemical formulae.

Fig. 1 Overview of all investigated compounds together with their abbreviation used in the text. The systems are sorted according to their overall degree of substitution (n_D = 0–4) which is given in parentheses after the full name of the system. Molecules highlighted in blue are used to train the initial correlation fits, which are then tested with the molecules in black.

Conformational designators are ′ (prime), * and t specifying the OH–OH hydrogen bond arrangement or lack thereof. If no prime is added it refers to an O–OH angle which is above 120° whereas a ′ indicates that it is below 120°. This is shown for rM-M in Fig. 2. In general a ′ implies a more orthogonal OH arrangement while unprimed conformations imply a more colinear arrangement. In some cases OH dipoles orient in a more antiparallel or crossed fashion (Fig. 2) instead of forming an intramolecular hydrogen bond. In these instances a * is added. In extreme cases the OH groups are no longer in direct contact at all and the OCCO dihedral angle is anti-periplanar. This is denoted with a t. An example for CP-MM is given in Fig. 2. The t label is also used in case of di-axial conformations (t5-5) or related conformations without hydrogen bonds (t4-4). Should a label repeat, letters a, b, c, d are added i.e. rM-Ma, rM-Ma′ or CP-MMat. Note that the labels need not to be correlated, so a and a′ may denote conformations differing by more than the difference in O–OH angle. Figures of all molecular structures are provided in Section S5 of the ESI.†

Fig. 2 Illustration of the naming convention for rM-M and CP-MM as examples.

2.2 Experimental methods

All spectra were recorded using our jet Raman setup which was previously described in detail.⁴⁸ This greatly simplifies the OH stretching spectra compared to higher temperature gas phase studies.^{30,35,43,49,50} Here, we just give a general description of the gas expansion setup which employs mixtures of helium gas with traces of the diol to be investigated. For all compounds except MM-MM a heatable gas flow saturator was necessary to reach a sufficiently high concentration. The tubing behind the heatable saturator was kept 10–20 K above the saturator to prevent condensation. Backing pressures ranged from 0.35 bar to 1.4 bar and in some cases argon was added to the gas mixture to promote collisional relaxation. This mixture was expanded continuously for up to 10 min through a slit nozzle. A 532 nm laser beam with 20 or 25 W, produced by a Spectra Physics Millenia 25 eV, crossed the expansion orthogonally 0.5 mm to 2 mm downstream of the nozzle. Details concerning the actual detection of the photons and further handling of the spectra can be found elsewhere.⁴⁸ The detailed conditions of each shown spectrum can be found in Table S1 in the ESI.† All assignments can be found in Section S4.2 of the ESI.† Note that due to band overlap and the limited predictive power of the harmonic calculations, not all band assignments are unique and unambiguous. We expect that less than 10% may be wrong, and typically, these refer to conformations with a low population.

2.3 Computational methods

Given the conformational complexity of some systems, structural search algorithms were used. Specifically, we employed CREST (Conformer-Rotamer Ensemble Sampling Tool, version 2.10.2) developed by Grimme and coworkers^51,52 which utilises the GFN2-xTB (Geometries Frequencies Non-covalent interactions – extended Tight Binding, version 6.3.3) functional.^53,54 The search itself was done with CREST's NCI mode enabled as well as with the standard iMTD-GC (iterative Meta-Dynamics – Genetic Crossing) procedure. The results where carefully checked by hand for potentially missing further conformers.

All DFT calculations were done with the ORCA (version 4.2.1) program package.^55,56 Only four functionals are explored in this experimentally driven work, two GGA and two hybrids to work out the generic difference between these two traditional approaches. The B3LYP,^57–59 PBE0,^60,61 PBE⁶² and BP86^57,63,64 functionals were used in conjunction with Grimme's D3 dispersion correction using Becke–Johnson damping as well as three body terms.^65,66 This dispersion correction will be implied in the following without explicit statement. We chose the ma-def2-TZVP Ahlrichs basis^67,68 set as a compromise between accuracy and computational cost and will abbreviate it as maTZ in the following, where appropriate. In our testing the augmentation raises the computational costs only slightly and does not change the frequencies much relative to the regular triple zeta basis set but significantly helps reduce the BSSE (Basis Set Superposition Error) related to the intramolecular hydrogen bond or contact. This becomes particularly relevant once anti-periplanar arrangements of the OCCO backbones are included. This general issue was previously discussed in more detail by Reiling et al.⁶⁹ for ethanediol and by Jensen⁷⁰ for ethanediol and propane-1,3-diol at the MP2 level of computation. Furthermore, density fitting (RI-J) was employed for BP86 and PBE with the corresponding auxiliary basis⁷¹ set whereas for B3LYP and PBE0 none was applied.

The geometries generated with CREST were optimised and an analytical frequency calculation was carried out within the double harmonic approximation. These computed analytical frequencies were used as a basis to assign the experimental results. Because the coupling of the vicinal local OH oscillators is weak,⁴⁰ there is typically no ambiguity in terms of free and bound modes. Since ORCA can only compute Raman activities for numerical frequency calculations, these were added using the RI-JCOSX⁷² approximation after additional energy sorting of the analytical frequency results. From these Raman activities the differential cross-sections are calculated which take setup specific factors into account. This conversion is described in more detail in ref. 73 and its ESI.

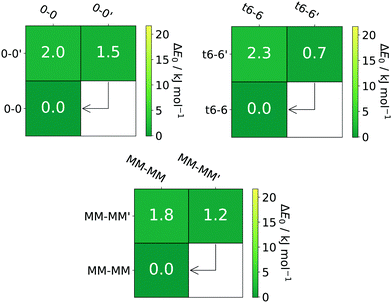
For the transition state search the NEB-CI (Nudged Elastic Band-Climbing Image) method⁷⁴ was used for the initial guess, as it is implemented in ORCA. A transition state optimisation was then carried out on the converged climbing image. During the optimisation an exact Hessian calculation was carried out on every third optimisation step. All barriers are always given relative to the less stable species. The results are shown in the form of an energy-matrix (see Fig. 3 and more extensive examples in the ESI,† some with arrows to guide the reader to experimentally feasible interconversions). The diagonal elements give the relative energy to the global minimum, increasing when moving from the bottom-left towards the top-right. All off diagonal elements represent the corresponding barrier where rows indicate all relaxation pathways away from the conformer while columns indicate all pathways towards a conformer. Based on previous examples and the results of Ruoff et al.⁷⁵ we expect and tentatively locate this relaxation threshold near 5 kJ mol⁻¹. This threshold only offers a coarse orientation, due to the large amount of influence parameters like expansion conditions and the gradual nature of conformational relaxation. Example inputs for the ORCA calculations can be found in Table S2 in the ESI.†

Fig. 3 Overview of the relative zero point corrected energies (diagonal) of the different conformers and barriers for the corresponding interconversion (off-diagonal) at the B3LYP/maTZ level for ethanediol (0-0), cyclohexanediol (t6-6) and pinacol (MM-MM). Barriers are given relative to the meta-stable conformer.

3 Goals and strategy

The main goal of this manuscript is to establish safe assignments for the diol spectra of increasing complexity, because a spectroscopic database with numerous misassignments can mislead theory. This in turn requires, besides new experimental data, robust help from theory in terms of qualitative energy order and barrier size information between conformations, and semiquantitative sequences of wavenumber shifts for the two coupled oscillators as a function of conformation for each species and between species. In principle, any reasonable dispersion corrected density functional can be used for this trend-exploiting purpose, but we focus on B3LYP because it has proven helpful in related assignment tasks. The line of spectroscopic argument is summarised briefly for each individual case, referring the reader to the ESI† for detailed lines of argument. Here, the key question is: How many and which diol conformations can be safely assigned and thus serve experimental benchmarking purposes?

Because the theory guidance is not perfect for individual systems, the experimental assignment task has to be split into three hierarchical stages. The first stage involves three symmetric, unquestionably assignable diols, the second one varies substitution patterns but leaves out further functionalisation or ring strain and the third stage introduces secondary chemical functionality or strain as a complicating factor. The key question is: Can such weak secondary hydrogen bond acceptors still be accommodated, before the generic failure of DFT in quantitatively describing normal hydrogen bond shifts⁵ bends the theory-experiment correlation?

In between these stages, there has to be a learning process which is carried out by a model which correlates harmonic theoretical OH stretching wavenumbers to experiment. Instead of two previously used types of one-parameter correlation (scaling and shifting), we start with a strongly covariant two-parameter correlation in which we subsequently fix the scaling parameter for each of four functionals at its mean value to fit only the shifting parameter. This experimentally driven parametric treatment leads to insights about a fundamental difference between GGA and hybrid functionals in describing weak hydrogen bonds in combination with the well-characterised alcohol substitution trends. For each of the two families of functionals, we use two representatives to avoid overinterpretation. In the end, the qualitatively different values of the obtained parameters in the two families are interpreted to confirm why B3LYP in hindsight has been and still is most useful for vibrational spectroscopists, because it yields fitting parameters which are closest to a diatomic spectroscopic picture of the OH bond in a weakly hydrogen-bonded environment. Here the key question is: How far can the use of evidently unphysical fitting parameters rescue the interpolating performance of other density functionals at the onset of hydrogen bonding?

The spectroscopically helpful three-tier approach requires an interplay of assignment and modelling description, which could also be useful for automated spectroscopic learning algorithms. The grossly different response of GGA and hybrid functionals to weak hydrogen bonding requires correlation figures which include the full range covered by all functionals, at the expense of subtle substitution effects, which are better followed in the linear regression coefficients and in the ESI.† A reader who is just interested in using the present experimental benchmark set for the testing of further density functionals which could replace B3LYP as perhaps the de facto standard in vibrational spectroscopy – an activity strongly encouraged by our work – can jump directly from Sections 4.2–5 before extracting the relevant experimental reference data from the ESI.†

4 Model building

4.1 Assignment for three symmetrically substituted diols

The experimental data for ethane-1,2-diol (0-0)^12,13 and trans-cyclohexane-1,2-diol (t6-6)¹³ have been previously published by our group. Both compounds allow for straightforward assignments because they only have two relevant conformers and B3LYP has already proven to make reliable predictions in these cases. We now extend their analysis to different functionals. An energetic comparison can be found in the ESI† (see Tables S3 and S11) indicating that functionals based on the generalised gradient approximation (GGA) like BP86 and PBE tend to overestimate the stability of primed (′) conformers. A recent study by Barone and co-workers also addressed t6-6 in solution via IR and VCD spectroscopy employing anharmonic calculations to simulate their spectra. They find similar energy differences at the B3LYP-D3(BJ)/jul-cc-pVTZ and B2PLYP-D3(BJ)/jun-cc-pVTZ level of computation as well as a comparable barrier.⁴⁴ A comparison of their anharmonic local mode and VPT2 (Vibrational Perturbation Theory of Second Order) results with our jet data suggests that the former is the more promising approach (see Table S19 in the ESI†). It should be noted though that the PCM (Polarizable Continuum Model) was applied to all vibrations except XH stretching type vibrations.

A system with similar conformational simplicity as 0-0 and t6-6 is pinacol (MM-MM). A compact energetic overview of all three systems is given in Fig. 3. The energy difference between the ground state and the excited conformation (′) as well as the energy barrier from the excited conformation to the ground state are rather similar and quite small, allowing for significant conversion if the energetical driving force does not vanish.

Fig. 4 shows that the simulated harmonic B3LYP spectra fit quite well to the experimental ones, once they are wavenumber scaled to align the dominant, least downshifted OH stretching fundamental with experiment. The required scaling factors are not identical but rather similar, indicating some substitution dependence of either the DFT error or anharmonicity. The small deviations between the scaled harmonic theory and experiment are not systematic in sign and size. The dominance of the respective global minimum structures is quite pronounced even in a helium expansion, as shown by the shrinking factors relative to the simulation above the black arrows for non-overlapping bands which range from about 0.2 to 0.5. This relaxation is expected for the 1.8–2.3 kJ mol⁻¹ barriers under jet conditions, despite the small predicted energy differences of 0.7–1.5 kJ mol⁻¹. It is in qualitative contrast to the GGA predictions for t6-6 (see Table S11, ESI†). For pinacol, Lomas et al. find a similar energy difference of about 1.9 kJ mol⁻¹ at the PBE0/cc-pVTZ//B3LYP/6-311+G(d,p) computational level.⁷⁶ Olschewski et al. also find a similarly low barrier.⁴¹ A comparison of our computational results with others^35,41,76 can be found in the ESI† (see Table S16). Earlier Ar-matrix FT-IR results by Dahlqvist et al. only observed the most stable conformer³⁵ (see Table S35 in the ESI†). It is also instructive to compare the wavenumber splitting between the two OH oscillators in pinacol as a function of phase state. In different solutions and also in the gas phase at room temperature,^{10,25,35,39,41,77} this splitting is below 50 cm⁻¹ and isomers cannot be distinguished due to thermal excitation. In an Ar cryomatrix,³⁵ it is close to 50 cm⁻¹, but the matrix isolation shift is comparable in size to spectral isomer differences and only the most stable isomer can be observed. Only jet cooling reveals two isomers separated by 11 and 14 cm⁻¹ with oscillator splittings of 53 and 56 cm⁻¹. It provides the best meeting point for theory, where only the B3LYP calculation predicts a (harmonic) oscillator splitting around 55 cm⁻¹, whereas all other explored methods predict splittings between 67 and 92 cm⁻¹.

Fig. 4 Experimental spectra (plotted upwards) and simulated spectra (plotted downwards) of ethanediol (0-0),¹³trans-cyclohexanediol (t6-6)¹³ and pinacol (MM-MM). To investigate the conformational relaxation behaviour, different admixtures of argon to helium were used in case of t6-6. Saturator (T_S) and nozzle temperatures (T_N) are provided. The simulation is based on B3LYP calculations and Boltzmann weighted according to T_N and the relative energies given in Fig. 3. Wavenumber scaling factors for the free OH mode for the most stable conformer are also given.

The relaxation and thus distinction between the two isomers can be further enhanced by the addition of argon to the carrier gas (see the t6-6 case), confirming the energy sequence. The shoulder of the 3658 cm⁻¹ signal in the MM-MM spectrum is caused by water impurities, also visible as a separate or overlapping signal for the other two diols. Separation of the water Q-branch and the actual band of interest can be achieved by monitoring the bands over extended periods of time, where the water band will continually decrease. It should be noted though that some residual water will remain for typical measurement periods.

When comparing the spectra for the three diols in Fig. 4, a progressive downshift of the bands with the degree of substitution from ethanediol to cyclohexanediol to pinacol is noticeable. It parallels the downshift observed from primary over secondary to tertiary saturated mono-ols.^9,11 However, diols allow for more differentiated substitution patterns including asymmetric variants, which shall be explored in later sections together with more challenging spectral assignments. Before doing this, it appears useful to train different correlation models between experimental and theoretical band positions with the three symmetric diols 0-0, t6-6 and MM-MM.

4.2 Model training and interpretation

There are two simple one-parameter strategies how to correlate quantum chemical harmonic predictions for OH stretching fundamental wavenumbers with experimental, anharmonic data. One is to scale the harmonic prediction by a multiplicative factor h, the other to shift it by a constant a2. The former is more popular, the latter is more physical from a local mode perspective, because it implies a uniform anharmonicity of the OH bond, which should be only weakly affected by the environment. For isolated alcohols, this anharmonicity is indeed quite independent on the degree of substitution at the alpha carbon.⁴ Obviously, any theory-experiment correlation also has to account for deficiencies in the electronic structure method, which can be formally absorbed into the anharmonic (a2) or the harmonic (h) correction.

Our approach is to take the three symmetric diols with established assignment and to initially fit all assigned transitions to a two-parameter expression

[small nu, Greek, tilde]_i = hω_i − a2 (1)

where h stands for a multiplicative harmonic correction and a2 for an additive anharmonic correction term, which is denoted as 2ω_ex_e for diatomic molecules. [small nu, Greek, tilde]_i is the experimental anharmonic wavenumber of the i-th mode and ω_i the harmonic wavenumber predicted by theory. An ideal quantum-chemical method would yield h ≈ 1 and a2 ≈ (175 ± 15) cm⁻¹ for weakly hydrogen-bonded and free OH groups.⁷⁸ In reality, for a given DFT level, the two parameters are strongly correlated, washing out any subtle substitution patterns among different diols. Therefore, the h value from the global fit to 12 transitions in the three symmetric diols for a given quantum-chemical level is subsequently frozen and the different diols are further discriminated by their best a2 fits. Due to the strong parameter correlation (see exemplary covariance matrices in Table S39 of the ESI†), it is not so important which value of h is used, and we arbitrarily round and freeze the global fit value to the second decimal place when a2 is fitted. A quantitatively poor method may still allow for meaningful predictions, in particular interpolations, based on such a training fit, but the parameters may lose their physical meaning.

Fig. 5 shows the result of such a strategy for the B3LYP predictions. One can see that h is slightly (but insignificantly) higher than 1.00. Because at the same time, the best fit a2 is rather close to twice the (negative) diagonal anharmonic constant for alcohols⁷⁸ and the net effect of off-diagonal contributions is small,^4,79 the diol OH bonds are seen to be slightly too soft for this hybrid functional. This combined statement is possible despite the strong fitting parameter correlation and associated large standard deviation. If one now freezes h = 1.01 (rounded to two decimal places from 1.008 of the two parameter all fit) and looks at the individual best fits for the three separate diols, a systematic (and now significant) trend of increasing a2 values with increasing substitution is found. This matches nicely the finding for isolated alcohols,⁴ but now includes weakly hydrogen-bonded situations.

Fig. 5 Correlation between the experimental and predicted band positions at the B3LYP (top) and PBE0 (bottom) level of computation. Fits for each compound are shown as well as a fit for all bands with one (solid line) and two free parameters (dashed line). The standard error (σ) of each fitted parameter is also given. N specifies the number of bands included in the all fit.

Fig. 5 also contains the results for PBE0, which was shown to be slightly superior to B3LYP in terms of the independence of a2 on the substitution pattern, for h = 1.00.⁴ Now, including weakly hydrogen-bonded situations in vicinal diols, the deviation is actually dependent on the predicted wavenumber value, i.e. on weak hydrogen bond-like contacts. Therefore, the unconstrained fit yields h ≈ 0.84, although only the fact that h < 1 is really significant and in part corresponds to the common knowledge that PBE0 predicts significantly too stiff OH bonds. Another important contribution to the low h value is the exaggerated PBE0 OH wavenumber lowering in electron-rich environments. By arbitrarily freezing h at 0.84, one therefore obtains a2-values which are much larger and of opposite sign than one would physically expect due to anharmonicity. As a positive aspect, PBE0 shows a smaller, hardly significant dependence on substitution pattern, like in the simple alcohol case.⁴ This is still the case when one constrains h to 1, although to a lesser extent (see Fig. S1 in the ESI†). Therefore, we freeze h at 0.84, suggesting that PBE0 somehow systematically overestimates the frequency lowering due to weak hydrogen bonding, if the true anharmonicity is invariant to weak hydrogen bonding.

This systematic overestimation of the frequency lowering due to hydrogen bonding is even more pronounced for GGA functionals, which are exemplified in Fig. S2 of the ESI† for PBE and BP86, again including empirical dispersion correction and using the same basis set. The global two-parameter fit yields h close to 2/3, whereas the magnitude of the a2 value exceeds 1000 cm⁻¹ to compensate for the reduced slope. This shows that the harmonic trends in GGAs are far too reactive to weak hydrogen bond interactions, if one assumes that the true anharmonicity does not change much. For correlation and prediction purposes, this is not necessarily detrimental, but any success of GGAs in predicting OH stretching frequencies is clearly for the wrong reason. Therefore, we will focus more on the two hybrid functionals in the next steps, which appear to be closer to the anharmonic reality. An overview of all fit parameters including their errors can be found in Section S4.3 of the ESI.†

4.3 Methyl substitutions and model testing

In this and the following subsections we will only briefly discuss our assignments. More detailed explanations can be found in Section S4.1 of the ESI.† A seemingly simple extension of ethanediol is propanediol (0-M) although its conformational landscape is vastly more complicated as indicated by 8 different conformers within 5 kJ mol⁻¹ and the experimental microwave data^80,81 which we will discuss in more detail later on. However, many of these conformers relax easily under jet conditions. This can be enhanced by adding Ar to the seeding gas, in line with the predicted barriers. Some relaxation is to be expected for all primed/unprimed pairs. In terms of its substitution, 0-M constitutes a new class (n_D = 1). By scaling the harmonic frequency calculations to coincide with the free OH vibration of the most stable conformer and by using the computed relative energy information we were able to assign 7 conformers, two more than a previous jet FTIR investigation.⁸²

0-M is of considerable interest to the astrochemical microwave community^80,81,83,84 as an extension of 0-0 which has been found in interstellar clouds.^85,86 A comparison of other computational data^{17,80–82,87,88} with ours can be found in the ESI† (Table S4). The hybrid functionals as well as the MP2 results agree with each other while the GGAs and HF fail to predict the correct energetic order as indicated by our vibrational and the rotational data.^80,81 The GGAs predict the primed species to be more stable, a deficiency recurring for other diols. Our results are consistent with Lovas et al., who investigated the relaxation pathways⁸⁰ and was also able to observe all conformers besides 0-Mc′. Arenas et al.⁸¹ observed all conformers besides 0-Mb′ and 0-Mc′ (more details are provided in Table S4 of the ESI,† where we also translate our nomenclature to the one introduced by Vázquez et al.⁸⁹).

A first candidate to test the previously established correlation for t6-6 is rac-butane-2,3-diol (rM-M) since it shares the same substitution pattern (secondary–secondary). Given the more symmetric nature of rM-M in comparison to 0-M the conformational landscape is reduced to 5 energetically relevant, partially interconverting conformers. The rM-M* conformer is only stable at the B3LYP/maTZ level of computation and will not be assigned. The remaining conformers were assigned with satisfactory agreement to the experimental results.

The previously mentioned study by Barone and co-workers⁴⁴ also investigated rM-M. The energetical landscape they found is similar to ours with regards to the relative energies as well as the interconversion pathways. A comparison of their anharmonic vibrational treatment can be found in Table S20 in the ESI.† The VPT2 approach performs significantly better while the local mode approach heavily underestimates the band positions in some instances (up to 87 cm⁻¹), although it looked quite promising for t6-6. Jesus et al. investigated rM-M via FT-IR matrix spectroscopy in Ar and Xe.⁴⁷ Their results are also compared to ours in Table S20 (ESI†) and highlight the importance of jet reference data since the matrix effects can be fairly substantial and non-uniform. They also only observe the rM-M and rM-Ma conformers. A comparison of our computational data with literature values^{19,36,37,44,47,88} can be found in the ESI† (Table S14). Besides the results by Wang et al.³⁶ the computational results agree reasonably well with each other. Furthermore whether or not rM-M* is a stable species (without imaginary frequencies) depends on the method used.

Diols allow for different local substitution patterns for the same overall degree of substitution at the vicinal carbons. For example 2-methyl-propane-1,2-diol (0-MM) has the same overall degree of substitution (n_D = 2) as the previously discussed t6-6 and rM-M. Therefore the derived correlation for t6-6 may have predictive power for 0-MM. Indeed, this is the case (see Fig. S15 ESI†), suggesting that the overall degree substitution is the deciding factor. Furthermore, the conformational landscape of 0-MM is similar to rM-M, including the stability issues of rM-M*/0-MM*. An energetic comparison with other tested functionals can be found in the ESI† (Table S8).

Another possible methyl substitution pattern is secondary-tertiary (n_D = 3) which is realised by methyl-butanediol (M-MM). In terms of its symmetry it is analogous to 0-M which results in a very similar conformational landscape with 8 energetically relevant conformers. The B3LYP energetic ordering varies slightly but the barriers are very similar. Therefore we expect a similar relaxation behaviour. The other tested functionals also behave similarly as they did for 0-M as can be seen in the ESI† (Table S15). The assignment procedure was analogous to that of 0-M, where 6 conformers were assigned in total (see Fig. S15 ESI†).

A surprisingly large and non-monotonic energetical preference is observed for diol hydrogen bonds pointing away from or towards a fully substituted carbon site (0-MM, M-MM, MM-MM) for both hybrid functionals. While this isomerism is absent for MM-MM, it prefers the direction towards the MM site by about 1.5 (for 0-MM) or even 2.3 kJ mol⁻¹ (for M-MM). In case of 0-M the 0 site is energetically favoured by 0.2 kJ mol⁻¹, instead.

4.4 Closing the training phase

With the new assignments correlation patterns can be found for all possible degrees of substitution and the analysis from the previous section can be repeated for the new cases. The results for B3LYP and PBE0 are shown in Fig. 6 and the results for BP86 and PBE can be found in the ESI† (Fig. S3). Dedicated fits for 0-M and M-MM as the new substitution class representatives are provided and their standard deviation is even smaller than for the previous substitution classes. To simplify the comparison only data points from the redundant class members rM-M and 0-MM are shown. In case of B3LYP the previous trend of a more positive a2 with an increasing degree of substitution continues. Both 0-M and M-MM fit nicely in between the 0-0/t6-6 and t6-6/MM-MM pairs, respectively. The resulting h from the combined (all) fit approaches 1 even more than before. Separate fits for rM-M and 0-MM yield about 143.4 cm⁻¹, very close to the results for t6-6 at 144.2 cm⁻¹ and further corroborating the assumption that the same overall degree of substitution leads to a similar correlation within B3LYP. We thus include the smallest possible set of 5 molecules into our final training set and leave the two redundant n_D = 2 cases rM-M and 0-MM for the start of an extensive test phase.

Fig. 6 Correlation between the experimental and predicted band positions at the B3LYP (top) and PBE0 (bottom) level of computation only showing the data points for the test sets introduced in Section 4.3. Fits for each compound are shown as well as a fit for all bands. The standard error (σ) of each fitted parameter is also given. N specifies the number of bands included in the all fit.

A final note on the B3LYP performance in the training set refers to the uniformly increasing downshift from theory with n_D to match experiment. A simple correlation [small nu, Greek, tilde]_i = ω_i − (137 + 3n_D) cm⁻¹ (all(n_D)) appears to fit all substitution classes within error bars. This is reminiscent of, but more systematic than the trend in alcohols (mono-ols),⁴ where the average correction between primary and tertiary alcohols is close to 2 × 3 cm⁻¹ but secondary alcohols resemble tertiary systems. We will come back to this physically looking elementary global fit alternative, although it is likely that the apparent stepwise increase of anharmonicity with degree of substitution is an artifact of the functional⁴ and the actual anharmonicity of the OH group is likely larger, being artificially attenuated by the intrinsically too soft OH oscillator at B3LYP level for this basis set.

In case of PBE0 the rounded h value remains unaffected by the enlarged training set. The fits for 0-0 and 0-M are significantly separated from each other whereas t6-6, M-MM and MM-MM are clustered closely together. The relative indifference to the degree of substitution of PBE0 relative to B3LYP still prevails. The slightly lower errors of the PBE0 combined (all) fit in comparison to B3LYP indicate a more global character of PBE0, whereas the individual fits perform slightly worse. If one had to come up with a substitution-parameterised global PBE0 fit like in the B3LYP case, it would perhaps be [small nu, Greek, tilde]_i = 0.84ω_i + (411 + 3n₀) cm⁻¹ (all(n₀)), where n₀ is the number of unsubstituted CH₂-groups in the vicinal diol scaffold.

Both GGAs deviate substantially from h = 1 with about 0.66 in either case and small or insignificant changes with the extension of the training set (see Fig. S2 and S3 of the ESI†). The 0-0, 0-M and t6-6 fits are still significantly separated from each other for both functionals, whereas M-MM and MM-MM cluster together for both GGAs. The individual fits for rM-M (BP86: −1228.8 ± 1.8; PBE: −1221.5 ± 1.8) and 0-MM (BP86: −1228.8 ± 2.2; PBE: −1221.5 ± 2.1) are again very close together, as in the other investigated functionals. However rM-M and 0-MM do not agree well with t6-6 for the GGA functionals. Overall, the individual fits of the GGAs do worse than those for the hybrid functionals but the combined (all) fits still perform reasonably well globally.

After this minimalistic n_D-dependent training (5 species of different n_D) and initial testing (2 species of the same n_D) of harmonic theory-experiment correlations for vicinal diols of alkanes without any other functional groups or ring strain, it must be checked how well the models hold up when modest chemical complexity is introduced.

4.5 Other hydrogen contacts (to π-clouds and F)

To further gauge possible correlations we investigated systems involving π-systems as well as fluorination. As rather simple candidates we have chosen butenediol (0-V), phenyl-ethanediol (0-Ph) and trifluoro-propanediol (0-F). In comparison to mono-ols the introduction of the second OH-group already provides a first “perturbation” which may be amplified, even cooperatively or competitively, by vinyl and phenyl groups or fluorine atoms.

The conformational landscape of 0-V is the most complicated yet with 9 conformers within 5 kJ mol⁻¹. However, many barriers are sufficiently low that relaxation under jet conditions is expected. In Table S6 of the ESI† the different tested functionals are compared showing a considerable dependence upon zero point correction. The n_D = 1 correlation works quite well with the notable exception of the 0-V′ conformer, where larger deviations for the bound OH mode (O–H⋯O–H) can be found. This can be explained by the direct involvement of the π-system in the hydrogen bond arrangement exclusive to this conformer. Additionally, the two OH stretching vibrations are considerably less localised in comparison to all other conformers. In total 7 conformers were assigned.

In contrast to 0-V phenyl-ethanediol is less conformationally complex with 7 energetically relevant conformers. Additionally, the relative energies increase more quickly and an anti-periplanar orientation may become relevant. The PBE0 results of Lomas⁸⁸ (Table S7, ESI†) agree with the B3LYP/maTZ energetic order. As for 0-V some relaxation is expected. The n_D = 1 correlation again fits well to the experimental data with larger deviations for the Pha′ conformer. Apart from a poorer match for both OH stretching vibrations, this behaviour is analogous to that of 0-V′. The structural motif is the same for both conformers as can be seen in Fig. S25 and S26 in the ESI.†

The effect of trifluorination is tested with trifluoro-propanediol (0-F). Only 6 conformations are potentially energetically relevant with very different relative energies in comparison to 0-M and only two conformers are expected to relax significantly. This is also the first system where a primed conformer i.e. 0-F′ constitutes the global minimum, likely due to hydrogen bonding towards the fluorine atom. The GGAs yield the same energetic order as the hybrid functionals which can be seen in Table S5 in the ESI.† Other than for π systems, the involvement of fluorine in the hydrogen bond arrangement does not result in a worse wavenumber description with the n_D = 1 model. In comparison to 0-V′ and 0-Pha′ the OH stretching vibrations of 0-F′ are more localised. Overall 3 conformers were experimentally assigned.

In summary, the B3LYP model yields good predictions for both 0-V and 0-Ph except for cases where the vinyl or phenyl group is directly involved in the hydrogen bonding. For 0-F, such a restriction is not required. This could indicate that the nature of the additional hydrogen bond acceptor is the deciding factor. There seems to be a systematic theoretical underestimation of the shift due to π-interaction for 0-V′ and 0-Pha′, which could be extrapolated to related systems.⁹⁰

The assigned bands are plotted together with the derived fits in Fig. 7 for B3LYP and PBE0. They cluster satisfactorily around the n_D = 1 (0-M) or n_D = 2 (t6-6) correlation for B3LYP while in case of PBE0 due to the uniform nature of the fits no clear favourite can be declared. A B3LYP fit including only the three n_D = 1 derivatives with weak additional hydrogen contact options 0-V, 0-Ph and 0-F yields a2 = (142.6 ± 0.6) cm⁻¹. If the conformers with actual weak hydrogen bonds 0-V′ and 0-Pha′ are excluded, a2 = (141.8 ± 0.5) cm⁻¹ moves closer to the trained n_D = 1 correlation. This already indicates that in the presence of stronger hydrogen bonds the current correlations have to be modified, most likely due to deficiencies of hybrid functionals in spectroscopically describing such hydrogen bonds in a balanced way. The high substitution sensitivity for B3LYP, which likely is also a subtle and specific deficiency,⁴ is confirmed. Fig. S4 in the ESI† shows the less systematic results for BP86 and PBE.

Fig. 7 Correlation between the experimental and predicted band positions at the B3LYP (top) and PBE0 (bottom) level of computation only showing the data points for the compounds introduced in Section 4.5. Conformers directly involving the π-system or F atoms in their hydrogen bond arrangement are shown with rotated symbols and include prominent outliers. The standard error (σ) of each fitted parameter is also given. N specifies the number of bands included in the all fit.

4.6 Cyclic systems

Another structural variation we explored is ring size, starting from the nearly unstrained case of trans-cyclohexanediol which is part of the training set. We provide a systematic progression going from trans-cyclobutanediol (t4-4) via trans-cyclopentanediol (t5-5) and trans-cyclohexanediol (t6-6) to trans-cycloheptanediol (t7-7). cis-Cyclohexanediol (c6-6), where the equatorial-axial hydrogen bond arrangements may provide a further challenge for theory, is added.

Before discussing each system in more detail we briefly look at the evolution of the intramolecular hydrogen bond/contact length with increasing ring size. For the most stable unprimed species OH–O distances are predicted to be 3.34 Å for t4-4, 2.67 Å for t5-5, 2.31 Å for t6-6, 2.25 Å for c6-6 and 2.23 Å for t7-7 at the B3LYP/maTZ level. This is reflected in the larger experimental downshifts when the ring size is increased and also supports similar Raman signal spreads for t6-6, c6-6 and t7-7. For 0-0 a distance of 2.38 Å is computed (experimental estimate: 2.36 Ź⁵), only slightly higher than for t6-6. This contrasts their substantially different spectral positions of the bound oscillators (Δ[small nu, Greek, tilde] ≈ 10 cm⁻¹) clearly indicating the importance of n_D besides the hydrogen bond length when judging the general downshift of different systems. Note again that the term hydrogen bond is used here in a purely phenomenological way in the context of OH stretching wavenumber downshifts, whereas bond critical points considered by some researchers to indicate hydrogen bonding require shorter distances.⁹¹

The rather long hydrogen bond in case of t4-4 leads to a more complicated conformational landscape in comparison to t6-6, where conformers with nothing resembling a hydrogen bond become energetically competitive. These conformers are designated with a t (e.g. t4-4t). In total 6 conformers are energetically relevant and connected by low, but sometimes wide and thus more relaxation-resistant barriers. A comparison of all computational results can be found in Table S9 in the ESI.† The B3LYP n_D = 2 correlation deviates considerably from the experimental spectrum. However, the most intense bands can be matched and 4 conformers can be assigned. The difficulties of the model can be attributed to the strong ring strain found in cyclobutane. The assignment of one band remains unclear but likely belongs to t4-4′ with B3LYP significantly underestimating the shift between the two OH vibrations. Higher level electronic structure methods or vibrational treatment might resolve this issue.

For t5-5 di-axial conformations (indicated by a t) become energetically relevant for a total of 8 relevant conformers. Similar to t4-4 barriers are quite low and unlike for t6-6 conversion from di-axial to di-equatorial conformations is feasible. An energetic overview of all tested functionals can be found in Table S10 in the ESI.† The B3LYP correlation appears to fit well at a first glance. However the lack of spacing between signals makes a proper assignment difficult. VPT2⁹² calculations carried out with Gaussian 16 (Revision A.03)⁹³ allow to analyse the possible involvement of hot bands of the most stable conformer at a nozzle temperature of 360 K. A summary of these calculations can be found in Table S21 of the ESI.† In general an assignment of di-axial conformers is difficult and also brings the intensities and indirectly barriers into question in some instances. Therefore, we restrict ourselves to the assignment of the two most stable conformers of t5-5 and leave higher energy conformations to a future, perhaps microwave-assisted investigation.

Among all discussed systems in this section c6-6 is the conformationally simplest, with 4 relevant structures. In contrast to the other systems some significantly higher barriers exist. Relative energies can be found in Table S12 in the ESI† and include a comparison with the results of Lomas.⁸⁸ The correlation predicts the band positions quite well. This suggests that axial–equatorial hydrogen bonds do not provide a challenge for the model. To gauge the relaxation behaviour spectra at different nozzle distances (d_N) were recorded. Closer to the nozzle 3 conformers can be assigned while further away this drops to 2.

As for t6-6, di-axial conformations are not energetically relevant for t7-7. For some other conformations, barriers are not expected to be overcome under jet conditions. An energetic comparison of all tested methods for t7-7 can be found in Table S13 of the ESI.† The n_D = 2 B3LYP model works quite well, making a total of 5 assignments possible.

The assigned bands are plotted together with the derived fits in Fig. S5 in the ESI,† for B3LYP and PBE0. It immediately becomes apparent that t4-4 cannot be described as a regular n_D = 2 system. This is somewhat expected since the ring strain is significantly higher than for all other cyclic systems. For both B3LYP and PBE0 t4-4 behaves more like an n_D = 0 or n_D = 1 diol. For B3LYP, the t6-6 (n_D = 2) correlation fits well to the other cyclic systems, while PBE0 behaves rather uniform among the fits for more than one substituent. In Fig. S6 in the ESI† the plots for BP86 and PBE show no improvement with regard to t4-4, but some larger deviations for t7-7.

4.7 Fully substituted systems

Another possible challenge is provided by connecting the carbon substituents of pinacol on each side of the OH groups. We investigated compounds with cyclopentane bridges that exert additional strain on the backbone. Specifically we looked at 1-(1-hydroxy-1-methylethyl)-cyclopentanol (CP-MM) and [1,1′-bicyclopentyl]-1,1′-diol (CP–CP) which are expected to systematically increase the difficulty of predicting correct results.

CP-MM is among the few systems studied here where t conformers are energetically feasible. Furthermore, with 11 conformers within 5.2 kJ mol⁻¹ it is also the most complex diol. Two families of conformers (t and non t) can convert to some degree within themselves but not among each other. An overview of the energetics for all tested methods can be found in Table S17 of the ESI.† The B3LYP n_D = 4 model still performs reasonably well, making an assignment of 6 conformers possible. However, no t conformers are included in the assignment.

In case of CP–CP t conformers are no longer energetically feasible and the amount of conformers to be considered is reduced to 8. There are again two families that are relaxing separately (CP–CPc/CP–CPc′ and all other conformers). Similar to 0-F, primed species constitute the most stable conformers for CP–CP. An overview of the energetics for all tested methods can be found in Table S18 of the ESI.† The addition of another cyclopentyl moiety also significantly increases the deviations of the B3LYP n_D = 4 model from the experiment. However, similar to t4-4 one can still make sense of the spectrum with some assignments remaining tentative, but all conformers being assigned. Additionally, it appears likely that the energetics of the 2 most stable conformers are reversed.

The assigned bands are plotted together with the derived fits in Fig. S7 in the ESI† for B3LYP and PBE0. As the plots indicate, CP-MM and progressively CP–CP are downshifted relative to the n_D = 4 (MM-MM) fit. This is further quantified by fitting the CP–CP data points separately. The deviations for both hybrid functionals are very similar. Fig. S8 in the ESI† shows the results for the GGAs which behave in line with the hybrid functionals as can be seen when comparing the individual CP–CP fits. For all methods the same substitution trend is found, different from the rather universal behaviour of PBE0, BP86 and PBE for CP-free systems. Judging from these observations as well as those for t4-4 it appears that closing the cycle from one carbon atom to the other of the 0-0 basic diol unit leads to an increase in wavenumber (decrease of a2, whether it is positive for B3LYP or negative for the other functionals) while closing it at the same carbon atom leads to a decrease in wavenumber (increase in a2). It may be speculated that for trans-cyclopropane-1,2-diol a2 would decrease even further while it should increase for [1,1′-bicyclobutyl]-1,1′-diol. Apart from these ring strain effects, the diol OH stretching wavenumbers can be modeled surprisingly well with a simple linear model and even better with some explicit dependence on the degree of substitution for the hybrid functionals. This shall be analysed in more quantitative detail in the next section.

5 Combined analysis

5.1 Absolute band predictions

The deviation of the 107 predicted absolute wavenumbers from the experimental wavenumbers without ring strain for each tested functional are shown as boxplots in Fig. 8 and 9, split according to the fit that was used. These are ordered in terms of the degree of substitution (n_D) which is outlined in Fig. 1. The training sets themselves are also included in the analysis. In case of n_D = 0 and n_D = 3 no test set is available. The solid blue lines are the median and the dotted lines are the arithmetic average values. The box represents the 25th to the 75th percentile while the whiskers represent at most 1.5 times the interquartile range relative to the 25th and 75th respectively (i.e. about 2.7σ) with crosses being outliers. CP–CP (n_D = 4) and t4-4 (n_D = 2) are excluded from their respective categories and the all fit since they behave considerably different from what their substitution pattern would suggest. All other diols are included in the appropriate n_D category, even if some like CP-MM or 0-Ph start to show systematic deviations.

Fig. 8 Boxplots indicating the deviation of the predicted absolute wavenumbers of the fits, depending on the degree of substitution (n_D), at the B3LYP/maTZ (top) and PBE0/maTZ (bottom) level from the experimental ones. N indicates the amount of datapoints included in the analysis. Positive values indicate overestimation and negative values underestimation relative to the experimental value. The solid blue lines is the median and the dotted line the arithmetic average values.

Fig. 9 Boxplots indicating the deviation of the predicted absolute wavenumbers of the fits, depending on the degree of substitution (n_D), at the BP86/maTZ (top) and PBE/maTZ (bottom) level from the experimental ones. N indicates the amount of datapoints included in the analysis. Positive values indicate overestimation and negative values underestimation relative to the experimental value. The solid blue lines are the median and the dotted line the arithmetic average values.

In Fig. 8 the hybrid functionals are compared. As was previously alluded to in Section 4.2 PBE0 is less dependent upon the substitution patterns which can also be seen from the all fit boxplot. The individual fits for each degree of substitution (relevant for conformational assignment) show a smaller deviation from the experimental results for B3LYP whereas the global fit performs better in case of PBE0. For all fits except n_D = 4 the median centers around 0 cm⁻¹, showing no clear trend for over- or underestimation. In case of the n_D = 4 substitution a general trend for both functionals towards overestimation can be found as indicated by the median being around +2.5 cm⁻¹. Fig. 8 also shows the pattern specific all fits (all(n_D) and all(n₀)) as introduced in Section 4.4. In case of B3LYP the median increases slightly while the spread decreases substantially. In case of PBE0 the median decreases slightly while the spread does not significantly change. This confirms the substitution dependence of B3LYP, whereas PBE0 behaves largely independent of the degree of substitution.

Fig. 9 shows the behaviour of the two tested GGAs. Both functionals perform similarly and significantly worse than in particular B3LYP for substitution-dependent fits. For the global fit, a somewhat opposite trend may be seen despite strongly unphysical GGA parameters, but PBE0 still performs best. The performance contrast between the combined (all) fit and the substitution specific ones for B3LYP further emphasises its unique behaviour in comparison to the GGAs, but there are also qualitative similarities (overestimation for n_D = 4,1, underestimation for n_D = 2). Overall, the global fit for BP86 and PBE could still be used for assignment purposes in cases where signals are well separated. However, a good substitution-dependent fit is a substantial assignment aid within a given diol or a class of related diols.

5.2 Hydrogen bond shifts

Since reliable calculated anharmonic band positions are often not available, relative harmonic hydrogen bond shifts tend to be used instead under the assumption that anharmonic effects will at least partially compensate each other. This approach should work best when looking at the shift between the acceptor OH mode and the donor OH mode of each conformer individually since the anharmonic effects should be the most similar in these instances, given the weakness of the hydrogen bond. This is illustrated for the tested hybrid functionals in Fig. 10 and for the GGAs in Fig. 11 as a function of n_D with separate treatment of t4-4 and CP–CP (but inclusion in the all fit). The B3LYP predictions fit quite well for all n_D while PBE0 overestimates the shifts throughout. However, for both of them the overestimation increases with n_D. A systematically increasing overestimation with n_D is common to both functionals and could be corrected for more reliable shift predictions. For PBE0, t4-4 is a clear exception, where the difference is shifted even less than 0-0 (n_D = 0).

Fig. 10 Boxplots indicating the deviation of the difference of the harmonic free OH mode and the bound OH mode at the B3LYP/maTZ (top) and PBE0/maTZ (bottom) level of computation relative to the experimental ones, depending on the degree of substitution (n_D). N indicates the amount of datapoints included in the analysis. Positive values indicate overestimation and negative values underestimation relative to the experimental value. The solid blue lines are the median and the dotted line the arithmetic average.

Fig. 11 Boxplots indicating the deviation of the difference of the harmonic free OH mode and the bound OH mode at the BP86/maTZ (top) and PBE/maTZ (bottom) level of computation relative to the experimental ones, depending on the degree of substitution (n_D). N indicates the amount of datapoints included in the analysis. Positive values indicate overestimation and negative values underestimation relative to the experimental value. A solid blue line marks the median and a dotted line the arithmetic average.

As can be seen from Fig. 11, the deviations for the GGAs are much larger with a broader spread than for the hybrid functionals. Both behave very similar to each other. A general trend towards overestimation with an increase of the degree of substitution can again be observed. Abberations for CP–CP and t4-4 are reminiscent of those for PBE0.

The average errors for the shifts between free and bound OH stretching fundamentals should be compared to the experimental median (43 cm⁻¹) and extreme values (0–81 cm⁻¹) for this shift in all assigned cases. From this perspective, the GGA performance is not very satisfactory. A normalised error evaluation based on the median absolute deviation (MAD) and the mean absolute error (MAE) can be found in the ESI† (Fig. S12), which further highlights this fact. Regular MAD and MAE variants can be found in Fig. S11 of the ESI.†

5.3 Behaviour of conformational families

Besides the degree of substitution one can also differentiate between the primed (M′) and unprimed (M) conformer families. These signals can be even further divided into hydrogen bond donors and acceptors. This is illustrated for all measured compounds in Fig. 12. Here the experimental band positions are plotted against the computed B3LYP, PBE0 and PBE results. BP86 is not shown for simplicity since it behaves very similar to PBE. Separate plots of all functionals can found in the ESI† (Fig. S9 and S10). In terms of wavenumber spread, the M and M′ families cover about the same range. The strongly downshifted signal at 3575 cm⁻¹ (experimental band position) is caused by conformer 0-F′ where a fluorine atom is directly involved in the hydrogen bond arrangement. The unusually high M′ donor band at 3654 cm⁻¹ is caused by t4-4′ with its loose hydrogen bond/contact. Furthermore, the M bands around 3690 cm⁻¹ are all caused by substances with a low degree of substitution i.e. 0-0, 0-M, 0-F, 0-F, 0-Ph with the notable exception of 0-MM. There is also a gap between the high frequency modes and the next signals below 3675 cm⁻¹. 0-MM also causes a primed band (3667 cm⁻¹) that is shifted to significantly higher wavenumbers than is generally the case. However a clear trend emerges where primed species exhibit signals at lower wavenumbers. This is reminiscent of the behaviour that can be found for the gauche/trans isomerism of mono-ols where gauche isomers, comparable to primed conformers, are shifted towards lower wavenumbers in case of primary alcohols although this trend does not persist for secondary and tertiary alcohols.⁴ Furthermore, the division between donors and acceptors clearly indicates that M′ conformers are better hydrogen bond acceptors. Additionally, a gap in the unprimed signals can be found roughly between 3640 cm⁻¹ and 3650 cm⁻¹ (experimental) which is exclusively covered by primed conformers. Both gaps persist for all tested functionals (see Fig. S10 for BP86 in the ESI†) and it remains unclear whether this is a universal diol property or just specific to the diols studied in this paper.

Fig. 12 Overview of the primed hydrogen bond donor (green) and acceptor (blue) bands as well as the corresponding unprimed donors (black) and acceptors (blue) of all measured compounds and the correlation of their experimental band positions relative to the DFT predictions. N indicates the total number of bands for each sub class. The numbers (#) on the lines correspond to functions of the form ω/cm⁻¹ + #. Points between light blue lines correspond to PBE predictions, those between grey lines to B3LYP and those between brown lines to PBE0.

The plot illustrates that h is close to the ideal value of 1 for B3LYP while the other functionals suggest values lower than 1, with PBE0 still being somewhat close. It also indicates an individual fitting of each of the four classes. This is illustrated in Fig. S6 and S7 of the ESI.† One could also think of mixing the B3LYP and PBE0 results with similar weights, to obtain the best overall correlation between theory and experiment and at the same time rather physical h and a2 values.

5.4 Transferability to oligomers

Lastly, we would like to emphasise the limited transferability of the derived monomer correlations to diol oligomers, where moderately strong hydrogen bonds become possible. For example, if one applies the B3LYP n_D = 0 fit to the most stable 0-0 dimer (4 intermolecular hydrogen bonds, S₄ symmetric) one obtains 3419 cm⁻¹ (A symmetry), 3452 cm⁻¹ (E symmetry) and 3493 cm⁻¹ (B symmetry). In comparison to the experiment (A: 3444 cm⁻¹, E: 3475 cm⁻¹, B: 3513 cm⁻¹)^12,13 the fit underestimates the band positions significantly. The deviation increases with decreasing wavenumber, such that the characteristic vibrational exciton splitting pattern between the three modes is exaggerated by about 7%. For GGA functionals like BP86, the extrapolation is about 40% more distortive. Similar, slightly attenuated trends can be found for the structurally related most stable dimer of t6-6 (n_D = 2). A maximum deviation of 22 cm⁻¹ for B3LYP and 30 cm⁻¹ for BP86 from the experimental results (A: 3416 cm⁻¹, E: 3448 cm⁻¹, B: 3493 cm^−1 13) is observed. For liquid diol hydrogen bonded dimer motifs, the deviations are likely larger.⁹⁴ The systematic substitution dependence (n_D = 0 to n_D = 2) observed for B3LYP persists in the most stable dimer. While these findings confirm that the presented correlations should not be extrapolated, they also indicate significant potential for a refined DFT-based model which includes stronger hydrogen bonds.

5.5 Lessons learned for DFT functionals describing weak OH⋯O hydrogen bonds

Dispersion corrected DFT functionals provide sufficiently accurate energy sequences and barriers for the assignment of the vicinal diol spectra, although the tested GGA functionals systematically overstabilise primed conformations. Given such a theory-assisted assignment, the functionals can be further rated in their ability to predict the subtly hydrogen bond-affected (anharmonic) OH stretching wavenumbers based on the harmonic approximation. This requires scaling and shifting parameters due to the onset of hydrogen bonding, other than for simple alcohols, where either scaling or shifting is sufficient.⁴ For some functionals, parameterising the alkyl substitution degree (but not pattern) improves the correlation between experiment and DFT prediction, although there is no evidence for a dominant anharmonic origin for this. Most importantly, hybrid functionals do not only yield more physical values for the best scaling and shifting parameters than GGA functionals, but they also perform better in describing absolute and relative experimental wavenumbers. PBE0 does so in a global fit, whereas B3LYP shows the best performance after including a dependence on substitution degree and thus within a given family of diols and their conformations. This rationalises the popularity and success of B3LYP-D3 in the vibrational spectroscopy of flexible molecules with weak hydrogen bonds and the experimental database developed in the present work may allow to identify even superior computational approaches for this purpose.

6 Conclusions

The present work perhaps provides the largest experimental database of weak and distant OH⋯OH gas phase hydrogen bonding signatures in the OH stretching fundamental range. It shows how different density functionals cope with the onset of hydrogen bonding in the harmonic approximation. While a poor performance might have been blamed on a strong variation in anharmonicity relative to an unbound OH oscillator before our work, it now more likely indicates a fundamental electronic structure deficiency in quantitatively describing the onset of hydrogen bonding. We characterise a large set of different systems with increasing complexity that can be used to test higher levels of computation than the ones presented here. Among the tested functionals B3LYP performs best, followed by PBE0, while two popular GGAs perform worse to a similar extent in terms of their derived correlations. In cases of strongly separated bands BP86 and PBE could still be used for assignment purposes, but PBE0 is superior and for conformational assignments within a given diol, B3LYP is unmatched. This is because the previously established trend for a significant dependence upon the degree of substitution of B3LYP for mono-ols⁴ is confirmed for the studied diols and invites substitution-specific correlations with systematic error cancellation. For these correlations, the total degree of substitution is the deciding factor while the actual substitution pattern can differ, i.e. a primary–tertiary substitution can be treated together with a secondary–secondary one.

In case of π and F hydrogen contacts, discussed in Section 4.5, the derived correlation for B3LYP still works sufficiently well, unless a π system cooperatively enhances the hydrogen bond. It is rewarding that the best slope of the linear experiment-theory correlation is very close to 1 for B3LYP and the offset qualitatively corresponds to the expected diagonal anharmonicity, whereas this is not the case for PBE0, PBE and BP86. On the other hand, the latter three functionals give offsets which depend less systematically on substitution (cf.Fig. 5 and Fig. S2 (ESI†), Fig. 8 and 9), which probably corresponds to slightly more physical behaviour.⁷⁸

All tested functionals follow a trend where a cyclic connection of one carbon atom to the other of the ethane-1,2-diol subunit results in an excessive increase of the wavenumber once ring sizes as small as cyclobutane are reached. Additionally, closing the ring on the same carbon atom with some ring strain leads to a progressive decrease of the OH stretching wavenumber relative to the best fits for open systems (cf. Fig. S7 and S8 ESI†). For all functionals a trend towards overestimation of intramolecular splittings induced by the weak hydrogen bond can be found with an increase of the degree of substitution, and also with the shortness of the intramolecular hydrogen bond. B3LYP performs best, followed by PBE0, while GGAs significantly overestimate such splittings (cf.Fig. 10 and 11), probably due to delocalisation error.⁹⁵

The overall good performance of B3LYP with the compelling multiplicative scaling factor h of 1 and a systematically substitution dependent anharmonicity correction a2 in eqn (1) should not be overinterpreted in terms of physical content, because the diagonal anharmonicity effects are likely larger and more uniform.^4,78 More physical a2 values can be obtained by fixing h at 1.01, leading to an all(n_D) fit of the form [small nu, Greek, tilde]_i = 1.01ω_i − (175 + 3n_D) cm⁻¹. This is also in line with small expected off-diagonal anharmonicity contributions for alcohols.^4,79 In the presence of ring strain, further systematic correction factors would have to be included. This simple formula is close to the best interpolation of the experimental data and at the same time semiquantitatively encodes the two remaining B3LYP deficiencies, i.e. the need to upscale the somewhat too soft computed harmonic frequencies by up to 1% and to make the (now reasonable) anharmonic correction somewhat too dependent on the degree of substitution. To illustrate the correlation between harmonic and anharmonic deficiencies, different fits with set h values can be found in the ESI† (Table S40). To underscore that the specific numbers depend on the basis set without changing the essential conclusions, we also include the h = 1.01 and h = 1.00 fits for the Gaussian16 B3LYP calculations using the may-cc-pVTZ^96–98 basis set as used in ref. 4. In this case, an all(n_D) fit of the form [small nu, Greek, tilde]_i = 1.01ω_i − (198 + 2n_D) cm⁻¹ or [small nu, Greek, tilde]_i = 1.00ω_i − (160 + 2n_D) cm⁻¹ would be more appropriate, indicating that the B3LYP deficiencies can be somewhat attenuated by the choice of a different basis set.

For practical purposes, a vibrational spectroscopist who wants to quickly predict OH stretching fundamentals for a single new vicinal diol is well advised to pick a diol with the same degree (and kind) of alkyl substitution from our database, do a B3LYP-D3 difference calculation between the new and the reference molecule and add this difference to the experimental value of the reference system.

Evidently, the main goal of this work is more far-reaching in different directions. Our deposited experimental spectra and structure files (ref. 99 and 100 and ESI†) help to expand the experimental benchmark sets for alcohols⁴ and provide a strong basis for the future testing of anharmonic frequency calculations as well as different underlying electronic structure methods for OH groups engaged in weak hydrogen bond like environments. It remains to be seen whether similarly successful and simple correlations between harmonic theory and experiment can be found for medium strength hydrogen bonds, where the DFT delocalisation error⁹⁵ grows, but anharmonic effects also become more important and perhaps less cancelling. It may be necessary to move to wavefunction-based methods and adequate anharmonic treatments to disentangle these two contributions.^5,78,79 Another avenue may be the improvement of conformational abundance predictions by adding single point energies from higher level electronic structure methods to the numerous DFT-predicted minima and saddle points reported in this work. However, the illustrated complexity of the relaxation processes in the context of non-equilibrium supersonic jet preparation of vicinal diols likely shifts that further into the future and will profit from further microwave characterisation of the cold conformations.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455 and 405832858 for computational resources. We thank Franz Kollipost, Hendrik Schröder, Daniel Falkowski and Axel Binning for preliminary IR work on the conformations of propane-1,2-diol and Robert Medel for valuable discussions.

References

1. A. Ben Faleh, S. Warnke and T. R. Rizzo, Anal. Chem., 2019, 91, 4876–4882.
2. C. J. Gray, L. G. Migas, P. E. Barran, K. Pagel, P. H. Seeberger, C. E. Eyers, G.-J. Boons, N. L. B. Pohl, I. Compagnon, G. Widmalm and S. L. Flitsch, J. Am. Chem. Soc., 2019, 141, 14463–14479.
3. C. Pavan, R. Santalucia, R. Leinardi, M. Fabbiani, Y. Yakoub, F. Uwambayinema, P. Ugliengo, M. Tomatis, G. Martra, F. Turci, D. Lison and B. Fubini, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27836–27846.
4. R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2021, 23, 5629–5643.
5. M. Heger, M. A. Suhm and R. A. Mata, J. Chem. Phys., 2014, 141, 101105.
6. D. Zimmermann, T. Häber, H. Schaal and M. A. Suhm, Mol. Phys., 2001, 99, 413–425.
7. R. A. Klein, J. Comput. Chem., 2002, 23, 585–599.
8. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266.
9. J. van der Maas and E. Lutz, Spectrochim. Acta, Part A, 1974, 30, 2005–2019.
10. F. Singelenberg and J. Van Der Maas, J. Mol. Struct., 1991, 243, 111–122.
11. B. T. Lutz and J. H. van der Maas, J. Mol. Struct., 1997, 436–437, 213–231.
12. F. Kollipost, K. E. Otto and M. A. Suhm, Angew. Chem., Int. Ed., 2016, 55, 4591–4595.
13. B. Hartwig, M. Lange, A. Poblotzki, R. Medel, A. Zehnacker and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 1122–1136 . Note that on page 1129, in the expression …barrier for het3 certainly prevents…, het3 should be replaced by het3*.
14. W. Caminati and G. Corbelli, J. Mol. Spectrosc., 1981, 90, 572–578.
15. P.-E. Kristiansen, K.-M. Marstokk, H. Møllendal, V. D. Parker and L. Niinistö, Acta Chem. Scand., 1987, 41a, 403–414.
16. W. Caminati, J. Mol. Spectrosc., 1981, 86, 193–201.
17. T. J. Lockley, J. I. Hearn, A. K. King and B. J. Howard, J. Mol. Struct., 2002, 612, 199–206.
18. A. Maris, L. B. Favero, A. Vigorito, C. Calabrese, L. Evangelisti and S. Melandri, J. Mol. Struct., 2020, 1205, 127643.
19. J. Paul, I. Hearn and B. J. Howard, Mol. Phys., 2007, 105, 825–839.
20. M. Onda, K. Hasunuma, T. Hashimoto and I. Yamaguchi, J. Mol. Struct., 1987, 159, 243–248.
21. W. Caminati, S. Di Bernardo, L. Schäfer, S. Q. Kulp-Newton and K. Siam, J. Mol. Struct., 1990, 240, 263–274.
22. D. Christen, L. Coudert, J. Larsson and D. Cremer, J. Mol. Spectrosc., 2001, 205, 185–196.
23. D. Christen and H. S. P. Müller, Phys. Chem. Chem. Phys., 2003, 5, 3600–3605.
24. H. S. Müller and D. Christen, J. Mol. Spectrosc., 2004, 228, 298–307.
25. L. P. Kuhn, J. Am. Chem. Soc., 1952, 74, 2492–2499.
26. E. L. Eliel and C. Pillar, J. Am. Chem. Soc., 1955, 77, 3600–3604.
27. J. Brimacombe, A. Foster, M. Stacey and D. Whiffen, Tetrahedron, 1958, 4, 351–360.
28. A. Foster, A. Haines and M. Stacey, Tetrahedron, 1961, 16, 177–184.
29. P. Krueger and H. Mettee, J. Mol. Spectrosc., 1965, 18, 131–140.
30. P. Buckley and P. A. Giguère, Can. J. Chem., 1967, 45, 397–407.
31. C. W. Davey, E. L. McGinnis, J. M. McKeown (née Chancellor), G. D. Meakins, M. W. Pemberton and R. N. Young, J. Chem. Soc. C, 1968, 2674–2682.
32. J. Bacon, J. van der Maas, J. Dixon, W. George and P. McIntyre, Spectrochim. Acta, Part A, 1989, 45, 1313–1318.
33. F. Singelenberg and J. Van Der Maas, J. Mol. Struct., 1990, 240, 213–223.
34. K. Yamamoto, Y. Nakao, Y. Kyogoku and H. Sugeta, J. Mol. Struct., 1991, 242, 75–86.
35. M. Dahlqvist, M. Hotokka and M. Räsänen, Chem. Phys., 1998, 229, 137–147.
36. F. Wang and P. L. Polavarapu, J. Phys. Chem. A, 2001, 105, 6991–6997.
37. A. J. Lopes Jesus, M. T. S. Rosado, M. L. P. Leitão and J. S. Redinha, J. Phys. Chem. A, 2003, 107, 3891–3897.
38. M. Plass and A. Kolbe, Z. Phys. Chem., 2003, 217, 1085–1096.
39. A. J. Lock, J. J. Gilijamse, S. Woutersen and H. J. Bakker, J. Chem. Phys., 2004, 120, 2351–2358.
40. X. Ma and J. Wang, J. Phys. Chem. A, 2009, 113, 6070–6076.
41. M. Olschewski, J. Lindner and P. Vöhringer, Angew. Chem., Int. Ed., 2013, 52, 2602–2605.
42. A. Lopes Jesus and J. Redinha, J. Mol. Struct., 2014, 1067, 104–111.
43. P. Das, P. K. Das and E. Arunan, J. Phys. Chem. A, 2015, 119, 3710–3720.
44. L. Paoloni, G. Mazzeo, G. Longhi, S. Abbate, M. Fusè, J. Bloino and V. Barone, J. Phys. Chem. A, 2020, 124, 1011–1024.
45. H. Takeuchi and M. Tasumi, Chem. Phys., 1983, 77, 21–34.
46. C. G. Park and M. Tasumi, J. Phys. Chem., 1991, 95, 2757–2762.
47. A. J. Lopes Jesus, M. T. S. Rosado, I. Reva, R. Fausto, M. E. Eusébio and J. S. Redinha, J. Phys. Chem. A, 2006, 110, 4169–4179.
48. T. Forsting, H. C. Gottschalk, B. Hartwig, M. Mons and M. A. Suhm, Phys. Chem. Chem. Phys., 2017, 19, 10727–10737.
49. D. L. Howard, P. Jørgensen and H. G. Kjaergaard, J. Am. Chem. Soc., 2005, 127, 17096–17103.
50. D. L. Howard and H. G. Kjaergaard, J. Phys. Chem. A, 2006, 110, 10245–10250.
51. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
52. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
53. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
54. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
55. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
56. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
57. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
58. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
59. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
60. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
61. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
63. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
64. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406.
65. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
66. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
67. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
68. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
69. S. Reiling, J. Brickmann, M. Schlenkrich and P. A. Bopp, J. Comput. Chem., 1996, 17, 133–147.
70. F. Jensen, J. Chem. Phys., 2017, 146, 184109.
71. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
72. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
73. M. Gawrilow and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 15303–15311.
74. V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945.
75. R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150.
76. J. S. Lomas, L. Joubert and F. Maurel, Magn. Reson. Chem., 2016, 54, 805–814.
77. D. A. Partridge, J. Chem. Educ., 1980, 57, 508.
78. F. Kollipost, K. Papendorf, Y.-F. Lee, Y.-P. Lee and M. A. Suhm, Phys. Chem. Chem. Phys., 2014, 16, 15948–15956.
79. E. Vogt, P. Bertran Valls and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 932–942.
80. F. Lovas, D. Plusquellic, B. H. Pate, J. L. Neill, M. T. Muckle and A. J. Remijan, J. Mol. Spectrosc., 2009, 257, 82–93.
81. B. E. Arenas, S. Gruet, A. L. Steber and M. Schnell, J. Mol. Spectrosc., 2017, 337, 9–16.
82. F. Kollipost, PhD thesis, Georg-August-Universität Göttingen, Germany, 2015, http://hdl.handle.net/11858/00-1735-0000-0023-9644-9.
83. J.-B. Bossa, M. H. Ordu, H. S. P. Müller, F. Lewen and S. Schlemmer, Astron. Astrophys., 2014, 570, A12.
84. O. Zakharenko, J.-B. Bossa, F. Lewen, S. Schlemmer and H. Müller, J. Mol. Spectrosc., 2017, 333, 23–26.
85. C. Favre, L. Pagani, P. F. Goldsmith, E. A. Bergin, M. Carvajal, I. Kleiner, G. Melnick and R. Snell, Astron. Astrophys., 2017, 604, L2.
86. M. Melosso, L. Dore, F. Tamassia, C. L. Brogan, T. R. Hunter and B. A. McGuire, J. Phys. Chem. A, 2020, 124, 240–246.
87. J. S. Lomas, F. Maurel and A. Adenier, J. Phys. Org. Chem., 2011, 24, 798–808.
88. J. S. Lomas, Magn. Reson. Chem., 2013, 51, 32–41.
89. S. Vázquez, R. A. Mosquera, M. A. Rios and C. Van Alsenoy, THEOCHEM, 1989, 184, 323–342.
90. R. Medel and M. A. Suhm, Phys. Chem. Chem. Phys., 2020, 22, 25538–25551.
91. R. A. Klein, Chem. Phys. Lett., 2006, 429, 633–637.
92. V. Barone, J. Chem. Phys., 2005, 122, 014108.
93. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016.
94. A. Jindal, V. Arunachalam and S. Vasudevan, J. Phys. Chem. B, 2021, 125, 5909–5919.
95. A. J. A. Price, K. R. Bryenton and E. R. Johnson, J. Chem. Phys., 2021, 154, 230902.
96. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
97. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
98. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034.
99. B. Hartwig and M. A. Suhm, Göttingen Research Online/Data, version V1, 2021 DOI:10.25625/CVAGRL.
100. B. Hartwig and M. A. Suhm, Göttingen Research Online/Data, version V1, 2021 DOI:10.25625/VJF95K.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details as well as the raw spectra (http://10.25625/CVAGRL), relative electronic and zero point corrected energies, additional plots, assignment arguments and results as well as structures including the xyz files (http://10.25625/VJF95K) are provided. See DOI: 10.1039/d1cp03367k

---