A nanosecond-resolved atomic hydrogen magnetometer†
Received
12th July 2021
, Accepted 12th September 2021
First published on 15th September 2021
Abstract
We introduce a novel and sensitive ns-resolved atomic magnetometer, which is at least three orders of magnitude faster than conventional magnetometers. We use the magnetic field dependence of the hyperfine beating of high-density spin-polarized H atoms, produced from the rapid photodissociation of HCl gas with sub-ns laser pulses and measured with a pick-up coil, to demonstrate ns-resolved magnetometry, and project sensitivity of a few nT for a spin-projection-limited sensor with 10 nl measurement volume after 1 ns measurement time. The magnetometer will allow ultrafast continuous B-field measurements in many fields, including spin chemistry, spin physics, and plasma physics.
Introduction
Sensitive detection of magnetic fields plays an important role in several fields, including biomedicine, materials science, security screening, geophysical and space surveys,1 as well as fundamental physics measurements, such as axion searches.2 In addition to the requirement for high sensitivity, numerous applications demand magnetic field detection with high temporal resolution. For instance, ultrafast magnetometry can be used as a sensitive probe of the pathways and kinetics of chemical reactions involving the production of electron or nuclear spin polarization, such as in photo-chemically induced dynamic nuclear polarization (photo-CIDNP).3–6 Similarly, studies of magnetodynamics can shed light on dynamical processes in magnetic materials7,8 and plasmas,9 enabling the development of new technologies. For imaging purposes or for mapping the magnetic field gradients, an important quality is the length scale of the magnetometer, as, in general, small-sized sensors allow for high spatial resolution.
A plethora of magnetometers has been developed to address the challenges in magnetic field sensing (see for example ref. 10 and references therein). Atomic magnetometers based on optically polarized alkali-metal atoms have realized the highest sensitivities,11 albeit at low bandwidths, typically up to a few tenths of kHz.12 Superconducting quantum interference devices (SQUIDs) have demonstrated similar sensitivities. Although in principle their frequency response can extend up to a few GHz, practical considerations related to the electronic circuitry for the signal readout reduce their bandwidth to the MHz range.13 Inductive-coil sensors feature high detection-bandwidth and broad applicability to different spin species and environments, but they present relatively low sensitivity compared with other state-of-the-art magnetometers (see however ref. 14 for an ultrasensitive, quantum limited inductive sensor). Optical approaches based on the Kerr effect have realized magnetometry in the picosecond temporal regime; nevertheless, their inherent sensitivity is limited and they are mainly used to probe rather large fields from magnetic materials.7,15 Nitrogen-vacancy defects in diamond offer an attractive platform for high spatial resolution.16 Yet, the demonstrated sensitivity does not rival alkali-atomic magnetometers or SQUIDs and elaborate dynamic decoupling techniques are required to realize broadband magnetometry.
Here, we present a novel atomic hydrogen magnetometer that can measure magnetic fields with high sensitivity and nanosecond time resolution. The sensitive detection results from realizing large spin densities, many orders of magnitude higher than conventional alkali-metal atomic sensors, while the temporal resolution derives from performing magnetometry at the hyperfine coherences of hydrogen (hyperfine frequency of 1.42 GHz and 0.327 GHz in H and D, respectively). The proposed magnetometer operates at room temperature, is technically simple to use and can be adjusted to sense sub-micrometer length-scales.
Principle of operation
High density spin-polarized hydrogen (SPH) is produced by photodissociating hydrohalide gas with a circularly-polarized UV laser pulse, by exciting a well-defined dissociative electronic state of the molecule (see ref. 17–19 for details). In hydrohalide photolysis, the fragments acquire a spin-orientation which is correlated to the spin of the dissociating photon, and their final polarization is limited by the dissociation path and by the random direction of the hydrohalide molecular bond with respect to the laser propagation direction. Under readily achieved experimental conditions concerning the laser wavelength and intensity, the photodissociation probability can be near unity, thereby the density of the atomic fragments can be made similar to the initial density of the parent molecule. With this process SPH densities of 1019 cm−3 and up to 40% polarization have been demonstrated for isotropic molecular bonds,18,20,21 whereas up to 100% is possible if the bonds are aligned along the photodissociation-laser polarization axis.22
Crucially for the operation of the magnetometer, photolysis is predominantly an electronic process occurring within sub-picosecond time-scales, during which the nuclear spin degrees of freedom are effectively frozen.20 For hydrogen halides, photodissociation with a sufficiently fast laser pulse typically generates fragments with electronically polarized spins, while the nuclear spins remain in their thermal unpolarized state.
Immediately after the photodissociation (assuming that the HCl bonds have been aligned parallel to the photodissociation polarization direction, and complete electron polarization), half of the generated H atoms are in the state
| |  | (1) |
and half of the polarized atoms are in the state
| |  | (2) |
Here, F is the total spin (sum electronic and nuclear spin) quantum number, ms, mI and mF are respectively the electronic, nuclear and total spin projection along the quantization axis, the subscripts u and c refer to the uncoupled and coupled angular momentum basis respectively, σ is the helicity of the photons (+1 or −1 for σ+ and σ− respectively), and the quantization axis is taken to be along the laser propagation direction. Unlike |ψ0〉, the state |ψ1〉 is not an eigenstate of the hyperfine interaction. Atoms prepared initially in |ψ1〉 experience hyperfine quantum beats, causing the electron and nucleus to exchange spin at the hyperfine frequency. In the absence of a magnetic field this frequency corresponds to the 21 cm hydrogen line at f0 ≈ 1.42 GHz.
A magnetic field parallel to the dissociation axis does not affect to first order the hyperfine coherences resulting from the photodissociation |0, 0〉c ↔ |1, 0〉c. However, the presence of a magnetic field perpendicular to the pumping direction modifies the hyperfine oscillation and induces a net precession of the spins. Taking the direction of magnetic field as the quantization axis, the evolution of |ψ1〉 can be written in the form (ignoring a global phase factor and small amplitude terms of order γHB/ω0):
| |  | (3) |
where
t is the time after the photodissociating pulse, the apostrophe distinguishes the quantization axis and the angular frequencies are given by the Breit–Rabi formula:
| |  | (4) |
In the above equation,
ω0 = 2π
f0,
γH ≈ 2π × 1.4 MHz G
−1 is the gyromagnetic ratio of total angular momentum for atomic H,
B is the magnetic field, and we have ignored the small nuclear gyromagnetic Landé factor. Information about the magnetic field can be deduced by monitoring the hyperfine dynamical evolution of the electron spin. In the case of H this is most easily performed with an inductive pickup coil, which measures the time-dependent ensemble magnetization, determined to a good approximation by the hydrogen electron spin.
Spin decoherence in SPH limits the performance of the magnetometer. The spin decay mechanism originates from depolarizing collisions of H with the particles in the ensemble, which include the photofragments and their secondary side-products from chemical reactions, as well as the parent molecules in the case of partial photodissociation (see ref. 21 and references therein). The impact of collisions to spin-relaxation depends on the density, the conditions of photolysis, and the halide species and a corresponding optimization should be performed according to the requirements for magnetometry. This optimization may involve compromising the SPH density in order to achieve larger coherence times as discussed in ref. 21.
Experiment
Experimental setup
We performed an experiment with a DC magnetic field to demonstrate the magnetometer operation. The experimental setup is based on the one described in ref. 20. Briefly, a circularly polarized 150 ps laser pulse at 213 nm was focused inside a cell filled with 2 bar of high purity (99.9%) HCl, as shown in Fig. 1a. A 4 mm long coil, 4.5 turns, radius of 1 mm and oriented with its axis along the laser pulse propagation, was employed to measure the time-dependent electron magnetization of the SPH atoms. The pickup coil signal was amplified by an RF amplifier and was recorded by a fast-sampling oscilloscope. The time-constant associated with the induction detector was much smaller than the sampling time, so that the recorded signal was directly proportional to the time derivative of the magnetic flux.
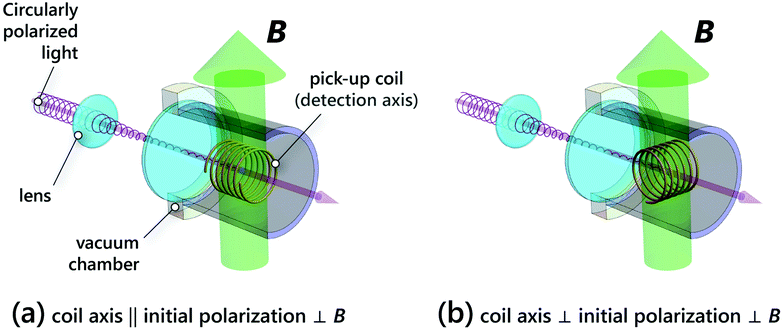 |
| | Fig. 1 (a) Experimental setup schematic for the proof of principle demonstration of the magnetometer. A 150 ps, circularly-polarized laser pulse (red arrow), is focused inside a high density HCl gas cell. A pickup inductive-coil, with its axis parallel to the pumping direction, monitors the ensemble magnetization, while a magnetic field (green arrow) perpendicular to the coil and pumping light is applied; (b) proposed configuration for sensitive detection of time varying magnetic fields. Compared to (a) the detection axis is perpendicular to both the magnetic field and the light pulse. | |
The pumping laser beam was weakly focused to a spot of approximately 100 μm in diameter, located at the center of the coil. For the energy of the laser pulse (3 mJ), the realized intensities were sufficient to dissociate only a small fraction (about 2%) of the HCl molecules inside the beam volume per pulse. Taking into account the HCl absorption cross section and the photodissociation efficiency we estimate an average SPH density of 1018 cm−3 over the coil volume.23 Even though this is about 2% of the parent molecule density, it is more than three orders of magnitude higher than the densities in alkali-metal atomic magnetometers.12 For this proof of principle experiment, we traded off SPH density for increased coherence times, as the spin-relaxation cross section for H–H and H–Cl collisions is much larger than that for H–HCl collisions.
We operated the magnetometer in an unshielded environment. This made the pick-up coil and the cables susceptible to electromagnetic interference, originating mainly from discharges in the laser unit. We filtered this noise by subtracting two consecutive measurements acquired with opposite spin orientations in the SPH ensemble. For this, the helicity of the dissociating laser pulse was reversed every laser shot, using a photoelastic modulator (PEM) and an appropriate electronic circuit to phase lock the low frequency laser emission rate with the higher PEM modulation frequency.23
A static transverse magnetic field was applied using two permanent round magnets (Neodymium grade N42, 10 mm diameter and 2 mm thickness) placed astride the measurement region with their magnetization vectors aligned. The magnets were attached on translation stages, which allowed us to control their separation. This way, a homogeneous, precisely tunable magnetic field, ranging from 10 G to 150 G was applied. A Hall probe was used to calibrate the magnetic field versus magnet separation at low fields, while at higher fields the field was estimated from extrapolation.
Results
The measured signals, averaged over 50 repetitions, and the corresponding Fourier transforms for various magnetic fields are shown in Fig. 2. The photodissociation pulse occurs at time t = 0. After a fast transient, which decays at sub-ns timescales, the oscillating signal reflects the H hyperfine coherences damped by collisions. For zero magnetic field (B = 0) a single frequency at f0 appears in the Fourier spectrum. A non-zero magnetic field, transverse to the pumping-axis, modifies the frequency of hyperfine coherence and two Fourier peaks appear in the signal, which can be found from eqn (4).
 |
| | Fig. 2 Measured signal in the time domain (left) and the corresponding amplitude of Fourier transform (right) for different values of magnetic fields. | |
Notice that the heights of the two Fourier peaks A+ and A− in Fig. 2, which correspond to the frequencies given by 4, become more unequal with larger B field, and their ratio is given by:
| | | A−/A+ = (ω−/ω+) × tan2(θ) | (5) |
Eqn (5) has two factors: the ratio of frequencies
ω−/
ω+, due to the frequency dependence of coil detection; and the tan
2(
θ) term, which is the ratio of the square of the projections of the initially prepared state onto the states of the system that beat at
ω− and
ω+. The angle
θ of the tan
2(
θ) term is given by tan(2
θ) = 1/
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif)
, where
B =
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif)
/
Bc, and
Bc = 50.7 mT is the critical field for H atoms.
24Eqn (5) then becomes:
| |  | (6) |
Note that for ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = 0, A−/A+ = 1, whereas when
= 0, A−/A+ = 1, whereas when ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) tends to infinity, the A− peak vanishes, and the ratio A−/A+ tends to 0.
tends to infinity, the A− peak vanishes, and the ratio A−/A+ tends to 0.
In Fig. 3 the measured frequencies are plotted versus the applied magnetic field as quantified from an independent calibration with the Hall probe. The peak frequencies were found using an algorithm which fits a Lorentzian curve to the three consecutive points with the highest amplitudes in the discrete Fourier transform.23 The agreement between the frequency peaks and the prediction of eqn (4) is excellent within the measurement resolution, demonstrating that the magnetic field can be estimated from the Fourier peaks. By repeating the measurement multiple times we estimate that the frequency statistical uncertainty (standard deviation) was around 40 kHz corresponding to approximately 30 mG sensitivity after 50 iterations. In this case, the sensitivity was limited by the poor resolution in Fourier transform, the electronic noise from an unoptimized electric circuitry and from discharge noise originating from pumping the photodissociating laser.
 |
| | Fig. 3 Measured hyperfine frequencies versus B, and predictions of eqn (2) (Δf1σ ≈ 40 kHz, smaller than the size of the points). | |
Extension to time-dependent magnetometry
The magnetometer that relies on the frequency content of Fourier power spectrum is not appropriate for characterizing a time-varying field. For such an estimation, the phase evolution of the signal should also be taken into account. In addition, high resolution detection requires first-order sensitivity to the magnetic field. The configuration that satisfies these conditions is shown in Fig. 1b: the dissociation/pumping axis, the magnetic field direction and the detection axis are all perpendicular to each other. With this scheme, the signal  (electromotive force in the detection coil) at time t after the optical pumping can be approximated to be (see 7 for details):
(electromotive force in the detection coil) at time t after the optical pumping can be approximated to be (see 7 for details):| |  | (7) |
where 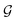 is a geometrical factor that relates the magnetic field from the spins to the flux in the region of the coil,
is a geometrical factor that relates the magnetic field from the spins to the flux in the region of the coil,  is the number of turns per unit length of the coil, μB is the Bohr magneton, NSPH the number of SPH atoms in the detection region, and T2 is the hyperfine coherence time. The above equation is an approximation in the limit where the magnetic field evolves much slower compared to the hyperfine frequency and when ω0 ≫ (1/T2, γHB). It also assumes an inductor detection time constant much shorter than the hyperfine period and neglects dipolar-interactions between the hydrogen spins. It can be seen that the information about the magnetic field appears as amplitude modulation of the carrier wave at the hyperfine frequency ω0. As a result, the evolution of magnetic fields at timescales longer than 1/ω0 should be faithfully captured with the proposed magnetometer as long as it is completed before significant spin-depolarization occurs.
is the number of turns per unit length of the coil, μB is the Bohr magneton, NSPH the number of SPH atoms in the detection region, and T2 is the hyperfine coherence time. The above equation is an approximation in the limit where the magnetic field evolves much slower compared to the hyperfine frequency and when ω0 ≫ (1/T2, γHB). It also assumes an inductor detection time constant much shorter than the hyperfine period and neglects dipolar-interactions between the hydrogen spins. It can be seen that the information about the magnetic field appears as amplitude modulation of the carrier wave at the hyperfine frequency ω0. As a result, the evolution of magnetic fields at timescales longer than 1/ω0 should be faithfully captured with the proposed magnetometer as long as it is completed before significant spin-depolarization occurs.
Simulations
In Fig. 4 we show the results of simulations for time-varying magnetic waveforms: (a) is for cosine waves at 1 MHz and 100 MHz, while (b) is for Gaussian magnetic pulses with durations (Gaussian RMS width) of 1 and 5 ns, centered at 30 ns after the pumping pulse. The same magnetic field amplitude (maximum value) was considered for all the cases. In all the simulations the depolarization time was taken to be 0.75 μs. The magnetic field was estimated by first demodulating the signal at frequency ω0 and then taking the time derivative of the demodulation output. For the demodulation we implemented a simple low pass filter, where the signal was multiplied by cos(ω0t) and the resultant was integrated over a single period 2π/f0. Subfigures (a) and (b) are plotted in the same (arbitrary) units for comparison. The response in the two cosine waves in (a) is similar despite a two orders of magnitude difference in frequencies. In (b) the retrieved Gaussian pulses (dotted blue lines) approximate well the actual Gaussian waveforms (red lines). In sub-figure (c), the response to a cosinusoidal magnetic field is plotted as a function of frequency. Here, the response is taken to be the maximum oscillation amplitude in the readout signal; in the examined frequency range, this maximum occurs at timescales much shorter than the decay time and is therefore not affected by the decay. The magnetometer bandwidth, defined as the frequency where the response has decreased by a factor of two, is approximately 450 MHz.
 |
| | Fig. 4 Numerical simulation assuming atomic spin decay time 0.75 μs, for the detection geometry in Fig. 1b. (a) B(t) = B0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πft), where B0 = 100 μG and f = 1 MHz (blue dashed line) or f = 100 MHz (red solid line). (b) cos(2πft), where B0 = 100 μG and f = 1 MHz (blue dashed line) or f = 100 MHz (red solid line). (b)  , where Δt = 1 ns and 5 ns, t0 = 30 ns and B0 = 100 μG. (c) Frequency response of the magnetometer (normalized to DC response). , where Δt = 1 ns and 5 ns, t0 = 30 ns and B0 = 100 μG. (c) Frequency response of the magnetometer (normalized to DC response). | |
Noise sources and sensitivity limit
The detection of magnetic fields is fundamentally limited by the spin-projection noise,11 originating from the Heisenberg uncertainty for spins. Considering the experimental setup shown in Fig. 1b, the effect of spin noise on the magnetometer depends on the magnetic waveform. We consider a magnetic field of the form:  , where B0 signifies the amplitude of magnetic field to be estimated from the magnetometer signal and
, where B0 signifies the amplitude of magnetic field to be estimated from the magnetometer signal and  is an arbitrary function of time t assumed to be known. By adopting a χ2 minimization, it can be shown (see 8) that the spin-projection noise limit for a single measurement run is given by:
is an arbitrary function of time t assumed to be known. By adopting a χ2 minimization, it can be shown (see 8) that the spin-projection noise limit for a single measurement run is given by:| |  | (8) |
where Tm is the measurement time after the photodissociation. For concreteness we consider the case of a cosinusoidal signal ( , where ω is the angular frequency) and the conditions described above: SPH density 1018 cm−3, measurement volume (100μm)2 × 1 mm = 10 nl and T2 ≈ 100 ns. Such a projection-noise-limited magnetometer presents sensitivity on the order of a few nanoTesla after measurement time of 1 ns. For Tm ∼ T2 the sensitivity is better than 200 pT per pulse; in this case, with a pulse repetition rate of 1 MHz, the projected sensitivity becomes better than
, where ω is the angular frequency) and the conditions described above: SPH density 1018 cm−3, measurement volume (100μm)2 × 1 mm = 10 nl and T2 ≈ 100 ns. Such a projection-noise-limited magnetometer presents sensitivity on the order of a few nanoTesla after measurement time of 1 ns. For Tm ∼ T2 the sensitivity is better than 200 pT per pulse; in this case, with a pulse repetition rate of 1 MHz, the projected sensitivity becomes better than  .
.
The magnetometer is also inflicted from thermal and quantum fluctuations in the detection coil and associated electric circuit. The impact of this noise source depends on the geometric arrangement of the spin-ensemble and the pick-up inductor. Furthermore, for non-spherical measurement volumes the dipolar interactions between the spins impair the magnetometer operation. We defer the consideration of these issues to a later study.
Outlook
The presented magnetometer is amenable for miniaturization. The measurement lengthscale, determined by the size of the photodissociation beam, can be readily adapted to the sub-micrometer region. Due to the high densities that can be achieved, the number of polarized atoms remains sufficient for high sensitivities even with such small measurement regions. Employing large spin-polarized density also relaxes the requirements on the induction coil. Unless high sensitivities are pursued or the measurement is performed from a very small region, moderate coil quality factor and room-temperature, standard electric circuitry should be adequate to detect the response of the polarized spins to the magnetic field. Another attractive feature is the large dynamic range and the capacity to operate in relatively high magnetic field backgrounds. The upper detection limit Bl is set by the condition γHBl ≪ ω0, which for SPH corresponds to Bl in the hundreds of Gauss range.
Contrary to the conventional alkali-metal atomic magnetometers, the proposed scheme does not rely on a magnetic resonance condition. Therefore the detection bandwidth is not determined by the decoherence rate, but only from the hyperfine frequency. In the new scheme the spin-state preparation results from a single-step mechanism (photodissociation of the parent molecule) and does not involve several excitation cycles or the application of magnetic pulses to create coherences. Unlike magnetometry with nitrogen-vacancy centers in diamond, the dense spin ensemble does not suffer from inhomogeneous broadening and high sensitivities can be achieved without the use of dynamic decoupling techniques. This approach can be applied to different alkali-metal halides with larger hyperfine splittings. For instance, operation with Cs instead of H will extend the range of application to the sub-ns regime.
This fast and atomic magnetometer can be improved further in time resolution and detection sensitivity, by replacing the pickup coil with optical detection (via Faraday rotation), as in conventional atomic magnetometers. This is not practical for H atoms, for which there are only transitions in the VUV. However, polarized atomic photofragments with high atomic number can have convenient probe transitions in the UV, visible, or IR, and can have hyperfine beating frequencies of around 10 GHz (e.g. Cs atoms), thus bringing fast magnetometry down to the 100 ps timescales. A magnetometer with such capabilities holds great promise for characterizing fast magnetization dynamics in chemical processes, including biologically relevant pathways, as well as in materials science and technology.
Conflicts of interest
There are no conflicts to declare.
Appendix A: time evolution
In the presence of a magnetic field B (which can be time varying), the SPH evolves according to the Hamiltonian (we neglect for the moment the relaxation):| |  | (9) |
where Î is the dimensionless nuclear spin operator, ω0 is the hyperfine frequency of H, μB is the Bohr magneton, gs ≈ 2 is the electron spin g-factor, Ĥ0 is the Hamiltonian for hyperfine interaction expressed in (angular) frequency units. In the above equation, we neglected the coupling of the magnetic field to nuclear spin, as this is three orders of magnitude smaller than the coupling to the electron spin.
For clarity we write the Hamiltonian in the coupled (subscript c) and uncoupled (subscript u) basis taking z (the magnetic field direction) as the quantization axis:
where
γH =
gsμB/2
ħ is the gyromagnetic ratio of atomic H. The above matrices are expressed in a basis with the following ordering:
| |  | (10) |
where
F is the total spin (sum of electronic and nuclear spin) quantum number,
ms,
mI and
mF are respectively the electronic, nuclear and total spin projection along the quantization axis.
Transformation of an arbitrary operator  or state vector |ψ〉 from one basis to the other can be performed according to the following rules:
or state vector |ψ〉 from one basis to the other can be performed according to the following rules:
| |  | (11) |
| |  | (12) |
The hydrohalide photo-dissociation occurs with a sub-nanosecond laser pulse and optical pumping effectively transfers angular momentum from light to the electronic spin, leaving the nuclear spin degrees of freedom in their thermal (completely unpolarized) state. Following the above basis ordering, after optical pumping half of the polarized H atoms are in the quantum state (expressed as a column vector):
| |  | (13) |
where the subscript
y denotes that the quantization axis for spin projections was taken in the
y direction (if no axis subscript appears it is implicitly assumed that the quantization axis is in the
z direction),
T is the transpose operation,
σ is the helicity of the pumping light pulse and

is the rotation matrix around the
x-axis applied to the uncoupled basis (two spins, each of spin 1/2):
| |  | (14) |
The other half of the polarized H atoms are in the state:
| |  | (15) |
For the observable  the contribution to signal of atoms initially at state |ψ(0)〉0 is a factor of γHB/ω0 smaller than the contribution of atoms initially at |ψ(0)〉1. In the case of γHB/ω0 ≪ 1, the magnetometer signal is mainly determined by the atoms initially at |ψ(0)〉1.
the contribution to signal of atoms initially at state |ψ(0)〉0 is a factor of γHB/ω0 smaller than the contribution of atoms initially at |ψ(0)〉1. In the case of γHB/ω0 ≪ 1, the magnetometer signal is mainly determined by the atoms initially at |ψ(0)〉1.
For static magnetic field, Schrödinger equation can be solved in a straightforward manner:
| |  | (16) |
where |
ψ(
t)〉 is the wavefunction at time
t after optical pumping. For |
ψ(0)〉 = |
ψ(0)〉
1 the wavefunction at time
t in the coupled basis is:
| |  | (17) |
where:

.
In the general case of a time varying magnetic field the Schrödinger equation cannot be solved analytically, as the Hamiltonian does not commute with itself at different times. For an approximate analytical solution it is convenient to work in the interaction picture (denoted by the ∼ symbol):
| | 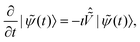 | (18) |
where
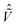
is the Hamiltonian describing the magnetic field coupling to the atoms:
| |  | (19) |
In the last equation

is expressed in the uncoupled basis.
The solution of eqn (18) can be expressed in the form of the Magnus series.25 For magnetic fields that change slowly with respect to the hyperfine frequency so that:
| |  | (20) |
the solution of
eqn (18) can be approximated by keeping only the first term in Magnus expansion. In this case:
| | 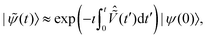 | (21) |
and the observable (taking into account the condition (20)) can be written as:
| |  | (22) |
The last approximation holds for
γHB ≪
ω0.
The condition stated in 20 implies that the magnetic field does not induce hyperfine transitions and the magnetic field can be treated as a perturbation to the energies of the hyperfine levels. Then, for small magnetic fields (γHB ≪ ω0) the Hamiltonian for H atoms (hyperfine levels with F = 0 and F = 1) can be approximated to be (as before the magnetic field direction is taken to be the quantization axis):
| | | Ĥ ≈ Ĥ0 + γHB(t)(Ŝz + Îz). | (23) |
This Hamiltonian commutes with itself at different times and the Schrödinger equation can be solved analytically:
| |  | (24) |
Decay
The evolution of spins is also affected by relaxation processes leading to non-Hamiltonian dynamics. We model these by introducing a decay term in the density matrix equation:| | 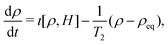 | (25) |
where 1/T2 is the decay rate, and ρeq corresponds to the state towards which the decay processes drive the system. We take this quantum state to be the completely unpolarized state, written in the form:| |  | (26) |
where ![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) 4×4 is the 4 × 4 identity matrix. For eqn (25) and (26) to be valid the population decay (hydrogen atom losses due to formation of molecules) should be significantly slower compared to (atomic) hydrogen spin-decoherence processes. This condition is justified in our case.
4×4 is the 4 × 4 identity matrix. For eqn (25) and (26) to be valid the population decay (hydrogen atom losses due to formation of molecules) should be significantly slower compared to (atomic) hydrogen spin-decoherence processes. This condition is justified in our case.
The density matrix at t = 0 is (z quantization axis the direction of magnetic field and optical pumping in the y axis):
| |  | (27) |
An analytical solution to the density matrix equation can be found for a static magnetic field or for an arbitrary field when the Hamiltonian can be approximated by
eqn (23). In the experimentally relevant limit of
ω0 ≫ (1/
T2,
γHB) the signal is (keeping lowest order terms in the harmonic amplitudes):
| |  | (28) |
Eqn (25) and (26) implies spin-damping occurs (at equal rate) for both electron and nuclear spin of H. However, the results derived here are general for the relevant approximations (ω0 ≫ (1/T2, γHB)) and condition (20). For instance, eqn (28) is reproduced also for decay mechanisms that relax only the electronic spin:
| |  | (29) |
Appendix B: spin-projection noise
In the following we will need to know the multi-time correlation| | 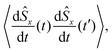 | (30) |
where we take| |  | (31) |
The last term (not derived from first principles) was introduced to account for the spin decay. We assume that the evolution of the density matrix ρ is given by eqn (25) (though the results are the same – within the relevant approximations – for the evolution described in eqn (29)).
The multi-time correlation can be written operationally in the form:
| |  | (32) |
where
U(
t,
t′) is the evolution operator of the density matrix from time
t′ to
t (
t >
t′), and
ρ(
t′) is the density matrix at time
t′:
ρ(
t′) =
U(
t′, 0)
ρ(0). The evolution operator
U cannot be written in the form of a matrix and is not associative. The evolved state

can be found from the general solution of
eqn (25) taking
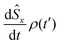
as the initial condition for the density matrix. For quantum noise analysis we can take the magnetic field to be zero in the calculation of the multi-time correlation, since quantum noise affects considerably magnetometry only at low fields. When
ω0T2 ≫ 1, it can be found that:
| |  | (33) |
In order to find what is the magnetic field uncertainty due to spin-projection noise, we have to specify a method for estimating the magnetic field from the detected signal  . Taking into account eqn (28), one way to do this (appropriate for arbitrary magnetic waveforms) is from considering the “quasi-instantaneous” amplitude of the frequency component at the hyperfine frequency:
. Taking into account eqn (28), one way to do this (appropriate for arbitrary magnetic waveforms) is from considering the “quasi-instantaneous” amplitude of the frequency component at the hyperfine frequency:
| |  | (34) |
where
Thf = 2π/
ω0 is the period of hyperfine oscillation and
n is an integer number. We assume that the magnetic field can be written in the form:

, where
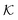
is a known (but other than this an arbitrary), time-dependent function. Spin-projection noise creates an uncertainty in the estimation of
B0.
We consider the case where the functions  and e−t/T2 evolve in time much slower compared to sin(ω0t) and can therefore be considered constant during the hyperfine period. Effectively this is the situation for ω0T2 ≫ 1 and the condition stated in 20. Then, the quasi-amplitude of the sine wave at hyperfine frequency is (we ignore the – irrelevant for noise purposes – −σ factor in the signal in eqn (28)):
and e−t/T2 evolve in time much slower compared to sin(ω0t) and can therefore be considered constant during the hyperfine period. Effectively this is the situation for ω0T2 ≫ 1 and the condition stated in 20. Then, the quasi-amplitude of the sine wave at hyperfine frequency is (we ignore the – irrelevant for noise purposes – −σ factor in the signal in eqn (28)):
| |  | (35) |
where the last approximation holds for small magnetic fields.
The magnetic field B0 can be estimated by minimizing with respect to the parameter B0 the χ2 function:
| |  | (36) |
where MT
hf is the total measurement time. The above equation can be viewed as a curve fitting problem with unknown parameter
B0 for a noisy signal. The solution to the curve fitting problem is:
| |  | (37) |
and the estimation uncertainty in
B0 due to the spin-projection noise is:
| |  | (38) |
From
eqn (33) and (34) we find (in the limit of
ω0 ≫
γ):
| |  | (39) |
so that:
| |  | (40) |
where
Tm is the measurement time for a single run of the experiment.
The above derivation applies to a measurement a single H atom. For NSPH independent (absence of spin-squeezing) H atoms the uncertainty in magnetic field estimation is:
| |  | (41) |
Acknowledgements
This work was supported by the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), grant agreement no. HFRI-FM17-3709 (project NUPOL) and by the project “HELLAS-CH” (MIS 5002735), which is implemented under the “Action for Strengthening Research and Innovation Infrastructures”, funded by the Operational Programme “Competitiveness, Entrepreneurship and Innovation” (NSRF 2014–2020) and cofinanced by Greece and the European Union (European Regional Development Fund). GEK acknowledges funding from the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT), under grant agreement No. [1789], and GV acknowledges funding from EU QuantERA Project PACE-IN (GSRT Grant No. T11EPA4-00015).
References
-
P. Ripka, Magnetic Sensors and Magnetometers, Artech House Publishers, 2001, ISBN 1580530575, 9781580530576 Search PubMed.
- R. Bradley, J. Clarke, D. Kinion, L. J. Rosenberg, K. van Bibber, S. Matsuki, M. Mück and P. Sikivie, Microwave cavity searches for dark-matter axions, Rev. Mod. Phys., 2003, 75, 777–817, DOI:10.1103/RevModPhys.75.777.
- O. I. Gnezdilov, A. E. Mambetov, A. A. Obynochny and K. M. Salikhov, Time-resolved epr study of electron spin polarization and spin exchange in mixed solutions of porphyrin stable free radicals, Appl. Magn. Reson., 2003, 250(1), 157, DOI:10.1007/BF03166974 , ISSN 1613-7507.
- M. Mompeán, R. M. Sánchez-Donoso, A. de la Hoz, V. Saggiomo, A. H. Velders and M. Victoria Gomez, Pushing nuclear magnetic resonance sensitivity limits with microfluidics and photo-chemically induced dynamic nuclear polarization, Nat. Commun., 2018, 90(1), 108, DOI:10.1038/s41467-017-02575-0 , ISSN 2041-1723.
- O. B. Morozova, K. L. Ivanov, A. S. Kiryutin, R. Z. Sagdeev, T. Köchling, H. M. Vieth and A. V. Yurkovskaya, Time-resolved CIDNP: An NMR way to determine the EPR parameters of elusive radicals, Phys. Chem. Chem. Phys., 2011, 130(14), 6619–6627 RSC.
- J. Klein-Seetharaman, M. Oikawa, S. B. Grimshaw, J. Wirmer, E. Duchardt, T. Ueda, T. Imoto, L. J. Smith, C. M. Dobson and H. Schwalbe, Long-range interactions within a nonnative protein, Science, 2002, 2950(5560), 1719–1722, DOI:10.1126/science.1067680 , ISSN 0036-8075.
- Y. Acremann, C. H. Back, M. Buess, O. Portmann, A. Vaterlaus, D. Pescia and H. Melchior, Imaging precessional motion of the magnetization vector, Science, 2000, 290, 491–495, DOI:10.1126/science.290.5491.492.
-
D. Atkinson, D. A. Allwood, M. D. Cooke and R. P. Cowburn. Nanosecond pulsed field magnetization reversal in thin-film permalloy studied by kerr effect magnetometry, in 2002 IEEE International Magnetics Conference (INTERMAG), 2002, p. GV4 DOI:10.1109/INTMAG.2002.1001512.
- M. Yamada, R. Kulsrud and H. Ji, Magnetic reconnection, Rev. Mod. Phys., 2010, 82, 603–664, DOI:10.1103/RevModPhys.82.603.
-
High Sensitivity Magnetometers. Smart Sensors, Measurement and Instrumentation 19, ed. S. C. Mukhopadhyay, A. Grosz and M. J. Haji-Sheikh, Springer International Publishing, 1st edn, 2017, ISBN 978-3-319-34070-8, 978-3-319-34068-5, https://books.google.es/books?id=t8gcDQAAQBAJLink Search PubMed.
- D. Budker and M. Romalis, Optical magnetometry, Nat. Phys., 2007, 3, 227–234, DOI:10.1038/nphys566.
- R. Jiménez-Martínez, W. C. Griffith, S. Knappe, J. Kitching and M. Prouty, High-bandwidth optical magnetometer, J. Opt. Soc. Am. B, 2012, 290(12), 3398–3403, DOI:10.1364/JOSAB.29.003398.
- R. L. Fagaly, Superconducting quantum interference device instruments and applications, Rev. Sci. Instrum., 2006, 770(10), 101101, DOI:10.1063/1.2354545.
- A. Bienfait, J. J. Pla, Y. Kubo, M. Stern, X. Zhou, C. C. Lo, C. D. Weis, T. Schenkel, M. L. W. Thewalt, D. Vion, D. Esteve, B. Julsgaard, K. Mølmer, J. J. L. Morton and P. Bertet, Reaching the quantum limit of sensitivity in electron spin resonance, Nat. Nanotechnol., 2016, 110(3), 253–257, DOI:10.1038/nnano.2015.282 , ISSN 1748-3395.
- J. McCord, Progress in magnetic domain observation by advanced magneto-optical microscopy, J. Phys. D: Appl. Phys., 2015, 480(33), 333001, DOI:10.1088/0022-3727/48/33/333001.
- H. Zheng, Z. Sun, G. Chatzidrosos, C. Zhang, K. Nakamura, H. Sumiya, T. Ohshima, J. Isoya, J. Wrachtrup, A. Wickenbrock and D. Budker, Microwave-free vector magnetometry with nitrogen-vacancy centers along a single axis in diamond, Phys. Rev. Appl., 2020, 13, 044023, DOI:10.1103/PhysRevApplied.13.044023.
- T. P. Rakitzis, P. C. Samartzis, R. L. Toomes, T. N. Kitsopoulos, A. Brown, G. G. Balint-Kurti, O. S. Vasyutinskii and J. A. Beswick, Spin-polarized hydrogen atoms from molecular photodissociation, Science, 2003, 3000(5627), 1936–1938, DOI:10.1126/science.1084809 , ISSN 0036-8075.
- D. Sofikitis, L. Rubio-Lago, L. Bougas, A. J. Alexander and T. P. Rakitzis, Laser detection of spin-polarized hydrogen from HCl and HBr photodissociation: Comparison of H- and halogen-atom polarizations, J. Chem. Phys., 2008, 1290(14), 144302, DOI:10.1063/1.2989803.
- T. P. Rakitzis, Pulsed-laser production and detection of spin-polarized hydrogen atoms, ChemPhysChem, 2004, 5, 1489–1494, DOI:10.1002/cphc.200400108.
- D. Sofikitis, C. S. Kannis, G. K. Boulogiannis and T. P. Rakitzis, Ultrahigh-density spin-polarized H and D observed via magnetization quantum beats, Phys. Rev. Lett., 2018, 121, 083001, DOI:10.1103/PhysRevLett.121.083001.
- A. K. Spiliotis, M. Xygkis, M. E. Koutrakis, K. Tazes, G. K. Boulogiannis, C. S. Kannis, G. E. Katsoprinakis, D. Sofikitis and T. P. Rakitzis, Ultrahigh-density spin-polarized hydrogen isotopes from the photodissociation of hydrogen halides: new applications for laser-ion acceleration, magnetometry, and polarized nuclear fusion, Light: Sci. Appl., 2021, 100(1), 35, DOI:10.1038/s41377-021-00476-y , ISSN 2047-7538.
- D. Sofikitis, P. Glodic, G. Koumarianou, H. Jiang, L. Bougas, P. C. Samartzis, A. Andreev and T. P. Rakitzis, Highly nuclear-spin-polarized deuterium atoms from the UV photodissociation of deuterium iodide, Phys. Rev. Lett., 2017, 118, 233401, DOI:10.1103/PhysRevLett.118.233401.
-
A. Spiliotis, Ultrahigh-Density Spin-Polarized Hydrogen Isotopes from the Photodissociation of Hydrogen Halides: Production, Detection, and Applications in Magnetometry, PhD thesis, University of Crete, 2020 Search PubMed.
- E. Steffens and W. Haeberli, Polarized gas targets, Rep. Progr. Phys., 2003, 660(11), 1887–1935, DOI:10.1088/0034-4885/66/11/r02.
- S. Blanes, F. Casas, J. A. Oteo and J. Ros, The magnus expansion and some of its applications, Phys. Rep., 2009, 4700(5), 151–238, DOI:10.1016/j.physrep.2008.11.001 , ISSN 0370-1573.
Footnotes |
| † PACS numbers: 07.55.Ge, 67.65.+z. |
| ‡ Permanent address: Department of Physics, University of Ioannina, Ioannina, Greece. |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
George E.
Katsoprinakis
ab,
Dimitrios
Sofikitis‡
ab,
George E.
Katsoprinakis
ab,
Dimitrios
Sofikitis‡
 ab,
Georgios
Vasilakis
ab and
T. Peter
Rakitzis
ab,
Georgios
Vasilakis
ab and
T. Peter
Rakitzis
 *ab
*ab





![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) , where B =
, where B = ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) /Bc, and Bc = 50.7 mT is the critical field for H atoms.24Eqn (5) then becomes:
/Bc, and Bc = 50.7 mT is the critical field for H atoms.24Eqn (5) then becomes:
![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) = 0, A−/A+ = 1, whereas when
= 0, A−/A+ = 1, whereas when ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) tends to infinity, the A− peak vanishes, and the ratio A−/A+ tends to 0.
tends to infinity, the A− peak vanishes, and the ratio A−/A+ tends to 0.
 (electromotive force in the detection coil) at time t after the optical pumping can be approximated to be (see 7 for details):
(electromotive force in the detection coil) at time t after the optical pumping can be approximated to be (see 7 for details):
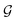 is a geometrical factor that relates the magnetic field from the spins to the flux in the region of the coil,
is a geometrical factor that relates the magnetic field from the spins to the flux in the region of the coil,  is the number of turns per unit length of the coil, μB is the Bohr magneton, NSPH the number of SPH atoms in the detection region, and T2 is the hyperfine coherence time. The above equation is an approximation in the limit where the magnetic field evolves much slower compared to the hyperfine frequency and when ω0 ≫ (1/T2, γHB). It also assumes an inductor detection time constant much shorter than the hyperfine period and neglects dipolar-interactions between the hydrogen spins. It can be seen that the information about the magnetic field appears as amplitude modulation of the carrier wave at the hyperfine frequency ω0. As a result, the evolution of magnetic fields at timescales longer than 1/ω0 should be faithfully captured with the proposed magnetometer as long as it is completed before significant spin-depolarization occurs.
is the number of turns per unit length of the coil, μB is the Bohr magneton, NSPH the number of SPH atoms in the detection region, and T2 is the hyperfine coherence time. The above equation is an approximation in the limit where the magnetic field evolves much slower compared to the hyperfine frequency and when ω0 ≫ (1/T2, γHB). It also assumes an inductor detection time constant much shorter than the hyperfine period and neglects dipolar-interactions between the hydrogen spins. It can be seen that the information about the magnetic field appears as amplitude modulation of the carrier wave at the hyperfine frequency ω0. As a result, the evolution of magnetic fields at timescales longer than 1/ω0 should be faithfully captured with the proposed magnetometer as long as it is completed before significant spin-depolarization occurs.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2πft), where B0 = 100 μG and f = 1 MHz (blue dashed line) or f = 100 MHz (red solid line). (b)
cos(2πft), where B0 = 100 μG and f = 1 MHz (blue dashed line) or f = 100 MHz (red solid line). (b)  , where Δt = 1 ns and 5 ns, t0 = 30 ns and B0 = 100 μG. (c) Frequency response of the magnetometer (normalized to DC response).
, where Δt = 1 ns and 5 ns, t0 = 30 ns and B0 = 100 μG. (c) Frequency response of the magnetometer (normalized to DC response). , where B0 signifies the amplitude of magnetic field to be estimated from the magnetometer signal and
, where B0 signifies the amplitude of magnetic field to be estimated from the magnetometer signal and  is an arbitrary function of time t assumed to be known. By adopting a χ2 minimization, it can be shown (see 8) that the spin-projection noise limit for a single measurement run is given by:
is an arbitrary function of time t assumed to be known. By adopting a χ2 minimization, it can be shown (see 8) that the spin-projection noise limit for a single measurement run is given by:
 , where ω is the angular frequency) and the conditions described above: SPH density 1018 cm−3, measurement volume (100μm)2 × 1 mm = 10 nl and T2 ≈ 100 ns. Such a projection-noise-limited magnetometer presents sensitivity on the order of a few nanoTesla after measurement time of 1 ns. For Tm ∼ T2 the sensitivity is better than 200 pT per pulse; in this case, with a pulse repetition rate of 1 MHz, the projected sensitivity becomes better than
, where ω is the angular frequency) and the conditions described above: SPH density 1018 cm−3, measurement volume (100μm)2 × 1 mm = 10 nl and T2 ≈ 100 ns. Such a projection-noise-limited magnetometer presents sensitivity on the order of a few nanoTesla after measurement time of 1 ns. For Tm ∼ T2 the sensitivity is better than 200 pT per pulse; in this case, with a pulse repetition rate of 1 MHz, the projected sensitivity becomes better than  .
.


 or state vector |ψ〉 from one basis to the other can be performed according to the following rules:
or state vector |ψ〉 from one basis to the other can be performed according to the following rules:


 is the rotation matrix around the x-axis applied to the uncoupled basis (two spins, each of spin 1/2):
is the rotation matrix around the x-axis applied to the uncoupled basis (two spins, each of spin 1/2):

 the contribution to signal of atoms initially at state |ψ(0)〉0 is a factor of γHB/ω0 smaller than the contribution of atoms initially at |ψ(0)〉1. In the case of γHB/ω0 ≪ 1, the magnetometer signal is mainly determined by the atoms initially at |ψ(0)〉1.
the contribution to signal of atoms initially at state |ψ(0)〉0 is a factor of γHB/ω0 smaller than the contribution of atoms initially at |ψ(0)〉1. In the case of γHB/ω0 ≪ 1, the magnetometer signal is mainly determined by the atoms initially at |ψ(0)〉1.

 .
.
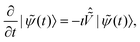
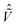 is the Hamiltonian describing the magnetic field coupling to the atoms:
is the Hamiltonian describing the magnetic field coupling to the atoms:
 is expressed in the uncoupled basis.
is expressed in the uncoupled basis.

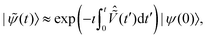


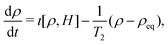

![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) 4×4 is the 4 × 4 identity matrix. For eqn (25) and (26) to be valid the population decay (hydrogen atom losses due to formation of molecules) should be significantly slower compared to (atomic) hydrogen spin-decoherence processes. This condition is justified in our case.
4×4 is the 4 × 4 identity matrix. For eqn (25) and (26) to be valid the population decay (hydrogen atom losses due to formation of molecules) should be significantly slower compared to (atomic) hydrogen spin-decoherence processes. This condition is justified in our case.



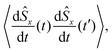


 can be found from the general solution of eqn (25) taking
can be found from the general solution of eqn (25) taking 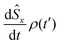 as the initial condition for the density matrix. For quantum noise analysis we can take the magnetic field to be zero in the calculation of the multi-time correlation, since quantum noise affects considerably magnetometry only at low fields. When ω0T2 ≫ 1, it can be found that:
as the initial condition for the density matrix. For quantum noise analysis we can take the magnetic field to be zero in the calculation of the multi-time correlation, since quantum noise affects considerably magnetometry only at low fields. When ω0T2 ≫ 1, it can be found that:
 . Taking into account eqn (28), one way to do this (appropriate for arbitrary magnetic waveforms) is from considering the “quasi-instantaneous” amplitude of the frequency component at the hyperfine frequency:
. Taking into account eqn (28), one way to do this (appropriate for arbitrary magnetic waveforms) is from considering the “quasi-instantaneous” amplitude of the frequency component at the hyperfine frequency:
 , where
, where 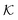 is a known (but other than this an arbitrary), time-dependent function. Spin-projection noise creates an uncertainty in the estimation of B0.
is a known (but other than this an arbitrary), time-dependent function. Spin-projection noise creates an uncertainty in the estimation of B0.
 and e−t/T2 evolve in time much slower compared to sin(ω0t) and can therefore be considered constant during the hyperfine period. Effectively this is the situation for ω0T2 ≫ 1 and the condition stated in 20. Then, the quasi-amplitude of the sine wave at hyperfine frequency is (we ignore the – irrelevant for noise purposes – −σ factor in the signal in eqn (28)):
and e−t/T2 evolve in time much slower compared to sin(ω0t) and can therefore be considered constant during the hyperfine period. Effectively this is the situation for ω0T2 ≫ 1 and the condition stated in 20. Then, the quasi-amplitude of the sine wave at hyperfine frequency is (we ignore the – irrelevant for noise purposes – −σ factor in the signal in eqn (28)):








