A photoelectron imaging and quantum chemistry study of the deprotonated indole anion

Abstract

Indole is an important molecular motif in many biological molecules and exists in its deprotonated anionic form in the cyan fluorescent protein, an analogue of green fluorescent protein. However, the electronic structure of the deprotonated indole anion has been relatively unexplored. Here, we use a combination of anion photoelectron velocity-map imaging measurements and quantum chemistry calculations to probe the electronic structure of the deprotonated indole anion. We report vertical detachment energies (VDEs) of 2.45 ± 0.05 eV and 3.20 ± 0.05 eV, respectively. The value for D₀ is in agreement with recent high-resolution measurements whereas the value for D₁ is a new measurement. We find that the first electronically excited singlet state of the anion, S₁(ππ*), lies above the VDE and has shape resonance character with respect to the D₀ detachment continuum and Feshbach resonance character with respect to the D₁ continuum.

---

1 Introduction

Indole, a prototypical polycyclic aromatic nitrogen heterocycle, plays an important role in defining the ultraviolet (UV) absorption and fluorescence spectra of tryptophan. It is also an important building block in other biological molecules, such as the chromophore of W7 cyan fluorescent protein (CFP) (Fig. 1), a blue-shifted analogue of green fluorescent protein (GFP) whose identification from the jellyfish Aequorea victoria revolutionised the life sciences by enabling a range of applications such as fluorescence imaging and biosensing.^1–3 CFP has a broad absorption spectrum with maxima at 434 nm and 455 nm, corresponding to the chromophore in neutral and deprotonated anionic forms respectively, and an equally broad bimodal fluorescence profile with maxima at 476 nm and 505 nm.⁴ As in GFP, it is the anionic form of CFP that fluoresces. However, the fluorescence from CFP is considerably less bright than that from GFP, suggesting that competing non-radiative decay processes play an important role in the excited-state dynamics of the CFP protein. In some ways, this is quite remarkable considering that the only difference between CFP and GFP is the substitution of a para-phenol building block in the GFP chromophore by an indole building block in the CFP chromophore.

Fig. 1 Structure of the deprotonated cyan fluorescent protein chromophore with the deprotonated indole moiety in black.

Experimentally, the most direct way of probing the electronic structure and non-radiative relaxation dynamics of molecules is photoelectron spectroscopy. In earlier work, we proposed that the electronic structure of GFP and CFP chromophores were governed by the deprotonated phenol and indole molecular units respectively.⁵ Recently, Anstöter et al. developed this idea further by suggesting that the basic electronic structure of photoactive chromophores can be understood by using Hückel theory to construct the molecular orbitals of a photoactive protein chromophore from linear combinations of the molecular orbitals of their constituent molecular building blocks.⁶ This implies that to understand the electronic structure and non-radiative relaxation dynamics of CFP requires a detailed understanding of the electronic structure of the deprotonated indole anion building block. The only gas-phase studies of the deprotonated indole anion reported to date are a low-resolution photoelectron spectroscopy study that determined the vertical detachment energy (VDE) to be 2.31 ± 0.15 eV⁵ and a recent high-resolution slow velocity-map imaging (SEVI) study that reported a very accurate value for the adiabatic detachment energy (ADE) of 2.4315 ± 0.0017 eV.⁷ Photodetachment spectroscopy has also been employed to study deprotonated tryptophan-containing peptides and their corresponding neutral radicals.^8,9 Here, we report the results of a new, combined photoelectron imaging and computational chemistry study of the deprotonated indole anion. We report values for the VDEs to both the ground and first electronically excited states of the neutral deprotonated indole radical and we determine the vertical excitation energy and resonance character of the first electronically excited state of the deprotonated indole anion.

2 Methods

2.1 Anion photoelectron spectroscopy

Photoelectron images were recorded using our electrospray ionisation (ESI) velocity map imaging (VMI) instrument that has been described elsewhere.¹⁰ Briefly, we generated gas-phase deprotonated indole by ESI of ∼1 mM indole in 1/1 (v/v) methanol–water with a few drops of aqueous ammonia. The anions were mass-selected by a quadrupole and guided into a hexapole ion trap. They were released from the trap at 20 Hz and focused into the source region of a collinear velocity map imaging spectrometer. Nanosecond laser pulses of wavelength 359–310 nm were generated by frequency doubling the output of a nanosecond YAG-pumped dye laser operating at 20 Hz. Photoelectrons generated in the interaction region were accelerated towards a position sensitive detector and imaged using a CCD camera. Laser only images were recorded without the ion-beam and subtracted from the overall signal to remove background electron counts arising from ionization of residual gas or scattered laser light.

The pBasex inversion method was used to obtain photoelectron velocity and angular distributions.¹¹ Electron kinetic energy (eKE) spectra were obtained by calibrating the radial photoelectron velocity distribution against the photoelectron spectrum of iodide¹² and the energy resolution, ΔE/E < 5%. Qualitative insight into the nature of the molecular orbitals from which the electrons are detached can be obtained from the photoelectron angular distributions (PADs) which, for a one-photon process, is given by

I(θ) ∝ 1 + β₂P₂(cos θ), (1)

where I(θ) is the probability of photoelectron emission at a particular angle θ, defined as the angle between the laser polarisation and the velocity vector of the photoelectron, P₂(cos θ) is the 2nd order Legendre polynomial and β₂ is the asymmetry parameter.

2.2 Computational chemistry calculations

The structures of the anionic chromophores and their corresponding neutral radicals were optimised using density functional theory (DFT) with B3LYP^13–16 and CAM-B3LYP¹⁷ functionals, with Pople (6-311++G(3df,3dp))¹⁸ and Dunning (aug-cc-pVDZ/pvTZ)¹⁹ basis sets. Frequency calculations were performed to confirm that minima in the potential energy surfaces were reached.

Vertical detachment energies (VDEs) were calculated using various methods. We used electron propagator theory (EPT),²⁰ a method that has been found to yield reliable VDEs in previous work.^21–24 We also used the equation-of-motion coupled-cluster method with single and double excitations for the calculation of ionisation potentials (EOM-IP-CCSD).²⁵ Both of these methods allowed us to calculate the VDE to the first electronically excited state of the neutral radical, D₁, as well as that to the electronic ground state of the neutral radical, D₀. We also used DFT to calculate the VDE as the energy difference between the anion and neutral radical at the optimised geometry of the anion. Calculating the VDE this way allowed us to make a direct comparison with the adiabatic detachment energy (ADE) calculated as the difference between the lowest vibrational state of the anion and the lowest vibrational state of the neutral radical (0–0 transition).

Vertical excitation energies (VEEs) of the excited singlet states of the anion were calculated using time-dependent DFT (TD-DFT)²⁶ with the CAM-B3LYP functional and 6-311++G(3df,3dp) and aug-cc-pVTZ basis sets. They were also calculated using the ADC(2)/6-311++G(2d,2p) method.^27,28 Due to the number of diffuse functions in the basis set, a huge number of continuum states were calculated. Thus, to assist with our interpretation of the ADC(2) calculations, we first used the 6-311G(2d,2p) basis set, which did not give accurate VEEs because it neglected the interaction of the resonance states with the continuum but it allowed us to determine the nature of the molecular orbitals involved in the transitions. Having identified the key molecular orbitals, we then added the diffuse functions to obtain more accurate VEEs. We chose to use the ADC(2) method having recently found it compared favourably with high-level SA-CASSCF(14,12)-PT2/cc-pVDZ calculations,²⁹ for a series of photoactive yellow protein chromophore anions,²¹ and high-level XMCQDPT2/(aug)-cc-pVTZ level calculations,³⁰ for a series of GFP chromophore anions.²²

Geometry optimisations, vibrational frequencies, TD-DFT and EPT calculations were performed using the Gaussian09 software suite,³¹ EOM-IP-CCSD and ADC(2) calculations were carried out using the Q-Chem software package.³²

The photoelectron spectrum was calculated using ezSpectrum (version 3.0).³³ These calculations require the equilibrium geometries, harmonic frequencies and normal mode vectors of the deprotonated indole anions and corresponding neutral radicals as input and we used those obtained using the CAM-B3LYP/aug-cc-pVTZ method. The Franck–Condon overlap integrals were calculated in ezSpectrum using the parallel normal mode approximation. The vibrational temperature of the anions was assumed to be 300 K and the minimum intensity threshold was set to 0.001. The maximum number of vibrational quanta in the anion and neutral radical were limited to 3 and 6, respectively. The resulting stick spectra were convoluted with Gaussian instrumental profiles with full-width at half maxima (FWHM) equivalent to the instrumental resolution, ΔE/E = 4% at 0.4 eV eKE.

PADs for direct detachment to D₀ and D₁ were calculated using ezDyson (version 3.3).^34,35 The Dyson orbitals were obtained from the EOM-IP-CCSD/aug-cc-pVDZ calculation and represent the overlap between the N electron molecular wavefunction of the anion in its ground electronic state and the N − 1 electron molecular wavefunction of the corresponding neutral radical. The PADs were calculated in ezDyson using the plane wave approximation.

3 Results

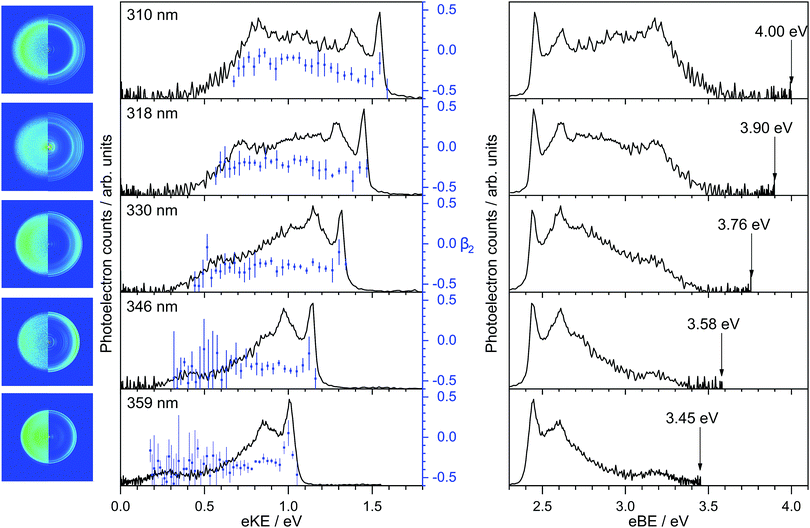
Photoelectron spectra of deprotonated indole were recorded as a function of eKE and are plotted in Fig. 2 together with the anisotropy parameters, β₂. The spectra are also presented as a function of electron binding energy, eBE = hν − eKE.

Fig. 2 Photoelectron spectra of deprotonated indole at wavelengths of 359 nm (3.45 eV), 346 nm (3.58 eV), 330 nm (3.76 eV), 318 nm (3.90 eV) and 310 nm (4.00 eV), plotted as a function of electron kinetic energy (eKE) and electron binding energy (eBE). β-parameters averaged over five data points (solid blue circles) are plotted as a function of eKE with error bars that are one standard deviation of this average. The maximum photon energy is marked on the spectra plotted as a function of eBE. Experimental and inverted velocity-map images are also presented; the polarisation axis of the laser light lies in the vertical direction.

All the photoelectron spectra have a relatively narrow peak centered at 2.45 ± 0.05 eV eBE, a broad unresolved feature at higher eBE and a peak centered around 3.20 ± 0.05 eV eBE. The peaks around 2.45 eV and 3.20 eV eBE remain at constant eBE for all photon energies, characteristic of direct photodetachment (PD). Between the two peaks at 2.45 eV and 3.20 eV is a feature that shifts to higher eBE with increasing photon energy, characteristic of an indirect PD process. More specifically, this feature is centered around 0.9–1.0 eV eKE and remains at constant eKE with increasing photon energy. The relative intensities of the first two peaks in the photoelectron spectra vary with increasing photon energy, another indication that indirect PD is contributing to the photoelectron spectrum.

The calculated VDEs for D₀–S₀ and D₁–S₀ processes are presented in Table 1. The calculated values for detachment to the D₀ continuum all lie in the range 2.4–2.6 eV and are in excellent agreement with our measured value of 2.45 ± 0.05 eV eBE. The VDEs are also very close to the CAM-B3LYP/aug-cc-pVTZ calculated 0–0 transition at 2.46 eV, suggesting that the geometry of the anion is similar to the geometry of the neutral radical in its ground electronic state. The calculated values for detachment to the D₁ continuum are very close to our experimental measurement of 3.20 eV eBE indicating that this feature arises from direct detachment to the continuum associated with the first electronically excited state of the neutral radical of deprotonated indole.

Table 1 Calculated vertical detachment energies (VDEs) for D₀–S₀ and D₁–S₀ processes in deprotonated indole compared with the maximum of the low eBE peak in the 346 nm experimental spectrum. All values are in eV

Method	D0	D1
B3LYP/6-311++G(3df,3dp)	2.36
B3LYP/aug-cc-pVDZ	2.36
B3LYP/aug-cc-pVTZ	2.44
CAM-B3LYP/6-311++G(3df,3dp)	2.47
CAM-B3LYP/aug-cc-pVDZ	2.45
CAM-B3LYP/aug-cc-pVTZ	2.46
EPT/6-311++G(3df,3dp)	2.56	3.11
EOM-IP-CCSD/aug-cc-pVDZ	2.37	3.00
Experiment	2.45 ± 0.05	3.20 ± 0.05

---

To assist with our interpretation of the structure in the photoelectron spectra, we have calculated the photoelectron spectrum corresponding to direct photodetachment from the S₀ state of the deprotonated indole anion to the D₀ state of the neutral radical. The photoelectron stick spectrum is convoluted with a Gaussian instrument function with FWHM ΔE/E = 4% and presented in Fig. 3 together with the experimental 359 nm and 346 nm photoelectron spectra. The most intense line in the stick spectrum is the 0–0 transition at 2.46 eV. The calculated spectrum allows us to identify the dominant features in the photoelectron spectra as a progression in the ν₂₉ mode (1468 cm⁻¹) of the neutral radical, an in-plane vibration (see inset of Fig. 3). Despite the excellent agreement between experiment and theory for the sharp peak at low eBE, there is additional photoelectron signal in the experimental spectra that is not accounted for in the calculation and the profile of this additional photoelectron signal varies with photon energy. Such variation in photoelectron signal is observed at all wavelengths (Fig. 2) and is consistent with indirect PD following photoexcitation of excited electronic states of the anion.

Fig. 3 Calculated D₀–S₀ stick spectrum at 300 K (blue), calculated stick spectrum convoluted with an instrument function (see text) (red) and experimental 359 nm and 346 nm photoelectron spectra (solid and dashed, respectively). The calculated spectra have been shifted −0.01 eV to match the experiment. All spectra are normalised to the maximum of the 0–0 transition. Inset: Atomic displacement vectors of the ν₂₉ mode of the neutral deprotonated indole radical.

The β₂-parameters plotted in Fig. 2 are fairly constant across the photoelectron spectra and slightly negative, as might be expected for photodetachment from a π-orbital. We have calculated the β₂-parameters that characterise the PADs corresponding to direct detachment from the S₀ state of the deprotonated indole anion to the D₀ and D₁ states of the neutral radical. The calculated β₂-parameters are plotted in Fig. 4, together with the experimental values. The experimental values are determined as intensity-weighted averages from regions of the photoelectron spectra corresponding to eBEs of 2.4–2.5 eV for D₀ and 3.0–3.4 eV for D₁, with appropriate intensity-averaged standard deviations. The experimental values are plotted as a function of eKE above the experimentally determined D₀ and D₁ VDEs (2.45 eV and 3.20 eV). The calculated and measured PADs are very similar to one another for both D₀ and D₁ detachment channels.

Fig. 4 Left: Calculated (lines) and experimental (symbols) β₂-parameters characterising the PADs following direct detachment from the S₀ state of the deprotonated indole anion to the D₀ (black) and D₁ (blue) states of the neutral radical, plotted as a function of eKE above the D₀ and D₁ VDEs. Right: Relevant Dyson orbitals for the D₀ (bottom) and D₁ (top) detachment channels.

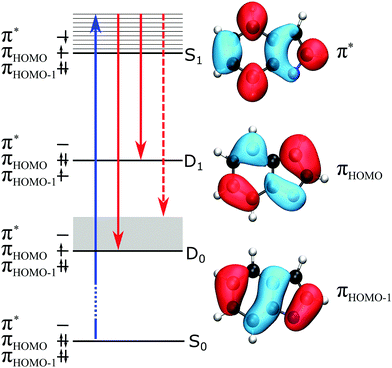
To identify the excited electronic state of the anion embedded in the detachment continuum, we calculated the VEEs of electronically excited singlet states of the deprotonated indole anion. The VEEs are summarised in Table 2 and suggest that there is a weak, but not insignificant, π_HOMO → π* transition with VEE around 3.8–4.0 eV, which is accessible with the photon energies employed in this work (3.5–4.0 eV). The ADC(2)/6-311G(2d,2p) molecular orbitals (MOs) involved in this transition are presented in Fig. 5. Both the highest occupied molecular orbital (HOMO) and π* state are delocalised across the whole molecular anion.

Table 2 Calculated vertical excitation energies (in eV) of the S₁ state of the deprotonated indole anion together with their oscillator strengths and main electronic configurations

Method	VEE (f)	Main configuration
CAM-B3LYP/aug-cc-pVTZ	3.97 (0.029)	0.55 (πHOMO → π*)
CAM-B3LYP/6-311++G(3df,3dp)	4.05 (0.032)	0.67 (πHOMO → π*)
ADC(2)/6-311++G(2d,2p)	3.84 (0.029)	0.44 (πHOMO → π*)

---

Fig. 5 Jablonski diagram illustrating the main electron detachment processes for deprotonated indole following photoexcitation in the range 359–310 nm (3.45–4.00 eV) and showing the main electron configurations and ADC(2)/6-311G(2d,2p) molecular orbitals involved in these processes. The vertical blue arrow represents photoexcitation and the vertical red arrows represent direct (solid) and indirect (dashed) electron detachment processes. The closely spaced horizontal lines represent the vibrational levels of S₁ and the solid grey block represents the vibrational energy in D₀ following indirect electron detachment from S₁.

4 Discussion

The VDE to the ground electronic state of deprotonated indole, D₀, was measured to be 2.45 ± 0.05 eV, which improves the accuracy of our earlier measurement of 2.31 ± 0.15 eV⁵ and is in agreement with a very accurate measurement of the ADE obtained using SEVI that was reported earlier this year (2.4315 ± 0.0017 eV).⁷ The VDE to the first electronically excited state of the neutral radical, D₁, has been measured to be 3.20 ± 0.05 eV. Both measured values are in excellent agreement with our calculations of VDEs to the D₀ and D₁ states of the neutral deprotonated indole radical (Table 1). Nelson et al.⁷ also observed a feature at 3.2 eV eBE in a photoelectron spectrum recorded with a photon energy of 3.49 eV, but believing the first excited state of the neutral radical to be inaccessible at this photon energy, left this feature unassigned. It is worth highlighting that the 0–0 transition (ADE) in the stick spectrum calculated using the CAM-B3LYP/aug-cc-pVTZ method (Fig. 3) lies at 2.46 eV, which is in remarkably good agreement with the SEVI measurement (within 1%).

In order to understand the indirect PD processes contributing to the broadening of the photoelectron spectra of deprotonated indole following photoexcitation in the range 359–310 nm (3.45–4.00 eV), it is useful to consider the main electronic configurations and molecular orbitals of the states involved; these are illustrated in a Jablonski diagram (Fig. 5). Direct PD from S₀ to D₀ and D₁ involve removal of an electron from the HOMO and the HOMO−1, respectively. Photoexcitation of S₁ involves excitation of a single electron from the HOMO to the π* molecular orbital and our calculations suggest that the VEE is around 3.8–4.0 eV. For the S₁ state of the deprotonated indole anion to be accessible in our experiments, the relaxation energy in S₁ would need to be 0.35–0.55 eV. The relaxation energy of the lowest lying ¹ππ* state of indole has been calculated to be around 0.5 eV, so this is not at all unreasonable.³⁶ The S₁ state has a hole in the HOMO so has shape resonance character with respect to the D₀ continuum but has Feshbach resonance character with respect to the D₁ continuum. Thus, we expect the S₁ state to couple strongly to the D₀ continuum and more weakly to the D₁ continuum and, therefore, autodetachment from S₁ to occur predominantly to D₀. The broadening of the D₀–S₀ photoelectron spectrum can be attributed to this autodetachment from S₁ to D₀. Despite the clear evidence for a resonance in the continuum, the experimental and calculated PADs are very similar (Fig. 4); this is interesting, since resonances can cause changes in PADs.⁶ We do not see any evidence of thermionic emission from the ground electronic state of the anion, characterised by a low eKE (high eBE) signal with exponential profile, I(eKE) ∝ exp(−eKE/k_BT),³⁷ which suggests that autodetachment from S₁ to D₀ is faster than internal conversion from S₁ to S₀.

Our original motivation for this work was to improve our understanding of the role of the deprotonated indole anion as a molecular building block of the CFP chromophore. In this respect, an important measurement is that of the VEE of deprotonated indole, 3.8–4.0 eV, which is higher than that of deprotonated phenol, 3.5 eV.⁶ If we consider the MOs of the excited states of the photoactive protein chromophore to be linear combinations of the excited states of their constituent molecular building blocks,⁶ replacing the deprotonated phenol anion with a deprotonated indole anion raises the energy of the π* MO of the substituent relative to the π* MO of the 2,3-dimethyl-5-methylene-3,5-dihydro-4H-imidazol-4-one molecular unit (grey in Fig. 1). Simple Hückel theory then predicts that the first electronically excited state of the deprotonated CFP chromophore will be higher than that of the deprotonated GFP chromophore, which is in agreement with gas-phase action absorption spectroscopy measurements of the deprotonated GFP (2.53 eV)³⁸ and CFP (2.70 eV)⁴ chromophores. Moreover, the higher lying excited state of the deprotonated CFP chromophore will be localised on the indole moiety and be lower in energy than that of the deprotonated GFP chromophore. Following photoexcitation of S₁, GFP has the ability to act as a light-induced electron donor in the presence of an oxidant,^39,40 which is valuable for monitoring redox processes in cells. Following UV photoexcitation of higher lying electronically excited states, GFP has been shown to undergo decarboxylation⁴¹ and it has been proposed that the primary step might involve electron emission from excited electronic states.⁴² Thus, since simple Hückel theory predicts that the excited states of the CFP chromophore are similar to those of the GFP chromophore, it seems reasonable to suppose that similar processes involving electron emission from electronically excited states will occur in CFP and that changing the substituent provides a means of tuning these photoinduced processes.

5 Summary

From the combination of photoelectron spectroscopy measurements and computational chemistry calculations, we have improved our understanding of the electronic structure of the deprotonated indole anion. We have determined the VDEs to be 2.45 ± 0.05 eV and 3.20 ± 0.05 eV for the ground and first electronically excited states of the neutral deprotonated indole radical, D₀ and D₁, respectively. The value for D₀ is in agreement with a recently published high resolution measurement and the value for D₁ is a new measurement. We have identified the lowest electronically excited singlet state of the deprotonated indole anion to arise from a HOMO → π* transition that is delocalised across the whole anion. This electronically excited state lies approximately 1.3–1.5 eV above the VDE to D₀ and has shape-resonance character with respect to the D₀ continuum and Feshbach resonance character with respect to the D₁ continuum. Improving our understanding of the electronic structure of indole and other small molecular building blocks that make up the chromophores of photoactive proteins is important for first principles design of new photoactive protein chromophores with specific characteristics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by EPSRC grant EP/L005646/1. We are grateful to Professor Graham Worth and Dr Mariana Assmann (UCL) for advice on the computational chemistry calculations and to Frank Otto for computational support.

References

1. S. R. Meech, Chem. Soc. Rev., 2009, 38, 2922–2934.
2. M. Chalfie, Y. Tu, G. Euskirchen, W. W. Ward and D. C. Prasher, Science, 1994, 263, 802–805.
3. A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2017, 117, 758–795.
4. S. Boyé, I. B. Nielsen, S. B. Nielsen, H. Krogh, A. Lapierre, H. B. Pedersen, S. U. Pedersen, U. V. Pedersen and L. H. Andersen, J. Chem. Phys., 2003, 119, 338–345.
5. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
6. C. S. Anstöter, C. R. Dean and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2017, 19, 29772–29779.
7. D. J. Nelson, A. M. Oliveira and W. C. Lineberger, J. Chem. Phys., 2018, 148, 064307.
8. L. Joly, R. Antoine, A.-R. Allouche and P. Dugourd, J. Am. Chem. Soc., 2008, 130, 13832–13833.
9. C. Brunet, R. Antoine, A.-R. Allouche, P. Dugourd, F. Canon, A. Giuliani and L. Nahon, J. Phys. Chem. A, 2011, 115, 8933–8939.
10. A. R. McKay, M. E. Sanz, C. R. S. Mooney, R. S. Minns, E. M. Gill and H. H. Fielding, Rev. Sci. Instrum., 2010, 81, 123101.
11. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989.
12. R. J. Peláez, C. Blondel, C. Delsart and C. Drag, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 125001.
13. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
14. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
15. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
16. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
17. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
18. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
19. R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
20. J. Linderberg and Y. Öhrn, Propagators in Quantum Chemistry, John Wiley and Sons, Hoboken, NJ, USA, 2014.
21. A. Henley, M. E. Diveky, A. M. Patel, M. A. Parkes, J. C. Anderson and H. H. Fielding, Phys. Chem. Chem. Phys., 2017, 19, 31572–31580.
22. C. McLaughlin, M. Assmann, M. A. Parkes, J. L. Woodhouse, R. Lewin, H. C. Hailes, G. A. Worth and H. H. Fielding, Chem. Sci., 2017, 8, 1621–1630.
23. M. A. Parkes, C. Phillips, M. J. Porter and H. H. Fielding, Phys. Chem. Chem. Phys., 2016, 18, 10329–10336.
24. C. R. S. Mooney, M. A. Parkes, A. Iskra and H. H. Fielding, Angew. Chem., Int. Ed., 2015, 54, 5646–5649.
25. P. U. Manohar and A. I. Krylov, J. Chem. Phys., 2008, 129, 194105.
26. E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000.
27. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
28. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299–2324.
29. F. F. García-Prieto, M. Á. Aguilar, F. J. Olivares del Valle, I. Fernández Galván, A. Muñoz-Losa, M. L. Sánchez and M. E. Martín, J. Phys. Chem. A, 2015, 119, 5504–5514.
30. A. V. Bochenkova, C. R. S. Mooney, M. A. Parkes, J. L. Woodhouse, L. Zhang, R. Lewin, J. M. Ward, H. C. Hailes, L. H. Andersen and H. H. Fielding, Chem. Sci., 2017, 8, 3154–3163.
31. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford, CT, 2009.
32. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
33. V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, http://iopenshell.usc.edu/downloads/ezspectrum.
34. S. Gozem and A. I. Krylov, ezDyson, http://iopenshell.usc.edu/downloads/ezdyson.
35. S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540.
36. C. Dedonder-Lardeux, C. Jouvet, S. Perun and A. L. Sobolewski, Phys. Chem. Chem. Phys., 2003, 5, 5118–5126.
37. J. B. Wills, F. Pagliarulo, B. Baguenard and C. Bordas, Chem. Phys. Lett., 2004, 390, 145–150.
38. H. V. Kiefer, H. B. Pedersen, A. V. Bochenkova and L. H. Andersen, Phys. Rev. Lett., 2016, 117, 243004.
39. A. M. Bogdanov, A. S. Mishin, I. V. Yampolsky, V. V. Belousov, D. M. Chudakov, F. V. Subach, V. V. Verkhusha, S. Lukyanov and K. A. Lukyanov, Nat. Chem. Biol., 2009, 5, 459–461.
40. A. M. Bogdanov, A. Acharya, A. V. Titelmayer, A. V. Mamontova, K. B. Bravaya, A. B. Kolomeisky, K. A. Lukyanov and A. I. Krylov, J. Am. Chem. Soc., 2016, 138, 4807–4817.
41. J. J. van Thor, T. Gensch, K. J. Hellingwerf and L. N. Johnson, Nat. Struct. Biol., 2002, 9, 37–41.
42. A. V. Bochenkova, B. Kaerke, D. B. Rahbek, J. Rajput, Y. Toker and L. H. Andersen, Angew. Chem., Int. Ed., 2014, 53, 9797–9801.

---

Footnote

† Electronic supplementary information (ESI) available: Optimised anion and radical geometries; vibrational frequencies and FCFs; ezSpectrum calculations; vertical excited energies and characters; molecular orbitals. See DOI: 10.1039/c8cp01902a

---