Open Access Article
Open Access ArticleInvestigation of Ni-catalyzed hydropyrolysis of hemicellulose via ReaxFF-MD simulation
Hong Xiana,
Linjia Yina,
Xiangkun Zhanga,
Muye Fengb and
Kaige Wang *a
*a
aState Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou 310027, China. E-mail: kaigewang@zju.edu.cn
bSchool of Mechanical and Power Engineering, Nanjing Tech University, Nanjing, 211816, China
First published on 20th March 2025
Abstract
Catalytic hydropyrolysis represents a crucial method in the conversion of biomass, particularly hemicellulose with diverse components and an ambiguous structure, into high-value chemical derivatives. The catalytic mechanism and the role of H2 remain challenging to fully elucidate due to the inherent complexity of the system. The mechanism of Ni-catalyzed hydropyrolysis of xylan at the molecular level is elucidated using ReaxFF molecular dynamics (ReaxFF-MD) simulations. The results show that the Ni catalyst not only provides strong chemical adsorption enabling reactants and H2 to interact through active Ni surface sites, but also reduces the global activation energy of xylan hydropyrolysis from 37.12 kcal mol−1 to 24.44 kcal mol−1, significantly enhancing both pyrolysis and hydrodeoxygenation (HDO) reactions. Additionally, the Ni catalyst further optimizes the product distribution by guiding the rearrangement and cracking reactions leading to the enhanced formation of alkenes, cycloalkanes, and furan derivatives. The effective HDO reactions result in a substantial reduction in the oxygen content of the xylan hydropyrolysis products, with the oxygen content of the light condensable products decreasing to 4.07 wt%, the overall oxygen content dropping to 12.8 wt%, and the deoxygenation degree reaching 74.23%. Moreover, the hydrogenation process effectively suppresses carbon deposition over the Ni catalyst attributed to the synergistic interaction between Ni and H2, but excessive H2 may lead to over-reduction of the catalyst surface, thereby diminishing its catalytic activity. This research could provide a valuable approach to elucidate the intricate mechanisms underlying biomass catalytic hydropyrolysis.
1. Introduction
The utilization of biomass is recognized as one of the most promising solutions to current energy and environmental challenges, as biomass is the only renewable energy source capable of being converted into condensable fuels and serving as feedstock for high-value chemical derivatives.1 Hemicellulose is the second most important component in lignocellulosic biomass, following cellulose, typically accounting for 15–30% of its composition.2 However, unlike cellulose which is composed of glucose polymers, hemicellulose has a more complex and less defined structure. It consists of a variety of highly branched pentose and hexose sugars, which makes its conversion process more challenging.3Fast pyrolysis provides a promising pathway for the conversion of hemicellulose, however, it faces challenges such as excessive coking, low calorific value and poor thermal stability of products.4,5 Hydropyrolysis, a method that introduces H2 or hydrogen-rich solvents during the pyrolysis process, addresses the issue of hemicellulose being deficient in hydrogen and rich in oxygen.6,7 Additionally, the incorporation of catalysts facilitates efficient product formation and selective enrichment, thereby enhancing the quality of the bio-oil.8–10 The Ni catalyst, owing to the superior hydrogenation activity and cost-effectiveness, has emerged as a significant subject of investigation in the realm of biomass catalytic hydropyrolysis. Zhou et al.11 performed hydropyrolysis of spent tea flowers using Ni nanoparticles. They observed that most oxygenated compounds were converted into aromatic and aliphatic compounds, with selectivities of 33.0% and 50.5% respectively. The oxygen content of the products was 3.90%, and the calorific value was relatively low at 41.8 MJ kg−1. Xia et al.12 developed a Ni–Re/AC catalyst supported on activated carbon, which demonstrated excellent catalytic performance in the hydrogenation of xylose to xylitol, achieving a yield of up to 98%. The catalyst also exhibited superior hydrogenation activity in the conversion of hemicellulose hydropyrolysis products. Liu et al.13 employed a Ni/ZSM-5 catalyst for the hydropyrolysis of rice straw hemicellulose, finding that the incorporation of Ni onto the ZSM-5 surface created new acidic sites, which significantly enhanced the selectivity for aromatic compounds, reaching 54%.
Although experimental investigations have provided valuable insights into the hydropyrolysis of hemicellulose, the reaction mechanisms and interactions remain challenging to fully elucidate. Computational methods such as DFT can provide deeper insights,14 however, a direct, clear, and comprehensive understanding of the complex catalytic hydropyrolysis process remains elusive. The development of ReaxFF-MD simulation makes it possible to directly obtain microscopic mechanisms such as molecular reactions and bond breaking that could not be directly achieved by previous methods. ReaxFF is a bond-order-based reactive force field developed by Van Duin and Goddard, and when combined with molecular dynamics,15 ReaxFF-MD can be used to describe dynamic bond breaking and formation of a complex molecular system as well as to simulate the dynamical evolution of radical intermediates and products during the catalytic hydropyrolysis of hemicellulose. Yin et al.16 used ReaxFF-MD simulations to investigate the role of H2 gas during the catalytic hydropyrolysis of β-O-4 lignin dimers. The initial reaction was found to begin with the cleavage of the Cβ–O bond, a process that was significantly enhanced in the presence of H2. Ku et al.17 used MD simulations to examine the time evolution of major pyrolysis products at different temperatures. The results indicated that relatively high temperatures accelerated the generation of key gas and tar. However, most studies on lignocellulosic biomass simulations have focused on pyrolysis under noncatalytic conditions, with limited research exploring the catalytic mechanisms of hemicellulose via ReaxFF-MD simulations.18–21 For instance, previous studies primarily focused on the product distribution and pyrolysis reaction pathways of lignocellulosic biomass during pyrolysis or gasification. However, due to limitations in product identification and chemical bond statistics for specific catalytic systems, as well as constraints in force field files, research on the pyrolysis reaction mechanisms of hemicellulose under catalytic conditions remained insufficient. In this study, leveraging the well-established Ni-inclusive force field files in the ReaxFF framework and the self-developed RMD_tools, the hydropyrolysis product distribution, key elementary reactions, and carbon deposition behavior of hemicellulose over Ni catalysts were systematically investigated. This approach provided detailed insights into the reaction mechanisms of hemicellulose Ni-catalyzed hydropyrolysis.
The molecular dynamics simulations based on the ReaxFF force field were conducted using LAMMPS software to investigate the catalytic hydropyrolysis of hemicellulose in this research. Xylan was chosen as the representative model compound, and Ni nanoparticles were employed as the catalyst. The effects of temperature, H2 on the product distribution, the carbon deposition over the Ni catalyst and catalytic mechanism were systematically investigated. This research contributes to a deeper molecular-level understanding of the catalytic hydropyrolysis of hemicellulose.
2. Methods
2.1 Model construction
As shown in Fig. 1(a), a long-chain model was constructed, consisting of nine β-1,4-linked xylose units, one α-1,3-linked α-L-arabinofuranose unit, and one α-1,2-linked 4-O-methyl-α-D-glucuronic acid unit. The model was established by referencing the study of Lu et al.22 and incorporating the 2D HSQC NMR and chemical composition analysis results. And the model was geometry-optimized using the Materials Studio Forcite module with the PCFF force field. | ||
| Fig. 1 (a) Constructed model of xylan, (b) initial simulation system of Ni-catalyzed hydropyrolysis of xylan, (c) experiment TGA result of xylan, and (d) simulation TGA result of xylan. | ||
As shown in the Fig. 1(c) and (d), a comparative analysis was conducted between experimental and simulated thermogravimetric analysis to verify the applicability and accuracy of the xylan molecular model in ReaxFF-MD simulations. The experiments were carried out using a TGA/DSC 3+ simultaneous thermal analyzer under nitrogen atmosphere, heating 10 mg samples from room temperature to 800 °C at a rate of 10 °C min−1, resulting in a TGA weight loss curve and DTG derivative thermogravimetric curve. In the simulation, the xylan pyrolysis system was heated from 400 K to 3000 K at a rate of 10 K ps−1. The mass of C40+ products was statistically approximated as residual solid material, and corresponding TGA and DTG curves were plotted. It was observed that the weight loss curve and the derivative thermogravimetric (DTG) curve followed a similar trend. It could be validated that the xylan model was accurate for ReaxFF-MD simulations. Notably, although the simulation temperature began at 400 K, weight loss was observed to commence at 1800 K during the simulation. It could be explained that ReaxFF-MD simulations require significantly higher temperatures than experimental conditions to facilitate molecular motion and collisions, which are necessary for chemical reactions to occur.23–25 This was the reason for selecting simulation temperatures in the range of 2000 K to 3000 K.
The thermal stability of Ni nanoparticles was closely related to the size, with larger diameters significantly increasing the melting temperature.26–28 Chen et al.29 demonstrated that a Ni nanoparticle with a radius of 15 Å had a melting temperature of approximately 1700 K, while increasing the radius to 20 Å raised the melting temperature to around 2000 K. At higher temperatures, although the shape of the Ni nanoparticle underwent some changes, it could still maintain an approximately spherical structure. Based on the thermal stability considerations, a radius of 20 Å for the Ni nanoparticle model was constructed by the NanoCrystal modeling program developed by Chatzigoulas et al.,30 and the minimum surface energies of Ni corresponding to the Miller indices of (111), (100) and (110) were based on the research results of Jiang et al.31 The Ni nanoparticle was also geometry optimized using Materials Studio with the same force field.
The simulation system illustrated in Fig. 1(b) was constructed using the PACKMOL tool,32 and consisted of 20 uniformly dispersed xylan chains, one Ni nanoparticle in the center, and a gradient amount of H2 (1000, 2000, 3000) into a periodic simulation box of 100 Å × 100 Å × 100 Å with the tolerance of 1.2 Å.
2.2 Simulation details
The simulation was performed using the built-in Reax/C module in the large-scale atomic/molecular massively parallel simulator (LAMMPS). The C/H/O/Ni ReaxFF force field developed by Adri C. T. van Duin et al.33 was adopted, which has been proven to be effective for the simulation of decomposition of hydrocarbons over Ni at high temperature.34,35 Prior to the simulation, the system was equilibrated through a 100 ps relaxation at 300 K in the NVT ensemble, using the conjugate gradient algorithm to remove internal stresses and achieve energy minimization. After the relaxation, the simulations were conducted in the NVT ensemble with a time step of 0.1 fs for 400 ps. The temperature was controlled using a Berendsen thermostat with a 100 fs damping constant in all simulations. The linear and angular momentum of the Ni nanoparticle were zeroed every 10 timesteps to slow down the melting process at high temperatures and facilitate the observation of the reaction process of reactants on the catalyst surface. All the visualizations were achieved with the Open Visualization Tool (OVITO). The data analysis such as product identification, chemical bond analysis and chemical reaction statistics were performed using the self-developed RMD_tools. The RMD_tools overcame the limitations in product identification and chemical bond statistics for specific catalytic systems inherent in existing mainstream open-source software. Based on the depth-first search (DFS) algorithm, it could accurately track and quantify specific chemical reaction events of interest in this study, providing precise data statistics support that facilitated an in-depth exploration of catalytic reaction mechanisms.3. Results and discussion
3.1 The effect of temperature on xylan hydropyrolysis
The time scale of ReaxFF-MD simulations is in the picosecond range, with a time step as small as 0.1 fs. This is much smaller than the second-scale times typical of micro-pyrolysis experiments. To overcome the limitations of the simulation time scale, ReaxFF-MD simulations often employ the strategy of artificially increasing the system temperature.24,25,30,31,36 The elevated temperatures used in the ReaxFF-MD simulations have been regarded as a form of “time scale compression” relative to the lower temperatures employed in experiments.37 Accordingly, the simulation temperatures were set at six distinct points between 2000 K and 3000 K in this research.The results of xylan hydropyrolysis at different simulation temperatures are presented in Fig. 2. The hydropyrolysis products were categorized into three groups: gas products containing 1 to 4 carbon atoms (C1–C4), light condensable products containing 5 to 14 carbon atoms (C5–C14), and heavy condensable products with more than 15 carbon atoms (C15+). This classification aided in a more comprehensive understanding of the evolution of hydropyrolysis products during the Ni-catalyzed hydropyrolysis of xylan. Fig. 2(a) and (b) depict the variations of gas and condensable products under different temperatures in the 2000 H2 system. It was evident that with the increase in simulation temperature, the hydropyrolysis reaction rate accelerated, leading to a greater degree of decomposition and consequently a higher yield of C1–C4 gas molecules. As shown in Fig. 2(b), the condensable products reached a peak around 40 ps and then gradually decreased. This was attributed to the cleavage and detachment of arabinose and 4-O-methyl-α-D-glucuronic acid branch units from the long xylan chains during the initial phase. Subsequently, the β-1,4-xyloside bonds were broken, and the xylan backbone progressively decomposed into C5+ products. Fig. 2(a) further reveals that alongside the macromolecule breakdown of xylan, small molecular fragments such as methyl and carboxyl groups were generated. The rapid increase in C1–C4 gas products followed a similar trend to the condensable products. At elevated temperatures, macromolecule cleavage occurred more quickly. The number of condensable products began to increase at about 100 ps, particularly at 2800–3000 K, where this increase was more pronounced. It was attributed to the higher temperatures facilitating the further decomposition of C15+ products into lighter condensable products.
Fig. 2(c) illustrates the changes in the quantities of the three types of products during the Ni-catalyzed hydropyrolysis of xylan in the 2000 H2 system under different simulation temperatures. The data showed that the amount of gas products gradually increased with rising temperature. In contrast, the quantity of condensable products remained relatively stable, without significant fluctuations corresponding to the temperature increase. It could be suggested that the notable rise in gas products could primarily be attributed to further decomposition of certain small-molecule gases under high-temperature conditions. Fig. 2(d) provides further details on the evolution of products with different carbon numbers (C1 to C14) as the temperature changes. It was found that with the increase in simulation temperature, the number of C1 products increased, whereas the number of C2 products decreased. Thus, the overall increase in gas products at higher temperatures was mainly due to the continued decomposition of C2 products into C1 products, with only minor changes observed in the quantities of C3 and C4 products. The number of condensable products decreased overall with increasing temperature. The fluctuation in the quantities of the three product categories became minimal at 400 ps, indicating that dynamic equilibrium had been reached. This suggested that a reaction duration of 400 ps was sufficient for the system to stabilize. Moreover, the simulation results indicated that the reaction temperature primarily affected the intermediate stage of the hydropyrolysis process between 40 and 200 ps, with little impact on the product distribution during the later stages of the hydropyrolysis reaction.
3.2 The effect of H2 on xylan hydropyrolysis
To simulate the Ni-catalyzed hydropyrolysis of xylan, a simulation system was constructed consisting of a Ni nanoparticle and xylan chains, with a gradient number of H2. Fig. 3 illustrates the evolution of xylan hydropyrolysis products under varying H2 numbers at 2000 K. The increase in the H2 number significantly affected product distribution during the Ni-catalyzed hydropyrolysis of xylan. As depicted in Fig. 2, during the initial stage of the simulation (0–50 ps), the rapid increase in gas and condensable products was attributed to the detachment of side chains and cleavage of the main xylan chains. As shown in Fig. 3(a)–(d), with increasing H2 number, both gas and condensable products rose. However, at 3000 H2, gas products increased significantly, while condensable products decreased. It could be explained that excessive H2 would facilitate secondary cracking reactions of the hydropyrolysis products.38 Furthermore, HDO reactions reduced carboxyl and phenolic hydroxyl groups in xylose, arabinose, and 4-O-methyl-α-D-glucuronic acid units, resulting in the formation of additional gas products, such as CO, CO2, CH4, C2H4, methanol, and acetic acid.Fig. 3(e) and (f) show the evolution of products with varying carbon numbers and the trends for typical gas and condensable products. As the H2 concentration increased, both C1 products (e.g., CO, CO2, CH4, methanol) and C2 products (e.g., acetic acid) showed a consistent increase, aligning with experimental observations reported by Wu et al.39 that higher H2 concentrations promoted the formation of light hydrocarbons and oxygenates, such as CH4 and acetic acid, during the catalytic pyrolysis of biomass. Among the condensable products in the C5–C14 range, furan and 2-methylfuran steadily increased, which could be explained that higher H2 concentrations enhanced the hydrogenation of furfural to furan and its derivatives during biomass pyrolysis.40 Meanwhile furfural, a representative aldehyde, exhibited a continuous decline, consistent with the HDO mechanism studied by Gupta et al.,41 which elucidates its conversion to furan and 2-methylfuran via hydrogenation and deoxygenation under elevated H2 levels. Interestingly, ketone compounds, including hydroxyacetone, 2-butanone, and cyclopentanone, exhibited an initial increase followed by a decline. This trend could be explained by the partial hydrogenation of intermediate oxygenates leading to the initial increase, and the subsequent decrease due to further hydrogenation and decomposition into saturated hydrocarbons under high H2 concentrations.42
In the field of biomass hydropyrolysis, the efficient removal of oxygen from condensable products is essential for producing bio-oils that meet fuel standards, with higher calorific value, improved stability, and reduced corrosiveness.43 The degree of deoxygenation is commonly used as an indicator of the extent to which oxygen atoms are removed from both gas and condensable products during HDO reactions.44 A higher deoxygenation degree corresponded to a lower oxygen content in the condensable products, which consequently improved the effective H/C ratio and the overall products quality.
Table 1 provides a comparative analysis of the oxygen content and deoxygenation degree of xylan hydropyrolysis. The initial molecular formula of xylan was C56H90O47, with the oxygen content of 49.67 wt%. In the pyrolysis system without Ni and H2, the oxygen content of the three product categories was similar, with the overall oxygen content of 48.57 wt%, and the deoxygenation degree of only 2.21%, which underscored the challenge of high oxygen content in bio-oils produced via fast pyrolysis. In contrast, the hydropyrolysis helped alleviate this issue to a certain extent, as HDO reactions reduced the oxygen content in all product categories. The overall oxygen content decreased to 40.32 wt%, with the deoxygenation degree of 18.82%.
| System | Oxygen content (wt%) | Deoxygenation degree (%) xylan (O-49.67 wt%) | |||
|---|---|---|---|---|---|
| Gas C1–C4 | Light condensable C5–C14 | Heavy condensable C15+ | All products | ||
| 0 H2–Ni | 32.32 | 28.52 | 0.87 | 37.44 | 24.62 |
| 1000 H2–Ni | 14.84 | 4.07 | 0.42 | 12.80 | 74.23 |
| 2000 H2–Ni | 14.80 | 2.19 | 0.31 | 11.89 | 76.06 |
| 3000 H2–Ni | 15.48 | 2.43 | 0.39 | 12.83 | 74.17 |
| 1000 H2–0Ni | 40.88 | 40.43 | 40.52 | 40.32 | 18.82 |
| 0 H2–0Ni | 50.65 | 44.87 | 50.35 | 48.57 | 2.21 |
The introduction of the Ni catalyst effectively enhanced the removal of oxygen, leading to a significant reduction in oxygen content. In the Ni-catalyzed hydropyrolysis system, with the same number of H2 (1000), oxygen content decreased to 12.80 wt%, and the oxygen content in the light condensable products reached 4.07 wt%, resulting in a deoxygenation degree of 74.23%. As the H2 number increased, the oxygen content of the products gradually decreased, although the rate of decrease diminished over time. It could be attributed to the synergistic effect between H2 and Ni, which effectively facilitated HDO reactions. The Ni catalyst promoted the adsorption of reactants and intermediates on the Ni surface, rather than in a highly dispersed state, significantly enhancing the contact between H2 and the reactants. As a result, when the H2 quantity in the catalytic system increased from 0 to 1000, the deoxygenation degree increased dramatically from 24.62% to 74.23%. It was noteworthy that with further increases in H2 number, the deoxygenation degree of the condensable products initially increased, but then decreased. This could be attributed to the fact that a lower H2 concentration initially favored hydrogenation reduction reactions, promoting oxygen removal and thus reducing the oxygen content in the condensable products. However, at higher H2 concentrations, H2 molecules may have saturated the reaction system, leading to excessive adsorption on the catalyst surface, which in turn reduced the reaction selectivity and diminished the deoxygenation efficiency.45 Moreover, the higher H2 number could have led to an increased generation of gas products, which further affected the deoxygenation efficiency of the condensable products.
3.3 Carbon deposition over the Ni catalyst during xylan hydropyrolysis
Carbon deposition was one of the primary causes of catalyst deactivation, particularly in processes such as catalytic cracking and hydropyrolysis. The formation of carbon deposition led to the blockage of catalyst surfaces and pores, inhibiting the effective utilization of active sites and subsequently reducing catalytic efficiency.46,47 The carbon deposition effect thus has become a significant issue in catalyst research. In the field of biomass catalytic pyrolysis, there were differing views on the mechanism of carbon deposition formation. Some studies suggested that carbon deposition occurred primarily within the catalyst, particularly in the pores or lattice, leading to catalyst deactivation.48 Other studies argued that carbon deposition was predominantly formed on the catalyst surface, where surface-adsorbed carbon species occupied active sites, thereby limiting catalyst regeneration.49As illustrated in Fig. 4(a), the radial distribution function (RDF) of the Ni nanoparticle was analyzed, categorizing the Ni catalyst into surface and core regions. Specifically, the region with a radius between 18 Å and 20 Å was assigned to the surface layer, while the region with a radius smaller than 18 Å was assigned to the core layer. A clearer understanding of the distribution and formation mechanisms of carbon deposition was enabled by this approach, offering a theoretical foundation for the investigation of catalyst deactivation.
The variation of cross-sectional views of the Ni nanoparticle over the simulation time is illustrated in Fig. 4(b)–(h) show the evolution of C, H, and O atoms over the Ni nanoparticle at 2000 K with the reaction time. Prior to the reaction, the reactants and H2 were highly dispersed around the Ni catalyst. As shown in Fig. 4(f)–(h), during the primary stages of the reaction (0–20 ps), the concentration of C, H, and O atoms on the Ni surface increased significantly. It could be seen that the reactants and H2 rapidly adsorbed onto the catalyst surface. In the subsequent stages, C, H, and O atoms gradually diffused into the interior of the Ni catalyst, with the number of Inner_C, H, and O atoms rising sharply. As illustrated in Fig. 4(c) and (d), the onset of carbon deposition was evident at 50 ps, and this phenomenon became more pronounced at 200 ps. Fig. 4(f) further reveals that both Surface_C and Inner_C over the Ni catalyst exhibited a stable growth trend, with Inner_C content surpassing the Surface_C. This suggested that although Surface_C predominates in the early reaction stages due to adsorption of the reactants, as the reaction progresses, the Inner_C accumulation gradually intensifies, primarily occurring within the pores and crystal lattice of the Ni catalyst.
The carbon deposition was likely intricately related to the pore structure, surface active sites, and diffusion behavior of reactant molecules over the Ni catalyst. During the early stages of the reaction, reactants and H2 primarily reacted at the active sites on the surface, leading to a rapid accumulation of Surface_C. As the reaction progressed, some C, H, and O atoms diffused into the interior of the catalyst, resulting in Inner_C deposition. The deposited carbon likely infiltrated the micropores and crystal lattice of the catalyst, gradually occupying its internal space and affecting both the porosity and surface activity, thereby reducing its catalytic efficiency. Moreover, over time, the accumulation of carbon deposition not only compromised the structural stability of the catalyst but also potentially led to surface coverage and blockage of active sites, resulting in a gradual decline in the catalytic performance.
Interestingly, as illustrated in Fig. 4(g) and (h), the number of O atoms within the Ni catalyst initially increased and then gradually decreased. The concentration of O atoms within the Ni catalyst peaked around 200 ps, and the number of Inner_O had diminished significantly at 400 ps. It could be explained by the fact that, as a typical transition metal, Ni was capable of adsorbing and incorporating atoms such as oxygen into its lattice sites under high temperature and pressure conditions. Once the oxygen atoms saturated the Ni surface, they were diffused into the interior of the catalyst. However, due to the presence of high-pressure H2 in the system, its strong reducing nature facilitated the entry of hydrogen molecules into the catalyst, resulting in the formation of volatile H2O molecules, thereby removing oxygen from the catalyst.
The variation of C, H, and O atoms over the Ni nanoparticle at 2000 K with the gradient H2 number is illustrated in Fig. 4(i)–(k). The increase in H2 concentration led to an increase in H atoms and a decrease in O atoms within the catalyst, owing to diffusion effects and the strong reducing nature of H2. Moreover, the increase in H2 effectively suppressed the carbon deposition over the Ni catalyst. As shown in Fig. 4(i), the introduction of H2 resulted in a significant increase in Surface_C on the Ni catalyst, owing to synergistic reactions between the reactants and H2 at the Ni catalytic sites. As the H2 number increased to 2000, carbon deposition on both the surface and interior of the Ni sphere was significantly reduced, due to H2's role in promoting hydrocarbon cracking and aromatization reactions, which decreased both Surface_C and Inner_C. However, at an H2 number of 3000, a slight rebound in carbon deposition over the Ni catalyst was observed. It could be explained that the excessive H2 may have led to the over-reduction of metal species on the Ni catalyst surface, resulting in the formation of metal hydrides like NiH and NiHx,50 thereby diminishing the catalytic activity.
3.4 Catalytic mechanism of the Ni catalyst during xylan hydropyrolysis
Fig. 5 illustrates the reaction processes of xylan hydropyrolysis under Ni-catalyzed and noncatalytic conditions, with the H2 atmosphere represented by the blue annulus. The left corresponded to noncatalytic hydropyrolysis, and the right depicted Ni-catalyzed hydropyrolysis. The reactions in both cases were subdivided into five stages: physical and chemical adsorption, pyrolysis, HDO, rearrangement and cracking, and desorption. Representative moments of each stage were captured using the visualization software OVITO, and chemical reaction statistics were generated using RMD_tools for a comparative analysis of the impact of the Ni catalyst on the reaction pathway of xylan hydropyrolysis.Under the noncatalytic system, xylan chains primarily underwent physical adsorption with the surface via van der Waals forces, which arise from transient dipoles between molecules. The weak interactions resulted in loose adsorption, leading to a short residence time of the reactants on the surface and, consequently, reduced reaction efficiency. Additionally, H2 was less effectively activated under these conditions, leading to slower reaction rates and lower selectivity. In contrast, under the Ni-catalyzed system, reactants and H2 were chemically adsorbed onto the Ni catalyst surface through stronger interactions, such as covalent bonding. The active sites on the catalyst surface effectively activated H2 and facilitated strong adsorption of reactants and intermediates. This chemical adsorption provided stable sites for hydropyrolysis and HDO reactions, significantly enhancing both the reaction rate and selectivity.
As the system temperature increased, the pyrolysis reaction began, resulting in the cleavage and detachment of the arabinose and 4-O-methyl-α-D-glucuronic acid branching units from the xylan chains. Simultaneously, the β-1,4-glycosidic bonds linking the xylose units in the main chain of xylan broke, resulting in the formation of numerous hydroxyl-containing units (R–OH) and hydroxyl radicals (HO·). Analysis of the chemical reaction statistics generated by RMD_tools revealed that the HDO process of reactants and intermediates during hydropyrolysis predominantly relied on H· rather than H2. It was contributed to the higher reactivity and lower activation energy of active H·. H2 was relatively stable (with an H–H bond energy of approximately 436 kJ mol−1) and thus less likely to directly react with oxygen or carbon atoms in organic molecules under noncatalytic conditions. During the xylan hydropyrolysis, H·, as a free radical, could quickly react with oxygen-containing functional groups such as hydroxyl and carbonyl groups, facilitating the HDO reaction. The H· in the xylan hydropyrolysis primarily originated from reactions 1 and 2 (reaction 1: R–OH → R· + HO·, reaction 2: H2 + HO· → H· + H2O), where H2 combined with the HO· radicals. Under Ni-catalyzed conditions, the abundant active sites on the catalyst surface significantly enhanced the cleavage of H2 (reaction 4: H2 → H· + H·), generating a large number of H·. These H· could further combine with the free HO· (reaction 2: H2 + HO· → H· + H2O) and participate in the HDO reactions (reaction 3: R–OH + H· → R· + H2O, reaction 5: R· + H· → R), which accelerated the reaction rate and improved efficiency, thereby promoting the effective conversion and deoxygenation of intermediates. As a result, more 2-methylfuran, furan, cyclopentanone, acetone, methane, and ethylene were formed, while the yields of furfural and hydroxyacetone significantly decreased. As shown in Table 1, the incorporation of the Ni catalyst led to a marked reduction in the oxygen content of the three product categories and a significant increase in the overall deoxygenation level, further confirming the catalytic enhancement effect of Ni in the xylan hydropyrolysis.
During the xylan hydropyrolysis, the Ni catalyst significantly enhanced the kinetic performance of cracking and rearrangement reactions, while improving the selectivity and quality of the products. As shown in Table 2, by providing metal active sites, the Ni catalyst effectively lowered the activation energy of cracking reactions, thereby increasing the cracking rate of xylan molecules and enhancing the selectivity of the cracking process, which resulted in a significant reduction of by-products such as coke and CO2. Simultaneously, the Ni catalyst also facilitated the rearrangement reactions of cracking products, including isomerization and aromatization, further optimizing the product distribution and generating more alkenes (e.g., methane, ethylene), cycloalkanes (e.g., cyclopentane, cyclopentanone), and furan derivatives (e.g., furan, dimethylfuran). In general, the Ni catalyst accelerated cracking, promoted deoxygenation, and facilitated rearrangement reactions, significantly enhancing the reaction efficiency and optimizing the composition of the products, which led to higher-quality outputs in the xylan hydropyrolysis.
| System | Fitting formula (R2) | Ea (kcal mol−1) | |
|---|---|---|---|
| This work | Ref. | ||
| 0 H2–Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 6.80–13 k = 6.80–13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211.41/T(0.99118) 211.41/T(0.99118) |
26.25 | 24.02–40.93(ref. 13 and 51) |
| 1000 H2–Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 6.59–12 k = 6.59–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.80/T(0.98018) 298.80/T(0.98018) |
24.44 | |
| 2000 H2–Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 6.54–11 k = 6.54–11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 901.45/T(0.98574) 901.45/T(0.98574) |
23.65 | |
| 3000 H2–Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 5.94–10 k = 5.94–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031.38/T(0.99179) 031.38/T(0.99179) |
19.93 | |
| 0 H2–0Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 8.94–21 k = 8.94–21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199.29/T(0.99740) 199.29/T(0.99740) |
42.12 | 29.17–47.80(ref. 52–54) |
| 1000 H2–0Ni | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = 8.17–18 k = 8.17–18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680.99/T(0.98254) 680.99/T(0.98254) |
37.12 | |
3.5 Global kinetic analysis of xylan hydropyrolysis
The global kinetics of xylan hydropyrolysis were also studied. The first-order kinetic equations are commonly employed in the study of reaction kinetics during MD simulations.35,55,56 Thus, it was assumed that the reaction process in this research followed first-order kinetics, and the chemical reaction rate of xylan hydropyrolysis was calculated accordingly. The global activation energy for the xylan hydropyrolysis system was subsequently determined using the Arrhenius equation. The first-order kinetic equation is presented in eqn (1):
 | (1) |
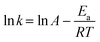 | (2) |
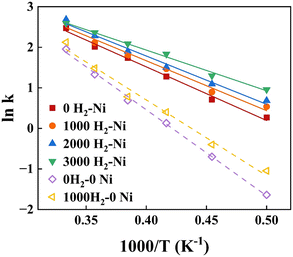
The kinetic fitting results of xylan hydropyrolysis under different systems are shown in Fig. 6. And the corresponding Arrhenius equations and activation energies (Ea) are presented in detail in Table 2. The introduction of the Ni catalyst significantly reduced the global activation energy of xylan hydropyrolysis from 37.12 kcal mol−1 to 24.44 kcal mol−1 compared to the noncatalytic system, under the same H2 number (1000). Furthermore, the global activation energy of the catalytic system under different H2 numbers was also analyzed, revealing that the introduction of H2 could reduce the global activation energy to some extent, although the effect was less pronounced than that of the Ni catalyst. Compared to previous experimental studies, the activation energy ranges for xylan hydropyrolysis and catalytic hydropyrolysis were 29.17–47.80 kcal mol−1 and 24.02–40.93 kcal mol−1 respectively.
The consistency between the experiments and simulation results demonstrated that the ReaxFF-MD simulation method employed in this study could effectively describe the reaction kinetics of xylan hydropyrolysis, particularly the reaction pathways and energy changes under the influence of Ni catalysts. It was worth noting that the activation energy of the Ni-catalyzed system in the simulations was slightly lower than the lower limit reported in experimental references. The discrepancy might have been attributed to high dispersion of Ni nanoparticles and optimized distribution of active sites on their surfaces in simulated systems. The precise control over the microstructure and reaction environment for catalysts allowed by simulation possibly contributed to higher catalytic efficiency.
4. Conclusions
The Ni-catalyzed hydropyrolysis of xylan was investigated using ReaxFF-MD simulations. The effects of temperature and H2 on the distribution of xylan hydropyrolysis products were studied, along with the reaction mechanism and carbon deposition over the Ni catalyst. The kinetic behavior of xylan during Ni-catalyzed hydropyrolysis was also analyzed.The results showed that the Ni catalyst not only provided substantial active sites which enabled xylan molecules and H2 to interact, but also reduced the global activation energy of xylan hydropyrolysis, significantly enhancing the pyrolysis and HDO reactions. Additionally, the Ni catalyst further optimized the product distribution by guiding the rearrangement and cracking reactions, leading to the enhanced formation of alkenes, cycloalkanes, and furan derivatives. The enhanced HDO reactions by the introduction of the Ni catalyst led to a significant reduction in the oxygen content of the xylan hydropyrolysis products, with the overall oxygen content dropping to 12.8 wt% and the deoxygenation degree reaching 74.23%. Moreover, the hydrogenation process effectively suppressed carbon deposition over the Ni catalyst, but excessive H2 could lead to over-reduction of the catalyst surface, thereby diminishing the catalytic activity. This research could provide a deeper insight into the catalytic mechanism and kinetic characteristics of xylan hydropyrolysis, offering valuable theoretical support for the future optimization of catalytic hydropyrolysis processes.
Data availability
All data included in this study are available upon request by contact with the corresponding author.Author contributions
Hong Xian: conceptualization, data curation, formal analysis, software, visualization, and writing – original draft. Linjia Yin: software. Xiangkun Zhang: software and data curation. Muye Feng: supervision, software, and validation. Kaige Wang: conceptualization, funding acquisition, project administration, supervision, writing – review & editing.Conflicts of interest
No potential conflict of interest was reported by the authors.Acknowledgements
The authors would like to acknowledge financial support from the National Key R&D Program of China (Grant No. 2023YFE0111600), the National Natural Science Foundation of China (Grant No. 52236011), the Fundamental Research Funds for the Central Universities (Grant No. 2022ZFJH004), and the Zhejiang Provincial Natural Science Foundation of China (Grant No. LTGS23E060001).References
- R. K. Srivastava, N. P. Shetti, K. R. Reddy, E. E. Kwon, M. N. Nadagouda and T. M. Aminabhavi, Environ. Pollut., 2021, 276, 116731 CAS.
- A. Ebringerová, Z. Hromádková and T. Heinze, in Polysaccharides I: Structure, Characterization and Use, ed. T. Heinze, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 1–67, DOI:10.1007/b136816.
- J. Rao, Z. Lv, G. Chen and F. Peng, Prog. Polym. Sci., 2023, 140, 101675 CAS.
- M. Sharifzadeh, M. Sadeqzadeh, M. Guo, T. N. Borhani, N. V. S. N. Murthy Konda, M. C. Garcia, L. Wang, J. Hallett and N. Shah, Prog. Energy Combust. Sci., 2019, 71, 1–80 Search PubMed.
- P. Li, X. Shi, X. Wang, J. Song, S. Fang, J. Bai, G. Zhang, C. Chang and S. Pang, J. Cleaner Prod., 2021, 328, 129613 CrossRef CAS.
- F. L. P. Resende, Catal. Today, 2016, 269, 148–155 CAS.
- M. Z. Stummann, M. Høj, J. Gabrielsen, L. R. Clausen, P. A. Jensen and A. D. Jensen, Renewable Sustainable Energy Rev., 2021, 143, 110960 CAS.
- T. M. H. Dabros, M. Z. Stummann, M. Høj, P. A. Jensen, J.-D. Grunwaldt, J. Gabrielsen, P. M. Mortensen and A. D. Jensen, Prog. Energy Combust. Sci., 2018, 68, 268–309 CrossRef.
- M. Z. Stummann, A. B. Hansen, L. P. Hansen, B. Davidsen, S. B. Rasmussen, P. Wiwel, J. Gabrielsen, P. A. Jensen, A. D. Jensen and M. Høj, Energy Fuels, 2019, 33, 1302–1313 CrossRef CAS.
- T. Li, J. Su, H. Wang, C. Wang, W. Xie and K. Wang, Appl. Energy, 2022, 316, 119115 CrossRef CAS.
- B. Zhou, X. Liu, F. L. P. Resende, J. Zhou, M. Wang and A. B. Dichiara, ACS Sustainable Chem. Eng., 2021, 9, 10827–10836 CrossRef CAS.
- H. Xia, L. Zhang, H. Hu, S. Zuo and L. Yang, Nanomaterials, 2020, 10(1), 73 CrossRef CAS PubMed.
- Nishu, C. Li, M. Chai, M. M. Rahman, Y. Li, M. Sarker and R. Liu, Renewable Energy, 2021, 175, 936–951 CrossRef CAS.
- G. Dai, G. Wang, K. Wang, Z. Zhou and S. Wang, Proc. Combust. Inst., 2021, 38, 4241–4249 CrossRef CAS.
- T. Hansson, C. Oostenbrink and W. van Gunsteren, Curr. Opin. Struct. Biol., 2002, 12, 190–196 CrossRef CAS PubMed.
- L. Yin, M. Feng, T. Li, J. Su, H. Xian, X. Zhang, H. Wang, H. Li and K. Wang, Chem. Eng. J., 2024, 488, 150811 CrossRef CAS.
- Z. Liu, X. Ku and H. Jin, ACS Omega, 2022, 7, 21075–21085 CrossRef CAS PubMed.
- Z. Hu and L. Wei, J. Compos. Sci., 2023, 7(9), 354 CAS.
- C. Chen, L. Zhao, J. Wang and S. Lin, Ind. Eng. Chem. Res., 2017, 56, 12276–12288 CrossRef CAS.
- J. B. Huang, D. Wu, H. Tong and W. M. Li, J. Energy Inst., 2013, 86, 189–193 CrossRef CAS.
- X. Zhou, W. Li, R. Mabon and L. J. Broadbelt, Energy Environ. Sci., 2018, 11, 1240–1260 RSC.
- B. Hu, W.-L. Xie, H. Li, K. Li, Q. Lu and Y.-P. Yang, Proc. Combust. Inst., 2021, 38, 4215–4223 CrossRef CAS.
- X.-M. Cheng, Q.-D. Wang, J.-Q. Li, J.-B. Wang and X.-Y. Li, J. Phys. Chem. A, 2012, 116, 9811–9818 CrossRef CAS PubMed.
- X. Li, M. Zheng, C. Ren and L. Guo, Energy Fuels, 2021, 35, 11707–11739 CrossRef CAS.
- C. Ashraf, A. Jain, Y. Xuan and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2017, 19, 5004–5017 RSC.
- F. A. Lindemann, Phys. Z., 1910, 11, 609–612 CAS.
- D. Errandonea, B. Schwager, R. Ditz, C. Gessmann, R. Boehler and M. Ross, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 132104 CrossRef.
- D. Errandonea, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 054108 CrossRef.
- C. Chen, R. Volpe and X. Jiang, Appl. Energy, 2021, 302, 117557 CrossRef CAS.
- A. Chatzigoulas, K. Karathanou, D. Dellis and Z. Cournia, J. Chem. Inf. Model., 2018, 58, 2380–2386 CrossRef CAS PubMed.
- Q. Jiang, H. M. Lu and M. Zhao, J. Phys.: Condens. Matter, 2004, 16, 521 CrossRef CAS.
- J. M. Martínez and L. Martínez, J. Comput. Chem., 2003, 24, 819–825 CrossRef PubMed.
- B. V. Merinov, J. E. Mueller, A. C. T. van Duin, Q. An and W. A. Goddard III, J. Phys. Chem. Lett., 2014, 5, 4039–4043 CrossRef CAS PubMed.
- M. Yu, C. Chen, Z. Xing and X. Jiang, Int. J. Hydrogen Energy, 2023, 48, 123–137 CrossRef CAS.
- J. Yu, Q. Dang, T. Wu, Y. Wu, T. Lei and F. Qi, J. Anal. Appl. Pyrolysis, 2023, 175, 106212 CrossRef CAS.
- F. Xu, H. Liu, Q. Wang, S. Pan, D. Zhao, Q. Liu and Y. Liu, Fuel Process. Technol., 2019, 195, 106147 CrossRef CAS.
- T.-R. Shan, A. C. T. van Duin and A. P. Thompson, J. Phys. Chem. A, 2014, 118, 1469–1478 CAS.
- J. Lin, S. Liu, Z. Han, R. Ma, C. Cui and S. Sun, Chem. Eng. J., 2023, 452, 139551 CrossRef CAS.
- C. Wu, Z. Wang, J. Huang and P. T. Williams, Fuel, 2013, 106, 697–706 CrossRef CAS.
- C. Zhao and J. A. Lercher, Angew. Chem., Int. Ed., 2012, 51, 5765 CrossRef CAS.
- K. Gupta, R. K. Rai and S. K. Singh, ChemCatChem, 2018, 10, 2326–2349 CrossRef CAS.
- A. Bjelić, M. Grilc, M. Huš and B. Likozar, Chem. Eng. J., 2019, 359, 305–320 Search PubMed.
- P. Lahijani, M. Mohammadi, A. R. Mohamed, F. Ismail, K. T. Lee and G. Amini, Energy Convers. Manage., 2022, 268, 115956 CAS.
- M. W. Nolte and B. H. Shanks, Energy Technol., 2017, 5, 7–18 CAS.
- L. He, Y. Huang, A. Wang, Y. Liu, X. Liu, X. Chen, J. J. Delgado, X. Wang and T. Zhang, J. Catal., 2013, 298, 1–9 CAS.
- J. Huo, J.-P. Tessonnier and B. H. Shanks, ACS Catal., 2021, 11, 5248–5270 CAS.
- D. Sutton, B. Kelleher and J. R. H. Ross, Fuel Process. Technol., 2001, 73, 155–173 CAS.
- E. T. C. Vogt, D. Fu and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2023, 62, e202300319 CAS.
- X.-W. Liu, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, Surf. Sci., 2012, 606, 733–739 CAS.
- J. Li, Y. Ma, J. C. Ho and Y. Qu, Acc. Chem. Res., 2024, 57, 895–904 CAS.
- Nishu, C. Li, D. Yellezuome, Y. Li and R. Liu, Renewable Energy, 2023, 209, 569–580 CrossRef CAS.
- L. Zhou, Y. Jia, T.-H. Nguyen, A. A. Adesina and Z. Liu, Fuel Process. Technol., 2013, 116, 149–157 CrossRef CAS.
- K. Cheng, W. T. Winter and A. J. Stipanovic, Polym. Degrad. Stab., 2012, 97, 1606–1615 CrossRef CAS.
- W.-H. Chen, C. F. Eng, Y.-Y. Lin and Q.-V. Bach, Energy Convers. Manage., 2020, 221, 113165 CrossRef CAS.
- M. Feng, X. Z. Jiang and K. H. Luo, Proc. Combust. Inst., 2019, 37, 5473–5480 CrossRef CAS.
- M. Wei, S. Wu, Q. Mao, Y. Wang, G. Guo and D. Zhang, Fuel, 2020, 275, 117989 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |