 Open Access Article
Open Access ArticleA theoretical framework to understand high electron mobilities in cable bacteria
Andrew J. Smitha and
David N. Beratan *abc
*abc
aDepartment of Chemistry, Duke University, Durham, NC 27708, USA
bDepartment of Physics, Duke University, Durham, NC 27708, USA
cDepartment of Biochemistry, Duke University, Durham, NC 27710, USA. E-mail: andrew.smith@duke.edu; david.beratan@duke.edu
First published on 19th January 2026
Abstract
Cable bacteria contain electron-transport pathways that are among the longest found in living systems, reaching the centimeter scale. These bacteria have very high electrical conductivities, and the electron- transport mechanism is poorly understood. We performed theoretical analysis to assess possible transport mechanisms in cable bacteria. While earlier studies suggested that extended carrier delocalization or the formation of large polarons might explain the measured conductivities, we find that vibronically coupled multi-step hopping appears to dictate the biological electron transport mechanisms on these very large length scale.
1 Introduction
Cable bacteria (CB) form filamentous, multicellular organisms with thousands of cells connected end-to-end in single file, and these multicellular organisms share a common outer membrane. CB possess cylindrical conductive structures embedded in a shared outer membrane, and these conductive structures are known as fibers. These multicellular organisms can grow to centimeter lengths, and it is believed1 that the redox potential drop between their two ends is correlated to their metabolism. CB oxidize sulfides at a buried terminus (low-oxygen environment) and reduce oxygen at the other end.2,3 CB were found to have high electrical conductivities (0.01–536 S cm−1).1,4 These values compare to conductivities <0.1 S cm−1 in OmcS bacterial nanowires,5 ∼30 S cm−1 in OmcZ bacterial nanowires5 and ∼10 S cm−1 in polyaniline-based conducting polymers.6 The high conductivity of CB was attributed to extended delocalization of electrons (over at least 10 nm length scales),7,8 or to the formation of large polarons.9 These suggested conduction mechanisms contrast with the small polaron hopping that is found elsewhere in biological energy transducing systems at shorter distances, where weak site–site interactions and disorder limit carrier delocalization. In our study, we find that incoherent multi-step hopping (engaging small polarons) can explain the observed high electrical mobility of CB. To address the novel 3D structure of CB, our study goes beyond existing linear transport network models that were established earlier to describe transport in highly conductive bacterial nanowires.10 We develop a model for the complex interconnected conducting networks of CB (see Section 2.1) and formulate a coarse grained strategy to treat the extraordinary centimeter scale transport in CB (see Section 2.3).1.1 Structural models for cable bacteria
The modeling choices made in our study are motivated by structural data that are available for CB. CB feature a shared extracellular, protein-rich matrix which is referred to as the fiber sheath after much, but not all, of the non-conductive material is chemically removed (see Fig. 1). Many parallel ridges in the sheath run the length of the sheath, and underneath the ridges are conductive fibers buried within the periplasm. CB that are probed in electrical measurements typically have 50–60 fibers.1,11 These fibers are joined by a cartwheel junction (indicated in blue in Fig. 1A) every ∼4 µm.11 | ||
| Fig. 1 Panel (A) shows transmission electron microscopy images of CB (adapted from Cornelissen et al.11) the dark lines (highlighted in orange) are the conductive fibers. The box to the left in blue indicates the structure of a conductive cartwheel junction. CB have ∼50–60 fibers11 (we assume 60 in our modeling). Panel (B) shows a schematic representation of the CB conductive sheath (i.e., the CB with much, but not all, of the non-conductive material chemically removed). See ref. 1, 4, 9 and 11 for a description of the fiber sheath extraction and preparation process. In Panel (B) (and throughout this paper) blue indicates cartwheel structures and orange indicates the conductive fibers. This schematic shows only 8 fibers and a single junction, for simplicity. | ||
Conducting atomic force microscope (AFM) measurements on CB indicate that the protein sheath is conductive1,4 and this conductivity is believed to originate from the fibers.7,8,12 Electrical experiments on the CB are typically performed on the extracted protein sheaths.1,4,13 An extracted sheath is represented schematically in Fig. 1B. Each conducting fiber has a diameter of >20 nm.11 Each of these fibers, in turn, contains many smaller individual conduction channels with a diameter of ∼2 nm.7,14 It is challenging to link chemical structure to transport mechanism(s). When structural data is very limited, forging this link is even more challenging. CB appear to contain a novel nickel-based cofactor could play a role in mediating charge flow.1 Within this limited structural context, we build a model for conduction in CB.
1.2 Experimental transport properties of CB
Electrical conductivities and mobilities are widely reported for CB. Electrical conductivity (σ) measures how the current density (J) varies with electric field (E): J = Eσ.15 The conductivity is proportional to the current density. The current density is the product of the average velocity of the particles that carry charge (〈v〉), the density of charge-carrying particles (n), and the particle charge (q): J = 〈v〉qn.15 The carrier density (n) is determined by the number of carriers per unit volume and thus by the placement of the carrier binding sites in the structure. 〈v〉 depends on the charge-carrier dynamics.15,16 The conductivity is defined as σ = nq〈v〉/E or σ = nqµ. Here, µ = 〈v〉/E is the electrical mobility.16 The electrical mobility describes how the carriers respond to applied electric fields.16 In this study, and in previous referenced experimental studies,13 the mobility is taken to be an intrinsic material property – not dependent on the applied electric field. As such, we will consider and model the mobility as an intrinsic property namely, the low-field, mobility defined as µ = lim|E|→0〈v〉/E which is commonly used when discussing the electrical properties of materials.17,18 The absence of an applied field allows us to neglect drift in our later random walk models. The fundamental relationship between the mobility and the charge transport mechanism motivates our modeling approach to the CB electrical mobilities.Electrical mobilities in CB derived from field effect transistor measurements are ∼0.19 cm2 V−1 s−1.13 A mobility of this magnitude is large for biological structures.13 Bacterial nanowires of Geobacter, for example, have mobilities of ∼0.01 cm2 V−1 s−1.19 One aim of our theoretical modeling is to understand the source(s) of the high conductivities and mobilities in CB. We focus on modeling the in vitro CB probed in the experiments.
Marine CB conductivity values are wide ranging, spanning four orders of magnitude (from 100s S cm−1 to 0.01 S cm−1).4,8,9 The values have a relative standard deviation of >300%. In CB, the highest observed conductivities are more than 20 times larger than the typical inter-quartile range outlier definition (see SI for analysis of published conductivity data).20,21 The origin of these wide ranging conductivity values is not understood quantitatively (although it is likely due at least in part to the experimental sample preparation), and it is challenging to assess which values are most relevant when developing minimalistic models (see SI for details on the variations in conductivity).
Despite the range of measured conductivity values, the measured electrical mobilities for CB are of the same order of magnitude, around ∼0.19 cm2 V−1 s−1.13 Experimental mobilities are more difficult to measure than conductivities, and mobility data are less frequently reported. At 300 K,13 >200 conductivity values are found in the literature for CB, while only four mobilities are found. We focus our modeling on mobilities, since the mobility most directly encodes the charge transport mechanism. In contrast, the conductivity encodes the mechanism via its dependence on the mobility and adds an additional explicit dependence on the charge carrier density. The small number of mobility measurements is a limitation, as future measurements may reveal a wider range of mobilities. However, we hope that future measurements of the mobility will present an opportunity to confirm (or reject) the theoretical model presented in this study (with mobility measurements around 0.1 cm2 V−1 s−1 consistent with the model and values that are orders of magnitude greater than 0.1 cm2 V−1 s−1 inconsistent with the model).
2 Hopping transport model
2.1 Kinetic model for CB transport
Neither the chemistry of the redox-active units nor their precise organization in the CB are known. We used the limited structural and compositional information to estimate the packing of the redox active units in the CB. We base our analysis on the assumption that transport occurs through a set of connected one-dimensional hopping paths that form a complex hopping network. Analysis based on a 3D lattice hopping model (see SI) finds qualitatively similar conclusions. We model the CB hopping network as consisting of N one-dimensional linear hopping chains which trace the path of the fibers and continue through star-shaped interconnections (cartwheels) (Fig. 2). It is crucial to note that we model a network composed of a single one of the smaller 2 nm diameter individual conduction channels in electrical isolation from other conduction channels. How these individual conduction channels interact is not known exactly; in the SI we demonstrate how this assumption of electrical independence can be relaxed. Although, for simplicity, we primarily depict the large electrical path through fibers and junctions, our model represents a single (much smaller) conduction channel which follows the geometry of these larger structures. | ||
| Fig. 2 Schematic representation of the hopping network model for CB. Squares (all colors) represent redox active units and the lines indicate hopping connections among them. All structures in orange are associated with fibers (pale orange represents obstructed features), and features in blue correspond to the cartwheels. The yellow squares are branch points, and the paths connecting them to the dark blue hub is denoted a spoke. For simplicity, the figure shows only 3 junctions; typical CB would have 100–1000 junctions11. Only 8 fibers are shown; typical CB would have 50–60 (ref. 11). | ||
The number of hopping sites in the fibers and cartwheels was estimated based on the hopping site placement in bacterial nanowires. We assume a center-to-center hopping site separation of 1 nm, typical of bacterial nanowires.22 The length of a fiber between two junctions of the nearest cartwheel (4 µm) is about twice the radius of the cartwheel structures (2 µm), based on the measurements of scanning electron microscopy.11 The diameter of the fibers is ≥20 nm.
The 1D fibers were estimated to have ∼4000 hopping sites between pairs of cartwheels, based on the structure of the CB11 and the assumed nanometer-scale hopping site separation found in bacterial nanowires. Using similar reasoning, we estimate 2000 electron transfer sites between the hub and the edge of each cartwheel structure (i.e., the spoke). Individual fibers persist for the entire CB length (cm scale), despite the fact that cartwheels occur about every 4 µm.
In the model developed here, electrons can hop between nearest-neighbor redox groups. Each hopping site at a branch point (the intersection of a spoke and a fiber) has three nearest neighbors. The cartwheel hubs contain 60 nearest neighbor redox groups (see Fig. 1A).11 All hopping sites, other than those at the branch points and hubs, have 2 nearest neighbors. We model the conductive properties as being uniform in the fibers and junctions. This assumption of uniformity is discussed further in the SI.
2.2 Kinetic analysis of the fiber-hub-cartwheel networks
To describe the electron mobility in the hopping network model, we use the Einstein–Smoluchowski relation
 | (1) |
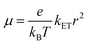 | (2) |
Our earlier model for transport in bacterial nanowires was based on nearest-neighbor hopping among periodically spaced charge localizing sites, and the carrier motion was assumed to be uncorrelated.10 Conduction in CB proceeds through many conducting fibers that are interconnected by cartwheel structures (see Fig. 1).11,12 We investigate how the 3D structure of CB may influence their electrical mobilities; we also explore the validity of approximating transport within arms of the CB using 1D hopping models. One-dimensional approximations to the hopping transport in arms of the CB may overestimate the mobility, because mobility drops with transport network dimensionality in periodic structures.26
The mean first passage time (MFPT) through a network describes how long it takes, on average, for a particle to travel a distance from its starting point. We calculate the ratio of the mean first passage times 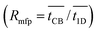 for CB models (built of cartwheel structures joined by linear chains – see Fig. 3A) compared to purely linear 1D chains (Fig. 3B). The hopping rates between nearest-neighbor sites are identical and equal to kET in the two models.
for CB models (built of cartwheel structures joined by linear chains – see Fig. 3A) compared to purely linear 1D chains (Fig. 3B). The hopping rates between nearest-neighbor sites are identical and equal to kET in the two models.
 | ||
| Fig. 3 Panel (A) shows the hopping network model for a CB as summarized in Fig. 2. Panel (B) shows that the CB network model reduced to an effective 1D chain without branching or converging paths. Sites in the 1D chain model are rendered in black in (B). All of the sites in this effective 1D model have two nearest neighbors (i.e., the distinction between the junction, hub, spoke, and fiber sites is suppressed). Both models maintain the geometry and color conventions in Fig. 2. In both panels, green outlines indicate hopping sites at the termini of the CB; these sites are used in the end-to-end MFPT analysis. The figure also indicates that all hopping rates, ki, are equal. | ||
We calculate MFPTs for these networks. MFPT analysis is favored over analyzing diffusion coefficients, since computing diffusion properties requires long-time simulations and trajectory averaging;23 MFPTs only require trajectory averaging. This allows us to run many more short simulations in parallel, making the calculations accessible. We use an unbiased random walk (see SI) to simulate electron hopping in linear 1D models for the CB and also in the multi-chain network with cartwheels (see Fig. 3). We calculate the first passage time from one end of the network to the other (start and end points indicated with green outlines in Fig. 3) for individual random walks by computing m/kET, where m is the number of steps taken to travel from end to end (see Fig. 3). To obtain MFPTs, we average the first passage times on many random walk trajectories. The convergence of the computations is described in the SI. Note that for a 1D chain the MFPT can be calculated analytically and we calculate 1D MFPTs numerically only to validate the random walk code (validation in SI).
Assuming equal nearest-neighbor hopping rates between redox groups in both the 1D and branched CB models, the ratio of the mean first passage times is equal to the inverse ratio of the corresponding mobilities (along the long transport axis, see SI).
 | (3) |
2.3 Coarse-graining of the transport networks
We are simulating transport through CB on the centimeter length scale. A 1 cm long CB with hopping sites spaced by <3 nm contains about 109 hopping sites. A 1D chain with this number of sites, and an unbiased random walk, requires an average of 1018 hops for end-to-end traversal.24 To enable the simulation of structures on this scale, we use coarse-graining.The coarse-graining defines effective redox active sites (depicted in green in Fig. 4) of diameter  at each branch point or hub. A redox site within a distance
at each branch point or hub. A redox site within a distance 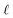 of the branch point or hub is absorbed into the coarse-grained bead (see Fig. 4). The remainder of the hopping network (fibers or spokes) is broken into clusters of
of the branch point or hub is absorbed into the coarse-grained bead (see Fig. 4). The remainder of the hopping network (fibers or spokes) is broken into clusters of  sites that are each merged into an effective site. Because we assumed a low carrier density, the effective redox sites are occupied by one or zero electrons (we further justify the low mobility assumption in the SI).
sites that are each merged into an effective site. Because we assumed a low carrier density, the effective redox sites are occupied by one or zero electrons (we further justify the low mobility assumption in the SI).
 | ||
Fig. 4 Summary of the coarse-graining procedure for the branched CB networks, illustrated with 4 fibers, 2 junctions, and an effective site diameter of 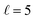 . The effective site diameter is the number of physicalsites traversed in each coarse-grained hop. The figure uses the color coding of Fig. 2. Panel (A) indicates the network with all redox units before coarse graining. Panel (B) shows the network with all effective redox units. Panel (C) shows how each effective unit replaces many physical redox site units, based on their spatial position within an effective coarse graining diameter. Panel (C) also shows that the distance traveled (in physical redox sites) for hopping between effective sites is constant. . The effective site diameter is the number of physicalsites traversed in each coarse-grained hop. The figure uses the color coding of Fig. 2. Panel (A) indicates the network with all redox units before coarse graining. Panel (B) shows the network with all effective redox units. Panel (C) shows how each effective unit replaces many physical redox site units, based on their spatial position within an effective coarse graining diameter. Panel (C) also shows that the distance traveled (in physical redox sites) for hopping between effective sites is constant. | ||
This distance between closest coarse-grained sites is fixed at  , where r is the distance (in nanometers) between physical redox sites. Fig. 4 shows that the distance (in physical sites) between the center of each effective site (shown in red) is the same number of physical sites (the distance between the effective site centers of diameter
, where r is the distance (in nanometers) between physical redox sites. Fig. 4 shows that the distance (in physical sites) between the center of each effective site (shown in red) is the same number of physical sites (the distance between the effective site centers of diameter  is always
is always  ). The effective rate is taken as the reciprocal of the MFPT to cross the distance between effective site centers.
). The effective rate is taken as the reciprocal of the MFPT to cross the distance between effective site centers.
 | (4) |
 is the MFPT to traverse a physical distance
is the MFPT to traverse a physical distance  . This time scale represents an average rate to hop between two neighboring effective sites. We approximate the structure of the CB as consisting of redox active groups with uniform spacings and equal reduction potentials. We explore the validity of the coarse-graining procedure for 1D chains and CB models with junctions in the SI. For the ratio of the MFPT in a 1D chain and the MFPT in a 2D square lattice, this coarse-graining procedure produces the expected analytical result for a ratio of end-to-end MFPTs with errors not exceeding 2.5%, regardless of the effective redox unit diameter
. This time scale represents an average rate to hop between two neighboring effective sites. We approximate the structure of the CB as consisting of redox active groups with uniform spacings and equal reduction potentials. We explore the validity of the coarse-graining procedure for 1D chains and CB models with junctions in the SI. For the ratio of the MFPT in a 1D chain and the MFPT in a 2D square lattice, this coarse-graining procedure produces the expected analytical result for a ratio of end-to-end MFPTs with errors not exceeding 2.5%, regardless of the effective redox unit diameter  that is chosen. As described in the SI, we find that errors incurred due to the coarse-graining method or the numerical methods amount to at most ∼6%. This magnitude of error does not qualitatively affect our conclusions.
that is chosen. As described in the SI, we find that errors incurred due to the coarse-graining method or the numerical methods amount to at most ∼6%. This magnitude of error does not qualitatively affect our conclusions.
2.4 Differences between branched and 1D transport networks
The random walk procedure described in Section 2.2 with the coarse-graining method described in Section 2.3 allows us to calculate a ratio of MFPTs CB modeled including junctions or as simple 1D linear chains. Fig. 5 shows that the ratio of MFPTs is approximately 3/2 (for an effective redox unit diameter of physical redox units) for CB on the 100s of µm scale with junctions. Based on this MFPT ratio, we use eqn (3) to calculate a correction for the overestimate of the mobility that arises from using a 1D chain model rather than a branched chain model: µCB = 2/3µ1D. Correcting the 1D mobility in this way allows us to write an analytical expression for the mobility, as described in the next section.
physical redox units) for CB on the 100s of µm scale with junctions. Based on this MFPT ratio, we use eqn (3) to calculate a correction for the overestimate of the mobility that arises from using a 1D chain model rather than a branched chain model: µCB = 2/3µ1D. Correcting the 1D mobility in this way allows us to write an analytical expression for the mobility, as described in the next section.
2.5 Transport dependence on the electron transfer parameters
Biological electron transport chains typically arise from sequential, vibronically coupled electron-transfer reactions (i.e., multi-step hopping or polaron transport). The hopping rates are often well described with a non-adiabatic Marcus-like electron-transfer rate with:27–29
 | (5) |
Corrections to the free energy dependence of the rate can be made if high frequency modes couple to the reaction.30,31
Non-adiabatic electron-transfer rates depend on the donor–acceptor coupling (HDA), reorganization energy (λ), and thermodynamic driving force (−ΔG(0)).27 We calculate the mobility of CB using one-dimensional chain simulations, with the correction factor described above, for a given set of electron-transfer parameters. Eqn (2), (3), and (5) were used to write:
 | (6) |
We assess the ability of the multi-step hopping mechanism to describe the observed electronic mobilities in CB for a range of physically plausible electron-transfer parameters. We derived coupling information from heme cofactors similar to that of bacterial nanowires that are in near van der Waals contact, as a starting point for our model.32 Hemes in close contact without solvent or protein have computed couplings of up to 60 meV at 1.5 nm center-to-center separation distances (0.35–0.7 nm edge-to-edge distances).32 We note that, when computed in proteins, these couplings are typically lower than (1–20 meV).22,33 However, because the electron-transfer cofactors in CB are believed to be non-heme,34 the cofactors may exhibit stronger electronic coupling than that typically found between hemes. To account for the possibility of higher couplings between cofactors, while maintaining biological plausibility, we consider coupling values well below the heme–heme coupling gas-phase limit of 60 meV,32 but above typical in-protein heme couplings (<20 meV), allowing a range of 0.1–30 meV.
Reorganization energies can be estimated from temperature-dependent mobilities13 and conductivities7,8 in CB, since the hopping rates are linked to µ and σ. For a (classical) activated process, the exponential temperature dependence (where Ea is the activation energy, and µ0 is the mobility at infinite temperature) is:
 | (7) |
The classical mobility equation and the non-adiabatic hopping rate of eqn (5) give:
 | (8) |
Eqn (8) allows us to extract electron-transfer parameters from temperature-dependent mobility data and (using σ = Neµ) from temperature-dependent conductivity data. Temperature-dependent studies of CB conductivity and mobility find λ values of 0.16 to 0.36 eV.7,8,13 These λ values were obtained by fitting temperature-dependent mobility/conductivity data from CB to compute an activation free energy (λ/4) at zero driving force. Values of λ near 0.2 eV are at the low end of typical biologically values.35 We take 0.2 eV as a starting point for our kinetic analysis.
For a 1 cm CB, we estimated 107 redox active groups on the shortest hopping pathway between the ends of the CB. With a potential drop on the 0.1 V36 over this distance, the potential drop per redox-active sites is negligible.
The coarse-graining description of CB averages out local differences on scales smaller than the coarse-graining diameter  . The assumption of very small ΔG(0) values for each hopping step was made by others,13 and may be used to estimate λ.30 The approximation that |ΔG(0)| ≃ 0 for the ET steps is also supported by the fact that CB are known to invert in an end-to-end sense, flipping the direction of electron flow from time to time.37 If ΔG(0) were strongly biased in one direction, the flips would not produce viable charge flow in both orientations. A flat free energy landscape (ΔG(0) ∼ 0) therefore favors function.
. The assumption of very small ΔG(0) values for each hopping step was made by others,13 and may be used to estimate λ.30 The approximation that |ΔG(0)| ≃ 0 for the ET steps is also supported by the fact that CB are known to invert in an end-to-end sense, flipping the direction of electron flow from time to time.37 If ΔG(0) were strongly biased in one direction, the flips would not produce viable charge flow in both orientations. A flat free energy landscape (ΔG(0) ∼ 0) therefore favors function.
3 Results
We computed mobilities for ∼1.16 million (see SI for further discussion of the choice of grid points) combinations of reorganization energies, inter-site distances, and couplings (based on the discussion in Section 2.5, we set 0.5 ≤ r ≤ 2.5 nm, 1 ≤ HDA ≤ 30 meV, 0.16 ≤ λ ≤ 0.36 eV, and ΔG(0) = 0 eV). 22.03% (∼255 thousand points) of the chosen values were within one standard deviation of the average reported electronic mobility (standard deviations of the experimental mobility measurements found in ref. 13). As well, 2.12% (∼24.5 thousand points) of the chosen values produce mobilities that differ from the average experimental value by less than the experimental uncertainties (0.01 cm2 V−1 s−1). We explored whether or not there are region of the non-adiabatic electron transfer parameter space that correspond to the observed CB mobilities. We found one isolated region parameter space that was consistent with a multi-step hopping transport mechanism so long as HDA ≥ 3 meV (see Fig. S8 and Section S6 in SI).4 Discussion
Fig. 6 shows that many sets of plausible electron transfer parameters are consistent with the reported electronic mobilities. Since many viable combinations of parameters are consistent with the reported mobilities, we conclude that a multi-step hopping mechanism is consistent with the experimental data. Earlier studies excluded multi-step hopping, based on the small reorganization energy values that were needed for data fitting (λ ≈ 0.2 eV).7,8 Such low values of λ, however, are not inaccessible for biological redox systems, nor do they require extended delocalization among hopping sites.7 We next discuss similar findings in bacterial nanowires and discuss how small λ values may arise in biological structures. | ||
| Fig. 6 Solid lines indicate the reorganization energies and couplings that generate experimental mobilities (the shaded areas are points within one-half of an experimental standard deviation) for 5 values of the inter-site distances noted in the inset (see eqn (6)). | ||
4.1 Sources of low λ values in proteins
Reorganization energies in proteins typically range from 0.2–2 eV.35,38 Photosynthetic reactions centers, cytochrome c, and cytochrome b5 have measured reorganization energies of 0.5–1.5 eV (with ruthenium complex or physiological partners, see ref. 39). Molecular dynamics based estimates of reorganization energies in dried bacterial nanowires are at the lower end of this range (some hemes have calculated reorganization energies below 0.2 eV (ref. 33)). Low reorganization energies arise from low dielectric environments (e.g., solvent drying), nonergodic effects in fast ET (ref. 40), and delocalized hopping sites (as within the porphyrin ring of hemes). More detailed first principles assessment of reorganization energies in CB awaits structural information about the redox-active sites and the associated protein folds. Since many CB experiments are conducted in dried media (and experimental data suggest that the conductive structures may be insulated from water by the surrounding biological matrix9), these conditions may produce low λ values and correspondingly high mobilities.13,39 Recent computational studies of bacterial nanowires, as well, indicate that drying may bring reorganization energies into the 0.2–0.3 eV range.33 Non-ergodic effects may further lower the value of λ, as suggested by Matyushov et al.41 Non-ergodic effects arise from differences between the electron transfer time scale and the time scale for reorganization of vibronically coupled nuclear modes.Charge delocalization among multiple redox sites can accelerate charge transport by a delocalization-assisted mechanism.42–44 In DNA, delocalization of holes over several neighboring stacked bases is believed to occur45–47 and may also arise in CB if the redox groups interact strongly.44 Delocalization-assisted hopping over length scales of more than 10 nm would represent a strong departure from expectations for hopping sites that are not covalently linked. Extended delocalization among hopping sites would likely manifest in characteristic optical signature for delocalization as well. Short range delocalization (over less than 5 nm) would be similar to observations in DNA, and may be allowed by the (currently unknown) electronic structure of the redox active units in CB. It is noteworthy that some species of CB exhibit substantially lower conductivities (≤0.1 S cm−1) compared to others (≥1 S cm−1).2,14 If these lower conductivity measurements reflect intrinsically reduced charge transport in these species, then correspondingly lower mobilities would be expected. In that case of lower mobilities, higher values of λ could remain consistent with the experimentally observed transport behavior.
4.2 Historical context
Early studies of transport in bacterial nanowires hypothesized that coherent transport might play a role.44,48–50 Theoretical analysis10 found that multi-step hopping could explain the charge-transport currents if low values of λ (∼0.2–0.4 eV) were assigned for hopping sites in near van der Waals contact.10 After the structure of the key nanowire proteins were determined,51 it became clear that multi-step hopping among hemes likely defined the conduction mechanism.22,33,52–54 Indeed, atomistic simulations of dried bacterial nanowires support small reorganization energy values.33 These insights from bacterial nanowires highlight how indirect measurement in complex systems, like CB, can be challenging to interpret. As such, there is a need for more direct examination of the charge transport mechanism in CB. Additional mobility measurements on high-conductivity samples (σ ≥ 50 S cm−1), together with quantitative control over experimental factors known to influence conductivity (such as oxygen exposure and uncertainties in sample cross-sectional area) would further clarify how transport properties vary between specimens. Such systematic measurements would provide the experimental foundations needed to develop theories of CB that can quantitatively account for both typical conductivities and the full observed range of reported conductivities that span 2.4 × 10−5 to 564 S cm−1.4.3 Extended-delocalization theories
Ref. 7 and 8 suggest that delocalization on a scale of at least 10 nm may underpin CB transport. Extensive delocalization was suggested as a means of explaining the high observed conductivity. However, long-range delocalization models overestimate the mobilities by nearly three orders of magnitude.7 This overestimation in large-scale delocalization models is due to pairing the high end of plausible coupling values (∼20 meV) with the low end of reorganization energy values (∼0.2 eV), and is also derived from large effective inter-site distances in the models (≥10 nm). Although our primary aim is to model the mobility and not the conductivity,1 our model captures the median experimental conductivity measurements at 300 K with as little as 10% site occupancy (see further details in the SI). Our simulations indicate that extended delocalization is not required to replicate the experimental mobilities with the electron transfer parameters investigated (0.5 ≤ r ≤ 2.5 nm, 1 ≤ HDA ≤ 30 meV, 0.16 ≤ λ ≤ 0.36 eV, and ΔG(0) = 0 eV) – so long as the coupling exceeded 3 meV (a value of the coupling similar to couplings between hemes in bacterial nanowires).4.4 Large polaron theories
Ref. 9 suggested a large polaron mechanism for electron transport in CB, similar to that in some high-purity organic crystals.55,56 Ref. 9 cites transient localization theory, which is frequently used to describe transport in organic crystals.55,56 Ref. 9 reports a cyclic voltammogram with no redox peaks and electrochemical gating experiments that did not show characteristic bell-shaped57 current-gate voltage relations in redox-based conduction. These two findings led the authors to conclude that CB contain no redox-active sites and that the charge-transfer mechanism must be “non-redox” mediated. However, the transient localization mechanism seems biologically unlikely, because transient localization theory generally predicts an anti-Arrhenius temperature dependence, counter to the experimental findings of Arrhenius temperature dependency in CB (see discussion in SI).13,55,58 Existing theoretical analysis56 (and our additional analysis in the SI) suggest that obtaining Arrehenius temperature dependent mobilities for 50–300 K (as seen in CB), would require a coupling in excess of 250 meV for transient localization theory to provide a viable description of CB transport (see SI). Because of the large coupling required to generate the experimentally reported Arrhenius temperature-dependent mobilities with transient localization theory, we find it unlikely that CB use a transient localization mechanism, although it is difficult to entirely dismiss the possibility of this mechanism.The primary evidence cited in support of a large polaron hopping mechanism in CB has been electrochemical gating and cyclic voltametry measurements of ref. 9. Electrochemical gating measurements find a plateau rather than Gaussian current-gate voltage relation (as typically seen in redox conduction). CB samples do not contain isolated conduction channels. There may be heterogeneity in proteins, redox cofactors, and redox potentials in different fibers, different fiber regions, or different parts of the CB (spokes, junctions, or fibers). Any heterogeneity in redox potentials could give rise to multiple overlapping Gaussians in the current vs. gate voltage curves. Previous studies of conducting polymers have seen overlapping Gaussians give rise to a plateau in the current vs. gate voltage curves – as observed for example in samples with chain length heterogeneity.57 The overlapping Gaussians interpretation of the electrochemical gating data would support a redox conduction mechanism, contrary to the “non-redox” mechanism of ref. 9. Still, the absence of redox peaks in the cyclic voltammetry data of ref. 9 is not as easily explicable. The high concentrations of metals observed in CB1 make it seem unlikely that CB are redox-inert. Many theories of charge transfer (including transient localization theory) require that charges eventually localize, which should give rise to signals in the cyclic voltammetry. As such, it remains an open challenge to find either a charge-transport mechanism compatible with the cyclic voltametry measurements (compatible with the absences of redox chemistry) or measurements that can probe the redox potentials of cofactors in CB more directly. While the values of cofactor redox potentials in CB have not been measured precisely, we conclude that the existing temperature dependent mobilities and conductivities are qualitatively incompatible with a large polaron-mediated mechanism of charge transport. This conflict is likely due to the requirement of a coupling in excess of 250 meV (as discussed in the SI), as well as the alternate interpretation of the electrochemical gating and cyclic voltamogram experiments of ref. 9 (which were the previous best evidence for a large polaron like mechanism of charge transport in CB).
5 Conclusions
We have modeled transport in 3D models for CB that include the influence of the novel cartwheel structures, moving beyond 1D models.10 We developed a coarse-graining procedure that alows us to address the cm length scale transport in CB. We computed the electronic mobilities in CB using our model for a range of coupling and reorganization energy parameters typical of biological electron transfer systems. We found that many plausible combinations of electron-transfer parameters for multi-step hopping models are consistent with the reported electronic mobilities of CB. Although reproducing the reported mobility data with hopping models require low reorganization energies,59 it is possible that cable drying, non-ergodic effects,41 and short-range (∼1 nm) delocalization assistance could contribute to low reorganization energies.51 We conclude that multi-step hopping between localized states likely accounts for transport in CB; extended delocalization among active groups is not required to explain the reported electronic mobility data.Author contributions
Andrew Smith contributed conceptualization, investigation, methodology, software, and writing. David Beratan contributed conceptualization, funding acquisition, project administration, resources, supervision, and writing.Conflicts of interest
The authors declare no conflicting interests.Data availability
Code used for calculations presented in this study can be found at https://github.com/ajsmit24/LDETDiffusionTopology.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5sc04393j.
Acknowledgements
A. J. S. thanks the NSF for the support through a GRFP. A. J. S. contribution to this material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-2139754. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors(s) and do not necessarily reflect the views of the National Science Foundation. D. N. B. thanks the National Institutes of Health, Grant GM-048043, for support of this research. We thank Prof. Peng Zhang for helpful discussions.Notes and references
- H. T. Boschker, P. L. Cook, L. Polerecky, R. T. Eachambadi, H. Lozano, S. Hidalgo-Martinez, D. Khalenkow, V. Spampinato, N. Claes and P. Kundu, et al., Nat. Commun., 2021, 12, 3996 CrossRef CAS PubMed.
- T. Yang, M. S. Chavez, C. M. Niman, S. Xu and M. Y. El-Naggar, eLife, 2024, 12, RP91097 Search PubMed.
- K. U. Kjeldsen, L. Schreiber, C. A. Thorup, T. Boesen, J. T. Bjerg, T. Yang, M. S. Dueholm, S. Larsen, N. Risgaard-Petersen and M. Nierychlo, et al., Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 19116–19125 Search PubMed.
- F. J. Meysman, R. Cornelissen, S. Trashin, R. Bonné, S. H. Martinez, J. van der Veen, C. J. Blom, C. Karman, J.-L. Hou and R. T. Eachambadi, et al., Nat. Commun., 2019, 10, 4120 CrossRef PubMed.
- S. E. Yalcin, J. P. O'Brien, Y. Gu, K. Reiss, S. M. Yi, R. Jain, V. Srikanth, P. J. Dahl, W. Huynh and D. Vu, et al., Nat. Chem. Biol., 2020, 16, 1136–1142 CrossRef CAS PubMed.
- K. Bednarczyk, W. Matysiak, T. Tański, H. Janeczek, E. Schab-Balcerzak and M. Libera, Sci. Rep., 2021, 11, 7487 CrossRef CAS PubMed.
- J. R. van der Veen, S. Valianti, H. S. van der Zant, Y. M. Blanter and F. J. Meysman, Phys. Chem. Chem. Phys., 2024, 26, 3139–3151 RSC.
- J. R. van der Veen, S. Hidalgo Martinez, A. Wieland, M. De Pellegrin, R. Verweij, Y. M. Blanter, H. S. van der Zant and F. J. Meysman, ACS Nano, 2024, 18(47), 32878–32889 CrossRef CAS PubMed.
- D. Pankratov, S. H. Martinez, C. Karman, A. Gerzhik, G. Gomila, S. Trashin, H. T. Boschker, J. S. Geelhoed, D. Mayer and K. De Wael, et al., Bioelectrochemistry, 2024, 157, 108675 CrossRef CAS PubMed.
- N. F. Polizzi, S. S. Skourtis and D. N. Beratan, Faraday Discuss., 2012, 155, 43–61 RSC.
- R. Cornelissen, A. Bøggild, R. Thiruvallur Eachambadi, R. I. Koning, A. Kremer, S. Hidalgo-Martinez, E.-M. Zetsche, L. R. Damgaard, R. Bonné and J. Drijkoningen, et al., Front. Microbiol., 2018, 9, 3044 CrossRef PubMed.
- R. Thiruvallur Eachambadi, R. Bonné, R. Cornelissen, S. Hidalgo-Martinez, J. Vangronsveld, F. J. Meysman, R. Valcke, B. Cleuren and J. V. Manca, Adv. Biosyst., 2020, 4, 2000006 CrossRef PubMed.
- R. Bonné, J.-L. Hou, J. Hustings, K. Wouters, M. Meert, S. Hidalgo-Martinez, R. Cornelissen, F. Morini, S. Thijs and J. Vangronsveld, et al., Sci. Rep., 2020, 10, 19798 CrossRef PubMed.
- L. Digel, M. L. Justesen, N. S. Madsen, N. Fransaert, K. Wouters, R. Bonné, L. E. Plum-Jensen, I. P. Marshall, P. B. Jensen and L. Nicolas-Asselineau, et al., EMBO Rep., 2025, 1–19 Search PubMed.
- E. M. Purcell, Electricity and Magnetism, Cambridge University Press, 2013 Search PubMed.
- C. Jacoboni, Theory of Electron Transport in Semiconductors: a Pathway from Elementary Physics to Nonequilibrium Green Functions, Springer Science & Business Media, 2010, vol. 165 Search PubMed.
- S. M. Sze, Semiconductor Devices: Physics and Technology, John Wiley & Sons, 2008 Search PubMed.
- C. Jacoboni and L. Reggiani, Rev. Mod. Phys., 1983, 55, 645 CrossRef CAS.
- S. Lampa-Pastirk, J. P. Veazey, K. A. Walsh, G. T. Feliciano, R. J. Steidl, S. H. Tessmer and G. Reguera, Sci. Rep., 2016, 6, 23517 CrossRef CAS PubMed.
- M. J. Crawley, Statistics: an Introduction Using R, John Wiley & Sons, 2014 Search PubMed.
- R. Dawson, J. Stat. Educ., 2011, 19(2) DOI:10.1080/10691898.2011.11889610.
- P. J. Dahl, S. M. Yi, Y. Gu, A. Acharya, C. Shipps, J. Neu, J. P. O'Brien, U. N. Morzan, S. Chaudhuri and M. J. Guberman-Pfeffer, et al., Sci. Adv., 2022, 8, eabm7193 CrossRef CAS PubMed.
- A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems, Oxford University Press, 2024 Search PubMed.
- H. C. Berg, Random Walks in Biology, Princeton University Press, 1993 Search PubMed.
- F. C. Grozema and L. D. Siebbeles, Int. Rev. Phys. Chem., 2008, 27, 87–138 Search PubMed.
- G. Klein, Proc. R. Soc. London, Ser. A, 1952, 211, 431–443 CAS.
- F. Di Giacomo, Introduction to Marcus Theory of Electron Transfer Reactions, World Scientific, 2020 Search PubMed.
- J. J. Hopfield, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 3640–3644 Search PubMed.
- D. N. Beratan, C. Liu, A. Migliore, N. F. Polizzi, S. S. Skourtis, P. Zhang and Y. Zhang, Acc. Chem. Res., 2015, 48, 474–481 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, Rev. Bioenerg., 1985, 811, 265–322 CrossRef CAS.
- J. D. Schultz, K. A. Parker, M. J. Therien and D. N. Beratan, J. Am. Chem. Soc., 2024, 146, 32805–32815 CrossRef CAS PubMed.
- D. M. Smith, K. M. Rosso, M. Dupuis, M. Valiev and T. Straatsma, J. Phys. Chem. B, 2006, 110, 15582–15588 Search PubMed.
- M. J. Guberman-Pfeffer, J. Phys. Chem. B, 2023, 127, 7148–7161 CrossRef CAS PubMed.
- G. Polycarpou and S. S. Skourtis, J. Phys. Chem. B, 2025, 129, 2992–3006 CrossRef CAS PubMed.
- H. Imahori, N. V. Tkachenko, V. Vehmanen, K. Tamaki, H. Lemmetyinen, Y. Sakata and S. Fukuzumi, J. Phys. Chem. A, 2001, 105, 1750–1756 CrossRef CAS.
- J. T. Bjerg, H. T. Boschker, S. Larsen, D. Berry, M. Schmid, D. Millo, P. Tataru, F. J. Meysman, M. Wagner and L. P. Nielsen, et al., Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5786–5791 CrossRef CAS PubMed.
- N. M. Geerlings, C. Karman, S. Trashin, K. S. As, M. V. Kienhuis, S. Hidalgo-Martinez, D. Vasquez-Cardenas, H. T. Boschker, K. De Wael and J. J. Middelburg, et al., Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5478–5485 CrossRef CAS PubMed.
- L. I. Krishtalik, Biochim. Biophys. Acta, Rev. Bioenerg., 2011, 1807, 1444–1456 CrossRef CAS PubMed.
- K. A. Sharp, Biophys. J., 1998, 74, 1241–1250 CrossRef CAS PubMed.
- D. V. Matyushov, J. Electrochem. Soc., 2022, 169, 067501 CrossRef CAS.
- D. V. Matyushov, J. Phys. Chem. Lett., 2012, 3, 1644–1648 CrossRef CAS PubMed.
- Y. Zhang, C. Liu, A. Balaeff, S. S. Skourtis and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10049–10054 CrossRef CAS PubMed.
- Z. Futera, I. Ide, B. Kayser, K. Garg, X. Jiang, J. H. Van Wonderen, J. N. Butt, H. Ishii, I. Pecht and M. Sheves, et al., J. Phys. Chem. Lett., 2020, 11, 9766–9774 CrossRef CAS PubMed.
- Y. Eshel, U. Peskin and N. Amdursky, Nanotechnology, 2020, 31, 314002 CrossRef PubMed.
- C. Liu, L. Xiang, Y. Zhang, P. Zhang, D. N. Beratan, Y. Li and N. Tao, Nat. Chem., 2016, 8, 941–945 CrossRef CAS PubMed.
- I. V. Kurnikov, G. S. M. Tong, M. Madrid and D. N. Beratan, J. Phys. Chem. B, 2002, 106, 7–10 Search PubMed.
- Y. Jin, X. Ru, N. Q. Su, Y. Mei, D. N. Beratan, P. Zhang and W. Yang, J. Phys. Chem. B, 2020, 124, 3428–3435 Search PubMed.
- C. Sanchez, Nat. Rev. Microbiol., 2011, 9, 700 CrossRef CAS PubMed.
- N. S. Malvankar, M. Vargas, K. Nevin, P.-L. Tremblay, K. Evans-Lutterodt, D. Nykypanchuk, E. Martz, M. T. Tuominen and D. R. Lovley, mBio, 2015, 6, 10–1128 CrossRef PubMed.
- N. S. Malvankar, M. Vargas, K. P. Nevin, A. E. Franks, C. Leang, B.-C. Kim, K. Inoue, T. Mester, S. F. Covalla and J. P. Johnson, et al., Nat. Nanotechnol., 2011, 6, 573–579 CrossRef PubMed.
- F. Wang, Y. Gu, J. P. O'Brien, M. Y. Sophia, S. E. Yalcin, V. Srikanth, C. Shen, D. Vu, N. L. Ing and A. I. Hochbaum, et al., Cell, 2019, 177, 361–369 CrossRef CAS.
- J. Huang, J. Zarzycki, M. Gunner, W. W. Parson, J. F. Kern, J. Yano, D. C. Ducat and D. M. Kramer, J. Am. Chem. Soc., 2020, 142, 10459–10467 CrossRef CAS PubMed.
- M. J. Guberman-Pfeffer, Front. Microbiol., 2024, 15, 1397124 CrossRef CAS PubMed.
- Y. Gu, M. J. Guberman-Pfeffer, V. Srikanth, C. Shen, F. Giska, K. Gupta, Y. Londer, F. A. Samatey, V. S. Batista and N. S. Malvankar, Nat. Microbiol., 2023, 8, 284–298 Search PubMed.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- S. Ciuchi and S. Fratini, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 86, 245201 CrossRef.
- M. D. Yates, S. M. Strycharz-Glaven, J. P. Golden, J. Roy, S. Tsoi, J. S. Erickson, M. Y. El-Naggar, S. C. Barton and L. M. Tender, Nat. Nanotechnol., 2016, 11, 910–913 Search PubMed.
- A. Landi, J. Phys. Chem. C, 2019, 123, 18804–18812 Search PubMed.
- C. E. Wise, A. E. Ledinina, D. W. Mulder, K. J. Chou, J. W. Peters, P. W. King and C. E. Lubner, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2117882119 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |

