 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Idealized modeling of stratospheric aerosol injection deployment scenarios with two non-cooperative actors
Anni Määttänen *a,
François Ravettaa,
Jérôme Bureaua,
Thibaut Lurtonb and
Olivier Boucherb
*a,
François Ravettaa,
Jérôme Bureaua,
Thibaut Lurtonb and
Olivier Boucherb
aLATMOS/IPSL, Sorbonne Université, UVSQ Université Paris-Saclay, CNRS, Paris, France. E-mail: anni.maattanen@latmos.ipsl.fr
bInstitut Pierre-Simon Laplace, Sorbonne Universite/CNRS, Paris, France
First published on 20th January 2026
Abstract
We investigate solar radiation management scenarios of two non-cooperative actors deploying stratospheric aerosol injection (SAI). We perform the idealized experiments with a four-box Energy Balance Model capable of predicting hemispheric temperatures and monsoon precipitation, coupled to PI-controllers. The controller models the behaviour of an actor that deploys SAI at a certain location in order to reach a certain climatic goal, such as an average temperature or a monsoon precipitation target. The goal of this work is to assess through case studies of idealized scenarios what could go wrong in a non-cooperative deployment. Continuous non-cooperative deployment by two actors provides the expected climate result in most of the cases studied, but it can lead to the actors not fully reaching their targets. Intermittent deployment, related to policy instability in our scenario design, can lead to a free-riding situation, or missing the climatic targets due to temperature oscillations induced by the intermittency. These results of our case studies point out the need for exploring more politically plausible scenarios in SRM modelling studies. More complex experiments, including multi-target controllers and coalitions of actors, will be possible with a future version of the model.
Environmental significanceSolar radiation management has been proposed as a possibility to alleviate the consequences of climate change through cooling the Earth with injecting reflective particles in the middle atmosphere. We explore with a simple climate model coupled to a controlling algorithm how non-cooperative deployment of solar radiation management by two actors could impact the climate. We show that despite the lack of coordination, if the actors perform continuous deployment, the resulting climatic state is relatively steady. If the solar radiation management is intermittent, the actors miss their targets and cause large climate variations. Environmental impacts of such deployment might be large, implying a need for a global engagement if solar radiation management were to be deployed in the future. |
1 Introduction
Solar radiation management or modification (SRM) is no substitute for deep greenhouse gas emissions reductions. Nevertheless, the current rate of mitigation efforts worldwide is largely insufficient to achieve the Paris Agreement targets1,2 and SRM is also seen as a way to reduce the risk of dangerous climate change occurring in the near- to medium-term3,4 because it has the potential to cool the Earth within a few years to a decade. SRM is certainly not a panacea: it does not completely cancel the impacts of climate change due to greenhouse gases5,6 and it is known to introduce a number of new risks7 as well as social and ethical concerns.8 As the science of SRM evolves rapidly, there is a need to regularly update assessments.9,10A key question when it comes to SRM deployment is how to set up a governance framework that determines the objectives of SRM and delivers them. Indeed “Who controls the Global Thermostat?” and “By how much?” were identified early on as key issues associated with SRM.7 Given that SRM cannot fully compensate for the impacts of greenhouse gases, it has been investigated to which extent it is possible to calibrate how SRM is deployed in a way that would minimize the regional damages according to some simple climate metrics.11 Other optimal strategies12 could also account for social or economical aspects, such as the disparity between those who will benefit/suffer from climate change and how it impacts their incentives for SRM deployment.
Stratospheric aerosol injection (SAI) is the most studied SRM method because there is confidence that it has the potential to cool the planet by at least 1 °C.13 Large volcanic eruptions provide a natural analogue that allow for testing and calibration of climate models used for studying them. Similarly, climate modeling has proved to be a useful approach to understand the strengths and limitations of SRM. Climate modelling has also been used to investigate the interactions of large volcanic eruptions and SAI deployment.14,15 However, SRM modelling research comes with its uncertainties19,20 that are yet to be comprehensively quantified.21 To attain the desired climate goals, SRM through SAI could be implemented in very different ways with injection at different possible latitudes, heights and seasons.16–18 Moreover, SRM is also increasingly seen as an optimal control problem,22–27 whereby SAI or other forms of SRM is adjusted iteratively over the years to stabilize the climate around one or several set targets. Typical targets include the global mean surface temperature (GMST) and interhemispheric or equator-to-pole temperature gradients. They can also include other climate variables such as regional precipitation amounts or patterns, soil moisture or ecosystem services.
All of the SRM scenarios so far have not explicitly included analyses on the geopolitical plausibility of the scenarios, and thus it is unclear whether any long-term deployment foreseen in the scenarios can be stable without some level of global consensus. Such scenarios have been criticized and challenged28–30 and there is indeed a lot of debate as to whether and how SRM can be effectively governed.31
Unilateral deployment of SRM could lead to the so-called “free driving” situation where a single actor deploys SRM thus affecting the global climate and exerting power over other nations. Game theory has been used to study the possibility of unilateral deployment,32 revealing that the decision to embark on the unilateral SRM deployment depends on the perceptions and the interactions between the deploying country and others and on weighting cost and gain for the deploying country.
A system of distributed SRM deployment responsibility has been proposed to overcome the free-driving problem and reduce the risk of termination shock in the case a deploying actor suddenly stops its deployment.33 The distributed responsibility (based, for example, on cumulative past emissions) would lead to an emergent policy on SRM governance. This scheme was labelled as “limited unilateral control” as it would not require a centralized power making decisions or forming a policy, except for the initial agreement on the maximum cooling from SRM deployment and the distribution of efforts among the deploying actors.
SRM research has come to a point where implementation scenarios are needed34,35 both because this is a necessary step to better understand its benefits, impacts and risks, and because this may feed back into the needed research on governance.36–38 Key questions include whether SRM should be governed in a centralized or in a decentralized manner,39 how to respond to unexpected events,14,40 and failures, whether they are real or perceived.41 There could be varying levels of cooperation or lack of cooperation in the case of multiple actors,42 and there could be rogue actors.43 In particular, different actors may have different climate objectives and not reach a consensus. It has also been argued that some actors could take counter-SRM measures through the release of powerful short-lived greenhouse gases,44 although such counter-measures could also have a purely dissuasive role.
This study aims to address some of these potential governance issues in an idealized but quantitative way. We rely on an Energy Balance Model (EBM) coupled to a Proportional–Integral controller to test SAI deployment scenarios that involve two actors pursuing the same or different goals but that do not cooperate with each other nor coordinate their actions. In addition to test cases of single-actor deployment and two actors with similar goals, we also try to propose new scenarios that include actors reacting to unilateral deployment and explore intermittency. The scenarios are highly idealised and do not represent a realistic implementation of SRM. The assumption that an actor does not know the actions of other actors is an extreme but useful one to test our scenarios. In practice some actors may choose to communicate their actions or an actor that has set up an observing system to monitor its own injections could use it to infer some information on the actions of the other actors. However, by exploring these scenarios with our model, we capture the main outcomes of the different scenarios. The main question that we address is the following: What are the implications for the climate system of a non-cooperative two-actor deployment scenario?
Section 2 describes our Energy Balance Model and controller wrapped around it, and lists the studied scenarios. Section 3 presents the results while Section 4 draws conclusions and directions for future work.
2 Methods
2.1 The energy balance model
We employ a two-layer Energy Balance Model (EBM)45 that we have extended to cover the Northern Hemisphere (NH) and the Southern Hemisphere (SH) separately. Thus the model is a two-hemisphere EBM that represents the climate system with four boxes for which the mean temperatures are prognostic variables. The temperatures TNH and TSH characterize the atmosphere and upper-ocean layers of the NH and SH, respectively, and T0,NH and T0,SH the deep ocean layers. The inter-hemispheric temperature gradients TNH–TSH and T0,NH–T0,SH are relaxed within a certain time scale. The EBM is driven by a radiative forcing that is the sum of a global warming scenario including a volcanic eruption, and SAI. We have also developed a parametrization of the Indian monsoon precipitation for the EBM. These different elements of the model are detailed below.The idealized scenario for global warming radiative forcing (RF), symmetric over the two hemispheres and including a moderate volcanic eruption, is shown in panel A of Fig. 1. RF ramps up linearly from 0 to 4 W m−2 in year 100, followed by a plateau between years 100 and 150 and a linear ramping down to 3 W m−2 between years 150 to 200. A temporary decrease of RF due to a volcanic eruption causing a negative forcing is applied in years 125 (−2 W m−2) and 126 (−1 W m−2). This scenario is used in all model experiments.
The radiative forcing caused by SAI (RF SRM) for each hemisphere is computed from hemispheric stratospheric aerosol optical depth (SAOD) and a radiative efficiency factor of −10 W m−2 per unit AOD.46 The SAOD is computed as the sum of impulse response functions convoluted with the time-varying emissions at the different injection points. Hence the different emitted plumes (at different locations or different times) do not interact with each other. The impulse response functions are derived from dedicated experiments of the IPSL-CM6A-LR model47 coupled to the sectional stratospheric aerosol model S3A that describes the stratospheric sulfate aerosol microphysics and is capable to simulate SAI through stratospheric SO2 injections.46,48 The IPSL-CM6A-LR simulations were made for injections at the Equator, 15°N/S, 30°N/S and 60°N/S with the injections of 10 TgS per year made at the altitude of 18 km (±0.5 km) and spread evenly over the first simulation year. The IPSL-CM6A-LR model is then run for a period of 6 years in total until the pulse emissions almost completely disappear from the stratosphere. The hemispheric impulse response functions resulting from the simulations are shown in Fig. 2 for both hemispheres and the seven injection points. In most of the cases, the SAOD peaks in year 2 and decays quickly thereafter. The interhemispheric asymmetry seen in the impulse response to equatorial and tropical injections, the NH always responding more strongly than the SH, is related to the asymmetry in stratospheric circulation. For a chosen SRM scenario in the model experiments (Section 2.3), the RF SRM is calculated from the response functions corresponding to the chosen injection locations by scaling them to the actual injection rates and then summing the resulting hemispheric RFs.
The total hemispheric radiative forcing leads to inter-hemispheric temperature gradients TNH–TSH and T0,NH–T0,SH in the two-hemisphere EBM that are reduced by relaxation terms that have timescales of 10 and 20 years for the surface ocean and atmospheric layer and the deep ocean layer, respectively. It was not possible to diagnose clearly the exchange rate from IPSL-CM6A-LR simulations and we have opted here for physically plausible values that are not invalidated by the IPSL-CM6A-LR simulations. We recognize though that these numbers are chosen somewhat ad hoc.
We also account for the heterogeneous distribution of continents on the two hemispheres by modulating the heat capacity of the surface ocean between the two hemispheres. In the original two-layer EBM,45 the effective heat capacity of the surface ocean was estimated as 7.3 W year per m2 per K from a multi-model global mean. Noting that the NH is approximately 40% land and 60% ocean while the SH is 20% land 80% ocean, we weigh the effective heat capacities of each hemisphere accordingly (for both the surface and the deep ocean layers).
Furthermore the change in Indian monsoon precipitation is parametrized in our EBM as a function the interhemispheric difference in SAOD and temperature. Previous work has shown that the monsoon is not a land-sea breeze system driven by the land-ocean contrast,49 and that the ITCZ shift is related to the interhemispheric difference in heating, the induced energy transport at the equator, and to a lesser degree to the interhemispheric difference in the near-surface temperatures.50–52 Later, it was also shown that the global scale southward shift of the ITCZ in the latter half of the last century was caused by the cooling of the NH due to the anthropogenic aerosols,53 and that an asymmetry in stratospheric aerosol radiative forcing impacts the African monsoon (in the Sahel).54 Thus monsoon precipitation change can be thought to be both a response to the interhemispheric difference in SAOD (which is responsible for an interhemispheric difference in RF) and a response to the interhemispheric difference in surface temperature, both of which can induce changes in circulation patterns. Our approach focuses on these two predictors, but this does not mean that there are no other predictors. For instance, it is well known that the monsoon is connected to large-scale modes of variability, which we do not resolve in our simple model, but we introduce a relatively large noise level for the monsoon (see below). We were also inspired by work that parameterized the monsoon change as a function of the interhemispheric SAOD gradient,55 and another parametrization that described the monsoon precipitation change as a function of the average global AOD and interhemispheric differences in AOD.56 Deconvolving the effects on the monsoon of both the interhemispheric SAOD and temperature gradients in climate model experiments that apply a constant-in-time SAOD perturbation is not possible. This is why we set up an idealized experiment whereby the interhemispheric difference in SAOD alternates suddenly, causing the interhemispheric surface temperature and SAOD differences to be out of phase. It is then possible to disentangle the contributions of surface temperature and SAOD on the monsoon precipitation. Specifically we ran two sets of simulations with the IPSL-CM6A-LR model where the S3A module is switched off but the SAOD is simply prescribed to a constant value on one hemisphere at a time. These simulations alternate 5 years with SAOD fixed to a constant and uniform value, SAOD = 0.4, in the NH only, followed by 5 years of constant SAOD = 0.4 in the SH only. The SAOD in the other hemisphere is set to zero. We repeat this succession of alternating hemispheric SAOD three times leading to a 30-year long simulation. A second, nearly identical simulation is performed expect that the initial SAOD perturbation occurs in the SH instead of the NH. We can then compute yearly statistics of interhemispheric surface temperature difference and JJAS Indian monsoon rainfall. This provides 60 datapoints, half of which with an interhemispheric SAOD difference of 0.4 and the other half with an interhemispheric SAOD difference of −0.4, all plotted on Fig. 3. Because the surface temperature takes some time to respond to SAOD changes, we get quite some variation in the interhemispheric surface temperature difference for each subset of datapoints, including a few datapoints where the surface temperature is larger in the NH than in the SH despite the hemispheric stratospheric layer being prescribed in the NH. We perform a multiple regression of the monsoon rainfall against the two predictors that indicates that the changes in Indian monsoon precipitation is more sensitive to the SAOD than to the surface temperature hemispheric differences (Fig. 3). Our parametrization thus has the following form for the change in Indian monsoon precipitation ΔP/P (%) as a function of the interhemispheric (NH–SH) SAOD and temperature differences:
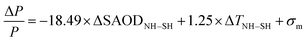 | (1) |
The EBM equations are integrated with a timestep of one tenth of a year, with the monsoon response calculated once a year. The controller call leading to the calculation of the new injections is also done once a year. We add to the hemispheric mean temperatures a time series of white noise with standard deviation σT = 0.11 K (see example in panel B of Fig. 1). The value of σT was calculated from the Berkeley Earth land/ocean temperature record GMST time series57 as the standard deviation in annual mean over the detrended 1980–2024 period. The noise time series is generated for each pair of simulations with and without SAI and is thus identical in the two simulations. However, it varies from one pair of simulations to the next. Similarly, we have added a time series of white noise with standard deviation σm = 10%, close to values found in the literature,58,59 to the monsoon precipitation change (see panel B of Fig. 1). As for the mean surface temperatures, the monsoon noise time series is identical for the simulations with and without SAI. The global mean surface temperature (GMST) is calculated as the average of the NH and SH surface temperatures (NHST and SHST, respectively).
2.2 Proportional–integral (PI) controller
Coupling controllers to climate models was introduced to SRM modeling about 15 years ago and is now routine in GeoMIP and ARISE simulations.22,24,25 We couple the EBM with PI-controllers that are based on the simple-pid python package (https://pypi.org/project/simple-pid/) to adjust the amount of SAI applied every year for a given target. Although the controller is a classical Proportional–Integral–Derivative (PID) controller, the actual implementation includes only the proportional and integral (PI) gain parameters (Kp and Ki) as in previous works. The controller does not include a feedforward term. The values of the gain parameters Kp and Ki (Table 1) were chosen by starting from those reported in previous studies,26 but were empirically adjusted so that the model response with the prescribed noise was adequate. We made sensitivity tests (not shown) by varying the parameters by a factor of two and ten. The model results were not very sensitive in this range. Larger Kp led to too strong a response of injections to noise, still reaching the climate goals, and smaller values allowed for less noisy injection timelines but delayed the convergence to the climate goals at the start of the SAI intervention. Smaller (larger) Ki smoothed more (less) strongly the injections in time. The chosen values are a good compromise where both the climate goals are met within a realistic time range and where the injection timeline remains sufficiently smooth, without exaggerated reactions to noise.| Surface temperature | Monsoon | |
|---|---|---|
| Proportional gain Kp | 0.8 (TgS per year)/°C | 0.08 (TgS per year)/% |
| Integral gain Ki | 0.6 (TgS per year)/°C per year | 0.06 (TgS per year)/% per year |
Each actor with a target is modeled with one controller and the actors operate independently. In the current implementation of our model, an actor can choose only one target among global mean surface temperature (GMST), Northern Hemisphere mean surface temperature (NHST), Southern Hemisphere mean surface temperature (SHST) or the Indian monsoon index (MON), but different actors can have different targets. The actors can also choose between injections points at the Equator, 15°N/S, 30°N/S and 60°N/S, for which impulse response functions have been implemented in the EBM (see Section 2.1 and Fig. 2). These latitudes are close to the optimal set for reaching different climate goals60 so these response functions should allow for a reasonably good exploration of the “SAI design space”. It should be noted that we do not attempt a full exploration of the space in this paper, but focus on a selection of cases with injections at the equator or at 15°N/S. We translate the fact that each actor has a limited deployment capacity by setting time-dependent maximum injection rates for each actor. This maximum value typically varies between 0 and 10 TgS per year and results in a corresponding maximum radiative forcing (that depends on the injection latitude and the SAOD impulse response functions) and therefore a maximum cooling capability. At the start of injections, the rate of increase of the injections is an adjustable parameter in the model, currently defined as a linear ramp-up from zero to the maximum rate within 20 years. In some experiments we program the controller to interrupt injections (by setting the maximum injection rate to zero) for a period of time when certain conditions are fulfilled (see description in the following section).
2.3 Implemented SRM scenarios
This subsection introduces the different deployment scenarios we implemented in our experiments. These experiments are not chosen as something “plausible”, for two reasons. First, the modelling system is idealized, not permitting to model fully realistic situations. Second, one of our goals was to test cases where “human behaviour” through deployment intermittence might have negative consequences on the climate, but this intermittence is not described through a realistic implementation of real-world situations.Table 2 summarizes the experiments discussed in this study and they are detailed hereafter. See details for each experiment and descriptions of what intermittency and cooling overshoot refer to in the following subsections.
| Experiment name | Actor A | Actor B | Intermitt. | ||
|---|---|---|---|---|---|
| Target | Location | Target | Location | ||
| Single-actor-NH | NHST | 15°N | — | — | No |
| Ownhemi | NHST | 15°N | SHST | 15°S | No |
| Coolglobe | GMST | EQ | GMST | EQ | No |
| NH-monsoon | NHST | 15°N | MON | 15°S | No |
| Freeride | GMST | EQ | GMST | EQ | Yes |
| Stopgo | GMST | EQ | GMST | EQ | Yes |
| Overcool | NHST | 15°N | SHST | 15°S | Yes |
First, the two complementary actors both intend to cool their own hemisphere (target: hemispheric surface temperature cools to the initial value) by injecting at latitudes 15°N and 15°S (Ownhemi).
Second, the two actors both aim at cooling the GMST to the initial value and both inject at the Equator (Coolglobe). Since the two actors do not cooperate, they both design their intervention as if they were working alone, and thus the choice of injections at the Equator is justified as it will provide the best impact when aiming at a global cooling.
In one of the scenarios, the actors have differing targets: one actor simply wants to cool the NHST whereas the other one does not have a temperature target but wants to stop the monsoon precipitation from decreasing due to the intervention of the first actor. The first actor injects at 15°N. The second injects at 15°S, starting 30 years later, as a way to compensate for the actions of the first actor (experiment NH-monsoon).
We have also attempted to include intermittence of SAI in the experiments. Such intermittence could be due to different reasons.
A free-riding scenario (labelled Freeride) has been designed whereby both actors initially work towards the same goal (GMST0) by injecting at the Equator (just like in the experiment Coolglobe). However, at some point in time, one of the actors stops injecting for 20 years and then resumes, resulting in a redistribution of the injection burden between the two actors.
Another type of intermittence may arise from, for example, situations where decision-makers change and have contrary opinions to their predecessors. Decision-makers might also simply change their opinion on SAI deployment. Perceived failure of SAI41 could lead to an interruption of injections in the case where it takes too long to detect the effect of SAI. Here, for sake of easy implementation of random intermittence, we consider that perceived failure occurs when SAI leads to overcooling (“cooling overshoot”). Two final scenarios, described below, address these aspects.
First, once again both actors cooperate towards the same goal (GMST0) by injecting at the Equator (just like in the experiment Coolglobe). Then one stops for 10 years, after which it resumes the injections, but then the other one stops for 10 years, and so on, in alternating roles. This scenario (Stopgo) describes intermittence with a certain periodicity.
The other intermittence experiment (Overcool) introduces irregularity in the intermittence. It uses two hemispheric actors that first both cool their own hemisphere by injecting at latitude 15°N/S (just like in the experiment Ownhemi). However, if the cooling of the hemisphere is too strong so that the temperature target is exceeded by more than 0.1 °C, the actor experiencing the cooling overshoot in their hemisphere immediately stops the injections. We assume that after five years either the decision-makers change their mind or new decision-makers overrule the decisions of their predecessors, and decide to restart injections to cool again. The threshold of 0.1 °C is chosen empirically based on the prescribed noise level (σT = 0.11 K) that allows for the cooling overshoot in our model due to this natural variability. This cooling overshoot is of course not realistic nor observable in the real world, but it has been implemented here to cause random interruptions of the injections, mimicking policy instabilities. It is a simple way to implement sporadic and random intermittence from perceived failure41 of SAI in our model. The experiment is meant to illustrate the possible behavior of ill-advised decision-makers under pressure from the general public after perceived failure of SRM (overcooling in our case). Keys et al.41 showed the perceived failure resulting from the natural variability of the climate masking the regional cooling effect of SAI on a decadal scale. In our experiment the perceived failure is implemented through overcooling, first because it is technically feasible, but also since our simple model only predicts the changes in global or hemispheric mean temperatures so looking at regional climate variability is not feasible.
3 Results
3.1 Single actor experiment
We start with the single actor experiment (Single-actor-NH) to check the model response (Fig. 4). In this experiment actor A cools the NH with an injection at 15°N. Injection ramps up as it is initially limited by the maximum injection rate. It then follows an evolution consistent with the RF history and the ocean thermal inertia. The NH mean temperature cools to the desired level in about 20 years. As the actor injects in the NH, the SH does not cool as much as the NH. This leads to a North–South temperature difference of about 1 K, and as a result the monsoon precipitation decreases by 7% on average.This experiment allows us also to test the reaction of the system to a sudden volcanic eruption occurring during SAI on simulation year 125. A volcanic eruption during SAI constitutes a risk identified by Laakso et al.14 In their experiments, if injections were continued despite a volcanic eruption, the supplementary cooling effect was felt for several years. They also concluded that if the injections were stopped altogether after the eruption, it would have been necessary to restart them within less than a year to be able to maintain the desired cooling. Besides using very different types of models (our EBM versus a global climate model and an Earth System Model), the main difference between the experiments in our study and in the previous study14 is that we dynamically adjust the injection rate every simulated year, allowing the SRM to adapt to the cooling caused by the eruption. Another study15 also modelled volcanic eruptions during SAI deployment and focused on the possibility to reduce volcanic eruption related risks with the adjustment of SAI. These experiments15 used a controller to adjust the SAI injections to keep the global mean temperatures at 1.5 K above the preindustrial in the SSP2-4.5 scenario, but the post-eruption modification of the injection scenario was prescribed. The authors15 showed that in particular when the eruption is of the same magnitude as the SAI deployment, the post-eruption risks can be efficiently mitigated by injection adjustments. If the eruption is much larger than the SAI injections, stopping injections right after eruption reduces somewhat the sudden cooling and the changes in precipitation.
As our ability to predict volcanic eruptions is very low, we assume that SAI reduction as a response to the cooling caused by the eruption can not be anticipated. The SAI could be stopped after the eruption through a feedforward term of the controller, which we have not implemented. Instead SAI is only adjusted after the eruption automatically by the controller once the temperature impact is detected. The controller detects that an external forcing is cooling the Earth and it adjusts the injection rate accordingly. Fig. 4 shows a clear drop in temperatures following the eruption and the injection rate decreases soon after as the controller reacts to the temperature change. The injection does not cease completely though, but only decreases slightly to adjust SAI to the new RF, and the impact of the volcanic eruption on the temperatures is felt during about five years. As the impact of the volcanic eruption on the temperatures is of the same order of magnitude as the noise, the detectability of the temperature change signal and the resulting SAI reduction timescale can be very variable.
3.2 Experiments with two actors with similar objectives
We now turn to experiments with two actors who have similar or complementary objectives.In the first two-actor experiment (Ownhemi), A cools the NH with a 15°N injection while B cools the SH with a 15°S injection. The results, shown on Fig. 5, indicate quite a fair outcome as the burden is shared between the two actors. Actor B needs to inject slightly more than A due to the NH/SH asymmetry in the AOD response (see Fig. 2) and the larger ocean fraction in the SH, but the difference remains small. The hemispheric SRM radiative forcings are very close to each other, and the hemispheric temperatures reach the target within about 10 years after SAI deployment starts. As the objectives are symmetrical between the two hemispheres, the monsoon is essentially unchanged. This is shown by the time series of monsoon variability being the same in both simulations (bottom right panel in Fig. 5). Thus in this experiment for this deployment scenario both actors reach their target and in addition the monsoon precipitation is not modified as a result of the SAI deployment.
 | ||
| Fig. 5 Same as Fig. 4 but for the Ownhemi experiment. The emissions from the two actors are shown with two different colors on the top left panel. Only the combined effects of their injections are shown on the other panels. | ||
The second two-actor experiment has both actors A and B aiming to cool the GMST by injecting at the Equator (Coolglobe, Fig. 6). Technically this means that the PI controller is the same for both actors. In this experiment the two actors share the burden almost equally. However, the hemispheric SRM radiative forcings are clearly different from in the previous experiment, the NH SRM RF being larger than for SH (Fig. Fig. 2). Thus, the NH cools slightly more than the SH (difference <0.5 K), leading to a small decrease (2.2%) of the monsoon precipitation.
 | ||
| Fig. 6 Same as Fig. 4 but for the Coolglobe experiment. | ||
The two experiments are very similar, but the interhemispheric differences in the SAI radiative forcing in the case of equatorial injections versus injections at 15°N/S and the slightly different targets (global versus hemispheric mean temperatures) causes notable deviations in the result, in particular concerning the monsoon. In the Coolglobe experiment the temperature target is reached, but the monsoon presents a negative anomaly in precipitation. This reflects the conclusion of our monsoon parametrization development (Section 2.1 and eqn (1)): the monsoon reacts mainly to the RF (or SAOD) difference between the hemispheres, as seen in the rightmost panels of Fig. 6. On the contrary, the Ownhemi experiment results in achieving the desired cooling with an unperturbed monsoon, since the resulting hemispheric RF are very similar. Essentially these results are expected due to the fact that the experiment Coolglobe has only one degree of freedom, whereas Ownhemi has two.
3.3 Scenarios with two actors with different objectives
In this subsection we discuss a scenario with two actors setting different climate objectives (NH-monsoon, Fig. 7). Actor A aims at cooling the NH whereas actor B has a monsoon target, due to the impacts of the deployment of SAI by A. In this scenario there is a built-in dependence of the actors, since B reacts to the monsoon change caused by A. However, despite this initial link between the two, both actors manage their SAI deployments independently. | ||
| Fig. 7 Same as Fig. 4 but for the NH-monsoon experiment. The dashed vertical lines indicate the start of SAI by actor A (year 50), the start of SAI by actor B (year 80), and the year 110 when both the interhemispheric RF gradient and temperature gradient disappear. | ||
First, actor A starts cooling the NH in simulation year 50 by injecting in the NH (15°N). After 30 years of SAI deployment by actor A (so on simulation year 80), as the monsoon precipitation is decreasing, actor B acts to improve the monsoon by injecting in the SH (at 15°S) and consequently ends up cooling the SH, too. As actor A starts its unilateral SRM, the monsoon precipitation decreases in simulation years 50–80 due to the interhemispheric temperature and RF gradients resulting from actor A's SAI deployment. When actor B starts SAI with a goal to fix the monsoon, the interhemispheric gradients start decreasing, but the impact of both gradients is visible until about year 110 when the temperature gradient disappears. Both achieve their primary targets: actor A cools the NH and B brings the monsoon precipitation to its normal level. However, both actors A and B cool also the SH, and actor B in particular needs to cool the SH down to the same level as NH (zero mean hemispheric temperature anomaly) in order to attain its monsoon goal.
3.4 Scenarios with two actors and SRM intermittence
With the last set of scenarios we investigate what happens if an actor starts, stops and then starts again its climate intervention. The intermittence could be due to many reasons, such as the advent of a new government with a contrary opinion on SRM, society changing its mind, or a public perception of a failure of SRM leading to decision-makers interrupting the injections. These experiments reveal the potential impacts of uncoordinated deployment by actors who are not committed to maintaining SAI injections and who are unprepared for perceived failure41 leading to doubt and potentially a change in public opinion. We have built three scenarios of this kind.In the first SRM intermittence scenario (Freeride, Fig. 8), both A and B aim to cool the GMST by injecting at the Equator (implemented as two PI controllers with the same parameters). They share the burden for a while, like in the Coolglobe scenario. Actor A stops SAI between years 100 and 120, and then resumes injecting.
 | ||
| Fig. 8 Same as Fig. 4 but for the Freeride experiment. The dashed vertical lines indicate the start and end of the period when actor A pauses SAI injections. | ||
As a result of A stopping injections, B ramps up its injections to its maximum capacity in an attempt to achieve its target. This is not fully sufficient and temperatures remain slightly (0.5 K) above the target. When A resumes, it does not need to inject as much as before, since B is injecting at its full capacity, which is almost sufficient to achieve their common target. This results in actor A free-riding at the expense of B. Since there is no direct communication between A and B nor any feedforward term, B does not really know that it could reduce its injections after year 120 and share the burden with A, so B continues to inject at nearly its maximum capacity until the GHG RF starts decreasing (at simulation year 150).
When A stops the injections, temperatures rise rapidly. This impact of stopping SRM is widely known as the termination shock,61 but here the impact is smaller in magnitude as only one actor stops and the other one continues. This result shows that even in lack of coordination, if two actors deploy SAI and have sufficient incentives, the termination shock can be avoided despite sudden halt of SAI by one of the actors.62
The second SRM intermittence scenario (Stopgo, Fig. 9) is similar to the previous one in that both A and B aim to cool the GMST by injecting at the Equator (they also have the same parameters for the PI controller). They share the burden for a while (50 years), but then keep changing their mind by stopping injections for ten years, each at a time, so that when one is not injecting the other one is, thus changing roles every ten years. This leads to oscillations in the SRM RF and a smaller average RF magnitude leading to the GMST missing the target by about +1 K. This scenario shows that intermittency is problematic and coordination and engagement would be needed to make sure that the goals are attained. This is a highly idealized scenario, designed for testing the achievability of the goals despite high levels of intermittence.
 | ||
| Fig. 9 Same as Fig. 4 but for the but for the Stopgo experiment. | ||
The intermittency stops in simulation year 180. In the end of the simulation a free-riding situation occurs, as actor A is nearly at its maximum capacity when actor B starts injecting again, the latter not needing to inject as much for reaching the target. Here the lack of a feedforward term is seen as in the previous case.
In the third SRM intermittence scenario (Overcool, Fig. 10) the actors have different targets. Actor A aims to cool the NH with an injection at 15°N while B aims to cool the SH with a 15°S injection. In this scenario, each actor stops for 5 years if they overcool their hemispheric mean temperature goal. The overcooling and stopping criteria occur irregularly, approximately every 15–20 years in this experiment. This intermittence results in temperatures rising in the target hemisphere although only one of the actors stops at a time. The irregular intermittence leads to fairly large (nearly 1 K) oscillations in hemispheric temperatures and the actors missing their target by +0.5 K, and to an increase in the monsoon variability (standard deviation of 10.6% versus 9.8% for the unperturbed monsoon).
 | ||
| Fig. 10 Same as Fig. 4 but for the Overcool experiment. | ||
4 Conclusion and future research
In this study, we have conducted several idealized numerical experiments to investigate the outcomes of uncoordinated SAI deployment by two actors. In particular, intermittent deployment can lead to severe oscillations of the target parameters and the actors missing the target. However, if the actors perform continuous deployment, the resulting climate converges (close) to the desired target(s).We have further shown that two non-cooperative actors implicitly learn from each other's actions through the monitoring of their own climatic targets, which induces some kind of indirect coordination. We have also shown that free riding may occur if one of the actors stops injections during a certain time and resumes while the other actor has already ramped up its deployment to a larger capacity. It should be noted that we have no feedforward term in our controller, so any change in actions of an actor are only based on a detection of change in the monitored parameters related to their climate goals (temperature or monsoon precipitation). Thus the changes can not be anticipated based on, for example, knowledge on stopping of injections by another actor or direct observation of a volcanic eruption that would be possible in reality.
We have also addressed intermittent deployment of SAI to mimic policy instabilities. Halting the injections is either prescribed or defined to happen when a certain condition (overcooling) is met. In our experiments, intermittence produces oscillations in the predicted temperatures and an increase in monsoon variability. These examples show that SRM intermittence can lead to missing the climatic target. This illustrates the need for a long-term (global) engagement if SRM is to be deployed. These experiments show that investigating non-ideal SRM scenarios is a critical line of research, including less ideal settings that account for political, societal, legal and geopolitical constraints, and failures of the SRM implementation.
Our model is simple, but fast to run, which makes it useful to potentially investigate more scenarios than the ones discussed in this study. The model could be made more complex to address new issues, but it is unlikely that a more complex model would lead to qualitatively different answers. Including different actors with controllers into a global model could be a follow up of our simple approach and remove some of the simplifications and biases of this model. Such an approach could for instance provide a more realistic link between regional RF and regional temperature response.63
There are also future perspectives for this work, using the same kind of a simple model. We could introduce a time delay in the controller response, related to political decision-making timescales. Here the study focused on two actors only, but further actors could be included, with different targets and/or different injection capabilities. Also, multi-target actors could be described with a modified controller (i.e. with multiple input and multiple output). It could also be possible to test the implementation of the suggested distributed deployment responsibility.33 Finally, a specific module could be developed to mimic a coalition of actors and their strategy in using SAI for their climatic goals.
Author contributions
A. M.: conceptualization, writing – original draft, methodology, investigation, formal analysis, visualization, validation, funding acquisition. F. R.: conceptualization, methodology, writing – review & editing. T. L.: investigation, writing – review & editing. J. B.: methodology, software, investigation, writing – review & editing. O. B.: conceptualization, writing – original draft, methodology, software, investigation, formal analysis, visualization, data curation, resources, supervision.Conflicts of interest
The authors have no conflicts of interest to declare.Data availability
The source code used for the final version of the article is available on zenodo: https://doi.org/10.5281/zenodo.18133164. The original code repository is available at https://github.com/OB-IPSL/two-actor-SRM.Acknowledgements
The IPSL-CM6 experiments were performed using the HPC resources of TGCC under the allocations 2022-A0120107732 and 2023-A0140107732 (project gencmip6) provided by GENCI (Grand Equipment National de Calcul Intensif). This study also benefited from the IPSL Data and Computing Center ESPRI which is supported by CNRS, Sorbonne Université, CNES and École Polytechnique. The authors acknowledge funding from the Institut de la transition environnementale de l'Alliance Sorbonne Université (SU-ITE).Notes and references
- J. Rogelj, T. Fransen, M. den Elzen, R. D. Lamboll, C. Schumer, T. Kuramochi, F. Hans, S. Mooldijk and J. Portugal-Pereira, Credibility gap in net-zero climate targets leaves world at high risk, Science, 2023, 380, 1014–1016 CrossRef CAS PubMed.
- UNEP, Emissions Gap Report 2024, United Nations Environment Programme Technical Report, 2024 Search PubMed.
- M. F. Quaas, J. Quaas, W. Rickels and O. Boucher, Are there good reasons against open-ended research into solar radiation management? A model of inter-generational decision-making under uncertainty, J. Environ. Econ. Manage., 2017, 84, 1–17 CrossRef.
- NAS, Reflecting Sunlight: Recommendations for Solar Geoengineering Research and Research Governance. Consensus Study Report, National Academies of Sciences, Engineering, and Medicine Technical Report, 2021 Search PubMed.
- A. Jones, J. Haywood and O. Boucher, A comparison of the climate impacts of geoengineering by stratospheric SO2 injection and by brightening of marine stratocumulus cloud, Atmos. Sci. Lett., 2011, 12, 176–183 Search PubMed.
- A. C. Jones, M. K. Hawcroft, J. M. Haywood, A. Jones, X. Guo and J. C. Moore, Regional Climate Impacts of Stabilizing Global Warming at 1.5 K Using Solar Geoengineering, Earth's Future, 2018, 6, 230–251 Search PubMed.
- A. Robock, A. Marquardt, B. Kravitz and G. Stenchikov, Benefits, risks, and costs of stratospheric geoengineering, Geophys. Res. Lett., 2009, 36, L19703 CrossRef.
- UNESCO, Report of the World Commission on the Ethics of Scientific Knowledge and Technology (COMEST) on the Ethics of Climate Engineering, United Nations Educational, Scientific and Cultural Organization Technical Report, 2023 Search PubMed.
- UNEP, One Atmosphere: an Independent Expert Review on Solar Radiation Modification Research and Deployment, United Nations Environment Programme Technical Report, 2023 Search PubMed.
- S. Tilmes, K. H. Rosenlof, D. Visioni, E. M. Bednarz, T. Felgenhauer, W. Smith, C. Lennard, M. S. Diamond, M. Henry, C. S. Harrison and C. Thompson, Research criteria towards an interdisciplinary Stratospheric Aerosol Intervention assessment, Oxford Open Clim. Change, 2024, 4, kgae010 CrossRef.
- P. J. Irvine and D. W. Keith, Halving warming with stratospheric aerosol geoengineering moderates policy-relevant climate hazards, Environ. Res. Lett., 2020, 15(4), 044011 CrossRef.
- W. Rickels, M. F. Quaas, K. Ricke, J. Quaas, J. Moreno-Cruz and S. Smulders, Who turns the global thermostat and by how much?, Energy Econ., 2020, 91, 104852 CrossRef.
- O. Boucher, D. Randall, P. Artaxo, C. Bretherton, G. Feingold, P. Forster, V.-M. Kerminen, Y. Kondo, H. Liao, U. Lohmann, P. Rasch, S. K. Satheesh, S. Sherwood, B. Stevens and X.-Y. Zhang, in Working Group I Contribution to the Fifth Assessment Report of the IPCC, ed. T. Stocker et al., Cambridge University Press, Cambridge, 2013, pp. 571–657 Search PubMed.
- A. Laakso, H. Kokkola, A.-I. Partanen, U. Niemeier, C. Timmreck, K. E. J. Lehtinen, H. Hakkarainen and H. Korhonen, Radiative and climate impacts of a large volcanic eruption during stratospheric sulfur geoengineering, Atmos. Chem. Phys., 2016, 16, 305–323 CrossRef CAS.
- I. Quaglia, D. Visioni, E. M. Bednarz, D. G. MacMartin and B. Kravitz, The Potential of Stratospheric Aerosol Injection to Reduce the Climatic Risks of Explosive Volcanic Eruptions, Geophys. Res. Lett., 2024, 51, e2023GL107702 CrossRef CAS.
- D. G. MacMartin, B. Kravitz, S. Tilmes, J. H. Richter, M. J. Mills, J.-F. Lamarque, J. J. Tribbia and F. Vitt, The Climate Response to Stratospheric Aerosol Geoengineering Can Be Tailored Using Multiple Injection Locations, J. Geophys. Res.: Atmos., 2017, 122, 12574–12590 CAS.
- D. Visioni, D. G. MacMartin, B. Kravitz, S. Tilmes, M. J. Mills, J. H. Richter and M. P. Boudreau, Seasonal Injection Strategies for Stratospheric Aerosol Geoengineering, Geophys. Res. Lett., 2019, 46, 7790–7799 CrossRef.
- W. R. Lee, D. Visioni, E. M. Bednarz, D. G. MacMartin, B. Kravitz and S. Tilmes, Quantifying the Efficiency of Stratospheric Aerosol Geoengineering at Different Altitudes, Geophys. Res. Lett., 2023, 50, e2023GL104417 CrossRef CAS.
- B. Kravitz and D. G. MacMartin, Uncertainty and the basis for confidence in solar geoengineering research, Nat. Rev. Earth Environ., 2020, 1, 64–75 CrossRef.
- D. Visioni, B. Kravitz, A. Robock, S. Tilmes, J. Haywood, O. Boucher, M. Lawrence, P. Irvine, U. Niemeier, L. Xia, G. Chiodo, C. Lennard, S. Watanabe, J. C. Moore and H. Muri, Opinion: The scientific and community-building roles of the Geoengineering Model Intercomparison Project (GeoMIP) – past, present, and future, Atmos. Chem. Phys., 2023, 23, 5149–5176 CrossRef CAS.
- A. Määttänen, T. Lameille, C. Kloeck, O. Boucher and F. Ravetta, Uncertainties and confidence in stratospheric aerosol injection modelling: a systematic literature review, Oxford Open Clim. Change, 2024, 4, kgae007 CrossRef.
- A. Jarvis, D. Leedal, C. J. Taylor and P. Young, Stabilizing global mean surface temperature: A feedback control perspective, Environ. Modell. Software, 2009, 24, 665–674 CrossRef.
- G. A. Ban-Weiss and K. Caldeira, Geoengineering as an optimization problem, Environ. Res. Lett., 2010, 5(3), 034009 Search PubMed.
- D. G. MacMartin, B. Kravitz, D. W. Keith and A. Jarvis, Dynamics of the coupled human-climate system resulting from closed-loop control of solar geoengineering, Clim. Dyn., 2014, 43(1–2), 243–258 Search PubMed.
- B. Kravitz, D. G. MacMartin, H. Wang and P. J. Rasch, Geoengineering as a design problem, Earth Syst. Dyn., 2016, 7(2), 469–497 CrossRef.
- B. Kravitz, D. G. MacMartin, M. J. Mills, J. H. Richter, S. Tilmes, J.-F. Lamarque, J. Tribbia and F. Vitt, First simulations of designing stratospheric sulfate aerosol geoengineering to meet multiple simultaneous climate objectives, J. Geophys. Res.: Atmos., 2017, 122(23), 12616–12634 Search PubMed.
- W. Lee, D. MacMartin, D. Visioni and B. Kravitz, Expanding the design space of stratospheric aerosol geoengineering to include precipitation-based objectives and explore trade-offs, Earth Syst. Dyn., 2020, 11, 1051–1072 Search PubMed.
- A. Tang, When looking is dangerous: How solar radiation management research can harm, Bull. At. Sci., 2023, msc1. https://thebulletin.org/2023/06/when-looking-is-dangerous-how-solar-radiation-management-research-can-harm/ Search PubMed.
- P. W. Keys, The plot must thicken: a call for increased attention to social surprises in scenarios of climate futures, Environ. Res. Lett., 2023, 18, 081003 CrossRef.
- W. Morrissey, Avoiding atmospheric anarchy: Geoengineering as a source of interstate tension, Environ. Secur., 2024, 2(2), 291–315 CrossRef.
- J. L. Reynolds, Is solar geoengineering ungovernable? A critical assessment of governance challenges identified by the Intergovernmental Panel on Climate Change, WIREs Clim. Change, 2021, 12, e690 CrossRef.
- C. M. Bell and P. W. Keys, Strategic logic of unilateral climate intervention, Environ. Res. Lett., 2023, 18, 104045 Search PubMed.
- A. Lockley, Distributed governance of Solar Radiation Management geoengineering: A possible solution to SRM's “free-driver”’ problem?, Front. Eng. Manage., 2019, 6, 551–556 CrossRef.
- D. G. MacMartin, D. Visioni, B. Kravitz, J. Richter, T. Felgenhauer, W. R. Lee, D. R. Morrow, E. A. Parson and M. Sugiyama, Scenarios for modeling solar radiation modification, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2202230119 CrossRef CAS PubMed.
- A. Lockley, Y. Xu, S. Tilmes, M. Sugiyama, D. Rothman and A. Hindes, 18 Politically relevant solar geoengineering scenarios, Curr. Opin. Environ. Sustainability, 2022, 4, 18127 Search PubMed.
- D. Bodansky, The who, what, and wherefore of geoengineering governance, Clim. Change, 2013, 121(3), 539–551 CrossRef.
- A. Gupta, I. Möller, F. Biermann, S. Jinnah, P. Kashwan, V. Mathur and S. Nicholson, Anticipatory governance of solar geoengineering: conflicting visions of the future and their links to governance proposals, Curr. Opin. Environ. Sustainability, 2020, 45, 10–19 CrossRef PubMed.
- F. Schenuit, J. Gilligan and A. Viswamohanan, A scenario of solar geoengineering governance: Vulnerable states demand, and act, Futures, 2021, 132, 102809 Search PubMed.
- J. L. Reynolds and G. Wagner, Highly decentralized solar geoengineering, Environ. Polit., 2020, 29(5), 917–933 CrossRef.
- S. Baum, T. Maher and J. Haqq-Misra, Double catastrophe: intermittent stratospheric geoengineering induced by societal collapse, Environ. Syst. Dec., 2013, 33, 168–180 CrossRef.
- P. W. Keys, E. A. Barnes, N. S. Diffenbaugh, J. W. Hurrell and C. M. Bell, Potential for perceived failure of stratospheric aerosol injection deployment, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2210036119 Search PubMed.
- K. L. Ricke, J. B. Moreno-Cruz and K. Caldeira, Strategic incentives for climate geoengineering coalitions to exclude broad participation, Environ. Res. Lett., 2013, 8(1), 014021 CrossRef.
- F. Rabitz, Going rogue? Scenarios for unilateral geoengineering, Futures, 2016, 84, 98–107 Search PubMed.
- D. Heyen, J. Horton and J. Moreno-Cruz, Strategic implications of counter-geoengineering: Clash or cooperation?, J. Environ. Econ. Manage., 2019, 95, 153–177 CrossRef.
- O. Geoffroy, D. Saint-Martin, D. J. L. Olivié, A. Voldoire, G. Bellon and S. Tytéca, Transient climate response in a two-layer energy-balance model. Part I: Analytical solution and parameter calibration using CMIP5 AOGCM experiments, J. Clim., 2013, 26, 1841–1857 Search PubMed.
- C. Kleinschmitt, O. Boucher and U. Platt, Sensitivity of the radiative forcing by stratospheric sulfur geoengineering to the amount and strategy of the SO2 injection studied with the LMDZ-S3A model, Atmos. Chem. Phys., 2018, 18, 2769–2786 CrossRef CAS.
- O. Boucher, J. Servonnat, A. L. Albright, O. Aumont, Y. Balkanski, V. Bastrikov, S. Bekki, R. Bonnet, S. Bony, L. Bopp, P. Braconnot, P. Brockmann, P. Cadule, A. Caubel, F. Cheruy, F. Codron, A. Cozic, D. Cugnet, F. D’Andrea, P. Davini, C. de Lavergne, S. Denvil, J. Deshayes, M. Devilliers, A. Ducharne, J.-L. Dufresne, E. Dupont, C. Éthé, L. Fairhead, L. Falletti, S. Flavoni, M.-A. Foujols, S. Gardoll, G. Gastineau, J. Ghattas, J.-Y. Grandpeix, B. Guenet, L. E. Guez, E. Guilyardi, M. Guimberteau, D. Hauglustaine, F. Hourdin, A. Idelkadi, S. Joussaume, M. Kageyama, M. Khodri, G. Krinner, N. Lebas, G. Levavasseur, C. Lévy, L. Li, F. Lott, T. Lurton, S. Luyssaert, G. Madec, J.-B. Madeleine, F. Maignan, M. Marchand, O. Marti, L. Mellul, Y. Meurdesoif, J. Mignot, I. Musat, C. Ottlé, P. Peylin, Y. Planton, J. Polcher, C. Rio, N. Rochetin, C. Rousset, P. Sepulchre, A. Sima, D. Swingedouw, R. Thiéblemont, A. K. Traore, M. Vancoppenolle, J. Vial, J. Vialard, N. Viovy and N. Vuichard, Presentation and evaluation of the IPSL-CM6A-LR climate model, J. Adv. Model. Earth Syst., 2020, 12, e2019MS002010 CrossRef.
- C. Kleinschmitt, O. Boucher, S. Bekki, F. Lott and U. Platt, The Sectional Stratospheric Sulfate Aerosol module (S3A-v1) within the LMDZ general circulation model: description and evaluation against stratospheric aerosol observations, Geosci. Model Dev., 2017, 10, 3359–3378 Search PubMed.
- S. Gadgil, P. A. Francis, K. Rajendran, R. S. Nanjundiah and S. A. Rao, in Role of Land-Ocean Contrast in the Indian Summer Monsoon Rainfall, 2021, ch. 1, pp. 3–12 Search PubMed.
- S. M. Kang, I. M. Held, D. M. W. Frierson and M. Zhao, The Response of the ITCZ to Extratropical Thermal Forcing: Idealized Slab-Ocean Experiments with a GCM, J. Clim., 2008, 21, 3521–3532 CrossRef.
- S. M. Kang, D. M. W. Frierson and I. M. Held, The Tropical Response to Extratropical Thermal Forcing in an Idealized GCM: The Importance of Radiative Feedbacks and Convective Parameterization, J. Atmos. Sci., 2009, 66, 2812–2827 Search PubMed.
- D. M. W. Frierson and Y.-T. Hwang, Extratropical Influence on ITCZ Shifts in Slab Ocean Simulations of Global Warming, J. Clim., 2012, 25, 720–733 CrossRef.
- Y.-T. Hwang, D. M. W. Frierson and S. M. Kang, Anthropogenic sulfate aerosol and the southward shift of tropical precipitation in the late 20th century, Geophys. Res. Lett., 2013, 40, 2845–2850 CrossRef.
- J. M. Haywood, A. Jones, N. Bellouin and D. Stephenson, Asymmetric forcing from stratospheric aerosols impacts Sahelian rainfall, Nat. Clim. Change, 2013, 3, 660–665 CrossRef CAS.
- S. Roose, G. Bala, K. Krishnamohan, L. Cao and K. Caldeira, Quantification of tropical monsoon precipitation changes in terms of interhemispheric differences in stratospheric sulfate aerosol optical depth, Clim. Dyn., 2023, 61, 4243–4258 Search PubMed.
- A. Xavier, G. Bala, S. Roose and U. KH, An investigation of the relationship between tropical monsoon precipitation changes and stratospheric sulfate aerosol optical depth, Oxford Open Clim. Change, 2024, 4, kgae016 CrossRef.
- R. A. Rohde and Z. Hausfather, The Berkeley Earth land/ocean temperature record, Earth Syst. Sci. Data, 2020, 12, 3469–3479 CrossRef.
- H. Annamalai, J. M. Slingo, K. R. Sperber and K. Hodges, The Mean Evolution and Variability of the Asian Summer Monsoon: Comparison of ECMWF and NCEP–NCAR Reanalyses, Mon. Weather Rev., 1999, 127, 1157–1186 CrossRef.
- V. Krishnamurthy and J. Shukla, Intraseasonal and Interannual Variability of Rainfall over India, J. Clim., 2000, 13, 4366–4377 CrossRef.
- Y. Zhang, D. G. MacMartin, D. Visioni and B. Kravitz, How large is the design space for stratospheric aerosol geoengineering?, Earth Syst. Dyn., 2022, 13, 201–217 Search PubMed.
- A. Jones, J. M. Haywood, K. Alterskjær, O. Boucher, J. N. S. Cole, C. L. Curry, P. J. Irvine, D. Ji, B. Kravitz, J. E. Kristjánsson, J. C. Moore, U. Niemeier, A. Robock, H. Schmidt, B. Singh, S. Tilmes, S. Watanabe and J.-H. Yoon, The impact of abrupt suspension of solar radiation management (termination effect) in experiment G2 of the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.: Atmos., 2013, 118, 9743–9752 Search PubMed.
- A. Parker and P. J. Irvine, The Risk of Termination Shock From Solar Geoengineering, Earth's Future, 2018, 6, 456–467 CrossRef.
- B. Zhang, M. Zhao, H. He, B. J. Soden, Z. Tan, B. Xiang and C. Wang, The Dependence of Climate Sensitivity on the Meridional Distribution of Radiative Forcing, Geophys. Res. Lett., 2023, 50, e2023GL105492 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |




