Heterogeneity-induced retraction in viscoelastic fluids following cessation of flow†
Patrick J.
McCauley‡
 ,
Satish
Kumar
,
Satish
Kumar
 * and
Michelle A.
Calabrese
* and
Michelle A.
Calabrese
 *
*
Department of Chemical Engineering and Materials Science, University of Minnesota Twin Cities, Minneapolis, Minnesota 55455, USA. E-mail: kumar030@umn.edu; mcalab@umn.edu; Tel: +1 612 625 2558 Tel: +1 612 625 2551
First published on 22nd May 2024
Abstract
Complex fluids including colloidal suspensions, microgels, and entangled wormlike micelles (WLMs) can develop heterogeneous flow regions under imposed steady shear. In some of these systems, the evolution to this flow state from rest is accompanied by flow reversal – when a portion of the fluid moves opposite to the imposed flow direction. Flow reversal was proposed to occur in shear startup when (1) the fluid has significant elasticity, and (2) the flow becomes heterogeneous immediately following the stress overshoot [McCauley et al., J. Rheol., 2023, 67, 661–681]. To verify this hypothesis, a new method is developed for measuring flow heterogeneity. Upon cessation of the imposed flow, elasticity and flow heterogeneity cause retraction of the fluid, which is quantified with particle tracking velocimetry. Flow is stopped at key times during shear startup in two systems: a gel-like WLM that exhibits flow reversal before heterogeneous flow and a viscoelastic, fluid-like WLM that does not. The degree of flow heterogeneity is inferred from the shape and magnitude of velocity profiles measured during retraction. Flow heterogeneity develops earlier in gel-like WLMs – supporting the proposed flow reversal criteria. For comparison, heterogeneous Couette flows described with the upper-convected Maxwell or Germann–Cook–Beris models are analyzed. These theoretical flow problems confirm that stark differences in rheological properties across the flow geometry can cause significant fluid retraction and reproduce key features of the experimentally observed retraction. This new method can be used to extract quantitative information about spatially heterogeneous flows in viscoelastic complex fluids, whether or not flow reversal occurs.
1 Introduction
Heterogeneous shear flows, where the microstructure and rheological properties of a flowing material vary spatially within the flow geometry, occur frequently in complex fluids ranging from colloidal suspensions to microgels and surfactants.1–3 In shear flows of entangled wormlike micelles (WLMs), substantial flow heterogeneity results in the formation of shear bands, regions of fluid with distinct shear rates, microstructures, and viscosities. Significant effort has been expended over the last few decades to understand how shear bands form in WLMs.4–7 To address this question, many studies have examined the evolution of shear-banded flow from an initially homogeneous solution at rest.8–12 In a frequently studied type of WLM, cetylpyridinium chloride surfactants with sodium salicylate (CPyCl-NaSal), shear bands are proposed to form by a “disentangle–re-entangle” mechanism10,11 in shear startup, a flow protocol where a constant shear rate is suddenly imposed on a solution at rest. Here, WLMs are hypothesized to be homogeneously entangled at rest, to homogeneously disentangle in the region of maximum stress, and then to partially re-entangle at long times following the onset of shear banding.McCauley et al. recently proposed a unique shear band formation mechanism in WLM gels – WLMs with very slow dynamics and an apparent yield stress13 – formed from triblock polymers known as poloxamers.14 Heterogeneous flows in these 15% wt poloxamer WLMs were likely due to a mechanism similar to that observed in some yield stress fluids.15,16 Here, elastic stresses accumulate near the beginning of startup flow, which eventually exceed the apparent static yield stress of the WLM gel. At this point, the WLM gel begins to fluidize. As the shear stress is not uniform in concentric cylinder flow geometries, only a portion of the WLM gel that is closer to the inner cylinder (where the shear stress is greater) fluidizes. In some yield stress fluids, this fluidized region expands over time and the flow heterogeneity eventually disappears.17 However, for these WLM gels, viscoelastic aging in the unyielded fluid region increases resistance to flow over time and prevents further fluidization, trapping the flow heterogeneity and creating distinct shear bands that persist indefinitely; this viscoelastic aging was shown to be related to an increase in the micelle entanglement density due to micelle elongation.14 These coexisting fluidized and unyielded regions were proposed to have very different rheological properties – relaxation times, viscosities, and elastic moduli – as inferred by the exceptionally large difference in shear rate in each region.
The most significant piece of evidence that suggested a unique shear band formation mechanism in these WLM gels was a period of flow reversal – when a portion of the fluid moves opposite to the direction of the moving boundary – during shear startup.12,14,18 Flow reversal preceding shear banding has been predicted in constitutive models of entangled polymer solutions and WLM fluids,19–23 and this phenomenon is expected to be more intense in geometries with greater underlying inhomogeneity (e.g. concentric cylinders with larger ratio of outer to inner radii).19,24 Despite these modeling predictions, flow reversal has not been observed experimentally in WLMs which form shear bands by the canonical disentangle–re-entangle mechanism.10,11,25 However beyond WLM gels,12,14,18,26 flow reversal has also been observed in complex fluids ranging from soft glassy materials to polymer solutions and microgels.27–30 Based on the commonality of this behavior across soft materials, McCauley et al. postulated two requirements for flow reversal:14 (1) the fluid must have substantial elasticity and (2) the flow must be heterogeneous when the shear stress decreases with time, immediately following the maximum stress “overshoot” in shear startup. In the 15% wt poloxamer WLM gels, flow reversal coincided with the rapid stress drop after the stress maximum. In the shear banding mechanism proposed for these WLM gels, the flow is heterogeneous during this time period because of the partial fluidization. However, in the disentangle–re-entangle mechanism, WLMs are homogeneously disentangled during the rapid drop in stress, and thus one criterion for flow reversal is not satisfied.
Validating the proposed heterogeneity criterion is difficult as measuring the evolution of the flow heterogeneity is challenging. Simultaneous rheology and particle tracking velocimetry (rheo-PTV), which is the primary technique used previously to quantify flow reversal,12,14,18 has the required spatiotemporal resolution, and qualitatively identifying heterogeneous flow regions from the velocity profile is fairly straightforward once the flow stabilizes. However, measuring flow heterogeneity is nontrivial during the transient period between initially homogeneous flow and shear-banded flow. For example, during flow reversal in poloxamer WLM gels, the velocity profile becomes highly nonlinear, and the location of distinct heterogeneous flow regions – if formed – cannot be clearly identified. Additionally, the underlying forward flow counteracts flow reversal, meaning this phenomenon can be suppressed at higher shear rates,14,26 which complicates correlations between flow reversal and flow heterogeneity.
To characterize flow heterogeneity, a classic rheology protocol, cessation of flow, is revisited here and investigated with rheo-PTV. In cessation of flow, shear startup is maintained for some time, tc, after which the strain is held constant and the fluid is allowed to relax. Previously, these protocols have been used to measure WLM microstructure recovery after shear startup, via flow-small angle neutron scattering (SANS) and flow-small angle light scattering (SALS).10,11 Rheo-PTV during flow cessation is not useful for purely viscous fluids, as the velocity must be zero across the flow geometry. However, fluids with elasticity can retract once the driving forces producing the flow are removed.31 Rheo-PTV measurements revealed regions of retracting fluid after step-strain in entangled polymer solutions32; later modeling efforts suggested this behavior could arise due to an underlying elastic consecutive instability, where small heterogeneities grow into shear flows.33
Here, the connection between flow heterogeneity and fluid retraction upon cessation of flow following shear startup is explored in wormlike micelles. This work shows that if elastic fluids, like the WLMs investigated here, have significant spatial heterogeneity in the stress dissipation rate, substantial fluid retraction accompanies stress relaxation during cessation of flow. Here, fluid retraction refers to the fluid moving in the direction opposite of the imposed shear flow after the imposed flow has been stopped, whereas flow reversal refers to a portion of the fluid moving opposite to the direction of the moving boundary during imposed shear flow. This large degree of fluid retraction can be subsequently related to flow heterogeneity.
In this article, fluid retraction upon flow cessation is examined comprehensively in two model aqueous poloxamer WLMs with spatially heterogeneous rheological properties, using experimental, theoretical, and computational methods. Both WLM solutions contain the same poloxamer, P234, but have been previously shown to exhibit drastically different rheological properties.14,34 Here, 4% wt P234 with 0.9 M sodium fluoride (NaF) forms a canonical, fast-breaking viscoelastic WLM solution,34 which is expected to exhibit shear banding via the “disentangle–re-entangle” mechanism. Conversely, 15% wt P234 with 2 M sodium chloride (NaCl) forms a WLM gel14 which is proposed to exhibit shear banding similar to that in aging yield stress fluids.
Flow heterogeneity during shear startup is characterized via cessation of flow experiments with rheo-PTV, where partial fluidization and fluid retraction are measured directly. These experiments are subsequently analyzed using refined rheo-PTV analysis methods; the simple, predictable trajectories of particles in the rheo-PTV flow geometry are exploited to accurately measure the velocity of particles that move very slowly. The experimental conclusions are then strongly supported by results from two theoretical flow problems: (1) Couette flow between parallel plates, and (2) Couette flow between concentric cylinders. In the first, the fluid constitutive behavior is modeled by two upper-convected Maxwell model fluids (two-UCM) with different rheological properties occupying adjacent but spatially distinct regions – a simplified representation of shear banded flow that can be solved analytically. In the second, the fluid behavior is modeled using the Germann–Cook–Beris (GCB) model,20,21 which captures key flow phenomena in poloxamer WLM gels including flow reversal and the onset of flow heterogeneity immediately following the stress overshoot in startup flows.
The different magnitudes of fluid retraction measured via rheo-PTV following cessation of flow strongly support the distinct shear band formation mechanisms proposed for each WLM system. The analytical solution to the first flow problem then reveals key quantitative relationships between heterogeneous fluid properties and fluid retraction. Finally, GCB model simulations are shown to capture key flow features from experiments. Importantly, the degree of fluid heterogeneity can either be directly controlled or calculated in the theoretical flow problems – which paired with experimental results, is used to show that fluid retraction provides a direct measure of flow heterogeneity and viscoelastic aging. These findings highlight the capability of cessation of flow paired with rheo-PTV to quantify flow heterogeneity in a wide range of viscoelastic complex fluids, providing spatial information not accessed by other techniques.
2 Theory
2.1 Couette flow of two adjacent UCM fluids between parallel plates
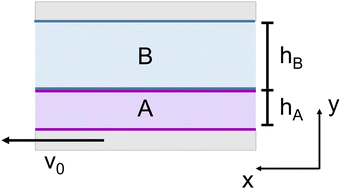
A simple approximation of shear-banded flow of WLMs is Couette flow between parallel plates of two upper-convected Maxwell model (UCM) fluids, separated perpendicular to the flow direction (Fig. 1). For simplicity, these fluid regions A and B (Fig. 1) are each composed of only one species, which have distinct relaxation times and viscosities. The benefit of this flow problem is that the flow field can be solved analytically, which provides key insights into fluid retraction behavior during cessation of flow. Additionally, these analytical results demonstrate that rheo-PTV using this flow protocol can measure flow heterogeneity. Although this model is a fairly crude approximation of shear-banded flow, the key behaviors predicted by this model in cessation of flow protocols will be shown to match the trends observed in experiments.The governing equations for Couette flow of two adjacent UCM fluids between parallel plates are:
 | (1) |
 | (2) |
Eqn (1) is the linear momentum balance, where v is the fluid velocity, ρ is the total mass density of the solution, p the pressure, and σ is the extra-stress tensor. Eqn (2) is the relationship of the extra-stress tensor for the UCM model, where τi is the relaxation time of fluid i = A, B, η0,i is the zero-shear viscosity of fluid i = A, B, and 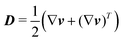 is the rate of strain tensor. The symbol
is the rate of strain tensor. The symbol  denotes the upper-convected derivative:
denotes the upper-convected derivative:
 | (3) |
The following criteria define the spatial extent of each fluid region within the gap:
| 0 ≤ y ≤ hA region A | (4) |
| hA ≤ y ≤ hA + hB = H region B | (5) |
These governing equations are simplified considerably by assuming the flow is one-dimensional, v = (vx,0,0), and inertial effects are negligible (creeping flow). These equations become:
| ∇·σ = 0 | (6) |
 | (7) |
 | (8) |
 . Eqn (7) describes the evolution of the shear stress, σyx, and eqn (8) describes the evolution of the normal stress, σxx; eqn (8) is not needed to solve for the velocity. From eqn (6), the shear stress is constant across the gap of the flow geometry
. Eqn (7) describes the evolution of the shear stress, σyx, and eqn (8) describes the evolution of the normal stress, σxx; eqn (8) is not needed to solve for the velocity. From eqn (6), the shear stress is constant across the gap of the flow geometry  . Therefore the shear rates,
. Therefore the shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) A and
A and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) B, described by eqn (7) are constant within their respective regions:
B, described by eqn (7) are constant within their respective regions: | (9) |
From eqn (7)–(9), a general solution for the evolution of the shear stress and shear rates in regions A and B is derived for a constant applied shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app (see Section SI.1, ESI†). With no-slip boundary conditions assumed at each solid–fluid boundary, the resulting equations are:
app (see Section SI.1, ESI†). With no-slip boundary conditions assumed at each solid–fluid boundary, the resulting equations are:
σyx(t) = η0,eff![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app + C app + C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τeff) exp(−t/τeff) | (10) |
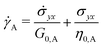 | (11) |
 | (12) |
 | (13) |
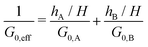 | (14) |
2.2 Couette flow of GCB model fluid between concentric cylinders
Analyzing Couette flow of adjacent UCM fluids between parallel plates reveals key insights about the nature of fluid retraction in heterogeneous flows. A second flow problem is explored using the GCB model, which allows spatiotemporal evolution of the microstructure and rheological properties and provides better qualitative agreement with experiments.37 Briefly, the GCB model to describe WLMs simplifies the continuous distribution of WLM lengths into two discrete populations, A and B, where micelles in population A are double the length of species B. The viscoelasticity of both species is described by the UCM model, and the number densities of species A and B change dynamically in response to deformation.20The flow geometry is two concentric cylinders – with a rotating inner cylinder of radius Ri and a stationary outer cylinder of radius Ro – which is the geometry used in most shear banding studies and the experiments performed here. An inherent radial stress gradient is present due to the curvature of the concentric cylinder geometry, which provides the initial source of heterogeneity to these flows. Couette flow of a GCB model fluid between concentric cylinders has been explored in-depth previously.21,38 The description of the flow problem and solution procedure here are identical to that in prior work39; thus full details about governing equations, non-dimensionalization, and solution method are deferred to Section SI.2 (ESI†). Key details related to this flow problem are discussed below.
The evolution of the flow field and species populations for a GCB model fluid between concentric cylinders are examined in shear startup and cessation of flow protocols. The flow geometry is represented in cylindrical coordinates (r, θ, z) and the velocity is assumed to be one dimensional in the azimuthal direction, v = (0, vθ, 0). To simulate shear startup, the following boundary condition is imposed at the inner cylinder:
vθ(t,r = Ri) = v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(at) tanh(at) | (15) |
vθ(t,r = Ri) = v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(at) − v0 tanh(at) − v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(a(t − tc)) tanh(a(t − tc)) | (16) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 = v0/H, where H is the gap width. Startup and cessation of flow are examined for one applied shear rate, which in dimensionless form is the Weissenberg number: Wi =
0 = v0/H, where H is the gap width. Startup and cessation of flow are examined for one applied shear rate, which in dimensionless form is the Weissenberg number: Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0τeff = 5, where τeff is the effective relaxation time of the GCB model. The dimensionless model parameters are fixed to values from ref. 39 (Table 1). Startup flow is stopped at several times tc to examine the impact of the flow heterogeneity on fluid retraction as the stress relaxes.
0τeff = 5, where τeff is the effective relaxation time of the GCB model. The dimensionless model parameters are fixed to values from ref. 39 (Table 1). Startup flow is stopped at several times tc to examine the impact of the flow heterogeneity on fluid retraction as the stress relaxes.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) Aeq and
Aeq and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) Beq are dimensionless equilibrium breakage and recombination rates for species A and B, respectively, and q = (Ro − Ri)/Ri is the curvature
Beq are dimensionless equilibrium breakage and recombination rates for species A and B, respectively, and q = (Ro − Ri)/Ri is the curvature
| Parameter | El−1 | β | ε | μ |
| Value | 0 | 7 × 10−5 | 1.2 × 10−3 | 2 |
| Parameter |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) Aeq
Aeq
|
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) Beq
Beq
|
q | |
| Value | 1 | 5 | 0.08 |
3 Materials and methods
3.1 Materials
Wormlike micelles were formed from poloxamer P234 (Synperonic PE/P84, Sigma Aldrich) dissolved in HPLC-grade water (Fischer Scientific). Samples were stirred for ≥12 h at 4 °C until the poloxamer fully dissolved and were stored at 4 °C. Two formulations are examined: (1) 15% wt poloxamer in 2 M NaCl (Fischer Scientific) and (2) 4% wt poloxamer in 0.9 M NaF (Sigma Aldrich); materials were used as received. For brevity, (1) is referred to as P234-NaCl, and (2) as P234-NaF. Both formulations form entangled WLMs based on prior work (performed in D2O),14,34 and have properties in water similar to those in D2O. Prior linear rheology measurements demonstrated that WLMs formed with NaF have faster relaxation dynamics than those formed with NaCl.34,40 These measurements also suggested that P234-NaF WLMs are fast-breaking, but did not provide sufficient evidence to discern if P234-NaCl WLMs have longer contour lengths, slower breakage dynamics, or a combination of these effects. Different P234 concentrations are required to produce WLMs with greatly contrasting rheological behavior – hypothesized to result from differences in WLM contour length as these WLMs have approximately equal cross-sectional radii.14,34 This work also builds upon previous nonlinear rheology characterization of 15% wt P234 WLMs.143.2 Shear rheology
Linear viscoelastic (LVE) rheology and nonlinear controlled stress and shear rate tests were done on an Anton Paar MCR 302 stress-controlled rheometer. Measurements were performed with an evaporation blocker, at 43.5 °C for P234-NaF and 38.5 °C for P234-NaCl. Circulating fluid around the outer cylinder maintains the setpoint temperature. The geometry, also used for rheo-PTV, is a black anodized aluminum bob of radius Ri = 16.35 mm and length L = 16.5 mm moving in a transparent quartz cylinder of radius Ro = 17.5 mm (gap-to-radius ratio ε = 0.07; aspect ratio Γ = L/(Ro − Ri) = 14.35).The rheological properties of P234-NaCl and P234-NaF are very different, thus distinct rheology protocols were used. P234-NaCl rheology is very sensitive to the thermal treatment and sample age;14 thus the pre-shear, thermal treatment, and rejuvenation protocols are almost identical to those in ref. 14. Flow curves were measured in P234-NaCl using both controlled stress (creep) and controlled shear rate protocols, where each data point was collected after 2–3 hours as done previously14; see Section SI.3 (ESI†) for complete rheology details. Note that due to aging effects, the shear stress may evolve even after these long measurement times, though not substantially.14 Although viscoelastic aging was not observed in P234-NaF, a ten-minute equilibration period at T = 43.5 °C preceded all measurements, and the sample was rejuvenated between trials using the same protocol as for P234-NaCl (see Section SI.3, ESI†). The P234-NaF flow curve was measured to identify the likely shear banding region. As these WLMs did not have a yield stress, a single ramp-up shear rate protocol (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.02–10 s−1) captured both the Newtonian region (low
= 0.02–10 s−1) captured both the Newtonian region (low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) and the shear-banding plateau (intermediate
) and the shear-banding plateau (intermediate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ). The sample was sheared for ten minutes at each shear rate. The onset of the shear banding plateau agreed with the expected value for viscoelastic WLMs
). The sample was sheared for ten minutes at each shear rate. The onset of the shear banding plateau agreed with the expected value for viscoelastic WLMs ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ ∼ 1,41 where the relaxation time τ was calculated from the crossover of G′ and G′′.
τ ∼ 1,41 where the relaxation time τ was calculated from the crossover of G′ and G′′.
3.3 Rheo-particle tracking velocimetry (rheo-PTV)
To visualize the flow field, simultaneous rheology and particle tracking velocimetry were performed using established instrumentation.10,42 The same geometry used for LVE and flow curve data was used for rheo-PTV. A 0.3 mm laser light sheet (60–150 mW CNI 532 nm low noise) illuminates a small region of the quartz cell. Tracer particles added to the sample (200 ppm 8–12 μm TSI Hollow-glass spheres) scatter the incident light. Samples were sonicated for ≥5 min prior to loading to ensure particles were well-dispersed. Particle addition was confirmed not to significantly alter the rheology.The shear protocol used in rheo-PTV measurements to probe the heterogeneity of the underlying fluid was a shear startup test followed by cessation of a flow, i.e. a period of time over which the strain is held constant. One shear rate in the shear banding region was characterized in-depth for each system: ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 s−1 for P234-NaF and
= 1 s−1 for P234-NaF and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.5 s−1 for P234-NaCl. The duration of startup prior to cessation of flow was chosen based on unique features in the stress response of long-shear startup trials.
= 0.5 s−1 for P234-NaCl. The duration of startup prior to cessation of flow was chosen based on unique features in the stress response of long-shear startup trials.
During these protocols, particles within a region of interest were recorded using a Lucam Lm165 CCD camera. Particle positions were identified and tracked between images using the open-source Trackpy Python package,43 which extends standard particle tracking algorithms.44 The particle locations are converted from the image pixel coordinates to cylindrical coordinates, the natural coordinate system describing the particle trajectories.
3.4 Velocity profile calculation
Data points in the velocity profiles correspond to the motion of individual particles, where the velocity of each particle was calculated using a trajectory-fitting approach described in Section SI.4 (ESI†). Briefly, this approach estimates a particle's velocity by fitting a displacement function to all of the particle's positions over a time interval.45 In typical rheo-PTV analysis, the velocity of a particle is calculated from its displacements between successive frame acquisitions.18,46–48 The difference between these approaches is subtle, but the approach used in this work better estimates the velocity and associated uncertainty for transient flows with slow-moving or rapidly accelerating particles, both of which are observed in cessation of flow (e.g. Fig. S1, ESI†). These two analysis methods are described and compared in Section SI.4 (ESI†) and rigorously in ref. 45.In shear startup, particle trajectories were fit assuming a constant particle velocity within short time intervals (∼1–2 s), as done previously.14 In cessation of flow, the velocity continuously decelerates and therefore the time interval must be adjusted dynamically. Velocities were first calculated using a slightly modified approach, by fitting full-duration trajectories with a decaying exponential-type function. This method was feasible because particles were present within the acquisition region throughout the duration of cessation of flow. For P234-NaF, a single exponential or sigmoid function was used; for P234-NaCl, a sum of two exponentials was used (see Section SI.4, ESI†). This approach provided time constants for the velocity decay and was compared with the averaging approach assuming constant velocity over short time intervals – where the time constants informed the time interval widths. Both approaches produced similar velocities (Fig. S4, ESI†).
For velocity profiles, the radial position in the gap is reported relative to the inner cylinder. The normalized gap position r/H = 0 at the inner cylinder and r/H = 1 at the outer cylinder. Uncertainty was estimated from the root-mean-square deviation of the predicted trajectory with velocity vavg from the measured particle trajectory. Velocity profiles at equal startup times prior to flow cessation were reproducible for both formulations (Fig. S6 and S8, ESI†).
4 Results and discussion
4.1 Wormlike micelle characterization
While WLMs form in both 4% wt P234 in 0.9 M NaF and 15% wt P234 in 2 M NaCl, the rheological properties dramatically differ (Fig. 2). The linear and nonlinear rheology of P234-NaF resembles that expected for typical viscoelastic WLMs. The frequency sweep of P234-NaF (Fig. 2a) is well described by a single relaxation time Maxwell model in the low-to-moderate frequency region (G0 = 3.7 ± 0.2 Pa and τ = 9.1 ± 0.6 s). At higher frequencies, G′′ deviates from this model, attributed to additional relaxation modes such as Rouse motion of the wormlike chains.23,49 The flow curve of P234-NaF (Fig. 2b) has a Newtonian region at low shear rates, where the stress increases linearly with applied shear rate, followed by an apparent plateau region with a power law index N = 0.06 (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≈ 0.2–2 s−1), where shear banding is anticipated. The shear rate at the onset of this plateau agrees well with the expected value for typical viscoelastic WLMs (
≈ 0.2–2 s−1), where shear banding is anticipated. The shear rate at the onset of this plateau agrees well with the expected value for typical viscoelastic WLMs (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ ≈ 2).8,41 The increase in shear stress at the end of the stress plateau likely corresponds to the onset of elastic instabilities, as seen in other WLM solutions.47,50–52
τ ≈ 2).8,41 The increase in shear stress at the end of the stress plateau likely corresponds to the onset of elastic instabilities, as seen in other WLM solutions.47,50–52
The gel-like rheological properties of P234-NaCl were previously characterized in D2O,14 but are characterized here due to differences in poloxamer batch and solvent. As a result, the viscoelastic aging rate is slightly faster in this formulation.14 The storage modulus monitored with SAOS (Fig. 2c) requires 20 minutes at 38.5 °C to reach G′ = 24 Pa – the benchmark storage modulus prior to startup. The flow curve of P234-NaCl here is similar to that previously reported.34 In contrast to P234-NaF, here an apparent static yield stress is observed based on controlled-stress (creep) measurements (Fig. 2d). The nature of this apparent yield stress in P234-NaCl was discussed in-depth previously.34 The static yield stress, 8 ≤ σ ≤ 12 Pa, is slightly lower than in the prior formulation;14 see Section SI.6 (ESI†) for full comparison.
The stark contrast in rheology between P234-NaF and P234-NaCl arises in part due to the different anion-specific interactions of fluoride anions compared to chloride anions,53 which were previously shown to impact the zero-shear viscosity and relaxation time of 4% wt poloxamer WLMs.34 Chloride anions promoted the formation of longer WLMs – with longer relaxation times – than fluoride anions. The increased poloxamer concentration in P234-NaCl compounds this effect, slowing the dynamics further and increasing the elastic modulus to roughly an order of magnitude greater than in P234-NaF. Most notably, these different formulations produce WLMs with distinct viscoelastic and gel-like properties, which have dramatically different transient behavior in shear startup.
4.2 Shear startup flows
Rheo-particle tracking velocimetry during shear startup confirms that both formulations exhibit heterogeneous flow or shear bands; however, the evolution of the velocity profiles is strikingly different (Fig. 3). These different routes to shear band formation are surprising if only the shear stress is considered; the evolution of the shear stress at applied shear rates![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 and 0.5 s−1 for P234-NaF and P234-NaCl, respectively, have similar features (Fig. 3a and b). In both cases, the shear stress increases at a nearly linear rate during the initial elastic deformation of the solution. Then, at a strain γ =
= 1 and 0.5 s−1 for P234-NaF and P234-NaCl, respectively, have similar features (Fig. 3a and b). In both cases, the shear stress increases at a nearly linear rate during the initial elastic deformation of the solution. Then, at a strain γ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) t ∼ O(1), the stress reaches a maximum and subsequently decreases at a rapid rate. As time progresses, the shear stress decreases more slowly. A much longer time than shown in Fig. 3 is likely required to reach a steady state stress.9
t ∼ O(1), the stress reaches a maximum and subsequently decreases at a rapid rate. As time progresses, the shear stress decreases more slowly. A much longer time than shown in Fig. 3 is likely required to reach a steady state stress.9
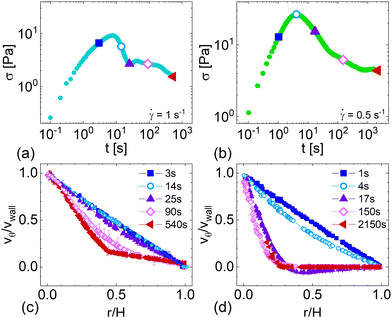 | ||
Fig. 3 Shear startups at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 s−1 for P234-NaF (a) and = 1 s−1 for P234-NaF (a) and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.5 s−1 for P234-NaCl (b). The shear stress evolves with similar features for both WLMs, but the velocity profile evolution starkly differs. Velocity profiles of P234-NaF (c) gradually evolve toward distinct shear bands whereas velocity profiles of P234-NaCl (d) become dramatically nonlinear early in startup, with a period of flow reversal. At t = 2150 s, the velocity near the inner cylinder cannot be determined due to strong WLM alignment, leading to substantial scattering of the light reflected from the particles.14 = 0.5 s−1 for P234-NaCl (b). The shear stress evolves with similar features for both WLMs, but the velocity profile evolution starkly differs. Velocity profiles of P234-NaF (c) gradually evolve toward distinct shear bands whereas velocity profiles of P234-NaCl (d) become dramatically nonlinear early in startup, with a period of flow reversal. At t = 2150 s, the velocity near the inner cylinder cannot be determined due to strong WLM alignment, leading to substantial scattering of the light reflected from the particles.14 | ||
For P234-NaF, shear bands form gradually during shear startup. The velocity profile is nearly linear throughout the stress overshoot of shear startup (Fig. 3c, t = 4 and 14 s). The velocity profile at the end of the stress overshoot only displays a slight degree of shear thinning (purple ▲, Fig. 3c, t = 25 s). As time progresses, the velocity profile gradually becomes more nonlinear, and eventually distinct shear bands form after a length of time much longer than the relaxation time (Fig. 3c, t = 540 s > 50τ). The evolution of the velocity profile for P234-NaF progresses similarly to that in typical viscoelastic WLM solutions like those formed from CPyCl-NaSal.9,10 These shear startup results thus suggest that P234-NaF forms shear bands by the disentangle–re-entangle mechanism. Interestingly, for r/H ≤ 0.1, the velocity profile is nearly linear and maintains the same slope at all times, indicating a local shear rate roughly equal to the gap-averaged shear rate. This peculiar, previously unreported behavior is discussed further in Section 4.7.
In contrast, the velocity profile becomes highly nonlinear early on in shear startup flow for P234-NaCl and eventually forms distinct fluidized and solid-like regions (Fig. 3d); this mechanism of shear band formation was analyzed in detail previously.14 Briefly, shear bands form due to partial fluidization during the stress overshoot that becomes trapped due to viscoelastic aging, like in some soft glassy materials.15,16 Unlike in P234-NaF, the velocity profile does not remain linear throughout the stress overshoot. Shear thinning in the velocity profile begins around the stress maximum (Fig. 3d, t = 4 s) and quickly develops into minor flow reversal as the stress rapidly decreases (Fig. 3d, t = 17 s). As time progresses, flow reversal subsides, and distinct regions form (Fig. 3d, t = 150 and 2150 s).
4.3 Cessation of flow experiments
The flow kinematics of P234-NaF and P234-NaCl evolve very differently in shear startup, where the key difference is the presence of flow reversal prior to shear-banded flow in P234-NaCl. Two criteria were proposed for flow reversal during shear startup14: fluid elasticity and heterogeneity in the rheological properties during the region of decreasing shear stress in the overshoot. While both WLM formulations are elastic, the magnitude and spatial distribution of heterogeneity in the rheological properties during this time period are unclear. One issue in comparing the shear startup behavior is that the base flow counteracts – and can suppress – fluid retraction.14 The cessation of flow experiments here remove this complication.Here, startup flow is stopped during three key periods of shear startup: during the initial elastic deformation, during the rapid drop in stress, and after shear bands have fully formed. For P234-NaCl, substantial fluid retraction is anticipated to occur when the imposed flow is stopped during flow reversal. A smaller degree of retraction occurs in cessation of flow at the other two stop times. The magnitude of retraction upon flow cessation at each stop time reflects the expected degree of flow heterogeneity.
 | ||
Fig. 4 Shear stress of P234-NaF in startup flow (a) at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 s−1 (vwall = 1.1 mm s−1) and in cessation of flow (b)–(d) after tc = 3, 14, and 540 s. Outlined symbols in (a) indicate the stress before flow cessation, σc; the shear stress in (b)–(d) is normalized by σc. (e)–(g) Corresponding velocity profiles at four times during cessation of flow (indicated by legend in (e), same for each tc). The magnitude of fluid retraction is greatest when shear banding precedes cessation of flow (g). The horizontal dotted line in (f) at vθ = 0 is for visual aid. See Section SI.7.1 (ESI†) for individual velocity profiles. = 1 s−1 (vwall = 1.1 mm s−1) and in cessation of flow (b)–(d) after tc = 3, 14, and 540 s. Outlined symbols in (a) indicate the stress before flow cessation, σc; the shear stress in (b)–(d) is normalized by σc. (e)–(g) Corresponding velocity profiles at four times during cessation of flow (indicated by legend in (e), same for each tc). The magnitude of fluid retraction is greatest when shear banding precedes cessation of flow (g). The horizontal dotted line in (f) at vθ = 0 is for visual aid. See Section SI.7.1 (ESI†) for individual velocity profiles. | ||
The majority of fluid retraction ceases ∼7.5 s into cessation of flow (Fig. 4e–g), well before the shear stress has fully relaxed (Fig. 4b–d). The time constant for this velocity decay, τv, is shown for each trial in Table 2. This short time constant τv varies as expected for the disentangle–re-entangle mechanism in viscoelastic WLMs. This time constant is largest at the earliest time when WLMs are fully entangled (tc = 3 s), drops in value when WLMs homogeneously disentangle (tc = 14 s), and increases when a portion of fluid re-entangles (tc = 540 s). Note this time constant also does not vary substantially with gap position (Fig. S5, ESI†).
Motivated by the presence of a fluid retraction timescale and prior work on CPyCl-NaSal surfactants during cessation of flow,11 the shear stress was fit with a sum of two decaying exponentials (Section SI.8.1, ESI†) with time constants τs,1 and τs,2 (Table 2). The larger time constant is a similar value to the relaxation time of the WLM solution at rest (τ = 9.1 s). The smaller time constant agrees well with the time scale for fluid retraction. The physical significance of each time constant is discussed in Section 4.7.
Interestingly, when the flow is heterogeneous (shear-banded), the velocity profile is slightly asymmetric (Fig. 4g). The location of the maximum fluid velocity in retraction (r/H ≈ 0.39) is close to the location of the shear band interface (r/H ≈ 0.43). The location of the maximum retraction velocity also moves toward the inner wall as time progresses (t − tc = 0.5 vs. 2.5 in Fig. 4g).
 | ||
Fig. 5 Shear stress of P234-NaCl in startup flow (a) at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.5 s−1 (vwall = 0.56 mm s−1) and in subsequent cessation of flow (b)–(d) started after tc = 1.2, 17, and 2150 s. Outlined symbols in (a) indicate σc; the shear stress in (b)–(d) is normalized by σc. Corresponding velocity profiles (e)–(g) are shown at four times during flow cessation; the same times are shown in (f) and (g). The fluid retraction magnitude is greatest during the rapid drop in stress after the stress maximum (f). See Section SI.7.2 (ESI†) for individual velocity profiles. = 0.5 s−1 (vwall = 0.56 mm s−1) and in subsequent cessation of flow (b)–(d) started after tc = 1.2, 17, and 2150 s. Outlined symbols in (a) indicate σc; the shear stress in (b)–(d) is normalized by σc. Corresponding velocity profiles (e)–(g) are shown at four times during flow cessation; the same times are shown in (f) and (g). The fluid retraction magnitude is greatest during the rapid drop in stress after the stress maximum (f). See Section SI.7.2 (ESI†) for individual velocity profiles. | ||
Beyond the large increase in fluid retraction speed after the shear stress maximum, the shape of the velocity profile also changes from symmetric to asymmetric (Fig. 5e vs. f, g). At tc = 1.2 s, the velocity profile is roughly symmetric (Fig. 5e) like in P234-NaF. After the stress maximum, a region of fluid close to the inner cylinder fluidizes and creates heterogeneous flow. The width of the fluidized regions remains roughly constant after forming. The apex of the velocity profile soon after stopping the flow (t − tc = 0.5 s) is located at r/H ≈ 0.3 for tc = 17 s and r/H ≈ 0.2 for tc = 2150 s (Fig. 5f and g, respectively). These positions are close to the interface between the distinct fluid regions during startup flow, r/H ≈ 0.25 (Fig. 3d). Note the band interface position fluctuates slightly in time during startup due to secondary flow in the fluidized region.14 Although the width of the fluidized and unyielded regions does not change significantly, the distinction between these regions becomes more refined as time progresses. The apex of the velocity profile becomes sharper and the shear rate becomes almost constant within each region when the shear startup is performed for a longer time (Fig. 5f vs. g). Interestingly, retraction is accompanied by wall slip for tc = 2150 s; in prior work,14 wall slip in P234-NaCl also increased after flow reversal ceased.
Characteristic timescales for relaxation of the shear stress and retraction velocity change with tc, revealing how the rheological properties of each region evolve during startup (Fig. 6). Fluid retraction and stress relaxation were measured for three more stop times (tc = 60, 150, 600 s); see Fig. S22 in Section SI.9 (ESI†) for shear stress and velocity profiles. Four time constants are estimated during cessation of flow for each tc: two from the decay of the velocity, τv,1 and τv,2, and two from the shear stress relaxation, τs,1 and τs,2. Time constants are obtained from fitting a sum of two decaying exponentials to the particle displacements (Section SI.4, ESI†) or shear stress (Section SI.8.2, ESI†). The time constants from particle displacements do not vary substantially with gap position (Fig. S5, ESI†).
 | ||
| Fig. 6 Cessation of flow time constants for P234-NaCl. Time constants were extracted from fitting particle trajectories: (a) τv,1 and (b) τv,2 (Section SI.4, ESI†), and shear stress: (c) τs,1 and (d) τs,2 (Section SI.8.2, ESI†). Wall slip increases the speed of the fast fluid retraction (gray region in (a) and (c)) near the start of cessation of flow. The longest time constant, τs,2, increases with tc, indicating viscoelastic aging in the unyielded region. | ||
All four time constants (Fig. 6a–d) decrease in value between the initial elastic deformation (tc = 1.2 s) and the rapid stress decrease after the maximum (tc = 17 s). Before the stress overshoot, the WLM solution is fully unyielded, and the structure and rheological properties across the flow geometry are mostly homogeneous. Notably, the time constants obtained from fitting the particle displacements and shear stress are similar.
After the stress overshoot, a large portion of the sample fluidizes. While the shorter time constants τv,1 and τs,1 remain similar (Fig. 6a and c), the longer time constants – which were similar before the overshoot (∼200 s) – are an order of magnitude different after the overshoot (tc = 17 s, τv,2 = 36 s vs. τs,2 = 184 s). The rapid drop in the time constant τv,2 suggests this relaxation time is related to relaxation of the fluidized region, which will be much faster than for the unyielded region. In contrast, τs,2 describes the relaxation of the unyielded region.
Assignments of these long relaxation times to particular fluid regions are verified by examining the evolution of these time constants as tc increases. The evolution of the shorter time constants, τv,1 and τs,1, is similar and characterizes the quick fluid retraction at the onset of flow cessation (also observed in P234-NaF). These constants increase at tc = 60 s and then decrease at larger tc when wall slip becomes noticeable (Fig. 5g and Fig. S22e, f, ESI†). With wall slip, an effective shear rate is applied in the direction of retraction, which accelerates this process. The intermediate time constant, τv,2, becomes roughly constant after flow reversal has ceased and distinct fluid regions have formed, tc ≥ 60 s; thus viscoelastic aging does not appear to impact this time constant. This observation and the magnitude suggest this time constant may depend primarily on the properties of the fluidized band.
Unlike the other time constants, τs,2, the longest time constant, increases with tc. The large value of τs,2 suggests that this time constant depends on the relaxation time of the unyielded region. The rate of increase of τs,2 slows as the shear startup progresses (Fig. 6d is a semi-logarithmic plot) – a characteristic feature of viscoelastic aging.54 Therefore the evolution of τs,2 strongly suggests that the unyielded region undergoes viscoelastic aging in shear startup; our prior work indicates that viscoelastic aging in this system is related to an increase in the micelle entanglement density, driven by an increase in the average contour length of the micelles.14 Together, the evolution of the velocity profiles and this time constant provide strong evidence for the hypothesized shear-band formation mechanism of P234-NaCl.14
4.4 Fluid retraction of two adjacent UCM fluids between parallel plates
To explain the observed fluid retraction in cessation of flow, a simple flow problem is considered. Here, the fluid velocity evolution for two adjacent UCM fluids between parallel plates (Section 2.1) is examined upon flow cessation, where the applied shear rate is set to zero following flow startup.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app is set to zero after startup flow has elapsed for a time tc, the stress will dissipate in time; however, flow will continue due to the heterogeneous properties of the fluid. To find a particular solution to eqn (10) for cessation of flow, the initial condition must be specified. For convenience, a time is defined since the onset of the cessation of flow protocol t* = t − tc. Therefore, the initial condition of the shear stress is σ(t* = 0) = σc(tc) where σc(tc), the shear stress obtained in shear startup at a constant applied shear rate
app is set to zero after startup flow has elapsed for a time tc, the stress will dissipate in time; however, flow will continue due to the heterogeneous properties of the fluid. To find a particular solution to eqn (10) for cessation of flow, the initial condition must be specified. For convenience, a time is defined since the onset of the cessation of flow protocol t* = t − tc. Therefore, the initial condition of the shear stress is σ(t* = 0) = σc(tc) where σc(tc), the shear stress obtained in shear startup at a constant applied shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app =
app = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0 maintained for a time tc, is given by:
0 maintained for a time tc, is given by:σc(tc) = η0,eff![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0(1 − exp(−tc/τeff)) 0(1 − exp(−tc/τeff)) | (17) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 0, the particular solution of eqn (10) for cessation of flow is:
app = 0, the particular solution of eqn (10) for cessation of flow is:| σyx(t*) = σc(tc)exp(−t*/τeff) | (18) |
Despite the similarity in shear stress evolution, the flow field during cessation of flow with two adjacent UCM fluids is very different from that of a homogeneous UCM fluid. For a single UCM fluid, no fluid motion would be expected during this flow protocol. As the shear rate is constant in regions of fluid where the rheological parameters are equal (eqn (9)), here the shear rate would be constant through the gap and equal to the applied shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 0 imposed by the boundary conditions.
app = 0 imposed by the boundary conditions.
However, with two adjacent UCM fluids, the fluid retracts during the stress relaxation because the relaxation time of each fluid region is different, which is revealed by solving for the shear rates in both regions of fluid A and B. For parallel plate flow, the shear stress must be uniform across each region at all times, and therefore the time derivative of the shear stress is also uniform:
 | (19) |
 | (20) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 0, the shear rates in either region must satisfy
app = 0, the shear rates in either region must satisfy ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) B = −
B = −![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) AhA/hB (found explicitly using the shear rate constraint of eqn (SI.1.3), ESI† and vw = 0). Substituting this relation between shear rates and the particular solution for shear stress in eqn (18) into eqn (20) yields an equation for the evolution of
AhA/hB (found explicitly using the shear rate constraint of eqn (SI.1.3), ESI† and vw = 0). Substituting this relation between shear rates and the particular solution for shear stress in eqn (18) into eqn (20) yields an equation for the evolution of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) A:
A: | (21) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) B:
B: | (22) |
The evolution of the shear stress and flow field in cessation of flow (eqn (18), (21) and (22)) is made clearer by the example in Fig. 7. Here, τB = 5τA, hB = 3hA, GB,0 = 3GA,0. The stress is assumed to reach steady state before cessation of flow:  , where
, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0τA = 5 is the normalized applied shear rate. For this parameter set, the shear stress decays exponentially with a time constant τeff/τA ≈ 1.7 (Fig. 7a). At the onset of flow cessation, significant fluid retraction occurs at a speed greater than the wall velocity of the preceding startup test, v0 (Fig. 7b). As time progresses, the shear rate – and thus fluid velocity – decays exponentially with the same time constant, τeff, as the shear stress (Fig. 7a inset shows decay of vmin(t), the minimum gap velocity).
0τA = 5 is the normalized applied shear rate. For this parameter set, the shear stress decays exponentially with a time constant τeff/τA ≈ 1.7 (Fig. 7a). At the onset of flow cessation, significant fluid retraction occurs at a speed greater than the wall velocity of the preceding startup test, v0 (Fig. 7b). As time progresses, the shear rate – and thus fluid velocity – decays exponentially with the same time constant, τeff, as the shear stress (Fig. 7a inset shows decay of vmin(t), the minimum gap velocity).
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) A,
A, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) B) is large when the relaxation times in each region are dissimilar, which is expected in shear-banded flow. This feature is clearly seen for flow cessation in P234-NaF (Fig. 4e–g), where the retraction velocity at tc = 540 s (flow is shear-banded and heterogeneous) is an order of magnitude greater than that at tc = 3 and 14 s (homogeneous flow).
B) is large when the relaxation times in each region are dissimilar, which is expected in shear-banded flow. This feature is clearly seen for flow cessation in P234-NaF (Fig. 4e–g), where the retraction velocity at tc = 540 s (flow is shear-banded and heterogeneous) is an order of magnitude greater than that at tc = 3 and 14 s (homogeneous flow).
Second, the magnitude of retraction depends not only on the heterogeneity in rheological properties, but also on the shear stress magnitude before cessation of flow, σc. The magnitude of the shear rate (retraction velocity) scales with the shear stress in P234-NaCl; the retraction velocity is an order of magnitude higher at tc = 17 s than at tc = 2150 s primarily due to the much lower shear stress at the latter time (Fig. 5f and g). The dependence of retraction speed on shear stress also implies that the change in flow heterogeneity for P234-NaF at tc = 540 s is understated, as σc at tc = 3 and 14 s is ∼6× greater than at tc = 540 s.
Third, in the two adjacent UCM model fluids, the magnitude of both shear rates decays exponentially, with the same time constant as the shear stress, τeff. Unlike this model, the shear stress relaxes by multiple processes with different time constants in experiments. However, in both P234-NaF and P234-NaCl, the shortest relaxation time governing fluid retraction and shear stress are similar (Table 2 and Fig. 6), and, overall, the retraction velocity does decay with the shear stress as predicted.
Finally, the magnitude of the shear rates is inversely proportional to the elastic moduli of fluid A and B. The elastic modulus describes the stiffness in response to deformation, and thus fluids that have a higher elastic modulus are stiffer and will deform less as the stress relaxes. This last observation is the reason that the maximum reaction speeds observed in P234-NaF (Fig. 4g) and P234-NaCl (Fig. 5f) are similar although the initial shear stress σc is over 10× higher in the latter case. The elastic modulus of P234-NaCl is an order of magnitude greater than P234-NaF, i.e. P234-NaCl WLMs are stiffer.
 equal – must be satisfied:
equal – must be satisfied: | (23) |
The time derivative of the shear stress depends on two terms: one proportional to the shear rate, which is responsible for the buildup of stress during flow, and one proportional to the shear stress, which dissipates shear stress. The dissipation terms for A and B are not equal if the relaxation times are different. Thus to maintain a constant stress relaxation rate, fluid motion occurs. The fluid with the faster relaxation time experiences a shear rate in the same direction as the applied shear rate (continued deformation), which will slow the rate of stress relaxation. The fluid with the slower relaxation time experiences a shear rate opposite to the direction of the applied shear rate (strain recovery), which accelerates the rate of stress relaxation. For example, in Fig. 7b, the shear rate is negative in the faster relaxation time region, A (r/H < 0.25), which is the same sign as the applied shear rate during shear startup, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0. Conversely, in Fig. 7b, the shear rate in the slower relaxation time region, B (r/H > 0.25), is positive (opposite sign of
0. Conversely, in Fig. 7b, the shear rate in the slower relaxation time region, B (r/H > 0.25), is positive (opposite sign of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0). The balance of the terms in eqn (23) across both fluids produces an effective relaxation rate intermediate to both fluids.
0). The balance of the terms in eqn (23) across both fluids produces an effective relaxation rate intermediate to both fluids.
While the GCB model and experimental systems have more complex dynamics than the flow problem with two adjacent UCM fluids, this principle holds true: substantial fluid deformation occurs during flow cessation when the fluid regions have much different relaxation times to offset large differences in the stress relaxation rate throughout the flow geometry.
4.5 Shear startup and fluid retraction of GCB model fluid between concentric cylinders
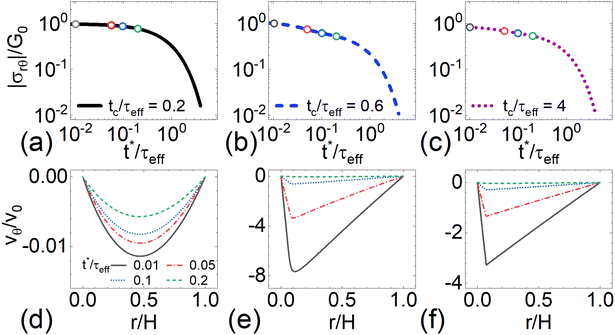
Whereas the first flow problem can be solved analytically, modeling the fluid behavior using the GCB model captures key flow phenomena in WLM gels in shear startup flows.14 This startup behavior is outlined briefly below and elsewhere,39 prior to focusing on behavior in cessation of flow.After the shear stress maximum, breakage of species A accelerates rapidly near the moving inner cylinder, and the populations nA and nB and flow field become highly nonuniform. At the halfway point in this stress drop (t/τeff = 0.6, blue ○ in Fig. 8a), substantial flow reversal develops, where the velocity is negative in a large portion of the gap (Fig. 8b). This flow reversal is accompanied by a highly nonuniform distribution of nA and nB across the gap, where nA is significantly smaller near the inner wall (r/H = 0) than near the outer wall (r/H = 1), indicative of flow-induced breakage (Fig. 8c). Soon afterward, the shear stress reaches a local minimum at time t/τeff = 0.75, and two distinct regions of different shear rates and populations of species A and B become more refined (Fig. 8b–d). At this time flow reversal has ceased: the velocity is positive at all r/H. As time progresses, eventually the shear stress approaches a steady state. At t/τeff = 4, sharply defined shear bands are apparent in the velocity profile, and nA and nB also change almost discontinuously across the band interface, where species B is more prevalent in the high-shear-rate band and species A is more prevalent in the low-shear-rate band.
Comparing the evolution of the shear stress, velocity profile, and populations of species A and B during shear startup reveals that flow reversal coincides with highly heterogeneous fluid microstructure. Flow reversal during startup flow occurs for the same reason that fluid retraction occurs in cessation of flow in the two adjacent UCM fluid model. Shortly after the stress maximum, a large portion of species A rapidly breaks into species B, which has a much faster relaxation time τB = ετA ≈ 10−3τA. This region rich in species B begins to rapidly dissipate the accumulated elastic shear stress, but the region rich in species A cannot dissipate stress at the same rate. Therefore, the region rich in A dissipates some of the elastic stress by retraction instead, like a rubber band retracts when tension is released. Here, the difference in the relaxation times of species A and B is so substantial that fluid retraction overcomes the base flow in shear startup.
During the initial ramp-up in shear startup (tc/τeff = 0.2), the flow is nearly homogeneous (Fig. 8c and d, τ/τeff = 0.2, solid-black line), and minimal fluid retraction occurs as the stress decays upon cessation of flow (Fig. 9a and d). Although the fluid is essentially homogeneous here prior to flow cessation, slight shear thinning occurs due to the inherent stress gradient of the concentric cylinder geometry – leading to a small change in stress relaxation rate across the gap and minor fluid retraction. In practice, this fluid motion measured with standard velocimetry will quickly become virtually undetectable; recall vmin is the largest magnitude negative velocity in the gap at a given time, and for a gap width of 1 mm, 10−3v0 ∼ 1 μm s−1.
Conversely, upon cessation of flow after the stress maximum (tc/τeff = 0.6, 4), the magnitude of fluid retraction is over two orders of magnitude larger than at tc/τeff = 0.2 (Fig. 9d vs. e, f). The population distribution of species A and B at tc/τeff = 0.2 is uniform, whereas the distribution of A and B at these later time points is highly heterogeneous (Fig. 8c and d, tc/τeff = 0.6, 4, dashed-blue and dotted-green lines). The magnitude of fluid retraction also depends on the magnitude of the shear stress immediately preceding flow cessation, σc; at tc/τeff = 0.6, σc and correspondingly the maximum magnitude of fluid retraction is over twice as large as those at tc/τeff = 4 (t*/τeff = 0.01 in Fig. 9b vs. c). While σc dictates the reversal magnitude for highly heterogeneous flows, the high degree of flow heterogeneity is a necessary precursor: the shear stress at tc/τeff = 0.2 is greater than at tc/τeff = 4, but the retraction magnitude is orders of magnitude larger in the latter case.
Notably, the retraction speed decelerates more quickly when the starting fluid is heterogeneous. For the two microstructurally-heterogeneous flows, fluid retraction has essentially ceased by t*/τeff = 0.2 (Fig. 9e and f), whereas retraction is still ongoing at this time for the microstructurally-homogeneous flow (Fig. 9d). The heterogeneous flows contain a much greater proportion of species B everywhere in the gap, which relaxes stress much more quickly than species A and accelerates the effective relaxation rate of the fluid. Additionally, fluid retraction practically ceases well before the shear stress fully relaxes (Fig. 9a–c vs. d–f), which differs from the prediction of the two adjacent UCM fluid model. At long times, the retraction speed decays at a similar rate in all cases, with a time constant roughly equal to the effective relaxation rate τeff (Fig. S24, ESI†).
Heterogeneity of the fluid microstructure can be inferred not only from the magnitude of the velocity during retraction, but also from the shape of the velocity profile in cessation of flow (Fig. 9d–f). When cessation of flow begins before the stress maximum of the shear startup (tc/τeff = 0.2), the velocity profile is nearly symmetric (Fig. 9d); in contrast, when cessation of flow begins after shear bands have fully formed (tc/τeff = 4, Fig. 9f), two distinct regions of nearly constant shear rate are observed in the velocity profile. The intersection of these regions is also precisely the location of the shear band interface. Interestingly, for cessation of flow that commences during the rapid drop in stress in shear startup (tc/τeff = 0.6, Fig. 9e), the velocity profile also has two regions of distinct shear rate, but the transition between these regions is not nearly as sharp as when shear-banded flow has fully formed prior to cessation.
The shapes of these velocity profiles correspond with the population distribution of species A and B during startup (Fig. 8c and d). When the population distribution changes gradually (tc/τeff = 0.2, 0.45), the change in shear rate – the slope of the velocity profile – is also gradual. However, if the microstructure changes rapidly over a small spatial region (tc/τeff = 0.6, 4), the shear rate also changes rapidly over that region. For shear-banded flow, the change in the fluid microstructure is essentially discontinuous, causing the discontinuity in shear rate in the velocity profile during cessation of flow.
Asymmetric velocity profiles indicate heterogeneous flow with the GCB model (Fig. 9e and f), where the apex of the velocity profile is located near the interface between the fluid regions during shear startup (r/H ≈ 0.1, Fig. 8b). Similar behavior is observed when shear-banded flow fully develops in both P234-NaF and P234-NaCl (Fig. 4g and 5g, respectively). The evolution of the shape and magnitude of fluid retraction during cessation of flow in the GCB model and P234-NaCl are remarkably similar (Fig. 5 and 9). This similarity arises because heterogeneity becomes substantial in the flow geometry at a similar time during the stress evolution in both cases: right after the stress maximum. However, the maximum relative retraction velocity predicted by the GCB model when the flow is heterogeneous vθ/v0 ≈ 3.8 (Fig. 9e and f, respectively) is much greater than the maximum observed in P234-NaF (vθ/v0 ≈ 0.1) or P234-NaCl (vθ/v0 ≈ 0.4). One potential explanation for this difference could be that heterogeneity develops more quickly or to a greater magnitude in the GCB model than in experiments, which could lead to greater retraction. Further analysis of the growth of instabilities using the GCB model should be pursued as has been performed for other constitutive models.24
Finally, in both the GCB model predictions and experiments, the majority of fluid retraction occurs during only a portion of the shear stress relaxation. In the GCB model, retraction is tied to the rapid relaxation of stress carried by species B (Section SI.10, ESI†), which is the dominant species in the high-shear-rate band of fluid (Fig. 8d). The origin of these time constants is discussed in Section 4.7.
4.6 Limitations of the model predictions
Despite the success of these models in predicting many of the behaviors observed during cessation of flow, some phenomena that impact the evolution of the shear stress and velocity profiles were not captured. For example, in P234-NaF, a layer of fluid roughly 1/10th of the gap width is practically immobile at all times during cessation of flow for tc = 3 and 540 s (Fig. 4e and g). Surprisingly, for tc = 14 s (Fig. 4f), the fluid within this layer moves in the positive flow direction for a brief period (see Section SI.7.1, ESI†). Interestingly, the distinct region near the inner wall (r/H < 0.1) was also noticeable in shear startup (Fig. 3c), where the velocity in this region was roughly linear at all times. However, none of this behavior is captured by the models.These results in shear startup and cessation suggest that the microstructure of P234-NaF changes near the boundary. Steady shear simulations that enforce a perpendicular orientation of the WLMs at the boundary55 have predicted velocity profiles that are reminiscent of the shear-banded flow in Fig. 3c. In those prior simulations, the curvature of the flow geometry and strength of stress-induced diffusion influenced the spatial extent of these regions. Measurements in geometries with different gap widths could help resolve these effects.
Another phenomenon accompanying fluid retraction absent from the models considered here is wall slip. For P234-NaCl, wall slip became significant during fluid retraction (Fig. 5g) and accelerates the initial fast fluid retraction (Fig. 6a and b). Taking a closer look at the velocity profiles plotted individually (Section SI.7.2, ESI†), wall slip is still present even after this initial retraction. However, wall slip does not significantly impact the slower time constants (Fig. 6c and d) because at longer times macroscopic motion is minimal; the shear stress primarily relaxes due to internal dissipation. Nonetheless, the impact of wall slip on fluid retraction is important, and if more quantitative information is desired, the impact of wall slip needs to be considered.
4.7 Cessation of flow with rheo-PTV as a novel method for characterizing flow heterogeneity
The combination of experimental, theoretical and computational results demonstrates that cessation of flow characterized by rheo-PTV can provide a wealth of insights into flow heterogeneity in complex fluids. Substantial macroscopic, heterogeneous fluid motion in cessation of flow has been reported previously in polymer liquids32; however, this study is the first to use this protocol to systematically study heterogeneous flow. Successful implementation of this protocol relies on newly developed analysis methods, where velocity is calculated from fits to particle trajectories rather than displacements between successive image acquisitions. The fluid velocity during cessation of flow often starts small and decays in time, and therefore the displacement between successive image acquisitions eventually becomes less than a fraction of the particle diameter. Velocity calculation from frame-to-frame displacements is impractical and will be plagued with noise. However, if particles are observed for long times, these displacements accumulate and become measurable. Therefore, even small velocities can be resolved when calculated by fitting the displacements. This method of velocity calculation is reminiscent of creep measurements used to characterize complex fluids: in creep, the shear rate is small, but because the cumulative strain is measured, even small shear rates can be discerned.A significant advantage to this approach is that cessation of flow effectively detects heterogeneity in the rheological properties – information only partially accessible via microstructural techniques such as flow-SANS,11,56 flow-SALS,10,57 nuclear magnetic resonance spectroscopy (NMR),58 and flow birefringence.59,60 Each technique characterizes flow-induced microstructural anisotropy at specific length scales. However, connecting the microstructure to rheological properties is difficult; the length scales accessed by any individual technique only partially contribute to the WLM shear stress and rheological properties.61,62
Nevertheless, microstructural measurements can help interpret the velocity evolution in cessation of flow. The P234-NaF relaxation times are compared to the microstructural relaxation of CPyCl-NaSal WLMs in cessation of flow, measured with flow-SANS11 and flow-SALS.10 Similar to P234-NaF, the shear stress in cessation of flow of CPyCl-NaSal WLMs – which appear to shear band via a similar mechanism – relaxed with two distinct relaxation times. The slow relaxation time was three times longer than the fast one.11 Interestingly, for P234-NaF the ratio of the relaxation times is similar (τslow/τfast ≈ 4). The initial fast shear stress decay correlated with the decay of large density fluctuations, indicated by the disappearance of butterfly patterns in flow-SALS.10Via flow-SANS, WLM segmental alignment was shown to decay at the same rate as the slow relaxation stress decay.11 In P234-NaF, the high-shear rate band is initially much brighter than the low-shear rate one, but this difference vanishes in ∼3 s, consistent with the observation that the shorter time constant corresponds to the relaxation of density fluctuations (Fig. S25 in Section SI.11, ESI†). The longer relaxation time of P234-NaF WLMs is thus presumed to decay with segmental alignment like in CPyCl-NaSal WLMs.
Linking the relaxation time constants in P234-NaCl to microstructural relaxation processes is more difficult. The shear banding mechanism is unique to these WLMs, and therefore no comparative microstructural studies exist. Unlike in P234-NaF, no visible brightness difference is apparent in the two fluid regions that can be attributed to density fluctuations. Additionally, three characteristic times describe the relaxation of shear stress and velocity in P234-NaCl instead of two like in P234-NaF. This extra relaxation time could be linked to the unique shear-banding mechanism of P234-NaCl. However, because the rheological properties of the fluid bands appear much more dissimilar in P234-NaCl than in P234-NaF, this timescale may just be better resolved for P234-NaCl. In P234-NaCl, the shortest relaxation time is two orders of magnitude faster than the longest, whereas the relaxation times are similar in P234-NaF. Complementary characterization is thus needed to resolve microstructural origins of these relaxation processes.
Although the timescales cannot be assigned to specific microstructural processes, the relatively large magnitude of these timescales in P234-NaCl may be related to the early development of flow heterogeneity. Prior work examining the origin of transient shear banding and fracture in polymer solutions found these phenomena can result from an elastic constitutive instability.24,33 In step-strain or at early times in rapid shear startup, these solutions behave like an elastic solid, which is expected to be unstable for 0 < dσ/dγ – when a stress overshoot occurs.63 The dynamics of P234-NaCl are sluggish enough that the initial deformation during shear startup at the shear rate examined here may be susceptible to a similar instability. The shear stress gradient inherent in the concentric cylinder geometry could provide the necessary inhomogeneity to amplify this elastic instability. Notably, in addition to strong flow heterogeneity after the stress maximum, prior work on P234-NaCl solutions found evidence of fracture when sample aging time was increased,14 which is also connected to the proposed elastic instability. Investigation of shear-band formation at a range of shear rates in these WLM solutions and in others with a wider range of rheological properties will be useful to understand the transition between the shear-banding behaviors observed P234-NaCl and P234-NaF.
5 Conclusion
This work showcases a novel rheology protocol combining cessation of flow with rheo-particle tracking velocimetry (PTV), which reveals new information about heterogeneous shear flows that can occur in wormlike micelle (WLM) solutions. Paired with new PTV analysis methods used to accurately calculate velocities of slowing particles, this approach then enables fluid retraction upon flow cessation to be precisely detected and quantified for the first time. While many WLM solutions develop flow heterogeneity, only a handful of experiments have observed flow reversal – when a portion of the fluid moves opposite to the direction of the moving boundary – despite predictions by constitutive models.To address this apparent discrepancy, this work aimed to experimentally and theoretically confirm two criteria previously proposed to be necessary to observe flow reversal based on evidence across wide-ranging soft materials. These criteria suggested that regardless of fluid composition, to observe flow reversal in shear startup: (1) the system must have elasticity; (2) flow must already be highly heterogeneous while the stress decreases in the stress overshoot region. To confirm these criteria, the base flow was removed and fluid retraction was directly measured upon flow cessation in two poloxamer WLMs – a viscoelastic, fluid-like WLM (P234-NaF) and a gel-like WLM (P234-NaCl).
Canonical WLMs (P234-NaF) were hypothesized to exhibit minimal retraction when flow was stopped in the decreasing region of the stress overshoot, whereas gel-like WLMs (P234-NaCl) were expected to significantly retract in this region due to earlier-onset heterogeneity formation. Subsequent experiments confirmed these hypotheses and were in qualitative agreement with results from two theoretical Couette flow problems: (1) two adjacent Upper Convected Maxwell (UCM) model fluids between parallel plates, and (2) a Germann–Cook–Beris model fluid between concentric cylinders.
The minimal retraction exhibited by P234-NaF following flow cessation in the stress overshoot region is consistent with the “disentangle–re-entangle” mechanism widely accepted for canonical WLMs. As heterogeneous flow forms far beyond the stress overshoot region via this mechanism, significant fluid retraction upon flow cessation occurs in P234-NaF only when flow is stopped after shear bands have stabilized. In contrast, heterogeneous flow forms near the stress maximum in P234-NaCl, leading to substantial retraction upon cessation of flow. Particle trajectories were then analyzed to extract time- and spatially-dependent relaxation behavior, confirming the prior hypothesis that the low shear rate band in this WLM gel becomes trapped by viscoelastic aging.
This work thus reveals that flow reversal upon shear startup is not observed in P234-NaF (or any previously-reported canonical, fast-breaking WLMs) despite model predictions due to the difference in when the heterogeneity manifests: models predict that these flows become heterogeneous in the stress overshoot region, whereas in experiments, heterogeneity onsets at far longer times. Strikingly, theoretical predictions from these simplified models regarding the magnitude, shape, and lifetime of the retraction velocity profile are highly consistent with experiments on gel-like WLMs, in part due to the similarity in the onset of flow heterogeneity. Conversely, canonical WLMs exhibit nearly homogeneous flow in the stress overshoot region, leading to minimal fluid retraction; thus flow reversal is not observed because the minimal fluid retraction cannot overcome the imposed flow. Notably, we also show that cessation of flow combined with PTV can be used to extract quantitative, spatially-dependent information about heterogeneous flows whether or not flow reversal occurs, making this technique applicable for characterizing wide-ranging complex fluids. Importantly, because the method proposed here analyzes displacements, even small retraction velocities can be observed when heterogeneity is minimal.
While this approach can be used to extract time- and spatially-dependent rheological behavior in wide-ranging soft materials, more work remains to extract more quantitative information about the rheological properties of the heterogeneous flow regions. For example, once shear bands have formed, the viscosity in each band can be estimated from the shear rate. Based on the analytical solution for the two adjacent UCM fluids, the elastic modulus and relaxation times in each fluid region may be able to be extracted by performing retraction experiments at additional shear rates. Quantifying the shear rate and total accumulated strain will also be useful to compare experiments to models and estimate these parameters.
A final outstanding question is to determine which properties dictate the shear band formation mechanism. Experimentally, complementary microstructural characterization via techniques like flow-small angle light and neutron scattering will be essential to achieve this goal. Additionally, further analysis of WLM models will be crucial for identifying key parameters that influence the amplification of flow heterogeneity. Perhaps a more sophisticated model than those used here can describe both shear-band formation mechanisms showcased in this work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation Graduate Research Fellowship (Award 2237827). The authors thank the Anton Paar VIP program for the rheometer used in this work.Notes and references
- T. Divoux, M. A. Fardin, S. Manneville and S. Lerouge, Annu. Rev. Fluid Mech., 2016, 48, 81–103 CrossRef.
- S. Lerouge and J.-F. Berret, Polymer Characterization, Springer, 2009, pp. 1–71 Search PubMed.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- P. D. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS.
- S. M. Fielding, Soft Matter, 2007, 3, 1262–1279 RSC.
- S. M. Fielding, J. Rheol., 2016, 60, 819–820 CrossRef.
- S. Manneville, Rheol. Acta, 2008, 47, 301–318 CrossRef CAS.
- J.-F. Berret, Langmuir, 1997, 13, 2227–2234 CrossRef CAS.
- O. Radulescu, P. Olmsted, J. Decruppe, S. Lerouge, J.-F. Berret and G. Porte, Europhys. Lett., 2003, 62, 230 CrossRef CAS.
- Y. T. Hu and A. Lips, J. Rheol., 2005, 49, 1001–1027 CrossRef CAS.
- C. R. López-Barrón, A. K. Gurnon, A. P. Eberle, L. Porcar and N. J. Wagner, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 042301 CrossRef PubMed.
- H. Mohammadigoushki, A. Dalili, L. Zhou and P. Cook, Soft Matter, 2019, 15, 5483–5494 RSC.
- S. R. Raghavan and Y. Feng, Wormlike Micelles, Royal Society of Chemistry, 2017, pp. 9–30 Search PubMed.
- P. J. McCauley, C. Huang, L. Porcar, S. Kumar and M. A. Calabrese, J. Rheol., 2023, 67, 661–681 CrossRef CAS.
- J. D. Martin and Y. T. Hu, Soft Matter, 2012, 8, 6940–6949 RSC.
- A. Kurokawa, V. Vidal, K. Kurita, T. Divoux and S. Manneville, Soft Matter, 2015, 11, 9026–9037 RSC.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef PubMed.
- P. Rassolov and H. Mohammadigoushki, J. Rheol., 2020, 64, 1161–1177 CrossRef CAS.
- J. Adams and P. D. Olmsted, Phys. Rev. Lett., 2009, 102, 067801 CrossRef CAS PubMed.
- N. Germann, L. Cook and A. N. Beris, J. Non-Newtonian Fluid Mech., 2013, 196, 51–57 CrossRef CAS.
- N. Germann, L. Cook and A. Beris, J. Non-Newtonian Fluid Mech., 2014, 207, 21–31 CrossRef CAS.
- L. Zhou, P. A. Vasquez, L. P. Cook and G. H. McKinley, J. Rheol., 2008, 52, 591–623 CrossRef CAS.
- L. Zhou, G. H. McKinley and L. P. Cook, J. Non-Newtonian Fluid Mech., 2014, 211, 70–83 CrossRef CAS.
- J. Adams, S. M. Fielding and P. D. Olmsted, J. Rheol., 2011, 55, 1007–1032 CrossRef CAS.
- E. Miller and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2007, 143, 22–37 CrossRef CAS.
- P. Rassolov and H. Mohammadigoushki, J. Rheol., 2023, 67, 169–181 CrossRef CAS.
- T. Divoux, C. Barentin and S. Manneville, Soft Matter, 2011, 7, 9335–9349 RSC.
- K. A. Erk, J. D. Martin, Y. T. Hu and K. R. Shull, Langmuir, 2012, 28, 4472–4478 CrossRef CAS PubMed.
- S. Ravindranath, S.-Q. Wang, M. Olechnowicz and R. P. Quirk, Macromolecules, 2008, 41, 2663–2670 CrossRef CAS.
- R. Benzi, T. Divoux, C. Barentin, S. Manneville, M. Sbragaglia and F. Toschi, Phys. Rev. Lett., 2021, 127, 148003 CrossRef CAS PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids. Vol. 1: Fluid mechanics, John Wiley and Sons Inc., New York, NY, 1987, pp. 78–79 Search PubMed.
- S.-Q. Wang, S. Ravindranath, P. Boukany, M. Olechnowicz, R. P. Quirk, A. Halasa and J. Mays, Phys. Rev. Lett., 2006, 97, 187801 CrossRef PubMed.
- O. S. Agimelen and P. D. Olmsted, Phys. Rev. Lett., 2013, 110, 204503 CrossRef PubMed.
- P. J. McCauley, S. Kumar and M. A. Calabrese, Langmuir, 2021, 37, 11676–11687 CrossRef CAS PubMed.
- M. Gvaramia, G. Mangiapia, V. Pipich, M.-S. Appavou, S. Jaksch, O. Holderer, M. D. Rukhadze and H. Frielinghaus, Colloid Polym. Sci., 2019, 297, 1507–1517 CrossRef CAS.
- M. Awad and Y. Muzychka, Exp. Therm. Fluid Sci., 2008, 33, 106–113 CrossRef CAS.
- N. Germann, L. Cook and A. Beris, J. Non-Newtonian Fluid Mech., 2016, 232, 43–54 CrossRef CAS.
- N. Germann, A. Kate Gurnon, L. Zhou, L. Pamela Cook, A. N. Beris and N. J. Wagner, J. Rheol., 2016, 60, 983–999 CrossRef CAS.
- P. J. McCauley, M. A. Calabrese and S. Kumar, J. Non-Newtonian Fluid Mech., 2023, 1, 1–2 Search PubMed.
- D. Y. Zhang and M. A. Calabrese, Soft Matter, 2022, 18, 3993–4008 RSC.
- N. Spenley, M. Cates and T. McLeish, Phys. Rev. Lett., 1993, 71, 939 CrossRef CAS PubMed.
- Y. T. Hu, C. Palla and A. Lips, J. Rheol., 2008, 52, 379–400 CrossRef CAS.
- D. B. Allan, T. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, soft-matter/trackpy: Trackpy v0.5.0, 2021.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
- P. J. McCauley, PhD thesis, Understanding self-assembly and flow heterogeneities in poloxamer wormlike micelles, University of Minnesota, 2023, pp. 57–75.
- S. Manneville, A. Colin, G. Waton and F. Schosseler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061502 CrossRef PubMed.
- M.-A. Fardin, T. Divoux, M. Guedeau-Boudeville, I. Buchet-Maulien, J. Browaeys, G. H. McKinley, S. Manneville and S. Lerouge, Soft Matter, 2012, 8, 2535–2553 RSC.
- P. Cheng, M. C. Burroughs, L. G. Leal and M. E. Helgeson, Rheol. Acta, 2017, 56, 1007–1032 CrossRef CAS.
- R. Granek and M. Cates, J. Chem. Phys., 1992, 96, 4758–4767 CrossRef CAS.
- S. Lerouge, M.-A. Fardin, M. Argentina, G. Grégoire and O. Cardoso, Soft Matter, 2008, 4, 1808–1819 RSC.
- M.-A. Fardin, B. Lasne, O. Cardoso, G. Grégoire, M. Argentina, J.-P. Decruppe and S. Lerouge, Phys. Rev. Lett., 2009, 103, 028302 CrossRef CAS PubMed.
- A. Briole, L. Casanellas, M.-A. Fardin, C. Py, O. Cardoso, J. Browaeys and S. Lerouge, J. Rheol., 2021, 65, 1187–1200 CrossRef CAS.
- B. A. Deyerle and Y. Zhang, Langmuir, 2011, 27, 9203–9210 CrossRef CAS PubMed.
- Y. M. Joshi and G. Petekidis, Rheol. Acta, 2018, 57, 521–549 CrossRef CAS.
- J. Adams, S. Fielding and P. Olmsted, J. Non-Newtonian Fluid Mech., 2008, 151, 101–118 CrossRef CAS.
- M. A. Calabrese, S. A. Rogers, L. Porcar and N. J. Wagner, J. Rheol., 2016, 60, 1001–1017 CrossRef CAS.
- J. Decruppe, S. Lerouge and J. Berret, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 022501 CrossRef CAS PubMed.
- E. Fischer and P. T. Callaghan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 011501 CrossRef CAS PubMed.
- J. Decruppe, R. Cressely, R. Makhloufi and E. Cappelaere, Colloid Polym. Sci., 1995, 273, 346–351 CrossRef CAS.
- S. Lerouge, J.-P. Decruppe and P. Olmsted, Langmuir, 2004, 20, 11355–11365 CrossRef CAS PubMed.
- E. Helfand and G. H. Fredrickson, Phys. Rev. Lett., 1989, 62, 2468 CrossRef CAS PubMed.
- M. E. Helgeson, P. A. Vasquez, E. W. Kaler and N. J. Wagner, J. Rheol., 2009, 53, 727–756 CrossRef CAS.
- G. Marrucci and N. Grizzuti, J. Rheol., 1983, 27, 433–450 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00203b |
| ‡ Current affiliation: Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, Delaware 19716, USA. |
| This journal is © The Royal Society of Chemistry 2024 |