Open Access Article
Open Access ArticleOptimizing anisotropic transport on bioinspired sawtooth surfaces†
Dillon G.
Gagnon
 *,
Dahbin
Park
,
Kevin
Yim
and
Svetlana
Morozova
*,
Dahbin
Park
,
Kevin
Yim
and
Svetlana
Morozova

Department of Macromolecular Science and Engineering, Case Western Reserve University, USA. E-mail: dgg28@case.edu
First published on 6th May 2024
Abstract
Species ranging from butterflies and other insects, to cactuses and lotus plants have evolved to use geometrically patterned surfaces to influence the transport of water droplets. While this phenomenon is well known, an ideal geometry has yet to be discovered. To determine the impact of surface geometry on droplet transport, we have studied the contact angle and droplet motion across anisotropically wetting patterned surfaces. The surface geometries tested were sawtooth patterns with angles (8.62–26.70°) and lengths (0.56–1.67 μm). The droplet contact angles were measured on 45° angled surfaces to simulate the droplet in motion. Velocities were measured using a high-speed camera shooting at 500 frames per second and the tailing edges of the droplets were hand tracked over 18 frames. It was found that travel along the sawtooth ridges is significantly faster than travel against the ridges for geometries with shallow angles. The optimal geometry was determined to be α = 8.62° and b = 1.67 μm and was replicated using nanoimprint lithography using materials with different surface energies. When replicated with acrylate resins and PDMS, the contact angles remained high, regardless of wettability, but we find that the overall velocity and velocity hysteresis depends on the hydrophobicity. More hydrophobic surfaces have overall higher hysteresis. The ability to tune imprinted surfaces to achieve ideal wetting characteristics using geometry will lead to interesting anisotropic material design.
Introduction
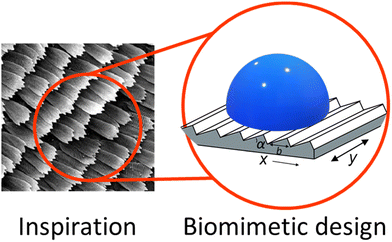
Anisotropically wetting surfaces are found often in nature with examples ranging from lotus leaves,1–5 to spider silk,6 rice leaves,7 cacti,8 and even butterfly wings.9 These surfaces are characterized by excellent, precise control of water droplet transport, allowing organisms to move water with high efficiency for either water collection or water repulsion. These phenomena have inspired many materials designed for more efficient surface water transport, for example in coatings that limit biofouling in medical devices.10 The control of solvent flows11–15 may allow for easier cleaning and better control of protein adsorption. Butterflies have adapted special structures to take advantage of anisotropic wetting properties.Many butterfly wings are covered in scales that help transport water droplets away from the central axis of the body. The scales range in length from around 500–2000 nm with most angles around 8°.16 Directional transport was demonstrated in butterfly wings by Zheng et al.17 They showed that Morpho aega scales, which are 585.5 ± 16.3 nm long with a shallow angle, can fully pin a 3 μL drop to prevent motion in the direction of the body, but allow the same drop to flow easily away from the body.17 This anisotropic control is attributed to the three phase (solid–liquid–gas) contact line. This boundary was thought to be only capable of adopting two states of interest, the Cassie–Baxter state, and the Wenzel state, low and high friction, respectively.14,18–23 Kusumaatmaja and Yeomans24 developed a model for the surface of butterfly scales. They found that when the droplet has full contact with the surface, the anisotropy in the velocity is maximized. In their work they also identified a partially suspended state to accompany the Cassie–Baxter18,25 and Wenzel states,24,26 where significant anisotropy in transport is still observed. On these surfaces, a low contact angle causes pinning, and a high contact angle leads to minimal friction. This intermediate wetting state was further studied by Choi et al. where they studied droplets of PDMS wetting a templated hoodoo surface.27 Through this they worked to improve the Cassie–Baxter model. This work showed that in asymmetric geometries the actual contact area is difficult to estimate due to the low stability of droplets on these geometries similar to what was shown in Eick et al. where they predicted metastable states in surfaces with sharp, near vertical angles.28 For example, on sawtooth geometries the droplets impact a vertical edge on one side of the ridge, which can cause metastable states which lead to a deviation from the classic Young's model of equilibrium wetting. Sawtooth geometries29 can be modelled by triangular ridges separated by a distance b, and raised at an angle α (Fig. 1). If the surface is hydrophobic, anisotropic droplet transport is predicted, depending on the wetting state.
Extensive previous work has been done to characterize anisotropic wetting on different surface geometries.30–32 Vertical ridges are the most studied surface geometry.7,8,14,20,33–37 Chen et al.38 discussed the forces at work and the geometry dependence of transport anisotropy on these surfaces. They performed significant analysis on the impact of water droplet volume on the contact angle. They also examined the impact of the width of the micro vertical ridges. Through this work they found that the parallel contact angle is highly dependent on water drop volume, increasing as the droplet volume increased.38 Xia, Johnson, and López4 demonstrated anisotropic wetting on striped surfaces as well as examined ratcheted geometries. Gao and McCarthy5 found that the advancing contact angle is directly correlated to the wetting state of droplets on ridged geometries similar to lotus leaves. Other geometries such as regular triangular ridges,14 and microchannels35,36,38–40 have been explored to a much lesser extent. Xu et al.14 modelled wetting on symmetric triangular ridges in order to better predict and model the Cassie–Baxter and Wenzel states. Wang et al.35 showed that micro patterned surface energies can influence wetting and transport directionality inside micro channels. Lee et al.41 showed that droplet formation on spikes came as a result of anisotropic wetting and this geometric effect also influence droplet transport and collision. While all these geometries show anisotropic wetting and transport, the asymmetric sawtooth pattern seen on butterfly wings is the only one that shows anisotropic transport along the same axis, meaning that motion in the +x and −x (with and against the ridges) directions differ as opposed to only differing with respect to x and y axes.17 These surfaces are typically patterned and replicated using photolithography.
The use of ratcheted hydrophobic surfaces has been explored extensively for its use in droplet propulsion.39,42,43 The directional geometry is well known to influence droplet transport with a variety of external stimuli ranging from heat to vibration. Lagubeau et al.42 showed that when heated sufficiently, ratcheted surfaces can take advantage of the Leidenfrost effect in order to propel droplets along these surfaces. Further work has been done to investigate the use of textured materials for droplet self-propulsion. Launay et al.44 showed that rail patterned micro grooved surfaces can use variable wetting conditions to pull droplets uphill with no exterior force. While this phenomenon is well known, replication of these surfaces is difficult leading to limited application outside the lab.
Much work has been done to study wettability of various materials,11,12,14,38,45 however, control of this property has been severely limited in the past. With advances in engineering practices46 and a focus on surface modification15 we hope to bring greater control of wetting to industry. This unique property is already being investigated for applications in medicine, where it can help eliminate biofouling.10 Further applications are being investigated in industrial longevity, where corrosion prevention is necessary.47 In all applications better control of solvent flow means better control of product degradation and a more consistent product. In the medical field, limiting biofouling means limiting chances of infection, one of the most critical focuses of any medical technology.
To understand the optimal geometry for anisotropic transport, we have studied water droplet motion on sawtooth ridges of varying geometries (Table 1). The surface is first treated with 1H,1H,2H,2H-perfluorodecyltrichlorosilane (FDTS), and contact angles are measured. By capturing videos of droplet motion driven by air flow, we have determined that the optimal geometry coincides with the largest contact angle hysteresis in the direction against the ridges. To test the effects of material surface energy, we also measure the droplet motion on hydrophilic acrylate surfaces and hydrophobic polydimethylsiloxane (PDMS) surfaces. Studying geometric effects on droplet transport will help guide the manufacturing of smart interfaces, with precise water propulsion control.
| α (°) | b (μm) | z (μm) | θ R(+x/−x/y) | θ A(+x/−x/y) |
|---|---|---|---|---|
| 8.62 | 1.67 | 0.25 | 97/109/102 | 117/138/122 |
| 10.37 | 0.83 | 0.15 | 96/109/99 | 114/135/110 |
| 12.48 | 0.56 | 0.12 | 104/100/108 | 104/100/122 |
| 17.45 | 0.83 | 0.25 | 104/107/106 | 120/126/123 |
| 17.45 | 1.67 | 0.5 | 99/102/101 | 124/132/119 |
| 26.70 | 0.83 | 0.37 | 124/135/104 | 124/135/119 |
Materials and methods
Materials
The blazed, sawtooth surfaces were purchased from Thorlabs (8.62°, 10.37°, 17.45°), and Edmund Optics (12.48°, 26.7°). Their geometries and surface properties are tabulated in Table 1, all gratings were purchased with an aluminum coating. 1H,1H,2H,2H-perfluorodecyltrichlorosilane (FDTS) was purchased from VWR and (Beantown Chemical). UV acrylate resin was purchased from Sigma Aldrich. Triton X-100 surfactant was purchased from Sigma Aldrich. Sylgard 184 PDMS resin kit was purchased from VWR. All reagents were used without further purification.Surface treatment
All Thorlabs and Edmund Optics blazed gratings were treated with 1H,1H,2H,2H-perfluorodecyltrichlorosilane (FDTS) through vapor deposition. For this process each surface was first UV-Ozone etched for 45 minutes with a Jelight Model 24 UV-Ozone cleaner to change the surface groups to highly reactive ozone. The surfaces were then placed in a desiccator under house vacuum along with 20 μL of 96% FDTS for a minimum of 30 minutes. This process results in a uniform monolayer of highly hydrophobic perfluoro tails protruding from the surface. In high humidity conditions surface hydration can lead to failed coatings. To mitigate this issue the surfaces were first dried at 80° under house vacuum, then ozone etched, then the coating was performed in an inert atmosphere. A glass coverslip was used as a control reference smooth geometry.Contact angle measurements
Contact angles were measured as a function of surface direction using an acA1920-155um – Basler ace camera and a tilt table. A 5 μL drop was deposited onto each surface and imaged at a 45° tilt. Between subsequent trials the surfaces were dried with a combination of canned and house air to avoid wetting effects. The apparent advancing and receding angles were then analysed using ImageJ. The apparent angles are tabulated in Table 1 and shown in Fig. 2 for each geometry and surface direction. All measurements were done in triplicate and were consistent throughout. Between subsequent trials the surfaces were dried with a combination of canned and house air to avoid wetting effects. We note that each subsequent run did not greatly deviate from the original.Droplet tracking
To image directional droplet motion in each direction, each surface was placed on a flat stage in between a backlight and the camera, with the air nozzle blowing from the right to left relative to the camera. Air was used to direct droplet motion as the droplets did not move due to gravity even on vertical surfaces. Air was blown at a constant 4 Liters per minute, to avoid changes in the airflow it was not shut off during testing. House air was used with a Brooks Instruments flowmeter. It was found that droplets did not move consistently at lower airflows. The airflow was then occluded using a plastic Petri dish. A 5 μL drop was then placed on the surface, recording was started, and the Petri dish was withdrawn quickly upward. This allowed the airflow to be applied across the surface uniformly. The surfaces were then recorded over eight seconds at 500 fps. Between subsequent trials the surfaces were dried with a combination of canned and house air to avoid wetting effects. We note that each subsequent run did not greatly deviate from the original. Tests were repeated with the glass coverslip control, varying the height of the stage until the droplets slid uniformly across the surface without lifting off. Video was then taken of each surface, first with motion in the +x direction, then rotating 90 degrees to the y direction, then rotating 90 degrees to the −x direction.The videos were then analyzed frame by frame in ImageJ. The dimensions of each surface were measured using vernier calipers to the nearest 0.1 mm. This scale was then used to track the distance of each droplet traveled. The droplets were tracked over 18 frames (36 milliseconds) this timeframe was found to best capture uniform, smooth motion of the droplets across the surfaces without any lifting or stalling. The tracking began from the first frame that showed deformation of the droplet shape. The distance was then tracked from the trailing edge of the droplet through 18 frames. This distance was measured by hand using the pixel count in the straight-line in ImageJ tool which could then be converted to mm using the known length of the surfaces. This distance traveled was then converted to velocity, dividing by the time elapsed, 36 milliseconds. Each measurement was repeated in triplicate then the results were individually averaged, and the sample standard deviation was taken for error.
Imprint lithography
Imprint lithography was used to make acrylate and PDMS surfaces. To mitigate wetting effects, Triton X-100 surfactant was dissolved at a concentration of 0.10 mM in UV curable acrylate resin. The UV-curable resin was then sandwiched between a flat, glass coverslip and one of the treated blazed gratings and then exposed to UV light through the coverslip. The acrylate was left to cure for 30 minutes under an everbeam 50 watt 395 nm lamp before carefully removing the blazed grating. These acrylate resin surfaces require no further modification.PDMS surfaces were prepared using Sylgard 184. The resin and cure agent were mixed in the manufacturer recommended 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight
1 weight![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) weight ratio. The resin is then sandwiched between a flat glass coverslip and a treated blazed grating. The resin is then oven cured at 85 °C for 4 hours before carefully removing the blazed grating. These PDMS surfaces require no further modification.
weight ratio. The resin is then sandwiched between a flat glass coverslip and a treated blazed grating. The resin is then oven cured at 85 °C for 4 hours before carefully removing the blazed grating. These PDMS surfaces require no further modification.
All resins were degassed under house vacuum for 30 minutes after mixing. The resin was further degassed for 1 hour after sandwiching prior to cure to remove gases incorporated during pipetting.
PDMS surfaces were tested when made fresh, they were then aged according to A. Hourlier-Fargette et al.48 This procedure aims to free uncrosslinked chains from PDMS.
Microscopy
Both optical and scanning electron microscopy were used to evaluate the quality of the templated surfaces. The optical microscopy was performed using a Leica DMI 4000 B microscope with a 100× oil objective with the surfaces imaged in bright field using a Basler acA640-750um camera. The surfaces for optical microscopy were prepared on and imaged through a Ted Pella no. 1 coverslip. Confocal microscopy was performed with the same Leica microscope, acrylate samples then had a silicone ring mold placed on them and filled with 200 μL of 0.01 mg mL−1 rhodamine B dyed water covered with another number 1 coverslip. This was then imaged using a 532 nm laser. A z scan was performed with 80 nm steps in the z direction starting from below the surface, and data are reported in the ESI.† SEM was performed on an Apreo 2 SEM. The surfaces for SEM were sputter coated with gold in the presence of argon at 1 kV and 20 mA for 90 seconds to give a gold layer with a thickness of 30.6 nm. All SEM images were taken at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× magnification.
000× magnification.
Results
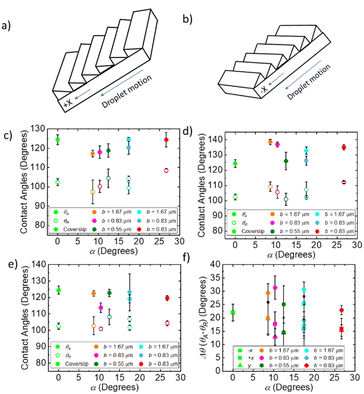
To determine the optimal geometry for anisotropic water transport, contact angles and droplet velocities were measured as a function of α and b in all directions on the surface (Fig. 1 and 2a, b). The surfaces with the optimal geometry were then replicated using lithography techniques to determine the effects of surface energy on anisotropic transport.The apparent contact angle, θ, has a slight dependence on the geometry, in the +x (Fig. 2c), −x (Fig. 2d), and y directions (Fig. 2e) and are summarized in Table 1. In all directions, hysteresis is observed between the receding, θR, and advancing angles, θA, measured by tilting the surface 45° (see ESI† for raw images). As shown in Fig. 2f, there is no change in hysteresis, Δθ = θA − θR, for the control coverslip surface in the +x, −x, and y directions, as expected. For blazed surfaces, there is a clear difference in Δθ between the +x (square points in Fig. 2f) and −x directions (circle points in Fig. 2f). This difference is shown in Fig. 2f as a function of α. Δθ is the same in the +x and y directions, for all geometries, including the coverslip. Interestingly, Δθ is much larger in the −x direction, compared to the +x direction, by about 10° for α = 8.62°, b = 1.67 μm (Fig. 2f), and by about 13.67° for α = 10.37°, b = 0.83 μm. This difference decreases as α increases to about 17° to 5°, and then increases slightly to 7° for α = 26.7. If the surfaces are in a Wenzel state, we expect, following Eick's28 arguments, that the advancing angle in the +x direction is θA = θE + α, where θA is the measured apparent advancing angle and θE is the equilibrium contact angle at the surface. We do observe a linear increase in θA that follows this theory however we expect the formation of metastable states or partial wetting results in the discrepancy between the equation and the observed. Similarly, we expect the advancing contact angles in the −x direction to follow θA = θE + 90 as the leading edge contacts the vertical faces of the ridges. We observe the constant trend that agrees with this prediction, but not the exact values. Once again, we believe the discrepancy results from the formation of metastable wetting states.
Droplet motion is observed by blowing 5 μL water droplets across flat surfaces with a constant air jet at a flow rate of 4 L min−1. Still frames from representative movies are shown in Fig. 3. From the movies, we observe that blaze angle appears to have an impact on both the top speed of the droplets as well as anisotropy in droplet transport. In all these surfaces there are 3 distinct types of motion, sliding, pinning, and liftoff. In sliding motion, we observe the droplet gliding smoothly along the surface with no sticking or lifting. In pinning we see the droplet seemingly adhere to the surface as it is trapped between the ridges. In liftoff we see the droplet fully release from the surface and a thin layer of air along the surface carries the droplet across the forward. These motion types give us information on the shear forces imposed on the droplets by the surface.
 | ||
| Fig. 3 Still frames of droplets being blown across glass surfaces (all scale bars 1 mm). Motion with the ridges (+x) is on the left, and against the ridges (−x) is on the right for each geometry. | ||
In some movies, the droplet gets pinned by the surface, after which the airflow is enough to peel the droplets off. In other cases, the droplet glides along the surface smoothly. The largest obvious difference is for the α = 8.62°, b = 1.67 μm and α = 10.37°, b = 0.83 μm geometries. In the +x direction, along the sawtooth pattern, in 0.02 s, the droplet slides smoothly 12.7 mm. In the −x, after 0.02 s, the droplet is pinned at 5 mm. Interestingly, for surfaces with the highest α angles and ridge heights (Table 1), the friction in both directions is highest. This is obvious from the elongated droplet shape almost immediately upon exposure to the air jet. This shape results from high shear.49 For surfaces with intermediate α angles and low ridge heights (Table 1), there is less pinning and the droplets slide in both directions freely (Fig. 3). This also leads to a tendency for the droplets to lift off. The shape of the droplets is also consistent with much less shear as compared to the α = 8.62°, b = 1.67 μm geometry.
The velocities of the droplets were compared in relation to both the blaze angle of the surface and the blaze length with the control being considered 0 for both. The results are shown in Fig. 4. This allows us to determine which dimension impacted each aspect of droplet motion. Fig. 4 shows both the top speed of the droplet compared to the control, as well as the hysteresis, defined as the difference between the velocity in +x direction and −x direction. In Fig. 4a we observe the absolute velocities in the −x direction (triangle points in Fig. 4a) of the extreme α geometries, high and low, tend to be lower than the intermediate α geometries and the control. For the α = 8.62° and α = 10.37° geometries, the velocities are about 0.03 m s−1 lower than for the α = 12.48° and α = 17.45° geometries. The α = 26.7° geometry has the lowest velocity in the −x direction, equal to 0.11 m s−1. However, in the +x direction (round points in Fig. 4a), the lowest α angles has the highest droplet velocity. The α = 26.7° geometry again has the lowest velocity in the +x direction, equal to 0.22 m s−1. For surfaces with constant surface energy, the velocity hysteresis (difference between +x and −x) on the low angle geometries is high, for α = 8.62° 0.13 m s−1 increasing to 0.18 m s−1 for α = 10.37°. The hysteresis then drops to 0.09 m s−1 for α = 12.48° then increases to around 0.1 m s−1 for α = 17.45–26.7°.
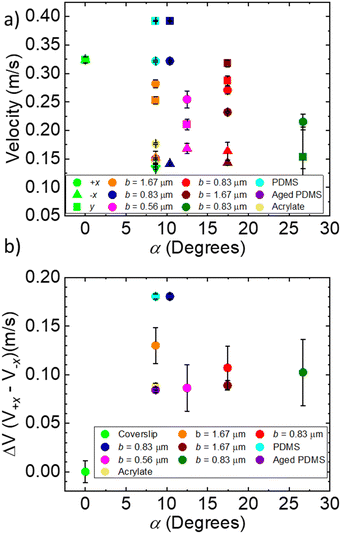 | ||
| Fig. 4 (a) Droplet velocities vs. α droplets were blown in the three primary directions +x, −x, y. (b) Difference in velocity between +x and −x directions. | ||
To determine the effect of surface energy, the α = 8.62°, b = 1.67 μm geometry was replicated using lithography techniques with acrylate resins mixed with Triton X-100 and PDMS (Table 2). These two materials show greatly different surface contact angles with water, ∼40° for acrylate resins mixed with Triton X-100 and ∼84° for PDMS, on a flat surface (Table 2). In Fig. 5, we show SEM and optical images of the surface texture on replicated surfaces. The surface appears to be well replicated using both materials, as indicated by the sharp lines spaced ∼1.7 μm apart. The contact angles in these surfaces (Table 2) very closely resemble those of the Thorlabs gratings. Aged PDMS shows some increased wettability over the virgin PDMS. We observe that contact angles in the +x and y directions decrease with the aging process and are overall closer to the hydrophilic acrylate surface (Table 2). This likely results from a slightly more hydrophilic surface as PDMS ages. UV acrylate with Triton X-100 surfaces had contact angle hysteresis of about 12° in the +x direction and about 29° in the −x direction. PDMS had contact angle hysteresis of about 16° in the +x direction and about 21° in the −x direction. Contact angle hysteresis decreased for aged PDMS. In the −x direction the hysteresis is 17° and 13° in the +x and y directions. In Fig. 5c, we observe 5 μL water droplet motion on acrylate templated surfaces with the α = 8.62°, b = 1.67 μm geometry. In the videos, there is some pinning indicative of shear. The droplet velocities recorded are 0.15 m s−1 in the +x direction and about 0.1 m s−1 in the −x direction. While the contact angle hysteresis is very similar to FDTS-coated Thorlabs gratings, the absolute velocity and velocity hysteresis decrease significantly from the more hydrophobic surfaces. The virgin PDMS – templated surfaces more closely resemble the FDTS-coated gratings. The droplet velocity in the +x-direction is 0.32 m s−1 and 0.14 m s−1 in the −x-direction. This data shows that the contact angle hysteresis and transport anisotropy is influenced by both surface energy and surface geometry. Geometric patterning influences wetting anisotropy in the range of flat surface contact angles from 40°–125°, where wetting and transport depend on the substrate geometry and surface energy.
| Resin – additive | +x(θA, θR) | −x(θA, θR) | y(θA, θR) |
|---|---|---|---|
| UV Acrylate – Triton X-100 | 106°, 94° | 126°, 97° | 104°, 96° |
| PDMS | 118°, 102° | 130°, 109° | 121°, 104° |
| Aged PDMS | 105°, 92° | 138°, 121° | 112°, 99° |
Discussion
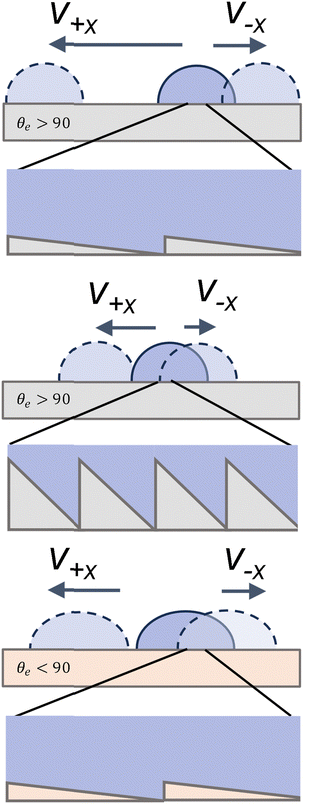
Though much work has been done to investigate anisotropic wetting and transport an ideal geometry has yet to be found. We have determined how the geometry influences droplet motion on sawtooth patterns as a function of angles (α = 8.62–26.70°) and lengths (b = 0.56–1.67 μm) (Fig. 1 and Table 1). We observe that the α = 8.62° and 10.37° surfaces exhibit the highest anisotropic droplet transport and the highest absolute velocities in the direction along the ridges (+x direction) and perpendicular to the ridges (y-direction). In this case, the shallow angle allows full droplet motion in one direction while pinning in the opposite direction.Maximum hysteresis, optimal wetting conditions for this experiment, is achieved when the droplet is in full contact (see ESI† for confocal images of the surface) with the surface with shallow angle geometries (α = 8.62° and 10.37°), as first described by Kusumaatmaja.24 For α = 8.62° and 10.37° surfaces, droplet motion along the ridges and perpendicular to the ridges has an absolute velocity similar to that of a flat coverslip. Significant pinning occurs as the droplet tries to slide against the ridges (motion in the −x direction (Fig. 2b)), based on the contact angle hysteresis and low droplet velocities. The full contact with the surface ensures pinning in the −x direction, and the shallow angle is necessary with minimal surface area for the droplet. In this way, friction is minimized in the +x direction (Fig. 2a) and maximized in the −x-direction. This geometry also corresponds most closely to that of butterfly wing scales which have α in the range of 5–10°. We also see that in motion in the +x direction the advancing contact angles tend to increase as α increases, we predict this occurs due according to the theoretical advancing contact angle θA = θE + α. Similarly, for the motion in the −x direction we see a trend closer to θA = θE + 90. This results from the advancing edge of the droplet impact only vertical faces of the ridges and remain in a metastable state.
As the α angle increases, the difference between contact angle hysteresis and velocity anisotropy changes. For α = 12–18° and b = 0.56–0.83 μm, we observe that droplets are able to slide freely in both the −x and +x directions (Fig. 2b and a respectively). The velocity in the −x direction is slightly higher than for shallower geometries. This is particularly true for the α = 12° angle with b = 0.56 μm. For this geometry, the ridge height is only 0.12 nm (Table 1), however, and leads to the lowest contact angle hysteresis and velocity hysteresis. As the ridge height increases, we once again observe pinning in the −x direction (Fig. 3).
At high angles and high ridge heights, we observe a significantly lower maximum droplet velocity in all directions and high friction indicated by the shear apparent in the videos. The velocities of sliding droplets in the +x direction drop by about 0.11 m s−1 from α = 10° to α = 26°. This change follows the predictions from simulation shown by Kussumatmaja.24 While we expect the droplets are fully wetting the geometry for both high and low α surfaces, (Fig. 6), significant pinning occurs in both directions for the α = 26.7° surface as opposed to primarily in the −x direction as seen in the 8.62° and 10.37° surfaces, and the hysteresis in the advancing angles is lower. As α increases to 26.7°, the droplets are pinned both along the ridges and against the ridges. As b decreases from 1.67 μm to 0.83 μm the ridge height decreases for the α = 18° surface from 500 nm to 250 nm, and we observe less droplet pinning in both directions. The overall velocity and velocity hysteresis however remains similar (Fig. 3 and Fig. 4b). While b plays a role in droplet motion and wetting on these surfaces, we see a dominating effect from changing α, which is apparent in the contact angle hysteresis, especially in the +x direction on all surfaces studied. Interestingly, regardless of α and b, all contact angles in the −x direction remain similar due to the underlying pinning geometry.
In many of the surfaces we see similar wetting in the +x and y directions. The similarity in contact angle likely arises from extremely fine geometry investigated. The sawtooth geometry demonstrates significant hysteresis in motion in the −x and +x directions. When droplets travel in the +x and y directions they flow over or along these faces respectively because the advancing edge is close to a flat surface due to the low α angle. This results in the drastic difference in pinning in the −x direction where the advancing edge of the droplet runs into the vertical face. This differs from many previously studied geometries where motion along parallel vectors is symmetric. Furthermore, the size regime of geometric texturing likely plays a role in the strength of the wetting effects seen. Many studies have been done concerning parallel ridged surfaces, however, the typical size of the features present are multiple microns wide and similar in depth.4,5 Our geometries are much smaller than this with the longest b = 1.67 μm and the depths ranging from 120–500 nm (Table 1).
We observe that droplet transport is dependent on both geometry and surface energy. For hydrophobic surfaces, both the absolute velocity and velocity hysteresis increase. While geometry is what enables and impacts the effectiveness of anisotropic droplet motion we still observe that droplets move at higher velocities on more hydrophobic surfaces, θe > 90 (Fig. 6). For hydrophilic surfaces like acrylate, we see a decrease in absolute velocities, which leads to a reduction in absolute hysteresis as well. Similar to acrylate we see the aged PDMS has lower absolute velocities and hysteresis. This likely results from the droplets more easily wetting these surfaces leading to a higher friction. This is consistent with the expected prediction by Eick et al.,28 who predict increasing hydrophobicity we tend to see an increase in contact angles. However, the predictions are not exact, and the contact angles remain higher than predicted for all surfaces, due to either the formation of metastable states or due to partial wetting. By using biological analogues with long b and low α we can achieve high droplet velocity hysteresis, which allows for directional transport across a wide range of surface energies.
Conclusion
The use of anisotropic droplet transport is ubiquitous in nature. Inspired by the wetting of butterfly wing scales, we have determined the effect of geometry of sawtooth patterned surfaces on the contact angle and droplet velocity. The contact angle hysteresis along the ridges (+x direction) and against the ridges (−x direction) changes as the ridge angle, α, increases from 8.62° to 26.7°. This coincides with a change in droplet velocity hysteresis, driven by air flow on the surface. For surfaces with shallow angle geometries, the highest hysteresis is observed in the direction against the ridges on hydrophobic surfaces. Droplets are pinned in the −x direction and travel freely in the +x direction, which results in the highest velocity hysteresis. As the angle increases, the droplets are pinned in both directions, which results in the lowest velocity hysteresis. This anisotropic transport persists on different surface energy materials like PDMS (virgin or aged) and acrylate. However, surface energy plays an important role effecting absolute droplet velocities and the magnitude of hysteresis. More hydrophilic substrates like acrylate have a higher global pinning force leading to reduced velocities in all directions but they maintain some directional hysteresis. By imparting sawtooth ridged textures onto any of the materials studied we can influence the droplet wetting and transport properties. Control of wetting and solvent flows has many applications, from antifouling to corrosion resistance, and lubricant films. By controlling material properties through texture, we hope we are able to use safer plastics in place of complex coatings.Author contributions
DGG led the experimental effort with DP and KY assisting in data collection. DGG performed data analysis, SAM provided assistance in analysis and production of figures. DGG wrote the first draft of the manuscript, final writing was split between SAM and DGG.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge The NSF Graduate Research Fellowship Program for funding this work grant number: 1937968. We would also like to acknowledge Sherwin Williams and their Protective and Marine team, Dr Jon York, Dr Travis S. Laws, and Dr Ilhan Ulkem for funding and support of this project. We would like to thank Sujata Dhakal and Dr Brittany Roopnarine for help with confocal imaging.References
- W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1–8 CrossRef CAS.
- M. Liu, Y. Zheng, J. Zhai and L. Jiang, Acc. Chem. Res., 2010, 43, 368–377 CrossRef CAS PubMed.
- Y. Y. Yan, N. Gao and W. Barthlott, Adv. Colloid Interface Sci., 2011, 169, 80–105 CrossRef CAS PubMed.
- R. Deying Xia, L. M. Johnson, G. P. López, D. Xia, L. M. Johnson and G. P. López, Langmuir, 2010, 26, 2700–2706 CrossRef PubMed.
- L. Gao and T. J. McCarthy, Langmuir, 2006, 22, 2966–2967 CrossRef CAS PubMed.
- Y. Zheng, H. Bai, Z. Huang, X. Tian, F. Q. Nie, Y. Zhao, J. Zhai and L. Jiang, Nature, 2010, 463, 640–643 CrossRef CAS PubMed.
- D. Kwon, S. Wooh, H. Yoon and K. Char, Langmuir, 2018, 34, 4732–4738 CrossRef CAS PubMed.
- K. Rykaczewski, J. S. Jordan, R. Linder, E. T. Woods, X. Sun, N. Kemme, K. C. Manning, B. R. Cherry, J. L. Yarger and L. C. Majure, Langmuir, 2016, 32, 9335–9341 CrossRef CAS PubMed.
- K. Ramanujan, Armor on butterfly wings protects against heavy rain|Cornell Chronicle, https://news.cornell.edu/stories/2020/06/armor-butterfly-wings-protects-against-heavy-rain (accessed 14 September 2021).
- H. Massoumi, M. K. Chug, G. H. Nguyen and E. J. Brisbois, J. Chem. Educ., 2022, 99, 2667–2676 CrossRef CAS PubMed.
- R. D. Davidson, T. E. O’Loughlin, T. E. G. Alivio, S. M. Lim and S. Banerjee, J. Chem. Educ., 2022, 99, 2689–2696 CrossRef CAS.
- H. R. Hong, J. S. Lee and C. H. Park, ACS Omega, 2022, 7, 26275–26288 CrossRef CAS PubMed.
- C. Xie, J. Shi, Y. Luo, G. Chu and H. Li, Langmuir, 2022, 38, 9822–9832 CrossRef CAS PubMed.
- Y. Xu, B. Han, K. Xiao, J. Yu, J. Zheng, S. Liang, X. Wang, G. Xu and X. Huang, Langmuir, 2022, 38(35), 10760–10767 CrossRef CAS PubMed.
- S. Park, J. Huo, J. Shin, K. J. Heo, J. J. Kalmoni, S. Sathasivam, G. B. Hwang and C. J. Carmalt, Langmuir, 2022, 38, 7825–7832 CrossRef CAS PubMed.
- Y. Ding, S. Xu and Z. L. Wang, J. Appl. Phys., 2009, 106, 74702 CrossRef.
- Y. Zheng, X. Gao and L. Jiang, Soft Matter, 2007, 3, 178–182 RSC.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- Y. Wang, M. Jian, H. Liu and X. Zhang, Langmuir, 2018, 35, 4387–4396 CrossRef PubMed.
- R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef CAS.
- H. Kusumaatmaja, M. L. Blow, A. Dupuis and J. M. Yeomans, EPL, 2008, 81, 36003 CrossRef.
- P. Papadopoulos, L. Mammen, X. Deng, D. Vollmer and H. J. Butt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3254–3258 CrossRef CAS PubMed.
- T. Koishi, K. Yasuoka, S. Fujikawa, T. Ebisuzaki and C. Z. Xiao, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8435–8440 CrossRef CAS PubMed.
- H. Kusumaatmaja and J. M. Yeomans, Soft Matter, 2009, 5, 2704–2707 RSC.
- G. Whyman and E. Bormashenko, Langmuir, 2011, 27, 8171–8176 CrossRef CAS PubMed.
- A. Giacomello, S. Meloni, M. Chinappi and C. M. Casciola, Langmuir, 2012, 28, 10764–10772 CrossRef CAS PubMed.
- W. Choi, A. Tuteja, J. M. Mabry, R. E. Cohen and G. H. McKinley, J. Colloid Interface Sci., 2009, 339, 208–216 CrossRef CAS PubMed.
- J. D. Eick, R. J. Good and A. W. Neumann, J. Colloid Interface Sci., 1975, 53, 235–248 CrossRef.
- M. J. Hancock, K. Sekeroglu and M. C. Demirel, Adv. Funct. Mater., 2012, 22, 2223–2234 CrossRef CAS PubMed.
- B. Wang, Y. Zhang, L. Shi, J. Li and Z. Guo, J. Mater. Chem., 2012, 22, 20112–20127 RSC.
- C. Ishino and K. Okumura, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 25, 415–424 CrossRef CAS PubMed.
- G. Sánchez-Balderas, J. D. H. Velázquez and E. Pérez, Langmuir, 2022, 38, 12804–12812 CrossRef PubMed.
- X. Li, L. Mao and X. Ma, Langmuir, 2013, 29, 1129–1138 CrossRef CAS PubMed.
- E. Mele, S. Girardo and D. Pisignano, Langmuir, 2012, 28, 5312–5317 CrossRef CAS PubMed.
- S. Wang, T. Wang, P. Ge, P. Xue, S. Ye, H. Chen, Z. Li, J. Zhang and B. Yang, Langmuir, 2015, 31, 4032–4039 CrossRef CAS PubMed.
- D. Xia, X. He, Y. B. Jiang, G. P. Lopez and S. R. J. Brueck, Langmuir, 2010, 26, 2700–2706 CrossRef CAS PubMed.
- M. Morita, T. Koga, H. Otsuka and A. Takahara, Langmuir, 2005, 21, 911–918 CrossRef CAS PubMed.
- F. Chen, D. Zhang, Q. Yang, X. Wang, B. Dai, X. Li, X. Hao, Y. Ding, J. Si and X. Hou, Langmuir, 2011, 27, 359–365 CrossRef CAS PubMed.
- C. Liu, J. Sun, J. Li, C. Xiang, L. Che, Z. Wang and X. Zhou, Sci. Rep., 2017, 7, 1–8 CrossRef PubMed.
- S. Daniel, M. K. Chaudhury and P. G. De Gennes, Langmuir, 2005, 21, 4240–4248 CrossRef CAS PubMed.
- C. L. Lee, T. S. Chan, A. Carlson and K. Dalnoki-Veress, Soft Matter, 2022, 18, 1364–1370 RSC.
- G. Lagubeau, M. Le Merrer, C. Clanet and D. Quéré, Nat. Phys., 2011, 7, 395–398 Search PubMed.
- M. Prakash and J. W. M. Bush, Int. J. Non-Linear Mech., 2011, 46, 607–615 CrossRef.
- G. Launay, M. S. Sadullah, G. McHale, R. Ledesma-Aguilar, H. Kusumaatmaja and G. G. Wells, Sci. Rep., 2020, 10, 1–8 CrossRef PubMed.
- X. Jing and Z. Guo, J. Mater. Chem. A, 2018, 6, 16731–16768 RSC.
- R. Feng, F. Song, Y. D. Zhang, X. L. Wang and Y. Z. Wang, Nat. Commun., 2022, 13, 1–8 Search PubMed.
- N. Kumar and A. Sharma, ACS Symp. Ser., 2022, 1418, 291–316 CrossRef CAS.
- A. Hourlier-Fargette, A. Antkowiak, A. Chateauminois and S. Neukirch, Soft Matter, 2017, 13, 3484–3491 RSC.
- A. Chahine, J. Sebilleau, R. Mathis and D. Legendre, Phys. Rev. Fluids, 2023, 8, 1–13 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm01669b |
| This journal is © The Royal Society of Chemistry 2024 |