Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical dynamics studies of the CH3 + HBr → CH4 + Br reaction: effects of isotope substitution and vibrational excitation of CH3†
Péter
Szabó
 *ab and
György
Lendvay
*ab and
György
Lendvay
 *cd
*cd
aDepartment of Chemistry, KU Leuven, Celestijnenlaan, 200F, Leuven, 3001, Belgium. E-mail: peter88szabo@gmail.com
bRoyal Belgian Institute for Space Aeronomy (BIRA-IASB), Avenue Circulaire 3, Brussels, 1180, Belgium
cInstitute of Materials and Environmental Chemistry, HUN-REN Research Centre for Natural Sciences, Magyar tudósok krt. 2., H-1117 Budapest, Hungary. E-mail: lendvay.gyorgy@ttk.hu
dCenter for Natural Sciences, Faculty of Engineering, University of Pannonia, Egyetem u. 10, Veszprém, 8200, Hungary
First published on 15th March 2024
Abstract
The rate coefficient for two deuterium substituted isotopologues of reaction CH3 + HBr → CH4 + Br has been determined using the quasiclassical trajectory (QCT) method. We used the analytical potential energy surface (PES) fitted to high-level ab initio points in earlier work. The PES exhibits a pre-reaction van der Waals complex and a submerged potential barrier. The rate coefficients of the deuterated isotopologue reactions, similarly to the pure-protium isotopologue, show significant deviation from the Arrhenius law, namely, the activation energy is negative below about 600 K and positive above it: k[CH3 + DBr] = 1.35 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(− 2472/T) + 5.85 × 10−13
exp(− 2472/T) + 5.85 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(335/T) and k[CD3 + HBr] = 2.73 × 10−11
exp(335/T) and k[CD3 + HBr] = 2.73 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(− 2739/T) + 1.46 × 10−12
exp(− 2739/T) + 1.46 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(363/T). The CH3 + DBr reaction is slower by a factor of 1.8, whereas CD3 + HBr isotopologue is faster by a factor of 1.4 compared to the HBr + CH3 system across a wide temperature range. The isotope effects are interpreted in terms of the properties of various regions of the PES. Quantum state-resolved simulations revealed that the reaction of CH3 with HBr becomes slower when any of the vibrational modes of the methyl radical is excited. This contradicts the assumption that vibrational excitation of methyl radicals enhances its reactivity, which is of historical importance: this assumption was used as an argument against the existence of negative activation energy in a decade-long controversy in the 1980s and 1990s.
exp(363/T). The CH3 + DBr reaction is slower by a factor of 1.8, whereas CD3 + HBr isotopologue is faster by a factor of 1.4 compared to the HBr + CH3 system across a wide temperature range. The isotope effects are interpreted in terms of the properties of various regions of the PES. Quantum state-resolved simulations revealed that the reaction of CH3 with HBr becomes slower when any of the vibrational modes of the methyl radical is excited. This contradicts the assumption that vibrational excitation of methyl radicals enhances its reactivity, which is of historical importance: this assumption was used as an argument against the existence of negative activation energy in a decade-long controversy in the 1980s and 1990s.
1 Introduction
Chemical kinetics offers itself to determine the heats of formation1 of reactive species such as radicals. The so-called second law method utilizes the relationship between activation energy and reaction energy: the latter is the difference between the activation energies of the forward and reverse reactions. Knowing the heats of formation of all but one species involved in the reaction, from the energy balance one can get the missing value. Heats of formation of a number of radicals were determined by measuring the activation energy of reactions of alkanes with Br or I atoms and assuming a small positive activation energy for the reverse reactions.2,3 A controversy arose when physical organic chemists realized4 that the heats of formation of alkyl radicals determined this way do not match the rest of the thermochemical data, from which it was concluded that at least one of the activation energies for each pair of reactions is not correct. The activation energy of the alkyl + HBr reactions was assumed to be between zero and 4 or 8 kJ mol−1, but in fact, the rate coefficients have not been measured. The only exception is the| CH3 + DBr → CH3D + Br | (R1) |
| CH3 + HBr → CH4 + Br | (R2) |
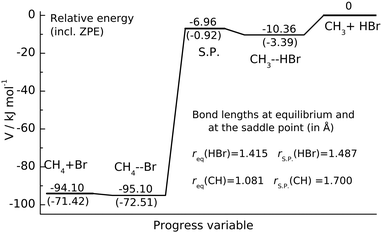 | ||
| Fig. 1 Potential energy profile of CH3 + HBr reaction. The energy levels of the stationary points characterizing the Czakó–Góger–Szabó–Lendvay PES13 are given in kJ mol−1. The zero-point energy corrected energies are shown in parentheses. The S.P. denotes the saddle point. | ||
Among the numerous arguments on the possible experimental errors behind negative activation energies, a particularly interesting objection was that the alkyl, including methyl radicals, when generated by laser flash photolysis, are vibrationally excited when formed and in the experiments there was not enough time for collisional relaxation. Remaining excited, they presumably reacted faster than the thermalized ones, discrediting the negative activation energy. This idea was raised and discussed again even as recently as 2014 at the Gas Kinetics Symposium in Szeged, Hungary. Although by now it is well established that the rate coefficients determined by the modern direct methods are reliable, we found it challenging to check whether vibrationally excited reactants react faster.
Reactions between alkane (R) and halogen atoms (X): RH + X → R + HX have been and continue to be a central subject of study in reaction dynamics over the past several decades.17–26 The PES of this reaction exhibits potential wells that may influence the reaction dynamics. The R + HX reactions where X = F, Cl, O are characterized by a large potential barrier19 which separates a pre-reactive complex from the product side. However, when X = Br, the reaction pathway features a van der Waals well along with a submerged barrier that lies in the entrance channel below the reactant's energy level. Understanding such reactions, and how the submerged barrier affects the dynamics, is far from complete.
Earlier, we performed quasiclassical trajectory (QCT) calculations on a reliable full-dimensional PES13 for reaction (R2) and obtained a number of interesting conclusions on the dynamics of the reaction.13,27–29 First, the experimental results were very well reproduced. Second, the excitation function, diverging at very low collision energy with decreasing Ecoll changes course and at higher collision energies increases with growing Ecoll. This suggests that the activation energy can be positive at higher temperatures. This expectation was confirmed in a combined experimental and theoretical work.29 Namely, reaction (R2) does have negative activation energy below about 500 K, but the rate coefficients pass minimum at about 650K, and start to increase with increasing temperature, producing a V-shaped Arrhenius plot. The experimental activation energy changes from −1.82 kJ mol−1 at 200 K to 13.5 kJ mol−1 at 1000 K. This confirms that the activation energy of (R2) is negative, but only at low temperatures, and a chance is given to researchers favoring positive Ea. An interesting consequence can be noticed when one follows the reverse path of the second-law method and calculates the activation energy of the reverse counterpart to (R2), the CH4 + Br reaction (−R2) from the reaction enthalpy and the measured, temperature-dependent activation energy of (R2). The reaction enthalpy and even its temperature dependence can now be calculated accurately from tabulated heats of formation that are reliable. The temperature dependence of the heats of formation of the four species involved, and so the reaction enthalpy calculated from tabulated data is mild29 (it changes non-monotonically, by less than 5 kJ mol−1 in the studied temperature range). As a result, similarly to the activation energy for (R2), that for (−R2) must also increase by about 20 kJ mol−1 (from about 70 kJ mol−1 at 200 K to about 90 kJ mol−1 at 1000 K), being about 71.2 kJ mol−1 at room temperature. The value used in the thermochemical calculations in the 1990s, 73.9 kJ mol−1 (considered as temperature-independent) is pretty close to this expectation, explaining why the alkyl heats of formation derived from the direct experiments were correct.
In this work, we intend to calculate the temperature dependence of the rate coefficients for reaction (R1) and evaluate the relationship between the experimental results of the two groups mentioned above. In addition, since NvKDW9 as well as Donaldson and Leone30 measured the rate coefficient for the
| CD3 + HBr → CD3H + Br | (R3) |
2 Methods
The QCT calculations were performed with our massively modified version of the 1988 edition of the VENUS code31 as detailed in ref. 13,27–29,32–37. The PES reported in ref. 13 was used (for some of its properties, see. Fig. 2; additional contour plots can be found in ref. 28 and 29). The impact parameter b was sampled with a weight proportional to b itself, and the maximum impact parameter was determined in exploratory trajectory batches and was varied between 4.5 and 11.0 to take into account all reactive events. In the rate coefficient calculations, the energy of all degrees of freedom was sampled from the appropriate Boltzmann distribution. 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run at every temperature using the velocity-Verlet integrator with the time step 0.07 fs to ensure energy conservation better than 0.05 kJ mol−1. To simulate the quantized nature of the vibration and rotation of the reactant molecules, the internal motion of molecules is described by ensembles of classical states that correspond to preselected quantum mechanical states. The ro-vibrational initial state of the HBr molecule is sampled by employing a quantized rotating Morse oscillator based on Porter–Raff–Miller method.38 The rotation of the methyl radical is described as an oblate symmetric top.39,40 The vibrational initial states of the methyl radical were selected randomly using normal mode sampling41 both in the calculations in thermal equilibrium and with vibrationally excited methyl radical.
000 trajectories were run at every temperature using the velocity-Verlet integrator with the time step 0.07 fs to ensure energy conservation better than 0.05 kJ mol−1. To simulate the quantized nature of the vibration and rotation of the reactant molecules, the internal motion of molecules is described by ensembles of classical states that correspond to preselected quantum mechanical states. The ro-vibrational initial state of the HBr molecule is sampled by employing a quantized rotating Morse oscillator based on Porter–Raff–Miller method.38 The rotation of the methyl radical is described as an oblate symmetric top.39,40 The vibrational initial states of the methyl radical were selected randomly using normal mode sampling41 both in the calculations in thermal equilibrium and with vibrationally excited methyl radical.
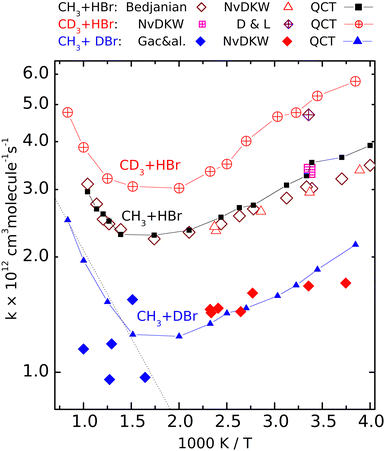 | ||
| Fig. 2 Calculated (QCT) rate coefficients for the CH3 + DBr (filled symbols), CH3 + HBr (open symbols) and CD3 + HBr (crossed symbols) reactions. The sources of the experimental data: NvKDW = Nicovich et al., ref. 9, D&L = Donaldson and Leone, ref. 20, Bedjanian, ref. 19, Gac&al, ref. 5. | ||
3 Results and discussion
3.1. Temperature dependence of rate coefficients for isotopologues of (R1)
Fig. 2 shows the rate coefficients calculated for the three isotopic variants (R1)–(R3), together with the experimental results. For reaction (R2) we show only the most complete data set, that of Bedjanian et al.,29 and the points measured by NvKDW9 whose results can be compared with their own measurements on reactions (R1) and (R3). To avoid congestion we do not present here the results of Seetula,10 Krasnoperov,42,43 and Seakins et al.8 because these are very close to the shown results, and they were amply discussed in our previous papers28,29 The QCT rate coefficients plotted for (R2) involving reactants with Boltzmann internal energy distributions are those we published earlier.That the V shape of the Arrhenius plot for (R2) predicted by the QCT calculations is correct is demonstrated by the excellent experiment-QCT agreement. This agreement extends to (R1) in the low-temperature regime where data from NvKDW9 are available. Note that similarly to (R2), for CH3 + DBr, all rate coefficients are in a narrow range, here between 1 × 10−12 and 2 × 10−12 cm3 molecule−1 s−1; we consider the capability of measuring a structured curve within this narrow range as a remarkable experimental achievement. For reaction R3, both of the room-temperature experiments9,30 provided somewhat larger rate coefficients than for the pure-protium reaction. The measured point of Donaldson and Leone et al.30 is very close to the nearby QCT points; it is roughly 1.5 times larger than the rate coefficient measured by Nicovich et al. The agreement is not as good between the QCT curve and the points reported by Gac et al. for reaction (R1).
Although the QCT curve runs between some of the experimental points, the latter, even considering their large scatter, cannot be claimed to follow the same tendency.
The Arrhenius plots for reactions (R1)–(R3) are well separated. The temperature dependence of the rate coefficients of the reactions involving deuterated reactants ((R1) and (R3)) follows the same tendency as the pure-protium (R2). At very high temperatures for reaction (R1) and elsewhere for (R3), only the QCT results are available. The good agreement with the experiments where the latter exist and the similarity to the Arrhenius plot of (R2) encourages us to consider the calculated results satisfactorily accurate. The curves are roughly parallel, and the location of the rate coefficient minima is close (around 550 and 600 K). The fastest is reaction (R3), the slowest is (R1).
The V shape of the Arrhenius plots means that at low temperatures the activation energy is negative, which by now became a widely accepted fact. That the activation energy at high temperatures is positive was first demonstrated experimentally by Bedjanian on (R2), whose measured rate coefficients agree very well with the QCT results. One can see that the other isotopologues also follow (R2) in that the activation energy at high temperatures is positive and exceeds the absolute value of the negative Ea below 400 K. In Fig. 2 (see also Fig. S1, ESI†) it is visible that for reaction (R1), the high-temperature points measured by Gac et al.5 look as if they formed a continuation of the lower-temperature data points of NvKDW9 However, the continuation of the straight Arrhenius line matching the latter data set to the region above 600 K does not follow the curvature of the QCT Arrhenius plot.
So, while it would be appealing to consider the two experimental data sets as consistent, one can conclude that the points measured using the early VLPP apparatus underestimate the rate coefficients for (R1) in that region and definitely do not follow the trend calculated by the QCT method which we consider realistic. As a result, even if the scatter of the Gac et al. measurements allowed the derivation of reasonable Arrhenius parameters, they would not be appropriate for thermochemical purposes, including the determination of the enthalpy of formation of the methyl radical, for which they were used by Gac et al.5 The activation energy in the 600 K–1000 K range, according to the QCT calculations for (R1) is roughly 8 kJ mol−1, exceeding even the upper uncertainty limit set by Benson and coworkers.1,2,11 Should an activation energy measured in this range combined with that for the reverse reaction – whose activation energy is also temperature-dependent – measured in a different temperature range, the resulting second-law heats of formation could become meaningless.
The rate coefficients of the CH3 + DBr and the CD3 + HBr isotopologue are smaller and larger, respectively than those of the CH3 + HBr variant. The experimental HBr/DBr kinetic isotope effect can be estimated to be around 1.7 from the data measured by NvKDW9 The corresponding QCT rate coefficient ratio on average is about 1.8. The remarkable rate lowering due to the substitution of the transferred H-atom by D, however, is not because of the less efficient tunnel effect as one could expect. Here the barrier is very flat (the imaginary frequency is 303i cm−1 for the CH3–H–Br isotopologue) and penetrating it would not make an appreciable advantage for the atom transfer.
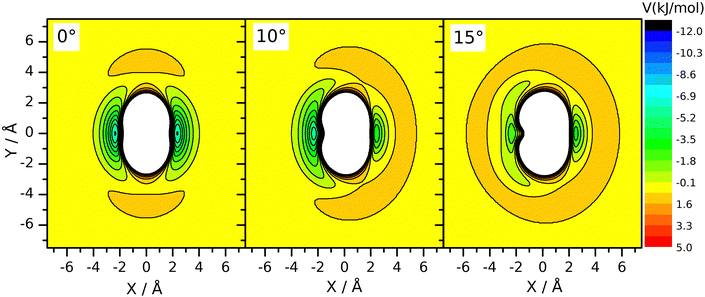
However, a dynamical effect connected to mass change does well explain the rate reduction. The preliminaries to this reasoning are as follows. We have seen earlier27 that for reaction (R2), the vibrational amplitude of the breaking bond's vibration has a critical role in determining the rate coefficient. The reason for this is that the shape of the potential energy surface is such that when the HBr molecule arrives at the neighborhood of CH3 in the H–Br vibrational phase when the bond is stretched significantly, an attraction arises between the two reactants. One can interpret this effect as if the attacking radical pulled the H-atom away from Br when seeing the H–Br bond halfway broken. This “dynamically induced attraction” has been manifested in the experiments of Smith and coworkers44 on the reaction of H atoms with water molecules excited by 4 stretch vibrational quanta as a huge, about 9 Å effective collision diameter. The effect was interpreted in QCT calculations44–48 and was seen as extreme rate enhancement in QCT simulations on other simple H-atom-transfer reactions involving reactants in which the breaking H–X bond is vibrationally excited, such as H + HF49 and F + H2 and H + HCl.50 In one of our recent papers27 we have shown that in the CH3 + HBr reaction, the amplitude of the H–Br oscillation is so large already in the vibrational ground state, that this kind of attraction arises whenever the H–Br oscillation is at the outer turning point and the CH3 reactant is close enough. Notably, when the H–Br vibrational amplitude is reduced by, for example, decreasing the vibrational excitation artificially below the zero-point (feasible in QCT simulations by setting the quantum number to non-integer negative values between –0.5 and 0) or by increasing the mass of the atom being transferred, the reaction can be frozen because the “dynamically induced attraction” will be inefficient or nil. The H/D isotope substitution in HBr involves such an amplitude reduction in the vibrational ground state, because the zero-point energy of DBr is smaller than that of HBr. The consequence is a sizeable primary isotope effect. The inverse secondary isotope effect arising when the H-atoms of the CH3 reactant are replaced by D can be traced back to a completely different reason: it is a steric effect, acting in conjuction with the zero-point vibration. Fig. 3 shows the potential energy of the HBr molecule pointing toward the carbon atom placed in various locations around the radical. One can see that the approach in the plane of the radical, which is set perpendicular to the plane of the figure, is not favorable. There is a “repulsive” ring around the edge of the radical, while its faces are attractive. When the umbrella mode oscillates and the out-of-plane angle changes, the side of the radical toward which the C–H bonds are bent becomes covered by a repulsive hemisphere, while the attraction on the other remains essentially the same. This makes one side of the methyl radical unattractive when the umbrella oscillation arrives to the outer turning point. This occurs alternately for the two sides of the radical, impeding the approach of the two reactants. At large amplitude, both sides are covered by a repulsive shell periodically. Thus, large-amplitude umbrella vibration is not favorable for the reaction. When the H atom is replaced by deuterium, the umbrella bending frequency and thus the zero-point energy is smaller. Consequently, the vibrational amplitude is reduced, just as we sketched in connection with the isotope replacement in HBr. In (R3), because the deviation of the CD3 umbrella bending angle from its equilibrium value remains small, the shielding effect is less efficient than with CH3. This explains the speed-up of (R3) wrt. (R2). In summary, the amplitude reduction upon H/D substitution in CH3 is also a zero-point energy effect: it occurs because the zero-point energy corresponding to the umbrella bending mode of CD3 is smaller than that of CH3.
3.2 The influence of the vibrational excitation of the CH3 radical on its reactivity toward HBr
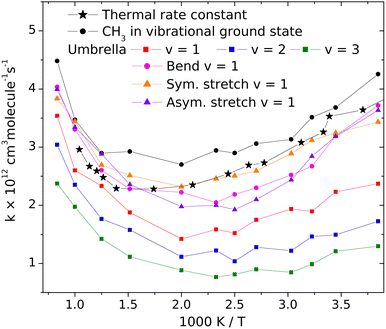
Changes of the vibrational amplitude that are found to cause remarkable isotope effect can also be induced by vibrational excitation. To explore the phenomenon, we calculated the rate coefficients with CH3 in vibrational ground state and when its vibrational modes are excited one at a time. This way the influence of vibrational excitation on the reactivity will also be assessed. The results are shown in Fig. 4 in Arrhenius representation. For reference, the rate coefficients simulated under thermal conditions (i.e. reactant vibrational excitation sampled from the Boltzmann distribution) are also shown (black stars). Each mode is separately excited by one vibrational quantum. For the lowest-frequency (umbrella) mode we tested the effect of higher excitations because these states can be populated even at moderate temperatures. The most reactive is CH3 in its ground state. Excitation of any of its vibrational modes hinders the reaction.The largest effect is caused by the excitation of the umbrella mode: the amplitude increases by so much due to excitation to the second energy level that the reactivity decreases by almost a factor of two below 500 K and somewhat less at higher temperatures. The second and third umbrella quanta cause further reactivity reduction, but the effect is less spectacular.
Among the remaining modes, the excitation of the symmetric stretching causes the smallest rate reduction; that induced by the amplitude increase of the in-plane bending or of the asymmetric stretch is larger and commensurable with each other. The reason for the adverse effect of the umbrella excitation is easy to find: it is the same that makes CH3 less reactive than CD3. The amplitude of the umbrella vibration increases with each vibrational quantum, inducing more and more efficient shielding of the reactive faces of the radical. There is probably a similar reason behind the effects of the other modes (Table 1).
| v umb = 1 | v umb = 2 | v umb = 3 | v bend = 1 | v sstr = 1 | v astr = 1 |
|---|---|---|---|---|---|
| 5.8 | 11.6 | 17.4 | 17.0 | 37.0 | 39.2 |
In addition to the decreasing reactivity, the activation energy at low temperatures is getting less and less negative with increasing umbrella excitation of the methyl radical. In this temperature range, the reaction rate is predominantly influenced by the capture of the reactants in the van der Waals well, induced by their attraction. It is known that the slower the reactants approach each other, the more efficient capture is. In thermal systems, this appears as a negative activation energy increasing in magnitude when the temperature decreases see the black dots in Fig. 3. When the attraction is reduced for some reason, for example, by the appearance of the little repulsive range when the umbrella amplitude is large (see Fig. 3), then its efficiency in bringing the reactants together will be smaller or cease, thus reducing the magnitude and the rate of increase of the activation energy with decreasing temperature.
The results on the effect of vibrational excitation of the methyl radical on its reactivity allow us to comment on the argument presented by Dobis and Benson11 about larger reaction rates due to unsatisfactory relaxation of the radicals after being generated in high-internal-energy states. We have seen that excitation of any CH3 mode is adverse to the reactions. As a result, incomplete vibrational relaxation would be unfavorable for the reaction, instead of enhancing the rate.
4 Summary
The rate coefficients of three isotopologs of the CH3 + DBr → CH3 D + Br reaction were determined using the quasiclassical trajectory method. During the 1990s, vivid discussion surrounded the sign of the activation energy of reactions in this class, a parameter that has a major role in the determination of heats of formation of free radicals using the “second law method” of thermochemical kinetics. In retrospect, it is easy to see that the origin of the controversy is the complexity arising because the reaction involves the temporary formation of a hydrogen-bonded CH3–HBr van der Waals complex and a potential barrier to product formation, and importantly the barrier to reaction is submerged. The microscopic mechanism corresponding to such a potential energy surface allows the variation of the activation energy so that it can be positive in one and negative in another temperature domain. The rate coefficient calculations on the CH3 + DBr isotopologue showed that of the two data sets measured experimentally, the high-temperature set5 contains too low rate coefficients and is not consistent with the positive activation energy expected in this range. The low-temperature experimental points are very close to the QCT rate coefficients and reflect accurately that the activation energy in this range is negative, which is consistent with what was found for the pure-protium isotopologue. The deuterium substitution in HBr causes a normal kinetic isotope effect which can be traced back to a vibrational mass effect associated with the zero-point energy. Namely, the attraction arising between the reactants when the breaking H–Br bond is in a highly stretched, partially broken phase of its vibrational period is less efficient in DBr than in HBr because the amplitude is smaller. The speed-up of the reaction observable when the H atoms of the other reactant, CH3 are replaced by D can be considered a steric effect also associated with the zero-point energy. More precisely, temporarily a less attractive or even repulsive “shield” arises when the umbrella displacement is large, and the mass increase upon deuterium substitution reduces the umbrella amplitude, i.e. the reactants attract each other with less hindrance. The vibrational excitation of any mode of CH3 was found to reduce the rate coefficient when it reacts with HBr, as compared with vibrational ground-state methyl radical. The largest effect is found for the excitation of the umbrella mode, which can be traced back to the same feature of the potential energy surface as seen above for the inverse CH3/CD3 kinetic isotope effect. Rate reduction due to vibrational excitation of reactants is not common and deserves attention. In the case of this specific reaction, this kind of rate reduction is particularly important: For this reaction, among other reactions in the alkyl + HBr class, to discredit the experiments providing negative activation energy, it was proposed that the reaction rates measured when the radicals are generated photolytically are too large. According to the argument, the reason for the assumed rate increase is vibrational excitation of the radicals that are not carefully relaxed before the reaction. The QCT calculations suggest that this reasoning has no foundation.Author contributions
P. Szabó; conceptualization, investigation; analysis; software; writing & editing; G. Lendvay: conceptualization; data analysis, funding acquisition; resources; validation; writing – review & editing.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
The research was funded by the Belgian Science Policy Office (BELSPO), FED-tWIN REVOCS. This article is based upon work from COST Action CA18212—Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology). Project K129140 for G. L. was implemented with the support provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the OTKA funding scheme.References
- S. W. Benson, Thermochemical Kinetics, Wiley Interscience, New York, 2nd edn, 1976 Search PubMed.
- D. M. Golden and S. W. Benson, Chem. Rev., 1969, 69, 125–134 CrossRef CAS.
- D. Gutman, Acc. Chem. Res., 1990, 23, 375–380 CrossRef CAS.
- W. Von Eggers Doering, Proc. Natl. Acad. Sci. U. S. A., 1969, 78, 5279–5283 CrossRef PubMed.
- N. A. Gac, D. M. Golden and S. W. Benson, J. Am. Chem. Soc., 1969, 91, 3091–3093 CrossRef CAS.
- J. J. Russell, J. A. Seetula, R. S. Timonen, D. Gutman and D. F. Nava, J. Am. Chem. Soc., 1988, 110, 3084–3091 CrossRef CAS.
- J. J. Russell, J. A. Seetula and D. Gutman, J. Am. Chem. Soc., 1988, 110, 3092–3099 CrossRef CAS.
- P. W. Seakins, M. J. Pilling, J. T. Niiranen, D. Gutman and L. N. Krasnoperov, J. Phys. Chem., 1992, 96, 9847–9855 CrossRef CAS.
- J. M. Nicovich, C. A. Van Dijk, K. D. Kreutter and P. H. Wine, J. Phys. Chem., 1991, 95, 9890–9896 CrossRef CAS.
- J. A. Seetula, Phys. Chem. Chem. Phys., 2002, 4, 455–460 RSC.
- S. W. Benson and O. Dobis, J. Phys. Chem., 1998, 102, 5175–5181 CrossRef CAS.
- M. Mozurkewich and S. W. Benson, J. Phys. Chem., 1984, 88, 6429–6435 CrossRef CAS.
- S. Góger, P. Szabó, G. Czakó and G. Lendvay, Energy Fuels, 2018, 32, 10100–10105 CrossRef.
- J. Chen, E. Tschuikow-Roux and A. Rauk, J. Phys. Chem., 1991, 95, 9832–9836 CrossRef.
- G. Czakó, J. Chem. Phys., 2013, 138, 134301 CrossRef PubMed.
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839 CrossRef PubMed.
- C. Yin and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 3083–3091 RSC.
- D. Papp and G. Czakó, J. Chem. Phys., 2021, 155, 154302 CrossRef CAS PubMed.
- G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839 CrossRef PubMed.
- J. C. Corchado, M. G. Chamorro1, C. Rangel and J. Espinosa-Garcia, Theo. Chem. Acc., 2019, 138, 26 CrossRef.
- J. Espinosa-Garcia, L. Bonnet and J. C. Corchado, J. Phys. Chem. A, 2017, 121, 4076 CrossRef CAS PubMed.
- J. Espinosa-Garcia, M. Garcia-Chamorro, J. C. Corchado, S. Bhowmick and Y. V. Suleimanov, Phys. Chem. Chem. Phys., 2020, 22, 13790–13801 RSC.
- H.-G. Yu and G. Nyman, J. Phys. Chem. A, 2001, 105, 2240 CrossRef CAS.
- N. Liu and M. Yang, J. Chem. Phys., 2015, 143, 134305 CrossRef PubMed.
- J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, J. Chem. Phys., 2016, 144, 171101 CrossRef PubMed.
- L. Sheng, Z. S. Li, J. Y. Liu and C. C. Sun, J. Chem. Phys., 2003, 119, 10585 CrossRef.
- B. Csorba, P. Szabó and G. Lendvay, J. Phys. Chem. A, 2021, 125, 8386–8396 CrossRef CAS PubMed.
- D. Gao, X. Xin, D. Wang, P. Szabó and G. Lendvay, Phys. Chem. Chem. Phys., 2022, 24, 10548–10560 RSC.
- J. Bedjanian, P. Szabó and G. Lendvay, J. Phys. Chem. A, 2023, 127, 6916–6923 CrossRef PubMed.
- D. J. Donaldson and S. R. Leone, J. Phys. Chem., 1986, 90, 936–941 CrossRef CAS.
- W. L. Hase, R. J. Duchovic, D.-H. Lu, K. N. Swamy, S. R. Vande, R. Linde and J. Wolf, VENUS: A General Chemical Dynamics Computer Program, 1988.
- A. L. Van Wyngarden, K. A. Mar, K. A. Boering, J. J. Lin, Y. T. Lee, S.-Y. Lin, H. Guo and G. Lendvay, J. Am. Chem. Soc., 2007, 129, 2866–2870 CrossRef CAS PubMed.
- A. V. Wyngarden, K. Mar, J. Quach, A. Nguyen, A. Wiegel, S.-Y. Lin, G. Lendvay, H. Guo, J. Lin, Y. Lee and K. Boering, J. Chem. Phys., 2014, 141, 064311 CrossRef PubMed.
- S. A. Lahankar, J. Zhang, T. K. Minton, H. Guo and G. Lendvay, J. Phys. Chem. A, 2016, 120, 5348–5359 CrossRef CAS PubMed.
- P. Szabó and G. Lendvay, J. Phys. Chem. A, 2015, 119, 7180–7189 CrossRef PubMed.
- P. Szabó and G. Lendvay, J. Phys. Chem. A, 2015, 119, 12485–12497 CrossRef PubMed.
- P. Szabó and G. Lendvay, AIP Conf. Proc., 2020, 2304, 020004 CrossRef.
- R. N. Porter, L. M. Raff and W. H. Miller, J. Chem. Phys., 1975, 63, 2214 CrossRef CAS.
- D. L. Bunker and E. A. Goring-Simpson, Faraday Discuss. Chem. Soc., 1973, 55, 93 RSC.
- R. J. Duchovic and W. L. Hase, J. Chem. Phys., 1985, 82, 3599 CrossRef CAS.
- W. L. Hase and D. G. Buckowski, Chem. Phys. Lett., 1980, 74, 284 CrossRef CAS.
- L. N. Krasnoperov and K. Mehta, J. Phys. Chem. A, 1999, 103, 8008–8020 CrossRef CAS.
- L. N. Krasnoperov, J. Peng and P. Marshall, J. Phys. Chem. A, 2006, 110, 3110–3120 CrossRef CAS PubMed.
- P. W. Barnes, P. Sharkey, I. R. Sims and I. W. M. Smith, Faraday Discuss., 1999, 113, 167–180 RSC.
- G. C. Schatz, G. Wu, G. Lendvay, D.-C. Fang and L. B. Harding, Faraday Discuss., 1999, 113, 151–165 RSC.
- P. Barnes, I. R. Sims, I. Smith, G. Lendvay and G. C. Schatz, J. Chem. Phys., 2001, 115, 4586–4592 CrossRef CAS.
- E. Bene, G. Lendvay and G. Póta, in Dynamics of Bimolecular Reactions of Vibrationally Excited Molecules, Theory of chemical reaction dynamics, Kluwer, Dordrecht, 2004 Search PubMed.
- E. Bene, G. Póta and G. Lendvay, J. Phys. Chem. A, 2005, 109, 8336–8340 CrossRef CAS PubMed.
- E. Bene and G. Lendvay, J. Phys. Chem. A, 2006, 110, 3231–3237 CrossRef CAS PubMed.
- A. Bencsura and G. Lendvay, J. Phys. Chem. A, 2012, 116, 4445–4456 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05610d |
| This journal is © the Owner Societies 2024 |