Open Access Article
Open Access ArticleMachine learning in energy chemistry: introduction, challenges and perspectives
Yuzhi
Xu†
ad,
Jiankai
Ge†
 *b and
Cheng-Wei
Ju
*b and
Cheng-Wei
Ju
 *c
*c
aDepartment of Chemistry, New York University, New York, New York 10003, USA
bChemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA. E-mail: jiankai2@illinois.edu
cPritzker School of Molecular Engineering, The University of Chicago, Chicago, Illinois 60637, USA. E-mail: cwju@uchicago.edu
dNYU-ECNU Center for Computational Chemistry at NYU Shanghai, Shanghai 200062, China
First published on 24th April 2023
Abstract
With the development of industrialization, energy has been a critical topic for scientists and engineers over centuries. However, due to the complexity of energy chemistry in various areas, such as materials design and fabrication of devices, it is hard to obtain rules beyond empirical ones. To address this issue, machine learning has been introduced to refine the experimental and simulation data and to form more quantitative relationships. In this review, we introduce several typical scenarios of applying machine learning to energy chemistry, including organic photovoltaics (OPVs), perovskites, catalytic reactions and batteries. In each section, we discuss the most recent and state-of-art progress in descriptors and algorithms, and how these tools assist and benefit the design of materials and devices. Additionally, we provide a perspective on the future direction of research in this field, highlighting the potential of machine learning to accelerate the development of sustainable energy sources. Overall, this review article aims to provide an understanding of the current state of machine learning in energy chemistry and its potential to contribute to the development of clean and sustainable energy sources.
1. Introduction
Energy consumption is rising accompanied by population growth and industrialization.1 Currently, fossil fuels such as coal, oil, and natural gas still dominate the global energy consumption.2,3 However, the burning of fossil fuels leads to a huge emission of carbon dioxide, which contributes to global warming and has negative impacts on the environment and human health.4,5 Therefore, it is increasingly important to develop sustainable and clean sources of energy in order to replace fossil fuels. Many attempts have been made over the last few decades to accomplish energy conversion and storage with high efficiency and little pollution, such as solar, wind, water, biofuel, and hydrogen.6 To be more specific, in the last 10 years, there has been significant progress in the field of sustainable and clean energy (Fig. 1). It is also an area that will continue to be a focus of research and development in the forthcoming years.7–9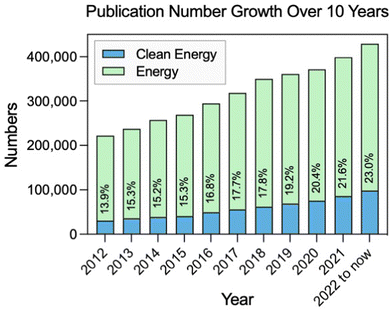 | ||
| Fig. 1 Change in the number and percentage of publications with clean energy and containing energy topics in the last decade (source: Web of Science). | ||
Photovoltaics (PV) is one of the clean energy technologies that utilize solar energy and has gained more and more attention. More particularly, solar energy is a source of energy that can be considered as physically infinite. Therefore, adopting solar energy is regarded as the most promising solution to address the energy crisis.10 PV can be divided into three categories: silicon-based solar cells, organic solar cells (OSCs), and the increasingly popular perovskite solar cells (PSCs).
Currently, over 90 percent of the global PV market is dominated by crystalline silicon solar cells.11 Silicon-based solar cells are mature and commercially available for large-scale manufacturing. However, in most buildings and agricultural production sites, the opaqueness and weight of crystalline silicon prevent it from being used as a cover.12 OSCs and PSCs are considered as potential alternatives to silicon-based solar cells, as they have the potential to be light weight, flexible, and produced at a lower cost. Nevertheless, compared to silicon-based solar cells, OSCs and PSCs are still in the development stage.13 The high power conversion efficiency (PCE), long-term stability and less efficiency loss while scaling up are the main challenges for OSCs and PSCs.14
Computational design of materials has become an essential part of PV design.15–17 By using computational methods, researchers can simulate and predict the performance of different materials and devices without costly and time-consuming experimental trials. Such methodology can greatly accelerate the materials design and device optimization process. In the past few decades, computational chemistry methods have mainly employed first principles method.18,19 One of the main advantages of first principles methods is that they can accurately and non-empirically predict the electronic and optical properties of materials, including the energy levels of electrons and holes, band gaps, and the absorption spectrum. In recent years, machine learning, a statistics-based technology, has become an important part of computation-aided materials design.20,21 Through machine learning, researchers can not only bypass complex formulas to explore relationships between different values but also generate novel compounds and materials. Many parameters in materials or devices for PV cannot be simply derived from theoretical equations or calculated using the first-principles method, while the usage of machine learning greatly facilitates research in these areas.
In addition to PV, the catalytic reaction is also an efficient tool in sustainable and energy chemistry. A lot of catalysts have been developed to accelerate different types of chemical reactions, like the oxygen reduction/evolution reaction (ORR/OER), hydrogen evolution reaction (HER), CO2 reduction reaction (CO2 RR), etc.22–24 However, the catalytic ability is limited by multiple factors such as synthesis conditions, morphology, measurement methods, etc.25–27 It is hard to develop theories or models to describe catalytic systems. Machine learning, with the benefits of multi-factor fitting and identifying trends, has great potential in catalytic fields. Similarly, with the help of machine learning, researchers may be able to improve the understanding of the structure–function relationship and predict the catalytic ability, thereby guiding the synthesis of catalysts.
To date, there are already many websites, books, and reviews on machine learning in chemistry or energy that describe machine learning algorithms and the related research process.28–30 To gain a better understanding of basic machine learning concepts such as what an algorithm is, what a dataset is, and how to manipulate and use machine learning, refering to these excellent works may help in comprehending the machine learning process.31–33 This review provides a perspective on input types, task types and state-of-the-art (SOTA) performances when using machine learning in energy chemistry. We expect that this review could help chemists and materials scientists to gain more insight into how machine learning empower the development of energy chemistry.
Here, we will introduce how machine learning could optimize and accelerate the development of energy chemistry, especially in designing of materials. More specifically, this review focuses on the recent advancements, applications, and future prospects of machine learning in the fields of PV, catalysis and batteries. These are essential areas of energy chemistry, where machine learning techniques have been applied to improve the prediction, design, and optimization of material properties. In Section 2, we provide a brief introduction to organic photovoltaics (OPV) and delve into the structural and electronic descriptors. We further discuss the development of de novo design of OPV materials. In Section 3, we summarize multiple types of features and prediction tasks for perovskites. After that, we discuss how machine learning helps in perovskite discovery through experiments and auto-synthesis. In Section 4, developing atomistic potentials and the prediction for heterogeneous catalytic reactions are presented. As a practical application, battery design and management are reviewed with typical examples in Section 5. Finally, a perspective on developing novel machine learning-based methodologies aimed at solving chemistry problems and their applications in energy chemistry is proposed. With the assistance of machine learning, scientists can benefit from developing materials designs on different scales, from predicting and optimizing properties, fitting atomistic force fields, to managing systems.
2. Organic photovoltaics
Compared with traditional crystalline silicon PVs, OPVs have the advantages of light weight, low-cost, and flexibility.34,35 One of the major advantages of commercial OPVs is that they can be solution-processed, which means that they can be cost-effectively produced on large-area PVs.36 OPVs have been under development for several decades, but their performance still lags behind that of crystalline silicon PVs, particularly in terms of PCE. It is imperative to search for novel and efficient OPV materials. Many factors can affect OPVs, such as electronic structure properties (HOMO, LUMO, and bandgaps), interfaces, and bulk heterojunction (BHJ) mixing. With the advent of machine learning, it is now possible to quickly predict these physical properties or efficiency before experiments, thereby saving time, resources, and manpower. Therefore, machine learning can be used as a powerful tool for high-throughput screening in the development of OPVs.37 Many accessible material databases that have been created based on previous calculation works provide a good data environment for using machine learning in exploring promising OPVs.38–40 Besides, researchers used to manually collect a large amount of data from previous papers to establish training databases.41,42 Leveraging these databases, many precise OPV prediction models have been proposed.2.1 OPV descriptors
Descriptors build a bridge between computer algorithms and physical understanding, which is critical for effectively predicting new materials or properties. Due to the complexity of OPV structures, the understanding of the quantitative structure–property relationship (QSPR) for OPVs is still inadequate even now. Thus, researchers invest significant effort in developing descriptors to uncover more hidden information within the structure of OPVs.There are multiple types of descriptors used in the process of converting raw data into features for OPVs, and these types can be divided into two categories: physical property representation and chemical structure representation. In physical property representation, researchers usually directly use electronic structure parameters or measurement values as the features. When constructing features using physical property data from different papers, it is important to ensure similar measurement conditions to avoid model bias or deviation. In chemical structure representation, various methods based on different structure description dimensions can be employed to describe the structure. It is important to note that these methods are often accompanied by a loss of information when converting a chemical structure to a feature. Therefore, the method of converting chemical structures into features may vary depending on the specific situation.
It is important to choose the suitable number and types of descriptors as features because adding more features in the model does not guarantee better prediction results. The inappropriate descriptors can add redundant information to the model and too much features may lead to model overfitting. Besides, it may also increase the dimensionality of the data, making the model training more expensive and difficult. Hence, feature engineering is usually required after manually selecting the descriptors to optimize the performance of the model.43 In actual practice, chemical structure descriptions and electronic descriptions typically complement one another.44
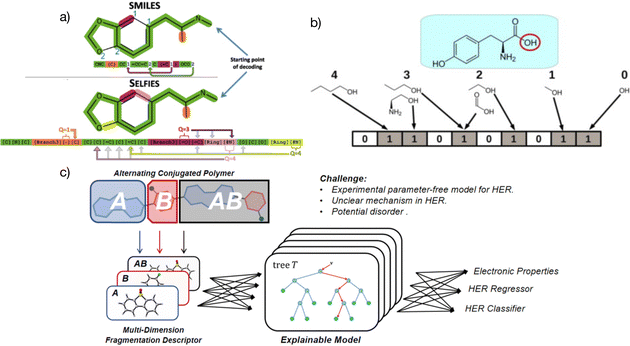 | ||
| Fig. 2 (a) Specific representation coding and differences between SELFIES and SMILES, with SELFIES having a more complex structure than SMILES.50 Reproduced from ref. 50 under the terms of the Creative Commons Attribution 4.0 license from IOP Publishing. (b) Simple representation of molecular fingerprints.54 Reprinted (adapted) with permission from ref. 54. Copyright 2014 Elsevier. (c) The multidimensional fragmentation descriptors strategy in a linear alternative polymer; A and B represent different fragments in the polymer and A–B stands for a monomer in the polymer. The features from different input dimensions work together and boost the prediction accuracy of the linear alternative polymers.51 Reprinted (adapted) with permission from ref. 51. Copyright 2021 American Chemical Society. | ||
In the chemical structure representation of OPVs, the whole polymer cannot be described directly using the machine learning algorithm for its complex components. As an approximation method, researchers usually adopt individual monomers to represent the polymers. Therefore, the process of describing small molecule and polymer structures is similar. In many cases of small molecule or protein design, 3D coordinates or 4D descriptors are useful as they provide detailed information about the molecular structure and conformation.55 However, the OPV structures are often more complex, and the use of these high dimensional descriptors may not be as effective. Besides, researchers are more concerned with OPV functionality than with subtle changes in the absolute position. Thus, 3D or 4D descriptors are rarely employed in the OPV machine learning work. In actual practice, structural descriptors are mainly classified into 2D and 3D categories. 2D descriptors can be mainly divided into SMILES (including different kinds of SMILES, such as canonical SMILES and SMILES with atomic mapping), InChI, Tensors and others. 3D descriptors can be divided into voxels, Coulomb matrix, tensor field networks and potential energy surface method. Using the concept of physical descriptors, Elton et al. introduced general descriptor production rules in two and three dimensions.56 Recently, the majority of OPV machine learning studies have used molecular fingerprints as the primary structure representation. This is because molecular fingerprints not only contain the original structure of the molecule but also capture some information from the surrounding atomic environment at a 2D level. This type of environmental information is generally in the range of 4–6 atoms such as extended-connectivity fingerprints (ECFP4 and ECFP6).57 Although molecular fingerprints lose long-range structural information, it is believed that with a large enough dataset, the environmental information supplemented by sub-segments can still capture this information. This is because OPV molecules have relatively fixed building blocks of the backbone structure. Note that very few OPV works simply use structures as the only descriptor. Generally, multiple descriptors including PV parameters and chemical structure information are featured together.
In many cases using fingerprints as descriptors, random forest (RF) and boosting decision tree (BDT) are the most suitable models in OPVs.58,59 Sun et al. manually constructed a database of more than 1700 experimentally tested real donor materials including both polymers and small molecules (with a median PCE of 3.48%).60 They compared the performance of image representation, ASCII strings, and seven molecular fingerprints in the binary classification of “high” or “low” PCE (two thresholds are 3.00% and 10.00%) with the algorithms of the back propagation neural network (BPNN), deep neural network (DNN), RF and support vector machines (SVMs). Besides, they also researched the influence of different lengths of the fingerprints. They found that using RF with daylight fingerprints61 an average prediction accuracy of 86.67% could be achieved and explored whether the fingerprints whose length is longer than 1000 bits including sufficient chemistry information are suitable candidates for building descriptors in PCE prediction models. Furthermore, Wu et al. established a small database of 565 donor/acceptors (D/A) combinations and used a fragment fingerprint method to build a PCE prediction model.62 In their work, the authors employed five different model methods including linear regression (LR), boosted regression trees (BRT), multinomial logistic regression (MLR), RF and artificial neural network (ANN) to perform ternary classification of PCE (power conversion efficiency) using thresholds of 7% and 11%. Among these methods, RF achieved the highest performance with 65.2% accuracy in the ternary classification of high-level PCE (>11%). They discovered six novel D/A combinations after virtual screening. After that, they compared the PCE values of the new materials with model prediction values and found that RF prediction values are closest to experimental values.
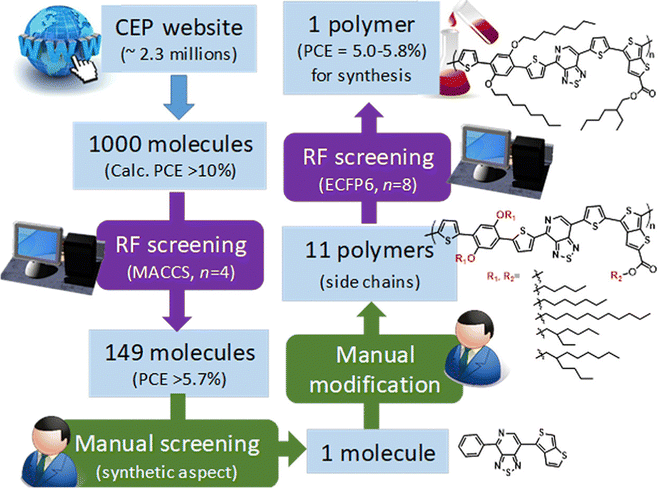
As mentioned before, small molecules are treated as monomers using fingerprints in OPVs without considering the molecular weight and binding situation. In some cases, if the structure is complex, it can lead to large deviations in material predictions. Nagasawa et al. used MACCS fingerprints and bandgaps, the HOMO, and weight-averaged molecular weight as the input with ANN and RF methods to build a PCE prediction model (Fig. 3).63 However, the predicted PCE of selected OPV molecules in the Harvard Clean Energy Project dataset was about 5.0%–5.8% while the experimental device values were 0.47 ± 0.04%. They concluded that the deviations between the machine learning and experiment values are due to the direction of combining and low molecular weight. Additionally, as an extension of the molecular structure, molecular graphs converted from SMILES can also be the structural descriptors in building PCE machine learning models. Eibeck et al. used the graph neural network (GNN) model and attention fingerprint model found by Xiong et al.64 in the PCE prediction and reported achieving the Pearson correlation coefficients of 0.68 and 0.57.65 In the field such as retrosynthesis66 and chemical reaction prediction,67 the molecular graph performed well, and with the development of the GNN and machine learning in chemistry, this method will contribute more to OPVs.
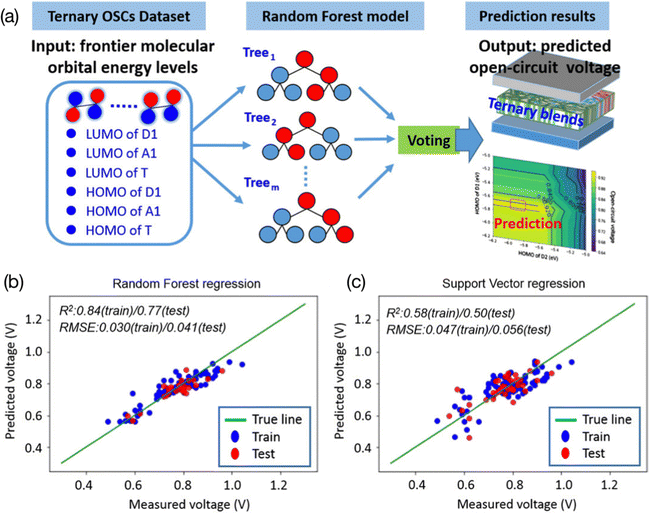 | ||
| Fig. 4 (a) Using the values of the HOMO and LUMO as features in the ternary OPV VOC prediction model. (b) The RF model and (c) SVM model.69 Reproduced from ref. 69 under the terms of the Creative Commons Attribution License from Wiley. | ||
Combining electronic descriptors with visualizing decision tree models, researchers can gain physical insights and experimental guidance from the trained models.51,70 To visualize a decision tree, the model is represented graphically as a tree-like structure. In the tree-like structure, there are four main types of nodes: root nodes, leaf nodes, internal nodes, and branch nodes. To be more specific, input data are located at the root nodes and the predictions are at the leave nodes. Each branch of the tree represents a decision made on the attributes, and the internal node shows the test on the attributes. This tree is constructed by repeatedly splitting the data based on the attributes that provide the most information gain. This process will continue until the stopping criteria are met. Decision tree visualization can help to understand the structure and decisions made using the model and can provide direct insights into the relationships between the input variables and the output predictions. For example, Lee used a ternary OPV machine learning model to verify the correlation between the electronic properties (HOMO and LUMO from donors, acceptors, and third components, respectively) of various materials and their PCE69 (Fig. 5). He employed the feature ranking mechanism of the RF algorithm to rank the contribution of each feature to the VOC and concluded that the donor's LUMO and HOMO had a primary impact on the VOC. Furthermore, he established an RF model for binary classification, with a threshold of 9%. After analyzing the logical flowchart of the classification of the two groups, it was found that the LUMO and HOMO of the donor, as well as the HOMO of the acceptor, were the key values that contributed to the classification model. This result is consistent with previous work in the field, which also identified these features as important for the classification of the two groups.
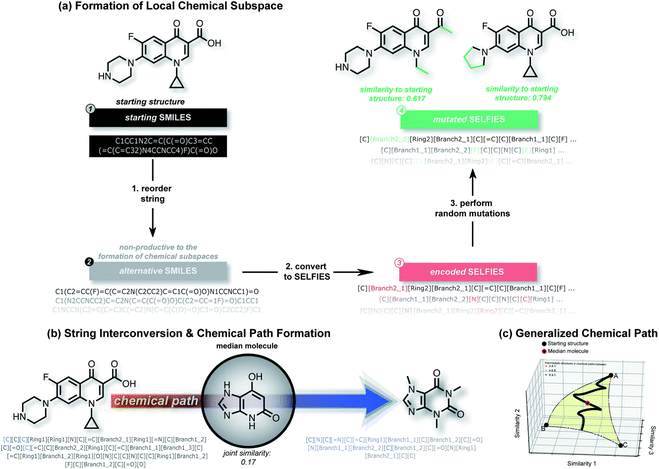 | ||
| Fig. 5 An overview of the STONED. (a) shows how STONED obtains the chemical subspaces. Reordering the SMILES string within the same molecule can generate different orders of SELFIES. Random mutation in SELFIES can yield vast different molecules with similar structures. (b) and (c) demonstrate how to form the path generated by two reference molecules and how to find the median molecule along the path, respectively.71 Reproduced from ref. 71 with permission from the Royal Society of Chemistry. | ||
2.2 De novo materials design
In OPVs, the main goal of using machine learning is to explore new materials. No matter whether chemical structural descriptors or electronic descriptors are used, the applications in which they are used are mostly focused on supervised learning, which requires the manual definition of data labels. However, the supervised learning model can only use the fragmentation methods to generate novel OPV molecules. In this method, researchers adopt a trained supervised learning model to score the manually defined fragments or building blocks from defined fragment combination libraries. Such libraries could be established using either expert knowledge or traversal searching methods.72,73 After identifying the well-performing fragments, researchers usually combine them into novel compounds. A trained prediction model is used to predict the properties of candidates.74 After that, the candidates with the desired properties are selected for further study and experimentation. A typical benefit of this approach is that new compounds are more likely to be synthesizable under real-world conditions. However, based on this method, chemical space is limited by the way of combinations and the types of fragments, which limits the diversity of new molecules. Recently, there has been an increasing number of researchers showing interest in the de novo design of compounds using deep learning methods.75–77 Using de novo design methods, researchers can generate new molecules without any pre-defined building blocks.Nigam et al. proposed a molecular generative neural network model based on the SELFIES description method for inverse molecular design, named superfast traversal, optimization, novelty, exploration and discovery (STONED) and the workflow is shown in Fig. 5. This model enables structure enumeration in chemical space and the discovery of transformation trajectories between any two molecules.71 The researchers utilized the ability of SELFIES to generate multiple structures by adding, deleting and changing random characters while maintaining a rational chemical structure. This allowed them to form local chemical subspaces. They also defined the chemical space path as a finite step change between two molecules to achieve a transformation from one end to the other. They tried to find the median molecule, which is similar to several reference molecules, in the path of the two reference molecules. In the application of the discovery of new OPV molecules, they took three properties (high LUMO energy, high dipole moment and high HOMO–LUMO energy gap) as end molecules and tried to find median molecules among them.
For the de novo design of a molecule, it is important to select the benchmarking task for the design. Currently, most of the insight into which threshold in machine learning to use derives from the researcher's own judgment and experience. A public benchmark is helpful in comparing the performance of different models. Nigam et al. reported a series of benchmarks named TARTARUS for designing molecules including OPV molecules.78 They demonstrated the utility of the TARTARUS benchmarks by evaluating several mature algorithms such as VAEs, long short-term memory hill climbing (LSTM-HC) models, REINVENT, JANUS, and a graph-based genetic algorithm (GB-GA). After the algorithm evaluation, they proposed six benchmarks based on the properties of the HOMO–LUMO gap, LUMO energy, molecular dipole moment and PCE, and put forward more detailed function combinations of these properties. According to these benchmarks, they designed a small organic donor and an acceptor molecule to be used in bulk heterojunction devices with [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) and poly[N-90-heptadecanyl-2,7-carbazolealt-5,5-(40,70-di-2-thienyl-20,10,30-benzothiadiazole), respectively. Although these benchmarks should not be viewed as the final performance judgments of any method used (design issues should be case by case), they can still provide preliminary insights. They also claimed that there is currently no champion algorithm capable of performing tasks on all benchmarks.
To date, de novo molecular design using deep learning still has much room for improvement. More advanced algorithms, broader and more comprehensive datasets, and more sophisticated guidance for design models are worthy of further consideration by researchers. Also, automated synthesis of molecules is currently a hot topic in high-throughput screening.79,80 In the near future, we believe that a series of on-demand designs for automated design and synthesis should take chemistry to the next level.
3. Perovskite
Perovskite was named after the Russian geologist Lev Perovski, and initially, it only referred to CaTiO3.81 Because of the development of a class of compounds with the same structure as CaTiO3 (ABO3), crystal structure compounds with perovskite-like structures can also adopt this first name as a general title. Perovskite is a face-centered cubic structure of the cubic crystal system, and many different cations can be embedded in this structure, allowing the development of a variety of engineered materials.82–84 This material has been successfully used as a photovoltaic adsorber (usually in a form of perovskite halides),85 and has the superiority of a high light absorption coefficient, tunable bandgap, high defect tolerance, and simple synthesis method. In recent years, the power conversion efficiency of perovskite solar cells has reached 36%.86 Owing to the outstanding performance, the perovskite materials have a wide range of applications in a variety of other optoelectronic and energy devices, including (but not limited to) light-emitting diodes,87,88 catalysts,89,90 batteries,91,92 photodetectors, etc.93,943.1 Features and descriptors
There are a lot of features that can be derived from the perovskite structure.95 In the perovskite structure, the topology of the crystal lattice constrains the positions of the atoms such that the relative positions of the A, B, and O atoms or ions are fixed. This means that when determining the available perovskite structure, researchers can mainly focus on the matching of the dimensions of the A, B, and O atoms. To evaluate the tolerance of ion size mismatch in perovskites when forming different structure types, Goldschmidt introduced a tolerance parameter t calculated from the A, B, O ionic radii ratio, which has been widely applied to study different structures of perovskite.96 Besides, the octahedral-factor pair μ is also from the basic perovskite structure calculated from the ratio between the ionic radii of anions and cations.97 With the development of structure research and more datasets for perovskites, the tolerate factors have improved. Bartel et al. proposed a new tolerance factor that can be applied to 576 types of materials, achieving a 92% accuracy in classifying whether the materials are perovskites or not.98 Lu et al. enhanced the tolerate factor and octahedral factor, which can cover almost all geometric elements of structural formability.99 Generally, these two descriptors are widely used not only in computation but also in experiments and their revised version is successfully employed in perovskite machine learning.100,101There are other common descriptors besides the structural features that can be used to represent perovskites, such as atomic, element level properties and macroscopic measurement properties. After considering the A-sites and B-sites, a huge number of microscopic descriptors can be extracted from the atom, such as atom mass, radius, electron affinity, Pauling electronegativity, etc. Similarly, macroscopic properties such as density and volume, and space groups can also be included in the feature input. Li et al. built a perovskite bandgap energy prediction model, which uses five structure relative factors (such as the tolerance factor) and an initial atomic feature set with 77 atomic physical, chemical and spatial properties.102 Isayev et al. proposed a concept of property-labeled material fragments (PLMFs), which combined the geometry structure with atom/element properties, including the multiplication and ratio of general element/atomic values, measured values and derived properties.102 Generally, it is possible to use different combinations of descriptors to create new descriptors using expert knowledge. Additionally, a data-driven method such as sure independence screening and sparsifying operator (SISSO) can also be used in exploring new descriptors. To be more specific, SISSO is a math model that is based on the LASSO approach. With the input of physical quantities, it could perform linear combination (unary or binary operators), which can select the best descriptor from a large space of parsed expressions (potential features).103,104 Many examples show that this method can produce numerous novel descriptors.105 Usually, using SISSO is accompanied by feature engineering (such as generating several potential descriptors and selecting the most suitable one). For example, Xie et al. used the SISSO with atomic radius, valence, electronegativity, permittivity, and nine operators to yield over 182 million descriptors (equations).106 Finally, after cross-validation, they selected the best features and successfully adopted them in octahedral tilting prediction with 81.7% accuracy. Notably, it is not a fact that the prediction result is better with more combinations of material properties. It is a problem that requires a tailored approach to feature selection. Xu et al. showcased that for predicting the properties of ferroelectric perovskites, the traditional machine learning workflow can perform better than the SISSO based method in specific surface area, bandgap, Curie temperature prediction.107 Therefore, in the choice of material electronic descriptors, multiple explorations can be used to find the optimal solution.
With the development of deep learning, a number of descriptors have been integrated to fit the DL input, which brings a new development in this area.108,109 Chen et al. proposed a novel neural network materials graph network (MEGNet) and represented a series of crystal perovskite structures as graphic structures.110 To be more specific, as shown in Fig. 6, they followed the GNN normal representation and defined the V, E, and U as atomic (node/vertex), bond (edge), and global state attributes, respectively. The original graph structure information is first updated from the original bond states to the new bond states. Subsequently, the atomic states are updated based on the previous state and bond states. Finally, a new graph structure is generated after using the previous global states. The previous steps are repeated in a cycles until the final result is achieved. 11 of the 13 properties predicted in MAE were under the generally accepted thresholds of chemical accuracy and better than the previous work using the QM9 database. This method also extends to predict the synthesizability and bandgap of perovskites.111,112
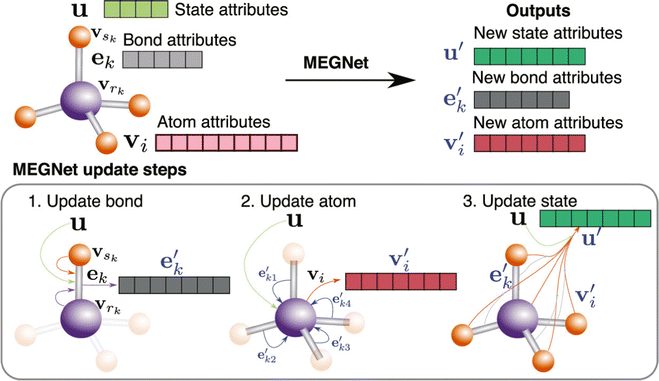 | ||
| Fig. 6 Overview of a MEGNet module, this figure shows how a graph represents a molecule in the MEGNet. The node attributes fall into three categories: bond, atom, and state. This figure also shows the updating steps in the MEGNet.110 Reprinted (adapted) with permission from ref. 110. Copyright 2019 American Chemical Society. | ||
Besides, automatic unsupervised learning methods can extract hidden information from the original input in the field of perovskites, leading to the formation of non-manual defined descriptors.113 From an encoding–decoding model such as variational autoencoders (VAE), original features are embedded into a series of compressed latent vectors, which can capture more in-depth features. Using the features extracted only from its chemical formula in the VAE model, Ihalage et al. defined the mean vector generated from VAE (μ) as the perovskite material fingerprint (Fig. 7).114 Furthermore, they verified this new fingerprint with the k-nearest neighbor method and found that in the fingerprint space, similar materials are located close to each other. 5-Nearest neighbors (5-NNs) can determine the correct experimental crystal system of the parent composition with a success rate of 71.8%. Furthermore, non-manual defined descriptors can be used to de novo design the perovskite. Based on the generative adversarial network (GAN) and transformer models in machine learning, Dan et al. and Wei et al. proposed material design models named MatGAN and crystal transformer.115,116 Wei et al. compared these two models and found that the transformer-based model is more suitable for exploration in known chemical spaces due to its ability to capture element interrelationships, whereas the GAN-based model is more appropriate for discovering new molecules in uncharted chemical spaces.
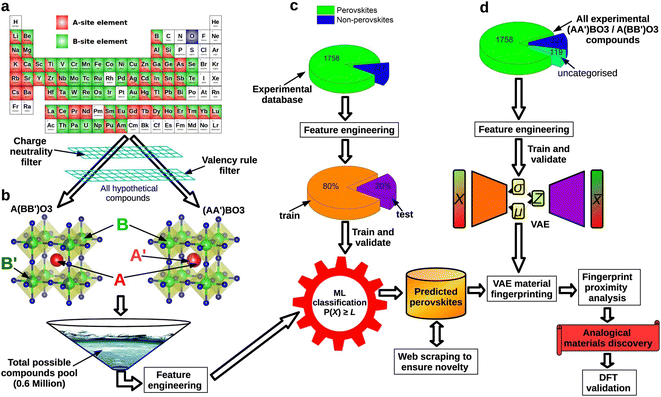 | ||
| Fig. 7 An overview of using VAE to make perovskite material fingerprints. (a and b) In the part of descriptor creation section, they explored the periodic table for elements that may fully or partially fill octahedral and interstitial positions and specified the following conditions: (1) in the generation, the average oxidation of site A should not be larger than that of site B; and (2) the average ionic radius of the A site should be more than or equal to the average ionic radius of the B site. (c and d) In the model training section, they trained the VAE model on over 2000 unlabeled experimental data sets. Calculation of Euclidean distances in fingerprint space between experimental components and potential perovskites.114 Reproduced from ref. 114 under the terms of the Creative Commons CC BY license. | ||
3.2 Types of perovskite prediction tasks
Despite the rapid development of perovskites in recent years, there are still several challenges that restrain perovskite industrialization.117,118 The first challenge is the requirement of potential new materials. Although lead-based halide perovskites currently have the highest PCE, their decomposition can lead to significant environmental concerns. However, non-lead halide perovskites have not been able to surpass lead-based perovskites in terms of efficiency currently, making it necessary to predict the PCE of materials using computational methods. Additionally, in experimental processes, it is common to judge whether a structure belongs to a perovskite structure or not, and find out how its physical properties (e.g., lattice constant, bandgap, lattice constant, etc.) can be regulated. These processes are time-consuming and need a series of experiments. Besides, some kinds of perovskites decompose rapidly in the presence of water vapor, light, increased heat, etc., which deviate from laboratory conditions. Machine learning can play a crucial role in addressing these challenges. Using the trained prediction models, researchers can make rapid and accurate analyses of perovskite structures and physical properties.Predicting the basic physical information of perovskites can be of great help in the exploration of new materials, the mapping of experimental parameters and the understanding of structure–function relationships. Many models have been developed to predict the physical properties of perovskites such as bandgaps,109,119 oxide ionic conductivity,120 thermodynamic stability,121,122 dielectric breakdown strength,123,124 lattice parameters,125 crystal structures.126 For example, Zhang et al. established a model to predict lattice constants based on cubic perovskites.127,128 Besides, Li et al. predicted formation energy, thermodynamic stability, crystal volume and oxygen vacancy formation energy using a variety of machine learning models.129 Saidi et al. constructed a convolutional neural (CNN) model for deriving relevant physical properties (e.g., lattice constants, octahedral tilt angles, etc.) from the given perovskite material.130 Compared to the first-principle methods such as density functional theory (DFT), these kinds of machine learning models can be used for low-cost large-scale screening of physical properties in perovskite materials.
A significant concern in perovskite research is the exploration of identifying potential perovskite structure types. This includes determining which elements can form perovskites and understanding the different structural and compositional variations that are possible within the perovskite structure.131,132 Many models are successfully established in different kinds of perovskites.133–135 Taking the electrical and geometrical factors into account, machine learning models established by Li et al. were used to predict the formation of perovskite structures and showcased 96.55% and 91.83% accuracy in the single and double perovskite databases.136 Combining first-principles calculations and machine learning, Talapatra et al. proposed to use energy above full = 50 meV as a threshold criterion for database stability and non-stability for perovskite screening.137 Based on 68 elements from the periodic table, they built a virtual database of 437![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828 stable perovskite structures. Based on SHAP analysis, Zhang et al. proposed that the formation of hybrid organic–inorganic perovskite (HOIP) structures is more likely to occur when the A site radius falls within the range of 1.95–3.25 Å and the B site radius falls within the range of 0.60–1.20 Å138 Besides, machine learning can also be adopted in identifying the perovskite structure in experimental characterization. Massuyeau et al. built RF/CNN models capable of identifying XRD peaks using XRD diffraction patterns as the training set, which can directly distinguish between perovskite and non-perovskite materials.139 All of these works provide good paradigms for identifying perovskites.
828 stable perovskite structures. Based on SHAP analysis, Zhang et al. proposed that the formation of hybrid organic–inorganic perovskite (HOIP) structures is more likely to occur when the A site radius falls within the range of 1.95–3.25 Å and the B site radius falls within the range of 0.60–1.20 Å138 Besides, machine learning can also be adopted in identifying the perovskite structure in experimental characterization. Massuyeau et al. built RF/CNN models capable of identifying XRD peaks using XRD diffraction patterns as the training set, which can directly distinguish between perovskite and non-perovskite materials.139 All of these works provide good paradigms for identifying perovskites.
Searching for the stability and high PCE lead-free halide perovskites140 is also an important downstream task of perovskite machine learning application. Using the property density distribution function (PDDF), Stanley et al. constructed features and applied them to predict the bandgap, formation energy, and convex hull distance of lead-free halide perovskites.141 Besides, machine learning can also be used in the design of new types of lead-free halide perovskites. Lu et al. reported a HOIP prediction model trained from 212 reported bandgap values.142 Using a combination of DFT optimization and machine learning prediction, they determined the range of tolerance factors, octahedral factors, metal electronegativity, and polarizability of potentially promising HOIP organic molecules and selected 3 thermal and environmental stable lead-free HOIPs with appropriate bandgaps from 5158 candidates. In addition, there have been research efforts that combine machine learning and DFT,143 for discovering lead-free hybrid perovskite,144 two-dimensional lead-free perovskite145 and others.118,146 These works provide a solid foundation for discovering more efficient and stable lead-free halide perovskites.
One of the major challenges that remains to be addressed in perovskite applications is the stability of devices. The stability of the perovskite devices falls short of mainstream silicon devices. Odabas et al. analyzed the hysteresis and reproducibility of perovskite solar cells and proposed materials and alternatives for perovskite deposition with low hysteresis and high reproducibility.147 In materials, in addition to thermodynamic stability, another more important aspect to consider is mechanical stability (or mechanical strength). Jaafreh et al. investigated the mechanical strength of perovskite-based materials using the AdaBoost algorithm with the volume and shear quantities of the elastic modulus and its scaling criterion (satisfying G/B smaller than 0.57 for ductility at room temperature (RT)). Based on the model, they identified about 770 perovskites with mechanical strength.148 Howard et al. proposed a reap-rest-recovery (3R) cycle machine learning framework to avoid permanent failure of perovskites due to exposure to water vapor and oxidation.149 Due to the complexity of factors such as device stability, more effective models with interpretability still need to be developed for evaluation to help find a suitable device.150
Compared with using virtual datasets, using real-world datasets is considered a more appropriate approach for predicting the properties of perovskite materials. However, one of the obstacles of this method is the time-consuming and labor-intensive process of manually collecting and cleaning large datasets from thousands of perovskite-relevant articles. Thanks to the development of natural language processing (NLP), much of the chemical text and information extraction toolkits are proposed such as ChemDataExtractor, OSCAR4, ChemicalTagger and others.151–154 Thus, it is possible to do text mining and build relatively large real-world datasets for perovskite prediction.155,156 Beard et al.157 adopted the ChemDataExtractor to build two datasets from 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 articles regarding dye-sensitized solar cells (DSCs) and perovskite solar cells (PSCs).157 Furthermore, using an automatic collection dataset can directly train the machine learning model. Kim et al. proposed a linguistic model-based approach for linking the scientific literature to material synthesis insights and successfully performed perovskite synthesizability screening (prediction of two precursors).158 Although there are few examples in the area of text-mining, it is likely that in the future the text-mining method will play an important role in building perovskite datasets as the amount of scientific literature data continues to grow.
720 articles regarding dye-sensitized solar cells (DSCs) and perovskite solar cells (PSCs).157 Furthermore, using an automatic collection dataset can directly train the machine learning model. Kim et al. proposed a linguistic model-based approach for linking the scientific literature to material synthesis insights and successfully performed perovskite synthesizability screening (prediction of two precursors).158 Although there are few examples in the area of text-mining, it is likely that in the future the text-mining method will play an important role in building perovskite datasets as the amount of scientific literature data continues to grow.
3.3 Experimental conditions and acceleration
In many cases, machine learning is often used as a powerful tool for experiment-free exploration in perovskite research. Although decision trees and SHAP's interpretable mechanisms can provide an intuitive understanding of how a model arrived at its predictions, it is not always clear if the underlying assumptions of the model are valid or if they accurately represent real physical processes. One explanation is that the experimental environment is usually more complex than the features input in the machine learning models.7,159 Additionally, data from different articles may be collected under different conditions, using different measurement techniques, or with different levels of measurement accuracy, making it difficult to compare and use in a machine learning model. It is important to validate the accuracy of machine learning models by combining the results of machine learning calculations with experimental work.160 This approach helps to ensure that the predictions made by the models are accurate and reliable. By using machine learning as a tool, it is also possible to accelerate perovskite discovery experiments in real-world conditions (usually with high throughput experiments)161,162 (Fig. 8). All of these works are considered as accelerating the speed of the experiments.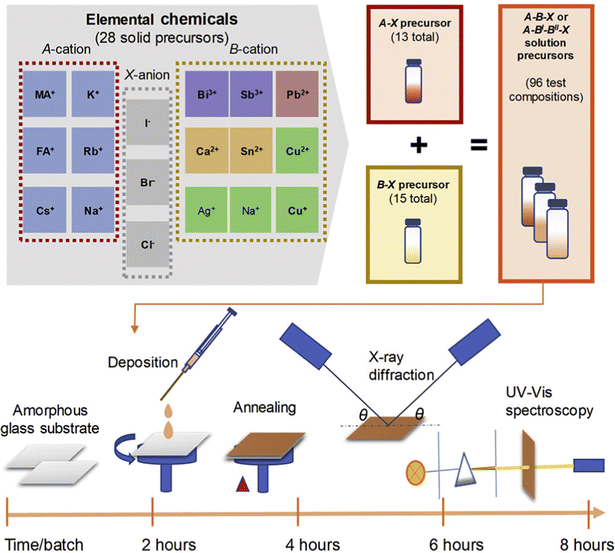 | ||
| Fig. 8 High throughput experiments conducted by Sun et al. Precursor solutions were prepared and a high throughput experimental cycle was designed. Three experiments and characterization were carried out to examine the structural and optical properties according to thin film deposition, X-ray diffraction and UV-visible spectroscopy.161 Reprinted (adapted) with permission from ref. 161. Copyright 2019 Elsevier. | ||
To be more specific, the accelerated experiments assisted by machine learning can be divided into two parts, to explore the experimental condition and realize verification.163 In the aspect of materials or experimental reagent selection, there are a lot of studies that have been reported. Yu et al. used machine learning to study the reactivity trends of different types of amines and suggested five property recommendations of amines for post-treatment of MAPbI3.164 By developing the capping layer, Hartono et al. used RF regression and SHAP values to find the features having the largest contribution to stability, and found that the most important properties for prolonging the onset of degradation were a low number of hydrogen bond donors and a small topological polar surface area.165 Furthermore, based on their model, they proposed and experimentally validated phenyltriethylammonium iodide (PTEAI) as the best capping layer material. They found that the stability lifetime of MAPbI3 was 4 ± 2 over bare MAPbI3 and 1.3 ± 0.3 over octylammonium bromide (OABr), which is SOTA at that time. They also gave a corresponding explanation based on XPS and FTIR results that the capping layer on top stabilizes MAPbI3 by changing the surface structure and chemistry, which match the previous experiment regulations.166,167 Besides, by machine learning and experimental verification, Cai et al. confirmed the ratio of Sn: Pb in MASnxPb1-xI3 holding an Sn–Pb alloy within the perovskite crystal.168
In exploring the device stability condition part, Hu et al. investigated the factors affecting the stability of perovskite solar cell devices through a combination of experiments and machine learning.169 Five factors affecting the efficiency and stability (grain size, defect density, bandgap, fluorescence lifetime and surface roughness) were selected using machine learning models and proposed that roughness and crystal size have a strong influence on long-term stability. Subsequently, based on a self-built PCE model, they designed different conditions to vary the surface roughness to achieve the best stability of perovskite devices at 25% humidity and 25 degrees Celsius.
Machine learning-assisted high throughput experiments for automated synthesis have an important role in replacing manual synthesis and a large-scale exploration of perovskites.170–172 More specifically, human-based operations are replaced with fully automated robotic working and the process is iterative between automated experiments and machine learning-based experiment planning. This method can speed up the experiment considerably compared to human labor. For example, Li et al. reported a high-throughput robotic perovskite synthesis system that takes 20-fold less time than manual synthesis.173 Bayesian optimization is the most commonly used algorithm, which performed well in low-dimensional parameter space.174,175 As shown in Fig. 9, MacLeod et al. developed an 8-step thin film modular robotic platform called ‘Adad’, which automatically synthesizes, processes, and characterizes thin-film samples. Using ChemOS in the previous work, a Bayesian optimization algorithm was applied to design the next sample for the experiment after the characterization.176,177 Besides, Higgins et al. used a pipetting robot to build a perovskite combinatorial library and used Gaussian regression (a form of Bayesian optimization) to analyze the physical properties of the constituent series.178 However, compared to the integrated pervasive API interface of machine learning, machine learning-assisted high-throughput experiments still require the development of a pervasive experimental system and software in the future.
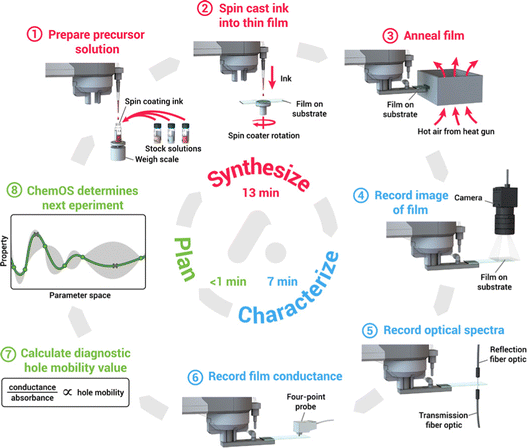 | ||
| Fig. 9 8-Step auto-platform combining synthesis, characterization, software machine learning calculation into a self-driving workflow to make thin film samples, this work reported by Macleod et al.176 Reproduced from ref. 176 under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC). | ||
4. Machine learning in catalytic reactions
Catalysis is important in energy storage systems.179,180 Catalytic reactions are complex due to multi-phase involved surfaces/interfaces, mass transfer effects, and various geometric/electronic structures of catalysts.181–187 Traditional methods for designing catalysts mainly focus on synthesis and computational-assisted design, hoping to understand the mechanisms and derive empirical rules for catalytic properties. However, it is greatly limited by the quality of experiments and the precision of calculations. Machine learning helps researchers to have a better understanding of the structure–property relationships and accelerate the discovery of new catalysts.4.1 Optimizing potentials
Machine learning is a powerful tool for optimizing interatomic potentials. Traditionally, a lot of physics-based potentials have been applied to Monte Carlo simulations and molecular dynamics (MD) simulations.188–191 However, the accuracy of these potentials cannot be guaranteed and is hard to improve. First-principles simulation can provide enough accuracy, but it is limited by the cost of calculations. It is impossible to run enough first-principles calculations for different types of potentials. With the development of machine learning, it becomes possible to train models with a practical number of first-principle calculations and obtain accurate atomistic potentials. This routine would accelerate MC/MD calculations and allow for long time scale simulations.192,193By using machine learning methods, machine learning potentials are obtained by fitting energy and force from DFT calculations. A classical method was proposed by Behler and Parrinello in 2007.194 Similar to empirical potentials, the total energy E could be expressed as a sum of atomic contributions Ei, an approach that is typically also used in empirical potentials.
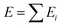 | (1) |
Another important method to calculate PESs was proposed by Bartok et al.,196 in which a kernal-based descriptor was applied. In this research, they started with forming a local atomic density related to neighbor atoms, and converted the PES to an interpolation of the atomic energy in the truncated bispectrum space. By using Gaussian process (GP) regression, they realized a good approximation to the atomic energy function. Then with different sparse configurations, they proposed a final expression called the Gaussian approximation potential (GAP) model. This model also performs well in bulk crystals at high temperature. As a typical method, it has been applied to develop smooth overlap of atomic positions (SOAPs).197 This proves that some widely used descriptors could be concluded using a general approach, where they applied a finite set of basis functions to expand the atomic neighborhood density function. To make a best estimate of atomic energy function, it assumes a Gaussian basis function as below:
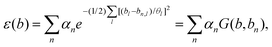 | (2) |
Thompson et al.198 proposed a new interatomic potential for solids and liquids, which is called spectral neighbor analysis potential (SNAP). Different from the GAP model proposed by Bartok,196 researchers proposed the bispectrum as its descriptor and assumed a linear relationship between atom energy and bispectrum components. In SNAP, the coefficients are determined by the weighted least-squares linear regression, which allows the model to fit a full set of quantum mechanics calculations. Also, the symmetry properties are applied to reduce the computational cost.
By utilizing graph convolutional neural networks (GCNNs), Schutt et al.199 developed a deep learning architecture SchNet to model atomic systems. By using continuous-filter convolutional layers, SchNet is able to predict the potential-energy surfaces and energy-conserving force fields of small molecules, which could be utilized in MD simulations. Also, GCNN has been applied to overcome the limitations of traditional methods, which do not consider the spatial information. Gasteiger et al.200 constructed a directional message passing neural network (DimeNet) that embeds the messages passed between atoms by considering directional information.
A deep learning method is promising in promoting the efficiency of calculating many-body potential energy. Zhang et al.201 designed a DeePMD-kit to build potential energy and force fields by using deep learning methods. The model used a function containing coordinates and elemental types as descriptors. By training the data from the AIMD to DeePMD model, the MD stimulations can accurately replicate the results of the original AIMD data. The DeePMD-kit is written with Python/C++ and interfaced with TensorFlow, which improves the training efficiency and user-friendly.
Also, a lot of software packages have been used to build deep learning potential energy surfaces. The promotion and application of machine learning models greatly benefits the development of atomistic potentials, as we listed several typical packages in below: 1. LASP:202 learning-based atomistic simulation package (LASP) is a software platform that merges the stochastic surface walking (SSW) method and global neural network (G-NN) potential for exploring and evaluating the PES. LASP provides various simulation techniques for PES data building, exchange, and G-NN potential generation within a single platform. 2. AMP:203 the atomistic machine-learning package (AMP) is a software package for building and using machine learning models for atomistic simulations. It is designed to handle large-scale simulations and includes features for parallelization and incorporating diverse training data. 3. SchNetPack:204,205 SchNetPack is an open-source software package for building neural network potentials for molecular and material simulations. It includes a variety of NN architectures, as well as tools for generating and analyzing training data. 4. MLIP:206–208 the machine learning interatomic potentials (MLIP) software package is a Python library for building interatomic potentials using machine learning models. It includes a variety of machine learning algorithms, as well as tools for generating and analyzing training data.
In conclusion, machine learning has been widely applied to find the PESs and atomic forces. With the development of machine learning algorithms, different descriptors and regression methods have been applied, leading to great progress. Compared with ab initio calculations, adopting machine learning could largely reduce the computational cost and maintain acceptable accuracy. It is promising to apply machine learning methods in MD/MC calculations.
4.2 Predicting catalytic ability
A lot of models and descriptors have been proposed to describe the catalytic activity. Among them, the d-band center theory is a classical descriptor for describing the relationship between the adsorption intensity and the energy of d-band center, which leads to different catalytic activities.209 However, calculating the d-band center of metals by applying the first-principles methods consumes a lot of CPU time. So it is convenient to predict d-band centers by using machine learning tools. Takigawa et al.210 compared with different regression models and applied the gradient boosting regression (GBR) method with six descriptors to predict the d-band center of 11 metals and their pairwise alloys. The result shows a reasonably accurate d-band center energy with an average root mean square error (RMSE) <0.5 eV.Adsorption decides the interaction intensity between active intermediates and the catalyst, and overpotential determines the behavior when assembling catalysts in batteries. Lian et al.211 investigated single-atom catalysts (SACs) for lithium–sulfur (Li-S) batteries. At first, researchers classified the adsorption process by the presence or absence of S–S bond breaking. Then, crystal graph convolutional neural network (CGCNN) was applied to complete the classification and regression.212 By obtaining 812 adsorption configurations on 203 SAC catalysts, researchers categorized them into 4 categories and excluded unstable catalytic configurations. After training the machine learning model, its prediction has a mean absolute error of 0.14 eV (Fig. 10a). As shown in Fig. 10b, for different elements, researchers calculated two elementary steps and plotted their free energy as ΔG1 and ΔG2. These two elementary steps were identified as potential limiting steps depending on the LiS* adsorption energy, which shows a volcano plot as shown in Fig. 10c. And by calculating the overpotential for different metal sites and supporter composites (Fig. 10d), researchers concluded that higher overpotential would lead to a limited catalytic activity. Based on the volcano plot and overpotential results, it could be applied to optimize the synthesis of SACs and predict catalytic activities.
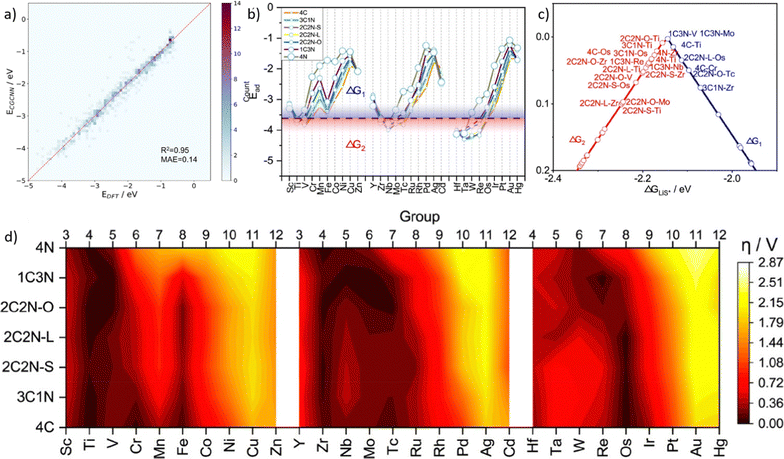 | ||
| Fig. 10 Taken from Fig. 3 and 4 in Lian et al.211 (a) DFT calculated and machine learning predicted adsorption energy of Li-polysulfides, (b) predicted adsorption energy of LiS*, (c) volcano plots for catalysts with an overpotential lower than 0.1 V, and (d) heat map of the predicted overpotential of different SACs. Reproduced with permission.211 Reprinted (adapted) with permission from ref. 211. Copyright 2021 American Chemical Society. | ||
The oxygen reduction reaction (ORR) and oxygen evolution reaction (OER) are key reactions for fuel cell and metal–air batteries.213–216 The ORR/OER are limited by 4 electron transfer and sluggish kinetics, so it is important to design efficient electrocatalysts for these two reactions. In recent years, SACs have been widely applied in the ORR/OER, and achieved high activities.217–219 And this has led to increased interest in investigating the key factors for these reactions, which could assist in understanding the mechanism. Ying et al.220 found a volcano-shaped relationship between the catalytic activity and ΔGO, and applied machine learning model based on the RF algorithm. With consideration of the scaling relationship and the feature importance, it determined the outer electron number and oxide formation enthalpy as the two most important factors. And the machine learning model could give an accurate prediction of ΔGO efficiently.
Furthermore, SACs still have some limitations, like compatible low stability and simple adsorption configurations. So researchers further introduced dual-metal-site catalysts (DMSCs),221,222 which could both enhance the activity and optimize surface adsorption. The increase in metal sites also increases the difficulty of investigating specific factors that contribute to reaction activity. So machine learning methods have been applied here to reveal the order of important factors,223 which benefits the optimization of catalysis design.224,225
Zhu et al.226 conducted DFT calculations to calculate the adsorption free energy and screen high ORR activity DMSCs as the flowchart shown in Fig. 11a. By training models based on the GBR algorithm,227 it showed a low RMSE of 0.036 eV. And mean impact value (MIV) has been applied here as an indicator to assess the importance of features. With this tool, researchers proposed 7 features that were mostly related to the catalytic activity of DMSCs, and determined that the electron affinity of metal atoms is the most important feature for the activity of DMSCs. This result provides a valuable insight for synthesizing DMSCs.
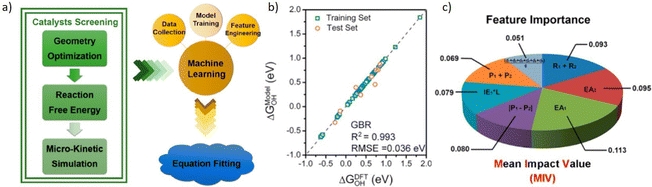 | ||
| Fig. 11 Taken from Fig. 4 by Zhu et al.226 (a) Schemetic plot of screening high efficient DMSCs from DFT calculation and trained with the machine learning model, (b) training results of ΔGOH, (c) feature importance based on the MIV. Reproduced with permission.226 Reprinted (adapted) with permission from ref. 226. Copyright 2019 American Chemical Society. | ||
5. Machine learning in batteries
Since the first commercial product came out in 1991, Li-ion batteries have been developed for over 30 years. As some of the most promising energy storage devices, they have wide applications in vehicles, electronic devices, and aerospace.228–230 The focus of development of Li-ion batteries is on the energy density, lifetime, and safety. To solve the bottlenecks in practical applications, it is important to design and optimize different parts of batteries. Currently, Li-ion batteries are suffering from low coulombic efficiency, poor electrode stability, and formation of dendrites.231–235 Researchers put a lot of effort into developing electrodes, electrolytes, and battery management systems to avoid these issues.A lot of effort has been made in finding new chemistry in battery electrodes, and electrolytes. However, each material has different electrochemical properties, and it is hard to optimize directly. With the development of machine learning, it becomes a powerful tool in dealing with complex factors and provides relationships between structure and their functions. Machine learning assists the design of batteries and boosts the discovery of energy storage materials.
5.1 Predicting electrode materials
For Li-ion batteries, electrode materials play a crucial part in determining voltage, capacity, Li storage ability, and stability of the structure and cycling.236–240 It is important to predict these properties based on the intrinsic properties of electrode materials. And finding a clear structure–function relationship would benefit researchers to gain insights into the behavior of electrode materials.241,242 Many machine learning models have been used to predict the properties of battery electrode materials. Joshi et al.243 applied DNN, SVM, and kernel ridge regression (KRR) as algorithms. Then, the model was trained with data taken from the Materials Project database,244,245 and a voltage profile of electrodes was obtained. By applying a total of 4250 data instances for 3580 intercalation-based electrode materials, researchers extended their predictions to different metal-ions (Li, Mg, Ca, Al, Zn, and Y) batteries. Their results showed a good fit for predicting the voltage of current electrode materials. The machine learning model is also able to investigate new electrode materials by replacing Li with other metals. The result shows a similar trend compared with experimental results.246Besides the voltage of electrode materials, the Li-ion conductivity is also a significant factor that decides the performance of batteries. For different electrode materials, the conductivity can differ in tens of magnitude,247,248 so how to develop high Li-ion conductivity materials is of great importance. Sendek et al.249 discovered a lot of crystalline solid materials through density functional theory simulations guided by machine learning-based methods. In this research, researchers compared the machine learning guided method with random search of material space, and received at least a 44 times improvement in the log-average of room temperature Li ion conductivity. It is also evaluated from the F1 score, which is 3.5 times better than completely random guesswork and much better than human brains. The screening result shows that most of the high conductivity materials are found by applying the machine learning guided search, which proves its superiority over the traditional guess and test method.
With the development of the Materials Project database, there are a lot of material data that could be utilized for training a machine learning model. However, the quality of models is greatly limited by the quality and quantity of data, and for each material, not all properties are well prepared. So developing an unsupervised learning method is valuable, as it could avoid labeling data and requires less data points. Zhang et al.250 proposed an unsupervised learning model to find materials for solid-state Li-ion conductors. As is shown in Fig. 12a, researchers applied an agglomerative hierarchical clustering method to train a mXRD dataset, and it shows similar characteristics with the real mXRD pattern (Fig. 12b and d), which means a good quality of classification. Then this model was used to find solid-state Li-ion conductors (SSLCs) with high Li-ionic conductivities and group them accordingly. (Fig. 12c). To confirm the superiority of the unsupervised learning, they conducted AIMD simulations, and the result shows that the model discovered 16 new fast Li-conductors with conductivities of 10−4 to 10−1 S cm−1.
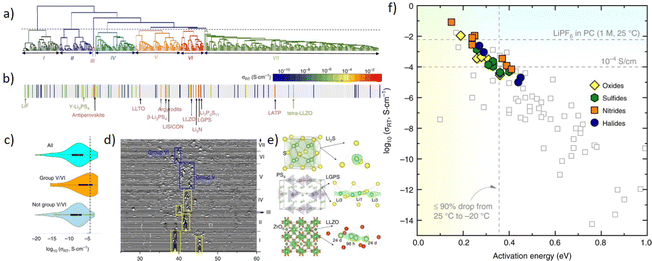 | ||
| Fig. 12 Plots remade from Fig. 2 and 3 by Zhang et al.250 (a) the tree diagram of the agglomerative hierarchical clustering method, (b) the dendrogram to the conductivity reveals grouping of known solid-state Li-ion conductors, (c) violin plots of σRT data grouped in the grouping, (d) mXRD of materials, (e) crystal structures (left) and (right) Li sites (green sphere) determined by local anion (yellow/red sphere) configurations, and (f) σRTvs. activation energy, ion conducting properties of newly predicted shown as filled symbols. Reprinted (adapted) with permission from ref. 250. Copyright 2019 Springer Nature. | ||
Previous works mainly focused on finding new compounds as electrode materials. Except for screening and designing electrode materials using components, optimizing heterogeneous electrode microstructures is also a powerful tool in designing batteries.251 Starting from microstructures could unveil the relationship between structures and functions clearly. With the help of machine learning, complex structures could be designed. The reconstruction routine consists of two major strategies, statistical sampling and optimization. A common method is to sample descriptors of different microstructures, and follow up with minimizing the difference between reconstructed structure and real structure. Based on this method, different modeling methods could be applied to build 3D electrode models, like physics-inspired Monte Carlo method and hierarchical reconstruction.252,253
5.2 Designing electrolytes
Electrolytes play an important role in Li-ion battery systems, like forming the solid electrolyte interphase (SEI) layer, conducting Li+, and the compatibility of electrodes.254–257 A lot of investigations have been made to find new chemistry of electrode materials and reactions, but the research on electrolytes is less. A typical commercial electrolyte is LiPF6 and organic carbonate solvents, as it is easy to operate and cheap.258,259 Plus, with the existence of electrolyte additives, it could stabilize the electrolyte skeleton and improve the formation of the SEI. So the design of electrolytes is focused on lifting the ionic conductivity, safety and stability.Machine learning is a strong tool for large scale screening materials and their properties. Jalem et al.260 proposed a NN method for screening potential solid state electrolyte (SSE) materials. In the research, researchers utilized NN and searched in the LiMXO4 group. The screening was mainly focused on two properties, the Li diffusion barrier and the cohesive energy. These two properties are important for Li-ion conductivity and bonding information. Researchers revealed the relationship between diffusion barrier, the cohesive energy and their structure descriptors in the materials space. Compared with traditional partial least squares, the application of multi-output node architecture could increase the accuracy of prediction.
Also, to realize the finding of new chemistry, the structure–function relationship needs to be investigated carefully. Kireeva et al.261 applied the support vector regression to investigate the composition–structure–Li ionic conductivity relationships. It could be utilized to define parameters that lead to high Li-ion conductivity, and search in a large material space, which could provide potential materials as SSE.
As shown in Fig. 13a, the model predicts the conductivity well with the experimental result. The accurate result could provide a significant insight into the co-doping effect, which is not completely issued by DFT calculation. Generally, the doping of different cations shows the same trend without outlier-by-prediction. Fig. 13b provides a model with an additional descriptor pool. It reveals the impact of different parameters on the property space.
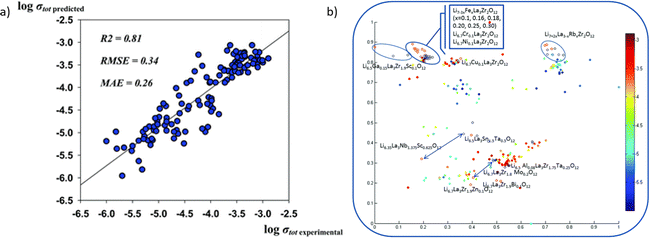 | ||
| Fig. 13 (a) The prediction accuracy of Li conductivity by machine learning models and (b) the conductivity results categorized using different synthesis methods, and adapt t-stochastic triplet embedding, where experimental results are served as an extra descriptor pool. Reproduced from ref. 261 with permission from the PCCP Owner Societies. | ||
Besides, machine learning could also be applied to predict mechanical properties like the growth of dendrites. Dendrite formation is a serious problem that affects the safety of batteries.262,263 Using solid electrolytes is a promising method to deduce dendrites, which could suppress the formation of dendrites greatly. Ahmad et al.264 calculated properties of mechanically isotropic and anisotropic interfaces as the criteria of dendrite initiation. Then a GCNN was trained on the shear and bulk moduli, and gradient boosting regressor and kernel ridge regression were used to train the elastic constants. With these machine learning methods, 20 mechanically anisotropic interfaces could be predicted between Li metal and four solid electrolytes as the candidate materials.
SSEs are also promising for addressing the flammability concerns, which requires to form a high quality SSE layer. To evaluate the quality of SSE films, both conductivity and uniformity are considered. Chen et al.265 proposed a high-quality SSE film synthesis method guided by machine learning. In this research, researchers adopted three algorithms (principal component analysis, K-means clustering, and support vector machine) to analyze the relationship between fabricating parameters and film quality. Principal component analysis has been used to determine the manufacturing conditions and converts it to a low dimensional subspace. Then K-means algorithm is applied to classify different films and defines its performance. Finally, a support vector machine unveils the effect of fabricating parameters on the quality of films. When assembling the whole cell, the SSE film shows a good stability, proving this method to be useful. The machine learning-assisted method successfully optimized the production of SSE films.
In conclusion, machine learning boosts the design of electrolytes and screening materials with superior physical properties. Compared with traditional first-principle methods, machine learning methods are able to consider more factors that determine the behavior of electrolytes and directly guide fabrication process in batteries.
5.3 Optimizing battery management
When fabricating commercial products, strict process control and optimization of parameters are important.266,267 Among all these parameters, how to maximize the lifetime of batteries and monitor the health condition has been considered as an important topic.267 Traditionally, lifetime testing of batteries needs long term experiments that may last for months.268 And with a variety of charge/discharge conditions for batteries, it is hard to predict a certain health condition directly. These issues bring trouble for sampling batteries and hinder the selection of representative data. Since machine learning is powerful in data learning and predicting, it is promising to develop advanced algorithms to optimize parameters in batteries and monitoring lifecycles.269To estimate the state of charge and health, it is significant to build efficient models to describe battery management systems. A main battery model that applies in battery systems is equivalent circuit models (ECMs),270,271 which simplifies complex systems to circuits and fits models. For further advancement, physics-based models (PBMs) are being developed for battery systems,272 which can take into account multi-dimensional information, like real time scale analysis, and battery dynamic parameters.273,274 These models are always limited by their complexity and require a large computational source to solve them. With the development of machine learning, a lot of methods and algorithms have been applied to simulate battery systems, including multiple regressions, NN, and Bayesian.275–277
An early-prediction strategy has been an important method for predicting the state of health (SoH) and remaining useful life (RUL) of batteries, as it could shorten the time of experiments and improve the efficiency of optimization. As shown in Fig. 14, Attia et al.,278 researchers proposed a closed-loop optimization (CLO) system, combining an early-prediction model and a Bayesian optimization algorithm to accelerate the time of identifying charge protocols. This strategy sampled the first 100 cycles and utilized it as input for a linear model via elastic net regression to find charging protocols.279 Compared with full cycle experiments, the early-prediction model accelerated more than 30 folds. Then, by applying a Bayesian optimization algorithm to early-prediction data, it could provide an optimized result for next-round charging protocols.280,281 With these two strategies, the article made a successful approximation to the average life cycle and uncertainty of protocols. Also, utilizing early-prediction results reduced the total optimization cost, which is beneficial for the wide application of the CLO system. Furthermore, the early prediction strategy could be extended and integrated with Monte Carlo simulation to predict the battery remaining useful life.282 Tong et al.282 proposed a deep learning algorithm, named adaptive dropout long short-term memory (ADLSTM). By obtaining early cycle capacity as training data, researchers trained the model, and used long term cycles as testing data. With a trained model, MC is applied to figure out the uncertainty of battery data, and enhanced the robustness of the model. This method showed the lowest errors compared with other algorithms.
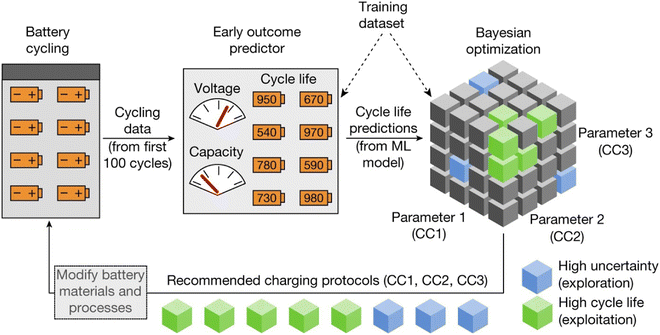 | ||
| Fig. 14 Schematic plot of the closed-loop optimization (CLO) system applied to predict the cycle life. Researchers adapted the first 100 cycles data as the first feeding data and applied Bayesian optimization to determine parameters. This method provides insights to designing parameters of batteries. Reprinted (adapted) with permission from ref. 278. Copyright 2019 Springer Nature. | ||
As a classical energy storage system, Li-ion batteries have been widely applied in daily life because of their high energy density.283–285 However, the degradation of Li-ion batteries, due to their complex and non-linear deactivation, has caused a lot of issues for recycling.286,287 To decide the state of health and remaining useful life of batteries, traditional methods mainly rely on multiscale simulations.288 But conventional simulation tools cannot perform well on a wide length scale and long time scale. So it is more accessible to combine different characterization and machine learning methods to generate a large amount of data and build an efficient statistical model.
For investigating battery systems, electrochemical impedance spectroscopy (EIS) is a classical method to measure the relationship between input and output, like capacity and resistance.289 However, it is hard to predict battery properties using EIS since the result of EIS contains both real and imaginary part, and still there are debates on if an electrical model could describe a complex battery system.290–292 Zhang et al.293 built a battery forecasting system with a GP model. By feeding over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 EIS results of commercial Li-ion batteries, the GP model could predict degradation and remaining useful life successfully. With one of the largest dataset, researchers could estimate the capacity and RUL of batteries by applying only one impedance test in different dimensions, like different temperatures and at different stages of life. Another article also applied EIS to measure the state of charge (SoC) and obtained a high accuracy model.294 By using a sensitivity analysis of data, researchers extracted most reliable features to predict the SoC. These methods help improving the prediction of battery conditions, and also benefit sampling methods of EIS.
000 EIS results of commercial Li-ion batteries, the GP model could predict degradation and remaining useful life successfully. With one of the largest dataset, researchers could estimate the capacity and RUL of batteries by applying only one impedance test in different dimensions, like different temperatures and at different stages of life. Another article also applied EIS to measure the state of charge (SoC) and obtained a high accuracy model.294 By using a sensitivity analysis of data, researchers extracted most reliable features to predict the SoC. These methods help improving the prediction of battery conditions, and also benefit sampling methods of EIS.
In conclusion, to make predictions for state of charge and health, researchers design a lot of machine learning algorithms and models, combining different characterization methods. These models provide valuable insights for designing and optimizing battery systems and accelerate the prediction, which are helpful for high throughput screening. Furthermore, by combining more physics insights with current machine learning algorithms, researchers can create models that can better explain the results.
6. Perspective
Despite numerous models that have been developed, machine learning-based energy chemistry is still in its early stages and there is still much room for improvement. In this section, we provide several perspectives based on our own knowledge and the relevant studies. We will focus more on the challenges and opportunities of machine learning in energy chemistry rather than the general problem of AI for science like data bias or limited data.6.1 Concept transformation: from drugs to energy materials
Over the past 20 years, drug-based machine learning has made significant progress, and become an important field in cheminformatics. This machine learning expertise is now being applied to energy chemistry, specifically in the field of OPVs which draws on many concepts and techniques from drug-based machine learning. For example, molecular fingerprints, such as MACCS, and Morgan fingerprints, were initially proposed and developed in small molecule drug research for virtual screening and molecular similarity comparison, but it has recently been widely applied in the field of organic photovoltaics in energy chemistry. Besides, the concept of QSPR has been adapted from the drug discovery field to the field of OPVs and other material machine learning work. In the relatively early stages of machine learning in energy chemistry, it is worthwhile to consider the inspiration and guidance from drug design. This concept can help to speed up the development of machine learning in energy chemistry and lead to more effective and efficient solutions.More recently, drug design for small molecules has kept pace with the development of applications in the field of SOTA machine learning technology, such as different transformer-based and GNN-based methods. But OPV machine learning models, which are also based on organic small molecule representation, are relatively limited and many of the current works still rely on using molecular fingerprinting with traditional machine learning. Compared to deep learning, traditional supervised learning requires less data and is more robust. This advantage can be extended and more adapted to the drawbacks of a small number of OPV datasets and low standardization of experimental data collected from the literature, which leads to better performance. However, using supervised learning cannot model complex relationships. With the development of OPVs and OPV data growth, the deep learning method could lead to a deeper understanding of underlying relationships in OPVs.
Transferring molecule-based models from one application to another is often simple since many molecule-based models have a high degree of applicability. For example, Some models based on small molecules can be used not only in drug discovery, but also in other areas such as materials science. Flam-Shepherd et al. showcased that their fragment-based 3D molecules model295 can be used in the design of both drug molecules and the materials of organic light-emitting devices (OLED). Besides, with relatively minor modifications, some molecule-based generalizable models such as SMILES transformer reported by Shion Honda et al.296 and SSVAE deep generative model reported by Kang et al.297 could potentially be used in other molecule-based prediction models in energy chemistry.
6.2 Trustworthy models
The lack of interpretability and experimental validation can be a major limitation for many applications of chemical machine learning, especially in the discovery of energy relevant materials. Without understanding the underlying mechanisms of a model's predictions and whether those predictions are reliable, it can be difficult for researchers to trust and use the model effectively because a model's predictions may not always be accurate. Researchers can use different methods to make their works into white-box models, which provide insights into how models work internally. This allows researchers to have a better understanding of the mechanisms behind their predictions and decision-making processes.Generally, some tools can help us to improve the interpretability of our models. Using visualization tools based on the NLP model or NN can visualize the weights of certain layers in a deep learning model. In some famous machine learning packages such as TensorFlow and Keras, it is easy to realize. This can make the model more acceptable; Rives et al. proposed a ESM-1b model which showed promising results in protein structural and functional prediction.298 They used the tsne technique to visualize their trained weight in their ESM-1b model and illustrated that the ESM-1b model can learn the physical and chemical information from the protein sequence. Besides the visualization tool, one useful tool is model-agnostic methods299 including the local interpretable model-agnostic explanations (LIME), SHAP, recursive feature elimination (RFE). The key attribute of model-agnostic methods is their independence from specific model structures, enabling their application across various model types. This flexibility allows for broad adoption in different model configurations.
In addition, experimental validation is an important part of ensuring the overall acceptance of the work by the researchers. With the development of chemistry machine learning, different researchers will come up with different solutions for the same task. Machine learning models with experimental validation are more acceptable to the people who want to apply them.
6.3 Benchmark and criteria
There are different criteria reported in different papers for manually collecting and incorporating data in the field of machine learning in energy chemistry. It is extremely difficult to determine which method is best suited for a particular project, which highlights the importance of benchmarking and comparison studies. To objectively evaluate different types of models and descriptors, benchmark and the comparison criteria should be established in a same downstream task. Using the public benchmark and criteria, researchers can have a better understanding of the strengths and weaknesses of each method.In many fields of machine learning, such as linguistics and biochemistry, many benchmarks have been established. Benchmark is one of the most important aspects of comparing models, which helps to clearly compare the performance of different models on different datasets. For molecules, several molecule benchmarks were set by Wu et al.300 and Nigam et al.78 However, more benchmarks are still needed to develop because many novel models in machine learning in chemistry are focusing on the descriptor and different works claim that their strategy is excellent but the training and test environments are different. Therefore, it is hard to compare different strategies. Although there are many public datasets for energy chemistry as mentioned above, we hope to have more public datasets in the future. Most of the current public datasets are collected in different methods, the average accuracy of validation with different datasets can be considered as an evaluation benchmark.
In summary, establishing more benchmarks helps to compare the quality of the corresponding algorithms or descriptors, which is more conducive to the development of chemical machine learning especially in energy chemistry.
6.4 Combining large language models with chemical science
The development of large language models (LLMs) has been very fast in recent years.301 Although LLMs have shown promising results in predicting protein structures and generation in the field of protein modeling, the use of LLM models in the field of materials science is still in its early stages. There are several LLMs that have been developed for molecules, such as DPA-1 and Molformer, which can be applied to potential energy surfaces and encoding molecules.302,303 In terms of extracting data from the materials science literature, there has been some recent progress. For example, MatBERT is a Bert-based model, which could be utilized to understand materials terminologies and paragraph-level scientific reasoning and achieve state-of-art results in several benchmark tests.302,303 These models can be used in specific downstream tasks after fine-tuning. In the future, we believe that in specific areas, we will see more and more applications of LLMs.Some LLMs, such as ChatGPT, are designed to help computers understand human language and generate natural language responses, making them valuable tools for various natural language processing (NLP) tasks. Such a chatbot could provide an accessible interaction way for researchers to leverage machine learning models, even if they are not familiar with programming or high-performance computing systems. Unluckily, a material-specific chatbot has not yet been developed. Nevertheless, the emergence of material-specific chatbots like ChatGPT that can interface with various downstream tasks and allow users to use pre-trained models for machine learning research is expected to lower the barrier to entry for machine learning research.
There is still much work to be done in this area. One challenge in building a LLM is the need for large amounts of high-quality data to train the model. Another challenge is to develop more specialized algorithms and architectures to handle the complex nature of materials science data. Despite these challenges, the development of LLMs has opened up new possibilities in the field of chemistry, and we can expect to see more exciting applications in the future.
Author contributions
Yuzhi Xu is responsible for conceptualization, finding resources, investigation, writing original drafts, and reviews and editing. Jiankai Ge is responsible for conceptualization, finding resources, investigation, writing original drafts, reviews and editing, and project administration. Cheng-Wei Ju is responsible for conceptualization, investigation, reviews and editing, and project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to express our gratitude to those who supported us in the revision of this review. Thanks to Zhewei Li from Tsinghua University for helping with proofreading. We also appreciate the invitation from The Royal Society of Chemistry.Notes and references
- K. Li and B. Lin, Renewable Sustainable Energy Rev., 2015, 52, 1107–1122 CrossRef CAS.
- G. R. Monama, K. E. Ramohlola, E. I. Iwuoha and K. D. Modibane, Results Chem., 2022, 100321 CrossRef CAS.
- A. Pudi, A. P. Karcz, S. Keshavarz, V. Shadravan, M. P. Andersson and S. S. Mansouri, Chem. Eng. Process., 2022, 174, 108883 CrossRef CAS.
- A. Goeppert, M. Czaun, J.-P. Jones, G. S. Prakash and G. A. Olah, Chem. Soc. Rev., 2014, 43, 7995–8048 RSC.
- D.-D. Zhou, X.-W. Zhang, Z.-W. Mo, Y.-Z. Xu, X.-Y. Tian, Y. Li, X.-M. Chen and J.-P. Zhang, EnergyChem, 2019, 1, 100016 CrossRef.
- I. Dincer and C. Acar, Inter. J. Energy Res., 2015, 39, 585–606 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- A. C. Mater and M. L. Coote, J. Chem. Inf. Model., 2019, 59, 2545–2559 CrossRef CAS PubMed.
- M. Meuwly, Chem. Rev., 2021, 121, 10218–10239 CrossRef CAS PubMed.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS.
- T. G. Allen, J. Bullock, X. Yang, A. Javey and S. De Wolf, Nat. Energy, 2019, 4, 914–928 CrossRef CAS.
- A. Polman, M. Knight, E. C. Garnett, B. Ehrler and W. C. Sinke, Science, 2016, 352, aad4424 CrossRef PubMed.
- G. C. Righini and F. Enrichi, Sol. Cells Light Manage., 2020, 1–32 CAS.
- J. Zhang, W. Zhang, H.-M. Cheng and S. R. P. Silva, Mater. Today, 2020, 39, 66–88 CrossRef CAS.
- Z. Wan, Q.-D. Wang, D. Liu and J. Liang, Comput. Mater. Sci., 2021, 198, 110699 CrossRef CAS.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 1–13 Search PubMed.
- X. Zhou, J. Jankowska, H. Dong and O. V. Prezhdo, J. Energy Chem., 2018, 27, 637–649 CrossRef.
- Y. S. Meng and M. E. Arroyo-de Dompablo, Energy Environ. Sci., 2009, 2, 589–609 RSC.
- L. Wang, G. Nan, X. Yang, Q. Peng, Q. Li and Z. Shuai, Chem. Soc. Rev., 2010, 39, 423–434 RSC.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, npj Comput. Mater., 2017, 3, 54 CrossRef.
- B. Ryu, L. Wang, H. Pu, M. K. Chan and J. Chen, Chem. Soc. Rev., 2022, 51, 1899–1925 RSC.
- N.-T. Suen, S.-F. Hung, Q. Quan, N. Zhang, Y.-J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365 RSC.
- N. Dubouis and A. Grimaud, Chem. Sci., 2019, 10, 9165–9181 RSC.
- C. Kim, F. Dionigi, V. Beermann, X. Wang, T. Möller and P. Strasser, Adv. Mater., 2019, 31, 1805617 CrossRef PubMed.
- F. M. Sapountzi, J. M. Gracia, H. O. Fredriksson and J. H. Niemantsverdriet, et al. , Prog. Energy Combust. Sci., 2017, 58, 1–35 CrossRef.
- Z. Liang, H. Zheng and R. Cao, ChemElectroChem, 2019, 6, 2600–2614 CrossRef CAS.
- C. Wei, S. Sun, D. Mandler, X. Wang, S. Z. Qiao and Z. J. Xu, Chem. Soc. Rev., 2019, 48, 2518–2534 RSC.
- A. Chen, X. Zhang and Z. Zhou, InfoMat, 2020, 2, 553–576 CrossRef CAS.
- X. Zhang, Y. Tian, L. Chen, X. Hu and Z. Zhou, J. Phys. Chem. Lett., 2022, 13, 7920–7930 CrossRef CAS PubMed.
- Z. Zhou, J. Mater. Chem. A, 2021, 9, 1295–1296 RSC.
- Z.-H. Zhou, Machine learning, Springer Nature, 2021 Search PubMed.
- S. Palkovits, ChemCatChem, 2020, 12, 3995–4008 CrossRef CAS.
- A. Bender, N. Schneider, M. Segler, W. Patrick Walters, O. Engkvist and T. Rodrigues, Nat. Rev. Chem., 2022, 6, 428–442 CrossRef PubMed.
- D. Zou, D. Wang, Z. Chu, Z. Lv and X. Fan, Coord. Chem. Rev., 2010, 254, 1169–1178 CrossRef CAS.
- C. J. Emmott, J. A. Röhr, M. Campoy-Quiles, T. Kirchartz, A. Urbina, N. J. Ekins-Daukes and J. Nelson, Energy Environ. Sci., 2015, 8, 1317–1328 RSC.
- Y. Hu, J. Wang, C. Yan and P. Cheng, Nat. Rev. Mater., 2022, 1–3 Search PubMed.
- A. Mahmood and J.-L. Wang, Energy Environ. Sci., 2021, 14, 90–105 RSC.
- P. C. St. John, C. Phillips, T. W. Kemper, A. N. Wilson, Y. Guan, M. F. Crowley, M. R. Nimlos and R. E. Larsen, J. Chem. Phys., 2019, 150, 234111 CrossRef PubMed.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- S. A. Lopez, E. O. Pyzer-Knapp, G. N. Simm, T. Lutzow, K. Li, L. R. Seress, J. Hachmann and A. Aspuru-Guzik, Sci. Data, 2016, 3, 1–7 Search PubMed.
- T. W. David, H. Anizelli, P. Tyagi, C. Gray, W. Teahan and J. Kettle, IEEE J. Photovolt., 2019, 9, 1768–1773 Search PubMed.
- H. Sahu, F. Yang, X. Ye, J. Ma, W. Fang and H. Ma, J. Mater. Chem. A, 2019, 7, 17480–17488 RSC.
- K. Wu, B. Natarajan, L. Morkowchuk, M. Krein and C. M. Breneman, Inf. Mater. Sci. Eng., Elsevier, 2013, pp. 385–422 Search PubMed.
- Y. Miyake and A. Saeki, J. Phys. Chem. Lett., 2021, 12, 12391–12401 CrossRef CAS PubMed.
- Z.-W. Zhao, M. del Cueto, Y. Geng and A. Troisi, Chem. Mater., 2020, 32, 7777–7787 CrossRef CAS.
- K. Kranthiraja and A. Saeki, Adv. Funct. Mater., 2021, 31, 2011168 CrossRef CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- U. V. Ucak, I. Ashyrmamatov and J. Lee, Chemrxiv, 2022.
- N. O'Boyle and A. Dalke, Chemrxiv, 2018.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, Machine Learning: Sci. Tech., 2020, 1, 045024 Search PubMed.
- Y. Xu, C.-W. Ju, B. Li, Q.-S. Ma, Z. Chen, L. Zhang and J. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 34033–34042 CrossRef CAS PubMed.
- L. Himanen, M. O. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- A. Cereto-Massagué, M. J. Ojeda, C. Valls, M. Mulero, S. Garcia-Vallvé and G. Pujadas, Methods, 2015, 71, 58–63 CrossRef PubMed.
- H. Kubinyi, Encycl. Comput. Chem., 1998, 1, 448–460 Search PubMed.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, Mol. Syst. Design Engineering, 2019, 4, 828–849 RSC.
- S. Riniker and G. A. Landrum, J. Cheminformatics, 2013, 5, 1–17 CrossRef PubMed.
- P. Xu, H. Chen, M. Li and W. Lu, Adv. Theory Simul., 2022, 5, 2100565 CrossRef.
- Q. Zhang, Y. J. Zheng, W. Sun, Z. Ou, O. Odunmbaku, M. Li, S. Chen, Y. Zhou, J. Li and B. Qin, et al. , Adv. Sci., 2022, 9, 2104742 CrossRef CAS PubMed.
- W. Sun, Y. Zheng, K. Yang, Q. Zhang, A. A. Shah, Z. Wu, Y. Sun, L. Feng, D. Chen and Z. Xiao, et al. , Sci. Adv., 2019, 5, eaay4275 CrossRef CAS PubMed.
- H. Matter and T. Pötter, J. Chem. Inf. Comput. Sci., 1999, 39, 1211–1225 CrossRef CAS.
- Y. Wu, J. Guo, R. Sun and J. Min, npj Comput. Mater., 2020, 6, 1–8 CrossRef.
- S. Nagasawa, E. Al-Naamani and A. Saeki, J. Phys. Chem. Lett., 2018, 9, 2639–2646 CrossRef CAS PubMed.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen and H. Jiang, et al. , J. Medic. Chem., 2019, 63, 8749–8760 CrossRef PubMed.
- A. Eibeck, D. Nurkowski, A. Menon, J. Bai, J. Wu, L. Zhou, S. Mosbach, J. Akroyd and M. Kraft, ACS Omega, 2021, 6, 23764–23775 CrossRef CAS PubMed.
- P. Han, P. Zhao, C. Lu, J. Huang, J. Wu, S. Shang, B. Yao and X. Zhang, Proceedings of the AAAI Conference on Artificial Intelligence, 2022, pp. 4014–4021.
- H. Wang, W. Li, X. Jin, K. Cho, H. Ji, J. Han and M. D. Burke, arXiv Preprint arXiv:2109.09888, 2021.
- D. Padula, J. D. Simpson and A. Troisi, Mater. Horizons, 2019, 6, 343–349 RSC.
- M.-H. Lee, Adv. Intell. Syst., 2020, 2, 1900108 CrossRef.
- T. W. David, H. Anizelli, T. J. Jacobsson, C. Gray, W. Teahan and J. Kettle, Nano Energy, 2020, 78, 105342 CrossRef CAS.
- A. Nigam, R. Pollice, M. Krenn, G. dos Passos Gomes and A. Aspuru-Guzik, Chem. Sci., 2021, 12, 7079–7090 RSC.
- C. Kunkel, J. T. Margraf, K. Chen, H. Oberhofer and K. Reuter, Nat. Commun., 2021, 12, 1–11 Search PubMed.
- Z. Chen, J. Li and Y. Xu, arXiv, 2021, Preprint arXiv:2107.02613.
- A. Saeki and K. Kranthiraja, Jpn. J. Appl. Phys., 2019, 59, SD0801 CrossRef.
- M. Lee and K. Min, J. Chem. Inf. Model., 2022, 62(12), 2943–2950 CrossRef CAS PubMed.
- Y. Xu, K. Lin, S. Wang, L. Wang, C. Cai, C. Song, L. Lai and J. Pei, Future Med. Chem., 2019, 11, 567–597 CrossRef CAS PubMed.
- T. Sousa, J. Correia, V. Pereira and M. Rocha, J. Chem. Inf. Model., 2021, 61, 5343–5361 CrossRef CAS PubMed.
- A. Nigam, R. Pollice, G. Tom, K. Jorner, L. A. Thiede, A. Kundaje and A. Aspuru-Guzik, arXiv, 2022, Preprint arXiv:2209.12487.
- X. Du, L. Lüer, T. Heumueller, J. Wagner, C. Berger, T. Osterrieder, J. Wortmann, S. Langner, U. Vongsaysy and M. Bertrand, et al. , Joule, 2021, 5, 495–506 CrossRef CAS.
- S. Langner, F. Häse, J. D. Perea, T. Stubhan, J. Hauch, L. M. Roch, T. Heumueller, A. Aspuru-Guzik and C. J. Brabec, Adv. Mater., 2020, 32, 1907801 CrossRef CAS PubMed.
- T. Wolfram and S. Ellialtioglu, Electronic and optical properties of d-band perovskites, Cambridge University Press, Cambridge, 2006 Search PubMed.
- H. S. Jung and N.-G. Park, Small, 2015, 11, 10–25 CrossRef CAS PubMed.
- J. Tian, Q. Xue, Q. Yao, N. Li, C. J. Brabec and H.-L. Yip, Adv. Energy Mater., 2020, 10, 2000183 CrossRef CAS.
- N. S. Kumar and K. C. B. Naidu, J. Materiomics, 2021, 7, 940–956 CrossRef.
- Q. Xu, D. Yang, J. Lv, Y.-Y. Sun and L. Zhang, Small Methods, 2018, 2, 1700316 CrossRef.
- C. Zhang, C. Liu, Y. Gao, S. Zhu, F. Chen, B. Huang, Y. Xie, Y. Liu, M. Ma and Z. Wang, et al. , Adv. Sci., 2022, 2204138 CrossRef CAS PubMed.
- A. Fakharuddin, M. K. Gangishetty, M. Abdi-Jalebi, S.-H. Chin, A. bin Mohd Yusoff, D. N. Congreve, W. Tress, F. Deschler, M. Vasilopoulou and H. J. Bolink, et al. , Nat. Electron., 2022, 5, 203–216 CrossRef CAS.
- C. Zhao, D. Zhang and C. Qin, CCS Chem., 2020, 2, 859–869 CrossRef CAS.
- Z. Bian, Z. Wang, B. Jiang, P. Hongmanorom, W. Zhong and S. Kawi, Renewable Sustainable Energy Rev., 2020, 134, 110291 CrossRef CAS.
- J. Hwang, R. R. Rao, L. Giordano, Y. Katayama, Y. Yu and Y. Shao-Horn, Science, 2017, 358, 751–756 CrossRef CAS PubMed.
- J. Yu, R. Ran, Y. Zhong, W. Zhou, M. Ni and Z. Shao, Energy Environ. Mater., 2020, 3, 121–145 CrossRef CAS.
- S. Narayanan, N. Parikh, M. M. Tavakoli, M. Pandey, M. Kumar, A. Kalam, S. Trivedi, D. Prochowicz and P. Yadav, Eur. J. Inorg. Chem., 2021, 1201–1212 CrossRef CAS.
- Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. I. Seok, M. D. McGehee, E. H. Sargent and H. Han, Science, 2018, 361, eaat8235 CrossRef PubMed.
- Y. Zhang, Y. Ma, Y. Wang, X. Zhang, C. Zuo, L. Shen and L. Ding, Adv. Mater., 2021, 33, 2006691 CrossRef CAS PubMed.
- M. R. Filip and F. Giustino, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5397–5402 CrossRef CAS PubMed.
- S. C. Tidrow, Ferroelectrics, 2014, 470, 13–27 CrossRef CAS.
- D. Ji, S. Feng, L. Wang, S. Wang, M. Na, H. Zhang, C. Zhang and X. Li, Vacuum, 2019, 164, 186–193 CrossRef CAS.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed.
- S. Lu, Q. Zhou, L. Ma, Y. Guo and J. Wang, Small Methods, 2019, 3, 1900360 CrossRef CAS.
- D. Jain, S. Chaube, P. Khullar, S. G. Srinivasan and B. Rai, Phys. Chem. Chem. Phys., 2019, 21, 19423–19436 RSC.
- G. Pilania, P. V. Balachandran, C. Kim and T. Lookman, Front. Mater., 2016, 3, 19 Search PubMed.
- C. Li, H. Hao, B. Xu, Z. Shen, E. Zhou, D. Jiang and H. Liu, Comput. Mater. Sci., 2021, 198, 110714 CrossRef CAS.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- R. Ouyang, E. Ahmetcik, C. Carbogno, M. Scheffler and L. M. Ghiringhelli, J. Phys.: Mater., 2019, 2, 024002 Search PubMed.
- J. L. Teunissen and F. Da Pieve, J. Phys. Chem. C, 2021, 125, 25316–25326 CrossRef CAS.
- S. R. Xie, P. Kotlarz, R. G. Hennig and J. C. Nino, Comput. Mater. Sci., 2020, 180, 109690 CrossRef CAS.
- P. Xu, D. Chang, T. Lu, L. Li, M. Li and W. Lu, J. Chem. Inf. Model., 2022, 62(21), 5038–5049 CrossRef CAS PubMed.
- Z. Wan, Q.-D. Wang and J. Liang, Int. J. Quantum Chem., 2021, 121, e26441 CAS.
- Z. Wan, Q.-D. Wang, D. Liu and J. Liang, New J. Chem., 2021, 45, 9427–9433 RSC.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- G. H. Gu, J. Jang, J. Noh, A. Walsh and Y. Jung, npj Comput. Mater., 2022, 8, 1–8 CrossRef.
- P. Omprakash, B. Manikandan, A. Sandeep, R. Shrivastava, P. Viswesh and D. B. Panemangalore, Comput. Mater. Sci., 2021, 196, 110530 CrossRef CAS.
- Q. Zhou, P. Tang, S. Liu, J. Pan, Q. Yan and S.-C. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6411–E6417 CAS.
- A. Ihalage and Y. Hao, npj Comput. Mater., 2021, 7, 1–12 CrossRef.
- Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- L. Wei, Q. Li, Y. Song, S. Stefanov, E. Siriwardane, F. Chen and J. Hu, arXiv, 2022, Preprint arXiv:2204.11953.
- C. W. Myung, A. Hajibabaei, J.-H. Cha, M. Ha, J. Kim and K. S. Kim, Adv. Energy Mater., 2022, 2202279 CrossRef CAS.
- L. Zhang, M. He and S. Shao, Nano Energy, 2020, 78, 105380 CrossRef CAS.
- Z. Guo and B. Lin, Sol. Energy, 2021, 228, 689–699 CrossRef CAS.
- L. Xu, L. Wencong, P. Chunrong, S. Qiang and G. Jin, Comput. Mater. Sci., 2009, 46, 860–868 CrossRef.
- G.-Q. Liang and J. Zhang, Comput. Mater. Sci., 2022, 204, 111172 CrossRef CAS.
- W. Li, R. Jacobs and D. Morgan, Comput. Mater. Sci., 2018, 150, 454–463 CrossRef CAS.
- C. Kim, G. Pilania and R. Ramprasad, J. Phys. Chem. C, 2016, 120, 14575–14580 CrossRef CAS.
- J. Li, Y. Peng, L. Zhao, G. Chen, L. Zeng, G. Wei and Y. Xu, Mater. Adv., 2022, 3, 8639–8646 RSC.
- L. Williams, A. Mukherjee and K. Rajan, J. Phys. Chem. Lett., 2020, 11, 7462–7468 CrossRef CAS PubMed.
- E. I. Marchenko, S. A. Fateev, A. A. Petrov, V. V. Korolev, A. Mitrofanov, A. V. Petrov, E. A. Goodilin and A. B. Tarasov, Chem. Mater., 2020, 32, 7383–7388 CrossRef CAS.
- Y. Zhang and X. Xu, CrystEngComm, 2020, 22, 6385–6397 RSC.
- Y. Zhang and X. Xu, ChemistrySelect, 2020, 5, 9999–10009 CrossRef CAS.
- R. Li, Q. Deng, D. Tian, D. Zhu and B. Lin, Crystals, 2021, 11, 818 CrossRef CAS.
- W. A. Saidi, W. Shadid and I. E. Castelli, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- P. V. Balachandran, A. A. Emery, J. E. Gubernatis, T. Lookman, C. Wolverton and A. Zunger, Phys. Rev. Mater., 2018, 2, 043802 CrossRef CAS.
- V. Shetty, S. Shedthi and J. Kumaraswamy, Mater. Today: Proc., 2022, 52, 457–461 CAS.
- J. Kim, E. Kim and K. Min, Adv. Theory and Simul., 2021, 4, 2100263 CrossRef CAS.
- W. Zheng, H. Cheng, Y. Liu, L. Chen, Y. Guo, Y. Yang, X. Yan and D. Wu, Comput. Mater. Sci., 2022, 209, 111394 CrossRef CAS.
- I. M. Pendleton, M. K. Caucci, M. Tynes, A. Dharna, M. A. N. Nellikkal, Z. Li, E. M. Chan, A. J. Norquist and J. Schrier, J. Phys. Chem. C, 2020, 124, 13982–13992 CrossRef CAS.
- L. Li, Q. Tao, P. Xu, X. Yang, W. Lu and M. Li, Comput. Mater. Sci., 2021, 199, 110712 CrossRef CAS.
- A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Chem. Mater., 2021, 33, 845–858 CrossRef CAS.
- H. A. Jame, S. Sarker, M. S. Islam, M. T. Islam, A. Rauf, S. Ahsan, S. S. Nishat, M. R. Jani, K. M. Shorowordi and J. Carbonara, et al. , ACS Appl. Mater. Interfaces, 2021, 14, 502–516 CrossRef PubMed.
- F. Massuyeau, T. Broux, F. Coulet, A. Demessence, A. Mesbah and R. Gautier, Adv. Mater., 2022, 2203879 CrossRef CAS PubMed.
- J. Yang and A. Mannodi-Kanakkithodi, MRS Bull., 2022, 1–9 Search PubMed.
- J. C. Stanley, F. Mayr and A. Gagliardi, Adv. Theory Simul., 2020, 3, 1900178 CrossRef CAS.
- S. Lu, Q. Zhou, Y. Ouyang, Y. Guo, Q. Li and J. Wang, Nat. Commun., 2018, 9, 1–8 CrossRef PubMed.
- Z. Gao, H. Zhang, G. Mao, J. Ren, Z. Chen, C. Wu, I. D. Gates, W. Yang, X. Ding and J. Yao, Appl. Surface Sci., 2021, 568, 150916 CrossRef CAS.
- Y. Wu, S. Lu, M.-G. Ju, Q. Zhou and J. Wang, Nanoscale, 2021, 13, 12250–12259 RSC.
- W. Hu, L. Zhang and Z. Pan, ACS Appl. Mater. Interfaces, 2022, 14(18), 21596–21604 CrossRef CAS PubMed.
- E. Meyer, D. Mutukwa, N. Zingwe and R. Taziwa, Metals, 2018, 8, 667 CrossRef.
- Ç. Odabas and R. Yldrm, Energy Tech., 2020, 8, 1901449 CrossRef.
- R. Jaafreh, A. Sharan, M. Sajjad, N. Singh and K. Hamad, Adv. Funct. Mater., 2022, 2210374 Search PubMed.
- J. M. Howard, E. M. Tennyson, B. R. Neves and M. S. Leite, Joule, 2019, 3, 325–337 CrossRef CAS.
- F. Häse, L. M. Roch, P. Friederich and A. Aspuru-Guzik, Nat. Commun., 2020, 11, 1–11 CrossRef PubMed.
- M. C. Swain and J. M. Cole, J. Chem. Inf. Model., 2016, 56, 1894–1904 CrossRef CAS PubMed.
- D. M. Jessop, S. E. Adams, E. L. Willighagen, L. Hawizy and P. Murray-Rust, J. Cheminformatics, 2011, 3, 1–12 CrossRef PubMed.
- L. Hawizy, D. M. Jessop, N. Adams and P. Murray-Rust, J. Cheminformatics, 2011, 3, 1–13 CrossRef PubMed.
- M. Krallinger, O. Rabal, A. Lourenco, J. Oyarzabal and A. Valencia, Chem. Rev., 2017, 117, 7673–7761 CrossRef CAS PubMed.
- H. Huo, Z. Rong, O. Kononova, W. Sun, T. Botari, T. He, V. Tshitoyan and G. Ceder, npj Comput. Mater., 2019, 5, 1–7 CrossRef.
- O. Kononova, T. He, H. Huo, A. Trewartha, E. A. Olivetti and G. Ceder, Iscience, 2021, 24, 102155 CrossRef PubMed.
- E. J. Beard and J. M. Cole, Sci. Data, 2022, 9, 1–19 CrossRef PubMed.
- E. Kim, Z. Jensen, A. van Grootel, K. Huang, M. Staib, S. Mysore, H.-S. Chang, E. Strubell, A. McCallum and S. Jegelka, et al. , J. Chem. Inf. Model., 2020, 60, 1194–1201 CrossRef CAS PubMed.
- J. Wei, X. Chu, X.-Y. Sun, K. Xu, H.-X. Deng, J. Chen, Z. Wei and M. Lei, InfoMat, 2019, 1, 338–358 CrossRef CAS.
- W. Yan, Y. Liu, Y. Zang, J. Cheng, Y. Wang, L. Chu, X. Tan, L. Liu, P. Zhou and W. Li, et al. , Nano Energy, 2022, 107394 CrossRef CAS.
- S. Sun, N. T. Hartono, Z. D. Ren, F. Oviedo, A. M. Buscemi, M. Layurova, D. X. Chen, T. Ogunfunmi, J. Thapa and S. Ramasamy, et al. , Joule, 2019, 3, 1437–1451 CrossRef CAS.
- J. Kirman, A. Johnston, D. A. Kuntz, M. Askerka, Y. Gao, P. Todorović, D. Ma, G. G. Privé and E. H. Sargent, Matter, 2020, 2, 938–947 CrossRef.
- Ç. Odabas and R. Yldrm, Sol. Energy Mater. Sol. Cells, 2020, 205, 110284 CrossRef.
- Y. Yu, X. Tan, S. Ning and Y. Wu, ACS Energy Lett., 2019, 4, 397–404 CrossRef CAS.
- N. T. P. Hartono, J. Thapa, A. Tiihonen, F. Oviedo, C. Batali, J. J. Yoo, Z. Liu, R. Li, D. F. Marrón and M. G. Bawendi, et al. , Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- A. Senocrate, T. Acartürk, G. Y. Kim, R. Merkle, U. Starke, M. Grätzel and J. Maier, J. Mater. Chem. A, 2018, 6, 10847–10855 RSC.
- S. Jariwala, S. Burke, S. Dunfield, R. C. Shallcross, M. Taddei, J. Wang, G. E. Eperon, N. R. Armstrong, J. J. Berry and D. S. Ginger, Chem. Mater., 2021, 33, 5035–5044 CrossRef CAS.
- X. Cai, F. Liu, A. Yu, J. Qin, M. Hatamvand, I. Ahmed, J. Luo, Y. Zhang, H. Zhang and Y. Zhan, Light: Sci. Appl., 2022, 11, 1–12 CrossRef PubMed.
- Y. Hu, X. Hu, L. Zhang, T. Zheng, J. You, B. Jia, Y. Ma, X. Du, L. Zhang and J. Wang, et al. , Adv. Energy Mater., 2022, 2201463 CrossRef CAS.
- R. W. Epps, K. C. Felton, C. W. Coley and M. Abolhasani, Lab Chip, 2017, 17, 4040–4047 RSC.
- M. Seifrid, R. Pollice, A. Aguilar-Granda, Z. Morgan Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu and A. Aspuru-Guzik, Acc. Chem. Research, 2022, 55, 2454–2466 CrossRef CAS PubMed.
- M. Ahmadi, M. Ziatdinov, Y. Zhou, E. A. Lass and S. V. Kalinin, Joule, 2021, 5, 2797–2822 CrossRef CAS.
- Z. Li, M. A. Najeeb, L. Alves, A. Z. Sherman, V. Shekar, P. Cruz Parrilla, I. M. Pendleton, W. Wang, P. W. Nega and M. Zeller, et al. , Chem. Mater., 2020, 32, 5650–5663 CrossRef CAS.
- S. Greenhill, S. Rana, S. Gupta, P. Vellanki and S. Venkatesh, IEEE Access, 2020, 8, 13937–13948 Search PubMed.
- Q. Song, Y. Bai and Q. Chen, J. Phys. Chem. Lett., 2022, 13, 10741–10750 CrossRef CAS PubMed.
- B. P. MacLeod, F. G. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. Yunker, M. B. Rooney and J. R. Deeth, et al. , Sci. Adv., 2020, 6, eaaz8867 CrossRef CAS PubMed.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. Yunker, J. E. Hein and A. Aspuru-Guzik, Sci. Robotics, 2018, 3, eaat5559 CrossRef PubMed.
- K. Higgins, S. M. Valleti, M. Ziatdinov, S. V. Kalinin and M. Ahmadi, ACS Energy Lett., 2020, 5, 3426–3436 CrossRef CAS.
- Z.-Y. Zhou, N. Tian, J.-T. Li, I. Broadwell and S.-G. Sun, Chem. Soc. Rev., 2011, 40, 4167–4185 RSC.
- S. P. Fisher, A. W. Tomich, S. Lovera, J. F. Kleinsasser, J. Guo, M. Asay, H. Nelson and V. Lavallo, Chem. Rev., 2019, 119, 8262–8290 CrossRef CAS PubMed.
- M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2, 2648–2663 CrossRef CAS.
- M. P. Duduković, F. Larachi and P. L. Mills, Catal. Rev., 2002, 44, 123–246 CrossRef.
- J. Huang, F. Cheng, B. P. Binks and H. Yang, J. Am. Chem. Soc., 2015, 137, 15015–15025 CrossRef CAS PubMed.
- E. L. Clark, J. Wong, A. J. Garza, Z. Lin, M. Head-Gordon and A. T. Bell, J. Am. Chem. Soc., 2019, 141, 4191–4193 CrossRef CAS PubMed.
- J. Greeley, J. K. Nørskov and M. Mavrikakis, Annu. Rev. Phys. Chem., 2002, 53, 319–348 CrossRef CAS PubMed.
- A. Nilsson, L. Pettersson, B. Hammer, T. Bligaard, C. H. Christensen and J. K. Nørskov, Catal. Lett., 2005, 100, 111–114 CrossRef CAS.
- J. Ge and B. Peters, Chem. Eng. J., 2023, 466, 143251 CrossRef CAS.
- B. Smit, J. Chem. Phys., 1992, 96, 8639–8640 CrossRef CAS.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. Pádua, Theor. Chem. Acc., 2012, 131, 1–11 Search PubMed.
- E. Vignola, S. N. Steinmann, B. D. Vandegehuchte, D. Curulla, M. Stamatakis and P. Sautet, J. Chem. Phys., 2017, 147, 054106 CrossRef PubMed.
- J. Westermayr, M. Gastegger, M. F. Menger, S. Mai, L. González and P. Marquetand, Chem. Sci., 2019, 10, 8100–8107 RSC.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- A. P. Thompson, L. P. Swiler, C. R. Trott, S. M. Foiles and G. J. Tucker, J. Comp. Phys., 2015, 285, 316–330 CrossRef CAS.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- J. Gasteiger, J. Groß and S. Günnemann, Proc. Int. Conf. Learn. Represent., 2019 Search PubMed.
- H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS.
- S.-D. Huang, C. Shang, P.-L. Kang, X.-J. Zhang and Z.-P. Liu, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415 CAS.
- A. Khorshidi and A. A. Peterson, Comput. Phys. Commun., 2016, 207, 310–324 CrossRef CAS.
- K. Schutt, P. Kessel, M. Gastegger, K. Nicoli, A. Tkatchenko and K.-R. Muller, J. Chem. Theory Comput., 2018, 15, 448–455 CrossRef PubMed.
- K. T. Schutt, S. S. Hessmann, N. W. Gebauer, J. Lederer and M. Gastegger, arXiv, 2022, preprint arXiv:2212.05517.
- A. Shapeev, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- E. V. Podryabinkin and A. V. Shapeev, Comput. Mater. Sci., 2017, 140, 171–180 CrossRef CAS.
- K. Gubaev, E. V. Podryabinkin, G. L. W. Hart and A. V. Shapeev, Comput. Mater. Sci., 2019, 156, 148–156 CrossRef CAS.
- B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240 CrossRef CAS.
- I. Takigawa, K.-i Shimizu, K. Tsuda and S. Takakusagi, RSC Adv., 2016, 6, 52587–52595 RSC.
- Z. Lian, M. Yang, F. Jan and B. Li, J. Phys. Chem. Lett., 2021, 12, 7053–7059 CrossRef CAS PubMed.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- R. Bashyam and P. Zelenay, Nature, 2006, 443, 63–66 CrossRef CAS PubMed.
- T. Zhou, H. Shan, H. Yu, C. Zhong, J. Ge, N. Zhang, W. Chu, W. Yan, Q. Xu and H. Wu, et al. , Adv. Mater., 2020, 32, 2003251 CrossRef CAS PubMed.
- X. Yu, T. Zhou, J. Ge and C. Wu, ACS Mater. Lett., 2020, 2, 1423–1434 CrossRef CAS.
- C. Zhong, T. Zhou, N. Zhang, M. Chen, Y. Xie, W. Yan, W. Chu, X. Zheng, Q. Xu, J. Ge and C. Wu, 2023, 533, 0304.
- P. Chen, T. Zhou, L. Xing, K. Xu, Y. Tong, H. Xie, L. Zhang, W. Yan, W. Chu and C. Wu, et al. , Angew. Chem., Int. Ed., 2017, 129, 625–629 CrossRef.
- J. Zhang, Y. Zhao, C. Chen, Y.-C. Huang, C.-L. Dong, C.-J. Chen, R.-S. Liu, C. Wang, K. Yan and Y. Li, et al. , J. Am. Chem. Soc., 2019, 141, 20118–20126 CrossRef CAS PubMed.
- Z. Jin, P. Li, Y. Meng, Z. Fang, D. Xiao and G. Yu, Nat. Catal., 2021, 4, 615–622 CrossRef CAS.
- Y. Ying, K. Fan, X. Luo, J. Qiao and H. Huang, J. Mater. Chem. A, 2021, 9, 16860–16867 RSC.
- W. Ye, S. Chen, Y. Lin, L. Yang, S. Chen, X. Zheng, Z. Qi, C. Wang, R. Long and M. Chen, et al. , Chem, 2019, 5, 2865–2878 CAS.
- N. Zhang, T. Zhou, J. Ge, Y. Lin, Z. Du, W. Wang, Q. Jiao, R. Yuan, Y. Tian and W. Chu, et al. , Matter, 2020, 3, 509–521 CrossRef.
- H. Surden, Wash. L. Rev., 2014, 89, 87 Search PubMed.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K.-I. Shimizu, ACS Catal., 2019, 10, 2260–2297 CrossRef.
- P. Schlexer Lamoureux, K. T. Winther, J. A. Garrido Torres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, ChemCatChem, 2019, 11, 3581–3601 CrossRef CAS.
- X. Zhu, J. Yan, M. Gu, T. Liu, Y. Dai, Y. Gu and Y. Li, J. Phys. Chem. Lett., 2019, 10, 7760–7766 CrossRef CAS PubMed.
- J. H. Friedman, Comput. Stat. Data Anal., 2002, 38, 367–378 CrossRef.
- V. Viswanathan, A. H. Epstein, Y.-M. Chiang, E. Takeuchi, M. Bradley, J. Langford and M. Winter, Nature, 2022, 601, 519–525 CrossRef CAS PubMed.
- X. Ke, Y. Liang, L. Ou, H. Liu, Y. Chen, W. Wu, Y. Cheng, Z. Guo, Y. Lai and P. Liu, et al. , Energy Storage Mater., 2019, 23, 547–555 CrossRef.
- Y. Chen, X. Ke, Y. Cheng, M. Fan, W. Wu, X. Huang, Y. Liang, Y. Zhong, Z. Ao and Y. Lai, et al. , Energy Storage Mater., 2020, 26, 56–64 CrossRef.
- J. Xiao, Q. Li, Y. Bi, M. Cai, B. Dunn, T. Glossmann, J. Liu, T. Osaka, R. Sugiura and B. Wu, et al. , Nat. Energy, 2020, 5, 561–568 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4, 3253–3266 RSC.
- C. Wang, A. Wang, L. Ren, X. Guan, D. Wang, A. Dong, C. Zhang, G. Li and J. Luo, Adv. Funct. Mater., 2019, 29, 1905940 CrossRef CAS.
- Y. Liang, Y. Chen, X. Ke, Z. Zhang, W. Wu, G. Lin, Z. Zhou and Z. Shi, J. Mater. Chem. A, 2020, 8, 18094–18105 RSC.
- G. Liu, Y. Yang, X. Lu, F. Qi, Y. Liang, A. Trukhanov, Y. Wu, Z. Sun and X. Lu, ACS Appl. Mater. Interfaces, 2022, 14, 31803–31813 CrossRef CAS PubMed.
- D. Liu, W. Zhu, J. Trottier, C. Gagnon, F. Barray, A. Guerfi, A. Mauger, H. Groult, C. Julien and J. Goodenough, et al. , RSC Adv., 2014, 4, 154–167 RSC.
- S. B. Peterson, J. Apt and J. Whitacre, J. Power Sources, 2010, 195, 2385–2392 CrossRef CAS.
- P. K. Nayak, E. M. Erickson, F. Schipper, T. R. Penki, N. Munichandraiah, P. Adelhelm, H. Sclar, F. Amalraj, B. Markovsky and D. Aurbach, Adv. Energy Mater., 2018, 8, 1702397 CrossRef.
- Y. Xie, M. Naguib, V. N. Mochalin, M. W. Barsoum, Y. Gogotsi, X. Yu, K.-W. Nam, X.-Q. Yang, A. I. Kolesnikov and P. R. Kent, J. Am. Chem. Soc., 2014, 136, 6385–6394 CrossRef CAS PubMed.
- G. Liu, N. Wang, F. Qi, X. Lu, Y. Liang and Z. Sun, Inorg. Chem. Front., 2023, 10, 699–711 RSC.
- L. Yaohua, K. Xi, L. Jun and S. Zhicong, Energy Storage Sci. Tech., 2017, 6, 1 Search PubMed.
- X. Ke, Z. Zhang, Y. Cheng, Y. Liang, Z. Tan, J. Liu, L. Liu, Z. Shi and Z. Guo, Sci. China Mater., 2018, 61, 353–362 CrossRef CAS.
- R. P. Joshi, J. Eickholt, L. Li, M. Fornari, V. Barone and J. E. Peralta, ACS Appl. Mater. Interfaces, 2019, 11, 18494–18503 CrossRef CAS PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al. , APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 RSC.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart and P. Lamp, et al. , Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Z. Zhang, Y. Shao, B. Lotsch, Y.-S. Hu, H. Li, J. Janek, L. F. Nazar, C.-W. Nan, J. Maier and M. Armand, et al. , Energy Environ. Sci., 2018, 11, 1945–1976 RSC.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Chem. Mater., 2018, 31, 342–352 CrossRef.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Nat. Commun., 2019, 10, 1–7 CrossRef PubMed.
- H. Xu, J. Zhu, D. P. Finegan, H. Zhao, X. Lu, W. Li, N. Hoffman, A. Bertei, P. Shearing and M. Z. Bazant, Adv. Energy Mater., 2021, 11, 2003908 CrossRef CAS.
- A. N. Mistry, K. Smith and P. P. Mukherjee, ACS Appl. Mater. Interfaces, 2018, 10, 6317–6326 CrossRef CAS PubMed.
- S. Hein, J. Feinauer, D. Westhoff, I. Manke, V. Schmidt and A. Latz, J. Power Sources, 2016, 336, 161–171 CrossRef CAS.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood III, Carbon, 2016, 105, 52–76 CrossRef CAS.
- E. Peled and S. Menkin, J. Electrochem. Soc., 2017, 164, A1703 CrossRef CAS.
- H. Zhang, C. Li, M. Piszcz, E. Coya, T. Rojo, L. M. Rodriguez-Martinez, M. Armand and Z. Zhou, Chem. Soc. Rev., 2017, 46, 797–815 RSC.
- Z. Wang, Y. Sun, L. Chen and X. Huang, J. Electrochem. Soc., 2004, 151, A914 CrossRef CAS.
- L. O. Valøen and J. N. Reimers, J. Electrochem. Soc., 2005, 152, A882 CrossRef.
- S. Lux, I. Lucas, E. Pollak, S. Passerini, M. Winter and R. Kostecki, Electrochem. Commun., 2012, 14, 47–50 CrossRef CAS.
- R. Jalem, M. Nakayama and T. Kasuga, J. Mater. Chem. A, 2014, 2, 720–734 RSC.
- N. Kireeva and V. S. Pervov, Phys. Chem. Chem. Phys., 2017, 19, 20904–20918 RSC.
- S.-H. Kim, K.-H. Choi, S.-J. Cho, E.-H. Kil and S.-Y. Lee, J. Mater. Chem. A, 2013, 1, 4949–4955 RSC.
- X.-B. Cheng, T.-Z. Hou, R. Zhang, H.-J. Peng, C.-Z. Zhao, J.-Q. Huang and Q. Zhang, Adv. Mater., 2016, 28, 2888–2895 CrossRef CAS PubMed.
- Z. Ahmad, T. Xie, C. Maheshwari, J. C. Grossman and V. Viswanathan, ACS Cent. Sci., 2018, 4, 996–1006 CrossRef CAS PubMed.
- Y.-T. Chen, M. Duquesnoy, D. H. Tan, J.-M. Doux, H. Yang, G. Deysher, P. Ridley, A. A. Franco, Y. S. Meng and Z. Chen, ACS Energy Lett., 2021, 6, 1639–1648 CrossRef CAS.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz and H. Tribukait, et al. , Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- K. A. Severson, P. M. Attia, N. Jin, N. Perkins, B. Jiang, Z. Yang, M. H. Chen, M. Aykol, P. K. Herring and D. Fraggedakis, et al. , Nat. Energy, 2019, 4, 383–391 CrossRef.
- K. Goebel, B. Saha, A. Saxena, J. R. Celaya and J. P. Christophersen, IEEE Instrum. Meas. Mag., 2008, 11, 33–40 Search PubMed.
- M.-F. Ng, J. Zhao, Q. Yan, G. J. Conduit and Z. W. Seh, Nat. Mach. Intell., 2020, 2, 161–170 CrossRef.
- A. E. Ruehli, IEEE Trans. Microw. Theory Tech., 1974, 22, 216–221 CrossRef.
- X. Hu, S. Li and H. Peng, J. Power Sources, 2012, 198, 359–367 CrossRef CAS.
- D. P. Finegan, J. Zhu, X. Feng, M. Keyser, M. Ulmefors, W. Li, M. Z. Bazant and S. J. Cooper, Joule, 2021, 5, 316–329 CrossRef.
- V. R. Subramanian, V. Boovaragavan and V. D. Diwakar, Electrochem. Solid-State Lett., 2007, 10, A255 CrossRef CAS.
- V. Boovaragavan, S. Harinipriya and V. R. Subramanian, J. Power Sources, 2008, 183, 361–365 CrossRef CAS.
- S. S. Mansouri, P. Karvelis, G. Georgoulas and G. Nikolakopoulos, IFAC-PapersOnLine, 2017, 50, 4727–4732 CrossRef.
- G. O. Sahinoglu, M. Pajovic, Z. Sahinoglu, Y. Wang, P. V. Orlik and T. Wada, IEEE Trans. Ind. Electron., 2017, 65, 4311–4321 Search PubMed.
- P. Khumprom and N. Yodo, Energies, 2019, 12, 660 CrossRef.
- P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins and Z. Yang, et al. , Nature, 2020, 578, 397–402 CrossRef CAS PubMed.
- H. Zou and T. Hastie, J. R. Stat. Soc. Series B Stat. Methodol., 2005, 67, 301–320 CrossRef.
- M. Hoffman, B. Shahriari and N. Freitas, Artificial Intelligence and Statistics, 2014, pp. 365–374 Search PubMed.
- A. Grover, T. Markov, P. Attia, N. Jin, N. Perkins, B. Cheong, M. Chen, Z. Yang, S. Harris and W. Chueh, et al., International Conference on Artificial Intelligence and Statistics, 2018, pp. 833–842.
- Z. Tong, J. Miao, S. Tong and Y. Lu, J. Clean. Prod., 2021, 317, 128265 CrossRef CAS.
- C. K. Chan, X. F. Zhang and Y. Cui, Nano Lett., 2008, 8, 307–309 CrossRef CAS PubMed.
- M. Saubanère, E. McCalla, J.-M. Tarascon and M.-L. Doublet, Energy Environ. Sci., 2016, 9, 984–991 RSC.
- M. Freire, N. V. Kosova, C. Jordy, D. Chateigner, O. Lebedev, A. Maignan and V. Pralong, Nat. Mater., 2016, 15, 173–177 CrossRef CAS PubMed.
- S. Abu-Sharkh and D. Doerffel, J. Power Sources, 2004, 130, 266–274 CrossRef CAS.
- A. Maheshwari, N. G. Paterakis, M. Santarelli and M. Gibescu, Appl. Energy, 2020, 261, 114360 CrossRef CAS.
- A. A. Franco, RSC Adv., 2013, 3, 13027–13058 RSC.
- D. D. Macdonald, Electrochim. Acta, 2006, 51, 1376–1388 CrossRef CAS.
- P. Singh, R. Vinjamuri, X. Wang and D. Reisner, Electrochim. Acta, 2006, 51, 1673–1679 CrossRef CAS.
- C. T. Love, M. B. Virji, R. E. Rocheleau and K. E. Swider-Lyons, J. Power Sources, 2014, 266, 512–519 CrossRef CAS.
- N. S. Spinner, C. T. Love, S. L. Rose-Pehrsson and S. G. Tuttle, Electrochim. Acta, 2015, 174, 488–493 CrossRef CAS.
- Y. Zhang, Q. Tang, Y. Zhang, J. Wang, U. Stimming and A. A. Lee, Nat. Commun., 2020, 11, 1–6 CrossRef PubMed.
- I. Babaeiyazdi, A. Rezaei-Zare and S. Shokrzadeh, Energy, 2021, 223, 120116 CrossRef CAS.
- D. Flam-Shepherd, A. Zhigalin and A. Aspuru-Guzik, arXiv, 2022, preprint arXiv:2202.00658.
- S. Honda, S. Shi and H. R. Ueda, arXiv, 2019, preprint arXiv:1911.04738.
- S. Kang and K. Cho, J. Chem. Inf. Model., 2018, 59, 43–52 CrossRef PubMed.
- A. Rives, J. Meier, T. Sercu, S. Goyal, Z. Lin, J. Liu, D. Guo, M. Ott, C. L. Zitnick and J. Ma, et al. , Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2016239118 CrossRef CAS PubMed.
- R. Dybowski, New J. Chem., 2020, 44, 20914–20920 RSC.
- Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing and V. Pande, Chem. Sci., 2018, 9, 513–530 RSC.
- Y. Hu and M. J. Buehler, APL Machine Learning, 2023, 1, 010901 CrossRef.
- D. Zhang, H. Bi, F.-Z. Dai, W. Jiang, L. Zhang and H. Wang, arXiv, 2022, preprint arXiv:2208.08236.
- A. Trewartha, N. Walker, H. Huo, S. Lee, K. Cruse, J. Dagdelen, A. Dunn, K. A. Persson, G. Ceder and A. Jain, Patterns, 2022, 3, 100488 CrossRef PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |