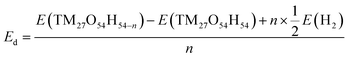Open Access Article
Open Access ArticleHigh-voltage deprotonation of layered-type materials as a newly identified cause of electrode degradation†
Junghoon
Yang
*ab,
Sungwon
Park
c,
Sungsik
Lee
d,
Jungpil
Kim
 b,
Di
Huang
a,
Jihyeon
Gim
b,
Di
Huang
a,
Jihyeon
Gim
 e,
Eungje
Lee
e,
Eungje
Lee
 e,
Gilseob
Kim
f,
Kyusung
Park
a,
Yong-Mook
Kang
*fg,
Eunsu
Paek
*c and
Sang-Don
Han
e,
Gilseob
Kim
f,
Kyusung
Park
a,
Yong-Mook
Kang
*fg,
Eunsu
Paek
*c and
Sang-Don
Han
 *a
*a
aMaterials, Chemical, and Computational Science Directorate, National Renewable Energy Laboratory, Golden, CO 80401, USA. E-mail: sang-don.han@nrel.gov
bCarbon and Light Materials Application R&D Group, Korea Institute of Industrial Technology, Jeonju, 54853, Republic of Korea. E-mail: jyang@kitech.re.kr
cDepartment of Chemical & Biomolecular Engineering, Clarkson University, Potsdam, NY 13699, USA. E-mail: epaek@clarkson.edu
dX-ray Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
eChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, IL 60439, USA
fDepartment of Materials Science and Engineering, Korea University, Seoul, 02841, Republic of Korea. E-mail: dake1234@korea.ac.kr
gKU-KIST Graduate School of Converging Science and Technology, Korea University, Seoul, 02841, Republic of Korea. E-mail: dake1234@korea.ac.kr
First published on 9th January 2023
Abstract
Further development of electrochemical devices and electric vehicles requires advanced secondary batteries with higher energy density, longer lifetime and enhanced thermal safety. Increasing the cell operating voltage is one of the realistic strategies to extend the energy density, but it is inevitably accompanied by irreversible structural changes and mechanical failure of the electrode materials and continuous parasitic reactions within the electrode–electrolyte interface resulting in capacity fading and subsequent battery failure along with safety issues. Herein, we report deprotonation of layered-type materials at high voltages (>4.5 V vs. Li/Li+) as a newly identified cause of electrode degradation, which has not been addressed previously. Electrochemical analysis and diagnostics combined with advanced characterization studies and computational simulations were employed to understand deprotonation mechanisms and investigate the effect of the deprotonation process on the electrode during high voltage operation. We demonstrated that protons act as charge carriers in lithium (Li)-free materials through the deprotonation process during the initial charging. In addition, this study shows that the deprotonation process is dependent upon transition metals and accordingly deteriorates the electrode by changing its structure and electrochemical properties.
Introduction
The importance of developing advanced electrochemical energy storage systems with higher energy density, longer lifetime and enhanced safety has been growing over the last few decades.1–3 Current Li-ion batteries (LIBs) are composed of layered structured electrodes based on an insertion-type ion storage mechanism.4 The energy density of a LIB is determined by the reversible capacities of the cathode and anode as well as the operating voltage window between them, so one of the proper design strategies toward higher energy density is to maximize the voltage difference between the anode and cathode, both of which have high capacities.5,6 Layered cathode materials have been attracting the attention of battery researchers thanks to their relatively higher reversible capacities and higher charging voltages. Among them, LiCoO2 had been popularly used as one of the commercial cathode materials through the 1990s and 2000s, but its capacity limit could not meet the substantial energy density required by electric vehicles (EVs).6 In this regard, nickel-based layered cathode materials (LiNi1−xMxO2, M = Co, Mn, Al, etc.) have been extensively developed to overcome the apparent limitation of LiCoO2.7 The target capacity of these nickel-based layered cathode materials is larger than 200 mA h g−1 and the charging voltages should be above 4.2 V (vs. Li/Li+, hereafter) to meet higher energy densities required for EV applications.8–13 Increasing the cell operating voltage, however, is inevitably accompanied by a plethora of electrode and electrolyte degradation mechanisms—irreversible structural changes, micro-fracture formation and continuous parasitic reactions within the electrode–electrolyte interface—that lead to rapid performance loss.14–20 Therefore, a fundamental and mechanistic understanding of underlying mechanisms in layered cathode materials during battery cycling at high voltages is critical for the development of next-generation LIBs.In addition to the aforementioned well-known observations at high voltages, recently an interesting phenomenon was observed from one of the layered cathode materials, birnessite (XMnO2·1.5H2O, X = alkali ions, such as Li, Na, and K) that has an intrinsically low amount of alkali ions (X < 0.4) in its as-prepared state due to the presence of crystal water and protons.21 Therein, the initial charge capacity should be lower than the subsequent discharge capacity considering the limited amount of alkali ions in its structure, but unexpectedly it shows higher charge capacity than the theoretical capacity implying that other electrochemical processes may be involved. Due to the low crystallinity of birnessite it is quite challenging to identify the origin of the unexpectedly high initial charge capacity, but the presence of protons in the structure may provide an important clue to unravel this interesting phenomenon: for example, the extracted protons in the structure could act as charge-carrier ions at high voltages (>4.5 V) instead of alkali ions. Considering the structural similarity between birnessite and other layered-type materials, it is highly possible to observe a similar interesting phenomenon in other layered-type materials containing protons, which motivates us to investigate its origin, detailed mechanisms and potential effects on the electrodes and cell performance. In addition, the role of a proton as a charge carrier in aqueous battery systems has been investigated by a number of research groups,22,23 but the presence of the proton and its role in non-aqueous battery systems during high-voltage operation is not well-studied. In general, the protons in the layered-type cathode materials originated from a direct exchange between Li+ and H+ due to exposure of the materials to a high-humidity atmosphere during the synthesis process.24 Several research studies reported that the activation energy of Li+ ion diffusion can be increased by blocking the Li+ ion channels due to the presence of protons in layered-type cathode materials, resulting in poor electrochemical performances.25,26
In this study, in order to provide a fundamental and mechanistic understanding of the correlation between deprotonation and electrochemical behaviors of layered-type materials in the non-aqueous electrolytes during high-voltage operation, layered-type transition-metal hydroxides, such as Mn0.5Ni0.5(OH)2−x, Ni(OH)2 and Co(OH)2, have been chosen as model materials. The electrochemical analysis and diagnostics combined with advanced characterization studies and first principles calculations enable us to investigate deprotonation mechanisms and its effects on these model materials. We observed that only Mn-containing hydroxide, Mn0.5Ni0.5(OH)2−x, showed a typical but strange initial charging behavior, whereas other model materials failed in electrochemical charging processes implying that deprotonation is a transition metal dependent phenomenon. In addition, we revealed that deprotonation degrades the structure and electrochemical properties of the electrode, and the extracted proton can be a potential capacity fading factor by forming corrosive HF in the LiPF6-based electrolyte systems. To the best of the authors' knowledge, there have been no previous literature reports of a high-voltage deprotonation mechanism and its detrimental effects on the proton containing layered-type cathode materials in a LIB.
Results and discussion
Structural properties and electrochemical behaviors of layered transition-metal hydroxides
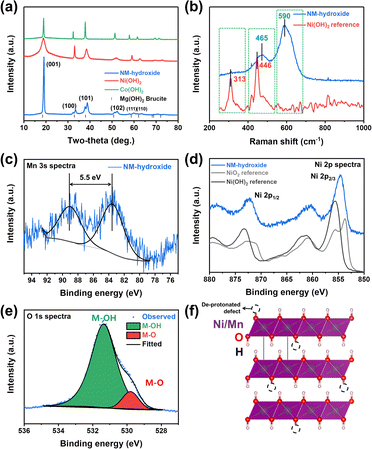
Powder-XRD analysis results indicate that Ni(OH)2, Co(OH)2 and Ni0.5Mn0.5(OH)2 (NM-hydroxide, hereafter) crystallize in a brucite (Mg(OH)2)-like structure with a space group of P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (Fig. 1a). These materials are built on transition metal (TM) hydroxide octahedra with Ni, Mn or Co atoms at the 1a (0, 0, 0) Wyckoff position, while O and H atoms are at the 2d (1/3, 2/3, z) position.27 These materials have interesting structural features of two different types of ionic TM–O bonds and covalent O–H bonds, which is different from typical Li-containing layered oxides that have only ionic TM–O and O–Li bonds. The peak split observed in NM-hydroxide indicates the coexistence of Ni and Mn in the material because pure Mn(OH)2 (Mn(II)) is unstable and readily changed to the Mn(hydro)-oxide phase that has a higher oxidation state of Mn(III) or Mn(IV).28
m1 (Fig. 1a). These materials are built on transition metal (TM) hydroxide octahedra with Ni, Mn or Co atoms at the 1a (0, 0, 0) Wyckoff position, while O and H atoms are at the 2d (1/3, 2/3, z) position.27 These materials have interesting structural features of two different types of ionic TM–O bonds and covalent O–H bonds, which is different from typical Li-containing layered oxides that have only ionic TM–O and O–Li bonds. The peak split observed in NM-hydroxide indicates the coexistence of Ni and Mn in the material because pure Mn(OH)2 (Mn(II)) is unstable and readily changed to the Mn(hydro)-oxide phase that has a higher oxidation state of Mn(III) or Mn(IV).28
Raman spectra of NM-hydroxide show two main bands centered at ∼465 cm−1 and ∼590 cm−1 as shown in Fig. 1b. The features are different from those of the typical transition metal hydroxide reference (e.g., Ni(OH)2) that shows main bands located at around ∼313 cm−1 and ∼446 cm−1. The first important observation in the Raman spectra of NM-hydroxide is the disappearance of a band centered at ∼313 cm−1. In a previous report, the Raman band at ∼313 cm−1 corresponds to the presence of a proton and specifically proton motion regarding the oxygen position (TM–OH rotational vibrational mode) in transition metal hydroxide.29 The vanishing of the signal may have originated from partial oxidation of TM–(OH)2 to TM–OOH in NM-hydroxide that is in the oxidized phase as a result of transition metal oxidation and the resultant deprotonation. In addition, the slight shift of a band from ∼446 cm−1 to ∼465 cm−1 with the appearance of a new band at ∼590 cm−1, as the second important change, demonstrates the partial oxidation of Mn0.5Ni0.5(OH)2 to Mn0.5Ni0.5(OOH2−x).29 As explained in the XRD results, the instability of the Mn(OH)2 phase induces oxidation of Mn and structural distortion of an ideal hydroxide structure that result in the changes in Raman spectra.
Additional XPS analysis was performed to confirm the partial oxidation of TM-hydroxide focusing on oxidation states of Mn and Ni in NM-hydroxide (Fig. 1c–e). Generally, the Mn 2p core level is known to possess complicated multiplet splitting that makes it difficult to resolve minute changes in the position and asymmetry of peaks from manganese.29 Therefore, the Mn 3s core level was analyzed to identify the valence state of Mn in NM-hydroxide (Fig. 1c). It is known that the Mn 3s core level energy (ΔE3s) is decreased as Mn valency is increased. For example, the ΔE3s of MnO (Mn2+) is ∼6 eV, that of Mn2O3 (Mn3+) is ∼5.5 eV and that of MnO2 (Mn4+) is ∼4.7 eV, respectively.30 For NM-hydroxide, thus, about 5.5 eV of ΔE3s indicates that the oxidation state of Mn is +3 rather than +2 by partial oxidation due to unstable Mn(OH)2. As shown in Fig. 1d, the Ni 2p core level spectra of NM-hydroxide are analyzed and compared with those of Ni(OH)2 and carefully treated NiO2 references with Ni2+ and Ni4+, respectively, to determine the valence state of Ni. Ni 2p spectra of NM-hydroxide consist of two spin–orbit doublets at binding energy values of ∼855.6 eV and ∼873.2 eV, and they can be assigned to Ni 2p2/3 and Ni 2p1/2, respectively. As can be seen from the two different reference materials, Ni 2p spectra have obvious differences in the peak position and peak shape. Ni 2p spectra of NiO2 can be clearly identified by the unique peak splitting for both Ni 2p3/2 and Ni 2p1/2, whereas neither of them are observed from Ni(OH)2. Also, the peak position of Ni 2p peaks of NiO is located at a lower value than that of Ni(OH)2.31 As NM-hydroxide shows similar Ni 2p spectra to that of the Ni(OH)2 reference material, it can be inferred that the state of Ni in the material is close to Ni2+ rather than Ni4+. Fig. 1e presents O1s core level spectra of NM-hydroxide. The O 1s peak can be deconvoluted into two components: the one at 529.8 eV is assigned to the typical bond of oxygen in metal oxides (M–O), while the other at 531.4 eV corresponds to hydroxide (M–OH), which is consistent with the previous report on Ni(OH)2.32 The dominant M–OH signal of O 1s spectra well supports the feature of hydroxide and the presence of M–O might be related to partial oxidation of NM-hydroxide. The XPS analysis results confirm that the oxidation states of Mn (as Mn3+) and Ni (as Ni2+) in NM-hydroxide indicating a partial deprotonated state from the ideal Ni0.5Mn0.5(OH)2 to Ni0.5Mn0.5(OH)2−x, and the deprotonated defect of TM–O–H may have occurred from Mn–O–H rather than Ni–O–H (Fig. 1f).
Electrochemical behaviors of NM-hydroxide were analyzed using coin-type cells with a Li metal counter/reference electrode and a Gen2 electrolyte (1.2 M lithium hexafluorophosphate (LiPF6) in ethylene carbonate (EC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl methyl carbonate (EMC), 3
ethyl methyl carbonate (EMC), 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
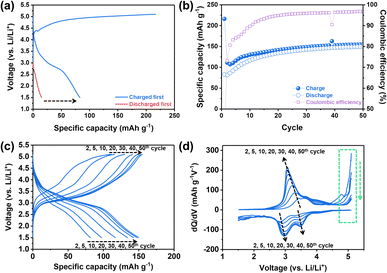
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 wt%, water content: <10 ppm). The specific capacity vs. voltage profile and the corresponding differential capacity (dQ/dV) plot for the 1st cycle were obtained by using two different electrochemical protocols (Fig. 2a and S1†): (1) charging first and then discharging (general electrochemical test protocol of cathode materials) and (2) discharging without the initial charging. Here, charging means applying a positive current to increase the cell voltage against the Li metal counter/reference electrode. In general, for lithium transition metal oxides (e.g., LiCoO2 and LiNixMnyCozO2), lithium ions, as charge carriers, are extracted during the initial charging process. It can be expected that, however, the electrochemical reactions of NM-hydroxide during initial charging are different from those of lithium transition metal oxides due to the absence of lithium ions in its initial structure. In particular, analysis of discharging capacities based on two different electrochemical protocols can provide potential origin (e.g., either one or a combination of factors including electrolyte decomposition, cathode–electrolyte interphase (CEI) formation, electrode structural changes, etc.) of the unexpectedly high charging capacity (∼216 mA h g−1 as shown in Fig. 2a). It is clear that the discharge capacities of NM-hydroxide are greatly dependent on the electrochemical test protocols (Fig. 2a). A minute discharge capacity of around 15 mA h g−1 without initial charging may be related to lithium ions insertion into the layered transition-metal hydroxides (Fig. S2†) as reported in previous studies demonstrating the electrochemical behaviors of layered transition-metal hydroxide as anode materials.33,34 On the other hand, it is noteworthy that the NM-hydroxide electrode tested with the initial charging protocol shows a significant increase in discharge capacity (approximately 83 mA h g−1) implying possible structural changes in NM-hydroxide that may allow the insertion of more lithium ions during subsequent cycles in addition to well-known reactions including oxidative electrolyte decomposition and CEI formation during charging.
7 wt%, water content: <10 ppm). The specific capacity vs. voltage profile and the corresponding differential capacity (dQ/dV) plot for the 1st cycle were obtained by using two different electrochemical protocols (Fig. 2a and S1†): (1) charging first and then discharging (general electrochemical test protocol of cathode materials) and (2) discharging without the initial charging. Here, charging means applying a positive current to increase the cell voltage against the Li metal counter/reference electrode. In general, for lithium transition metal oxides (e.g., LiCoO2 and LiNixMnyCozO2), lithium ions, as charge carriers, are extracted during the initial charging process. It can be expected that, however, the electrochemical reactions of NM-hydroxide during initial charging are different from those of lithium transition metal oxides due to the absence of lithium ions in its initial structure. In particular, analysis of discharging capacities based on two different electrochemical protocols can provide potential origin (e.g., either one or a combination of factors including electrolyte decomposition, cathode–electrolyte interphase (CEI) formation, electrode structural changes, etc.) of the unexpectedly high charging capacity (∼216 mA h g−1 as shown in Fig. 2a). It is clear that the discharge capacities of NM-hydroxide are greatly dependent on the electrochemical test protocols (Fig. 2a). A minute discharge capacity of around 15 mA h g−1 without initial charging may be related to lithium ions insertion into the layered transition-metal hydroxides (Fig. S2†) as reported in previous studies demonstrating the electrochemical behaviors of layered transition-metal hydroxide as anode materials.33,34 On the other hand, it is noteworthy that the NM-hydroxide electrode tested with the initial charging protocol shows a significant increase in discharge capacity (approximately 83 mA h g−1) implying possible structural changes in NM-hydroxide that may allow the insertion of more lithium ions during subsequent cycles in addition to well-known reactions including oxidative electrolyte decomposition and CEI formation during charging.
It is also important to understand the main factors—generally, redox centers and charge carriers—related to the redox behaviors of materials. For example, LiCoO2 is known to have cobalt (Co) as a definite redox center and Li+ ion as a charge carrier. In classical electrochemical reactions, Co3+/4+ ions release or uptake the electrons, while Li+ ions deinsert/insert from/into the cathode to maintain the charge neutrality of the material.35,36 Also, a recent study revealed that oxygen (O) also participates in electrochemical reactions as a redox center instead of TM under certain conditions, which is called an anionic redox reaction.37 In both classical and anionic redox reactions, it is a matter of which element in the material is the redox center (TM vs. oxygen) while the Li+ ions still act as charge carriers for those reactions.37 Considering that there were no Li+ ions in the as-prepared NM-hydroxide, however, it is important to understand which element in the structure acts as a charge carrier to contribute the initial charge capacity of ∼216 mA h g−1. The aforementioned reactions at high voltages including electrolyte decomposition, CEI formation and electrode structure changes are attributed to the initial charge capacity, but a significant increase in discharge capacity with initial charging indicates additional possible redox reactions by protons in NM-hydroxide as charge carriers. As shown in Fig. S3,† the initial discharge capacities of the NM-hydroxides are ∼31 and ∼82 mA h g−1, when the NM-hydroxides were charged up to 4.8 and 5.1 V, respectively, indicating that the electrochemical behavior of the NM-hydroxides is charge voltage-dependent.
To further understand electrochemical behaviors of NM-hydroxide upon cycling, the reversible specific capacities of up to 50 cycles were analyzed. As shown in Fig. 2b, the reversible capacities of NM-hydroxide are gradually increased and stabilized to around 150 mA h g−1. Interestingly, this value is close to half of the theoretical capacity of a typical TM oxide (LiTMO2) when only half of the Li+ ions in the structure participated in electrochemical reactions. The specific capacity vs. voltage profiles and the corresponding differential capacity (dQ/dV) plots of NM-hydroxide for different cycle numbers (Fig. 2c and d) indicate that the gradual increase of reversible capacity originated from the activated redox reactions at ∼3.2 V for charging and ∼3.5 and ∼3.0 V for discharging with the decrease in overpotential upon cycling. The voltage regions for the activated redox reactions correspond to manganese redox (Mn3+/4+) rather than nickel redox (Ni2+/4+), so it can be assumed that Mn may dominantly play a role as a redox center in NM-hydroxide. To verify this assumption, the same electrochemical verification of commercially available Ni(OH)2 and Co(OH)2 was conducted, and neither of them showed a typical electrochemical charging behavior (Fig. S4†).
Analysis of transition metal dependent redox chemistry and structural changes upon electrochemical processes
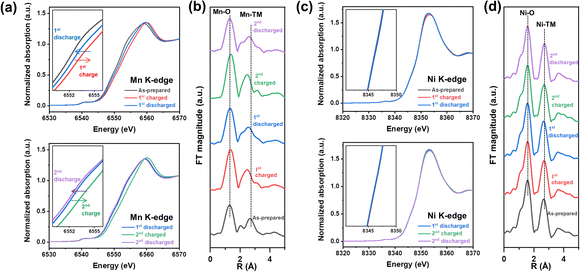
Mn and Ni K-edge X-ray absorption spectroscopy (XAS) analysis was conducted to explore the origin of redox centers in NM-hydroxide by analyzing the changes in the valence state and local coordination environment of transition metals in elementally selective ways. Fig. 3 shows the normalized X-ray absorption near edge structure (XANES) spectra and extended X-ray absorption fine structure (EXAFS) spectra obtained from the as-prepared, fully charged and fully discharged samples for the 1st and 2nd cycles. As shown in Fig. 3a and c, the Mn K-edge XANES spectra show clear edge shifts to higher energy upon charging and shifts to lower energy upon discharging, whereas the Ni K-edge XANES spectra represent a negligible change, indicating that Mn is a dominant redox center for the electrochemical processes in NM-hydroxide. Specifically, the Mn K-edge XANES spectra obtained from the discharged electrodes for the 1st and 2nd cycles support the observed electrochemical behavior (Fig. 2c). For instance, the edge position of the 2nd discharged electrode spectra shifts to lower energy compared to that of the 1st discharged electrode spectra, which implies that reduced Mn (Mn3+) is gradually increased due to continuous activation of electrochemically active Mn species in NM-hydroxide. The gradual increase in reversible capacity and the reduced overpotential in redox reactions at around 3.0–3.5 V during cycling (Fig. 2b and d) corroborate this.The local structural changes in NM-hydroxide are also analyzed based on Mn and Ni K-edge EXAFS spectra as shown in Fig. 3b and d. In Fourier transformed (FT) EXAFS spectra for the Mn and Ni K-edge regions, the strongest peak at ∼1.5 Å is attributed to the closest oxygen (Mn–O/Ni–O), while the peaks between ∼2.5 and ∼3.0 Å can be assigned to Mn–TM/Ni–TM bonds. Similar to the XANES results, there are negligible changes in Ni K-edge EXAFS spectra upon electrochemical processes (Fig. 3d). On the other hand, the local coordination around Mn is significantly changed during the electrochemical reactions (Fig. 3b): EXAFS peaks located between ∼2.5 and ∼3.0 Å corresponding to Mn–TM bonds show clear peak splitting and merging. In general, the peaks at ∼2.5 and ∼3.0 Å assigned to Mn in the adjacent octahedra with edge-sharing (Mn–Mnedge) and corner-sharing (Mn–Mncorner, longer Mn–Mn distance), respectively.38 It can be speculated that splitting and merging of the peaks corresponding to Mn-TM bonds originated from the formation of a locally present 3D structure in short-range order. For example, α-MnOOH—partially de-protonated material from layered Mn(OH)2—has the co-presence of edge-sharing and corner-sharing MnO6 octahedra in its distorted 3D structure.39 Also, it is known that δ-MnO2 consisting of only edge-sharing MnO6 shows a single intense peak corresponding to Mn–Mnedge, whereas β-MnO2 consisting of both edge-sharing and corner-sharing MnO6 represents the double peaks corresponding to Mn–Mnedge and Mn–Mncorner in the EXAFS spectra.40 Based on the observation in the Mn EXAFS spectra, the crystal structure of NM-hydroxide which changed during electrochemical processes is not an ideal layered structure, but rather a complicated 3D structure. This could be accompanied by changes in Mn coordination according to the migration of Mn from its octahedral sites to the adjacent Li sites, similar to the previously reported changes in layered LiMnO2.41
To gain a deeper insight into the deprotonation reaction mechanisms and structural changes during the electrochemical processes, we employed Raman spectroscopic and XRD analyses (Fig. 4). Before the analyses, we hypothesized that there are two possible actuating mechanisms in the redox reactions of NM-hydroxide at high voltages: (1) participation of H+ ions as charge carriers instead of Li+ ions and (2) insertion/deinsertion of PF6− anions. Anion (de)insertion is less common than cation (de)insertion, but charge compensation mechanisms based on anion (de)insertion at high voltages were already reported in layered cathode material. For instance, reversible co-insertion/-deinsertion of both cations and anions into/from the P3-type Na0.5Ni0.25Mn0.75O2 electrodes was studied in the NaClO4-based electrolyte systems, which demonstrates (de)insertion of ClO4− anions, accompanied by an anionic (O2− ↔ O−) reversible redox, at relatively higher voltages compared to (de)insertion of Na+ cations.42 As shown in Fig. 4a, Raman spectra of the electrodes cycled at different states of charge (SOC) and depths of discharge (DOD) were analyzed to verify the possible insertion/deinsertion of PF6− anions into/from NM-hydroxide at high voltages by focusing on the peak at around741 cm−1 in the spectra corresponding to the PF6− stretching band.43 No signal from a specific peak position, however, implies that PF6− anions (de)insertion may not occur in redox reactions of NM-hydroxide.
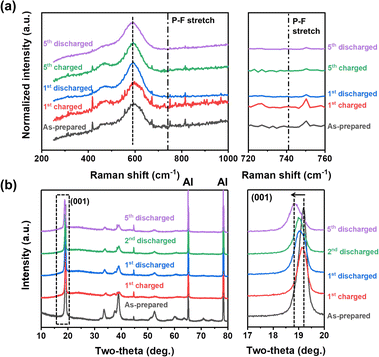 | ||
| Fig. 4 (a) Raman spectra and (b) XRD patterns of the as-prepared, fully charged and fully discharged NM-hydroxide samples in different cycles. | ||
The structural changes in NM-hydroxide induced by electrochemical reactions were further analyzed using ex situ XRD. Specifically, the changes of the (001) peak position—mainly related to interlayer-spacing between adjacent octahedra of TM–OH slabs—were analyzed. In general, the interlayer spacing is mostly affected by the shielding effect of repulsive forces between oxygen atoms located in adjacent layers. Transition metal hydroxides, however, have distinctive structural characteristics with covalent bonding of O and H (Fig. 1f), which makes the repulsive forces between adjacent O atoms relatively weak and thus have a narrower interlayer spacing than that of conventional lithium containing transition metal oxides. If the PF6− anion insertion occurs during the electrochemical reactions, the interlayer spacing should be expanded due to the larger size of PF6− anions compared with that of Li+ cations. As shown in Fig. 4b, the (001) peak position after the initial charging process is similar to that of the as-prepared state indicating no significant change in interlayer spacing, whereas the interlayer spacing of NM-hydroxide is expanded after the initial discharging process. Therefore, it seems reasonable to exclude PF6− insertion in the first charging process.
The electrochemical reactions after the initial charging process are quite complicated due to the co-contribution of protons and Li+ ions as charge carriers. The (001) peaks of discharged states for the 2nd and 5th cycles are found at lower two-theta angles indicating gradual expansion of interlayer spacing, while the increase of the full width at half maximum (FWHM) of those peaks is related to the loss of crystallinity (Fig. S5†) due to the local re-arrangement of Mn as shown in XAS analysis (Fig. 3). Specifically, gradual expansion of interlayer spacing may be correlated with the formation of Li-containing layered-type oxides as a result of repetitive electrochemical substitution of protons for Li+ ions over the cycles.
Computational study on transition metal dependent deprotonation mechanisms
Density functional theory (DFT) calculations were performed to examine how the structure, energy and electronic properties of the transition metal hydroxide (TM(OH)2) electrodes are influenced by the progressive deprotonation. The deprotonation energy (Ed) was calculated first to predict the energy cost to extract a single proton from the system. In the simulation, Ed was calculated as follows:where n denotes the number of extracted hydrogen atoms, and E(TM27O54H54), E(TM27O54H54−n) and E(H2) are the total energies of a pristine electrode, a dehydrogenated electrode, and an isolated hydrogen molecule, respectively. Note that in the simulation, the removal of a hydrogen atom from the simulation domain can be considered equivalent to the removal of a proton since the released electron from the cathode flows to the anode via the external circuit to maintain the overall neutrality. Here, we randomly removed 1, 3, 6, and 12 hydrogens from the electrodes which correspond to the removal of 2%, 6%, 11%, and 22% protons, respectively.
The calculated deprotonation energies (Table 1) show all positive values for the considered systems, implying that proton extraction is not a favorable reaction. The results show that the Mn systems exhibit the lowest deprotonation energies compared to the Co and Ni systems at all degrees of deprotonation. For example, Ed for the Mn system is 1.51 eV (vs. 1.79 and 2.41 eV for Co and Ni systems) when n = 1, and Ed for the Mn system is 1.46 eV (vs. 1.97 and 2.33 eV for Co and Ni systems) when n = 12. Interestingly, in the case of the Mn system, the required energy for single proton extraction remains consistent at varying degrees of deprotonation (Ed = 1.51, 1.52, 1.51 and 1.46 eV at n = 1, 3, 6, and 12, respectively), while the deprotonation energies for Co or Ni are increased or slightly fluctuated with increasing n. DFT calculation results indicate that protons could be relatively easily extracted from Mn27O54H54 compared to Co27O54H54 and Ni27O54H54.
| E d (eV) | ||||
|---|---|---|---|---|
| n = 1 | n = 3 | n = 6 | n = 12 | |
| a n represents the number of extracted protons from TM27O54H54 (TM = Mn, Co, and Ni). | ||||
| Mn | 1.51 | 1.52 | 1.51 | 1.46 |
| Co | 1.79 | 1.88 | 1.92 | 1.97 |
| Ni | 2.41 | 2.35 | 2.39 | 2.33 |
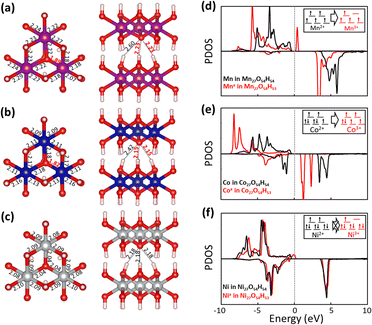
Fig. 5 shows fully relaxed configurations of TM27O54H53 (n = 1, single proton removal) with TM–O and H–O distances. First, slightly distorted structures near the deprotonated O are observed for both Mn27O54H53 and Co27O54H53. The distortion leads to the shortened bond length between Mn (Co) and the deprotonated O being 1.89 (1.82) Å compared with the other two bond lengths of 2.22 (2.18) Å (Fig. 5a and b). Note that the bond length between Mn (Co) and O in the pristine electrodes is 2.23 (2.14) Å, which is well consistent with the experimental value of 2.196 (2.116) Å.44,45 In the case of Ni27O54H53, the structural symmetry is well preserved near the deprotonated O site with identical Ni–O bond and H–O bond lengths of 2.04 Å—slightly shorter than the original value of 2.08 Å—and 2.18 Å, respectively. The structural evolutions upon progressive deprotonation were further investigated by calculating the distribution of TM–O–TM angles (Fig. S6†). At a low deprotonation level (n = 3, three proton removal), TM–O–TM angles exhibit a relatively narrower peak distribution with a main peak position of 97° for the three systems (see the bottom three panels in Fig. S6†). As the deprotonation degree increases (n = 6 and 12, six and twelve proton extraction), the distribution of angles becomes broadened as the structures are further disordered. Our results also show that the degree of disorder upon deprotonation strongly depends on the type of transition metal atom. Specifically, the angular distribution of Ni–O–Ni (Fig. S6c†) is likely to maintain its initial shape with a slightly broadened distribution, indicative of a relatively rigid framework upon deprotonation. The Mn system, however, shows a broader angular distribution than the Co and Ni systems at the same deprotonation level, implying that the Mn-based system possesses a largely distorted structure upon deprotonation.
To investigate the transition metal dependent distortion, we calculated the projected density of states (PDOS) of TM in pristine TM27O54H54, and TM with distortion in TM27O54H53. For Mn (black line in Fig. 5d) in Mn27O54H54, the spin-up states are only filled up while the spin-down states are mostly unoccupied, indicating that Mn is in the +2 state.46 The extraction of a proton pushes the spin-up orbitals over the Fermi level (red line), resulting in the formation of an Mn3+ ion. The transition of Mn oxidation states can be quantitatively confirmed by calculating the magnetic moment values of 4.64μB (Mn2+) and 4.04μB (Mn3+), respectively. Therefore, the distortion of Mn27O54H53 could be associated with the strong Jahn–Teller effect on an Mn3+ ion, which is commonly observed in Mn-based layered oxide materials.47,48 Similarly, Co2+ (2.78μB) in pristine Co27O54H54 is oxidized to Co3+ (3.13μB) upon deprotonation, resulting in the Jahn–Teller distortion effect within the structure. For Ni in the pristine system (Fig. 5f), both spin-up and spin-down states are occupied, while some of the down-spin d orbitals are unoccupied, representing the typical low spin states of Ni2+.49 It is worth noting that a noticeable change was not observed in the electronic structure of Ni with deprotonation, indicating that Ni is redox-inactive during the proton extraction process. The calculated magnetic moment of a Ni ion is marginally changed from 1.81μB to 1.74μB with deprotonation, resulting in inactive Jahn–Teller distortion.
Potential detrimental effect of deprotonation on electrochemical cells
A potential detrimental effect of deprotonation which occurred at high voltages was studied by visual observation and surface chemistry analysis on both electrodes cycled in two different electrolytes—Gen2 and LiTFSI–EC/EMC (1.0 M lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC, 3
EMC, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 wt%)—compared with pristine electrodes. Different from the cells fabricated with the Gen2 electrolyte, the cells tested in the LiTFSI–EC/EMC electrolyte failed to demonstrate reasonable electrochemical performance (Fig. S7†) due to severe aluminum (Al) corrosion which occurred at around 3.8 V in the presence of LiTFSI salt.50 As shown in Fig. 6a and b, the cycled and washed Li metal facing the NM-hydroxide electrodes in the Gen2 electrolyte displays a drastic discoloration with strong attachment of a separator (Fig. S8†) after the 1st charging, while this is not the case for the LiTFSI–EC/EMC electrolyte.
7 wt%)—compared with pristine electrodes. Different from the cells fabricated with the Gen2 electrolyte, the cells tested in the LiTFSI–EC/EMC electrolyte failed to demonstrate reasonable electrochemical performance (Fig. S7†) due to severe aluminum (Al) corrosion which occurred at around 3.8 V in the presence of LiTFSI salt.50 As shown in Fig. 6a and b, the cycled and washed Li metal facing the NM-hydroxide electrodes in the Gen2 electrolyte displays a drastic discoloration with strong attachment of a separator (Fig. S8†) after the 1st charging, while this is not the case for the LiTFSI–EC/EMC electrolyte.
The energy-dispersive X-ray spectroscopy (EDS) technique was utilized to further investigate the surface chemistry changes of Li metal cycled in the Gen2 electrolyte. It is noted that the attached separator was not fully removed as shown in Fig. 6a, so this may affect the EDS signals. As shown in Fig. 6c, the most distinctive elemental signals from Li metal cycled in the Gen2 electrolyte are F, O, P and C that could have originated from the solid–electrolyte interphase (SEI) layers formed from the reduction of electrolyte components, such as EC, EMC and LiPF6. In particular, we could observe the weak Ni and Mn signals which originated from dissolved and cross-talked transition metals of the NM-hydroxide electrode by deprotonation and the subsequent highly corrosive HF formation. It is well known that the protons from a trace amount of water in the LiPF6-based electrolyte results in the continuous formation of HF based on the following reactions:51
| H+ + PF6− ↔ H–F–PF5 | (1) |
| H–F–PF5 ↔ HF + PF5 | (2) |
On the other hand, O, F, S, C and Al have distinctive signals from the cycled Li metal in the LiTFSI–EC/EMC electrolyte. The O, F, S and C signals could have originated from the SEI layers formed from the reduction of electrolyte components including EC, EMC and LiTFSI, while the relatively stronger Al signal (compared with that of the Gen2 electrolyte) originates from dissolved and cross-talked Al traces due to Al current collector corrosion in the LiTFSI-based electrolyte. The edge damaged Al current collector of the cycled NM-hydroxide electrode also well demonstrates the Al corrosion issue in the LiTFSI–EC/EMC electrolyte (Fig. 6d).
Fig. 6e shows the SEM images of the pristine NM-hydroxide particles and the collected particles from the charged NM-hydroxide electrodes in two different electrolytes. The NM-hydroxide particles were synthesized by the co-precipitation method, and the secondary particles have a spherical shape with a size of ∼10 μm. Each secondary particle is composed of plate-like primary particles with a size of ∼100–300 nm as shown in Fig. S9.† Contrary to severe changes in the cycled Li metal anode in the Gen2 electrolyte, the NM-hydroxide secondary particles obtained from the charged cathodes in the Gen2 electrolyte showed a negligible change possibly due to the decomposition of the CEI by the formed HF.52 The LiPF6-based electrolytes are the most successful and heavily used for commercial LIBs, but the demonstrated potential issues of transition metal dissolution and crosstalk and decomposition of electrolyte–electrode interphases (EEIs) because of deprotonation and HF formation should be addressed for the development of advanced LIBs. It is noteworthy that layered-type transition metal oxide materials typically contain the protons through Li+–H+ exchange during ambient air synthesis and storage due to their high surface reactivity, which may cause similar problems as shown in the model NM-hydroxide.53
Conclusions
In summary, we have studied the detailed mechanisms of the deprotonation process in layered transition-metal hydroxide materials at a high-voltage region (>4.5 V) and its detrimental effects on electrochemical performance using a combination of electrochemical analysis and diagnostics, advanced characterization studies and computational simulations. Our study reveals critical electrochemical behaviors of layered structured materials during high-voltage charging: (1) protons in a layered structure can be deprotonated in the initial charge process; (2) extracted protons can play a role as charge carrier in Li-free materials; (3) deprotonation process is dependent upon transition metals and accordingly deteriorates the electrode by changing its structure and electrochemical properties; and (4) extracted protons can form corrosive HF in a LiPF6-based electrolyte resulting in detrimental effects, such as transition metal dissolution and crosstalk, decomposition of EEIs and continuous capacity fading during cell cycling. The detailed research newly suggests that the deprotonation process should be considered in the development of high-voltage cathode materials along with previously reported irreversible structural changes and oxidative electrolyte decomposition during high-voltage charging. We believe that the knowledge obtained from the fundamental and mechanistic studies will allow for rational design of advanced high-voltage cathodes and/or new electrolyte formulations for the development of next-generation rechargeable batteries with higher energy density, longer lifespan and enhanced safety.Experimental
Material synthesis
Layered nickel–manganese hydroxide, Ni0.5Mn0.5(OH)2, was synthesized by the co-precipitation method with transition metal solution consisting of a desired molar ratio of transition metals prepared by dissolving NiSO4·6H2O and MnSO4·5H2O (Sigma-Aldrich) in distilled water. The prepared metal solution (2 M) was continuously fed into a continuously stirred tank reactor (CSTR, 4 L), while an appropriate amount of an aqueous ammonia solution (5 M) as a chelating agent was pumped into the reactor at an appropriate feed rate to retain the ratio of metal and ammonia. The pH was kept at 10.6 by controlling the feed of sodium hydroxide solution and temperature was maintained at 55 °C to produce a homogeneous composition with an expected morphology. The product from the CSTR with 24 hours reaction was washed and filtered several times with distilled water to remove any unreacted sulfate and ammonia. The filtered powder was dried in nitrogen flowed oven overnight to avoid any oxidation.Material characterization studies
The crystal structures of the samples were analyzed by powder X-ray diffraction (PXRD, Rigaku D/Max, Cu Kα, operating at a voltage of 40 kV and a current of 250 mA). X-ray photoelectron spectroscopy (XPS) measurements were performed in a Thermo/K-Alpha ESCA System photoelectron spectrometer under ultrahigh vacuum (UHV) conditions. The morphology and microstructure of the samples were characterized using a field emission scanning electron microscope and energy dispersive X-ray spectroscopy (FE-SEM and EDS, Hitachi). The Mn and Ni K-edge XAS were measured at beamline 12-BM of the Advanced Photon Source in the Argonne National Laboratory. Raman spectroscopic analysis was conducted by using a Horiba XploRA™ PLUS V1.2 Multiline Confocal Raman microscope (30 mW air cooled laser diode (638 nm) and 0.5 numerical aperture).Electrochemical property evaluations
All electrochemical tests were conducted using CR2032 coin-type cells. The working electrode consisted of 80 wt% active materials, 10 wt% conductive carbon (super C65) and 10 wt% polyvinylidene fluoride (PVdF) binder. The mixture was dispersed in N-methyl pyrrolidone (NMP) and then hand ground for 30 min using a mortar and a pestle. The slurry was cast onto an Al foil and dried at 120 °C for 12 h under vacuum. The loading density of the electrode was ∼5 mg cm−2. The coin-type cells were assembled using a Celgard 2325 as the separator, a Li metal disc as the counter and reference electrodes, and 50 μL of “Gen2” electrolyte (1.2 M lithium hexafluorophosphate (LiPF6) in ethylene carbonate (EC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl methyl carbonate (EMC), 3
ethyl methyl carbonate (EMC), 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 wt%) as the electrolyte. Cell assembly was performed in an Ar-filled glove box. Galvanostatic charge and discharge tests and cyclic voltammetry (CV) were conducted using a Maccor battery cycler (Series 4000).
7 wt%) as the electrolyte. Cell assembly was performed in an Ar-filled glove box. Galvanostatic charge and discharge tests and cyclic voltammetry (CV) were conducted using a Maccor battery cycler (Series 4000).
Computational simulation
The atomic and electronic structures were calculated using density functional theory (DFT) within the Perdew–Becke–Ernzerhof generalized gradient approximation (GGA-PBE), as implemented in the Vienna Ab Initio Simulation Package (VASP).54 We employed the projector augmented wave (PAW) method to describe the interaction between core and valence electrons, and a planewave basis set with a kinetic energy cutoff of Ecut = 520 eV. The TM(OH)2 systems were modeled using a 3 × 3 × 3 supercell; each supercell had 27 TM (TM = Mn, Co and Ni), 54 O and 54 H atoms as shown in Fig. S10.† We used a (2 × 2 × 1) gamma-centered k-point mesh for the geometry optimization and energy calculations, and a (5 × 5 × 2) gamma-centered k-point mesh for the projected density of states (PDOS). The Hubbard U correction was used to reflect the strong correlation of 3 d electrons in transition metal ions. The values of U for Mn, Co and Ni were set to 4.5, 4.9 and 6.5 eV, respectively.55,56 Grid based Bader charge analysis was employed to determine the charge redistributions.57Author contributions
Junghoon Yang: conceptualization, investigation, formal analysis, validation, visualization, writing – original draft, funding acquisition; Sungwon Park: software, formal analysis, visualization, writing – original draft; Sungsik Lee: investigation, formal analysis; Jungpil Kim: investigation, formal analysis; Di Huang: investigation; Jihyeon Gim: resources, writing – review & editing; Eungje Lee: writing – review & editing; Gilseob Kim: investigation; Kyusung Park: review & editing; Yong-Mook Kang: writing – review & editing, funding acquisition; Eunsu Paek: writing – software, formal analysis, review & editing; Sang-Don Han: conceptualization, methodology, supervision, writing – original draft, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was authored in part by the Alliance for Sustainable Energy, LLC, and the manager and operator of the National Renewable Energy Laboratory (NREL) for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Support from the Vehicle Technologies Office (VTO), Hybrid Electric Systems Program, David Howell (Manager), Battery R&D, and Peter Faguy (Technology Manager), at the U.S. DOE, Office of Energy Efficiency and Renewable Energy, is gratefully acknowledged. The XAS research used beamline 12-BM of the Advanced Photon Source (APS), a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by the Argonne National Laboratory (ANL) under Contract No. DE-AC02-06CH11357. The authors acknowledge the Texas Advanced Computing Center (TACC) for providing HPC resources that have contributed to the research results reported within this paper. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes. J. Yang acknowledges funding from the National Research Foundation of Korea (NRF) under grant number NRF-2022R1F1A1071444 and the Korea Institute of Industrial Technology (KITECH UR-22-0020). Y.-M. K. acknowledges funding from the National Research Foundation of Korea (NRF) under grant numbers NRF-2017M3D1A1039561, NRF-2017R1A5A1015365, NRF-2017R1A2B3004383, and NRF-2020M3D1A1110527.References
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359 CrossRef CAS PubMed.
- M. Aramand and J. M. Tarascon, Nature, 2008, 451, 652 CrossRef PubMed.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167 CrossRef CAS PubMed.
- H. Xia, L. Lu, Y. S. Meng and G. Ceder, J. Electrochem. Soc., 2007, 154, A337 CrossRef CAS.
- J. B. Goodenough, Acc. Chem. Res., 2014, 46, 1053 CrossRef PubMed.
- M. Winter, J. O. Besenhard, M. E. Spahr and P. Novák, Adv. Mater., 1998, 10, 725 CrossRef CAS.
- W. Li, B. Song and A. Manthiram, Chem. Soc. Rev., 2017, 46, 3006 RSC.
- C. M. Julien and A. Mauger, Ionics, 2013, 19, 951 CrossRef CAS.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691 CrossRef CAS.
- L. Croguennec and M. R. Palacin, J. Am. Chem. Soc., 2015, 137, 3140 CrossRef CAS PubMed.
- H. Kawai, M. Nagata, H. Tukamoto and A. R. West, J. Power Sources, 1999, 81–82, 67 CrossRef CAS.
- W. Zhang, L. Liang, F. Zhao, Y. Liu, L. Hou and C. Yuan, Electrochim. Acta, 2020, 340, 135871 CrossRef CAS.
- F. Zhao, X. Li, Y. Yan, M. Su, L. Liang, P. Nie, L. Hou, L. Chang and C. Yuan, J. Power Sources, 2022, 524, 231035 CrossRef CAS.
- S.-M. Bak, E. Hu, Y. Zhou, X. Yu, S. D. Senanayake, S.-J. Cho, K.-B. Kim, K. Y. Chung, X.-Q. Yang and K.-W. Nam, ACS Appl. Mater. Interfaces, 2014, 6, 22594 CrossRef CAS PubMed.
- M. R. Palacin and A. de Guibert, Science, 2016, 351, 1253292 CrossRef CAS PubMed.
- J. Vetter, P. Novák, M. R. Wagner, C. Veit, K.-C. Möller, J. O. Besenhard, M. Winter, M. Wohlfahrt-Mehrens, C. Vogler and A. Hammouche, J. Power Sources, 2005, 147, 269 CrossRef CAS.
- Y. Zhang, C. Y. Chung, L. X. Sun and M. Zhu, Mater. Chem. Phys., 2008, 107, 254 CrossRef CAS.
- A. Mukhopadhyay and B. W. Sheldon, Prog. Mater. Sci., 2014, 63, 58 CrossRef CAS.
- J. P. Pender, G. Jha, D. H. Youn, J. M. Ziegler, I. Andoni, E. J. Choi, A. Heller, B. S. Dunn, P. S. Weiss, R. M. Penner and C. B. Mullins, ACS Nano, 2020, 14, 1243 CrossRef CAS PubMed.
- L. Liang, W. Zhang, F. Zhao, D. K. Denis, F. Zaman, L. Hou and C. Yuan, Adv. Mater. Interfaces, 2020, 7, 1901749 CrossRef CAS.
- M. R. Jo, Y. Kim, J. Yang, M. Jeong, K. Song, Y.-I. Kim, J.-M. Lim, M. Cho, J.-H. Shim, Y.-M. Kim, W.-S. Yoon and Y.-M. Kang, Nat. Commun., 2019, 10, 3385 CrossRef PubMed.
- D. Chao, W. Zhou, F. Xie, C. Ye, H. Li, M. Jaroniec and S.-Z. Qiao, Sci. Adv., 2020, 6, eaba4098 CrossRef CAS.
- J.-L. Yang, J.-M. Cao, X.-X. Zhao, K.-Y. Zhang, S.-H. Zheng, Z.-Y. Gu and X.-L. Wu, EnergyChem, 2022, 4, 100092 CrossRef CAS.
- N. V. Faenza, L. Bruce, Z. W. Lebens-Higgins, I. Plitz, N. Pereira, L. F. Piper and G. G. Amatucci, J. Electrochem. Soc., 2017, 164, A3727 CrossRef CAS.
- T. Toma, R. Maezono and K. Hongo, ACS Appl. Energy Mater., 2020, 3, 4078 CrossRef CAS.
- X. Gu, J.-L. Liu, J.-H. Yang, H.-J. Xiang, X.-G. Gong and Y.-Y. Xia, J. Phys. Chem. C, 2011, 115, 12672 CrossRef CAS.
- P. Treviño, A. C. Garcia-Castro, S. López-Moreno, A. Bautista-Hernández, E. Bobocioiu, B. Reynard, R. Caracasf and A. H. Romero, Phys. Chem. Chem. Phys., 2018, 20, 17799 RSC.
- H. Jung, B. Lee and Y.-S. Jun, Lanmuir, 2016, 32, 10735 CrossRef CAS PubMed.
- J. L. Bantignies, S. Deabate, A. Righi, S. Rols, P. Hermet, J. L. Sauvajol and F. Henn, J. Phys. Chem. C, 2008, 112, 2193 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. Smart, Appl. Surf. Sci., 2011, 257, 2717 CrossRef CAS.
- A. P. Grosvenor, M. C. Biesinger, R. S. Smart and N. S. McIntyre, Surf. Sci., 2006, 600, 1771 CrossRef CAS.
- Y. Z. Su, K. Xiao, N. Li, Z. Q. Liu and S. Z. Qiao, J. Mater. Chem. A, 2014, 2, 13845 RSC.
- B. Li, H. Cao, J. Shao, H. Zheng, Y. Lu, J. Yin and M. Qu, Chem. Commun., 2011, 47, 3159 RSC.
- J. Jiang, J. Zhu, R. Ding, Y. Li, F. Wu, J. Liu and X. Huang, J. Mater. Chem., 2011, 21, 15969 RSC.
- J. Yang, S. Muhammad, M. R. Jo, H. Kim, K. Song, D. A. Agyeman, Y.-I. Kim, W.-S. Yoon and Y.-M. Kang, Chem. Soc. Rev., 2016, 45, 5717 RSC.
- S. H. Min, M. R. Jo, S.-Y. Choi, Y.-I. Kim and Y.-M. Kang, Adv. Energy Mater., 2016, 6, 1501717 CrossRef.
- G.-H. Lee, J. Wu, D. Kim, K. Cho, M. Cho, W. Yang and Y.-M. Kang, Angew. Chem., Int. Ed., 2020, 59, 8681 CrossRef CAS PubMed.
- N. Zhang, F. Cheng, J. Liu, L. Wang, X. Long, X. Liu, F. Li and J. Chen, Nat. Commun., 2017, 8, 405 CrossRef PubMed.
- B. A. Magar, N. Paudel, T. N. Lambert and I. Vasiliev, J. Electrochem. Soc., 2020, 167, 020557 CrossRef CAS.
- A. Bergmann, I. Zaharieva, H. Dau and P. Strasser, Energy Environ. Sci., 2013, 6, 2745 RSC.
- S.-J. Hwang, H.-S. Park and J.-H. Choy, Solid State Ionics, 2002, 151, 275 CrossRef CAS.
- Q. Li, Y. Qiao, S. Guo, K. Jiang, Q. Li, J. Wu and H. Zhou, Joule, 2018, 2, 1134 CrossRef CAS.
- Y. Ha, B. J. Tremolet de Villers, Z. Li, Y. Xu, P. Stradins, A. Zakutayev, A. Burrell and S.-D. Han, J. Phys. Chem. Lett., 2020, 11, 286 CrossRef CAS PubMed.
- A. Nørlund Christensen and G. Ollivier, Solid State Commun., 1972, 10, 609 CrossRef.
- F. Pertlik, Monatsh. Chem., 1999, 130, 1083 CAS.
- A. C. Garcia-Castro, R. Ospina and A. H. Romero, J. Phys.: Conf. Ser., 2019, 1247, 012046 CrossRef CAS.
- P. He, H. Yu, D. Li and H. Zhou, J. Mater. Chem., 2012, 22, 3680 RSC.
- K. Zhang, D. Kim, Z. Hu, M. Park, G. Noh, Y. Yang, J. Zhang, V. W. Lau, S.-L. Chou, M. Cho, S.-Y. Choi and Y.-M. Kang, Nat. Commun., 2019, 10, 5203 CrossRef CAS PubMed.
- H. Wang and C. Song, Eur. Phys. J. B, 2019, 92, 1 CrossRef CAS.
- K. Matsumoto, K. Inoue, K. Nakahara, R. Yuge, T. Noguchi and K. Utsugi, J. Power Sources, 2013, 231, 234 CrossRef CAS.
- S. F. Lux, I. T. Lucas, E. Pollak, S. Passerini, M. Winter and R. Kostecki, Electrochem. Commun., 2012, 14, 47 CrossRef CAS.
- T. Yoon, J. Soon, T. J. Lee, J. H. Ryu and S. M. Oh, J. Power Sources, 2021, 15, 230051 CrossRef.
- R. Jung, R. Morasch, P. Karayaylali, K. Phillips, F. Maglia, C. Stinner, Y. Shao-Horn and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, A132 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- H. Chen, J. A. Dawson and J. H. Harding, J. Mater. Chem. A, 2014, 2, 7988 RSC.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta07496f |
| This journal is © The Royal Society of Chemistry 2023 |