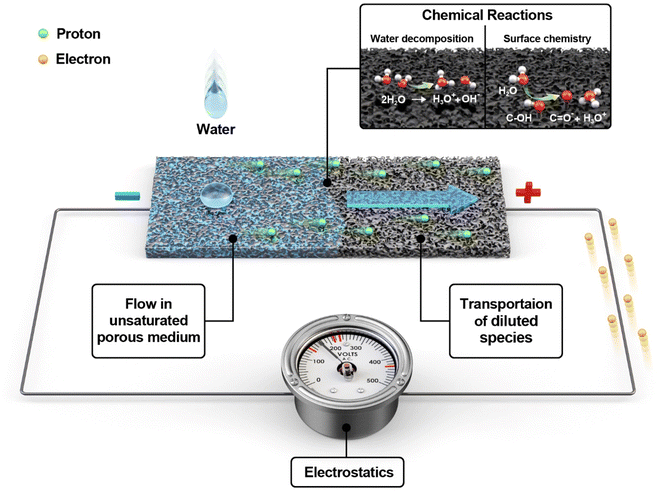
Why does water in porous carbon generate electricity? Electrokinetic role of protons in a water droplet-induced hydrovoltaic system of hydrophilic porous carbon†
Hyunseok
Ko
a,
Wonkyeong
Son
bf,
Min Sung
Kang
d,
Han Uk
Lee
d,
Chan-Yeup
Chung
a,
Seungwu
Han
c,
Changsoon
Choi
b and
Sung Beom
Cho
 *de
*de
aCenter of Materials Digitalization, Korea Institute of Ceramic Engineering and Technology, Jinju, Gyeongsang-namdo 52851, Republic of Korea
bDepartment of Energy and Materials Engineering, Dongguk University-Seoul, Seoul, 04620, Republic of Korea
cDepartment of Materials Science and Engineering, Research Institute of Advanced Materials, Seoul National University, Seoul, 08826, Republic of Korea
dDepartment of Energy Systems Research, Ajou University, Suwon, 16499, Republic of Korea. E-mail: csb@ajou.ac.kr
eDepartment of Materials Science and Engineering, Ajou University, Suwon, 16499, Republic of Korea
fDepartment of Energy Science, Sungkyunkwan University, Suwon, 16419, South Korea
First published on 23rd December 2022
Abstract
As emerging technology, hydrovoltaics harvests energy from water by flowing it through nanostructured materials. However, the poor understanding of the principles of hydrovoltaics has impeded its advancement. The process is complex and involves multiple simultaneous physico-chemical steps, and there has been extensive debate on aspects such as the streaming potential and ion flow. Herein, we report the first multiscale and multiphysics model for hydrovoltaic phenomena to provide in-depth interpretation and analysis of the working principles. Supported by experimental validation, this model explicitly considers the hydrodynamics in unsaturated porous media, ion transport, chemical reactions, and electrostatics. We found that protonation and ionic dynamics are the key factors for electricity generation. The difference in electric potential is mainly driven by the asymmetric proton concentration gradient, with a relatively small contribution from the streaming potential. Furthermore, the parametric effects of porosity, substrate geometry, catalytic activation energy, and room humidity were examined in detail. The results suggest a promising strategy to optimize the electrical performance of hydrovoltaic devices.
1. Introduction
Water covers 71% of the Earth's surface and is never still. Due to the depletion of fossil fuels and accelerating global warming, there is an urgent need to extract energy from the hydrosphere in the form of tides,1 seawater,2 raindrops,3–5etc.6 Recent years have witnessed the emergence of hydrovoltaic generators, which generate electricity from the interaction between water and materials,7 utilizing water droplets8–10 or moisture.11–13 Hydrovoltaics produces electricity sustainably by the flow of water/moisture through a nanostructured material and natural evaporation in ambient environment. A strong advantage of hydrovoltaics is its capability to generate volt-level potentials without any external force.14,15 Porous carbon materials are widely utilized for this purpose because they can absorb water through capillary pressure in the nanochannels and have a large carbon–water interface per unit volume.16–18 For instance, carbon black (CB)19–21 and porous carbon sheets (CS)22,23 were reported to output voltages of up to 1 V when water evaporated from them after passing through the micro- and nanochannels. Recently, a voltage of 4 V and a current of 18 μA were measured for a sandwich structure (CS–Al2O3 nanoparticle layer–CS).15However, despite these promising results, the applications of hydrovoltaics are still at the conceptual stage and additional research is needed to improve their performance for practical blue energy applications.7 In particular, the exact mechanism of electricity generation from the interaction between water and nanostructured materials remains controversial because it is not easy to identify it with experimental measurements. The proposed principles of electricity generation in hydrovoltaics can be classified into two types,24,25i.e., water flow-induced (e.g., streaming potential26 and electron drag27) and ion flow-induced (e.g., gradient of protons or ions11,28). The water flow mechanism is from the perspective of conventional streaming potential in a nanochannel or a porous medium.19,20,29 The charged surfaces in a channel interact with the intrinsic dipole of water molecules and align the latter in specific directions. Either the transport of charged species through a diffusive layer of electric double layer (EDL) or the flow of aligned dipoles produces an electric current, which is proposed as one of the major mechanisms.30 The ion flow mechanisms are based on the ion concentration gradient originating from the different diffusivity between anions and cations, particularly protons and hydroxyls in diluted water.31 This type of concentration gradient can also be induced either by the direct chemical interaction between water and a substrate32 or the dissolution of water accompanied by charge transfer between water and a surface.33 When the protons and hydroxyl ions are spatially separated, they produce an electric field, which leads to the generation of electricity. However, the above-mentioned mechanisms are highly speculative because experimental measurement is challenging and there is a lack of quantitative theoretical models, and this uncertainty hinders the optimization of hydrovoltaic devices. Furthermore, reported experimental studies used different setups (e.g., stationary immersion, cyclic immersion, and droplets) and substrates differing in porosity, liquid conductivity (the conductivity depends on the medium but is rarely considered), etc. Thus, to address these bottlenecks, recent review articles on this topic considered it essential to perform a comprehensive theoretical study of hydrovoltaics.24,34
The present work aimed to develop an in-depth theoretical model of hydrovoltaics by incorporating multi-physics phenomena to emulate realistic energy harvesting devices. We designed a carbon-coated hydrophilic surface that harvests electricity from a single water droplet. This model includes four physico-chemical processes including water flow in an unsaturated porous medium, chemical reactions, transport of dilute species, and electrostatics. We employed realistic parameter values, where those for the chemical reactions were obtained from first-principles calculations, and the others were ambient-condition values or literature values. We used theoretical and computational methods to obtain and analyze the output characteristics of the hydrovoltaic device, which agreed well with the experimental observations both quantitatively and qualitatively. The developed base model revealed that the electrokinetic effect induced by the proton gradient is dominant compared to the conventional streaming current. Proton flow is governed by the competition between diffusive and electrophoretic fluxes. We also performed a parametric study of the hydrovoltaic performance upon varying the porosity, substrate geometry, catalyst effect, and room humidity. Based on these results, we suggest a strategy to maximize the voltage output.
2. Theoretical model for hydrovoltaic device
2.1. Multiphysics model
The finite element method (FEM) was used to model a hydrovoltaic device (Fig. 1) using a carbon-coated porous sheet with dimensions close to that of real devices. The model incorporates four different types of physics, as follows: (i) flow in the unsaturated porous medium, (ii) chemical reactions, (iii) transportation of ions, and (iv) electrostatics. FEM calculations under open-circuit conditions were carried out using the COMSOL Multiphysics software. The following modules provided by COMSOL were employed: porous media and subsurface flow, chemistry, transport of diluted species, and electrostatics. The application built from the model is provided in the ESI.†Table 1 presents the nomenclature for the parameters used in this study.| Symbol description | Units |
|---|---|
| Q m mass source of water | [kg (m−3 s−1)] |
| u flux of water | [kg (m−2 s−1)] |
| S e effective saturation | — |
| C m specific moisture capacity (as a function of Se) | [m−1] |
| H p hydraulic pressure | [cm] |
| K r relative permeability | [m s−1] |
| p VS partial pressure of water on CB film | [Pa] |
| ϕ electrostatic potential | [V] |
| J i ionic flux of species i | [mol m−2] |
| c i concentration of species i | [mol m−3] |
| D i diffusion coefficient of species i | [m2 s−1] |
| z i charge of species i | — |
| ρ V charge density | [e m−3] |
The substrate is assumed to be a surface coated with carbon black (CB), which is a material that has been extensively studied before.35 The surface of CB is treated as hydrophilic and assumed to be mostly hydroxylated (further discussion in 2.1.2). The thickness of the substrate (0.2 mm) is set much smaller than its width and length (3 and 9 cm, respectively). At the beginning of the simulation, a water droplet falls on one side of the CB sheet (left side in the model), followed by water dispersion on and through the porous CB. The relative humidity (RH) of 60%, temperature of 20 °C, and ambient atmospheric pressure (1 atm) were set as the standard conditions. The geometry and domains can be found in ESI1† and Fig. S1.
A porous substrate greatly facilitates water transport through its abundant channels and vaporization in the surrounding air. Because the pores contain both air and water, the unsaturated zone is generally referred to as a two-phase (air–water) porous medium system. The hydrodynamics is governed by Richard's equation,38 a general partial differential equation describing water movement in unsaturated non-swelling soils. For a medium with a porosity of εp, Richard's equation for the fluid flux (u) can be written as follows:
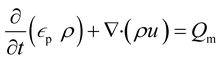 | (1) |
In this mass balance equation, the rate of change in a pore (first term in eqn. (1)) plus the rate of change of the total flux in and out of that volume (second term in eqn. (1)) equals the mass source Qm.
To describe the water occupation in the pores, we adopted the water retention model proposed by van Genuchten.37 The van Genuchten equation defines saturation similar to when the fluid reaches atmospheric pressure (i.e., Hp = 0). It also defines parameters in terms of the effective saturation (Se), which is evaluated in each domain as follows:
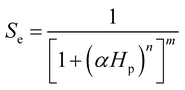 | (2) |
S e can also be expressed as [(θ − θr)/(θs − θr)], where θ is the water content, θr is the residual water content, and θs is the saturated water content. θs is set to the substrate porosity in the model. The other parameters in the van Genuchten model as a function of Se are explained in ESI 2.† Here, α, n, and m are empirical parameters, and their values were taken from the study of soil with sub-millimeter particle size (resembles the pores of cotton fabric) under unsaturated condition.39,40 Subsequently, the first term in eqn (1) becomes:
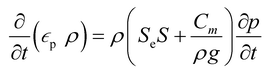 | (3) |
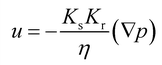 | (4) |
Evaporation is an important part of the hydrovoltaic operation. Under ambient conditions, liquid water vaporizes spontaneously because the vapor pressure above the water surface (pVS) is always higher than the partial pressure of water in the surrounding air (pVa). Thus, evaporation strongly depends on the vapor pressure difference between the atmosphere and the water surface,36 and the evaporation rate (Ev, kg m−2 s−1) is computed from the water vapor transport equation39 as follows:
| Ev = −XEεpρ·(pVS − pVA) | (5) |
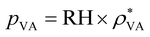 , where
, where 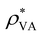 is the saturated water vapor pressure at 25 °C and 2.5 kPa. In general, the evaporation rate is greater for a more porous substrate and a wetter area (i.e., higher water concentration).
is the saturated water vapor pressure at 25 °C and 2.5 kPa. In general, the evaporation rate is greater for a more porous substrate and a wetter area (i.e., higher water concentration).
| R1: H2O ↔ H3O+ + OH− | (6) |
The natural dissociation of water occurs at pH = 7, and the equilibrium constant is 1 × 10−14.
Secondly, protons can be transferred between water and functional groups on the substrate surface. The surface of carbon materials often contains functional groups, commonly oxygen, nitrogen, sulfur, phosphorus and halogens, originating from their synthesis or naturally. In the case of carbon black, its surface includes considerable amounts of oxygen-containing functional groups, which frequently become hydroxylated, as confirmed by XPS analysis (ESI 3†) and previous study.41 In principle, acidic functionals such as carboxylic, lactones, and phenolic groups, which can easily release protons in aqueous condition, can be considered for the above-mentioned mechanism, but here we only focus on hydroxyl functionals for CB case. The hydroxyl on carbon surface can easily transfer a proton to water42,43via the deprotonation process (R2):
| R2: (C–OH) + H2O ↔ (C–O)− + H3O+ | (7) |
The total areal concentration of surface functional groups was set as 60 μM m−2, which is approximately 25% of the surface atomic density, which were assumed to be hydroxyl functionals given that they are the dominant species on CB,41 as shown in Table 2. Density functional theory (DFT) was used to calculate the binding energies of hydroxyl and deprotonated (C–O)− on graphene (0.45 and 0.88 eV, respectively42) to obtain the activation barriers for the forward and backward reactions of eqn (7).
The above discussion shows that abundant charge carriers can be generated when a bulk material enriched with surface groups is exposed to moisture. Combined with a gradient in water concentration, a gradient in H3O+ concentration is established, giving rise to proton diffusion in the material as well as an electric current. In this study, DI water was used to elucidate the fundamental mechanism of hydrovoltaic generators in general by avoiding complications due to the ions. Therefore, H3O+ and OH−are the only mobile charge carriers considered in this model. Other ions and their interactions with the substrates can become crucial44,45 especially for harvesters utilizing natural water sources (e.g., Na+ ions on surface can have equivalent effect of p-doped carbon and plausibly impose electron gradient8), but the present study only focused on the case of diluted water.
In the absence of species generation and ionic drift, the concentration of an ionic species i (ci) is described by the conservation of mass through the Nernst–Planck equation, as follows:
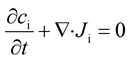 | (8) |
The ionic flux (Ji) can be expressed as:
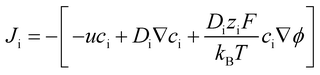 | (9) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)−).
O)−).
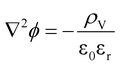 | (10) |
| ρV = Σzieci | (11) |
The streaming potential is an electric current generated during the development of an electric double layer (EDL) on the wall when there is fluid flow driven by pressure. In this study, the streaming potential was analytically solved from time-dependent partial differential equations using the Helmholtz–Smoluchowski equation,34 as follows:
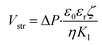 | (12) |
The open-circuit voltage (VOC) was calculated by taking the difference of the average electrostatic surface potentials (ϕ) between the left end (adjacent to the droplet, “head”) and the right end (away from the droplet, “tail”) of the substrate, as illustrated in Fig. S1.† The right boundary was grounded to avoid numerical instability.
3. Mechanism and principles of the hydrovoltaic model
3.1. Model validation and the mechanisms
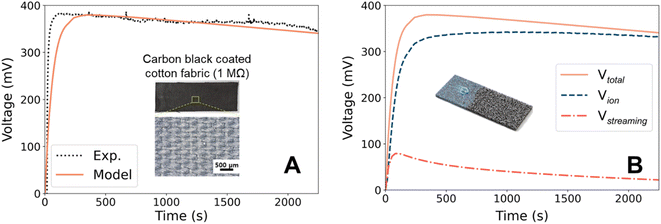
In the previous section, we described the physics necessary for modeling the hydrovoltaic generator. The default values for the key parameters in the base model (Table 2) are from either theoretical or experimental studies to match the practical applications. Herein, we first validate the model output with experimental results, and then discuss the time evolution of the model in detail.Fig. 2A shows the open-circuit voltage from the droplet hydrovoltaic model. The calculated VOC has a maximum value of 381 mV, which agrees with the range from previous studies on droplets.21,49,50 The measured current and calculated power are illustrated in ESI 4.† To further validate the model, we designed a surrogate experiment. A fabric (3 cm × 9 cm × 0.2 cm) composed of cotton fibers was used as the pristine substrate and coated with CB (inset of Fig. 2A). A coating solution was prepared by dispersing CB powder (0.5 g) in DI water (60 mL) with sodium dodecylbenzenesulfonate (SDBS) (0.2 g) surfactant, followed by sonication for 30 min to ensure the uniform dispersion of CB. After dip coating and drying, the CB powder was uniformly coated on the fabric surface. The CB-coated cotton fabric had a resistance of 1 MΩ,34 which was sufficiently high to measure the saturated voltage. Due to the high resistivity of the CB coating (lacks percolation at low concentration51), electron transport is highly unlikely. Likewise, the charge transfer along the surface or through CB is assumed to be negligible. Fig. 2A shows the experimental VOC profile (black) and prediction from the base model. In the experiment, a 0.3 mL water droplet was placed on the negative electrode of the CB-coated fabric, and the measured maximum voltage was 387 mV. It is worth noting that hydrophilic porous materials such as the CB film contains the water in their pores under ambient humidity, empowering the ionic flux even in the early stage21 (though electrodes are connected to materials). The voltage profile predicted by the model using appropriate conditions agrees well with the experimental results. However, there is a discrepancy in the time required to reach the maximum voltage, which is attributed to the difference in the area set for VOC measurement. In our laboratory-scale experiment, the jigs were connected to a small area, whereas the model calculation used both ends of the rectangular substrate. We believe that the latter setup is more reasonable for higher power production, although it takes longer to reach the maximum voltage.
The validity of the developed model can be further verified by comparison with previous studies. Yun et al.21 used a CB-coated hydrophilic cotton fabric, on which a 0.25 mL droplet generated a voltage of ∼350 mV. These experimental conditions are similar to our model, and their measured VOC is also in good agreement. Moreover, we found that a slower evaporation rate results in a lower calculated VOC (see ESI 7† for details), which is consistent with the tendency observed in previous experiments. For example, Xue et al.19 found that the induced VOC was significantly suppressed at a higher humidity (i.e., a diminished evaporation rate), and similar behaviors have also been reported elsewhere.5,28,52–54 In addition, Qin et al.45 showed that the VOC increased from 280 to 400 mV when the temperature increased from 20 °C to 65 °C, which was attributed to faster water flow through the nanochannels driven by accelerated evaporation at elevated temperatures. Thus, this agreement with various CB-based experimental studies demonstrates the validity of this model.
3.2. Underlying principles of hydrovoltaic electricity generation
We mentioned earlier that there is an ongoing debate about the exact mechanism of hydrovoltaic for evaporation-driven electricity generation because the corresponding experimental exploration is not trivial. Two types of mechanisms have been proposed, namely water flow- or ion flow-induced. Although both are expected to contribute to energy generation, their contribution ratio has not been quantitatively determined. Using the theoretical model developed here, we quantitatively evaluated contributions from the streaming potential and ion flow for the first time.In Fig. 2B, the voltage profile calculated from the droplet-based base model is broken down into contributions from the streaming potential (Vstr) and from ion flow (Vion). Vstr is evaluated by solving the partial differential equation at every step. Vion is the combined effect from mobile ions (H3O+ and OH−), with the contribution of H3O+ always at least one order of magnitude higher than that of OH−. Vstr is dominant in the early stage of water transport and evaporation because the water flow rate is relatively fast under the highly anisotropic initial condition. However, the contribution of Vstr to the total voltage is only up to 17%, indicating that ion transportation dominates electricity generation in the droplet-CB film hydrovoltaic device. Although previous studies hypothesized that ions play a key role,12,28,49 this is the first theoretical evidence that ion flow is the main contributor to hydrovoltaic electricity generation. This is mainly due to the strong water-surface interaction. Thus, it is suggested that ions, specifically protons from the carbon surface, are important in the design of hydrovoltaics.
In the case of ion flow, the entire picture is more sophisticated than it seems, where the ion flow is not merely accomplished by diffusion, it involves fluid flow in a porous medium, electrostatic field, and most of all, material–water interactions. The charge transfer between a material and water is considered in our model as charged functional groups, and these surface functional groups continuously give/take charges, while interacting with water. Together with ions, these surface functional groups contribute to the space charge, which appropriately account for the electrostatics across the CB film. In the following section, we present the analysis of the time evolution of ions and the driving forces for the ion flow across the CB film.
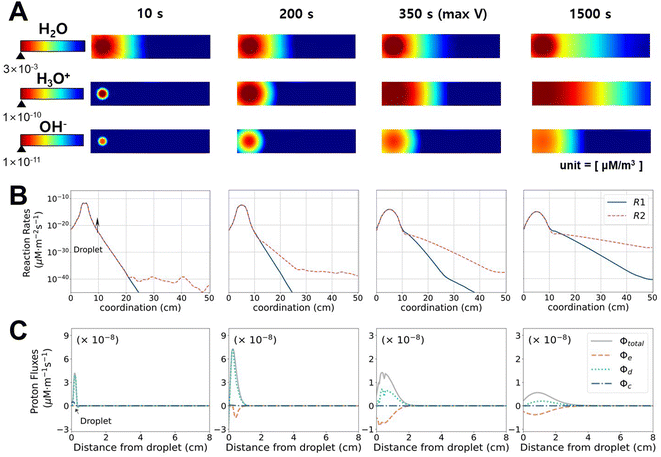
To investigate how the system changes with time, we analyzed the time evolution of ion concentrations, chemical reaction rates, and proton fluxes. Fig. 3A displays the concentrations of each chemical species (note that the range for the colormap varies in each frame for better visualization purpose, also see ESI Video†). The maximum value marked under the scale bar corresponds to the maximum value at t = 10 s because the concentrations always decrease with time. Once the droplet was deposited on the CB surface, water immediately spread out towards the unwetted regions, and water flow toward the tail continued up to 1500 s. It is noteworthy that the wetting occurs immediately, where it approximately takes 1.1 s to reach the opposite electrode in our simulations (also consistent with our experiment (0.5 < t < 1.0 s) and another CB study (∼1.0 s)21). The concentrations of H3O+ and OH− also increased with the dispersion of water droplets till t = 10 s and propagated along the direction of water movement to t = 2000 s.
For t ≥ 200 s, cH3O+ is greater than c−OH by 1–2 orders of magnitude, which can be explained by the chemical reaction rates, as shown in Fig. 3B. In the initial stage, both R1 and R2 are active due to the high H2O concentration. As time passes (t ≥ 200 s), R2 (reaction with CB) becomes dominant over R1 (dissociation of water) at a distance from the droplet. The amount of generated H3O+ is greater at the front of water movement because R2 is more active with the “unreacted surface”, while R1 only depends on cH2O but not on the location. Although the distribution of protons (whether released from R1 or R2) is also determined by the diffusion or ionic flow along with water, it is clear that the surface reaction R2 is the dominant protonation mechanism, which is accompanied by movement of the water front. The functional groups in R2 can redistribute across the CB as time passes, and when the gradient in the functional groups and water become minute, H3O+ saturates across electrodes, and then electricity production ceases.
To analyze the driving forces for the transportation of H3O+, the total flux in the x-direction (ϕtotal) is decomposed into diffusive (ϕd), convective (ϕc), and electrophoretic (ϕe) fluxes, as shown in Fig. 3C. It should be noted that ϕc in a porous medium is negligible compared to ϕe and ϕd, given that the latter two driving forces (gradients in charge and concentration, respectively) are much stronger in the x-direction. Because of the highly focused cH2O in the initial stage, ϕtotal increases and reaches the maximum at 100 s. Before reaching the maximum voltage (t = 350 s), ϕtotal is governed by ϕd, which is driven by a concentration imbalance. A negative flux of ϕe is developed at t ≥ 10 s. R2 leads to a higher concentration of immobile C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O−, whose reaction is more active at the front of the flow, and therefore electrostatically attracts protons. At 350 s, when VOC reaches the maximum, the contributions of ϕe and ϕd become comparable with the opposite signs, and VOC decreases afterward. From this point (t = 350–1500 s), the total flux is notably reduced compared to the initial stage. The slightly higher value of ϕe compared to ϕd favors H3O+ movement in the x-direction. Consequently, the concentration gradient and Voc decrease gradually. Theoretically, considering the high diffusivity of protons in water, the proton gradient should become small quickly, and the electrical output only lasts for seconds.15 The unique presence of immobile C
O−, whose reaction is more active at the front of the flow, and therefore electrostatically attracts protons. At 350 s, when VOC reaches the maximum, the contributions of ϕe and ϕd become comparable with the opposite signs, and VOC decreases afterward. From this point (t = 350–1500 s), the total flux is notably reduced compared to the initial stage. The slightly higher value of ϕe compared to ϕd favors H3O+ movement in the x-direction. Consequently, the concentration gradient and Voc decrease gradually. Theoretically, considering the high diffusivity of protons in water, the proton gradient should become small quickly, and the electrical output only lasts for seconds.15 The unique presence of immobile C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O− on carbon-based materials slows down the proton flux via electrophoresis to enable durable electricity generation.
O− on carbon-based materials slows down the proton flux via electrophoresis to enable durable electricity generation.
Briefly, the time-dependent voltage profile can be explained by the change in the distributions and fluxes of H3O+. The production of H3O+ is governed by surface reaction between water and the CB film, and its transportation is closely related to the flow of water induced by either capillary force in a porous medium or evaporation. Because ion flow contributes > 80% of the total VOC (Fig. 2B), our results firmly suggest that protons are the key to voltage generation in a hydrovoltaic device. In a recent study, it was shown that natural evaporation from nanostructured carbon films can produce a sustainable volt-level potential free from the streaming potential, i.e., an evaporating potential, which is directly generated by carrier transfer driven by evaporation of polar molecules.55
4. Effects of various parameters on hydrovoltaic performance
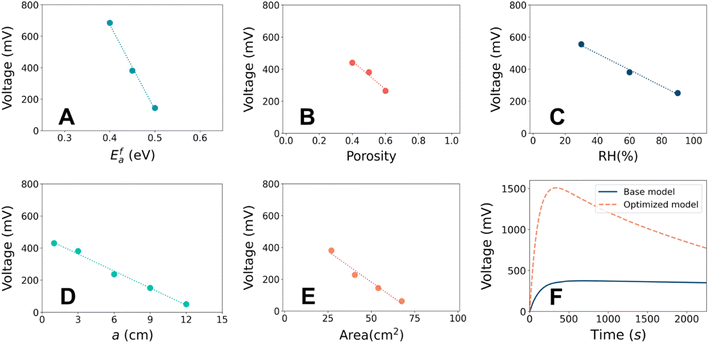
It is known that hydrovoltaic energy harvesters can be driven by multiple factors, such as nano-channels of the porous substrate, chemical interaction between the substrate and water, and anisotropic vaporization of water. Nevertheless, it is unclear how these factors influence the output and how much impact they have in experimental studies. This is mainly because of the difficulty in decomposing the total effect into the contributions from individual parameters, as well as the different experimental setups used in previous studies. The parametric effects can serve as a guideline for rational design to maximize the electrical output. A basic understanding of the output characteristics of the hydrovoltaic model will allow us to analyze influence of the most important design parameters. Herein, we investigated four crucial factors, namely, the porosity,56 substrate geometry,14 chemical reactions,8,57 and evaporation.13The sensitivities of each parameter were assessed and summarized in Fig. 4A–E. Most of the parameters showed a monotonous relationship with VOC. The parameters can be ranked by the sensitivity in the order of catalytic activation energy (Ea) > porosity (εp) > relative humidity (RH). The catalytic activation energy showed the highest sensitivity by exhibiting the steepest change when Efa changed by ± 5% (Fig. 4A). Accelerated protonation reaction leads to a higher concentration of H3O+ and a greater electrostatic potential difference across the CB film (ESI 5†). The porosity was also found to be a crucial parameter. A higher porosity leads to a lower VOC (Fig. 4B) and a change in εp by ± 20% caused VOC to change by ∼ ± 20%. The water can settle without severe evaporation and develop a maximum proton concentration difference between the head and tail (ESI 6†). It should be noted that the micro-pore distribution is crucial in the determination of hydrovoltaic performance, and although the mean-field approximation is applied in the current model due to the computational cost and sophistication, the effect of pore distribution was not treated as trivial. VOC is also sensitive to the humidity, where it increases when the RH at the right half of the CB substrate (RHt) is reduced (i.e., a drier atmosphere), and a consistent tendency had been observed experimentally.19–22 A lower RHt stimulates evaporation at the tail end, and thus enhances the gradient of water concentration (Fig. S9B†). This causes enhanced protonation in the CB film (R2), given that the dispersed water molecules encounter “fresh” CB with a higher C–OH concentration (ESI 7†). The geometric parameters (Fig. 4D and E) also have an effect but are considered relatively less relevant compared to the other considered parameters because larger geometric parameters always diminish VOC. The corresponding discussion is available in ESI 8.† In summary, the VOC is the most sensitive to protonation through the chemical reaction between water and functional groups on the CB surface, followed by the porosity and the room humidity.
The above-mentioned findings suggest the great potential to improve hydrovoltaics under realistic conditions by controlling the surface reaction rate and porosity. Because the reaction rate follows the Arrhenius equation (∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT)), lowering the catalytic activation barrier (which can be a separate challenge to engineer) or increasing temperature can increase the reaction rate by hundreds of times even at room temperature. A previous first-principles calculation also demonstrated that a more reactive carbon nanotube surface can produce approximately 50 times more electrons.33 Hence, materials with a reactive surface are desirable for enhancing electricity generation. Alternatively, porosity governs the capillary flow, which dominates the transportation behavior of ions together with water. A lower porosity means slow but steady water flow (i.e., permeation and evaporation), which results in a higher voltage profile and longer lifetime. Meanwhile, an extremely low porosity will hinder water flow and transportation of charged species. Therefore, the porosity also should be controlled at an optimal level. Overall, the priority in material design will be finding materials that promote proton release, while having satisfactory porosity.
exp(−Ea/kBT)), lowering the catalytic activation barrier (which can be a separate challenge to engineer) or increasing temperature can increase the reaction rate by hundreds of times even at room temperature. A previous first-principles calculation also demonstrated that a more reactive carbon nanotube surface can produce approximately 50 times more electrons.33 Hence, materials with a reactive surface are desirable for enhancing electricity generation. Alternatively, porosity governs the capillary flow, which dominates the transportation behavior of ions together with water. A lower porosity means slow but steady water flow (i.e., permeation and evaporation), which results in a higher voltage profile and longer lifetime. Meanwhile, an extremely low porosity will hinder water flow and transportation of charged species. Therefore, the porosity also should be controlled at an optimal level. Overall, the priority in material design will be finding materials that promote proton release, while having satisfactory porosity.
Fixing CB as the substrate material and the volume of water droplet, we tried to improve the output voltage by adjusting other parameters in the hydrovoltaic model. A maximum VOC of ∼1.5 V was achieved at εp = 0.4, a = 3 cm, b = 3 cm, RH = 30%, and Efa = 0.41 eV, as depicted in Fig. 4F. Compared to the base model, this represents an ∼350% improvement in VOC without employing any special material or complicated geometry. The amount of protonation induced by water-surface reaction was found to be the most influential parameter. Therefore, the hydrovoltaic performance may be enhanced by maneuvering the film properties and environmental conditions in an appropriate generator setup.
Based on our developed model, it can be further extended to other hydrophilic systems. However, its extension will require brute force, which is beyond our scope, and thus the inference of the current study is stressed here. For systems in which adsorption–desorption exchange at the interface is controlled,13,19–21 including our model, the water and the proton concentration along the material will play a key role in its mechanism. When the surface reactivity with water is modified on carbon materials or equivalent hydrophilic materials, i.e., engineered surface functional groups,23,57 the reaction rate becomes crucial and the proton gradient will be determined accordingly. Hence, other systems can be simulated by adjusting the variables of the present model, with appropriate experimental references. Alternatively, for hydrophobic systems including graphene surfaces, the electrokinetics at the surface governs the hydrovoltaic output (e.g., sliding droplet10,58 and evaporation through nanochannels45). In fibrous biofilms with a porous structure,59 the biofilms contain many amphiphilic surface groups, and these groups repel charged ions, and the streaming potential is likely to be the dominant mechanism in the immersion/evaporation-based hydrovoltaic device. However, the application of the present model is limited in hydrophobic systems given that it does not describe the geometrical charges in water.
5. Conclusions
A theoretical study of droplet-based hydrovoltaic energy harvesters was performed to not only provide fundamental principles of electricity generation but also useful design strategies. After experimental validation of the hydrovoltaic generator model, analysis suggested that the ion concentration gradient (especially that of proton) is responsible for the output voltage in a porous carbon material. Proton production is governed by surface reaction between water and the CB film, and its transportation is closely related to the water flow induced by either capillary motion in a porous medium or evaporation. These complex interactions create a proton concentration gradient, which generates electricity. Besides the working principles, we also discussed in depth the influence of porosity, geometry, chemical reactions, and evaporation. Given that the chemical reaction between water and surface functional groups is the most important factor, our theoretical calculation clearly indicates that increasing the rate of protonation through this reaction can improve the voltage output. Finally, simple adjustments to the surface chemistry, porosity, substrate dimension, and relative humidity can enhance the output voltage by approximately 400% under the optimized conditions. It is noteworthy that this model can be further improved with more precise parametrizations, given that some parameters such as dynamic evaporation resistance and water retention of CB films are inevitably taken from the most relevant empirical references. This work is the first in-depth theoretical investigation on the working principle of a hydrovoltaic generator. By developing the current model for other types of hydrovoltaic systems, the underlying physics can be revealed for other hydrovoltaic applications (different types of materials (e.g., porous and hydrophilic), type of water source (e.g., immersion and vapor), frequency of water source (e.g., wave and stationary)). The proposed design criteria serve as a guideline for maximizing the electrical output.Conflicts of interest
All authors have no conflict of interest to declare.Acknowledgements
This study is supported from Basic Science Research Program through the National Research Foundation of Korea (2022R1F1A1063060) and Virtual Engineering Platform Project through the Ministry of Trade, Industry, and Energy of Korea (P0022336). The computational resource for the DFT is supported from Korea Supercomputing Center (KSC-2022-CRE-0042).References
- J. Scruggs and P. Jacob, Science, 2009, 323, 1176–1178 CrossRef CAS PubMed.
- G. Zhu, Y. Su, P. Bai, J. Chen, Q. Jing, W. Yang and Z. L. Wang, ACS Nano, 2014, 8, 6031–6037 CrossRef CAS PubMed.
- Z.-H. Lin, G. Cheng, S. Lee, K. C. Pradel and Z. L. Wang, Adv. Mater., 2014, 26, 4690–4696 CrossRef CAS PubMed.
- J. Nie, Z. Wang, Z. Ren, S. Li, X. Chen and Z. Lin Wang, Nat. Commun., 2019, 10, 2264 CrossRef.
- W. Xu, H. Zheng, Y. Liu, X. Zhou, C. Zhang, Y. Song, X. Deng, M. Leung, Z. Yang, R. X. Xu, Z. L. Wang, X. C. Zeng and Z. Wang, Nature, 2020, 578, 392–396 CrossRef CAS.
- Z. Zhang, X. Li, J. Yin, Y. Xu, W. Fei, M. Xue, Q. Wang, J. Zhou and W. Guo, Nat. Nanotechnol., 2018, 13, 1109–1119 CrossRef CAS PubMed.
- J. Yin, J. Zhou, S. Fang and W. Guo, Joule, 2020, 4, 1852–1855 CrossRef.
- H. Cai, Y. Guo and W. Guo, Nano Energy, 2021, 84, 105939 CrossRef CAS.
- L. E. Helseth, J. Electrost., 2016, 81, 64–70 CrossRef CAS.
- J. Yin, X. Li, J. Yu, Z. Zhang, J. Zhou and W. Guo, Nat. Nanotechnol., 2014, 9, 378–383 CrossRef CAS PubMed.
- T. Xu, X. Ding, Y. Huang, C. Shao, L. Song, X. Gao, Z. Zhang and L. Qu, Energy Environ. Sci., 2019, 12, 972–978 RSC.
- F. Zhao, Y. Liang, H. Cheng, L. Jiang and L. Qu, Energy Environ. Sci., 2016, 9, 912–916 RSC.
- X. Liu, H. Gao, J. E. Ward, X. Liu, B. Yin, T. Fu, J. Chen, D. R. Lovley and J. Yao, Nature, 2020, 578, 550–554 CrossRef CAS PubMed.
- S. Zhang, S. Fang, L. Li and W. Guo, Sci. China: Technol. Sci., 2021, 64, 629–634 CrossRef CAS.
- X. Zhao, J. Feng, M. Xiao, D. Shen, C. Tan, X. Song, J. Feng, W. W. Duley and Y. N. Zhou, ACS Appl. Mater. Interfaces, 2021, 13(23), 27169–27178 CrossRef CAS.
- Q. Tang and P. Yang, J. Mater. Chem. A, 2016, 4, 9730–9738 RSC.
- Y. Xu, P. Chen and H. Peng, Chem. – Eur. J., 2018, 24, 6287–6294 CrossRef CAS PubMed.
- Z. Zhao, M. Xue, H. Qiu, W. Guo and Z. Zhang, Cell Rep. Phys. Sci., 2022, 3(4), 100822 CrossRef CAS.
- G. Xue, Y. Xu, T. Ding, J. Li, J. Yin, W. Fei, Y. Cao, J. Yu, L. Yuan, L. Gong, J. Chen, S. Deng, J. Zhou and W. Guo, Nat. Nanotechnol., 2017, 12, 317–321 CrossRef CAS.
- J. Bae, T. G. Yun, B. L. Suh, J. Kim and I.-D. Kim, Energy Environ. Sci., 2020, 13, 527–534 RSC.
- T. G. Yun, J. Bae, A. Rothschild and I.-D. Kim, ACS Nano, 2019, 13, 12703–12709 CrossRef CAS PubMed.
- T. Ding, K. Liu, J. Li, G. Xue, Q. Chen, L. Huang, B. Hu and J. Zhou, Adv. Funct. Mater., 2017, 27, 1700551 CrossRef.
- K. Liu, P. Yang, S. Li, J. Li, T. Ding, G. Xue, Q. Chen, G. Feng and J. Zhou, Angew. Chem., Int. Ed., 2016, 55, 8003–8007 CrossRef CAS.
- D. Shen, W. W. Duley, P. Peng, M. Xiao, J. Feng, L. Liu, G. Zou and Y. N. Zhou, Adv. Mater., 2020, 32, 2003722 CrossRef.
- J. Xie, L. Wang, X. Chen, P. Yang, F. Wu and Y. Huang, in Green Energy and Environment, IntechOpen, 2019, p. 45 Search PubMed.
- W. Olthuis, B. Schippers, J. Eijkel and A. van den Berg, Sens. Actuators, B, 2005, 111–112, 385–389 CrossRef CAS.
- P. Král and M. Shapiro, Phys. Rev. Lett., 2001, 86, 131–134 CrossRef.
- S. G. Yoon, Y. Yang, J. Yoo, H. Jin, W. H. Lee, J. Park and Y. S. Kim, ACS Appl. Electron. Mater., 2019, 1, 1746–1751 CrossRef CAS.
- S. Zhang, W. Chu, L. Li and W. Guo, J. Phys. Chem. C, 2021, 125, 8959–8964 CrossRef CAS.
- F. H. J. Van Der Heyden, D. Stein and C. Dekker, Phys. Rev. Lett., 2005, 95(11), 116104 CrossRef.
- S. H. Lee and J. C. Rasaiah, J. Chem. Phys., 2011, 135, 124505 CrossRef PubMed.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200 CrossRef CAS.
- S. He, Y. Zhang, L. Qiu, L. Zhang, Y. Xie, J. Pan, P. Chen, B. Wang, X. Xu, Y. Hu, C. T. Dinh, P. De Luna, M. N. Banis, Z. Wang, T.-K. Sham, X. Gong, B. Zhang, H. Peng and E. H. Sargent, Adv. Mater., 2018, 30, 1707635 CrossRef.
- Y. Huang, H. Cheng and L. Qu, ACS Mater. Lett., 2021, 3, 193–209 CrossRef CAS.
- M. A. Gabris and J. Ping, Nano Energy, 2021, 90(A), 106494 CrossRef CAS.
- M. Bittelli, F. Ventura, G. S. Campbell, R. L. Snyder, F. Gallegati and P. R. Pisa, J. Hydrol., 2008, 362, 191–205 CrossRef.
- M. T. van Genuchten, Soil Sci. Soc. Am. J., 1980, 44, 892–898 CrossRef.
- L. A. Richards, Physics, 1931, 1, 318–333 CrossRef.
- T. Fetzer, J. Vanderborght, K. Mosthaf, K. M. Smits and R. Helmig, Water Resour. Res., 2017, 53, 1080–1100 CrossRef.
- D. Jougnot, N. Linde, A. Revil and C. Doussan, Vadose Zone J., 2012, 11(1), 272–286 Search PubMed.
- H. Han, J. Lee, D. W. Park and S. E. Shim, Macromol. Res., 2010, 18, 435–441 CrossRef CAS.
- N. Ghaderi and M. Peressi, J. Phys. Chem. C, 2010, 114, 21625–21630 CrossRef CAS.
- F. Mouhat, F.-X. Coudert and M.-L. Bocquet, Nat. Commun., 2020, 11, 1566 CrossRef CAS.
- S. G. Yoon, B. J. Park, H. Jin, W. H. Lee, J. Han, Y. H. Cho, H. Yook, J. W. Han and Y. S. Kim, Small Methods, 2021, 5, 2100323 CrossRef CAS.
- Y. Qin, Y. Wang, X. Sun, Y. Li, H. Xu, Y. Tan, Y. Li, T. Song and B. Sun, Angew. Chem., Int. Ed., 2020, 59, 10619–10625 CrossRef CAS.
- B. O. Kalejaiye and S. S. S. Cardoso, Water Resour. Res., 2005, 41(10), W10407 CrossRef.
- S. A. Fischer, B. I. Dunlap and D. Gunlycke, Chem. Sci., 2018, 9, 7126–7132 RSC.
- G. B. Westermann-Clark and J. L. Anderson, J. Electrochem. Soc., 1983, 130, 839–847 CrossRef CAS.
- H. Jin, S. G. Yoon, W. H. Lee, Y. H. Cho, J. Han, J. Park and Y. S. Kim, Energy Environ. Sci., 2020, 13, 3432–3438 RSC.
- J. Park, S. Song, C. Shin, Y. Yang, S. A. L. Weber, E. Sim and Y. S. Kim, Angew. Chem., Int. Ed., 2018, 57, 2091–2095 CrossRef CAS PubMed.
- M. Barekat, R. S. Razavi and S. Bastani, Adv. Mater. Res., 2012, 472–475, 110–113 CAS.
- C. Li, K. Liu, H. Liu, B. Yang and X. Hu, Mater. Res. Bull., 2017, 90, 81–86 CrossRef CAS.
- B. Shao, Z. Song, X. Chen, Y. Wu, Y. Li, C. Song, F. Yang, T. Song, Y. Wang, S.-T. Lee and B. Sun, ACS Nano, 2021, 15, 7472–7481 CrossRef CAS PubMed.
- C. Shao, B. Ji, T. Xu, J. Gao, X. Gao, Y. Xiao, Y. Zhao, N. Chen, L. Jiang and L. Qu, ACS Appl. Mater. Interfaces, 2019, 11, 30927–30935 CrossRef CAS.
- S. Fang, J. Li, Y. Xu, C. Shen and W. Guo, Joule, 2022, 6, 690–701 CrossRef.
- J. H. Park, S. H. Park, J. Lee and S. J. Lee, ACS Sustainable Chem. Eng., 2021, 9(14), 5027–5037 CrossRef CAS.
- J. Li, K. Liu, T. Ding, P. Yang, J. Duan and J. Zhou, Nano Energy, 2019, 58, 797–802 CrossRef CAS.
- S. Yang, Y. Su, Y. Xu, Q. Wu, Y. Zhang, M. B. Raschke, M. Ren, Y. Chen, J. Wang, W. Guo, Y. Ron Shen and C. Tian, J. Am. Chem. Soc., 2018, 140, 13746–13752 CrossRef CAS PubMed.
- X. Liu, T. Ueki, H. Gao, T. L. Woodard, K. P. Nevin, T. Fu, S. Fu, L. Sun, D. R. Lovley and J. Yao, Nat. Commun., 2022, 13, 4369 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta05281d |
| This journal is © The Royal Society of Chemistry 2023 |