Deforming active droplets in viscoelastic solutions†
Prateek
Dwivedi
,
Atishay
Shrivastava
,
Dipin
Pillai
,
Naveen
Tiwari
and
Rahul
Mangal
 *
*
Department of Chemical Engineering, Indian Institute of Technology Kanpur, PIN-370210 Kanpur, Uttar Pradesh, India. E-mail: mangalr@iitk.ac.in
First published on 1st May 2023
Abstract
The motion of biological swimmers in typical bodily fluids is modelled using a system of micellar solubilization driven active droplets in a viscoelastic polymeric solution. The viscoelastic nature of the medium, as perceived by the moving droplet, characterized by the Deborah number (De), is tuned by varying the surfactant (fuel) and polymer concentration in the ambient medium. At moderate De, the droplet exhibits a steady deformed shape, markedly different from the spherical shape observed in Newtonian media. A theoretical analysis based on the normal stress balance at the interface is shown to accurately predict the droplet shape. With a further increase in De, time-periodic deformation accompanied by an oscillatory transition in swimming mode is observed. The study unveils the hitherto unexplored rich complexity in the motion of active droplets in viscoelastic fluids.
1. Introduction
Biological micro-organisms such as bacteria, protozoa, and sperm cells utilize non-reciprocal motion of the appendages attached to their surface, such as flagella or cilia, for swimming at very low Reynolds number. The propulsion of these micro-organisms is heavily influenced by their interactions with the environment, resulting in their capability to sense and respond to the surrounding hydrodynamic and chemical fields. In the presence of external flow, bacteria and sperm cells have been reported to exhibit up-stream rheotaxis.1–4 The presence of molecular solutes can also trigger chemotaxis or negative chemotaxis based on the nature of interaction of the solute with the swimmer.5,6 Similarly, the presence of macromolecular solutes such as proteins and enzymes induces viscoelasticity to the environment. Such a macromolecular matrix not only acts as a physical and chemical barrier for the microorganisms but also affects their propulsion characteristics and influences the growth of colonies. Over the years, scientists have investigated the motion of biological micro-organisms in both Newtonian and complex environments.7–15 Patteson et al. demonstrated that the addition of a small amount of polymer in a Newtonian medium can drastically reduce tumbling tendency of E. coli due to enhanced viscosity while increasing their swimming speed due to enhanced elasticity. Similarly, the impact of viscoelasticity and shear-thinning nature of the surrounding fluid on the locomotion of Caenorhabditis elegans has been studied. It has been shown that the activity of Caenorhabditis elegans is reduced due to the development of hyperbolic points near the nematode's surface, inducing large extensional viscosities brought in by the viscoelastic nature of the bulk fluid.13 We suggest some recent articles that present a thorough overview of the dynamics of biological microorganisms in complex environments.16,17Inspired by the unique ability of micro-organisms to survive and propel in a variety of complex environments, recent scientific attempts have focused on synthesizing artificial micro-swimmers capable of extracting energy from their surroundings and executing spontaneous mechanical motion.18 Their non-equilibrium transport characteristics have garnered significant interest due to their potential implications in a multitude of applications, including cargo delivery in microscopic domains,19 healthcare,20 environmental remediation,21 among others. One popular artificial microswimmer is that of an active Janus particle, which is a single particle with its two halves made of two different surface chemistry. These particles typically employ self-generated local gradients of a physicochemical field by interacting asymmetrically with the surrounding fluid to propel via a mechanism known as phoresis.22 A gradient of chemical solutes around the particle leads to propulsion due to self-diffusiophoresis.22,23 Similar self-propulsion has been achieved using mechanisms such as self-thermophoresis (temperature gradient)24 and self-electrophoresis (electric field gradient).25,26 Apart from exploring the dynamics of active particles in conventional Newtonian environments, their behavior in non-Newtonian environments such as polymer solutions,27–31 bulk passive tracer bath32 and under external flows33 has also been investigated.
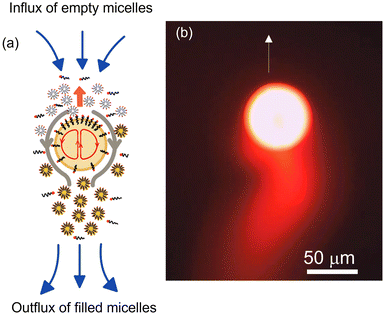
Another popular class of artificial microswimmers is that of active droplets. These active swimmers self-propel due to the Marangoni stress induced by interfacial tension gradient along the droplet interface. In an otherwise isotropic droplet with uniform surfactant coverage, the required asymmetry is spontaneously generated by either a targeted chemical reaction,34–36 droplet phase separation,37 or micellar solubilization.38–41 Due to its ease of use and non-reactive nature of the constituents, micellar solubilization is the most commonly preferred method to produce stable and persistent droplet propulsion. Here, a surfactant concentration (≫Critical Micellar Concentration (CMC)) in the bulk phase is maintained, which results in a high droplet solubilization rate. Under these circumstances, minor disturbances in the droplet position or local fluctuation in the surfactant density around the droplet are sufficient to generate a spontaneous asymmetry of interfacial tension gradient resulting in the onset of Marangoni stress at the interface. This generates a flow from the region of low interfacial tension to high interfacial tension region along the droplet surface causing the droplet to move in the direction opposite to the interfacial flow. During this propulsive movement, the droplet encounters more empty micelles at is the front and leaves a trail of filled micelles in the rear region, which ensures that the asymmetry in the surfactant concentration at the droplet interface is maintained. Thus, the self-sustained Marangoni stress results in a persistent droplet locomotion (see Fig. 1).
In recent years, several experimental and theoretical studies have investigated different aspects of active droplet behavior in diverse ambient conditions.40,42–55 For example, an increase in droplet speed with increasing surfactant concentration and droplet size has been reported.46 Further studies have shown that active droplets respond to gradients in bulk surfactant concentration leading to a unique chemotactic behavior.52 In the presence of external flows within a microchannel, active droplets have been reported to perform upstream locomotion.53,54 Similar effects of droplet size,47,48 addition of molecular solutes,40,49 boundary walls50,51 and gravity,55 have also been been investigated on active droplet behavior. Most of these studies have limited their focus to a Newtonian bulk environment. For a comprehensive review on such studies we recommend a few recent review articles.56–58 Recently, Dwivedi et al.,59 experimentally investigated the dynamics of a thermotropic liquid crystal 4-pentyl-4-cyanobiphenyl (5CB) active droplet in an aqueous trimethyl tetradecyl ammonium bromide (TTAB) surfactant solution doped with polyethylene oxide (PEO) as polymer. The study was, however limited to weakly viscoelastic systems. Since most biological microswimmers live in complex biological fluids, it is crucial to understand the dynamics of artificial active droplets in complex environments. In contrast to active colloids, the deformability of active droplets render them as ideal candidates to biomimic the swimming strategies employed by micro-organisms in complex media.
In this article, we report the active motion of 5CB droplets in ambient media with significant viscoelasticity. Unlike previously explored Newtonian/weakly viscoelastic media, here we show that the normal elastic stresses generated by the stretching polymer chains at the droplet interface produce significant deformation of the motile droplets. The deformation of active droplets due to the ambient elasticity is shown to be inextricably linked to the swimming mode employed by the active droplets.
2. Experimental methodology
2.1 Materials
5CB liquid crystal was used as the dispersed oil-phase and deionized water was used as the continuous aqueous phase. TTAB was used as a cationic surfactant, and polyethylene oxide of molecular weights (Mw's) 1 × 106 and 8 × 106 Da were used as macromolecular additives. All chemicals were purchased from Sigma Aldrich and used as received. For particle image velocimetry (PIV) experiments, red-colored fluorescent tagged colloids of size 500 nm were obtained from Thermo Fisher Scientific.2.2 Sample preparation and rheological measurements
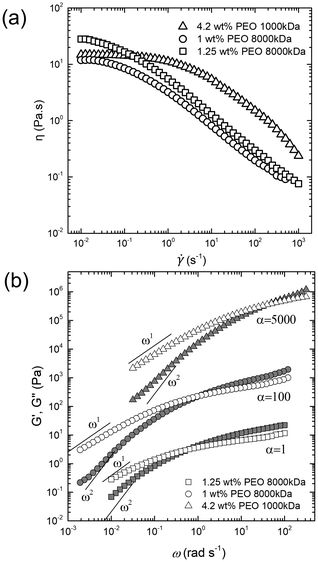
Aqueous TTAB solutions with varying concentrations of PEO with different Mws were prepared. For uniform mixing, samples were stirred overnight at a very low speed. The bulk viscosity (η0) and polymer relaxation time (τ) of the samples were measured using steady shear and frequency sweep (strain of 1%) oscillatory rheology at 25 °C using rheometer with a Couette assembly (TA Instruments DHR3). The relaxation time (τ) was calculated by analyzing the crossover of the storage modulus G′(ω) and the loss modulus G′′(ω) (cf.Fig. 4). Table 1 lists the physico-chemical properties of the different samples used in this study.| System description | Rheological features | ||||
|---|---|---|---|---|---|
| Fluid | c TTAB | M w,PEO | c PEO | η 0 | τ |
| wt% | Da | wt% | Pa s | s | |
| 1 | 6 | NA | NA | 0.001 | 0 |
| 2 | 6 | 8 × 106 | 1 | 11 | 1 |
| 3 | 21 | 8 × 106 | 1 | 11 | 1 |
| 4 | 21 | 1 × 106 | 4.2 | 13 | 0.025 |
| 5 | 21 | 8 × 106 | 1.25 | 28 | 2 |
2.3 Droplet production and flow visualization
Using a micro-injector (Femtojet 4i), 5CB droplets were injected into the surfactant-laden aqueous solutions (with and without polymer). By tuning the injection pressure, injection time, and compensation pressure of the Femtojet 4i, droplets of nearly uniform diameter ∼50 μm were produced. A low number density of droplets was maintained to avoid droplet–droplet interaction. The resulting emulsion was subsequently injected into a custom-made Hele–Shaw optical cell (length and width of 1 cm and vertical height of 50 μm), prepared using cleaned (ultrasonicated in ethanol, and subsequently plasma treated and nitrogen dried) glass slides. To avoid evaporative losses, the optical cell was properly sealed using wax. Fresh optical cells were used for every sample. The optical cell was placed on a temperature-controlled stage on an upright polarized optical microscope (Olympus BX53) at a target temperature of 25 °C (see Fig. 2). Isolated active droplets were visualized using an Olympus LC30 camera with 2048 × 1532 pixels2 resolution in brightfield mode at 20 fps. The motion of the droplets was tracked using Image-J software. We duplicated a series of images and converted them to binary masks, which represented the droplet in each image. Subsequently, using an outline command boundary of the droplet shape in each frame was traced. From the X and Y coordinates of the droplet's boundary, we determined the geometrical center of the shape, allowing us to track the droplet trajectory in each image. To obtain the hydrodynamic field around the droplet, the surrounding medium was doped with red fluorescent tracers (500 nm Polystyrene particles), and Particle Image Velocimetry (PIV) experiments were conducted using fluorescence microscopy. The experiments were captured using an ORX-10G-71S7C-C, FLIR camera with 3208 × 2200 pixels2 resolution, with a constant exposure setting throughout the video.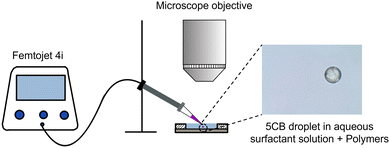 | ||
| Fig. 2 Schematic representation of the experimental setup along with a micrograph depicting an active droplet with a diameter of 50 μm. | ||
3. Results and discussions
First, we describe the characteristics of active motion of 5CB droplets in an aqueous surfactant solution with cTTAB = 6 wt% with no added PEO (fluid 1). Consistent with earlier reports on active motion in Newtonian media,39,40,48 at short time scales, the droplets exhibit ballistic motion (U ∼ 15 μm s−1), retaining their spherical shape (Fig. 3(a)). Next, we perform experiments with 1 wt% PEO of Mw,1 = 8 × 106 Da added to the surfactant solution, i.e., fluid 2. Due to the increased viscosity (η0 = 11 Pa s) of the solution, droplets move slower (U ∼ 2–3 μm s−1) while retaining their shape (see Fig. 3(b)), consistent with our earlier report.59 Further, keeping the PEO concentration at 1 wt%, we increase the surfactant concentration from 6 wt% to 21 wt% (fluid 3). Upon increasing the surfactant concentration, U is enhanced (∼8–10 μm s−1), which is also in agreement with previous studies.48,60 However, in this case, the increase in speed is interestingly accompanied with significant droplet deformation, with the droplet being elongated at its rear end. (see Fig. 3(c) and Movie S1, ESI†)Under an externally imposed Newtonian flow field, past studies have investigated droplet shape deformation well in detail.61–67 A competition between the viscous stresses and the interfacial tension characterized by the capillary number  and the viscosity ratio
and the viscosity ratio  determines the shape of the droplet. Here ηi and η0 are the droplet and the bulk phase viscosity, U is the droplet speed, and σ is the interfacial tension. It has been shown that typically, Ca > 0.1 results in droplet deformation due to strong viscous stresses. In our system, Ca is of the order of 10−3–10−2. Further to also rule out the effect of viscosity ratio in the case of fluid 3 (λ ∼ 0.01), we conducted additional experiments in fluid 4 (Mw,1 = 1 × 106 Da, cTTAB = 21 wt%) with an identical viscosity ratio as fluid 3 (λ ∼ 0.01). Interestingly, in contrast to fluid 3, the droplets maintained their spherical shape during self-propulsion in fluid 4. (see Fig. 3(d)). These observations conclusively demonstrate that observed droplet deformation in our active 5CB droplets is not dependent on factors such as Ca or λ. Instead, the elasticity of the surrounding medium may play a significant role in the deformation.
determines the shape of the droplet. Here ηi and η0 are the droplet and the bulk phase viscosity, U is the droplet speed, and σ is the interfacial tension. It has been shown that typically, Ca > 0.1 results in droplet deformation due to strong viscous stresses. In our system, Ca is of the order of 10−3–10−2. Further to also rule out the effect of viscosity ratio in the case of fluid 3 (λ ∼ 0.01), we conducted additional experiments in fluid 4 (Mw,1 = 1 × 106 Da, cTTAB = 21 wt%) with an identical viscosity ratio as fluid 3 (λ ∼ 0.01). Interestingly, in contrast to fluid 3, the droplets maintained their spherical shape during self-propulsion in fluid 4. (see Fig. 3(d)). These observations conclusively demonstrate that observed droplet deformation in our active 5CB droplets is not dependent on factors such as Ca or λ. Instead, the elasticity of the surrounding medium may play a significant role in the deformation.
Several past studies have shown that rising bubbles and droplets exhibit shape deformation due to the viscoelasticity of the ambient medium.68,69 Therefore, to quantify the strength of elasticity of the ambient media in our experiments, we determined the Deborah number De (=Uτ/a), defined as the product of polymer relaxation time (τ) and the characteristic strain rate 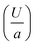 . Here U is the droplet speed and a is the droplet diameter. The relaxation time (τ) for different polymer solutions was obtained using the rheological measurement as described earlier (see Fig. 4(b)). Table 2 lists U, and the resulting De values for the different fluids. Clearly, at low De, for fluids (1, 2 and 4) no deformation is observed, and only beyond a moderate De, i.e., De > 0.20 in the case of fluid 3, noticeable deformation was observed.
. Here U is the droplet speed and a is the droplet diameter. The relaxation time (τ) for different polymer solutions was obtained using the rheological measurement as described earlier (see Fig. 4(b)). Table 2 lists U, and the resulting De values for the different fluids. Clearly, at low De, for fluids (1, 2 and 4) no deformation is observed, and only beyond a moderate De, i.e., De > 0.20 in the case of fluid 3, noticeable deformation was observed.
| System description | Propulsion characteristics | |||||
|---|---|---|---|---|---|---|
| Fluid | c TTAB | M w,PEO | c PEO | U | De | Deformed |
| wt% | 106 Da | wt% | μm s−1 | Yes/no | ||
| 1 | 6 | NA | NA | 15 | 0 | No |
| 2 | 6 | 8 | 1 | 12 | 0.04 | No |
| 3 | 21 | 8 | 1 | 10 | 0.20 | Yes |
| 4 | 21 | 1 | 4.2 | 6 | 0.003 | No |
| 5 | 21 | 8 | 1.25 | 2–16 | 0.10–0.60 | Yes |
Although active droplets are known to be weak pushers,36,70 as a first approximation we assume the surrounding flow field and the resulting elastic stresses to be qualitatively given by a droplet driven by an external field. With this assumption, we determine the droplet shape following the methodology outlined in Noh et.al.69 The ambient fluid is treated as a Boger fluid that accounts for the viscoelastic stresses in the medium. The shear viscosity is taken to be a constant. Such a model helps to isolate the physics of viscoelasticity from shear-thinning in polymer solutions. Although the polymer medium has a shear thinning behavior, it cannot lead to the observed droplet deformation. This is because the rear end with a larger curvature would have stronger velocity gradients (thereby lower local viscosity) than the front end (with higher local viscosity). Hence, the local capillary number would be larger at the front end as compared to the rear end, leading to conclude that a larger deformation is to be expected at the front end, contradicting the experimental observations. Hence, viscoelasticity of the ambient medium must be the dominant physics behind droplet deformation. Therefore, this minimalist Boger fluid model is shown to satisfactorily predict the experimentally observed shape deformations. Consider a uniform streaming flow of the ambient fluid in the droplet frame (see Fig. 5). We assume the flow around the droplet to be creeping flow. At leading order, the creeping flow solution for the streaming flow of a Newtonian fluid past a spherical bubble is given by
 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
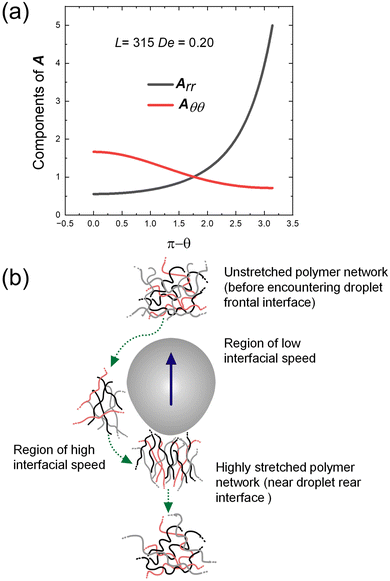
From the initial conditions, we find that Arθ = 0 and Aθθ = Aϕϕ at θ = π. It is thus evident from eqn (5) that Arθ = 0 and Aθθ = Aϕϕ in the entire domain of θ. We thus solve the ODEs numerically to obtain the distribution of A along the droplet surface that quantifies the polymeric chain orientation and thus its contribution to the additional normal elastic stress. Fig. 6(a) depicts the result for L = 315 and De = 0.5, where
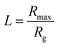 . Rmax and Rg are the contour length and the radius of gyration of the polymer respectively. Rmax of 8 × 106 molecular weight PEO is calculated using its monomer size of 0.28 nm.72 Assuming water to be a good solvent, Rg of PEO in water is determined using Rg = 0.02M0.58,73 where M is the molecular weight of PEO. From the figure, it is clear that the polymer chain is stretched at both front and rear stagnation points. At the front (θ = π), the local flow field causes the polymer chains to be stretched in directions parallel to the droplet surface. However, at the rear stagnation point, the stretching is in the direction normal to the surface as indicated by the diverging values of Arr (see Fig. 6(a)). This shows that the stretched polymer chains contribute to droplet elongation at the rear stagnation point through Arr in the form of an additional normal stress at the rear end.
. Rmax and Rg are the contour length and the radius of gyration of the polymer respectively. Rmax of 8 × 106 molecular weight PEO is calculated using its monomer size of 0.28 nm.72 Assuming water to be a good solvent, Rg of PEO in water is determined using Rg = 0.02M0.58,73 where M is the molecular weight of PEO. From the figure, it is clear that the polymer chain is stretched at both front and rear stagnation points. At the front (θ = π), the local flow field causes the polymer chains to be stretched in directions parallel to the droplet surface. However, at the rear stagnation point, the stretching is in the direction normal to the surface as indicated by the diverging values of Arr (see Fig. 6(a)). This shows that the stretched polymer chains contribute to droplet elongation at the rear stagnation point through Arr in the form of an additional normal stress at the rear end.
 | ||
| Fig. 5 Schematic of a deformed droplet as adapted from ref. 69. | ||
 | ||
| Fig. 6 (a) Variation of components of A along the droplet surface. (b) Schematic representation of polymer network evolving around an active droplet with rear deformation. | ||
The droplet shape deformation is quantitatively determined using the normal stress condition at the interface, given as
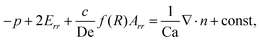 | (6) |
 | (7) |
 | (8) |
To quantify the degree of deformation, a metric called the deformation index, ψ, is defined as the standard deviation of the distance of points along the droplet perimeter with respect to its geometrical center. The shape of the deformed droplets predicted by the model is compared with the experimentally observed shapes in Fig. 7. A satisfactory agreement of the experimentally obtained shape with the numerical prediction validates the hypothesis that the droplet deformation near the rear stagnation point arises due to the additional elastic normal stress associated with the stretching of polymer chains at the droplet interface.
 | ||
| Fig. 7 Experimentally obtained shape of the deformed droplets overlaid with the model prediction for three different values of De. | ||
To investigate the effect of enhanced viscoelasticity further, we conducted experiments in fluid 5 (see Table 2), where cPEO is increased to 1.25 wt%. In this medium, the active droplet exhibits a well-defined periodic zigzag motion (Fig. 8a). The droplet first propels smoothly in one direction followed by a deflection in direction by ∼70–90°. The droplet then continues moving smoothly along this new direction for around the same time, until being deflected again, this time however in the opposite direction (see Movie S2, ESI†). It is to be noted that this zigzag motion is different from the previously reported jittery motion49,59,75 with repeated stop-and-go events, where the directional fluctuations are random (Fig. 8b). Additionally, the resting state in jittery motion is attributed to the non-propulsive quadrupolar flow-field mode, whereas, no such quadrupolar mode is observed in the zigzag motion (discussed later in the manuscript).
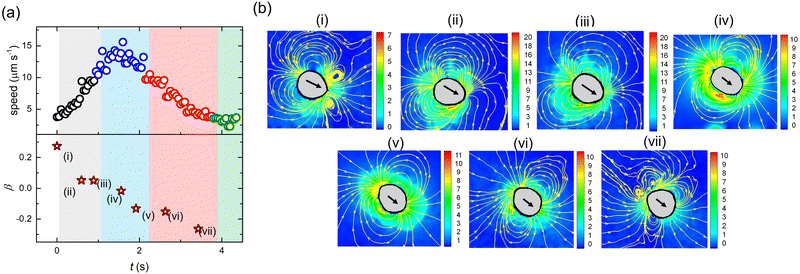
Fig. 9(a) depicts a representative section of the zigzag trajectory, color coded by U. The enlarged inset demonstrates the smooth intermediate section between two successive turning events of the periodic trajectory. The optical micrographs correspond to the droplet images captured at different instances. These images reveal a time-dependent shape deformation exhibited by the droplet. First, the droplet is at its lowest speed and is nearly spherical with minimum deformation. Subsequently, it accelerates while getting deformed at its front. Thereafter, with further increase in speed, at around half the time period, the deformation shifts to the equatorial region of the droplet rendering it elongated. Next, the droplet slows down, while getting deformed at its rear end. Finally, the droplet regains its original shape with negligible deformation and slow speed, before switching the direction and repeating the cycle. Fig. 9(b) depicts the in-phase time-dependent variation in U, ψ and De for a few zigzag cycles. The maximum deformation occurs at the highest U corresponding to the highest De, wherein the droplet has an elongated shape. The least deformation is observed during the change in droplet direction, when the droplet is the slowest with the lowest value of De.
In 2019 Hokamabad et al.76 demonstrated that 5CB nematic shells (i.e. 5CB droplet encapsulating a water droplet as core) exhibit shark fin meandering motion with significant curvature in their trajectories. The curvature in the trajectories was attributed to the off-centre displacement of the isotropic core, resulting in elasto-nematic effects, and the sudden deflection in motion was a result of chemotactic repulsion. The speed of the shells was observed to first decay gradually followed by a sudden rise, which led to a strong curvature in the trajectory. However, in our observations, the patterns resemble saw-tooth shapes with minimal curvature. Further, the temporal variation of droplet speed is symmetric in its decelerating and accelerating phase. In order to rule out the possibility of elasto-nematic effects being responsible for the observed zig–zag motion, we repeated the experiments with CB-15 ((S)-4-cyano-4'-(2-methylbutyl)biphenyl), an isotropic isomer of 5CB, as the droplet phase in fluid 5 (21 wt% TTAB and 1.25 wt% 8 × 106 Da PEO). The results are presented in Fig. S1 (ESI†), which show that the isotropic droplet also undergoes a zig–zag motion along with deformation. This confirms that the nematic elasticity of 5CB phase is not responsible for droplet deformation.
Next, to visualize the flow field around the droplet we seeded the surrounding medium with fluorescent tracers (500 nm polystyrene particles) and particle image velocimetry (PIV) was used to compute the tangential velocity u(R,θ) at the droplet interface in the co-moving frame of reference. The interfacial velocity, u(R,θ), can be described using only the first two modes of the squirmer model77,78 as  The ratio,
The ratio,  determines the swimming mode. The droplet is a puller for β > 0, neutral for β = 0, and pusher for β < 0.79
determines the swimming mode. The droplet is a puller for β > 0, neutral for β = 0, and pusher for β < 0.79
Fig. 10(a) depicts the variation in U and β with time during one cyle of the zigzag motion. Fig. 10(b(i–vii)) are the snapshots of the flow field around the droplet at intermediate instances. With time, β decreases continuously showing a transition of swimming mode from puller (deformed at the front) to neutral (elongated at the equatorial region) to pusher (deformed at the rear). At the beginning of the cycle with the puller and neutral mode the direction of motion remains nearly unchanged. Subsequently, the motion undergoes direction change when the droplet acquires the pusher mode. We also note that towards the end of the cycle, the pusher strength increases, characterized by the large magnitude of β (<0). This behavior is in agreement with previous reports demonstrating that the pusher mode is more susceptible to directional fluctuations.47,59
In 2011, Zhu et al.80 numerically demonstrated that for a spherical pusher, the polymer chains are primarily stretched at the rear end, generating a localized normal stress therein. Likewise, in a spherical puller, the polymer chains are mainly stretched at the sides generating a localized normal stress at the equator. Our experimental observations are in line with these numerical predictions. During the pusher mode, the flow-field around the droplet ensures that polymer chains are radially stretched (large local values of Arr as captured by the model) close to the rear end. This results in additional normal stress at the droplet interface, causing the droplet to deform at the rear end, adopting a pusher mode. During the puller/neutral mode in agreement with the predictions of Zhu et al.,80 the local velocity field stretches the polymer chains along the equatorial region. The resulting additional normal stress produces noticeable deformation at the frontal/equatorial region. Our results also validate the predictions of Daddi-Moussa-Ider et al.81 and Nasouri et al.82 that for swimmers with the front-end deformation, the puller mode is optimal. Whereas, for swimmers with rear-end deformation, the pusher mode is optimal.
Finally, the question remains as to why the droplet exhibits a zigzag motion. Using a numerical analysis, a similar mode-switching periodic motion, albeit without deformation, was predicted by Li.83 The study proposed that depending on the competing effects of advection and diffusion of micelles, i.e., 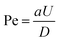 (where a is the droplet diameter, U is the droplet speed and D is the micelle diffusivity), a higher Pe can result in a periodic zigzag motion. With further increase in Pe, aperiodic zig–zag oscillations, characterized by a combination of triangle, quadrangle, and mixed waves while transitioning between pusher and puller states were predicted. The reason for such unexpected deflections was proposed to be the emergent interactions between the secondary and primary wakes of low surfactant concentration. However, in one of our earlier experimental works,59 it was demonstrated that at vanishing De, droplets retain their spherical shape, and the mode of propulsion is mainly dictated by the competition between the advection and diffusion of the micelles, i.e., Pe. Increasing Pe only leads to a change in droplet swimming mode from puller to pusher and quadrupolar, manifesting as a decrease in the droplet persistence length, and an increase in jitteriness. However, no periodic zig–zag motion was observed, which is also consistent with other experimental reports wherein similar Pe based mode-switching has been reported.47,49,59 In fact, using the metholody reported in ref. 59, for this study we determined D ∼ 3 μm2 s−1 resulting in similar Pe ∼ 70 for both pusher and puller mode (Fig. 10(b(i) and (vii))) during the zig–zag cycle. This confirms that Pe alone cannot explain the zig–zag motion.
(where a is the droplet diameter, U is the droplet speed and D is the micelle diffusivity), a higher Pe can result in a periodic zigzag motion. With further increase in Pe, aperiodic zig–zag oscillations, characterized by a combination of triangle, quadrangle, and mixed waves while transitioning between pusher and puller states were predicted. The reason for such unexpected deflections was proposed to be the emergent interactions between the secondary and primary wakes of low surfactant concentration. However, in one of our earlier experimental works,59 it was demonstrated that at vanishing De, droplets retain their spherical shape, and the mode of propulsion is mainly dictated by the competition between the advection and diffusion of the micelles, i.e., Pe. Increasing Pe only leads to a change in droplet swimming mode from puller to pusher and quadrupolar, manifesting as a decrease in the droplet persistence length, and an increase in jitteriness. However, no periodic zig–zag motion was observed, which is also consistent with other experimental reports wherein similar Pe based mode-switching has been reported.47,49,59 In fact, using the metholody reported in ref. 59, for this study we determined D ∼ 3 μm2 s−1 resulting in similar Pe ∼ 70 for both pusher and puller mode (Fig. 10(b(i) and (vii))) during the zig–zag cycle. This confirms that Pe alone cannot explain the zig–zag motion.
Based on our earlier findings59 and the predictions by Li,83 we suspect that zig–zag trajectories are a consequence of the droplet periodically adopting pusher and puller swimming modes. Such a periodic mode-switching has never been observed in the absence of droplet deformation. In the current work with stronger viscoelastic effects, i.e., above a critical De, droplet deforms and adopts a puller-neutral-pusher swimming mode, resulting in a zig–zag motion and periodic reorientation events. Using the schematic shown in Fig. 11(a), we aim to provide an explanation for the systematic deflections associated with the zig–zag behavior. At the end of one zig–zag cycle, the droplet adopts a pusher mode with supply of fresh surfactant/empty micelles being localized at the equatorial region. Therefore, the chemotactic bias causes the droplet to align its propulsion in the direction of fresh feed. For the maiden cycle, the equatorial feed is expected to be symmetric with respect to the propulsion direction so that the droplet can turn either way. The diffusion time scale for filled micelles released from the droplet, 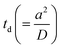 , is obtained to be ∼833 s, which is roughly two orders of magnitude higher than the time scale (∼8 s) between alternate deflections observed in the droplet motion. Thus, the droplet experiences significant negative autochemotactic effect52 from its micelle-filled primary and secondary wakes, resulting in a periodic zigzag motion. Regarding the associated time-period of the oscillations, we speculate it to depend on the time scale of micelle diffusion and convection captured by the corresponding Pe. To verify this hypothesis, for our experimental system in fluid 5, we adjusted the Pe by changing droplet size while maintaining the higher De values to invoke droplet deformation. We observed that at low Pe, the droplet (diameter ∼ 30 μm) undergoes a steady motion while getting deformed from its rear. Increasing the Pe with droplet size of 50 μm results in a zig–zag motion with a time period of 4 s (see Fig. 11(b) and (c)). Further increasing the droplet size to ∼100 μm results in aperiodic zig–zag motion with a shorter time period of 2 s (see Fig. 11(b) and (c)). Increasing the droplet size beyond 150 μm, resulted in a jittery motion. This confirms our hypothesis that Pe plays a major role in setting the time-scale of oscillations. We have tried to summarize and qualitatively illustrate our findings on Pe and De with the help of a potential phase diagram (see Fig. 11(d)) which we can foresee emerging from all of our experiments, including the work already discussed in ref. 59. Nonetheless, we maintain that a separate and comprehensive study is necessary to obtain a deeper understanding of the exact time period of oscillations and constructing a complete phase-diagram. For reaction-driven swimming droplets, Schmitt and Stark84 predicted that at high Marangoni number a similar mode-swithcing oscillating state can be achieved.
, is obtained to be ∼833 s, which is roughly two orders of magnitude higher than the time scale (∼8 s) between alternate deflections observed in the droplet motion. Thus, the droplet experiences significant negative autochemotactic effect52 from its micelle-filled primary and secondary wakes, resulting in a periodic zigzag motion. Regarding the associated time-period of the oscillations, we speculate it to depend on the time scale of micelle diffusion and convection captured by the corresponding Pe. To verify this hypothesis, for our experimental system in fluid 5, we adjusted the Pe by changing droplet size while maintaining the higher De values to invoke droplet deformation. We observed that at low Pe, the droplet (diameter ∼ 30 μm) undergoes a steady motion while getting deformed from its rear. Increasing the Pe with droplet size of 50 μm results in a zig–zag motion with a time period of 4 s (see Fig. 11(b) and (c)). Further increasing the droplet size to ∼100 μm results in aperiodic zig–zag motion with a shorter time period of 2 s (see Fig. 11(b) and (c)). Increasing the droplet size beyond 150 μm, resulted in a jittery motion. This confirms our hypothesis that Pe plays a major role in setting the time-scale of oscillations. We have tried to summarize and qualitatively illustrate our findings on Pe and De with the help of a potential phase diagram (see Fig. 11(d)) which we can foresee emerging from all of our experiments, including the work already discussed in ref. 59. Nonetheless, we maintain that a separate and comprehensive study is necessary to obtain a deeper understanding of the exact time period of oscillations and constructing a complete phase-diagram. For reaction-driven swimming droplets, Schmitt and Stark84 predicted that at high Marangoni number a similar mode-swithcing oscillating state can be achieved.
4. Conclusions
We report that in viscoelastic solutions, the extension of polymeric chains at the active droplet interface leads to the generation of additional normal elastic stress localized at the droplet interface, resulting in droplet deformation. The extent of deformation is controlled by the Deborah number, De, of the ambient fluid that can be tuned by varying the ambient surfactant and polymer concentration. We show that the combined effect of associated Péclet number (Pe) of droplet, its deformation induced mode-switching and negative autochemotaxis results in zigzag trajectories. We foresee that with synergistic efforts from experiments, theory and simulations, a more comprehensive understanding of the self-propulsion of active droplets in complex fluids will be achieved. While our observations are for synthetic active droplets, we envisage that it provides essential insights into the diverse range of active motion displayed in nature by biological swimmers.Author contributions
PD and RM conceptualized the research, PD and RM designed the methodology of the experiments, PD performed the experiments, PD, AS and RM analyzed the experimental data, NT determined the droplet shapes using theoretical model. PD, DSP, NT and RM wrote the paper.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We acknowledge the funding received by the Science and Engineering Research Board (Grant numbers SB/S2/RJN105/2017 and ECR/2018/000401), Department of Science and Technology, India.Notes and references
- Marcos, H. C. Fu, T. R. Powers and R. Stocker, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4780–4785 CrossRef CAS PubMed
.
- Z. Zhang, J. Liu, J. Meriano, C. Ru, S. Xie, J. Luo and Y. Sun, Sci. Rep., 2016, 6, 23553 CrossRef CAS PubMed
.
- K. Miki and D. E. Clapham, Curr. Biol., 2013, 23, 443–452 CrossRef CAS PubMed
.
- A. J. Mathijssen, N. Figueroa-Morales, G. Junot, É. Clément, A. Lindner and A. Zöttl, Nat. Commun., 2019, 10, 3434 CrossRef PubMed
.
- G. H. Wadhams and J. P. Armitage, Nat. Rev. Mol. Cell Biol., 2004, 5, 1024–1037 CrossRef CAS PubMed
.
- D. J. Webre, P. M. Wolanin and J. B. Stock, Curr. Biol., 2003, 13, R47–R49 CrossRef CAS PubMed
.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed
.
- H. A. Stone and A. D. Samuel, Phys. Rev. Lett., 1996, 77, 4102 CrossRef CAS PubMed
.
- E. Lauga and R. E. Goldstein, Phys. Today, 2012, 65, 30 CrossRef
.
- W. Poon, Proc. Int. Sch. Phys. Enrico Fermi, 2013, 184, 317–386 CAS
.
- D. Alizadehrad, T. Krüger, M. Engstler and H. Stark, PLoS Comput. Biol., 2015, 11, e1003967 CrossRef PubMed
.
- Y. Magariyama and S. Kudo, Biophys. J., 2002, 83, 733–739 CrossRef CAS PubMed
.
- X. Shen and P. E. Arratia, Phys. Rev. Lett., 2011, 106, 208101 CrossRef CAS PubMed
.
- A. Patteson, A. Gopinath, M. Goulian and P. Arratia, Sci. Rep., 2015, 5, 15761 CrossRef CAS PubMed
.
- A. E. Patteson, A. Gopinath and P. E. Arratia, Curr. Opin. Colloid Interface Sci., 2016, 21, 86–96 CrossRef CAS
.
- E. Lauga, Annu. Rev. Fluid Mech., 2016, 48, 105–130 CrossRef
.
- S. E. Spagnolie and P. T. Underhill, arXiv, 2022, preprint, arXiv:2208.03537 DOI:10.1146/annurev-conmatphys-040821-112149.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef
.
- S. Sundararajan, P. E. Lammert, A. W. Zudans, V. H. Crespi and A. Sen, Nano Lett., 2008, 8, 1271–1276 CrossRef CAS PubMed
.
- A. Ghosh, W. Xu, N. Gupta and D. H. Gracias, Nano Today, 2020, 31, 100836 CrossRef CAS PubMed
.
- M. Guix, J. Orozco, M. Garcia, W. Gao, S. Sattayasamitsathit, A. Merkoci, A. Escarpa and J. Wang, ACS Nano, 2012, 6, 4445–4451 CrossRef CAS PubMed
.
- J. R. Howse, R. A. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed
.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed
.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed
.
- W. F. Paxton, K. C. Kistler, C. C. Olmeda, A. Sen, S. K. Angelo, Y. Cao, T. E. Mallouk, P. E. Lammert and V. H. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS PubMed
.
- A. M. Brooks, M. Tasinkevych, S. Sabrina, D. Velegol, A. Sen and K. J. Bishop, Nat. Commun., 2019, 10, 495 CrossRef CAS PubMed
.
- J. R. Gomez-Solano, A. Blokhuis and C. Bechinger, Phys. Rev. Lett., 2016, 116, 138301 CrossRef PubMed
.
- H. Raman, S. Das, H. Sharma, K. Singh, S. Gupta and R. Mangal, ACS Phys. Chem. Au, 2023 DOI:10.1021/acsphyschemau.2c00056
.
- J. R. Gomez-Solano and C. Bechinger, New J. Phys., 2015, 17, 103032 CrossRef
.
- C. Lozano, J. R. Gomez-Solano and C. Bechinger, New J. Phys., 2018, 20, 015008 CrossRef
.
- S. Saad and G. Natale, Soft Matter, 2019, 15, 9909–9919 RSC
.
- K. Singh, A. Yadav, P. Dwivedi and R. Mangal, Langmuir, 2022, 38, 2686–2698 CrossRef CAS PubMed
.
- B. R. Si, P. Patel and R. Mangal, Langmuir, 2020, 36, 11888–11898 CrossRef CAS PubMed
.
- H. Kitahata, N. Yoshinaga, K. H. Nagai and Y. Sumino, Phys. Rev. E, 2011, 84, 015101 CrossRef PubMed
.
- A. Hirono, T. Toyota, K. Asakura and T. Banno, Langmuir, 2018, 34, 7821–7826 CrossRef CAS PubMed
.
- S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021 CrossRef
.
- S. Thakur, P. S. Kumar, N. Madhusudana and P. A. Pullarkat, Phys. Rev. Lett., 2006, 97, 115701 CrossRef PubMed
.
- K. Peddireddy, P. Kumar, S. Thutupalli, S. Herminghaus and C. Bahr, Langmuir, 2012, 28, 12426–12431 CrossRef CAS PubMed
.
- C. Krüger, G. Klös, C. Bahr and C. C. Maass, Phys. Rev. Lett., 2016, 117, 048003 CrossRef PubMed
.
- P. Dwivedi, B. R. Si, D. Pillai and R. Mangal, Phys. Fluids, 2021, 33, 022103 CrossRef CAS
.
- Z. Izri, M. N. Van Der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed
.
- S. I. Cheon, L. B. C. Silva, A. S. Khair and L. D. Zarzar, Soft Matter, 2021, 17, 6742–6750 RSC
.
- M. Morozov and S. Michelin, J. Fluid Mech., 2019, 860, 711–738 CrossRef CAS
.
- M. Morozov and S. Michelin, J. Chem. phys., 2019, 150, 044110 CrossRef PubMed
.
- M. Morozov, Soft Matter, 2020, 16, 5624–5632 RSC
.
- A. Izzet, P. G. Moerman, P. Gross, J. Groenewold, A. D. Hollingsworth, J. Bibette and J. Brujic, Phys. Rev. X, 2020, 10, 021035 CAS
.
- S. Suda, T. Suda, T. Ohmura and M. Ichikawa, Phys. Rev. Lett., 2021, 127, 088005 CrossRef CAS PubMed
.
- M. Suga, S. Suda, M. Ichikawa and Y. Kimura, Phys. Rev. E, 2018, 97, 062703 CrossRef CAS PubMed
.
- B. V. Hokmabad, R. Dey, M. Jalaal, D. Mohanty, M. Almukambetova, K. A. Baldwin, D. Lohse and C. C. Maass, Phys. Rev. X, 2021, 11, 011043 Search PubMed
.
- N. Desai and S. Michelin, Phys. Rev. Fluids, 2021, 6, 114103 CrossRef
.
- C. de Blois, M. Reyssat, S. Michelin and O. Dauchot, Physical Review Fluids, 2019, 4, 054001 CrossRef
.
- C. Jin, C. Krüger and C. C. Maass, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5089–5094 CrossRef CAS PubMed
.
- P. Dwivedi, A. Shrivastava, D. Pillai and R. Mangal, Phys. Fluids, 2021, 33, 082108 CrossRef CAS
.
- R. Dey, C. M. Buness, B. V. Hokmabad, C. Jin and C. C. Maass, Nat. Commun., 2022, 13, 2952 CrossRef CAS PubMed
.
- A. C. Castonguay, R. Kailasham, C. M. Wentworth, C. H. Meredith, A. S. Khair and L. D. Zarzar, 2022 DOI:10.1103/PhysRevE.107.024608.
- P. Dwivedi, D. Pillai and R. Mangal, Curr. Opin. Colloid Interface Sci., 2022, 101614 CrossRef CAS
.
- S. Birrer, S. I. Cheon and L. D. Zarzar, Curr. Opin. Colloid Interface Sci., 2022, 101623 CrossRef CAS
.
- S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101 CrossRef
.
- P. Dwivedi, A. Shrivastava, D. Pillai and R. Mangal, arXiv, 2022, preprint, arXiv:2207.13318 DOI:10.48550/arXiv.2207.13318.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Soft Matter, 2014, 10, 7008–7022 RSC
.
- S. Guido and V. Preziosi, Adv. Colloid Interface Sci., 2010, 161, 89–101 CrossRef CAS PubMed
.
- H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65–102 CrossRef
.
- G. Soligo, A. Roccon and A. Soldati, Meccanica, 2020, 55, 371–386 CrossRef
.
- J. Rallison, Annu. Rev. Fluid Mech., 1984, 16, 45–66 CrossRef
.
- M. Ohta, Y. Akama, Y. Yoshida and M. Sussman, J. Fluid Mech., 2014, 752, 383–409 CrossRef CAS
.
- C. Kim and L. Bernal, 38th Aerospace Sciences Meeting and Exhibit, 2000, p. 855.
- Z. Jiang, Y. Gan and Y. Luo, Phys. Fluids, 2020, 32, 053301 CrossRef CAS
.
- R. Poryles and R. Zenit, Fluids, 2018, 3, 54 CrossRef
.
- D. S. Noh, I. S. Kang and L. G. Leal, Phys. Fluids A, 1993, 5, 1315–1332 CrossRef CAS
.
- C. Jin, Y. Chen, C. C. Maass and A. J. Mathijssen, Phys. Rev. Lett., 2021, 127, 088006 CrossRef CAS PubMed
.
- M. Chilcott and J. Rallison, J. Non-Newtonian Fluid Mech., 1988, 29, 381–432 CrossRef CAS
.
- F. Oesterhelt, M. Rief and H. Gaub, New J. Phys., 1999, 1, 6 CrossRef
.
- N. Ziebacz, S. A. Wieczorek, T. Kalwarczyk, M. Fiałkowski and R. Hołyst, Soft Matter., 2011, 7, 7181–7186 RSC
.
- P. Singh and L. Leal, J. Non-Newtonian Fluid Mech., 1996, 67, 137–178 CrossRef CAS
.
- P. Dwivedi, B. R. Si, D. Pillai and R. Mangal, Phys. Fluids, 2021, 33, 022103 CrossRef CAS
.
- B. V. Hokmabad, K. A. Baldwin, C. Krüger, C. Bahr and C. C. Maass, Phys. Rev. Lett., 2019, 123, 178003 CrossRef CAS PubMed
.
- J. R. Blake, J. Fluid Mech., 1971, 46, 199–208 CrossRef
.
- M. Lighthill, Commun. Pure Appl. Math., 1952, 5, 109–118 CrossRef
.
- T. J. Pedley, IMA J. Appl. Math., 2016, 81, 488–521 CrossRef
.
- L. Zhu, E. Lauga and L. Brandt, Phys. Fluids, 2012, 24, 051902 CrossRef
.
- A. Daddi-Moussa-Ider, B. Nasouri, A. Vilfan and R. Golestanian, J. Fluid Mech., 2021, 922, R5 CrossRef CAS
.
- B. Nasouri, A. Vilfan and R. Golestanian, Phys. Rev. Lett., 2021, 126, 034503 CrossRef CAS PubMed
.
- G. Li, J. Fluid Mech., 2022, 934, A20 CrossRef CAS
.
- M. Schmitt and H. Stark, EPL, 2013, 101, 44008 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00228d |
| This journal is © The Royal Society of Chemistry 2023 |


![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)