Are MXenes suitable for soft multifunctional composites?†
Cerwyn
Chiew
a and
Mohammad H.
Malakooti
 *ab
*ab
aDepartment of Mechanical Engineering, University of Washington, Seattle, WA 98195, USA. E-mail: malakoot@uw.edu
bInstitute for Nano-Engineered Systems, University of Washington, Seattle, WA 98195, USA
First published on 30th August 2023
Abstract
MXenes are a family of two-dimensional (2D) nanomaterials known for their high electrical and thermal conductivity, as well as high aspect ratios. Recent research has focused on dispersing MXenes within compliant polymer matrices, aiming to create flexible and stretchable composites that harness MXenes’ exceptional conductivity and aspect ratios. Experimental findings demonstrate the potential of MXene polymer composites (MXPCs) as flexible electrical, thermal conductors, and high dielectric materials, with promising applications in soft matter engineered systems. However, the 2D structure of MXene inclusions and their relatively large elastic modulus can impart increased stiffness to the polymer matrix, posing limitations on the mechanical flexibility of these functional materials. Here, we introduce a modeling platform to predict the mechanics and functionality of MXene elastomer composites and assess their suitability as soft multifunctional materials. Our investigation primarily focuses on understanding the influence of MXenes’ size, layered structure, and percolation arrangements on the effective properties of the resulting composites. Through our model, we successfully determined the elastic modulus, thermal conductivity, and dielectric constant of MXene elastomer composites, and our results exhibit strong agreement with those obtained through finite element analysis. By utilizing this framework, we can theoretically identify the necessary microstructures of MXenes and guide the experiments, enabling the creation of MXPCs with the desired synergistic mechanical and functional properties.
New conceptsThis study introduces a novel concept that focuses on integrating monolayer and multilayer MXenes as filler materials in soft polymers, such as elastomers, for applications in flexible electronics, wearable devices, and soft robotics. While previous research has explored the use of MXenes in composite materials, the emphasis has mainly been on structural polymer composites and monolayer MXene fillers. In contrast, our study uncovers the untapped potential of multilayer MXenes and investigates their distinct influence on the overall properties of soft matter composites. We demonstrate that the layered structure and aspect ratio of MXenes play a crucial role in determining the mechanical, thermal, and dielectric behavior of the composites, offering a novel approach for tailoring their properties. Furthermore, our research highlights the significance of interphase engineering and percolating microstructures in achieving the desired properties of MXene-based composites, providing valuable guidelines for their design and synthesis. By better understanding of the role of microstructures in MXene–polymer composites, our work offers additional insights in this field and paves the way for accelerated development of soft multifunctional materials with enhanced performance characteristics. |
1 Introduction
Two dimensional carbides and nitrides, called MXenes, are a rising family of functional nanomaterials that can show excellent electrical, thermal, and optical properties in different systems.1–3 MXenes are atomically thin 2D materials composed of early-transition metals (M element, e.g., Ti, Zr, or Mo), and carbon or nitrogen (X element). When ‘A’ atoms are chemically removed from the MAX phase precursor, MXene flakes are obtained with a general chemical formula of Mn+1XnTx where Tx is the surface functional groups that can consist of oxygen, hydroxyl, chloride, or fluoride groups. Titanium carbide (Ti3C2Tx) is one of the commonly studied MXenes (Fig. 1a). These Ti3C2Tx nanoflakes can have high thermal conductivity (55.8 W m−1 K−1)4 and electrical conductivity (i.e., <20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 S cm−1)5–7 with a wide range of lateral sizes (100 nm–10 μm)6–8 as a single or highly ordered multilayer nanostructures.
000 S cm−1)5–7 with a wide range of lateral sizes (100 nm–10 μm)6–8 as a single or highly ordered multilayer nanostructures.
 | ||
| Fig. 1 (a) Micrograph of Ti3C2Tx before exfoliation process, (b) schematic of MXene polymer composites with multilayered MXene clusters. | ||
MXene polymer composites are currently gaining attentions because of their potential application as multifunctional and intelligent materials.9,10 In these composites, exfoliated MXene nanosheets are dispersed in a polymer matrix. For instance, epoxy and water-soluble polymers such as polyvinyl alcohol has been used as the matrix material to produce high-strength functional nanocomposites.4,11,12 More recently, MXenes are considered as a nanoscale building blocks for creating soft multifunctional composites.13 In these composites, MXenes are embedded in compliant polymers such as elastomers (e.g., polydimethylsiloxane – PDMS) and gels. Even at low volume fractions of MXene nanosheets, the following soft multifunctional composites exhibit promising electromagnetic shielding behavior,14–16 triboelectricity,17–20 thermal management,15,20 and high strain sensitivity21,22 which makes MXPCs desirable for applications in wearable electronics, soft robotics, and human–computer interactions.
The nanostructure, volume fraction, and orientation of embedded MXenes are several primary microstructure parameters that dictate the effective properties of MXene polymer composites. Unlike zero-dimensional functional nanomaterials (i.e., solid nanoparticles), the alignment and orientation of dispersed MXenes contribute to the anisotropic mechanical and conductive behaviors of their nanocomposites.23 In addition, synthesized MXenes can have several to multiple layered structures with various lateral sizes.1,8,24 Large MXenes with several layered structures are often selected to create high dielectric25,26 and thermally conductive27,28 MXene polymer composites at low concentration, while the mechanical stiffening in MXene-based soft composites is found proportional to the lateral size of embedded Ti3C2Tx.27,29 As illustrated in Fig. 1b, utilizing multilayered MXenes allows the sustainable production of MXPCs because layered MXenes can be synthesized close up to 100% yield without the several exfoliation and washing steps that are required for producing monolayer MXenes.8,30 Therefore, material design tools must be developed to predict the effective properties of MXene polymer composites.
Most current studies investigate the mechanical behaviors of MXene polymer nanocomposites using computational techniques. For instance, finite element method (FEM) is used to study the effects of MXenes’ multilayer structure on the fracture toughness, strength, and stiffness of MXene epoxy composites.31 In other studies, FEM simulations are used to investigate the effective Young's modulus32 and damage mechanics33 of multiphase epoxy composites with other 2D fillers such as graphene. The same FEM technique can also be used to computationally demonstrate how agglomerated MXene platelets with non-uniform aspect ratios and random orientations can suppress the stiffening effects in their polymer composites.33 Most of these modeling efforts focus on approximating the mechanical behaviors of MXene nanocomposite with stiff polymer matrices (elastic modulus of ∼1 GPa) while also emphasizing the structural reinforcement of the composite enabled by MXenes. On the contrary, the stiffening effect of MXPCs should be minimized for soft-matter engineering applications while the enhancement of thermal conductivity and dielectric constants (i.e., functional properties) are improved. To achieve this goal, the size, shape, structure, and volume fraction of embedded MXenes must be optimized. Thus, we develop a micromechanics model that can consider the influence of these microstructures on the bulk properties of soft multifunctional MXene polymer nanocomposites. Furthermore, this model can consider the percolation behavior and the layered structure of MXenes. The results of this study will help outline the tradeoff between the stiffness and functional behaviors of MXene polymer composites based on the size and structural arrangement of MXenes. To the best of our knowledge, this is the first micromechanics model that is formulated to predict the effective behaviors of soft multifunctional MXene polymer composites.
2 Modeling approach
2.1 Micromechanics model formulation
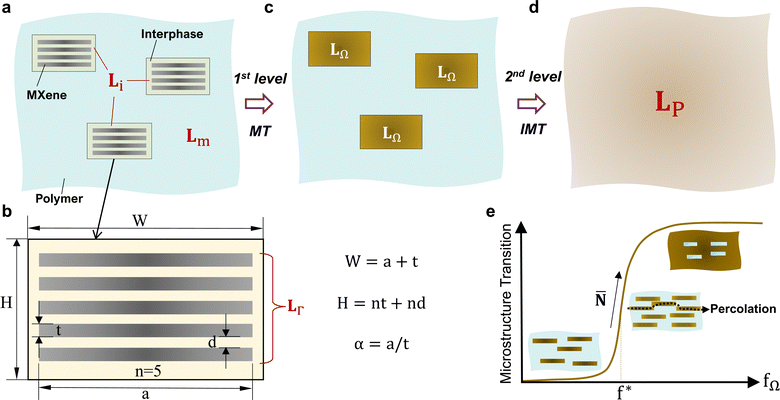
Mori–Tanaka (MT) theory is the common micromechanics model used to estimate the effective mechanical and functional properties of composites with 2D inclusions.34,35 However, when these 2D inclusions have high aspect ratios such as MXene and are embedded in polymer matrix with low elastic modulus, the accuracy of this model declines even at mild filler volume fractions.36 Moreover, Mori–Tanaka theory generally assumes that each of the inclusions in consideration are well separated and always surrounded by the matrix material. However, this configuration contradicts the fact that most MXenes in their composites have tightly layered arrangements. To address this modeling incompatibility, we had modified the existing Interpolated Mori–Tanaka (IMT) model37,38 to consider MXene's highly ordered nanostructure and percolation behaviors by incorporating Cauchy's interpolating function.39–41 This modified IMT model is used to evaluate the effective properties of MXPCs based on the properties of polymer matrix and the homogenized properties of clustered or multilayered MXenes which have been determined first by MT theory. This two-level homogenization approach is necessary for our IMT model to consider the multilayer structure, lateral lengths, interphase, orientations, and interactions between suspended MXenes at different length scales in the composite. In this section, the IMT model will be formulated to determine the general properties of MXPCs before eventually being redefined to predict the effective mechanical and functional behaviors of the composite.MXene polymer composites can be treated as a three-phase composite which constitutes the isotropic polymer matrix, interphase, and MXenes (Fig. 2a and b). To include the influence of MXenes’ multilayer structure or cluster on the final properties of MXPCs, an equivalent medium (Ω) is used to represent the locally averaged properties of MXene clusters (MC) which will be evaluated by MT theory at the first level of homogenization. The overall property of the MC depends on the properties of interphase (Li), monolayer MXene (LΓ), thickness (t), diameter (a), distance between single layer MXenes (d), and number of stacked layers (n) as shown in Fig. 2b. In addition, the shape of this equivalent medium is assumed to be aligned and centered to the flat cylindrical shape of layered MXenes (Fig. 2b and c).
The ratio of volume fraction of MXenes (fΓ) to those of equivalent medium (fΩ = fΓ + fi) is defined by expression R which does not depend on the number of layers (n) of MXenes in the cluster (eqn (1)). Instead, R converges to one when the interlaminar distance (d) approaches zero as the thickness to diameter ratio of MXene is very small. If the gap between monolayer MXenes is equal to the thickness of single layer MXene, R will converge to 0.5 because the width (W) of MC remains unchanged (Fig. 2b). In the case of MXPCs without MXene clusters (n = 1), R will be one (t = 0) unless a distinct interphase with finite thickness exists which alternately will have R = a2/(a + t)2. In general, the relationship between the volume fraction of polymer matrix (fm), interphase (fi), and MXenes (fΓ) in the composite is determined by eqn (2) where their total summation must be one.
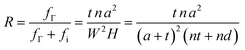 | (1) |
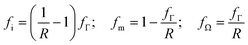 | (2) |
2.2 Effective properties of MXene clusters
Mori–Tanaka model is first used to determine the effective property of the MXene clusters which is the equivalent medium (LΩ) as shown in eqn (3). In this method, a global field concentration tensor (AΓ,Ω) is computed to relate the average field in the MXene phase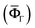 with the average field in the equivalent medium
with the average field in the equivalent medium 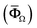 (eqn (4) and (5)). For elastic properties, this field concentration tensor will become the strain concentration tensor. Thus, when a strain field is applied on the composite, AΓ,Ω quantifies the load transfer efficiency between the interphase and MXene nanosheets within the equivalent medium. According to eqn (6), AΓ,Ω is dependent on the local field concentration tensor (BLi,LΓ) which is a quantity that considers the field concentration values when single layer MXenes are clustered or layered within their interphase of the equivalent medium or MC. In eqn (4) and (6), the term I represents the general identity matrix while ‘:’ is the multiplication operator either for 2nd (functional properties) or 4th (elastic properties) order tensors.
(eqn (4) and (5)). For elastic properties, this field concentration tensor will become the strain concentration tensor. Thus, when a strain field is applied on the composite, AΓ,Ω quantifies the load transfer efficiency between the interphase and MXene nanosheets within the equivalent medium. According to eqn (6), AΓ,Ω is dependent on the local field concentration tensor (BLi,LΓ) which is a quantity that considers the field concentration values when single layer MXenes are clustered or layered within their interphase of the equivalent medium or MC. In eqn (4) and (6), the term I represents the general identity matrix while ‘:’ is the multiplication operator either for 2nd (functional properties) or 4th (elastic properties) order tensors.| LΩ = Li + R(LΓ − Li) : AΓ,Ω | (3) |
| AΓ,Ω = fΩBLi,LΓ : (fiI + fΓBLi,LΓ)−1 | (4) |
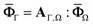 | (5) |
| BLi,LΓ = (I + SΓ : (Li−1 : LΓ − I))−1 | (6) |
The improved properties of the equivalent medium (LΩ) rely on the morphology of the encircled monolayer MXenes which behaves as field polarizers or reinforcement bodies of the MC (Fig. 2b). Hence, IMT model must consider the aspect ratio (α = a/t) of single layer MXene in the first homogenization step. This can be achieved by employing Eshelby's tensors (SΓ) to analytically determine the average strain, electric potential field, or thermal gradient in MXenes.42–46 These Eshelby's tensors can be defined as eqn (S1) and (S13) (ESI†) when evaluating the mechanical and functional properties of the equivalent medium, respectively. For instance, the mechanical Eshelby's tensor (SΓ) in BLi,Lf will depend on the Poisson's ratio of the interphase (νi) and the aspect ratio (α) of monolayer MXenes. On the other hand, to determine the functional properties of the equivalent medium, the same Eshelby's tensors (SΓ) will be replaced by a 2nd order (eqn (S13), ESI†) Eshelby's tensor which is only dependent on the aspect ratio of MXene (α). It is also important to emphasize that the current study utilizes flat cylinder47,48 instead of standard flat ellipsoid Eshelby's tensor43 to model the field polarization behaviors of 2D MXene inclusions. This is because the modified micromechanics model in this study is found to significantly overestimate the properties of soft MXPCs when the embedded MXenes are simplified as flat ellipsoids or as penny shapes. Although actual synthesized MXenes can have more complex polygon- or rectangular-like morphologies, it is impractical to consider such shapes in the current IMT modeling framework as the Eshelby's tensor for these inclusion shapes are not explicit.49,50
2.3 Effective properties of MXene composites
Once the effective properties of MXene clusters or the equivalent medium (LΩ) is determined, IMT method is applied in the second homogenization step. In this step, the homogenized MXene clusters are now the field polarizers or reinforcement bodies in a polymer matrix phase (Fig. 2c and d). Therefore, IMT model is used here to determine the effective anisotropic property (LP) of MXPCs with aligned MXene clusters (eqn (7)). However, in most synthesized composites, the embedded MXene clusters are either misoriented or randomly oriented, resulting in the presence of anisotropy among MXPCs. Hence, it could be necessary to estimate the effective property of MXPCs (Lfp) with randomly oriented MC (eqn (8)). This can be done by conducting numerical orientation averaging (〈·〉) on the second term of eqn (8).51 The definition of this orientation averaging operation for 4th order (mechanical property) and 2nd order (functional properties) tensors are expressed by eqn (S16) and (S20) (ESI†), respectively.| Lp = Lm + fΩ(LΩ − Lm) : AΩ,P | (7) |
| Lrp = Lm + fΩ〈(LΩ − Lm) : AΩ,P〉 | (8) |
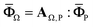 | (9) |
| β = w/H | (10) |
AΩ,P = ![[N with combining macron]](https://www.rsc.org/images/entities/b_char_004e_0304.gif) : (fmI + fΩ : (fmI + fΩ![[N with combining macron]](https://www.rsc.org/images/entities/b_char_004e_0304.gif) )−1 )−1 | (11) |
![[N with combining macron]](https://www.rsc.org/images/entities/b_char_004e_0304.gif) = ((1 − τ)(BLm,LΩ)−1 + τBLΩ,Lm)−1 = ((1 − τ)(BLm,LΩ)−1 + τBLΩ,Lm)−1 | (12) |
| BLm,LΩ = (I + SΩ : (Lm−1 : LΩ − I))−1 | (13) |
| BLΩ,Lm = (I + Sm : (LΩ−1 : Lm − I))−1 | (14) |
At the final homogenization of MXPCs, the role of the field concentration tensor (AΩ,P) of IMT model is to relate the average field in the overall composite body 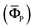 with the average field in the equivalent medium
with the average field in the equivalent medium 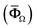 (eqn (9)). Since MC can have large aspect ratios (eqn (10)), these fillers are very likely to interact and form a percolating network when the volume fraction of the clusters is high. To consider this effect, AΩ,P is made dependent on the interpolated field concentration tensor (
(eqn (9)). Since MC can have large aspect ratios (eqn (10)), these fillers are very likely to interact and form a percolating network when the volume fraction of the clusters is high. To consider this effect, AΩ,P is made dependent on the interpolated field concentration tensor (![[N with combining macron]](https://www.rsc.org/images/entities/b_char_004e_0304.gif) ) (eqn (11). As the volume fraction (fΩ) of MC increases,
) (eqn (11). As the volume fraction (fΩ) of MC increases, ![[N with combining macron]](https://www.rsc.org/images/entities/b_char_004e_0304.gif) will interpolate between the local field concentration tensor evaluated when the distance between neighboring layered MXenes is large (BLm,LΩ) and when embedded MC are so densely interconnected that the polymer phase appears disconnected (BLΩ,Lm) (Fig. 2e). The interpolation progression between these two tensors is dictated by Cauchy's cumulative probability function (τ) which realistically simulate the percolation evolution of layered MXenes (Ω) as their volume fraction (fΩ) approaches and exceed a percolation threshold (f*) from a scale of zero to one.39–41,52
will interpolate between the local field concentration tensor evaluated when the distance between neighboring layered MXenes is large (BLm,LΩ) and when embedded MC are so densely interconnected that the polymer phase appears disconnected (BLΩ,Lm) (Fig. 2e). The interpolation progression between these two tensors is dictated by Cauchy's cumulative probability function (τ) which realistically simulate the percolation evolution of layered MXenes (Ω) as their volume fraction (fΩ) approaches and exceed a percolation threshold (f*) from a scale of zero to one.39–41,52
In the second homogenization step, the flat cylinder Eshelby's tensors are dependent on the aspect ratio (β) of the equivalent medium which is now treated as the reinforcement body for the polymer matrix. When modeling the functional property of MXPCs, both SΩ and Sm are 2nd order tensors (eqn (S13)) (ESI†) which solely depends on β. On the other hand, when evaluating the stiffness of MXPCs, SΩ is a 4th order Eshelby's tensor (eqn (S1), ESI†) that relies on the Poisson's ratio (νm) of polymer matrix and β. Similarly, Sm will be a 4th order Eshelby's tensor which depends on the Poisson's ratio of MXene (νΓ) in addition to β. This is done because the composite's microstructure represented by BLΩ,Lm suggests that the polymer phase is disconnected and appears as 2D shaped inclusions surrounded by MC when MXenes’ volume fraction (fΩ ≅ 1) is high (Fig. 2e). Also, it is important to clarify that in eigenstrain theory for elasticity, Sm (Mechanical Eshelby's tensor) would be dependent on the anisotropic property of the equivalent medium which is non-trivial to solve.43 Instead, Sm is assumed to be dependent on MXene's Poisson's ratio as an upper approximation for BLΩ,Lm.
2.4 Interchangeability of materials constants
In the formulation of interpolated Mori–Tanaka model, the property tensors of each λth phase in MXPCs are represented as Lλ. This general term is interchangeable when evaluating the mechanical or functional properties of MXene polymer composites.53 Table S2 (ESI†) summarizes the appropriate replacement of Lλ in eqn (3)–(14) when the effective stiffness (Cp), relative permittivity (εp), and thermal conductivity (κP) of MXPCs are evaluated. Also, the introduced general average field vector (![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/b_char_e0c1.gif) λ) can be considered as the strain, electric potential field, and temperature gradient of λth phase when the mechanical, dielectric, and thermal properties of MXPCs are respectively evaluated.
λ) can be considered as the strain, electric potential field, and temperature gradient of λth phase when the mechanical, dielectric, and thermal properties of MXPCs are respectively evaluated.
2.5 Cauchy's cumulative probability function
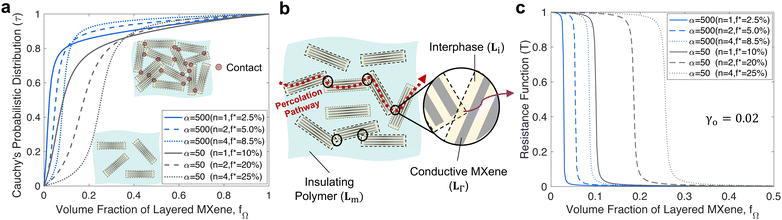
Single or layered MXenes are initially sparsely distributed in MXene polymer composites when the volume fraction is below a percolation limit (f*). As the volume fraction (fΩ) of MXene clusters increases, the probability of MXenes forming multiple interparticle contacts increases (Fig. 3a). Eventually, when the volume fraction exceeds a percolation limit, MXPCs will be saturated with layered MXenes that the polymer phase becomes disconnected. This microstructure transition can be simulated by Cauchy's cumulative probability (CCP) function (eqn (15)) before incorporated into IMT model (eqn (12).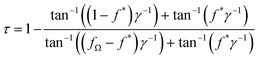 | (15) |
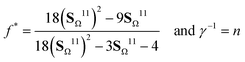 | (16) |
Based on eqn (15), the CCP function increases rapidly at the percolation limit (f*) which depends on the first component (SΩ11) of the Eshelby's tensor (SΩ).39,40 The concise expression for SΩ11 is given in eqn (S14) (ESI†). Since SΩ11 is only dependent on the aspect ratio of multilayer MXene (β), f* will be strictly dependent on the morphologies of MC (Fig. S2, ESI†). The estimated f* assumes that the embedded MXenes are randomly dispersed in a composite and is used to approximate the percolation limit of MXene clusters in their composites. Based on Fig. S2 (ESI†), f* is expected to decrease when the aspect ratio of MC (ζ−1 = β) in MXPCs is large which occurs when the number of layer (n) increases or the size (a) of the single layer MXenes decreases.
The rapid increase of Cauchy's cumulative probability function (τ) reflects the formation of percolation microstructures within MXPCs. For instance, CCP function suggests that MXPCs with large MXenes (α = 500) will form percolation microstructure at lower volume fraction than MXPCs with small (α = 50) MXene fillers (Fig. 3a). When the size of MXene is unchanged, a greater number of stacked layers (n) of embedded MXenes will cause the formation of percolation pathways to delay (f* shift higher) but the formation rate (γ−1) to increase (eqn (16)). This trend is realistic because for the same volume fraction and diameter, multilayer MXenes cannot form wider interconnected networks than few layer MXenes within their polymer composite. To create wider percolation networks, additional volume fraction of MC is needed to saturate the polymer matrix.
2.6 Resistance function for functional properties
MXenes’ percolation microstructure leads to the commonly observed sudden thermal conductivity and dielectric constant enhancement of MXPCs at a concentration threshold. This is because when percolation networks are formed, numerous neighboring MC will be in close contact with their respective interphase partially intersects each other (Fig. 3b). As a result, these overlapped interphases (Li) undergo large localized thermal conductivity or dielectric constant enhancement which respectively contributes to the sharp thermal or dielectric property improvement of MXPCs. Hence, a resistance function (T) is introduced to associate the function's resistance drop to the sudden enhancement in the local thermal conductivity (κi) and dielectric constant (εi) within the percolated MXene clusters (eqn (17) and (18)). In thermal property modeling, the sharp drop of resistance function within the interphase signifies the reduction in the interfacial (Kapitza resistance) or contact thermal resistance among percolated MC.41,54 Alternately, in dielectric property modeling, the rapid drop of resistance function mimics the spontaneous formation of nanocapacitors or the onset of Maxwell–Wagner–Sillars (MWS) effects among percolated MC. Therefore, Fig. 3c suggests that MXPCs with large (α = 500) monolayer MXenes will have a sharp decrease in resistance function or large functional property enhancement at 2.5% volume fraction. In contrast, MXPCs with small (α = 50) monolayer MXenes will have an acute drop in resistance function or sudden functional property improvement at 10% volume fraction.| Li = LmT−1 when Lλ = κλ or ελ | (17) |
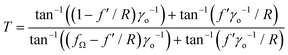 | (18) |
In this study, a scaling parameter (γ0) of 0.02 is used which is the approximated statistical value previously used for modeling the percolation evolution in graphene polymer composites.41 For simplicity, the percolation threshold (f*) used to model CCP function and the critical volume fraction (f′) for resistance function are assumed equal when modeling MXPCs with different sizes or layers of MXenes. It is also important to notice that at low volume fraction, eqn (18) suggests that the thermal or dielectric property of interphase converges to those of polymer matrix (Li = Lm) because of negligible interparticle interactions.
2.7 Finite element analysis
Finite element analysis is an effective way to validate the results of micromechanics model and to identify potential limitations of the model when predicting the effective properties of composites.46,55,56 To achieve this, the representative volume element (RVE) chosen for finite element evaluation needs to be sufficiently large to realistically reflect the microstructures of MXene polymer composite while is small enough to reduce computational resources.57 Hence, we chose the breadth (b) and height (h) of RVE to be at least two times larger than the diameter (a) and thickness (t) of MXenes, respectively (Fig. 4a). In this cubic RVE, there are hexagonal arrangements of flat cylinders representing MC dispersed in polymer matrix. In addition, the embedded MXenes can have several (n = 1 to 3) clustered flat cylinders uniformly separated by the thickness (d = t) of single layer MXene. For RVE with larger volume fraction of MXenes, the height of RVE is increased but the breadth is unchanged because the aspect ratio of MXenes is fixed. Each flat cylinders will have a diameter of 500 and thickness of one unit length in order to represent single layer MXene with aspect ratio of 500. We evaluated twenty four RVE of MXPCs with volume fraction of MC ranging between 1% to 10% and clustered layers of one to three. In all these RVE, both the bodies of the polymer and thin cylindrical MXenes are meshed with three node elements in ANSYS where the maximum allowable mesh size is set 500 times smaller than the breadth of RVE.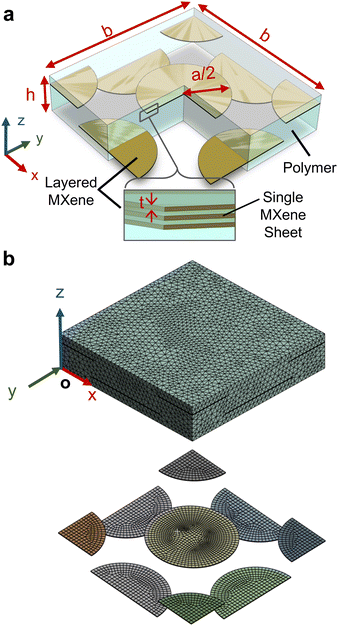 | ||
| Fig. 4 (a) RVE of MXPC with several layered MXenes. (b) The meshed body of the RVE with the layered MXenes configured as hexagonal packing. | ||
To prevent wall effects, the meshed RVEs are constructed to satisfy the material periodicity so the volume element behaves as they originate from the bulk nanocomposite.57 To do this, the thin plate inclusions (stacked or single layer) at the corners or boundaries of RVE are allowed to penetrate the borders but must reappear at the opposite edge (Fig. 4b). This guarantees that the opposites sides to have similar property and the evaluated final properties of the RVE to be transversely isotropic. Finally, homogeneous boundary conditions are used to evaluate the anisotropic elastic modulus, thermal conductivity, and static dielectric constants of the RVE. The detailed assembly of these boundary conditions are in the ESI.†
3 Results and discussion
To accurately predict the effective properties of MXene polymer composites, a realistic range of input material properties for monolayer MXene and polymer matrix is needed. These input material properties are summarized in Table S3 (ESI†) which includes the measured elastic modulus of single layer Ti3C2Tx by atomic force microscopy test58 and the measured elastic modulus of the polymer matrix (Sylgard 184) obtained from conducted tensile tests.59 The measured elastic modulus of single layer MXene can vary between 9 GPa and 70 GPa.58 In this modeling, the elastic modulus of MXene sheet is assumed to be 9 GPa (isotropic) as the effective stiffness of MXPCs with soft polymer matrix is found negligibly unchanged when MXenes’ elastic modulus ranges from the lowest (9 GPa) to the highest (70 GPa) stiffness (Fig. S4a, ESI†). Moreover, the Poisson's ratio (νλ) of Sylgard 184 and MXene is approximated as νm = 0.49 and νΓ = 0.2, respectively. Table S3 (ESI†) also includes the selected dielectric constants and thermal conductivity of the polymer matrix (Sylgard 184) and MXenes (Ti3C2Tx) which are used to predict the effective functional properties of MXPCs. Lastly, we assumed that the thickness (t) and separation distance (d) of MXenes are 1 nm. This approximation is justified based on X-ray diffraction measurements, which indicate that the separation distance of multilayer MXenes typically falls within the range of 0.5 to 1 nm.3.1 Mechanical properties
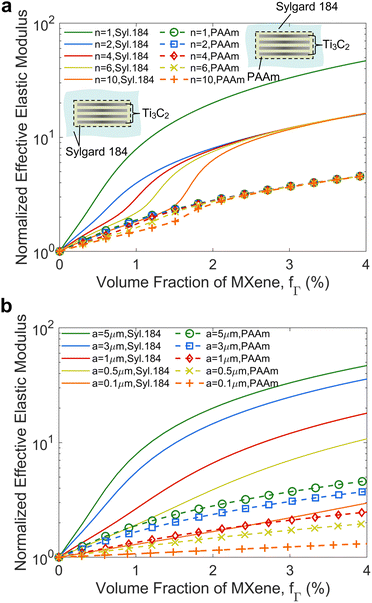
As the number of layers of large (a = 5 μm) Ti3C2Tx inclusions increases from one to ten layers, the large elastic modulus enhancement of MXene in Sylgard 184 composite (MXene-Sylgard 184) shifts to higher volume fraction (fΓ). This behavior is predicted because the mechanical reinforcement behavior of the composite depends on the filler distribution (Fig. 5a) and involves MXenes’ microstructure transitions when their volume fraction increases. When the number of layers of embedded MXenes are small (n < 4), this interpolation function surges at low volume fraction (fΩ < 2.4%). As a result, the elastic modulus of MXene-Sylgard 184 with single and two-layer MXenes (a = 5 μm) increases by 800% (∼12 MPa) and 400% (∼6 MPa), respectively at 1% volume fraction (Fig. 5b). In contrast, when the embedded MXenes have ten layers, the increase in the elastic modulus of the composite is initially slow (<200%) but escalates near 1.5% volume fraction. According to Fig. 5a, this volume fraction (fΓ ∼ 1.5%) is consistent to the volume fraction (fΩ = fΓ/R ≅ 3%) where the corresponding interpolation function of ten layer MXene clusters begins to increase. At above 3% volume fraction (fΓ), the predicted stiffness of MXene-Sylgard 184 with two or more layers of MXene inclusions becomes approximately equivalent to each other. These results indicate that the large stiffening effects of MXPCs at low volume fraction can be minimized when multilayer instead of single layer Ti3C2Tx inclusions are selected.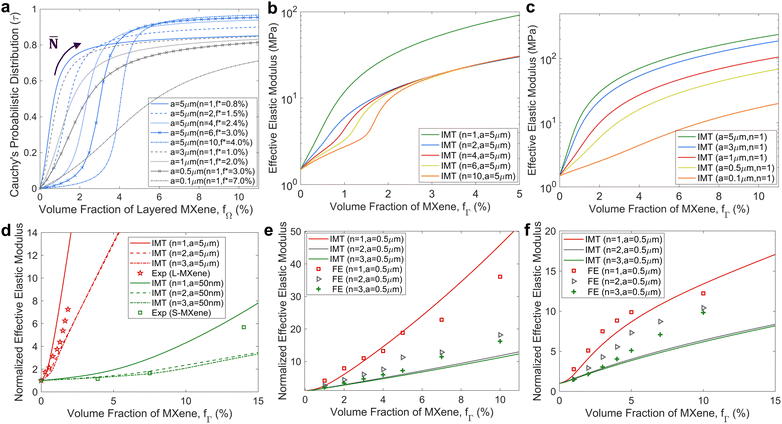 | ||
| Fig. 5 (a) Interpolation function for MXene inclusions with varying lateral diameter and layered structure. (b) Model prediction of effective elastic modulus of MXene–PDMS (Sylgard 184) with fixed MXene size (a = 5 μm) but different number of layers. (c) Effects of aspect ratio of monolayer MXenes on the stiffness of MXene–PDMS composite. (d) Comparison between predicted values and experimental data for the elastic modulus of MXene-Sylgard 184 with L-MXene and MXene–NBR with S-MXene.27,29 Elastic modulus of unfilled NBR chosen as 2.24 MPa and for unfilled PDMS as 0.4 MPa. Comparison of (e) longitudinal and (f) transverse elastic modulus evaluated from FEM with prediction results of the theoretical model. | ||
MXene-Sylgard 184 with nanosized single layer Ti3C2Tx sheets will have lower stiffness enhancements than MXene-Sylgard 184 with microscale single layer MXene sheets (Fig. 5c). For example, at 4% volume fraction, the effective elastic modulus of MXene-Sylgard 184 with large (a = 5 μm) and small (a = 100 nm) single layer MXenes are predicted to improve by 53 times (∼80 MPa) and 3 times (∼4.5 MPa), respectively. In addition, the stiffness increment of MXPCs with small monolayer Ti3C2Tx remains mild even at 10% volume fraction (fΓ). This is because as the volume fraction of smaller size MXenes increases, the microstructure transition (τ) of these fillers from sparse (low fΩ) to dense (high fΩ) distribution occurs much gradually. As a result, the stress or strain field around the smaller MXene fillers is only close enough to interact with their neighboring fillers when the filler volume fraction is sufficiently high.
3.2 Elastic modulus validations
The results of the Interpolated Mori–Tanaka model are being compared to the measured Young's modulus of MXene elastomer composites. As most fabricated MXene nanocomposites have randomly oriented MXenes, we approximate the orientations of MXene inclusions as random for this experimental validation. With this assumption, the Interpolated Mori–Tanaka model accurately predicts the measured Young's modulus of the MXene–PDMS composite, which incorporates large 5 μm size MXenes (referred to as L-MXene) as shown in Fig. 5d. For instance, when single, double, or triple layers of L-MXenes are randomly distributed in the PDMS composite, the predicted effective elastic modulus matches the measured stiffness of MXene–PDMS up to 3% volume fractions. This layer range is chosen based on the reported thickness measurement of several nanometers for embedded MXenes, suggesting predominantly few-layered structures with an approximate thickness of 1 nm. Upon closer comparison, the measured elastic modulus of the MXene–PDMS composite appears to fall between the predicted elastic moduli of composites with single and double-layered MXene clusters (Fig. 5d). This discrepancy could be attributed to a mixture of single and several-layer MXene fillers with variable lateral sizes in the test specimens, leading to a slight gap between experimental and theoretical results.The interpolated Mori–Tanaka model accurately estimates the measured elastic modulus of MXene–nitrile-butadiene-rubber composite (MXene–NBR), which contains small-sized MXenes (referred to as S-MXene).27 Initially, the measured elastic modulus of MXene–NBR shows a negligible increase up to 8% volume fractions, consistent with the predictions of the IMT model assuming two to three layers of MXene clusters (Fig. 5d). However, at approximately 14% volume fraction, the measured elastic modulus of MXene–NBR increases sixfold, which contradicts the IMT model's prediction based on randomly dispersed single-layer MXenes in the composite. Fabricating composites with only monolayer MXenes is highly challenging due to the aggressive agglomeration of nanosized MXenes at such high concentrations, leading to decreased mechanical reinforcement of the composite. Thus, unaccounted factors such as irregular lateral size distribution, orientation, and shapes of MXenes may contribute to the observed discrepancies between the predicted and measured results.
To further validate our modeling results, we compare the anisotropic elastic modulus (longitudinal and transverse) of MXene-Sylgard 184 predicted by the IMT model with the results of finite element method (FEM). In the IMT model predictions, we assume a fixed diameter of 500 nm (α = 500) for individual MXenes, consistent with the size of MXenes in the RVE shown in Fig. 4a. Due to the high aspect ratio, alignment, and separation of MXenes in the RVEs, the IMT model's percolation threshold (f*) is approximated to be close to zero (f* = ∼0.01), while the formation rate (γ−1) of the CCP function is set to one. These parameters are chosen based on the predicted percolation threshold for randomly oriented MXenes with an aspect ratio (ζ−1) of 500 (Fig. S2, ESI†). Thus, we can use the same modeling parameters to validate the thermal and dielectric properties of MXene polymer composites using FEM.
Comparing the longitudinal elastic modulus, both the IMT model and FEM results exhibit similar prediction behaviors. The elastic modulus predicted by the IMT model and FEM for composites with single-layer MXenes show the best agreement up to 5% volume fraction. However, the agreement between the theoretical and experimental results for composites with two and three layers of MXenes is limited to lower volume fractions before deviating at higher filler concentrations (Fig. 5e). Similarly, the transverse elastic modulus of MXPCs predicted by both the IMT model and FEM follows a comparable trend. However, the predicted transverse elastic modulus by the micromechanics model remains in close agreement with the FEM results only up to several percent volume fraction (Fig. 5f). At higher filler concentrations, particularly for MXene-Sylgard 184 with single and two-layer Ti3C2Tx inclusions, the IMT model underpredicts the transverse elastic modulus evaluated by FEM. This discrepancy arises because the interface of layered MXenes approaches the boundaries of the RVE at high volume fractions, leading to significant wall effects that reduce the accuracy of the FEM results. Nonetheless, most of the anisotropic elastic modulus of MXPCs predicted by both FEM and the IMT model closely align up to 3% volume fraction, which realistically represents the concentration limit for uniformly dispersed MXenes of this size in their composites.
3.3 The role of compliant interphase
The addition of an interphase surrounding MXene clusters can facilitate the synthesis of MXene nanocomposites and influence their mechanics. In our two-step homogenization model, we explore the effects of a softer interphase on the overall stiffness of MXPC. For instance, incorporating a hydrogel interphase, such as polyacrylamide (PAAm), which is assumed to be approximately five times more compliant (300 kPa) than Sylgard 184, can decrease the overall stiffness of MXene-Sylgard 184 by several orders of magnitude. Our micromechanics model reveals that the substantial stiffening behavior of MXPCs can be suppressed by the presence of a soft interphase. This holds true for composites containing either microscale multilayer MXenes (Fig. 6a) or single-layer MXene nanosheets (Fig. 6b). For example, when 5 μm size single-layer MXenes are embedded in Sylgard 184 at a 1% volume fraction, the predicted stiffness enhancement of MXPCs is only 1.9 times when a soft interphase is present, compared to an increase of up to 8 times without the soft interphase (i.e., perfect bonding). The model assumes that, in the absence of a soft interphase, the stiffness of the interphase and the polymer matrix are equivalent (Fig. 6a).The reduction in elastic modulus enhancement in MXene-Sylgard 184 composites, achieved by incorporating a soft PAAm interphase, is more pronounced for composites containing single-layer MXenes than for those with layered MXenes. For instance, the final elastic modulus of MXene-Sylgard 184 composites with one- and two-layer MXenes of the same lateral size (5 μm) becomes approximately equal when a PAAm interphase is introduced. Furthermore, the model shows that the soft interphase is particularly effective in mitigating the structural reinforcement caused by large single-layer MXenes (Fig. 6b). For instance, when a hydrogel interphase is introduced, the normalized elastic modulus of MXene-Sylgard 184 composites containing 5 μm and 100 nm monolayer MXenes reduces from 50 to 5 and from 10 to 2, respectively, at a 4% concentration. These modeling results suggest that the surface treatment of multilayer MXenes with a soft interphase can be a promising processing technique for creating highly flexible MXene polymer composites.
3.4 Predicting thermal properties
Using the interpolated Mori–Tanaka (IMT) model, we can investigate the influence of the micro or nano structures of MXenes on the thermal conductivity of their composites. Our model predicts that the thermal conductivity improvement of MXene-Sylgard 184 composites depends on the number of layers of large (5 μm) Ti3C2Tx MXenes, shifting from low to high volume fractions (Fig. 7a). For example, a thermal conductivity improvement of approximately 7 times (∼2 W m−1 K−1) can be achieved with either a 2.0% volume fraction of monolayer MXenes or a 2.5% volume fraction of ten-layered MXenes. This is because monolayer MXenes have a larger surface area-to-volume ratio, allowing them to form wider thermal networks at low volume fractions. In contrast, multilayer MXenes (n > 1) are locally clustered in the composite and are unable to form similarly wide conductive networks at the same low concentration, despite having the same size. At very low filler volume fractions (<0.5%), where percolation does not occur, the predicted thermal conductivity of MXene-Sylgard 184 becomes approximately the same regardless of the number of layers in the embedded MXene clusters.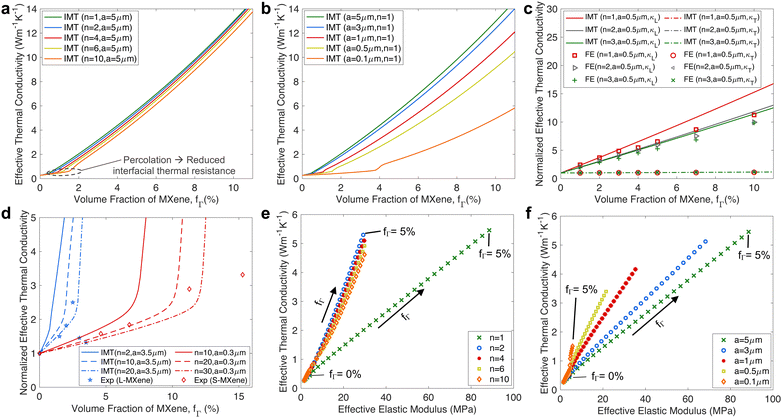 | ||
| Fig. 7 (a) Predicted longitudinal thermal conductivity of MXPCs with varying layers of MXene clusters. (b) Predicted longitudinal thermal conductivity of MXPCs with different diameters of MXene monolayers. (c) Comparison of FEM results with predicted thermal conductivity. (d) Comparison between predicted conductivity and experimental results.20,28 Thermal conductivity values of MXene-Sylgard 184 and MXene-PVDF are normalized by the thermal conductivity of unfilled Sylgard 184 (κm = 0.27) and unfilled PVDF (κm = 0.19), respectively. (e) Correlation between longitudinal thermal conductivity and elasticity of MXPCs with changes in MXenes’ layered structures (fixed 5 μm diameter). (f) Correlation between longitudinal thermal conductivity and elasticity of MXPCs with changes in the diameter of monolayer MXenes. | ||
High aspect ratio MXenes exhibit a more pronounced enhancement in the thermal properties of MXene-Sylgard 184 composites compared to those with low aspect ratio MXenes, particularly at low filler concentrations. For example, the thermal conductivity improvement of MXene-Sylgard 184 is approximately 7 times (2 W m−1 K−1) for a 2% volume fraction of 5 μm monolayer Ti3C2Tx and 1.5 times (0.4 W m−1 K−1) for a 2% volume fraction of 100 nm monolayer Ti3C2Tx (Fig. 7b). This is because as the size of monolayer MXenes decreases, the volume fraction at which there are enough MXene fillers to form thermally conductive pathways and reduce interfacial thermal resistance increases. The IMT model captures these trends by considering the critical volume fraction (percolation limit) that governs the microstructure transition (inflection point of CCP function) and reduced interfacial thermal resistance (resistance drop), which are inversely proportional to the aspect ratio (β) of the embedded MXene clusters.
3.5 Thermal conductivity validations
To validate our model, we compare the predicted thermal conductivity of MXene-Sylgard 184 composites (longitudinal – κL and transverse – κT) with FEM results in Fig. 7c. The IMT model assumes equal thermal conductivity between the interphase and polymer matrix (κi = κm) due to the separation of multilayer MXenes in the created RVEs. Results show reasonable agreement between the IMT model and FEM, especially at low volume fractions. The model indicates similar thermal conductivities for composites with two- and three-layer MXenes, while the single-layer MXene composite exhibits the highest thermal enhancement.In MXene composites with aligned clusters, in-plane thermal conductivity is high, but out-of-plane enhancement is negligible due to insulating interphases and the polymer matrix separating the aligned clusters. However, realistic MXPCs may not have ideal filler separation. Experimental studies have shown that transverse thermal conductivity can still improve significantly in MXene epoxy composites with aligned MXenes, likely due to smaller MXene flakes creating additional heat transfer bridges within the interphase or between aligned clusters.60 While our study does not fully consider these specific arrangements, the IMT model generally explains the impact of MXene orientation and multilayer structure on the effective thermal properties of MXene polymer composites.
Recently, a combined density functional theory (DFT) and effective medium theoretical calculations have also been used as another theoretical avenue to also predict the thermal conductivity of MXPCs with monolayer MXenes at low concentration.61 Upon comparison with our IMT model predictions, the calculated thermal conductivity of MXene in epoxy composites is also shown to be in close agreement with those predicted by interpolated Mori–Tanaka model. The IMT model appears to predict slightly larger thermal conductivity than the results from DFT evaluations (Table S4, ESI†). This is because of the absence of percolation considerations in the following combined DFT and effective medium theoretical calculations.
For further validation with experiments, we compare our prediction results with the measured thermal conductivity data of MXene polymer composites containing large (3.5 μm) and small (300 nm) MXene fillers.20 Our micromechanics model closely approximates the measured thermal conductivity of MXene-Sylgard 184 with 3.5 μm size MXenes (L-MXene) when assuming random suspension of ten to twenty MXene clusters in the composite (Fig. 7d). Additionally, the IMT model accurately predicts the thermal conductivity of embedded MXenes in polyvinylidene fluoride (MXene-PVDF), with approximately 300 nm size MXenes (S-MXene).28 We found that the model matches the measured thermal conductivity when assuming MXene clusters consisting of twenty to thirty layers. These layer assumptions are realistic, as most synthesized MXene clusters consist of multiple layers, with only a small number being single layers. Hence, it is reasonable to assume an average number of layers in the fabricated composites in our model.
Above the percolation volume fractions, the IMT model predicts a continuous significant increase in the thermal properties of MXPCs. However, experimental results show a slowdown in the thermal conductivity improvement of MXene-PVDF with large MXenes, and a decrease in the measured thermal conductivity of MXene-Sylgard 184 with small MXenes beyond the percolation limit (fΓ) of 2.2%. The theoretical model, on the other hand, predicts a continued escalation of thermal properties. This discrepancy arises because the micromechanics model assumes uniformly dispersed MXene clusters in the composite, while agglomeration void formation usually occurs as the volume fraction of MXenes increases during the synthesis. As a result, the contact surface area available for maintaining or expanding thermal pathways is reduced, impeding heat transfer within the polymer matrix.
3.6 Thermal conductivity and elastic modulus correlation
To address the suitability of MXene for soft multifunctional composites, material property charts were created to correlate the predicted values of thermal conductivity and elastic modulus of MXene-Sylgard 184. These charts provide insights into the tradeoffs between stiffness and thermal conductivity in MXene-based composites. Two correlations were examined: one considering the number of layers in MXene clusters (Fig. 7e), and the other focusing on the size of dispersed monolayer MXenes (Fig. 7f).The first correlation revealed that by favoring layered MXene fillers (n > 1) instead of single-layer MXenes, it is possible to preserve thermal conductivity enhancement while reducing the stiffening effects of MXPCs. For example, at a 5% volume fraction, the longitudinal elastic modulus and thermal conductivity of MXene-Sylgard 184 with 5 μm size single-layer MXenes were predicted to converge to 88 MPa and 5.5 W m−1 K−1, respectively. In contrast, at the same filler concentration, using 5 μm diameter MXene clusters with two layers resulted in predicted values of 30 MPa for the longitudinal elastic modulus and 5.3 W m−1 K−1 for the longitudinal thermal conductivity. This finding is promising because it was previously shown that the introduction of a soft interphase (PAAm) around the embedded clusters can further minimize the stiffening effects without compromising thermal conductivity, if the thermal properties of the interphase and the polymer matrix are similar. Notably, the selection of layered MXene clusters to minimize stiffening effects is effective when there is a large elastic modulus difference between the fillers and the polymer matrix. However, in a stiff epoxy matrix, both layered and monolayer MXenes exhibit similar mechanical reinforcement behavior (Fig. S4b, ESI†).
The second correlation examined the impact of the size of dispersed monolayer MXene nanosheets on thermal conductivity and elastic modulus. At a 5% volume fraction, MXene-Sylgard 184 with nanosized (100 nm) monolayer MXenes showed the lowest longitudinal thermal conductivity (∼1.5 W m−1 K−1) and smallest longitudinal elastic modulus (∼5.7 MPa) enhancement. In contrast, using larger (5 μm) MXene fillers resulted in higher thermal conductivity and larger Young's modulus at the same filler concentration. Therefore, without the presence of MXene clusters, it appears challenging to suppress the substantial stiffness reinforcement while maintaining the thermal property improvements of MXPCs. Theoretically, increasing the volume fraction (>5%) of small single-layer Ti3C2Tx sheets could potentially enhance the thermal conductivity-to-stiffness ratio of MXPCs. However, in practice, nanosized fillers tend to locally bind due to strong van der Waals interactions, limiting the formation of thermal conduction networks within the polymer matrix and leading to a deterioration in the effective thermal conductivity improvement.
3.7 Dielectric properties
Fig. 8a illustrates the predicted longitudinal dielectric constants of MXene-Sylgard 184 composites with 5 μm-sized Ti3C2Tx fillers of varying number of layers. The dielectric constant enhancement shifts from low to high volume fraction as the number of layers increases. For instance, a significant increase in dielectric constants is observed at 1.5% and 0.4% volume fractions for composites with ten-layer and one-layer Ti3C2Tx fillers, respectively. At low volume fractions, composites with one to several layer MXenes exhibit a dominant increase in dielectric constants due to the microstructure transition (Fig. 5a) and the onset of Maxwell–Wagner–Sillars effects (Fig. S3, ESI†) within MXene clusters. These factors indicate that composites with larger-sized MXenes and fewer layers can achieve high electrical permittivity at low concentrations. However, at high filler volume fractions (>4%), composites with ten-layer MXenes exhibit higher dielectric constants compared to those with fewer layers. This is because the introduction of additional multilayer MXenes saturates the composite more rapidly and reduces the average interparticle distance. It should be noted that the continuous improvement in dielectric behavior is contingent upon the absence of electron tunneling through ohmic conduction at the interphase, which occurs when neighboring MXene clusters are in direct contact with each other.62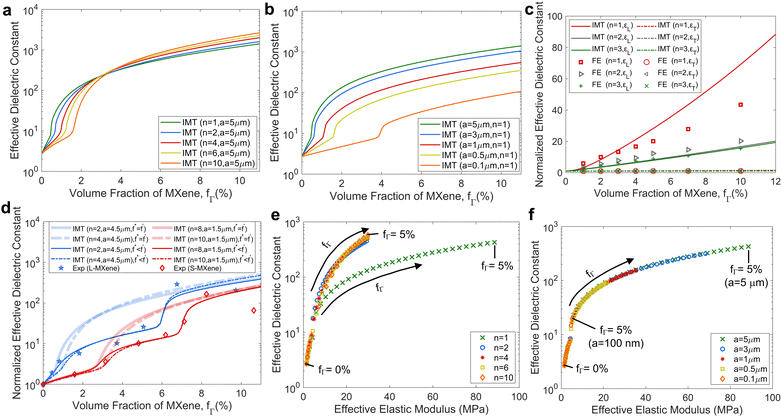 | ||
| Fig. 8 (a) Longitudinal dielectric constant of MXene–PDMS composites due to variations in the number of layers with a fixed 5 μm diameter. (b) Dielectric constant of MXene-Sylgard 184 with different sizes of monolayer MXenes. Dielectric constants are normalized with respect to the dielectric constant of unfilled Sylgard 184 (εm = 2.7). (c) Comparison of FEM results with predicted longitudinal (εL) and transverse (εT) dielectric constants of MXene-Sylgard 184. (d) Comparison between modeling results and experimental data63 for the dielectric constants of PVDF-Ti3C2Tx with assumed randomly oriented small (S-MXenes) and large MXenes (L-MXenes). (e) Correlation between predicted dielectric constants and stiffness predictions for MXene–PDMS composites with varying number of layers. (f) Correlation between predicted dielectric constants and stiffness predictions for MXene–PDMS with different sizes of monolayer MXenes. Both plots show up to 5% volume fraction (fΓ) of MXenes. | ||
The dielectric constants of the composites can also be enhanced by incorporating nanosized MXenes. However, achieving maximum dielectric constants in the composite requires a high-volume fraction of these nanoscale fillers. For instance, to obtain MXene-Sylgard 184 with a longitudinal dielectric constant of 10, either a 4% volume fraction of 100 nm-sized single layer MXene or a 0.5% volume fraction of 5 μm-sized monolayer Ti3C2Tx can be used (Fig. 8b). Consequently, smaller MXene fillers are less efficient in enhancing the dielectric constants of their composites. This is because a high filler volume fraction is necessary to ensure a sufficiently short average neighboring distance (near percolation) that induces large electric field polarization or significant nanocapacitance effects. The behavior observed in our micromechanics model aligns with these expectations, as the percolation microstructure transition (Fig. 5a) and the MWS effects for MXPCs with small monolayer MXenes theoretically occur at high volume fractions, where the suspended MXene clusters are probabilistically closest to each other (Fig. S3, ESI†).
3.8 Dielectric constant validations
FEM can be used to estimate the anisotropic dielectric constants of MXPCs. In our FEM simulations, we predict the dielectric constants of MXene-Sylgard 184, which consists of unidirectional MXenes with a diameter of 500 nm (Fig. 8c). We assume that the relative permittivity of the interphase is equivalent to that of the polymer matrix since there are no Maxwell–Wagner–Sillars effects and the MXene clusters are well separated in the RVE.When increasing the volume fraction of MXenes in MXene-Sylgard 184, both the interpolated Mori–Tanaka model and FEM solutions predict a similar improvement trend for the longitudinal dielectric constants (εL) of the composite. The models suggest that MXPCs with single-layer Ti3C2Tx exhibit the largest improvement in εL, while composites with two- and three-layer MXene fillers show lower and nearly equivalent εL at the same filler concentration. Comparing the predictions with FEM results, the relative permittivity predictions closely match the FEM results up to 3% volume fraction for single-layer MXenes. However, there is better agreement between both models when estimating the longitudinal dielectric constants of MXene-Sylgard 184 with two or three layers of MXene fillers. Therefore, the proposed IMT model can be a reliable predictive tool for evaluating the dielectric constants of MXPCs with low volume fraction or composites with layered and large size MXenes.
In contrast to the longitudinal dielectric constants, the Interpolated Mori–Tanaka model predicts much smaller transverse dielectric constants (εT) for MXPCs, showing negligible improvements even at high filler volume fraction. This is due to the smaller electrically insulating gaps between aligned multilayer MXenes in the longitudinal direction compared to the transverse direction, especially at high concentrations. Additionally, in the transverse orientation, the nano/micro capacitors formed by aligned MXene clusters can be considered in series connection,62 which can lead to lower effective capacitance or relative permittivity. As a result, there is lower interfacial electric field polarization at the interphase and a smaller enhancement in the effective dielectric constant in the orientation perpendicular to the suspended MXenes compared to the parallel direction.26 Hence, the orientation of multilayer Ti3C2Tx has a major effect on the dielectric properties of MXPCs.
To further validate our model as a reliable material design tool, we compare its predictions with the measured dielectric constants of MXene–polymer composites. Specifically, we focus on MXene-P[VDF-TrFE-CFE] composites containing large (L-MXenes – 4.5 μm) and small (S-MXenes – 1.5 μm) MXene fillers.25,63 Both types of fillers are assumed to be randomly oriented in the polymer matrix and have a thickness of one nanometer. According to Fig. 8d, the model closely predicts the measured dielectric constants of MXene-P[VDF-TrFE-CFE] composites with L-MXenes. This agreement is achieved when assuming embedded Ti3C2Tx clusters to have two to four layers. Similarly, the model accurately estimates the measured dielectric constants of MXene-P[VDF-TrFE-CFE] composites with S-MXenes when assuming randomly suspended Ti3C2Tx clusters to have eight to ten layers. These layer ranges chosen in the model are reasonable and consistent with the actual filler microstructures of most MXPCs. However, to obtain the best agreement, the critical volume fraction (f′) of the resistance function needs to be empirically determined from the experiments, which is found to be 6% and 7% (largest jump) for L-MXenes and S-MXenes, respectively.
In the original formulation of the IMT model, if the critical and percolation volume fractions are assumed to be equal (f* = f′), the model overestimates the dielectric constants of these composites even at moderate concentrations (>1%). This is because the peak microstructure transition (inflection point of CCP function) and MWS effects occur simultaneously. However, in the synthesized composites, the largest enhancement in the dielectric constants occurs at a higher filler concentration than the theoretical percolation limit (f* < 4%). This discrepancy can be attributed to potential differences in the morphologies (multilayer structure, polydispersity, etc.) of suspended MXenes at high volume fractions compared to low volume fractions. Agglomeration of large MXene clusters at high filler concentrations can significantly raise the real critical volume fraction or percolation limit, as our micromechanics model assumes uniform structures and distributions for all suspended MXenes, regardless of concentration. Additionally, particle agglomeration at high filler concentrations reduces the formation of more nano/micro capacitors in the composite, limiting the occurrence of MWS effects unless additional filler volume fraction is introduced. This can explain the secondary jump observed in the measured dielectric constant of MXene-P[VDF-TrFE-CFE].
As the volume fraction continues to increase, both MXPCs with large and small MXenes show decreasing measured dielectric constants. However, the micromechanics model predicts that the dielectric constants will continue to improve. This discrepancy arises because the IMT model assumes that once MWS effects take place, they remain active even with further increases in filler concentration. However, the stored charges among highly percolated MXene clusters will eventually experience electron or charge leakages, turning them into electrical conductors. Consequently, this phenomenon negates the effective charge storage and the enhancement of the composite's dielectric properties.
3.9 Relative permittivity and elastic modulus correlation
We can explore the tradeoffs between dielectric constants and elastic modulus in MXene polymer composites by correlating the predicted values of these properties. Fig. 8e shows the correlation between the predicted longitudinal dielectric constants and the predicted longitudinal elastic modulus of MXene-Sylgard 184. The composite includes one to ten layers of 5 μm size Ti3C2Tx inclusions. Similarly, Fig. 8f correlates the predicted longitudinal dielectric constants with the predicted longitudinal Young's modulus of MXene-Sylgard 184, considering the size of single-layer MXenes ranging from 100 nm to 5 μm.From Fig. 8e, it can be observed that MXene-Sylgard 184 with multilayer Ti3C2Tx can achieve dielectric constants in the order of hundreds while experiencing minimal enhancement in elastic modulus (<30 MPa) at low volume fractions (<5%). For instance, at 5% volume fraction, MXPCs with ten-layer Ti3C2Tx and 5 μm size exhibit dielectric constants of 580 and an elastic modulus of 30 MPa. In contrast, MXene-Sylgard 184 with single-layer Ti3C2Tx and 5 μm diameter shows dielectric constants of 430 and a stiffness of 90 MPa at the same volume fraction. These modeling results suggest that large-size MXene fillers with a multilayer structure can create MXene polymer composites with high dielectric constants and minimal mechanical stiffening. Conversely, large MXenes with single to a few layered structures are more suitable for creating stiff and high-strength composite materials where high dielectric constant is not a priority.
It is also possible to use small single or a few layer MXenes to create soft functional matter. However, according to our model, it would be challenging to achieve both high dielectric constants and low stiffness with these fillers in MXene-Sylgard 184. When the size of single-layer MXenes is reduced to 100 nm, the composite is predicted to have low elastic modulus (20 MPa) and dielectric constants (20) at 5% volume fraction (Fig. 8f). In contrast, composites with large (5 μm) single-layer MXenes exhibits high dielectric constants (∼400) and a large Young's modulus (90 MPa) at the same volume fraction. Therefore, based on these correlations, MXene fillers with large single or a few layered structures may not be suitable for creating MXPCs that require both high dielectric constants and high mechanical compliance.
4 Conclusion
In this study, we introduced an interpolated Mori–Tanaka model to predict the properties of MXene polymer composites. The model considered factors such as multilayer structure, size, orientation, interphase, and percolation microstructure. Comparisons with finite element method results and experimental data confirmed the accuracy of the model, particularly at low to moderate filler concentrations. Our findings suggest that MXene–PDMS composites with optimal properties can be achieved by incorporating large and aligned multilayer MXene fillers in a compliant matrix. The number of layers in the embedded MXenes influenced the stiffness of the composites. Conversely, MXPCs with large single-layer MXenes showed enhanced mechanical and functional properties with increasing volume fraction. These results emphasize the advantages of using large-sized multilayer MXene fillers in the design of soft multifunctional MXene polymer composites. Overall, this research provides valuable insights for tuning MXene nanostructures and microstructures to optimize the mechanical and functional properties of composites in various soft matter engineering applications such as stretchable electronics and wearable devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge support from the University of Washington Royalty Research Fund (grant no. A153081).References
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, 25th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- Y. Gogotsi and B. Anasori, The Rise of MXenes, ACS Nano, 2019, 13, 8491–8494 CrossRef CAS PubMed.
- A. VahidMohammadi, J. Rosen and Y. Gogotsi, The world of two-dimensional carbides and nitrides (MXenes), Science, 2021, 372, eabf1581 CrossRef CAS PubMed.
- R. Liu and W. Li, High-Thermal-Stability and High-Thermal-Conductivity Ti3C2Tx MXene/Poly(vinyl alcohol) (PVA) Composites, ACS Omega, 2018, 3, 2609–2617 CrossRef CAS.
- T. S. Mathis, et al., Modified MAX Phase Synthesis for Environmentally Stable and Highly Conductive Ti3C2 MXene, ACS Nano, 2021, 15, 6420–6429 CrossRef CAS.
- C. (John) Zhang, et al., Transparent, Flexible, and Conductive 2D Titanium Carbide (MXene) Films with High Volumetric Capacitance, Adv. Mater., 2017, 29, 1702678 CrossRef.
- S. Faisal, et al., Electromagnetic interference shielding with 2D transition metal carbides (MXenes), Science, 2016, 353(1137–1140), 2016 Search PubMed.
- C. E. Shuck, et al., Scalable Synthesis of Ti3C2Tx MXene, Adv. Eng. Mater., 2020, 22, 1901241 CrossRef CAS.
- M. Carey and M. W. Barsoum, MXene polymer nanocomposites: a review, Mater. Today Adv., 2021, 9, 100120 CrossRef CAS.
- K. Gong, K. Zhou, X. Qian, C. Shi and B. Yu, MXene as emerging nanofillers for high-performance polymer composites: A review, Composites, Part B, 2021, 217, 108867 CrossRef CAS.
- L. Wang, et al., Fabrication on the annealed Ti3C2Tx MXene/Epoxy nanocomposites for electromagnetic interference shielding application, Composites, Part B, 2019, 171, 111–118 CrossRef CAS.
- Y. Sliozberg, et al., Interface binding and mechanical properties of MXene-epoxy nanocomposites, Compos. Sci. Technol., 2020, 192, 108124 CrossRef CAS.
- C. Ma, M.-G. Ma, C. Si, X.-X. Ji and P. Wan, Flexible MXene-Based Composites for Wearable Devices, Adv. Funct. Mater., 2021, 31, 2009524 CrossRef CAS.
- X. Wu, et al., Compressible, durable and conductive polydimethylsiloxane-coated MXene foams for high-performance electromagnetic interference shielding, Chem. Eng. J., 2020, 381, 122622 CrossRef CAS.
- H. Liu, et al., Electrical insulating MXene/PDMS/BN composite with enhanced thermal conductivity for electromagnetic shielding application, Compos. Commun., 2021, 23, 100593 CrossRef.
- W. Yang, et al., Multifunctional MXene/natural rubber composite films with exceptional flexibility and durability, Composites, Part B, 2020, 188, 107875 CrossRef CAS.
- C. Jiang, et al., A multifunctional and highly flexible triboelectric nanogenerator based on MXene-enabled porous film integrated with laser-induced graphene electrode, Nano Energy, 2019, 66, 104121 CrossRef CAS.
- M. Salauddin, et al., A Novel MXene/Ecoflex Nanocomposite-Coated Fabric as a Highly Negative and Stable Friction Layer for High-Output Triboelectric Nanogenerators, Adv. Energy Mater., 2021, 11, 2002832 CrossRef CAS.
- Y. W. Cai, et al., A flexible ultra-sensitive triboelectric tactile sensor of wrinkled PDMS/MXene composite films for E-skin, Nano Energy, 2021, 81, 105663 CrossRef CAS.
- D. Wang, Y. Lin, D. Hu, P. Jiang and X. Huang, Multifunctional 3D-MXene/PDMS nanocomposites for electrical, thermal and triboelectric applications, Composites, Part A, 2020, 130, 105754 CrossRef CAS.
- Q. Guo, et al., Protein-Inspired Self-Healable Ti3C2 MXenes/Rubber-Based Supramolecular Elastomer for Intelligent Sensing, ACS Nano, 2020, 14, 2788–2797 CrossRef CAS.
- K. Zhang, et al., Self-Healing Ti3C2 MXene/PDMS Supramolecular Elastomers Based on Small Biomolecules Modification for Wearable Sensors, ACS Appl. Mater. Interfaces, 2020, 12, 45306–45314 CrossRef CAS PubMed.
- M. Yang, et al., Anisotropic Electromagnetic Absorption of Aligned Ti3C2Tx MXene/Gelatin Nanocomposite Aerogels, ACS Appl. Mater. Interfaces, 2020, 12, 33128–33138 CrossRef CAS.
- M. Li, et al., Element Replacement Approach by Reaction with Lewis Acidic Molten Salts to Synthesize Nanolaminated MAX Phases and MXenes, J. Am. Chem. Soc., 2019, 141, 4730–4737 CrossRef CAS PubMed.
- S. Tu, Q. Jiang, X. Zhang and H. N. Alshareef, Large Dielectric Constant Enhancement in MXene Percolative Polymer Composites, ACS Nano, 2018, 12, 3369–3377 CrossRef CAS PubMed.
- W. Ma, K. Yang, H. Wang and H. Li, Poly(vinylidene fluoride-co-hexafluoropropylene)-MXene Nanosheet Composites for Microcapacitors, ACS Appl. Nano Mater., 2020, 3, 7992–8003 CrossRef CAS.
- M. Aakyiir, et al., Electrically and thermally conductive elastomer by using MXene nanosheets with interface modification, Chem. Eng. J., 2020, 397, 125439 CrossRef CAS.
- K. Rajavel, et al., 2D Ti3C2Tx MXene/polyvinylidene fluoride (PVDF) nanocomposites for attenuation of electromagnetic radiation with excellent heat dissipation, Composites, Part A, 2020, 129, 105693 CrossRef CAS.
- L. Wei, et al., Enhanced Dielectric Properties of a Poly(dimethyl siloxane) Bimodal Network Percolative Composite with MXene, ACS Appl. Mater. Interfaces, 2020, 12, 16805–16814 CrossRef CAS PubMed.
- M. Alhabeb, et al., Guidelines for Synthesis and Processing of Two-Dimensional Titanium Carbide (Ti3C2Tx MXene), Chem. Mater., 2017, 29, 7633–7644 CrossRef CAS.
- G. Monastyreckis, et al., Micromechanical modeling of MXene-polymer composites, Carbon, 2020, 162, 402–409 CrossRef CAS.
- S. Kilikevičius, et al., Numerical investigation of the mechanical properties of a novel hybrid polymer composite reinforced with graphene and MXene nanosheets, Comput. Mater. Sci., 2020, 174, 109497 CrossRef.
- S. Kilikevičius, et al., Novel Hybrid Polymer Composites with Graphene and MXene Nano-Reinforcements: Computational Analysis, Polymers, 2021, 13, 1013 CrossRef.
- Y. Benveniste, A new approach to the application of Mori–Tanaka’s theory in composite materials, Mech. Mater., 1987, 6, 147–157 CrossRef.
- T. Mori and K. Tanaka, Average stress in matrix and average elastic energy of materials with misfitting inclusions, Acta Metall., 1973, 21, 571–574 CrossRef.
- S. Tarasovs and A. Aniskevich, Influence of the formation of clusters on the effective elastic properties of platelet reinforced polymers, Mech. Mater., 2022, 167, 104247 CrossRef.
- E. Ghossein and M. Lévesque, A comprehensive validation of analytical homogenization models: The case of ellipsoidal particles reinforced composites, Mech. Mater., 2014, 75, 135–150 CrossRef.
- G. Lielens, P. Pirotte, A. Couniot, F. Dupret and R. Keunings, Prediction of thermo-mechanical properties for compression moulded composites, Composites, Part A, 1998, 29, 63–70 CrossRef.
- R. Hashemi and G. J. Weng, A theoretical treatment of graphene nanocomposites with percolation threshold, tunneling-assisted conductivity and microcapacitor effect in AC and DC electrical settings, Carbon, 2016, 96, 474–490 CrossRef CAS.
- X. Xia, Z. Zhong and G. J. Weng, Maxwell–Wagner–Sillars mechanism in the frequency dependence of electrical conductivity and dielectric permittivity of graphene-polymer nanocomposites, Mech. Mater., 2017, 109, 42–50 CrossRef.
- Y. Su, J. J. Li and G. J. Weng, Theory of thermal conductivity of graphene-polymer nanocomposites with interfacial Kapitza resistance and graphene-graphene contact resistance, Carbon, 2018, 137, 222–233 CrossRef CAS.
- J. D. Eshelby, The determination of the elastic field of an ellipsoidal inclusion, and related problems, Proc. R. Soc. London, Ser. A, 2007, 241, 376–396 Search PubMed.
- T. Mura, Theory of Inclusions and Inhomogeneities, Mechanics of Elastic and Inelastic Solids, 1987 DOI:10.1007/978-94-009-3489-4.
- C. Friebel, I. Doghri and V. Legat, General mean-field homogenization schemes for viscoelastic composites containing multiple phases of coated inclusions, Int. J. Solids Struct., 2006, 43, 2513–2541 CrossRef.
- I. Doghri and A. Ouaar, Homogenization of two-phase elasto-plastic composite materials and structures study of tangent operators, cyclic plasticity and numerical algorithms, Int. J. Solids Struct., 2003, 40, 1681–1712 CrossRef.
- C. Chiew and M. H. Malakooti, A double inclusion model for liquid metal polymer composites, Compos. Sci. Technol., 2021, 208, 108752 CrossRef CAS.
- P. Franciosi, Mean and axial green and Eshelby tensors for an inclusion with finite cylindrical 3D shape, Mech. Res. Commun., 2014, 59, 26–36 CrossRef.
- P. Franciosi, S. Barboura and Y. Charles, Analytical mean Green operators/Eshelby tensors for patterns of coaxial finite long or flat cylinders in isotropic matrices, Int. J. Solids Struct., 2015, 66, 1–19 CrossRef.
- K. Zhou, et al., A review of recent works on inclusions, Mech. Mater., 2013, 60, 144–158 CrossRef.
- S. Trotta, F. Marmo and L. Rosati, Evaluation of the Eshelby tensor for polygonal inclusions, Composites, Part B, 2017, 115, 170–181 CrossRef.
- G. M. Odegard, T. S. Gates, K. E. Wise, C. Park and E. J. Siochi, Constitutive modeling of nanotube–reinforced polymer composites, Compos. Sci. Technol., 2003, 63, 1671–1687 CrossRef CAS.
- Y. Wang, J. W. Shan and G. J. Weng, Percolation threshold and electrical conductivity of graphene-based nanocomposites with filler agglomeration and interfacial tunneling, J. Appl. Phys., 2015, 118, 65101 CrossRef.
- M. Taya, Electronic Composites, University Press, Cambridge, 2005 DOI:10.1017/CBO9780511550508.
- Y. Sheng, et al., Multiscale modeling of thermal conductivity of hierarchical CNT-polymer nanocomposite system with progressive agglomeration, Carbon, 2023, 201, 785–795 CrossRef CAS.
- M. H. Malakooti and H. A. Sodano, Multi-Inclusion modeling of multiphase piezoelectric composites, Composites, Part B, 2013, 47, 181–189 CrossRef CAS.
- K. Hbaieb, Q. X. Wang, Y. H. J. Chia and B. Cotterell, Modelling stiffness of polymer/clay nanocomposites, Polymer, 2007, 48, 901–909 CrossRef CAS.
- I. M. Gitman, H. Askes and L. J. Sluys, Representative volume: Existence and size determination, Eng. Fract. Mech., 2007, 74, 2518–2534 CrossRef.
- J. Come, et al., Nanoscale Elastic Changes in 2D Ti3C2Tx (MXene) Pseudocapacitive Electrodes, Adv. Energy Mater., 2016, 6, 1502290 CrossRef.
- F. Schneider, T. Fellner, J. Wilde and U. Wallrabe, Mechanical properties of silicones for {MEMS}, J. Micromech. Microeng., 2008, 18, 65008 CrossRef.
- C. Ji, et al., Ice-Templated MXene/Ag–Epoxy Nanocomposites as High-Performance Thermal Management Materials, ACS Appl. Mater. Interfaces, 2020, 12, 24298–24307 CrossRef CAS PubMed.
- M. Wang, Y. Liu, H. Zhang, Y. Wu and L. Pan, Thermal conductivities of Ti3C2Tx MXenes and their interfacial thermal performance in MXene/epoxy composites – a molecular dynamics simulation, Int. J. Heat Mass Transfer, 2022, 194, 123027 CrossRef CAS.
- C.-W. Nan, Y. Shen and J. Ma, Physical Properties of Composites Near Percolation, Annu. Rev. Mater. Res., 2010, 40, 131–151 CrossRef CAS.
- S. Tu, et al., Enhancement of Dielectric Permittivity of Ti3C2Tx MXene/Polymer Composites by Controlling Flake Size and Surface Termination, ACS Appl. Mater. Interfaces, 2019, 11, 27358–27362 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00916e |
| This journal is © The Royal Society of Chemistry 2023 |