Machine learning-assisted optimization of multi-metal hydroxide electrocatalysts for overall water splitting†
Carina Yi Jing
Lim
 a,
Riko
I Made
a,
Riko
I Made
 a,
Zi Hui Jonathan
Khoo
a,
Zi Hui Jonathan
Khoo
 ab,
Chee Koon
Ng
ab,
Chee Koon
Ng
 a,
Yang
Bai
a,
Yang
Bai
 ac,
Jianbiao
Wang
ac,
Jianbiao
Wang
 a,
Gaoliang
Yang
a,
Gaoliang
Yang
 a,
Albertus D.
Handoko
a,
Albertus D.
Handoko
 *ab and
Yee-Fun
Lim
*ab and
Yee-Fun
Lim
 *ab
*ab
aInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Innovis #08-03, Singapore 138634, Republic of Singapore
bInstitute of Sustainability for Chemicals, Energy and Environment (ISCE2), Agency of Science, Technology and Research (A*STAR), 1 Pesek Road, Singapore 627833, Republic of Singapore. E-mail: Handoko_Albertus@isce2.a-star.edu.sg; limyf@isce2.a-star.edu.sg
cDepartment of Electrical and Computer Engineering, University of Toronto, Toronto, Ontario M5S 3G4, Canada
First published on 21st August 2023
Abstract
Green hydrogen produced via electrochemical water splitting is a suitable candidate to replace emission-intensive fuels. However, the successful widespread adoption of green hydrogen is contingent on the development of low-cost, earth-abundant catalysts. Herein, machine learning models built on experimental data were used to optimize the precursor ratios of hydroxide-based electrocatalysts, with the objective of improving the product's electrocatalytic performance for overall water splitting. The Neural Network-based models were found to be the most effective in predicting and minimizing the overpotentials of the catalysts, reaching a minimum in two iterations. The relatively mild reaction conditions of the synthesis procedure, coupled with its scalability demonstrated herein, renders the optimized catalyst relevant for industrial implementation in the future. The optimized catalyst, characterized to be a molybdate-intercalated CoFe LDH, demonstrated overpotentials of 266 and 272 mV at 10 mA cm−2 for oxygen and hydrogen evolution reactions respectively in alkaline electrolyte, alongside unwavering stability for overall water splitting over 50 h. Overall, our results reflect the efficacy and advantages of machine learning strategies to alleviate the time and labour-intensive nature of experimental optimizations, which can greatly accelerate electrocatalysts research.
New conceptsWe demonstrate a relatively straightforward implementation of machine learning for the optimization of synthesis parameters to yield the best-performing catalysts for overall water splitting in a given material space. In contrast to the majority of first-principles based machine learning approaches in the literature, this work highlights how simple machine learning methods can be practically integrated into experimental workflows to expedite electrocatalysis performance optimization. Specifically, we show how the experimental overpotentials of both electrocatalytic hydrogen and oxygen evolution reactions can be correlated directly to the input parameters – namely the molar fractions of the 5 metal-based precursors, leading to rapid performance optimisation. Computationally and experimentally-intensive steps of ascertaining structure–property-performance relations can then be reserved for better performing catalysts. As the machine learning models used herein are open source and easily adaptable, we expect wider implementation of the concept beyond electrocatalysis field. |
1. Introduction
Electrochemical water splitting can produce green hydrogen from renewable energy or off-peak surplus electricity, which is poised as a suitable low-carbon alternative to fossil fuels.1,2 Unfortunately, existing catalysts for water splitting are dominated by platinum group metals that are both rare and expensive. To accelerate industrial-scale applications, development of efficient and stable bifunctional catalysts based on earth-abundant elements for both half-reactions of water electrolysis is highly desirable.3,4 To further reduce manufacturing complexity and cost, the preparation of these electrocatalysts should also be simple and scalable.Layered double hydroxides (LDHs) are one such class of bifunctional electrocatalysts demonstrating noteworthy overall electrochemical water-splitting activity due to their unique lamellar structure and tuneable compositions.5 The structure of LDHs may be described as brucite-like metal hydroxide layers, but with 3+ oxidation states metals introduced into the 2+ metal hydroxide host structure, thereby leading to the intercalation of anion between the layers to compensate for additional positive charges.6 The electrocatalytic performances of these LDH structures have been shown to be further enhanced via diverse strategies including utilizing multi-metallic compositions,7,8 doping and defect engineering,9–12 as well as heterostructures and hierarchical architectures.13,14 In addition, it has been reported that introducing different intercalated ions also affect the electrochemical performance of the catalysts. This includes the influence of intercalated electrolyte cations15 as well as anions introduced into the interlayer spacing during the preparation of the LDH.16–18 For example, molybdate,19 and tungstate20 intercalated nickel–iron (NiFe) LDHs have significantly enhanced oxygen evolution (OER) activities. Systematic compositional studies via high-throughput experimentations have been used to investigate the electrocatalytic activity of complex multi-metallic (oxy)hydroxides.21,22 Alas, such approaches require screening of the entire material space to be fully effective, which remains extremely tedious and relies heavily on costly high-throughput instrumentation.
Beyond the full-scale high-throughput experiments, machine learning (ML)-aided approaches have also garnered increasing attention in electrocatalysis.23 Many of these ML studies and discussions are centred around computational models and density functional theory (DFT)-based catalyst screening (inverse design).24–29 However, it is common to observe a very wide disparity between the theoretically predicted potential and experimental reality, arising from a myriad of factors that remain very challenging to model accurately – such as the synthesis viability, reaction micro-environment, side reactions, and catalyst stability.30 Whilst there have been many recent advances in ML models based on experimental data for electrocatalysis,29,31,32 none for LDH systems have been reported to our knowledge. Ergo, the objective of this work is to implement a straightforward ML-driven optimization of LDH synthesis for overall water splitting based solely on the elemental composition of the electrocatalyst, with a small initial training dataset generated in-house and efficient convergence towards optimum performance via optimum tuning of the Bayesian Optimization process.33
Given the rich literature on NiFe,6,13,34 cobalt–iron (CoFe),35–37 and NiCoFe7,38 LDH-based catalysts and the abovementioned molybdate- and tungstate-intercalated LDHs, we seek an optimized LDH synthesis for overall water splitting centred around these five metal components. Given the five-dimensional material space selected, a typical full-scale optimization approach would be extremely time- and resource-intensive. Rather than approaching catalyst synthesis with a preferred composition and material in mind, we instead allow the ML models to optimize the metal precursor ratios based on the performance of the catalysts alone, facilitating the exploration of the parameter space with fewer human biases. The optimization of the synthesis parameters is entirely based on the experimental electrochemical performance of the catalysts, bypassing the need to obtain the composition–structure–property relationship of each datapoint. Such a straightforward approach aims to reflect practical implementation of ML in experimental workflows and demonstrate the efficacy of simple ML approaches without the use of extremely large datasets generated by high-throughput set-ups nor computationally-intensive calculations, given that both of which remain inaccessible to many experimentalists.
Despite the relatively small initial dataset of 53 samples, the ML models – particularly that from the neural network algorithm – were found to be efficient in optimizing the synthesis of electrocatalysts for overall water splitting. At present, we demonstrate the convergence of the models in as little as two iterations with the neural network predictive oracle, with a molybdate-intercalated CoFe hydroxide as the best performing overall electrochemical water splitting catalyst in alkaline conditions, with OER and HER overpotentials of 267 and 272 mV at 10 mA cm−2 when deposited on an Ni foam.
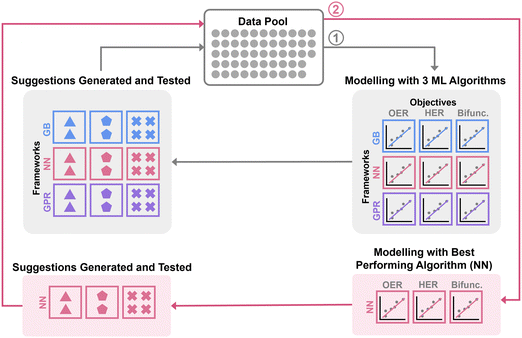
2. Results and discussion
A wet-chemistry approach based on NiFe LDH synthesis39 was adopted in this work. This triethanolamine-assisted route is selected for its mild reaction conditions of 95 °C in aqueous medium, without the need for strict monitoring and control of the solution pH. These mild conditions are amenable to automated workstations while retaining the ease of scaling up toward commercial production in the future. Five metal salts, namely cobalt(II) nitrate hexahydrate, nickel(II) nitrate hexahydrate, iron(III) nitrate nonahydrate, ammonium molybdate (para) tetrahydrate, and ammonium tungsten oxide hydrate were employed as Co, Ni, Fe, Mo, and W metal precursors respectively. Automated synthesis of the catalysts was conducted on a Lissy Chemical Workstation from Zinsser Analytics, which allows for pre-programmed steps of pipetting, shaking, and heating (full synthesis methods in Section S1.2, ESI†). The synthesized catalysts were then re-dispersed, drop-casted onto glassy carbon electrodes, and tested in a typical three-electrode rotating disc set-up in 1 M potassium hydroxide electrolyte (Section S1.4, ESI†).2.1. Machine learning optimization of synthesis parameters
The input parameters were chosen to be the molar ratio of the five metal precursors (X). With that the true number and identity of the active sites are difficult to ascertain, we adopt the recommendation where turnover frequency of the catalysts considers all relevant metal sides as active sites.40 Hence, the molar amount of all metal species – both cationic and anionic – is kept constant. In other words, X represents a set of five molar ratios, each varying between 0 and 1, with the sum of the five ratios equalling to 1.An initial dataset was constructed by obtaining OER and HER overpotentials at 10 mA cm−2 (ηOER and ηHER) and bifunctional activity metric (Ybifunc. = −(ηOER2 + ηHER2)−1) from linear sweep voltammetry (LSV) measurement at 10 mV s−1 of 53 samples synthesized with random varying ratios of the five metal precursors (Fig. S3.1–3, samples labelled i-{}, ESI†). The initial dataset is relatively diverse (Fig. S2.7, ESI†), with ηOER values between 279 to 409 mV; ηHER values from 348 to 562 mV; and Ybifunc. values between −2.18 and −4.90.
The overall machine learning workflow is summarised in Fig. 1. For model construction, the dataset was split into training and test sets with proportions of 70% and 30% of the dataset size respectively (Fig. S2.1, ESI†). We applied (trained and hyperparameters optimized) three commonly used machine learning (ML) algorithms, namely Gaussian process regression (GPR), gradient boosting (GB), and neural network (NN) to the dataset. GPR and GB were implemented in Python using scikit_learn library,41 while NN was implemented using pytorch library.42
We utilized Bayesian-Optimization with Gaussian process surrogate (BO-GP) to search for the optimum set of hyperparameters for each machine learning algorithm. The gp_minimize function, implemented in scikit-optimize,43 was used for hyperparameter tuning across the algorithms via minimization of the mean squared error (MSE) of the predictions for a third of the test set. The full description of the machine learning methods may be found in Section S2.1 (ESI†).
The objectives were to optimize the synthesis of electrocatalysts for oxygen evolution reaction (OER), hydrogen evolution reaction (HER), and collectively for both reactions. Machine learning surrogate models for these three objectives were then built for each of the algorithms as follows:
| ηOER = fOER(X) | (1) |
| ηHER = fHER(X) | (2) |
| Y(bifunc.) = −(ηOER2 + ηHER2)−1 = fbifunc.(X) | (3) |
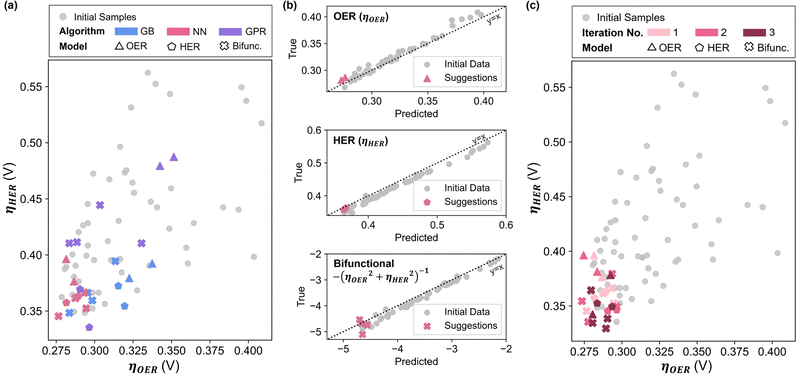
Comparing the overpotentials prediction (ηOER, ηHER, Ybifunc.), it is apparent that NN-suggested X* consistently show much better performance compared to GB and GPR in all objectives (Fig. 2a). NN also shows the highest prediction accuracy relative to GB and GPR, suggested by the closer datapoints to the parity line across all objectives (Fig. 2b and Fig. S2.6, ESI†). As such, NN was chosen as the preferred technique for subsequent iterations. Interestingly, Ni ratios seem to be suppressed or completely excluded from most of the models’ suggestions (Fig. S3.4, ESI†), which is contradictory to existing literature on LDH since Ni appears to be central to LDH's water splitting performance.5 In addition, the GB models also tend to favour higher ratios of W, as opposed to the NN suggestions where Mo is preferred.
Combining the additional 24 data points with the initial data set, the NN models were refitted, and new X* were generated (Fig. S3.6, ESI†). Due to significantly higher ηHER relative to ηOER, reducing ηHER has a greater effect in minimizing Ybifunc., consequently leading to similar compositions in the suggestions to minimise ηHER and Ybifunc.. Similar to the initial iteration, two suggestions each from the fOER(X) and fHER(X) models as well as four suggestions from the bifunctional model were synthesized and tested (Fig. S3.7, ESI†) for each iteration, and all data points were combined into the dataset to be re-fitted in the next iteration.
After the 3rd iteration, the activities seem to have already converged to a local minimum (Fig. 2c). NN-12, synthesized with only Co, Fe and Mo precursors from the 2nd NN iteration, was found to have the lowest Ybifunc. value amongst all samples at −5.28. NN-12 has ηOER and ηHER values of 277.5 mV and 335.4 mV respectively (Fig. 3b and c). Although NN-12 had the most negative Ybifunc., NN-13 from the 2nd iteration had the overall lowest ηOER at 273.4 mV while NN-21 from the 3rd iteration had the lowest ηHER at 329.4 mV.
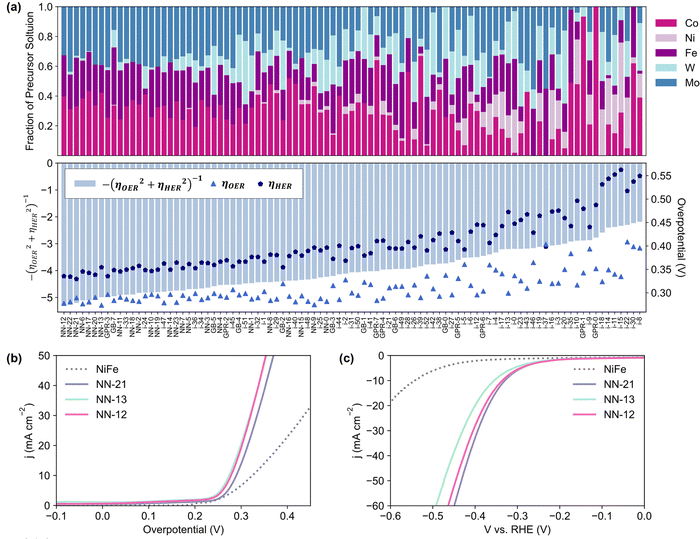 | ||
| Fig. 3 (a) Composition of catalysts synthesized and tested, sorted in order of ascending Ybifunc and their corresponding Ybifunc, ηOER, and ηHER values. (b) OER and (c) HER linear sweep voltammograms of the best performing bifunctional (NN-12), HER (NN-21), and OER (NN-13) catalysts, benchmarked against NiFe LDH synthesized as per literature,39 with comparable ηOER to the reported value. Linear sweep voltammograms collected at 10 mV s−1 on half-cell rotating disc electrode set-up in Ar-purged 1 M KOH. | ||
We note that the difference between the overpotentials of the 10 best-performing catalysts is less than 25 mV and may be within experimental error. The compositions of these catalysts follow an apparent trend, where lower overpotentials are achieved with catalysts that excludes Ni alongside low to no amounts of W (Fig. 3a). Consistently high Fe is also favoured, which is unsurprising given that Fe incorporation has been found to significantly increase the activity of Ni/Co(oxy)hydroxides relative to their unary oxides.46,47 The exclusion of Ni is unexpected, especially for OER, since typical NiFe systems generally outperform CoFe,48,49 and further characterisation and investigation is conducted below to better understand this trend. Nevertheless, the optimized catalyst significantly outperforms similarly-synthesized NiFe LDH which exhibited ηOER and ηHER values of 324.5 mV and 542.5 mV respectively, consistent with the ηOER reported value for this synthesis method.39 Additional discussion on the influence of the five metal precursors is included in the ESI,† Section S2.2 and Fig. S2.8, based on the NN models’ SHapley Additive exPlanations (SHAP) values.50
2.2. Characterisation of the optimized catalyst
Both energy dispersive X-ray (EDX) and X-ray photoelectron spectroscopy (XPS) spectra confirm that NN-12 predominantly comprises of Co, Fe, Mo, and O, with trace amounts of N also observed from contaminant TEA or urea decomposition (Fig. S4.1, ESI†).To validate the potential of the synthesis procedure to be translated towards industrial adoption, the synthesis of NN-12 was also scaled up by a factor of 10 from the scale used in the automated workstation (Section S1.2, ESI†). Similar morphologies resembling agglomerated nanosheets were observed from scanning electron micrographs of samples obtained from the automated and scaled-up synthesis method (Fig. 4a and b). EDX mappings of the two samples also reveal good homogeneity throughout the samples (Fig. S4.3, ESI†), with less than 1.25 at% variation of metal composition difference between the synthesis methods (Table S4, ESI†). High-resolution XPS scans of both samples are also similar (Fig. 4c–f and Fig. S4.4, ESI†), with multiplets corresponding to Co(OH)2 observed in the Co 2p at 780.4, 782.2, 786.0, and 790.4 eV51,52 (Fig. 4c). Meanwhile, the Fe 2p spectra (Fig. 4d) suggest that the Fe predominantly exists as Fe(III),53 while a pair of peaks identifies the Mo species as Mo(VI) from the molybdate54,55 (Fig. 4e). In the O 1s range (Fig. 4f), several peaks are observed: adsorbed water at 533.0 eV; lattice hydroxides at 531.1 eV; and metal–O species at 529.9 eV, which are largely attributed to the molybdate anions.52,56 No major change in the metal oxidation states from their precursors is observed, which is expected given the lack of strongly oxidising or reducing precursors.
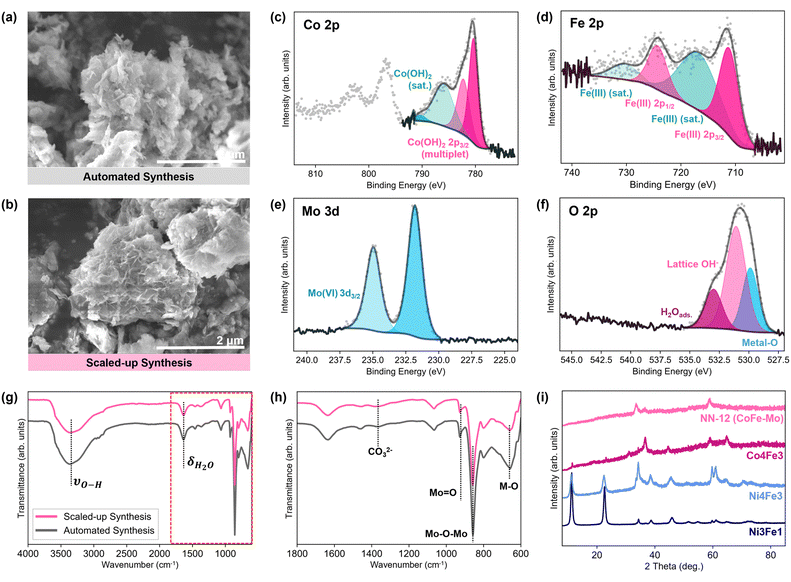 | ||
| Fig. 4 Scanning electron micrographs of NN-12 synthesized via (a) the automated workstation and (b) the scaled-up synthesis. Deconvoluted high-resolution X-ray photoelectron spectra for (c) Co 2p, (d) Fe 2p, (e) Mo 3d, and (f) O 2p of NN-12 synthesized by the automated workstation. (g) Fourier transform infrared spectrometry-attenuated total reflectance spectra of the catalysts and (h) an enlarged portion of the spectra as demarcated by broken lines in (g). (i) X-ray diffraction patterns of NN-12 alongside additional samples with systematic compositional changes,39 including NiFe from the original synthesis procedure (Ni3Fe1), Ni4Fe3 and Co4Fe3. | ||
Fourier transform infrared spectrometry-attenuated total reflectance (FTIR-ATR) spectra of the catalysts (Fig. 4g and h) corroborates the presence of O–H groups from the XPS O 1s spectra. A broad absorption band, red-shifted from the 3600 cm−1 band of free water molecules, is observed around 3370 cm−1 and is attributed to the stretching vibrations of the hydroxyl groups of the LDH as well as surface and interlayer water molecules.57 This is accompanied by a weaker band at 1625 cm−1, assigned to the O–H bending. Strong features associated with the presence of molybdates are also observed around 900 cm−1, most notably bands related to O–Mo–O and M![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 856 and 926 cm−1 respectively.57,58 Meanwhile, other peaks at wavenumbers below 800 cm−1 are usually attributed to metal–O/–OH bonding.59,60
O at 856 and 926 cm−1 respectively.57,58 Meanwhile, other peaks at wavenumbers below 800 cm−1 are usually attributed to metal–O/–OH bonding.59,60
Interestingly, a well-defined peak at ∼1350 cm−1, typically observed for carbonate anion-intercalated LDH structures from the anti-symmetric stretching mode of carbonate,61–63 is absent. Such a strong peak was reported in the NiFe FTIR spectrum obtained from the synthesis procedure this work was built upon,39 and was attributed to the intercalation of carbonate anions from urea decomposition to neutralize the positive charge generated by Fe3+ substitution within Ni(OH)2. The absence of such a carbonate feature further supports our hypothesis that molybdate anions may be intercalated into the LDH structure, in place of the carbonate anions.
Peaks identified in the Raman spectra (Fig. S4.5, ESI†) of both samples are also consistent with the presence of molybdate species seen with FTIR-ATR, with the strongest features at 328 cm−1, 820 cm−1, and 932 cm−1 assigned to its bending, asymmetric stretching, and symmetric stretching modes respectively.64,65 A weaker peak observed at 523 cm−1 is attributed to metal–oxygen vibrations observed for FeOOH34,66 or the Co–O (Ag) symmetric stretching mode,52 and is consistent with the previous spectra for CoFe LDHs.17,67
No differences were apparent between the X-ray diffraction (XRD) patterns of the samples from either synthesis method as well (Fig. S4.6, ESI†). Both patterns reflect poor crystallinity and are comparable to previous reports of molybdate-doped and intercalated NiFe LDHs.19,68 A strong (00l) peak at ∼10° typically observed for regular LDH structures is absent, suggesting lower periodicity in the direction perpendicular to the layers.19 No XRD peaks belonging to Co(II)- or Fe(III)-molybdate crystals are observed,69,70 supporting the case for molybdate ions intercalation between hydroxide sheets as opposed to a composite of molybdate salts and metal hydroxides or alloying.
Overall, the characterisation of our best catalyst suggests that the ML-optimized parameters yields a molybdate-intercalated CoFe LDH. The promising overall water splitting activity of this ML-suggested material is consistent with a recent report on Mo-doped CoFe LDH synthesized via electrochemical oxidation of CoFe Prussian-blue nanocubes, demonstrating excellent performance for overall water splitting.11 Although studies on molybdate-intercalated CoFe are limited, molybdate intercalation into NiFe LDH structures have been widely studied, particularly for improving the electrocatalytic activity for OER. To elaborate, the molybdate species were found to facilitate the reconstruction of the OER-active M-OOH phases,71–73 by undergoing dissolution and re-adsorption process at OER conditions. Molybdate anions were similarly observed to promote the reconstruction of α-Co(OH)2 nanosheets to active Co-OOH phases,74 and we posit similar effects may be operating in our NN-12 sample. In addition, prior literature also suggest that Mo doping could induce redistribution of the surface electron density to accelerate charge transfer and promote the formation of the *OOH intermediate for NiFe LDH structures as well.11,68,71,75 Congruent with these prior observations, NN-12 also exhibits significantly lower charge transfer resistance (Rct) than the original NiFe LDH,39 as observed from electrochemical impedance spectroscopy (Fig. S5.4, ESI†).
To better understand the physical phenomenon behind the ML suggestion, four additional samples were synthesised and characterised, varying the Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratio, replacing Ni and Co, as well as replacing the molybdate from NN-12 with tungstate (Section S4.2, ESI†). It was found that the incorporation of Co, exacerbated by the high Fe content and molybdate incorporation, compromises the crystallinity and stacking order of the LDH, as shown from the diminishing (00l) peaks (Fig. 4i). Given that the stability of the bulk LDH structure has been found to be affected by interlayer anions,76 the incorporation of molybdate may decrease the cohesion between the LDH sheets, leading to the disruption of the turbostratic structure. Relative to well stacked layers, structures with poor crystallinity and stacking have increased surface area, exposure of rich active sites as well as defects, all of which may contribute to enhanced electrochemical activity.77,78 Meanwhile, the incorporation of tungstate seems to induce the precipitation of electrically insulating FeOOH phase (Fig. S4.7, ESI†), which degrades the electrochemical performance. The full discussion may be found in the ESI,† Section S4.2. Overall, although the NiFe LDH is expected to have higher OER activity than CoFe LDH from literature,48 we hypothesise that this may be outweighed by the influence of the catalysts’ nanostructures arising from the effects of the different precursors used during synthesis.
Fe ratio, replacing Ni and Co, as well as replacing the molybdate from NN-12 with tungstate (Section S4.2, ESI†). It was found that the incorporation of Co, exacerbated by the high Fe content and molybdate incorporation, compromises the crystallinity and stacking order of the LDH, as shown from the diminishing (00l) peaks (Fig. 4i). Given that the stability of the bulk LDH structure has been found to be affected by interlayer anions,76 the incorporation of molybdate may decrease the cohesion between the LDH sheets, leading to the disruption of the turbostratic structure. Relative to well stacked layers, structures with poor crystallinity and stacking have increased surface area, exposure of rich active sites as well as defects, all of which may contribute to enhanced electrochemical activity.77,78 Meanwhile, the incorporation of tungstate seems to induce the precipitation of electrically insulating FeOOH phase (Fig. S4.7, ESI†), which degrades the electrochemical performance. The full discussion may be found in the ESI,† Section S4.2. Overall, although the NiFe LDH is expected to have higher OER activity than CoFe LDH from literature,48 we hypothesise that this may be outweighed by the influence of the catalysts’ nanostructures arising from the effects of the different precursors used during synthesis.
2.3. Catalyst stability
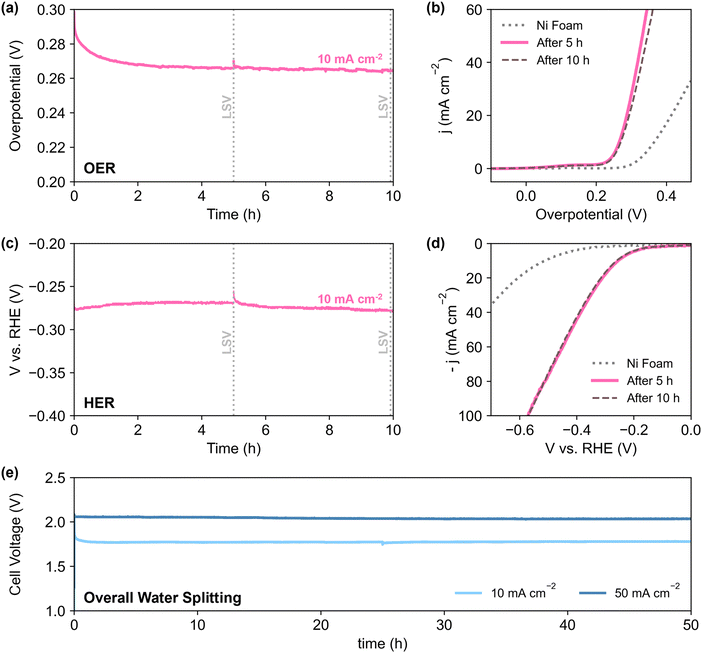
To better reflect the performance of the catalyst in practical applications, NN-12 from the scaled-up synthesis procedure was also tested on larger stationary electrodes, where the catalysts are air-brushed onto both sides of 0.3 mm Ni foams (Section S1.4, ESI†). Electrode areas measuring 1 × 1 cm (geometric active area = 2 cm2 per electrode) were isolated using epoxy resin to minimise possible current contributions from electrolyte ingress.Half-cell chronopotentiometry of NN-12/Ni foam electrodes was conducted at 10 mA cmgeo−2, delivering overpotentials of 266 and 272 mV for OER and HER respectively (averaged from the 2nd to 10th hour, Fig. 5a and c). Higher initial overpotentials observed is common amongst similar catalysts,79 and may be attributed to the ongoing reconstruction of the catalysts as these foam electrodes are not pre-treated. Apart from the formation of active metal hydroxide phases,48,80 the reconstruction process may also include dynamic dissolution and re-adsorption of the molybdate anions71–74,81 as mentioned earlier. No significant degradation was observed from LSV measured after 10 h (Fig. 5b and d), alluding to the good long-term stability of the catalyst. In addition, the observed OER Tafel slope of 59 mV dec−1 (Fig. S5.2a, ESI†) is in agreement with the proposed mechanisms for alkaline conditions, with reaction kinetics limited by the coverage of M*OOH sites.82 Meanwhile, the Tafel slope value for HER of 170 mV dec−1 (Fig. S5.2b, ESI†) is comparable to prior literature of LDH-based catalysts with no heteroatom doping.83 The deviation from cardinal HER Tafel values suggests possible Volmer–Heyrovsky mechanism,83,84 coupled with higher *H coverage and pH effects.82
The performance for overall water splitting was also evaluated via chronopotentiometry with the NN-12/Ni foam electrodes serving as both the cathode and anode. At 10 and 50 mA cmgeo−2, the cell voltage stabilised at around 1.78 and 2.04 V respectively, with no significant loss of activity after 50 h. Further quantification of hydrogen gas evolved during HER via gas chromatography yields average faradaic efficiency of 99.5% over more than 4 h at 10 mA cm−2 (Fig. S5.3, ESI†). Given its simple synthesis and structure, with no further modifications nor dopants, NN-12 delivers respectable performance and catalytic durability for overall water splitting, with comparable catalytic activities to some of the best LDH catalysts from prior literature (Table S5, ESI†).
3. Conclusion
In summary, we demonstrate the optimization of a simple synthesis and scalable procedure for bifunctional water splitting electrocatalysts. An optimum composition with the lowest bifunctional overpotential was found with merely two experimental iterations of our machine learning workflow. The syntheses were conducted in an automated workstation and the optimization was driven via ML through NN models built upon experimental data of 53 samples. The best-performing catalyst, NN-12, was tested to possess the characteristics of molybdate-intercalated CoFe LDHs, alongside good activity and stability for overall water splitting. Nevertheless, there remains much room for improvement and exploration in this work, such as increasing the material space and input parameters to be optimized. Possible expansion of this work includes the optimisation of heteroatom dopant species and content, with prior literature reporting promising electrocatalytic85–88 and photoelectrocatalytic88,89 water splitting activity with late transition metal dopants, especially copper and zinc.Consideration of experimental uncertainty as well as predicted uncertainty in the models may also allow for more robust ML models.90 In addition, whilst a simple negative inverse sum of squares approach was used herein to optimize for overall water splitting, there also exists well-established methods for multi-objective optimizations such as Chimera,44 which are particularly suited for more complex multi-objective optimizations.
Our key message is to highlight the efficacy of ML in assisting the optimization of experimental parameters and encourage experimentalists to tap into ML-assisted workflows to accelerate the time and labour-intensive nature of experimental work – particularly those with numerous parameters to be simultaneously optimized. Moreover, the use of ML may also aid in material discovery by removing human biases from the experimental process. Herein, the exclusion of Ni surprisingly led to better catalytic performances – which would not have been otherwise considered based on our preconception that Ni-based LDHs would yield better performances than Co-based LDHs. Other methods such as Phoenics91 have also been developed with chemistry and experimentation in mind, which is also an incredible tool for experimental catalyst discovery and optimization. Nevertheless, there remain many areas for further development. For example, developing better models suitable for smaller datasets would further increase the accessibility of ML to experimentalists, particularly for experiments conducted without high-throughput or automated set-ups to generate large data volumes. Such machine learning methods may be further expanded upon to facilitate the discovery and optimization of electrocatalysts over a wider material space, with greater efficiency relative to the Edisonian approach typically adopted in experimental catalysis research.
Code availability
Code available upon reasonable request.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work is supported by the Agency for Science, Technology and Research (A*STAR), and carried out within the framework of the Accelerated Catalysis Development Platform (grant number A19E9a0103). The authors acknowledge Dr Debbie Seng Hwee Leng, Dr Jian Liang Cheong and Dr Sebastian Yongsen Quek for their assistance in XPS and ATR-FTIR measurements.References
- M. Noussan, P. P. Raimondi, R. Scita and M. Hafner, Sustainability, 2020, 13, 298 CrossRef.
- X. Fu, R. Shi, S. Jiao, M. Li and Q. Li, J. Energy Chem., 2022, 70, 129–153 CrossRef CAS.
- J. Wang, X. Yue, Y. Yang, S. Sirisomboonchai, P. Wang, X. Ma, A. Abudula and G. Guan, J. Alloys Compd., 2020, 819, 153346 CrossRef CAS.
- B. You and Y. Sun, Acc. Chem. Res., 2018, 51, 1571–1580 CrossRef CAS PubMed.
- Y. Wang, D. Yan, S. El Hankari, Y. Zou and S. Wang, Adv. Sci., 2018, 5, 1800064 CrossRef PubMed.
- F. Dionigi and P. Strasser, Adv. Energy Mater., 2016, 6, 1600621 CrossRef.
- M. Oliver-Tolentino, J. Vazquez-Samperio, M. Tufiño-Velázquez, J. Flores-Moreno, L. Lartundo-Rojas and R. de Gonzalez-Huerta, J. Appl. Electrochem., 2018, 48, 947–957 CrossRef CAS.
- F. Qin, Z. Zhao, M. K. Alam, Y. Ni, F. Robles-Hernandez, L. Yu, S. Chen, Z. Ren, Z. Wang and J. Bao, ACS Energy Lett., 2018, 3, 546–554 CrossRef CAS.
- H. S. Jadhav, A. Roy, B. Z. Desalegan and J. G. Seo, Sustainable Energy Fuels, 2020, 4, 312–323 RSC.
- P. F. Liu, S. Yang, B. Zhang and H. G. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 34474–34481 CrossRef CAS PubMed.
- G. Zhao, B. Wang, Q. Yan and X. Xia, J. Alloys Compd., 2022, 902, 163738 CrossRef CAS.
- H. Sun, L. Chen, Y. Lian, W. Yang, L. Lin, Y. Chen, J. Xu, D. Wang, X. Yang, M. H. Rümmerli, J. Guo, J. Zhong, Z. Deng, Y. Jiao, Y. Peng and S. Qiao, Adv. Mater., 2020, 32, 2006784 CrossRef.
- Y. Ma, D. Liu, H. Wu, M. Li, S. Ding, A. S. Hall and C. Xiao, ACS Appl. Mater. Interfaces, 2021, 13, 26055–26063 CrossRef CAS PubMed.
- Y. Tang, Q. Liu, L. Dong, H. B. Wu and X.-Y. Yu, Appl. Catal., B, 2020, 266, 118627 CrossRef CAS.
- J. Zaffran, M. B. Stevens, C. D. M. Trang, M. Nagli, M. Shehadeh, S. W. Boettcher and M. Caspary Toroker, Chem. Mater., 2017, 29, 4761–4767 CrossRef CAS.
- D. Zhou, Z. Cai, Y. Bi, W. Tian, M. Luo, Q. Zhang, Q. Zhang, Q. Xie, J. Wang, Y. Li, Y. Kuang, X. Duan, M. Bajdich, S. Siahrostami and X. Sun, Nano Res., 2018, 11, 1358–1368 CrossRef CAS.
- G. Xiao, W. Chen, Y. Cai, S. Zhang, D. Wang and D. Cai, Catalysts, 2022, 12, 688 CrossRef CAS.
- B. M. Hunter, W. Hieringer, J. R. Winkler, H. B. Gray and A. M. Müller, Energy Environ. Sci., 2016, 9, 1734–1743 RSC.
- N. Han, F. Zhao and Y. Li, J. Mater. Chem. A, 2015, 3, 16348–16353 RSC.
- X. Xue, F. Yu, B. Peng, G. Wang, Y. Lv, L. Chen, Y. Yao, B. Dai, Y. Shi and X. Guo, Sustainable Energy Fuels, 2019, 3, 237–244 RSC.
- J. A. Haber, C. Xiang, D. Guevarra, S. Jung, J. Jin and J. M. Gregoire, ChemElectroChem, 2014, 1, 524–528 CrossRef.
- J. B. Gerken, S. E. Shaner, R. C. Massé, N. J. Porubsky and S. S. Stahl, Energy Environ. Sci., 2014, 7, 2376–2382 RSC.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- M. Karthikeyan, D. M. Mahapatra, A. S. A. Razak, A. A. M. Abahussain, B. Ethiraj and L. Singh, Catal. Rev., 2022, 1–31 CrossRef.
- L. Chen, X. Zhang, A. Chen, S. Yao, X. Hu and Z. Zhou, Chin. J. Catal., 2022, 43, 11–32 CrossRef CAS.
- N. K. Pandit, D. Roy, S. C. Mandal and B. Pathak, J. Phys. Chem. Lett., 2022, 13, 7583–7593 CrossRef CAS PubMed.
- L. Chen, Y. Tian, X. Hu, S. Yao, Z. Lu, S. Chen, X. Zhang and Z. Zhou, Adv. Funct. Mater., 2022, 32, 2208418 CrossRef CAS.
- X. Zhang, Y. Tian, L. Chen, X. Hu and Z. Zhou, J. Phys. Chem. Lett., 2022, 13, 7920–7930 CrossRef CAS PubMed.
- H. Mai, T. C. Le, D. Chen, D. A. Winkler and R. A. Caruso, Chem. Rev., 2022, 122, 13478–13515 CrossRef CAS PubMed.
- J. Resasco, F. Abild-Pedersen, C. Hahn, Z. Bao, M. T. M. Koper and T. F. Jaramillo, Nat. Catal., 2022, 5, 374–381 CrossRef.
- A. Zheng, Y. Wang, F. Zhang, C. He, S. Zhu and N. Zhao, iScience, 2021, 24, 103430 CrossRef CAS PubMed.
- M. R. Karim, M. Ferrandon, S. Medina, E. Sture, N. Kariuki, D. J. Myers, E. F. Holby, P. Zelenay and T. Ahmed, ACS Appl. Energy Mater., 2020, 3, 9083–9088 CrossRef CAS.
- Y.-F. Lim, C. K. Ng, U. S. Vaitesswar and K. Hippalgaonkar, Adv. Intell. Syst., 2021, 3, 2100101 CrossRef.
- Z. Qiu, C.-W. Tai, G. A. Niklasson and T. Edvinsson, Energy Environ. Sci., 2019, 12, 572–581 RSC.
- R. Yang, Y. Zhou, Y. Xing, D. Li, D. Jiang, M. Chen, W. Shi and S. Yuan, Appl. Catal., B, 2019, 253, 131–139 CrossRef CAS.
- D. S. Patil, S. A. Pawar, S. H. Lee and J. C. Shin, J. Electroanal. Chem., 2020, 862, 114012 CrossRef CAS.
- L. Feng, A. Li, Y. Li, J. Liu, L. Wang, L. Huang, Y. Wang and X. Ge, ChemPlusChem, 2017, 82, 483–488 CrossRef CAS PubMed.
- A. T. N. Nguyen, M. Kim and J. H. Shim, RSC Adv., 2022, 12, 12891–12901 RSC.
- S. Jaśkaniec, C. Hobbs, A. Seral-Ascaso, J. Coelho, M. P. Browne, D. Tyndall, T. Sasaki and V. Nicolosi, Sci. Rep., 2018, 8, 4179 CrossRef PubMed.
- F. Song, L. Bai, A. Moysiadou, S. Lee, C. Hu, L. Liardet and X. Hu, J. Am. Chem. Soc., 2018, 140, 7748–7759 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, E. Duchesnay and G. Louppe, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Z. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, in 33rd Conference on Neural Information Processing Systems, ed. H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox and R. Garnett, Curran Associates, Inc., Vancouver, Canada, 2019, pp. 8024–8035 Search PubMed.
- T. Head, M. Coder, G. Louppe, I. Shcherbatyi Fcharras, Z. Vinícius Cmmalone, C. Schröder, N. Campos, T. Young, S. Cereda, T. Fan, R. Rex, K. K. Shi, J. Schwabedal, C. H. Labs, M. Pak, F. Callaway, L. Estève, L. Besson, M. Cherti, K. Pfannschmidt, F. Linzberger, C. Cauet, A. Gut, A. Mueller and A. Fabisch, 2018.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Chem. Sci., 2018, 9, 7642–7655 RSC.
- L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, arXiv:1802.03426.
- M. B. Stevens, L. J. Enman, E. H. Korkus, J. Zaffran, C. D. M. Trang, J. Asbury, M. G. Kast, M. C. Toroker and S. W. Boettcher, Nano Res., 2019, 12, 2288–2295 CrossRef CAS.
- M. S. Burke, M. G. Kast, L. Trotochaud, A. M. Smith and S. W. Boettcher, J. Am. Chem. Soc., 2015, 137, 3638–3648 CrossRef CAS PubMed.
- F. Dionigi, Z. Zeng, I. Sinev, T. Merzdorf, S. Deshpande, M. B. Lopez, S. Kunze, I. Zegkinoglou, H. Sarodnik, D. Fan, A. Bergmann, J. Drnec, J. F. D. Araujo, M. Gliech, D. Teschner, J. Zhu, W.-X. Li, J. Greeley, B. R. Cuenya and P. Strasser, Nat. Commun., 2020, 11, 2522 CrossRef CAS PubMed.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schäfer, Chem. Soc. Rev., 2022, 51, 4583–4762 RSC.
- S. M. Lundberg and S.-I. Lee, in 31st Conference on Neural Information Processing Systems (NIPS), ed. U. v. Luxburg, I. Guyon, S. Bengio, H. Wallach and R. Fergus, Curran Associates Inc., Long Beach, CA, USA, 2017, pp. 4768–4777 Search PubMed.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- J. Yang, H. Liu, W. N. Martens and R. L. Frost, J. Phys. Chem. C, 2010, 114, 111–119 CrossRef CAS.
- T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441–2449 CrossRef CAS.
- Y. Lu, M. Zhao, R. Luo, Q. Yu, J. Lv, W. Wang, H. Yan, T. Peng, X. Liu and Y. Luo, J. Solid State Electrochem., 2018, 22, 657–666 CrossRef CAS.
- Z.-Q. Liu, L.-Y. Tang, N. Li, K. Xiao, J. Wang, J.-H. Zhang, Y.-Z. Su and Y.-X. Tong, J. Electrochem. Soc., 2012, 159, D582 CrossRef CAS.
- J.-C. Dupin, D. Gonbeau, P. Vinatier and A. Levasseur, Phys. Chem. Chem. Phys., 2000, 2, 1319–1324 RSC.
- K. Nejati, A. R. Akbari, S. Davari, K. Asadpour-Zeynali and Z. Rezvani, New J. Chem., 2018, 42, 2889–2895 RSC.
- R. Zavoianu, R. Birjega, O. D. Pavel, A. Cruceanu and M. Alifanti, Appl. Catal. A, 2005, 286, 211–220 CrossRef CAS.
- D. Sun, C. Li, S. Lu, Q. Yang and C. He, RSC Adv., 2021, 11, 20258–20267 RSC.
- S. Lee, M. Govindan and D. Kim, Chem. Eng. J., 2021, 416, 127918 CrossRef CAS.
- T. S. Munonde, H. Zheng and P. N. Nomngongo, Ultrason. Sonochem., 2019, 59, 104716 CrossRef CAS PubMed.
- F. Z. Mahjoubi, A. Khalidi, M. Abdennouri and N. Barka, J. Taibah Univ. Sci., 2017, 11, 90–100 CrossRef.
- M. Yasaei, M. Khakbiz, E. Ghasemi and A. Zamanian, Appl. Surf. Sci., 2019, 467–468, 782–791 CrossRef CAS.
- R. L. Frost, A. W. Musumeci, W. N. Martens, M. O. Adebajo and J. Bouzaid, J. Raman Spectrosc., 2005, 36, 925–931 CrossRef CAS.
- J. Wu, Z. Wang, S. Li, S. Niu, Y. Zhang, J. Hu, J. Zhao and P. Xu, Chem. Commun., 2020, 56, 6834–6837 RSC.
- K. Zhu, J. Chen, W. Wang, J. Liao, J. Dong, M. O. L. Chee, N. Wang, P. Dong, P. M. Ajayan, S. Gao, J. Shen and M. Ye, Adv. Funct. Mater., 2020, 30, 2003556 CrossRef CAS.
- E. Musella, I. Gualandi, E. Scavetta, A. Rivalta, E. Venuti, M. Christian, V. Morandi, A. Mullaliu, M. Giorgetti and D. Tonelli, J. Mater. Chem. A, 2019, 7, 11241–11249 RSC.
- Z. Yin, X. Liu, M. Cui, Z. Cao, A. Liu, L. Gao, T. Ma, S. Chen and Y. Li, Mater. Today Sustainability, 2022, 17, 100101 CrossRef.
- G. Harichandran, S. Radha, J. Yesuraj and B. Muthuraaman, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 627 CrossRef CAS.
- H. Oudghiri-Hassani, Catal. Commun., 2015, 60, 19–22 CrossRef CAS.
- Y. Gan, Y. Ye, X. Dai, X. Yin, Y. Cao, R. Cai and X. Zhang, J. Colloid Interface Sci., 2023, 629, 896–907 CrossRef CAS PubMed.
- H. Liao, X. Zhang, S. Niu, P. Tan, K. Chen, Y. Liu, G. Wang, M. Liu and J. Pan, Appl. Catal., B, 2022, 307, 121150 CrossRef CAS.
- J. Liu, P. Ding, Z. Zhu, W. Du, X. Xu, J. Hu, Y. Zhou and H. Zeng, Small, 2021, 17, 2101671 CrossRef CAS PubMed.
- Y.-L. Meng, Y. Li, Z. Tan, X. Chen, L.-L. Wu, L.-W. Ji, Q.-S. Wang, X.-Z. Song and S. Song, Energy Fuels, 2021, 35, 2775–2784 CrossRef CAS.
- Y. Gan, Z. Li, Y. Ye, X. Dai, F. Nie, X. Yin, Z. Ren, B. Wu, Y. Cao, R. Cai, X. Zhang and W. Song, ChemSusChem, 2022, 15, e202201205 CrossRef CAS PubMed.
- J. Zaffran, M. Nagli, M. Shehadeh and M. C. Toroker, Theor. Chem. Acc., 2017, 137, 3 Search PubMed.
- P. M. Bodhankar, P. B. Sarawade, G. Singh, A. Vinu and D. S. Dhawale, J. Mater. Chem. A, 2021, 9, 3180–3208 RSC.
- F. Song and X. Hu, Nat. Commun., 2014, 5, 4477 CrossRef CAS PubMed.
- L. Trotochaud, J. K. Ranney, K. N. Williams and S. W. Boettcher, J. Am. Chem. Soc., 2012, 134, 17253–17261 CrossRef CAS PubMed.
- X. Liu, J. Meng, K. Ni, R. Guo, F. Xia, J. Xie, X. Li, B. Wen, P. Wu, M. Li, J. Wu, X. Wu, L. Mai and D. Zhao, Cell Rep. Phys. Sci., 2020, 1, 100241 CrossRef.
- Y. Wang, Y. Zhu, S. Zhao, S. She, F. Zhang, Y. Chen, T. Williams, T. Gengenbach, L. Zu, H. Mao, W. Zhou, Z. Shao, H. Wang, J. Tang, D. Zhao and C. Selomulya, Matter, 2020, 3, 2124–2137 CrossRef.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- H. Yang, Z. Zhou, H. Yu, H. Wen, R. Yang, S. Peng, M. Sun and L. Yu, J. Colloid Interface Sci., 2023, 636, 11–20 CrossRef CAS PubMed.
- H. Chen, X. Liang, Y. Liu, X. Ai, T. Asefa and X. Zou, Adv. Mater., 2020, 32, 2002435 CrossRef PubMed.
- J. Han, J. Zhang, T. Wang, Q. Xiong, W. Wang, L. Cao and B. Dong, ACS Sustain. Chem. Eng., 2019, 7, 13105–13114 CrossRef CAS.
- L. Yan, B. Zhang, Z. Liu and J. Zhu, Chem. Eng. J., 2021, 405, 126198 CrossRef CAS.
- H. Wang, X. Liu, G. Liu, Y. Wang, X. Du and J. Li, Chem. Catal., 2023, 3, 100552 CrossRef CAS.
- J. Zaffran and M. C. Toroker, ChemPhysChem, 2016, 17, 1630–1636 CrossRef CAS PubMed.
- J. Zaffran and M. C. Toroker, ChemistrySelect, 2016, 1, 911–916 CrossRef CAS.
- F. Strieth-Kalthoff, F. Sandfort, M. H. S. Segler and F. Glorius, Chem. Soc. Rev., 2020, 49, 6154–6168 RSC.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh00788j |
| This journal is © The Royal Society of Chemistry 2023 |