Open Access Article
Open Access ArticleCollision-induced state-changing rate coefficients for cyanogen backbones NCN 3Σ− and CNN 3Σ− in astrophysical environments†
Lola
González-Sánchez
 a,
Ersin
Yurtsever
a,
Ersin
Yurtsever
 b,
Jorge Alonso
de la Fuente
b,
Jorge Alonso
de la Fuente
 c,
Cristina
Sanz-Sanz
c,
Cristina
Sanz-Sanz
 c,
Roland
Wester
c,
Roland
Wester
 d and
Francesco A.
Gianturco
d and
Francesco A.
Gianturco
 *d
*d
aDepartamento de Química Física, University of Salamanca Plaza de los Caídos sn, 37008, Salamanca, Spain
bDepartment of Chemistry, Koc University Rumelifeneriyolu, Sariyer TR 34450, Istanbul, Turkey
cDepartamento de Quimica Fisica Aplicada, Modulo 14, Universidad Autonoma de Madrid, 28049 Madrid, Spain
dInstitut für Ionenphysik und Angewandte Physik, Universität Innsbruck Technikerstr., 25 A-6020, Innsbruck, Austria. E-mail: francesco.gianturco@uibk.ac.at
First published on 25th October 2023
Abstract
We report quantum calculations involving the dynamics of rotational energy-transfer processes, by collision with He atoms in interstellar environments, of the title molecular species which share the presence of the CN backbone and are considered of importance in those environments. The latter structural feature is taken to be especially relevant for prebiotic chemistry and for its possible role in the processing of the heterocyclic rings of RNA and DNA nucleobases in the interstellar space. We carry out ab initio calculations of their interaction potentials with He atoms and further obtain the state-to-state rotationally inelastic cross sections and rate coefficients over the relevant range of temperatures. The similarities and differences between such species and other similar partners which have been already detected are analyzed and discussed for their significance on internal state populations in interstellar space for the two title molecular radicals.
1 Introduction
The study of the molecular complexity in the interstellar medium (ISM) provides us with fundamental information on the chemical storage of species and on the energy available for the formation of stars and planets.1 It also gives us useful indication about the chemical inventory that the primitive Earth may have inherited and about the formation paths of many of the species increasingly discovered by direct observations.2 In particular, the molecular species with the nitrogen–carbon (CN) backbone are especially relevant for prebiotic chemistry, since e.g. the heterocyclic rings of RNA and DNA nucleobases contain such a structure.3It is in fact notable that a simple molecule like HCN is already ubiquitous in the solar system and beyond, having been detected on comets,4 in various planets as shown by Tokunaga et al.5 and in Lellouch et al.,6 in dwarf planets and in the interstellar medium,7 as well as in the atmosphere of Saturns moon Titan.8 Furthermore, HCN also lies at the roots of reaction networks proposed to explain the origins of RNA, protein, and lipid precursors, as discussed in ref. 9 and also in ref. 10. Various biomolecular building blocks, such as nucleobases, cofactors, and amino acids, e.g. see: Oro’11 and Ferris et al.,12 have been detected among the reaction products of HCN polymerization experiments.
More specifically for the present study, and for the general case of CN-bearing molecules, the last decade of observations has brought to light the presence of such species like cyanamide (NH2CN): Fahrenbach et al.13 and Powner et al.14 just to mention one example of a molecule bearing the backbone in question. Furthermore, its isomer carbodiimide (HNCNH), Merz et al.,15 and urea (NH2CONH2): Becker et al.16 are indeed also considered key molecular precursors for the synthesis of RNA and DNA ribonucleotides which can occur under the early earth conditions. It is also interesting to note that all the three above examples have been recently detected in the Interstellar Medium (ISM) environment: see Turner et al.,17 McGuire, B. A. et al.,18 and Belloche et al.19 Additionally, the simpler cynomidyl radical HNCN has also been observed very recently in the direction of the G + 0.693 − 0.027 molecular cloud, e.g. see: Rivilla et al.20 The latter has been considered as an ideal target to detect new molecular species since it has shown a very rich chemistry of complex organic molecules, and in particular of N-bearing species like cyanamide (NH2CN) Zeng et al.,21 iminopropyne (HCCCHNH) Bizzocchi et al.22 and ethanolamine (NH2CH2CH2OH) Rivilla et al.23 In fact, it has been in that direction that several rotational transitions of the HNCN millimeter spectrum have been observed by Rivilla et al.20
It is also important to mention at this point that more than 30 interstellar molecules indeed contain the strong bond of the CN group and that cyanogen, NCCN, has been successfully identified in comets and in Titan's atmosphere while recently the polar metastable isomer isocyanogen (CNCN) has been confirmed in interstellar space by Agundez et al.24 This isomer has been observed in L483 and tentatively in TMC-1 by identifying various rotational transitions in the λ3 mm band. Furthermore, another simple triatomic species like CCN X2Π, a linear carbon-nitrogen chain framework, has been finally detected in IRC + 10216 by Anderson and Ziurys,25 thus reinforcing the likelihood that such simple (C,N)-bearing species could also play a role within the astrochemical processes. All of the above molecules are structurally related to the species we are discussing in the present work: NCN and CNN, both structurally described as 3Σ− electronic states. It therefore would be useful to add more knowledge on their dynamical behaviour and make comparisons with the behaviour already found from recent calculations on the other, similar systems mentioned in this Introduction in spite of the fact that their existence in the ISM has not yet been confirmed: see Bizzocchi et al.22
In order to further have additional information on the role which the above species might have in storing and transferring part of their internal energy via their dynamical interaction with the most abundant baryons of that environment, like He atoms or H2 molecules, one needs to gather data on the shape and strength of the corresponding interaction forces and then employ them to derive the temperature behaviour and relative size of the relevant state-to-state inelastic rate coefficients, especially those involving the rotational states of these title molecules. In the present work we shall start with the He atom as the prime partner of these energy-transfer processes and discuss in the following the calculation of their potential energy surfaces, followed by the evaluation via quantum dynamics of the inelastic cross sections and inelastic rate coefficients. The more complex dynamical study of the collision with the molecular partner H2 could be bypassed by performing a realistic scaling of the rate coefficients obtained for the He partner, a procedure employed in the literature with varying success, e.g. see: Gianturco et al.26
The present work will involve first the discussion of the potential energy surfaces (PESs) for all two species with He as a partner, presented in the next Section II. The details of the relevant quantum formulation of the scattering dynamics and the evaluation of the corresponding rate coefficients will be given in Section III, while all the results which we have obtained will be given in Section IV. Our final Conclusions will then be presented in the last Section V.
2 The ab initio computed interaction potentials
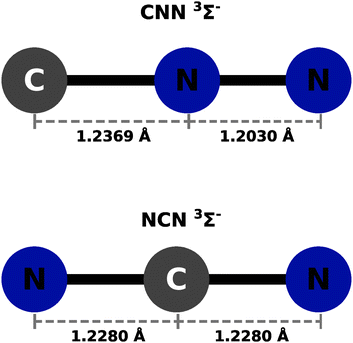
The calculations were carried out using the GAUSSIAN09 set of codes as in ref. 27 with the UCCSD(T) approach based on initial UHF orbital expansion using the aug-cc-pVTZ. The usual BSSE correction was applied for both systems as discussed in ref. 27–29. In all the ab initio calculations we used an angular grid of 2.5° intervals. The optimized bond distances in the CNN partner were taken to be: 1.2369 Å for the R(CN) and 1.2030 Å for the R(NN), in line with what was reported in earlier studies in ref. 22. In the case of the NCN partner, the optimized bond distances were both the same and placed at 1.228 Å. The resulting potentials were then described by only the distance R and the polar angle θ, both being the usual 2D Jacobi coordinates. The radial variable R's range is from either 2.2 Å or from 2.3 Å depending on the particular angular orientation and their values went out to 20 Å. Intervals of 0.2 to 0.4 Å were used depending on the range region. A pictorial view of the neutral partner radical species is presented in Fig. 1 as a summary of the above discussion. The actual computed raw points from the initial calculations are given in complete form in the ESI.†Both neutral molecules are found to be linear radical of 3Σ− symmetry in the ground electronic states. This specific feature will be further discussed below when their interaction with He atoms will be presented.
2.1 NCN and CNN interaction potentials with He atoms
The data reported by Fig. 2 and 3 show a pictorial representation of the spatial anisotropy displayed by the interaction potentials of the two radical species with the He atom. The former figure reports the NCN target while the latter shows the CNN partner with the helium atom.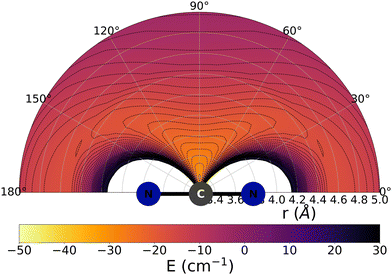 | ||
| Fig. 2 Pictorial representation of the spatial features of the interaction between the NCN radical and an He atom. See main text for further details. | ||
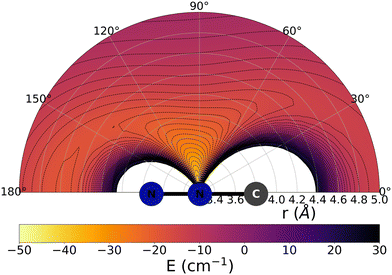 | ||
| Fig. 3 Pictorial representation of the spatial interaction between the CNN radical and the He atom. See main text for further details. | ||
Some significant structural features of the two PESs mapped pictorially in Fig. 2 and 3 are reported by the data of Table 1. For each of the interaction forces we show there the geometries of their stationary points, both of which present the T-shaped configurations of the two complexes. We further report their global minima that indicate the presence of well depths sufficiently deep to support one of more bound states, although to study such structural features in the present dynamical study is at the moment outside our principal aims. In any event, the above details point at the presence of only one global minimum for each system, without the presence of either further local/global minima or of global/local maxima features.
| NCN + He | |||
|---|---|---|---|
| θ (He–C–N) | R (Å, He–C) | E (cm−1) | Stationary point |
| 90.00 | 3.4 | −30.244 | Global minimum |
| CNN + He | |||
|---|---|---|---|
| θ (He–N1–C) | R (Å, He–N1) | E (cm−1) | Stationary point |
| 97.50 | 3.2 | −40.047 | Global minimum |
We clearly see the strong similarities between the interaction strengths of the two radical partners, while however also realizing that the differences in inversion symmetry between the two produce different mapping of their spatial anisotropy. To better understand this structural point, we shall discuss below another, well-known way of presenting the spatial shape of these interaction potentials.
In the standard procedures employed for solving the Coupled-Channel (CC) scattering equations, it is usually convenient, in fact, to expand at each value of R the interaction potential V(R,θ) into orthogonal angular functions Arthurs and Dalgarno,30 Secrest,31 Kouri and Hoffman,32 Gianturco.33 Hence, the spatial anisotropy around the CNN and NCN radical fragments, given by the extensive 2D grid of points obtained from the quantum chemical calculations mentioned before, can be given in terms of the familiar Legendre polynomials in their standard (R,θ) form:
V(R,θ) = ΣλVλ(R)Pλ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ) | (1) |
The actual expansions were carried out to λ values up to λ = 18, to ensure numerical convergence. We report in Fig. 4 a comparison between the lower six coefficients for the present molecular radicals to indicate the relative strength of the angular coupling that will be active for the various radial regions of the two interactions. The actual numerical values of all the radial coefficients are given in the ESI.†
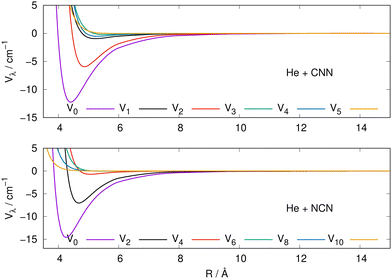 | ||
| Fig. 4 Radial multipolar coefficients for the interaction potential energy surfaces between the CNN (upper panel), NCN (lower panel) radicals and the He atom. See main text for further comments. | ||
As it is to be expected, the spherical interactions with λ = 0 exhibit the largest well depths for their attractive regions, while the next strong interactions come from the λ = 2 coefficients for both radical partners. These coefficients are both attractive in the long-range regions and present well depths of similar strengths. The significance for the quantum dynamics of having this particular radial coefficient providing the largest anisotropic coupling will be discussed in the next Section.
It is also instructive to view the same radial coefficients over an enlarged range of distances, as done in Fig. 5 for the case of CNN radical. The situation is very similar for the NCN system, so we only show one for brevity, while reporting the latter in the ESI.† The data in Fig. 5 clearly show that the multipolar coefficient with λ = 2 has the outermost turning point and further shows a marked attractive well which is next in size only to the one of the spherical interaction of λ = 0. These clear strength dominance features play a significant role for the cross section behaviour, since they are indicators of strong direct coupling induced by the interaction between target rotational states with Δj = 2.
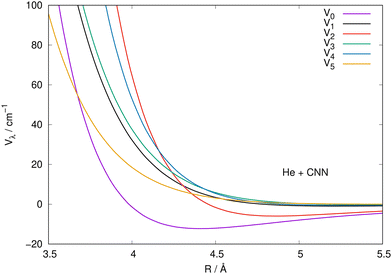 | ||
| Fig. 5 Same coefficients as those in Fig. 4 but here for an enlarged view of the shorter radial distances involving the CNN radical partner. See main text for further details. | ||
The actual multipolar radial functions were numerically fitted with standard polynomial forms and further connected smoothly to the asymptotically correct long-range potential representing the polarizability of the He partner and also the dipole term for the CNN radical partner. Hence, the long range potential is given by the following leading terms
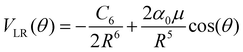 | (2) |
The computed rotational constants for the two neutral radicals, treated at the simplified level of linear, rigid rotors in pseudo-1Σ states (see further discussion below) were found to be fairly close to each other, as is to be expected: Be = 0.3991 cm−1 for the NCN molecule and 0.4375 cm−1 for CNN. For a comparison between the rotational energy levels within the pseudo-singlet simplification, we report in the ESI,† the lower rotational states within about 100 cm−1 of energy. We see there that excited rotational levels up to j = 14 or 15 become energetically accessible at the T conditions expected to be present in the diffuse molecular clouds environment.
To see more clearly the relative role and abundances of a large number of states which can be available, we have prepared two additional figures, reported in the ESI,† where we show the equilibrium populations up to about 150 K of the rotational states of the two present systems. One sees there that rotational states up to about jmax = 20 could be significantly contributing to an equilibrium population up to 80 K if one expects the diffuse cloud environments to have reached local thermal equilibrium (LET). This structural features will further be discussed later when we shall examine the results from the scattering processes for both neutral radicals and the efficiency of the collision-driven inelastic processes causing state changes in the expected ISM environments.
3 Rotationally inelastic quantum dynamics
The present molecular species have both a 3Σ− electronic term, hence their physical rotational levels are split by electronic spin-rotation coupling dynamics that requires the electronic spin angular momentum to be coupled to the molecular rotational angular momentum.36 Following the Hund's case (b), we can write that the electronic spin angular momentum S couples with the nuclear rotational angular momentum N to form the total angular momentum j| j = N + S | (3) |
It thus follows that each j level (with j ≥ 1) is split into three subleves F1, F2, F3 which have the following rotational wavefunctions:
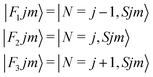 | (4) |
For a given value of N, the molecular rotational quantum number, the corresponding relative energies for the three levels defined in eqn (5), and associated with the three different rotational wavefunctions, are given by:36
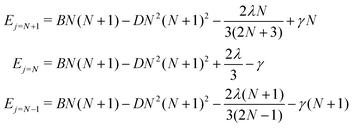 | (5) |
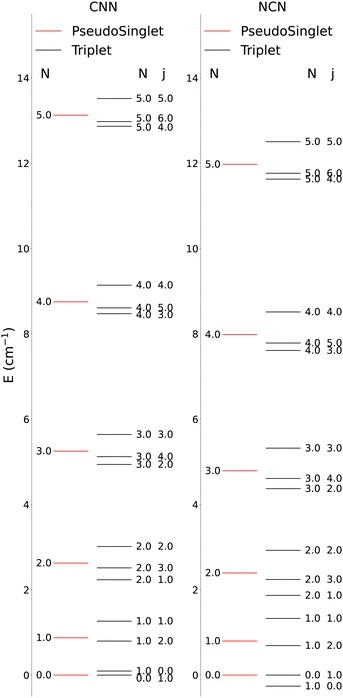
The lower-lying rotational energy levels when spin-rotation effects are included are given by Fig. 6. As mentioned before, due to their relative smallness, the centrifugal distortions have been neglected in these calculations.
One clearly sees in Fig. 6 that the ΔN ≠ 0 and the Δj ≠ 0 transitions involve larger energy gaps than those transitions were only the spin S quantum number changes: spin-flip processes therefore involve much smaller energy transfers during inelastic collisions, hence we shall not further discuss them for the present study since they are expected to contribute only marginally to state-changes induced by collision paths. This aspect of the dynamics has already been illustrated by us in our earlier work39 on similar molecules. We also see in Fig. 6 that, by removing the spin-rotational coupling which causes the energy splitting terms, we could obtain an approximate picture for the rotational structures of the target molecules described as a pseudo-1Σ cases, with the corresponding simplification of the energy spacings reported by the figure given in the ESI,† where we cover a larger range of rotational levels. The validity of such a recoupling scheme was recently tested by us for the Hydrogen Molecular Ions (HMIs) in collision with He, see: Hernández Vera et al.40 and for the OH+ cation, also colliding with He atoms in: González-Sánchez et al.39 In the following discussion we shall verify once again this simplification and therefore decide to generate the necessary rate coefficients only for the pseudo-1Σ case.
In order to check in our two systems the validity of the recoupling simplification, we need to treat the quantum dynamics for a specified state |Fijm〉 for each target molecule which interacts with the He atom as a structureless partner. Hence we need to generate the scattering eigenfunctions of the total angular momentum J, which describe the total collisional system, and which can be written as in González-Sánchez et al.:39
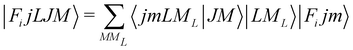 | (6) |
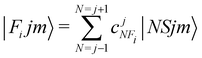 | (7) |
To now solve the correct coupled-channel (CC) equations we need to generate the transition matrix elements between the fine-structure states defined by 7 which are now coupled via the anisotropic PES discussed in the previous Section. One should note here that the quantum dynamics involves a potential coupling which is only electrostatic in nature and therefore does not directly involve spin-flipping effects González-Sánchez et al.,39 Hernández Vera et al.40 Such effects are only indirectly brought in by the recoupling of the changed rotational quantum numbers, during a state-changing collision (ΔN ≠ 0), with the electronic spin angular momentum to produce a different set of coefficients of the changed Fi values in eqn (7). We shall further discuss this effect later on in this work. For a fixed value of J, the relevant potential-coupled matrix elements are given as Franz et al.41
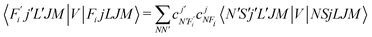 | (8) |
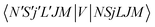 .40,41
.40,41
We have carried out calculations by solving the relevant coupled-channel equations for all the initial states from N = 0 to N = 5 using our in-house quantum scattering code ASPIN, as described in López-Durán et al.,34 Martinazzo et al.,35 and solved both the full fine-structure coupling scheme of the 3Σ− target and the pseudo-closed shell (i.e. spin zero) simplified coupling scheme of the 1Σ target Franz et al.41 The total angular momentum values were extended, when needed, up to Jmax = 65. Several closed channels were included in order to obtain convergence of the collisional cross sections: the range of integration was extended, in some cases, out to a radial distance of 200 Å maximum and at least ten closed channels were included in each expansion López-Durán et al.34 The final cross sections have been checked to be numerically converged within 1-to-5% of their values.
We have collected in Table 2 the actual values of the scattering parameters employed in our calculations.
| System | Rend (Å) | j max | J max |
|---|---|---|---|
| CNN | 200 | 40 | 64 |
| NCN | 200 | 38 | 63 |
When the pseudo-1Σ− modifications are employed during the collisional event (as is in our case), the total scattering wave function can be expanded in terms of asymptotic target rotational eigenfunctions (within the rigid rotor approximation) which are taken to be spherical harmonics and whose eigenvalues are given by Bej(j + 1) where Be is the rotational constant mentioned earlier for the present systems30–33 and considered when ignoring vibrational effects. The channel components for the CC formulation are therefore expanded into products of total angular momentum eigenfunctions and of radial functions.30 These functions are in turn the elements of the solutions matrix which appear in the familiar set of coupled, second order homogeneous differential equations:
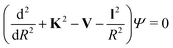 | (9) |
The scattering observables are obtained in the asymptotic region where the Log-Derivative matrix has a known form in terms of free-particle solutions and unknown mixing coefficients. For example, in the asymptotic region the solution matrix can be written in the form:
| Ψ(R) = J(R) − N(R)K | (10) |
| (N′ − YN) = J′ − YJ | (11) |
From the K matrix the S-matrix is easily obtained and from it the state-to-state cross sections. We have already published an algorithm that modifies the variable phase approach to solve that problem, specifically addressing the latter point and we defer the interested reader to these references for further details.34,35 In the present calculations we have followed the above simplified, decoupling method and generated a broad range of state-to-state rotationally inelastic cross sections from the collisions of NCN and CNN with He.
Once the state-to-state inelastic integral cross sections are known, the rotationally inelastic rate coefficients kj→j′(T) can be evaluated as the convolution of the cross sections over a Boltzmann distribution of the Etrans values:
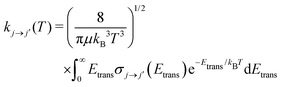 | (12) |
The reduced mass value for the NCN/He and CNN/He systems was of 3.6385636 a.u. The individual rate coefficients were obtained at intervals of 1 K, starting from 5 K and going up to 80 K.
4 Discussion of results
In the following subsections we shall discuss the present computational results involving state-changing processes for the two title systems in collision with He atoms. The next Section 4.1 reports our results for the inelastic cross sections correctly calculated within the CC scheme and treating the targets as 3Σ− rotors and compared with the simplified results within the approximate pseudo-1Σ− treatment of the molecular radicals. The following Section 4.2 will discuss more extensively the present results obtained within the CC treatment but for simple linear rotors of the pseudo-singlet-states of the radical molecules. The resulting rate coefficients are reported in the Section 4.3.4.1 Rotationally inelastic cross sections for 3Σ− rotors
The calculations reported in the panels of the two four-panel figures, which are given in the ESI,† are comparing the values of the inelastic cross sections calculated exactly by following the inclusion of the spin-rotation coupling mechanism outlined in the previous Section. The exact data are given by dots, while the results from the decoupling scheme that treat the targets as pseudo-1Σ− rotors are given as continuous lines of different colours. The reported calculations clearly indicate that the two types of cross sections are essentially coincident and that to implement the faster, and simpler, decoupling scheme for the dynamics yields for both radicals results which are practically indistinguishable from the exact calculations. Such findings therefore confirm once more that it makes sense to carry out our production cross sections and inelastic rates for the rotational populations of the title molecules by using only the decoupling scheme.4.2 Rotationally inelastic cross sections for pseudo-1Σ− rotors
We have therefore computed a broad range of state-to-state rotationally inelastic cross sections for the title systems, employing the exact Coupled-Channel (CC) method outlined in the previous Section 3 but treating the rotating molecules as simple linear rotors in their 1Σ− pseudo-state without any coupling induced by the electronic spin discussed earlier. The values of the index for the multipolar coefficients included in the expansion potentials described in the previous subsection went up to λ = 10 for the CNN radical and up to λ = 16/17 for the NCN radical. The number of coupled channels has been extended according to the involved collision energy, covering all available open channels. For the case of CNN we included a varying range of coupled channels up to j = 30-to-38 depending on collision energies and with a minimum number of 11 closed channels. For the NCN radical j values were between 22 and up to 38 with a minimum of 3 closed rotational channels. The range of radial integration was extended with the long-range terms discussed earlier and went out to 200 Å at all the energies. Collision energy values went from 0.0001 cm−1 up to 340 cm−1 for CNN and up to 415 cm−1 for NCN.It is also interesting to note here that in the case of the target molecule with inversion symmetry, the NCN radical, the rotational j index can separately have either odd or even values, with the sequence ladders separated by the Δj = 2 selection rule. On the other hand, the CNN system, the asymmetric polar radical, allows both even and odd j values within the same coupling sequence so that both types of transitions, with the Δj = 1 and 2 selection rules.
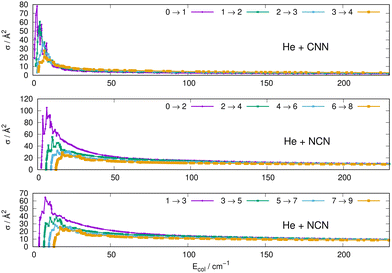
Some of the obtained results are reported by the panels in Fig. 7 and 8, where both types of transitions involving even and odd j values, with the Δj = 2 selection rule, are given for the pseudo-singlet state of the NCN symmetric radical, while transitions involving both even and odd rotational states, and with all the types of selection rules, are reported for the CNN radical.
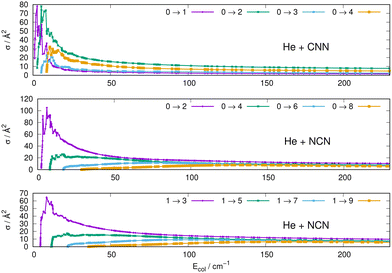 | ||
| Fig. 7 Computed excitation cross sections from the ground rotational states (odd and even j values) for the CCN (upper panel), NCN (middle and lower panels). See main text for further details. | ||
The following comments can be made from a perusal of the data in Fig. 7 and 8:
(i) at all energies considered in the panels of Fig. 7, but especially from the data near thresholds, we see that the transitions involving Δj =2 steps are systematically the largest cross sections, both for the even and odd j values, when in comparison with processes involving both smaller and larger j changes. This behaviour is obviously linked to the different coupling strengths displayed in the previous Section 2 by the different multipolar coefficients representing the original points of the PESs. Both of their interactions, in fact, indicated the λ = 2 term as having the strongest coupling range and therefore to be more efficient when involving transitions with Δj = 2 processes.
(ii) the inelastic transitions displayed by the three panels of Fig. 8 report a comparison between excitations with Δj = 1 (top panel) and processes with Δj = 2 in the middle and bottom panels. Right after the threshold regions where resonant processes are indicated by the oscillatory behaviour of these cross sections, we clearly see that, once again, transitions with Δj = 2 provide the larger cross sections. The smaller differences shown in their behaviour are additionally linked to the values of the energy gaps between involved levels. As shown by the energy ladders of Fig. 6, the gaps increase between excited levels and therefore the efficiency of the corresponding inelastic coupling decreases when excited levels are involved.
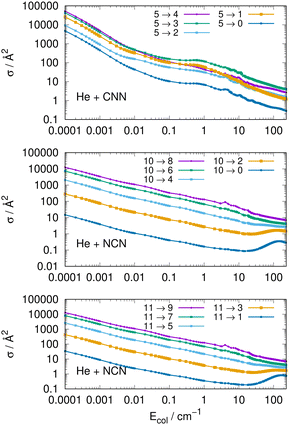
Another interesting type of behaviour is reported on a log scale by the three panels of Fig. 9. What we present there are the computed cross sections involving de-excitation (rotational cooling) processes over a very broad range of collision energies.
The results of Fig. 9 show clearly the dramatic effect of the collision energy on the size of the computed de-ecitation cross sections. Over a range of seven orders of magnitude for the relative collision energies the corresponding cross sections decrease by about six orders of magnitude, in the top panel, for transitions with different −Δj = values starting from the j = 5 excited initial state. On the other hand, when de-excitation processes involve initially a higher excited level, e.g. the j = 10 level in the middle panel, we see that the dominant factor in controlling de-excitation efficiency is the value of the Δj change since for the Δj = −10 we already have much smaller cross sections even close to the threshold opening, so that the overall decrease is just about two orders of magnitude. The same type of behaviour is also displayed by the transitions between odd j reported by the bottom panel for the NCN radical. This effect is due to the interplay between the involved energy gap and the increase of the interaction times for the larger −Δj changes: longer interaction times induce less efficient energy-transfer processes.
In terms of comparison between the energy-transfer behaviour of two radicals, our calculations of both the excitation and de-excitation cross sections between different rotational states indicate that the polar CNN radical displays larger cross sections and greater efficiency for its collision-driven state-changing processes than we see for the case of the homonuclear radical NCN. Such differences in size and behaviour will also have, as expected, direct consequences on the general features of the inelastic rate coefficients discussed in the next Section 4.3.
4.3 Inelastic rate coefficients
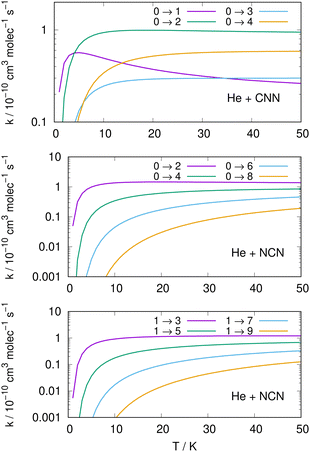
Following the numerical integration process of eqn (12) we have employed the computed inelastic cross sections discussed in the previous Section 4.2 to generate inelastic rate coefficients over a range of about 50 K, which is the expected range of temperatures relevant to the CSE environments where detection of the present radical is been surmised, as we have already discussed in our Introduction.Examples of the present results are displayed and compared with each other in the panels of the following figures. The data in Fig. 10 report the rate coefficients for excitation processes which start from the lowest available rotational states of the radical molecules and show increasingly larger Δj values, while the data in Fig. 11 report rate coefficients for the excitation transitions only with Δj =1 and 2.
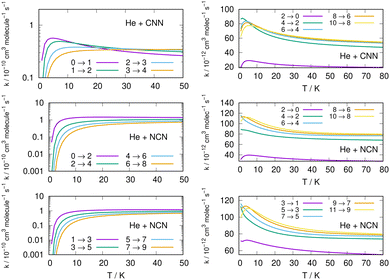 | ||
| Fig. 11 Left column: Excitation rate coefficients from a variety of initial rotational states (odd and even j values) for the CCN (upper panel), NCN (middle and lower panels) over the same range of temperature values as in Fig. 10. Right column: De-excitation (cooling) rate coefficients from several initial rotational states (odd and even j values) for the CCN (upper panel), NCN (middle and lower panels) the range of temperature values is up to 80 K. | ||
When we look at the data involving excitations from the ground rotational states (even and odd j values) for the two molecular radicals (reported by Fig. 10), we clearly see that all the rate coefficients pertaining to excitation processes with Δj = 2 transitions are uniformly the largest ones. Furthermore, in the T range above 10 K all the largest rates are very similar in size for all three panels, stressing the similarities between coupling potentials and energy gap values for the two molecules.
Different sets of inelastic rate coefficients are reported in the two columns of data shown by Fig. 11. In fact, we present there, on the left, excitation processes which originate From different levels, while we give in the panels of the right column de-excitation processes also from different initial levels. We easily see that, when excitation processes initiate from higher rotational states, and the Δj = 1 or = 2 transitions are considered, we find that the corresponding rates decrease in value when the excitation moves up from the ground initial levels and are also much larger when the polar radical species is involved (middle and lower panels in that figure). Once more, the changing energy gap values largely control the efficiency of the transitions involved, as already discussed earlier in this Section.
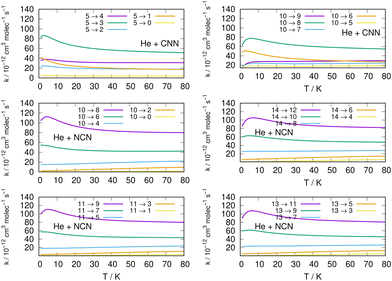
We now turn to an analysis of the de-excitation (collisional cooling) processes which are presented in the right column of the same Fig. 11, as well as in the various panels of the two columns in Fig. 12. We compare processes which start from different initial states of the title molecules.
Several specific considerations could be made from a perusal of the data reported in the various columns of these figures. If we start from the three panels on the right in Fig. 11, we focus there on de-excitation processes involving Δj = −2 transitions from a variety of initial levels up to j = 10 and j = 11 excited initial states. We see there that cooling transitions from the higher excited rotational states are now producing in all cases the largest rates, both for the CNN radical (upper panel) and the NCN radical reported in the next two panels. Since the energy ladder of the involved levels (given in the previous Fig. 6) showed that the energy gaps become larger as j increases, the collisional efficiency indicates here that the largest energy release from the target molecules is linked to the rate coefficients where the Δj = −2 transitions occur. They confirm once more that the cooling mechanism is most efficient when the Δj = −2 transitions are involved and start from one of the higher initial states since the increased energy gaps now allow for shorter interaction times and for more sudden processes, a feature we discussed many times in our earlier work, e.g. see: Gianturco.33 The swifter collisions, in classical terms, are generally associated with more efficient energy releases.
4.4 Assessing state-changing efficiency from collisional pathways
An interesting aspect that can be gleaned from our information on the inelastic rate coefficients involving rotational levels in both radical molecules is the general trend of the relative efficiency of the state-transfer processes which are induced by the collisional events in the ISM environments where we expect these molecules should be present. Furthermore, since similar cyanogen-bearing species have also been detected and computationally evaluated (e.g. see: NCCN in ref. 42 and CNCN in ref. 2) it will be useful to compare the state-changing efficiencies exhibited by the latter two systems with the present radicals. One should also bear in mind, in fact, that the involved rotational constants turn out to be somewhat similar to those discussed here: thus, the Be = 0.157 cm−1 for NCCN and Be = 0.172 cm−1 for CNCN, to be compared with 0.3991 cm−1 for NCN and 0.4375 cm−1 for CNN, which are nearly a factor of 3 larger.The data shown by the three panels of the first of them, i.e.Fig. 13, present excitation processes involving the two radicals of this study in the upper and middle panels and the already published data for the NCCN radical in the bottom panel of that figure. We report, at three different temperatures given by different colour lines, transitions from different initial rotational states and involving the dominant Δj = 2 excitations. The efficiency of the excitation processes for the present radicals, given in the upper and middle panels, gets smaller as T decreases, which is what to expect from our previous data analysis of the dynamical coupling during collisions. Furthermore, the excitation rate coefficient values become smaller as one starts from the more highly excited initial states, a feature related once more to the increase of both the energy gaps and the interaction times as the initial j increases. The bottom panel further shows the same type of processes involving the NCCN cyano-derivative, already detected in the ISM and recently studied in collision with He by Chhabra et al.42 In spite of the fact that this system has a smaller rotational constant than both our title systems, we see that its rotational excitation rate coefficients are similar in size, follow a less marked pattern as j increases and exhibit a rather weak dependence on temperatures. Such features are linked here to the smaller energy gaps existing between transition levels, while however the general effects are the same as in the present molecules. Since NCCN has been observed, while those of the present study have been so far only surmised, it stands to reason to suggest that our systems, if further searched, could become observationally available and should follow a similar non-LTE behaviour as that indicated for the NCCN radical.42
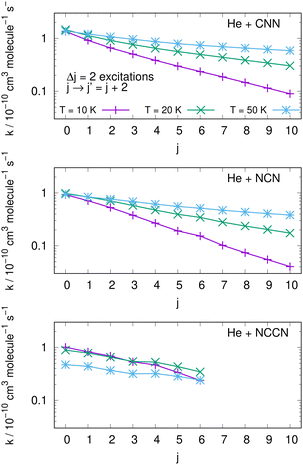 | ||
| Fig. 13 Computed excitation rate coefficients for the two molecules of the present study (upper two panels) and for the NCCN molecule from ref. 42 (in the bottom panel). Transitions with Δj = 2 from different initial levels are shown for three different temperatures labelled with different colours. See main text for further details. | ||
Comparisons between computed data are further reported in the three panels of Fig. 14 for the same three molecules discussed in previous Fig. 15. We are showing a series of de-excitation processes which all initiate from the excited rotational state of j = 10 and report rate coefficients at four different temperature values. The top and middle panels show our present calculations for the CNN and the even-j levels of NCN, while the bottom panel compares our results with those obtained in ref. 2 for the cyano-derivative CNCN. The following considerations can be made:
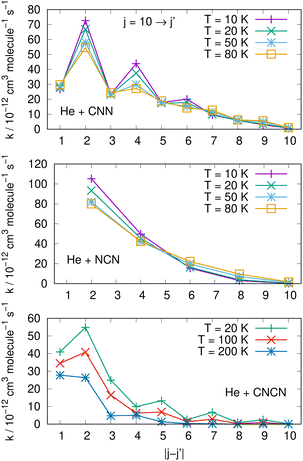 | ||
| Fig. 14 Comparing de-excitation rates from the initial level of j = 10 for the present molecules (top and middle panels) and for the CNCN from ref. 2 (bottom panel). Different T values are shown in the various panels and are labeled with different colours. See main text for further details. | ||
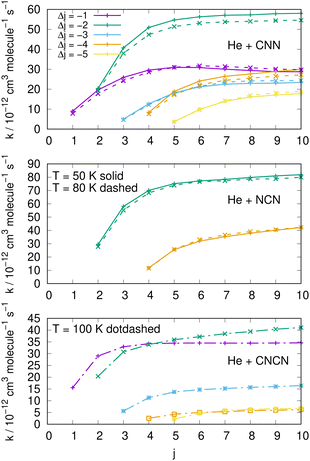 | ||
| Fig. 15 Comparing cooling processes over a range of initial rotational states and for five different values of the −Δj variation. The top two panels report data for the present molecules while the bottom panel comes from the CNCN derivative studied in ref. 2. Two different temperature values are reported for the present molecules while only one is available for the CNCN. See main text for further details. | ||
(i) the rapid oscillations of the relative efficiency among state-changing processes confirm once more that the cooling transitions which yield the largest rate coefficient values correspond to the largest energy release during the de-excitation paths. Differences however exist between systems: the top panel shows oscillatory behaviour between even- and odd-j values for the CNN system, indicating once more the importance of Δj = −2 coupling dynamics, while the middle panel exhibits uniform decrease for the NCN system where all transitions obey the Δj = −2 selection rule. The decrease in size as the Δj increases is most rapid in the bottom panel for the CNCN molecule where no such selection rule applies;
(ii) the temperature dependence of the 'cooling' processes we are considering now indicates that the collisional de-excitation paths are more efficient the lower the T regime one is considering and decrease uniformly at higher T values, a feature related once more to the relative changes of the interaction times;
(iii) the present radical molecules show their largest de-excitation efficiency to be of the order of about 10−11 cm3 molecule−1 s−1, as indicated by the top two panels in Fig. 14. On the other hand, the same quantities for the CNCN molecule, and shown in the bottom panel of that same figure, clearly indicate that the de-excitation efficiency for this molecule is about 50% smaller. This interesting result does confirm that the two bio-fragments which are the object of the present study can indeed undergo collisional state-changing processes at the same, or higher level of efficiency as those from similar molecules which have been already observed in ISM environments.
The results reported in the three panels of Fig. 15 additionally present an analysis of the de-excitation paths which compares the present radicals with the CNCN cyano-derivative of a previous study.2 Five different state-changing processes are shown and compared at two different temperatures. The following comments could be made:
(i) the largest de-excitation rate coefficients stem from 'cooling' paths involving Δj = −2 transitions for the CNN radical and for the NCN radical. All the other processes involving different values of Δj show invariably smaller collisional efficiency. Thus, the dominant efficiency of that direct rotational coupling term of their potentials is confirmed;
(ii) in the case of the CNCN molecule, on the other hand, we see both transitions with Δj = −1 and −2 are comparable in size and show the largest rate coefficient values. Such values, on the other hand, are again about 50% smaller than those shown in the upper panels by the present radical molecules;
(iii) the results in the top two panels also show that the temperature effects around the two values examined are rather negligible and the relative cooling efficiency remain largely the same at the two temperatures.
In conclusion, our present calculations indicate that both title radicals exhibit rather efficient rotational state-changing probabilities from collision with He atoms and therefore are likely to be present in the ISM environments in some of their rotationally excited levels, from which radiative emissions can occur and probably be sighted.
5 Present conclusions
In the work reported here we have discussed in some detail the inelastic dynamics of two important cyanogen-related molecules, believed to provide the molecular backbones of several systems considered to be precursors to bio species in the ISM. We provide computational evidence on how such molecules could exist in rotationally excited internal states by undergoing efficient collisions with the He atoms, abundant component of the same environment. Such data, obtained from accurate quantum dynamics, could also be employed in principle to estimate the same rate coefficients, but for the H2 molecular partner, by usings scaling procedures already present in the current literature Gianturco et al.26Neither CNN nor NCN have so far been observed in Molecular Clouds, but their presence has been surmised and searched, as discussed in our Introduction. This means that to have additional information on their energy-transfer behaviour via their interaction with He atoms, in the CSE environments where they could be located, would certainly help us to provide additional data on their relative populations of internal states which can be in turn be detected by radiative emission, at least in the case of the CNN radical. To be able to model the collision-driven processes which can lead to LTE (Local Thermal Equilibrium) rotational populations is therefore one of the products of the present calculations.
To this end, we have first obtained, from accurate ab initio calculations, their interaction potentials with the He atom and we have shown that it is computationally accurate to treat the dynamics of the NCN 3Σ− and the CNN 3Σ− rotating radicals, to a first approximation, as behaving like pseudo-singlet rotors. We have, in fact, directly tested by calculation that the actual differences between the two types of inelastic cross sections are not significant and therefore we carried out the production of final inelastic rate coefficients from quantum dynamics within the pseudo-singlet rotor decoupling scheme, using the exact CC treatment to solve the scattering problem.
Inelastic cross sections were therefore calculated for a variety of initial and final rotor states and the corresponding inelastic rate coefficients were obtained up to 80 K, in keeping with the expected T-range within the CSE environments where these molecules have been searched so far.
The inelastic rate coefficients which we have obtained here turned out to be significant in size, indicating a good efficiency of the collision paths to state-changing processes, even in comparison with those associated with similar systems which had been treated before: CNCN2 and NCCN,42 and which have been already observed. Our present calculations therefore indicate that the rotationally inelastic rate coefficients from collisions with He atoms, in the same environments where the latter molecules had been detected, can provide significant effects on the question of possible LTE rotational state distributions of both radical species and therefore could make more likely their observational detections from internal radiative emissions off the populated excited states, at least in the case of the polar CNN radical.
Author contributions
E. Y. carried out the ab initio structure calculations. L. G.-S., J. A. F. and C. S.-S. carried out the quantum dynamics cross section and rate coefficient calculations, F. A. G. designed the plan of the project, discussed the results and drafted the manuscript, R. W. was involved in the data assessment and in the writing of the final manuscript. All authors analysed the data, discussed the results and evaluated their significance during the whole drafting of the final manuscript.Data availability
The data that support the findings of this study are available within the article and its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
FAG acknowledges the support of the Computing Center of Innsbruck University where part of the present calculations were carried out. L. G.-S. acknowledges the financial support by Ministerio de Ciencia e Innovación (Spain) MCIN/AEI/10.13039/501100011033 (Ref. PID2020-113147GA-I00 and PID2021-122839NB-I00) and C.S-S. further acknowledges the financial support by Ministerio de Ciencia e Innovación (Spain) Ref. PID2021-122549NB-C22.Notes and references
- J. Lequeux, E. Falgarone and C. Ryter, The Interstellar Medium, Springer, Berlin, 2005 Search PubMed.
- D. Ben Abdallah, M. Mogren Al Mogren, S. Dhaif Allah Al Harbi and M. Hochlaf, J. Chem. Phys., 2018, 149, 064305 CrossRef CAS PubMed.
- V. Le Page, T. Snow and V. Bierbaum, ApJ, 2009, 704, 274 CrossRef CAS.
- S. D. Rodgers and S. B. Charnley, Astrophys. J., 1998, 501, L227–L230 CrossRef CAS.
- A. T. Tokunaga, S. C. Beck, J. H. Geballe, T. R. Lacy and E. Serabyn, Icarus, 1981, 48, 283–289 CrossRef CAS.
- E. Lellouch, P. N. Romani and J. Rosenqvist, Icarus, 1994, 108, 112–136 CrossRef CAS.
- D. Buhl and L. E. Snyder, Nature, 1970, 228, 267–269 CrossRef CAS PubMed.
- L. Tanguy, B. Bezard, A. Marten, D. Gautier, E. Gerard, G. Paubert and A. Lecacheux, Icarus, 1990, 85, 43–57 CrossRef CAS.
- J. D. Sutherland, Angew. Chem., Int. Ed., 2016, 55, 104–121 CrossRef CAS PubMed.
- B. H. Patel, C. Percivalle, D. J. Ritson, C. D. Duffy and J. D. Sutherland, Nat. Chem., 2015, 7, 301–307 CrossRef CAS PubMed.
- J. Oro’, Biochem. Biophys. Res. Commun., 1960, 2, 8407–8412 Search PubMed.
- J. P. Ferris, P. C. Joshi, J. G. Edelson and E. H. Lawless, J. Mol. Evol., 1978, 11, 8293–8311 CrossRef PubMed.
- A. C. Fahrenbach, C. Giurgiu, L. Tam, C. P. Li, Y. Hongo, M. Aono and J. W. Szostak, J. Am. Chem. Soc., 2017, 139, 8780 CrossRef CAS PubMed.
- M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242 CrossRef CAS PubMed.
- K. M. Merz, E. C. Aguilar and J. da Silva, J. Phys. Chem. A, 2014, 118, 3637 CrossRef CAS PubMed.
- S. Becker, J. Feldmann, S. Wiedemann, H. Okamura, C. Schneider, C. Iwan, A. Crisp, M. Rossa, T. Amatov and T. Carell, Science, 2019, 366, 76 CrossRef CAS PubMed.
- B. E. Turner, H. S. Listz, N. Kaifu and A. G. Kisliakov, ApJ, 1975, 201, L149 CrossRef CAS.
- B. A. McGuire, et al. , ApJL, 2012, 758, L33 CrossRef.
- A. Belloche, R. T. Garrod, H. S. P. Mueller, K. M. Menten, I. Medvedev, J. Thomas and Z. Kisiel, Anesth. Analg., 2019, A10, 628 Search PubMed.
- V. M. Rivilla, J. Jimenez-Serra, J. Garcia de la Concepcion, J. Martin-Pintado, L. Colzi, L. F. Rodriguez-Almeida, B. Tercero, F. Rico-Villas, S. Zeng, S. Martin, M. A. Requena-Torres and P. de Vicente, Mon. Not. R. Astron. Soc., 2021, 506, L79–L84 CrossRef CAS.
- S. Zeng, Q. Zhang, I. Jimenez-Serra, B. Tercero, X. Lu, J. Martin-Pinado, P. de Vicente, V. M. Rivilla and S. Li, MNRAS, 2020, 497, 14896–14909 CrossRef PubMed.
- L. Bizzocchi, D. Prudenzano, V. M. Rivilla, A. Pietropolli-Charmet, B. M. Giuliano, P. Caselli, J. Martin-Pintado, I. Jimenez-Serra, S. Martin, M. A. Requena-Torres, F. Rico-Villas, S. Zeng and J. C. Guillemin, Anesth. Analg., 2020, 640, A98 CAS.
- V. M. Rivilla, I. Jimenez-Serra, J. Martin-Pintado and M. A. Requena-Torres, Proc. Natl. Acad. Sci. U. S. A., 2021, 22, 118 Search PubMed.
- M. Agúndez, N. Marcelino and J. Cernicharo, Astrophys. J. Lett., 2018, 861, L22 CrossRef PubMed.
- J. Anderson and L. Ziurys, ApJ. Lett., 2014, 795, L1 CrossRef.
- F. A. Gianturco, K. Giri, L. González-Sánchez, E. Yurtsever, N. Sathyamurthy and R. Wester, J. Chem. Phys., 2021, 154, 054311 CrossRef CAS PubMed.
- M. J. Frisch, H. B. Trucks, G. W. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc, Wallingford, CT, USA, 2009 Search PubMed.
- M. J. O. Deega and P. J. Knowles, Chem. Phys. Lett., 1994, 227, 321–326 CrossRef.
- D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS.
- A. M. Arthurs and A. Dalgarno, Proc. R. Soc. A, 1960, 256, 540 Search PubMed.
- D. Secrest, Rotational Excitation-I: The Quantal Treatment, Plenum, New York, 1979 Search PubMed.
- Multiparticle Quantum Scattering With Applications to Nuclear, Atomic and Molecular Physics, ed. D. Kouri, D. Hoffman, D. G. Truhlar and B. Simon, Springer, New York, NY, 1997, 89 Search PubMed.
- F. Gianturco, The Transfer of Molecular Energies by Collisions: Recent Quantum Treatments, Springer Verlag, Berlin, 1979 Search PubMed.
- D. López-Durán, E. Bodo and F. A. Gianturco, Comput. Phys. Commun., 2008, 179, 821 CrossRef.
- R. Martinazzo, E. Bodo and F. A. Gianturco, Comput. Phys. Commun., 2003, 151, 187 CrossRef CAS.
- J. Hougen, The Calculation of Rotational Energy Levels and Rotational Line Intensities in Diatomic Molecules, U.S. National Bureau of Standards, 1970 Search PubMed.
- H. Ganser, C. Hill, J. George, J. Brown and M. Jackson, J. Mol. Spectrosc., 2021, 382, 111547 CrossRef CAS.
- M. Curtis, A. P. Levick and P. Sarre, Laser Chem., 1988, 9, 359–368 CrossRef CAS.
- L. González-Sánchez, R. Wester and F. A. Gianturco, ChemPhysChem, 2018, 19, 1866 CrossRef PubMed.
- M. Hernández Vera, F. A. Gianturco, R. Wester, H. da Silva Jr., O. Dulieu and S. Schiller, J. Chem. Phys., 2017, 146, 124310 CrossRef PubMed.
- J. Franz, B. Mant, L. González-Sánchez, R. Wester and F. Gianturco, J. Chem. Phys., 2020, 152, 234303–234315 CrossRef CAS PubMed.
- S. Chhabra, A. Kushwaha and T. J. D. Kumar, J. Chem. Phys., 2018, 149, 174312 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The multipolar coefficients for the Legendre expansion of the rigid rotor interaction potentials for both NCN/He and CNN/He and the computed inelastic cross sections, and corresponding rate coefficients, from the 2D-RR-PESs employed. The raw ab initio PESs of the rigid rotor potentials for NCN 3Σ− and CNN 3Σ− with He, the computed rotationally inelastic cross sections and inelastic rate coefficients from the two 2D-RR-PESs employed in this work are available as ESI, to the present publication. The different folders of the ESI, therefore contain: (i) NCN: containing all the additional Information regarding that molecule. Specifically four different folders which include: (i) the PES raw points; (ii) the calculated rates discussed in the paper; (iii) the multipolar coefficients reporting the scattering-oriented PES; (iv) the computed cross sections using both the triplet and the pseudo-singlet approaches. (ii) CNN: containing the same types of folders as above but this time referred to the CNN− molecular species. (iii) Additional – Fig.: it contains the pdf versions of six additional figures discussed in the main paper but not displayed there. For all six figures also their.eps version is given. See DOI: https://doi.org/10.1039/d3cp03316c |
| This journal is © the Owner Societies 2023 |