Perovskite crystal symmetry and oxygen-ion transport: a molecular-dynamics study of perovskite†
Elisabeth
Robens
a,
Robert
Rauschen
 a,
Johannes
Kaub
a,
Jana P.
Parras
a,
Johannes
Kaub
a,
Jana P.
Parras
 a,
Dennis
Kemp
a,
Dennis
Kemp
 a,
Colin L.
Freeman
a,
Colin L.
Freeman
 b and
Roger A.
De Souza
b and
Roger A.
De Souza
 *a
*a
aInstitute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, Germany. E-mail: desouza@pc.rwth-aachen.de; Fax: +49 241 80 92128; Tel: +49 241 80 94739
bDepartment of Materials Science and Engineering, University of Sheffield, Sheffield, UK
First published on 4th October 2021
Abstract
Many ABX3 perovskite compounds adopt at temperatures of interest a low-symmetry structure, rather than the ideal (cubic) structure. The prototypical case is the mineral perovskite (CaTiO3), which exhibits orthorhombic symmetry over a wide range of temperatures, attaining ideal, cubic symmetry only at very high temperatures. In this study, we made use of this behaviour to examine the effect of crystal symmetry on oxygen diffusion in a single perovskite material. Employing molecular dynamics (MD) simulations, we calculated oxygen tracer diffusion coefficients in CaTiO3, doped with various acceptor species, in the range 1000 ≤ T/K ≤ 2500. The activation enthalpy of oxygen tracer diffusion was found to be larger for the orthorhombic structure (0.58 eV) than for the cubic structure (0.43 eV). In addition, oxygen tracer diffusion was found to be adversely affected by the presence of acceptor-type cation defects, with stronger effects being observed for the low-symmetry structure. Our results also allow us to suggest explanations for the large scatter observed in experimental transport studies; to derive trends for the alkaline-earth perovskites; and to emphasise the merits of using MD simulations, rather than static calculations, to obtain activation barriers for ion migration in the high-symmetry forms of distorted perovskites.
1 Introduction
Anion transport in ABO3 perovskite-type oxides is widely believed to occur most readily in those compositions that display the highest symmetry. Indeed, the best perovskite-based oxygen-ion conductors—materials that constitute some of the best oxygen-ion conductors currently known:1–6 LaGaO3-based electrolytes,7–9 (Na,Bi)TiO3-based electrolytes,10–13 and mixed ionic–electronic conductors in the (La,Ba,Sr)(Co,Fe)O3 system14–19—display cubic symmetry (or small distortions thereof). Quantitative correlations between transport rate and crystal symmetry have suffered, however, from comparisons being made between materials that have different structures and compositions.20–25 Comparing oxygen-ion conduction, for instance, in cubic BaZr0.9Y0.1O2.95 and in orthorhombic CaZr0.9In0.1O2.95,25 one finds faster transport in the higher symmetry system. These two compositions differ, though, not only in terms of their symmetry, but also in terms of their A-site cations (Ba vs. Ca) and their acceptor-type substituents (Y vs. In). Thus, the effects on ion transport arising from the composition need to be separated from those arising from the crystal symmetry, and this may be far from trivial for concentrated solid solutions. A superior approach would be to study oxygen-ion transport in a single, weakly doped perovskite-type oxide that undergoes with increasing temperature a series of transitions to increasingly higher symmetry forms.In this sense, the eponymous mineral is an ideal system. CaTiO3 is considered in various studies,26–29 though not all,30,31 to undergo the following sequence of symmetry changes with increasing temperature:
Pbnm ↔ Cmcm ↔ I4/mcm ↔ Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. m. | (1) |
The transition from orthorhombic Pbnm to orthorhombic Cmcm occurs at T = (1380 ± 10) K, with the subsequent transition to tetragonal I4/mcm occurring at T = (1500 ± 20) K and the final transition to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at T = (1600 ± 10) K.26–29 The intermediate orthorhombic (Cmcm) phase is not always observed in experiment,30,31 and this may be due to its structural and thermodynamic similarity to the orthorhombic Pbnm phase.29 The four phases correspond to tilting of the TiO6 octahedra about 3, 2, 1 and 0 pseudo-cubic axes, respectively.32–34
m at T = (1600 ± 10) K.26–29 The intermediate orthorhombic (Cmcm) phase is not always observed in experiment,30,31 and this may be due to its structural and thermodynamic similarity to the orthorhombic Pbnm phase.29 The four phases correspond to tilting of the TiO6 octahedra about 3, 2, 1 and 0 pseudo-cubic axes, respectively.32–34
In a different sense, CaTiO3 is not an ideal system for examining the correlation between symmetry and ion transport. Experimental studies of oxide-ion transport in nominally un-doped CaTiO3 (ref. 35–39) report isothermal oxygen diffusion coefficients that differ by four or more orders of magnitude, with the corresponding activation enthalpies of oxygen diffusion (ΔHD) scattering between 0.6 eV and 4 eV (see Fig. 1). Some variation in oxygen diffusivity is to be expected, since nominally un-doped samples will contain varying levels of acceptor impurities. But variations in impurity level of four orders of magnitude are implausible in this case, and such variations cannot explain the large scatter in reported activation enthalpies.
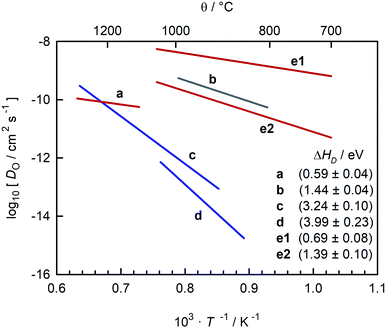 | ||
Fig. 1 Comparison of oxygen diffusion coefficients obtained for CaTiO3: a (George and Grace35), b (Iwahara et al.36) c (Gautason and Muehlenbachs37), d (Sakaguchi and Haneda38), e (Bak et al.39). Data converted from conductivities (grey), tracer diffusivities (blue), or chemical diffusivities (red). Tracer data converted via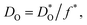 with f* = 0.69; chemical data assuming DO = DδOnv/3 and nv = 1.86 × 10−4; and conductivity data via the Nernst–Einstein equation. with f* = 0.69; chemical data assuming DO = DδOnv/3 and nv = 1.86 × 10−4; and conductivity data via the Nernst–Einstein equation. | ||
A closer examination indicates that the activation enthalpies fall puzzlingly into three groups, with ΔHD ≈ 0.6 eV,35,39 ΔHD ≈ 1.4 eV,36,39 and ΔHD > 3 eV.37,38 Equally puzzling is the huge discrepancy between studies that are often regarded as unambiguous: the activation barrier for oxygen-vacancy migration in orthorhombic CaTiO3 was reported in classical40,41 and quantum-mechanical42 simulations to be <1 eV, whereas tracer diffusion measurements of single crystals yield ΔHD ≈ 4 eV.38 Furthermore, the problems, whatever they are, do not afflict all CaTiO3-based systems. All studies of oxygen diffusion in CaTi0.9Fe0.1O3−δ agree, as pointed out by Salles et al.,43 that the activation enthalpy of diffusion is ΔHD ≈ 0.9 eV.43–46
In this study, we performed classical molecular dynamics (MD) simulations of oxygen tracer diffusion in CaTiO3 as a function of temperature, first, in order to bring some clarity to published experimental data;35–39 and second, in order to examine the relationship between crystal symmetry and oxygen-ion transport in a perovskite-type oxide. There are two benefits to carrying out MD simulations of ion transport. Data interpretation does not have to rely solely on the activation enthalpy (as is the case for static simulations) but can also make use of the absolute magnitude of the oxygen diffusivity. And in comparison with experimental work, the number and type of point defects are known exactly for the systems under study.
Lastly, we comment on our choice of classical MD simulations over MD simulations based on Density-Functional-Theory (DFT) calculations. The latter are restricted currently to short simulation times, very small simulation cells, and often, excessively high simulation temperatures. These restrictions translate into inadequate statistics (i.e. an insufficiently large number of successful ion jumps, and thus imprecise diffusion data); extremely high defect concentrations (i.e. well beyond the limit of a dilute solution); and the necessity to extrapolate data from temperatures several thousand kelvin above the solid's melting point down to the temperatures of experimental interest. Our choice of classical MD simulations was dictated, therefore, by the need to obtain precise diffusion data for dilute solutions of point defects at physically reasonable temperatures.
Classical MD simulations, it is sometimes claimed, are unsuited for studying ion migration in solids, for they do not include bond breaking and formation. Such claims appear to be based mainly on misconceptions of both the simulation methods and the migration process. They also ignore entirely a substantial body of evidence. For example, classical simulation methods employing the set of empirical pair potentials (EPP) derived by Pedone et al.47 are able to predict quantitatively the rate of defect migration and its temperature dependence for oxygen-vacancy diffusion in BaTiO3,48–51 and for oxygen-vacancy diffusion52–57 and strontium-vacancy diffusion58–60 in SrTiO3. If ion migration did involve bond breaking and bond formation, such agreement between simulation and experiment would be impossible: there would always be discrepancies, and this is not the case. Given the evident capabilities of the EPP set derived by Pedone et al.47 for quantitatively describing ion migration in BaTiO3 and SrTiO3, we employ them here to study oxygen diffusion in CaTiO3.
2 Computational
In all simulations performed in this study, the constituent ions of the solid were treated as classical particles, each bearing a charge and interacting with other particles through a long-range coulombic potential and a short-range EPP. As noted above, we used the pairwise potentials derived by Pedone et al.,47 in which ions bear partial charges and the short-range interactions are described by a Morse function and an additional repulsive (r−12) term. That is, the potential between ions i and j as a function of separation r takes the form of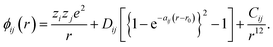 | (2) |
The values for the empirical parameters (Dij, aij, r0 and Cij) were taken directly from Pedone et al.47 and are summarized in Table 1. Long-range coulombic interactions were evaluated by an Ewald summation61 with an accuracy of 10−6, and short-range interactions were evaluated up to 15 Å.
| Ion pair | D ij /meV | a ij /Å−1 | r 0/Å | C ij /eV Å12 |
|---|---|---|---|---|
| Ca+1.2–O−1.2 | 30.211 | 2.241334 | 2.923245 | 5.0 |
| Ti+2.4–O−1.2 | 24.235 | 2.254703 | 2.708943 | 1.0 |
| Al+1.8–O−1.2 | 361.581 | 1.900442 | 2.164818 | 0.9 |
| Fe+1.8–O−1.2 | 418.981 | 1.620376 | 2.382183 | 2.0 |
| O−1.2–O−1.2 | 42.395 | 1.379316 | 3.618701 | 22.0 |
The MD simulation cell consisted of 12 × 12 × 12 unit cells of Ca4Ti4O12 (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 560 ions) with periodic boundary conditions applied in all three spatial directions. Point defects were introduced by either removing or replacing ions at random from the simulation cell. If the total charge of all defects was not zero, the excess was compensated by means of an uniform background charge. MD simulations were performed within the NpT ensemble, i.e., particle number N, pressure p and temperature T were held constant, while energy U and volume V were allowed to vary. The system's temperature (pressure) was controlled by means of a Nose–Hoover thermostat (barostat), with damping parameters of 1 ps (10 ps). A timestep of 1 fs was used. The LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code62 was used.
560 ions) with periodic boundary conditions applied in all three spatial directions. Point defects were introduced by either removing or replacing ions at random from the simulation cell. If the total charge of all defects was not zero, the excess was compensated by means of an uniform background charge. MD simulations were performed within the NpT ensemble, i.e., particle number N, pressure p and temperature T were held constant, while energy U and volume V were allowed to vary. The system's temperature (pressure) was controlled by means of a Nose–Hoover thermostat (barostat), with damping parameters of 1 ps (10 ps). A timestep of 1 fs was used. The LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code62 was used.
For each MD simulation, the cell was first allowed to equilibrate for 40 ps (after which U and V were observed to only fluctuate around constant values). Thereafter, the simulation was run for 500 ps, and the mean-squared-displacement of the oxide ions 〈RO2〉 was monitored. For every simulation in which the evolution of 〈RO2〉 as a function of time was smooth and linear, we calculated a tracer diffusion coefficient of oxygen from the standard Einstein relation
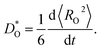 | (3) |
The activation barriers for oxygen-ion migration were also determined by means of molecular-statics simulations. Climbing-image nudged-elastic-band (CI-NEB) calculations were performed at constant volume with 25 images, as implemented in the GULP code.63 The (static) lattice energies of various CaTiO3 perovskite phases were also calculated with the GULP code.
3 Results
In correlating crystal symmetry and ion transport, one needs to identify the exact phase in which ion transport is taking place. In the present case, that meant we had to identify the phases that this set of EPP yield in the MD simulations before we studied oxygen diffusion. In fact, we took a step back and considered first the relative (static) lattice energies of various CaTiO3 perovskite phases.3.1 Lattice energies
Although it is now universally agreed that the CaTiO3 lattice displays Pbnm symmetry at room temperature and adopts Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry at sufficiently high temperature, there are debates concerning the intermediate phases. It has been argued that a direct transition is unlikely,32–34 so that the question is not so much whether there are intermediate phases but rather what the intermediate phases are.
m symmetry at sufficiently high temperature, there are debates concerning the intermediate phases. It has been argued that a direct transition is unlikely,32–34 so that the question is not so much whether there are intermediate phases but rather what the intermediate phases are.
Taking our lead from Amisi et al.,64 who studied the crystal structures of the related perovskite SrZrO3 and their instabilities with regard to octahedral tilting, we performed energy minimisation calculations of the most likely perovskite crystal symmetries of CaTiO3 [see sequence eqn (1)], as well as of some possible alternatives. The results are shown in Fig. 2. Examining the differences in lattice energy relative to that of the cubic phase, we find that, according to these EPP, intermediate orthorhombic and tetragonal phases are plausible, with Cmcm being preferred over Imma for the intermediate orthorhombic phase and I4/mcm being preferred over P4/mbm for the intermediate tetragonal phase. Our static simulations are thus in agreement with data from calorimetry,26 Raman spectroscopy,27 neutron powder diffraction,28 and thermodynamic modelling29 studies.
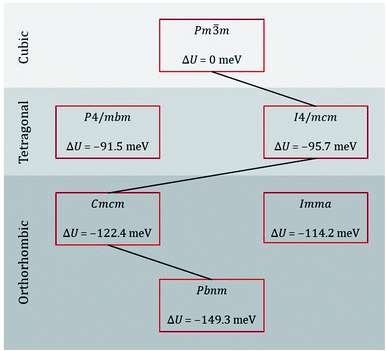 | ||
| Fig. 2 Lattice energy U of various phases of CaTiO3 relative to that of the ideal cubic phase. The black line indicates the probable sequence of transitions. | ||
3.2 Temperature-dependent lattice parameters
In Fig. 3(a) we plot the pseudo-cubic lattice parameters obtained for CaTiO3 in our MD simulations. Changes in the behaviour are observed at T1/2 = (1225 ± 5) K, T2/3 = (1295 ± 5) K, and T3/4 = (1335 ± 5) K. From these data it is not possible to identify the exact space group, but it is evident that phase 1 is orthorhombic (apc ≠ bpc ≠ cpc); phase 3 is tetragonal (apc = bpc < cpc); and phase 4 is cubic (apc = bpc = cpc). Phase 2 appears to be tetragonal, but apc and bpc are only approximately equal and close examination indicates apc ≠ bpc ≠ cpc. On the basis of the results obtained in the previous section, we ascribe phases 1–4 to Pbnm, Cmcm, I4/mcm and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space groups.
m space groups.
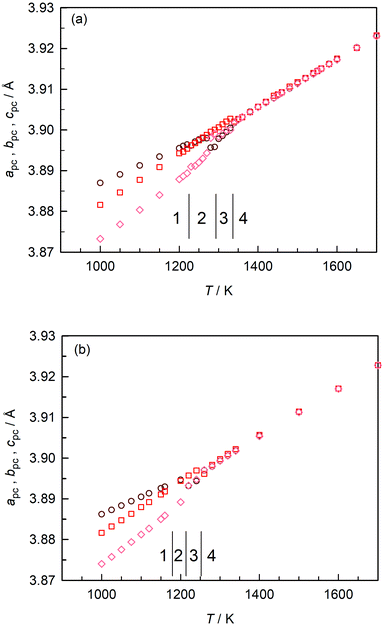 | ||
| Fig. 3 Pseudo-cubic lattice parameters obtained as a function of temperature: (a) stoichiometric CaTiO3; (b) oxygen-deficient CaTiO3. | ||
These transition temperatures are much lower than the experimental values26,28,29 of T = (1380 ± 10) K, T = (1500 ± 20) K and T = (1600 ± 10) K. The differences between simulation and experiment get larger, the higher the transition temperature. This is not particularly surprising, though, since these EPP were not fitted to crystal data for CaTiO3 (but to data for binary oxides and glasses47). Here, it is sufficient that different phases are stable in the MD simulations because it means that MD simulations with these EPP can be used to examine oxygen diffusion in these different phases.
Upon introducing oxygen vacancies into the simulation cell at a site fraction of nv = 0.2% (and compensating their charge with a background charge), we observed that the transition temperatures shifted to lower values [Fig. 3(b)]: (1180 ± 20) K, (1210 ± 10) K, and (1250 ± 10) K. We believe that the direction of the shifts is predicted correctly because increasing x in the CaTi1−xFexO3−x/2 system decreases the transition temperatures65 and because reducing BaTiO3 decreases the ferroelectric–paraelectric transition temperature.51 The magnitude of the shifts (up to 85 K) are rather large, though, and we cannot rule out that these shifts are overestimated. Nevertheless, the data of Fig. 3 do clearly indicate that there is an effect from oxygen vacancies alone, their charge being compensated in these specific simulations by a background charge. In experiment, a compensating defect is always present, e.g. acceptor substituents or electrons produced upon sample reduction, and this complicates the assignment to a specific point defect.
3.3 Oxygen tracer diffusion
We first consider oxygen tracer diffusion in a system containing only oxygen vacancies, since this allows us to examine the dynamic behaviour of oxygen vacancies without having to take interactions with acceptor cations into account. Subsequently, we consider oxygen diffusion in systems with the same number of vacancies but also containing specific acceptor cations as charge compensation. All data presented in this section refer to cells containing 0.2% oxygen vacancies (or 42 vacancies in a cell containing 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 oxygen-ion sites).
736 oxygen-ion sites).
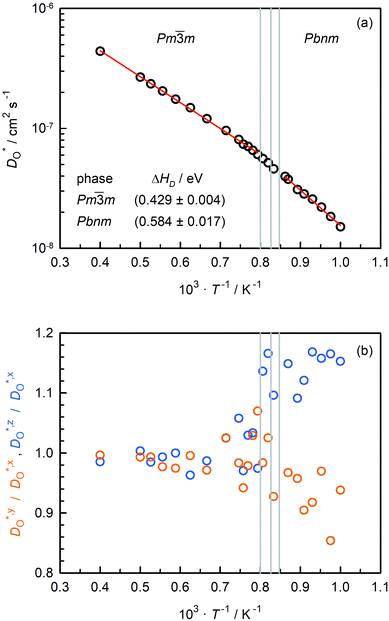
Oxygen tracer diffusion coefficients obtained for the system with only oxygen vacancies as a function of temperature are shown in Fig. 4(a). The temperatures of the phase transitions determined in Sec. 3.2 are also shown, and there are no evident jumps in 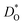 at these temperatures. For the two intermediate phases, the stability ranges are too small to allow activation enthalpies to be determined. We focus, therefore, on the end phases and obtain activation enthalpies of ΔHD* = (0.584 ± 0.017) eV for the Pbnm phase and of ΔHD* = (0.429 ± 0.004) eV for the Pm
at these temperatures. For the two intermediate phases, the stability ranges are too small to allow activation enthalpies to be determined. We focus, therefore, on the end phases and obtain activation enthalpies of ΔHD* = (0.584 ± 0.017) eV for the Pbnm phase and of ΔHD* = (0.429 ± 0.004) eV for the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. The tracer diffusion of oxygen is clearly characterised by a far larger activation enthalpy in the low-symmetry phase.
m phase. The tracer diffusion of oxygen is clearly characterised by a far larger activation enthalpy in the low-symmetry phase.
In Fig. 4(b), the ratios of the axis-specific tracer diffusion coefficients are plotted, 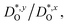 and
and 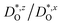 . This plot confirms the analysis of Sec. 3.2, since the two ratios are both approximately unity for the isotropic Pm
. This plot confirms the analysis of Sec. 3.2, since the two ratios are both approximately unity for the isotropic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase but differ substantially from unity and from one another for the non-isotropic Pbnm phase. Incidentally, the two intermediate phases behave as expected: in the tetragonal phase, one ratio is approximately unity and one isn't; and for the intermediate orthorhombic phase, both ratios deviate from unity.
m phase but differ substantially from unity and from one another for the non-isotropic Pbnm phase. Incidentally, the two intermediate phases behave as expected: in the tetragonal phase, one ratio is approximately unity and one isn't; and for the intermediate orthorhombic phase, both ratios deviate from unity.
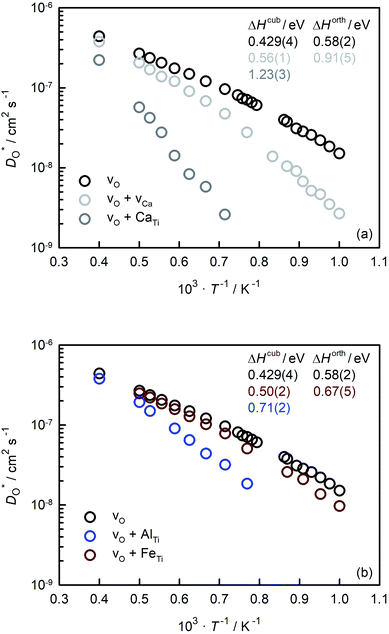
In Fig. 5(a) and (b) we examine the effect of compensating acceptor-type defects on 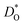 (at constant nv = 0.2%). The data are divided into native (divalent) acceptor-type species (vCa, CaTi) and foreign (trivalent) acceptor-type species (AlTi, FeTi). No reliable data was obtained for cells containing vTi and vO, or at lower temperatures for cells containing CaTi and vO, or AlTi and vO. As expected,13,66–68 all acceptor-species cause the rate of oxygen diffusion at a given temperature to decrease (even though the vacancy site fraction is constant) and the effective activation enthalpy to increase. The effects are stronger for the lower-symmetry phase, as indicated by the larger increases in ΔHD*. For example, in the presence of vCa, the activation enthalpy of oxygen diffusion increases by 0.13 eV for the cubic phase but by 0.33 eV for the orthorhombic phase. The changes in
(at constant nv = 0.2%). The data are divided into native (divalent) acceptor-type species (vCa, CaTi) and foreign (trivalent) acceptor-type species (AlTi, FeTi). No reliable data was obtained for cells containing vTi and vO, or at lower temperatures for cells containing CaTi and vO, or AlTi and vO. As expected,13,66–68 all acceptor-species cause the rate of oxygen diffusion at a given temperature to decrease (even though the vacancy site fraction is constant) and the effective activation enthalpy to increase. The effects are stronger for the lower-symmetry phase, as indicated by the larger increases in ΔHD*. For example, in the presence of vCa, the activation enthalpy of oxygen diffusion increases by 0.13 eV for the cubic phase but by 0.33 eV for the orthorhombic phase. The changes in 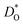 and ΔHD* can be attributed to acceptor-type cation defects trapping oxygen vacancies in their vicinity and modifying the barriers for oxygen-vacancy migration in their vicinity.66 The use of a background charge works as a ‘perfect’ acceptor-dopant, introducing vO, but not affecting their behaviour.
and ΔHD* can be attributed to acceptor-type cation defects trapping oxygen vacancies in their vicinity and modifying the barriers for oxygen-vacancy migration in their vicinity.66 The use of a background charge works as a ‘perfect’ acceptor-dopant, introducing vO, but not affecting their behaviour.
3.4 Activation barriers from static calculations
There are eight oxygen ions that can jump into a neighbouring vacant site in the perovskite structure. In the un-doped cubic phase, all eight jumps are symmetry equivalent, and hence, oxygen-vacancy migration is characterised by one single barrier. In the un-doped Pbnm phase, there are five symmetry-inequivalent jumps. Introducing acceptor-type cation species into these lattices modifies the barriers for ion migration not only around but also towards and away from the acceptor-type species,66 generating a more complex energy landscape with multiple possible barriers even for the cubic phase. For this reason, and also to make two specific points, we focus here on migration in the un-doped phases (i.e. in those containing only oxygen vacancies).The activation barriers determined for the five jumps in the un-doped, orthorhombic phase by means of NEB calculations are listed in Table 2. The effective activation enthalpy of long-range oxygen diffusion will be a weighted means of those barriers that connected together provide low-energy paths through the structure. Consideration of how the barriers listed in Table 2 are connected indicates that the highest barrier of 0.73 eV does not need to be traversed for long-range diffusion. This leaves barriers that are rather similar, of 0.54 eV, 0.60 eV, 0.61 eV and 0.63 eV. Given these possibilities, ions will jump most often over the lowest barrier, but also over the other barriers, since the relative jump rates at the temperatures of interest [∝ exp(−ΔHmig,v/kBT)] do not differ by orders of magnitude. This picture is consistent with the effective activation enthalpy of oxygen diffusion of (0.584 ± 0.017) eV obtained in the MD simulations.
| Jump | ΔHmig,v/eV |
|---|---|
| O1–O2 | 0.61 |
| O1–O2 | 0.54 |
| O1–O2 | 0.73 |
| O2–O2 | 0.60 |
| O2–O2 | 0.63 |
NEB calculations of oxygen-ion migration in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase were unreliable: with a 4 × 4 × 4 supercell of cubic CaTiO3, an activation barrier of 0.59 eV was obtained, and with a 6 × 6 × 6 supercell, 0.57 eV. These values, though physically reasonable, are clearly representative of the orthorhombic structure, rather than of the (starting) cubic structure [cf.Fig. 4(a)]. The problem is that NEB calculations refer to zero kelvin, and at this temperature the Pbnm phase, with its tilted octahedra, has the lowest energy. Examination of the NEB simulation cells indicated that coordinated tilting of the octahedra had indeed occurred. Although even-number-sized supercells are obligatory for coordinated tilting of the octahedra to occur, the use of an odd-number-sized supercell, e.g. 3 × 3 × 3, produced unreasonable results, namely, an asymmetric energy profile with an intermediate minimum, whose maximal barrier height was only 0.17 eV. NB: all problems encountered in NEB calculations of oxygen-vacancy migration in cubic CaTiO3 did not plague analogous calculations for SrTiO3, whose ground state structure, according to these EPP, is cubic.
m phase were unreliable: with a 4 × 4 × 4 supercell of cubic CaTiO3, an activation barrier of 0.59 eV was obtained, and with a 6 × 6 × 6 supercell, 0.57 eV. These values, though physically reasonable, are clearly representative of the orthorhombic structure, rather than of the (starting) cubic structure [cf.Fig. 4(a)]. The problem is that NEB calculations refer to zero kelvin, and at this temperature the Pbnm phase, with its tilted octahedra, has the lowest energy. Examination of the NEB simulation cells indicated that coordinated tilting of the octahedra had indeed occurred. Although even-number-sized supercells are obligatory for coordinated tilting of the octahedra to occur, the use of an odd-number-sized supercell, e.g. 3 × 3 × 3, produced unreasonable results, namely, an asymmetric energy profile with an intermediate minimum, whose maximal barrier height was only 0.17 eV. NB: all problems encountered in NEB calculations of oxygen-vacancy migration in cubic CaTiO3 did not plague analogous calculations for SrTiO3, whose ground state structure, according to these EPP, is cubic.
In order to frustrate the coordinated tilting of the octahedra, one could perform Mott–Littleton (ML) calculations69 with a relatively small inner region I. As ionic relaxations are only fully permitted within region I and not within the adjacent region IIa, the alignment of tilts between regions I and IIa can in principle force the system to maintain artificially high symmetry. We found that a region I size of ca. 7 Å yielded an activation barrier of oxygen-vacancy migration in the cubic structure of 0.42 eV, a value consistent with the MD results. Evidently, this region I size is sufficient to capture ionic relaxation for both the initial and transition-state configurations and prevent octahedral tilting from occurring.
In general, it may be difficult to determine definitively from a molecular-statics simulation (NEB or ML) whether a specific initial or transition-state configuration exhibits distortions characteristic of a lower symmetry phase. It is only because we have values from MD simulations at finite temperatures that we are able to judge the fidelity of the barriers obtained from NEB and ML calculations.
4 Discussion
4.1 Comparison with experimental data for CaTiO3
The best level for comparing transport data is at the level of defect diffusivities because Dv is independent of defect concentration, at least for non-interacting solutions of charge carriers. Dv can be obtained from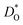 according to
according to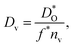 | (4) |
Another benefit of considering Dv is that its temperature dependence directly yields the activation enthalpy of oxygen-vacancy migration,
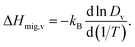 | (5) |
In contrast, the activation enthalpy of oxygen diffusion is the sum of ΔHmig,v and ΔHgen,v, the latter indicating how strongly nv varies with temperature:
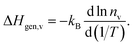 | (6) |
In Fig. 6 we compare oxygen-vacancy diffusivities with the two sets of literature data for which the vacancy diffusivity can be confidently calculated from oxygen diffusion data.35,39 (The reason for confidence is that, if chemical diffusion is examined in a regime for which the electronic conductivity dominates the overall conductivity, Dv is simply given by DδO/3.)25 One finds that the closest agreement in terms of absolute magnitude is with dataset e1.39 The difference between experiment and simulation could be due to one or more factors: f* for oxygen-vacancy migration in an orthorhombic perovskite differing from the value for the cubic structure; a slight overestimation of Dv in the MD simulations; or a slightly underestimation of Dv in the chemical diffusion experiments. At present none of these possibilities can be ruled out. The experimental activation enthalpy appears to be too high, ΔHmig,v = (0.69 ± 0.08) eV,39 but the error is substantial. [And ΔHmig,v decreases to (0.59 ± 0.17) eV if, for example, the lowest-temperature data point is ignored.] Importantly, one recognises from Fig. 6 that agreement in terms of activation enthalpy is not sufficient to judge data. There is a substantial difference in vacancy diffusivities between datasets a and f, even though the activation enthalpies agree well.
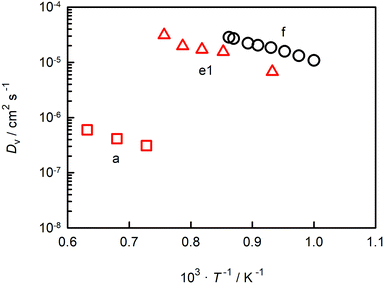 | ||
| Fig. 6 Oxygen-vacancy diffusion coefficients in CaTiO3 as a function of inverse temperature: a (George and Grace35), e1 (Bak et al.39), f (this study). | ||
The oxygen diffusion coefficients obtained in tracer diffusion studies37,38 are, as shown in Fig. 1, orders of magnitude lower than the dataset e1 of Bak et al.,39 and they have very high activation enthalpies. We suggest that these tracer diffusion data are incorrect for two reasons. First, in both cases the interpretation of the experimental data is questionable. Sakaguchi and Haneda38 obtained isotope profiles in the solid—isotope profiles with two features, and they attributed the first feature to bulk diffusion and the second to fast-diffusion along twin boundaries. We propose that the correct assignment of the two features is to diffusion through a depletion space-charge layer followed by diffusion in a homogeneous bulk phase.71,72 A surface space-charge zone has already been identified previously for acceptor-doped SrTiO3,55,73–76 acceptor-doped BaTiO3,49 and for acceptor-doped Pb(Zr,Ti)O3.77,78 It would be extremely surprising if acceptor-doped CaTiO3 did not have a depletion space-charge zone at its surface. One consequence of an incorrect assignment would be that the conclusion of Sakaguchi and Haneda,38 of fast oxygen diffusion along domain walls, would be incorrect, too. In the other tracer study, Gautason and Muehlenbachs37 conducted gas-phase monitoring of isotope exchange and assumed that the kinetics were governed by bulk diffusion. They employed, however, powdered samples, and for such samples, the exchange kinetics are generally limited by the process of surface exchange.79,80 In fact, their activation enthalpy of (3.24 ± 0.10) eV37 is reasonably close to the activation enthalpy of isotope exchange measured for acceptor-doped SrTiO3, ΔHk* ≈ 3 eV.55 In other words, in both cases37,38 there are more plausible explanations for the low values of 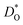 and for the high values of ΔHD*.
and for the high values of ΔHD*.
The second reason to question the tracer diffusion data37,38 is that the high values of ΔHD* require ΔHmig,v to be improbably high. Under the oxidising conditions of the experiments, typical fixed-valence acceptor impurities in perovskite titanates, such as Mg and Al, yield ΔHgen,v ≈ 0, while variable valence acceptor dopants, such as Fe, yield ΔHgen,v = (0.1 to 0.2) eV.81 As a consequence, ΔHmig,v (=ΔHD* − ΔHgen,v) would have to be (3 to 4) eV, which seems very unlikely.
Lastly, even though there are no experimental results for the cubic phase with which to compare our MD data, we contend that the data are fairly accurate, in particular the small activation enthalpy of oxygen-vacancy migration of 0.43 eV, because our data for the orthorhombic structure are in good agreement with experiment and because MD data for SrTiO3 and BaTiO3 obtained with these EPP show excellent agreement with literature values.49,51–55,57
4.2 Comparison with computational data for CaTiO3
There are three static computational studies of oxygen-ion migration by a vacancy mechanism in CaTiO3. Two studies40,41 employed Mott–Littleton calculations, with different sets of EPP to the set used here, and reported for Pbnm symmetry a single barrier40 of 0.58 eV and three barriers41 of 0.51 eV, 0.43 eV and 0.55 eV for migration along the three axes of the orthorhombic unit cell. These data are in reasonable agreement with our NEB results [five barriers between 0.54 eV and 0.73 eV, see Table 2] and with our MD results [an effective activation enthalpy of (0.584 ± 0.017) eV, see Fig. 4(a)].A more recent DFT study42 reported, for small supercells with either Pbnm or Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m starting symmetry, activation barriers that are suspiciously similar, at 0.71 eV and 0.75 eV, and that are too high. On the basis of our NEB and ML simulations (Sec. 3.4), we suggest that the similarity is an artefact, arising from octahedral tilting in the cubic supercell. And on the basis of the systematic DFT study of oxygen-vacancy migration in SrTiO3 by Zhang et al.,57 we suggest that the use of small supercells is responsible for the overestimation of the activation barriers.
m starting symmetry, activation barriers that are suspiciously similar, at 0.71 eV and 0.75 eV, and that are too high. On the basis of our NEB and ML simulations (Sec. 3.4), we suggest that the similarity is an artefact, arising from octahedral tilting in the cubic supercell. And on the basis of the systematic DFT study of oxygen-vacancy migration in SrTiO3 by Zhang et al.,57 we suggest that the use of small supercells is responsible for the overestimation of the activation barriers.
4.3 CaTiO3versus other titanate perovskites
Fig. 7(a) compares the oxygen-vacancy diffusivity calculated in this study for CaTiO3 with those reported in the literature for SrTiO3 (ref. 56) and BaTiO3.50 The three datasets are strictly comparable, as they all were obtained from MD simulations with the EPP of Pedone et al.47 and refer to dilute solutions of non-interacting oxygen vacancies. (As noted in the Introduction, the MD data for SrTiO3 and BaTiO3 show excellent agreement with experimental values.49,51–55) Isothermal values of Dv are seen to increase in the order: Dv(BaTiO3) < Dv(SrTiO3) < Dv(CaTiO3). The temperature dependence, i.e. ΔHmig,v, decreases in the same order. Particularly surprising is that orthorhombic CaTiO3 displays faster rates of oxygen-vacancy diffusion with a lower activation enthalpy of migration than cubic SrTiO3. Evidently, symmetry is not the decisive factor in determining the activation barrier, but it is an important factor, as indicated by ΔHcubmig,v < ΔHorthmig,v for CaTiO3.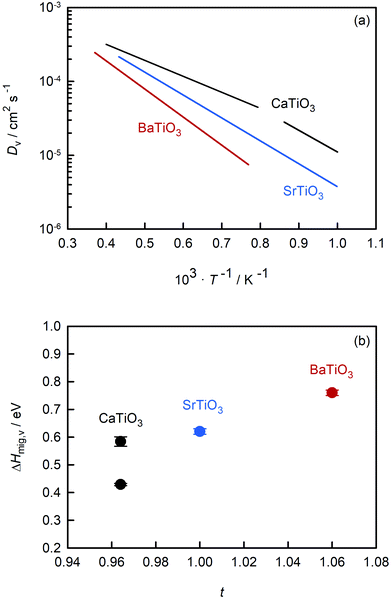 | ||
| Fig. 7 Comparison of data for titanate perovskites obtained from MD simulations: (a) oxygen-vacancy diffusivities versus inverse temperature, (b) activation enthalpy for oxygen-vacancy migration versus Goldschmidt tolerance factor. CaTiO3 (this study), SrTiO3 (Waldow and De Souza56), BaTiO3 (Kaub et al.50). | ||
Also of interest is how the behaviour evident in Fig. 7(a) changes upon the addition of acceptor species. Regardless of whether weakly doped material or a solid solution containing high concentrations of oxygen vacancies and acceptor cations, the general trend of Fig. 7(a), we suppose, will be maintained. (And Fe substitution will shift the phase transition temperatures for CaTiO3.65) Acceptor species will for each of the three systems decrease the rate of oxygen diffusion and increase its activation enthalpy, maybe not all to exactly the same degree but certainly not to hugely varying degrees. With the exception of Fe-doped SrTiO3,82 there are no experimental transport data for weakly doped systems. But for 10–20% Fe-substituted systems, the limited experimental evidence43,83,84 appears to support this supposition: oxygen diffusion is fastest in the CaTiO3-based system and slowest in the analogous BaTiO3-based system.
One reason for comparing the behaviour of these perovskites is to identify trends, and in this way, superior ion-conducting perovskites. Over the years, researchers have attempted to link isothermal conductivities or activation enthalpies to characteristic structural parameters, such as lattice volume, lattice free volume, the critical radius at the transition state, or the Goldschmidt tolerance factor.22–24,84–86 Here, we examine ΔHmig,v for these three perovskites as a function of the Goldschmidt tolerance factor t. We have restricted the analysis to these alkaline-earth titanates because the data refer to the diffusion of non-interacting vacancies and are thus strictly and directly comparable with each other; and we restrict the analysis to this one parameter (t), not because it is the best descriptor (we don't believe it is), but because it is useful for our discussions, i.e., it allows us to make several specific points.
The Goldschmidt tolerance factor is defined as87
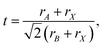 | (7) |
An optimal tolerance factor of t = 0.96 suggests that small degrees of structural distortion away from the ideal cubic form are beneficial for oxygen-ion transport, but high degrees are detrimental. This would account for orthorhombic CaTiO3 exhibiting higher oxygen diffusivity than cubic SrTiO3 [Fig. 7(a)], but it would not explain why. This brings us to the major, open question: what is so special about a tolerance factor of t = 0.96? Hayashi et al.22 proposed that t = 0.96 represents a balance between the tolerance factor and the specific free volume (the proportion of a unit cell not occupied by the ions). Regardless of whether this is correct or not, the larger issue is that, as pointed out by Mogensen et al.,23 this proposal does not explain why optimal behaviour occurs at t = 0.96. And at present it is still not clear. A detailed study based on the working hypothesis that Coulomb interactions play the key role in determining the migration barrier for X moieties in ABX3 perovskites13,92,93 is underway.
5 Concluding remarks
We performed molecular-dynamics simulations of oxygen-deficient CaTiO3, obtaining oxygen tracer diffusion coefficients for Pbnm (orthorhombic) and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (cubic) phases. From these data we determined activation enthalpies of oxygen tracer diffusion (for non-interacting oxygen vacancies) of ΔHorthmig,v = (0.584 ± 0.017) eV and ΔHcubmig,v = (0.429 ± 0.004) eV. We thus show that for a single, weakly doped perovskite system the lower symmetry phase exhibits a larger activation enthalpy of oxygen diffusion.
m (cubic) phases. From these data we determined activation enthalpies of oxygen tracer diffusion (for non-interacting oxygen vacancies) of ΔHorthmig,v = (0.584 ± 0.017) eV and ΔHcubmig,v = (0.429 ± 0.004) eV. We thus show that for a single, weakly doped perovskite system the lower symmetry phase exhibits a larger activation enthalpy of oxygen diffusion.
The second major result concerns the effect of acceptor-type cation defects (vacancies, antisites, dopants) on oxygen diffusion. We found that their presence decreases the oxygen tracer diffusivity and increases its activation enthalpy, as for other perovskites, and we discovered that these decreases in 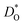 and increases in ΔHD* are more pronounced for the low-symmetry phase.
and increases in ΔHD* are more pronounced for the low-symmetry phase.
Third, based on an analysis of diffusion data for the alkaline-earth titanate perovskites, we showed that orthorhombic CaTiO3 displays faster rates of oxygen-vacancy diffusion with a lower activation enthalpy of migration than cubic SrTiO3, and we argued in favour of the hypothesis that the rate of oxygen diffusion in perovskite oxides reaches a maximum for those systems with a Goldschmidt tolerance factor of t = 0.96. The origin of this behaviour remains unclear.
Fourth, we demonstrated two particular benefits of classical MD simulations. For the orthorhombic phase, with its multiple activation barriers, MD simulations yielded data that refer to long-range diffusion and are thus directly comparable with experimental values. For the cubic phase, which is only stable at elevated temperatures, the MD simulations provided a reliable method for obtaining the activation barrier of ion migration. NEB calculations of ion migration in the cubic phase were found to be unreliable. This is an intrinsic problem afflicting static supercell calculations of ion migration in the high-symmetry phases of ABX3 perovskites whose ground state structure has lower symmetry.
Lastly, this study constitutes another example of classical MD simulations providing as a function of temperature precise diffusion coefficients that allow experimental transport data for perovskite materials to be clarified and interpreted.50,68,94 Standard ab initio MD cannot be relied upon, but ab initio metadynamics simulations95 do offer exciting possibilities.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding from German Research Foundation (DFG) within the framework of the collaborative research centre SFB917, “Nanoswitches”, is gratefully acknowledged. Simulations were performed with computing resources granted by RWTH Aachen University under projects thes0229, thes0847, rwth0254 and rwth0655.Notes and references
- B. C. H. Steele, Mater. Sci. Eng., B, 1992, 13, 79–87 CrossRef
.
- J. C. Boivin and G. Mairesse, Chem. Mater., 1998, 10, 2870–2888 CrossRef CAS
.
- V. Kharton, F. Marques and A. Atkinson, Solid State Ionics, 2004, 174, 135–149 CrossRef CAS
.
- S. Hull, Rep. Prog. Phys., 2004, 67, 1233–1314 CrossRef CAS
.
- A. Orera and P. R. Slater, Chem. Mater., 2010, 22, 675–690 CrossRef CAS
.
- J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS
.
- T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803 CrossRef CAS
.
- M. Feng and J. Goodenough, Eur. J. Solid State Inorg. Chem., 1994, 31, 663–672 CAS
.
- T. Ishihara, J. A. Kilner, M. Honda and Y. Takita, J. Am. Chem. Soc., 1997, 119, 2747–2748 CrossRef CAS
.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35 CrossRef CAS PubMed
.
- L. Koch, S. Steiner, K.-C. Meyer, I.-T. Seo, K. Albe and T. Frömling, J. Mater. Chem. C, 2017, 5, 8958–8965 RSC
.
- F. Yang, M. Li, L. Li, P. Wu, E. Pradal-Velázque and D. C. Sinclair, J. Mater. Chem. A, 2017, 5, 21658–21662 RSC
.
- H. Zhang, A. H. H. Ramadan and R. A. De Souza, J. Mater. Chem. A, 2018, 6, 9116–9123 RSC
.
- J. E. ten Elshof, M. H. R. Lankhorst and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 1060–1067 CrossRef
.
-
S. J. Benson, R. J. Chater and J. A. Kilner, Proc. Third Intl. Symp. Ionic and Mixed Conducting Ceramics, Pennington, NJ, USA, 1997, pp. 596–609 Search PubMed
.
- R. A. De Souza and J. A. Kilner, Solid State Ionics, 1998, 106, 175–187 CrossRef CAS
.
- L. Wang, R. Merkle, J. Maier, T. Acartürk and U. Starke, Appl. Phys. Lett., 2009, 94, 071908 CrossRef
.
- A. Berenov, A. Atkinson, J. Kilner, E. Bucher and W. Sitte, Solid State Ionics, 2010, 181, 819–826 CrossRef CAS
.
- A. Egger, E. Bucher, M. Yang and W. Sitte, Solid State Ionics, 2012, 225, 55–60 CrossRef CAS
.
- A. F. Sammells, R. L. Cook, J. H. White, J. J. Osborne and R. C. MacDuff, Solid State Ionics, 1992, 52, 111–123 CrossRef CAS
.
- K. Nomura and S. Tanase, Solid State Ionics, 1997, 98, 229–236 CrossRef CAS
.
- H. Hayashi, H. Inaba, M. Matsuyama, N. Lan, M. Dokiya and H. Tagawa, Solid State Ionics, 1999, 122, 1–15 CrossRef CAS
.
- M. Mogensen, D. Lybye, N. Bonanos, P. Hendriksen and F. Poulsen, Solid State Ionics, 2004, 174, 279–286 CrossRef CAS
.
- T. Shibasaki, T. Furuya, S. Wang and T. Hashimoto, Solid State Ionics, 2004, 174, 193–203 CrossRef CAS
.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326–6342 CrossRef CAS
.
- F. Guyot, P. Richet, P. Courtial and P. Gillet, Phys. Chem. Miner., 1993, 20, 141–146 CrossRef CAS
.
- P. Gillet, F. Guyot, G. D. Price, B. Tournerie and A. L. Cleach, Phys. Chem. Miner., 1993, 20, 159–170 CrossRef CAS
.
- B. J. Kennedy, C. J. Howard and B. C. Chakoumakos, J. Phys.: Condens. Matter, 1999, 11, 1479–1488 CrossRef CAS
.
- Y. Gu, K. Rabe, E. Bousquet, V. Gopalan and L.-Q. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064117 CrossRef
.
- S. A. T. Redfern, J. Phys.: Condens. Matter, 1996, 8, 8267–8275 CrossRef CAS
.
- R. Ali and M. Yashima, J. Solid State Chem., 2005, 178, 2867–2872 CrossRef CAS
.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32–43 CrossRef
.
- C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789 CrossRef
.
- K. S. Aleksandrov, Ferroelectrics, 1976, 14, 801–805 CrossRef CAS
.
- W. George and R. Grace, J. Phys. Chem. Solids, 1969, 30, 889–892 CrossRef CAS
.
- H. Iwahara, T. Esaka and T. Mangahara, J. Appl. Electrochem., 1988, 18, 173–177 CrossRef CAS
.
- B. Gautason and K. Muehlenbachs, Science, 1993, 260, 518–521 CrossRef CAS PubMed
.
- I. Sakaguchi and H. Haneda, J. Solid State Chem., 1996, 124, 195–197 CrossRef CAS
.
- T. Bak, J. Nowotny and C. Sorrel, J. Phys. Chem. Solids, 2004, 65, 1229–1241 CrossRef CAS
.
- K. Wright and G. D. Price, J. Geophys. Res.: Solid Earth, 1993, 98, 22245–22253 CrossRef
.
- G. C. Mather, M. Islam and F. Figueiredo, Adv. Funct. Mater., 2007, 17, 905–912 CrossRef
.
- J. J. Brown, Z. Ke, W. Geng and A. J. Page, J. Phys. Chem. C, 2018, 122, 14590–14597 CrossRef CAS
.
- C. Salles, J. Bassat, J. Fouletier, D. Marinha and M.-C. Steil, Solid State Ionics, 2018, 324, 103–108 CrossRef CAS
.
- S. Marion, A. I. Becerro and T. Norby, Phase Transitions, 1999, 69, 157–168 CrossRef CAS
.
- L. Dunyushkina and V. Gorelov, Solid State Ionics, 2013, 253, 169–174 CrossRef CAS
.
- A. Murashkina, A. Demina, A. Demin, V. Maragou and P. Tsiakaras, Solid State Ionics, 2008, 179, 1615–1619 CrossRef CAS
.
- A. Pedone, G. Malavasi, M. C. Menziani, A. N. Cormack and U. Segre, J. Phys. Chem. B, 2006, 110, 11780–11795 CrossRef CAS PubMed
.
- O. Kanert, H. Schulz and J. Albers, Solid State Commun., 1994, 91, 465–469 CrossRef CAS
.
- M. Kessel, R. A. De Souza and M. Martin, Phys. Chem. Chem. Phys., 2015, 17, 12587–12597 RSC
.
- J. Kaub, J. Kler, S. C. Parker and R. A. De Souza, Phys. Chem. Chem. Phys., 2020, 22, 5413–5417 RSC
.
- F. Cordero, F. Trequattrini, D. Quiroga and P. Silva, J. Alloys Compd., 2021, 874, 159753 CrossRef CAS
.
- D. B. Schwarz and H.
U. Anderson, J. Electrochem. Soc., 1975, 122, 707–710 CrossRef CAS
.
- A. Hackmann and O. Kanert, Radiat. Eff. Defects Solids, 1991, 119–121, 651–656 CrossRef
.
- F. Cordero, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 172106 CrossRef
.
- R. A. De Souza, V. Metlenko, D. Park and T. E. Weirich, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174109 CrossRef
.
- S. P. Waldow and R. A. De Souza, ACS Appl. Mater. Interfaces, 2016, 8, 12246–12256 CrossRef CAS
.
- L. Zhang, B. Liu, H. Zhuang, P. Kent, V. R. Cooper, P. Ganesh and H. Xu, Comput. Mater. Sci., 2016, 118, 309–315 CrossRef CAS
.
- H. J. Heelweg and R. A. De Souza, Phys. Rev. Mater., 2021, 5, 013804 CrossRef CAS
.
- K. Gömann, G. Borchardt, M. Schulz, A. Gömann, W. Maus-Friedrichs, B. Lesage, O. Kaïtasov, S. Hoffmann-Eifert and T. Schneller, Phys. Chem. Chem. Phys., 2005, 7, 2053–2060 RSC
.
- R. Meyer, R. Waser, J. Helmbold and G. Borchardt, Phys. Rev. Lett., 2003, 90, 105901 CrossRef PubMed
.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC
.
- S. Amisi, E. Bousquet, K. Katcho and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064112 CrossRef
.
- A. I. Becerro, S. A. T. Redfern, M. A. Carpenter, K. S. Knight and F. Seifert, J. Solid State Chem., 2002, 167, 459–471 CrossRef CAS
.
- M. Schie, R. Waser and R. A. De Souza, J. Phys. Chem. C, 2014, 118, 15185–15192 CrossRef CAS
.
- H. Zhang and R. A. De Souza, J. Mater. Chem. A, 2019, 7, 25274–25278 RSC
.
- J. M. Börgers and R. A. De Souza, Phys. Chem. Chem. Phys., 2020, 22, 14329–14339 RSC
.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC
.
- T. Ishigaki, S. Yamauchi, K. Kishio, J. Mizusaki and K. Fueki, J. Solid State Chem., 1988, 73, 179–187 CrossRef CAS
.
- R. A. De Souza and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2356–2367 RSC
.
- H. Schraknepper and R. A. De Souza, J. Appl. Phys., 2016, 119, 064903 CrossRef
.
- R. A. De Souza, J. Zehnpfenning, M. Martin and J. Maier, Solid State Ionics, 2005, 176, 1465–1471 CrossRef CAS
.
- R. A. De Souza, F. Gunkel, S. Hoffmann-Eifert and R. Dittmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 241401 CrossRef
.
- K. K. Adepalli, J. Yang, J. Maier, H. L. Tuller and B. Yildiz, Adv. Funct. Mater., 2017, 27, 1700243 CrossRef
.
- H. Schraknepper, T. E. Weirich and R. A. De Souza, Phys. Chem. Chem. Phys., 2018, 20, 15455–15463 RSC
.
- R.-V. Wang and P. C. McIntyre, J. Appl. Phys., 2005, 97, 023508 CrossRef
.
- S. Gottschalk, H. Hahn, S. Flege and A. G. Balogh, J. Appl. Phys., 2008, 104, 114106 CrossRef
.
- H. Bouwmeester, H. Kruidhof and A. Burggraaf, Solid State Ionics, 1994, 72, 185–194 CrossRef CAS
.
- C.-Y. Yoo and H. J. M. Bouwmeester, Phys. Chem. Chem. Phys., 2012, 14, 11759 RSC
.
- V. Metlenko, W. Jung, S. R. Bishop, H. L. Tuller and R. A. De Souza, Phys. Chem. Chem. Phys., 2016, 18, 29495–29505 RSC
.
- J. Claus, M. Leonhardt and J. Maier, J. Phys. Chem. Solids, 2000, 61, 1199–1207 CrossRef CAS
.
-
S. Steinsvik, T. Norby and P. Kofstad, Proc. Electroceramics IV, Aachen, Germany, 1994, pp. 691–696 Search PubMed
.
- V. A. Kolotygin, A. P. Viskup, E. V. Pivak and V. V. Kharton, Russ. J. Electrochem., 2020, 56, 110–117 CrossRef CAS
.
- J. A. Kilner and R. J. Brook, Solid State Ionics, 1982, 6, 237–252 CrossRef CAS
.
- M. Cherry, M. S. Islam and C. R. A. Catlow, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS
.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- K. Kreuer, Solid State Ionics, 1999, 125, 285–302 CrossRef CAS
.
- N. Kurita, N. Fukatsu, K. Ito and T. Ohashi, J. Electrochem. Soc., 1995, 142, 1552–1559 CrossRef CAS
.
- R. A. De Souza, J. A. Kilner and C. Jeynes, Solid State Ionics, 1997, 97, 409–419 CrossRef CAS
.
- J. P. Parras, A. R. Genreith-Schriever, H. Zhang, M. T. Elm, T. Norby and R. A. De Souza, Phys. Chem. Chem. Phys., 2018, 20, 8008–8015 RSC
.
- R. A. De Souza and D. Barboni, Chem. Commun., 2019, 55, 1108–1111 RSC
.
- D. Barboni and R. A. De Souza, Energy Environ. Sci., 2018, 11, 3266–3274 RSC
.
- J. Koettgen, P. C. Schmidt, T. Bučko and M. Martin, Phys. Rev. B, 2018, 97, 024305 CrossRef CAS
.
Footnote |
| † Roger De Souza writes: John Kilner played a formative role in my scientific career. He introduced me to the world of defects, diffusion and perovskites some 30 years ago, providing illuminating and captivating guidance. It seems fitting, therefore, to contribute to his Festschrift with a paper on defects and diffusion in the mineral perovskite. |
| This journal is © The Royal Society of Chemistry 2022 |