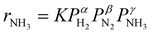Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced promotion of Ru-based ammonia catalysts by in situ dosing of Cs†
Vahid
Shadravan‡
 ,
Ang
Cao‡
,
Ang
Cao‡
 ,
Vanessa J.
Bukas§
,
Vanessa J.
Bukas§
 ,
Mette K.
Grønborg
,
Christian D.
Damsgaard
,
Zhenbin
Wang
,
Mette K.
Grønborg
,
Christian D.
Damsgaard
,
Zhenbin
Wang
 ,
Jakob
Kibsgaard
,
Jakob
Kibsgaard
 ,
Jens K.
Nørskov
,
Jens K.
Nørskov
 * and
Ib
Chorkendorff
* and
Ib
Chorkendorff
 *
*
Department of Physics, Technical University of Denmark, 2800 Kongens Lyngby, Denmark. E-mail: jkno@dtu.dk; ibchork@fysik.dtu.dk
First published on 24th June 2022
Abstract
Ammonia synthesis via the high-temperature and -pressure Haber–Bosch (HB) process at large centralized facilities has a significant contribution to global CO2 emissions. Radically new catalysts should be discovered to enable sustainable ammonia synthesis processes that can operate at much lower temperatures to relax the demand for high pressure in the current HB process. In this manner, the capital requirement and energy consumption for making ammonia would decrease considerably and a de-centralized production could become feasible. Herein, we present a new class of ruthenium-based catalysts promoted with metallic cesium using an in situ preparation technique. The catalysts prepared with this new technique showed up to a factor of ∼10 higher activity compared to the ones prepared by traditional ex situ promotion methods. The in situ promoted catalyst also has a smaller apparent activation energy and is less susceptible to H2 poisoning. We systematically investigate the promotional role of in situ dosed Cs and propose a detailed model supported by extensive density functional theory calculations to explain the difference between the promotional effect of the in situ and traditionally ex situ prepared catalysts.
As the precursor and main building block of various N-containing fertilizers, ammonia has played an important role in nourishing the global population since the beginning of the modern era.1,2 Recently, ammonia has also been considered for hydrogen storage (i.e., chemical storage of sustainable energy resources) and carbon-free fuel.3,4 The Haber–Bosch (HB) process (N2 + 3H2 → 2NH3) has been the main industrial ammonia synthesis route for more than a century.5–7 As the hydrogen input for the HB process typically comes from steam reforming of methane,7 ammonia production is responsible for around 1% of both global energy consumption and carbon emission.8,9 Ammonia production plants are usually built in areas with access to low-cost fossil resources,10 and combined with the harsh conditions of the HB process (∼400 °C and ∼150 bar) and substantial capital costs (which are increasing exponentially by increasing pressure11), this results in large centralized facilities.
There is an intense search for alternative processes with a lower carbon footprint (e.g., photochemical,12 electrochemical,9 thermal looping,13 and plasma14 processes). At the moment, the most straightforward alternative consists of green hydrogen production from water electrolysis15 (or other electrified processes16) combined with the traditional high pressure and temperature HB process. An efficient ammonia synthesis process under milder conditions could help make this approach more compatible with small-scale green hydrogen production units. To move away from the centralized high-pressure ammonia production, it is necessary to decrease the process temperature to minimize the limiting effects of thermodynamic equilibrium on ammonia synthesis. In this case, it is essential to discover a better catalyst that can produce ammonia under mild conditions (ideally <200 °C and <40 bar)17 with a reasonably high yield.
Inspired by the work of Aika et al.,18,19 using metal vapors in a low pressure batch-type reactor to compare the promotional effects of different alkali metals on Ru, we present here a new in situ technique for promoting a carbon supported Ru catalyst with Cs for ammonia synthesis. In this technique, the Ru/C catalyst is getting promoted directly by metallic Cs vapor in a high-pressure plug-flow reactor, while keeping the internal partial pressure of O2 and H2O very close to zero. Our in situ promoted catalyst gives rates that are more than an order of magnitude higher than those for a conventional ex situ promoted catalyst at temperatures below 350 °C. We also find a considerably lower activation energy, making the catalyst more suitable for ammonia synthesis at low temperatures. Finally, we developed a promotion model using density functional theory calculations to explain both the higher rate and the lower activation energy.
Results
In situ promotion of Ru/C with metallic Cs
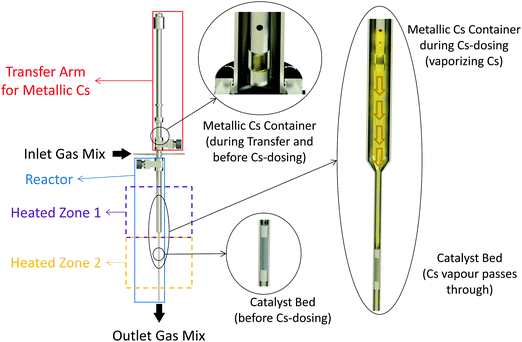
It has been shown that even trace amounts of oxygen-containing compounds, such as water, are detrimental to low-temperature ammonia synthesis and it is thus essential to mitigate oxygen poisoning.20 Minimizing or complete removal of the oxygen impurities (especially O2 and H2O) from the reactants’ gas stream may significantly enhance the ammonia synthesis rate on any active catalyst. Therefore, in this work, Ru/C samples were directly promoted with metallic Cs vapor and tested without any exposure to air. To this end, an add-on to the reactor setup was designed and used for in situ dosing of metallic Cs to the catalysts Fig. 1. The system consists of an ultra-high vacuum compatible transfer arm equipped with a small cup for loading metallic Cs. The transfer arm was loaded with metallic Cs (≥99.95% trace metals basis, Sigma-Aldrich) in an Ar-glovebox. The arm was then connected to the setup, allowing the Cs loaded cup to be moved inside the reactor near the catalyst bed. The system was then evacuated and purged with Ar several times ensuring no oxygen is left in the system. For vaporizing Cs, the temperature of the Cs loaded cup was controlled independently from the catalyst bed temperature. The Cs was dosed to the catalysts in Ar flow at 10 bar while the Cs cup was kept at 450 °C and the catalyst bed was at 400 °C. After a few hours, the flow was switched to the N2 + H2 mixture for different measurements.Besides the in situ promoted catalysts, a series of ex situ promoted catalysts were prepared by wet impregnation of the Ru/C samples with Cs precursor solutions. More details about these can be found in the Methods section.
Catalytic performance of in situ and ex situ promoted Ru/C
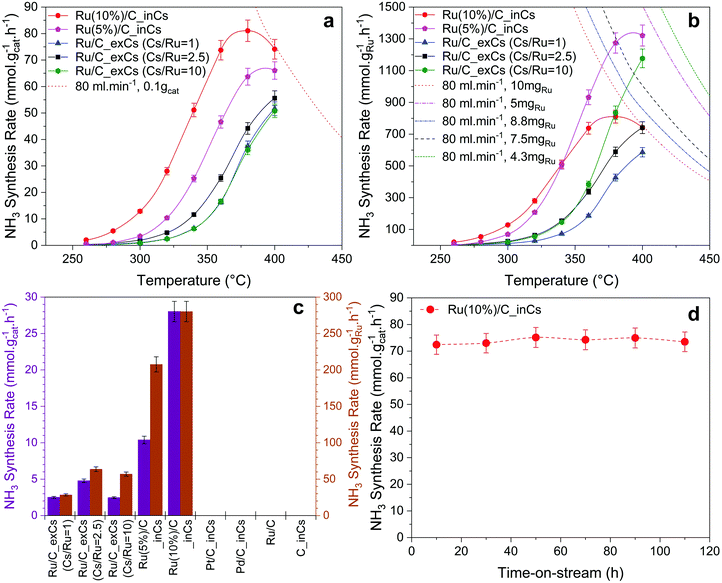
To investigate the effect of the oxygen-free promotion (here named Ru/C_inCs) and compare it with the conventional in-air ex situ promotion (named Ru/C_exCs) a series of catalyst activity measurements were carried out (the activity of the Ru/C_exCs catalyst is within the range of reported RuCs catalysts in the literature, see Table S1, ESI†). The activity of each catalyst is reported as the rate of ammonia synthesis per weight of the loaded catalyst (Fig. 2a) or the Ru content (Fig. 2b) in the catalyst bed. The dashed/dotted lines in Fig. 2a and b represent the equilibrium rate of ammonia synthesis. At temperatures away from equilibrium (<360 °C) where the kinetics dominate, the in situ promoted catalysts have up to a factor of ∼10 higher activity compared to the ex situ promoted ones. This observation is independent of calculating the NH3 synthesis rates normalized by the total mass of the catalyst or the mass of Ru.Due to the nature of our in situ promotion technique in its current form, it is difficult to control how much evaporated Cs will end up on the actual catalyst bed and not just pass through the bed. Therefore, the ex situ promoted catalysts were prepared with three different ratios of the Cs to Ru (Cs/Ru) content. A relation between the Cs/Ru ratio and ammonia synthesis rate for Ru/C_exCs catalysts was observed similar to the observations reported by others, which often shows that there is an optimum value for Cs/Ru to achieve the highest activity.21,22 Here, the main purpose of varying the Cs/Ru ratio for the Ru/C_exCs catalysts was to rule out the scenario that the performance difference of in situ and ex situ promoted catalysts is simply because of the Cs content.
The ammonia synthesis rate over the Ru/C_exCs catalysts was almost the same by varying the Cs/Ru ratio from 1 to 10 as shown in Fig. 2a. Here the activity based on the total weight of the loaded catalyst is plotted as a function of temperature for various catalysts. Similarly in Fig. 2b, where the activity is shown based on the weight of the Ru content of the catalyst, it is seen that by increasing the Cs/Ru ratio from 2.5 to 10 the enhancement effect of Cs is not significant. This observation is specifically important to compare the performance of Ru/C_exCs catalysts with the in situ promoted ones. Assuming that all of the evaporated Cs was condensed on the catalyst bed during in situ promotion, the Cs/Ru ratio is around 10 for the in situ promoted catalysts (the relative loadings of Cs over different in situ and ex situ promoted catalysts are presented in Table S3, ESI†). Therefore, the higher ammonia synthesis rate of in situ promoted catalysts cannot be simply due to a higher Cs/Ru ratio. Moreover, particle size distribution was evaluated for the in situ and ex situ promoted catalysts (Table S4, ESI†). It is found that the particles over these samples are within the same order of magnitude (the in situ sample has around a factor of 3 larger particles Fig. S3, ESI†). This relatively similar particle size over the in situ and ex situ promoted catalysts also confirms that the higher activity of the in situ promoted catalysts is not simply due to the smaller particle size and thus a greater number of surface active sites. In contrast, the ex situ catalyst has even smaller particles.
The stability of the in situ promoted catalyst was tested and is presented in Fig. 2d. It is observed that the catalyst could have a stable performance for up to 110 h, when the experiment was stopped. One important point for the stable performance of the in situ promoted catalyst is that our system is ultra-clean in terms of being free from O-containing compounds. The high activity of the in situ promoted catalyst can be extremely affected by introducing small amounts of water to the system (Fig. S5, ESI†).
Kinetics and the effect of H2 poisoning
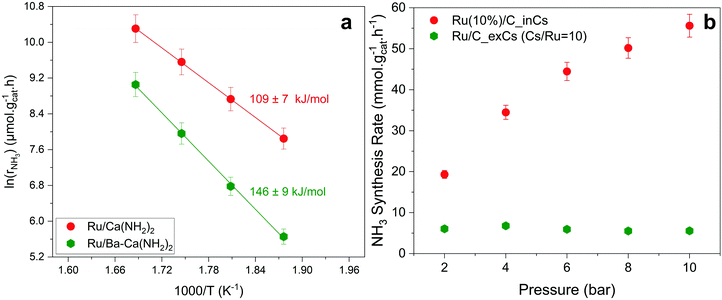
Fig. 3a shows an Arrhenius plot and measured apparent activation energies for Ru/C catalysts promoted with Cs by in situ and ex situ techniques. A significant difference between the activation energies of these catalysts is observed. Moreover, Table 1 and Fig. S4 (ESI†) present the calculated reaction orders over these catalysts. Ammonia inhibition is a well-known characteristic of most ammonia synthesis processes, especially over Fe-based catalysts23 since nitrogen is bonding too strongly. The ammonia inhibition effect has also been reported for Ru-based catalysts to a lesser extent while H2 inhibition has a more significant effect on most Ru-based catalysts.24 Although a catalyst may have very active sites for N2 activation, both NH3 and H2 inhibition can negatively affect the performance of ammonia in the catalyst. Ammonia inhibition acts as a self-poisoning effect for the catalyst and hydrogen inhibition suppresses the catalyst performance at higher pressures (i.e., higher partial pressure of H2 resulting in more H2 poisoning).| Catalyst | α(H2) | β(N2) | γ(NH3) |
|---|---|---|---|
| Ru/C_inCs | −0.6 | 1.5 | −0.3 |
| Ru/C_exCs | −1.3 | 1.8 | −0.5 |
Here, assuming a simplified power law rate expression 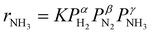 , the calculated N2 reaction orders of both Ru/C_inCs and Ru/C_exCs are roughly equal, 1.5 and 1.8, respectively (if the NH3 order is assumed to be 0, the calculated N2 orders will be 1.1 and 1.3 for Ru/C_inCs and Ru/C_exCs, respectively). The values of N2 order above 1 might be due to the oversimplification of the rate expression. In addition, a slight NH3 inhibition effect is observed for both catalysts.
, the calculated N2 reaction orders of both Ru/C_inCs and Ru/C_exCs are roughly equal, 1.5 and 1.8, respectively (if the NH3 order is assumed to be 0, the calculated N2 orders will be 1.1 and 1.3 for Ru/C_inCs and Ru/C_exCs, respectively). The values of N2 order above 1 might be due to the oversimplification of the rate expression. In addition, a slight NH3 inhibition effect is observed for both catalysts.
Although the NH3 and N2 orders are more or less the same for the in situ and ex situ Cs promoted catalysts, the H2 reaction orders (indicating the H2 inhibition effect) are significantly different (Fig. 3b and Fig. S4c, ESI†). In this case, H2 inhibition is much less for the in situ promoted catalyst compared to the ex situ promoted one. The less H2 inhabitation on the in situ promoted catalyst results in an increase of activity by a factor of ∼3 when the pressure is increased from 2 to 10 bar, while the performance of the ex situ promoted catalyst does not change by increasing the reaction pressure due to the very strong H2 inhibition effect (see Fig. 3b).
Investigation of Cs as the active material
After observing the enhancement effect of promoting Ru/C with metallic Cs vapor, three hypotheses were first considered:(1) Cs or Cs/C may be able to activate both N2 and H2 to produce NH3.
(2) Cs may be able to activate N2 and enhance activity by providing new N2 activation sites.
(3) As Cs is an extremely reducing element with high O2- and H2O-capturing abilities, its role may be to act solely as an oxygen trap resulting in less oxygen poisoning of the catalyst and thus higher activity.
To investigate the first two hypotheses, the in situ Cs promotion technique was also used for a pure carbon support as well as Pd/C and Pt/C catalysts. No ammonia synthesis activity was detected for either after in situ dosing with Cs under our testing conditions (Fig. 2c). By observing the inactivity of C_inCs, it is concluded that in situ dosed Cs does not have any ammonia production activity in itself. The Pd and Pt experiments were done to test the second hypothesis, where Pt and Pd were intentionally included as H2 activation sites25 for Cs. However, neither the Pd/C_inCs nor Pt/C_inCs catalysts showed any ammonia synthesis activity. To check the possibility of the third hypothesis, a set of experiments were performed where the feed gas passed through a separate tube containing metallic Cs prior to entering the reactor packed with Ru/C (no Cs vapor entering the reactor). Fig. S2 (ESI†) shows that the ammonia synthesis activity is not enhanced over Ru/C when Cs is used as an O2/H2O trap in this manner. On the other hand, it is observed that NH3 synthesis activity is enhanced significantly after the metallic Cs vapor passes through the reactor. We therefore conclude that none of the three hypotheses involving a separate role of Cs are valid. In the following we continue by further analyzing the Cs promotion effect of the Ru catalyst. These tests also rule out that any ammonia was generated from the reactor, or the steel wool used for making an oxygen free packing the plug of catalysts.
A promoter model
The experimental results described above suggest that activity enhancement is due to a promoter effect on the Ru surface. This poses three fundamental questions:(1) How can the in situ dosing give a rate which is up to a factor of ∼10 higher than the ex situ promotion below 340 °C?
(2) How can a change in the rate of a factor of ∼10 be compatible with a change in apparent activation energy of ∼0.4 eV (∼40 kJ mol−1)? At 340 °C this should give a rate difference on the order of 2000 for the same pre-exponential factor.
(3) How can a different promotion procedure give rise to a change in the reaction order in H2 from −0.6 with ex situ promotion to −1.3 with in situ promotion?
To answer these questions, we first calculated the surface phase diagram to explore the nature of the active phase, see Fig. 4. For details of the density functional theory calculations, see the Methods section. The figure shows a comparison of the free energy of Cs in different precursor compounds (i.e., bulk Cs2O, CsOH, CsN3 and CsH) to the free energy of Cs at a Ru step modelled by a Ru(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 5) surface under typical ammonia synthesis conditions (T = 340 °C, PH2 = 7.125 bar, PNH3= 0.25 bar (N2 conversion of 5% and PH2O = 10−6 bar (0.1 ppm of water in the feed to illustrate a very clean gas)). The step site has been shown theoretically and experimentally to be the active site for N2 dissociation over Ru.26 We consider adsorbed Cs*, co-adsorbed Cs and O (presented as (Cs–O)*), as well as co-adsorbed Cs and OH (presented as (Cs–OH)*), at the step (for configurations see Fig. 4a).
5) surface under typical ammonia synthesis conditions (T = 340 °C, PH2 = 7.125 bar, PNH3= 0.25 bar (N2 conversion of 5% and PH2O = 10−6 bar (0.1 ppm of water in the feed to illustrate a very clean gas)). The step site has been shown theoretically and experimentally to be the active site for N2 dissociation over Ru.26 We consider adsorbed Cs*, co-adsorbed Cs and O (presented as (Cs–O)*), as well as co-adsorbed Cs and OH (presented as (Cs–OH)*), at the step (for configurations see Fig. 4a).
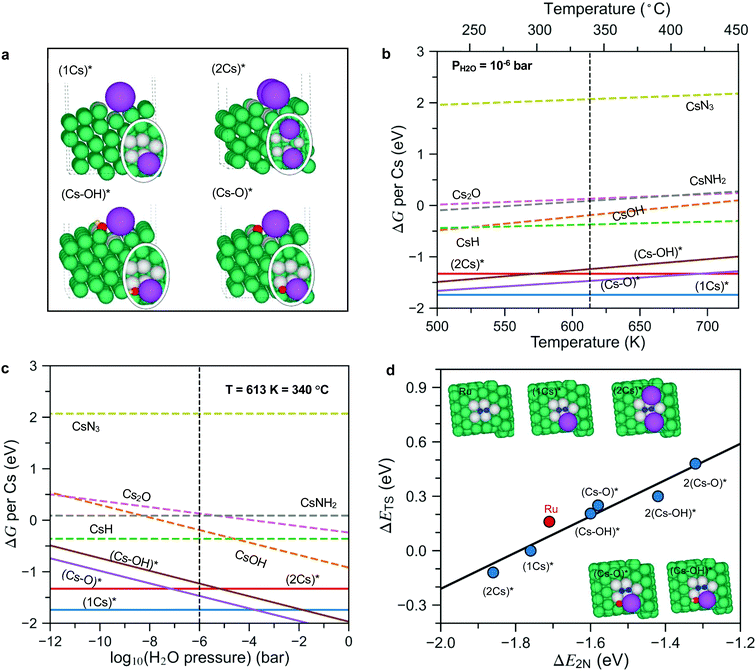 | ||
| Fig. 4 (a) Side and top (in oval) views of co-adsorbed 1Cs*, 2Cs*, (Cs–O)* and (Cs–OH)* species at the step of the Ru surface. (b and c) The phase diagrams of Cs promoted Ru in equilibrium with its oxides, hydroxides, hydrides, amides and nitrides under reaction conditions as a function of temperature and H2O pressure. The reaction conditions for panel (b) are PH2 = 7.125 bar, PNH3 = 0.25 bar (N2 conversion of 5%), PH2O = 10−6 bar, chosen to simulate an extremely dry reactant gas. The reaction conditions for panel (c) are T = 340 °C, PH2 = 7.125 bar, PNH3 = 0.25 bar (N2 conversion of 5%; phase diagrams based on N2 conversion of 2% and 10% are also calculated and presented in Fig. S9, ESI†). Bulk species are shown as dashed lines, while adsorbed species are shown as full lines and identified by a *. All energies are per Cs atom and relative to bulk Cs. (d) Scaling relations for the N2 dissociation barrier (ΔETS) as a function of N2 dissociation energy (ΔE2N) on pristine Ru steps as well as Cs*, (Cs–O)* and (Cs–OH)* covered Ru steps (extended data are presented in Fig. S10, ESI†). Green, purple, red, yellow, and blue spheres represent Ru, Cs, O, H, and N atoms, respectively. To see more clearly, the Ru atoms at the active sites are labeled in grey. | ||
Fig. 4b shows that at a low water content (10−6 bar) and a temperature of 340 °C, bulk Cs2O, CsOH, CsN3 and CsH are unstable and can be reduced to form adsorbed Cs*, and low Cs coverage ((1Cs)* coverage of ¼ along the step) is considerably more stable than a high coverage phase ((2Cs)* coverage of ½ along the step). This reflects a repulsive (dipole–dipole) interaction between adsorbed Cs atoms, which have given up a good fraction of their valence electrons to the Fermi level of the metal surface. The formation of (2Cs)* only becomes favorable relative to the co-adsorbed (Cs–O)* species as the temperature increases (above 700 K) or the water content decreases (below 10−8 bar, Fig. 4c). Importantly, only non-oxidized Cs* acts as a promoter by lowering the N2 dissociation transition state energy, see Fig. 4d. (Cs–O)* and (Cs–OH)* both increase the activation energy and therefore act as inhibitors for ammonia synthesis.
All in all, the results summarized in Fig. 4 suggest that if the promoter is introduced as an oxide or hydroxide as in the ex situ case, only a low coverage of Cs without O or OH attached will be available for promotion – the promoter oxide or hydroxide phase will provide a background level of water that is likely to make the higher Cs coverage patches O- or OH-poisoned. This is different for in situ promotion, where we can keep the promoter water free (hence no (Cs–O)* and (Cs–OH)*). This suggests that the in situ promotion gives a higher Cs coverage than the ex situ promotion. If we could reduce the ex situ sample well enough at an extremely low O content, we should in principle be able to reach the same level of promotion as the in situ method. As long as there are unreduced Cs oxides and hydroxides in the sample, it is, however, very difficult to reach this state – as can be seen in Fig. 4b and c, the highly promoted in situ sample is much more prone to oxygen poisoning than the ex situ, low Cs coverage, system. We suggest that this is the reason that no one has observed this state before now. We also note that the Cs is bound very strongly at the step and will not easily desorb, in good agreement with experimental results for Ru(0001) showing a high temperature tail in the thermal desorption spectrum above 1200 K which we attribute to the Cs bound at step sites.27
In the following we use the ¼ and ½ Cs step-coverage to model the ex situ and in situ promotion, respectively. This is a simple model, but should capture the trend. Fig. 4d shows that the transition state energy for N2 dissociation decreases monotonically from the clean to the low to the high coverage Cs case (Fig. 4d), implying that Cs* is a good promoter for N2 dissociation and more so for a high Cs coverage. This explains qualitatively the further enhanced rate for the in situ promoted catalyst. The reason that the high Cs coverage catalyst promotes better is as follows: the promotion effect of the adsorbed Cs is related to the attractive interaction between the Cs-induced electric field outside the surface and the dipole induced by the N2 molecule in the transition state at the surface.28 At the high Cs coverage, the transition state molecule is close to two Cs atoms (Fig. 4d, insets), meaning the field is ∼twice as large, and hence the larger stabilization of the transition state.
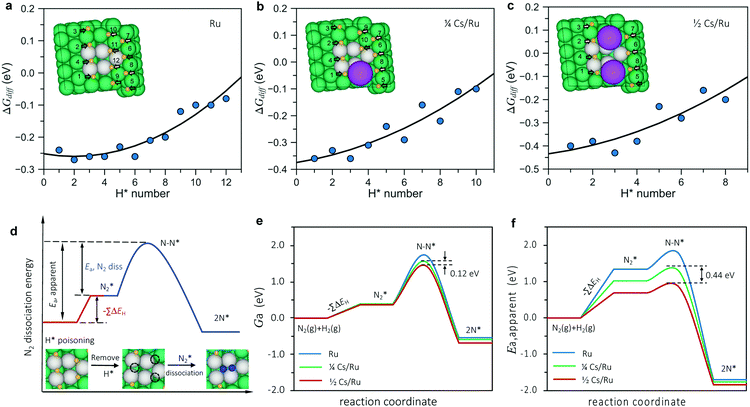
The change (0.1 eV) in the transition state energy between the ¼ and ½ Cs cases (ex situ and in situ promotion, respectively) does not explain the large difference in the apparent activation energy (0.4 eV) observed in the experiments. To understand that we need to include the effect of co-adsorbed species, the point being that the apparent activation energy (Ea,apparent) measured experimentally includes both the activation energy for N2 dissociation (Ea,N2diss = ETS − EN2-gas) and the energy needed to free an active site from co-adsorbed species (ΔE), see e.g. ref. 29:
| Ea,apparent = Ea,N2diss + ΔE (create a free site for N2 activation) | (1) |
The calculated surface phase diagram (Fig. S11, ESI†) shows that H* species bind to the Ru surface stronger than other intermediates (N*, NH*, NH2* and NH3*). To investigate the coverage of H on the surface, we first studied the adsorption energies of H atoms at various adsorption sites in detail and labeled the order of H adsorption in Table S5 (ESI†). We found that under the experimental conditions, the free energies for all H atoms around the N2 dissociation site are all below 0 eV, which means that the active step sites (and all surrounding sites) are completely covered by hydrogen on both non-promoted Ru and at ¼ and ½ Cs coverage, as shown in Fig. 5a–c (extended data in Table S5, ESI†). This means we need to pay the energy of getting rid of co-adsorbed H* species before N2 dissociation.
As illustrated in Fig. 5d, three H* atoms around the active site (one at the upper step and two at the lower step) need to be removed prior to N2 dissociation on the pristine Ru surface. In the model for the low Cs coverage, one Cs atom replaces one of the blocking H* adsorption sites at the lower steps (Fig. 5b), so another two H atoms (one at the lower step and the other one at the upper step site) must be removed. For the high Cs coverage model, only one H atom at the upper step site needs to be removed since two Cs atoms can block all the H* adsorption sites at the lower step (Fig. 5c).
The apparent activation energy therefore can be simply expressed by
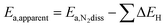 | (2) |
The apparent activation free energy is calculated in the same way as eqn (2) except free energies enter the equation instead of electronic energies. This is the activation energy that determines the rate. The main difference between the free energies and the electronic energies is the entropy loss when a molecule loses its translational degrees of freedom upon adsorption (or in the transition state). Entropy effects at the surface are included in the harmonic approximation.
Fig. 5e and f (extended data in Table S6, ESI†) shows a summary of the calculated free energies and adsorption energies in the model (eqn (2)) for the most relevant sites that block N2 dissociation. It can be seen that the simple model describes the observations quite well. It describes the promotion of the synthesis rate in terms of the decrease in (apparent) activation free energy upon promotion. The difference in the apparent activation free energy between the low and high promoter coverage is 0.12 eV corresponding to a difference in the rate on the order of 10 at 340 °C, close to the experimentally observed difference at this temperature. The difference in apparent activation energy between the two cases is 0.44 eV very close to the experimentally observed difference (0.4 eV). The trend is therefore well described both qualitatively and quantitatively. Given the simplicity of the model, this is quite encouraging. In addition, we performed a full kinetic analysis on the basis of the calculated energies, and found it to be completely consistent with the simple (transparent) analysis, with respect to the difference in apparent activation energy and rate for the two Cs coverages, see the methods section and Fig. S12 (ESI†).
Finally, we address the question of the reaction orders. The model assumes N2 dissociation to be rate-limiting in all cases giving an order in N2 of ∼ 1. The order in H2 should be ∼−0.5 for the high Cs coverage model since only one H atom with negative adsorption free energy needs to be removed prior to dissociation. The H2 order in the model for the low coverage case is ∼−1 where two H atoms must be removed. The observation of a large change in measured activation energy accompanied by a relatively small change in rate is an example of the so-called compensation effect – the change in the apparent activation energy is accompanied by an almost compensating change in the apparent pre-exponential factor. The reason is quite simple. As described above, the high Cs coverage case corresponding to ex situ promotion has one less adsorbed H atom to remove to allow N2 dissociation than the low Cs coverage case. The binding energy of this adsorbed H is ∼0.4 eV – this is the main contribution to the higher activation energy for the low Cs coverage surface (the rest of the difference being given by a slightly different adsorption energy of the other H atom in the active site and the difference in the N2 transition state energy of the two samples). This is almost canceled by the entropy contribution to the adsorption free energy of the adsorbed H atom of −TΔS ∼ 0.3 eV at 340 °C, the majority of which is associated with the loss of gas phase translational entropy of hydrogen upon adsorption. The entropy contribution to the apparent activation free energy will show up as a change in the pre-factor (eΔS/kB) in an Arrhenius expression. A similar model has been used previously to explain the compensation effect observed in ammonia synthesis when varying the catalyst and more generally in heterogeneous catalysis.30
Concluding remarks
In conclusion, we provide insight into the promotional effect of Cs and show that in situ dosing of pure metallic Cs is substantially better for ammonia synthesis than the conventionally prepared Ru catalysts ex situ promoted with Cs. The performance of in situ promoted catalysts reported here is in the same order as the most recent state-of-the-art and highly active materials reported in the literature presented in Fig. S1 and extended data of Table S1 (ESI†). Although the highly active in situ promoted catalyst could not reach the ideal mild conditions criteria (i.e., < 200 °C), one of the main advantages of this work is providing insight into the promotional effect which opens a route to the discovery of highly active catalysts for ammonia synthesis under mild conditions that can be used in a sustainable HB process coupled with green-H2 facilities in decentralized plants. Moreover, the in situ promoted catalyst shows that there is a huge potential for enhancing the performance of known highly active ammonia catalysts via employing the in situ promotion technique. This technique and its potential could help the ammonia catalyst research field by moving away from using rare-elements and complex precursor compounds to synthesise new catalysts.Methods
Catalyst preparation
Ru/C and Ru/C_exCs catalysts were prepared by the incipient wetness impregnation method. High surface area carbon (PBX-51) was used as oxygen-free support. For Ru/C samples, ruthenium(III) nitrosyl nitrate solution in dilute nitric acid (1.5 wt%, Sigma-Aldrich) was used as the Ru precursor. The Ru solution was further diluted with Milli-Q water to reach the desired volume of the precursor solution. The solution then was added dropwise to the carbon powder and stirred continuously. The slurry was dried in an Ar stream at 200 °C. The Ru/C_exCs catalysts were prepared by impregnation of Ru/C samples with aqueous cesium carbonate (99.995% trace metal basis, Sigma-Aldrich). The Ru/C_exCs slurries were dried in Ar flow at 400 °C. All catalysts were reduced in a reactor at 400 °C and H2 flow prior to each experiment.Activity measurements and the setup
Catalyst activity measurements were performed in a fixed bed tubular reactor. Typically, 100 mg of sized catalyst particles (150–300 μm) were loaded in a reactor. To avoid the presence of any oxygen containing compounds inside the reactor, the catalyst particles were supported by a layer of stainless steel fine wool on each side of the bed. The tests were performed in the temperature range of 260–400 °C, pressure range of 2–10 bar and total flow rates of 40–120 ml min−1 (H2/N2 = 3). Ultra high purity H2, N2 and Ar gases (99.9999%, Air Liquide) were used for the experiments. The gas mixtures were further purified to be oxygen and moisture free by a series of oxygen (heated iron-based) and moisture (cold molecular sieve) traps prior to entering the reactor. Feed and product streams were analyzed by two mass spectrometers: a quadrupole (QMS) and Time-of-Flight (ToFMS). The QMS was used for continuous monitoring of selected masses during the experiment while the high resolution (m/Δm > 2000) and calibrated ToFMS were used for quantitative purposes. The high resolution of ToFMS is especially important for distinguishing OH and NH3 at mass 17 (Fig. S13, ESI†). By using ToFMS we could always make sure that the oxygen and water content is always below the detection limit (sub-ppm levels) during the experiments. Due to the utilization of a custom-made sniffer system (consisting of disks with micrometer size orifices and modified connections), the system's response time is on the scale of a few seconds. The whole setup is also assembled by using UHV compatible copper-gasket sealed fittings to ensure high purity and maintain O-free experiments.Gas cleaning with a Cs-based trap
For further cleaning of the inlet gas mixture from O-containing species, a Cs-based trap was used in some experiments. The trap was a U-tube with two valves. The Cs-based trap contained carbon powder and metallic Cs, which were loaded inside an Ar-glovebox. The trap was installed in the feed stream before the reactor with the possibility of being bypassed. The trap was kept at 250 °C and it was made sure that no Cs vapor can escape the trap and enter the reactor. In the first phase of this experiment, the feed gas was passing through the Cs-based trap and then entered the reactor. In the second phase, the Cs-based trap was bypassed and Cs vapor was dosed into the reactor on the Ru/C catalyst bed.Kinetic measurements
Activation energy and reaction order measurements were performed under conditions where the produced NH3 concentration is far from equilibrium. The reaction order was measured following the experimental method as explained in the literature.23Computational methods
DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP),31,32 employing the generalized gradient approximation (GGA)33 with the Revised PBE functional34 to account for the electron exchange and correlations. Valence electrons were described with plane-waves with an energy cutoff of 450 eV, whereas core electrons were represented by projector augmented-wave (PAW) pseudopotentials.35For bulk and all surface calculations, Monkhorst–Pack k-point grids36 of 12 × 12 × 12 and 2 × 2 × 1 were used. A lattice constant optimization was performed on the HCP bulk structure of Ru. The (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 5) surface was generated using 4-layer 4 × 6 cells to represent the stepped surface on Ru based on our previous models, as shown in Fig. S8 (ESI†).20 The resulting unit cell had six by four surface atoms and included two steps per unit cell. Here we choose the B-type step in the following calculations since the B5-site on the B-type step was designated to be the active site for ammonia synthesis,26 while no B5 site was present on the A-type step. At the same time, the binding energy of Cs on other Ru step surface, such as removing a few rows from the first layer of the Ru(0001) surface to build a step surface as shown in a previous study,37 was calculated to be the same as that on the Ru(1015) surfaces. A vacuum of 15 Å separated the slabs in the z-direction, and dipole correction was applied. The bottom two layers of each slab were constrained to their original positions, while the upper layers were allowed to relax. All slabs and bulk were relaxed until all forces converged to less than 0.05 eV.
5) surface was generated using 4-layer 4 × 6 cells to represent the stepped surface on Ru based on our previous models, as shown in Fig. S8 (ESI†).20 The resulting unit cell had six by four surface atoms and included two steps per unit cell. Here we choose the B-type step in the following calculations since the B5-site on the B-type step was designated to be the active site for ammonia synthesis,26 while no B5 site was present on the A-type step. At the same time, the binding energy of Cs on other Ru step surface, such as removing a few rows from the first layer of the Ru(0001) surface to build a step surface as shown in a previous study,37 was calculated to be the same as that on the Ru(1015) surfaces. A vacuum of 15 Å separated the slabs in the z-direction, and dipole correction was applied. The bottom two layers of each slab were constrained to their original positions, while the upper layers were allowed to relax. All slabs and bulk were relaxed until all forces converged to less than 0.05 eV.
Transition states (TS) of the reactions were located by the climbing image nudged elastic band (Cl-NEB) method38 with at least five images generated between the initial and final states. The TS structures obtained by this method were further refined until the forces on atomic centers reach 0.05 eV Å−1. Zero-point energies and entropic contributions were calculated within the harmonic approximation. Free energy corrections of gas-phase species were obtained using the Shomate equation.39
The formation energy (ΔEf) of the adsorbed species (Cs*/O*/OH*/) on the metal surface was calculated by
| ΔE(species) = E(slab + Cs + HxOy) − E(slab) − E(Cs) − xEH − yEO | (3) |
The formation energy of bulk (CsHxOy) per Cs atom is
| Cs + H2 + H2O → (CsHxOy) | (4) |
| ΔE(bulk) = E(CsHxOy) − E(Cs) − xEH − yEO | (5) |
The adsorption energy of adsorbates (H*, NH*, NH2*, NH3*) is calculated by
| ΔE(adsorbates) = E(slab + adsorbates) − E(slab) − xEH − yEN | (6) |
The energy barrier of the N–N transition state is calculated by
| ΔE(TS) = E(slab + TS) − E(slab) − EN2 | (7) |
The free energy (ΔG) is given by
| ΔG = ΔE + ΔEzpe + ΔH − TΔS | (8) |
Microkinetic model
A steady state kinetic model was solved using the free energy corrections described in the Methods section, and the CatMap steady state solver.40 The reaction mechanism for ammonia synthesis is shown in eqn (9)–(15).| ‘N2_g + 2* → N2*’, | (9) |
| ‘N2* ↔ N–N* + * → 2N*’, | (10) |
| ‘2*_h + H2_g → 2H_h’, | (11) |
| ‘N* + H_h ↔ N–H* + *_h → NH* + *_h’, | (12) |
| ‘NH* + H_h ↔ NH–H* + *_h → NH2* + *_h’, | (13) |
| ‘NH2* + H_h ↔ NH2–H* + *_h → NH3* + *_h’, | (14) |
| ‘NH3* → NH3_g + *’, | (15) |
The TOF calculation is shown simply in the following steps.
| γi = 1 (i = 2–6) | (16) |
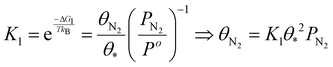 | (17) |
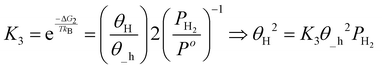 | (18) |
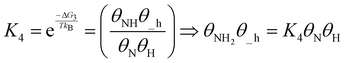 | (19) |
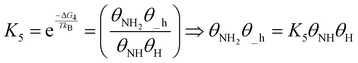 | (20) |
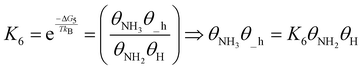 | (21) |
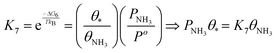 | (22) |
| θ* + θN2 + θN + θNH + θNH2 + θNH3 = 1 | (23) |
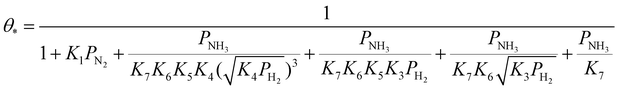 | (24) |
| Rate(TOF) = k2PN2θ*2(1 − γ) | (25) |
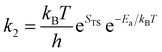 | (26) |
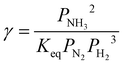 | (27) |
| Keq = K1K2K33K42K52K62K72 | (28) |
Transmission electron microscopy (TEM)
After catalytic tests, the reactor was sealed with two valves (one on each side of the reactor) from the atmosphere and transferred into an argon glovebox. The samples were unloaded from the reactor in the glovebox. Tested samples were loaded on a 300-mesh lacey carbon Cu TEM-grid (AGS166-3H, Agar Scientific) and mounted on a Fischione 2070 vacuum transfer tomography holder inside the glovebox. The transfer from the glovebox to the transmission electron microscope was done in less than 10 minutes. Size-distributions were measured on samples by drawing the outline of each observed nanoparticle, measuring the area and calculating a corresponding circular diameter.Powder X-ray diffraction (XRD)
The tested catalysts were transferred outside of the glovebox in ambient air to prepare the XRD samples using zero background sample holders. The XRD patterns were collected using an Empyrean (Malvern PANalytical) diffractometer, operating at 45 kV and 40 mA using a Cu Kα (Kα = 1.540598 Å) radiation source. The diffracted beam was filtered through a monochromator.Inductively coupled plasma mass spectrometry (ICP-MS)
An iCAP-QC (Thermo Fisher Scientific) ICP-MS instrument was used to determine the chemical composition of the samples. Typically around 5–10 mg of each sample were dissolved in aqua regia and aged for 48 h. The sample solutions were further sequentially diluted (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and 1
10 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) in 0.67% HNO3 (Suprapur, Merck). External calibration for quantitative analyses was done using four different concentrations of standard reference samples. Internal calibration was also done for cross-validation of the quantitative analyses.
100) in 0.67% HNO3 (Suprapur, Merck). External calibration for quantitative analyses was done using four different concentrations of standard reference samples. Internal calibration was also done for cross-validation of the quantitative analyses.
X-ray photoelectron spectroscopy (XPS)
Powder samples were prepared either in ambient air or in an argon glovebox for XPS measurements. The powder samples were first crushed into fine particles and then pressed into small disks (diameter ≈ 7 mm and thickness ≈ 0.5 mm). The samples that were prepared in ambient air were heated at 120 °C for 4 h and then were immediately transferred to an Ar glovebox to be loaded into a custom-made transfer arm. The samples that were prepared in the glovebox were directly loaded into the transfer arm. The transfer arm is a custom made system for transferring samples from the Ar glovebox to the UHV chamber without any exposure to an ambient air atmosphere. XPS measurements were performed using a ThermoScientific Thetaprobe instrument equipped with an Al Kα X-ray source. An Ar sputtering gun was also used to sputter the samples (1 kV, 1 μA) for 300 s. XPS analyses were performed after each sputtering.Data availability
The datasets generated during and/or analysed during the current study are available in DOI: https://doi.org/10.11583/DTU.16708681.Author contributions
JKN, JK, and IC conceived the project. VS did the experiments, data collection and analysis. MKG helped to do experiments. AC, VJB and ZW performed the DFT calculations and data analysis. VS and AC wrote the manuscript. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from Villum Fonden V-SUSTAIN (grant no. 9455) (VS, AC, VJB, MKG, CDD, ZW, JK, IC, and JKN). VS would like to thank Mattia Saccoccio for his contribution in developing the transfer system from the glovebox to the XPS UHV chamber. VS would like to thank Jens-Peter Baernholdt Haraldsted for his help with ICP-MS sample preparation.References
- G. Ertl, Angew. Chem., Int. Ed., 2008, 47, 3524–3535 CrossRef CAS PubMed.
- M. Appl, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011 Search PubMed.
- R. F. Service, Science, 2018, 361, 120–123 CrossRef CAS PubMed.
- C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111, 140–144 CrossRef CAS.
- F. Haber and R. Le Rossignol, Z. Elektrochem. Angew. Phys. Chem., 1913, 19, 53–72 CAS.
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, Nat. Geosci., 2008, 1, 636–639 CrossRef CAS.
- R. Schlögl, Angew. Chem., Int. Ed., 2003, 42, 2004–2008 CrossRef PubMed.
- I. Rafiqul, C. Weber, B. Lehmann and A. Voss, Energy, 2005, 30, 2487–2504 CrossRef CAS.
- S. Z. Andersen, M. J. Statt, V. J. Bukas, S. G. Shapel, J. B. Pedersen, K. Krempl, M. Saccoccio, D. Chakraborty, J. Kibsgaard, P. C. K. Vesborg, J. Nørskov and I. Chorkendorff, Energy Environ. Sci., 2020, 13, 4291–4300 RSC.
- L. E. Apodaca, Nitrogen (Fixed) – Ammonia, Mineral Commodity Summaries, U.S. Geological Survey, 2020 Search PubMed.
- D. E. Garrett, Chemical Engineering Economics, Springer Netherlands, 1989 Search PubMed.
- A. J. Medford and M. C. Hatzell, ACS Catal., 2017, 7, 2624–2643 CrossRef CAS.
- R. Michalsky, A. M. Avram, B. A. Peterson, P. H. Pfromm and A. A. Peterson, Chem. Sci., 2015, 6, 3965–3974 RSC.
- P. Peng, Y. Li, Y. Cheng, S. Deng, P. Chen and R. Ruan, Plasma Chem. Plasma Process., 2016, 36, 1201–1210 CrossRef CAS.
- M. F. Lagadec and A. Grimaud, Nat. Mater., 2020, 19, 1140–1150 CrossRef CAS PubMed.
- S. T. Wismann, J. S. Engbæk, S. B. Vendelbo, F. B. Bendixen, W. L. Eriksen, K. Aasberg-Petersen, C. Frandsen, I. Chorkendorff and P. M. Mortensen, Science, 2019, 364, 756–759 CrossRef CAS PubMed.
- Research needs towards sustainable production of fuels and chemicals, ed. J. K. Nørskov, A. Latimer and C. F. Dickens, 2019 Search PubMed.
- A. Ozaki, K. Aika and H. Hori, Bull. Chem. Soc. Jpn., 1971, 44, 3216 CrossRef CAS.
- K. Aika, H. Hori and A. Ozaki, J. Catal., 1972, 27, 424–431 CrossRef CAS.
- B. A. Rohr, A. R. Singh and J. K. Nørskov, J. Catal., 2019, 372, 33–38 CrossRef CAS.
- K.-I. Aika, Catal. Today, 2017, 286, 14–20 CrossRef CAS.
- K. Aika, T. Takano and S. Murata, J. Catal., 1992, 136, 126–140 CrossRef CAS.
- S. Hagen, R. Barfod, R. Fehrmann, C. J. H. Jacobsen, H. T. Teunissen and I. Chorkendorff, J. Catal., 2003, 214, 327–335 CrossRef CAS.
- M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S. W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940 CrossRef CAS PubMed.
- M. Johansson, E. Skúlason, G. Nielsen, S. Murphy, R. M. Nielsen and I. Chorkendorff, Surf. Sci., 2010, 604, 718–729 CrossRef CAS.
- S. Dahl, A. Logadottir, R. C. Egeberg, J. H. Larsen, I. Chorkendorff, E. Törnqvist and J. K. NØrskov, Phys. Rev. Lett., 1999, 83, 1814–1817 CrossRef.
- Y. Kim, Y. Zhu, S. Wendt, A. Seitsonen, S. Schwegmann, H. Bludau, H. Over and A. Morgante, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8455–8461 CrossRef CAS.
- N. D. Lang, S. Holloway and J. K. Nørskov, Surf. Sci., 1985, 150, 24–38 CrossRef CAS.
- P. Stoltze and J. K. Nørskov, J. Catal., 1988, 110, 1–10 CrossRef CAS.
- T. Bligaard, K. Honkala, A. Logadottir, J. K. Nørskov, S. Dahl and C. J. H. Jacobsen, J. Phys. Chem. B, 2003, 107, 9325–9331 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 32–34 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. Monkhorst and J. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. Kent, R. E. Green, J. Madden, a a Dadda, P. Cammarano, M. W. Pienkowski, J. D. Wilson, R. B. Bradbury, M. F. Heath, E. Signals, E. Assess-, E. Communities, J. a Mcneely, S. J. Scherr, J. G. Robinson, P. F. Donald, D. Southgate, K. Brown, P. E. Waggoner, D. T. Avery, E. B. Barbier, J. C. Burgess, A. Angelsen, D. Kaimowitz, A. Intensification, E. Development, C. B. Barrett, D. R. Lee, N. E. Borlaug, I. M. Goklany, M. W. Sprague and S. Development, Science, 2005, 4963, 2003–2006 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- C. H. Shomate, J. Phys. Chem., 1954, 58, 368–372 CrossRef CAS.
- A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee00591c |
| ‡ These authors have contributed equally. |
| § Present address: Fritz-Haber-Institut der Max-Planck-Gesellschaft, 14195 Berlin, Germany. |
| This journal is © The Royal Society of Chemistry 2022 |