Unusual stoichiometry, band structure and band filling in conducting enantiopure radical cation salts of TM-BEDT-TTF showing helical packing of the donors†‡
Flavia
Pop
a,
Cécile
Mézière
a,
Magali
Allain
a,
Pascale
Auban-Senzier
b,
Naoya
Tajima
c,
Daichi
Hirobe
def,
Hiroshi M.
Yamamoto
de,
Enric
Canadell
 *g and
Narcis
Avarvari
*g and
Narcis
Avarvari
 *a
*a
aUniv. Angers, CNRS, MOLTECH-Anjou, SFR MATRIX, F-49000 Angers, France. E-mail: narcis.avarvari@univ-angers.fr
bLaboratoire de Physique des Solides, Université Paris-Saclay CNRS UMR 8502, Bât. 510, 91405 Orsay, France
cDepartment of Physics, Toho University, Funabashi, Chiba 274-8510, Japan
dInstitute for Molecular Science, Myodaiji, Okazaki 444-8585, Japan
eSOKENDAI (Graduate University for Advanced Studies), Myodaiji, Okazaki 444-8585, Japan
fPRESTO, Japan Science and Technology Agency (JST), Kawaguchi 332-0012, Japan
gInstitut de Ciència de Materials de Barcelona, ICMAB-CSIC, Campus de la UAB, E-08193 Bellaterra, Spain. E-mail: canadell@icmab.es
First published on 16th April 2021
Abstract
Electrocrystallization of tetramethyl-bis(ethylenedithio)-tetrathiafulvalene (TM-BEDT-TTF) (1) as pure (S,S,S,S) and (R,R,R,R) enantiomers in the presence of (n-Bu4N)2(Mo6O19) and chloroform or bromoform afforded a series of four isostructural enantiopure radical cation salts [(S/R)-1]9(Mo6O19)5·(CHX3)2 (X = Cl, Br) crystallizing in the trigonal non-centrosymmetric space group R32. In the formula unit there are six donors of type A and three donors of type B showing, respectively, (ax, ax, eq, eq) and all-ax conformations (ax = axial, eq = equatorial) of the methyl substituents. The donors form a hexagonal network in the ab plane with a helical twist between them leading to lateral orbital overlap interactions. Electrocrystallization of the racemic donor provided the compound [(rac)-1]2(Mo6O19) which crystallized in the monoclinic system P21/n. Single crystal resistivity measurements show semiconducting behaviour of the enantiopure materials with a relatively high room temperature conductivity of 0.8–1.2 S cm−1, but rather insensitive to applied pressures of up to 2.3 GPa. Analysis of the electronic structure of the conducting solids through extended Hückel tight-binding band structure calculations indicates a Mott insulator behaviour explaining the semiconducting character and suggests that these compounds are valuable candidates for Dirac cone materials. Further insight into the conducting properties is provided by preliminary field effect transistor measurements.
1. Introduction
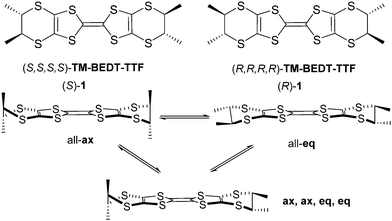
(S,S,S,S)-Tetramethyl-bis(ethylenedithio)-tetrathiafulvalene (TM-BEDT-TTF) was the first reported enantiopure tetrathiafulvalene (TTF) derivative back in 1986 by Wallis and Dunitz,1 while the (R,R,R,R) enantiomer was described later on by Sugawara and Kawada ((S)-1 and (R)-1 in Scheme 1).2 The initial interest on chiral TTF precursors was arisen by the possibility to access chiral conductors which were intuitively thought to show emergent properties related to the application of external electric and magnetic fields.1 It was only about fifteen years later that Rikken et al. reported first experimental evidences on the synergy between chirality, conductivity and magnetic field through the electrical magnetochiral anisotropy (eMChA) effect observed as non-reciprocal electron transport in metallic helical bismuth wires3 and chiral single-walled nanotubes,4 and, much more recently, in elemental tellurium.5 Note that in these compounds the chirality is extensively expressed at the material level. Intensive research on chiral TTF materials6,7 led us to the first observation of eMChA in chiral bulk crystalline molecular conductors, namely the (R,R) and (S,S) enantiomeric mixed valence salts of the dimethyl-ethylenedithio-tetrathiafulvalene (DM-EDT-TTF) donor, (DM-EDT-TTF)2ClO4.8 However, besides the direct synergy between chirality and electron transport, expressed as the eMChA effect, differences of conductivity in chiral TTF based radical cation salts can also occur as a consequence of different packing between enantiopure and racemic forms,9,10 or structural disorder in the latter.11,12 Another important aspect of this field of research is the quest for chiral molecular superconductors which are still to be reported. Indeed, while occurrence of a superconducting transition was claimed for the enantiopure phase κ-[(S,S)-DM-BEDT-TTF]2ClO4,13 based on the dimethyl-BEDT-TTF (DM-BEDT-TTF) donor, our recent investigations on both enantiomers of this chiral material ruled out this initial assumption.14 Whereas several methyl substituted chiral BEDT-TTF and EDT-TTF derivatives, such as DM-BEDT-TTF,13–16 DM-EDT-TTF,8–10,17 DM-EDT-TTF diamides,18 or Me-EDT-TTF,19,20 provided interesting conducting materials, TM-BEDT-TTF still remains the flagship donor of this family of chiral precursors when considering the number of reported radical cation salts based on the enantiomers of TM-BEDT-TTF and various anions of different shapes, charge and magnetic properties. Indeed, several crystalline salts formulated as (TM-BEDT-TTF)2XF6 (X = P, As, Sb),21 (TM-BEDT-TTF)I3,22 (TM-BEDT-TTF)3(XO4)2 (X = Cl, Re),23 (TM-BEDT-TTF)x[MnCr(ox)3] (ox = oxalate),24 (TM-BEDT-TTF)[(rac)-TRISPHAT],25 (TM-BEDT-TTF)3(PPh4)[KFe(Cl2An)3] (Cl2An = dichloroanilate),26 or (TM-BEDT-TTF)2(Re6S6Cl8),27 obtained by electrocrystallization and showing semiconducting or metallic behaviour, have been described over the years since the initial report on TM-BEDT-TTF.1 However, in spite of the presence of stereogenic centres on the donor and, thus, crystallization in non-centrosymmetric space groups, expression of chirality at the crystal level, such as helical packing, was never achieved within TM-BEDT-TTF salts contrary to DM-EDT-TTF in (DM-EDT-TTF)2ClO4, for which the two enantiomeric compounds crystallized in the enantiomorphic hexagonal space groups P6222 and P6422, with, however, the helical axis perpendicular to the stacking direction of the donors.8 Extensive expression of chirality at the material level thanks to chirality transfer from the molecular level may enhance the eMChA effect, although no microscopic theory for eMChA in bulk chiral conductors has been developed so far. Another peculiar structural aspect in the TM-BEDT-TTF based salts is related to the conformational equilibrium between axial (ax) and equatorial (eq) conformers of TM-BEDT-TTF (Scheme 1), highly impacting the packing of the donors and, consequently, the intermolecular interactions.While in most of the salts described to date the donors show an all-eq conformation, favouring intermolecular face-to-face overlap, the all-ax27 and mixed (ax, ax, eq, eq)26 conformations have been occasionally observed as well. In our ongoing search for chiral TTF based crystalline conductors with extensive expression of chirality in the packing we have focused on the association of TM-BEDT-TTF with the Lindqvist type dianion [Mo6O19]2−. The latter was successfully used as counter-ion in radical cation salts with TTF,28 BEDT-TTF,29 or other TTF functional precursors,30–32 but never with chiral TTF precursors. We hypothesized that its propensity to crystallize on special positions in the lattice thanks to the presence of threefold symmetry axes, combined with the inherent non-centrosymmetry of the donor might favour the occurrence of original structures not encountered with the more ‘classical” anions used in TTF materials. We describe herein conducting enantiopure TM-BEDT-TTF based radical cation salts with the [Mo6O19]2− anion, showing unprecedented stoichiometry and helical packing of the donors. Extended Hückel tight-binding calculations indicate very unusual band structure and band filling for these chiral materials.
2. Results and discussion
2.1 Synthesis and structure of the radical cation salts
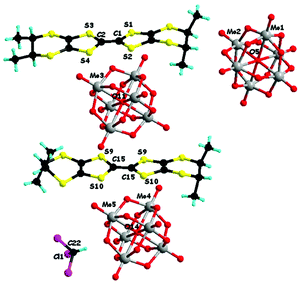
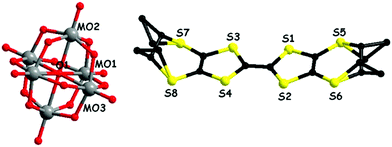
In a first set of experiments, enantiopure (S)-1 and (R)-1 have been electrocrystallized in the presence of (TBA)2(Mo6O19) (TBA = tetra-n-butyl-ammonium) in a mixture of solvents chloroform/acetonitrile 1/1, affording millimetre size black hexagonal plate-like crystals on the platinum electrodes (Fig. S1, ESI‡). Single crystal X-ray diffraction analysis revealed that the two enantiomeric salts crystallized in the trigonal non-centrosymmetric space group R32. They are isostructural and formulated as [(S)-1]9(Mo6O19)5·(CHCl3)8.67 and [(R)-1]9(Mo6O19)5·(CHCl3)10, respectively. This very peculiar stoichiometry results from the composition of the asymmetric unit consisting in one independent TTF molecule in general position (S1–S4, molecule A, ESI‡), half of another TTF molecule (S9 and S10, molecule B, ESI‡) which generates the corresponding half through a C2 axis oriented in the mean plane of the molecule and perpendicular to the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, two independent one third (Mo1–Mo2 and Mo4–Mo5) and one independent one sixth (Mo3) anions, with the central μ6 oxygen atoms O5, O14 and O11 located respectively on special positions of multiplicity 3, 3 and 6 (Fig. 1 for [(S)-1]9(Mo6O19)5 and Fig. S2 (ESI‡) for [(R)-1]9(Mo6O19)5). Finally, one third of CHCl3 solvent molecule, with the C atom on a threefold special position, completes the asymmetric unit, thus providing two molecules of CHCl3 per formula unit [1]9(Mo6O19)5, while the remaining number of highly disordered crystallization solvent molecules, i.e. 6.67 for (S) and 8 for (R) per formula unit, was attributed through the SQUEEZE procedure. From now on, for clarity reasons, only the two located solvent molecules will be specified in the formula unit.
C bond, two independent one third (Mo1–Mo2 and Mo4–Mo5) and one independent one sixth (Mo3) anions, with the central μ6 oxygen atoms O5, O14 and O11 located respectively on special positions of multiplicity 3, 3 and 6 (Fig. 1 for [(S)-1]9(Mo6O19)5 and Fig. S2 (ESI‡) for [(R)-1]9(Mo6O19)5). Finally, one third of CHCl3 solvent molecule, with the C atom on a threefold special position, completes the asymmetric unit, thus providing two molecules of CHCl3 per formula unit [1]9(Mo6O19)5, while the remaining number of highly disordered crystallization solvent molecules, i.e. 6.67 for (S) and 8 for (R) per formula unit, was attributed through the SQUEEZE procedure. From now on, for clarity reasons, only the two located solvent molecules will be specified in the formula unit.
In the course of our investigations on the salts [1]9(Mo6O19)5·(CHCl3)2 it appeared that the crystallinity of the materials was slowly deteriorating at room temperature very likely because of the loss of disordered solvent, thus making delicate the resistivity measurements (vide infra). We have therefore replaced chloroform by bromoform, much less volatile, in a second series of electrocrystallization experiments, which provided, as hypothesized, the two enantiomeric salts [(S)-1]9(Mo6O19)5·(CHBr3)8.67 and [(R)-1]9(Mo6O19)5·(CHBr3)8.67 as hexagonal crystals (Fig. S3, ESI‡), showing the same composition of the unit cell as their CHCl3 counterparts (Fig. S4 and S5, ESI‡). This choice proved to be judicious since it allowed the preparation of more robust isostructural crystalline materials, also demonstrating that the C3 symmetry of the solvent is crucial in order to favour crystallization in the R32 space group and hence occurrence of this unusual donor/anion stoichiometry.
Several peculiar structural features can be disclosed for these salts. First, the C3 symmetry of the anion and solvent is translated at the crystal level, as they are located on threefold symmetry rotation axes, favouring crystallization in a trigonal space group, which has to be necessarily non-centrosymmetric because of the donor. Since one donor A and half a donor B are independent, in the formula unit there are six equivalent donors A and three equivalent donors B for five dianions [Mo6O19]2−, leading to an average charge per donor of +1.11, which is very uncommon. In fact, the analysis of the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds and average internal C–S bonds distances (Table 1), which are the most sensitive to the oxidation state of TTF, would tend to suggest that donors A bear an approximate charge +1, while donors B are over-oxidized, although the esd values of the bond lengths are too high to allow an accurate estimation of the charge on each donor. However, comparison with the corresponding values of the racemic salt [(rac)-1]2(Mo6O19) (vide infra), showing a much simpler structure with the donors in oxidation state +1, would indeed indicate an oxidation state +1 for donors A in the four isostructural enantiopure compounds. Considering that in the formula unit there are six donors A and three donors B bearing a total charge of +10, it results that each donor B should have a charge +1.33.
C bonds and average internal C–S bonds distances (Table 1), which are the most sensitive to the oxidation state of TTF, would tend to suggest that donors A bear an approximate charge +1, while donors B are over-oxidized, although the esd values of the bond lengths are too high to allow an accurate estimation of the charge on each donor. However, comparison with the corresponding values of the racemic salt [(rac)-1]2(Mo6O19) (vide infra), showing a much simpler structure with the donors in oxidation state +1, would indeed indicate an oxidation state +1 for donors A in the four isostructural enantiopure compounds. Considering that in the formula unit there are six donors A and three donors B bearing a total charge of +10, it results that each donor B should have a charge +1.33.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths (Å) and average internal C–S bonds (Å) of [1]9(Mo6O19)5 for donors A and B and of [(rac)-1]2(Mo6O19)
C bond lengths (Å) and average internal C–S bonds (Å) of [1]9(Mo6O19)5 for donors A and B and of [(rac)-1]2(Mo6O19)
| [(S)-1]9(Mo6O19)5·CHCl3 | [(R)-1]9(Mo6O19)5·CHCl3 | [(S)-1]9(Mo6O19)5·CHBr3 | [(R)-1]9(Mo6O19)5·CHBr3 | [(rac)-1]2(Mo6O19) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–S | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–S | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–S | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–S | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
C–S | |
| A | 1.36(3) | 1.715 | 1.402(19) | 1.71 | 1.37(2) | 1.715 | 1.380(19) | 1.72 | 1.381(6) | 1.724 |
| B | 1.41(3) | 1.68 | 1.43(2) | 1.67 | 1.42(3) | 1.682 | 1.39(3) | 1.69 | ||
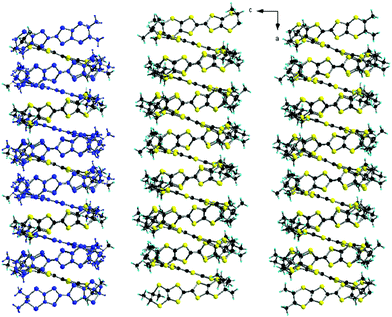
Interestingly, the two donors A and B show, respectively, the much less frequent (ax, ax, eq, eq) and all-ax conformations. The former was encountered only in the compound (TM-BEDT-TTF)3(PPh4)[KFe(Cl2An)3],26 coexisting with the predominant all-eq conformation, in a charge transfer complex with TCNQ21 and in a cycloadduct with tetrachlorocatecholate.33 Clearly, location of the methyl substituents in the axial position does not favour establishment of the usual face-to-face stacking of donors, but mostly interactions of the lateral type. Moreover, the presence of threefold rotation axes generates in the ab plane an unprecedented helical packing of the donors, characterized by rather short lateral intermolecular S⋯S distances (Fig. 2).
 | ||
| Fig. 2 Crystal packing of [(S)-1]9(Mo6O19)5·(CHCl3)2 in the ab plane (donors A are highlighted in blue). CHCl3 molecules have been omitted. | ||
There is no classical organic–inorganic segregation in the packing, but formation of mixed layers of donors surrounding the polyoxometallate anions Mo3 and Mo4–Mo5, alternating along the c direction with layers of polyoxometallates Mo1–Mo2 and crystallization solvent. Consequently, there is no donor⋯donor interaction along c (Fig. 3).
Since the chiral information provided by the donors is extensively expressed in the crystal packing of the enantiopure phases discussed thus far, we have further proceeded to the electrocrystallization of a racemic mixture of TM-BEDT-TTF 1 in the same conditions. The resulting crystalline radical cation salt, formulated as [(rac)-1]2(Mo6O19), shows a striking different structure when compared to the enantiopure counterparts. The compound crystallized in the monoclinic centrosymmetric space group P21/n with one independent donor and half anion in the unit cell (Fig. 4).
 | ||
| Fig. 4 Detail of the crystal structure of [(rac)-1]2(Mo6O19). Both ethylene bridges of the donor are disordered. Hydrogen atoms have been omitted. | ||
Considering that both ethylene bridges are disordered, the two enantiomers are equally statistically present on the same crystallographic site. In spite of this disorder and since this time there is no inclusion of ill-defined crystallization solvent, the quality of the structure is very accurate and allows correlation between the +1 oxidation state of the donor and the values of the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and internal C–S bond lengths (Table 1). In the packing, the donors arrange in face-to-face centrosymmetric dimers with very short intermolecular S⋯S distances of 3.35 Å (S2⋯S3) and 3.44 Å (S1⋯S4) (Fig. S6, ESI‡). This strong dimerization, facilitated by the all-eq conformation adopted by the methyl substituents, should confer an insulating character to the material (vide infra).
C and internal C–S bond lengths (Table 1). In the packing, the donors arrange in face-to-face centrosymmetric dimers with very short intermolecular S⋯S distances of 3.35 Å (S2⋯S3) and 3.44 Å (S1⋯S4) (Fig. S6, ESI‡). This strong dimerization, facilitated by the all-eq conformation adopted by the methyl substituents, should confer an insulating character to the material (vide infra).
2.2 Single crystal conductivity measurements and band structure calculations
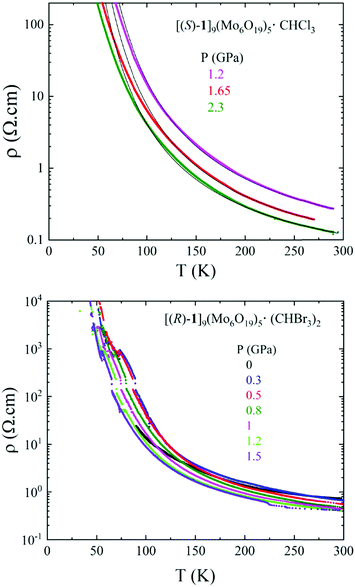
In view of their similar structures, single crystal resistivity of one enantiomeric salt of each solvate, i.e. (S) for CHCl3 and (R) for CHBr3, for which the crystal size was appropriate for four point contact measurements, was investigated.Both compounds show semiconducting behaviour, with room temperature conductivity values of 0.8 S cm−1 for [(S)-1]9(Mo6O19)5·(CHCl3)2 and 1.2 S cm−1 for [(R)-1]9(Mo6O19)5·(CHBr3)2 (Fig. 5 and Fig. S7, ESI‡). As anticipated, the CHBr3 solvate was more robust and, therefore, allowed full temperature range measurement at ambient pressure, while accurate curves were obtained for the CHCl3 solvate only under pressure. For pressures as high as 2.3 GPa for the latter and 1.5 GPa for the former the materials remain semiconductors, their resistivity being in fact, rather surprisingly, quite insensitive to the application of pressure (Fig. S8, ESI‡). This behaviour is very likely due to the stiffness of the structures caused by the lack of organic–inorganic segregation and classical face-to-face stacking of the donors.
Let us now analyse the correlation between these peculiar solid state structures and conducting properties from a band structure perspective. The donor layers of [(S)-1]9(Mo6O19)5·(CHCl3)2 contain two different donors (A and B in Fig. 6) and four different intermolecular interactions (I to IV in Fig. 6).
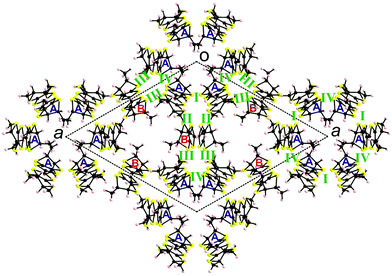 | ||
| Fig. 6 Donor layer of the [(S)-1]9(Mo6O19)5·(CHCl3)2 salt where the different donors and intermolecular interactions are labeled. | ||
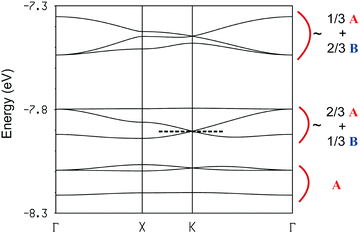
The hexagonal unit cell contains six donors of type A and three donors of type B. Since the average charge deduced from the stoichiometric formula is +1.11, i.e. ten holes per unit cell but nine donors, it is challenging to understand the correlation between the transport properties and the charge distribution in the solid. With this goal in mind we have studied the band structure of the system which is reported in Fig. 7.
The band structure contains nine bands almost exclusively based on the HOMO (highest occupied molecular orbital) of the TM-BEDT-TTF donor. These bands can be arranged in three different groups according to their character. The set of three lowest energy bands are mostly made of the HOMO of donors A. Then, there is another set of three bands with character of both types of donors, A and B, although the HOMO of donors A is still dominant. Finally at higher energy there is a third set of three bands with the opposite character. Since the stoichiometry dictates that the HOMO bands must have ten holes, the equivalent of four bands must be filled assuming double occupation of the levels. This would put the Fermi level at the K point of the Brillouin zone. However, since two bands are degenerate at this point because of the symmetry of the lattice, this situation would correspond to a metallic behaviour, something which is in contradiction with the activated character of the conductivity. We thus must conclude that the present salt is a Mott localized system containing two localized electrons per unit cell. Such localization is likely because the dispersion of the partially filled bands is quite small. The electronic structures of the [(R)-1]9(Mo6O19)5·(CHCl3)2 and [(R)-1]9(Mo6O19)5·(CHBr3)2 salts are practically identical (Fig. S9 and S10 for the band structures and Tables S2 and S3 for the interaction energies, ESI‡) so that the following discussion applies to all of these salts.
The suggestion of a Mott localized system, even if in agreement with the transport measurements, is quite puzzling. It is not easy to reconcile the localized nature of the system with the fact that there are ten holes to be distributed among two sets of six and three donors, respectively. Certainly, the band structure of Fig. 7 suggests that six electrons must be formally assigned to the six donors of type A so that for the time being each of them would hold a positive charge. However, this leaves us with two localized electrons. How should they be allocated to the six A- or three B-type donors of the lattice? Although charge (i.e. holes in the present case) attributions based on integer values must often be considered as formal charges, for a Mott localized system, at least in principle, it should be possible to derive a chemically meaningful localized description. As mentioned before, there are four types of HOMO⋯HOMO interaction in the donor layers: two are between donors of type A (interactions I and IV in Fig. 6) and two between donors of type A and B (interactions II and III in Fig. 6). The S⋯S contacts shorter than 3.9 Å as well as the absolute values of the βHOMO–HOMO interaction energies34 (eV) for the four different donor⋯donor interactions are reported in Table 2. At first sight the four interactions seem to be quite sizeable. However, one must note that the two donors differ considerably in terms of their HOMO energy: the HOMO of donors A is substantially lower in energy (Δ = 0.39 eV) and this fact has an important consequence. The strength of the interaction between two HOMOs is proportional to the square of their overlap but inversely proportional to their energy difference. In molecular conductors the overlaps are always relatively weak so that sizeable HOMO energy differences like the present one strongly reduce the effective interactions. This is what happens in the present case. Although the strength of the A–A and A–B interactions seem to be of the same order according to the S⋯S short contacts and |βHOMO–HOMO| values of Table 2, the A–B interactions are really considerably weaker.
| Interaction (type) | S⋯S (<3.9 Å) | |βHOMO–HOMO| (eV) |
|---|---|---|
| I (A–A) | 3.510 (×2), 3.545 (×2), 3.617, 3.674 (×2) | 0.1501 |
| II (A–B) | 3.650, 3.651, 3.738, 3.807, 3.852, 3.868 | 0.0996 |
| III (A–B) | 3.554, 3.592, 3.604, 3.662, 3.673, 3.732, 3.796 | 0.2085 |
| IV (A–A) | 3.497, 3.510 (×2), 3.583 (×2), 3.759 (×2) | 0.2644 |
As shown in Fig. 6 the donor lattice of the present salt contains cyclic hexameric units of donors A bridged by donors B. The weak interaction between donors A and B is ultimately the reason for the small dispersion of all the bands in Fig. 7. The two interactions of type A–A are however very sizeable. As a result, the six levels of one of these cyclic A6 hexameric units exhibit a substantial splitting of approximately 0.6 eV (Fig. 8), i.e. larger than the energy separation between the HOMOs of donors A and B. This means that the six donors of type A interact strongly enough to be considered as a unit as far as the HOMO⋯HOMO interactions are concerned. In other words, the donor lattice of the present salt can be described as a series of hexameric units of donors A which are weakly connected through donors B. This leads to a natural explanation of the charge distribution and activated conductivity. The three lower-lying orbitals of the hexamer (Fig. 8) are filled with three pairs of electrons and the two degenerate levels right above are each filled with one unpaired electron. In that way the A6 hexameric unit can formally hold eight electrons even if it is made of six donors. This means that there is full delocalization of the unpaired electrons within the A6 units but the weak coupling between such units through donors B does not allow a full delocalization throughout the donor lattice. Consequently, the unpaired electrons (i.e. the charge carriers) remain mostly confined within these hexameric units and an activation energy must be overcome for the hopping of carriers through the lattice. Let us emphasize that such formal localized view providing an intuitive description of the origin of the activated conductivity is not in contradiction with the previous analysis of the charge distribution based on the donor bond lengths. This structural approach implicitly takes into account the communication of the A6 units through the B donors so that the slight delocalization implicates some shift of charge from the A6 units to the B donors thus conciliating both descriptions. The two views provide complementary hints on different aspects of the material.
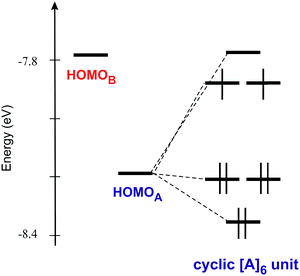 | ||
| Fig. 8 HOMO energy levels of the isolated A and B donors and a cyclic hexameric unit of donors A with the proposed level occupation. | ||
Consequently, if the coupling through donors B could be reinforced, for instance through applied pressure, and the metallic state could be stabilized, the Fermi level would occur at the K point and thus would coincide with a Dirac cone which could lead to the exotic transport properties predicted for this situation.35 Among molecular conductors, only (EDT-TTF-CONH2)6[Re6Se8(CN)6],36,37 α-(BEDT-TTF)2I3 under pressure,38 [Pd(dddt)2] (dddt = 5,6-dihydro-1,4-dithiin-2,3-dithiolate) under pressure,39 [Pt(dmdt)2] (dmdt = dimethyl-tetrathiafulvalene-dithiolate)40 and, very recently, α-(BETS)2I3 (BETS = bis(ethylenedithio)-tetraselenafulvalene)41 have been previously shown to exhibit such an uncommon electronic feature. Unfortunately, our measurements suggest that in the present salts the electrons remain localized at the pressures we could reach.
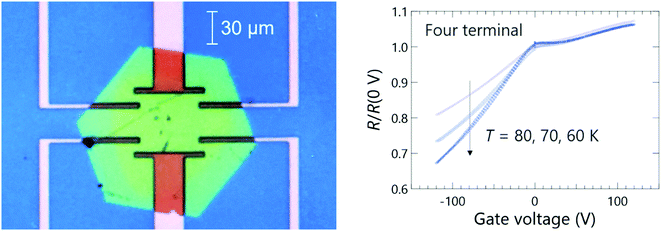
In order to obtain further information on the insulating nature of this salt, a field effect transistor (FET) was made, and its electric-field dependent resistivity was measured as shown in Fig. 9. In the case of a Mott-insulating state, it is known that electrostatic doping by FET will result in an ambipolar behaviour because both hole- and electron-doping will collapse the Mott gap due to the commensurability mismatching between the lattice density and carrier concentration at the doped state.42,43 In the present case, the FET basically showed a p-type behaviour from 60 K to 80 K, where the resistance decreases as the gate voltage is decreased (hole-doping). However, it is interesting to see an anomaly around zero gate voltage which implies that the system is a combination of wide-range p-type FET with a slight portion of ambipolar fraction. The details of the FET behaviour need to be more thoroughly investigated in future experiments to clarify the operation mechanism associated with the origin of the insulating state.
We have further analysed the electronic structure of the racemic material [(rac)-1]2(Mo6O19). The crystal structure of this salt can be described as containing layers of the TM-BEDT-TTF donor stacked along the (a–c)-direction (Fig. 10a). The donors in such layers are strongly dimerized (Fig. 10b) with S⋯S short contacts of 3.348 Å (×2), 3.439 Å (×2), 3.714 Å (×2) and 3.796 Å (×2). However no S⋯S contacts shorter than 4.17 Å are found within the layers of Fig. 10b. The only short S⋯S contacts occur along the a-direction (purple dashed lines in Fig. 10c), 3.540 Å.
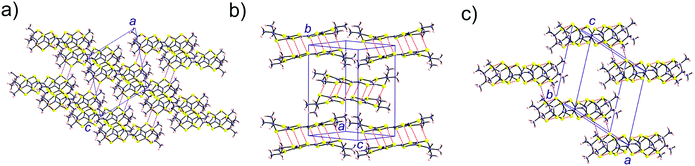 | ||
| Fig. 10 Donor sublattice of the [(rac)-1]2(Mo6O19) salt. The S⋯S contacts shorter than 3.9 Å are shown as dashed red (intra-dimer) and purple (inter-dimer) lines. | ||
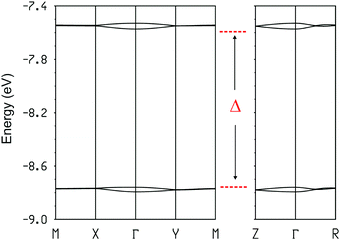
Thus, this salt contains dimer chains along the a-direction. The calculated absolute values of the βHOMO–HOMO interaction energies are 0.9840 and 0.0027 eV for the intra- and inter-dimer interactions, respectively. Despite a relatively short S⋯S contact, the inter-dimer interaction is very small because of the dimerization and the fact that the overlap is of the lateral type between two outer S atoms (whose contribution to the HOMO is only ∼1/3 that of the inner ones). Consequently, from the viewpoint of the HOMO⋯HOMO interactions this salt contains quite isolated strong dimers. In agreement with this analysis, the calculated three-dimensional band structure of the donor sublattice of [(rac)-1]2(Mo6O19) (Fig. 11) contains two pairs of well separated and almost non dispersive bands. Since there are two dianions per unit cell, the HOMO bands contain four holes so that only the lower pair of bands is filled. Consequently, this salt should be a semiconductor with a relatively low conductivity.
3. Conclusions
Electrocrystallization of the enantiopure donor TM-BEDT-TTF 1 in the presence of the Lindqvist type precursor (TBA)2(Mo6O19) provided the series of crystalline radical cation salts [(S/R)-1]9(Mo6O19)5·(CHX3)2 (X = Cl, Br) characterized by a very unusual donor/anion stoichiometry and unprecedented helical packing of the donors thanks to the symmetry operations of the trigonal non-centrosymmetric R32 space group. The two crystallographically independent donors A and B, bearing, respectively, approximate charges +1 and +1.33, show the uncommon (ax, ax, eq, eq) and all-ax orientations for the methyl substituents in TM-BEDT-TTF based radical cation salts, favouring lateral interactions instead of face-to-face overlap between the donors. Single crystal resistivity measurements are in agreement with a semiconducting behaviour of the chiral materials, with room temperature conductivity values of 0.8–1.2 S cm−1 at ambient pressure, while applying hydrostatic pressures of up to 2.3 GPa only slightly enhance the conductivity. Band structure calculations reveal a very peculiar electronic structure for the four isostructural enantiopure salts, suggesting a possible Dirac cone behaviour since, in the case of metallic conductivity, the Fermi level would be at the K point of the Brillouin zone where two bands are degenerate. Instead, very likely because of the small dispersion of the partially filled bands, the materials are Mott insulators. Field effect transistor (FET) measurements were made on a thin single crystal of [(S)-1]9(Mo6O19)5·(CHBr3)2 to obtain information on the insulating state at low temperatures. The gate voltage dependence of the device resistance suggested that the device was wide-range p-type FET with a slight portion of ambipolar fraction, deviating from a dominant ambipolar behaviour of the ideal Mott-insulating state. The paramount role of the donor's chirality has been also emphasized through the preparation of the racemic salt [(rac)-1]2(Mo6O19), which shows drastically different crystal structure, with the donors in the radical cation state forming strong dimers.The enantiopure conductors we describe in this work are very promising for future investigations. Further improving the robustness of the crystals by using, for example, iodoform as a co-crystallization agent, and enhancing the intermolecular interactions between the donors, by applying very high pressures, are valuable prospects aiming at conferring metallic character to these salts which are candidates for unprecedented chiral Dirac cone materials. The preliminary FET results are also encouraging in view of modulation of the effect by applying a magnetic field. Moreover, the helical packing of the donors in combination with the conducting properties are important features of our materials towards the investigation of the chirality induced spin selectivity (CISS) effect44,45 in the linear response regime, a situation of much interest which has been only very recently reported.46,47
4. Experimental
4.1 Materials and methods
Reactions were carried out under argon; solvents acetonitrile (Carlo Erba) and chloroform HPLC grade (VWR) were used. Bromoform was purchased from Alfa Aesar and stored on dry potassium carbonate. TM-BEDT-TTF was synthesized according to the published procedures.1,24.2 Synthesis
4.3 X-Ray structure determinations
Details about data collection and solution refinement are given in Table S1 (ESI‡). Single crystals of the compounds were mounted on plastic loops using a viscous hydrocarbon oil to coat the crystal and then transferred directly to a cold nitrogen stream for data collection. X-Ray data collection was performed at 150 K on a Rigaku Oxford Diffraction SuperNova with micro-focus CuKα (λ = 1.54184 Å) or on a Nonius Kappa CCD diffractometer, using graphite-monochromated MoKα radiation (λ = 0.71073 Å). The structures were solved by direct methods with the SHELXS-97 and SIR92 programs and refined against all F2 values with the SHELXL-97 program48 using the WinGX graphical user interface.49 All non-H atoms were refined anisotropically. Hydrogen atoms were introduced at calculated positions (riding model), included in structure factor calculations but not refined. The four structure refinements containing solvent molecules showed disordered electron density which could not be reliably modeled and the program PLATON/SQUEEZE (A. L. Spek V290617 (1980–2019)) was used to remove the corresponding scattering contribution from the intensity data. This electron density could be attributed to chloroform or bromoform molecules. The assumed solvent compositions were used in the calculation of the empirical formula, formula weight, density, linear absorption coefficient, and F(000).Crystallographic data for the five structures have been deposited with the Cambridge Crystallographic Data Centre, deposition numbers CCDC 2068677 ([(S)-1]9(Mo6O19)5·(CHCl3)2), 2068680 ([(R)-1]9(Mo6O19)5·(CHCl3)2), 2068681 ([(S)-1]9(Mo6O19)5·(CHBr3)2), 2068682 ([(R)-1]9(Mo6O19)5·(CHBr3)2), and 2068683 ([(rac)-1]2(Mo6O19)).‡
4.4 Conductivity measurements
The electrical conductivity of [(S)-1]9(Mo6O19)5·(CHCl3)2 was measured on platelet-shaped single crystals 0.3–0.5 mm long. Gold wires were glued with silver paste on four aligned gold contacts previously evaporated on one face of the single crystals. Resistivity measurements were performed using an AC current of 1 μA and low-frequency (<100 Hz) with lock-in amplifier detection. High hydrostatic pressures are applied in a homemade NiCrAl clamp type cell up to 2.3 GPa. The pressure is measured at room temperature when the pressure is varied using a manganin gauge and silicon oil (Idemitsu Daphne-oil 7373) is used as the pressure transmitting medium. Low temperature was achieved with a cryostat equipped with a 4 K pulse-tube.The measurements of electrical conductivity on [(R)-1]9(Mo6O19)5·(CHBr3)2 were done by using a conventional DC method with six-probes. Gold wires with the diameter of 15 μm were attached on the sample using carbon paste. Two electrodes were used for the current supply and another four electrodes for voltage sensors. A sample to which six electrical leads were attached was encased in a Teflon capsule filled with pressure medium (Idemitsu DN-oil 7373). The capsule was set in a clamp-type pressure cell made of MP35N hard alloy and hydrostatic pressure of up to 1.5 GPa was applied.
4.5 Band structure calculations
The tight-binding band structure and molecular calculations were of the extended Hückel type.50 A modified Wolfsberg-Helmholtz formula was used to calculate the non-diagonal Hμν values.51 All valence electrons were taken into account in the calculations and the basis set consisted of Slater-type orbitals of double-ζ quality for C 2s and 2p, S 3s and 3p and of single-ζ quality for H. The ionization potentials, contraction coefficients and exponents were taken from previous work.52Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in France by the National Agency for Research (ANR, Project 15-CE29-0006-01 ChiraMolCo), the CNRS and the University of Angers. Work at Bellaterra (Spain) was supported by the Spanish MICIU through Grant PGC2018-096955-B-C44 and the Severo Ochoa FUNFUTURE (CEX2019-000917-S) Excellence Centre distinction as well as by Generalitat de Catalunya (2017SGR1506). This work was also partially supported in Chiba, Japan by MEXT = JSPJ KAKENHI under Grants No. 16H06346 and 20K03870. Work in Okazaki was supported by Grant-in-Aid for Scientific Research (A) (Grant Number 19H00891) and Grant-in-Aid for Challenging Research (Exploratory) (Grant Number 20K20903) from JSPS as well as PRESTO (Grant Number JPMJPR20L9) from JST.Notes and references
- J. D. Dunitz, A. Karrer and J. D. Wallis, Helv. Chim. Acta, 1986, 69, 69–70 Search PubMed.
- S. Matsumiya, A. Izuoka, T. Sugawara, T. Taruishi and Y. Kawada, Bull. Chem. Soc. Jpn., 1993, 66, 513–522 Search PubMed.
- G. L. J. A. Rikken, J. Fölling and P. Wyder, Phys. Rev. Lett., 2001, 87, 236602 Search PubMed.
- V. Krstic, S. Roth, M. Burghard, K. Kern and G. L. J. A. Rikken, J. Chem. Phys., 2002, 117, 11315–11319 Search PubMed.
- G. L. J. A. Rikken and N. Avarvari, Phys. Rev. B, 2019, 99, 245153 Search PubMed.
- N. Avarvari and J. D. Wallis, J. Mater. Chem., 2009, 19, 4061–4076 Search PubMed.
- F. Pop, N. Zigon and N. Avarvari, Chem. Rev., 2019, 119, 8435–8478 Search PubMed.
- F. Pop, P. Auban-Senzier, E. Canadell, G. L. J. A. Rikken and N. Avarvari, Nat. Commun., 2014, 5, 3757 Search PubMed.
- F. Pop, P. Auban-Senzier, A. Frąckowiak, K. Ptaszyński, I. Olejniczak, J. D. Wallis, E. Canadell and N. Avarvari, J. Am. Chem. Soc., 2013, 135, 17176–17186 Search PubMed.
- F. Pop, P. Auban-Senzier, E. Canadell and N. Avarvari, Chem. Commun., 2016, 52, 12438–12441 Search PubMed.
- C. Réthoré, N. Avarvari, E. Canadell, P. Auban-Senzier and M. Fourmigué, J. Am. Chem. Soc., 2005, 127, 5748–5749 Search PubMed.
- A. M. Madalan, C. Réthoré, M. Fourmigué, E. Canadell, E. B. Lopes, M. Almeida, P. Auban-Senzier and N. Avarvari, Chem. – Eur. J., 2010, 16, 528–537 Search PubMed.
- J. S. Zambounis, C. W. Mayer, K. Hauenstein, B. Hilti, W. Hofherr, J. Pfeiffer, M. Bürkle and G. Rihs, Adv. Mater., 1992, 4, 33–35 Search PubMed.
- N. Mroweh, C. Mézière, F. Pop, P. Auban-Senzier, P. Alemany, E. Canadell and N. Avarvari, Adv. Mater., 2020, 32, 2002811 Search PubMed.
- S. Matsumiya, A. Izuoka, T. Sugawara, T. Taruishi, Y. Kawada and M. Tokumoto, Bull. Chem. Soc. Jpn., 1993, 66, 1949–1954 Search PubMed.
- F. Pop, M. Allain, P. Auban-Senzier, J. Martínez-Lillo, F. Lloret, M. Julve, E. Canadell and N. Avarvari, Eur. J. Inorg. Chem., 2014, 3855–3862 Search PubMed.
- N. Mroweh, C. Mézière, M. Allain, P. Auban-Senzier, E. Canadell and N. Avarvari, Chem. Sci., 2020, 11, 10078–10091 Search PubMed.
- N. Mroweh, F. Pop, C. Mézière, M. Allain, P. Auban-Senzier, N. Vanthuyne, P. Alemany, E. Canadell and N. Avarvari, Cryst. Growth Des., 2020, 20, 2516–2526 Search PubMed.
- N. Mroweh, P. Auban-Senzier, N. Vanthuyne, E. Canadell and N. Avarvari, J. Mater. Chem. C, 2019, 7, 12664–12673 Search PubMed.
- N. Mroweh, P. Auban-Senzier, N. Vanthuyne, E. B. Lopes, M. Almeida, E. Canadell and N. Avarvari, Crystals, 2020, 10, 1069 Search PubMed.
- S. Yang, F. Pop, C. Melan, A. C. Brooks, L. Martin, P. Horton, P. Auban-Senzier, G. L. J. A. Rikken, N. Avarvari and J. D. Wallis, CrystEngComm, 2014, 16, 3906–3916 Search PubMed.
- F. Pop, S. Laroussi, T. Cauchy, C. J. Gómez-García, J. D. Wallis and N. Avarvari, Chirality, 2013, 25, 466–474 Search PubMed.
- A. Karrer, J. D. Wallis, J. D. Dunitz, B. Hilti, C. W. Mayer, M. Bürkle and J. Pfeiffer, Helv. Chim. Acta, 1987, 70, 942–953 Search PubMed.
- J. R. Galán-Mascarós, E. Coronado, P. A. Goddard, J. Singleton, A. I. Coldea, J. D. Wallis, S. J. Coles and A. Alberola, J. Am. Chem. Soc., 2010, 132, 9271–9273 Search PubMed.
- F. Riobé, F. Piron, C. Réthoré, A. M. Madalan, C. J. Gómez-García, J. Lacour, J. D. Wallis and N. Avarvari, New J. Chem., 2011, 35, 2279–2286 Search PubMed.
- M. Atzori, F. Pop, P. Auban-Senzier, R. Clérac, E. Canadell, M. L. Mercuri and N. Avarvari, Inorg. Chem., 2015, 54, 3643–3653 Search PubMed.
- F. Pop, P. Batail and N. Avarvari, Crystals, 2016, 6, 8 Search PubMed.
- S. Triki, L. Ouahab, J.-F. Halet, O. Peña, J. Padiou, D. Grandjean, C. Garrigou-Lagrange and P. Delhaes, J. Chem. Soc., Dalton Trans., 1992, 1217–1227 Search PubMed.
- S. Triki, L. Ouahab, D. Grandjean and J.-M. Fabre, Acta Crystallogr., 1991, C47, 645–648 Search PubMed.
- E. Coronado and C. J. Gómez-García, Chem. Rev., 1998, 98, 273–296 Search PubMed.
- A. Dolbecq, A. Guirauden, M. Fourmigué, K. Boubekeur, P. Batail, M.-M. Rohmer, M. Bénard, C. Coulon, M. Sallé and P. Blanchard, J. Chem. Soc., Dalton Trans., 1999, 1241–1248 Search PubMed.
- N. Avarvari and M. Fourmigué, Chem. Commun., 2004, 1300–1301 Search PubMed.
- F. Pop, J. Lacour and N. Avarvari, Rev. Roum. Chim., 2012, 57, 457–462 Search PubMed.
- M.-H. Whangbo, J. M. Williams, P. C. W. Leung, M. A. Beno, T. J. Emge and H. H. Wang, Inorg. Chem., 1985, 24, 3500–3502 Search PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. M. Geim, Rev. Mod. Phys., 2009, 81, 109–162 Search PubMed.
- S. A. Baudron, P. Batail, C. Coulon, R. Clérac, E. Canadell, V. Laukhin, R. Melzi, P. Wzietek, D. Jérome, P. Auban-Senzier and S. Ravy, J. Am. Chem. Soc., 2005, 127, 11785–11797 Search PubMed.
- S. Carlson, L. Zorina, D. R. Allan, J. P. Attfield, E. Canadell and P. Batail, Inorg. Chem., 2013, 52, 3326–3333 Search PubMed.
- S. Katayama, A. Kobayashi and Y. Suzunura, J. Phys. Soc. Jpn., 2006, 75, 054705 Search PubMed.
- R. Kato, H. Cui, T. Tsumuraya, T. Miyazaki and Y. Suzumura, J. Am. Chem. Soc., 2017, 139, 1770–1773 Search PubMed.
- B. Zhou, S. Ishibashi, T. Ishii, T. Sekine, R. Takehara, K. Miyagawa, K. Kanoda, E. Nishibori and A. Kobayashi, Chem. Commun., 2019, 55, 3327–3330 Search PubMed.
- S. Kitou, T. Tsumuraya, H. Sawahata, F. Ishii, K. Hiraki, T. Nakamura, N. Katayama and H. Sawa, Phys. Rev. B, 2021, 103, 035135 Search PubMed.
- Y. Kawasugi, H. M. Yamamoto, N. Tajima, T. Fukunaga, K. Tsukagoshi and R. Kato, Phys. Rev. B, 2011, 84, 125129 Search PubMed.
- Y. Kawasugi, K. Seki, Y. Edagawa, Y. Sato, J. Pu, T. Takenobu, S. Yunoki, H. M. Yamamoto and R. Kato, Nat. Commun., 2016, 7, 12356 Search PubMed.
- K. Michaeli, N. Kantor-Uriel, R. Naaman and D. H. Waldeck, Chem. Soc. Rev., 2016, 45, 6478–6487 Search PubMed.
- R. Naaman, Y. Paltiel and D. H. Waldeck, Nat. Rev. Chem., 2019, 3, 250–260 Search PubMed.
- A. Inui, R. Aoki, Y. Nishiue, K. Shiota, Y. Kousaka, H. Shishido, D. Hirobe, M. Suda, J. Ohe, J. Kishine, H. M. Yamamoto and Y. Togawa, Phys. Rev. Lett., 2020, 124, 166602 Search PubMed.
- Y. Nabei, D. Hirobe, Y. Shimamoto, K. Shiota, A. Inui, Y. Kosaka, Y. Togawa and H. M. Yamamoto, Appl. Phys. Lett., 2020, 117, 052408 Search PubMed.
- G. M. Sheldrick, (2013–2018) SHELXS-2013, SHELXL-2016 or 2018, Program for Crystal Structure solution and Crystal Structure refinement, University of Gottingen, Germany.
- L. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 Search PubMed.
- M.-H. Whangbo and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 6093–6098 Search PubMed.
- J. H. Ammeter, H.-B. Bürgi, J. Thibeault and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 3686–3692 Search PubMed.
- A. Pénicaud, K. Boubekeur, P. Batail, E. Canadell, P. Auban-Senzier and D. Jérome, J. Am. Chem. Soc., 1993, 115, 4101–4112 Search PubMed.
Footnotes |
| † Dedicated to Professor Concepció Rovira and Professor Jaume Veciana on the occasions of their 70th birthdays. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2068677 and 2068680–2068683. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc01112j |
| This journal is © The Royal Society of Chemistry 2021 |