Open Access Article
Open Access ArticleRevealing the bonding of solvated Ru complexes with valence-to-core resonant inelastic X-ray scattering†
Elisa
Biasin
 *a,
Daniel R.
Nascimento
b,
Benjamin I.
Poulter
*a,
Daniel R.
Nascimento
b,
Benjamin I.
Poulter
 c,
Baxter
Abraham
d,
Kristjan
Kunnus
ae,
Angel T.
Garcia-Esparza
c,
Baxter
Abraham
d,
Kristjan
Kunnus
ae,
Angel T.
Garcia-Esparza
 d,
Stanislaw H.
Nowak
d,
Thomas
Kroll
d,
Robert W.
Schoenlein
d,
Stanislaw H.
Nowak
d,
Thomas
Kroll
d,
Robert W.
Schoenlein
 ae,
Roberto
Alonso-Mori
e,
Munira
Khalil
ae,
Roberto
Alonso-Mori
e,
Munira
Khalil
 c,
Niranjan
Govind
c,
Niranjan
Govind
 *b and
Dimosthenis
Sokaras
*b and
Dimosthenis
Sokaras
 *d
*d
aStanford PULSE Institute, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA. E-mail: ebiasin@stanford.edu
bPhysical and Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland, Washington 99352, USA. E-mail: niri.govind@pnnl.gov
cDepartment of Chemistry, University of Washington, Seattle, Washington 98195, USA
dSSRL, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA. E-mail: dsokaras@slac.stanford.edu
eLCLS, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
First published on 29th January 2021
Abstract
Ru-complexes are widely studied because of their use in biological applications and photoconversion technologies. We reveal novel insights into the chemical bonding of a series of Ru(II)- and Ru(III)-complexes by leveraging recent advances in high-energy-resolution tender X-ray spectroscopy and theoretical calculations. We perform Ru 2p4d resonant inelastic X-ray scattering (RIXS) to probe the valence excitations in dilute solvated Ru-complexes. Combining these experiments with a newly developed theoretical approach based on time-dependent density functional theory, we assign the spectral features and quantify the metal–ligand bonding interactions. The valence-to-core RIXS features uniquely identify the metal-centered and charge transfer states and allow extracting the ligand-field splitting for all the complexes. The combined experimental and theoretical approach described here is shown to reliably characterize the ground and excited valence states of Ru complexes, and serve as a basis for future investigations of ruthenium, or other 4d metals active sites, in biological and chemical applications.
1. Introduction
Ruthenium complexes exhibit unique photophysical and photochemical properties and are widely used in light harvesting technologies,1 photocatalysis,2 biological applications,3 and information storage.4 In particular, polypyridyl based Ru(II) complexes have been widely investigated as functional materials, thanks to their stability in solution, strong absorption throughout the UV-vis light regions, and long excited state lifetimes.5,6 In these systems, the functional properties are dictated by the relative energies and composition of the excited states, which can be tuned by changing the ligand environment. For instance, the efficiency of Ru(II) photosensitizer relies on lower-lying metal-to-ligand charge transfer (MLCT) states accessible though transfer on an electron from the Ru 4d orbitals to a ligand-based π* orbital.1,6 For some photocatalytic or biological applications, such as those that exploit ligand substitution, the excited state reactivity is governed instead by the metal-centered (MC) states.4,7,8 The elucidation of the ground- and excited-state valence structures of Ru-complexes, which governs their properties and ultimate functions, and their dependence on the ligand environment has been the focus of numerous experimental and computational studies.9,10 Even though systematic efforts have certainly enhanced our understanding of Ru-complexes, particularly for bipyridine ligands,2,10 a universal description of their 4d electronic coupling, their complex manifold of valence excited states, as well as their metal–ligand interactions remains an experimental and computational challenge. A comprehensive understanding of Ru complexes, especially their functional excited states formed under photoexcitation or catalytic conditions, is a crucial step for accelerating the development of the next-generation functional materials.The continuous development and availability of element-specific experimental methods, such as X-ray spectroscopic techniques, has guided the progress of electronic structure elucidation in transition metal complexes. X-ray absorption spectroscopy (XAS) is commonly used to probe unoccupied valence state in these systems, even in dilute solutions.11 For Ru-complexes, XAS at either the Ru L- or K-edge has provided unique insights on the 4d electronic configuration as a function of local geometry/symmetry and ligand environment.12–17 Simultaneously, density functional theory (DFT) and time-dependent density functional theory (TDDFT) calculations have played a key role for correlating the experimental XAS spectral fingerprints with the electronic structure of Ru complexes.7,18,19 Valence-to-core (VtC) X-ray emission spectroscopy (XES) is a complementary technique to XAS, since it probes the occupied valence states with element specificity. Although such experiments are more challenging to perform than XAS, they are now well-established in the hard X-ray regime and especially for 3d transition metals.20–22 VtC XES measurements are often described well by ground state DFT calculations using the single electron transition picture and, therefore, provide straightforward access to local electronic and geometric structure and metal–ligand bonding.23–27 Ru 4d → 2p VtC XES has been very recently explored in a series of concentrated (solid-state) model complexes and found to be sensitive to oxidation state, ligand identity, and covalency.28 However, VtC XES studies for any 4d elements remain quite scarce,28–31 mainly due to the unavailability of instruments operating in the tender X-ray regime with a high enough detection throughput. Additionally, the technique sensitivity is limited by the appreciable contribution of the core-hole lifetime broadening of 4d elements, which amounts approximately to 5 and 2 eV for 1s-hole and 2p-hole, respectively.32
VtC resonant XES, also known as Resonant Inelastic X-ray Scattering (RIXS), is a two-step excitation-relaxation process probing both occupied and unoccupied valence states.33 When interpreting such resonant emission spectra on an energy-loss axis, information on valence excitations is extracted with element and chemical sensitivity. The energy resolution is not limited by the lifetime broadening of the (intermediate) core-hole state, but dictated by the smaller lifetime broadening of the (final) valence-excited state and by other contributions, such as the energy-resolution of the measurements and vibronic effects. VtC RIXS measurements have provided invaluable insights into the electronic configuration of 3d transition metals.34 In particular, 2p3d RIXS (initial 2p-hole, final 3d-hole) have been used to provide detailed information on the nature of the 3d frontier orbitals, metal–ligand interactions, energies and nature of charge separated states, including dd transitions,35–38 and have also been extended to the time-domain.39,40 Similarly to the VtC XES, VtC RIXS measurements on 4d elements have been very scarce and only for bulk and concentrated systems.41–43 Such studies are even more demanding than the VtC XES: experimentally, they require both high detection throughput and a high-enough energy resolution; theoretically, calculations of a large manifold of core- and valence-excited states are required.
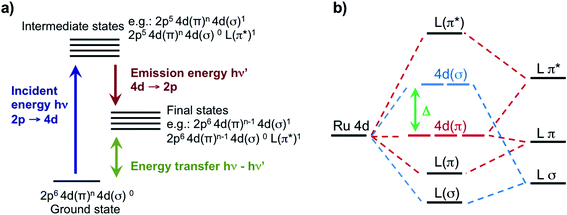
In this work, we leverage our recent advances in high-energy-resolution tender X-ray spectroscopy44 and our theory developments45 to reveal direct insights on the valence structure of a series of Ru-complexes with different oxidation state and metal–ligand bond strength. Specifically, we perform Ru L-edge measurements on two Ru(III)-complexes: [RuIII(NH3)6]3+, containing only σ-donating amine ligands, and [RuIII(NH3)5Cl]2+, where one amine ligand is substituted with one π-donating Cl ligand; and three Ru(II)-complexes: the prototypical [RuII(bpy)3]2+, a variation [RuII(bpy)2Cl2], and [RuII(CN)6]4−, which is a typical π back-donating system. Uniquely, we perform Ru 2p4d RIXS measurements of the Ru-complexes in dilute aqueous solution. This is made possible by the combination of a high incident flux beamline and a new in-vacuum, high resolution (∼0.6 eV) and low background tender X-ray spectrometer that integrates an ambient pressure sample sub-chamber hosting a free flowing liquid jet.44 The 2p4d RIXS process, which is illustrated in Fig. 1a, allows us to directly access the valence excitations of the solvated Ru-complexes and to gain information about the composition of the local orbitals. We combine our observations with a newly developed theoretical approach based on TDDFT, which accounts for the multideterminant character of the excited states within the space of single excitations.45 We show this approach is sufficiently accurate and predictive to capture the experimental spectra reliably. We find that the Ru 2p4d RIXS features uniquely identify the MC, ligand-centered (LC), and charge transfer (CT) states, directly extract ligand field splitting energies, and reveal detailed information on metal–ligand covalency for all the Ru complexes. We underline the uniqueness of the information provided by the RIXS spectra through comparison with the 2p → 4d XAS and the 4d → 2p VtC XES measurements, which are also reported in this work and analysed at the same TDDFT theoretical level. For instance, the ground-state ligand-field energy splitting of the Ru(II)-complexes is experimentally accessed for the first time by our 2p4d RIXS experiment. The approach described here is broadly applicable to novel studies of 4d metal based systems, and holds the promise to significantly improve the design of new molecules with optimal photophysical and photochemical properties.
2. Methods
2.1 Samples
Tris(2,2′-bipyridyl)ruthenium(II) chloride hexahydrate (Ru(bpy)3(H2O)6), potassium hexacyanoruthenate(II) hydrate (K4[Ru(CN)6]xH2O), hexaammineruthenium(III) chloride ([Ru(NH3)6]Cl3), pentaamminechlororuthenium(III) chloride ([Ru(NH3)5Cl]Cl2), and cis-bis(2,2′-bipyridine)-dichlororuthenium(II) hydrate, ([Ru(bpy)2Cl2]xH2O)) were purchased from Sigma Aldrich and used without further purification. The five complexes were dissolved in water yielding 50 mM ([RuII(bpy)3]2+), 100 mM ([RuII(CN)6]4−), 100 mM ([RuIII(NH3)6]3+), 10 mM ([RuIII(NH3)5Cl]2+) and 10 mM ([RuII(bpy)2Cl2]) solutions.2.2 Data collection and analysis
The high resolution X-ray emission spectroscopy studies were performed at beamline 6-2a at the Synchrotron Radiation Light Source (SSRL). A liquid nitrogen cooled Si(111) monochromator delivered an incident beam flux of ∼3 × 1012 photons per s at 3.0 keV (vicinity of Ru L3 absorption edge) with an energy resolution of about 400 meV and a beamsize with a full width half maximum (FWHM) of 400 × 250 μm2 (v × h). The measurements were performed using a high-resolution Johansson-type spectrometer equipped with a cylindrically bent Si(111) analyzer with energy resolution of ∼0.6 eV.44 The energy calibration of the spectrometer was performed with elastic scattering measurements. The monochromator energy was calibrated using the published L3 XAS spectra of [RuII(bpy)3]2+.14 Although the main volume of the spectrometer was under vacuum conditions, in order to minimize the attenuation of these low X-ray energies, the isolated sample sub-chamber with ambient He gas atmosphere permitted the integration of a free flowing liquid jet system. An HPLC pump was used to flow (7 ml min−1 flow rate) the samples through a 250 μm (inner diameter) Kapton capillary. A catcher placed 10 mm below the capillary was used to re-feed the pump and enabled a closed loop re-circulation of the solution. The X-ray beam interaction point was set ∼2 mm below the tip of the Kapton capillary. A downstream ionization chamber was also used for the quick alignment of the jet to the incident beam.An in-vacuum 2-dimensional (2048 × 2048 pixels) charge couple device (CCD) camera was used as a position sensitive detector to record the dispersively analyzed X-rays. The procedure used for the image processing is described in detail in ref. 44. Briefly, each 2D image is corrected for background and geometrical effects before being projected along the energy dispersion axis to yield the emission spectrum. A low-intensity threshold is also applied to isolate X-ray events from electronic noise. Total acquisition time for the spectra presented in this work varied from 20 to 120 minutes and they are reported in ESI Section 1.†
2.3 Calculations
All excited state calculations were performed within the linear-response TDDFT framework46–49 implemented in NWChem.50,51 Within TDDFT, the core-excited states were computed with the restricted excitation window approach,52 where the excitation space was restricted to the 2p ground state orbitals and no restrictions on the target unoccupied states, thus yielding the L3-XAS spectrum. VtC-XES calculations were also performed using a TDDFT-based protocol as outlined in ref. 53, and the final emission spectra were assembled by considering both α and β 2p orbitals. Spectral profiles for all L3-XAS and VtC-XES simulated spectra are generated by convolving the discrete excitations with natural (Lorentzian) widths of 1.5 eV.RIXS calculations considering an absorbed photon with energy ℏω and an emitted photon with energy ℏω′ were performed by solving the Kramers–Heisenberg equation within the electric dipole approximation,
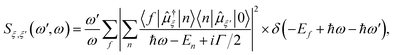 | (1) |
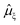 is the ξ-component of the electric dipole operator. Final RIXS spectra are calculated summing over the ξ-components, taking into account the experimental geometry.54
is the ξ-component of the electric dipole operator. Final RIXS spectra are calculated summing over the ξ-components, taking into account the experimental geometry.54
The ground-L3 and L3-valence dipole couplings were obtained via the TDDFT pseudo-wavefunction ansatz.55,56 Details of our approach is given in ref. 45. In order to generate the manifold of Ru L3-edge excited states, a total of 200 roots were computed for each complex; while the manifold of valence excited states was comprised of 200 roots for the [RuIII(NH3)6]3+ and [RuIII(NH3)5Cl]2+ complexes and 1300 roots for [RuII(bpy)3]2+, [RuII(bpy)2Cl2], and [RuII(CN)6]4− complexes, respectively. The minimum number of roots was chosen so that the calculated states would span the energy range of interest (i.e. 0–15 eV for the final states), and the maximum number of roots was dictated by computational resources. In implementing eqn (1), a uniform lifetime broadening, Γ, of 2.4 eV was used, and the Dirac delta was approximated by a Gaussian function with a FWHM of 1.2 eV. These broadening constants were chosen based on the comparison with the measurements.
All excited-state calculations employed the B3LYP functional,57,58 the Sapporo-DKH3-TZP-2012 basis set59 for the Ru atoms and the 6-311G** basis set60 for all the remaining atoms. Solvent (water) effects were included implicitly via the Conductor-like Screening Model (COSMO),61,62 and scalar relativistic effects were included via the Zeroth-order Regular Approximation (ZORA) model potential of van Lenthe et al.63–65 We have neglected the spin–orbit splitting in the calculations, since (1) in an earlier work we have shown that ligand field multiplet and spin–orbit effects do not strongly influence the L3-edges of Ru,18 and (2) the 4d spin orbit coupling constant is small (∼0.1 eV66) with respect to the energy resolution and ligand field effects.67,68 L3-XAS and VtC-XES calculations were performed with NWChem (version 6.8.1), while the RIXS were computed with a development version. The ground-state geometries of the complexes were previously optimized using the ORCA quantum chemistry package69 at the B3LYP/def2-TZVP level of theory. Solvent effects were modeled via the conductor-like polarizable continuum model (CPCM).70 The geometries of the complexes are provided in the ESI Section 6.†
3. Results and discussion
3.1 Ru L3-edge X-ray absorption
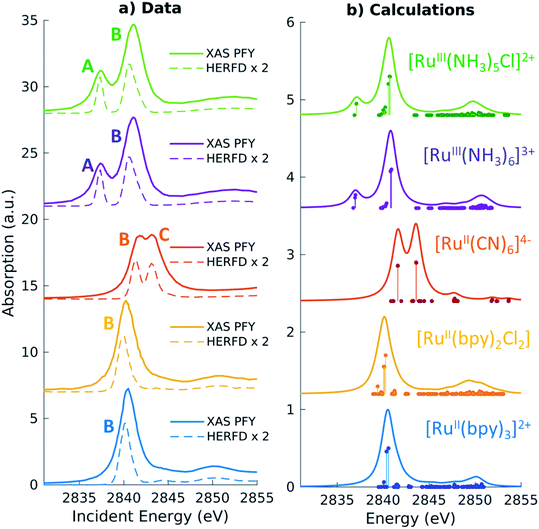
For the five model Ru-complexes investigated in our study, we initially measured the 3d → 2p fluorescence (Lα1,2) as a function of incident energy in the 2820–2900 eV range, corresponding to the L3 (2p3/2 → 4d) Ru absorption edge. This yields two-dimensional RIXS maps, from which we obtain: (1) the absorption spectrum in partial fluorescence yield (PFY) by integrating the signal over all detected X-ray emission energies, and (2) the high energy resolution fluorescence detected (HERFD) X-ray absorption signal, by integrating the signal measured in a narrow region (∼0.6 eV) centered at the peak of the Lα1 emission line above the edge jump (∼2557 eV). Fig. 2a shows the measured PFY and HERFD XAS signals for the five Ru model complexes. Strong spectral features (labeled A, B, and C) appear in the pre-edge region, which are sharper in the HERFD spectrum. These features have been previously assigned14,17,18 and can be qualitatively understood by considering molecular orbitals (MOs) derived from ligand field theory. Fig. 1b illustrates possible molecular orbitals arising from the mixing of the Ru 4d orbitals with the σ or π orbitals of the ligands. The Ru 4d orbitals are split by the ligand field into higher lying 4d(σ) and lower lying 4d(π) orbitals, and Ru(II) and Ru(III) complexes have low-spin d6 and d5 configurations, respectively. With this in mind, the B peak present in all measured XAS spectra (∼2840.5 eV) is mainly due to transitions from the 2p orbitals to the unoccupied 4d(σ) orbitals. On the lower energy side, Ru(III)-complexes show an additional A feature due to transitions to the 4d(π) orbitals vacancy. Finally, [RuII(CN)6]4− presents a C peak on the high energy side due to transitions from the 2p to the unoccupied CN(π*) orbitals. Spectral features above the edge jump (at around 2850 eV) are due to quasi bound above-ionization resonances. These states have been previously discussed,14,17 and will not be investigated further in this work.The position of the labeled spectral features (A, B, C) have been determined by fitting Voigt profiles to the PFY-XAS data, after pre-edge background removal, and are reported in Table 1. These peak positions were used to select the resonant incident energies for the 2p4d RIXS measurements described below. The position of the absorption peaks report on the effective charge density at the metal, and also on effects such as metal–ligand covalency and ligand field strength.71 For instance, the B peak shifts to higher energy upon oxidation due to reduced screening of the 2p orbitals, which effectively lowers the 2p energy (closer to the core). However, the B peak of [RuII(CN)6]4− is found at a higher energy compared with the B peak of the Ru(III)-complexes investigated in this study. We also notice that the B peak is slightly blueshifted for [RuIII(NH3)6]3+ ([RuII(bpy)3]2+) with respect to [RuIII(NH3)5Cl]2+ ([RuII(bpy)2Cl2]).
| Molecule | Experiment | Calculationsa | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | Δ peaks | A | B | C | Δ peaks | |
| a A global shift of 2.3 eV is applied to the calculated spectra. b Δ peaks are calculated before rounding to the first digit. | ||||||||
| [RuIII(NH3)5Cl]2+ | 2837.4 | 2840.9 | 3.5 | 2837.2 | 2840.6 | 3.4 | ||
| [RuIII(NH3)6]3+ | 2837.3 | 2841.1 | 3.7 | 2837.0 | 2840.8 | 3.8 | ||
| [RuII(CN)6]4− | 2841.5 | 2843.4 | 1.9 | 2841.6 | 2843.6 | 2 | ||
| [RuII(bpy)2Cl2] | 2840.3 | 2040.1 | ||||||
| [RuII(bpy)3]2+ | 2840.5 | 2840.5 | ||||||
Quantitative information can be obtained by the analysis of the TDDFT calculated L3-edge XAS spectra, which are shown in Fig. 2b. The spectra have been shifted by aligning the calculated B peak of [RuII(bpy)3]2+ with the experimental value. Following this universal shift, the position of the A, B and C features are determined by fitting the spectra with a sum of Lorentzian profiles and the results are reported in Table 1. The calculations reproduce the features and the trends observed in the experimental spectra. For instance, the calculations can be used to disentangle the information encoded in the B peak position. We find that the calculated 2p orbitals energies correlate with the position of the B peak, with the exception of the [RuII(CN)6]4− complex (see ESI Fig. 1†). Even though [RuII(CN)6]4− has the highest energy for the 2p orbitals with respect to the other complexes, the B peak position can be explained by the high energy of the 4d(σ) orbitals.
In order to analyze the character of the calculated core-excited states, we first identify and group the relevant ground state (GS) molecular orbitals (i.e. those containing Ru 4d character) according to their energy and label them considering their atomic orbital contributions and bonding character. Table 2 shows the results of this analysis. We estimate the atomic orbital contributions based on the respective squared atomic orbital coefficients which are normalized such that the sum of all the squared coefficients for each MO is equal to 1. Illustrations of the MOs can be found in the ESI.† Based on this classification, we inspect the composition of the core-excited states with the highest oscillator strength for each molecular complex, and confirm that the ligand field picture described above accounts for the dominant contribution of the transitions relative to the A, B, and C features in the calculated XAS spectra. Additionally, for the Ru(III)-complexes, the B features contain a small contribution (<1%) from 2p → 4d(π) transitions. For [RuII(CN)6]4−, the B features contain a ∼3% contribution from transitions with 2p → CN(π*) character and the C peak has a 3% contribution from 2p → 4d(π) transitions. Finally, we find that the B features of the [RuII(bpy)3]2+ and [RuII(bpy)2Cl2] XAS spectra also exhibit an intensity contribution from Ru 2p → bpy(π*) transitions (∼30% for [RuII(bpy)3]2+). We note that these percentages, as well as the percentages in Tables 2 and 3, depend on the choice of the basis set; however, they provide a qualitative interpretation of the spectral features and rationalize the trends observed in the data. These calculated core-excited states will be used as the intermediate states for the Ru 2p4d RIXS calculations described below.
| Ru 5s | Ru 4d | N 2p | N 2s | C 2p | C 2s | Cl 3p | Cl 2p | H 1s | |
|---|---|---|---|---|---|---|---|---|---|
| [Ru III (NH 3 ) 6 ] 3+ | |||||||||
| 4d(σ) | 56% | 13% | 18% | 13% | |||||
| 4d(π) | 91% | 2% | 7% | ||||||
| NH3(σ) | 33% | 55% | 7% | 5% | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| [Ru III (NH 3 ) 5 Cl] 2+ | |||||||||
| 4d(σ) | 3% | 51% | 11% | 15% | 8% | 12% | |||
| 4d(π) | 83% | 11% | 6% | ||||||
| Cl(π) | 9% | 6% | 5% | 80% | |||||
| NH3(σ) | 29% | 50% | 7% | 9% | 5% | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| [Ru II (CN) 6 ] 4− | |||||||||
| CN(π*) | 23% | 26% | 28% | 20% | |||||
| 4d(σ) | 51% | 5% | 23% | 12% | 8% | ||||
| 4d(π) | 76% | 24% | |||||||
| CN(5σ) | 18% | 49% | 10% | 18% | |||||
| CN(π) | 19% | 46% | 35% | ||||||
| CN(4σ) | 15% | 5% | 23% | 9% | 48% | ||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| [Ru II (bpy) 3 ] 2+ | |||||||||
| 4d(σ) | 37% | 11% | 8% | 23% | 11% | 10% | |||
| bpy(π*) | 6% | 25% | 1% | 66% | 1% | ||||
| 4d(π) | 76% | 2% | 16% | 4% | |||||
| bpy | 12% | 17% | 3% | 51% | 2% | 15% | |||
| Molecule | Peak | Pos. (eV) | Character | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp.b | Calc.a | Ru 5s | Ru 4d | N 2p | N 2s | C 2p | C 2s | Cl p | H 1s | ||
| a A global shift of 96.3 eV is applied to the calculated spectra. b n.a. = peak is not well-defined in the experimental data. | |||||||||||
| [RuIII(NH3)5Cl]2+ | a | 2837.7 | 2838.0 | 60% | 14% | 26% | |||||
| b | 2833.3 | 2833.3 | 3% | 58% | 36% | 2% | |||||
| c | n.a. | 2829.8 | 4% | 91% | 5% | ||||||
| [RuIII(NH3)6]3+ | a | 2838.1 | 2838.2 | 95% | 5% | ||||||
| b | 2833.2 | 2833.8 | 2% | 38% | 53% | 7% | |||||
| c | n.a. | 2830.6 | 9% | 91% | |||||||
| [RuII(CN)6]4− | a | 2837.0 | 2837.1 | 94% | 4% | 1% | |||||
| b | 2833.0 | 2832.5 | 38% | 43% | 10% | 2% | 7% | ||||
| c | 2830.7 | 2830.2 | 34% | 9% | 10% | 47% | |||||
| [RuII(bpy)3]2+ | a | 2837.3 | 2837.3 | 90% | 6% | 1% | 3% | ||||
| b | n.a. | 2832.7 | 38% | 2% | 42% | 2% | 16% | ||||
| c | n.a. | 2830.2 | 30% | 16% | 40% | 7% | 7% | ||||
3.2 Non-resonant Ru L3-edge VtC X-ray emission
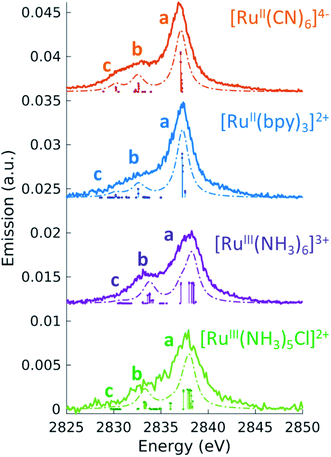
Before turning to the 2p4d RIXS measurements, we present for comparison the non-resonant VtC (Lβ2,15) XES emission spectra. These spectra were measured at an incident energy of 2950 eV (above the Ru L3-edge ionization potential and below the L2-edge) and are shown as solid lines in Fig. 3. All the measured spectra manifest a main peak (at around 2837.5 eV) and a less intense broad feature on the lower energy side. The lower signal-to-noise for the [RuIII(NH3)5Cl]2+ spectrum arises from both the lower concentration of the sample (10 mM vs. >50 mM) and lower acquisition time (40 m vs. ∼2 h) with respect to the other complexes. Same considerations apply for the [RuII(bpy)2Cl2] spectrum, which is not reported here since it is found to be nominally identical to the [RuII(bpy)3]2+ spectrum (see ESI Fig. 3†).To interpret the measured non-resonant VtC XES spectra, we perform TDDFT calculations as described in the Methods section. 4d → 2p transitions are calculated for the relaxed 2p-hole ionized state of each Ru model complex and shifted in energy to overlap the measured and calculated position of the most intense feature in the [RuII(bpy)3]2+ spectrum. As shown in Fig. 3, the calculations reproduce the experimental measurements well. They show an intense peak (labeled a) and two low-energy weaker features (labeled b and c). Table 3 also reports the peaks positions of the measured and calculated spectra, determined by fitting the spectra with a sum of Voigt and Lorentzian profiles, as described in ESI Section 4.† We notice that the calculations show two lower energy side peaks for each complex (b and c). However, experimentally, the fit can only robustly disentangle these two low-energy side features for [RuII(CN)6]4−. This is due the resolution of the measured spectra, which is limited by the natural lifetime of the 2p-hole (∼1.75 eV72).
To analyze the character of the spectral features, we utilize a previously described weighting scheme.73 After identifying the most dominant transitions within a specific energy range (i.e. the transitions of peaks a, b, c), we decompose their valence molecular orbitals contributions into weighted sums of atomic orbitals. The analysis is detailed in the ESI† and the results are reported in Table 3. It is clear that we can correlate the intensity of the 4d → 2p peaks to their percent 4d character, reported in Table 3. For [RuII(bpy)3]2+, [RuII(CN)6]4−, and [RuIII(NH3)6]3+, we find that peak a is dominated by 4d(π) → 2p transitions. From the values reported in Table 3, we notice that the 4d(π) orbitals of the 2p-hole ionized systems have higher Ru 4d contribution with respect to the GS orbitals (see Table 2). This is due to the fact that the ionization lowers the energy of the 4d orbitals, which decreases the 4d(π) back-donation. For [RuIII(NH3)5Cl]2+, peak a also contains contributions from Cl(π) → 2p transitions. Similarly to what discussed for the XAS measurements and as further detailed in ESI Section 2,† the peak a position encodes information on both the effective charge at the metal and the ligand field strength. Finally, we observe that peak a is wider for Ru(III)-complexes than for Ru(II)-complexes. The calculations capture this same trend and indicate that this is due to the broken degeneracy of the unfilled 4d(π) orbitals for d5 configurations.
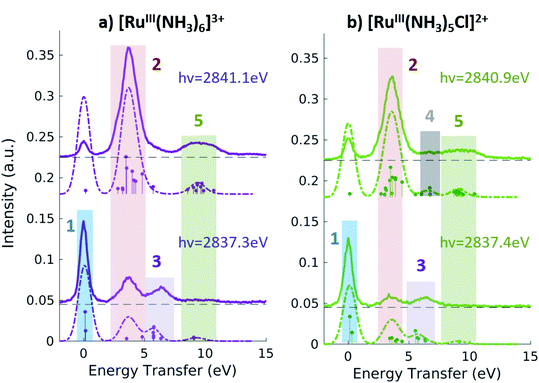
3.3 Ru L3-edge VtC resonant inelastic X-ray scattering
For all Ru-complexes, 4d → 2p X-ray emission spectra were collected with incident X-ray energy at the position of the A, B, and C peaks of the respective PFY-XAS spectra (see Table 1). This process is illustrated in Fig. 1a and yields Ru 2p4d RIXS spectra, which are shown as a function of energy transfer in Fig. 4 and 5 (solid lines). All spectra show an elastic peak at 0 eV, a dominant peak between 3.5 and 5 eV, and some less intense peaks at higher energy transfers. As for the VtC XES spectra described in the previous section, the intensity of the peaks reflects the contribution of Ru 4d orbital character to the transitions and it is therefore indicative of the metal–ligand covalency. Qualitatively, the dominant peak arises mostly from 4d(π) → 2p transitions, while the less intense peaks arise from transitions from occupied π and/or σ ligand orbitals mixed with Ru 4d characters. The peak positions report directly on the energy of the valence-excited states with respect to the ground state, as discussed below.The dashed lines in Fig. 4 and 5 show corresponding theoretical spectra obtained using TDDFT calculated core-excited (intermediate) and valence-excited (final) states in eqn (1). The calculated spectra reproduce reliably all the experimental features, except for the intensity of the resonant elastic peak. The cause of the overestimated elastic scattering intensity is discussed in ref. 28, and this does not affect the description and interpretation of the inelastic features that we focus on here. Fig. 4 and 5 also show discrete transitions below each calculated spectrum. These represent the couplings between the final states and the one intermediate state with the highest oscillator strength in the incident energy range of the X-ray absorption resonance considered (see Fig. 2). By examining the character of the final states that have the strongest couplings, we identify the dominant transitions between the GS orbitals (which are classified in Table 2) for each of the calculated spectral features. The results are shown in Table 4 and discussed below.
| Peak | Pos. (eV) | Character | Main contribution | |
|---|---|---|---|---|
| Exp. | Calc. | |||
| [Ru II (CN) 6 ] 4− | ||||
| 1 | 5.0 | 5.1 | MC | 4d(π)−1 4d(σ)+1 |
| 2 | 6.2 | 6.3 | MLCT | 4d(π)−1 CN(π*)+1 |
| 3 | 9.9 | 10.0 | LMCT | CN(π)−1 4d(σ)+1 |
| 4 | 10.9 | 10.5 | LC | CN(5σ)−1 CN(π*)+1 |
| 5 | ∼12 | 12.5 | LMCT | CN(4σ)−1 4d(σ)+1 |
| 6 | ∼13 | 12.7 | LC | CN(4σ)−1 CN(π*)+1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| [Ru III (NH 3 ) 6 ] 3+ | ||||
| 1 | 0 | 0.1 | — | 4d(π)+1/−1 |
| 2 | 3.7 | 3.7 | MC | 4d(π)−1 4d(σ)+1 |
| 3 | 6.3 | 5.7 | LMCT | NH3(σ)−1 4d(π)+1 |
| 5 | 9.5 | 9.4 | LMCT | NH3(σ)−1 4d(σ)+1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| [Ru III (NH 3 ) 5 Cl] 2+ | ||||
| 1 | 0 | 0.1 | — | 4d(π)+1/−1 |
| 2 | 3.6 | 3.6 | (A) LMCT (B) MC | (A) Cl(π)−1 4d(π)+1 (B) 4d(π)−1 4d(σ)+1 |
| 3 | 6.4 | 5.7 | LMCT | NH3(σ)−1 4d(π)+1 |
| 4 | n.a. | 6.6 | LMCT | Cl(π)−1 4d(σ)+1 |
| 5 | 9.2 | 9.0 | LMCT | NH3(σ)−1 4d(σ)+1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| [Ru II (bpy) 3 ] 2+ | ||||
| 1 | 4.0 | 3.8 | MLCT + MC | 4d(π)−1 bpy(π*)+1 + 4d(π)−1 4d(σ)+1 |
| 2 | ∼8.5 | 8–10 | LC + LMCT | bpy−1bpy(π*)+1 + bpy−14d(σ)+1 |
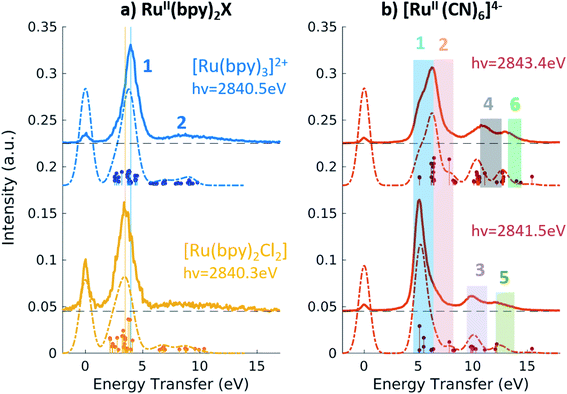
Fig. 4a shows the spectra of [RuII(bpy)3]2+ and [RuII(bpy)2Cl2] measured with incident energy set at the B PFY-XAS peak of each complex. As detailed above, for these complexes the B peak is dominated by 2p → 4d(π) transitions, but also contains a contribution from 2p → bpy(π*) transitions. Therefore, we find that the most intense feature of the RIXS spectra (peak 1 in Fig. 4) includes both 4d(π)−1 bpy(π*)+1 (MLCT) and 4d(π)−1 4d(σ)+1 (MC) final-state configurations. In our notation, −1/+1 refer to a loss/gain of an electron. Specifically for [RuII(bpy)3]2+, we find that the MLCT transitions dominate the spectra below 2.9 eV, while the MC excitations dominate at higher energy transfer. This is consistent with the known excited state dynamics of the complex, which exhibit long-lived lower-lying MLCT states.10 In summary, the peak position of feature 1, which is found at ∼4 eV, can be considered as a direct measure of the energy of the MC state (with respect to the GS) in [RuII(bpy)3]2+ and similarly in [RuII(bpy)2Cl2]. Specifically, we find it to be 4.0 eV for [RuII(bpy)3]2+ and 3.5 eV for [RuII(bpy)2Cl2]. The difference between these two values reflects the different ligand field strengths of the two complexes due to the substitution of one bpy ligand with two Cl ligands, in agreement with the spectrochemical series. We note that a previous approximate measurement of the ligand field of [RuII(bpy)3]2+ was possible only through a time-resolved laser pump X-ray probe L3-edge XAS experiment, and reported to be 3.75 eV.14
The broad low-intensity feature (feature 2) centered at ∼8.5 eV in the [RuII(bpy)3]2+ and [RuII(bpy)2Cl2] spectra reports on the manifold of high-energy valence-excited states, mostly of ligand-to-metal charge transfer (LMCT) and LC character. The broadness of this feature reflects the high density of non-degenerate ligand orbitals due to the relatively electron rich bpy ligands, and its relatively low-intensity is indicative of low metal–ligand covalency. We notice that the calculations describe the transitions up to ∼9.8 eV, which is the calculated final state with the highest energy. Increasing the number of calculated valence-excited states (i.e. more than 1300 that are used for these calculations) would lead to a complete description of the high energy transfer feature. This calculation, however, is computationally expensive.
Fig. 4b shows the 2p4d RIXS spectra collected for [RuII(CN)6]4−, with incident energy set at the B and C PFY-XAS peaks. Table 4 summarizes the assignment of the experimental features through comparison with the calculations. Feature 1 (at 5.0 eV) corresponds to a MC excitation (4d(π)−1 4d(σ)+1). We are not aware of any previous measurement of the MC state energy for this complex. Feature 2 corresponds to a MLCT transition (4d(π)−1 CN(π*)+1). As expected, feature 1(2) is more intense when resonant at the B(C) peak of the XAS spectrum, whereas the remaining intensity at the C(B) peak is mainly due to the finite 2p-hole lifetime, and in part also to the mixed-character of the core-excited states. This is shown by the presence of discrete transitions (i.e. the vertical sticks plotted below the calculated spectra) for feature 1(2) at the C(B) peak, indicating a non-zero coupling between the core-excited state populated at the B(C) peak and the MLCT(MC) final state. Finally, high energy transfer peaks are mainly due to LMCT and LC transitions, as detailed in Table 4. We note that the measurements allow us to distinguish charge transfer states that are ∼1 eV apart in energy. For instance the difference between the energy of the MC and the MLCT states is found to be 1.2 eV (difference between feature 1 and 2 and between features 5 and 6 in Fig. 4b and Table 4).
Fig. 5 shows the resonant emission spectra measured at the A and B resonances of the [RuIII(NH3)6]3+ and [RuIII(NH3)5Cl]2+ PFY-XAS spectra. When measuring resonantly at the A peak of the PFY-XAS spectrum, the 4d(π) → 2p transitions yield a quasi-elastic peak at ∼0 eV energy transfer (feature 1). In the calculations, the peak position of feature 1 (∼0.1 eV) reflects the loss of degeneracy of the 4d(π) orbitals due to the d5 configuration. Feature 2 correspond to the 4d(π)−1 4d(σ)+1 configuration and, again, is a direct measure of the ligand field of the complex. We find a value of 3.7 eV for [RuIII(NH3)6]3+ and 3.6 eV for [RuIII(NH3)5Cl]2+, indicating the weakening of the ligand environment containing Cl atoms. These numbers are within 0.1 eV agreement with the values obtained from the splitting of the A and B peaks in the PFY-XAS spectra (see Table 1). However, the small differences between the ligand field splitting energies extracted through XAS and VtC RIXS can be due to the 2p-hole presence in the XAS measurements. In contrast, VtC RIXS is not affected by the 2p-hole and therefore could extract the ligand field splitting energy more accurately (see also discussion below).
The peaks above 5 eV energy transfer are attributed to LC excitations. Noticeably, feature 4 (∼6.6 eV) is present only for the [RuIII(NH3)5Cl]2+ at the B resonance, both in data and calculation, and absent in the [RuIII(NH3)6]3+ calculated and measured spectra. By analysis of the calculations, the main character of the this peak is assigned to a Cl(π)−1 4d(σ)+1 final state. This confirms the sensitivity of the 2p4d RIXS measurements to the ligand environment around the metal.
In summary, the measured Ru 2p4d RIXS features have been assigned to valence excitations through comparison with calculations. For all Ru-complexes, measuring the RIXS spectrum resonantly at the B peak of the PFY-XAS spectrum yields a direct measure of the energy of the MC state. MC excitations are usually obscured in the UV-vis spectrum and, in case of Ru(II)-complexes, cannot be observed in XAS measurements. In our RIXS measurements, the MC state energies can be compared to the energies of other valence excitations, such as MLCT transitions, to reveal information on the functional properties of the Ru-complexes. For instance, the fact that Ru-polypyridyl complexes have MC states with higher energy than the MLCT states is crucial for the photochemistry of these molecules. On the contrary, in Fe-polypyridyl complexes, MLCT states usually decay quickly to lower-lying MC states, leading, for instance, to worse photosynthetic efficiency. For comparison, the energy of the MC state of [FeII(bpy)3]2+ and [FeII(CN)6]4− are reported to be ∼2.2 eV38 and 3.5 eV,36 respectively.
Fig. 6 summarizes the values obtained for the MC state energies for the complexes investigated in this study. These values correspond to the ligand field splitting energies, since the dd multiplet effects for 4d systems are known to be small.68 Specifically, we have calculated the dd multiplet effects for Ru atoms to be ∼0.1 eV (see ESI Section 5†). The sensitivity of the Ru 2p4d RIXS measurements to the ligand environment allowed us to quantify the difference in ligand field splitting energies between complexes that differ for only one ligand; and additional spectral features are observed in the [RuIII(NH3)5Cl]2+ spectrum with respect to the [RuIII(NH3)6]3+ spectrum. This level of sensitivity to the ligand environment could not be obtained from the non-resonant VtC XES measurements shown in the previous section, and it is due to the higher resolution of the RIXS spectra with respect to VtC XES (and XAS) spectra. Moreover, we find that the 2p4d resonant spectra of the Ru-complexes are approximately ten times more intense than the corresponding non-resonant VtC XES spectra (see also ESI Fig. 4†), allowing for faster collection time and improved signal-to-noise. The approach presented here is applicable to the study of Ru-complexes and 4d metal complexes in general, and will enable the study of these systems in a large range of applications and chemical environments.
4. Conclusion
We have investigated the chemical bonding of Ru(II) and Ru(III) complexes solvated in water with a combination of X-ray absorption, VtC emission, and VtC RIXS measurements at the Ru L3-edge. All the experimental spectra have been described well by TDDFT calculations, and have thus allowed us to quantify the experimental observations in terms of the valence electronic structure. Through comparison with calculations, we have shown that measurements report on the metal–ligand covalency, oxidation state, ligand field splitting energy, and ligand identity of the Ru-complexes; and that greater sensitivity on these quantities is achieved with the RIXS measurements, with respect to XAS and VtC XES. In particular, the ligand field splitting energy can be directly extracted from the RIXS measurements and we have found it to be 5.0 eV for [RuII(CN)6]4−, 4.0 eV for [RuII(bpy)3]2+, 3.7 eV for [RuIII(NH3)6]3+, 3.6 eV for [RuIII(NH3)5Cl]2+, and 3.5 eV for [RuII(bpy)2Cl2]. In general, we have demonstrated that the 2p4d RIXS can directly measure the energies of the MC, LC, and CT states of the Ru complexes.Measuring the MC state energies is particularly important for complexes with fully filled 4d(π) orbitals, since the ligand field splitting energy cannot be accessed with ground-state XAS studies. Moreover, MC transitions are often obscured in the UV-vis spectrum by intense CT absorption bands; therefore the approach presented here can be of unique value for Ru and other 4d metals, in general. At the same time, the suppression of the core-hole lifetime broadening within the RIXS spectral features enables distinguishing sub-eV differences between valence excitations, such as closely separated MC and MLCT states. The interplay between the competing decay pathways is well understood for bipyridine complexes but is substantially less investigated for other types of ligands. 2p4d RIXS studies can therefore be used to investigate and screen multiple Ru-complexes and help the understanding of the formation and stabilization of charge separated states in these complexes. Moreover, the TDDFT approach presented here has allowed us to quantify the molecular orbitals contributions to the experimental VtC RIXS spectra; this will be helpful in predicting the role of different ligand environment when trying to design new Ru-complexes or tailor their properties. Finally, extending these methods to the time-resolved regime will enable the photoinduced dynamics to be followed for such systems. These advances can accelerate the development of novel functional materials.
In conclusion, we have performed a systematic experimental and computational study for characterizing the bonding properties of Ru(II) and Ru(III) complexes solvated in water. We have shown that state-of-the-art high-energy resolution tender X-ray spectroscopy methods and TDDFT calculations can now uniquely shed light on the valence structure of solvated 4d metal complexes.
Author contributions
E. B., B. A., A. T. G.-E., T. K., R. A.-M., and D. S. prepared and conducted the experiment at the SSRL. E. B., B. P., K. K., S. H. N., R. W. S., M. K., and D. S. analysed and/or interpreted the experimental data. D. R. N. and N. G. performed the TDDFT calculations. E. B., N. G., and D. S. wrote the article with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division under Award No. DE-AC02-76SF00515 (E. B., R. W. S.), KC-030105172685 (D. R. N., N. G.), DE-SC0019277 (B. P. and M. K.). B. P. acknowledges support by the NSF GRFP (No. DGE-1762114). Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. This research benefited from computational resources provided by EMSL, a DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research and located at PNNL. PNNL is operated by Battelle Memorial Institute for the United States Department of Energy under DOE Contract No. DE-AC05-76RL1830. This research also used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231.References
- Y. Qin and Q. Peng, Ruthenium sensitizers and their applications in dye-sensitized solar cells, Int. J. Photoenergy, 2012, 2012, 291579 CrossRef.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Visible light photoredox catalysis with transition metal complexes: applications in organic synthesis, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- B. S. Howerton, D. K. Heidary and E. C. Glazer, Strained ruthenium complexes are potent light-activated anticancer agents, J. Am. Chem. Soc., 2012, 134, 8324–8327 CrossRef CAS PubMed.
- A. W. King, L. Wang and J. J. Rack, Excited state dynamics and isomerization in ruthenium sulfoxide complexes, Acc. Chem. Res., 2015, 48, 1115–1122 CrossRef CAS PubMed.
- F. Heinemann, J. Karges and G. Gasser, Critical overview of the use of Ru(ii) polypyridyl complexes as photosensitizers in one-photon and two-photon photodynamic therapy, Acc. Chem. Res., 2017, 50, 2727–2736 CrossRef CAS PubMed.
- G. C. Vougioukalakis, A. I. Philippopoulos, T. Stergiopoulos and P. Falaras, Contributions to the development of ruthenium-based sensitizers for dye-sensitized solar cells, Coord. Chem. Rev., 2011, 255, 2602–2621 CrossRef CAS.
- A. A. Cordones, et al., Transient metal-centered states mediate isomerization of a photochromic ruthenium-sulfoxide complex, Nat. Commun., 2018, 9, 1989 CrossRef PubMed.
- P. S. Wagenknecht and P. C. Ford, Metal centered ligand field excited states: their roles in the design and performance of transition metal based photochemical molecular devices, Coord. Chem. Rev., 2011, 255, 591–616 CrossRef CAS.
- A. Juris, et al., Ru(ii) polypyridine complexes: photophysics, photochemistry, electrochemistry, and chemiluminescence, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- D. W. Thompson, A. Ito and T. J. Meyer, [Ru(bpy)3]2+* and other remarkable metal-to-ligand charge transfer (MLCT) excited states, Pure Appl. Chem., 2013, 85, 1257–1305 CAS.
- M. W. Mara, et al., Metalloprotein entatic control of ligand-metal bonds quantified by ultrafast X-ray spectroscopy, Science, 2017, 356, 1276–1280 CrossRef CAS PubMed.
- K. Getty, M. U. Delgado-Jaime and P. Kennepohl, Assignment of pre-edge features in the Ru K-edge X-ray absorption spectra of organometallic ruthenium complexes, Inorg. Chim. Acta, 2008, 361, 1059 CrossRef CAS PubMed.
- G. Assat, A. Iadecola, C. Delacourt, R. Dedryvère and J.-M. Tarascon, Decoupling cationic–anionic redox processes in a model Li-rich cathode via operando X-ray absorption spectroscopy, Chem. Mater., 2017, 29, 9714–9724 CrossRef CAS.
- W. Gawelda, et al., Electronic and molecular structure of photoexcited [Ruii(bpy)3]2+ probed by picosecond X-ray absorption spectroscopy, J. Am. Chem. Soc., 2006, 128, 5001–5009 CrossRef CAS PubMed.
- J.-Y. Kim, et al., 4d Electronic structure analysis of ruthenium in the perovskite oxides by Ru K- and L-edge XAS, J. Synchrotron Radiat., 2001, 8, 722–724 CrossRef CAS PubMed.
- B. E. Van Kuiken, et al., Probing the electronic structure of a photoexcited solar cell dye with transient X-ray absorption spectroscopy, J. Phys. Chem. Lett., 2012, 3, 1695–1700 CrossRef CAS PubMed.
- T. K. Sham, X-ray absorption spectra of ruthenium l edges in hexaammineruthenium trichloride, J. Am. Chem. Soc., 1983, 105, 2269–2273 CrossRef CAS.
- B. E. Van Kuiken, et al., Simulating Ru L3-edge X-ray absorption spectroscopy with time-dependent density functional theory: Model complexes and electron localization in mixed-valence metal dimers, J. Phys. Chem. A, 2013, 117, 4444–4454 CrossRef CAS PubMed.
- I. Alperovich, et al., Understanding the electronic structure of 4d metal complexes: from molecular spinors to L-edge spectra of a di-Ru catalyst, J. Am. Chem. Soc., 2011, 133, 15786–15794 CrossRef CAS PubMed.
- C. J. Pollock and S. DeBeer, Insights into the geometric and electronic structure of transition metal centers from valence-to-core X-ray emission spectroscopy, Acc. Chem. Res., 2015, 48, 2967–2975 CrossRef CAS PubMed.
- P. Glatzel and U. Bergmann, High resolution 1s core hole X-ray spectroscopy in 3d transition metal complexes—electronic and structural information, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS . Synchrotron Radiation in Inorganic and Bioinorganic Chemistry.
- D. Sokaras, et al., A seven-crystal Johann-type hard X-ray spectrometer at the stanford synchrotron radiation lightsource, Rev. Sci. Instrum., 2013, 84, 053102 CrossRef CAS PubMed.
- A. M. March, et al., Probing transient valence orbital changes with picosecond valence-to-core x-ray emission spectroscopy, J. Phys. Chem. C, 2017, 121, 2620–2626 CrossRef CAS PubMed.
- K. Ledbetter, et al., Excited state charge distribution and bond expansion of ferrous complexes observed with femtosecond valence-to-core X-ray emission spectroscopy, J. Chem. Phys., 2020, 152, 074203 CrossRef CAS PubMed.
- C. J. Pollock and S. DeBeer, Valence-to-core X-ray emission spectroscopy: a sensitive probe of the nature of a bound ligand, J. Am. Chem. Soc., 2011, 133, 5594–5601 CrossRef CAS PubMed.
- Y.-T. Tseng, et al., To transfer or not to transfer? Development of a dinitrosyl iron complex as a nitroxyl donor for the nitroxylation of an Feiii–porphyrin center, Chem.–Eur. J., 2015, 21, 17570–17573 CrossRef CAS PubMed.
- V. Martin-Diaconescu, et al., Kβ valence to core X-ray emission studies of Cu(i) binding proteins with mixed methionine–histidine coordination. Relevance to the reactivity of the M-and H-sites of peptidylglycine monooxygenase, Inorg. Chem., 2016, 55, 3431–3439 CrossRef CAS PubMed.
- N. Levin, et al., Ruthenium 4d-to-2p X-ray emission spectroscopy: a simultaneous probe of the metal and the bound ligands, Inorg. Chem., 2020, 59, 8272–8283 CrossRef CAS PubMed.
- B. Ravel, et al., Nonresonant valence-to-core X-ray emission spectroscopy of niobium, Phys. Rev. B, 2018, 97, 125139 CrossRef CAS PubMed.
- C. J. Doonan, et al., High-resolution X-ray emission spectroscopy of molybdenum compounds, Inorg. Chem., 2005, 44, 2579–2581 CrossRef CAS PubMed.
- R. G. Castillo, J. T. Henthorn, J. McGale, D. Maganas and S. DeBeer, Kβ X-ray emission spectroscopic study of a second-row transition metal (Mo) and its application to nitrogenase-related model complexes, Angew. Chem., Int. Ed., 2020, 59, 12965–12975 CrossRef CAS PubMed.
- M. O. Krause, Atomic radiative and radiationless yields for K and L shells, J. Phys. Chem. Ref. Data, 1979, 8, 307–327 CrossRef CAS.
- U. Bergmann and P. Glatzel, X-ray emission spectroscopy, Photosynth. Res., 2009, 102, 255 CrossRef CAS PubMed.
- M. Lundberg and P. Wernet, Resonant inelastic X-ray scattering (RIXS) studies in chemistry: present and future, in Synchrotron Light Sources and Free-Electron Lasers: Accelerator Physics, Instrumentation and Science Applications, 2nd edn, 2019 Search PubMed.
- M. M. van Schooneveld, et al., A multispectroscopic study of 3d orbitals in cobalt carboxylates: the high sensitivity of 2p3d resonant X-ray emission spectroscopy to the ligand field, Angew. Chem., Int. Ed., 2013, 52, 1170–1174 CrossRef CAS PubMed.
- K. Kunnus, et al., Viewing the valence electronic structure of ferric and ferrous hexacyanide in solution from the Fe and cyanide perspectives, J. Phys. Chem. B, 2016, 120, 7182–7194 CrossRef CAS PubMed.
- A. W. Hahn, et al., Probing the valence electronic structure of low-spin ferrous and ferric complexes using 2p3d resonant inelastic X-ray scattering (RIXS), Inorg. Chem., 2018, 57, 9515–9530 CrossRef CAS PubMed.
- R. M. Jay, et al., The nature of frontier orbitals under systematic ligand exchange in (pseudo-)octahedral Fe(ii) complexes, Phys. Chem. Chem. Phys., 2018, 20, 27745–27751 RSC.
- R. M. Jay, et al., Disentangling transient charge density and metal–ligand covalency in photoexcited ferricyanide with femtosecond resonant inelastic soft X-ray scattering, J. Phys. Chem. Lett., 2018, 9, 3538–3543 CrossRef CAS PubMed.
- P. Wernet, et al., Orbital-specific mapping of the ligand exchange dynamics of Fe(Co)5 in solution, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- R. Thomas, et al., Resonant inelastic X-ray scattering of molybdenum oxides and sulfides, J. Phys. Chem. C, 2015, 119, 2419–2426 CAS.
- H. Suzuki, et al., Spin waves and spin-state transitions in a ruthenate high-temperature antiferromagnet, Nat. Mater., 2019, 18, 563–567 CrossRef CAS PubMed.
- B. W. Lebert, et al., Resonant inelastic X-ray scattering study of $\alpha$-RuCl3: a progress report, J. Phys.: Condens. Matter, 2020, 32, 144001 CrossRef CAS PubMed.
- S. Nowak, et al., A versatile Johansson-type tender X-ray emission spectrometer, Rev. Sci. Instrum., 2020, 91, 033101 CrossRef CAS PubMed.
- D. R. Nascimento, et al., A time-dependent density functional theory protocol for resonant inelastic X-ray scattering calculations, arXiv: 2010.03092 (physics.chem-ph), 2020.
- M. Petersilka, U. Gossmann and E. Gross, Excitation energies from time-dependent density-functional theory, Phys. Rev. Lett., 1996, 76, 1212 CrossRef CAS PubMed.
- M. E. Casida and D. Chong, Recent advances in density functional methods, Recent Advances in Computational Chemistry, 1995, DOI:10.1142/2914.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory for radicals: an improved description of excited states with substantial double excitation character, Chem. Phys. Lett., 1999, 302, 375–382 CrossRef CAS.
- M. Valiev, et al., Nwchem: a comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- E. Aprà, et al., Nwchem: past, present, and future, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, Linear-response and real-time time-dependent density functional theory studies of core-level near-edge X-ray absorption, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, Simulating valence-to-core X-ray emission spectroscopy of transition metal complexes with time-dependent density functional theory, J. Chem. Theory Comput., 2015, 11, 5804–5809 CrossRef CAS PubMed.
- F. Gel'mukhanov and H. Ågren, Resonant inelastic X-ray scattering with symmetry-selective excitation, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 4378–4389 CrossRef PubMed.
- X. Zhang and J. M. Herbert, Analytic derivative couplings in time-dependent density functional theory: quadratic response theory versus pseudo-wavefunction approach, J. Chem. Phys., 2015, 142, 064109 CrossRef PubMed.
- Q. Ou, G. D. Bellchambers, F. Furche and J. E. Subotnik, First-order derivative couplings between excited states from adiabatic TDDFT response theory, J. Chem. Phys., 2015, 142, 064114 CrossRef PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- T. Noro, M. Sekiya and T. Koga, Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n= D, T, Q), Theor. Chem. Acc., 2012, 131, 1124 Search PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. Klamt and G. Schüürmann, Cosmo: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- D. M. York and M. Karplus, A smooth solvation potential based on the conductor-like screening model, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic total energy using regular approximations, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- C. van Wüllen, Molecular density functional calculations in the regular relativistic approximation: method, application to coinage metal diatomics, hydrides, fluorides and chlorides, and comparison with first-order relativistic calculations, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- P. Nichols, N. Govind, E. J. Bylaska and W. A. de Jong, Gaussian Basis Set and Planewave Relativistic Spin-Orbit Methods in NWChem, J. Chem. Theory Comput., 2009, 5, 491–499 CrossRef CAS PubMed.
- R. D. Cowan, The Theory of Atomic Structure and Spectra, University of California Press, Berkeley, CA, USA, 1981 Search PubMed.
- E. Ronca, F. De Angelis and S. Fantacci, Time-dependent density functional theory modeling of spin–orbit coupling in ruthenium and osmium solar cell sensitizers, J. Phys. Chem. C, 2014, 118, 17067–17078 CrossRef CAS.
- F. M. F. de Groot, et al., Differences between L3 and L2 X-ray absorption spectra of transition metal compounds, J. Chem. Phys., 1994, 101, 6570–6576 CrossRef.
- F. Neese, Software update: the orca program system, version 4.0, WIREs Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- V. Barone and M. Cossi, Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Kubin, et al., Probing the oxidation state of transition metal complexes: a case study on how charge and spin densities determine mn L-edge X-ray absorption energies, Chem. Sci., 2018, 9, 6813–6829 RSC.
- M. Ohno and G. A. van Riessen, Hole-lifetime width: a comparison between theory and experiment, J. Electron Spectrosc. Relat. Phenom., 2003, 128, 1–31 CrossRef CAS.
- W. M. Holden, E. P. Jahrman, N. Govind and G. T. Seidler, Probing sulfur chemical and electronic structure with experimental observation and quantitative theoretical prediction of Kα and valence-to-core Kβ X-ray emission spectroscopy, J. Phys. Chem. A, 2020, 124, 5415–5434 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc06227h |
| This journal is © The Royal Society of Chemistry 2021 |