Coarse-grained simulations of ionic liquid materials: from monomeric ionic liquids to ionic liquid crystals and polymeric ionic liquids†
Yong-Lei
Wang‡§
 *a,
Bin
Li‡
*a,
Bin
Li‡
 b and
Aatto
Laaksonen
acde
b and
Aatto
Laaksonen
acde
aDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, SE-10691 Stockholm, Sweden. E-mail: wangyonl@gmail.com
bSchool of Chemical Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, P. R. China
cState Key Laboratory of Materials-Oriented and Chemical Engineering, Nanjing Tech University, Nanjing 210009, P. R. China
dCentre of Advanced Research in Bionanoconjugates and Biopolymers, Petru Poni Institute of Macromolecular Chemistry, Aleea Grigore Ghica-Voda, 41A, 700487 Iasi, Romania
eDepartment of Engineering Sciences and Mathematics, Division of Energy Science, Luleå University of Technology, SE-97187 Luleå, Sweden
First published on 13th August 2021
Abstract
Ionic liquid (IL) materials are promising electrolytes with striking physicochemical properties for energy and environmental applications. Heterogeneous structures and transport quantities of monomeric and polymeric ILs are intrinsically intercorrelated and span multiple spatiotemporal scales, which is more feasible for coarse-grained (CG) simulations than atomistic modelling. Herein we constructed a novel CG model for ethyl-imidazolium tetrafluoroborate ILs with varied cation alkyl chains ranging from C2 to C20, and the interaction parameters were validated against representative static and dynamic properties that were obtained from atomistic reference simulations and experimental characterizations at relevant thermodynamic states. This CG model was extended to study thermotropic phase behaviors of monomeric ILs and to explore ion association structures and ion transport quantities in polymeric ILs with different architectures. A systematic analysis of structural and dynamical quantities identifies an evolution of liquid morphology from homogeneous to nanosegregated structures and then a smectic mesomorphism via a gradual lengthening of cation alkyl chains, and thereafter a distinct structural transition characterized by a monotonic decrease in orientational and translational order parameters in a sequential heating cascade. Backbone and pendant polymeric ILs exhibit evident anion association structures with cation monomers and polymer chains, and striking intra- and interchain coordinations between cation monomers owing to an intrinsic polymer architecture effect. Such a peculiar ion pairing association leads to a progressive increase in anion intrachain hopping probabilities, and a concomitant decrease in anion interchain hopping events with a gradual lengthening of polymeric ILs. The anion diffusivities in polymeric ILs are intrinsically correlated with ion pairing association lifetimes and ion structural relaxation times via a universal power law correlation D ∼ τ−1, irrespective of polymer architectures.
I. Introduction
Ionic liquids (ILs) are an emerging class of molten salts entirely composed of bulky organic cations and weakly coordinating anions with their melting points below 100 °C.1–4 Recent years have seen a great enthusiasm for imidazolium-based ILs regarding their utilities as fascinating functional materials in diverse applications ranging from material synthesis and catalysis to gas adsorption and separation, electrotunable lubrication and tribology, and electrochemical devices for energy storage and harvesting.5–9 These promising applications of imidazolium ILs are mainly attributed to multifaceted physicochemical characteristics of ILs, such as nonflammability and negligible volatility, reasonable viscosity-conductivity features, high electrochemical- and thermal-oxidative stabilities, wide electrochemical windows, and exceptional affinities to molecular compounds having varied polarities.1–5 These remarkable properties of imidazolium ILs are intrinsically correlated with inherent ion structures and delicate intra- and intermolecular interactions ranging from weak, isotropic and nonspecific forces to strong, anisotropic and specific forces among constituent ions.2–4 Additionally, these fascinating quantities can be widely tuned in a controllable fashion via a judicious selection of cation–anion moieties and by mutating specific atoms in constituent ions, leading to the formation of remarkable liquid structures and endowing imidazolium ILs with abundant phase behaviors.4,10–14Both experimental and computational studies have demonstrated that imidazolium ILs can form segregated liquid organization at nanoscopic level when cation alkyl chains are longer than C4. This is intrinsically attributed to electrostatic interactions among charged species which force cation alkyl chains and other hydrophobic groups to aggregate and form apolar domains that are either segregated or interpenetrated with polar network in IL matrices.2,4,15–18 Furthermore, the dispersion associations among apolar units increase with lengthening cation alkyl chains, and when cation alkyl chains are adequately long, the strength of their preferential dispersion interactions facilitates the alignment of alkyl chains in parallel and the formation of peculiar ionic liquid crystalline (ILC) phase that has unique features beyond traditional liquid crystals.12,13,19,20 Applications of imidazolium ILCs are mainly concentrated on their anisotropic ion transport properties as they are promising electrolyte materials for electrochemical applications.5,7,13,14,21
The macroscopic functionalities of imidazolium ILs can be further expanded via polymerization of imidazolium cations.22–25 The imidazolium-based poly(ionic liquid)s (PILs), either backbone or pendant type, present additional promising characteristics, such as high electrochemical and mechanical stabilities, and distinct ion transport quantities compared with monomeric ILs.26–32 These intrinsic characteristics of PILs have triggered significant enthusiasm in the pursuit of polyelectrolyte materials possessing an optimal combination of mechanical strength, ion conductivity, and transference number for a wide range of energy storage and conversion applications.5,7,24,25 In contrast to extensive experimental and computational characterizations of physicochemical properties of pure ILs and IL-based mixtures, there are sporadic investigations concerning these quantities of PILs and salt-doped PIL materials. Recent experimental studies reported significant deviation in the dependency of ion conductivity from polymer segmental dynamics,27,28,33–35 and subsequent atomistic simulations30,32,36 demonstrated that anion mobility in PILs occurs via a combination of intra- and interchain ion hopping events through the formation and breaking of ion association structures between anions and PIL cation monomers. This feature is substantially different to transport quantities of anions in monomeric ILs, where anion diffusion is closely correlated with structural relaxation of surrounding ionic medium.4,11,37 Such a discrepancy was suggested to be the main origin of experimental observation in which long PILs exhibit higher ion conductivity than short PILs and monomeric ILs when compared at the same glass-transition-normalized temperature.38 The decoupling of ion transport quantities from segmental dynamics of PILs is essentially correlated with microstructures and mesoscopic morphologies of PILs, as revealed from recent multiscale modelling of imidazolium PILs consisting of varied anion moieties.5,29,36 This leads to complicated microstructural relaxations and the corresponding lifetimes spanning multiple temporal scales for ion association, ion hopping and diffusion,4,39–41 and spatial rearrangements of polar and apolar domains in bulk materials and in selective solvents.42,43 In this regard, multiscale modelling of monomeric IL and PIL materials combining all-atomistic (AA) and coarse-grained (CG) simulations is a promising procedure to explore complex phase behaviors of these ion-containing materials at extended spatiotemporal scales with a modest computational cost.3,4,44–48
Roy and coworkers proposed an idealized four-site CG model having characteristics resembling those of 1-butyl-3-methylimidazolium hexafluorophosphate ([C1C4IM][PF6]) IL for simulating solvation dynamics and charge transfer phenomena on microsecond time scale.49 The adopted coarse-graining strategy is similar in spirit to CG models for imidazolium ILs developed by Wang et al.15,44,50 and Karimi-Varzaneh et al.51 for studying aggregation structures of polar and apolar domains and ensuing dynamical quantities in heterogeneous IL matrices. The derived interaction parameters for CG beads were able to reproduce structural and energetic properties of a prototypical [C1C4IM][PF6] IL but with slaved transport quantities at a wide temperature range, which could be significantly improved via a rescaling of ion charges.52 Such a CG representation was adapted by Merlet and coworkers to explore capacitive properties of ILs used as electrolyte materials in electrochemical devices.53–56
Besides these CG representations, we made endeavors in previous studies to develop CG models for ILs consisting of imidazolium cations coupled with spherical anions.48,57 Instead of using analytical functions representing intermolecular interactions between CG beads, we derived tabulated potentials from reference radial distribution functions that were calculated from underlying AA MD simulations using the Newton Inversion and iterative Boltzmann Inversion methods.51,58 The developed CG models were further calibrated so as to capture essential physicochemical and structural features, and solute-based dynamics of model ionic fluids over a wide temperature range while being simple enough to be computationally economical.48
It should be particularly mentioned that these proposed CG models have been widely used to study static and dynamic quantities of isotropic phase of imidazolium ILs having short cation alkyl chains, and are rarely used to explore relevant properties of ILCs and PILs, as well as their functionalities in promising applications, due to limited transferability of these CG models in describing phase behaviors of ILs having long alkyl chains and of PILs with different polymer architectures. In the current work, following the parametrization strategy used in Bresme's work,59 we first adopt the coarse-graining scheme to construct CG model for 1-alkyl-3-ethylimidazolium tetrafluoroborate ([C2CnIM][BF4]) ILs, and thereafter calibrate interaction parameters against representative thermodynamics, structural, and dynamic properties that were obtained from reference AA MD simulations and experimental characterizations at relevant thermodynamic states. The constructed CG model for [C2CnIM][BF4] ILs and the derived effective interaction parameters between CG beads are extended to study thermotropic phase behaviors of monomeric ILs and to explore ion association structures and ion transport quantities in PILs with different architectures at extended spatiotemporal scales.
II. Description of coarse-grained model and validation of interaction parameters
A. The CG model for [C2CnIM][BF4] ILs
The CG model for [C2CnIM][BF4] ILs is constructed with the following principles: the planar imidazolium ring is represented by a single bead tagged as “IM” carrying a partial charge of +1.0e; the [BF4] anion is mapped into a single CG bead labelled as “BF” carrying a partial charge of −1.0e; each ethyl or ethylene unit is coarsened into one neutral CG bead, in which the head and tail beads are labelled as “CH” and “CT”, respectively, and the others are termed as “CE” for convenience of discussion (all these neutral CG beads have the same set of interaction parameters). Such a mapping scheme for a representative [C2C4IM][BF4] is illustrated in Fig. 1. The relative positions of these CG beads are determined from the center-of-mass of the corresponding atomistic units. It is noted that such a constructed CG model is compatible with that developed in previous studies for methyl-imidazolium ILs coupled with varied anion species,44,46–51,53,54,60 and exhibit considerable transferability to triazolium-based ILs.61The bonded interactions between CG beads consisting of bond stretching, angle bending and dihedral terms have a similar form with those for the corresponding atomistic models but with different force constant parameters, which were originally taken from previous works,48,59 and thereafter calibrated to reproduce probability distributions of bond lengths, angles, and dihedrals that were extracted from extensive atomistic reference simulations of [C2CnIM][BF4] ILs at different thermodynamic states. The interaction potential forms, the determined interaction parameters for constructed CG model for [C2CnIM][BF4] ILs, and AA and CG MD simulation protocols are provided in the ESI.†
B. Structural properties and liquid organizations
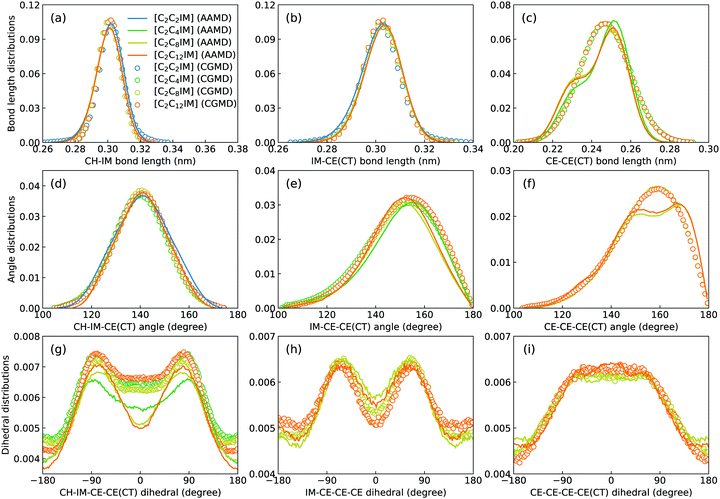
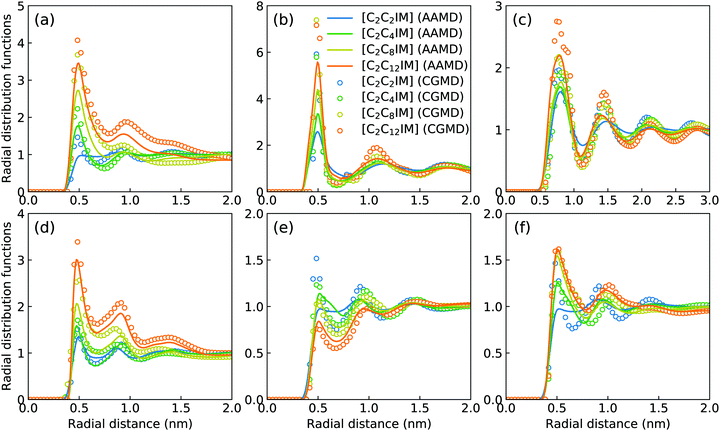
Fig. 2 presents a comprehensive comparison of probability distributions of bond lengths, angles, and dihedrals among CG beads obtained from CG MD simulations with those determined from reference atomistic modelling systems at relevant thermodynamic states. It is clearly illustrated that probability distributions of bond lengths and angles are quantitatively reproduced from CG MD simulations. The marginal discrepancy between AA and CG MD simulations of CE–CE(CT) bond length (Fig. 2(c)) and CE–CE–CE(CT) angle distribution (Fig. 2(f)) is mainly attributed to dihedral preference and constrained distribution of C–H bonds having gauche and trans configurations around C–C bond in the ethyl group in atomistic model, which are totally averaged out in the simplified CG model, leading to the smooth distribution of CE–CE(CT) bond length and CE–CE–CE(CT) angle obtained from CG MD simulations. The bimodal feature in probability distributions for CH–IM–CE–CE(CT) and IM–CE–CE–CE dihedrals and the flat arch character for CE–CE–CE–CE(CT) dihedral distributions determined from the constructed CG model exhibit qualitative agreement with that calculated from reference AA MD simulations.The intermolecular structures of CG beads are quantified via the calculation of site–site radial distribution functions (RDFs) to concrete their specific spatial correlations in heterogeneous IL matrices. Fig. 3 presents representative RDFs for CG bead pairs, and these RDFs are compared with their counterparts determined from atomistic reference simulations at similar thermodynamic states. Both peak positions and plot shapes of reference RDFs determined from atomistic simulations are well reproduced from CG MD simulations, indicating that the constructed CG model and the calibrated interaction parameters can essentially retain local ion structures in [C2CnIM][BF4] ILs having different cation alkyl chains. The IM–IM pair RDFs (Fig. 3(a)) exhibit considerably short-ranged correlations, which are comparable with those for CH–CH pair RDFs (Fig. 3(d)) due to their intrinsic positions in cation framework. The existence of multiple secondary peaks in IM–BF (Fig. 3(b)) and BF–BF (Fig. 3(c)) pair RDFs indicates strong structural correlations among these charged beads via electrostatic interactions, which is an intrinsic characteristic of a model system dominated by coulombic interactions among charged species. These ion-related structures in IL matrices have an impact on the number of counterions present in solvation shells of a given ion, and an even significant effect on spatial distributions of ions with like charges nearby.
It should be noted that there are marginal variations of peak intensities and peak positions in RDF plots obtained from CG MD simulations compared with those determined from atomistic reference simulations, which can be essentially rationalized by the simplification of atomistic model for [C2CnIM][BF4] ILs and the absence of some conformational constraints in the developed CG model for [C2CnIM] cations.44,46,48,49,54,59 In fact, these disparities can be minimized with a gradual lengthening of cation alkyl chains from C4 to C12, indicating that the constructed CG model and the derived interaction parameters for CG beads are effective in predicting microstructures of reference atomistic modelling systems at different thermodynamic states.
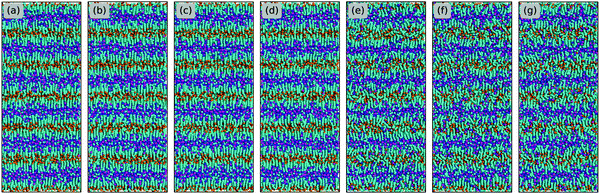
The evolution of microstructures in [C2CnIM][BF4] ILs with a gradual lengthening of cation alkyl chains is visualized by representative snapshots in Fig. 4, and is rationalized by competitive associations between preferential electrostatic interactions among charged beads and collective solvophobic coordinations among neutral beads.15,49,51,57 For ILs consisting of short cation alkyl chains, such as [C2C2IM][BF4] (Fig. 4(a)) and [C2C4IM][BF4] (Fig. 4(b)), the mesoscopic liquid structures are characterized by homogeneous distributions of CG beads in IL matrices. A progressive lengthening of cation alkyl chains leads to an aggregation of neutral beads and the formation of apolar domains owing to their mutual solvophobic characteristics.15,49,57 For ILs consisting of intermediate cation alkyl chains, like [C2C8IM][BF4] (Fig. 4(c)), the mesoscopic liquid structures are described by bi-continuous sponge-like arrangements of interpenetrating polar and apolar networks. The further lengthening of cation alkyl chains leads to a significant permeation of polar network by expanded apolar domains, the former of which tends to persist but has to accommodate the growing apolar domains by loosing part of its connectivity in IL matrices, resulting in the segregation of polar domains within apolar framework. These computational results obtained from CG MD simulations using a simplified ion model are in qualitative agreement with experimental observations in characterizing variations of microstructures and liquid organizations of imidazolium ILs with a progressive lengthening of cation alkyl chains.16–18
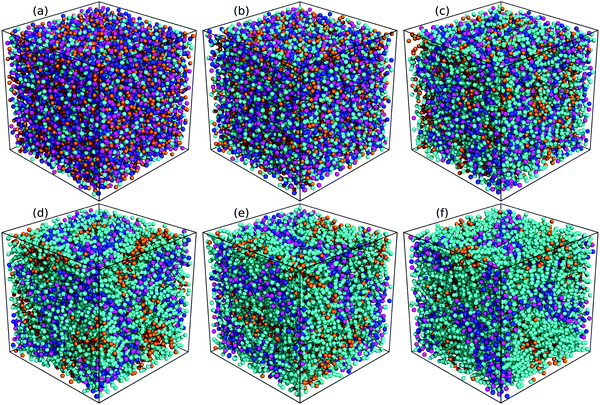 | ||
| Fig. 4 Representative liquid morphologies of (a) [C2C2IM][BF4], (b) [C2C4IM][BF4], (c) [C2C8IM][BF4], (d) [C2C12IM][BF4], (e) [C2C16IM][BF4], and (f) [C2C20IM][BF4] ILs at 400 K. The color codes of these CG beads are the same as those shown in Fig. 1 except that the tail CT beads in [C2CnIM] cations are highlighted with orange spheres to visualize their distinct distributions in apolar domains in IL matrices. | ||
The charge ordering phenomena in IL matrices can be quantified using a charge distribution function, Qi(r), which is defined such that 4πr2qiQi(r)dr is the net charge from a central ion i located at ri having a partial charge qi. The total charge distribution function can be obtained by a summation of partial charge distribution functions for [C2CnIM] cations (QCA) and [BF4] anions (QAN) via Q(r) = QCA(r) + QAN(r), in which QCA and QAN are correlated with RDFs among charged beads through QCA(r) = ρ(gCA–CA(r) − gCA–AN(r)) and QAN(r) = ρ(gAN–AN(r) − gCA–AN(r)), respectively.46,57ρ = ρCA + ρAN is the total number density of charged beads in CG modelling systems. Fig. 5(a) presents the total charge distribution functions for [C2CnIM][BF4] ILs calculated from reference AA and CG MD simulations. Charge oscillations are strongly damped in all studied IL matrices, indicating that these modelling systems exhibit striking charge ordering phenomenon.
 | ||
| Fig. 5 (a) Charge distribution functions for [C2CnIM][BF4] ILs calculated from AA and CG MD simulations, and (b) charge screening lengths of electrostatic correlations for [C2CnIM][BF4] ILs with varied cation alkyl chains. The charge screening length data for [C1CnIM][PF6] ILs are taken from ref. 46 for a comparative purpose. | ||
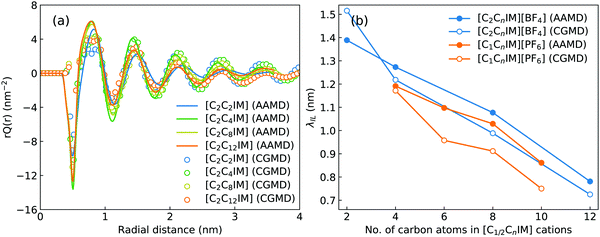
Such a charge ordering phenomenon in modelling systems dominated by coulombic interactions among charge beads can be quantified via fitting charge distribution functions to an asymptotic form 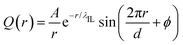 , in which the parameter of interest is the charge screening length (λIL) quantifying a distance beyond which the local charge neutrality is achieved in bulk liquid region.46,62 The estimated charge screening lengths λIL for [C2CnIM][BF4] ILs, as shown in Fig. 5(b), demonstrate that the constructed CG model and the derived interaction parameters can generate consistent results with those obtained from atomistic reference simulations. In addition, these computational results are comparable with those for [C1CnIM][PF6] ILs obtained by Moradzadeh et al. if we ignore the marginal difference between [BF4] and [PF6] anions.46,49,57 The charge screening length data for [C2CnIM][BF4] and [C1CnIM][PF6] ILs decrease with lengthening cation alkyl chains, which is expected due to enhanced microstructural heterogeneities in modelling systems that are originated from competitive associations between electrostatic interactions among charged beads and solvophobic forces among neutral spheres.
, in which the parameter of interest is the charge screening length (λIL) quantifying a distance beyond which the local charge neutrality is achieved in bulk liquid region.46,62 The estimated charge screening lengths λIL for [C2CnIM][BF4] ILs, as shown in Fig. 5(b), demonstrate that the constructed CG model and the derived interaction parameters can generate consistent results with those obtained from atomistic reference simulations. In addition, these computational results are comparable with those for [C1CnIM][PF6] ILs obtained by Moradzadeh et al. if we ignore the marginal difference between [BF4] and [PF6] anions.46,49,57 The charge screening length data for [C2CnIM][BF4] and [C1CnIM][PF6] ILs decrease with lengthening cation alkyl chains, which is expected due to enhanced microstructural heterogeneities in modelling systems that are originated from competitive associations between electrostatic interactions among charged beads and solvophobic forces among neutral spheres.
C. Thermodynamic and dynamic quantities of [C2CnIM][BF4] ILs
Besides the reproduction of microstructures of atomistic reference modelling systems, the constructed CG model and the derived interaction parameters can produce a reasonable linear scaling of liquid densities of [C2CnIM][BF4] ILs against temperatures. It is noted that there are limited density data for [C2CnIM][BF4] ILs, and therefore we provide experimental density data for [C1CnIM][BF4] ILs for a comparative propose. It is shown in Fig. 6 that the temperature-dependent liquid densities of [C2CnIM][BF4] ILs are consistent with those determined from experimental measurements63–65 with a maximum uncertainty of 3.5%. The slopes of these computational density data against temperatures are thermal expansion coefficients, which generally fall within the range for typical imidazolium ILs obtained from numerous experimental measurements and computational calculations.46,49,51,57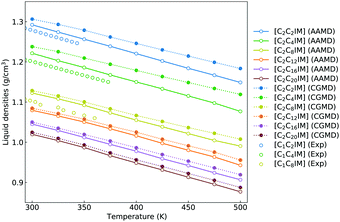 | ||
| Fig. 6 Temperature-dependent liquid densities of [C2CnIM][BF4] ILs obtained from reference AA and CG MD simulations are compared with experimental density data for [C1CmIM][BF4] ILs (m = 2, 4, and 8) taken from ref. 63–65 for a comparative purpose. | ||
It should be further noted that the constructed CG model and the derived interaction parameters exhibit a good transferability and representability in generating consistent microstructural and thermodynamic quantities (provided in the ESI†) of triazolium ILs.61 Therefore it is expected that this model can be used as a generic bead-spring model to explore phase behaviors of imidazolium and triazolium ILs, and even ion groups bearing heteroaromatic ring planes at varied thermodynamic conditions.
To go beyond microstructures and thermodynamic properties, we examine translational and rotational dynamics of [C2CnIM] cations at a wide temperature range to explore the dependence of these dynamic quantities on alkyl chain lengths and temperatures in bulk IL matrices. The diffusion coefficients of [C2CnIM] cations and [BF4] anions determined from mean square displacements in AA and CG MD simulations are shown in Fig. 7, and these computational data are compared with relevant experimental data.66 The diffusion coefficients of [C2CnIM] cations and [BF4] anions fall within the order of 10−12–10−8 m2 s−1 at 300–500 K, which is consistent with computational results obtained from previous studies using varied CG models.46,48,49,51,54,59 In addition, the diffusion coefficients determined from CG MD simulations are larger than the corresponding experimental values and atomistic simulation data by a factor of 2–7, indicating that the constructed CG model and the derived interaction parameters can essentially capture temperature-dependant and alkyl chain length-dependent translational dynamics of ion species in [C2CnIM][BF4] ILs at a wide temperature range.
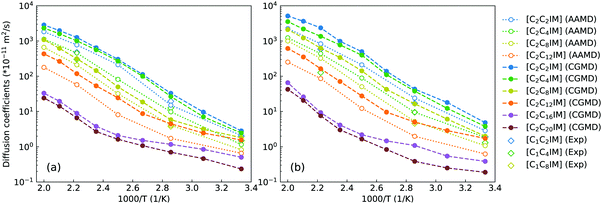 | ||
| Fig. 7 Comparison of temperature-dependent translational diffusion coefficients (unit in 10−11 m2 s−1) for (a) [C2CnIM] cations and (b) [BF4] anions obtained from reference AA and CG MD simulations with those determined from experimental measurements for [C1CmIM][BF4] (m = 2, 4, and 8) ILs at relevant thermodynamic conditions.66 | ||
At given temperatures, the comparable mobilities of charged IM and BF beads suggest their preferential associations in local ionic domains because of electrostatic interactions,4,46,48,49,59 whereas the neutral tail CT beads in CG [C2CnIM] cations exhibit the fastest translational diffusivities due to their distributions in local cavities of apolar domains, as clearly visualized in the lower panels in Fig. 4. Lengthening cation alkyl chains leads to a substantial decrease in diffusivities of [C2CnIM] cations and [BF4] anions, which can be rationalized by a distinct evolution of mesoscopic liquid morphologies of ILs. The mobilities of CG [C2CnIM] cations and [BF4] anions can be qualitatively sorted into three categories depending on cation alkyl chain lengths. For [C2CnIM][BF4] ILs with short cation alkyl chains, such as n = 2 and n = 4, the spatial distributions of ion groups in IL matrices are relatively homogeneous and there is no phase segregation of polar and apolar domains. The comparable diffusions of CG cations and anions are mainly influenced by strong electrostatic coordinations among charged beads. For cation alkyl chains longer than C4, the hydrophobic alkyl chains tends to aggregate and form apolar clusters, apolar domains and then interpenetrating apolar network in heterogeneous IL matrices with a gradual lengthening of cation alkyl chains. Such a striking microstructural transition leads to a significant decrease in mobilities of cations and anions, as clearly manifested in diffusion coefficient data for [C2C8IM][BF4], [C2C12IM][BF4] and [C2C16IM][BF4] ILs. However, the further lengthening of cation alkyl chains from C16 to C20 leads to marginal changes in microstructures and liquid morphologies. Therefore, even the translational diffusivities of ion groups in [C2C20IM][BF4] IL are considerably decreased, the magnitude of reduction is not so significant compared with that from [C2C4IM][BF4] to [C2C16IM][BF4] ILs.
The translational diffusivities of all CG beads and ion species exhibit an exponential increase with increasing temperatures, indicating that these temperature-dependent diffusion data can be depicted by a classic Arrhenius equation D = D0eEa/RT, where Ea is the activation energy. Fitting diffusion coefficients to the Arrhenius expression gives the activation energies of ion species, which lie within a range of 20–35 kJ mol−1 depending on constituent ions in modelling systems. The activation energies for charged CG beads are comparable, and are considerably larger than those for neutral beads in CG cation model, indicating that ion structures consisting of charged beads are more difficult to break in stiff ionic framework, in contrast to neutral tail beads in “soft” apolar domains.
In concert with translational dynamics, the rotational relaxations of CG [C2CnIM] cations have been investigated by calculating the rotational correlation functions represented by the first rank Legendre polynomial P1(t) = 〈ê(0)·ê(t)〉, in which ê is a unitary vector connecting head CH and tail CT beads in CG [C2CnIM] cations.32,40,41Fig. 8 presents representative rotational correlation functions of CG [C2CnIM] cations at different temperatures. The rotational relaxations of [C2CnIM] cations are complicated and heterogeneous depending on the relative relaxations of charged and neutral moieties. The charged moieties are locally liberated in ion cages in polar region while neutral moieties freely swing in solvophobic domains, and additionally, a gradual lengthening of cation alkyl chains slows down rotational relaxations of [C2CnIM] cations, which is intrinsically correlated with cation sizes and their spatial distributions in heterogeneous IL matrices. This is compatible with their translational dynamics determined from AA and CG simulations, and microstructural relaxations of ILs determined by charged and neutral probes using ultrafast vibrational spectroscopy.9,48,51
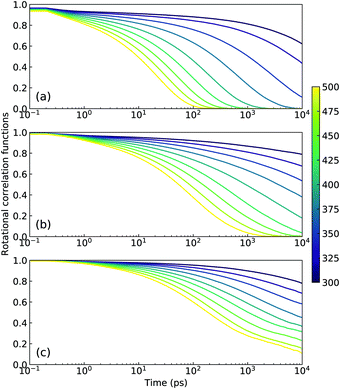 | ||
| Fig. 8 Rotational correlation functions of CG (a) [C2C2IM], (b) [C2C8IM], and (c) [C2C16IM] cations at varied temperatures. | ||
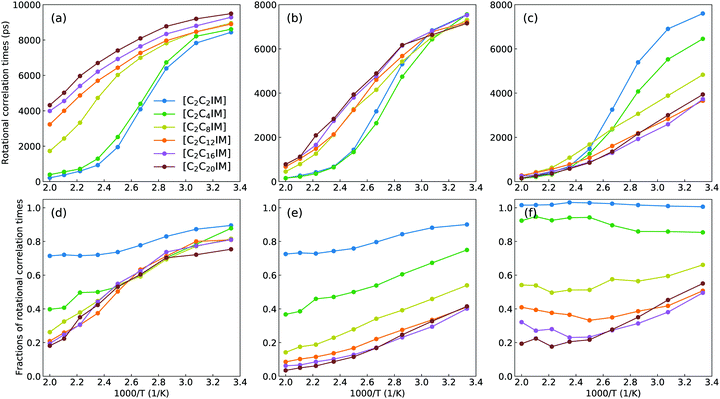
It should be addressed that these asymptotic rotational correlation functions can be best fitted to a stretched bi-exponential decay function C(t) = C0 + C1e−t/τ1 + C2e−t/τ2.41,67 The accessible fitting parameters τ1 and τ2 represent two rotational modes of a rotational body, usually a slow mode and a fast mode with different rotational timescales. The detailed description of these fitting parameters was comprehensively discussed in previous works.41,61,67 The total rotational correlation times τ for [C2CnIM] cations are determined by a numerical integration of the fitted functions using 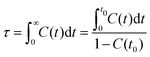 . In addition, the rotational correlation times for head units (τhead), represented by a vector connecting CH and IM beads, and for tail groups (τtail), described by a vector connecting the last two tail beads (IM–CT for [C2C2IM] and CE–CT for other cations), are determined from the corresponding rotational correlation functions. The obtained rotational correlation times, as shown in Fig. 9, demonstrate distinct rotational relaxations of polar units and apolar groups in [C2CnIM] cations. The first feature is that an increase in temperature leads to enhanced rotational dynamics with a concomitant decrease in rotational correlation times for head units and tail groups, as well as for the whole [C2CnIM] cations. The second character is that lengthening alkyl chains in [C2CnIM] cations leads to a substantial increase in rotational correlation times for head units and the whole cations at relevant temperatures, and a concomitant decrease in rotational correlation times for tail groups in cations.
. In addition, the rotational correlation times for head units (τhead), represented by a vector connecting CH and IM beads, and for tail groups (τtail), described by a vector connecting the last two tail beads (IM–CT for [C2C2IM] and CE–CT for other cations), are determined from the corresponding rotational correlation functions. The obtained rotational correlation times, as shown in Fig. 9, demonstrate distinct rotational relaxations of polar units and apolar groups in [C2CnIM] cations. The first feature is that an increase in temperature leads to enhanced rotational dynamics with a concomitant decrease in rotational correlation times for head units and tail groups, as well as for the whole [C2CnIM] cations. The second character is that lengthening alkyl chains in [C2CnIM] cations leads to a substantial increase in rotational correlation times for head units and the whole cations at relevant temperatures, and a concomitant decrease in rotational correlation times for tail groups in cations.
These computational results, as we discussed in previous subsections, are intrinsically correlated with a transition of microstructures and mesoscopic liquid morphologies for [C2CnIM][BF4] ILs with a gradual lengthening of cation alkyl chains. For [C2C2IM] and [C2C4IM] cations having short alkyl chains, the head CH–IM units are strongly coupled with anions, constraining neutral CT beads in local cavities, and therefore rotational dynamics of all cations are strongly dependent on relaxations of head CH–IM units in cations. For [C2CnIM] cations with alkyl chains longer than C4, the neutral beads tend to aggregate and form apolar domains, which is highlighted by spatial distributions of neutral CT beads (orange spheres) in Fig. 4. This leads to increased rotations of tail CE–CT groups in apolar domains, and marginal changes for rotational dynamics of head CH–IM units in polar domains. It is noted that lengthening cation alkyl chains from C12 to C20 leads to a progressive increase in rotational correlation times for the whole [C2CnIM] cations, which might be attributed to the contributions of other neutral CE beads between head CH–IM units and tail CE–CT groups in cations.
Additional physical insights for temperature-dependant and cation alkyl chain length-dependent rotational correlation times for [C2CnIM] cations, head CH–IM units and tail (IM)CE–CT groups in cations can be obtained via calculating fractions of rotational correlation times for different moieties at varied temperatures shown in lower panels in Fig. 9. In [C2C2IM][BF4] and [C2C4IM][BF4] ILs, the head CH–IM units and tail (IM)CE–CT groups in cations have comparable contributions to rotational relaxations of cations. This is expected as in these two modelling systems the tail (IM)CE–CT groups are covalently bonded to head CH–IM units in cations, and therefore their rotational dynamics are strongly coupled with that for head CH–IM units in cations. For [C2CnIM] cations with alkyl chains longer than C8, the contributions of head CH–IM units exhibit negligible changes, whereas tail CE–CT groups demonstrate stepwise decrease in their contributions to rotational relaxations of cations, manifesting that microstructures and spatial distributions of tail CE–CT groups in apolar domains have marginal changes in these ILs with a further lengthening of cation alkyl chains from C8 to C20. The rotational heterogeneities, embedded in charged and neutral moieties and the whole cations, indicate that charged units are actually difficult to rotate because of a strong cation–anion association caging effect and therefore charged units have longer rotational correlation times; in contrast, neutral groups have a relatively free rotational motion due to a small energy barrier for neutral chains to rotate and diffuse in apolar domains and therefore neutral groups have shorter rotational correlation times.41,68–70 These two rotational modes exhibit a prevalent competitive and temperature-dependent feature in affecting the total rotational dynamics of [C2CnIM] cations in heterogeneous IL matrices.
III. Coarse-grained simulations of ionic liquid crystalline phases
A. Phase behaviors and number density profiles
Prior investigations have established that ILs with an appropriate combination of cation alkyl chains and anion types can form striking liquid phases exhibiting ILC characteristics and long range mesoscopic ordering structures over extended temperature range.13,71–73 The specific combination feature for [C1CnIM][BF4] ILs has been experimentally determined to be n ≥ 12.14,74 In addition, long alkyl chains are needed for imidazolium cations to form stable ILC structures when they are coupled with large anion groups.73–75 The main driving force for the formation of ILC phase, very often of smectic type mesomorphism, is the phase segregation of hydrophobic chains from ionic layers. Herein, we investigate the transferability of the constructed CG model and the derived interaction parameters in describing ILC characteristics of [C2CnIM][BF4] ILs at varied thermodynamic states. It should be noted that in regular CG MD simulations the ILC structures are routinely obtained via annealing isotropic ILs from high to low temperatures, which, however, are highly dependent on annealing procedures, and more significantly, modelling systems are readily trapped at different metastable states.72,73,76–78 Therefore the transition from isotropic to crystalline structures is complicated and hardly being observed during normal simulations without enhanced sampling techniques. As such, we adopt another straightforward procedure to first generate starting configurations of IL ion pairs characterized by crystalline structures on regular lattices, and thereafter heat modelling systems to target temperatures and perform full equilibrations before taking statistical analysis.Three model ILs, [C2C4IM][BF4], [C2C12IM][BF4] and [C2C20IM][BF4], are selected to explore ILC characteristics of [C2CnIM][BF4] ILs with short, intermediate, and long cation alkyl chains. Fig. 10 presents representative configurations of CG [C2C12IM][BF4] ILs in equilibrated simulation systems in a sequential heating cascade from 50 to 500 K. A generic smectic phase is identified and IL microstructures are much ordered at lower temperatures (<350 K) than those at higher temperatures (>350 K). The equilibrated ion structures of [C2C4IM][BF4] and [C2C20IM][BF4] ILs (provided in ESI†), and ensuing structural analysis demonstrate that the former IL displays isotropic liquid phase behaviors, whereas the latter exhibits distinct ILC characteristics within a wide temperature range. All these computational results are essentially attributed to an alkyl chain length effect in [C2CnIM] cations.
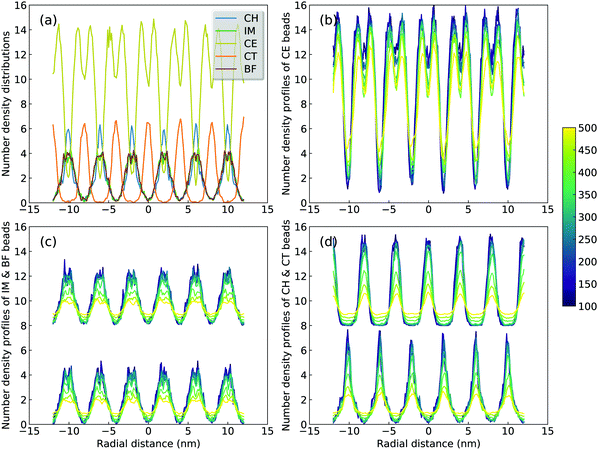
A sophisticated identification of smectic phase is complemented by analyzing number density distributions (Fig. 11), pair distribution functions (Fig. 12), orientational and translational order parameters (Fig. 13) of modelling systems. The number density profiles for CG beads in [C2C12IM][BF4] ILs at 300 K, as shown in Fig. 11(a), indicate a well-defined head-to-head and tail-to-tail crystalline pattern between ionic and hydrophobic layers with little overlap. The head CH and tail CT beads exhibit similar peak intensities but with displaced peak positions (Fig. 11(d)), and IM and BF beads have comparable density profiles (Fig. 11(c)) due to their strong coulombic interactions, as expected. An increase in temperature from 300 K leads to a considerable modulation of smectic phase with boarder density distributions, which is quantitatively consistent with number density profiles of the corresponding atomistic reference groups in modelling systems at relevant thermodynamic states.72,73,78,79
 | ||
| Fig. 13 Variations of (a) orientational and (b) translational order parameters for [C2CnIM] cations at different temperatures. | ||
B. In-plane structures and dynamics
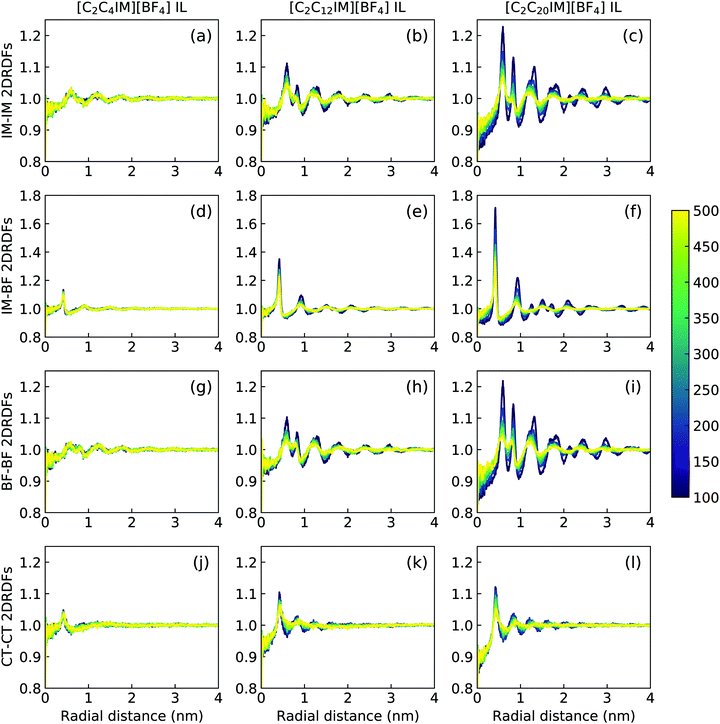
The descriptions of ILC and smectic phase structures of [C2C4IM][BF4], [C2C12IM][BF4], and [C2C20IM][BF4] ILs are complemented by in-plane pair distribution functions at xy plane perpendicular to phase director (z-axis). The [C2C4IM][BF4] IL is characterized by isotropic liquid structures, and therefore all in-plane RDFs (the first column in Fig. 12) exhibit mean distributions at all studied temperatures, which is not different from what usually observed in isotropic phase of ILs. However, the [C2C20IM][BF4] IL exhibits highly ordering in-plane structures consisting of alternating ion layering characteristics. The in-plane RDFs for charged beads (IM–IM, IM–BF, and BF–BF pairs) span beyond three nanometers, indicating a persistent modulation of long-ranged two dimensional ordering pattern as would be expected in a crystalline phase.79,80 The [C2C12IM][BF4] IL has intermediate in-plane structural properties consisting of alternating ion layers. The distributions of neutral CT beads in [C2C12IM] cations are limited within few ionic radii and are consistent with a liquid-like structure of hydrophobic layers.
Fig. 13 presents orientational and translational order parameters of [C2CnIM] cations to quantify their orientational and translational distributions in layering IL matrices. The orientational order parameter is defined as an ensemble average of the second-order Legendre polynomial, S = 〈P2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β)〉, where β is the angle between phase director (z-axis) and the directional vector pointing from head CH to tail CT beads in [C2CnIM] cations.78–80 The orientational order parameters for cations with long alkyl chains, such as [C2C16IM] and [C2C20IM], are around 0.9 at low temperatures, indicating that these cations take uniform arrangements along the same direction in modelling systems. As temperature increases, molecular conformations of [C2CnIM] cations become less orientationally ordered, corresponding to a solid–solid phase transition from crystalline to smectic A phase. This observation is generally consistent with experimental observations as these ILs indeed exhibit microstructural transitions with increasing temperatures.72,73 However, for cations having short alkyl chains, such as [C2C2IM] and [C2C4IM], the orientational order parameters are almost zero and do not show appreciable changes with decreasing temperatures, indicating that these simulation systems exhibit isotropic structures with minimal phase segregation between polar and apolar moieties, even at low temperatures. The orientational order parameters for cations with intermediate alkyl chains, like [C2C12IM], lie between those for [C2C8IM] and [C2C16IM] ILs, and exhibit significant changes with temperatures. It is shown that at low temperatures, the orientational order parameters for [C2C12IM] cations are close to 0.8, and present stepwise decrease from 100 to 350 K, and then an evident decrease at around 400 K. This indicates that microstructures in [C2C12IM][BF4] IL apparently lose crystalline mesomorphism and transform to smectic phase and then isotropic phase with less ordering characteristics, in which [C2C12IM] cations are more interdigitated and alkyl chains exhibit more flexibilities with less spatial constraints than those exhibit aligned distributions at lower temperatures. This corresponds to a smectic–isotropic structural transition of [C2C12IM][BF4] IL as those observed in previous experiments and computational studies.72,73
β)〉, where β is the angle between phase director (z-axis) and the directional vector pointing from head CH to tail CT beads in [C2CnIM] cations.78–80 The orientational order parameters for cations with long alkyl chains, such as [C2C16IM] and [C2C20IM], are around 0.9 at low temperatures, indicating that these cations take uniform arrangements along the same direction in modelling systems. As temperature increases, molecular conformations of [C2CnIM] cations become less orientationally ordered, corresponding to a solid–solid phase transition from crystalline to smectic A phase. This observation is generally consistent with experimental observations as these ILs indeed exhibit microstructural transitions with increasing temperatures.72,73 However, for cations having short alkyl chains, such as [C2C2IM] and [C2C4IM], the orientational order parameters are almost zero and do not show appreciable changes with decreasing temperatures, indicating that these simulation systems exhibit isotropic structures with minimal phase segregation between polar and apolar moieties, even at low temperatures. The orientational order parameters for cations with intermediate alkyl chains, like [C2C12IM], lie between those for [C2C8IM] and [C2C16IM] ILs, and exhibit significant changes with temperatures. It is shown that at low temperatures, the orientational order parameters for [C2C12IM] cations are close to 0.8, and present stepwise decrease from 100 to 350 K, and then an evident decrease at around 400 K. This indicates that microstructures in [C2C12IM][BF4] IL apparently lose crystalline mesomorphism and transform to smectic phase and then isotropic phase with less ordering characteristics, in which [C2C12IM] cations are more interdigitated and alkyl chains exhibit more flexibilities with less spatial constraints than those exhibit aligned distributions at lower temperatures. This corresponds to a smectic–isotropic structural transition of [C2C12IM][BF4] IL as those observed in previous experiments and computational studies.72,73
The translational order parameter τ is described by τ = 〈cos(2πz/d)〉, where z is the position of [C2CnIM] cation beads along phase director, d is the layer spacing, and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 represents an ensemble average.73,80–82 It is shown in Fig. 13(b) that the translational order parameters for all modelling systems exhibit similar variations as orientational order parameters with increasing temperatures. More pertinently, the translational order parameters for specific modelling systems at relevant temperatures are smaller than the corresponding orientational order parameters shown in Fig. 13(a), indicating that orientational distributions of [C2CnIM] cations, either exhibiting crystalline, smectic mesomorphism, or isotropic nanosegregated structures, are somewhat significant compared with the corresponding translational distributions in characterizing phase structures of modelling systems, akin to that observed in CG MD simulations of ILs using a generic CG model represented by Gay–Berne potential.82
〉 represents an ensemble average.73,80–82 It is shown in Fig. 13(b) that the translational order parameters for all modelling systems exhibit similar variations as orientational order parameters with increasing temperatures. More pertinently, the translational order parameters for specific modelling systems at relevant temperatures are smaller than the corresponding orientational order parameters shown in Fig. 13(a), indicating that orientational distributions of [C2CnIM] cations, either exhibiting crystalline, smectic mesomorphism, or isotropic nanosegregated structures, are somewhat significant compared with the corresponding translational distributions in characterizing phase structures of modelling systems, akin to that observed in CG MD simulations of ILs using a generic CG model represented by Gay–Berne potential.82
It should be noted that herein we do not observe a sudden apparent jump in orientational and translational order parameters with increasing temperatures, which might be attributed to the simplified CG model for [C2CnIM][BF4] ILs.78,80 Although there are some discrepancies of transition temperatures between computational results and experimental observations due to some computational tricks, this does not prevent us from a qualitative understanding of experimental phenomena using CG MD simulations as the relative trends still provide insightful information on thermotropic phase behaviors of [C2CnIM][BF4] ILs at varied thermodynamic states. In addition, the comprehensive analysis of number density profiles, in-plane radial distribution functions, orientational and translational order parameters can provide further physical insights for microstructural transitions of [C2CnIM][BF4] ILs with a gradual lengthening of cation alkyl chains. The [C2CnIM][BF4] ILs with cation alkyl chains shorter than C4 are isotropic liquids, whereas [C2CnIM][BF4] ILs with intermediate cation alkyl chains (4 < n < 12) are heterogeneous liquids with a distinct segregation between polar and apolar domains. The spatial distributions of charged and neutral beads in these modelling systems do not allow a complete segregation of polar and apolar domains at mesoscopic level, which necessarily results in a perturbation of ion pairing interactions by alkyl chains, and vice versa.78 A further lengthening of cation alkyl chains (n ≥ 12) leads to their preferential alignments, in which polar and apolar domains are completely segregated, and as a consequence, ionic layers are not readily perturbed by long alkyl chains, which, however, have a significant effect on orientational ordering distributions of cations.73
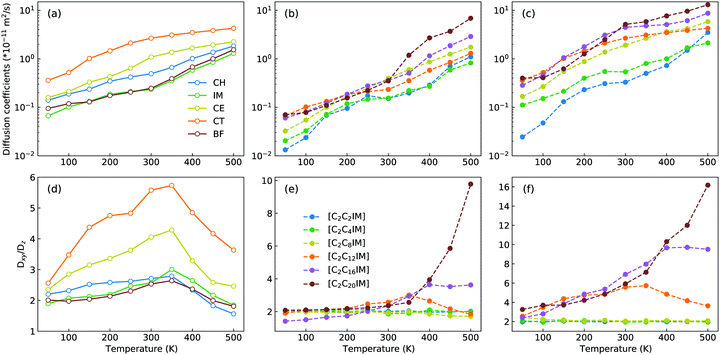
The microstructures of [C2CnIM][BF4] ILs, either characterized by crystalline, smectic mesomorphism, or isotropic nanosegregated structures, have a direct impact on translational mobilities of charged and neutral CG beads in modelling systems at different temperatures. An increase in temperature leads to enhanced translational mobilities of CG beads with neutral spheres having larger diffusion coefficients (DCT > DCE > DCH) than charged IM and BF beads at a wide temperature range, in which the latter two are strongly coupled via coulombic interactions, as shown in representative diffusion coefficient data for all CG beads in [C2C12IM][BF4] IL in Fig. 14(a).
Besides the total diffusion coefficients, the microstructures of [C2CnIM][BF4] ILs have additional effect on mobilities of CG beads at xy plane and along z-axis. Fig. 14(d) presents fractions of in-plane diffusion coefficient data of CG beads in [C2C12IM][BF4] IL over their counterparts along z-axis. The neutral beads have distinct mobilities at xy plane compared with their diffusions along z-axis owing to intrinsic crystalline structures of ILs at low temperatures, and such mobilities are significantly increased with temperatures due to their enhanced in-plane diffusivities in apolar domains in modelling systems. The fractions for all CG beads are maximized at around 350 K, beyond which the values of Dxy/Dz decrease with increasing temperatures, which is rationalized by a phase transition of [C2C12IM][BF4] IL from crystalline mesomorphism to smectic and isotropic structures.
The variations of cation alkyl chains have a straightforward effect on in-plane mobilities of CG beads over their counterparts along z-axis, and representative results for charged IM beads and neutral CT spheres are present in Fig. 14(e) and (f), respectively. For cations with alkyl chains shorter than C12, the in-plane mobilities of CG beads over their counterparts along z-axis are almost constant. This is expected as these ILs have homogeneous structures or form nanosegregated apolar domains within a framework consisting of charged beads but not smectic phase due to an imbalance of polar and apolar moieties in IL matrices. Therefore all CG beads in these modelling systems, either charged IM (and BF) beads or neutral CT (also CH and CE) spheres, exhibit comparable mobilities in three dimensional space. However, for cations with alkyl chains longer than C12, all CG beads exhibit enhanced diffusivities at xy plane over their counterparts along z-axis, in which neutral beads hold more significance than charged spheres due to intrinsic phase structures and specific distributions of these CG beads in modelling systems.
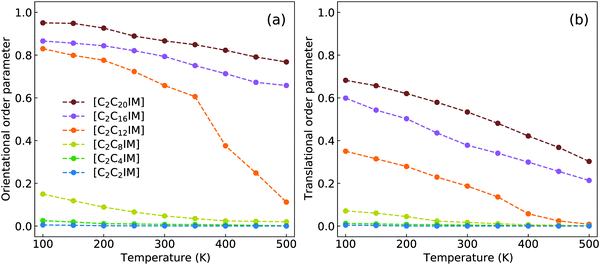
Dvinskikh and coworkers studied thermotropic phase behaviors of [C1C12IM][BF4] and [C1C12IM]Br ILs and found heterogeneous mobilities of cations in ordered liquid environment characterized by smectic A phase.83,84 Compared with these experimental measurements, it is shown in Fig. 15 that the developed CG model for [C2CnIM][BF4] ILs can essentially capture heterogeneous diffusivities, including the total diffusion coefficients and the values of Dxy/Dz, of [C2C12IM] cations in varied thermodynamic and structural states. In addition, the experimental diffusion data for [C1C12IM]Br IL at relevant temperatures are also provided in Fig. 15 for a comparative purpose. These comparisons demonstrate that the developed CG model can be specifically adopted to study thermodynamic and structural properties of ILs consisting of imidazolium cations coupled with spherical anions, and can be adapted to explore striking phase behaviors of other ILs consisting of cation having a polar head and hydrophobic tails coupled with anions characterized by different molecular shapes and sizes at varied thermodynamic states, which will be a central scheme for our computational studies in future.
 | ||
| Fig. 15 Comparison of (a) the total diffusion coefficient data and (b) the fractions of in-plane diffusion coefficients (Dxy) over those along z-axis (Dz) of [C2C12IM] cations in [C2C12IM][BF4] IL obtained from current CG MD simulations with experimental measurements of [C1C12IM][BF4] IL at relevant temperatures.83 The experimental data for [C1C12IM]Br IL at different temperatures are also provided for a comparative purpose.84 | ||
IV. Ion association structures and ion hopping dynamics in polymerized ionic liquids
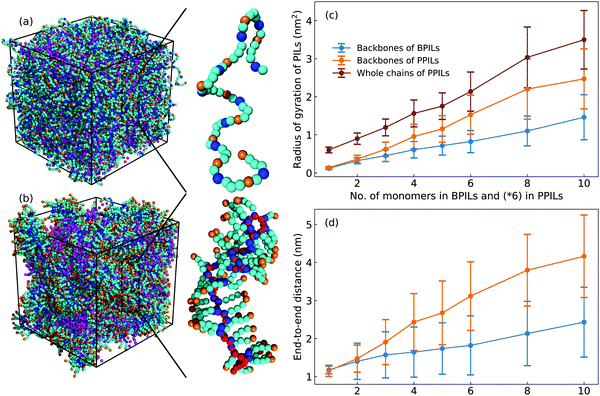
Imidazolium-based PILs are of interest as next-generation ion transport materials because of their particularities in combining mechanical stabilities of polymers with ion transport quantities of imidazolium ILs.7,22,23,25,31,85 Great endeavors have been focused on PILs where charged groups are pendant to polymer backbones. As PIL backbones and most pendent groups are apolar units, the charged moieties in cation monomers have strong coordinations with anions and form peculiar ionic aggregates, which has been observed in related experimental characterizations.23,28,86,87 The ensuing modelling works demonstrated that the formation of intriguing morphologies from spheres to strings of ionic aggregates depends on the degree of neutralization, ion types, and polymer architectures.32,36,88–90 It was further suggested that placing charged moieties in PIL backbones (ionenes) instead of pendant groups leads to the formation of substantially percolated ionic aggregates spanning the entire sample geometry, which has profound implications on ion conductivity and transport quantities of backbone PILs compared with their pendant analogous.28,31,88 Motivated by these reports, in the current study, we adopt the constructed CG model for [C2C8IM] cation to probe structural and ion transport properties in a set of backbone and pendant polymerized ionic liquids (labelled as BPILs and PPILs, respectively, and representative configurations of BPIL and PPIL chains are provided in Fig. 16) as previous CG MD simulations have demonstrated that [C2C8IM][BF4] IL exhibits distinct phase segregation between polar and apolar domains but without obvious IL crystalline mesomorphism. Backbone and pendant polymerized [C2C8IM] cations are constructed with PIL backbone lengths ranging from 6 to 60 to explore the effects of PIL architectures and PIL molecular weights on ion mobilities and the mechanism underlying ion association structures and ion hopping dynamics in PIL materials. More specifically, a series of BPIL chains consisting of 1, 2, 3, 4, 5, 6, 8, and 10 [C2C8IM] cation monomers with a head-to-tail polymerization manner is constructed, leading to BPIL backbones consisting of 6, 12, 18, 24, 30, 36, 48, and 60 CG beads (each [C2C8IM] cation consists of 6 CG beads). Likewise, multiple PPIL chains are constructed in a head-to-head polymerization form with PPIL backbones containing 6, 12, 18, 24, 30, 36, 48, and 60 CH beads. Each modelling system contains 3600 [C2C8IM][BF4] ion pairs with different number of BPIL and PPIL chains. The detailed modelling protocols of BPIL and PPIL simulation systems are provided in ESI.†A. Ion association structures
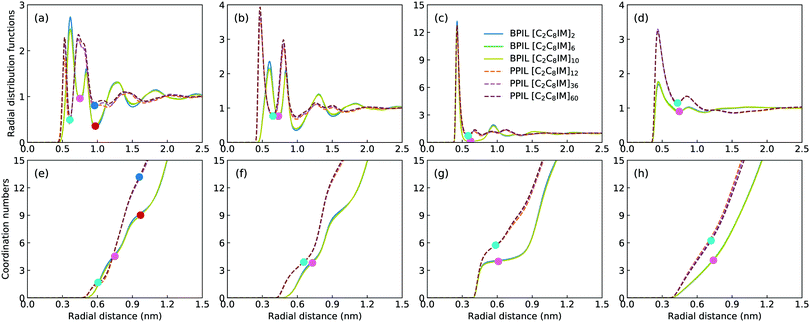
Fig. 16 presents representative morphologies and configurations of BPILs and PPILs in modelling systems. Both charged IM beads and tail CT spheres in [C2C8IM] cations exhibit localized distributions in PPILs compared with their counterparts in BPILs, which can be rationalized by relative locations of IM and CT beads in PILs. In PPILs, the CH beads are covalently bonded together, leading to a close contact of IM beads. The strong electrostatic repulsions among charged IM beads result in a distinct aggregation of anions near IM beads to neutralize local charges, and therefore charged IM and BF beads exhibit distinct localizations in PPIL modelling systems (Fig. 16(b)). However, in BPILs, the charged IM beads are separated by five neutral beads, which can effectively reduce electrostatic repulsions between IM beads in neighboring [C2C8IM] cation monomers, leading to the BPILs having coil-like structures in bulk regions. Such a distinct PIL architecture effect leads to varied conformational properties, such as radius of gyration (Fig. 16(c)) and end-to-end distance (Fig. 16(d)), of BPILs and PPILs, and thereafter results in striking ion transport properties that will be discussed in following paragraphs.The local ion structures in BPILs and PPILs are qualitatively characterized by calculating radial distribution functions and the corresponding accumulated coordination numbers shown in Fig. 17. For CT–CT and IM–BF pairs, both BPILs and PPILs have similar cutoffs for the first solvation shell. However, a large coordination number is present for CT–CT and IM–BF pairs in PPILs compared with that in BPIL counterparts, indicating a preferential association between neutral CT beads of alkyl chains in apolar domains and a strong coordination between charged beads with unlike charges in polar domains, respectively, which are clearly visualized in Fig. 16. Such a strong coordination pattern between unlike charges leads to distinct correlations among charged beads with like charges.32,89 The BF–BF RDF plot has enhanced peak intensities at short radial distances in PPILs compared with that in BPILs, but with an almost equal probability for a central anion to coordinate with neighboring ones within the first solvation shell. The spacial correlations among neighboring IM beads exhibit a peculiar characteristic depending on PIL architectures. In PPILs, the IM–IM correlations have a small radius and thereafter a slightly reduced number of coordinating ions in the first solvation shell, whereas have a comparable radius but with a large number of coordinating ions in the second coordination shell in contrast to their analogues in BPILs. In addition, the out-of-phase feature at short distance in RDF plots is a ubiquitous signature of charge alternation in ionic systems mediated by anions to neutralize cation charges, which may contribute to their varied capabilities in trapping charge carriers and thereafter affecting ion transport and hopping dynamics in BPILs and PPILs.
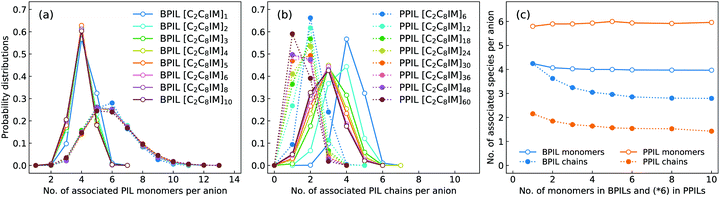
In order to have a comprehensive understanding of anion association patterns with neighboring polymerized cations, we have calculated the probability distribution for an anion to coordinate with n PIL cation monomers and with N PIL chains in BPILs and PPILs. An ion association state is defined for a specific ion pair with their relative distance smaller the cutoff of the first solvation shell in the corresponding RDF plot.30,32,36,89 It is displayed in Fig. 18(a) that the probabilities for anions in BPIL modelling systems exhibit sharply peaked distributions at n = 4, indicating a preferential coordination of an anion with four cation monomers in BPILs. However, a broad distribution with comparable probabilities centered at n = 5 and n = 6 corresponds to the most probable associations of an anion with approximately six cation monomers in PPIL modelling systems, which further confirms the localized coordination of anions with PPIL cation monomers in contrast to their associations with BPIL cation monomers.90 It should be noted that these characteristics are invariant among BPILs and PPILs with different backbone lengths, as illustrated in Fig. 18(c), indicating that such a probability distribution represents an inherent coordination feature of an anion with four BPIL cation monomers and with six PPIL cation monomers in their respective modelling systems.
The associated characteristics of anions with PIL chains, as shown in Fig. 18(b), highlight significant variations for an anion to coordinate with different numbers of BPIL and PPIL chains. For monomeric [C2C8IM][BF4] IL, an anion exhibits its maximal coordination with four [C2C8IM] cations. A head-to-tail polymerization manner of [C2C8IM] cation monomers leads to a gradual shift of peak positions from N = 4 to N = 3, corresponding to a coordination pattern of an anion with fewer BPIL chains due to rigidity of BPIL backbones.90 Such an associating state is also observed for PPILs with the most probably coordinated PPIL chains gradually shifted from N = 2 for PPILs with short backbones to N = 1 for PPILs with long backbones. These changes are clearly manifested in Fig. 18(c) addressing variations of the averaged numbers of associated PIL cation monomers and PIL chains per anion with a gradual lengthening of backbones in BPILs and PPILs.
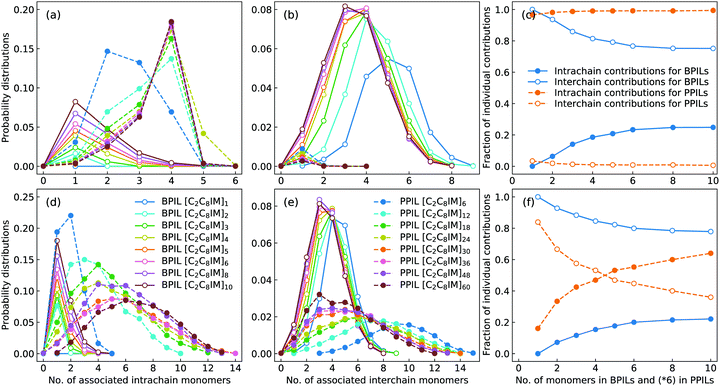
The intra- and interchain coordinations between cation monomers in the first and second solvation shells, which are determined by the first and second minima in the corresponding RDF plots in Fig. 17, in BPILs and PPILs are illustrated in Fig. 19. All cations in monomeric IL matrix (BPIL with a polymerization degree of 1) have interchain associations in the first and second solvation shells. Lengthening BPIL backbones leads to a considerable increase in intrachain coordinations for cation monomers (Fig. 19(a)), and a concomitant decrease in interchain associations from a maximal coordination probability with five interchain monomers to a maximal association probability with three interchain monomers (Fig. 19(b)). More specifically, for the BPIL with the polymerization degree equals to 10, it is shown that approximately 25% of cation monomer coordinations in the first solvation shell comes from intrachain associations, and the left 75% is described by interchain associations (Fig. 19(c)). Similar computational results are observed for associating BPIL cation monomers within the second solvation shell with comparable intra- and interchain contributions.
For intra- and interchain coordinations between cation monomers in PPILs, it is demonstrated that almost all PPIL cation monomers have intrachain associations with neighboring ones in the first solvation shell (Fig. 19(a)), and these associations exhibit a substantial shift of maximal distribution from n = 2 for [C2C8IM]6 PPIL to n = 4 for [C2C8IM]60 PPIL with a gradual lengthening of PPIL backbones.91,92 Meanwhile, intrachain coordinations between PPIL cation monomers in the second solvation shell exhibit a gradual transition from a sharp probability distribution localized at n = 2 to that characterized by board distributions centered at around n = 6 (Fig. 19(d)), and a concomitant shift for maximal interchain associations from n = 10 to n = 3 (Fig. 19(e)). The individual contributions of intrachain coordinations between PPIL cation monomers in the second solvation shell are increased from 16% for [C2C8IM]6 PPIL to 64% for [C2C8IM]60 PPIL, and correspondingly, the contributions of interchain coordinations are gradually decreased from 84% to 36% with a gradual lengthening of PPIL backbones (Fig. 19(f)). Such a spatial constraint of anions around cation monomers in PPILs, on the one hand, leads to their decreased diffusions in PPILs, and on the other head, may have a significant effect on the mobility of other charge carriers, such as lithium ions in lithium salt-doped PPILs which are promising electrolyte materials for batteries, supercapacitors, and other electrochemical devices.
B. Ion hopping dynamics
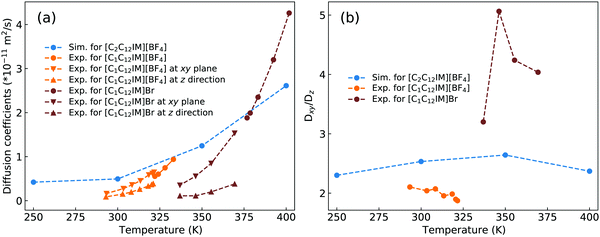
The diffusion coefficients of cation monomers and anions as shown in Fig. 20(a) demonstrate that these ion groups exhibit enhanced mobilities in BPILs compared with their counterparts in PPILs due to distinct spatial constraints of anions around PPIL cation monomers. More pertinently, both cation monomers and anions exhibit monotonic decrease in their mobilities with a gradual lengthening of BPIL and PPIL backbones, and concomitantly, BPILs and PPILs have reduced ion conductivities (Fig. 20(b)) and enhanced anion transference numbers (Fig. 20(c)). | ||
| Fig. 20 (a) Diffusion coefficients of cation monomers and anions, (b) ion conductivities, and (c) anion transference numbers in BPILs and PPILs with varied PIL backbone lengths. | ||
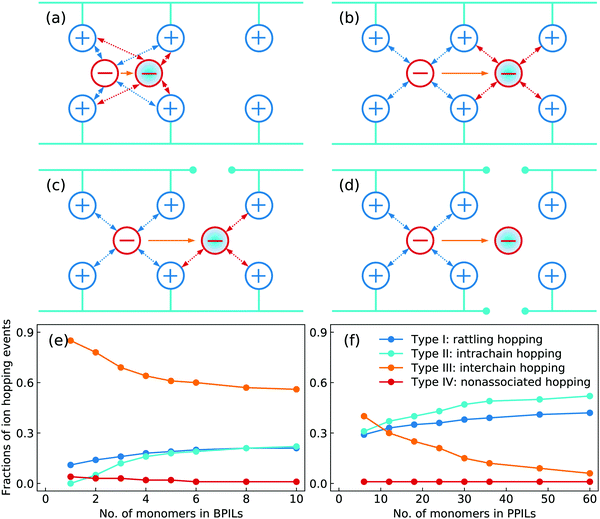
Based on a systematic analysis of ion association structures and ion diffusivities, we proceed to examine different ion hopping features and their variations with lengthening backbones in BPILs and PPILs. An ion hopping event is considered to occur when an ion pair association breaks or a new association forms.30,32,36,90 With identifications of associated anions with PIL cation monomers, the anion hopping events can be classified into four distinct types that are sketched in Fig. 21. The type I is termed as rattling hopping, where anions are associated with the same cation monomers within a time interval Δt. The type II is labelled as intrachain hopping, in which anions are associated with different cation monomers in the same PIL chains before and after Δt. The type III is described as interchain hopping, where anions are associated with cation monomers in different PIL chains as time elapses from t = 0 to t = Δt. The type IV is tagged as nonassociated hopping, in which anions are transitioned from associated to nonassociated states within Δt. The fractions of these four ion hopping types in BPILs and PPILs are illustrated in Fig. 21(e) and (f), respectively.
A substantial fraction of rattling hopping (type I) is observed, making up of approximately 20% and 42% in BPILs and PPILs, respectively, indicating that a considerable amount of anions do not experience breaking or forming of ion pairing associations within a time interval Δt. Such a striking feature for rattling hopping is even more distinct in PPILs compared with that in BPILs, owing to peculiar ion pairing associations of anions with cation monomers that have been rationalized by RDFs and accumulated coordination numbers shown in Fig. 17 and by ion associating probability distributions present in Fig. 18. This leads to enhanced probabilities of intrachain hopping (type II) in PPILs, which is roughly 52% of the total anion hopping events compared with that of 22% in BPILs. For interchain hopping (type III) of anions in BPILs and PPILs, a common feature is that such a hopping event has less probabilities with a gradual lengthening of PIL backbones, whereas a different character is that in BPILs this hopping mode is overwhelmingly dominant compared with other hopping modes and in PPILs this hopping type is progressively replaced by rattling and intrachain hopping modes. It is noted that the probability for nonassociated ion hopping event is essentially negligible, which is attributed to strong associations among anions and cation monomers in BPILs and PPILs via decisive coulombic interactions.
The detailed analyses of ion associations between anions and cation monomers and anion hopping modes in BPILs and PPILs indicate that PIL architectures indeed have a significant effect on ion transport quantities in PIL materials. To quantify correlations of ion diffusivities with ion structural relaxation times and ion association lifetimes, we calculate continuous ion pairing correlation function, 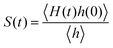 , and intermittent ion pairing correlation function,
, and intermittent ion pairing correlation function, 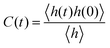 , in which h(t) is assigned to unity if an ion pairing association is present at t = 0 and remains intact at time t, and H(t) has a value of unity if an ion pairing coordination that exists at t = 0 remains intact continuously up to time t.32,36,90 Therefore, S(t) measures continuous ion pairing coordinations and C(t) describes intermittent ion structural associations before their permanent dissociations, and the corresponding time scales, τS and τC, quantifies the average lifetimes of ion pairing coordinations and ion structural relaxations, respectively. τS and τC can be derived by fitting the corresponding correlation functions, S(t) and C(t), respectively, to stretched exponential functions and thereafter integrating the fitted analytical forms.
, in which h(t) is assigned to unity if an ion pairing association is present at t = 0 and remains intact at time t, and H(t) has a value of unity if an ion pairing coordination that exists at t = 0 remains intact continuously up to time t.32,36,90 Therefore, S(t) measures continuous ion pairing coordinations and C(t) describes intermittent ion structural associations before their permanent dissociations, and the corresponding time scales, τS and τC, quantifies the average lifetimes of ion pairing coordinations and ion structural relaxations, respectively. τS and τC can be derived by fitting the corresponding correlation functions, S(t) and C(t), respectively, to stretched exponential functions and thereafter integrating the fitted analytical forms.
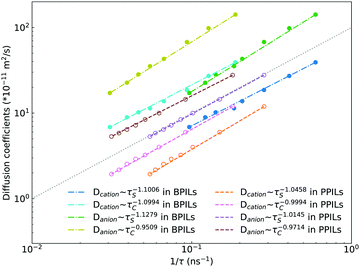
Fig. 22 presents diffusion coefficients of PIL cation monomers and anions against ion pairing association times (τS) and ion structural relaxation times (τC). It is clearly demonstrated that diffusion coefficients of ion species are inversely correlated with their relaxation times and follow a universal power law correlation of D ∼ τ−1, indicating an intrinsic correlation of ion diffusivities and ion hopping dynamics with ion pairing associations and ion structural relaxations in PILs, irrespective of PIL architectures. This observation is generally consistent with atomistic computational results from previous works.30,32,36,90 Recalling that S(t) decays with an initial breaking of cation–anion ion pairing coordinations and C(t) decays with a final dissociation of cation–anion ion structural associations, it can be conceptually addressed that τS should be comparable with the time scale for rattling hopping mode (type I) as both quantities reflect an instant breaking of ion pairing coordinations. This rattling hopping mode does not contribute to effective ion transport, but is an indicative of probability of ion pairing dissociation. A small τS (fast decay of S(t)) corresponds to an associated ion pair that can be readily dissociated in a short time interval. Such an ion dissociation probability can be substantially increased via external stimuli, such as introduction of inorganic salts or imposing external electric field for specific applications of BPILs and PPILs as electrolyte materials in electrochemical devices. C(t) is intrinsically correlated with ion “caging” effect constraining a vibrational motion of associated or semi-associated ion pairs in local ionic environment before their final dissociation, and therefore τC is an appropriate index to describe effective ion hopping dynamics (types II and III, and even type IV) and their lifetimes in modelling systems.
V. Concluding remarks and outlook
In this work we have constructed a novel CG model for [C2CnIM][BF4] ILs with cation alkyl chains up to C20 to study phase behaviors of monomeric and polymeric ILs with different architectures. The interaction parameters for this CG model were validated against representative thermodynamics (liquid densities), structural (radial distribution functions and probability distributions of bond lengths, angles and dihedrals), and dynamic properties (diffusion coefficients) that were obtained from atomistic reference simulations and experimental measurements at relevant thermodynamic states.This constructed CG model was adopted to study thermotropic characteristics of monomeric ILs with varied cation alkyl chains. A structural evolution from homogeneous to nanosegregated liquid structures and then a smectic crystalline mesomorphism was identified via a gradual lengthening of cation alkyl chains from C2 to C20. In addition, a systematic structural analysis (density profiles, in-plane pair distribution functions, diffusion coefficients, orientational and translational order parameters) illustrates a distinct structural transition in a sequential heating cascade characterized by a monotonic decrease in orientational order parameters, which is qualitatively consistent with experimental thermotropic phase behaviors of ILCs at a wide temperature range.
This CG model was further extended to explore ion association structures and the molecular mechanism underlying ion hopping phenomena in BPILs and PPILs with different PIL backbone lengths. Anions demonstrate comparable probabilities to coordinate with PIL cation monomers, but striking association features with PIL chains. PIL cation monomers illustrate distinct intra- and interchain coordinations depending on specific PIL architectures and spatial distributions of cation monomers around reference units, leading to a substantial decrease in ion transport properties and anion hopping dynamics with a gradual lengthening of PIL backbones. A considerable amount of anions has local rattling hopping inside ion cages without cation–anion association breaking and reforming, whereas significant differences manifest that lengthening PIL backbones leads to a progressive increase in anion intrachain ion hopping probabilities and a concomitant decrease in anion interchain ion hopping events, underscoring a PIL architecture effect as that hypothesized in previous atomistic simulations. Ion diffusivities of PIL cation monomers and anions are inversely correlated with ion pairing association lifetimes and ion structural relaxation times via a universal power law correlation D ∼ τ−1, irrespective of PIL architectures, mirroring qualitatively the ion hopping interpretation of ion conductivity data for PILs in earlier experimental and computational investigations.
Altogether, these computational studies of thermotropic phase behaviors of monomeric ILs with varied cation alkyl chains and of ion association and transport properties in BPILs and PPILs indicate that the constructed CG model for [C2CnIM][BF4] ILs and the derived interaction parameters are effective in reproducing relevant properties of IL-based materials at different thermodynamic states and providing physical insights in local ion association structures and ion hopping dynamics in PIL materials. It is expected that such a CG model will be a generic bead-spring model representing a series of IL-based materials having different ion structures and varied polymer architectures, and is adequate to reveal molecular-level quantities underlying peculiar structure–property relationships for ion-containing (polymeric) materials. This will be of particular significance for building a library of specific structure–property ontology and for a systematic computational design of novel ion-containing materials at mesoscopic level to meet specific requirements in electrochemical applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y.-L. W. acknowledges financial support from Knut and Alice Wallenberg Foundation (KAW 2018.0380) and partial support from Swedish Research Council. B. L. acknowledges financial support from National Natural Science Foundation of China (No. 22003080), and Fundamental Research Funds for Central Universities (No. 20lgpy76). A. L. acknowledges Swedish Research Council for financial support, and partial support from Ministry of Research and Innovation of Romania (CNCS – UEFISCDI, project number PN-III-P4-ID-PCCF-2016-0050, within PNCDI III). We thank Prof. Jiayin Yuan in Stockholm University for insightful discussion. These computations were enabled by resources provided by Swedish National Infrastructure for Computing (SNIC) at PDC, HPC2N, and NSC partially funded by Swedish Research Council through grant agreement no. 2016-07213.References
- E. W. Castner Jr, C. J. Margulis, M. Maroncelli and J. F. Wishart, Annu. Rev. Phys. Chem., 2011, 62, 85 CrossRef PubMed.
- R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357 CrossRef CAS PubMed.
- D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell Jr, B. Roux and C. Schroder, Chem. Rev., 2019, 119, 7940 CrossRef CAS PubMed.
- Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798 CrossRef CAS PubMed.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621 CrossRef CAS PubMed.
- F. Zhou, Y. Liang and W. Liu, Chem. Soc. Rev., 2009, 38, 2590 RSC.
- D. R. MacFarlane, M. Forsyth, P. C. Howlett, M. Kar, S. Passerini, J. M. Pringle, H. Ohno, M. Watanabe, F. Yan and W. Zheng, et al. , Nat. Rev. Mater., 2016, 1, 15005 CrossRef CAS.
- Z. Zhang, J. Song and B. Han, Chem. Rev., 2016, 117, 6834 CrossRef PubMed.
- J. Y. Shin, S. A. Yamada and M. D. Fayer, J. Am. Chem. Soc., 2017, 139, 11222 CrossRef CAS PubMed.
- K. Goossens, P. Nockemann, K. Driesen, B. Goderis, C. Görller-Walrand, K. Van Hecke, L. Van Meervelt, E. Pouzet, K. Binnemans and T. Cardinaels, Chem. Mater., 2008, 20, 157 CrossRef CAS.
- D. A. Turton, J. Hunger, A. Stoppa, G. Hefter, A. Thoman, M. Walther, R. Buchner and K. Wynne, J. Am. Chem. Soc., 2009, 131, 11140 CrossRef CAS PubMed.
- S.-C. Luo, S. Sun, A. R. Deorukhkar, J.-T. Lu, A. Bhattacharyya and I. J. Lin, J. Mater. Chem., 2011, 21, 1866 RSC.
- K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Chem. Rev., 2016, 116, 4643 CrossRef CAS PubMed.
- Y. Nozaki, K. Yamaguchi, K. Tomida, N. Taniguchi, H. Hara, Y. Takikawa, K. Sadakane, K. Nakamura, T. Konishi and K. Fukao, J. Phys. Chem. B, 2016, 120, 5291 CrossRef CAS PubMed.
- Y. Wang and G. A. Voth, J. Am. Chem. Soc., 2005, 127, 12192 CrossRef CAS PubMed.
- A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, J. Phys. Chem. B, 2007, 111, 4641 CrossRef CAS PubMed.
- D. W. Bruce, C. P. Cabry, J. N. Canongia Lopes, M. L. Costen, L. D’Andrea, I. Grillo, B. C. Marshall, K. G. McKendrick, T. K. Minton and S. M. Purcell, et al. , J. Phys. Chem. B, 2017, 121, 6002 CrossRef CAS PubMed.
- J. Haddad, D. Pontoni, B. M. Murphy, S. Festersen, B. Runge, O. M. Magnussen, H.-G. Steinrück, H. Reichert, B. M. Ocko and M. Deutsch, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E1100 CrossRef CAS PubMed.
- Y. Ji, R. Shi, Y. Wang and G. Saielli, J. Phys. Chem. B, 2013, 117, 1104 CrossRef CAS PubMed.
- G. Casella, V. Causin, F. Rastrelli and G. Saielli, Liq. Cryst., 2016, 43, 1161 CrossRef CAS.
- J. Sakuda, M. Yoshio, T. Ichikawa, H. Ohno and T. Kato, New J. Chem., 2015, 39, 4471 RSC.
- J. Yuan, D. Mecerreyes and M. Antonietti, Prog. Polym. Sci., 2013, 38, 1009 CrossRef CAS.
- W. Qian, J. Texter and F. Yan, Chem. Soc. Rev., 2017, 46, 1124 RSC.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190 CrossRef CAS PubMed.
- S.-Y. Zhang, Q. Zhuang, M. Zhang, H. Wang, Z. Gao, J.-K. Sun and J. Yuan, Chem. Soc. Rev., 2020, 49, 1726 RSC.
- J.-H. Choi, Y. Ye, Y. A. Elabd and K. I. Winey, Macromolecules, 2013, 46, 5290 CrossRef CAS.
- J. R. Sangoro, C. Iacob, A. Agapov, Y. Wang, S. Berdzinski, H. Rexhausen, V. Strehmel, C. Friedrich, A. Sokolov and F. Kremer, Soft Matter, 2014, 10, 3536 RSC.
- C. M. Evans, C. R. Bridges, G. E. Sanoja, J. Bartels and R. A. Segalman, ACS Macro Lett., 2016, 5, 925 CrossRef CAS.
- C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, ACS Macro Lett., 2017, 6, 941 CrossRef CAS.
- S. Mogurampelly, J. R. Keith and V. Ganesan, J. Am. Chem. Soc., 2017, 139, 9511 CrossRef CAS PubMed.
- P. Kuray, T. Noda, A. Matsumoto, C. Iacob, T. Inoue, M. A. Hickner and J. Runt, Macromolecules, 2019, 52, 6438 CrossRef CAS.
- X. Luo, H. Liu and S. J. Paddison, ACS Appl. Polym. Mater., 2021, 3, 141 CrossRef CAS.
- J. R. Sangoro and F. Kremer, Acc. Chem. Res., 2012, 45, 525 CrossRef CAS PubMed.
- Z. Wojnarowska, J. Knapik, J. Jacquemin, S. Berdzinski, V. Strehmel, J. Sangoro and M. Paluch, Macromolecules, 2015, 48, 8660 CrossRef CAS.
- J. Bartels, G. E. Sanoja, C. M. Evans, R. A. Segalman and M. E. Helgeson, Macromolecules, 2017, 50, 8979 CrossRef CAS.
- Z. Zhang, B. K. Wheatle, J. Krajniak, J. R. Keith and V. Ganesan, ACS Macro Lett., 2019, 9, 84 CrossRef.
- R. Yan, M. Antonietti and M. Oschatz, Adv. Energy Mater., 2018, 8, 1800026 CrossRef.
- F. Fan, W. Wang, A. P. Holt, H. Feng, D. Uhrig, X. Lu, T. Hong, Y. Wang, N.-G. Kang and J. Mays, et al. , Macromolecules, 2016, 49, 4557 CrossRef CAS.
- W. Zhao, F. Leroy, B. Heggen, S. Zahn, B. Kirchner, S. Balasubramanian and F. Müller-Plathe, J. Am. Chem. Soc., 2009, 131, 15825 CrossRef CAS PubMed.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. Lett., 2015, 6, 700 CrossRef CAS PubMed.
- Y.-L. Wang, J. Phys. Chem. B, 2018, 122, 6570 CrossRef CAS PubMed.
- B. Bhargava and M. L. Klein, Soft Matter, 2009, 5, 3475 RSC.
- J. Yuan, S. Soll, M. Drechsler, A. H. Müller and M. Antonietti, J. Am. Chem. Soc., 2011, 133, 17556 CrossRef CAS PubMed.
- Y. Wang, S. Izvekov, T. Yan and G. A. Voth, J. Phys. Chem. B, 2006, 110, 3564 CrossRef CAS PubMed.
- M. Salanne and Phys Chem, Chem. Phys., 2015, 17, 14270 CAS.
- A. Moradzadeh, M. H. Motevaselian, S. Y. Mashayak and N. R. Aluru, J. Chem. Theory Comput., 2018, 14, 3252 CrossRef CAS PubMed.
- F. Uhlig, J. Zeman, J. Smiatek and C. Holm, J. Chem. Theory Comput., 2018, 14, 1471 CrossRef CAS PubMed.
- Y.-L. Wang, Y.-L. Zhu, Z.-Y. Lu and A. Laaksonen, Soft Matter, 2018, 14, 4252 RSC.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410 CrossRef CAS PubMed.
- Y. Wang, S. Feng and G. A. Voth, J. Chem. Theory Comput., 2009, 5, 1091 CrossRef CAS PubMed.
- H. A. Karimi-Varzaneh, F. Müller-Plathe, S. Balasubramanian and P. Carbone, Phys. Chem. Chem. Phys., 2010, 12, 4714 RSC.
- D. Roy and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 12629 CrossRef CAS PubMed.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, J. Phys. Chem. C, 2011, 115, 16613 CrossRef CAS.
- C. Merlet, M. Salanne and B. Rotenberg, J. Phys. Chem. C, 2012, 116, 7687 CrossRef CAS.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306 CrossRef CAS PubMed.
- C. Péan, C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, B. Daffos, M. Salanne and P. Simon, ACS Nano, 2014, 8, 1576 CrossRef PubMed.
- Y.-L. Wang, A. Lyubartsev, Z.-Y. Lu and A. Laaksonen, Phys. Chem. Chem. Phys., 2013, 15, 7701 RSC.
- A. Lyubartsev, A. Mirzoev, L. Chen and A. Laaksonen, Faraday Discuss., 2010, 144, 43 RSC.
- O. Y. Fajardo, S. Di Lecce and F. Bresme, Phys. Chem. Chem. Phys., 2020, 22, 1682 RSC.
- L. I. Vazquez-Salazar, M. Selle, A. H. De Vries, S. J. Marrink and P. C. Souza, Green Chem., 2020, 22, 7376 RSC.
- Y.-L. Wang, J. Phys. Chem. B, 2020, 124, 7452 CrossRef CAS PubMed.
- P. Keblinski, J. Eggebrecht, D. Wolf and S. Phillpot, J. Chem. Phys., 2000, 113, 282 CrossRef CAS.
- K. R. Harris, M. Kanakubo and L. A. Woolf, J. Chem. Eng. Data, 2006, 51, 1161 CrossRef CAS.
- J. Salgado, T. Regueira, L. Lugo, J. Vijande, J. Fernández and J. Garca, J. Chem. Thermodyn., 2014, 70, 101 CrossRef CAS.
- D. Song and J. Chen, J. Chem. Eng. Data, 2014, 59, 257 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593 CrossRef CAS.
- I. Skarmoutsos, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3675 RSC.
- Z. Hu and C. J. Margulis, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 831 CrossRef CAS PubMed.
- J. J. Hettige, J. C. Araque, H. K. Kashyap and C. J. Margulis, J. Chem. Phys., 2016, 144, 121102 CrossRef PubMed.
- B. Wu, J. P. Breen and M. D. Fayer, J. Phys. Chem. C, 2020, 124, 4179 CrossRef CAS.
- K. V. Axenov and S. Laschat, Materials, 2011, 4, 206 CrossRef CAS PubMed.
- M. E. Di Pietro, T. Margola, G. Celebre, G. De Luca and G. Saielli, Soft Matter, 2019, 15, 4486 RSC.
- W. Cao, B. Senthilkumar, V. Causin, V. P. Swamy, Y. Wang and G. Saielli, Soft Matter, 2020, 16, 411 RSC.
- Y. V. Nelyubina, A. S. Shaplov, E. I. Lozinskaya, M. I. Buzin and Y. S. Vygodskii, J. Am. Chem. Soc., 2016, 138, 10076 CrossRef CAS.
- T. Li, F. Xu and W. Shi, Chem. Phys. Lett., 2015, 628, 9 CrossRef CAS.
- A. Erbas and M. O. De La Cruz, Phys. Chem. Chem. Phys., 2016, 18, 6441 RSC.
- G. Saielli and Y. Wang, J. Phys. Chem. B, 2016, 120, 9152 CrossRef CAS PubMed.
- W. Cao, Y. Wang and G. Saielli, J. Phys. Chem. B, 2018, 122, 229 CrossRef CAS PubMed.
- G. Saielli, J. Phys. Chem. B, 2016, 120, 2569 CrossRef CAS PubMed.
- G. Saielli, Soft Matter, 2012, 8, 10279 RSC.
- M. Bates and G. Luckhurst, J. Chem. Phys., 1999, 110, 7087 CrossRef CAS.
- G. Saielli, T. Margola and K. Satoh, Soft Matter, 2017, 13, 5204 RSC.
- M. Cifelli, V. Domenici, B. B. Kharkov and S. V. Dvinskikh, Mol. Cryst. Liq. Cryst., 2015, 614, 30 CrossRef CAS.
- D. Majhi, J. Dai, A. V. Komolkin and S. V. Dvinskikh, Phys. Chem. Chem. Phys., 2020, 22, 13408 RSC.
- D. Mecerreyes, Prog. Polym. Sci., 2011, 36, 1629 CrossRef CAS.
- U. H. Choi, Y. Ye, D. Salas de la Cruz, W. Liu, K. I. Winey, Y. A. Elabd, J. Runt and R. H. Colby, Macromolecules, 2014, 47, 777 CrossRef CAS.
- Y. Shao, Y.-L. Wang, X. Li, A. K. Kheirabad, Q. Zhao, J. Yuan and H. Wang, Angew. Chem., Int. Ed., 2020, 59, 17187 CrossRef CAS PubMed.
- L. M. Hall, M. J. Stevens and A. L. Frischknecht, Phys. Rev. Lett., 2011, 106, 127801 CrossRef.
- J. R. Keith, N. J. Rebello, B. J. Cowen and V. Ganesan, ACS Macro Lett., 2019, 8, 387 CrossRef CAS.
- J. R. Keith and V. Ganesan, J. Chem. Phys., 2019, 151, 124902 Search PubMed.
- J. R. Keith, S. Mogurampelly, F. Aldukhi, B. K. Wheatle and V. Ganesan, Phys. Chem. Chem. Phys., 2017, 19, 29134 RSC.
- Q. Zhao and C. M. Evans, Macromolecules, 2021, 54, 3395 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02662c |
| ‡ These authors contributed equally to this work. |
| § Present address: Department of Electrochemical Energy Storage, Helmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109 Berlin, Germany. |
| This journal is © the Owner Societies 2021 |