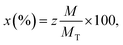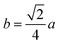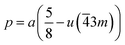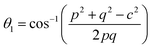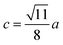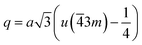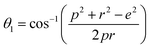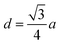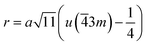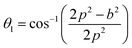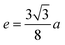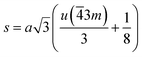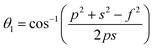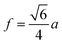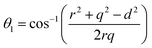Open Access Article
Open Access ArticleMagnetic and structural properties of single-phase Gd3+-substituted Co–Mg ferrite nanoparticles
El. Abouzira,
M. Elansary a,
M. Belaiche
a,
M. Belaiche *a and
H. Jazirib
*a and
H. Jazirib
aNanomaterials and Nanotechnology Unit, E.N.S, Energy Research Centre, Faculty of Sciences, Mohammed V University, B.P. 5118 Takaddoum, Rabat, Morocco. E-mail: med.belaiche@um5.ac.ma
bGenetics and Molecular Biology, E.N.S, Mohammed V University, B.P. 5118 Takaddoum, Rabat, Morocco
First published on 18th March 2020
Abstract
Nanocrystalline Gd3+-doped Co–Mg ferrite nanoparticles with the chemical formula Co0.7Mg0.3Fe(2−x)GdxO4 (x = 0.02) were prepared by coprecipitation for the first time. The properties of the nanoparticles were investigated by X-ray diffraction, confirming a single-phase, highly crystalline cubic spinel structure in the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and an average crystallite size of 54 nm. The Fourier-transform infrared spectrum showed two fundamental absorption bands in the wavenumber range of 437–748 cm−1 attributed to the stretching vibration of tetrahedral and octahedral sites in the spinel structure. Scanning electron microscopy analysis showed that the nanoparticles are different in shape and slightly agglomerated. Energy-dispersive X-ray spectroscopy demonstrated the purity of the nano-ferrite powder. Magnetic measurements revealed ferrimagnetic behavior at room and low temperatures with high coercivity and a high saturation magnetization of 95.68 emu g−1, larger than that of pure bulk cobalt ferrite (80.8 emu g−1). Only ferrite cobalt synthesized sonochemically has been reported to have a higher saturation magnetization (92.5 emu g−1).
m and an average crystallite size of 54 nm. The Fourier-transform infrared spectrum showed two fundamental absorption bands in the wavenumber range of 437–748 cm−1 attributed to the stretching vibration of tetrahedral and octahedral sites in the spinel structure. Scanning electron microscopy analysis showed that the nanoparticles are different in shape and slightly agglomerated. Energy-dispersive X-ray spectroscopy demonstrated the purity of the nano-ferrite powder. Magnetic measurements revealed ferrimagnetic behavior at room and low temperatures with high coercivity and a high saturation magnetization of 95.68 emu g−1, larger than that of pure bulk cobalt ferrite (80.8 emu g−1). Only ferrite cobalt synthesized sonochemically has been reported to have a higher saturation magnetization (92.5 emu g−1).
Introduction
Research in the past decades has suggested that nanotechnology will have crucial long-term effects on all industrial sectors. Compared to bulk materials, nanomaterials have increased reactivity due to their increased solubility and higher proportion of surface atoms. The magnetic, electrical, mechanical, and optical properties along with the specific electronic states of nanomaterials are also totally different from those of the equivalent bulk materials.The specific properties of nanomaterials give them a variety of physical and chemical functionalities that are highly desirable for applications in numerous industrial sectors.1–3 The unique structural characteristics, energetics, tailoring, and production strategies of nanostructures constitute the experimental and conceptual background for the field of nanoscience. The suitable control of nanostructure properties and activity can lead to new devices and technologies. The deviation of the properties of nanosized materials from those of the corresponding bulk materials is related to surface effects, which mainly depend upon the ratio of surface area to volume, the particle size, the chemical composition, and interactions between the particles. It should be noted that rapid developments in the field of nanotechnology have opened up vast possibilities for understanding and using magnetic materials.
In addition, many physical phenomena become more noticeable as the size of the system approaches the nanoscale. In recent years, a lot of work has been done on nanocrystalline materials because of their unusual and interesting properties compared to bulk materials.4,5 Several research groups are investigating spinel oxide nanoparticles and particularly nano-ferrites because of their potential applications in magnetic devices, microwave technology, high-density magnetic recording media, cancer treatment, drug delivery systems, magnetic resonance imaging, and other fields.
The composition and synthetic method play crucial roles in determining the physical and chemical properties of ferrites. Several researchers have synthesized substituted nanoscale ferrites using the standard ceramic technique,6 solid-state methods,7 coprecipitation,8,9 sol–gel methods,10 molten salt routes,11 electrodeposition,12 and mecanosynthesis.13 Other studies have focused on improving the physical properties of these nanomaterials. For example, Li et al. have shown that at the nanoscale, the shape, particle size, and cationic distribution play crucial roles in determining the physical properties of spinel ferrite.14,15 They also demonstrated that the magneto-resistance of spinel ferrite decreases as the average grain size is reduced.16,17
Liu et al.14 established a correlation between the coupling of the orbital angular momentum of electron spin in CoFe2O4 and the superparamagnetic properties of spinel ferrite nanoparticles (MgFe2O4) and deduced that due to the strong magnetic coupling of the Co2+ lattice sites, the blocking temperature of the CoFe2O4 nanoparticles was at least 150 °C higher than that of MgFe2O4 nanoparticles of the same size. On the other hand, rare earth (RE) elements possess high magnetic moments, high magneto-crystalline anisotropy, and very high magnetostriction at low temperature due to the localized nature of 4f electrons. Thus, doping with small quantities of REs can improve the magnetic properties of nano-ferrites, particularly the magnetic coercivity, making them suitable for different applications (e.g., the treatment of hyperthermia and other biomedical applications).17,18 Although numerous nanometric cobalt ferrites have been produced by coprecipitation, few studies have been compared the cationic distributions and magnetic properties of RE-substituted cobalt powders. To our knowledge, the cation distributions and microstructural distributions of RE-doped Co–Mg nano-ferrites have not been reported. Despite the different synthetic techniques, no reports are available on gadolinium-substituted Co–Mg nano-ferrites. In this study, a coprecipitation method was used to synthesize Co0.7Mg0.3Fe1.98Gd0.02O4 nano-ferrites. This method was chosen for its simplicity, short reaction time, low cost, and ability to product fine and homogeneous crystalline powders without any risk of contamination.
The objective of this work was to determine the effects of doping with Gd3+ on the structural, magnetic, and morphological properties of Co0.7Mg0.3Fe(2−x)GdxO4 (x = 0.02) nanoparticles prepared via coprecipitation. To the best of our knowledge, no similar work has been reported to date.
Characterization
The synthesized powder was characterized by X-ray diffraction (XRD; PANalytical PW3050/60) to determine the crystalline phase. The lattice parameters and crystallite sizes were calculated using Rietveld refinement and the Debye–Scherrer formula, respectively. Fourier-transform infrared (FTIR) spectra were recorded on a VERTEX 70 FTIR spectrometer over the range of 400–4000 cm−1. Scanning electron microscopy (SEM; Quanta 200) coupled with energy-dispersive X-ray spectrometry (EDS) was used to determine the particle morphology and the chemical composition of the sample. Magnetic measurements were conducted using a Magnetic Property Measurement System (Quantum Design MPMS-XL-7AC SQUID) to study the magnetic behavior.Experimental details
Gd3+-doped Co–Mg ferrite with the chemical formula Co0.7Mg0.3Fe2−xGdxO4 (x = 0.02) was synthesized by chemical coprecipitation. First, CoCl2·5H2O (≥98% pure, Sigma-Aldrich), FeCl3 (≥99.0% pure, Sigma-Aldrich), Gd(NO3)3·6H2O (≥99.0% pure, Sigma-Aldrich), and Mg(NO3)2 (≥99.0% pure, Sigma-Aldrich) were dissolved stoichiometrically in deionized water. The mixture was stirred with a magnetic stirrer until the solution became homogeneous. The pH of the solution was adjusted to 12 via the dropwise addition of sodium hydroxide under constant stirring. The coprecipitated products were washed several times with deionized water to remove unwanted residual salts. The precipitates were then filtered and dried overnight in an oven at 100 °C. The resulting powders were calcined at 800 °C and 900 °C.Results and discussion
XRD analysis
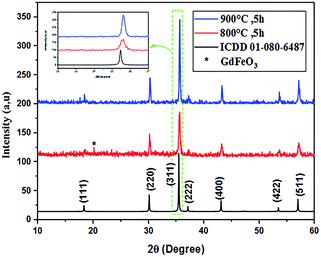
The powder XRD patterns of Co0.7Mg0.3Fe1.98Gd0.02O4 calcined at 800 °C and 900 °C are shown in Fig. 1. The patterns of both samples indicate a highly pure, single-phase spinel crystal structure. The spectrum of the powder calcined at 800 °C has a parasitic peak corresponding to GdFeO3 impurity, which is attributed to incomplete crystallization. In the spectrum of the powder calcined at 900 °C, the diffraction peaks located at 2θ values of 18.41°, 30.24°, 35.65°, 37.25°, 43.22°, 53.60°, and 57.16° correspond to the (111), (220), (311), (222), (400), (422), and (511) planes, respectively, which match exactly with the ICDD data card no #01-080-6487 (for CoFe2O4). These results confirm the formation of single-phase products. Thus, all dopants simply replaced the Co2+–Fe3+ ions without distorting the cubic symmetry of the host cobalt ferrite, resulting in a single-phase cubic spinel structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m); no other impurities were detected in the high-purity cobalt ferrite both with and without gadolinium doping.
m); no other impurities were detected in the high-purity cobalt ferrite both with and without gadolinium doping.
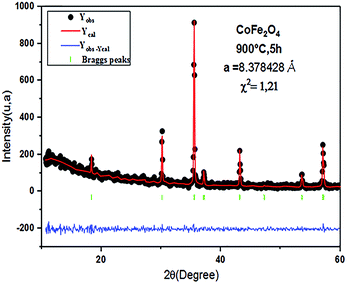
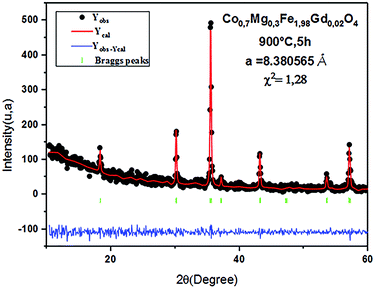
The Rietveld refinement of the average intensity profiles of nanocrystalline CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 calcined at 900 °C was carried out using the program FULLPROF to determine the structural properties. The fitted patterns are in good agreement with the respective experimental data with good fitting parameters; the obtained lattice parameters a are 8.3784 and 8.3805 Å for CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4, respectively. All the peaks can be indexed to a spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Fig. 2 and 3 show the typical refinements for CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 after the final cycle of Rietveld refinement.
m. Fig. 2 and 3 show the typical refinements for CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 after the final cycle of Rietveld refinement.
The average crystallite size D of each sample was determined from the full width at half maximum (FWHM) using the Debye–Scherrer formula:19
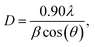 | (1) |
The theoretical density ρX-ray is determined by the following relation:20
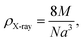 | (2) |
The values of D and ρX-ray determined from eqn (1) and (2) along with the a values calculated by Rietveld refinement are listed in Table 1.
The lattice parameter a = 8.3805 Å for Co0.7Mg0.3Fe1.98Gd0.02O4 was larger than that of CoFe2O4 (a = 8.3784 Å). This can be attributed to the larger ionic radii of Gd3+ (0.094 nm) and Co2+ (0.074 nm) at the octahedral site compared to the radii of Fe3+ (0.067 nm) and Mg2+ (0.072 nm), which resulted in an overall expansion of the lattice.
As shown in Table 1, The calculated value of the average crystallite size (D), of the doped sample Co0.7Mg0.3Fe1.98Gd0.02O4 is smaller than that of the undoped cobalt ferrite CoFe2O4, a result that is similar to those reported for RE-doped ferrites. Indeed, by comparing our results with those found in the literature, we noticed that we observed similar structural behavior with that described in previous work, in terms of an increase in the lattice parameter and decrease in the average crystallite size, but totally different magnetic behavior.21–24 Indeed, in the case of the two substitutions by magnesium and gadolinium, the saturation magnetization and coercivity decrease, whereas in our case the saturation magnetization and coercivity increase drastically despite having been doped with a low concentration of gadolinium. This phenomenon will be better elucidated later when discussing the magnetic properties.
From a structural point of view, this situation can result from the fact that the higher binding energy of Gd3+–O2− compared to Fe3+–O2−. In fact, a large amount of energy is necessary to replace Fe3+ with Gd3+. As a result, Gd3+-substituted ferrites have higher thermal stability than pure cobalt ferrites. The smaller crystallite size may also be related to the pressure created by the larger crystals of Gd3+ ions (large ionic rays) on the grain boundaries.25,26
The calculated ρX-ray value of Co0.7Mg0.3Fe1.98Gd0.02O4 is small compared to that of pure CoFe2O4. This can be explained by the decrease in molecular weight upon doping with Gd3+ and Mg2+. The relative molecular weight decreases as more Co2+ is replaced by Mg2+ since the atomic weight of Co2+ is greater than that of Mg. In addition, the atomic percentage of Gd3+ in this compound is much smaller than that of Mg2+.
Bulk cobalt ferrite has an inverse spinel structure that shifts to a partially inverted structure in the case of nano-ferrites. In the inverse spinel, eight of the tetrahedral sites are occupied by Fe3+, and half of the octahedral sites are occupied by Co2+ and Fe3+. When the size is reduced to the nanoscale, some of the Co2+ ions at the octahedral site migrate to the tetrahedral site, leading to a partially inverted structure. Cobalt ferrite belongs to space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and the lattice parameter is typically close to 8.39 Å.27
m, and the lattice parameter is typically close to 8.39 Å.27
In the literature, MgFe2O4 has been reported to have a partially inverted spinel ferrite structure.28 The distribution of metal ions in MgFe2O4 is given as (Mg1−xFex)[MgxFe2−x]O4, where the parenthesis and square brackets denote cation sites of tetrahedral (A-sites) and octahedral [B-sites] coordination, respectively.29
Studies have been conducted on the effects of the substitution of Co by Mg on the physicochemical properties of cobalt ferrite and vice versa. Several studies have been reported on the effect of metal ion substitution on the structure and magnetic properties of MgFe2O4. The main objective of these studies was to synthesize pure nanocrystalline powders with the general formula MgxCo1−xFe2O4 (0.00 ≤ x ≤ 1.00).
The structural, morphological, electrical, dielectric, and magnetic properties of Co–Mg ferrite have been studied30 while continuing to verify and improve the quality of ferrite for various applications. Several experimental techniques have been used to evaluate the degree of inversion in these spinel systems, including X-ray absorption, neutron and X-ray diffraction, and Raman and Mössbauer spectroscopy. However, these methods alone cannot determine the cation distribution in CoxMg1−xFe2O4 because they only target iron ions (reported results are summarized in Table 2). Therefore, it is interesting to study the properties of Co–Mg ferrite nanoparticles doped with gadolinium because the expected improvement in the structure can lead to the improvement of the magnetic properties.
| Site A | Site B | Method | Reference | |
|---|---|---|---|---|
| Coprecipitation | [Mg0.1Fe0.9] | [Co0.7Mg0.2Fe1.08Gd0.02] | Mathematical model | Present work |
| [Mg0.1Fe0.9] | [Mg0.4Co0.5Fe1.1] | XRD | 31 | |
| [Co0.31Fe0.69] | [Co0.69Gd0.03Fe1.28] | Rietveld analysis | 32 | |
| Sol–gel | [Co0.106Mg0.049Fe0.85] | [Mg0.007Co0.85Fe1.2] | Mössbauer spectroscopy | 33 |
| [Mg0.51Fe0.49] | [Mg0.29Co0.2Fe1.51] | Mathematical model | 34 | |
| [Mg0.159Fe0.841] | [Mg0.841Fe1.159] | Rietveld analysis | 35 | |
| [Mg0.15Fe0.85] | [Mg0.86Fe1.15] | Mössbauer spectroscopy | 36 | |
| [Mg0.14Fe0.86] | [Mg0.87Fe1.13] | Raman spectroscopy | ||
| Ceramic method | [Zn0.5Mg0.08Fe0.62] | [Mg0.62Fe1.38] | Mössbauer spectroscopy | 37 |
According to the literature and in the light of the considerations mentioned above, the suggested cation distribution for the Co0.7Mg0.3Fe1.98Gd0.02O4 samples in this study can be written as
| [MgδFe1−δ]A[Co1−δ−γMgγFe0.98+δGd0.02]BO4, |
The mean ionic radii of ions at the tetrahedral site rtet and octahedral site roct can be described in terms of their concentrations as
| rtet = [δrMg2+ + (1 − δ)rFe3+], | (3) |
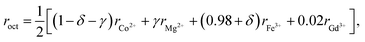 | (4) |
The lattice parameter can be calculated theoretically by the following equation:38
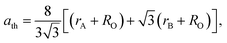 | (5) |
A mathematical model based on the formula proposed for cation distribution was constructed to search for the best match between the theoretical and experimental values of the lattice constant for the sample by optimizing the values of the parameters δ and γ over the tetrahedral and octahedral sites; the obtained cation distribution is shown in Table 3.
| aexp | ath | rA | rB | Cation distribution | |
|---|---|---|---|---|---|
| A-site | B-site | ||||
| 8.3805 | 8.38016 | 0.6750 | 0.7022 | Mg0.1Fe0.9 | Co0.7Mg0.2Fe1.08Gd0.02 |
The results obtained from the proposed model are in very good agreement with those obtained experimentally by Nakagomi et al.36 using Mössbauer and Raman spectroscopy.
From the results reported previously, it is clear that the tetrahedral site A is mainly occupied by Fe3+ ions and a low percentage of Mg2+ ions, while the octahedral site B is occupied by Fe3+, Gd3+, Co2+, and Mg2+ ions, in good agreement with other results obtained by different experimental methods (Table 2).
The spinel structure has a cubic arrangement of O2− ions (fcc); each unit cell contains eight AB2O4 units with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The atom locations in the spinel depend on the choice of the origin in the space group Fd
m. The atom locations in the spinel depend on the choice of the origin in the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The conventional choices for the origin in the cells of the spinel unit are either a cation site A with
m. The conventional choices for the origin in the cells of the spinel unit are either a cation site A with ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m symmetry or an octahedral vacancy with
3m symmetry or an octahedral vacancy with ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry.39
m symmetry.39
If the cation site A with ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m symmetry is taken as the origin, the oxygen position parameter or the anionic parameter u, which is the distance between the oxygen ion and the face of the edge along the cube diagonal of the spinel lattice, is calculated by40
3m symmetry is taken as the origin, the oxygen position parameter or the anionic parameter u, which is the distance between the oxygen ion and the face of the edge along the cube diagonal of the spinel lattice, is calculated by40
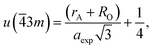 | (6) |
The calculated values of u(![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m) are 0.37886 and 0.3874 Å for the CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 samples, respectively. The decrease in the oxygen positional parameter can be explained by the occupation of the Gd3+ only the octahedral sites but Mg2+ ions at the octahedral and tetrahedral sites. Consequently, the distance between the A and O2− ions decreased, while that between B and O2− increased.41
3m) are 0.37886 and 0.3874 Å for the CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 samples, respectively. The decrease in the oxygen positional parameter can be explained by the occupation of the Gd3+ only the octahedral sites but Mg2+ ions at the octahedral and tetrahedral sites. Consequently, the distance between the A and O2− ions decreased, while that between B and O2− increased.41
FTIR spectra
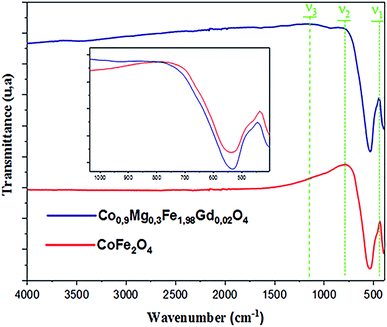
FTIR spectroscopy makes it possible to predict the presence of the different bonds in a crystal. The FTIR spectra of the CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 samples were recorded at room temperature in the wavenumber range of 400–4000 cm−1 (Fig. 4).The positions of the vibrational bands of CoFe2O4 and Co0.7Mg0.3Fe1.98Gd0.02O4 are given in Table 4. For spinel ferrites, the vibrational band at around 750–850 cm−1 corresponds to the stretching vibration of the tetrahedral site, while the vibrational band at around 400–500 cm−1 corresponds to the stretching vibration of the octahedral site.33,42
| ν1 (cm−1) | ν2 (cm−1) | ν3 (cm−1) | |
|---|---|---|---|
| CoFe2O4 | 437.0807 | 779.7678 | — |
| Co0.7Mg0.3Fe1.98Gd0.02O4 | 445.28849 | 812.0047 | 1165.5477 |
Table 4 indicates that the vibrational spectra consist of two main bands (ν1 = 437.0807 cm−1 and ν2 = 779.7678 cm−1) for CoFe2O4 and three bands (ν1 = 445.28849 cm−1, ν2 = 812.0047 cm−1, and ν3 = 1165.5477 cm−1) for Co0.7Mg0.3Fe1.98Gd0.02O4. The absorption band ν1 is assigned to the stretching vibration mode of metal–oxygen at tetrahedral sites, whereas ν2 is attributed to octahedral sites. The positions of the two strong bands are clearly related to the difference in the Fe–O bond lengths at the A- and B-sites. The presence of the band ν3 in Co0.7Mg0.3Fe1.98Gd0.02O4 is related to the stretching vibration of the nitrate group (NO3).43
Compared to CoFe2O4, the FTIR bands of Co0.7Mg0.3Fe1.98Gd0.02O4 are shifted toward higher frequency, as indicated in the inset of Fig. 4 (v1 = 437–445 cm−1 and v2 = 749–812 cm−1). These shifts are explained by the changes in the bond strength, bond length, and broadening of the tetrahedral and octahedral sites.44
The changes in the octahedral site were greater than those in the tetrahedral site after doping with gadolinium. Thus, it can be concluded that the gadolinium ions have a greater effect on the octahedral sites. The doping ions can increase the absorption band length of the tetrahedral and octahedral site lattice. In addition, Fe3+, Co2+, Mg2+, and Gd3+ mainly occupy the B-sites in the spinel structure, inducing stress at the octahedral and tetrahedral sites. This leads to an increase in the ionic rays at both sites, leading to a change in frequency.
Morphological study
The external morphology of Co0.7Mg0.3Fe1.98Gd0.02O4 was visualized by SEM (Fig. 5). The nanoparticles agglomerated due to their mutual magnetic interactions and high surface energy. The shapes of the particles appeared to be non-spherical.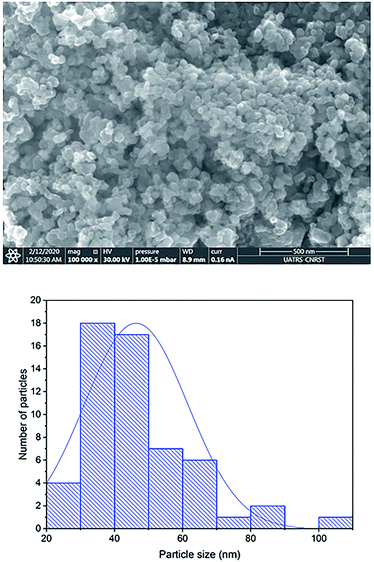 | ||
| Fig. 5 SEM image of Co0.7Mg0.3Fe1.98Gd0.02O4 nanoparticles and the corresponding particle size distribution. | ||
The particle size distribution was analyzed using ImageJ software. The particle size at the surface was roughly estimated to be in the range of 30–70 nm for the Gd-doped ferrite sample, close to the value of D obtained by XRD analysis (Scherrer's method) for the same sample.
The elemental composition of the Co0.7Mg0.3Fe1.98Gd0.02O4 nanomaterial sample was investigated by EDS and the elemental mapping is shown in Fig. 6. The EDS spectrum and elemental mapping confirm the presence of Co, Mg, Gd, Fe, and O in the synthesized nanoparticles; no other traceable impurities were detected within the resolution limit of EDS. The theoretical elemental composition x was calculated using the following formula:
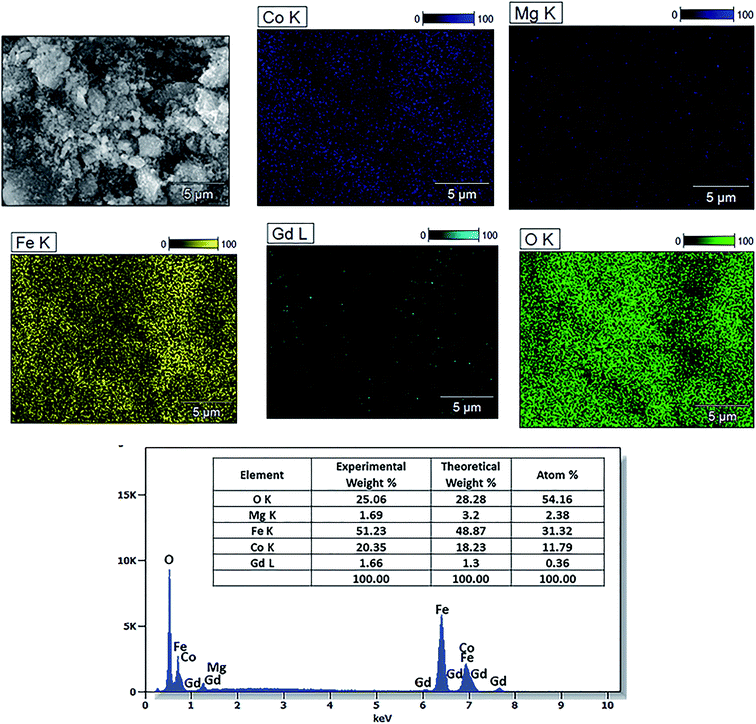 | ||
| Fig. 6 EDS spectrum and elemental maps of Co0.7Mg0.3Fe1.98Gd0.02O4 and the corresponding elemental composition. | ||
Magnetic properties
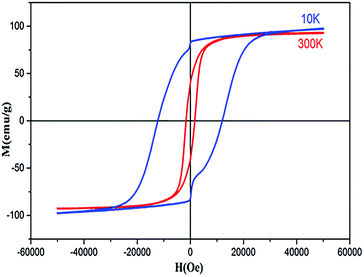
The magnetic properties of Co0.7Mg0.3Fe1.98Gd0.02O4 were investigated using a magnetic property measurement system. Fig. 6 shows the measured magnetic hysteresis loops at low and room temperature (10 and 300 K) under an applied external field of ±50 kOe. The loops indicate ferrimagnetic behavior.The MS values of the two curves were determined by fitting the high-field (1/H → 0) data using the following function:19
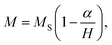 | (7) |
| Ms (emu g−1) | Mr (emu g−1) | Hc (Oe) | Mr/Ms | nB (μB) | K × 105 (erg cm−3) | |
|---|---|---|---|---|---|---|
| 300 K | 95.68 | 39.99 | 1702.28 | 0.41 | 3.87 | 1.69 |
| 10 K | 109.53 | 82.58 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959.53 959.53 |
0.75 | 4.43 | 13.64 |
The data in Table 5 show that MS and Mr increased with decreasing temperature from 300 to 10 K for the doped sample, and these MS and Mr values were higher than those of undoped cobalt ferrite. In contrast, the MS values of some RE-doped ferrites were reported to be lower compared to that of bulk cobalt ferrite.22 The MS determined at 10 K was higher than that determined at 300 K. This can be explained by the decrease in thermal energy at low temperature, which leads to the alignment of magnetic moments parallel to the direction of the applied magnetic field, resulting in an increase in saturation.45 The mechanism is exactly the opposite at high temperature, where the surface spins show some disordered states, weakening their response to the applied magnetic field and thus reducing magnetization. The higher values of MS at high and low temperature are attributed to the migration of some ferric ions from the octahedral site to the tetrahedral site. This observed variation in the MS and Mr can be understood by considering the structure of the ferrimagnetic cubic spinel. The number of octahedral sites (B-sites) is twice the number of tetrahedral sites (A-sites), and the magnetic moments on the octahedral and tetrahedral sites are antiparallel to each other, leading to a net magnetic moment M(cal) = MB − MA. In addition, the increase in size can be correlated with the transformation of the multi-domain structure into a monodomain structure40,41 upon doping the Co–Mg nano-ferrite with Gd3+. At tetrahedral sites further from the proposed cation distribution, magnesium and ferric ions exhibit A–A exchange interactions; in contrast, at octahedral sites, cobalt, magnesium, ferric, and gadolinium ions exhibit B–B interactions. At tetrahedral and octahedral sites, bivalent (Co2+ and Mg2+) and trivalent (Fe3+ and Gd3+) metal ions exhibit superexchange A–B interactions. The superexchange A–B interactions are practically superior to the A–A and B–B interactions at the respective sites. The superexchange A–B interactions can increased upon the addition of Gd3+ in spinel nano-ferrite Co0.7Mg0.3Fe1.98Gd0.02O4. This increase in A–B interaction implies an increase in MS and nB. Based on the literature, the particle size of pure cobalt ferrite synthesized via coprecipitation is between 10 and 30 nm, while MS is in the range of 55–75 emu g−1 (Table 6). In the case of Co0.7Mg0.3Fe1.98Gd0.02O4, as demonstrated by XRD analysis, the particle size is 54 nm, indicating that MS increases with particle size.
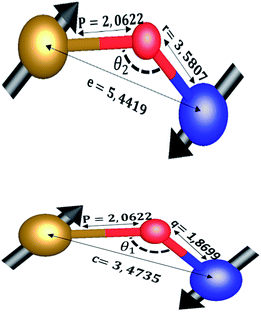
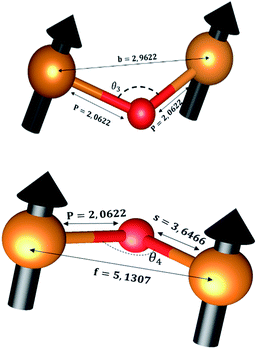
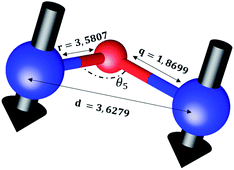
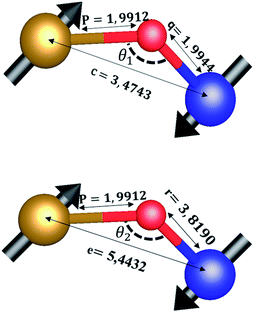
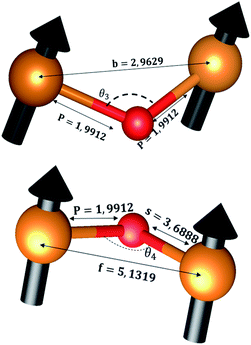
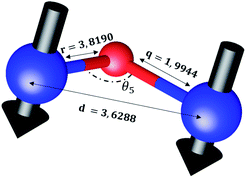
The distances along with the angles between the ions play a crucial role in determining the magnetic exchange interactions. In general, for spinel ferrites, these binding angles and inter-ionic distances greatly affect the magnetic characteristics. Thus, the inter-ionic distances between the cation and anion (Me–O; p, q, r, and s) and between the cation and cation (Me–Me; b, c, d, e, and f) as well as the bond angles (θ1, θ2, θ3, θ4, and θ5) between the cation and cation–anion were calculated using the equations presented in Table 7.40
Tables 8, 9 and 11 show that doping with Mg2+ and Gd3+ caused the bond lengths between Me–O (r, q, and s) and Me–Me (b to f) to increase, while p decreased. An increase in site radius may be expected due to the replacement of smaller Fe3+ (0.067 nm) by larger Mg2+ (0.072 nm) and Gd3+ (0.094 nm) at octahedral sites. The ionic radius of a Gd3+ (0.094 nm) is large for the tetrahedral site; therefore, Gd3+ ions are forced to occupy octahedral sites. Similarly, Co2+ (0.074 nm) prefers to occupy octahedral sites because of its site preference binding energy. Fe3+ partially migrates from octahedral to tetrahedral sites.θ1 and θ2 are related to the A–B interaction, θ3 and θ4 are related to the B–B interaction, and θ5 is related to the A–A interaction. The obtained inter-ionic binding angles are given in Table 11. Doping with Mg2+ and Gd3+ caused θ1, θ2, and θ5 to decrease, while θ3 and θ4 increased. The increase in θ5 indicates a strengthening of A–A interactions, while the increases in θ3 and θ4 suggest an increase in the strength of B–B exchange interactions. Thus, we can deduce that Fe3+, Mg2+, Gd3+, and Co2+ ions at B sites along with Fe3+ and a low concentration of Mg2+ at A sites reinforce the superexchange interaction A–B, leading to increased saturation magnetization. This enhancement in magnetic properties is also attributed to the higher magnetic moment (4f7 orbital, S = 7/2, L = 0, J = 7/2) and spin magnetic moment of Gd3+ compared to Fe3+ (3d5) and Co2+ (3d7, L = 3, S = 3/2, J = 9/2) due to strong L–S coupling. Recently, many studies have been devoted to the effects of various REE dopants on the physicochemical properties of ferrites, including Li–Ni, Ni–Zn, Mn–Zn, Mg–Cu, Cu–Zn.50–54 In most of these studies, MS decreased upon doping. Reports of increases in MS upon doping with REs are much rarer. Rare earth ions generally occupy octahedral sites and have limited solubility in the spinel lattice due to their large ionic rays. However, their precise solubility in the spinel network has not been determined. It should also be noted that doping with low concentrations of REs causes MS to increase, while high dopant concentrations cause MS to decrease.55 Our results are in good agreement with the theoretical studies of Hou Y. H. et al.,56 who found that the net magnetic moment of CoFe2O4 increased upon doping with Gd3+. Yu-Hua et al. also showed that the rare earth ions prefer to substitute for Fe3+ located at octahedral sites, and the lattice constant of CoFe1.875RE0.125O4 (RE = La, Ce, Pr, Nd, Eu, and Gd) decreased due to the decreasing ionic radius of the RE with increasing atomic number. The saturation magnetization of CoFe2O4 increases upon doping only with Eu and Gd because there are more unpaired 4f electrons for Eu3+ and Gd3+. Similarly, Torkian et al.55 reported that the magnetization of Gd3+-doped Mn–Zn ferrite increased for Gd3+ substitution of up to 15%. The most significant result of this work is the production of Gd-doped Co–Mg nano-ferrites with magnetization much higher than that of bulk cobalt ferrite. To the best of our knowledge, this result has not been previously reported. Similar findings have been reported for sonochemically produced CoFe2O4 and ZnxCo(1−x)Fe2O4 synthesized using complex precursors (Table 10).
| Parameter | b (Å) | c (Å) | d (Å) | e (Å) | f (Å) | p (Å) | q (Å) | r (Å) | s (Å) |
|---|---|---|---|---|---|---|---|---|---|
| CoFe2O4 | 2.9622 | 3.4735 | 3.6279 | 5.4419 | 5.1307 | 2.0622 | 1.8699 | 3.5807 | 3.6466 |
| Co0.7Mg0.3Fe1.98Gd0.02O4 | 2.9629 | 3.4743 | 3.6288 | 5.4432 | 5.1319 | 1.9912 | 1.9944 | 3.8190 | 3.6888 |
| Parameter | θ1 (°) | θ2 (°) | θ3 (°) | θ4 (°) | θ5 (°) |
|---|---|---|---|---|---|
| CoFe2O4 | 124.0221 | 148.1105 | 91.8114 | 125.6836 | 76.3662 |
| Co0.7Mg0.3Fe1.98Gd0.02O4 | 121.3193 | 136.7599 | 96.1482 | 126.6282 | 69.2622 |
| Compound | Method of synthesis | MS (emu g−1 at 300 K) | Ms (emu g−1 at 5 K) | HC (Oe at 300 K) | HC (Oe at 5 K) | Mr/Ms (300 K) | Mr/Ms (5 K) | Reference |
|---|---|---|---|---|---|---|---|---|
| Co0.7Mg0.3Fe1.98 Gd0.02O4 | Coprecipitation | 95.68 | 109.5 | 1702.28 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959.53 959.53 |
0.4179 | 0.7539 | Present work |
| CoFe2O4 | Classical ceramic method | 88 | — | 141 | — | — | — | 57 |
| CoFe2O4 | — | 80.8 | 93.9 | — | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
— | 58 | |
| CoFe2O4 | Sonochemical method | 92.5 | — | 807 | — | — | — | 59 |
| CoFe2O4 | Chemical complexes | 92 | 109 | — | 12 | — | — | 60 |
The experimental magnetic moment per formula unit (nB of Co0.7Mg0.3Fe1.98Gd0.02O4 was be calculated as follows:61
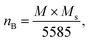 | (8) |
According to the proposed cation distribution (Mg0.1Fe0.9)A[Co0.7Mg0.2Fe1.08Gd0.02]BO4 and using the magnetic moment values of Mg2+ (0 μB), Fe3+ (5 μB), Gd3+ (7 μB), and Co2+ (3 μB), the net magnetic moment M(cal) was calculated as M(cal) = MB − MA, where MA and MB represent the net magnetic moments of lattice sites A and B, respectively. The calculated value of M(cal) is 3.14 μB, comparable with the determined experimental value. Further from the proposed cation distribution, at tetrahedral locations, magnesium and ferric ions exhibit A–A exchange interactions; in contrast, at octahedral sites, cobalt, magnesium, ferric, and gadolinium ions exhibit B–B interactions. At tetrahedral and octahedral sites, the metal ions (Mg2+ and Fe3+) exhibit superexchange A–B interactions with Co2+, Mg2+, Fe3+, and Gd3+. Superexchange A–B interactions are practically superior to A–A and B–B interactions at the respective sites. There may be an increase in A–B superexchange interactions with the addition of Gd3+ to Co0.7Mg0.3Fe1.98Gd0.02O4 spinel nano-ferrites. This increase in A–B interaction suggests an increase in the measured values of saturation magnetization and magnetic moment. In this work, MS and nB increased upon the addition of Gd3+ in Co0.7Mg0.3Fe1.98Gd0.02O4 ferrite spinels. This increase in magnetic parameters can be correlated with the bonding angles. The bonding angles θ1, θ2, and θ5 decreased upon doping, suggesting decreased A–A interactions. Meanwhile, θ3 and θ4 increased, indicating an increase in B–B and A–B interactions. The complete solubility of large Gd3+ ions at B sites could be responsible for the change in the magnetic behavior of the Co0.7Mg0.3Fe1.98Gd0.02O4 nano-ferrites. This is probably why high MS and nB values have been obtained with low concentrations of gadolinium. For ferrites doped with high concentrations of other REs, the decrease in saturation magnetization and magnetic moment can be interpreted based on the migration of rare earth ions to the grain boundaries, resulting in weak magnetic behavior. Moreover, the magnetic parameters of spinel ferrites depend upon various factors, including the synthetic technique, sintering temperature, crystallite size, grain size, and redistribution of cations among A and B sites.
The effective anisotropy constant K can be calculated using the relationship62
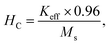 | (9) |
The coercivity of the sample increased from 1702.28 Oe at 300 K to 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 959.53 Oe at 10 K. The enhanced coercivity is attributed to the reduced thermal fluctuation energy at 10 K, which is less effective in reducing the effects of magneto-crystalline anisotropy energy. In addition, the enhanced coercivity could be interpreted as a result of the energy barriers in the nanoparticles becoming more apparent at low temperature. While these barriers always exist, they have been suggested to become more pronounced at low temperature; hence, these barriers might delay the alignment of magnetic moments in the direction of the applied magnetic field.
959.53 Oe at 10 K. The enhanced coercivity is attributed to the reduced thermal fluctuation energy at 10 K, which is less effective in reducing the effects of magneto-crystalline anisotropy energy. In addition, the enhanced coercivity could be interpreted as a result of the energy barriers in the nanoparticles becoming more apparent at low temperature. While these barriers always exist, they have been suggested to become more pronounced at low temperature; hence, these barriers might delay the alignment of magnetic moments in the direction of the applied magnetic field.
As indicated in Fig. 7, the hysteresis loops show “kink” behavior at 10 K. Various explanations have been suggested for these types of loops, including the magnetic coupling between two different magnetic phases with different coercivities. However, in this work, no secondary phase was observed. The kink behavior may also be explained by the oxidation of soft magnetic layers in the presence of atmospheric oxygen. Otherwise, this anomaly can only be attributed to the reordering of magnetic spins at 10 K under the influence of the applied field. These spin reorientations are responsible for constraining the M–H loop, which can be attributed to the reorientation of surface spins around particles and to the domain wall pinning of the potential wells formed by the directional order.65
The squareness ratio (Mr/MS) at 300 K (0.4179) increased to 0.7539 at 10 K. At 300 K, Mr/MS tends towards 0.5, corresponding to randomly oriented uniaxial anisotropic ferromagnetic particles. In contrast, at 10 K, Mr/MS approaches 1, corresponding to typical isolated single-domain ferromagnetic particles. In the same vein, Stoner and Wohlfarth66 reported that the quadratic ratio of 0.5 indicates non-interactive, randomly oriented particles that undergo coherent rotation under the effect of the applied magnetic field. For quadratic ratios below 0.5, the particles interact only through magnetostatic interactions. Exchange coupling only manifests for a quadratic ratio of higher than 0.5.
The squareness ratio obtained at 10 K confirms that we synthesized nanosized materials with high surface area; the surface effects of the magnetic nanoparticles are responsible for their uniaxial anisotropy. Kodama67 effectively suggested that due to the high surface areas of nanomaterials, the spins at the surfaces are canted, and Néel's model of two sublattices is no longer valid. This spin canting at the surface results in higher magneto-crystalline anisotropy in nanomaterials, in good agreement with the results of this study. Such effects may be approved by the contribution from the single-ion anisotropy of Gd3+ in the crystal lattice in conjunction with the surface effects resulting from the alteration of the magnetic structures on the surfaces of the nanoparticles.68
Conclusion
In the present work, coprecipitation was found to be an economical and efficient method for the synthesis of gadolinium-doped mixed Co–Mg ferrite nanoparticles. Structural analysis indicated a single-phase cubic spinel structure of ferrite after sintering at 900 °C, while GdFeO3 was observed as a secondary phase after sintering at 800 °C. The crystallite size calculated from the XRD data was in the order of 54 nm. Rietveld refinement of the XRD pattern indicated an increase in the lattice constant after doping with Gd3+, which enhanced the crystallinity and induced compression deformations. The spinel structure was further confirmed by FTIR spectroscopy. EDS spectroscopy confirmed the presence of Co, Mg, Fe, Gd, and O in the investigated sample, verifying its purity and the good reactivity of gadolinium at 900 °C. The proposed cation distribution suggests that Co2+ and Gd3+ have strong preferences for the octahedral B sites, whereas Mg2+ and Fe3+ prefer to occupy tetrahedral A sites and octahedral B sites. The experimental and theoretical lattice constants were comparable. The measured saturation magnetization values at 10 and 300 K indicated that Gd3+ substitution in the mixed Co–Mg ferrite enhanced the saturation magnetization, which was attributed to the higher spin magnetic moment and anisotropy of Gd3+ compared Fe3+ along with the strong L–S coupling of Co2+. Coercivity increased upon Gd3+ doping, which can be explained by the strong L–S coupling and weak crystal field of Co2+, resulting in stronger magneto-crystalline anisotropy related to the increase in the concentration of high-spin Co2+ ions at octahedral sites. The enhancements in magnetic properties (MS and nB) after doping with Gd3+ were correlated with the changes in bond angles. Finally, we note that the obtained saturation magnetization was much higher than that of bulk cobalt ferrite.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.References
- P. M. Ajayan, M. Pulickel, L. S. Schadler, and P. V. Braun, Nanocomposite science and technology, John Wiley & Sons, 2006 Search PubMed.
- D. Astruc, E. Boisselier and C. Ornelas, Chem. Rev., 2010, 110, 1857–1959 CrossRef CAS PubMed.
- E. Boisselier and D. Astruc, Chem. Soc. Rev., 2009, 38, 1759 RSC.
- C. D. Stanciu, A. V. Kimel, F. Hansteen, A. Tsukamoto, A. Itoh, A. Kirilyuk and Th. Rasing, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 220402 CrossRef.
- R. K. Panda and D. Behera, J. Alloys Compd., 2014, 587, 481–486 CrossRef CAS.
- A. Lakshman, P. S. V. Subba Rao and K. H. Rao, J. Magn. Magn. Mater., 2004, 284, 352–357 CrossRef CAS.
- S. K. Sharma, R. Kumar, V. V. Siva Kumar, M. Knobel, V. R. Reddy, A. Gupta and M. Singh, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 248, 37–41 CrossRef CAS.
- M. Thomas and K. C. George, Appl. Phys., 2009, 47, 6 Search PubMed.
- L. Wang, J. Li, W. Ding, T. Zhou, B. Liu, W. Zhong, J. Wu and Y. Du, J. Magn. Magn. Mater., 1999, 207, 111–117 CrossRef CAS.
- P. Brown and L. J. Hope-Weeks, J. Sol-Gel Sci. Technol., 2009, 51, 238–243 CrossRef CAS.
- S. L. Darshane, R. G. Deshmukh, S. S. Suryavanshi and I. S. Mulla, J. Am. Ceram. Soc., 2008, 91, 2724–2726 CrossRef CAS.
- M. K. Roy and H. C. Verma, J. Magn. Magn. Mater., 2006, 306, 98–102 CrossRef CAS.
- T. M. Clark and B. J. Evans, IEEE Trans. Magn., 1997, 33, 3745 CrossRef CAS.
- C. Liu, B. Zou, A. J. Rondinone and Z. J. Zhang, J. Am. Chem. Soc., 2000, 122, 6263–6267 CrossRef CAS.
- J.-M. Li, X.-L. Zeng and Z.-A. Xu, Appl. Phys. Lett., 2013, 103, 232410 CrossRef.
- J.-M. Li, A. C. H. Huan, L. Wang, Y.-W. Du and D. Feng, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 6876–6878 CrossRef CAS.
- I. Apostolova and J. M. Wesselinowa, Solid State Commun., 2009, 149, 986–990 CrossRef CAS.
- P. Kumar, J. Chand, S. Verma and M. Singh, Int. J. Theor. Appl. Sci., 2011, 3(2), 10–12 Search PubMed.
- Y. Mouhib, M. Belaiche and S. Briche, Phys. Status Solidi A, 2018, 215, 1800469 CrossRef.
- T. Prabhakaran, R. V. Mangalaraja, J. C. Denardin and J. A. Jiménez, J. Alloys Compd., 2017, 716, 171–183 CrossRef CAS.
- Q. Lin, Y. He, J. Lin, F. Yang, L. Wang and J. Dong, J. Magn. Magn. Mater., 2019, 469, 89–94 CrossRef CAS.
- Q. Lin, J. Lin, Y. He, R. Wang and J. Dong, J. Nanomater., 2015, 1–6 Search PubMed.
- M. M. Rashad, R. M. Mohamed and H. El-Shall, J. Mater. Process. Technol., 2008, 198, 139–146 CrossRef CAS.
- L. Zhao, H. Yang, L. Yu, Y. Cui, X. Zhao, Y. Yan and S. Feng, Phys. Lett. A, 2004, 332, 268–274 CrossRef CAS.
- L. Zhao, H. Yang, L. Yu, W. Sun, Y. Cui, Y. Yan and S. Feng, Phys. Status Solidi A, 2004, 3121–3128 CrossRef CAS.
- A. A. Sattar, A. M. Samy, R. S. El-Ezza and A. E. Eatah, Phys. Status Solidi A, 2002, 8, 86–93 CrossRef.
- A. Franco, F. L. A. Machado and V. S. Zapf, J. Appl. Phys., 2011, 110, 53913 CrossRef.
- N. Aliyan, S. M. Mirkazemi, S. M. Masoudpanah and S. Akbari, Appl. Phys. A, 2017, 123, 446 CrossRef.
- S. K. Pradhan, S. Bid, M. Gateshki and V. Petkov, Mater. Chem. Phys., 2005, 93, 224–230 CrossRef CAS.
- L. Sun, R. Zhang, Q. Ni, E. Cao, W. Hao, Y. Zhang and L. Ju, Phys. B, 2018, 545, 4–11 CrossRef CAS.
- D. Varshney, K. Verma and A. Kumar, J. Mol. Struct., 2011, 1006, 447–452 CrossRef CAS.
- S. Joshi, M. Kumar, S. Chhoker, A. Kumar and M. Singh, J. Magn. Magn. Mater., 2017, 426, 252–263 CrossRef CAS.
- G. P. Nethala, R. Tadi, A. V. Anupama, S. L. Shinde and V. Veeraiah, Mater. Sci., 2018, 36, 310–319 CAS.
- N. Thomas, P. V. Jithin, V. D. Sudheesh and V. Sebastian, Ceram. Int., 2017, 43, 7305–7310 CrossRef CAS.
- N. K. Thanh, T. T. Loan, N. P. Duong, L. N. Anh, D. T. T. Nguyet, N. H. Nam, S. Soontaranon, W. Klysubun and T. D. Hien, Phys. Status Solidi A, 2018, 215, 1700397 CrossRef.
- F. Nakagomi, S. W. da Silva, V. K. Garg, A. C. Oliveira, P. C. Morais and A. Franco, J. Solid State Chem., 2009, 182, 2423–2429 CrossRef CAS.
- A. M. Gismelseed, K. A. Mohammed, H. M. Widatallah, A. D. Al-Rawas, M. E. Elzain and A. A. Yousif, J. Phys.: Conf. Ser., 2010, 217, 012138 CrossRef.
- R. A. Pawar, S. M. Patange, A. R. Shitre, S. K. Gore, S. S. Jadhav and S. E. Shirsath, RSC Adv., 2018, 8, 25258–25267 RSC.
- S. Panchal, S. Raghuvanshi, K. Gehlot, F. Mazaleyrat and S. N. Kane, AIP Adv., 2016, 6, 055930 CrossRef.
- V. K. Lakhani, T. K. Pathak, N. H. Vasoya and K. B. Modi, Solid State Sci., 2011, 13, 539–547 CrossRef CAS.
- N. Najmoddin, A. Beitollahi, H. Kavas, S. Majid Mohseni, H. Rezaie, J. Åkerman and M. S. Toprak, Ceram. Int., 2014, 40, 3619–3625 CrossRef CAS.
- M. S. Khandekar, R. C. Kambale, J. Y. Patil, Y. D. Kolekar and S. S. Suryavanshi, J. Alloys Compd., 2011, 509, 1861–1865 CrossRef CAS.
- B. M. Ali, M. A. Siddig, Y. A. Alsabah, A. A. Elbadawi and A. I. Ahmed, Adv. Nanoparticles, 2018, 07, 1 CrossRef CAS.
- H. S. Mund and B. L. Ahuja, Mater. Res. Bull., 2017, 85, 228–233 CrossRef CAS.
- S. R. Naik, A. V. Salker, S. M. Yusuf and S. S. Meena, J. Alloys Compd., 2013, 566, 54–61 CrossRef CAS.
- Z. Karimi, Y. Mohammadifar, H. Shokrollahi, Sh. K. Asl, Gh. Yousefi and L. Karimi, J. Magn. Magn. Mater., 2014, 361, 150–156 CrossRef CAS.
- A. K. Nikumbh, R. A. Pawar, D. V. Nighot, G. S. Gugale, M. D. Sangale, M. B. Khanvilkar and A. V. Nagawade, J. Magn. Magn. Mater., 2014, 355, 201–209 CrossRef CAS.
- S. Amiri and H. Shokrollahi, J. Magn. Magn. Mater., 2013, 345, 18–23 CrossRef CAS.
- R. Safi, A. Ghasemi, R. Shoja-Razavi and M. Tavousi, J. Magn. Magn. Mater., 2015, 396, 288–294 CrossRef CAS.
- M. F. Al-Hilli, S. Li and K. S. Kassim, Mater. Sci. Eng., B, 2009, 158, 1–6 CrossRef CAS.
- A. C. F. M. Costa, A. P. A. Diniz, A. G. B. de Melo, R. H. G. A. Kiminami, D. R. Cornejo, A. A. Costa and L. Gama, J. Magn. Magn. Mater., 2008, 320, 742–749 CrossRef CAS.
- D. Ravinder and K. V. Kumar, Bull. Mater. Sci., 2001, 24, 505–509 CrossRef CAS.
- N. Rezlescu, E. Rezlescu, F. Tudorache and P. D. Popa, J. Optoelectron. Adv. Mater., 2004, 6, 695 CAS.
- J. Jiang, L. Li, F. Xu and Y. Xie, Mater. Sci. Eng., B, 2007, 137, 166–169 CrossRef CAS.
- S. Torkian, A. Ghasemi and R. S. Razavi, J. Supercond. Nov. Magnetism, 2016, 29, 1617–1625 CrossRef CAS.
- Y. H. Hou, Y. L. Huang, S. J. Hou, S. C. Ma, Z. W. Liu and Y. F. Ouyang, J. Magn. Magn. Mater., 2017, 421, 300–305 CrossRef CAS.
- G. Dascalu, T. Popescu, M. Feder and O. F. Caltun, J. Magn. Magn. Mater., 2013, 333, 69–74 CrossRef CAS.
- M. Grigorova, H. J. Blythe, V. Blaskov, V. Rusanov, V. Petkov, V. Masheva, D. Nihtianova, Ll. M. Martinez, J. S. Muñoz and M. Mikhov, J. Magn. Magn. Mater., 1998, 183, 163–172 CrossRef CAS.
- M. Abbas, B. Parvatheeswara Rao, Md. Nazrul Islam, K. W. Kim, S. M. Naga, M. Takahashi and C. Kim, Ceram. Int., 2014, 40, 3269–3276 CrossRef CAS.
- V. Mameli, A. Musinu, A. Ardu, G. Ennas, D. Peddis, D. Niznansky, C. Sangregorio, C. Innocenti, N. T. K. Thanh and C. Cannas, Nanoscale, 2016, 8, 10124–10137 RSC.
- S. E. Shirsath, M. L. Mane, S. M. Patange, S. S. Jadhav and K. M. Jadhav, J. Phys. Chem. C, 2011, 115, 20905–20912 CrossRef.
- A. Nairan, M. Khan, U. Khan, M. Iqbal, S. Riaz and S. Naseem, Nanomaterials, 2016, 6, 73 CrossRef PubMed.
- Modern magnetic materials: principles and applications, ed. C. Oh. Robert and O. Handley, John Wiley Sons Inc, N. Y., 2000 Search PubMed.
- B. A. Calhoun and M. J. Freiser, J. Appl. Phys., 1963, 34, 1140–1145 CrossRef CAS.
- Q. Gao, G. Hong, J. Ni, W. Wang, J. Tang and J. He, J. Appl. Phys., 2009, 105, 07A516 CrossRef.
- E. C. Stoner and E. P. Wohlfarth, IEEE Trans. Magn., 1991, 27, 3475–3518 CAS.
- R. H. Kodama, J. Magn. Magn. Mater., 1999, 200, 359–372 CrossRef CAS.
- R. N. Panda, J. C. Shih and T. S. Chin, J. Magn. Magn. Mater., 2003, 257, 79–86 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |