Liquid-phase bottom-up synthesis of graphene nanoribbons

Abstract

Graphene nanoribbons (GNRs) – an emerging family of carbon-based semiconductors – can be precisely synthesised from small molecules such as benzene derivatives through bottom-up approaches. This review outlines a summary of the development of bottom-up synthesis of GNRs in liquid phase. The strategies are classified based on edge structures and widths of the materials, which are the crucial factors for properties of GNRs. In addition, views on challenges in the field and the future outlook are also provided.

---

Ki-Young Yoon

Ki-Young Yoon obtained a BS and an MS in Chemistry from the Seoul National University (South Korea), where he did his research on polymerization-induced self-assembly with Prof. Tae-Lim Choi. He received his PhD degree in Organic Chemistry from the University of Chicago under the guidance of Prof. Guangbin Dong. At UChicago, his research focused on metal-catalysed synthesis of macromolecules including graphene nanoribbons. As a Postdoctoral Fellow, he is currently working with Prof. Robert H. Grubbs at the California Institute of Technology.

Guangbin Dong

Guangbin Dong received his BS degree from Peking University and completed his PhD degree in chemistry from Stanford University with Professor Barry M. Trost, where he was a Larry Yung Stanford Graduate fellow. In 2009, he began his research with Professor Robert H. Grubbs at California Institute of Technology, as a Camille and Henry Dreyfus Environmental Chemistry Fellow. In 2011, he joined the department of chemistry and biochemistry at the University of Texas at Austin as an assistant professor and a CPRIT Scholar. Since 2016, he has been a Professor of Chemistry at the University of Chicago.

---

1. Introduction

Organic semiconductors hold great promise for enabling inexpensive productions of printed electronics and flexible displays.^1–3 However, to realise more practical and efficient devices from organic semiconductors, it is important to achieve precise bandgap engineering, as well as better charge carrier mobility, solution processability, and synthetic scalability of these materials.^2,4 In this context, graphene nanoribbons (GNRs), regarded as quasi-one-dimensional subunits of graphene, are considered to be a highly promising class of organic semiconductors. As a special type of conjugated polymers, GNRs possess a non-zero band gap because of the lateral quantum confinement; yet, they could maintain sufficiently high charge-carrier mobility (>200 cm² V⁻¹ s⁻¹) stemming from their mother material, graphene.^5–7

The electronic properties of GNRs including bandgap and charge-carrier mobility critically depend on their chemical structures, such as edge types (armchair, zigzag, cove, fjord, etc.), width and length of the materials.^8–10 To date, “top-down” approaches, such as lithographic cutting of graphene sheets, unzipping of carbon nanotubes, or sonochemical extraction, have been used to provide GNRs from higher dimensional carbon materials.¹¹ However, these methods produce a mixture of GNRs with different lengths, widths, and edge structures. In addition, it is extremely challenging to obtain narrow GNRs (<2 nm) via a top-down approach, whose bandgaps are expected to be similar to those of conventional silicon semiconductors (∼1.1 eV).¹⁰

In contrast, the “bottom-up” approaches allow for control of the structures of GNRs, because the judicious design of monomer structures, after polymerisation and/or graphenisation, not only dictates the widths and edge structures of GNRs but also permits precise doping at specific positions.^12–15 Currently, liquid-phase and surface-assisted syntheses constitute two different approaches for the “bottom-up” preparation of GNRs. The surface-assisted protocol prepares GNRs from organic monomers on conductive metal surfaces after annealing, which generally gives materials of high quality that can be directly monitored by scanning tunneling microscopy (STM) or atomic force microscopy (AFM) without any casting process. It avoids dealing with the solubility issues of the GNRs formed. In addition, these efforts have led to better characterisation and understanding of the properties of GNRs.^12,15 On the other hand, as a complementary technique, the liquid-phase bottom-up synthesis is beneficial for (potential large-area) device fabrication in terms of scalability and processability of GNRs. The liquid-phase synthesis is generally operated under milder conditions (e.g. much lower reaction temperature); as a consequence, various functional groups or side chains could be introduced by this approach.^12,14

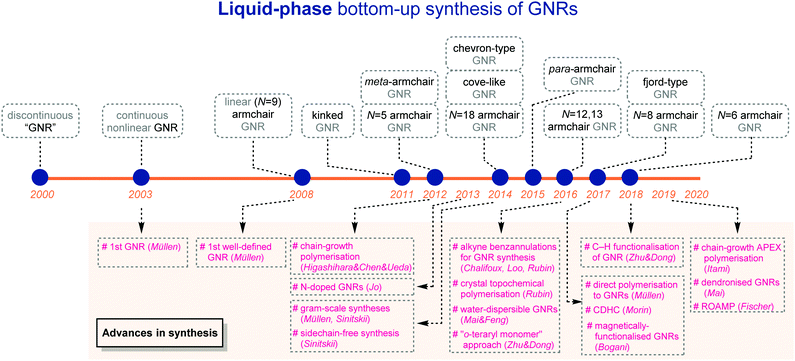
Inspired by a number of excellent reviews/accounts on GNR synthesis,^{7,9–11,14–23} this review is focused on liquid-phase bottom-up synthetic strategies and is categorised based on edge structures and widths, the crucial factors for properties of GNRs (Fig. 1). On-surface GNR syntheses and syntheses of polyaromatic hydrocarbons/nanographenes have been reviewed previously,^{15,18,22–28} and are beyond the scope of this article. As a general note, when relative molecular weights of polymers are mentioned, the number-average molecular weights (M_ns) based on polystyrene standards from size exclusion chromatography (SEC) are used in order to compare with one another in a fair manner.

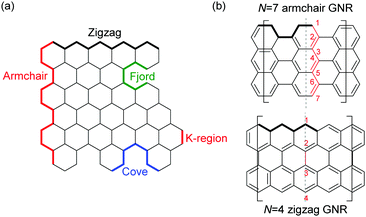Fig. 1 (a) Terminologies of GNR edges. (b) Examples of the width naming. N: the number of rows of atoms forming the ribbon width.

2. Graphene nanoribbons with armchair edges

The properties of GNRs with armchair-shaped edges, namely armchair GNRs, have been most studied from theory.^8,29–32 Since armchair GNRs with N = 3k (semiconducting), 3k + 1 (semiconducting), and 3k + 2 (semimetallic) – N is defined as the number of rows of atoms forming the ribbon width and k is an integer – are predicted to display different characteristics,^8,32 syntheses of armchair GNRs in each family are summarised here. In addition to conventional N-armchair GNRs, other armchair-like GNRs are also covered in this section.

2.1 N = 3k armchair graphene nanoribbons

N = 9 Armchair GNRs. In 2000, Müllen reported an A₂B₂-type Diels–Alder polymerisation of dicyclopentadienone M1c with 1,4-diethynylbenzene (M1a) (Fig. 2). Subsequent cyclodehydrogenation of the resulting polymer (P1a) (AlCl₃, Cu(OTf)₂) resulted in an array of nanographenes (G1a) rather than a (continuous) GNR structure.³³ To prepare a continuous GNR structure, the same group later replaced the monomer M1a with 1,4-diethynyl-2,5-di(4′-tert-butylphenyl)benzene (M1b), and the same polymerisation reaction afforded branched polyphenylenes (P1b) that contain three isomeric polymeric units (trans, linear, cis). The following cyclodehydrogenation of P1b with FeCl₃ yielded a kinked GNR (G1b) with an unclear absorption onset point corresponding to the optical bandgap of ∼1.1 eV.³⁴

Fig. 2 Synthesis of a kinked N = 9 armchair GNR.

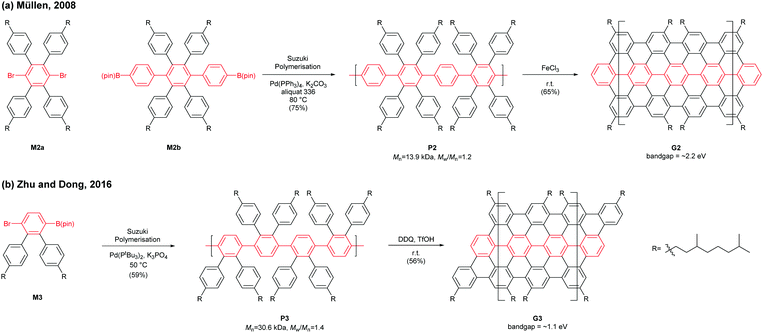
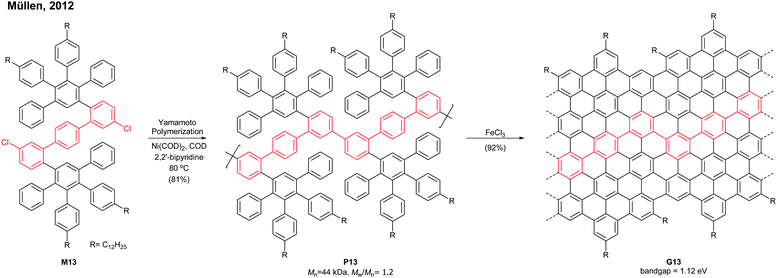
In 2008, Müllen developed a seminal synthetic route to a linear armchair GNR via an A₂B₂-type Suzuki–Miyaura polymerisation of diiodobenzene M2a with bis(boronic ester) compound M2b (Fig. 3a).³⁵ Each monomer contained bulky 3,7-dimethyloctyl groups as side-chains to increase the processability of armchair GNRs. The resulting poly(p-phenylene) (PPP, P2) (M_n = 13.9 kDa and Đ = 1.2 after Soxhlet extraction, where Đ is the molar mass dispersity (M_w/M_n)) was graphenised (94% efficiency) in the presence of FeCl₃ to generate the first well-defined N = 9 armchair GNR (G2) with a length up to 12 nm. The relatively short G2 presented excellent dispersity in common organic solvents; it possessed a relatively large optical bandgap of ∼2.2 eV.

Fig. 3 Synthesis of (linear) N = 9 armchair GNRs.

In 2016, our group developed a new synthetic route to an N = 9 armchair GNR via an AB-type Suzuki–Miyaura polymerisation based on a simple triaryl monomer (M3) (Fig. 3b).³⁶ The monomer can be easily prepared in 4 steps from 1,2-dibromobenzene. The polymerisation afforded a higher-molecular-weight PPP (P3) of M_n = 30.6 kDa and Đ = 1.4 (after Soxhlet extraction) with excellent solubility. The oxidative cyclodehydrogenation with 2,3-dichloro-5,6-dicyanobenzoquinone (DDQ) and triflic acid (TfOH) transformed P3 to a longer armchair GNR (G3, 99% graphenisation efficiency) with an optical bandgap of ∼1.1 eV. The DDQ/TfOH condition was found to be more efficient and selective for cyclodehydrogenation than FeCl₃ in this case. From the bandgap discrepancy between similar GNRs (G2 and G3) one can infer that, besides width and edge structures, length (due to the finite-length effect)³⁷ and/or structural integrity of GNRs could also affect bandgaps.

N = 18 Armchair GNRs. Feng, Müllen, and Samori in 2014 prepared an N = 18 armchair GNR (G4) and then blended it with P3HT for OFET applications because an N = 18 armchair GNR was expected to have an ionisation energy close to that of P3HT.³⁸G4 was produced by an AA-type Yamamoto polymerisation of dichloride M4, followed by oxidative cyclodehydrogenation with FeCl₃ (Fig. 4). G4 with a length up to 10 nm, made from P4 (M_n = 7.4 kDa, Đ = 1.4), was detected by MALDI-TOF MS. The optical bandgap, which is theoretically predicted to be smaller than that of the narrower N = 9 armchair GNR (vide supra, 1.1 eV for G3),⁸ was measured to be 1.6 eV, and this could be possibly due to the short length of G4.³⁷ The fabricated device of P3HT with 24 wt% G4 displayed increased field-effect mobility (3.3 × 10⁻² cm² V⁻¹ s⁻¹) compared to that of pristine P3HT (7.3 × 10⁻³ cm² V⁻¹ s⁻¹).

Fig. 4 Synthesis of N = 18 armchair GNRs.

N = 12 Armchair GNR. In 2016, Rubin reported a unique method to prepare an N = 12 armchair GNR through crystal topochemical polymerisation (Fig. 5).³⁹ The crystal topochemical polymerisation is not a typical wet chemistry process but can be still regarded as liquid-phase bottom-up synthesis of GNRs rather than on-surface synthesis, given that crystals are grown in solution and polymerisation occurs without metal surfaces. Crystals of diacetylene monomers (M5) were polymerised under heat or light to give poly(diacetylene)s P5. The consecutive benzannulation and cyclodehydrogenation under an inert heating atmosphere (300 °C) yielded G5. While fused/cross-linked GNRs were observed, G5 with an optical bandgap of 1.4 eV offered excellent properties for FET applications, including an average mobility of 0.15 cm² V⁻¹ s⁻¹ and an on–off current ratio of 5.

Fig. 5 Synthesis of an N = 12 armchair GNR.

N = 6 Armchair GNRs. An N = 6 armchair GNR, the narrowest member in the N = 3k armchair GNR family, was prepared by our group in 2018 (Fig. 6).⁴⁰ Utilising simple monomers M6a and M6d, an A₂B₂-type Suzuki–Miyaura polymerisation yielded a PPP P6a (M_n = 28.9 kDa, Đ = 1.71 after Soxhlet extraction). P6a was treated with DDQ and TfOH to afford G6a with a bandgap of 1.21 eV. Due to the modular synthetic approach, bandgap engineering of GNRs was achieved simply by using different monomers (e.g.M6b or M6c) instead of M6a. Just as donor–acceptor-type alternating conjugated copolymers, GNRs bearing electron-deficient heteroaryl units (G6b and G6c) possessed lower bandgaps than the pristine GNR (G6a) because of the intramolecular charge transfer. G6b and G6c also featured rare unsymmetrical edges. Capitalising on the heterocyclic moiety, post-functionalisation of G6b was realised via an N-directed C–H borylation (Fig. 7) toward G6b-B, which provided a further decreased optical bandgap (0.95 eV).

Fig. 6 Synthesis of N = 6 armchair GNRs.

Fig. 7 Post-functionalisation of the N = 6 armchair GNR bearing heterocycles.

2.2 N = 3k + 1 armchair graphene nanoribbons

N = 13 armchair GNR. In 2016, Loo fabricated a field-effect device exhibiting ambipolarity (hole: 1.3 × 10⁻⁷ cm² V⁻¹ s⁻¹, electron: 1.0 × 10⁻⁷ cm² V⁻¹ s⁻¹ at 78 K) in an accumulation mode, which was made of a novel N = 13 armchair GNR.⁴¹ This observation was similar to Jo's previous report with kinked GNRs (G24–G26, vide infra).⁴² Notably, the N = 13 GNR G7 was built up from a poly(p-phenylene ethynylene) (PPE) instead of typical PPPs, which was advantageous because it is generally easier to obtain high-molecular-weight PPEs than PPPs (Fig. 8). Indeed, the A₂B₂-type Sonogashira polymerisation of M7a and M7b afforded P7 with a high M_n = 106.5 kDa and Đ = 1.85 (SEC-MALLS). By utilising the copper-catalysed benzannulation⁴³ of the internal alkyne unit of P7 with aldehyde M7c, GNR precursor polymer P7ben was prepared, and then the following cyclodehydrogenation produced G7 with a length of 50 nm (based on the molecular weight of P7). The optical bandgap of a dispersion of G7 was observed to be 1.1 eV; however, the solid-state optical bandgap of G7 on the device was observed to be lower than 0.4 eV, which can relate to the low on–off current ratios (1.8 to 3.1) observed in the device of G7.

Fig. 8 Synthesis of an N = 13 armchair GNR.

2.3 N = 3k + 2 armchair graphene nanoribbons

N = 5 armchair GNRs. The width of N = 5 armchair GNRs is the same as that of naphthalene or perylene. Although oligorylenes have been extensively studied and synthesised in various manners,⁴⁴ polyrylenes (N = 5 armchair GNRs) were not prepared until recently. In 2012, Higashihara, Chen, and Ueda synthesised a polythiophene bearing phenyl groups at the 3-position (P8) by the Grignard-metathesis-method (GRIM) polymerisation of M8a (Fig. 9). P8 was then oxidised by 50 equiv. of FeCl₃ to afford GNR G8via the oxidative cyclodehydrogenation, which can be considered as a sulfur-annulated N = 5 armchair GNR.⁴⁵ Owing to the living chain-growth nature of GRIM, a block copolymer, poly(3-hexylthiophene) (P3HT)-block-G8, was prepared in the same manner. The optical bandgap (∼1.9 eV) and the average hole mobility (1.1 × 10⁻⁵ cm² V⁻¹ s⁻¹) of P3HT-block-G8 (M_n = 7.5 kDa, Đ = 1.29) were similar to those of the P3HT homopolymer possibly due to the short G8 block (degree of polymerisation (DP) = <8).

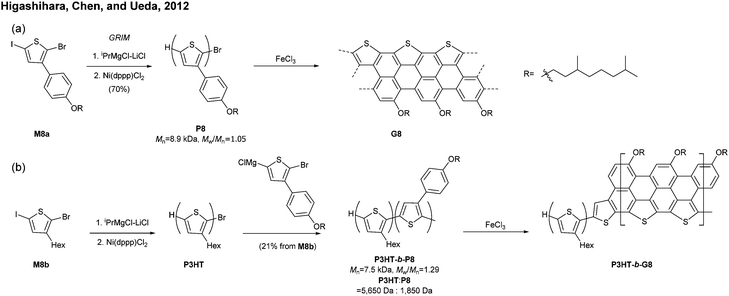Fig. 9 (a) Synthesis of a S-annulated N = 5 armchair GNR and (b) a block copolymer containing S-annulated N = 5 armchair GNRs.

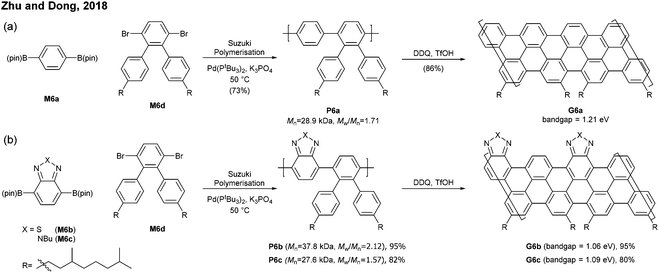
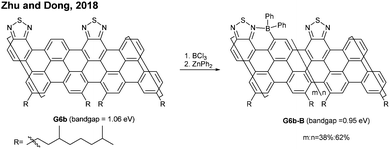
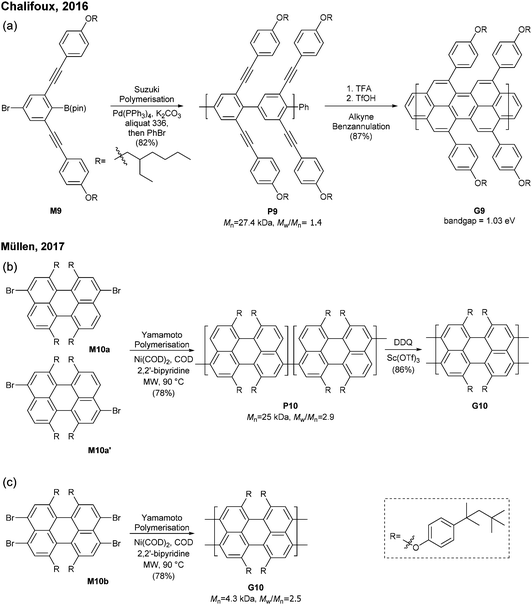
The successful synthesis of longer N = 5 armchair GNRs was reported in 2016 by Chalifoux (Fig. 10a).⁴⁶ The monomer M9 was polymerised via Suzuki–Miyaura coupling to give bis(alkynyl)PPP (P9) with M_n = 27.4 kDa and Đ = 1.4. Then, P9 was further cyclised by benzannulation under acidic conditions in the absence of any oxidant to afford armchair GNR G9 with an average estimated length of 35 nm. The optical bandgap of this narrow GNR was measured to be 1.03 eV. In contrast to poorly soluble G8, G9 featured excellent solubility in common organic solvents such as THF and chloroform. Contrary to the recent observation by Wu that cyclopenta-ring-fused oligorylenes have intrinsic high reactivity coming from a diradical character,⁴⁷G9 was not reported to have specific instability. Above all, the synthetic route to G9 shows an important alternative of the oxidative cyclodehydrogenation for the graphenisation step.

Fig. 10 Synthesis of N = 5 armchair GNRs.

In 2017, Müllen developed a synthesis approach to a poly(perylene) (P10) with M_n = 25 kDa and Đ = 2.9 via an AA-type Yamamoto polymerisation of 3,9/3,10-dibromo-1,6,7,12-tetrakis[tert-octylphenoxy]perylene (M10a/M10a′) (Fig. 10b). The polyperylene P10 was converted to N = 5 armchair GNR G10 through oxidative cyclodehydrogenation with DDQ and Sc(OTf)₃.⁴⁸ After the typical polymerisation–graphenisation approach, Müllen further attempted a concise approach to prepare an N = 5 armchair GNR (G10) directly from a perylene monomer, just as surface-assisted synthesis. Tetrabromo-monomer M10b was polymerised through Yamamoto coupling to directly generate G10. Although the G10 prepared by this method was significantly shorter (M_n = 4300, Đ = 2.5), it eliminated the harsh graphenisation step.

N = 8 armchair GNR. Crystal topochemical polymerisation was revisited by Rubin in 2017 to synthesise N = 8 armchair GNRs (Fig. 11a).⁴⁹ Crystals of diacetylene monomers containing different side-chains (M11a–d) were polymerised under light to give poly(diacetylene)s P11a–d, respectively. Heating of poly(diacetylene)s under an inert atmosphere (500–600 °C) promoted a cascade cyclisation with the polymer backbone, cyclodehydrogenation, and side-chain thermolysis, which quantitatively yielded N = 8 armchair GNR G11 with no side-chains.

Fig. 11 Synthesis of N = 8 armchair GNRs.

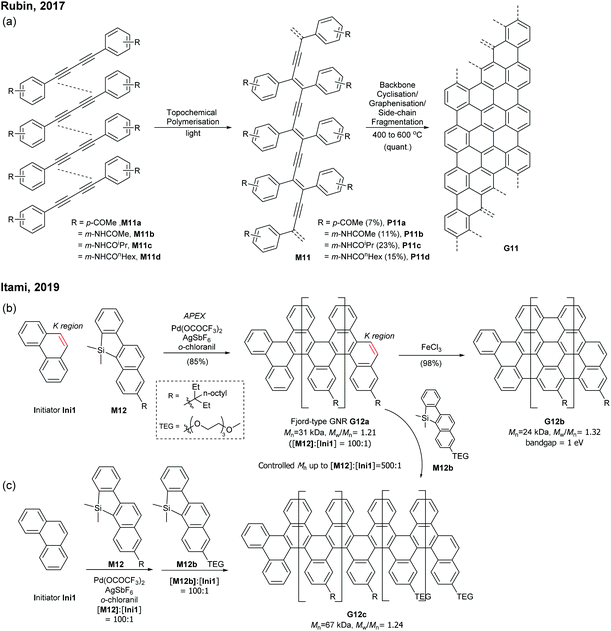
Very recently, Itami disclosed an innovative way to synthesise N = 8 armchair GNRs.⁵⁰ Annulative π-extension (APEX), which was previously shown for nanographene synthesis,^27,28 was successfully extended to polymerisation, first affording Fjord-type GNR G12 in a living chain-growth manner (Fig. 11b). The initiation occurred at the K-region (see Fig. 1) of phenanthrene (Ini1) reacting with monomer M12, and then the chain-propagation continuously occurred at the K-regions that are newly generated by APEX. The molecular weights of G12a were controlled up to the monomer-to-initiator ratio of 500 (DP = 500), the length of which was calculated to be 169 nm. The living chain-growth character also enabled block copolymerisation for a block GNR G12c. Furthermore, the cyclodehydrogenation successfully converted G12a to N = 8 armchair GNR G12b (Fig. 11c). The optical bandgap of the resulting N = 8 armchair GNR (∼1 eV) was observed to be larger than that of the theoretically predicted pristine N = 8 armchair GNR (0.42 eV²⁹); however, the origin of this discrepancy was unclear.

2.4 Isomeric armchair graphene nanoribbons

meta-Armchair GNR. An uncommon GNR was synthesised by Müllen in 2012 (Fig. 12).⁵¹ An AA-type Yamamoto polymerisation of M13 produced a polyphenylene containing an alternative meta–para connectivity (P13) with M_n = 44 kDa and Đ = 1.2 (after prep SEC), which, upon treatment with FeCl₃, formed a unique armchair-like GNR (G13), namely meta-armchair GNR. The wide GNR G13 exhibited an optical bandgap of 1.12 eV, similar to the bandgap of silicon-based semiconductors (1.1 eV).

Fig. 12 Synthesis of a meta-armchair GNR.

para-Armchair GNR. In 2015, Feng and Müllen synthesised a new GNR that is isomeric to meta-armchair GNRs, which is named as a para-armchair GNR. Using the A₂B₂-type Suzuki–Miyaura polymerisation, the PPP P14a (M_n = 4060, Đ = 1.7) was afforded in 73% yield, and the following cyclodehydrogenation with FeCl₃ afforded a para-armchair GNR G14a, which showed an optical bandgap of 1.44 eV (Fig. 13a).⁵²

Fig. 13 Synthesis of para-armchair GNRs.

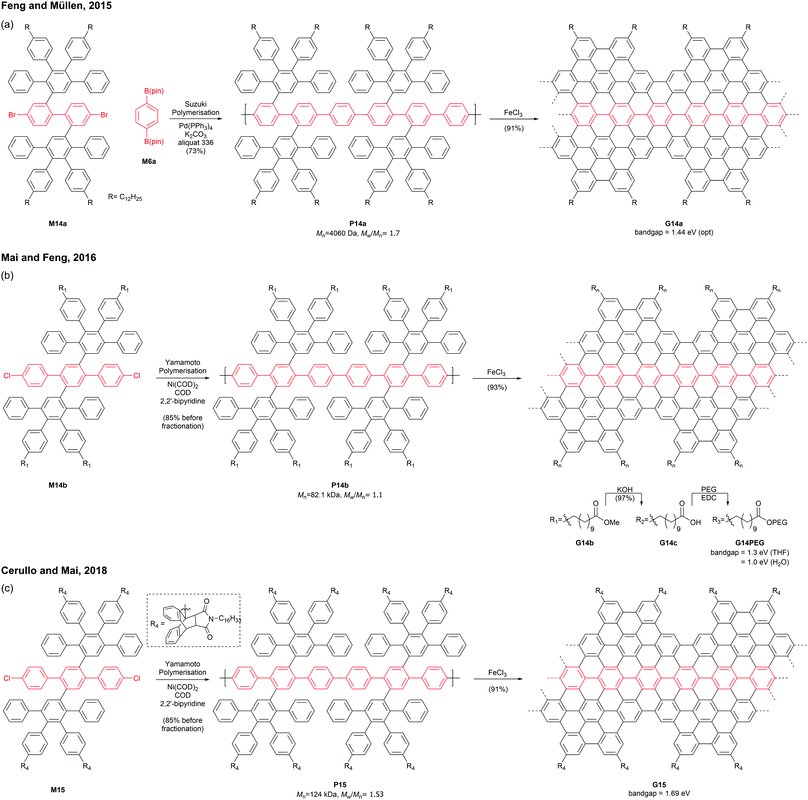
Mai and Feng discovered that an AA-type Yamamoto polymerisation afforded a similar PPP P14b with a higher molecular weight (M_n = 82.1 kDa, Đ = 1.1 after prep SEC fractionation),⁵³ which was graphenised to give para-armchair GNR G14b (Fig. 13b).⁵⁴ The ester side-chains of G14b can be hydrolysed under basic conditions and functionalised with poly(ethylene glycol)s (PEGs) via EDC coupling. The post-functionalised GNR G14PEG (46% PEG grafting) was well-dispersed in THF (1 mg mL⁻¹) as well as in water (0.2 mg mL⁻¹), owing to the hydrophilic PEG-containing side-chains. The optical bandgap of G14PEG in water (1.0 eV) was lower than that in THF (1.3 eV), probably owing to more aggregation of this material in water.⁵⁴ In 2018, Cerullo and Mai prepared a similar para-armchair GNR G15 with bulky side-chains synthesised through a Diels–Alder reaction of anthracenyl units and N-hexadecyl maleimide (Fig. 13c).⁵⁵ The bulky side groups on G15 effectively suppressed the aggregation of GNR chains, exhibiting excellent dispersibility (5 mg mL⁻¹) in many organic solvents such as THF, DCM, and toluene. Dilute dispersions in THF consisted mainly of nonaggregated ribbons, which displayed the optical bandgap of a single GNR G15 (1.69 eV) without contamination of light-scattering signals by GNR aggregates.^56,57 In addition, this GNR showed near-IR emission with a high quantum yield (9.1%) and a long lifetime (8.7 ns).

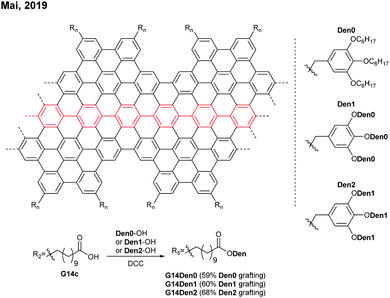
Later in 2019, Mai functionalised G14c with benzyl ether-type dendrons, instead of PEG, via DCC coupling (Fig. 14).⁵⁸ The dendronised GNRs, G14Den0, G14Den1, and G14Den2 (59–68% dendron grafting), were more well-dispersed in THF (1.5–3 mg mL⁻¹) than G14PEG. Interestingly, one-dimensional self-assembled structures of G14Den0 (long nanowires), G14Den1 (long helices) and G14Den2 (short nanofibers) were observed in solution. G14Den2 showed a similar optical bandgap (1.3 eV) to G14PEG in THF, whereas more ordered aggregates of G14Den0 and G14Den1 in THF showed red-shifted absorption.

Fig. 14 Synthesis of dendronised GNRs with para-armchair edges.

3. Graphene nanoribbons with non-armchair edges

3.1 Zigzag graphene nanoribbons

The successful bottom-up synthesis of zigzag GNRs has been demonstrated by Müllen and Fasel through surface-assisted protocols.⁵⁹ However, liquid-phase synthesis of zigzag GNRs has not been reported yet.

3.2 Cove/cove-type graphene nanoribbons

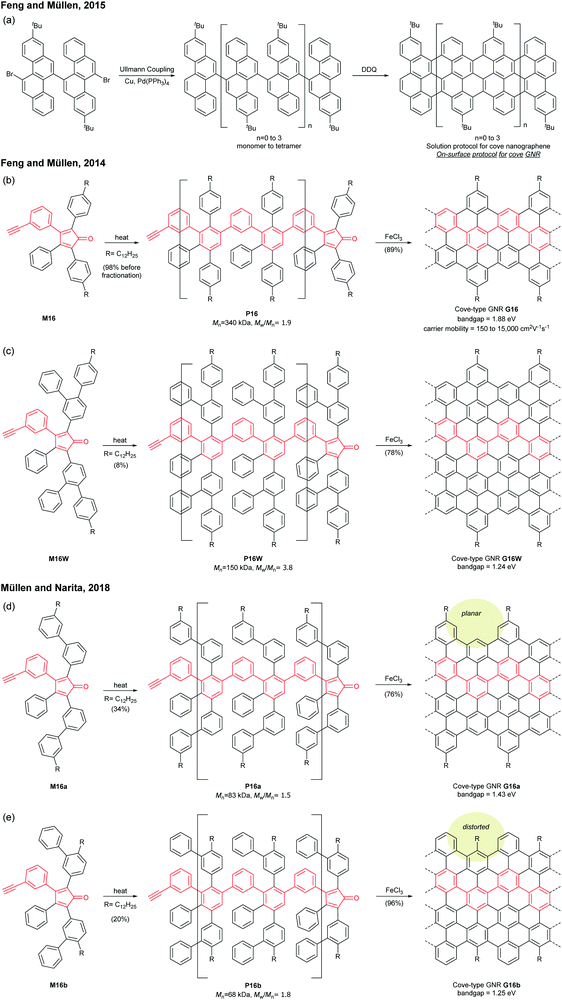
Cove GNRs are zigzag GNRs with periodic carbon atom vacancies on both edges (Fig. 1).⁶⁰ A pristine cove GNR was first synthesised by Feng and Müllen (Fig. 15a).⁶¹ In this case, oligomers were produced in solution via Ullmann coupling followed by DDQ oxidation, whereas the corresponding cove GNR was prepared on a metal surface.

Fig. 15 Synthesis of cove-type GNRs.

On the other hand, GNRs with cove-like edges have also been successfully prepared in solution. In 2014, based upon their previous protocols for the synthesis of nanographenes,^62–64 the same research group developed an elegant metal-free bottom-up approach to synthesise cove-type GNRs, where the AB-type Diels–Alder reaction between cyclopentadienones and alkynes was employed (Fig. 15b).⁶ The polymerisation initially produced precursor polymer P16 with a broad molecular weight dispersity (M_n = 41 kDa, Đ = 13), but SEC fractionation successfully isolated P16 with high-molecular-weight portions (M_n = 340 kDa, Đ = 1.9), which was subjected to cyclodehydrogenation conditions to give long GNR G16 (>200 nm). Cove-type edges containing bulky side-chains on their peripheral positions effectively alleviated the aggregation of long G16, thus displaying decent dispersibility in common organic solvents such as THF and chlorobenzene. The optical bandgap of G16 was measured to be 1.88 eV, which is relatively high compared to the bandgaps of armchair GNRs with similar widths. In addition, G16 featured a high carrier mobility of 150–15 000 cm² V⁻¹ s⁻¹. The same protocol has also been employed to synthesise a wider cove-type GNR G16W, which possessed a lower bandgap than G16 (1.24 vs. 1.88 eV) (Fig. 15c).⁶⁵

Apart from the lateral extension, Müllen and Narita presented a different approach for compressing the bandgaps of cove-type GNRs (Fig. 15d and e). In 2018, they achieved the synthesis of planar G16a and nonplanar G16b from the precursor polymers prepared via the Diels–Alder polymerisation, P16a (M_n = 83 kDa, Đ = 1.5 after prep SEC) and P16b (M_n = 68 kDa, Đ = 1.8 after prep SEC).⁶⁶ With the same aromatic core structure, the peripheral benzo-rings of G16b were distorted by ca. 24° from planarity, while G16a was flat. The optical bandgap of G16b (1.25 eV) was 0.18 eV lower than that of G16a (1.43 eV), which is associated with a lower conduction band. This was likely due to the fact that the structural distortion at the edge alleviates the aggregation of cove GNRs. This approach is free from the drawback of the lateral extension strategy – the trade-off between bandgap compression and processability.

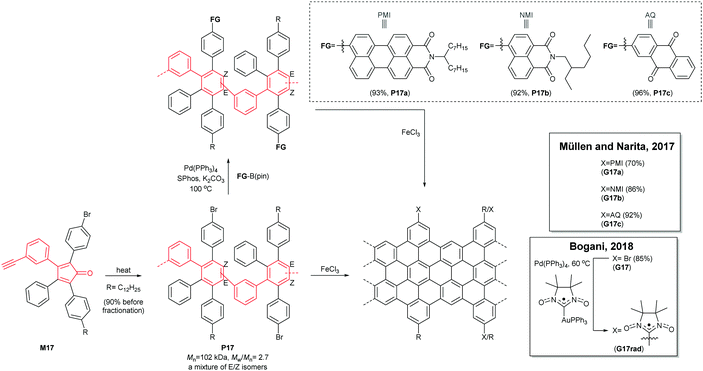
A divergent protocol for edge functionalisation of cove-type GNRs was also developed by Müllen and Narita in 2017 (Fig. 16).⁶⁷ Bromo-functionalised P17 (M_n = 102 kDa, Đ = 2.7 after purification), prepared from mono-bromo-functionalised monomer M17via the Diels–Alder polymerisation, was diversified by introduction of perylene monoamide (PMI), naphthalene monoamide (NMI) and anthraquinone (AQ) units at the peripheral positions of P17 by Suzuki–Miyaura coupling. The consecutive cyclodehydrogenation of P17a–c with FeCl₃ yielded edge-functionalised G17a–c. In 2018, Bogani disclosed a cove-type GNR functionalised with spin-bearing radical groups (Fig. 16).⁶⁸ After graphenisation of P17, nitronyl nitroxide radicals as magnetic injectors were introduced onto G17via palladium-catalysed cross-coupling, affording a magnetically functionalised G17rad.⁵⁹ Spin injection from the nitronyl nitroxide radicals into the GNR core induced magnetic edge states of GNRs, which opens a door for the potential spintronic applications of GNRs.

Fig. 16 Edge functionalisation of cove-type GNRs.

3.3 Chevron-type graphene nanoribbons

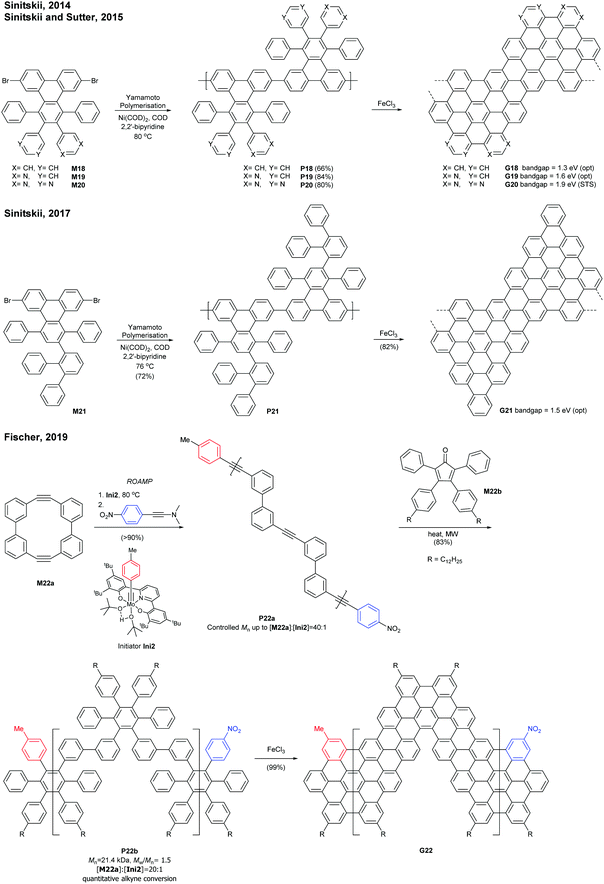
Sinitskii reported a gram-scale synthetic approach for chevron-type GNRs G18 (Fig. 17). An AA-type Yamamoto polymerisation was used to construct the GNR precursor P18, followed by oxidative cyclodehydrogenation with FeCl₃.⁶⁹ It is noted that G18 featured GNRs with no side-chains in stark contrast to the general GNRs with bulky side-chains as solubilising groups. The absence of side-chains facilitated scanning probe microscopic/spectroscopic analyses (e.g. STM, STS, AFM), but made characterisation of GNR precursors (e.g. NMR, SEC) and liquid-phase processes of the GNRs challenging. The limitation of processability was partially resolved by the efforts of Sinitskii and Lyding, respectively. Sinitskii developed a new fabrication method that makes films of single-GNR thick (2 nm), which exploits the high dispersibility of G18 in chlorosulfonic acid and water–air interfacial self-assembly.⁷⁰ On the other hand, Lyding reported a clean deposition method of G18 onto the hydrogen-terminated Si(100) surface.⁷¹

Fig. 17 Synthesis of chevron-type GNRs.

The edge structures of chevron GNRs are difficult to define though large portions of them are armchair-edged. The optical bandgap of G18 was 1.3 eV, which is similar to that of N = 6 or N = 9 armchair GNRs (see Fig. 3 and 6). Later, a laterally extended chevron-type GNR G21 was also prepared by Sinitski by a similar approach, which found application as a gas sensor for methanol and ethanol.⁷²

In addition, nitrogen-doped chevron-type GNRs, G19 and G20, were synthesised analogously by Sinitskii and Sutter.^73,74 The nitrogen doping significantly affects inter-GNR interactions (e.g. N⋯H–C hydrogen bonding interactions, van der Waals interactions, and π–π interactions at the basal planes of G19 and G20), which consequently generated the hierarchical self-assembly of N-doped GNRs into ordered structures.

In 2019, Fischer developed a creative route to a chevron-type GNR. The ring-opening alkyne metathesis polymerisation (ROAMP) of strained cyclic diynes (M22a) afforded P22a in a controlled chain-growth manner. The molecular weights of P22a were controlled up to the monomer-to-initiator ratio of 40 (DP = 40), the length of which was calculated to be 68 nm. The alkynes of P22a were quantitatively converted to phenylene units by Diels–Alder reactions with cyclopentadienone M22b, and the resulting GNR precursor polymer P22b was subsequently cyclodehydrogenated to give a chevron GNR G22.⁷⁵

3.4 Kinked graphene nanoribbons

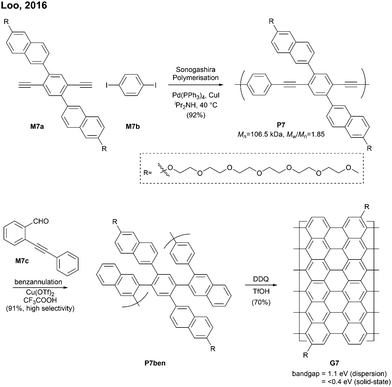
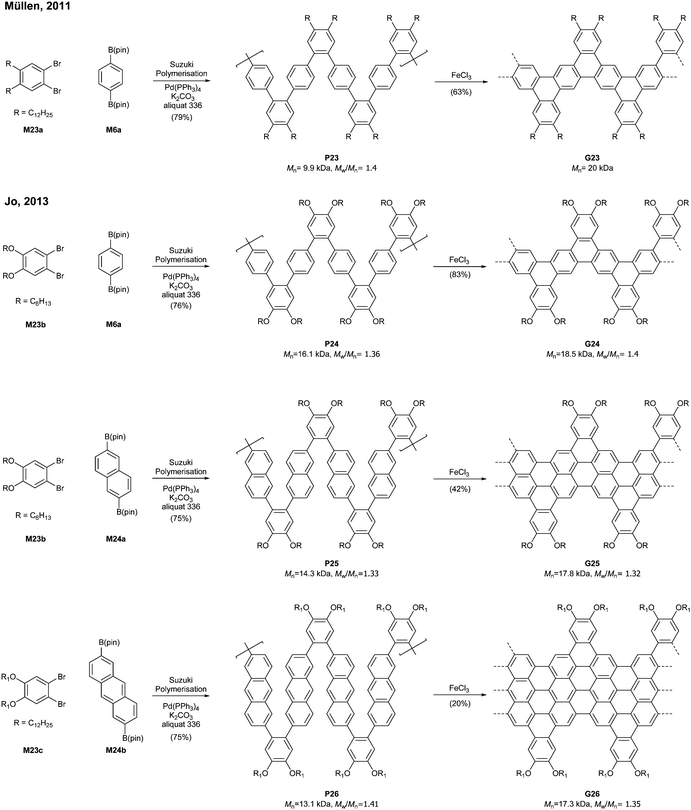
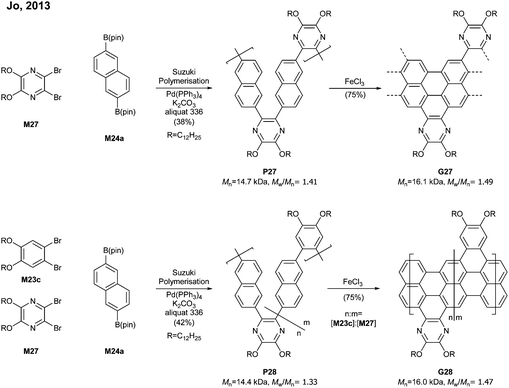
Relatively flexible kinked GNRs were designed to address the solubility issue of GNRs derived from rigid PPPs (e.g.G1b and G2). In 2011, Müllen synthesized soluble kinked GNRs G23 (M_n = 20 kDa) via the Suzuki–Miyaura polymerisation followed by oxidative cyclodehydrogenation (Fig. 18).⁷⁶

Fig. 18 Synthesis of soluble “kinked” GNRs.

The lateral extension of kinked GNRs was achieved, by Jo in 2013, where naphthalene diboronic ester M24a or anthracene diboronic ester M24b was polymerised instead of M6a. While the cyclodehydrogenation from P24 to G24 was successful, incomplete graphenisation was observed in the case of G25 (78%) and G26 (75%). Thin-film transistors (TFTs) were fabricated with these kinked GNRs, which displayed ambipolar transport behaviour, just as the device made of G7 (vide supra). In particular, TFTs made of G26 exhibited better performance (µ_hole = 3.25 × 10⁻² cm² V⁻¹ s⁻¹ and µ_electron = 7.11 × 10⁻³ cm² V⁻¹ s⁻¹) than those made of G24 and G25 due to better π–π stacking.⁴²

By switching 1,2-dibromobenzene to a pyrazine-derived monomer (M27) and via the Suzuki–Miyaura polymerisation followed by cyclodehydrogenation (>95% efficiency) one can achieve nitrogen-doped G27 (M_n = 16.1 kDa, Đ = 1.49) (Fig. 19). In addition, the degree of nitrogen doping can be simply controlled through a copolymerisation process by changing the feed ratio of M27 (pyrazine) to M23c (benzene) (e.g.G28). The electron mobility of G27 (0.102 cm² V⁻¹ s⁻¹) was two orders of magnitude higher than that of G25 (4.57 × 10⁻³ cm² V⁻¹ s⁻¹), which showed that the nitrogen doping modified the electronic transport behaviour from ambipolar to n-type.⁷⁷

Fig. 19 Synthesis of nitrogen-doped “kinked” GNRs.

3.5 Fjord-type graphene nanoribbons

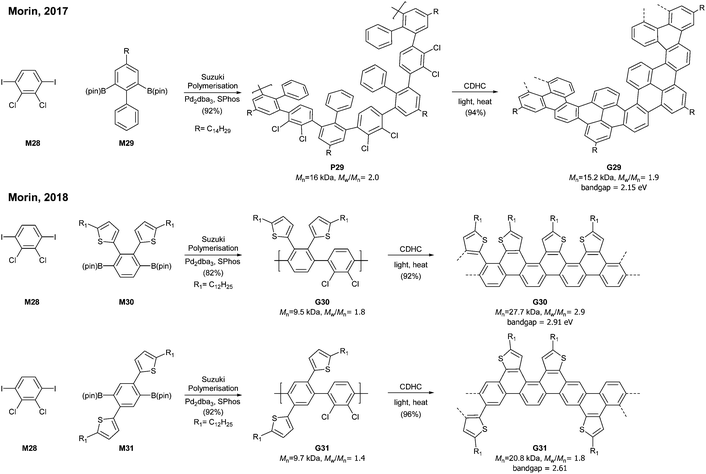
A photochemical cyclodehydrochlorination (CDHC) reaction was first employed for GNR synthesis by Morin. This reaction is not only a relatively mild alternative to the commonly used oxidative methods in the graphenisation step but also a nice way to construct fjord-type edge structures.

In 2017, Morin developed the synthesis of a helically coiled GNR G29 from a polychlorinated poly(m-phenylene) P29via CDHC (Fig. 20).⁷⁸ Given that one helical pitch consists of six monomeric units, the DP value of 32 represents ca. 5 helical pitches. Another structural feature of G29 was the fjord-type inner edge. G29 showed a large optical band gap (2.15 eV) compared to other GNRs and was highly emissive both in solution and in the solid state. It is unclear whether these characters resulted from the fjord edge and/or the helical structure.

Fig. 20 Synthesis of fjord-type GNRs.

Later, Morin also reported an approach to prepare thiophene-edged graphene nanoribbons (G30 and G31) from thiophene-containing polychlorinated PPPs (P31 and P31) via CDHC.⁷⁹ The substitution positions of the thiophenyl groups on PPPs played a critical role in the electronic properties of the GNR. For example, the optical bandgap of G31 (2.61 eV) is 0.3 eV lower than that of G30 (2.91 eV). In addition, G29 and G30 featured unsymmetrical edge structures, similar to the N = 6 armchair GNRs (Fig. 6). As mentioned in the previous section (vide supra, Fig. 11), the APEX polymerisation of M12 directly afforded fjord GNR G12a (M_n = 150 kDa, Đ = 1.22), which showed the optical bandgap to be >2.5 eV.

4. Conclusions and outlook

Since 2000, great advances in liquid-phase bottom-up syntheses have been achieved, which provide access to GNRs with a variety of structures in laboratories, as covered in this review (Fig. 21). Yet, this young research field still demands more important breakthroughs to meet high expectations for (industrial) practical applications.

Fig. 21 A timeline of liquid-phase bottom-up synthesis of GNRs.

First, liquid-phase bottom-up approaches hold great potential for edge functionalisation. The functional groups on the GNR edges could allow for manipulating and fine-tuning the properties of the materials, including band gap engineering, water solubility and binding ability of metal ions. Currently, the graphenisation step in most syntheses requires strong acids, strong oxidants, and/or high temperatures, which would limit the types of functional groups to be introduced due to chemical compatibility. While a few recent efforts, e.g. alkyne benzannulation and cyclodehydrohalogenation, have alleviated the constraint to some extent, general and milder graphenisation approaches (e.g. no acid at r.t.) are still highly sought.

Another ongoing challenge is to confirm the structural integrity of GNRs, that is, to rapidly identify defects. Common solid-state spectroscopic analyses (solid-state NMR, MALDI, IR, Raman, XPS, etc.) are helpful and complementary to each other, but still disputable. Interdisciplinary efforts would be needed to discover conclusive protocols for GNR characterisation.

The self-assembly of GNRs is another ongoing interest. Recent progress in living chain-growth polymerisation for GNRs enables the length control of GNRs as well as block copolymer synthesis, which opens up the possibility of systemic preparation of high-ordered nanostructures from block co-GNRs. In addition, the inter-GNR interactions enabled by nitrogen-doped GNRs have created new opportunities for hierarchical assembly through non-covalent bonds.

Finally, targeted as the next-generation semiconductors, GNRs ought to be produced cost effectively and subjected to large scales. While gram-scale synthesis of GNRs has been achieved in liquid phase to date, further scale-up could be hampered by the overall synthetic efficiency. This in turn calls for better design and more streamlined syntheses of GNR monomers, as well as more selective, efficient and controlled polymerisation and graphenisation methods.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The University of Chicago and NSF (CHE 1707399) are acknowledged for research support.

References

1. A. Facchetti, Mater. Today, 2007, 10, 28–37.
2. H. Klauk, Organic electronics: materials, manufacturing, and applications, John Wiley & Sons, 2006.
3. T. B. Singh and N. S. Sariciftci, Annu. Rev. Mater. Res., 2006, 36, 199–230.
4. X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908.
5. J. Wang, R. Zhao, M. Yang, Z. Liu and Z. Liu, J. Chem. Phys., 2013, 138, 084701.
6. A. Narita, X. Feng, Y. Hernandez, S. A. Jensen, M. Bonn, H. Yang, I. A. Verzhbitskiy, C. Casiraghi, M. R. Hansen, A. H. R. Koch, G. Fytas, O. Ivasenko, B. Li, K. S. Mali, T. Balandina, S. Mahesh, S. De Feyter and K. Müllen, Nat. Chem., 2014, 6, 126–132.
7. S. Dutta and S. K. Pati, J. Mater. Chem., 2010, 20, 8207–8223.
8. Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
9. O. V. Yazyev, Acc. Chem. Res., 2013, 46, 2319–2328.
10. A. Celis, M. N. Nair, A. Taleb-Ibrahimi, E. H. Conrad, C. Berger, W. A. de Heer and A. Tejeda, J. Phys. D: Appl. Phys., 2016, 49, 143001.
11. L. Ma, J. Wang and F. Ding, ChemPhysChem, 2013, 14, 47–54.
12. A. Narita, Z. Chen, Q. Chen and K. Mullen, Chem. Sci., 2019, 10, 964–975.
13. A. Narita, X. Feng and K. Mullen, Chem. Rec., 2015, 15, 295–309.
14. M. Shekhirev and A. Sinitskii, Phys. Sci. Rev., 2017, 2, 12807–12821.
15. L. Talirz, P. Ruffieux and R. Fasel, Adv. Mater., 2016, 28, 6222–6231.
16. Y. C. Teo, H. W. H. Lai and Y. Xia, Chem. – Eur. J., 2017, 23, 14101–14112.
17. Y. Segawa, H. Ito and K. Itami, Nat. Rev. Mater., 2016, 1, 15002.
18. X.-Y. Wang, A. Narita and K. Müllen, Nat. Rev. Chem., 2017, 2, 0100.
19. W. Niu, J. Liu, Y. Mai, K. Müllen and X. Feng, Trends Chem., 2019, 1, 549–558.
20. J. F. Morin, A. Jolly, D. Miao and M. Daigle, Angew. Chem., Int. Ed., 2019 DOI:10.1002/anie.201906379.
21. A. D. Senese and W. A. Chalifoux, Molecules, 2019, 24, 118.
22. K. Müllen, ACS Nano, 2014, 8, 6531–6541.
23. L. Chen, Y. Hernandez, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2012, 51, 7640–7654.
24. A. Narita, X.-Y. Wang, X. Feng and K. Müllen, Chem. Soc. Rev., 2015, 44, 6616–6643.
25. X.-Y. Wang, X. Yao and K. Müllen, Sci. China: Chem., 2019, 9, 1099–1144.
26. X. Feng, W. Pisula and K. Müllen, Pure Appl. Chem., 2009, 81, 2203–2224.
27. H. Ito, Y. Segawa, K. Murakami and K. Itami, J. Am. Chem. Soc., 2018, 141, 3–10.
28. H. Ito, K. Ozaki and K. Itami, Angew. Chem., Int. Ed., 2017, 56, 11144–11164.
29. D. Prezzi, D. Varsano, A. Ruini, A. Marini and E. Molinari, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041404.
30. H. Raza and E. C. Kan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245434.
31. S. Osella, A. Narita, M. G. Schwab, Y. Hernandez, X. Feng, K. Müllen and D. Beljonne, ACS Nano, 2012, 6, 5539–5548.
32. X. Zhu and H. Su, J. Phys. Chem. A, 2011, 115, 11998–12003.
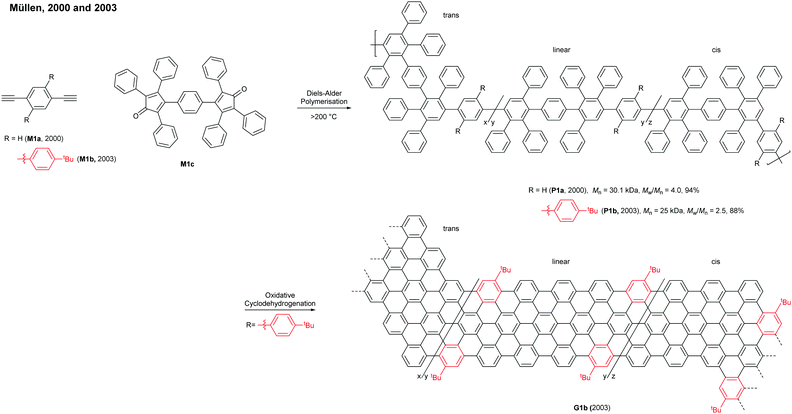
33. Z. B. Shifrina, M. S. Averina, A. L. Rusanov, M. Wagner and K. Müllen, Macromolecules, 2000, 33, 3525–3529.
34. J. Wu, L. Gherghel, M. D. Watson, J. Li, Z. Wang, C. D. Simpson, U. Kolb and K. Müllen, Macromolecules, 2003, 36, 7082–7089.
35. X. Yang, X. Dou, A. Rouhanipour, L. Zhi, H. J. Räder and K. Müllen, J. Am. Chem. Soc., 2008, 130, 4216–4217.
36. G. Li, K.-Y. Yoon, X. Zhong, X. Zhu and G. Dong, Chem. – Eur. J., 2016, 22, 9116–9120.
37. O. Hod, J. E. Peralta and G. E. Scuseria, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 233401.
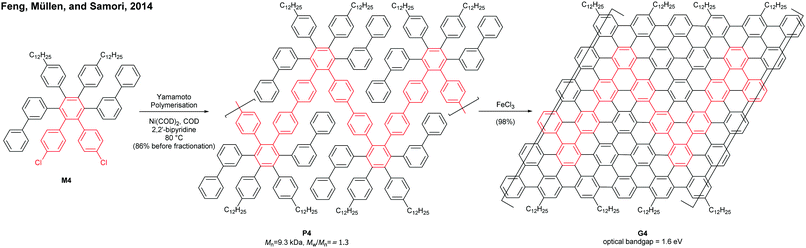
38. M. El Gemayel, A. Narita, L. F. Dössel, R. S. Sundaram, A. Kiersnowski, W. Pisula, M. R. Hansen, A. C. Ferrari, E. Orgiu, X. Feng, K. Müllen and P. Samorì, Nanoscale, 2014, 6, 6301–6314.
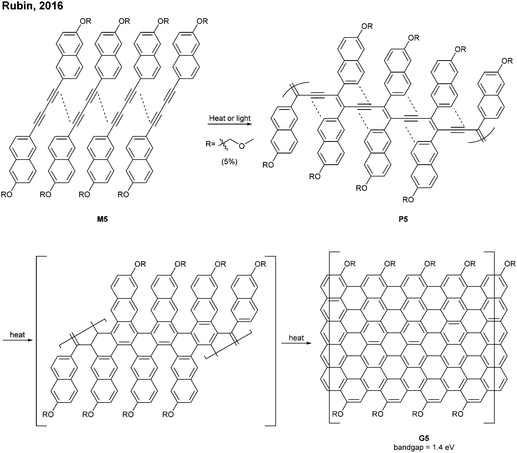
39. R. S. Jordan, Y. Wang, R. D. McCurdy, M. T. Yeung, K. L. Marsh, S. I. Khan, R. B. Kaner and Y. Rubin, Chem, 2016, 1, 78–90.
40. G. Li, K.-Y. Yoon, X. Zhong, J. Wang, R. Zhang, J. R. Guest, J. Wen, X.-Y. Zhu and G. Dong, Nat. Commun., 2018, 9, 1687.
41. J. Gao, F. J. Uribe-Romo, J. D. Saathoff, H. Arslan, C. R. Crick, S. J. Hein, B. Itin, P. Clancy, W. R. Dichtel and Y.-L. Loo, ACS Nano, 2016, 10, 4847–4856.
42. K. T. Kim, J. W. Jung and W. H. Jo, Carbon, 2013, 63, 202–209.
43. S. J. Hein, D. Lehnherr, H. Arslan, F. J. Uribe-Romo and W. R. Dichtel, Acc. Chem. Res., 2017, 50, 2776–2788.
44. J. T. Markiewicz and F. Wudl, ACS Appl. Mater. Interfaces, 2015, 7, 28063–28085.
45. A. Takahashi, C.-J. Lin, K. Ohshimizu, T. Higashihara, W.-C. Chen and M. Ueda, Polym. Chem., 2012, 3, 479–485.
46. W. Yang, A. Lucotti, M. Tommasini and W. A. Chalifoux, J. Am. Chem. Soc., 2016, 138, 9137–9144.
47. W. Zeng, H. Phan, T. S. Herng, T. Y. Gopalakrishna, N. Aratani, Z. Zeng, H. Yamada, J. Ding and J. Wu, Chem, 2017, 2, 81–92.
48. D. Jänsch, I. Ivanov, Y. Zagranyarski, I. Duznovic, M. Baumgarten, D. Turchinovich, C. Li, M. Bonn and K. Müllen, Chem. – Eur. J., 2017, 23, 4870–4875.
49. R. S. Jordan, Y. L. Li, C.-W. Lin, R. D. McCurdy, J. B. Lin, J. L. Brosmer, K. L. Marsh, S. I. Khan, K. N. Houk, R. B. Kaner and Y. Rubin, J. Am. Chem. Soc., 2017, 139, 15878–15890.
50. Y. Yano, N. Mitoma, K. Matsushima, F. Wang, K. Matsui, A. Takakura, Y. Miyauchi, H. Ito and K. Itami, Nature, 2019, 20, 387–392.
51. M. G. Schwab, A. Narita, Y. Hernandez, T. Balandina, K. S. Mali, S. De Feyter, X. Feng and K. Müllen, J. Am. Chem. Soc., 2012, 134, 18169–18172.
52. M. G. Schwab, A. Narita, S. Osella, Y. Hu, A. Maghsoumi, A. Mavrinsky, W. Pisula, C. Castiglioni, M. Tommasini, D. Beljonne, X. Feng and K. Müllen, Chem. – Asian J., 2015, 10, 2134–2138.
53. Y. Huang, Y. Mai, X. Yang, U. Beser, J. Liu, F. Zhang, D. Yan, K. Müllen and X. Feng, J. Am. Chem. Soc., 2015, 137, 11602–11605.
54. Y. Huang, Y. Mai, U. Beser, J. Teyssandier, G. Velpula, H. van Gorp, L. A. Straasø, M. R. Hansen, D. Rizzo, C. Casiraghi, R. Yang, G. Zhang, D. Wu, F. Zhang, D. Yan, S. De Feyter, K. Müllen and X. Feng, J. Am. Chem. Soc., 2016, 138, 10136–10139.
55. Y. Huang, F. Xu, L. Ganzer, F. V. A. Camargo, T. Nagahara, J. Teyssandier, H. van Gorp, K. Basse, L. A. Straasø, V. Nagyte, C. Casiraghi, M. R. Hansen, S. De Feyter, D. Yan, K. Müllen, X. Feng, G. Cerullo and Y. Mai, J. Am. Chem. Soc., 2018, 140, 10416–10420.
56. L. Dong, G. Shang, J. Shi, J. Zhi, B. Tong and Y. Dong, J. Phys. Chem. C, 2017, 121, 11658–11664.
57. K.-Y. Yoon, Y. Xue and G. Dong, Macromolecules, 2019, 52, 1663–1670.
58. F. Xu, C. Yu, A. Tries, H. Zhang, M. Kläui, K. Basse, M. R. Hansen, N. Bilbao, M. Bonn, H. I. Wang and Y. Mai, J. Am. Chem. Soc., 2019, 141, 10972–10977.
59. P. Ruffieux, S. Wang, B. Yang, C. Sanchez-Sanchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, Nature, 2016, 531, 489–492.
60. Y.-L. Lee, F. Zhao, T. Cao, J. Ihm and S. G. Louie, Nano Lett., 2018, 18, 7247–7253.
61. J. Liu, B.-W. Li, Y.-Z. Tan, A. Giannakopoulos, C. Sanchez-Sanchez, D. Beljonne, P. Ruffieux, R. Fasel, X. Feng and K. Müllen, J. Am. Chem. Soc., 2015, 137, 6097–6103.
62. D. Wasserfallen, M. Kastler, W. Pisula, W. A. Hofer, Y. Fogel, Z. Wang and K. Müllen, J. Am. Chem. Soc., 2006, 128, 1334–1339.
63. M. Kastler, J. Schmidt, W. Pisula, D. Sebastiani and K. Müllen, J. Am. Chem. Soc., 2006, 128, 9526–9534.
64. Y. Fogel, L. Zhi, A. Rouhanipour, D. Andrienko, H. J. Räder and K. Müllen, Macromolecules, 2009, 42, 6878–6884.
65. A. Narita, I. A. Verzhbitskiy, W. Frederickx, K. S. Mali, S. A. Jensen, M. R. Hansen, M. Bonn, S. De Feyter, C. Casiraghi, X. Feng and K. Müllen, ACS Nano, 2014, 8, 11622–11630.
66. Y. Hu, P. Xie, M. De Corato, A. Ruini, S. Zhao, F. Meggendorfer, L. A. Straasø, L. Rondin, P. Simon, J. Li, J. J. Finley, M. R. Hansen, J.-S. Lauret, E. Molinari, X. Feng, J. V. Barth, C.-A. Palma, D. Prezzi, K. Müllen and A. Narita, J. Am. Chem. Soc., 2018, 140, 7803–7809.
67. A. Keerthi, B. Radha, D. Rizzo, H. Lu, V. Diez Cabanes, I. C.-Y. Hou, D. Beljonne, J. Cornil, C. Casiraghi, M. Baumgarten, K. Müllen and A. Narita, J. Am. Chem. Soc., 2017, 139, 16454–16457.
68. M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691–695.
69. T. H. Vo, M. Shekhirev, D. A. Kunkel, M. D. Morton, E. Berglund, L. Kong, P. M. Wilson, P. A. Dowben, A. Enders and A. Sinitskii, Nat. Commun., 2014, 5, 3189.
70. M. Shekhirev, T. H. Vo, M. Mehdi Pour, A. Lipatov, S. Munukutla, J. W. Lyding and A. Sinitskii, ACS Appl. Mater. Interfaces, 2016, 9, 693–700.
71. A. Radocea, T. Sun, T. H. Vo, A. Sinitskii, N. R. Aluru and J. W. Lyding, Nano Lett., 2016, 17, 170–178.
72. M. M. Pour, A. Lashkov, A. Radocea, X. Liu, T. Sun, A. Lipatov, R. A. Korlacki, M. Shekhirev, N. R. Aluru, J. W. Lyding, V. Sysoev and A. Sinitskii, Nat. Commun., 2017, 8, 820.
73. T. H. Vo, M. Shekhirev, D. A. Kunkel, F. Orange, M. J. F. Guinel, A. Enders and A. Sinitskii, Chem. Commun., 2014, 50, 4172–4174.
74. T. H. Vo, U. G. E. Perera, M. Shekhirev, M. Mehdi Pour, D. A. Kunkel, H. Lu, A. Gruverman, E. Sutter, M. Cotlet, D. Nykypanchuk, P. Zahl, A. Enders, A. Sinitskii and P. Sutter, Nano Lett., 2015, 15, 5770–5777.
75. S. von Kugelgen, I. Piskun, J. H. Griffin, C. T. Eckdahl, N. N. Jarenwattananon and F. R. Fischer, J. Am. Chem. Soc., 2019, 141, 11050–11058.
76. L. Dössel, L. Gherghel, X. Feng and K. Müllen, Angew. Chem., Int. Ed., 2011, 50, 2540–2543.
77. K. T. Kim, J. W. Lee and W. H. Jo, Macromol. Chem. Phys., 2013, 214, 2768–2773.
78. M. Daigle, D. Miao, A. Lucotti, M. Tommasini and J.-F. Morin, Angew. Chem., Int. Ed., 2017, 56, 6213–6217.
79. D. Miao, M. Daigle, A. Lucotti, J. Boismenu-Lavoie, M. Tommasini and J.-F. Morin, Angew. Chem., Int. Ed., 2018, 57, 3588–3592.

---