Open Access Article
Open Access ArticleMacrocycles of higher ortho-phenylenes: assembly and folding†
Zacharias J.
Kinney
 ,
Viraj C.
Kirinda
,
Viraj C.
Kirinda
 and
C. Scott
Hartley
and
C. Scott
Hartley
 *
*
Department of Chemistry & Biochemistry, Miami University, Oxford, OH 45056, USA. E-mail: scott.hartley@miamioh.edu
First published on 9th August 2019
Abstract
Higher-order structure in abiotic foldamer systems represents an important but largely unrealized goal. As one approach to this challenge, covalent assembly can be used to assemble macrocycles with foldamer subunits in well-defined spatial relationships. Such systems have previously been shown to exhibit self-sorting, new folding motifs, and dynamic stereoisomerism, yet there remain important questions about the interplay between folding and macrocyclization and the effect of structural confinement on folding behavior. Here, we explore the dynamic covalent assembly of extended ortho-phenylenes (hexamer and decamer) with rod-shaped linkers. Characteristic 1H chemical shift differences between cyclic and acyclic systems can be compared with computational conformer libraries to determine the folding states of the macrocycles. We show that the bite angle provides a measure of the fit of an o-phenylene conformer within a shape-persistent macrocycle, affecting both assembly and ultimate folding behavior. For the o-phenylene hexamer, the bite angle and conformer stability work synergistically to direct assembly toward triangular [3 + 3] macrocycles of well-folded oligomers. For the decamer, the energetic accessibility of conformers with small bite angles allows [2 + 2] macrocycles to be formed as the predominant species. In these systems, the o-phenylenes are forced into unusual folding states, preferentially adopting a backbone geometry with distinct helical blocks of opposite handedness. The results show that simple geometric restrictions can be used to direct foldamers toward increasingly complex folds.
Introduction
The structures of biomacromolecules demonstrate that molecular folding is an effective strategy for the generation of large-scale structural complexity. Decades of study have thus provided many examples of abiotic foldamers1 that adopt well-defined secondary structures, ranging from peptides that hew closely to their biochemical inspirations to aromatic oligomers that offer distinctly different structures and properties.2–6 However, despite the importance of hierarchical structure in biochemistry, tertiary structure remains rare in abiotic foldamers, especially in the context of non-peptidic systems.7–11 That is, folding into helices, and to some extent other secondary structures,12 is fairly common, but these locally folded segments are rarely studied within larger architectures.Combining foldamer subunits within a macrocycle represents a simple strategy toward higher-order structure, placing multiple secondary structures into well-defined spatial relationships (note that this approach is distinct from macrocycles that themselves fold13–18 or with a single folded unit19,20). Foldamer-based macrocycles raise questions about how the foldamer moieties interact when confined within a larger structure, and about how folding and macrocyclization affect each other. For example, Huc has demonstrated homochiral self-sorting in macrocycles of aromatic oligoamides,21 and Chmielewski and Otto have very recently demonstrated a dynamic library that yields an emergent folding pattern.22 In related work, Sawada and Fujita have used foldamers as the components of complex assemblies based on metal coordination.23,24
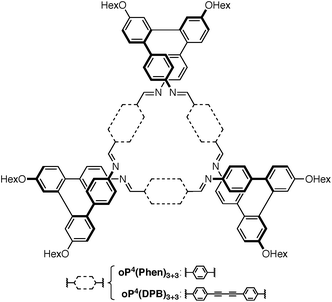
Our work has focused on the o-phenylenes, simple polyphenylenes25 that adopt helical conformations in solution driven by (offset) arene–arene stacking interactions parallel to the helical axis.26–34 In previous work on o-phenylene-based macrocycles, we showed that amino-functionalized o-phenylene tetramers could be co-assembled with a series of rod-shaped dialdehyde linkers, giving, for example, the [3 + 3] macrocycles oP4(Phen)3+3 and oP4(DPB)3+3 shown in Chart 1 (i.e., 3 o-phenylenes + 3 linkers).35 The resulting twisted macrocycles36–40 are shape-persistent but have well-defined degrees of conformational freedom via the foldamer moieties. They exhibit rich stereochemical behavior, with both homochiral D3-symmetric and heterochiral C2-symmetric diastereomers distinguishable by NMR spectroscopy. Later work showed that variation in linker geometry can be used to direct the assembly toward [2 + 2] and [1 + 1] macrocycles.41
These results provided a proof of concept for the use of dynamic covalent chemistry to assemble o-phenylene foldamers into closed architectures (i.e., macrocycles and cages). However, o-phenylene tetramers are the absolute simplest that can fold, with only a single relevant degree of conformational freedom (the central biaryl bond). In a sense, they cannot misfold: an o-phenylene tetramer can adopt only two possible backbone geometries, not counting enantiomers, both of which are helical.
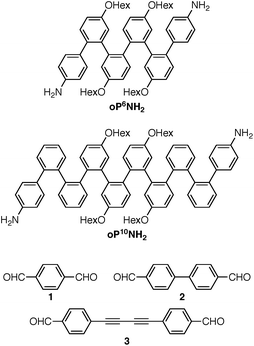
Understanding the relationships between folding, self-assembly, and macrocyclic structure requires components with more-complex conformational energy landscapes. Here, we extend our results to include longer o-phenylene components oP6(NH2) and oP10(NH2), shown in Chart 2, which have been co-assembled with rod-shaped linkers 1, 2, and 3. Increasing the length of the o-phenylenes to six or ten repeat units greatly increases the complexity of these systems: the hexamer gives two full turns of the helix when perfectly folded and can potentially adopt ten unique backbone geometries (five folding states and their enantiomers). The decamer gives 3.3 turns of the helix when perfectly folded and can potentially adopt 74 unique geometries (37 folding states and their enantiomers). This added complexity has a substantial effect on both self-assembly and the folding behavior of the macrocycles. Importantly, it affords new insights into how the subcomponents' folding propensities relate to the efficiency of assembly and how they respond to structural constraints imposed by the macrocycle. The behavior can be explained using simple models derived from conformational energy landscapes of the parent oligomers.
Results and discussion
Synthesis of components
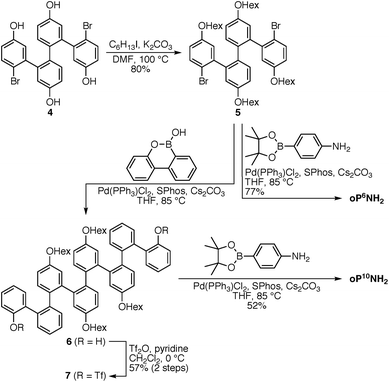
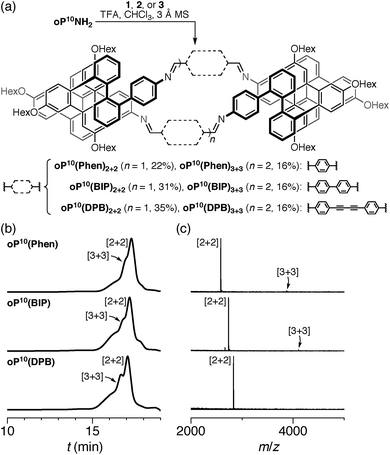
The diamino o-phenylenes oP6(NH2) and oP10(NH2) were synthesized as shown in Scheme 1. Known29 hydroxy-functionalized o-phenylene tetramer 4 was first alkylated to give 5. This oligomer could then be terminated by Suzuki coupling to give oP6(NH2), or extended further through Suzuki coupling (6) and then triflation to give octamer 7. We had originally intended to uniformly functionalize the longer oligomer with hexyloxy groups. However, despite multiple attempts, we were unable to couple 5 with the appropriate 10-hydroxy-10,9-boroxarophenanthrene42 derivative. It is likely that steric hindrance between the larger hexyloxy groups with the (predominantly folded) conformations of 5 prevented coupling. This limitation turned out to be useful, however, as the sequence of distinct repeat units in oP10(NH2) allowed them to be more easily distinguished by NMR spectroscopy (see below).The dialdehyde linkers were either commercially available (1) or were prepared according to literature procedures (2 and 3).43,44
Hexamer assembly
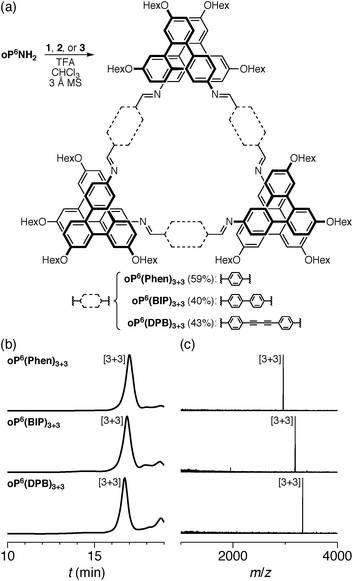
We first examined the assembly of the o-phenylene hexamer oP6(NH2), using the same conditions as previously used for the assembly of tetra(o-phenylene) macrocycles.35 As shown in Fig. 1a, oP6(NH2) (1.1 eq.) was combined with linkers 1, 2, or 3 (1.0 eq.) in chloroform (1.5 mM aldehyde) in the presence of TFA (0.10 eq.) and 3 Å molecular sieves. Monitoring of the reaction by 1H NMR spectroscopy indicated that, in all three cases, the reaction mixtures reached a steady state after 5 d. At this point, the reactions were quenched with triethylamine to stop assembly and facilitate analysis.45–47 Gel permeation chromatography (GPC, Fig. 1b) of the resulting crude products showed a single predominant peak, indicating that assembly occurs efficiently in all three cases to give a single species (or set of species of very similar hydrodynamic radii). MALDI mass spectra (Fig. 1c) indicated that the major products are the [3 + 3] macrocycles oP6(Phen)3+3, oP6(BIP)3+3, and oP6(DPB)3+3. These macrocycles could be isolated by semi-preparative GPC in moderate yields,48 and were then fully characterized by NMR spectroscopy and mass spectrometry.From the GPC and mass spectrometry results, it is clear that o-phenylene hexamer oP6(NH2) assembles effectively with rod-shaped linkers into quasi-triangular [3 + 3] macrocycles, much like the previously reported o-phenylene tetramers in Chart 1. What role does their folding play in macrocyclization?
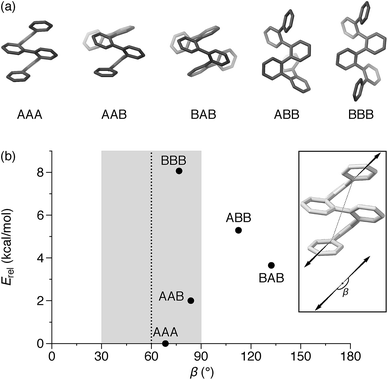
The conformational analysis of o-phenylenes has been reviewed elsewhere.26 Briefly, for an o-phenylene with n repeat units, the backbone folding state will be defined by the n − 3 internal biaryl dihedral angles. To a first approximation, these dihedrals can assume four values, approximately −55°, +55, +135°, and −135°, which we refer to as the A, A′, B, and B′ states, respectively. Every second ring along the backbone must be nearly coplanar; it follows that within a single o-phenylene molecule only the A/B or A′/B′ states can coexist. Thus, the total population of oligomers can be divided into two enantiomeric pools of oligomers (A/B and A′/B′). The limiting conformations, AA⋯A and BB⋯B, are both helical; the AA⋯A conformer is a compact left-handed helix and BB⋯B is an extended right-handed helix. The overall conformational distribution is then governed by two simple principles: (1) each “A” state results in a single arene–arene stacking interaction, worth on the order of 0.5 kcal mol−1 for unsubstituted o-phenylenes (in CDCl3 around 0 °C). (2) The “ABA” sequence of dihedrals is strongly disfavored because it introduces unfavorable steric clashes. Thus, the “perfectly folded” AA⋯A state is favored for simple o-phenylenes.27,49
This model is admittedly simplified: it fails, for example, to account for steric effects of substituents, and the twisting of the backbone in longer oligomers can certainly lead to additional conformational stabilization via other interactions beyond arene–arene stacking (e.g., edge-to-face arene–arene interactions).33 However, it provides a very useful framework within which to understand o-phenylene folding, and can be refined by using DFT calculations to more-accurately predict conformer energies.49
An o-phenylene hexamer can therefore adopt five unique conformations in the A/B pool (and their enantiomers in the A′/B′ pool), shown in Fig. 2a for (unsubstituted) hexa(o-phenylene). While the AAA conformer typically predominates, both the AAB and BAB conformers are usually observable.26,49,50
In the context of macrocyclization, we also must consider the fit to the product geometry.51 For example, for a shape-persistent triangular [3 + 3] macrocycle, we expect the corners to make angles of roughly 60°.52 The potential for each folding state to fit into this architecture can be approximated via its “bite” (or “bend”) angle β; that is, the angle made by the points of attachment to the o-phenylene moiety. This is a straightforward application of the concept of the minimization of strain in the assembly of macrocycles and cages, well-known in both metal-coordination and dynamic covalent systems.51–55
Both the relative stabilities of different o-phenylene folding states Erel and bite angles β are straightforward to predict using DFT optimizations. For simplicity and efficiency, and anticipating the more-complex deca(o-phenylene) systems discussed below, we decided to focus on the unsubstituted hexa(o-phenylene); while the substituents will certainly affect the stabilities of o-phenylene conformers, the trend in stabilities and the bite angles should be consistent. The optimized geometries, shown in Fig. 2a, were obtained at the PCM(CHCl3)/B97-D/cc-pVDZ level.56 This method was found to reproduce the results of the previously used B97-D/TZV(2d,2p) method49,57 but in a fraction of the computational time (about 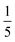 for hexa(o-phenylene)). Note, however, that the calculated Erel values from both methods overestimate the differences in stability that are actually observed in solution. They should nevertheless accurately predict the relative stabilities, which is sufficient for the analysis presented here. Bite angles β were calculated from the geometries in Fig. 2a using the vectors shown in the inset (see ESI†).
for hexa(o-phenylene)). Note, however, that the calculated Erel values from both methods overestimate the differences in stability that are actually observed in solution. They should nevertheless accurately predict the relative stabilities, which is sufficient for the analysis presented here. Bite angles β were calculated from the geometries in Fig. 2a using the vectors shown in the inset (see ESI†).
A plot of Erel against β, shown in Fig. 2b, makes it immediately clear why oP6(NH2) assembles efficiently into [3 + 3] macrocycles with linkers 1, 2, or 3. A reversible system at equilibrium will favor macrocycles that balance their strain against size (i.e., smaller macrocycles are favored entropically but can only form if they do not introduce significant strain).51,58 For this system, [1 + 1] macrocycles (the smallest conceivable) should be impossible given the geometries of oP6(NH2) and any of the linkers. In their simplest form, [2 + 2] macrocycles would require β ≈ 0°,52 which is not found for any possible conformers of hexa(o-phenylene). The next-largest [3 + 3] macrocycle requires β ≈ 60°, and here multiple conformers have well-matched intrinsic bite angles, including the most-stable AAA geometry (β = 68°). Thus, this size is favored both entropically and enthalpically and should be assembled efficiently, as was observed.
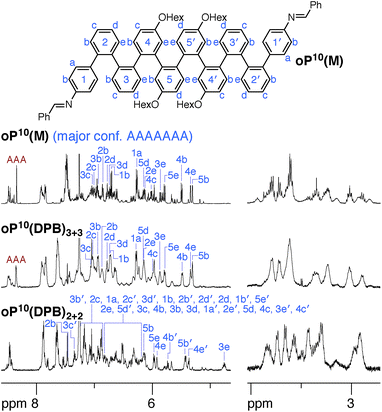
NMR spectroscopy provides insight into how the o-phenylenes are folded within the macrocycles. One of the most useful features for the conformational analysis of o-phenylenes is that their backbones are typically in slow conformational exchange on the NMR time scale around room temperature (but fast exchange on the lab time scale).26,59 Thus, their NMR spectra are a superposition of contributions from different folding states. Importantly, the 1H chemical shifts are very sensitive to the geometry, in some cases varying by >1 ppm. In general, this dependence can be quantitatively predicted using ab initio methods. NMR spectroscopy therefore allows the folding states of o-phenylenes to be determined and quantified. While crystallography would have provided useful structural information, it would be very challenging to crystallize the array of macrocyclic geometries expected in solution (see below), and even then the prevalence of each species in the overall population would not be determined. Since our focus was the behavior of mixtures of stereoisomers and folding states, the oligomers were decorated with hexyloxy groups to promote solubility and crystals suitable for X-ray diffraction were not obtained.
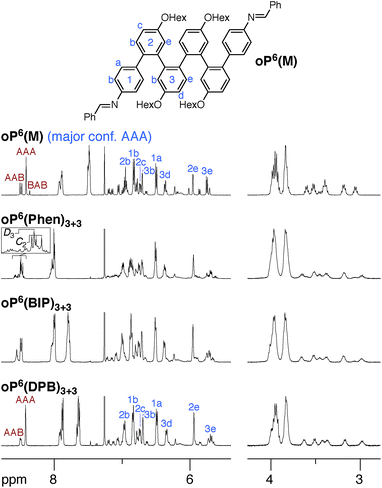
We synthesized oP6(M), an acyclic analogue of the o-phenylene hexamer moieties within the macrocycles, as a reference point (see ESI†). Its 1H NMR spectrum (CDCl3, 0 °C) is shown in Fig. 3 (top).60 As expected, the spectrum is relatively complicated, with contributions from misfolded states in the alkoxy (i.e., –CH2O–, 3–4 ppm), aromatic, and imine regions. EXSY experiments show that the protons giving rise to these minor signals are in exchange with those for major signals, confirming that they are different conformational states and not impurities (see ESI†). It was straightforward to assign the signals corresponding to the major (twofold-symmetric) conformer using standard 2D NMR experiments (COSY, HSQC, HMBC). Following a strategy now used many times for o-phenylenes,26,59 a simplified computational model of oP6(M) was optimized in all five possible backbone geometries at the PCM(CHCl3)/B97-D/cc-pVDZ level and NMR isotropic shieldings were calculated for each at the PCM(CHCl3)/WP04/6-31G(d) level.61,62 Comparison of the experimental and predicted NMR data confirmed that the major conformer does indeed correspond to the AAA state (see ESI†). By analogy with previous results,26,49,50,59,63 the minor conformers were assigned to the AAB and BAB geometries; this is probably most easily seen in the imine region around 8.5 ppm, which shows two equal-intensity imine signals for an unsymmetrical conformer (i.e., AAB) and a single smaller signal for a symmetrical conformer (BAB), labeled in Fig. 3.
The 1H NMR spectra of macrocycles oP6(Phen)3+3, oP6(BIP)3+3, and oP6(DPB)3+3 are also shown in Fig. 3. A cursory inspection indicates that the spectra are all similar (disregarding the signals associated with the linkers themselves), and similar to that of oP6(M). This similarity suggests that the folding behavior has not been dramatically perturbed; however, there are some clear differences. First, the spectrum of oP6(Phen)3+3, and to a lesser extent oP6(BIP)3+3, is more complex than the others. Close inspection of the imine signals (inset in Fig. 3) shows that there are far more signals than in the spectrum for oP6(M), suggesting many distinct species in solution. In our previous work on oP4(Phen)3+3, we found that the p-phenylene linker was sufficiently rigid that the different diastereomeric forms of the macrocycle could be identified;35 that is, the single imine signal for the D3-symmetric homochiral (PPP, MMM) stereoisomer was readily distinguished from the three imine signals for the C2-symmetric heterochiral (PMM, MPP) stereoisomers. The behavior of oP6(Phen)3+3 appears to be similar, except that there is also the added complication of oligomer misfolding. Indeed, the four most-prominent imine signals are consistent with the homochiral-D3 (1 signal) and heterochiral-C2 (3 signals) configurations of the perfectly folded (AAA)3 macrocycle (inset in Fig. 3), with the smaller peaks corresponding to macrocycles with at least one of the o-phenylenes misfolded. The D3- and C2-symmetric stereoisomers of the (AAA)3 configuration appear to be present in approximately the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio attributable to symmetry alone.
3 ratio attributable to symmetry alone.
Clearly, there is little stereochemical control in these systems, as was expected from the previous results for oP4(Phen)3+3. However, the specific folding state of the hexa(o-phenylene) moieties within macrocycles oP6(Phen)3+3, oP6(BIP)3+3, and oP6(DPB)3+3 is a separate issue. o-Phenylene conformations with close to the optimum β should be preferred by the [3 + 3] macrocycle (Fig. 2b, shaded region). This analysis suggests that, of the three conformers that should be observed in solution, AAA, AAB, and BAB, only the AAA and AAB geometries should fit.
The coexistence of multiple stereoisomers of each macrocycle complicates assignment of the 1H NMR spectra of oP6(Phen)3+3 and oP6(BIP)3+3. Fortunately, the diphenylbutadiyne linker in oP6(DPB)3+3 is sufficiently flexible64 that the different stereoisomers no longer give distinct 1H NMR signals. That is, multiple stereoisomers of oP6(DPB)3+3 presumably coexist, but they give indistinguishable spectra because the linker does not communicate the configuration between o-phenylenes (as had been previously observed for oP4(DPB)3+3).35 Thus, analysis is no more difficult than it was for oP6(M): as before, each of the aromatic protons on the backbone of the major conformer could be assigned using standard 2D NMR experiments (see ESI†). The assignments, shown in Fig. 3, are a close match to those for oP6(M), suggesting that the o-phenylene subunits of oP6(DPB)3+3 are also in the AAA configuration.
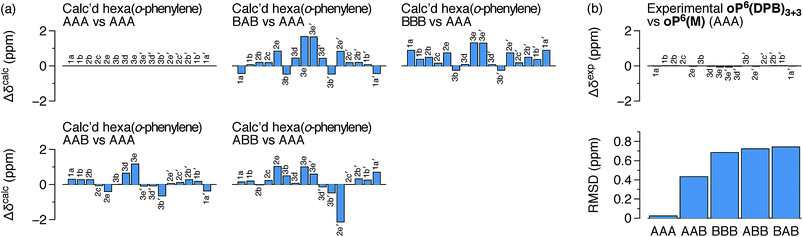
It is conceivable that other backbone geometries could give similar NMR spectra to the AAA state of an o-phenylene hexamer. We therefore compared the 1H chemical shifts in oP6(DPB)3+3 and oP6(M) more quantitatively (this analysis also anticipates the much more complex case of the deca(o-phenylenes) discussed below). We focused on the chemical shift differences Δδ for analogous protons between the o-phenylene within the macrocycle and in the model oP6(M). For example, for proton H1a (see Fig. 3 for labeling), the experimentally observed Δδexp1a is given by
| Δδexp1a = δ1a(oP6(DPB)3) − δ1a(oP6(M)) | (1) |
We focus on Δδ (rather than δ) because substituent effects on chemical shift should cancel out: while the hexyloxy groups and imines should significantly affect the chemical shifts of nearby protons, their contributions to Δδ, which are primarily dependent on the orientations of the protons with respect to the shielding zones of nearby aromatic rings, should be negligible. This assumption allows us to carry out computational work on the library of unsubstituted conformers and apply the results to experimental systems regardless of o-phenylene substitution pattern or structural context, ignoring, for example, the relative orientations of attached functionality.
Computational Δδcalc values were then predicted for each of the five optimized geometries of hexa(o-phenylene) (Fig. 2) at the GIAO/PCM(CHCl3)/WP04/6-31G(d) level. They were calculated relative to the AAA conformer; for example, for proton H1a in conformer AAB, the predicted difference in chemical shift Δδcalc1a(AAB) is given by
| Δδcalc1a(AAB) = σ1a(AAA) − σ1a(AAB) | (2) |
The predicted Δδcalc vary from the trivial case of the AAA conformer, for which, by definition, Δδcalc = 0 for all protons, to more than 2 ppm for some key protons in other conformers. Each conformer gives a unique pattern of Δδcalc1a, shown in Fig. 4a, that should serve as a fingerprint for the folding state of an o-phenylene moiety. The experimental differences Δδexp for the major o-phenylene conformer in oP6(DPB)3+3, shown in Fig. 4b, are all very close to 0 (≤0.06 ppm). They are very clearly the best match for the AAA configuration, with a root-mean-squared deviation (RMSD) of only 0.02 ppm between the experimental and predicted Δδ. As shown in Fig. 4b, this match is substantially better than the next-best comparison (to AAB, RMSD = 0.43 ppm), significant at the 99.9% confidence level (see ESI for details†).
The regions of the spectra corresponding to the alkoxy groups (3–4 ppm), also shown in Fig. 3, provide corroborating evidence that the o-phenylenes remain well-folded within the macrocycles. These signals should be largely unaffected by changes in linker structure or relative o-phenylene stereochemistry but are very sensitive to o-phenylene folding state.65 These regions of the spectra are very similar for oP6(M) and all three macrocycles, indicating similar overall folding behavior in all cases.
Although the o-phenylenes within the macrocycles remain predominantly folded into the AAA state, there are differences in the relative populations of the different conformers. This is most easily seen in the imine regions of the spectra in Fig. 3. For oP6(M), integration of the imine singlets gives a ratio of 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 for AAA
7 for AAA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) AAB
AAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BAB. In contrast, for oP6(DPB)3+3 we obtain 69
BAB. In contrast, for oP6(DPB)3+3 we obtain 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, which is significantly different even taking into account the 5–10% error typically assumed for NMR integration. This result is consistent with expectations based on Fig. 2: the AAA state (β = 68°) was expected to be the best match for the [3 + 3] macrocyclic geometry, and indeed it is amplified in the macrocycle. The AAB state is still observed (β = 84°), although it is less populated, but the BAB state (β = 132°) is eliminated entirely.
0, which is significantly different even taking into account the 5–10% error typically assumed for NMR integration. This result is consistent with expectations based on Fig. 2: the AAA state (β = 68°) was expected to be the best match for the [3 + 3] macrocyclic geometry, and indeed it is amplified in the macrocycle. The AAB state is still observed (β = 84°), although it is less populated, but the BAB state (β = 132°) is eliminated entirely.
This result implies that the bite angle is a useful parameter for assessing the fit of an o-phenylene conformer within a shape-persistent architecture. In our previous work on o-phenylene tetramer macrocycles (e.g., oP4(DPB)3+3), we had noted that macrocyclization led to improved folding.35 This conclusion was drawn on the basis of characteristic changes in chemical shifts for key protons in rapid exchange.66 Macrocycle oP6(DPB)3+3 confirms this result by allowing direct observation of a change in the conformational population.
To visualize the structure of the o-phenylene hexamer macrocycles, we performed geometry optimizations on  , a simplified version of oP6(DPB)3+3 with the alkoxy groups removed, at the PCM(CHCl3)/B97-D/cc-pVDZ level. Of course, even with structural simplifications and the relative simplicity of the linkers, there remain many conformational degrees of freedom that must be accounted for. Thus, the larger structures were built up by systematically optimizing key dihedral angles for smaller fragments, as described in the ESI.† We stress that the strategy does not guarantee the identification of the global conformational energy minimum; however, it should provide a good indication of the fit of the o-phenylene within the macrocyclic framework.
, a simplified version of oP6(DPB)3+3 with the alkoxy groups removed, at the PCM(CHCl3)/B97-D/cc-pVDZ level. Of course, even with structural simplifications and the relative simplicity of the linkers, there remain many conformational degrees of freedom that must be accounted for. Thus, the larger structures were built up by systematically optimizing key dihedral angles for smaller fragments, as described in the ESI.† We stress that the strategy does not guarantee the identification of the global conformational energy minimum; however, it should provide a good indication of the fit of the o-phenylene within the macrocyclic framework.
The geometries of oP6(DPB)3+3 in two of its configurations, homochiral-(AAA)3 and homochiral-(AAA)2(AAB), are shown in Fig. 5. The heterochiral-(AAA)3 conformer (not shown) is energetically very similar to the homochiral isomer (ΔE = 0.01 kcal mol−1). Conversely, the mixed homochiral-(AAA)2(AAB) geometry is predicted to less stable than the fully folded (AAA)3-homochiral macrocycle by 3.6 kcal mol−1. This is significantly larger than the inherent preference for the AAA conformer over AAB (2.5 kcal mol−1 at the same level of theory), suggesting that the poorer fit of the AAB state, because of its less-well-matched β, introduces additional strain (i.e., by forcing the o-phenylene moiety away from its optimum AAB geometry).
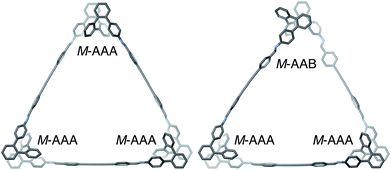 | ||
Fig. 5 Optimized geometries (PCM(CHCl3)/B97-D/cc-pVDZ) of  in its homochiral-(AAA)3 (left) and homochiral-(AAA)2(AAB) (right) configurations. in its homochiral-(AAA)3 (left) and homochiral-(AAA)2(AAB) (right) configurations. | ||
Decamer assembly
We then turned to the assembly of the oP10(NH2) system, as shown in Fig. 6a. Reaction with linkers 1, 2, and 3 was carried out under the same conditions as for oP6(NH2). In all three cases, assembly was found to occur more slowly, with the best results obtained after 11 d. At this point, GPC analysis of the quenched reaction mixtures, shown in Fig. 6b, gave qualitatively similar results for all three linkers. Two distinct peaks corresponding to two major products (overlapping at approximately 17 min) were observed along with a broad peak corresponding to larger species. Beyond 11 d, additional molecular sieves had to be added to maintain the same distribution of products but no net improvement could be obtained. Thus, we cannot conclusively say that the GPC traces in Fig. 6b represent equilibrium distributions for these systems. It is, however, clear that assembly is less efficient for oP10(NH2) compared to oP6(NH2). MALDI mass spectra of the crude reaction mixtures show dominant peaks corresponding to the [2 + 2] macrocycles along with small signals for the [3 + 3] macrocycles in two cases (Fig. 6c). Careful purification by multiple semi-preparative GPC injections allowed the two major products to be isolated in reasonable yields and conclusively identified as the [2 + 2] and [3 + 3] macrocycles by NMR and mass spectrometry. Isolated yields of the [2 + 2] macrocycles increase in the order oP10(Phen)2+2 < oP10(BIP)2+2 < oP10(DPB)2+2. As the GPC chromatograms of the crude mixtures are very similar in all three cases, this trend likely reflects greater ease of purification of the macrocycles with longer linkers rather than greater efficiency of self-assembly.Of course, the conformational landscape available to an unconstrained o-phenylene decamer is substantially larger than of a hexamer, with 37 possible folding states (not including enantiomers). A library of all of these possibilities for the unsubstituted deca(o-phenylene) was optimized as before (PCM(CHCl3)/B97-D/cc-pVDZ). The corresponding relative stabilities Erel and bite angles β are plotted in Fig. 7. Like hexa(o-phenylene) (Fig. 2), the most stable conformer of deca(o-phenylene) is the perfectly folded state (AAAAAAA). This conformer has a β = 69° and would be expected to fit well into a roughly triangular [3 + 3] macrocycle. Unlike hexa(o-phenylene), deca(o-phenylene) has many folding geometries with β near 0°, several of which should be energetically accessible (bearing in mind that the Erel overestimate the absolute energetic differences between conformers). These smaller bite angles should be a good match to the smaller [2 + 2] architecture.
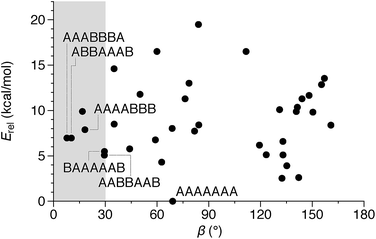 | ||
| Fig. 7 Calculated Erelvs. β for all conformers of deca(o-phenylene) (PCM(CHCl3)/B97-D/cc-pVDZ). Selected conformations are labeled. | ||
The complexity of the deca(o-phenylene) conformational energy landscape explains why mixtures are obtained from assembly of oP10(NH2) with linkers 1, 2, or 3 as well as the slight preference for assembly into [2 + 2] macrocycles. As briefly discussed for the hexamer-based system, the equilibria between macrocycles of various o-phenylene geometries and sizes will be governed, at least to a first approximation, by (1) the entropic favorability of smaller macrocycles, as commonly exploited in self-assembly (including dynamic covalent assembly),51 and (2) the strain associated with misfolding.67 For the o-phenylene decamer system, Fig. 7 predicts that these two effects work against each other: while the AAAAAAA conformer is the most inherently stable, it is not sufficiently favored to overcome the entropic favorability of (misfolded) smaller macrocycles. This behavior contrasts with that of the shorter o-phenylene tetramers and hexamers, which offer no conformers that can reasonably fit within a macrocycle smaller than [3 + 3].
This inherent frustration implies that confinement within smaller architectures forces the foldamer subunits toward structurally complex misfolded states. We therefore explored the folding of the o-phenylene moieties as before. Model compound oP10(M) was prepared for comparison (see ESI†), with its 1H NMR spectrum shown in Fig. 8 (top). While complex, the signals corresponding to its major conformer are straightforward to assign and the geometry can be established as AAAAAAA by comparison with DFT predictions of chemical shifts (see ESI†). Nevertheless, there are several other observed conformers, most easily seen in the imine region of the spectrum. Integration shows that approximately 25% of the population is perfectly folded.
The 1H NMR spectra of the macrocycles resulting from the three linkers are shown in the ESI.† Close examination of the alkoxy group region (–CH2O–) suggests that the folding of the o-phenylenes within a particular macrocycle size ([2 + 2] or [3 + 3]) is similar, but that there are differences between the two sizes themselves. The aromatic regions of the 1H NMR spectra of macrocycles resulting from linkers 1 and 2 (oP10(Phen)2+2, oP10(Phen)3+3, oP10(BIP)2+2, and oP10(BIP)3+3) are complex, again reflecting the coexistence of many stereoisomers. We therefore focused on the macrocycles from more-flexible linker 3 (oP10(DPB)2+2 and oP10(DPB)3+3), which again give more easily interpreted spectra, shown in Fig. 8, since the stereoisomers are indistinguishable.
The behavior of the [3 + 3] macrocycle oP10(DPB)3+3 is straightforward and closely parallels that of oP6(DPB)3+3. While its 1H NMR signals are slightly broadened, there is very little difference between its spectrum and that of oP10(M) in both the alkoxy and aromatic regions. Explicit assignments of the aromatic protons in the major conformer were made through analysis of 2D spectra. Differences in chemical shifts Δδexp were calculated relative to the AAAAAAA conformer of oP10(M) and were all ≤0.02 ppm. These were then compared to predicted changes in chemical shifts Δδcalc for the full 37-conformer library relative to the AAAAAAA conformer of deca(o-phenylene). The best match was, unsurprisingly, to the AAAAAAA conformer of the library, with a RMSD of 0.01 ppm. Thus, the o-phenylene decamers in the [3 + 3] macrocycle remain well-folded, with little difference in behavior relative to freely mobile acyclic oligomers. Integration of the imine region indicates a slight increase in preference for the well-folded conformer within the macrocycle, with 40% of the oligomers in the AAAAAAA state (vs. 25%).
Folding in the [2 + 2] macrocycle oP10(DPB)2+2 is very different. A quick inspection of the 1H NMR spectra (Fig. 8, bottom) shows that there is a marked difference in overall appearance, including in the alkoxy region.68 While challenging, it was possible to assign all of the significant signals in the aromatic region of the spectrum to two principal conformers that are present in an approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.69 The major conformer, whose assignments are shown in Fig. 8, is unsymmetrical, with unique 1H signals along the entirety of its backbone. The minor conformer is twofold symmetric (see ESI† for assignments).
1 ratio.69 The major conformer, whose assignments are shown in Fig. 8, is unsymmetrical, with unique 1H signals along the entirety of its backbone. The minor conformer is twofold symmetric (see ESI† for assignments).
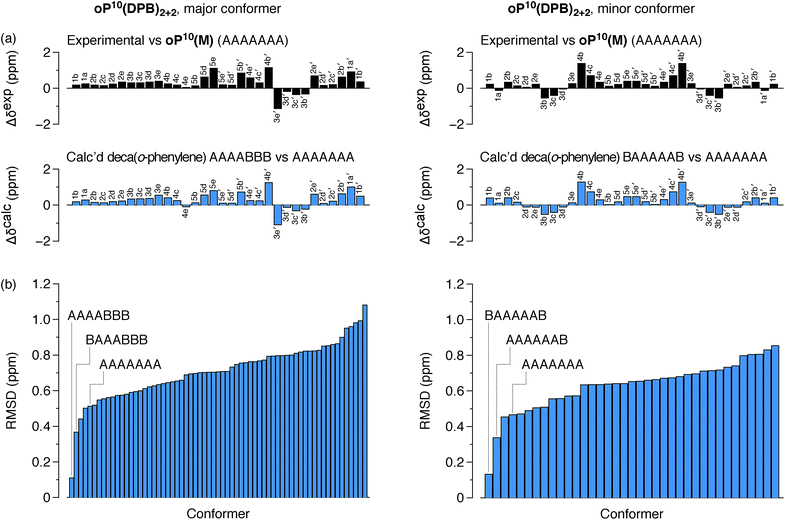
The differences in chemical shift Δδexp between both the major and minor conformers of oP10(DPB)2+2 and the AAAAAAA state of oP10(M) were then determined and are shown in Fig. 9a (top). They are substantially larger than was observed in oP6(DPB)3+3 and oP10(DPB)3+3. For example, proton H3e in the major conformer is shifted upfield by 1.1 ppm (to 4.74 ppm), indicating that it must be deep within the shielding zone of a nearby aromatic ring. It was therefore clear that neither conformer corresponds to the AAAAAAA state. The experimental Δδexp were then compared with the Δδcalc values predicted for the library of deca(o-phenylene) conformers. Clear matches were identified: the major conformer corresponds to the AAAABBB folding state, whereas the minor conformer corresponds to the BAAAAAB folding state. In both cases the similarity between the experimental data and the NMR predictions for the parent deca(o-phenylene) conformer library is striking (Fig. 9a). Quantitative comparisons to the full library were made by comparing the RMSD values for each possible conformer, as shown in Fig. 9b. For both of the experimentally observed folds, the best matches have RMSD values on the order of 0.1 ppm, typical for NMR comparisons made for o-phenylenes.26 The second-best matches are significantly worse (>0.3 ppm), with the differences statistically significant at a >99% confidence level (see ESI†).
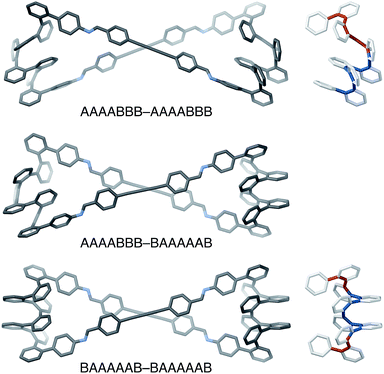
The AAAABBB and BAAAAAB folding states are highlighted in the plot of Erelvs. β in Fig. 7. They are indeed among the configurations that would be predicted to be good matches to the [2 + 2] geometry, with low bite angles (β < 30°) and relatively good stabilities. To confirm that they should be well-accommodated within a [2 + 2] macrocycle, we optimized the geometries of the (AAAABBB)2, (BAAAAAB)2, and (AAAABBB)(BAAAAAB) configurations of a simplified version of oP10(DPB)2+2 with the alkoxy groups removed, 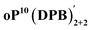 , at the PCM(CHCl3)/B97-D/cc-pVDZ level. All possible relative configurations of the o-phenylenes and, in the case of (AAAABBB)2, their relative direction (i.e., parallel or antiparallel) were considered. The most stable geometries for each species are shown in Fig. 10. Clearly, the assumption that the [2 + 2] architecture requires β ≈ 0° is an oversimplification, with the linkers crossing in all three geometries. The results do confirm, however, that both observed o-phenylene folding states are good matches to this size. The product presumably comprises a mixture of these geometries, but unfortunately we cannot be more specific at this time.
, at the PCM(CHCl3)/B97-D/cc-pVDZ level. All possible relative configurations of the o-phenylenes and, in the case of (AAAABBB)2, their relative direction (i.e., parallel or antiparallel) were considered. The most stable geometries for each species are shown in Fig. 10. Clearly, the assumption that the [2 + 2] architecture requires β ≈ 0° is an oversimplification, with the linkers crossing in all three geometries. The results do confirm, however, that both observed o-phenylene folding states are good matches to this size. The product presumably comprises a mixture of these geometries, but unfortunately we cannot be more specific at this time.
Fig. 7 suggests that there are other configurations that would also have been expected to be competitive, with smaller bite angles, higher stabilities, or both compared to the observed conformers (e.g., AAABBBA or ABBAAAB). Why are these not observed? There are two likely explanations. First, the true optimum β, as mentioned above, is not predictable by the macrocycle stoichiometry alone. Because the [2 + 2] macrocycles can adopt geometries with crisscrossed linkers, somewhat larger bite angles are tolerated (e.g., 43° in the homochiral-(AAAABBB)2 macrocycle). Second, the stabilities in Fig. 7 are predicted for the unsubstituted deca(o-phenylene). Substituted oligomers will experience additional interactions involving the substituents that are not accounted for in these models. For example, steric clashes between the relatively large hexyloxy groups will disfavor some conformers with congested structures. Indeed, optimization of several of the alternate backbone geometries with explicit methoxy groups indicates that they are less stable than would have been predicted using the library of parent conformers (see ESI†). This is an important caveat; however, the optimization of the geometries of unsubstituted oligomers is so much simpler, and the NMR predictions so useful, that explicit consideration of the substituents does not seem worthwhile.
Unlike the o-phenylene tetramer and hexamer systems, the assembly and structure of the oP10(NH2)-derived macrocycles demonstrates that new structural complexity can emerge in these systems once the baseline conformational behavior is sufficiently complex. The distribution of products highlights an important feature of the o-phenylenes: the overall driving force for folding is relatively weak; thus, it is competitive with the entropic driving force for smaller macrocycles. It follows that thermodynamically controlled approaches can be used to prepare closed architectures with the foldamers in misfolded states. While quantitative yields may not be feasible, once isolated these species offer added structural complexity, with the foldamer moieties restricted to a predictable region of their conformational energy landscapes. In principle, it should be possible to use perturbations (e.g., host–guest binding) to select for macrocycles of various sizes,70 and it could also be possible to perturb assembly by tuning the o-phenylene folding propensity.63
The minor o-phenylene folding observed in oP10(DPB)2+2, BAAAAAB, is not unexpected given that fraying at the ends of o-phenylenes is commonly observed.59 The major state, AAAABBB, is much more unusual, however, and shows that simple geometric constraints can be used to access folding patterns that are otherwise unavailable. This geometry has a fascinating structure: the “AAAA” end is folded by analogy with all other o-phenylenes, into a compact helix with arene–arene stacking. In contrast, the “BBB” end is pulled into the extended helix that has not, to our knowledge, been observed for simple o-phenylenes (but is commonly found for the analogous poly(quinoxaline-2,3-diyls)71,72). o-Phenylene moieties in this conformation thus have two distinct helical blocks twisting in opposite directions, left then right handed for AAAABBB, as is shown in Fig. 10, or right then left handed for A′A′A′A′B′B′B′.
Unlike the hierarchical structure in proteins, the AAAABBB folding in oP10(DPB)2+2 does not result from structural complexity programmed into the o-phenylenes themselves. The reactant oP10(NH2) is symmetrical and its sequence does not code for anything more complex than the perfectly folded AAAAAAA pattern, as is clear from model oP10(M). Instead, the o-phenylene moiety in the macrocycle adopts a more complex geometry as a consequence of the constraints on folding imposed by the larger architecture via β. Of course, the fact that this geometry is structurally interesting, with opposing helical twists, is presumably just a coincidence; this just happens to be one of the conformers with the appropriate β. o-Phenylenes of other lengths would likely adopt very different folding motifs in strained macrocycles, but this should be predictable, to some extent, by determining the stabilities and bite angles of conformer libraries for the parent acyclic oligomers.
Conclusions
In summary, o-phenylene hexamer oP6(NH2) and decamer oP10(NH2) have been co-assembled with a series of rod-shaped linkers 1, 2, and 3. Assembly occurs effectively in the case of oP6(NH2) to give [3 + 3] macrocycles. Analysis of NMR spectra shows that within the macrocycles, the o-phenylene moieties remain predominantly folded into the AAA state, with a greater proportion of perfectly folded oligomers than is observed for an analogous acyclic model compound (oP6(M)) but little stereocontrol. In contrast, oP10(NH2) assembles in all three cases into a mixture of [2 + 2] and [3 + 3] macrocycles. In the [3 + 3] macrocycles, the behavior of the o-phenylene decamers directly parallels that of the hexamers and (previously reported) tetramers: an increased preference for the perfectly folded AAAAAAA state, and again no evidence for stereocontrol. In the [2 + 2] macrocycles, the oligomers are forced to misfold, and instead adopt the AAAABBB state as their major conformation. Not only has this state not been previously observed (nor expected) for acyclic oligomers, but it is an unusual fusion of two helical blocks with distinct geometries and opposite twist senses.The trade-off between inherent conformer stability (Erel) and the bite angle (β) made by the linkages to the o-phenylene appears to be the key to understanding the relationship between folding and macrocyclization in these systems. Both of these parameters are predictable using ab initio calculations of conformer libraries of unsubstituted o-phenylenes. These libraries also provide a powerful framework for relating the NMR spectra to folding state via substituent-independent changes in chemical shifts (Δδ), which provide a spectral fingerprint that can be used to identify new folding patterns.
The work described here does not yet represent a viable strategy toward high yields of structurally complex and well-defined species. Most importantly, we still lack control over the absolute and relative stereochemistry of the o-phenylene moieties. Nevertheless, the results show that foldamers within shape-persistent macrocycles can exhibit folding behavior that is distinctly different from the analogous acyclic species in solution. This strategy offers the potential of generating structural complexity efficiently and predictably through geometric restrictions on folding rather than, for example, monomer sequence. Studies of the effect of tuning the overall folding propensity on assembly and efforts to improve stereocontrol in these systems are ongoing.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the National Science Foundation (CHE-1608213) for support of this work, the Volwiler Distinguished Research Professorship, and Dr Dominik Konkolewicz for the use of his analytical GPC.Notes and references
- S. H. Gellman, Acc. Chem. Res., 1998, 31, 173–180 CrossRef CAS.
- D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, Chem. Rev., 2001, 101, 3893–4011 CrossRef CAS PubMed.
- G. Guichard and I. Huc, Chem. Commun., 2011, 47, 5933–5941 RSC.
- D.-W. Zhang, X. Zhao, J.-L. Hou and Z.-T. Li, Chem. Rev., 2012, 112, 5271–5316 CrossRef CAS PubMed.
- T. A. Martinek and F. Fülöp, Chem. Soc. Rev., 2012, 41, 687–702 RSC.
- B. A. F. Le Bailly and J. Clayden, Chem. Commun., 2016, 52, 4852–4863 RSC.
- S. De, B. Chi, T. Granier, T. Qi, V. Maurizot and I. Huc, Nat. Chem., 2018, 10, 51–57 CrossRef CAS PubMed.
- N. Delsuc, M. Hutin, V. E. Campbell, B. Kauffmann, J. R. Nitschke and I. Huc, Chem.–Eur. J., 2008, 14, 7140–7143 CrossRef CAS PubMed.
- K. L. George and W. S. Horne, Acc. Chem. Res., 2018, 51, 1220–1228 CrossRef CAS PubMed.
- N. Delsuc, S. Massip, J.-M. Léger, B. Kauffmann and I. Huc, J. Am. Chem. Soc., 2011, 133, 3165–3172 CrossRef CAS PubMed.
- H.-Y. Hu, J.-F. Xiang, Y. Yang and C.-F. Chen, Org. Lett., 2008, 10, 69–72 CrossRef CAS PubMed.
- L. Sebaoun, V. Maurizot, T. Granier, B. Kauffmann and I. Huc, J. Am. Chem. Soc., 2014, 136, 2168–2174 CrossRef CAS PubMed.
- P. Reiné, J. Justicia, S. P. Morcillo, S. Abbate, B. Vaz, M. Ribagorda, Á. Orte, L. Álvarez de Cienfuegos, G. Longhi, A. G. Campaña, D. Miguel and J. M. Cuerva, J. Org. Chem., 2018, 83, 4455–4463 CrossRef PubMed.
- K. Urushibara, Y. Ferrand, Z. Liu, H. Masu, V. Pophristic, A. Tanatani and I. Huc, Angew. Chem., Int. Ed., 2018, 57, 7888–7892 CrossRef CAS PubMed.
- R. Katoono, Y. Tanaka, K. Fujiwara and T. Suzuki, J. Org. Chem., 2014, 79, 10218–10225 CrossRef CAS PubMed.
- R. Katoono, K. Kusaka, K. Fujiwara and T. Suzuki, Chem.–Asian J., 2014, 9, 3182–3187 CrossRef CAS PubMed.
- F. Chen, T. Tanaka, Y. Hong, W. Kim, D. Kim and A. Osuka, Chem.–Eur. J., 2016, 22, 10597–10606 CrossRef CAS PubMed.
- T. Hjelmgaard, L. Nauton, F. De Riccardis, L. Jouffret and S. Faure, Org. Lett., 2018, 20, 268–271 CrossRef CAS PubMed.
- N. Fuentes, A. Martin-Lasanta, L. Alvarez de Cienfuegos, R. Robles, D. Choquesillo-Lazarte, J. M. García-Ruiz, L. Martínez-Fernández, I. Corral, M. Ribagorda, A. J. Mota, D. J. Cárdenas, M. C. Carreño and J. M. Cuerva, Angew. Chem., Int. Ed., 2012, 51, 13036–13040 CrossRef CAS PubMed.
- H. Wu, A. Acharyya, Y. Wu, L. Liu, H. Jo, F. Gai and W. F. DeGrado, ChemBioChem, 2018, 19, 902–906 CrossRef CAS PubMed.
- C. Tsiamantas, X. de Hatten, C. Douat, B. Kauffmann, V. Maurizot, H. Ihara, M. Takafuji, N. Metzler-Nolte and I. Huc, Angew. Chem., Int. Ed., 2016, 55, 6848–6852 CrossRef CAS PubMed.
- B. Liu, C. G. Pappas, E. Zangrando, N. Demitri, P. J. Chmielewski and S. Otto, J. Am. Chem. Soc., 2019, 141, 1685–1689 CrossRef CAS PubMed.
- T. Sawada, A. Matsumoto and M. Fujita, Angew. Chem., Int. Ed., 2014, 53, 7228–7232 CrossRef CAS PubMed.
- T. Sawada, M. Yamagami, K. Ohara, K. Yamaguchi and M. Fujita, Angew. Chem., Int. Ed., 2016, 55, 4519–4522 CrossRef CAS PubMed.
- B. A. G. Hammer and K. Müllen, Chem. Rev., 2016, 116, 2103–2140 CrossRef CAS PubMed.
- C. S. Hartley, Acc. Chem. Res., 2016, 49, 646–654 CrossRef CAS PubMed.
- S. Ando, E. Ohta, A. Kosaka, D. Hashizume, H. Koshino, T. Fukushima and T. Aida, J. Am. Chem. Soc., 2012, 134, 11084–11087 CrossRef CAS PubMed.
- E. Ohta, H. Sato, S. Ando, A. Kosaka, T. Fukushima, D. Hashizume, M. Yamasaki, K. Hasegawa, A. Muraoka, H. Ushiyama, K. Yamashita and T. Aida, Nat. Chem., 2011, 3, 68–73 CrossRef CAS PubMed.
- G. N. Vemuri, R. R. Pandian, B. J. Spinello, E. B. Stopler, Z. J. Kinney and C. S. Hartley, Chem. Sci., 2018, 9, 8260–8270 RSC.
- Y. Tokoro, N. Ohtsuka, A. Kusakabe and S.-i. Fukuzawa, Eur. J. Org. Chem., 2017, 2353–2358 CrossRef CAS.
- D. Lotter, A. Castrogiovanni, M. Neuburger and C. Sparr, ACS Cent. Sci., 2018, 4, 656–660 CrossRef CAS PubMed.
- A. Muraoka and H. Kiwaki, Chem. Lett., 2018, 47, 487–489 CrossRef CAS.
- D. Lehnherr, C. Chen, Z. Pedramrazi, C. R. DeBlase, J. M. Alzola, I. Keresztes, E. B. Lobkovsky, M. F. Crommie and W. R. Dichtel, Chem. Sci., 2016, 7, 6357–6364 RSC.
- Y. Mizukoshi, K. Mikami and M. Uchiyama, J. Am. Chem. Soc., 2015, 137, 74–77 CrossRef CAS PubMed.
- Z. J. Kinney and C. S. Hartley, J. Am. Chem. Soc., 2017, 139, 4821–4827 CrossRef CAS PubMed.
- R. Katoono, S. Kawai, K. Fujiwara and T. Suzuki, Chem. Sci., 2015, 6, 6592–6600 RSC.
- H. Sato, J. A. Bender, S. T. Roberts and M. J. Krische, J. Am. Chem. Soc., 2018, 140, 2455–2459 CrossRef CAS PubMed.
- A. M. Castilla, W. J. Ramsay and J. R. Nitschke, Acc. Chem. Res., 2014, 47, 2063–2073 CrossRef CAS PubMed.
- A. U. Malik, F. Gan, C. Shen, N. Yu, R. Wang, J. Crassous, M. Shu and H. Qiu, J. Am. Chem. Soc., 2018, 140, 2769–2772 CrossRef CAS PubMed.
- G. Naulet, L. Sturm, A. Robert, P. Dechambenoit, F. Röhricht, R. Herges, H. Bock and F. Durola, Chem. Sci., 2018, 9, 8930–8936 RSC.
- Z. J. Kinney and C. S. Hartley, Org. Lett., 2018, 20, 3327–3331 CrossRef CAS PubMed.
- Q. J. Zhou, K. Worm and R. E. Dolle, J. Org. Chem., 2004, 69, 5147–5149 CrossRef CAS PubMed.
- M. Kozáková, M. Buděšínský and J. Hodačová, Synth. Commun., 2005, 35, 161–167 CrossRef.
- Y. B. Borozdina, E. Mostovich, V. Enkelmann, B. Wolf, P. T. Cong, U. Tutsch, M. Lang and M. Baumgarten, J. Mater. Chem. C, 2014, 2, 6618–6629 RSC.
- Although catalytic amounts of primary amines, which would be expected in the present systems even after quenching with NEt3, can catalyze transimination by themselves (ref. 46 and 47), previous work has shown that this is not significant under the conditions used here (ref. 35).
- M. Ciaccia, S. Pilati, R. Cacciapaglia, L. Mandolini and S. Di Stefano, Org. Biomol. Chem., 2014, 12, 3282–3287 RSC.
- M. Ciaccia, R. Cacciapaglia, P. Mencarelli, L. Mandolini and S. Di Stefano, Chem. Sci., 2013, 4, 2253–2261 RSC.
- The macrocycles were carefully purified through multiple GPC injections; thus, the isolated yields are likely low compared to the actual efficiency of assembly.
- S. M. Mathew, J. T. Engle, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2013, 135, 6714–6722 CrossRef CAS PubMed.
- S. M. Mathew and C. S. Hartley, Macromolecules, 2011, 44, 8425–8432 CrossRef CAS.
- C. Yu, Y. Jin and W. Zhang, Dynamic Covalent Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2017, pp. 121–163 Search PubMed.
- R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918 CrossRef CAS PubMed.
- W. Zhang and J. S. Moore, Angew. Chem., Int. Ed., 2006, 45, 4416–4439 CrossRef CAS PubMed.
- J. Bunzen, J. Iwasa, P. Bonakdarzadeh, E. Numata, K. Rissanen, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2012, 51, 3161–3163 CrossRef CAS PubMed.
- T. P. Moneypenny II, A. Yang, N. P. Walter, T. J. Woods, D. L. Gray, Y. Zhang and J. S. Moore, J. Am. Chem. Soc., 2018, 140, 5825–5833 CrossRef PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS PubMed.
- G. M. Whitesides, J. P. Mathias and C. T. Seto, Science, 1991, 254, 1312–1319 CrossRef CAS PubMed.
- C. S. Hartley and J. He, J. Org. Chem., 2010, 75, 8627–8636 CrossRef CAS PubMed.
- NMR spectra throughout this work have been run at 0 °C, which typically gives slightly sharper peaks.
- K. W. Wiitala, T. R. Hoye and C. J. Cramer, J. Chem. Theory Comput., 2006, 2, 1085–1092 CrossRef CAS PubMed.
- R. Jain, T. Bally and P. R. Rablen, J. Org. Chem., 2009, 74, 4017–4023 CrossRef CAS PubMed.
- S. Mathew, L. A. Crandall, C. J. Ziegler and C. S. Hartley, J. Am. Chem. Soc., 2014, 136, 16666–16675 CrossRef CAS PubMed.
- S. Toyota, Chem. Rev., 2010, 110, 5398–5424 CrossRef CAS PubMed.
- In the spectrum of oP6(M), individual signals vary by nearly 1 ppm over different conformers.
- o-Phenylene tetramers are in fast backbone conformational exchange on the NMR time scale.
- We do not expect there to be significant differences in entropy between specific foldamer conformers (beyond those associated with their symmetries) since they are composed of rigid subunits and conformationally well-defined. Likewise, the behavior of the linkers is not expected to be strongly dependent on macrocycle size; this is consistent with the very similar outcomes of assembly for all systems examined thus far (e.g., as assessed by GPC).
- The 1H NMR spectrum of oP10(DPB)2+2 was also acquired in acetone-d6. The appearance was very similar to that in CDCl3, suggesting at least qualitatively similar folding behavior in both solvents.
- Here, “significant” signals are defined as those with cross-peaks observable in an HSQC spectrum and related signals from an HMBC spectrum.
- P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652–3711 CrossRef CAS PubMed.
- Y. Ito, E. Ihara, M. Murakami and M. Sisido, Macromolecules, 1992, 25, 6810–6813 CrossRef CAS.
- Y. Nagata, H. Hasegawa, K. Terao and M. Suginome, Macromolecules, 2015, 48, 7983–7989 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supplemental figures and discussion referred to in the text, experimental procedures, NMR spectra, and computational data. See DOI: 10.1039/c9sc02975c |
| This journal is © The Royal Society of Chemistry 2019 |