Metal-to-insulator transition in SmNiO3 induced by chemical doping: a first principles study†
Pilsun
Yoo
and
Peilin
Liao
 *
*
School of Materials Engineering, Purdue University, West Lafayette, IN 47906, USA. E-mail: lpl@purdue.edu
First published on 11th January 2018
Abstract
Rare-earth perovskite RNiO3 (R = Sm, Pr, Nd, etc.) has been investigated during the past decades due to a variety of tunable physical properties such as electrical conductivity and optical properties. Chemical doping in SmNiO3 was confirmed by experiments as a new way to drive metal-to-insulator transition under isothermal conditions. However, detailed crystal and electronic structure changes remain unknown. Here, we applied first principles density functional theory (DFT) to understand the mechanism of chemical doping with H and Li in SmNiO3. We showed that the DFT+U method with the PBEsol functional and Ueff = 2 eV produced results in good agreement with experiments for both insulating and metallic phases of SmNiO3. We examined the changes in geometry and electronic structures at various hydrogen and lithium doping concentration up to the experimental 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H(Li)
1 H(Li)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio. We observed a band gap opening of ∼3.0 eV (predicted by HSE06) at H
Ni ratio. We observed a band gap opening of ∼3.0 eV (predicted by HSE06) at H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 1
Ni = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, in good agreement with experiments. We further investigated the migration of H or Li along the [001] direction of SmNiO3. We found a migration barrier of ∼0.3 eV for hydrogen and ∼0.4 eV for lithium. These current findings pave the way for future theoretical and experimental investigation to develop efficient metal–insulator switching devices using rare earth perovskites.
1, in good agreement with experiments. We further investigated the migration of H or Li along the [001] direction of SmNiO3. We found a migration barrier of ∼0.3 eV for hydrogen and ∼0.4 eV for lithium. These current findings pave the way for future theoretical and experimental investigation to develop efficient metal–insulator switching devices using rare earth perovskites.
Design, System, ApplicationMetal-to-insulator transition (MIT) is of interest for both fundamental understanding of materials and development of electronic devices. Recently, Ramanathan's group applied electron doping to the SmNiO3 thin film surface to initiate MIT. The large change in conductivity opens up vast opportunities for applications in electronics, photonics, and solid oxide fuel cells. Computationally, the accurate prediction of perovskite with transition metal elements is challenging. Here we carefully benchmarked computational methods for predicting perovskite in various magnetic configurations and symmetry groups. We studied the changes in geometry and electronic structures as dopants were incorporated at different concentrations and discussed the origin of the MIT based on Ni 3d orbital occupation. Our results provide fundamental understanding of MIT in SmNiO3via a chemical route. |
1. Introduction
Sharp metal–insulator transition (MIT) in rare earth perovskite oxides RNiO3 (R = rare earth elements) has provoked research interest in fundamental understanding of the underlying physics and in developing electronic devices in industrial applications.1,2 X-ray and neutron diffraction and resistivity studies revealed correlation between crystal structures and electronic states,1–3 which sets forth the following questions: (1) what is the origin of MIT, and (2) what are the possible ways to tailor the MIT temperature (TMIT)?To answer the first question, researchers investigated the crystal structures, electronic, and magnetic properties of RNiO3. Symmetry breaking was observed along with MIT. RNiO3 experiences structural transition from an orthorhombic perovskite structure (Pbnm space group) in the metallic phase above TMIT (ref. 4) to monoclinic perovskite symmetry (P21/n space group) in the insulating phase below TMIT.5–7 The insulating monoclinic phase is marked by a breathing mode distortion of two Ni sublattices, which is not observed in the metallic orthorhombic structure.8 The origin of the insulating phase of RNiO3 has been under debate for a long time. Early studies suggested that charge disproportionality exists between two Ni sublattices, which opens up the Mott–Hubbard gap among Ni sites and generates alternating bond lengths from equivalent Ni sites with symmetry breaking.9–11 More recent computational studies found only small charge disproportionality and suggested a different mechanism through charge transfer of O anion to Ni.12,13 In the metallic phase, an electron was transfer from O anions to Ni, forming a 3d8![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) electron configuration with Ni2+ (3d8) and a ligand hole on O anions (
electron configuration with Ni2+ (3d8) and a ligand hole on O anions (![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) ). In the insulating phase, the two Ni sites become 3d8
). In the insulating phase, the two Ni sites become 3d8![[L with combining low line]](https://www.rsc.org/images/entities/i_char_004c_0332.gif) 2 for small Ni sites and 3d8 for large Ni sites. The presence of ligand holes near small Ni sites was used to explain shorter bond lengths and tight binding, consistent with the strong breathing mode observed. Most recently, Varignon et al.14 looked into different rare earth nickelates RNiO3 (R = Pr, Nd, Sm, Eu, Gd, Tb and Dy) to study bonding character using DFT+U with PBEsol functional and Ueff (U–J) = 2 eV. By analyzing the charge and magnetic moments on Ni, as well as the orbital shapes through maximally-localized Wannier function analysis, the authors proposed a mechanism that reconciles the charge disproportion and charge transfer models. They showed that indeed the two Ni sites disproportionate into low-spin +4 and high-spin +2 states. Meanwhile, O 2p electrons are strongly hybridized towards Ni4+, which gives rise to the final small charge difference between the two different types of nickel sites. To date, there is not yet a conclusive agreement on the thermal MIT in RNiO3.
2 for small Ni sites and 3d8 for large Ni sites. The presence of ligand holes near small Ni sites was used to explain shorter bond lengths and tight binding, consistent with the strong breathing mode observed. Most recently, Varignon et al.14 looked into different rare earth nickelates RNiO3 (R = Pr, Nd, Sm, Eu, Gd, Tb and Dy) to study bonding character using DFT+U with PBEsol functional and Ueff (U–J) = 2 eV. By analyzing the charge and magnetic moments on Ni, as well as the orbital shapes through maximally-localized Wannier function analysis, the authors proposed a mechanism that reconciles the charge disproportion and charge transfer models. They showed that indeed the two Ni sites disproportionate into low-spin +4 and high-spin +2 states. Meanwhile, O 2p electrons are strongly hybridized towards Ni4+, which gives rise to the final small charge difference between the two different types of nickel sites. To date, there is not yet a conclusive agreement on the thermal MIT in RNiO3.
The second question stimulates research interests to understand how to tune the TMIT for practical applications of RNiO3. The sharp change of the Ni–O bond and Ni–O–Ni angle at TMIT indicates correlation between the structural distortion with different R elements in RNiO3 and TMIT.3,4 Smaller rare earth metal cations in RNiO3 induce octahedral rotation to fill the open space, which influences the Ni–O bond distance and Ni–O–Ni angles. It was reported that the TMIT increases as the rare-earth metal size decreases.4,5 Different methods have been proposed to modify TMIT for practical applications: doping in the R site with elements of different ionic radii to produce distortion by a steric effect, using an RNiO3 heteroepitaxial thin film accompanied by substrates with lattice mismatch to generate strain effects, and employing an external electric field to induce deviation of the MIT from bulk materials.15–18 However, these methods are all subjected to the constraint that temperature should be varied to derive MIT.
Recently, Ramanathan's group applied chemical doping to SmNiO3 thin film surfaces to directly drive MIT.19,20 They demonstrated that electronic conductivity can be decreased by about 8 orders of magnitude by adding hydrogen atoms, which are ionized to donate electrons. They proposed that the additional electrons induce an electron configuration change in the Ni d-orbital from Ni3+ (3d7:t2g6eg1) to Ni2+ (3d8:t2g6eg2). They suggested that further addition of electrons to eg orbitals of Ni2+ ions is subjected to strong Coulomb repulsion, which suppresses the electronic conductivity. As a result, the addition of hydrogen to SmNiO3 produces an insulating phase, which is characterized as the Mott-insulator. Based on this finding, Ramanathan's group19 proposed that doping with hydrogen, lithium or magnesium in the interstitial sites of SmNiO3 is an effective strategy to induce MIT without changing temperature or strain to the thin film. The large change in conductivity with electron doping opens up vast opportunities for robust applications in electronics,19 plasmonic optics,21 solid oxide fuel cells,20 and devices that mimic the behavior of neurons in the brain.22 Furthermore, Zuo et al.22 performed a first principles study with explicit electron doping (direct addition of electrons without physical dopants) and confirmed the change in the electronic structure. However, the mechanism of incorporating chemical doping elements was unclear. Detailed information on the crystal structure and occupation sites of interstitial dopants (H, Li, Mg) is necessary for further improving their properties for advanced applications.
In this work, we applied first principles electronic structure calculations to investigate the chemical doping driven MIT in SmNiO3. The rest of the manuscript is organized as follows: section 2 provides the computational model, section 3 presents the bulk calculations to validate our computational model, chemical doping results and migration barriers of dopants, and section 4 concludes.
2. Computational details
2.1 Bulk SmNiO3
First principles spin-polarized DFT calculations in this study were conducted with the Vienna ab initio simulation package (VASP, version 5.4.4).23,24 The projected augmented wave (PAW) pseudopotentials25 were used with Ni 4s23d8, O 2s22p4 and Sm 5s25p64f16s2 treated as valence electrons. In the case of Sm, five of the f electrons are kept in the core to reduce self-interaction errors as suggested by Kiejna et al.26The DFT+U method27–29 was used with the PBEsol (Perdew–Burke–Ernzerhof revised for solids)30 exchange-correlation functional and Ueff = 2 eV. Several studies31,32 use Ueff > 2 eV for Ni to correct for the self-interaction errors in transition metal oxides. In Varignon et al.’s work,14 they used Ueff = 2 eV, and obtained results in good agreement with experiments for a series of rare earth nickelates. They also reported that, contrary to the experimental findings, large values of Ueff resulted in a metallic antiferromagnetic (AFM) state for both monoclinic and orthorhombic symmetries.14 In this study, we adopted the same PBEsol+U with the Ueff = 2 eV setting (denoted as PBEsol+2 below). Our results in section 3.1 indicate that this Ueff value is capable of accurate predictions for both insulating phase and metallic phase for SmNiO3.
An 80-atom (2 × 1 × 2) supercell was adopted for studying bulk insulating phase and metallic phase. The cutoff energy was set to 500 eV. A Γ-centered k-point mesh of 3 × 6 × 4 was used along with a Gaussian smearing of 0.1 eV. Overall, this setting converges the total energy to within 1 meV per atom with respect to the higher energy cutoff or denser k-point mesh. The conjugated-gradient algorithm was used for all geometry optimizations, and the optimization stops when the change in the total energy between the subsequent steps is less than 1 meV. The Γ-centered k-point grid of 6 × 12 × 8 and the tetrahedron method with Blöchl correction33 are used for density of state calculations.
We studied both monoclinic (P21/n space group) and orthorhombic (Pbnm space group) SmNiO3 as they have been reported at different temperatures and with different electronic structures.34,35 In the rest of this manuscript, monoclinic and orthorhombic SmNiO3 are denoted as M-SNO and O-SNO, respectively. The magnetic configuration was characterized by neutron diffraction to have the propagation vector K = (½, 0, ½).36 Several possible magnetic configurations satisfying this condition were suggested and studied by first principles calculations.14,37 We chose to study three most stable magnetic configurations in SmNiO3: T-type AFM (T-AFM), A-type AFM (A-AFM) and ferromagnetic (FM).14 The specific magnetic configurations for T-AFM and A-AFM are illustrated in Fig. S1 in the ESI.† A-AFM is a simple AFM configuration in which the magnetic moments of neighboring Ni layers are opposite. The T-AFM case is more complicated. It has a stairwise pattern of magnetic moments of Ni. We performed full geometry optimization of M-SNO for both T-AFM and A-AFM. M-SNO was unstable in the FM state and was optimized without changing the cell shape for systematic comparison in magnetic ordering. Similarly, O-SNO is stable in the FM state. O-SNO in the AFM states is optimized without changing the cell shape.
2.2 Chemical doping by hydrogen or lithium
To examine the doping concentration effects on the MIT, we studied different H doping concentrations in a 1 × 1 × 1 unit cell of SmNiO3 with 20 atoms (4 Sm, 4 Ni and 12 O). The 1 × 1 × 1 unit cell satisfies the symmetry requirements and was used for testing different H doping concentrations. The H concentration increases from 0 H (H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 0
Ni = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 as in pure SmNiO3) to 1.0 H (H
4 as in pure SmNiO3) to 1.0 H (H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 4
Ni = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, addition of 4 hydrogens), which is the same as the concentration of doped hydrogen near the surface in X-ray photoelectron spectroscopy.19 It was reported that there was no significant structural distortion after the chemical doping within the resolution of X-ray diffraction.20 Hence, we assumed that the crystal mainly experiences volume expansion, and relaxed the volume while keeping the cell shape fixed for the initial screening of H location in the doping studies. We used Γ-centered 6 × 6 × 4 k-point grid with a Gaussian smearing of 0.1 eV. The density of states was obtained by single point calculation with the Γ-centered 12 × 12 × 8 k-point mesh and the tetrahedron method with Blöchl correction. Since DFT+U may underestimate band gaps,38 we performed the single point HSE06 (ref. 39 and 40) calculation over the optimized PBEsol+2 geometry to obtain additional predictions. Γ-centered 4 × 4 × 3 k-point mesh is used for the HSE06 calculations. Bader charge analysis41 was employed to estimate the charge values before and after chemical doping in the system. The magnetic moments of Ni in Fig. 5 were calculated as the difference between Ni spin up and spin down electrons from Bader charge analysis.
4, addition of 4 hydrogens), which is the same as the concentration of doped hydrogen near the surface in X-ray photoelectron spectroscopy.19 It was reported that there was no significant structural distortion after the chemical doping within the resolution of X-ray diffraction.20 Hence, we assumed that the crystal mainly experiences volume expansion, and relaxed the volume while keeping the cell shape fixed for the initial screening of H location in the doping studies. We used Γ-centered 6 × 6 × 4 k-point grid with a Gaussian smearing of 0.1 eV. The density of states was obtained by single point calculation with the Γ-centered 12 × 12 × 8 k-point mesh and the tetrahedron method with Blöchl correction. Since DFT+U may underestimate band gaps,38 we performed the single point HSE06 (ref. 39 and 40) calculation over the optimized PBEsol+2 geometry to obtain additional predictions. Γ-centered 4 × 4 × 3 k-point mesh is used for the HSE06 calculations. Bader charge analysis41 was employed to estimate the charge values before and after chemical doping in the system. The magnetic moments of Ni in Fig. 5 were calculated as the difference between Ni spin up and spin down electrons from Bader charge analysis.
3. Results and discussion
3.1 Bulk SmNiO3
In this section, we validate our computational approach by comparing the predicted SmNiO3 crystal structures and electronic properties in different symmetries (O-SNO and M-SNO) and magnetic configurations (T-AFM, A-AFM, and FM) to experimental results. Experimentally, the insulating phase was found to become monoclinic perovskite with breathing mode distortion below TMIT ≈ 400 K, and to change to metallic phase in the orthorhombic perovskite structure at higher temperature.Table 1 summarizes the structural parameters such as the lattice constant, volume and band gap in different space groups and magnetic systems for SmNiO3. We systematically compare our calculation results to the experimental results above and below TMIT from Rodriguez-Carvajal et al.42 The FM configuration is used as the reference state with ΔE = EAFM − EFM. As discussed in section 2.1, M-SNO is only stable in T-AFM, and O-SNO is only stable in FM. Different magnetic configurations were obtained from constraining the cell shape to test their relative stability. Overall, the relative energy of magnetic ordering is predicted to be T-AFM < FM < A-AFM. The ΔE values predicted for M-SNO and O-SNO are quite similar. T-AFM is more stable than the FM state by 0.16 eV and 0.18 eV in M-SNO and O-SNO, respectively. On the other hand, FM is more stable than the A-AFM state by 0.17 eV and 0.11 eV in M-SNO and O-SNO, respectively. The relative magnetic ordering is in agreement with experiments; SmNiO3 experiences magnetic transition from AFM to paramagnetic (PM) at TN ≈ 192 K with its magnetic structure characterized by neutron diffraction study.1,14,36,43
| Experiment42 | PBEsol+2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| At 375 K, PM | At 410 K, PM | T-AFM14 | T-AFM | A-AFM | FM | T-AFM | A-AFM | FM | |
| Space group | Orthorhombic (Pbnm) | Monoclinic (P21/n) | Orthorhombic (Pbnm) | ||||||
| Electronic phase | Insulator | Metal | Insulator | Insulator | Insulator | Metal | Insulator | Insulator | Metal |
| a (Å) | 5.430 | 5.424 | 5.395 | 5.405 (−0.5%) | 5.416 (−0.3%) | 5.405 (−0.4%) | 5.311 (−2.2%) | 5.419 (−0.1%) | 5.416 (−0.2%) |
| b (Å) | 5.330 | 5.332 | 5.225 | 5.247 (−1.6%) | 5.251 (−1.5%) | 5.247 (−1.6%) | 5.294 (−0.7%) | 5.251 (−1.5%) | 5.253 (−1.5%) |
| c (Å) | 7.680 | 7.556 | 7.478 | 7.475 (−2.7%) | 7.489 (−2.5%) | 7.475 (−1.1%) | 7.495 (−1.1%) | 7.489 (−0.9%) | 7.471 (−1.1%) |
| α (°) | 90.00 | 90.00 | 90.05 | 90.03 | 90.01 | 90.03 | 90.00 | 90.00 | 90.00 |
| β (°) | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 |
| γ (°) | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 | 90.00 |
| Volume (Å3) | 222.3 | 218.8 | 210.8 | 212.0 (−4.6%) | 213.2 (−4.2%) | 212.0 (−3.2%) | 210.7 (−3.8%) | 213.1 (−2.5%) | 212.5 (−2.7%) |
| Band gap (eV) | — | — | 0.54 | 0.51 | 0.19 | 0 | 0.47 | 0.17 | 0 |
| ΔE (eV) (EAFM − EFM) | — | — | −0.15 | −0.16 | 0.17 | 0 | −0.18 | 0.11 | 0 |
Deviation from experiments was calculated by comparing the insulating AFM results to insulating phase at 375 K and the metallic FM results to metallic phase at 410 K (Table 1). For the T-AFM insulating phase, the lattice constants for all directions in PBEsol+2 were underestimated by <3%, with the z-axis of the unit cell being the most underestimated. Our results for T-AFM M-SNO were in reasonable agreement with previously reported computational results.14 For the FM metallic phase, the deviation from experiments was smaller than those of the T-AFM case. Maximum lattice constant deviation was <1% and the volume difference was ∼3%.
Fig. 1 shows the projected density of states (PDOS) for T-AFM M-SNO and FM O-SNO. Fig. S2† shows the total density of states (TDOS) for all magnetic configurations and symmetries investigated. Similar band gaps are predicted for two symmetry groups with the same types of AFM: T-AFM (A-AFM) SmNiO3 showed an ∼0.5 (∼0.2) eV gap opening with splitting of DOS at the Fermi level. The exact experimental band gap for SmNiO3 at low temperature is unknown due to the inconsistency with the single conduction mechanism.44 Our prediction agrees with the 0.54 eV value reported by Varignon et al. using PBEsol+2 for T-AFM SmNiO3.14 For the FM state, however, the two symmetry groups gave different electronic structures. There is a splitting of band gap in FM M-SNO, while FM O-SNO shows the metallic character with continuous spin up states across the Fermi level. This prediction of metallic FM O-SNO is in good agreement with experiments.45 The agreement in both magnetic and electronic structures supports the use of a single Ueff parameter of 2 eV to investigate the current system.
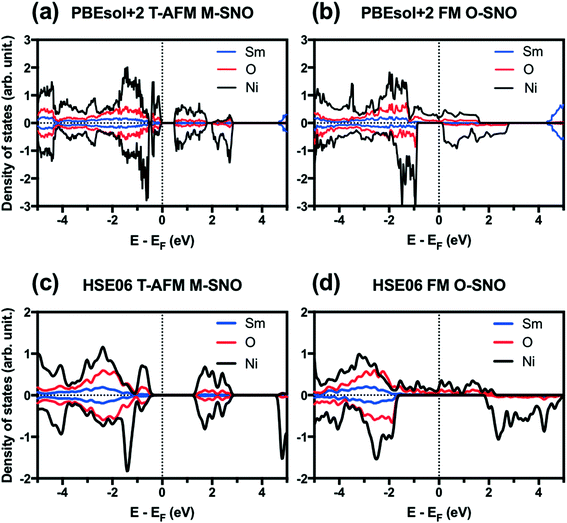 | ||
| Fig. 1 Projected density of states (PDOS) for (a) PBEsol+2 T-AFM M-SNO, (b) PBEsol+2 FM O-SNO, (c) HSE06 T-AFM M-SNO, and (d) HSE06 FM O-SNO. Vertical dotted lines are added to indicate Fermi level. | ||
We further tested two additional exchange-correlation functionals: the SCAN functional (strongly constrained and appropriately normed meta-generalized gradient approximation (GGA))46 and the hybrid functional HSE06.39,40 The SCAN functional is a recently developed meta-GGA functional with good overall performance for both molecular and condensed matter systems.46,47 The SCAN functional predicted both AFM M-SNO and FM O-SNO to be metallic (Fig. S3†), which disagrees with experiments and highlights the difficulty in obtaining accurate predictions for this particular system. Compared with PBEsol+2, HSE06 predicted the metallic phase for FM O-SNO and the insulating phase for T-AFM N-SNO with a band gap of ∼1.2 eV (Fig. 1).
Both the experiments and the ab initio calculations suggested that the “breathing mode” distortion of neighboring Ni octahedra in M-SNO was related to the emergence of the insulating phase.5,8,14,35 We computed the breathing mode in both space groups by investigating the volume difference in percent deviation from the neighboring Ni octahedra (Table S1† and Fig. 2). In M-SNO, all magnetic systems give the presence of the breathing mode distortion except for the PM system (non-spin-polarized calculation in DFT). These values are similar to previous calculation results reported by Varignon et al.14 (orange dash line in Fig. 2(c)). In contrast, the breathing mode was not observed at all in O-SNO systems. This implies that the M-SNO symmetry is more suitable for insulating phase study. Therefore, the presence/observation of the breathing mode further supports our assumption that M-SNO can be used to model a low-temperature insulator while O-SNO can be used to model the high temperature metallic phase. As a result, we can use PBEsol+2 with a single Ueff = 2 eV to completely describe the physical properties of SmNiO3 at different temperatures. Hence, in the following, we will investigate the chemical doping in SmNiO3 by hydrogen and lithium using the FM O-SNO configuration as experimental chemical doping occurs above TMIT.
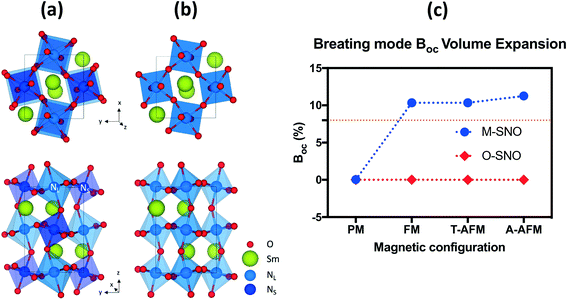 | ||
| Fig. 2 (a) M-SNO with breathing mode distortion and (b) O-SNO in the absence of breathing mode distortion. (c) Breathing mode octahedral volume difference (BOC) in different magnetic systems in both M-SNO and O-SNO. BOC was calculated as the percent difference in volumes of two neighboring NL and NS. The orange dashed line shows previously reported breathing distortion values.14 | ||
3.2 Chemical doping induced MIT
To systematically investigate the spatial distribution of dopants inside SmNiO3, we first investigated the preferential sites for a single hydrogen atom. The search for the most stable sites for single hydrogen doping yielded 4 stable interstitial sites in the (001) planes near the edges of Ni octahedra and another 4 metastable interstitial sites in the (001) planes near the edges of Sm polyhedra (Fig. S4†). In all cases, H atoms are bonded to oxygen anions. From these results, degenerate sites (distance below 1 Å) were treated as a single site, and these simplified interstitial sites were used to generate configurations for higher doping concentrations. Since the interstitial sites in the Ni octahedron plane are more stable than those in the Sm polyhedron plane (by ∼0.3 eV for the lowest energy configurations of the two (Fig. S4†)), in the next step, sites for 4 hydrogens were selected from the first pool to achieve 1.0 H concentration (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H
1 H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni) in SmNiO3. We selected two sites from each Ni octahedron plane, which results in a combination of
Ni) in SmNiO3. We selected two sites from each Ni octahedron plane, which results in a combination of 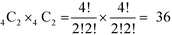 different configurations in the SmNiO3 unit cell.
different configurations in the SmNiO3 unit cell.
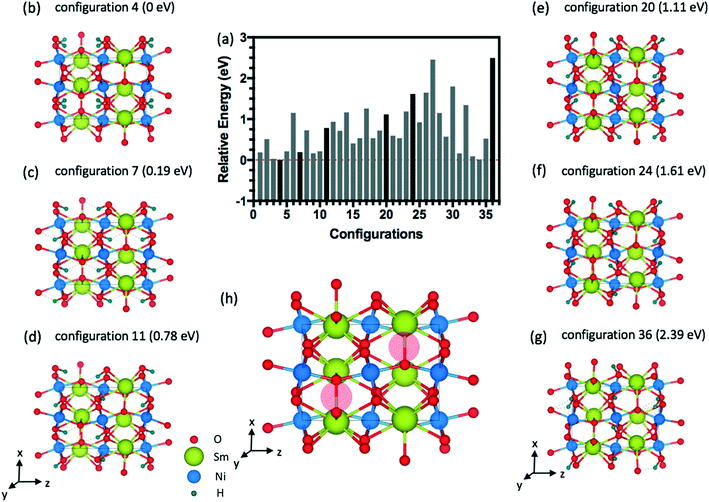
The energy distributions and several configurations are shown in Fig. 3. We notice that stable configurations have hydrogens close to the void space in the Sm layers denoted with red circles in Fig. 3(h). For example, configuration 4 in Fig. 3(b) has hydrogens that are all heading towards the interstitial sites in a single Sm layer. More specifically, two hydrogens are heading towards +z direction from the bottom Ni layer and two other hydrogens are heading towards −z direction in Fig. 3(b). Meanwhile, the other higher energy configurations (Fig. 3(c)–(g)) have more hydrogens away from these interstitial sites. Further studies on doping with hydrogens were conducted with this lowest energy configuration 4 shown in Fig. 3(b). Similarly, stable configurations for doping with lithium were determined and are shown in Fig. 4.
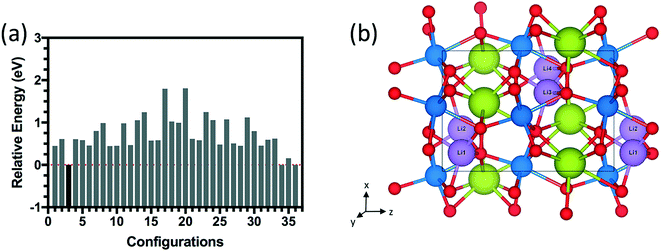 | ||
| Fig. 4 (a) Relative energy difference for 36 configurations of 1.0 Li doping concentration (4 Li atoms) inside the 20-atom O-SNO unit cell. (b) Lowest energy structure among the 36 configurations. | ||
Table 2 indicates the structural changes with different doping concentrations from 0 H (pure SmNiO3) to 1.0 H concentration (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; H
1; H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni) in the unit cell of SmNiO3. Lower concentrations such as 0.25 H, 0.5 H, and 0.75 H were calculated by removing 1 H each time from the lowest energy configuration of the 1.0 H structure. For H doping, the lattice constant increases from +0.8% at 0.25 H to +4.1% at 1.0 H, while the volume expands from +2.4% at 0.25 H to +12.7% at 1.0 H. Experimentally, the shift of the X-ray diffraction peak suggests that the lattice expanded by 10% along the out-of-plane [001] direction.19 This measurement relates closely to the region below the Pt electrode in which the hydrogen could be directly adsorbed on SmNiO3. On the other hand, the SmNiO3 surface exposed to atmosphere in the peripheral region of the Pt electrode experienced lattice expansion by about 4% in the [001] direction. Therefore, our results with an increase of ∼4.1% in the lattice parameter along [001] for 1.0 H are consistent with the experimental finding.20 We investigated the same process for chemical doping in SmNiO3 with different concentrations of Li (0.25 Li, 0.5 Li, 0.75 Li, and 1.0 Li). The lowest energy configuration for 1.0 Li (Fig. 4) was different from the case of 1.0 H SmNiO3; Li atoms are in between the Ni and Sm layers. Since the ionic radius of Li is larger than that of H, larger expansion in lattice constants and volume was observed: ∼11% increase in the lattice constant and 37% increase in the volume for 1.0 Li concentration.
Ni) in the unit cell of SmNiO3. Lower concentrations such as 0.25 H, 0.5 H, and 0.75 H were calculated by removing 1 H each time from the lowest energy configuration of the 1.0 H structure. For H doping, the lattice constant increases from +0.8% at 0.25 H to +4.1% at 1.0 H, while the volume expands from +2.4% at 0.25 H to +12.7% at 1.0 H. Experimentally, the shift of the X-ray diffraction peak suggests that the lattice expanded by 10% along the out-of-plane [001] direction.19 This measurement relates closely to the region below the Pt electrode in which the hydrogen could be directly adsorbed on SmNiO3. On the other hand, the SmNiO3 surface exposed to atmosphere in the peripheral region of the Pt electrode experienced lattice expansion by about 4% in the [001] direction. Therefore, our results with an increase of ∼4.1% in the lattice parameter along [001] for 1.0 H are consistent with the experimental finding.20 We investigated the same process for chemical doping in SmNiO3 with different concentrations of Li (0.25 Li, 0.5 Li, 0.75 Li, and 1.0 Li). The lowest energy configuration for 1.0 Li (Fig. 4) was different from the case of 1.0 H SmNiO3; Li atoms are in between the Ni and Sm layers. Since the ionic radius of Li is larger than that of H, larger expansion in lattice constants and volume was observed: ∼11% increase in the lattice constant and 37% increase in the volume for 1.0 Li concentration.
| Concentration | 0 H | 0.25 H | 0.50 H | 0.75 H | 1.0 H | 0.25 Li | 0.50 Li | 0.75 Li | 1.0 Li |
|---|---|---|---|---|---|---|---|---|---|
| a (Å) | 5.248 | 5.290 | 5.343 | 5.396 | 5.462 | 5.407 | 5.563 | 5.715 | 5.828 |
| b (Å) | 5.409 | 5.451 | 5.506 | 5.560 | 5.629 | 5.572 | 5.733 | 5.889 | 6.006 |
| c (Å) | 7.470 | 7.528 | 7.604 | 7.679 | 7.773 | 7.695 | 7.918 | 8.134 | 8.294 |
| Volume (Å3) | 212.1 | 217.1 | 223.7 | 230.4 | 239.0 | 231.9 | 252.6 | 273.8 | 290.4 |
| Lattice expansion (%) | 0 | 0.8 | 1.8 | 2.8 | 4.1 | 3.0 | 6.0 | 8.9 | 11.1 |
| Volume expansion (%) | 0 | 2.4 | 5.5 | 8.6 | 12.7 | 9.3 | 19.1 | 29.1 | 36.9 |
| Differential adsorption energy (eV) | 0 | −2.01 | −2.48 | −2.84 | −1.94 | −0.24 | −1.41 | −1.38 | −2.16 |
| Average adsorption energy (eV) | 0 | −2.01 | −2.25 | −2.45 | −2.32 | −0.24 | −0.83 | −1.01 | −1.30 |
We reported both the differential and average H/Li adsorption energy in Table 2. The differential adsorption energy was calculated as 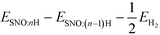 and ESNO:nLi − ESNO:(n−1)Li − ELibcc. The average adsorption energy was calculated as
and ESNO:nLi − ESNO:(n−1)Li − ELibcc. The average adsorption energy was calculated as 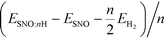 and (ESNO:nLi − ESNO − nELibcc)/n. n is the number of H or Li (n = 1, 2, 3, 4), ESNO:nH (ESNO:nLi) is the total energy with n H (Li) in doped SmNiO3, ESNO is the total energy of pristine SmNiO3, EH2 is the energy of a hydrogen molecule, and ELibcc is the energy per Li atom in bcc Li. The differential and average adsorption energies of H remain relatively constant in the range of −2.0 to −2.8 eV. In contrast, the initial adsorption of Li is only weakly favorable with an adsorption energy of −0.2 eV for the first Li and gradually becomes more favorable, with a differential adsorption energy of ∼−2.2 eV at Li
and (ESNO:nLi − ESNO − nELibcc)/n. n is the number of H or Li (n = 1, 2, 3, 4), ESNO:nH (ESNO:nLi) is the total energy with n H (Li) in doped SmNiO3, ESNO is the total energy of pristine SmNiO3, EH2 is the energy of a hydrogen molecule, and ELibcc is the energy per Li atom in bcc Li. The differential and average adsorption energies of H remain relatively constant in the range of −2.0 to −2.8 eV. In contrast, the initial adsorption of Li is only weakly favorable with an adsorption energy of −0.2 eV for the first Li and gradually becomes more favorable, with a differential adsorption energy of ∼−2.2 eV at Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni 1
Ni 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 concentration. The average adsorption energy for H(Li)
1 concentration. The average adsorption energy for H(Li)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni = 1
Ni = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is −1.3 eV for Li, about 1 eV higher than that (−2.3 eV) for H. The less negative adsorption energy of Li implies that Li doping is harder than H to be incorporated into the SmNiO3 lattice. We suggest that the large expansion in unit cell volume with Li insertion may be the cause of the less favorable adsorption energy.
1 is −1.3 eV for Li, about 1 eV higher than that (−2.3 eV) for H. The less negative adsorption energy of Li implies that Li doping is harder than H to be incorporated into the SmNiO3 lattice. We suggest that the large expansion in unit cell volume with Li insertion may be the cause of the less favorable adsorption energy.
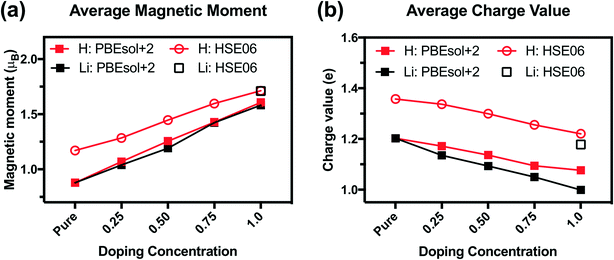
We analyze the electronic structures in terms of changes in charges, magnetic moments, and band gaps for different H and Li concentrations. Fig. 5(a) shows that the magnetic moments of Ni monotonously increased with increasing hydrogen and lithium in a similar slope. The PBEsol+2 and HSE06 predictions show similar trends, but differ by an almost constant offset. For PBEsol+2 predictions, Ni in pure SmNiO3 has a magnetic moment of 0.86μB. At 1.0 H (or 1.0 Li), the magnetic moments of Ni significantly increase to ∼1.6μB. We assumed that 0.86μB is the magnetic moment of a single electron in the eg orbital of Ni3+. A Ni magnetic moment of ∼1.6μB in 1.0 H and 1.0 Li was almost twice the magnetic moment of pure SmNiO3. This increase indicates the filling of eg orbital in Ni, supporting the transition of electron configuration in Ni ions from a single eg orbital occupation (Fig. 6(c)) to half-filled eg orbital occupation (Fig. 6(d)). Fig. 6(a) and (b) show the spatial distribution of magnetic moments of Ni. It is worth noting that the magnetic moments of individual Ni ions in Fig. 5 do not deviate from the averaged values in 1.0 H (Fig. 5(a)).
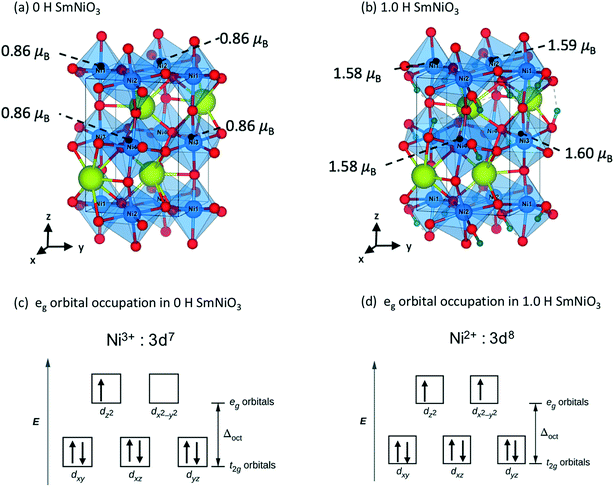 | ||
| Fig. 6 Magnetic moments of Ni in (a) 0 H O-SNO and (b) 1.0 H O-SNO. Electron configuration of the Ni 3d orbital in (c) 0 H O-SNO and (d) 1.0 H O-SNO. | ||
The charge of Ni monotonously decreases with the addition of H (Fig. 5(b)). Again, the PBEsol+2 and HSE06 predictions exhibit the same trend but differ by a constant offset. This implies that Ni ions take electrons from the dopants. Based on these results, we suggest that Ni in 1.0 H SmNiO3 is close to Ni2+ (3d8:t2g6eg2). The singly occupied eg orbital in pure SmNiO3 is known to be the origin of the metallic state with the electron transfer between Ni eg orbitals above TMIT. Adding one electron to each Ni creates half-filled eg orbitals. The strong Coulomb d–d repulsion from these half-filled orbitals prevents the facile transfer of electrons. This explains the 8 orders of magnitude change in the conductivity in H-doped SmNiO3.
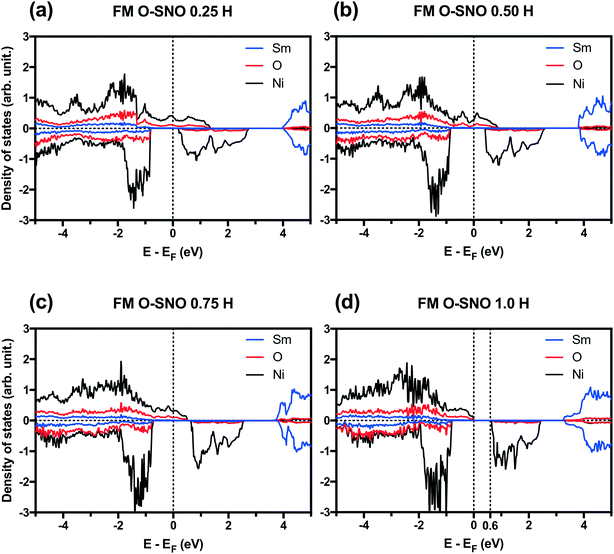
PBEsol+2 PDOS for different hydrogen concentrations are provided in Fig. 7. As hydrogen atoms are added into SmNiO3 in Fig. 7(a)–(d) for up to 1.0 H, the density of states of spin up electrons at the Fermi level became split and transitioned from the metallic phase to the insulating phase. At 0 H concentration in Fig. 1(a), the metallic character of SmNiO3 above TMIT is attributed to the transition of Ni eg electrons to nearby Ni eg orbital. At 1.0 H concentration, the Ni 3d spin up states moved below the Fermi level. Overall, the occupied Ni spin down states in t2g orbitals and unoccupied Ni spin down states in eg orbitals remain almost unchanged with doping.
In terms of DFT predicted band gap values, PBEsol+2 predicted a band gap of ∼0.6 eV for complete hydrogen doping at 1.0 H concentration, similar to the value of ∼0.5 eV predicted for the T-AFM insulating phase of M-SNO. Additional single point calculations with the HSE06 functional were performed over the PBEsol+2 structures. HSE06 predicted a band gap value of ∼3.0 eV for the 1.0 H concentration (Fig. 8), much larger than the ∼1.2 eV predicted for T-AFM M-SNO discussed in section 3.1. Experimentally, the band gap after hydrogen doping was reported to be ∼3 eV,19 estimated from the order of magnitude change in conductivity. Therefore, the results of HSE06 are in excellent agreement with experiments. Although PBEsol+2 underestimated the band gap compared to the HSE06 functional, it can provide accurate description for bulk phases and predict the transition for chemical doping in SmNiO3. Considering the low computational cost of PBEsol+2 compared with HSE06, we suggest that PBEsol+2 is a valuable tool for studying electronic structures in this rare earth nickelate system.
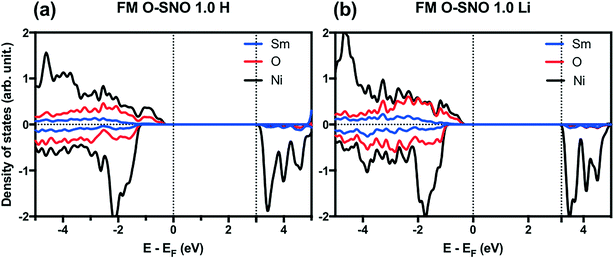 | ||
| Fig. 8 HSE06 PDOS for (a) 1.0 H concentration in O-SNO and (b) 1.0 Li concentration in O-SNO. Vertical dotted lines are added to the Fermi level and the bottom of conduction bands. | ||
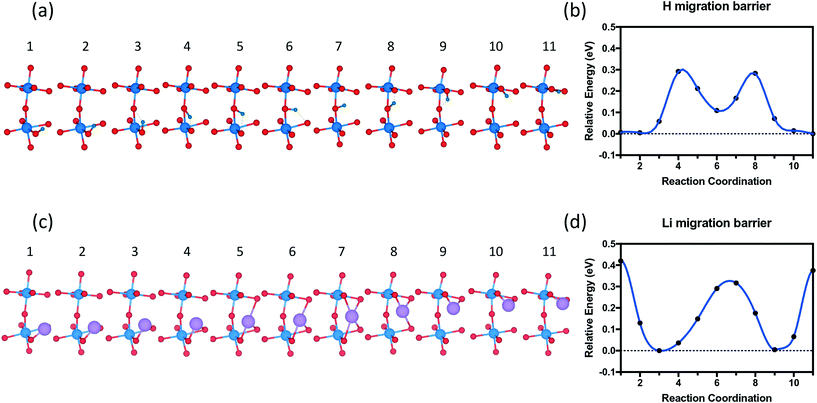
The migration pathway of hydrogen along the [001] direction of SmNiO3 was computed to investigate the activation energy for hydrogen intercalation (Fig. 9). Experimentally, the H atoms were transferred from the top of Pt to the SmNiO3 film grown in [001], and the lattice was found to expand more underneath Pt than in the peripheral region.20 We assumed that the [001] migration is the primary direction for hydrogen adsorption to consider. We performed climbing image nudged elastic band (CI-NEB) calculations48 to study the migration pathway along the [001] direction. We applied full geometry relaxation with 0.25 H concentration (1 hydrogen or lithium in the unit cell). The barrier for H migrating from the Ni–O layer to the Sm–O layer is predicted to be ∼0.3 eV, followed by a barrier of ∼0.2 eV for the transfer from the Sm–O layer to the next Ni–O layer. A different path was found for Li migration along the [001] direction. The Li ion is stable between the Ni–O and Sm–O layers. There is a single barrier of ∼0.35 eV through the Sm–O layer to the next interstitial site, and a higher barrier of ∼0.45 eV through the Ni–O layer to the next available site. In our results, both barriers are higher than those for the hydrogen migration. We attribute the higher energy barrier for the Li migration to more distortion induced by Li than H. This barrier difference could be overcome by external excitation, which was observed experimentally with external electric field or application of gate voltage.19 Larger distortion further implies that if the system can be prepared with tensile strain on SmNiO3,49 the barrier height could be modulated for easier migration of interstitial dopants.
4. Conclusion
In summary, we applied PBEsol+2 to study the bulk phase of SmNiO3, the mechanism of chemical doping with H or Li in SmNiO3, as well as the migration barriers of the dopants. We showed that PBEsol+2 is capable of predicting correctly the low-temperature insulating phase and high temperature metallic phase, as well as the chemical doping induced MIT in SmNiO3. We observed the breathing mode distortion with a band gap of ∼0.5 eV in AFM M-SNO by PBEsol+2, which agrees with the experimental findings in the low-temperature insulating phase. By changing the magnetic configuration from AFM to FM, metallic O-SNO was stabilized in the system. Chemical doping in O-SNO revealed that eg orbital occupancy induces transition to insulator due to strong Coulomb repulsion. A critical concentration of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for H(Li)
1 for H(Li)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni was found for all Ni eg orbitals to be half filled and the MIT to occur. While PBEsol+2 predicts similar band gap values for T-AFM M-SNO at low temperature and chemical doped SmNiO3, single point HSE06 calculations based on PBEsol+2 geometries were able to predict larger band gaps for the latter chemical doping case, which is in excellent agreement with experiments. We further calculated the migration pathway of H or Li along the [001] direction, and obtained barriers of ∼0.3 eV for H and ∼0.4 eV for Li. Overall, our results explained the mechanism of MIT with chemical doping and demonstrated the predictive capability of DFT calculations for this novel strategy. These findings will be helpful for future experimental or theoretical research to synthesize materials with low migration barriers, test other chemical doping methods, and develop a facile synthesis of perovskite materials with different elements.
Ni was found for all Ni eg orbitals to be half filled and the MIT to occur. While PBEsol+2 predicts similar band gap values for T-AFM M-SNO at low temperature and chemical doped SmNiO3, single point HSE06 calculations based on PBEsol+2 geometries were able to predict larger band gaps for the latter chemical doping case, which is in excellent agreement with experiments. We further calculated the migration pathway of H or Li along the [001] direction, and obtained barriers of ∼0.3 eV for H and ∼0.4 eV for Li. Overall, our results explained the mechanism of MIT with chemical doping and demonstrated the predictive capability of DFT calculations for this novel strategy. These findings will be helpful for future experimental or theoretical research to synthesize materials with low migration barriers, test other chemical doping methods, and develop a facile synthesis of perovskite materials with different elements.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. L. gratefully acknowledges the startup support from the School of Materials Engineering at Purdue University. This research was supported in part through computational resources provided by the Information Technology department at Purdue, West Lafayette, Indiana.References
- J. Torrance, P. Lacorre, A. Nazzal, E. Ansaldo and C. Niedermayer, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 8209–8212 CrossRef CAS.
- J. L. García-Muñoz, J. Rodríguez-Carvajal, P. Lacorre and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4414–4425 CrossRef.
- P. Lacorre, J. B. Torrance, J. Pannetier, A. I. Nazzal, P. W. Wang and T. C. Huang, J. Solid State Chem., 1991, 91, 225–237 CrossRef CAS.
- M. L. Medarde, J. Phys.: Condens. Matter, 1999, 9, 1679–1707 CrossRef.
- J. A. Alonso, J. L. García-Muñoz, M. T. Fernández-Díaz, M. A. G. Aranda, M. J. Martínez-Lope and M. T. Casais, Phys. Rev. Lett., 1999, 82, 3871–3874 CrossRef CAS.
- M. Medarde, M. T. Fernández-Díaz and P. Lacorre, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 212101 CrossRef.
- C. Girardot, J. Kreisel, S. Pignard, N. Caillault and F. Weiss, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104101 CrossRef.
- N. C. Bristowe, J. Varignon, D. Fontaine, E. Bousquet and P. Ghosez, Nat. Commun., 2015, 6, 6677 CrossRef CAS PubMed.
- S.-J. Kim, G. Demazeau, I. Presniakov, K. Pokholok, A. Baranov, A. Sobolev, D. Pankratov and N. Ovanesyan, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 014427 CrossRef.
- J. L. García-Muñoz, J. Rodríguez-Carvajal and P. Lacorre, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 978–992 CrossRef.
- I. I. Mazin, D. I. Khomskii, R. Lengsdorf, J. A. Alonso, W. G. Marshall, R. M. Ibberson, A. Podlesnyak, M. J. Martínez-Lope and M. M. Abd-Elmeguid, Phys. Rev. Lett., 2007, 98, 176406 CrossRef.
- Y. Bodenthin, U. Staub, C. Piamonteze, M. García-Fernández, M. J. Martínez-Lope and J. A. Alonso, J. Phys.: Condens. Matter, 2011, 23, 036002 CrossRef CAS PubMed.
- H. Park, A. J. Millis and C. A. Marianetti, Phys. Rev. Lett., 2012, 109, 156402 CrossRef PubMed.
- J. Varignon, M. N. Grisolia, J. Íñiguez, A. Barthélémy and M. Bibes, npj Quantum Materials, 2017, 2, 21 CrossRef.
- S. W. Cheong, H. Y. Hwang, B. Batlogg, A. S. Cooper and P. C. Canfield, Phys. B, 1994, 194-196, 1087–1088 CrossRef.
- J. S. Zhou and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 153105 CrossRef.
- B. Torriss, J. Margot and M. Chaker, Sci. Rep., 2017, 7, 40915 CrossRef CAS PubMed.
- R. Scherwitzl, P. Zubko, I. G. Lezama, S. Ono, A. F. Morpurgo, G. Catalan and J.-M. Triscone, Adv. Mater., 2010, 22, 5517–5520 CrossRef CAS PubMed.
- J. Shi, Y. Zhou and S. Ramanathan, Nat. Commun., 2014, 5, 4860 CrossRef CAS PubMed.
- Y. Zhou, S. Lee, H. Liu, S. Ramanathan, S. Adam, X. Guan, H. Zhou, K. Ramadoss, J. Shi, M. Tsuchiya and D. D. Fong, Nature, 2016, 534, 231 CrossRef CAS PubMed.
- Z. Li, Y. Zhou, H. Qi, Q. Pan, Z. Zhang, N. N. Shi, M. Lu, A. Stein, C. Y. Li, S. Ramanathan and N. Yu, Adv. Mater., 2016, 28, 9117–9125 CrossRef CAS PubMed.
- F. Zuo, P. Panda, M. Kotiuga, J. Li, M. G. Kang, C. Mazzoli, H. Zhou, A. Barbour, S. Wilkins, B. Narayanan, M. Cherukara, Z. Zhang, S. K. R. S. Sankaranarayanan, R. Comin, K. M. Rabe, K. Roy and S. Ramanathan, 2017, arXiv:1703.01209, pp. 1–29 Search PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 47, 558–561 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- A. Kiejna, G. Kresse, J. Rogal, A. De Sarkar, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035404 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- V. I. Anisimov, in Spectroscopy of Mott Insulators and Correlated Metals, Springer Berlin Heidelberg, Berlin, Heidelberg, 1995, vol. 119, pp. 106–116 Search PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- M. Wang, Solid State Ionics, 2004, 166, 167–173 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 603 Search PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- J. A. Alonso, M. J. Martínez-Lope, M. T. Casais, M. A. G. Aranda and M. T. Fernández-Díaz, J. Am. Chem. Soc., 1999, 121, 4754–4762 CrossRef CAS.
- S. Johnston, A. Mukherjee, I. Elfimov, M. Berciu and G. A. Sawatzky, Phys. Rev. Lett., 2014, 112, 106404–106405 CrossRef PubMed.
- J. Rodríguez-Carvajal, S. Rosenkranz, M. Medarde, P. Lacorre, M. Fernandez-Díaz, F. Fauth and V. Trounov, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 456–464 CrossRef.
- G. Giovannetti, S. Kumar, D. Khomskii, S. Picozzi and J. van den Brink, Phys. Rev. Lett., 2009, 103, 156401 CrossRef PubMed.
- P. Liao and E. A. Carter, Phys. Chem. Chem. Phys., 2011, 13, 15189–15199 RSC.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106–224106 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- J. Rodríguez-Carvajal, M. Hennion, F. Moussa, A. H. Moudden, L. Pinsard and A. Revcolevschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R3189–R3192 CrossRef.
- J. L. García-Muñoz, J. Rodríguez-Carvajal, P. Lacorre and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4414–4425 CrossRef.
- R. Jaramillo, S. D. Ha, D. M. Silevitch and S. Ramanathan, Nat. Phys., 2014, 10, 304–307 CrossRef CAS.
- M. Medarde, A. Fontaine, J. L. García-Muñoz, J. Rodríguez-Carvajal, M. de Santis, M. Sacchi, G. Rossi and P. Lacorre, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14975–14984 CrossRef CAS.
- J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdew, Nat. Chem., 2016, 8, 831–836 CrossRef CAS PubMed.
- Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Phys. Rev. B, 2017, 96, 1203 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. H. Aydogdu, S. D. Ha, B. Viswanath and S. Ramanathan, J. Appl. Phys., 2011, 109, 124110 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8me00002f |
| This journal is © The Royal Society of Chemistry 2018 |