The mechanisms behind the extreme susceptibility of photon avalanche emission to quenching

Abstract

The photon avalanche (PA) process that emerges in lanthanide-doped crystals yields a threshold and highly nonlinear (of the power law order >5) optical response to photoexcitation. PA emission is the outcome of the excited-state absorption combined with a cross-relaxation process, which creates positive and efficient energy looping. In consequence, this combination of processes should be highly susceptible to small perturbations in energy distribution and can thus be hindered by other competitive “parasitic” processes such as energy transfer (ET) to quenching sites. Although luminescence quenching is a well-known phenomenon, exact mechanisms of the susceptibility of PA to resonant energy transfer (RET) remain poorly understood, limiting its practical applications. A deeper understanding of these mechanisms may pave the way to new areas of PA exploitation. This study focuses on the investigation of the LiYF₄:3%Tm³⁺ PA system co-doped with Nd³⁺ acceptor ions, which are found to impact both the looping and emitting levels. This effectively disrupts the PA emission, causing an increase in the PA threshold (I_th) and a decrease in the PA nonlinearity (S_max). Our complementary modelling results reveal that ET from the looping level increases I_th and S_max, whereas ET from the emitting level diminishes S_max and the final emission intensity. Ultimately, significant PA emission quenching demonstrates a high relative sensitivity (S_R) to infinitesimal amounts of Nd³⁺ acceptors, highlighting the potential for PA to be utilized as an ultra-sensitive, fluorescence-based reporting mechanism that is suitable for the detection and quantification of physical and biological phenomena or reactions.

---

New concepts

In this study, extreme susceptibility of photon avalanche (PA) emission to intentionally conceived quenching was demonstrated and explained for the first time. In particular, the PA emission intensity, PA threshold and PA non-linearity of 3% Tm³⁺-doped inorganic LiYF₄ fluoride microcrystals as a model PA system were evaluated for the rising concentration of volumetrically added acceptors (Nd³⁺ ions), which have been specifically chosen to enable the Tm-to-Nd resonant energy transfer (RET). Uniquely, three possible quenching scenarios of the key PA relevant energy levels (i.e., emitting, looping and both levels) have been proposed, discussed and experimentally verified, thus enabling an understanding of the mechanisms and drawing generic conclusions on the PA susceptibility to RET. Importantly, the probing of PA quenching deeply within the subsurface volume of the microcrystals minimized unspecific quenching and other issues related to the homogeneity of doping, surface ligands or defects present in nanocrystals. Therefore, the fundamental and yet unresolved questions concerning the severe susceptibility of PA emission to infinitely small disruption of energy looping in these materials could be ultimately addressed. Finally, these novel materials and observations, supported by phenomenological modelling, laid foundations for a new concept of a remote, luminescence-based reporter towards generic ultrasensitive sensing applications, featuring an in situ expandable dynamic detection range.

1. Introduction

A photon avalanche (PA) is a special type of energy transfer up-conversion that yields a highly nonlinear pump-power (I_P) dependent luminescence emission intensity I_L = (I_P − I_TH)^S,¹ where I_TH is a pump-power threshold and the order of nonlinearity S ranges from 5 to 46.^2–4 In comparison, an ordinary up-conversion process generally achieves an S of 2–4.^5,6 High nonlinearity grants the possibility of deploying PA materials in many applications such as the sensing of physical, chemical, and biological quantities,^7–10 sub-diffraction imaging,^2,3,11–14 reservoir computing,¹⁵ and data storage,¹⁶ and may become a key enabling technology for security inks and solar energy harvesting.¹⁷ The PA process can only occur after the fulfillment of two primary conditions (Fig. 1(a)).^1,18,19 First of all, the ground-state absorption (GSA) must be negligible with regard to the excited-state absorption (ESA). Thus, the ratio σ_ESA/σ_GSA of the two absorption cross-sections must be equal to or higher than typically 10⁴.^17,20 After the initial multiphonon-assisted GSA from the ground (GL) to the looping level (LL), an efficient ESA occurs and populates the emitting level (EL) directly or through the nonradiative multiphonon relaxation (MPR) from the upper level. From this emitting level, a few processes can occur including other ESA to higher states,^16,21 radiative and non-radiative recombinations, non-radiative relaxations, or cross-relaxation (CR) energy transfer. The emergence of the CR between two adjacent lanthanide ions is the second critical requirement for efficient energy looping and storage. During CR, the population of the looping level doubles with each iteration of the looping cycle. After achieving a certain population of the looping state across many lanthanide ions, which is realized by increasing the excitation power up to a threshold level, the material becomes a good absorber (through ESA), and the luminescence emission intensity starts to grow in a highly nonlinear manner with a further increase in the photoexcitation intensity. The PA pump power threshold corresponds to the situation when the number of ions entering the energy looping is larger than the number of ions leaving.

Fig. 1 Explanation of PA quenching. (a) Simplified energy-level diagram showing the PA process: inefficient GSA from the ground level (GL) is followed by efficient ESA, energy CR in a positive loop, followed by photon emission; (b) diagram illustrating the acceptor energy levels in close proximity to the looping and emitting levels of lanthanide ions, demonstrating three distinct scenarios of resonant energy transfer (ET) pathways leading to quenching of the PA emission: (I) D–A ET from the looping level LL (Q_I), (II) D–A ET from the emitting level EL (Q_II), and (III) D–A ET from both looping and emitting levels of D emitting ion (Q_III); (c) simulated “S” shape data schematically showing the impact of quenching on the PA emission characteristics; (d) diagram schematically compares two scenarios: the pure, unperturbed PA emission (PA) with PA quenched by Q_I and Q_II acceptor species (PA + RET) and highlights the mechanisms of RET quenching within the whole branches of the energy looping ions subnetwork, leading to less efficient PA emission and increased PA threshold.

PA is a highly nonlinear phenomenon governed by complex energy distribution dynamics and many interdependent processes. It can be easily perturbed by numerous quenching processes, such as unintentionally co-doped impurities, crystal vacancies, dislocations, and other crystal defects.^14,22,23 Additionally, in nanomaterials, surface quenching by ligands and solvent molecules becomes an additional path for disrupting the PA energy looping and emission.¹⁴ Initial studies on avalanching nanoparticles (ANPs) with varying shell thicknesses demonstrated that any process capable of modifying the relaxation rate of the looping state (e.g., unspecific surface quenching) affects I_th.¹⁴ Nevertheless, these negative processes, when properly managed and understood, may become novel, sensitive luminescence reporters for the (bio)sensing of chemical surroundings. For example, it has been suggested that the perturbation of PA emission in nanomaterials by resonant surface acceptors may effectively increase the resonant energy transfer (RET) sensitivity range beyond the Förster distance.²⁴ Nevertheless, the specific contributions of the energy transfer (ET) from the looping and emitting states are still not entirely understood, and remain speculative without experimental evidence. While the conventional understanding of luminescence quenching refers to the quenching of the emitting levels, PA is significantly more complex as it is a collective and excitation history-dependent phenomenon. The major motivation and novelty of the studies presented here is to both qualitatively and quantitatively understand the principles behind PA quenching, as well as critically and generically discuss these phenomena with future applications of PA emission in mind.

Because every PA system involves at least three states (Fig. 1(a)), ground (n₁), looping (n₂), and emitting (n₃) levels, we distinguished three scenarios of PA quenching by the resonant acceptor (Fig. 1(b)): (Q_I) ET from the looping level, (Q_II) ET from the PA-emitting level, and (Q_III) a combination of both. The latter reflects the real-world scenario studied here, where the acceptor possesses a complex energy-level structure with many absorption bands. In the presence of such a Q_III acceptor, an increased pump-power threshold for PA emission is expected (Fig. 1(c)) because the energy transfer from the looping and emitting states inhibits the population growth of the looping state. Furthermore, it is anticipated that the energy transfer from both levels will reduce the emission intensity of PA. The order of nonlinearity in the PA emissions is also expected to decrease as the CR competes with the new non-radiative process. Compared with pure PA (Fig. 1(d), PA left branch), the presence of energy acceptors should hinder the excited-state population buildup and photon emission (Fig. 1(d), PA + RET right branch) by disturbing the smooth and efficient ESA (Q_I) and CR (Q_II), deferring energy looping directly (Q_I) or indirectly (Q_II).

In our study, we take advantage of the remarkable PA emission exhibited by Tm³⁺ ions. The Tm³⁺ ions were incorporated into a crystalline matrix of LiYF₄, with a 3% doping level to assure PA emission generation and simultaneously avoid any potential photodarkening effect (explained by PA electron trapping in surface defects), which has been observed in nanocrystals doped with Tm³⁺ ions at a concentration above 8%.²⁵ This concentration not only shows satisfactory nonlinear properties to understand the general principles behind PA quenching, but also attains a lower power-excitation threshold compared with higher concentrations.² PA in Tm³⁺ ions can be achieved by non-resonant GSA at 1059 nm, leading to the excitation of the ³H₅ level (Fig. 2(a)). Non-radiative relaxation ³H₅ → ³F₄ populates the long-living looping state. As soon as the looping state becomes preliminarily populated, the resonant ESA process further excites higher-lying energy levels, such as ³F₃ and ³F₂. With another non-radiative relaxation ³F₃/³F₂ → ³H₄, the emitting state becomes populated. Both GSA and ESA must occur with phonon assistance to populate the crucial looping and emitting states. With the populated ³H₄ level, efficient CR occurs between adjacent ions, doubling the ³F₄ population and further enhancing the ESA until saturation (SAT) is reached. Radiative recombination at the ³H₄ level yields the most intense PA emission at 800 nm (Fig. 2(b)).

Fig. 2 (a) Energy level diagram of Tm³⁺ showing the radiative and non-radiative processes leading to and accompanying the PA process, and the energy diagram of the Nd³⁺ acting as an acceptor and leading to the parasitic energy transfer from the Tm³⁺ looping (mechanism I) and emitting (mechanism II) states; (b) experimental 1059 nm pump-power-dependent 800 nm emission showing three PA zones, i.e., low emission intensity ESA based up-conversion (ESA), PA emission (PA) and the saturation regime (SAT); (c) SEM image of LiYF₄:3%Tm³⁺ microcrystals. (d) Bright field white light image, with the 1059 nm laser beam focused on the surface of the microcrystal.

To understand the quenching of the two key levels on the PA excitation and emission, the capability of individual quenching of the emitting and the looping levels are critical. Although a wide range of organic or inorganic species exhibit absorption bands corresponding to the Tm^{3+ 3}H₄ emitting level (800 nm) (e.g., IR808, Ag₂S QDs, etc.), there is a limited availability of those that can resonantly and specifically interact with the looping state (³F₄ level E ∼ 5180–5972 cm⁻¹, ca. at ∼1674–1930 nm). Even if such two acceptors to be anchored on the surface of the ANP are available, their conjugation chemistry and ANP surface coverage may not be homogenous. Thus, such experiment would not resolve the question about the nature, mechanism and importance of the two levels in PA emission quenching. To make the studies reliable and comparable, we evaluated how the intended co-doping of the Tm³⁺ energy-looping system with various concentrations of Nd³⁺ acceptor ions influenced the processes leading to PA emission from the Tm³⁺ ions. The other lanthanides (e.g., Er³⁺, Ho³⁺etc.) could help to elucidate the mechanism of quenching the PA emission too, however, we have deliberately chosen Nd³⁺ ions, whose energy levels overlap with the two critical levels in Tm³⁺ that are involved in PA machinery. Moreover, at up to 1% Nd³⁺ doping, Nd³⁺ does not show significant self-concentration quenching in fluoride hosts.²⁶ In particular, neodymium possesses energy levels ⁴F_5/2 and ²H_9/2 (12 005–12 933 cm⁻¹), which energetically overlap with the emitting Tm³⁺ level ³H₄ (12 180 to 12 891 cm⁻¹), as well as the ⁴I_15/2 (5328–6432 cm⁻¹) level that energetically overlaps with the Tm³⁺ looping level ³F₄ (5180–5972 cm⁻¹).²⁷ In this case, the PA quenching should arise from both the emitting and looping levels, which corresponds to the Q_III quenching scheme. Consequently, it is challenging to split and discuss the specific effects of quenching that result from separate ET processes originating from either the emitting or looping level. However, to investigate the individual contributions to PA quenching, we employed photon avalanche differential rate equations (PADRE) to model the behavior of PA luminescence. Furthermore, considering the many nonspecific quenching mechanisms that could potentially influence the PA emission in nanoparticles,¹⁴ coupled with the issues related to the NP themselves and the NP passivating shell formation (i.e., shell thickness variability, dopant concentration gradient across the NPs, local and particle-to-particle inhomogeneities, ion intermixing/migration between subsequent NP layers, access of surface ligands and solvent vibration, surface defects), we deliberately mitigated these concerns. This was achieved by utilizing large microcrystals (ca. 60 μm) (Fig. 2(c) and Fig. S1, ESI†) and investigating PA properties deeply within the subsurface volume of such microcrystals using a tightly focused laser beam (Fig. 2(d), ϕ = 1.2 μm diameter, which is ca. 50-fold smaller than the single microcrystal). The structural purity and uniform morphology of these samples were confirmed by X-ray diffraction (XRD) and scanning electron microscopy (SEM) (Fig. S1 and S2, ESI†).

2. Results and discussion

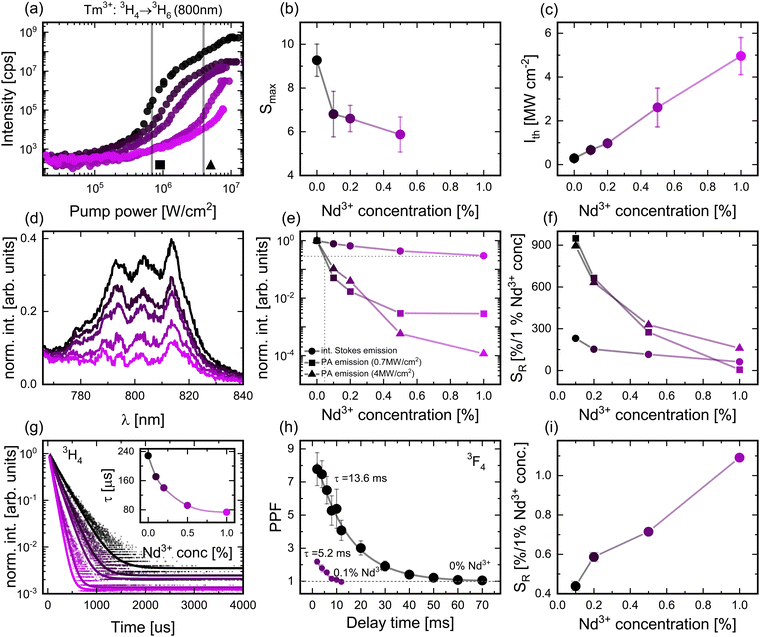
Energy transfer between lanthanide ions depends largely on the spectral overlap integral between the respective levels and the physical distance between the donor and acceptor species. With the matching energy levels of the Nd³⁺ and Tm³⁺ ions, one can anticipate a relatively effective energy transfer between them despite the forbidden nature of the f–f dipole–dipole transitions. Here, we investigated the impact of the presence and concentration of Nd³⁺ ions on the pump-power-dependent PA emission intensity of Tm³⁺ ions under 1059 nm photoexcitation. It is important to state, as discussed in the ESI,† that LiYF₄ crystals doped with ≤1% Nd³⁺ ions remain transparent under 1059 nm excitation at RT and do not exhibit PA-like behavior by themselves, supporting the idea to use Nd³⁺ ions as energy acceptors (through mechanism Q_III) from the avalanching Tm³⁺. The measured up-conversion spectra of the singly Tm³⁺-doped sample reveal six emission bands at 450 nm, 477 nm, 511 nm, 648 nm, 700 nm and the most intense one at 800 nm, which can be ascribed to the ¹D₂ → ³F₄, ¹G₄ → ³H₆, ¹D₂ → ³H₅, ¹G₄ → ³H₆, ³F₃ → ³H₆, and ³H₄ → ³H₆ transitions, respectively (Fig. S4, ESI†). The introduction of Nd³⁺ ions notably hindered the intensity of every emission band, which confirms efficient ET from Tm³⁺ to Nd³⁺ ions. Following the ET pathways between donor and acceptor presented in Table S1 (ESI†), this can be either (Tm;Nd)(³H₄;⁴I_9/2) → (³H₆; ⁴F_5/2 + ²H_9/2) or (Tm;Nd)(³F₄;⁴I_9/2) → (³H₆; ⁴I_11/2) Tm³⁺ to Nd³⁺ resonant energy transfers corresponding to Q_I (LL) or Q_II (EL) mechanisms, respectively. Co-doping the Tm³⁺ PA system with Nd³⁺ ions brings about a notable and gradual (as Nd³⁺ concentration rises) alteration in the characteristic pump-power dependences (Fig. 3(a) and Fig. S4, ESI†). This co-doping hinders the PA process by reducing the nonlinearity (Fig. 3(b)) and emission intensity (Fig. 3(e)), as well as increasing the photoexcitation power threshold, I_th (Fig. 3(c)), necessary to achieve the PA regime. The excitation threshold I_th is known to be proportional to the cross-section ESA coefficient, and inversely proportional to the luminescence lifetime of the looping state and cross-section GSA absorption coefficient according to the I_th ∼ [σ_ESA/(τ₂σ_GSA)]^1/2.²⁸ Since σ_ESA and σ_GSA strictly depend on the wavelength choice and type of the absorbing ion, they remain constant for Tm³⁺ ions independently of Nd³⁺ co-doping. Hence, the increase in I_th must be associated with a decrease in τ₂, indicating the emergence of ET from the looping level. Moreover, the presence of acceptor ions reduced the maximum nonlinearity order, S_max (Fig. 3(b)). This suggests that the Nd³⁺ ions hinder the smooth occurrence of the CR process, which is responsible for the nonlinear behavior observed in the PA emission.²⁸ To underscore the scale of quenching in the PA emission intensity, we collected Stokes 800 nm emission spectra (Fig. 3(d) and Fig. S6, ESI†) for comparative analysis (Fig. 3(e)). At a constant excitation power of 4 MW cm⁻², it is evident that the introduction of 1% Nd³⁺ doping results in a remarkable four-order magnitude reduction in the 800 nm PA emission intensity compared to the singly Tm³⁺ doped sample, where the corresponding integrated Stokes emission is approximately only four times less intense in the same and corresponding microcrystals (Fig. 3(e)). The observed exceptional PA emission quenching in response to increasing acceptor concentration indicates that the PA phenomenon has huge application potential as a luminescent reporting feature, and is suitable for the ultrasensitive sensing of physical (e.g., temperature, force, and plasmonic interactions), chemical (e.g., pH), and biological (FRET sensing) processes.

Fig. 3 Comparison of PA and Stokes emission quenching. (a) Pump power-dependent 800 nm (³H₄→ ³H₆) Tm³⁺ PA emission upon quenching by co-doping with 0.1, 0.2, 0.5 and 1% Nd³⁺ acceptors; corresponding (b) averaged maximum order of nonlinearity and (c) excitation intensity threshold as a function of Nd³⁺ concentration; (d) 800 nm Stokes emission quenching for 0, 0.1, 0.2, 0.5 and 1% Nd³⁺ concentration; (e) normalized Stokes emission under 356 nm excitation wavelength (●) and PA emission at 0.7 MW cm⁻² (■) and 4 MW cm⁻² (▲) enables emission intensity quenching comparison; (f) relative sensitivity based on the Stokes and PA emission intensity (i.e. based on (e) data); (g) normalized Stokes 800 nm emission decay fitted with mono-exponential decay, the inset depicts the time decay as a function of the Nd³⁺ concentration; (h) paired pulse facilitation described as the ratio of I₂/I₁ of 800 nm PA emission as a function of the delay time for the 0% and 0.1% Nd³⁺ concentrations, depicting the looping level population decay; (i) relative sensitivity of the studied PA material determined based on the time decay of the 800 nm Stokes emission (i.e. based on (g) data).

To quantify the superiority of PA emission over Stokes emission in acceptor sensing, we calculated the relative sensitivity (S_R) for both processes, as defined by S_R = 1/I_LUM·ΔI_LUM/ΔConc_Nd (Fig. 3(f)), which quantitatively depicts the susceptibility of luminescence intensity to a unit change of acceptor concentration. PA emission at two fixed power densities (0.7 and 4 MW cm⁻²) demonstrated significantly higher S_R, reaching up to 900% at low concentrations and decreasing with higher concentrations down to the 7–160% range. In contrast, the Stokes emission covers a sensitivity range of lower but still reasonable 280% down to 60%. Notably, PA quenching is particularly suitable for detecting low acceptor concentrations owing to its superior sensitivity within this range. Nevertheless, such extreme sensitivities originating from the susceptibility of the PA mechanism to minute amounts of acceptor/quenching species have the other side of the coin, as PA may non-specifically be affected by other material factors (e.g., nano/micro crystal size, doping homogeneity, surface effects) (Fig. S7, ESI†), excitation (e.g., pump power density, pump power, and wavelength short- and long-term stability), or the properties of the actual sample (e.g., variation in pump power due to variations in light scattering). Therefore, it is critical to devise methodologies capable of reducing artifacts in order to enable reliable and reproducible sensing. Although one such approach has been proposed previously,²⁴ which suggests a comparison of luminescence under photoexcitation of avalanche materials through ESA and GSA, the lack of exact knowledge of the pumping intensity within scattering samples remains an open problem.

Another prominent evidence of the scale of quenching is the shortening of the Stokes luminescence lifetime. Stokes emission decays at 800 nm emission were measured and fitted with the mono-exponential decay function y = A₁e^−x/τ, yielding a time decay τ characteristic for the ³H₄ state (Fig. 3(g)). The ET efficiency can be determined based on the Stokes lifetime of the donor emission in the presence (τ_DA) or absence of an acceptor (τ_D) in accordance with the formula, η = (1 − τ_DA/τ_D)·100%. Thus, when considering Nd³⁺ concentrations of 0.1, 0.2, 0.5, and 1%, the ET efficiency of the ³H₄ → ³H₆ transition reaches 25, 39, 60 and 68%, respectively. The relative sensitivity based on the Stokes ³H₄ → ³H₆ emission decay was comparable to the emission intensity variation approach (Fig. 3(i)), and demonstrated relatively low sensitivity (i.e., 0.5 to 1%/1%Nd³⁺) for the 0.1–1% Nd³⁺ concentration range. Measuring the luminescence kinetics in the PA regime would be very informative, but because the looping level energetically falls within the NIR range (1670 nm), a specialized and typically noisy NIR detector is required to measure the emission and emission decays. An alternative method using the pump–probe technique was proposed to probe the looping level lifetime through 800 nm PA emission (Fig. S8, ESI†). Two subsequent pulses (pulse width d = 10 ms) were used with different delay times (δ = 1–70 ms), where the first pulse is responsible for the initial population of the ³F₄ level through GSA. The duration and power of the pulse are sufficient to initiate not only GSA and ESA, but also the CR process, leading to 800 nm emission. Because the ³F₄ level is a reservoir level characterized by decay times of several milliseconds^29,30 and is responsible for preserving some oddment population that has been established with the first pulse, it is capable of facilitating faster and more efficient ESA during the subsequent pulse. Thus, it should show enhanced luminescence intensity despite the pump pulses being equal in terms of energy and pulse width. The ratio I₂/I₁ of the emission intensities induced by these two subsequent pulses - i.e. the intensity in response to the second pulse (I₂) versus the intensity in response to the first one (I₁), collected as a function of the time delay between the two pulses (δ), provides information on how fast the ³F₄ decays (Fig. 3(h)). When the ratio equals 1, there is no enhancement, which indictes that during the delay time between the two pulses, the population of the ³F₄ level decays completely. The I₂/I₁ ratio is called paired pulse facilitation (PPF = I₂/I₁), and was initially used to highlight the similarities between PA materials and biological synapses.¹⁵ The lifetimes of the ³F₄ level obtained from the exponential fitting of the PPF(δ) dependence were investigated for Nd³⁺ concentrations of 0% and 0.1% only. This is because the quenching effect of the Nd³⁺ ions is so strong that even at delay times ranging from 0.1 to 1 ms, samples with higher Nd³⁺ concentrations did not demonstrate any emission intensity facilitation during the subsequent pulse. The lifetime decreases from 13.6 ms (in agreement with other literature results, i.e., 15.25 ms^29,30 for LiYF₄:3%Tm³⁺) down to 5.2 ms upon co-doping with as little as 0.1% Nd³⁺ (S_R = 618%/1%Nd; η = 62%). This is a clear indication of the emergence of the new non-radiative process, which in PA mode is additionally competing with processes such as ESA and CR. These results prove that the population of the ³F₄ looping-level growth is significantly hindered by low acceptor concentrations, resulting in a higher I_th.

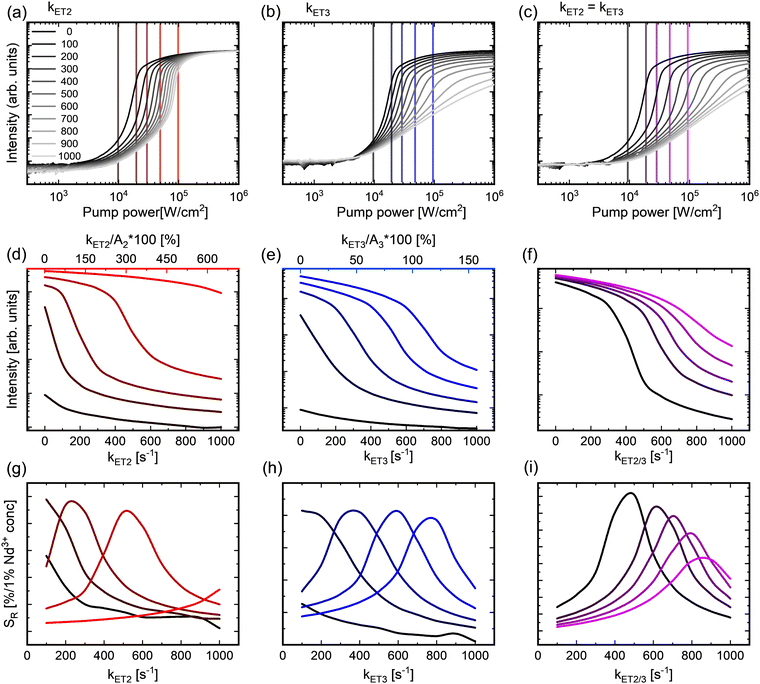
It has been demonstrated that the PA process becomes progressively disrupted in the presence of Nd³⁺ ions, but it is still unclear which specific mechanism underlies the observed changes, namely, whether PA is affected specifically by ET occurring by mechanism Q_I (from looping ³F₄) and/or mechanism Q_II (from emitting ³H₄). Therefore, the differential rate equation (DRE)-based modelling of PA (PADRE) was used to investigate how ET from the looping and emitting levels affects the PA performance (eqn (S1), ESI†). Instead of reproducing the complex and interdependent PA behavior of the Nd³⁺ co-doped LiYF₄:Tm³⁺ system, a simplified PADRE model was employed to describe the PA emission at 800 nm, in which only ³H₆ (ground), ³F₄ (looping), and ³H₄ levels (emissive) of Tm³⁺ and ⁴F_5/2, ⁴I_15/2 and ⁴I_9/2 (ground) Nd³⁺ levels were considered.¹¹ To quantify the interaction between the two ions, the PADRE model was extended with ET from Tm³⁺ to Nd³⁺ by adding k_ET2 and k_ET3 parameters, which denote the nonradiative resonant energy transfer rates from the ³F₄ and ³H₄ levels to the respective ⁴I_15/2 and ⁴F_5/2 Nd³⁺ levels.

Increasing the k_ET2 and k_ET3 factors in the range of 0–1000 s⁻¹ shows how individual ET from either looping, emitting, or both levels affects PA behavior (Fig. 4(a)–(c)). At a first glance, k_ET2 mainly affects the excitation threshold I_th, whereas k_ET3 significantly reduces the intensity and order of nonlinearity of the PA emission. To further investigate the influence of ET at each level on the PA emission, the pump-power-dependent order of nonlinearities was determined (Fig. S9, ESI†). The factor k_ET2 not only increases I_th, but also contributes to the S factor, i.e., the order of nonlinearity. At the same time, k_ET3 does not seem to influence I_th and is mainly responsible for the S_max value decline. Since k_ET3 is a process directly competing with CR, it is clear that it substantially affects the order of nonlinearity. Intriguingly, k_ET2 seems to have an opposite effect on the order of nonlinearity compared to that of k_ET3 (Fig. S9, ESI†). This effect could be attributed to the fact that ET from the looping level contributes to the depopulation of the electrons excited through GSA, which are necessary to initialize PA. However, they are competing with CR at the PA regime. The power-excitation threshold I_th is known to be inversely proportional to the luminescence lifetime of the looping state, which is solely affected by the k_ET2 process. Further analysis of S_max as a function of mechanisms Q_I and Q_II supports (Fig. S10 and S11, ESI†) our hypothesis on the critical role of the looping-level population. Although the PA luminescence risetimes could be a source of additional information, because of the fact that the PA kinetic profiles under pulsed excitation strongly depend on the pump power, and the Nd³⁺ acceptor additionally modifies the PA thresholds significantly, we decided to perform simulations aiming to indicate the direction of changes of the risetimes that can be expected (Fig. S12, ESI†). All three quenching mechanisms, i.e., Q_I (through k_ET2 increase), Q_II (through k_ET3 increase) and Q_III (through simultaneous k_ET2 and k_ET3 increase) make the risetimes shorter and reduce the PA emission intensity in a similar way. The simulations and experimental studies provide evidence for the generic understanding of quenching in PA materials and for further considerations of sensing of homogenous physical fields or quantities (e.g., temperature, pressure), when the homogenous 3D mixture of the donor and acceptor species is considered. The next level of complexity, which is beyond the scope of the current work, should be expected when bio-specific interactions between an avalanching nanoparticle (comprising thousands of interacting Tm³⁺ ions) and the NP surface-bound acceptors is taken into account. In such a case, the volumetric interactions between the looping Tm³⁺ and homogenously incorporated acceptor species are replaced with the interactions of ANP (as an energy donor nanoparticle) and surface-bound acceptors.^31,32

Fig. 4 Simulations of photon avalanche emission intensities in response to different quenching mechanisms and strength. (a)–(c) The pump power-dependent 800 nm PA emission intensities were calculated based on the differential rate equations for varying energy transfer rates (0–1000 s⁻¹) and for scenarios involving ET (a) from the looping state via k_ET2, (b) from the emitting state via k_ET3, and (c) from both states equally with k_ET2 = k_ET3; (d)–(f) the ET rate-dependent PA emission intensities (derived from a–c correspondingly along vertical lines) at fixed power densities of 10, 20, 30, 50 and 100 kW cm² in function of (d) k_ET2,(e) k_ET3 and (f) k_ET2 = k_ET3; the top axes of the (d) and (e) show the relative values as compared to the A₂ and A₃ radiative rates; (g)–(i) the relative, pump power-dependent sensitivities derived from the determined PA emission intensities variation (dervied from d–e correspondingly) as a function of (g) k_ET2,(h) k_ET3 and (i) k_ET2 = k_ET3, respectively.

Similar to the experiments performed, the PADRE model-based simulated PA luminescence intensities (Fig. 4(d)–(f)), as well as the theoretical S_R were determined (Fig. 4(g)–(i)) at fixed power densities (vertical lines in Fig. 4(a)–(c)). The quenching-rate-dependent PA emission intensities monotonically and rapidly decreased in both experiments (Fig. 3(e)) and simulations (Fig. 4(d)–(f)). In addition to understanding the fundamental interactions and susceptibility of PA emissions to the presence and characteristics of quenching strength and mechanism, these results clearly suggest the possibility of exploiting the studied mechanisms for multiple types of sensing. In metrology, the sensitivity and response dynamic range are key features of the transducing element, which are typically fixed. The simulation performed for PA luminescence suggests that the dynamic response range can be adjusted dynamically in situ by adjusting the pump power intensities, while preserving high sensitivity. Such a feature would be extremely valuable in situations where a wide detection range is required. However, experimental data only partially confirm these observations and hypotheses. This inconsistency between the theoretical and experimental S_R can be attributed to the limitations of the simplified three-level model of the donor, where the presence of an acceptor is expressed solely by two additional non-radiative quenching parameters (k_ET2 and k_ET3), which fails to fully replicate the dynamics occurring in the actual LiYF₄:3%Tm³⁺ co-doped with the Nd³⁺ ion system. Moreover, the simulations offer a much wider and ideal dynamic range of the possible populations of the ground and excited levels, whereas typical photodetectors are limited in this respect and are susceptible to background noise and other artifacts. Based on the simulation, both k_ET2 and k_ET3 contribute to the S_R range tunability. Thus, this effect should be further investigated with more bio-relevant acceptors with simple energetic structures, such as dyes, that are capable of absorbing either at 800 nm or 1670 nm.

3. Conclusions

PAs in nanomaterials have attracted increased interest owing to their extreme nonlinearity and the possibility of applying these interesting materials to numerous fields of science and technology. Although the advantages of the PA phenomenon (i.e., threshold behavior and extreme nonlinear response to photoexcitation, NIR to Vis/NIR conversion, etc.) and its target applications (i.e., labels for simple PASSI subdiffractional imaging and data storage, all-optical data reservoir processing, sensing of physical quantities, or chemical species) have been clearly identified, further progress may be hindered without a deeper understanding of the susceptibility of PA to external chemical/physical factors, such as temperature, crystalline host, or quencher type and concentration. Although luminescence quenching in lanthanide-doped (nano)materials has been extensively studied, the unique character of the PA emission stemming from a complex combination of GSA/ESA and energy looping presents more challenges in understanding and managing newly developed materials and metrology with luminescent reporters. Therefore, the impact of energy transfer from photon-avalanching Tm³⁺ ions, either from the looping or emitting states, or both, to intentionally admixed quenching Nd³⁺ ions, was evaluated in LiYF₄ microcrystals. The experiments were planned to purposefully exclude surface effects that typically non-specifically quench the luminescence of conventional nanophosphors and to address specific resonant energy transfer to the acceptor, aiming to mimic the principles behind luminescence (bio)sensing. Interestingly, thulium emission quenching by Nd³⁺ ions significantly differs, depending on the photoexcitation regime: a spectacular 4-order of magnitude PA emission quenching was observed in 1%Nd³⁺ co-doped crystals (800 nm emission under 1059 nm photoexcitation), whereas only 4-fold Tm³⁺ emission (800 nm emission under 475 nm photoexcitation) quenching was observed for the same 3%Tm 1%Nd LiYF₄ microcrystals under Stokes excitation as compared to pristine 3%Tm LiYF₄ microcrystals. Moreover, the experimental data provide evidence of not only significant PA emission intensity quenching, but also a maximum order of nonlinearity reduction and a linear pump power-excitation threshold increase. These studies facilitate our understanding of the generic mechanism behind PA quenching and the critical role of the looping level in PA generation.

In addition to the experimental evaluations, a phenomenological model was developed to determine the nature and strength of this susceptibility in the presence and varying concentrations of quenching species. This modelling indicates that this is mostly the ET from the looping level, which leads to an increase in I_th and S_max, whereas the ET from the emitting state should be associated with a decrease in S_max and a decrease in the final emission intensity in the saturation regime. The extreme susceptibility of PA emission to quenching, compared to Stokes emission, makes the PA phenomenon and PA excitation scheme a novel ultrasensitive sensing mechanism with high and potentially in situ tunable relative sensitivity. Moreover, both experiments and modelling confirmed the previous hypotheses that the extreme susceptibility of PA to quenching may potentially extend its effective (bio)detection range. Even though the resonant energy transfer occurs through Förster mechanism and is governed by the distance power −6 (r⁻⁶) law, it is important to note that a 4-fold luminescence drop in response to quenching by 1%Nd³⁺ in the Stokes mode is equal to the effects achieved in the PA mode (dotted lines in Fig. 3(e)) for as little as 0.08% Nd³⁺. In the first approximation, such a comparison suggests that meaningfully smaller concentrations of acceptors may be detected in PA mode than in the conventional Stokes mode. This suggests that PA luminescence is equally quenched at a D–A distance of 13.83 Å, as the Stokes luminescence with a D–A distance of 6.25 Å – namely, at 2.2-fold longer range. Such effects are advantageous for (bio)chemical sensing, where the length of the molecules responsible for specific biorecognition anchored to the surface of donor nanoparticles present a challenge for ordinary up-converters owing to their relatively large size (typically 20 nm in diameter), lack of inherent biological specificity, and limited effective Förster distance from Ln³⁺ donor ions to organic acceptors. Consequently, the FRET sensitivity is reduced, and most of the advantages of upconverting nanoparticles as luminescence donors for bioassays are not realized.³¹ Moreover, PA luminescence shows a very steep dynamic decline within the 0–0.1% Nd³⁺ concentration range, suggesting it is extremely and unproportionally more sensitive to tiny perturbations. Since the PA process is far more complex than other up-conversion processes, one can deduce that it will surpass this problem by achieving a higher effective Förster distance.³³ Having a photon avalanching donor nanoparticle would thus solve a serious issue of conventional UCNPs-based biosensors, preserving all other advantages that the lanthanide ions and efficient anti-Stokes emission offer, such as narrow band absorption and emission, photo- and chemical stability and non-blinking, as well as anti-Stokes NIR-to-NIR emission. However, one should be aware that the system studied here cannot be simply and directly translated to biosensing schemes. Here, the avalanching and quenching species are homogenously and volumetrically mixed, which differs from typical biosensing scheme where the ANP sensor would contain only avalanching ions and the quenching centers are anchored through biorecognition molecules a few nanometers away from the surface of the avalanching sensor. Mimicking the latter case, non-specific quenching was recently demonstrated in single ANPs by varying passive shell thickness and distance to surface ligands,¹⁴ which agrees with observations and conclusions made by us. The ANP (bio)specific sensors will definitely require the small size of the ANPs to enlarge the surface-to-volume ratio, and quench PA within the (still enhanced) specific interaction radius around the looping ions. Moreover, the appropriate quenching species must be tested, such as QDs, fluorescent dyes or lanthanide complexes. The selection of those available acceptors may redirect efforts to obtain PA in nanoparticles through energy looping levels located in the visible spectral range, where these acceptors have their excited states.

While qualitative correspondence exists between the experiments and modelling (e.g., Fig. 3(e)vs.Fig. 4(d)–(f)), the specific and detailed behaviors differ slightly. For example, the corresponding relative sensitivities S_R based on the simulation were not fully consistent with those based on the experimental data. However, we expect the simulations to show a much broader concentration range than that of the experiments. The capability to in situ tune the sensitivity range – the conclusion which was derived from the modelling, is so far only partially supported by the measurements (Fig. 3(e) and (f), ▲ vs. ■, as compared to Fig. 4(g)–(i), respectively). Alternatively, we assume that some differences between the real Tm–Nd system and the simplified PADRE model occur; for example, the applied PADRE model may not include other factors, such as excited-state absorption by the Nd³⁺ ions, energy cross relaxation between Nd³⁺ ions (at increased Nd³⁺ concentration), or back energy transfer from Nd³⁺ to Tm³⁺, which are currently excluded from the analysis.

Despite their impressively high relative sensitivity (S_R), PA-based sensors still need to address issues related to reproducibility and reliable readout. We assume that the extreme nonlinearity of the PA phenomenon, which defines the suitability of this mechanism for ultrasensitive detection, shows the other side of the coin. In the PA regime, the infinitesimal variation in the pumping intensity (of the light source, but potentially also due to light scattering in the heterogeneous biological samples) may not specifically modulate the output luminescence. This indicates that instabilities in the photoexcitation and photodetection paths are critical for the reproducibility of the readout. Therefore, special care must be taken to ensure the perfectly stable operation of the PA luminescence excitation and detection.

The advantages of PA emission, which were demonstrated and modelled in this work, indicate that the highly nonlinear responsivity has key features that are of great value for the ultrasensitive detection and sensing of physical quantities, chemical environments, and biological reactions. The use of luminescence opens new possibilities for remote, nondestructive, nonelectric/magnetic field interference sensing with simple and robust optical instruments, even at sub-diffraction spatial resolution.² Recent achievements in PA technology and an understanding of this phenomenon may therefore enable the design of photonic chips or complex platforms that combine sensing,⁸ data interpretation,¹⁵ and storage.¹⁶

4. Experimental

Chemicals

The LiYF₄:TmNd microcrystals were prepared using commercially available reagents. Yttrium oxide Y₂O₃ (99.999%) and thulium oxide Tm₂O₃ (99.995%) were purchased from Chemicals 101 Corp. Nd₂O₃ (99.99%) and ammonium fluoride NH₄F (≥98.0%) were purchased from Sigma Aldrich. Ethanol (96% pure p.a.) was purchased from POCH S.A. Lithium fluoride LiF and EDTA ≥99% (Ethylenediaminetetraacetic acid) were purchased from POL-AURA.

Synthesis protocol

LiYF₄:Tm³⁺Nd³⁺ microcrystals were synthesized according to a previously published hydrothermal synthesis method, with some modifications.³⁴ First, 20 mmol of RE(NO₃)₃ (Y(NO₃)₃, Tm(NO₃)₃ and Nd(NO₃)₃) was dissolved in 15 mL of distilled water, and added dropwise to 15 mL of a 1.06 g EDTA solution. The mixture was stirred vigorously at room temperature for 1 h. Simultaneously, 20 mmol LiF and 60 mmol NH₄F were mixed with 30 mL distilled water. The RE-EDTA solution was then added dropwise to the fluoride solution under vigorous stirring. The thick white mixture was then stirred for 30 min and transferred to a 100 mL Teflon-lined autoclave. Synthesis was performed for 12 h at 200 °C. The resulting microcrystals were separated from the supernatant, and washed with distilled water and ethanol in an ultrasonic bath. The product was then dried on a hot plate at 100 °C for 1 h.

Experimental details

Pump-power-dependent PA measurements were conducted under a 1059 nm excitation source (single fiber laser diode) on a custom optical setup (Fig. S3, ESI†) consisting of an inverted microscope (Nikon Ti2 Eclipse), two photomultiplier tubes (PMT, PMT1001M, PMT2001M, Thorlabs), and a photon counter (quTAG, quTools). An arbitrary waveform generator (AWG Handyscope5, TiePie) controlling the laser diode voltage was used for the pump–probe experiments. The PA spectra were collected using a commercial Czerny–Turner spectrometer (Shamrock 500i). The Stokes spectra and emission decay were measured using a commercial Czerny–Turner photoluminescence spectrometer (FLS1000, Edinburgh Instruments). A more detailed description is provided in ESI.†

Data modelling

The simulations were executed using custom MATLAB code. PADRE equations were developed and studied in ref. 11 and expanded here to account for the RET between Tm and Nd (eqn (S1), ESI†), utilized to reproduce the nonlinear PA behavior and emission quenching.

Author contributions

Scientific concepts, ideas, and experimental designs were the result of interactions and discussions between the authors. M. Mi synthesized and characterized these particles. M. Ma performed all spectroscopic measurements, as well as modelling, analyses and prepared the draft of figures and manuscript. A. B. conceived the idea, provided resources & funding, and contributed to analyses, software development and modelling. All authors wrote, reviewed and edited the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors declare that they have no competing interests. This research was funded in whole by the 2021/43/B/ST5/01244 project funded by the National Science Center, Poland. All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† The authors are grateful to Mrs E. Bukowska and Dr D. Szymański for XRD and SEM measurements.

References

1. J. S. Chivian, W. E. Case and D. D. Eden, Appl. Phys. Lett., 1979, 35, 124–125.
2. C. Lee, E. Z. Xu, Y. Liu, A. Teitelboim, K. Yao, A. Fernandez-Bravo, A. M. Kotulska, S. H. Nam, Y. D. Suh, A. Bednarkiewicz, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2021, 589, 230–235.
3. Y. Liang, Z. Zhu, S. Qiao, X. Guo, R. Pu, H. Tang, H. Liu, H. Dong, T. Peng, L. D. Sun, J. Widengren and Q. Zhan, Nat. Nanotechnol., 2022, 17, 524–530.
4. H. Deng, S. Yang, S. Xiao, H. M. Gong and Q. Q. Wang, J. Am. Chem. Soc., 2008, 130, 2032–2040.
5. C. Chen, L. Ding, B. Liu, Z. Du, Y. Liu, X. Di, X. Shan, C. Lin, M. Zhang, X. Xu, X. Zhong, J. Wang, L. Chang, B. Halkon, X. Chen, F. Cheng and F. Wang, Nano Lett., 2022, 22, 7136–7143.
6. A. B. Kostyuk, A. D. Vorotnov, A. V. Ivanov, A. B. Volovetskiy, A. V. Kruglov, L. M. Sencha, L. Liang, E. L. Guryev, V. A. Vodeneev, S. M. Deyev, Y. Lu and A. V. Zvyagin, Nano Res., 2019, 12, 2933–2940.
7. E. P. Santos, C. V. T. Maciel, R. F. da Silva, D. F. Luz, J. F. Silva, C. Jacinto, L. J. Q. Maia, F. G. Rego-Filho and A. L. Moura, J. Lumin., 2022, 245, 118645.
8. Z. Korczak, M. Dudek, M. Majak, M. Misiak, Ł. Marciniak, M. Szalkowski and A. Bednarkiewicz, Low Temp. Phys., 2023, 49, 322.
9. H. Qian, T. Zhang, X. Jiang, H. Wang, W. Yang and C. Li, J. Mater. Sci.: Mater. Electron., 2022, 33, 22718–22727.
10. L. Marciniak, A. Bednarkiewicz and K. Elzbieciak, J. Mater. Chem. C, 2018, 6, 7568–7575.
11. M. Dudek, M. Szalkowski, M. Misiak, M. Ćwierzona, A. Skripka, Z. Korczak, D. Piątkowski, P. Woźniak, R. Lisiecki, P. Goldner, S. Maćkowski, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Adv. Opt. Mater., 2022, 10, 2201052.
12. A. Bednarkiewicz, E. M. Chan, A. Kotulska, L. Marciniak and K. Prorok, Nanoscale Horiz., 2019, 4, 881–889.
13. D. Denkova, M. Ploschner, M. Das, L. M. Parker, X. Zheng, Y. Lu, A. Orth, N. H. Packer and J. A. Piper, Nat. Commun., 2019, 10, 1–12.
14. K. W. C. Kwock, C. Lee, A. Teitelboim, Y. Liu, K. Yao, S. B. Alam, B. E. Cohen, E. M. Chan and P. J. Schuck, J. Phys. Chem. C, 2021, 125(43), 23976–23982.
15. A. Bednarkiewicz, M. Szalkowski, M. Majak, Z. Korczak, M. Misiak and S. Maćkowski, Adv. Mater., 2023, 2304390.
16. C. Lee and P. J. Schuck, Annu. Rev. Phys. Chem., 2023, 74, 415–438,  DOI:10.1146/annurev-physchem-082720-032137.
17. P. Kumar, S. Singh and B. K. Gupta, Nanoscale, 2016, 8, 14297–14340.
18. M. Dudek, M. Szalkowski, M. Misiak, M. Ćwierzona, A. Skripka, Z. Korczak, D. Piątkowski, P. Woźniak, R. Lisiecki, P. Goldner, S. Maćkowski, E. M. Chan, P. J. Schuck and A. Bednarkiewicz, Adv. Opt. Mater., 2022, 2201052.
19. M. F. Joubert, S. Guy, B. Jacquier and C. Linarés, Opt. Mater., 1994, 4, 43–49.
20. M. F. Joubert, Opt. Mater., 1999, 11, 181–203.
21. A. Skripka, M. Lee, X. Qi, J.-A. Pan, H. Yang, C. Lee, P. J. Schuck, B. E. Cohen, D. Jaque and E. M. Chan, Nano Lett., 2023, 23, 7100–7106.
22. Z. Zhang, A. Skripka, J. C. Dahl, C. Dun, J. J. Urban, D. Jaque, P. J. Schuck, B. E. Cohen and E. M. Chan, Angew. Chem., Int. Ed., 2023, 62, e202212549.
23. A. Teitelboim, B. Tian, D. J. Garfield, A. Fernandez-Bravo, A. C. Gotlin, P. J. Schuck, B. E. Cohen and E. M. Chan, J. Phys. Chem. C, 2019, 123, 2678–2689.
24. A. Bednarkiewicz, E. M. Chan and K. Prorok, Nanoscale Adv., 2020, 2, 4863–4872.
25. C. Lee, E. Z. Xu, K. W. C. Kwock, A. Teitelboim, Y. Liu, N. Fardian-Melamed, C. C. S. Pedroso, H. S. Park, J. Kim, S. D. Pritzl, S. H. Nam, T. Lohmueller, P. Ercius, Y. D. Suh, B. E. Cohen, E. M. Chan and P. J. Schuck, Nature, 2023, 618, 951–958.
26. A. Bednarkiewicz, D. Wawrzynczyk, M. Nyk and W. Strek, Opt. Mater., 2011, 33, 1481–1485.
27. A. Aleksandrovich. Kaminskiĭ, Crystalline lasers: physical processes and operating schemes, CRC Press, 1996.
28. S. Guy, M. Joubert and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 8240.
29. U. Demirbas, J. Thesinga, M. Kellert, F. X. Kärtner and M. Pergament, Opt. Mater. Express, 2022, 12, 4712.
30. U. Demirbas, U. Demirbas, J. Thesinga, E. Beyatli, M. Kellert, M. Pergament, F. X. Kärtner, F. X. Kärtner and F. X. Kärtner, Opt. Express, 2022, 30, 41219–41239.
31. A. Pilch-Wrobel, A. Kotulska, S. Lahtinen, T. Soukka and A. Bednarkiewicz, Small, 2022, 18, 2200464.
32. A. M. Kotulska, A. Pilch-Wróbel, S. Lahtinen, T. Soukka and A. Bednarkiewicz, Light: Sci. Appl., 2022, 11, 1–14.
33. A. Bednarkiewicz, E. M. Chan and K. Prorok, Nanoscale Adv., 2020, 2, 4863–4872.
34. Z. Qiu, S. Wang, W. Wang and S. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 29835–29843.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00362d

---