Covalency-aided electrochemical CO2 reduction to CO on sulfide-derived Cu–Sb†
Daniel Yong Yi
Goh
 ab,
Kah Meng
Yam
de,
Lavie
Rekhi
ab,
Kah Meng
Yam
de,
Lavie
Rekhi
 d,
Albertus Denny
Handoko
d,
Albertus Denny
Handoko
 c,
Ying Chuan
Tan
c,
Ying Chuan
Tan
 c,
Yong
Wang
c,
Yong
Wang
 a,
Joel Ming Rui
Tan
af,
Tej Salil
Choksi
a,
Joel Ming Rui
Tan
af,
Tej Salil
Choksi
 *de,
Yanwei
Lum
*de,
Yanwei
Lum
 *b and
Lydia Helena
Wong
*b and
Lydia Helena
Wong
 *af
*af
aSchool of Materials Science and Engineering, Nanyang Technological University, 639798, Singapore. E-mail: lydiawong@ntu.edu.sg
bInstitute of Materials Research and Engineering, Agency for Science, Technology and Research, 138635, Singapore. E-mail: lumyw@nus.edu.sg
cInstitute of Sustainability for Chemicals, Energy and Environment, Agency for Science, Technology and Research, 138635, Singapore
dSchool of Chemistry, Chemical Engineering and Biotechnology, Nanyang Technological University, 637459, Singapore. E-mail: tej.choksi@ntu.edu.sg
eCambridge Centre for Advanced Research and Education in Singapore, 138602, Singapore
fSingapore-HUJ Alliance for Research and Enterprise (SHARE), Campus for Research Excellence and Technological Enterprise (CREATE), 138602, Singapore
First published on 22nd December 2023
Abstract
p-Block dopants like sulfur have been shown to break scaling relations in the electrocatalytic CO2 reduction reaction (CO2RR) by providing alternative binding sites with altered *CO binding energy. However, most sulfide-derived catalysts reported to date tend to produce formate or hydrogen during the CO2RR by shifting the reaction pathway away from C-bound intermediates. In this work, we discovered highly selective CO production on a bimetallic Cu–Sb–S derived catalyst. The high CO selectivity is in contrast with the individual control samples of CuSx and SbSx that demonstrate a preference towards the formate product. Interestingly, different starting phases and atomic ratios of Cu–Sb–S affect the CO2RR selectivity. Post-catalysis characterization coupled with DFT calculations indicates that the key enabler towards CO formation is the substitution of Sb sites with sulfur which improves *COOH binding relative to *CO, breaking scaling relations and facilitating subsequent CO (g) formation. The highest CO production of FECO = 80.5% was observed on the tetrahedrite Cu–Sb–S-derived sample at −1.0 V RHE with 37.6 mA cm−2 geometric partial current density.
Introduction
As part of the energy transition to renewable energy, efforts are underway to decarbonize industry. Electrocatalysis is regarded as a key solution to this issue, with ongoing research efforts in electrochemical CO2 reduction (CO2RR) to decarbonize the chemical and polymer industries. Carbon monoxide (CO) in particular is a crucial intermediate for the formation of value-added chemicals such as ethylene, methanol (via the hydrogenation reaction),1 and synthetic diesel/kerosene (via the Fischer–Tropsch process).2,3 Currently, CO is produced as part of syngas, made from the gasification of coal or steam reforming of methane which can then be further processed or hydrogenated to form useful chemicals. However, this introduces fossil carbon into the carbon cycle which contributes to global warming. As part of the electrification of the energy system via renewables, such products should be produced via electrolysis or otherwise clean processes. Electrochemical CO2 reduction is an emerging solution to produce chemicals via the recycling of waste CO2 from hard-to-abate sectors such as steel and cement, where the main profitable products currently are CO and HCOO−.4,5 However, the state-of the-art CO2RR catalysts for CO production, made from Ag or Au, are costly. This has spurred a search for cheaper catalysts with high CO selectivity.Modification of the catalyst oxidation state and composition has been instrumental in achieving the desired catalytic selectivity. Oxide-derived catalysts, for example, have been shown to boost selectivity for liquid products.6 However, the exact mechanism of selectivity improvements is still highly debated.7–10 Other interesting examples of modification include bimetallics and catalysts with p-block dopants.11–14 In particular, sulfide-derived catalysts have been widely reported to promote HCOO−.15–17 Among them, the CuSx-derived catalyst system is an interesting case because the sulfide-derived variation changes the selectivity of the Cu metal completely, from CO (and C2+) to HCOO−.18–22 The selectivity switch has been attributed to the presence of remnant surface sulfur, which weakens M–C binding, in turn favouring the H2 evolution reaction (HER).23–25 This weakening effect seems to be observed also on other metals with p-block dopants, especially those metals with relatively strong *CO binding.
The M–C behaviour is more convoluted when metals with weaker *CO binding are doped with p-block elements. For example, Kim's group found that p-block dopants did not affect *COOH and *CO equally on the Ag surface.26 In an ideal case, this unusual scaling relation violation could be exploited to enhance the CO2RR to CO (g), by selecting dopants that would lead to stronger *COOH while allowing weaker *CO binding. However, controlling the p-block dopant content down to the level predicted by the theoretical calculation is challenging, due to the facile formation of stoichiometric compounds.27 Unfortunately, excessive p-block element content often results in increased *H coverage leading to prominent H2 evolution (HER).20,28 Thus, high performance CO2RR to CO demonstration on p-block doped metals with relatively weaker *CO binding (e.g., Ag/Au/Zn) is usually performed in non-aqueous electrolytes.29,30
As a different strategy, we propose that p-block dopants can be introduced into alloys of strong and weak *CO binding metals. Bimetallic post transition metal alloys with Cu such as Cu–In, Cu–Sn, or Cu–Sb are prime targets for this investigation, as there are many stoichiometric ternary phases that can be exploited to control the p-block element fraction. Additionally, these alloys have shown some CO2RR intrinsic activity in aqueous electrolyte.31–33 We hypothesise that the considerably different *CO binding strength in the metal pair may resist the HER boosting seen on many single metal systems, as the p-block dopants may be stabilised only on certain favourable sites. Additionally, the doping content can be further reduced, as the leaving group and gases can be evolved under cathodic conditions.
With these considerations in mind, we selected Cu–In, Cu–Sn, and Cu–Sb as possible base alloys and sulfur (S) as the p-block dopant to construct suitable pre-catalysts for the CO2RR. We found Cu–Sb–S to be more suitable for the CO2RR compared to Cu–In–S and Cu–Sn–S, as the latter systems are very difficult to reduce and remain in the semiconductive sulfide form after 45 min at −1.0 V vs. the reversible hydrogen electrode (RHE; all potentials are reported against RHE). Cu–Sb–S is also a suitable system as there are multiple stoichiometric phases that can be exploited to modulate the metal and p-block element ratio (Fig. S17†), providing an effective d-band centre tuning knob.
More interestingly, we found that tetrahedrite phase (TH; Cu12Sb4S13) derived Cu–Sb outperformed the control Cu–Sb bimetallic for CO production. DFT calculations reveal that the substitution of Sb with S improves the energetics of CO formation. An optimal CO faradaic efficiency (FE) of about 80.5% on a TH-derived catalyst was obtained at an applied voltage of −1.0 V vs. the reversible hydrogen electrode (RHE; all potentials are reported against RHE unless stated).
Results and discussion
Material screening
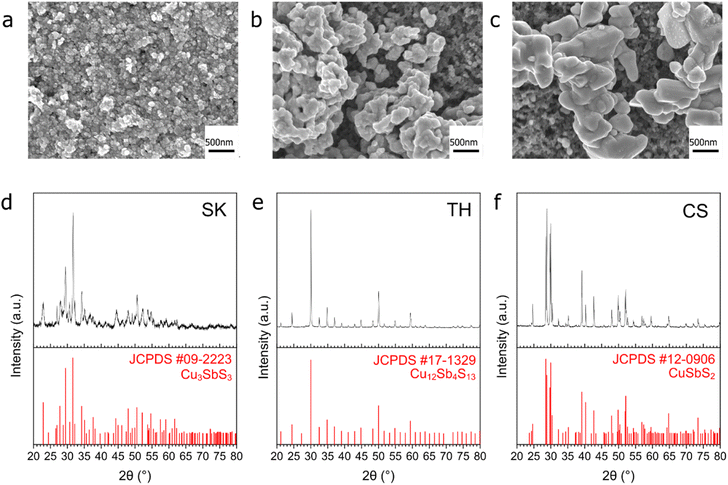
We first synthesized the sulfides of Cu–In, Cu–Sn, and Cu–Sb. The preliminary CO2RR at −1.0 V found that H2 and HCOO− were the major products on Cu–In–S and Cu–Sn–S (Fig. S1a†), while some CO was observed on Cu–Sb–S. Post catalysis X-ray diffraction (XRD) analysis of these compounds revealed that Cu–In–S and Cu–Sn–S were unreduced (Fig. S1b and c†), while Cu–Sb–S was reduced completely to Cu–Sb (Fig. S1d†). As both Cu–Sn–S and Cu–In–S were not reduced during the CO2RR and generate primarily H2 and HCOO−, we focused on Cu–Sb–S for this study.Characterization of Cu–Sb–S phases
Three Cu–Sb–S phases, skinnerite (SK; Cu3SbS3), tetrahedrite (TH; Cu12Sb4S13), and chalcostibite (CS; CuSbS2) were synthesized using a one-pot heat-up synthesis method34 to observe the effect of atomic composition on CO2RR selectivity. XRD characterization confirms the identity of the respective phases (Fig. 1d–f). Field emission scanning electron microscopy (FE-SEM) showed distinct morphologies with particle size in the order of SK < TH < CS (Fig. 1a–c and S2†). In terms of length, SK showed nanoplates on the order of tens of nm, TH showed agglomerated particles of about 100 nm, while CS has the largest particle size at about 500 nm to 1 μm.We then analysed the elemental composition of our samples using energy-dispersive X-ray spectroscopy (EDX) and X-ray photoelectron spectroscopy (XPS) (Fig. 2, S3, and S4†). The elemental composition of our samples before reduction is close to the stoichiometric ratios, thus confirming the successful synthesis of Cu–Sb–S catalysts. XPS analysis showed two distinct species of Cu, Sb, and S each which originate in the catalyst. We attribute the two Cu species to major Cu+ and minor Cu2+ (due to surface oxidation), the two Sb species to major Sb3+ and minor Sb–O (due to surface oxidation), and the two S species to S2− and adsorbed dodecanethiol (the sulfur source used for synthesis).35,36
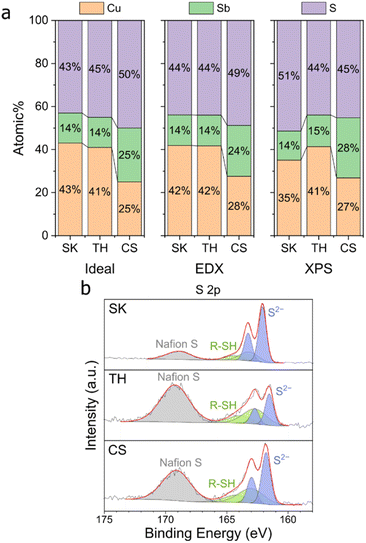 | ||
| Fig. 2 EDX and XPS characterization of the samples before reduction. (a) elemental composition of samples on carbon paper. (b) XPS S 2p peaks of the samples on carbon paper. | ||
Electrochemical performance of Cu–Sb–S phases
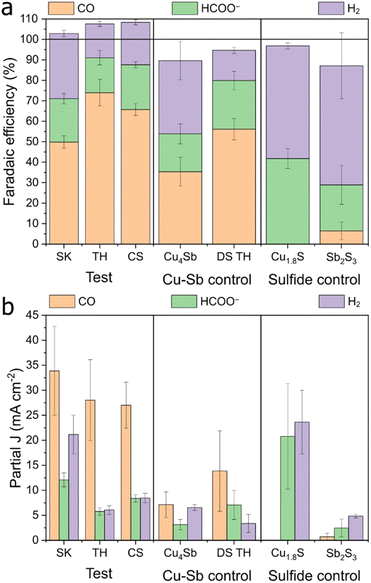
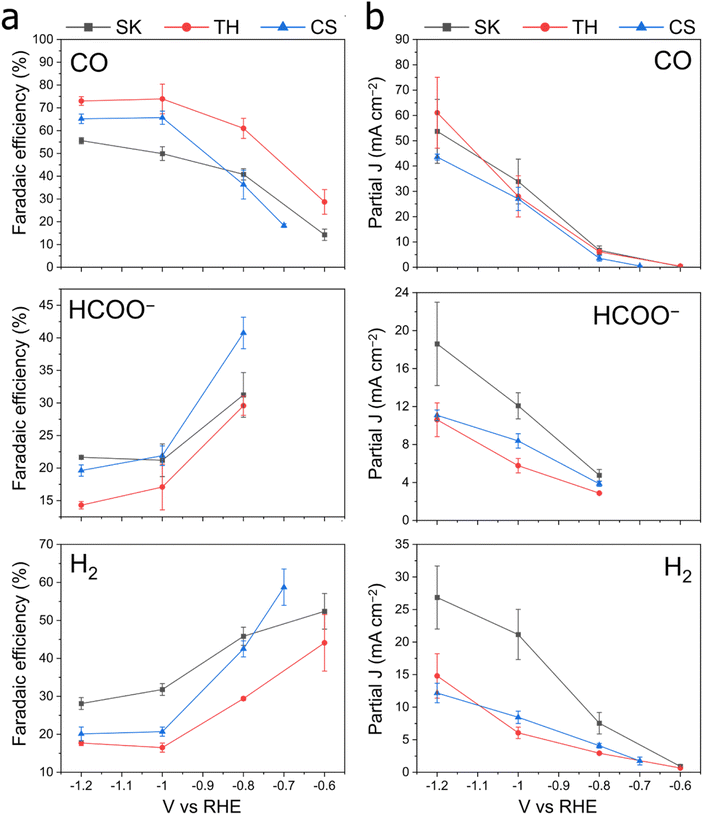
We tested the synthesized Cu–Sb–S phases as catalysts by airbrushing the catalyst ink onto a GDE and testing it in a three-compartment flow cell with 1 M KHCO3 electrolyte. It was found that all Cu–Sb–S catalysts (SK, TH, and CS) produced a substantial amount of CO (FECO ≈ 50–75%) at −1.0 V (Fig. 3). This is in contrast with the pure metal sulfide control samples of Cu1.8S and Sb2S3 (characterisation in Fig. S5†), where HCOO− is the dominant CO2RR product as also seen in Fig. 3, in line with the literature.18–20 While we note that the CuSb alloy also produces a fair amount of CO (FECO ≈ 35%), Cu–Sb–S catalysts significantly outperform the CuSb alloy in terms of CO production; hence, the S chalcogen may be responsible for boosting the catalytic activity.We then proceeded to test the Cu–Sb–S catalysts for CO2 reduction in a wider potential range, from the onset potential to −1.2 V. The full electrochemical CO2RR results are shown in Fig. 4. We found that FECO increases with more cathodic potentials and reaches a maximum of 60 to 80% at a potential of −1.0 to −1.2 V. These high efficiencies contrast with FEH2 and FEHCOO−, which decreased at more cathodic potentials to <30% each at −1.0 to −1.2 V. We also performed a constant current CO2RR measurement at 200 mA cm−2 where the catalysts retain >60% faradaic efficiency (Fig. S6†). The TH catalyst demonstrated good stability over a period of 24 h, with stable FECO in the 60–80% range (Fig. S7†). We obtain a maximum FECO of 80.5% at an applied voltage of −1.0 V for the TH sample, which is comparable with the literature maximum FECO of 80–95% for Cu–Sb materials (Table S1†). We note however, that the literature reports of Cu–Sb are not pristine (deposited on Cu nanowires)37 or not well-mixed (galvanic-displaced or composites)38,39 and may not be accurate sulfur-free reference standards to compare our samples against. It may be that if both structural control and sulfur doping are simultaneously engineered, an even better Cu–Sb-based catalyst performance can be achieved. Our best-performing TH had a geometric partial current density of CO of about 37.6 mA cm−2 at −1.0 V in a 1 M KHCO3 GDE flow cell, which is approximately seven times that of literature values of ∼5 mA cm−2 at the same voltage in 0.1 M KHCO3 H-type cells (Table S1†). We note that this is partially due to a difference in cell type (GDE flow cell vs. H-cell) and electrolyte concentration; thus the increase in current density due to only the catalyst would be smaller. Current densities of HCOO− and H2 at −1.0 V for the TH catalyst were 5.7 mA cm−2 and 6.0 mA cm−2 respectively.
The onset potential for CO formation is −0.6 V for the Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb 3
Sb 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phases (SK and TH) and −0.7 V for the Cu
1 phases (SK and TH) and −0.7 V for the Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sb 1
Sb 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 phase (CS). Electrochemically active surface area (ECSA) measurements were performed on the samples after pre-reduction (Fig. S8 and S9†), which show that SK and TH have similar total current densities when normalized to the active surface area (by adding up the total J in Fig. 3 and dividing by the double layer capacitances). The double layer capacitance showed SK > TH ≫ CS, which is approximately in the reverse order compared to the particle size seen in FE-SEM.
1 phase (CS). Electrochemically active surface area (ECSA) measurements were performed on the samples after pre-reduction (Fig. S8 and S9†), which show that SK and TH have similar total current densities when normalized to the active surface area (by adding up the total J in Fig. 3 and dividing by the double layer capacitances). The double layer capacitance showed SK > TH ≫ CS, which is approximately in the reverse order compared to the particle size seen in FE-SEM.
To investigate the kinetics of the reaction, Tafel slopes of the current density readings were plotted as shown in Fig. 5. The best performing TH catalyst had a lower Tafel slope of 104 mV dec−1 compared to the other two catalysts which each registered 118 mV dec−1. According to the literature, an ideal Tafel slope of 120 mV dec−1 corresponds to an electron transfer step as the rate-determining step: * + CO2 + e− → *CO2−.40 Conversely, an ideal Tafel slope of 60 mV dec−1 corresponds to a protonation step as the rate-determining step: *CO2− + H+ → *COOH. Based on the Tafel slopes, it is possible that although the electron transfer step is the main rate-determining step, some reaction sites on the TH sample might have better kinetics with the protonation step as the rate-determining step, resulting in better CO faradaic efficiency.
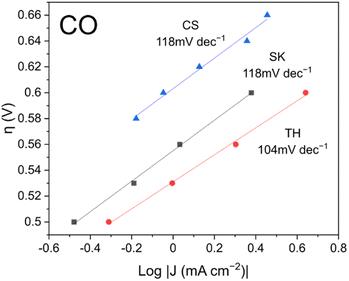 | ||
| Fig. 5 CO Tafel slopes of the catalysts. Catalysts were pre-reduced for 5 min at −1.0 V vs. RHE prior to the experiment. | ||
Post-reduction characterization and remnant sulfur
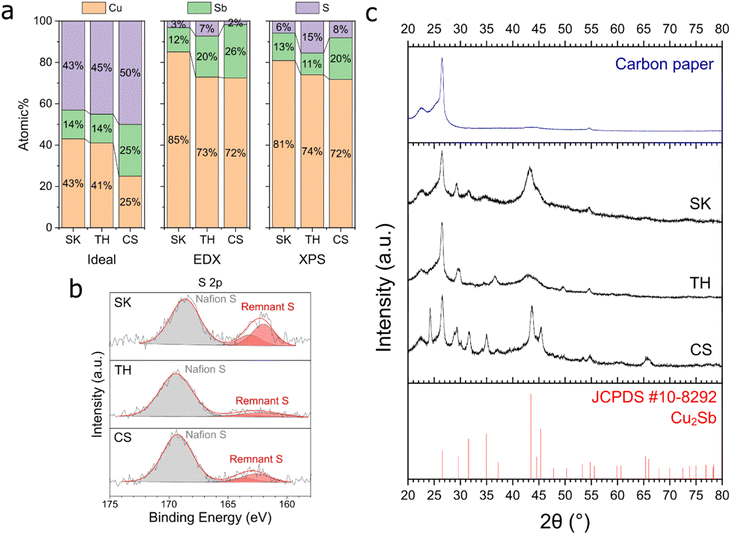
CV scans were performed on the three Cu–Sb–S phases to determine the reduction potential of these samples (Fig. S10†). From the inflection point of the cathodic sweep first derivative,41,42 the reduction potentials of our samples (−0.55, −0.60, and −0.70 V for SK, TH, and CS respectively, Fig. S11†) were determined to be the same or more positive than the CO2RR to CO onset (between −0.6 and −0.7 V, Fig. 4), indicating that the CO2RR to CO occurs after the reduction process of the sulfide phases.The observation that sulfide reduction occurs before the CO2RR onset is corroborated by EDX and XPS analyses post-reduction at −1.0 V (Fig. 6). A drastic decrease in the S at% was observed on all samples. Interestingly, only a small Sb at% decrease was detected. One reason for this could be because Sb forms a stable alloy with Cu, and thus it is not as easily leached compared to S. This proposition is supported by further ICP measurements of the electrolytes collected post reduction, showing that Sb had been leached at a similar rate to Cu (Table S2†), possibly due to surface reconstruction.43
Post catalysis XPS (Fig. S13†) showed that Cu2+ satellite peaks appeared and the oxidized Cu2+ and Sb–O peaks are noticeably enlarged, while the original Sb3+ peaks at approx. 529.5 eV completely disappeared. The presence of oxidized Cu and Sb is likely due to surface reoxidation as the XPS measurements were performed ex situ. The presence of O in EDX and XPS most likely originated from catalyst re-oxidation post-electrolysis (Fig. S12 and S13†). We excluded O in our elemental composition analysis due to the large variation of oxygen content between samples.
As a result of the drastic decrease in sulfur content in the catalysts after electrochemical reduction, the active phase of our catalysts should thus be regarded as Cu–Sb alloys with remnant sulfur atoms as defects. XRD results (Fig. 6c) also showed that the dominant crystalline phase present after reduction was Cu2Sb, supporting the assignment of this phase as the active surface during the electrochemical CO2RR.
Taking the XRD data together with EDX and XPS in Fig. 6, the S and Sb amounts appear to be correlated with the crystallinity/crystallite size of the samples. The CS sample with higher Sb composition showed much smaller full-width half maximum (FWHM) peaks compared to SK and TH. TH also shows particularly broad Cu2Sb peaks, which is proposed to be linked to much higher S content. Post-reduction selected area electron diffraction (SAED, Fig. S14†) results showed very diffuse peaks that correspond to the XRD data. SEM micrographs of the catalysts after reduction showed no major changes on the micrometre scale (Fig. S15†), while TEM images of the catalysts after reduction (Fig. S16†) showed small crystallite size on the order of a few nm that corroborates the XRD findings above.
Rietveld refinement of SK detected phase segregation of Cu2Sb and Cu (Fig. S18 and Table S3†). We posit that our SK sample contains a mixture of two phases, an S-doped Cu–Sb phase and an S-doped Cu rich phase as predicted by the phase diagram (Fig. S17†). As S-doped Cu has been shown to prefer HCOO− and H2 production in the literature,18–22 it is expected that the SK catalyst shows lower CO selectivity. Conversely, TH and CS catalyst compositions are closer to the Cu2Sb alloy region, which imply lower S-doped Cu content. Thus, a lower Cu amount may be advantageous to avoid Cu phase segregation and thus suppress H2 and HCOO−. This is supported by the control experiments on Cu1.8S that show a majority of H2 and HCOO− products (Fig. 3a).
DFT calculations
Density functional theory (DFT) provides a theoretical framework for understanding the structure–activity relations of Cu–Sb–S. This information can help guide the design of experiments and catalysts for CO2 reduction and improve our understanding of how these materials work. We first determine the stability of sulfur atoms in the parent phases, i.e., tetrahedrite (TH), chalcostibite (CS), and skinnerite (SK) and identify the likely contributors for improved catalytic performance.Post-electrochemical characterisation showed significant removal of sulfur in the three parent phases. The TH phase retains the largest amount of S (7% from EDX; 15% from XPS), which is about double that in SK (3% from EDX; 16% from XPS) and in CS (2% from EDX; 8% from XPS). We then calculated the energy penalty to form a sulfur vacancy according to eqn (S1) (ESI Section S5.2)† in primitive cells of bulk TH, CS and SK. This energy penalty reflects the likelihood of sulfur being retained in the structures. We find that the energy penalty trends as TH (5.46 eV) > CS (5.33 eV) > SK (5.23 eV) with sulfur being most strongly bound in the TH phase. This trend is consistent with the experiments wherein the TH phase retains the highest percentage of sulfur after electrochemical tests.
Characterization studies after electrochemical testing indicated that the active phase during the 2e−-CO2RR is tetragonal Cu2Sb of space group P4/nmm. We calculated the Cu2Sb primitive cell lattice parameters (a = b = 3.98 Å, c = 6.09 Å, α = β = γ = 90°) and obtained good agreement with literature values (a = b = 4.00 Å, c = 6.10 Å, α = β = γ = 90°).44 Surface energies calculated for various Cu2Sb facets presented in Table S6† indicate that the (100) surface is the lowest energy facet. To simulate the catalytic active phases of Cu–Sb–S having low sulfur content, we considered nine active site motifs (Fig. S19b and c†) based on pristine Cu2Sb(100), with sulfur adatoms and substitutionally doped sulfur in the topmost and next atomic layer.
Due to possibilities of S-removal, we also considered three active site motifs with copper and antimony vacancies at the Cu1, Cu2 and Sb1 sites (Fig. S19a†). We hence first investigated the stability of sulfur-decorated and vacancy surface motifs (ESI Section S5.2†). We found that SCu3@Cu2Sb(100) is not likely to be stable under operating conditions (Table S4†) and hence will not be considered further.
Then, we tested the adsorption of the four key intermediates: *H, *COOH, HCOO* and *CO involved in the 2e-CO2RR (additional details in ESI Section S5.4†). By comparing the adsorption energies on all surfaces against those on Cu2Sb(100) (Table S5†), seven surfaces (SCu3@Cu2Sb(100), SCu3Sb@Cu2Sb(100), SCu1/Cu2Sb(100), SCu2/Cu2Sb(100), SSb1/Cu2Sb(100), SSb2/Cu2Sb(100), and VCu2/Cu2Sb(100)) bind *CO less strongly than both Cu (111) and Cu2Sb (100). It has been demonstrated that CO2RR catalysts that are selective towards the 2e− products experimentally possess a *CO binding energy that is weaker than that on Cu(111).45 The weaker binding of *CO on the seven surfaces will promote *CO desorption rather than further reduction to *CHO or *COH. Since the CS, SK, and TH samples showed a high selectivity towards the 2e-CO2RR products even at a more negative applied voltage of −1.2 V, these seven active site motifs are more likely to be present in the catalytic active Cu–Sb–S phases.
With the remaining seven active site motifs, we employ a selectivity analysis towards CO or HCOOH formation similar to that adopted by Tang et al.24 (additional details in ESI Section S5.5†). Essentially, a motif that provides a larger driving force for *COOH formation (ΔR1G in eqn (S10)†) than for HCOO* (ΔR2G in eqn (S11)†) is selective towards the CO pathway. If the converse is true, the active site is more selective towards HCOOH. Another important consideration is the availability of H* for the formation of HCOO*. This availability of H* is given by using eqn (S12).† One can thus use ΔR1G − ΔR2G as a descriptor: a negative (positive) value indicates a larger driving force for the CO (HCOOH) pathway. The values for ΔR1G, ΔR2G, ΔR1G − ΔR2G and ΔR3G for the seven relevant active site motifs are in Table 1 while the values for all site motifs considered in this work are in Table S8.†
| Surface structure | ΔR1G (eV) | ΔR2G (eV) | ΔR1G − ΔR2G (eV) | ΔR3G (eV) |
|---|---|---|---|---|
| Cu(111) | −0.42 | −0.28 | −0.15 | −1.17 |
| Cu2Sb(100), reference | −0.34 | 0.14 | −0.48 | −1.05 |
| SCu3@Cu2Sb(100) | −0.30 | 0.36 | −0.66 | −0.92 |
| SCu3Sb@Cu2Sb(100) | −0.15 | 0.24 | −0.39 | −0.86 |
| SCu1/Cu2Sb(100) | −0.04 | 0.32 | −0.36 | −0.78 |
| SCu2/Cu2Sb(100) | −0.27 | 0.38 | −0.65 | −0.91 |
| SSb1/Cu2Sb(100) | −0.23 | 0.15 | −0.38 | −0.94 |
| VCu2/Cu2Sb(100) | −0.25 | 0.33 | −0.58 | −1.08 |
| SSb2/Cu2Sb(100) | −0.71 | −0.15 | −0.56 | −0.99 |
At an operating potential of −1.0 V, all seven Cu2Sb-based motifs indicate that the formation of *COOH is thermodynamically favourable. We found that Cu2Sb(100) is more selective towards CO formation as compared to Cu(111) due to a more negative ΔR1G − ΔR2G value. ΔR1G − ΔR2G values on the other seven motifs are negative, indicating that the CO pathway is thermodynamically favoured. In fact, the ΔR1G − ΔR2G values on SCu3@Cu2Sb(100), SCu2/Cu2Sb(100), VCu2/Cu2Sb(100), and SSb2/Cu2Sb(100) are more negative than that on Cu2Sb(100). The higher CO selectivity in Cu2Sb-based motifs can be ascribed to a weaker H* adsorption, which leads to a more positive ΔR2G value and thus a more negative ΔR1G − ΔR2G value. One finds that H* adsorption is 0.12 eV weaker on Cu2Sb(100) than on Cu(111) and this H* adsorption strength can be further modulated by the presence of sulfur. In fact, we noticed that the presence of sulfur in the six S-decorated motifs (i.e., SCu3@Cu2Sb(100), SCu3Sb@Cu2Sb(100), SCu1/Cu2Sb(100), SCu2/Cu2Sb(100), SSb1/Cu2Sb(100), and SSb2/Cu2Sb(100)) further weakens *H adsorption as compared with that on Cu2Sb(100). We note from adsorption data in Table S5† that SSb2/Cu2Sb(100) binds HCOO* stronger than Cu2Sb(100) while the five other motifs with sulfur as an adatom or as a substitutional dopant in the topmost layer bind HCOO* weaker. The simultaneous weakening of H* adsorption and HCOO* in turn results in positive ΔR2G values for SCu3@Cu2Sb(100), SCu3Sb@Cu2Sb(100), SCu1/Cu2Sb(100), SCu2/Cu2Sb(100) and SSb1/Cu2Sb(100). On the other hand, the enhancement of HCOO* adsorption is greater than the weakening of *H, hence giving an overall negative ΔR2G value for SSb2/Cu2Sb(100). While these seven Cu2Sb-based motifs are all selective towards CO formation, HCOOH and H2 were also produced in the electrochemical tests. We rationalize these pathways with the Gibbs energy diagrams in the next section.
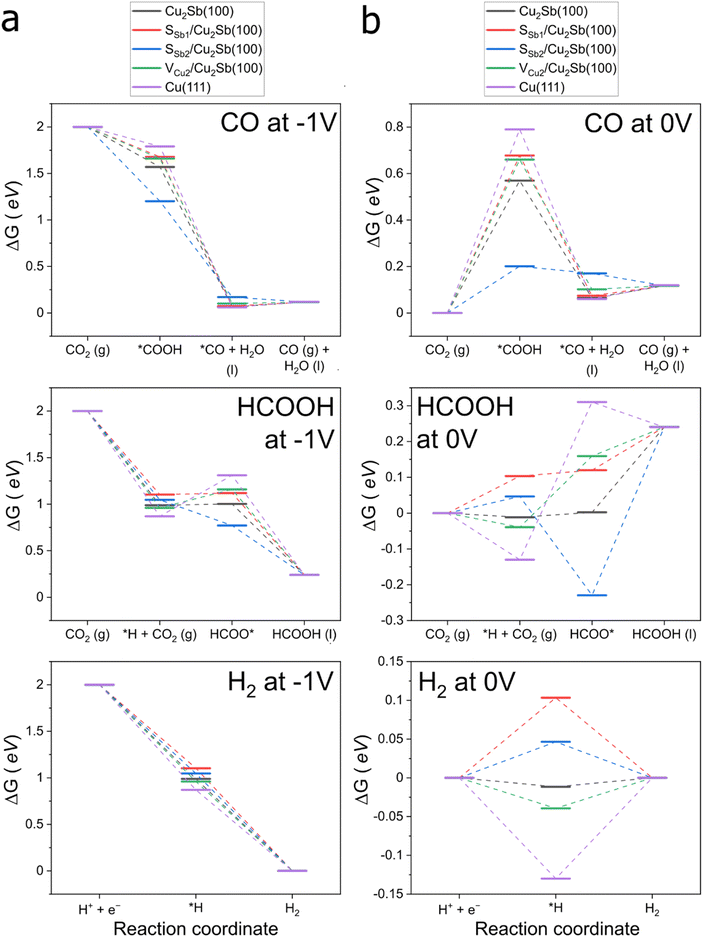
From the seven sites shortlisted from the reactivity analysis, sulfur stability analysis (ESI Section S5.2†) was carried out to narrow the list down further to four surface motifs that are most likely to be present throughout the electrochemical operation: pristine Cu2Sb(100), SSb1/Cu2Sb(100), SSb2/Cu2Sb(100) and VCu2/Cu2Sb(100). These four surface motifs are expected to be stable at −1.0 V and adsorb *CO weaker than Cu(111) to form only 2e-CO2RR products. We finally plotted the Gibbs energy diagrams at 0 V and −1.0 V to have an overview of the CO pathway (eqn (S13)–(S15)†), HCOOH pathway (eqn (S16)–(S18)†) and hydrogen evolution reaction (HER) (eqn (S19) and (S20)†) in Fig. 7 respectively. The Gibbs energy diagrams for all the surface motifs considered at 0.0 V can be found in Fig. S21.† We tabulated the Gibbs energy changes for the CO, HCOOH and HER pathways at 0.0 V in Tables S9–S11† respectively.
Before we discuss the CO2RR pathways, we first evaluated the HER performance by using different surface models. We included Pt(111), which is known to be the best prototypical electrocatalyst towards the HER (ΔG(*H) = −0.38 eV). Although all the four surface motifs perform worse than Pt(111), the HER is exergonic at −1.0 V, which is why H2 is always produced.
Moving to the CO pathway, we find from the Gibbs energy diagrams at 0.0 V in Fig. 7 that the potential determining step is the electrochemical hydrogenation of CO2 to *COOH for Cu2Sb(100), SSb1, VCu2 and SSb2. This is consistent with the finding for the CO Tafel slopes shown in Fig. 5, with values close to 120 mV dec−1 for the three catalytic active phases. This Tafel slope indicates that the rate determining step is an electrochemical step, which is unlikely to be *CO desorption. At −1.0 V, the hydrogenation of CO2 to *COOH for the four motifs is exergonic. The desorption of *CO is expected to involve an energy barrier of less than 0.10 eV that was easily overcome.
From the free energy diagrams for the HCOOH pathway at 0.0 V, we found that in general, the PDS for HCOOH formation is the chemical step involving hydrogenation of CO2 to form HCOO*. The exception being SSb2/Cu2Sb(100), on which the hydrogenation of HCOO* is potential limiting. At −1.0 V, the HCOOH pathway on SSb2/Cu2Sb(100) is exergonic for all elementary steps. This means that SSb2/Cu2Sb(100) can produce both CO and HCOOH, consistent with the negative values of ΔR1G and ΔR2G presented earlier. It was noted that HCOOH was always produced in the electrochemical tests at −1.0 V. We found that the energy barrier of the potential determining step for the HCOOH pathway on pristine Cu2Sb(100), SSb1/Cu2Sb(100) and VCu2/Cu2Sb(100) surface motifs only require 0.01 eV, 0.02 eV and 0.20 eV at −1.0 V, which can be overcome under ambient conditions. Since the pristine Cu2Sb(100) surface motif should predominate in the three samples CS, SK and TH, such a barrier can be overcome which explains why HCOOH was always produced in the electrochemical tests at −1.0 V just like H2.
Overall, the computational results are consistent with the experimental results, which showed a high selectivity towards the 2e-CO2RR products even at a more negative applied voltage of −1.0 V. The results also help explain why the TH phase retains the highest percentage of sulfur after electrochemical tests, and they provide insight into the active phase and surfaces involved in the 2e-CO2RR process.
Conclusions
In summary, sulfide-derived Cu–Sb electrocatalysts for CO2 reduction have been studied in a GDE-based cell. Three-different Cu–Sb–S phases were synthesized by a heat-up colloidal nanoparticle route which demonstrated different selectivity for the CO2RR with CO as the main product. Based on elemental composition characterization after reduction, we have shown that these different selectivity patterns were due to the different elemental compositions when the parent phases are reduced. Less Cu minimizes phase segregation into detrimental S-doped Cu which forms HCOO− and H2, while more sulfur disrupts crystallinity and encourages CO formation. This is seen in the TH sample having the highest residual sulfur and demonstrating the highest CO FE of about 80.5% at −1.0 V with a geometric partial current density of 37.6 mA cm−2. DFT calculations show that substitution of Sb sites with S likely contributes to this improved performance. These findings run contrary to the expectation that sulfide-derived electrocatalysts for the CO2RR encourage HCOO−, which has been the case for most of the studies in this category so far. This study challenges this assumption and could likely open the door to studies on other chalcogenides with surprising selectivity patterns and could also point the way to engineering better catalysts to produce CO in sulfur-rich environments such as the flue gas CO2RR.46Methods
Synthesis of nanoparticles
We synthesized three of the four major phases of the copper antimony sulfide (Cu–Sb–S) system: skinnerite (SK; Cu3SbS3), tetrahedrite (TH; Cu12Sb4S13), and chalcostibite (CS; CuSbS2)34,47 that have different Cu/Sb/S stoichiometric ratios. These phases were synthesized by a heat-up colloidal nanoparticle route as follows:• For SK, Cu3SbS3, 3.75 mmol of copper(II) acetylacetonate, 1.25 mmol of antimony(III) acetate, 3 mL of 1-dodecanethiol and 3 mL of oleylamine were dissolved in 24 mL of 1-octadecene in a 250 mL three-neck flask and the mixture was degassed under flowing nitrogen for 30 min at 150 °C. The mixture was then heated to 220 °C for 1 h under a nitrogen atmosphere for the formation of nanoparticles.
• For TH, Cu12Sb4S13, 3.75 mmol of copper(II) acetylacetonate, 1.25 mmol of antimony(III) acetate, 3 mL of 1-dodecanethiol and 3 mL of oleylamine were dissolved in 24 mL of 1-octadecene in a 250 mL three-neck flask and the mixture was degassed under flowing nitrogen for 30 min at 150 °C. The mixture was then heated to 260 °C for 1 h under a nitrogen atmosphere for the formation of nanoparticles.
• For CS, CuSbS2, 2 mmol of copper(II) acetylacetonate, 2 mmol of antimony(III) acetate, 3 mL of 1-dodecanethiol and 3 mL of oleylamine were dissolved in 24 mL of 1-octadecene in a 250 mL three-neck flask and the mixture was degassed under flowing nitrogen for 30 min at 150 °C. The mixture was then heated to 250 °C for 1 h under a nitrogen atmosphere for the formation of nanoparticles.
The resulting suspensions are then topped up to 45 mL with ethanol, sonicated and centrifuged at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 5 min using a Thermo Scientific Sorvall Legend x1. Then, the nanoparticles are centrifuged in ethanol for the removal of polar impurities. Subsequently, the nanoparticles are centrifuged three times with a hexane/ethanol mixture in 25
000 rpm for 5 min using a Thermo Scientific Sorvall Legend x1. Then, the nanoparticles are centrifuged in ethanol for the removal of polar impurities. Subsequently, the nanoparticles are centrifuged three times with a hexane/ethanol mixture in 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, 15
20, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 and 5
30 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 mL ratios for the removal of organic impurities.
40 mL ratios for the removal of organic impurities.
The CuSbS2 powder is additionally immersed in 0.5 M NaOH for 30 min and centrifuged to etch Sb2S3 impurities, followed by centrifugation in deionized water to remove the remaining NaOH.
Finally, the nanoparticles are centrifuged in isopropyl alcohol and dried in an oven at 70 °C for an hour.
Preparation of the catalyst layer on gas diffusion electrodes
27 mg of the catalyst was dispersed in 2 mL of ethanol with 100 μl of nafion ionomer solution (5%) and ultrasonicated for 30 min. The prepared catalyst ink was then airbrushed with an airbrush gun (Paasche) onto a 6 × 6 cm2 CeTech (CT) GDL280 carbon paper.Electrochemical measurements in a three-compartment flow cell
The electrochemical measurements were carried out in a three-compartment gas diffusion electrode (GDE) flow cell,48 with an anion exchange membrane (Fumasep FAA-3-pk-130) and nickel foam clamped between the catholyte and anolyte compartments and carbon paper with catalyst ink clamped between the gas and catholyte compartments. The geometric area of the working electrode was 1 cm2. The reference electrode placed in the catholyte compartment was an AgCl electrode filled with 3 M KCl.The applied voltage was compensated for 80% of the measured iR drop using an Autolab PGSTAT302N. The resulting voltage was then converted to the RHE scale using the formula:
| ERHE = EAg/AgCl + 0.197 + 0.0591 × pH | (1) |
Chronoamperometry experiments were carried out with an Autolab PGSTAT302N, with an Alicat MC-100SCCM-D mass flow controller to control the flow of CO2 to the gas inlet. A mass flow of 40 sccm was used for all experiments. 25 mL of catholyte and 25 mL of anolyte were used, pumped at a rate of 28.5 mL min−1. Gas products were quantified with a gas chromatograph (Shimadzu Nexis GC-2030) equipped with a thermal conductivity detector (TCD) and flame ionization detector (FID) with an optional methanizer setting. Liquid products were quantified with a liquid chromatograph (Shimadzu LC-2030) equipped with a UV detector and a refractive index detector (RID).
The faradaic efficiency (gas product) was calculated with the equation:
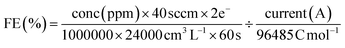 | (2) |
The faradaic efficiency (liquid product) was calculated with the equation:
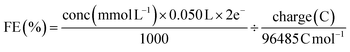 | (3) |
Catalyst characterization
X-ray diffraction (XRD) was carried out using a Panalytical X'Pert Pro with Cu-Kα radiation operated at 40 kV and 30 mA. Field emission scanning electron microscopy (FE-SEM) images were taken using a JEOL JSM-7600F equipped with an INCA – XAct 10 mm2 X-ray detector for energy-dispersive X-ray (EDX) analysis. Transmission electron microscopy (TEM) was obtained using a JEOL 2100F. X-ray photoelectron spectroscopy (XPS) data were collected using a Kratos AXIS Supra.DFT calculations
All density functional theory calculations were performed using Quantum ESPRESSO49,50 within an atomic simulation environment (ASE). Core electrons were represented using Vanderbilt ultra-soft pseudopotentials.51 A plane wave basis set with a kinetic energy and density cut-off of 500 eV and 5000 eV, respectively, were used. A Fermi-level smearing width of 0.1 eV was adopted to accelerate the convergence of metallic systems. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was adopted.52 Long range dispersion corrections were accounted for using Grimme's D3 approach.53 The convergence criteria for the total energy and Hellmann–Feynman force per atom set were at 10−6 eV and 0.05 eV Å−1 respectively.The primitive cell was used for the calculation of bulk Cu, Pt, Sb and Cu2Sb and they were sampled with (8,8,8), (8,8,8), (8,8,8), and (6,6,4) k-point grids, respectively, in the first Brillouin zone generated in the Monkhorst–Pack scheme.54 The primitive cell of the three parent phases chalcostibite (CS), skinnerite (SK) and tetrahedrite (TH) were also used, sampled with (6,4,2), (4,3,2), and (3,3,3) Monkhorst–Pack grids, respectively.
We created orthogonal asymmetric slabs encompassing only the surface primitive cell of different facets of Cu2Sb to calculate the surface energies. The number of atomic layers used and fixed in the asymmetric slabs are tabulated in Table S6† along with the lateral lattice parameters, (a and b), the surface area of the cell, and the surface energy. The surface primitive cells of (100), (101), (110) and (001) were sampled with (6,4,1), (4,6,1), (4,4,1), and (6,6,1) Monkhorst–Pack grids, respectively.
All gas-phase species were calculated in a 21 Å × 22 Å × 23 Å simulation cell sampled with the Γ-point. The surface slabs of Cu(111), Pt(111), Cu2Sb(100) and Cu2Sb(101) were constructed as (3 × 3 × 4), (3 × 3 × 4), (3 × 2 × 6), and (2 × 2 × 6) with the bottom two atomic layers fixed to their bulk positions. These surface slabs were sampled using (3,3,1), (3,3,1), (3,4,1), and (3,3,1) k-point grids, respectively. A vacuum of at least 15 Å and a dipole correction were included in the direction perpendicular to the surface to mitigate spurious electrostatic interactions for all surface calculations.55
Additional information, including surface energy calculations (Table S6†) and the gas-phase and adsorbate Gibbs energy correction adopted for this work (Table S7†) can be found in the ESI.†
Author contributions
D. Y. Y. G., Y. L. and L. H. W. conceived the study. J. M. R. T. designed the heat-up colloidal synthesis procedure and D. Y. Y. G. carried out the synthesis. D. Y. Y. G. carried out the electrochemical testing, most of the characterization and analyzed the experimental data. Y. W. carried out the TEM characterization. K. M. Y., R. L. and T. S. C. carried out the DFT modelling. Y. L. and L. H. W. supervised the project, while A. D. H. and Y. C. T. contributed to the discussion of the data and the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was financially supported by grants from the National Research Foundation, Prime Minister's Office, Singapore, under its Campus of Research Excellence and Technological Enterprise (CREATE) program as well as the Singapore Ministry of Education (MOE) Tier 1 grant (Award ID RG68/21), Tier 2 grant (MOE T2EP50120-0008) and Agency for Science, Technology and Research (A*STAR) Career Development Award (Project No. 202D800037). We thank Mengyuan Zhang for the initial discussion on this project. We acknowledge the Facility for Analysis, Characterisation, Testing and Simulation, Nanyang Technological University, Singapore, for use of their electron microscopy/X-ray facilities, with thanks to Weiling Liu and Teddy Salim for their help in XPS. We also thank Anqi Sng of the Institute of Materials Research and Engineering, A*STAR for her help in performing ICP measurements. K. M. Y., L. R., and T. S. C acknowledge the financial support of the Singapore National Research Foundation (NRF) through the Campus for Research Excellence and Technological Enterprise (CREATE) programme, and from the Ministry of Education Academic Research Fund Tier-1: RG5/22. We thank the High Performance Computing (HPC) team at the HPC Centre, Nanyang Technological University (NTU) for technical assistance and computing resources. The computational work for this article was partially performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg/). This work used computational resources of the supercomputer Fugaku provided by Riken through the HPCI system research project (Project ID: hp220158). L. R. acknowledges NTU for a research scholarship. D. Y. Y. G. wishes to thank Zheng Hao Tan, Ying Fan Tay, Surani bin Dolmanan, Meltem Yilmaz, Mahmoud Ahmed, Vincent and Roong Jien Wong for helpful discussions.References
- J. Gao, C. Jia and B. Liu, Catal. Sci. Technol., 2017, 7, 5602–5607 RSC.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120, 7984–8034 CrossRef CAS PubMed.
- C. Chen, J. F. Khosrowabadi Kotyk and S. W. Sheehan, Chem, 2018, 4, 2571–2586 CAS.
- H. Shin, K. U. Hansen and F. Jiao, Nat. Sustainability, 2021, 4, 911–919 CrossRef.
- C. W. Li, J. Ciston and M. W. Kanan, Nature, 2014, 508, 504–507 CrossRef CAS PubMed.
- Y. Lum and J. W. Ager, Angew. Chem., Int. Ed., 2018, 57, 551–554 CrossRef CAS PubMed.
- D. Gao, I. Zegkinoglou, N. J. Divins, F. Scholten, I. Sinev, P. Grosse and B. Roldan Cuenya, ACS Nano, 2017, 11, 4825–4831 CrossRef CAS PubMed.
- A. D. Handoko, C. W. Ong, Y. Huang, Z. G. Lee, L. Lin, G. B. Panetti and B. S. Yeo, J. Phys. Chem. C, 2016, 120, 20058–20067 CrossRef CAS.
- L. C. Pardo Pérez, A. Arndt, S. Stojkovikj, I. Y. Ahmet, J. T. Arens, F. Dattila, R. Wendt, A. Guilherme Buzanich, M. Radtke, V. Davies, K. Höflich, E. Köhnen, P. Tockhorn, R. Golnak, J. Xiao, G. Schuck, M. Wollgarten, N. López and M. T. Mayer, Adv. Energy Mater., 2022, 12, 2103328 CrossRef.
- W. Zhu, B. M. Tackett, J. G. Chen and F. Jiao, Top. Curr. Chem., 2018, 376, 41 CrossRef PubMed.
- Y. Wu, S. Cao, J. Hou, Z. Li, B. Zhang, P. Zhai, Y. Zhang and L. Sun, Adv. Energy Mater., 2020, 10, 2000588 CrossRef CAS.
- H. Song, Y. C. Tan, B. Kim, S. Ringe and J. Oh, ACS Appl. Mater. Interfaces, 2021, 13, 55272–55280 CrossRef CAS PubMed.
- L. Wang, H. Peng, S. Lamaison, Z. Qi, D. M. Koshy, M. B. Stevens, D. Wakerley, J. A. Zamora Zeledón, L. A. King, L. Zhou, Y. Lai, M. Fontecave, J. Gregoire, F. Abild-Pedersen, T. F. Jaramillo and C. Hahn, Chem Catal., 2021, 1, 663–680 CrossRef CAS.
- A. Mukherjee, M. Abdinejad, S. S. Mahapatra and B. C. Ruidas, J. Mater. Chem. A, 2023, 11, 9300–9332 RSC.
- W. Ma, S. Xie, X.-G. Zhang, F. Sun, J. Kang, Z. Jiang, Q. Zhang, D.-Y. Wu and Y. Wang, Nat. Commun., 2019, 10, 892 CrossRef PubMed.
- X. Zheng, P. De Luna, F. P. García de Arquer, B. Zhang, N. Becknell, M. B. Ross, Y. Li, M. N. Banis, Y. Li, M. Liu, O. Voznyy, C. T. Dinh, T. Zhuang, P. Stadler, Y. Cui, X. Du, P. Yang and E. H. Sargent, Joule, 2017, 1, 794–805 CrossRef CAS.
- T. Shinagawa, G. O. Larrazábal, A. J. Martín, F. Krumeich and J. Pérez-Ramírez, ACS Catal., 2018, 8, 837–844 CrossRef CAS.
- K. R. Phillips, Y. Katayama, J. Hwang and Y. Shao-Horn, J. Phys. Chem. Lett., 2018, 9, 4407–4412 CrossRef CAS PubMed.
- Y. Huang, Y. Deng, A. D. Handoko, G. K. L. Goh and B. S. Yeo, ChemSusChem, 2018, 11, 320–326 CrossRef CAS PubMed.
- W. Luc, B. H. Ko, S. Kattel, S. Li, D. Su, J. G. Chen and F. Jiao, J. Am. Chem. Soc., 2019, 141, 9902–9909 CrossRef CAS PubMed.
- Y. Deng, Y. Huang, D. Ren, A. D. Handoko, Z. W. Seh, P. Hirunsit and B. S. Yeo, ACS Appl. Mater. Interfaces, 2018, 10, 28572–28581 CrossRef CAS PubMed.
- R. García-Muelas, F. Dattila, T. Shinagawa, A. J. Martín, J. Pérez-Ramírez and N. López, J. Phys. Chem. Lett., 2018, 9, 7153–7159 CrossRef PubMed.
- M. T. Tang, H. Peng, P. S. Lamoureux, M. Bajdich and F. Abild-Pedersen, Appl. Catal., B, 2020, 279, 119384 CrossRef CAS.
- R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082 CrossRef CAS PubMed.
- H.-K. Lim, H. Shin, W. A. Goddard, Y. J. Hwang, B. K. Min and H. Kim, J. Am. Chem. Soc., 2014, 136, 11355–11361 CrossRef CAS PubMed.
- S. D. Deshmukh, R. G. Ellis, D. S. Sutandar, D. J. Rokke and R. Agrawal, Chem. Mater., 2019, 31, 9087–9097 CrossRef CAS.
- X.-L. Zhang, P.-C. Yu, X.-Z. Su, S.-J. Hu, L. Shi, Y.-H. Wang, P.-P. Yang, F.-Y. Gao, Z.-Z. Wu, L.-P. Chi, Y.-R. Zheng and M.-R. Gao, Sci. Adv., 2023, 9, eadh2885 CrossRef CAS PubMed.
- H.-i. Nam, K. Ryeol Park, Y.-W. Choi, H.-j. Sim, K. Yong Sohn and D.-H. Lim, Appl. Surf. Sci., 2023, 612, 155646 CrossRef CAS.
- S. Liu, H. Tao, Q. Liu, Z. Xu, Q. Liu and J.-L. Luo, ACS Catal., 2018, 8, 1469–1475 CrossRef CAS.
- Y. Lai, R. J. R. Jones, Y. Wang, L. Zhou, M. H. Richter and J. Gregoire, J. Mater. Chem. A, 2019, 7, 26785–26790 RSC.
- S. Rasul, D. H. Anjum, A. Jedidi, Y. Minenkov, L. Cavallo and K. Takanabe, Angew. Chem., Int. Ed., 2015, 54, 2146–2150 CrossRef CAS PubMed.
- S. Sarfraz, A. T. Garcia-Esparza, A. Jedidi, L. Cavallo and K. Takanabe, ACS Catal., 2016, 6, 2842–2851 CrossRef CAS.
- K. Ramasamy, H. Sims, W. H. Butler and A. Gupta, Chem. Mater., 2014, 26, 2891–2899 CrossRef CAS.
- T. J. Whittles, T. D. Veal, C. N. Savory, A. W. Welch, F. W. de Souza Lucas, J. T. Gibbon, M. Birkett, R. J. Potter, D. O. Scanlon, A. Zakutayev and V. R. Dhanak, ACS Appl. Mater. Interfaces, 2017, 9, 41916–41926 CrossRef CAS PubMed.
- C. H. M. van Oversteeg, F. E. Oropeza, J. P. Hofmann, E. J. M. Hensen, P. E. de Jongh and C. de Mello Donega, Chem. Mater., 2019, 31, 541–552 CrossRef CAS PubMed.
- S. Mou, Y. Li, L. Yue, J. Liang, Y. Luo, Q. Liu, T. Li, S. Lu, A. M. Asiri, X. Xiong, D. Ma and X. Sun, Nano Res., 2021, 14, 2831–2836 CrossRef CAS.
- H. Li, T.-W. Jiang, X. Qin, J. Chen, X.-Y. Ma, K. Jiang, X.-G. Zhang and W.-B. Cai, ACS Catal., 2021, 11, 6846–6856 CrossRef CAS.
- Y. Li, S. Chu, H. Shen, Q. Xia, A. W. Robertson, J. Masa, U. Siddiqui and Z. Sun, ACS Sustain. Chem. Eng., 2020, 8, 4948–4954 CrossRef CAS.
- C. W. Lee, N. H. Cho, S. W. Im, M. S. Jee, Y. J. Hwang, B. K. Min and K. T. Nam, J. Mater. Chem. A, 2018, 6, 14043–14057 RSC.
- E. M. Espinoza, J. A. Clark, J. Soliman, J. B. Derr, M. Morales and V. I. Vullev, J. Electrochem. Soc., 2019, 166, H3175–H3187 CrossRef CAS.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206 CrossRef CAS.
- Y.-G. Kim, J. H. Baricuatro and M. P. Soriaga, Electrocatalysis, 2018, 9, 526–530 CrossRef CAS.
- W. B. Pearson, Z Kristallogr Cryst Mater., 1985, 171, 23–40 CrossRef CAS.
- K. P. Kuhl, T. Hatsukade, E. R. Cave, D. N. Abram, J. Kibsgaard and T. F. Jaramillo, J. Am. Chem. Soc., 2014, 136, 14107–14113 CrossRef CAS PubMed.
- B.-U. Choi, Y. C. Tan, H. Song, K. B. Lee and J. Oh, ACS Sustain. Chem. Eng., 2021, 9, 2348–2357 CrossRef CAS.
- B. J. Skinner, F. D. Luce and E. Makovicky, Econ. Geol., 1972, 67, 924–938 CrossRef CAS.
- Y. C. Tan, W. K. Quek, B. Kim, S. Sugiarto, J. Oh and D. Kai, ACS Energy Lett., 2022, 7, 2012–2023 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta04777f |
| This journal is © The Royal Society of Chemistry 2024 |