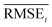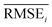Open Access Article
Open Access ArticleMaterials discovery with extreme properties via reinforcement learning-guided combinatorial chemistry†
Hyunseung
Kim‡
 a,
Haeyeon
Choi‡
bc,
Dongju
Kang‡
a,
Won Bo
Lee
a,
Haeyeon
Choi‡
bc,
Dongju
Kang‡
a,
Won Bo
Lee
 *a and
Jonggeol
Na
*a and
Jonggeol
Na
 *bc
*bc
aSchool of Chemical and Biological Engineering, Seoul National University, Republic of Korea. E-mail: wblee@snu.ac.kr
bDepartment of Chemical Engineering and Materials Science, Ewha Womans University, Republic of Korea. E-mail: jgna@ewha.ac.kr
cGraduate Program in System Health Science and Engineering, Ewha Womans University, Republic of Korea
First published on 24th April 2024
Abstract
The goal of most materials discovery is to discover materials that are superior to those currently known. Fundamentally, this is close to extrapolation, which is a weak point for most machine learning models that learn the probability distribution of data. Herein, we develop reinforcement learning-guided combinatorial chemistry, which is a rule-based molecular designer driven by trained policy for selecting subsequent molecular fragments to get a target molecule. Since our model has the potential to generate all possible molecular structures that can be obtained from combinations of molecular fragments, unknown molecules with superior properties can be discovered. We theoretically and empirically demonstrate that our model is more suitable for discovering better compounds than probability distribution-learning models. In an experiment aimed at discovering molecules that hit seven extreme target properties, our model discovered 1315 of all target-hitting molecules and 7629 of five target-hitting molecules out of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trials, whereas the probability distribution-learning models failed. Moreover, it has been confirmed that every molecule generated under the binding rules of molecular fragments is 100% chemically valid. To illustrate the performance in actual problems, we also demonstrate that our models work well on two practical applications: discovering protein docking molecules and HIV inhibitors.
000 trials, whereas the probability distribution-learning models failed. Moreover, it has been confirmed that every molecule generated under the binding rules of molecular fragments is 100% chemically valid. To illustrate the performance in actual problems, we also demonstrate that our models work well on two practical applications: discovering protein docking molecules and HIV inhibitors.
1 Introduction
The task of discovering materials that are superior to those currently known is a challenging problem in various fields of materials science, including pharmaceutical substances,1–4 electrical and electronic materials,5–11 energy materials,11–14 metals and ceramics,10 nanomaterials,15 and polymeric materials.16,17 Some of these studies aim to discover materials with two or more target properties that contradict each other, meaning it is difficult for them to coexist.18 For example, super engineering plastics used in automobiles should be lighter than metals yet have similar mechanical strength.16,17 Similarly, transparent conductors used in display panels should be both optically transparent (requiring a large bandgap) and electrically conductive (requiring high carrier concentration, which generally has a low bandgap).5,18 In some cases, the aim is to discover materials that have properties with either extremely high or low values. For example, the development of a better organic light-emitting diode (OLED) requires chemists to discover novel materials with higher efficiency and stability.6–8 Here, the problem is that there are no (or few) known samples that have such properties compared to common substances. This makes it difficult for chemists to gain insights or knowledge from the known materials, that could help to infer the molecular structures of the desired materials. Unfortunately, this situation also holds for most machine learning models that learn the data. Therefore, it is necessary to develop a model that can discover materials, even in regions with little or no known data. In this paper, we refer to this problem as materials extrapolation.In recent years, it has been reported that machine learning techniques can solve many challenging problems in a wide range of fields, including materials discovery. In particular, models for goal-directed inverse molecular design are attractive because they can directly infer the molecular structures that meet a set of given target conditions such as scaffolds,2,21 physical properties,15,22–24 and biological activities.2,4,24 Some of these studies have proposed models based on neural machine translation (NMT) such as seq2seq24,25 and Transformer,26 which translate input target conditions to corresponding molecular structures. Models based on conditional generative models have also been proposed, such as conditional generative adversarial networks (cGANs)27 and conditional variational autoencoders (cVAEs).28 These models directly generate molecular structures to meet a set of given target conditions.15,21–23 In contrast, there are also ways to obtain the desired materials from unconditional generative models, such as generative adversarial networks (GANs)29 and variational autoencoders (VAEs).30 These approaches use additional methods to find appropriate latent code, which is required to generate the target-hitting substances. Navigating policies of latent space trained by reinforcement learning (RL)31,32 and optimization techniques33–35 belong here.
Unfortunately, all of the previously mentioned models (NMT, GAN, and VAE-based) are difficult to use in materials extrapolation for discovering novel materials with properties that are out of training data distribution. To generate realistic molecules with these models, the models should be trained to generate molecular data that approximate the probability distribution of the real-world chemical system. However, since it is impossible to know the true probability of the real-world chemical system, the models are trained to generate data that approximate the empirical probability of the training data. Regrettably, the empirical data at our disposal may exhibit biases due to various factors, consequently leading to models trained on such biased data failing to generate some molecules that even exist in the real world (Fig. 1a). Hence, the probability distribution-learning models are not suitable for generating molecules in regions with little or no known data (such as materials extrapolation). Furthermore, there are several ongoing discussions about whether probability distribution-learning models are suitable for extrapolation problems.9,10,19,36 In the same vein, we believe that employing an approach that either avoids using data or minimizes data usage, such as RL and genetic algorithm (GA), is appropriate for materials extrapolation. Since GA is a method for deriving a set of optimal solutions rather than a problem-solving policy, it cannot guarantee the diversity of the derived solution set. On the contrary, RL involves learning action policies to obtain solutions based on the given current state. This advantage enables RL to infer a wider variety of solutions. Therefore, we intend to utilize RL in our approach. Despite several recent studies utilizing RL in molecular design,2,4,37 the majority of them do not prioritize presenting RL as a means to address the limitations of probability distribution-learning models for discovering substances beyond their trained domains.
 | ||
Fig. 1 Probability distribution-learning models for molecular generation. (a) Data distribution of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P–TPSA. The pink dots denote the molecules in MOSES19 training data. The other colored dots denote the molecules generated by MOSES baseline models which were trained with the MOSES training data. Since the MOSES baseline models are probability distribution-learning models such as NMT, GAN, VAE, and AAE, the distribution of generated molecules approximates the distribution of their training data. The magenta triangles and blue diamonds indicate real molecules in ChEMBL20 database, which have extrapolated properties from MOSES training data distribution. ① CHEMBL3216345; ② CHEMBL3230084; ③ CHEMBL3358630; ④ CHEMBL300801; ⑤ CHEMBL501130; ⑥ CHEMBL52004. (b–d) Types of inverse molecular designer. Xi, Yi, and z denote i-th molecular structure, properties of the i-th molecule, and latent code, respectively. P–TPSA. The pink dots denote the molecules in MOSES19 training data. The other colored dots denote the molecules generated by MOSES baseline models which were trained with the MOSES training data. Since the MOSES baseline models are probability distribution-learning models such as NMT, GAN, VAE, and AAE, the distribution of generated molecules approximates the distribution of their training data. The magenta triangles and blue diamonds indicate real molecules in ChEMBL20 database, which have extrapolated properties from MOSES training data distribution. ① CHEMBL3216345; ② CHEMBL3230084; ③ CHEMBL3358630; ④ CHEMBL300801; ⑤ CHEMBL501130; ⑥ CHEMBL52004. (b–d) Types of inverse molecular designer. Xi, Yi, and z denote i-th molecular structure, properties of the i-th molecule, and latent code, respectively. | ||
Combinatorial chemistry38 was invented in the 1980s and can generate molecules with properties out of known data. These types of methods use a set of molecular fragments and rules for fragment combination. Breaking of retrosynthetically interesting chemical substructures (BRICS)39 is an example of combinatorial chemistry. This technique involves combining randomly selected BRICS fragments with their template-based fragment combination rules, which is similar to assembling Lego blocks. Therefore, combinatorial chemistry can create all chemically possible molecular structures that can be obtained from the combination of molecular fragments. According to our estimation, approximately 4 × 1016 types of small molecules (≤500 Da) can be combined with 2207 BRICS fragments. Considering that the total number of small molecules was roughly estimated to be 1060 in ref. 40, this means that it can cover a fairly wide area. However, there is the limitation that the combinatorial chemistry-based molecular generator does not know which molecular fragments to be selected and combined to complete the desired molecule. In other words, it has no policy to guide the selection of molecular fragments to obtain the target molecule. Hence, it proceeds with countless attempts to combine randomly selected fragments and selects the best compound from the generated molecular candidates, which can result in a combinatorial explosion.41 If we assume that it takes 1 ms to assemble one molecule, it would take 1.27 × 106 years to enumerate all possible small organic molecules using 2207 molecular fragments; 4 × 1016 molecules × 1 ms = 1.27 × 106 years.
Herein, we introduce RL to provide combinatorial chemistry with a molecular fragment selection policy that guides the generating molecule toward the target. With a randomly selected initial fragment, the RL-guided policy iteratively selects the subsequent fragment to be combined. In the training phase, the policy is learned by giving a higher reward if the properties of the generated molecule are closer to the target. Therefore, the learned policy enables an efficient search of chemical space and helps to escape from the combinatorial explosion problem by providing direction to the target. Moreover, the proposed model—RL-guided combinatorial chemistry (RL-CC)—has the potential to enable materials extrapolation, which is impossible for probability distribution-learning models. To demonstrate the potential empirically, we apply RL-CC and two probability distribution-learning models to a toy problem of molecules discovery that hits multiple extreme target properties simultaneously. The results indicate that our model can discover extreme target molecules that probability distribution-learning models cannot reveal. Furthermore, we theoretically demonstrate why the probability distribution-learning models are not suitable for problems involving materials extrapolation. To illustrate the performance in actual problems, we conduct two practical experiments. The first is to discover protein docking molecules to a 5-hydroxytryptamine receptor 1B (5-HT1B receptor) with high binding affinity. The second is the discovery of human immunodeficiency virus (HIV) inhibitors with high potency. These two experiments demonstrate that the proposed approach can discover compounds with extreme properties, which shows the potential to be extended as materials extrapolation when it utilizes a set of domain-specific molecular fragments and their combination rules.
2 Results and discussion
2.1 Theoretical review of probability distribution-learning models
Inverse molecular design models based on NMT, VAE, and GAN learn the empirical probability distribution of training data Pdata. Let X, Y = (X1, Y1), …, (XN, YN) denote N-sampled training data. Here, Xi = (xi,1, …, xi,T′) denotes sequence data of the i-th molecular structure, and Yi = (yi,1, …, yi,T) denotes a set of properties of the i-th molecule. The NMT-based models are trained to translate the input Yi = (yi,1, …, yi,T) into a paired output sequence Xi = (xi,1, …, xi,T′). Here, xi,t is a one-hot encoded vector of the t-th token constituting a molecule Xi. The θ-parameterized translator GNLPθ should be trained to select a token xi,t iteratively over t = 1, …, T′, by maximizing the likelihood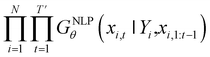 empirically. The actual training process is conducted by minimizing its negative log-likelihood
empirically. The actual training process is conducted by minimizing its negative log-likelihood 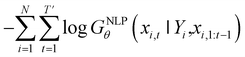 , which is equivalent to minimizing cross-entropy H(·, ·) of hypothesis
, which is equivalent to minimizing cross-entropy H(·, ·) of hypothesis ![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ from training data X:
θ from training data X: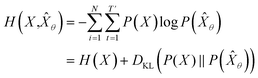 | (1) |
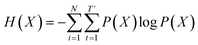 denotes the entropy42 of training data X, and DKL(P(X)‖P(
denotes the entropy42 of training data X, and DKL(P(X)‖P(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ)) is the Kullback–Leibler (KL) divergence43 of hypothesis probability P(
θ)) is the Kullback–Leibler (KL) divergence43 of hypothesis probability P(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ) from Pdata. Since H(X) is not a function of trainable parameter θ, minimizing the cross-entropy H(X,
θ) from Pdata. Since H(X) is not a function of trainable parameter θ, minimizing the cross-entropy H(X,![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ) is equivalent to minimizing the KL divergence term in eqn (1). Thus, the optimal GNLPθ* is obtained by approximating P(
θ) is equivalent to minimizing the KL divergence term in eqn (1). Thus, the optimal GNLPθ* is obtained by approximating P(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ)—which is the probability distribution of data generated by GNLPθ—to Pdata. It means that GNLPθ learns the empirical probability distribution of training data Pdata, not the true probability distribution of the system P.
θ)—which is the probability distribution of data generated by GNLPθ—to Pdata. It means that GNLPθ learns the empirical probability distribution of training data Pdata, not the true probability distribution of the system P.
Second, VAE-based models are types of generative self-learning models that learn the empirical probability distribution of training data Pdata. The models are trained to encode training data X = X1, …, XN in the latent space with encoder QVAEϕ and reconstruct it with decoder GVAEθ. The difference from autoencoders is that the latent variables z are constrained to follow a prior distribution such as a normal distribution. The VAEs are trained using the following objective function:30
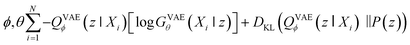 | (2) |
When looking at the VAEs from the perspective of a generative model, the KL divergence term simply acts like a regularizer in the training process. The expectation term measures the reconstruction error of GVAEθ and it is approximated by using the following L-number of Monte-Carlo sampling:
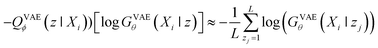 | (3) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ,z from training data X:
θ,z from training data X: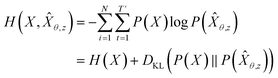 | (4) |
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) θ,z) to the Pdata. This means that GVAEθ(X|z) with z ∼ QVAEϕ(z|X) approximates Pdata.
θ,z) to the Pdata. This means that GVAEθ(X|z) with z ∼ QVAEϕ(z|X) approximates Pdata.
Third, GAN is also a model to obtain a generator GGANθ that approximates Pdata. Here, GGANθ learns the Pdata in the learning process to generate data that sufficiently resembles training data X to deceive the discriminator DGANϕ. Note that it has been proved that the global minimum of the virtual training criterion of the generator is achieved if (and only if) Pdata = GGANθ(z).29 This means that the optimal GGANθ* is obtained by approximating the hypothesis probability P(![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) z) to the probability of training data Pdata.
z) to the probability of training data Pdata.
Therefore, it can be concluded that models based on NMT, VAE, and GAN used for inverse molecular design are models to derive an approximator of Pdata. Unfortunately, since Pdata derived from the observed empirical data is not equal to the true probability P of chemical system, it cannot guarantee that the probability-distribution learning models will work well for problems involving materials extrapolation.
2.2 RL-guided combinatorial chemistry with BRICS
The RL-CC illustrated in Fig. 2 is applicable to various tasks of materials discovery, by designing a target molecule with the selected molecular fragments. A trained RL-guided policy iteratively selects the subsequent fragment to be combined. Here, the RL-guided policy serves as a guide to generate a target-hitting molecule. This approach has three main phases: configuration settings (Fig. 2b–d), training (Fig. 2a), and inference (Fig. 3).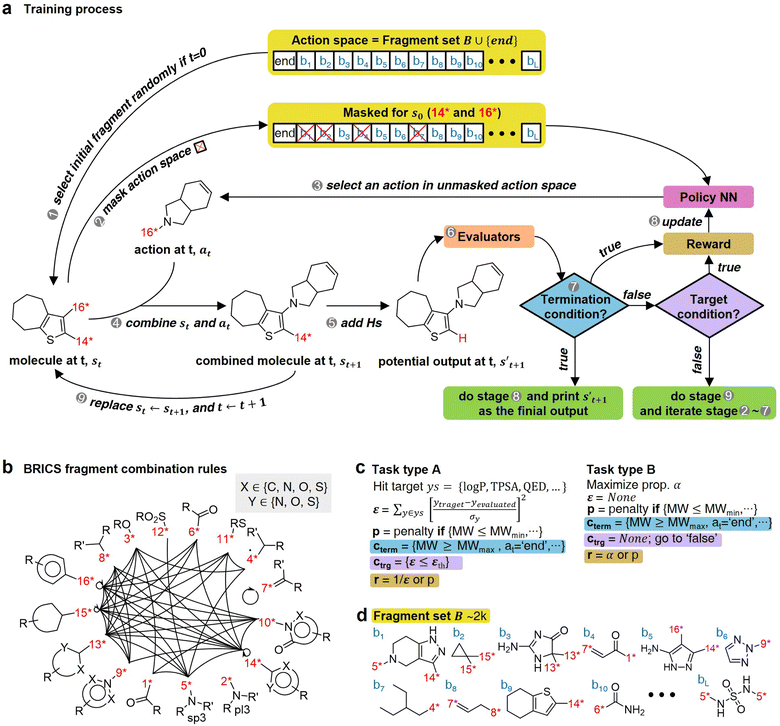 | ||
| Fig. 2 Overview of RL-guided combinatorial chemistry with BRICS. (a) Training process. (b) Modified BRICS39 fragment combination rules. Here, the RDKit44 version 2020.09.1.0 of the modified BRICS rules is adopted. This figure is modified from Degen et al., 2008, ChemMedChem, 10(3), 1503–1507,39 with permission of Wiley-VCH GmbH. (c) Type of tasks. Task type A is to discover molecules that hit the specific values of given target properties and Task type B is to discover molecules that maximize the given target properties. (d) Fragment set B. Here, B ∪ {end} is defined as action space. | ||
 | ||
| Fig. 3 Inference process for molecular generation. (a) An example of a molecular generation process. (b) Property changes for generated molecules. | ||
In the configuration settings phase, all settings necessary for reinforcement learning are customized. Accordingly, the task for materials discovery must be specified. There are two types of tasks for this (Fig. 2c): the discovery of molecules to hit specific values of the multiple target properties (Task type A), and the discovery of molecules to maximize a specific property (Task type B). Depending on the type of given task, the user designs the reward function r, target error function ε, termination conditions cterm, and target conditions ctrg. The reward function r is designed to give a higher reward the better a given task is performed. For Task type A, the target error function ε and reward function r are designed as sum errors for the multiple target properties and the reciprocal of the target error function ε, respectively. In the case of Task type B, the property itself is used as the reward function r; hence, maximizing r is equivalent to maximizing the property. For the minimization case of Task type B, the negative property is used as the reward function r. We can also consider the constraints p, which are reflected in the reward function r by giving penalties if one of the constraints p is not satisfied. Here, the minimum molecular weight (MWmin) and the minimum number of fragments (nmin) that make up a molecule can be used as constraints p. These enable the model to generate various molecules by preventing premature termination, which would cause the generation of molecules that were too small and uniform.
The termination conditions (cterm) and target conditions (ctrg) pertain to deciding when to terminate the process of selecting and combining additional molecular fragments, which determines the characters of the final output molecule. Hence, the termination conditions cterm and target conditions ctrg are designed considering the given task. The molecular generation process is terminated early if one of the termination conditions cterm is satisfied. Accordingly, maximum molecular weight (MWmax) and maximum number of fragments (nmax) are used to design the termination conditions cterm. It should be noted that the process is also terminated if there are no more sites for binding fragments to the combined molecule at step t (st+1) or if the policy selects end-action at step t. These are included in the termination conditions cterm. The target conditions ctrg are the target bounds to hit, which are applied only to Task type A.
To evaluate the previously mentioned functions and conditions, the evaluators (stage 6 in Fig. 2a) for the interesting properties are utilized selectively to calculate the properties of potential output molecule at step  . In order to calculate the properties of the molecule, the molecule must not have any unfilled binding site. Hence,
. In order to calculate the properties of the molecule, the molecule must not have any unfilled binding site. Hence,  is derived by attaching hydrogen to the unfilled binding sites of the combined molecule at step t (st+1) if st+1 has any unfilled binding site (stage 5 in Fig. 2a). RDKit44 was selectively used to evaluate the calculated octanol–water partition coefficient (log
is derived by attaching hydrogen to the unfilled binding sites of the combined molecule at step t (st+1) if st+1 has any unfilled binding site (stage 5 in Fig. 2a). RDKit44 was selectively used to evaluate the calculated octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P),45 topological polar surface area (TPSA),46 quantitative estimates of drug-likeness (QED),47 number of hydrogen bond acceptors (HBA), number of hydrogen bond donors (HBD), and molecular weight (MW). A quantitative structure–activity relationship (QSAR) model24 and QVina2,48 which is a tool for discovering the minimum-energy docking conformation of a tested molecule and calculating its docking score, are also selectively used to evaluate drug activity for dopamine receptor D2 (DRD2) and the binding affinity to the 5-HT1B receptor, respectively.
P),45 topological polar surface area (TPSA),46 quantitative estimates of drug-likeness (QED),47 number of hydrogen bond acceptors (HBA), number of hydrogen bond donors (HBD), and molecular weight (MW). A quantitative structure–activity relationship (QSAR) model24 and QVina2,48 which is a tool for discovering the minimum-energy docking conformation of a tested molecule and calculating its docking score, are also selectively used to evaluate drug activity for dopamine receptor D2 (DRD2) and the binding affinity to the 5-HT1B receptor, respectively.
For combinatorial chemistry, fragment set B and its combination rules should be set. Accordingly, a modified version44 of the BRICS39 system was adopted (Fig. 2b,d). Since the best performance was achieved for approximately 2k action spaces in the preliminary experiments (ESI Note 2†), approximately 2k fragments were sampled from BRICS 40k for fragment set B. The BRICS fragment combination rules are rules to bind 16 molecular templates, where each template has a unique binding site (red digit in Fig. 2b).
In the training phase, our model was trained using the proximal policy optimization (PPO) algorithm,49 which is known to perform well in RL problems with discrete actions. This is because it has the advantages of stable training, sample efficiency, scalability, and flexibility. In the preliminary experiments, PPO performed optimally for our problem among several state-of-the-art RL algorithms (ESI Note 3†). An episode iteratively proceeds the process of selecting and combining molecular fragments from steps 0 to T (Fig. 2a). If one of the termination conditions cterm or target conditions ctrg are satisfied, the episode is prematurely terminated at the step. At step 0, an episode is started with a randomly selected fragment s0 (stage 1 in Fig. 2a), and the randomness of the initial fragment s0 creates more diverse output molecules  . Subsequently, action masking (stage 2 in Fig. 2a) is performed, which masks the actions that are not applicable to s0. Thereby, the fragment selection policy is enforced not to select the masked actions. This action masking helps to generate molecules that do not violate the chemical valence rule and enables efficient learning by reducing the action space. In this way, the fragment selection policy selects an action at step 0 (a0) from the unmasked actions.
. Subsequently, action masking (stage 2 in Fig. 2a) is performed, which masks the actions that are not applicable to s0. Thereby, the fragment selection policy is enforced not to select the masked actions. This action masking helps to generate molecules that do not violate the chemical valence rule and enables efficient learning by reducing the action space. In this way, the fragment selection policy selects an action at step 0 (a0) from the unmasked actions.
If the selected action at step t(at) is the end-action, the process is terminated. However, if at is a fragment, at is combined with st to make a combined molecule at step t (st+1). To evaluate the properties of a molecule, the molecule should not have any unfilled binding sites. Hence, the potential output molecule at step 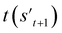 is derived by attaching hydrogen to the remaining binding site of st+1. Then, the interesting properties of
is derived by attaching hydrogen to the remaining binding site of st+1. Then, the interesting properties of 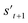 are evaluated to obtain the target error εt+1 and reward rt+1 at step t. Now, to check whether one of the termination conditions cterm or target conditions ctrg is satisfied, at, εt+1, and rt+1 are considered. If one of the termination conditions cterm or target conditions ctrg is satisfied, the reward rt+1 is used to update the policy. If any of the termination conditions cterm and target conditions ctrg is not satisfied, the environment outputs the combined molecule st+1. Then, the model iteratively proceeds to the next step of the process until either one of the termination conditions cterm or target conditions ctrg is satisfied. This process is repeated for a preset number of iterations to train the model.
are evaluated to obtain the target error εt+1 and reward rt+1 at step t. Now, to check whether one of the termination conditions cterm or target conditions ctrg is satisfied, at, εt+1, and rt+1 are considered. If one of the termination conditions cterm or target conditions ctrg is satisfied, the reward rt+1 is used to update the policy. If any of the termination conditions cterm and target conditions ctrg is not satisfied, the environment outputs the combined molecule st+1. Then, the model iteratively proceeds to the next step of the process until either one of the termination conditions cterm or target conditions ctrg is satisfied. This process is repeated for a preset number of iterations to train the model.
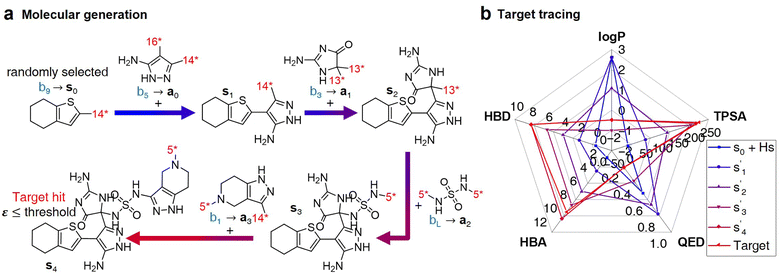
After the training is completed, the trained policy is used to generate a target molecule in the inference phase. Fig. 3a displays an example of molecular generation, in which new molecular fragments are selected and combined to complete a target molecule from steps 0 to 3. In the process, the properties of the generated potential output molecules (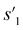 to
to 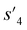 ), which are derived from hydrogen attachment of the combined molecules (s1 to s4), change from the properties of hydrogen attached initial fragment (s0 + Hs) to the target properties (log
), which are derived from hydrogen attachment of the combined molecules (s1 to s4), change from the properties of hydrogen attached initial fragment (s0 + Hs) to the target properties (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P: −0.488, TPSA: 220.83, QED: 0.207, HBA: 9, HBD: 8). In step 3, the properties of the potential output molecule
P: −0.488, TPSA: 220.83, QED: 0.207, HBA: 9, HBD: 8). In step 3, the properties of the potential output molecule 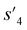 (log
(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P: −0.488, TPSA: 211.09, QED: 0.205, HBA: 10, HBD: 8) are close to the target properties (Fig. 3b). Since the target error ε4 is lower than the maximum target error εmax, the process is early terminated at step 3. Hence, the potential output molecule at step 3
P: −0.488, TPSA: 211.09, QED: 0.205, HBA: 10, HBD: 8) are close to the target properties (Fig. 3b). Since the target error ε4 is lower than the maximum target error εmax, the process is early terminated at step 3. Hence, the potential output molecule at step 3 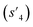 becomes the final output molecule.
becomes the final output molecule.
2.3 Materials extrapolation to hit multiple extreme target properties
In this section, we empirically demonstrate that RL-guided combinatorial chemistry enables the discovery of extrapolated compounds, which is not possible with probability distribution-learning models. To achieve this, we adopt two different types of probability distribution-learning models and compare their performance with our model in terms of materials extrapolation. One of the adopted models is a conditional recurrent neural network (cRNN).24 It serves as an NMT-based translator, translating input target properties into the corresponding molecular chemical language. As it operates as a translator, the input target properties and the corresponding molecular chemical language are one-to-one matched. The other model is the generative chemical transformer (GCT),23 a cVAE-based generative model. It utilizes the transformer's architecture as the backbone and incorporates a conditional latent space between its encoder and decoder. GCT generates chemical language corresponding to input target properties and sampled noise. As it functions as a generator using randomly sampled noise, it generates various molecular chemical languages with a single set of target properties.For the demonstration, we conducted experiments on generating molecules to hit multiple target properties. The experimental setup was borrowed from ref. 24. In the experiments, the following seven drug-related target properties were given to the models to generate target-hitting molecules: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA, QED, HBA, HBD, MW, and DRD2. This experiment falls under Task type A as specified in Fig. 2c. Since ε has multiple terms to minimize and multiple constraints, this toy problem covers complex optimization problems. By even changing the signs of some terms of ε, it is possible to cover complex optimization problems that involve a mix of minimization and maximization. Detailed information about the properties is summarized in Methods. Here, RDKit and a QSAR model for DRD2 (ref. 24) were adopted as evaluators.
P, TPSA, QED, HBA, HBD, MW, and DRD2. This experiment falls under Task type A as specified in Fig. 2c. Since ε has multiple terms to minimize and multiple constraints, this toy problem covers complex optimization problems. By even changing the signs of some terms of ε, it is possible to cover complex optimization problems that involve a mix of minimization and maximization. Detailed information about the properties is summarized in Methods. Here, RDKit and a QSAR model for DRD2 (ref. 24) were adopted as evaluators.
First, the original performances of cRNN24 and GCT23 in interpolation points were evaluated (Table 2). The two models were trained and tested with datasets24 curated from the ChEMBL database.20 Here, how well target-hitting molecules were generated for the given target properties—which were gathered from 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 molecules in the curated ChEMBL test data24—was evaluated. In contrast to the two methodologies, the proposed RL-CC approach in this paper requires retraining for each set of target properties. This makes it impractical for a realistic performance comparison in terms of interpolation, as training needs to be conducted individually for 149
679 molecules in the curated ChEMBL test data24—was evaluated. In contrast to the two methodologies, the proposed RL-CC approach in this paper requires retraining for each set of target properties. This makes it impractical for a realistic performance comparison in terms of interpolation, as training needs to be conducted individually for 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 properties. Additionally, RL-CC focuses on generating molecules with extreme properties, and thus, model performance in interpolation was not assessed for RL-CC.
679 properties. Additionally, RL-CC focuses on generating molecules with extreme properties, and thus, model performance in interpolation was not assessed for RL-CC.
To conduct the experiments on materials extrapolation, we adopted another molecular dataset with properties that were more widely distributed than the trained data:24 PubChem SARS-CoV-2 clinical trials50 (Fig. 4). Among the molecules in this dataset, 10 molecules were sampled whose properties were outside the trained data, which were then set as the extrapolated targets (C1 to C10). Since these 10 molecules were real molecules that exist in the real world, their properties would be physically feasible targets to generate. For each extrapolated target, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular generations were tried with cRNN24 and GCT.23
000 molecular generations were tried with cRNN24 and GCT.23
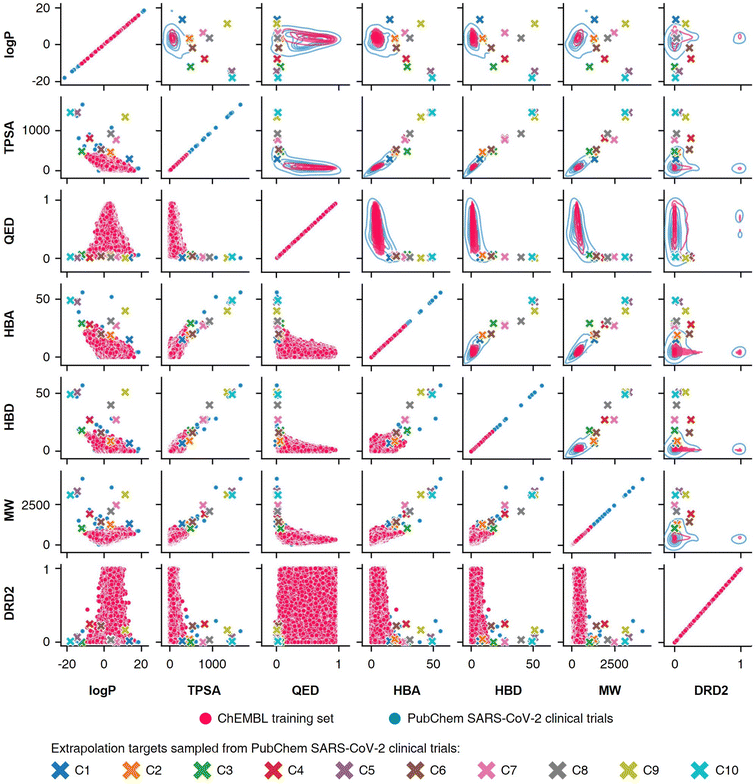 | ||
Fig. 4 Targets for materials extrapolation. The PubChem SARS-CoV-2 clinical trials dataset50 is more widely distributed than the ChEBML training dataset.20 The properties of five molecules in PubChem SARS-CoV clinical trials that deviated from the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P–TPSA distribution of the ChEMBL training dataset were set as extrapolation targets C1 to C5, and the properties of five molecules that deviated from the TPSA–QED distribution were set as extrapolation targets C6 to C10. P–TPSA distribution of the ChEMBL training dataset were set as extrapolation targets C1 to C5, and the properties of five molecules that deviated from the TPSA–QED distribution were set as extrapolation targets C6 to C10. | ||
To evaluate the performance of generating molecules that hit multiple target properties, the criteria for determining whether each target property was hit should be defined. Accordingly, in the experiment of materials interpolation with cRNN24 and GCT,23 the root mean squared error of each target property i (RMSEi) was analyzed (Table 1). Since all RMSEi for cRNN and GCT were not significantly different from each other, we determined that the magnitude of the average RMSEi represents the difficulty of generating molecules that hit the target property i. Therefore, by setting
represents the difficulty of generating molecules that hit the target property i. Therefore, by setting 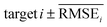 as the target bound of i, a wide bound was assigned to targets that were difficult to hit and a narrow bound was assigned to any targets that were easy to hit. In this context, the term ‘target-hitting molecule’ refers to molecules with properties that fall within the range of
as the target bound of i, a wide bound was assigned to targets that were difficult to hit and a narrow bound was assigned to any targets that were easy to hit. In this context, the term ‘target-hitting molecule’ refers to molecules with properties that fall within the range of 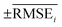 from the target values for each property.
from the target values for each property.
Table 2 shows the results for materials interpolation. In Table 2, the results of interpolation for a total of 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 target properties were rescaled to 10
679 target properties were rescaled to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for comparison with the extrapolation results. Since the number of attempted molecular generations for materials interpolation and extrapolation were different, the rescaled results based on 10
000 for comparison with the extrapolation results. Since the number of attempted molecular generations for materials interpolation and extrapolation were different, the rescaled results based on 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trials are summarized in Table 2 for comparison. For materials interpolation, the cRNN24 generated 2948 molecules that hit all of the seven targets (log
000 trials are summarized in Table 2 for comparison. For materials interpolation, the cRNN24 generated 2948 molecules that hit all of the seven targets (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA, QED, HBA, HBD, MW, and DRD2) simultaneously and 3774 molecules hit the five targets (log
P, TPSA, QED, HBA, HBD, MW, and DRD2) simultaneously and 3774 molecules hit the five targets (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA, QED, HBA, and HBD) simultaneously. With the same criteria, the GCT23 generated 2321 molecules that hit all seven targets and 3480 molecules hit the five targets simultaneously. These results confirmed that both models are able to generate target-hitting molecules in the trained region.
P, TPSA, QED, HBA, and HBD) simultaneously. With the same criteria, the GCT23 generated 2321 molecules that hit all seven targets and 3480 molecules hit the five targets simultaneously. These results confirmed that both models are able to generate target-hitting molecules in the trained region.
| Model | # Of valid mols (# of unique mols) | # Of all target-hitting mols w/o MW & DRD2 (# of unique mols.) | # Of all target-hitting mols (# of unique mols) | # Of each target-hitting mols | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
TPSA | QED | HBA | HBD | MW | DRD2 | ||||
| cRNN24 | 8475 (8475) | 3774 (3774) | 2948 (2948) | 6263 | 6459 | 6653 | 7627 | 8077 | 6897 | 7796 |
| GCT23 | 8715 (8715) | 3480 (3436) | 2321 (2290) | 6289 | 6916 | 6693 | 7013 | 8200 | 5890 | 8114 |
Results for materials extrapolation are shown in Table 3 and Fig. 5. According to the results, both probability distribution-learning models achieved poor results in terms of molecular extrapolation. For each target from C1 to C10 outside the trained data, we conducted 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trials to generate the molecules per target. As shown in the results for the targets C1 to C10 of Table 3 and Fig. 5, both probability distribution-learning models failed to generate molecules that hit all of the targets and did not generate molecules that hit the five targets. GCT23 only succeeded in generating seven valid and unique molecules that satisfied the chemical valence rule out of 100
000 trials to generate the molecules per target. As shown in the results for the targets C1 to C10 of Table 3 and Fig. 5, both probability distribution-learning models failed to generate molecules that hit all of the targets and did not generate molecules that hit the five targets. GCT23 only succeeded in generating seven valid and unique molecules that satisfied the chemical valence rule out of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trials, with four and three molecules being generated for targets C1 and C3, respectively. cRNN24 generated a total of 15
000 trials, with four and three molecules being generated for targets C1 and C3, respectively. cRNN24 generated a total of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068 chemically valid molecules, although only 21 were unique. In particular, 15
068 chemically valid molecules, although only 21 were unique. In particular, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 out of the 15
054 out of the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068 valid molecules were nonsensical outcomes that were overlapped and too small, such as CH4, CH4S, H2O, H2S, SO, H2OS, and H2S2. The MWs of these small molecules range from 16 and 66 Da. Considering that the target MWs of C1 to C10 ranged from 1026 to 3124 Da, it was difficult to conclude whether it operated correctly. Moreover, other generated molecules exhibited considerable deviations from the intended targets. Detailed information on the generated molecules is summarized in Tables S1–S4.†
068 valid molecules were nonsensical outcomes that were overlapped and too small, such as CH4, CH4S, H2O, H2S, SO, H2OS, and H2S2. The MWs of these small molecules range from 16 and 66 Da. Considering that the target MWs of C1 to C10 ranged from 1026 to 3124 Da, it was difficult to conclude whether it operated correctly. Moreover, other generated molecules exhibited considerable deviations from the intended targets. Detailed information on the generated molecules is summarized in Tables S1–S4.†
| Model | Extrapolated targets | # Of valid mols (# of unique mols) | # Of all target-hitting mols w/o MW & DRD2 (# of unique mols) | # Of all target-hitting mols (# of unique mols) | # Of each target-hitting mols | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P P |
TPSA | QED | HBA | HBD | MW | DRD2 | |||||
| RL-CC (this work) | C10 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9999) 000 (9999) |
23 (23) | 0 (0) | 820 | 1133 | 9978 | 5533 | 2618 | 0 | 35 |
| C9 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (10 000 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
289 (289) | 0 (0) | 3919 | 1432 | 9995 | 7880 | 3223 | 1 | 15 | |
| C8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9998) 000 (9998) |
181 (181) | 0 (0) | 2999 | 974 | 9992 | 6273 | 2379 | 466 | 133 | |
| C7 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9996) 000 (9996) |
321 (321) | 0 (0) | 3686 | 1420 | 9971 | 7832 | 3588 | 531 | 28 | |
| C6 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9981) 000 (9981) |
1709 (1708) | 311 (311) | 3769 | 3450 | 9890 | 8636 | 7301 | 1445 | 8729 | |
| C5 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (10 000 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
14 (14) | 0 (0) | 1607 | 1377 | 9981 | 7381 | 2363 | 0 | 26 | |
| C4 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9969) 000 (9969) |
439 (439) | 50 (50) | 1972 | 1452 | 9809 | 7283 | 4384 | 572 | 9493 | |
| C3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9869) 000 (9869) |
913 (877) | 233 (224) | 3143 | 2296 | 9940 | 8392 | 7143 | 1128 | 8310 | |
| C2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9987) 000 (9987) |
2424 (2424) | 366 (366) | 6738 | 3145 | 9928 | 8415 | 8635 | 1388 | 4970 | |
| C1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (9994) 000 (9994) |
1317 (1317) | 355 (355) | 5202 | 2282 | 9918 | 9347 | 8622 | 1849 | 9406 | |
| cRNN24 | C10 | 422 (2) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 422 |
| C9 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C8 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C7 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C6 | 6 (6) | 0 (0) | 0 (0) | 0 | 0 | 6 | 1 | 0 | 0 | 5 | |
| C5 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C4 | 9836 (1) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C3 | 3022 (5) | 0 (0) | 0 (0) | 0 | 0 | 4 | 2 | 1 | 0 | 3022 | |
| C2 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C1 | 1788 (10) | 0 (0) | 0 (0) | 0 | 0 | 4 | 1 | 1 | 0 | 1788 | |
| GCT23 | C10 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C9 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C8 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C7 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C6 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C5 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C4 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C3 | 3 (3) | 0 (0) | 0 (0) | 0 | 0 | 3 | 1 | 0 | 0 | 3 | |
| C2 | 0 (0) | 0 (0) | 0 (0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| C1 | 4 (4) | 0 (0) | 0 (0) | 0 | 0 | 1 | 0 | 0 | 0 | 4 | |
For the targets C1, C2, C3, C4, and C6, our RL-guided combinatorial chemistry generated a total of 1315 target-hitting molecules that hit all seven targets simultaneously. Here, 355, 366, 233, 50, and 311 molecules that hit all targets were generated for targets C1, C2, C3, C4, and C6, respectively. For targets C5, C7, C8, C9, and C10, RL-guided combinatorial chemistry could not generate molecules that hit all seven target properties. However, it successfully generated a total of 828 molecules that hit five target properties that failed with the probability distribution-learning models. Here, 14, 321, 181, 289, and 23 molecules that hit five targets were generated for targets C5, C7, C8, C9, and C10, respectively.
Also, in fact, it is hard to assert that it completely failed to hit the seven target properties simultaneously for the targets C5, C7, C8, C9, and C10. For these targets, the generated molecules exhibited low target-hitting errors. This means that if the target bounds were more broadly set, there would be more molecules that were counted as molecules that hit all targets. It should be noted that the employed MW target bound ±7.113 Da and DRD2 target bound ±0.105 were fairly narrow (see Table 1). The target bound of MW 7.113 Da was so small that it was less than the weight of a single atom. Furthermore, the target bound of DRD2 0.105 was considerably smaller than the commonly known drug activity prediction accuracy of QSAR models. In ref. 24, the QSAR model for DRD2 was used as a binary classifier to evaluate as either active (when the predicted value was >rbin 0.5) or inactive (≤0.5). For this reason, we believe that the number of molecules hitting the targets MW and DRD2 was less counted than the number of molecules hitting the other targets (see MW-column and DRD2-column of RL-CC in Table 3). Hence, we conducted a supplementary experiment on another dataset to generate five target-hitting molecules, excluding MW and DRD2 (ESI Note 1†). As a result, we confirmed that our model successfully generated molecules with extreme properties outside the known domain, which is not possible with probability distribution-learning models.
Moreover, RL-CC uses a selective binding approach within combinable molecular fragments based on the BRICS fragment combination rules. As a result, all generated molecules adhered to the chemical valence constraints, ensuring a 100% chemically valid. Furthermore, even when extreme target properties were specified, the diversity of chemically valid generated molecules remained remarkably high as seen in Fig. 5.
When choosing the molecular candidates, it is also important to consider the synthesizability of the generated molecules. Thus, we have analyzed the synthetic accessibility (SA) score of the generated molecules using RDKit, which represents the ease of chemical compounds to be synthesized or produced. SA score is evaluated by considering how common the fragments composing the molecule are and the complexity of intricate ring structures such as fused rings. The SA scores for the generated molecules are presented in Fig. S6.† The calculated results indicate that the generated molecules consistently exhibit low SA scores, excluding cases with extremely high molecular weights as seen in the experiment for generating molecules with extreme target properties. This suggests a reasonable level of synthesizability for the generated molecules.
2.4 Application to the discovery of protein docking molecules
The discovery of small molecules that dock to a target protein is a practical problem in drug discovery. Moreover, binding affinity to a target receptor is an important indicator for measuring drug–target interactions.3 Since molecules with higher binding affinity to the target protein (compared to other proteins) can be considered as having high selectivity and docking ability, the discovery of molecules that maximize target binding affinity is a key objective in protein docking drug discovery.51 Therefore, to generate molecules with a low docking score, which means to generate molecules that can bind strongly with 5-HT1B in this case, the trained policy attaches fragments that can maximize the reward.In this section, we demonstrate that RL-guided combinatorial chemistry can discover molecules that maximize the binding affinity towards the 5-hydroxytryptamine receptor 1B (5-HT1B receptor), which is related to mental diseases. A detailed description of the 5-HT1B receptor is summarized in Methods. We adopted QVina2 (ref. 48) (a data-free molecular docking simulator) to discover the minimum-energy docking conformation. This simulator evaluates the docking score quickly and reliably. Since the docking score is an indicator that is inversely proportional to the binding affinity, the reward function was set as the negative docking score.
To evaluate the performance of RL-guided combinatorial chemistry, the docking scores of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecules from our model were compared with the docking scores of two other molecular sets. One was a set of 1871 molecules that were generated to maximize the negative docking score towards the 5-HT1B receptor using fragment-based generative RL with explorative experience replay for drug design (FREED),2 which is reported in the paper. The other set was 10
000 generated molecules from our model were compared with the docking scores of two other molecular sets. One was a set of 1871 molecules that were generated to maximize the negative docking score towards the 5-HT1B receptor using fragment-based generative RL with explorative experience replay for drug design (FREED),2 which is reported in the paper. The other set was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules that were randomly sampled from ChEMBL20 drug-like molecules. The docking scores of the three sets are summarized in Fig. 6a, which were calculated with QVina2. The calculation configuration is described in ESI Note 4.† The best molecule with the lowest docking score was discovered from our model and the median docking score for the sets was also the lowest. The top 10 generated molecular structures with the highest pIC50 for CCR5, INT, and RT are illustrated in Fig. S8–S10.†
000 molecules that were randomly sampled from ChEMBL20 drug-like molecules. The docking scores of the three sets are summarized in Fig. 6a, which were calculated with QVina2. The calculation configuration is described in ESI Note 4.† The best molecule with the lowest docking score was discovered from our model and the median docking score for the sets was also the lowest. The top 10 generated molecular structures with the highest pIC50 for CCR5, INT, and RT are illustrated in Fig. S8–S10.†
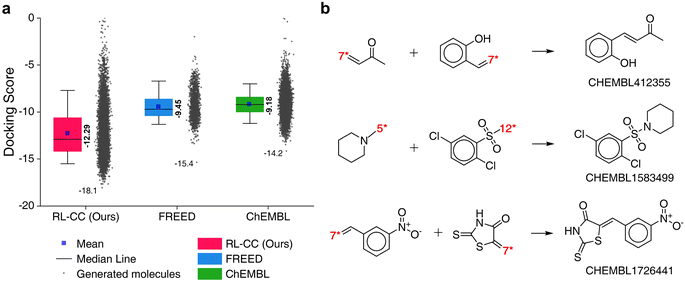 | ||
Fig. 6 Generated 5-HT1B receptor docking materials. (a) Comparison of docking scores for the three molecular sets. Pink indicates the docking scores of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecules from RL-guided combinatorial chemistry. Green indicates the docking scores of 10 000 generated molecules from RL-guided combinatorial chemistry. Green indicates the docking scores of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 drug-like molecules that were randomly sampled from ChEMBL20 database. Blue indicates the docking scores of 1871 molecules generated by FREED.2 The 1871 molecules have been reported as de novo cases with 4-step in the paper. It should be noted that the maximum number of fragments constituting a compound was the same as ours. The docking scores of the 1871 molecules were re-evaluated using QVina2 (ref. 48) under the same calculation configuration as ours. The mean and minimum docking score for each outcome are represented numerically, while the box is set with percentiles 25 and 75, and the whiskers extend to the 5th and 95th percentiles. (b) Three molecular examples that were generated by RL-guided combinatorial chemistry, which exactly matched with active drug molecules reported in the PubChem Bioassay database.52 000 drug-like molecules that were randomly sampled from ChEMBL20 database. Blue indicates the docking scores of 1871 molecules generated by FREED.2 The 1871 molecules have been reported as de novo cases with 4-step in the paper. It should be noted that the maximum number of fragments constituting a compound was the same as ours. The docking scores of the 1871 molecules were re-evaluated using QVina2 (ref. 48) under the same calculation configuration as ours. The mean and minimum docking score for each outcome are represented numerically, while the box is set with percentiles 25 and 75, and the whiskers extend to the 5th and 95th percentiles. (b) Three molecular examples that were generated by RL-guided combinatorial chemistry, which exactly matched with active drug molecules reported in the PubChem Bioassay database.52 | ||
To check if potential drug molecules were found among the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecules, we investigated whether any generated molecules were an exact match with the drug-like molecules in the ChEMBL20 database. There were 23 molecules whose molecular structures exactly matched with real drug-like molecules in the ChEMBL database, of which 13 out of the 23 molecules had labels on drug activity (active or inactive). It should be noted that ref. 40 roughly estimated the number of small organic molecules as 1060, of which only 2.2 × 106 were included in the ChEMBL database.20 Hence, it was difficult to find molecules with an exact match. An interesting finding is that five (CHEMBL1583499, CHEMBL1726441, CHEMBL412355, CHEMBL2261013, and CHEMBL99068) of the 13 molecules had been reported as active for some targets. Among these, three (CHEMBL1583499, CHEMBL1726441, and CHEMBL412355) were active in the related roles in which the 5-HT1B docking molecules have been reported to have an effect. For example, CHEMBL1726441 is reported to be active for various targets such as corticotropin-releasing factor receptor 2, Rap guanine nucleotide exchange factor 4, Nuclear factor erythroid 2-related factor 2, and Geminin. These targets have been reported to act in the human brain and peripheral tissues, playing a psychopathological role53 and controlling brain function.54 These investigations were conducted with the PubChem Bioassay database.52 The other investigated results for the two remaining molecules (CHEMBL2261013 and CHEMBL99068) are summarized in Table S7.†
000 generated molecules, we investigated whether any generated molecules were an exact match with the drug-like molecules in the ChEMBL20 database. There were 23 molecules whose molecular structures exactly matched with real drug-like molecules in the ChEMBL database, of which 13 out of the 23 molecules had labels on drug activity (active or inactive). It should be noted that ref. 40 roughly estimated the number of small organic molecules as 1060, of which only 2.2 × 106 were included in the ChEMBL database.20 Hence, it was difficult to find molecules with an exact match. An interesting finding is that five (CHEMBL1583499, CHEMBL1726441, CHEMBL412355, CHEMBL2261013, and CHEMBL99068) of the 13 molecules had been reported as active for some targets. Among these, three (CHEMBL1583499, CHEMBL1726441, and CHEMBL412355) were active in the related roles in which the 5-HT1B docking molecules have been reported to have an effect. For example, CHEMBL1726441 is reported to be active for various targets such as corticotropin-releasing factor receptor 2, Rap guanine nucleotide exchange factor 4, Nuclear factor erythroid 2-related factor 2, and Geminin. These targets have been reported to act in the human brain and peripheral tissues, playing a psychopathological role53 and controlling brain function.54 These investigations were conducted with the PubChem Bioassay database.52 The other investigated results for the two remaining molecules (CHEMBL2261013 and CHEMBL99068) are summarized in Table S7.†
2.5 Application to discovery of HIV inhibitors
This section describes experiments in which RL-guided combinatorial chemistry was applied to discover HIV inhibitors. Here, we selected three HIV inhibition targets: C–C chemokine receptor type 5 (CCR5), HIV integrase (INT), and HIV reverse transcriptase (RT). Detailed information about the targets is summarized in Methods. To evaluate the HIV inhibition potency of molecules, pIC50 predictors4 for the three HIV inhibition targets were adopted. It should be noted that pIC50 is equal to −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IC50, where IC50 is an indicator that measures the amount of a particular inhibitory substance required to inhibit a given biological process or biological component by 50%. In other words, the lower the value of IC50, the higher the HIV inhibition potency. Moreover, the higher the value of pIC50, the higher the HIV inhibition potency. Therefore, we set pIC50 as the reward function to make our model discover HIV inhibitors with high potency.
IC50, where IC50 is an indicator that measures the amount of a particular inhibitory substance required to inhibit a given biological process or biological component by 50%. In other words, the lower the value of IC50, the higher the HIV inhibition potency. Moreover, the higher the value of pIC50, the higher the HIV inhibition potency. Therefore, we set pIC50 as the reward function to make our model discover HIV inhibitors with high potency.
In total, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecules from our model were compared with the same number of molecules randomly combined by no-policy combinatorial chemistry (Fig. 7a). For all the HIV inhibition targets, molecules generated by our model exhibited significantly higher pIC50 values compared to those of random combination without a policy (original combinatorial chemistry). This result indicated that our model learned the fragment-selection policy to discover the intended substances. The benchmark results compared to the other four generators for HIV inhibitors are summarized in Table S9,† in which our model achieved the highest pIC50 values for targets CCR5 and RT. The top 10 generated molecular structures with the lowest docking score are illustrated in Fig. S7.†
000 generated molecules from our model were compared with the same number of molecules randomly combined by no-policy combinatorial chemistry (Fig. 7a). For all the HIV inhibition targets, molecules generated by our model exhibited significantly higher pIC50 values compared to those of random combination without a policy (original combinatorial chemistry). This result indicated that our model learned the fragment-selection policy to discover the intended substances. The benchmark results compared to the other four generators for HIV inhibitors are summarized in Table S9,† in which our model achieved the highest pIC50 values for targets CCR5 and RT. The top 10 generated molecular structures with the lowest docking score are illustrated in Fig. S7.†
 | ||
Fig. 7 Results for HIV inhibitors discovery with high pIC50 for three HIV inhibition targets: CCR5, INT, and RT. (a) Comparison of pIC50 for two molecular sets. Pink indicates pIC50 for a set of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules generated by RL-guided combinatorial chemistry. Blue indicates pIC50 for a set of 10 000 molecules generated by RL-guided combinatorial chemistry. Blue indicates pIC50 for a set of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 drug-like molecules that were randomly sampled from the ChEMBL database.20 The mean and maximum pIC50 values for each outcome are represented numerically, while the box is set with percentiles 25 and 75, and the whiskers extend to the 5th and 95th percentiles. (b) Policy changes in BRICS molecular fragment selection according to the training steps. The left-hand side of the figure shows the number of appearances for 25 molecular fragments with the biggest change. The vertical and horizontal axes of the left-hand side blue–red plot represent the type of fragment and the training iteration, respectively. Blue–red indicates the number of generated molecules that have the fragment among the 10 000 drug-like molecules that were randomly sampled from the ChEMBL database.20 The mean and maximum pIC50 values for each outcome are represented numerically, while the box is set with percentiles 25 and 75, and the whiskers extend to the 5th and 95th percentiles. (b) Policy changes in BRICS molecular fragment selection according to the training steps. The left-hand side of the figure shows the number of appearances for 25 molecular fragments with the biggest change. The vertical and horizontal axes of the left-hand side blue–red plot represent the type of fragment and the training iteration, respectively. Blue–red indicates the number of generated molecules that have the fragment among the 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 generated molecules. 000 generated molecules. | ||
To analyze the policy change of molecular fragment selection in the training phase, we generated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules at the end of every training iteration. The derived frequencies (how many molecules had the fragment) for 25 fragments with the biggest change are plotted on the left of Fig. 7b. In the initial state (where no policy was learned), the frequency of all fragments was similar. As the training progressed, the frequency of each fragment became varied. Although the selected frequency of some fragments increased as training proceeded, some of them decreased at certain points. This is because the agent found the combinations of molecular fragments that provided a high reward. Hence, the selection of other fragments that did not have any merit in the pIC50 score rapidly decreased. The most selected fragments differed according to the type of HIV inhibition targets. Since the fragments were most often used to maximize the pIC50 for each target, we hypothesize that they may be key structures for HIV inhibitors on each target.
000 molecules at the end of every training iteration. The derived frequencies (how many molecules had the fragment) for 25 fragments with the biggest change are plotted on the left of Fig. 7b. In the initial state (where no policy was learned), the frequency of all fragments was similar. As the training progressed, the frequency of each fragment became varied. Although the selected frequency of some fragments increased as training proceeded, some of them decreased at certain points. This is because the agent found the combinations of molecular fragments that provided a high reward. Hence, the selection of other fragments that did not have any merit in the pIC50 score rapidly decreased. The most selected fragments differed according to the type of HIV inhibition targets. Since the fragments were most often used to maximize the pIC50 for each target, we hypothesize that they may be key structures for HIV inhibitors on each target.
2.6 Expansion potential for discovery of organic materials
Fig. 8a and b illustrate the results of fragmenting TADF emitters for single-layer OLED by leveraging the BRICS fragment combination rules in reverse. Examination of the fragments depicted in Fig. 8a reveals that by inversely applying the BRICS fragment combination rules, it is possible to fragment the emitter into acceptor, donor, and bridge components, aligning with the knowledge of designing photoactive materials. However, the emitter shown in Fig. 8b displays a chunk where the combination of acceptor and bridge remains undivided. This occurrence is due to the BRICS rules covering only the bonds between C, N, O, and S elements, lacking rules for bonds at the B–X binding sites marked in blue in Fig. 8b. Consequently, this highlights a limitation that for the BRICS rules to encompass a wider range of organic materials beyond drugs, there is a need to incorporate additional rules for various elemental bonds. Fig. 8c and d show the fragmentation results of organic flame retardant materials using the BRICS fragment combination rules in reverse. These results indicate that if the BRICS fragment combination rules are well-expanded and inversely applied to construct the fragment set of targeted materials, RL-CC has the potential to be sufficiently extended to the discovery of organic materials.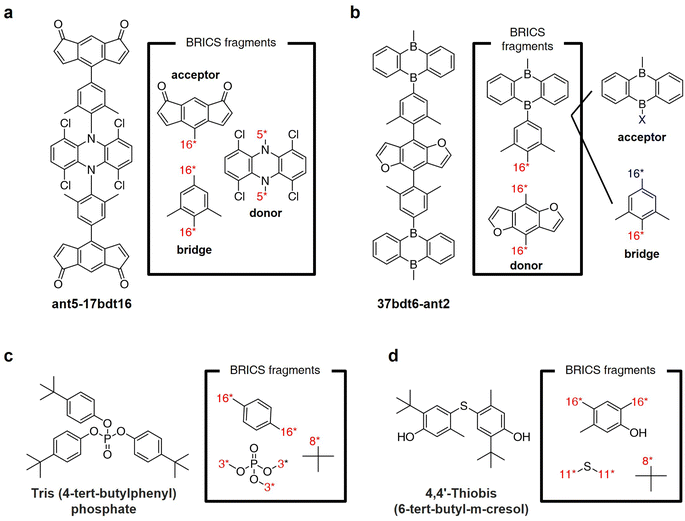 | ||
| Fig. 8 BRICS fragmentation of organic materials. (a and b) Thermally-activated delayed fluorescence (TADF) emitters for single-layer OLED reported in ref. 55. (c and d) Flame retardant materials reported in ref. 56. | ||
3 Conclusion
From a data science perspective, the discovery of better than previously known is to find new substances with properties outside outliers. In particular, research on inverse molecular design models with extrapolated target properties can be considered as fundamental groundwork for materials extrapolation. Most of the reported inverse molecular design models are based on data probability distribution-learning models, such as machine translators and generative models (including Seq2Seq,25 Transformer,26 GAN,29 and VAE30). However, these models are too limited for use in materials extrapolation, which requires discovering substances in the untrained area. To solve this problem, we adopted combinatorial chemistry,38 which generates molecules from combinations of randomly selected molecular fragments. Fundamentally, it is a rule-based molecular designer for generating all chemically possible molecular structures that can be obtained from the combination of molecular fragments. However, since the lack of a molecular fragment selection policy can cause a combinatorial explosion,41 RL is applied to train its fragment-selection policy to provide a direction toward target substances.This paper contains three major contributions. First, we theoretically demonstrated that most inverse molecular design models based on probability distribution-learning of data are too limited for use in materials extrapolation. Second, we empirically demonstrated that our proposed RL-guided combinatorial chemistry works well on various discovery problems with extreme/extrapolated properties, such as the discovery of multiple target-hitting molecules, protein docking molecules, and HIV inhibitors. Since the BRICS39 system is designed based on drug-like molecules, our applications were limited to the discovery of drug molecules. For these reasons, we have shown the feasibility of applying the proposed methodology to the discovery of organic materials by using the BRICS fragment bonding rules in reverse to decompose molecules of organic materials. This also highlights the limitations of the BRICS fragment combination rules that need to be addressed in order to further extend the scope of materials discovery. The problems addressed in this study exhibit significant overlap with practical materials discovery issues. For instance, photoactive materials used in applications such as organic light-emitting displays, solar cells, optical sensors, bioelectronic devices, and liquid crystal displays are compounds designed through combinations of molecular fragments. The common goals of these photoactive materials discovery are finding new and better materials that satisfy target properties, such as the energies of the S0, S1, T1 states, and their gaps. Additionally, considerations for band gaps in semiconductors and transport properties in battery electrolytes fall within these kinds of problems. Third, the limitations of our model were also analyzed in Methods. One of these was that re-training would be required to discover multiple target-hitting molecules if the targets were changed. The other limitation was a sparse reward problem that interrupted the discovery of materials with extreme properties. However, ongoing research efforts aimed at addressing these limitations suggest that they can be resolved through future studies.
4 Methods
4.1 Molecular descriptors
For the experiment in materials extrapolation, where the aim was to hit multiple extreme target properties, seven properties were set: logarithm of the calculated octanol–water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P);45 topological polar surface area (TPSA);46 quantitative estimate of drug-likeness (QED);47 number of hydrogen bond acceptors (HBA); number of hydrogen bond donors (HBD); molecular weight (MW); and drug activity for dopamine receptor D2 (DRD2). Each property is considered important in the field of drug discovery. The term log
P);45 topological polar surface area (TPSA);46 quantitative estimate of drug-likeness (QED);47 number of hydrogen bond acceptors (HBA); number of hydrogen bond donors (HBD); molecular weight (MW); and drug activity for dopamine receptor D2 (DRD2). Each property is considered important in the field of drug discovery. The term log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P is a descriptor for the lipophilicity of a molecule, which refers to a molecule's capacity to dissolve in fats or oils. This is an important property in drug design since it has an impact on the molecule's capacity for penetrating cell membranes and reaching its intended target. The term TPSA is a calculated descriptor of the polar surface area (PSA) of a molecule, which refers to the area of a molecule having polar functional groups that could form hydrogen bonds with water molecules. A molecule is less polar and more likely to be able to penetrate cell membranes if it has a lower PSA value. The terms HBA and HBD are also important properties in drug design because they can affect a molecule's capacity to interact with other molecules through hydrogen bonding. Hydrogen bonding is frequently used in drug design to facilitate the binding of a molecule to the target receptor. Moreover, hydrogen bonding can affect a drug molecule's solubility and permeability, which influence its pharmacological properties. Term MW is a descriptor used in drug discovery, as it can affect a drug's pharmacokinetics, efficacy, and safety. This is because the size of the molecules can influence a drug's absorption, distribution, metabolism, or degree of penetration into the cell membrane. The correct molecular weight of a drug depends on its application. However, most drugs generally comprise small molecules with a molecular weight of less than 500 Da. This is because drug molecules have a higher likelihood of passing through a cell's membrane and have a lower likelihood of being affected by biometabolic reactions. The term QED is a metric used to evaluate a molecule's overall drug-likeness, which is a geometric mean of log
P is a descriptor for the lipophilicity of a molecule, which refers to a molecule's capacity to dissolve in fats or oils. This is an important property in drug design since it has an impact on the molecule's capacity for penetrating cell membranes and reaching its intended target. The term TPSA is a calculated descriptor of the polar surface area (PSA) of a molecule, which refers to the area of a molecule having polar functional groups that could form hydrogen bonds with water molecules. A molecule is less polar and more likely to be able to penetrate cell membranes if it has a lower PSA value. The terms HBA and HBD are also important properties in drug design because they can affect a molecule's capacity to interact with other molecules through hydrogen bonding. Hydrogen bonding is frequently used in drug design to facilitate the binding of a molecule to the target receptor. Moreover, hydrogen bonding can affect a drug molecule's solubility and permeability, which influence its pharmacological properties. Term MW is a descriptor used in drug discovery, as it can affect a drug's pharmacokinetics, efficacy, and safety. This is because the size of the molecules can influence a drug's absorption, distribution, metabolism, or degree of penetration into the cell membrane. The correct molecular weight of a drug depends on its application. However, most drugs generally comprise small molecules with a molecular weight of less than 500 Da. This is because drug molecules have a higher likelihood of passing through a cell's membrane and have a lower likelihood of being affected by biometabolic reactions. The term QED is a metric used to evaluate a molecule's overall drug-likeness, which is a geometric mean of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, HBA, HBD, PSA, number of rotatable bonds (ROTB), number of aromatic rings (AROM), and number of structural alerts (ALERTS). A molecule with a high QED value is more likely to be a promising drug candidate. Finally, DRD2 refers to a drug's activity toward dopamine receptor D2. The dopaminergic neurotransmission is regulated by the G protein-coupled receptor dopamine receptor D2, which is mainly expressed in the brain.
P, HBA, HBD, PSA, number of rotatable bonds (ROTB), number of aromatic rings (AROM), and number of structural alerts (ALERTS). A molecule with a high QED value is more likely to be a promising drug candidate. Finally, DRD2 refers to a drug's activity toward dopamine receptor D2. The dopaminergic neurotransmission is regulated by the G protein-coupled receptor dopamine receptor D2, which is mainly expressed in the brain.
In the experiment aimed at discovering protein docking molecules, QVina2 (ref. 48)—a tool to discover the minimum-energy docking conformation and calculate its docking score—was employed to compute a docking score. This score is proportional to the binding strength between a drug molecule and its target. QVina2 calculates the docking score by simulating how a drug molecule interacts with a given target receptor in a three-dimensional simulation box. We targeted the protein receptor 5-HT1B. Many studies have reported that activating 5-HT1B receptors outside the brain has vascular effects (such as pulmonary vasoconstriction, which can help treat angina57). Moreover, reduced 5-HT1B heteroreceptor activity can increase impulsive behavior, whereas reduced 5-HT1B autoreceptor activity can have an antidepressant-like effect.58,59
In the experiment aimed at discovering HIV inhibitors, we selected three HIV-related targets: C–C chemokine receptor 5 (CCR5), HIV integrase (INT), and HIV reverse transcriptase (RT). Here, CCR5 is the immune system-related protein, which is found on the surface of white blood cells. Along with C–X–C chemokine receptor 4, it is a key co-receptor for HIV entry.60 The second target was INT, which is involved in viral replication and facilitates the viral cDNA's insertion into the infected cells.1 The final target was RT, which triggers the reverse transcription process. Here, the process can cause mutation and recombination that form the genetic diversity of HIV, enabling the formation of viral variants that could evade host immune responses, rendering the virus resistant to medication treatments.61 For each target in the experiment, we tried to maximize its pIC50 value, which is a descriptor for the potency of a drug in inhibiting a biological activity. It is calculated as the negative logarithm of the IC50 value, which is the amount of a drug that inhibits 50% of the biological activity. In other words, the drug's potency increases as the IC50 value decreases. In drug discovery, IC50 is commonly utilized to compare the effectiveness of potential drug candidates.
4.2 Fragment set configuration
Two types of fragment sets were used in this study. One set contained 2207 BRICS fragments that appeared more than 150 times in the training set24 curated from the ChEMBL database20 (release version 25). This fragment set was used for three major experiments: the discovery of seven target-hitting molecules, protein docking materials, and HIV inhibitors. For the supplementary experiment aimed at discovering five target-hitting molecules (ESI Note 1†), another fragment set containing 2547 BRICS fragments that appeared more than 100 times in the training set of the MOSES database19 was used. The detailed reasoning for using these fragment sets is described in ESI Note 2.†4.3 Action masking
For efficient learning, we applied action masking to our model (stage 2 in Fig. 2a). Based on the molecule in the current state, the list of actions that the agent can choose is limited by action masking. Since our model combines fragments according to BRICS fragment combination rules, the fragments that could not be connected to the molecule in the current state were masked. Thereby, more efficient learning was possible since the number of selectable actions in the current state was reduced, which improved the performance of our model (ESI Note 3†).4.4 Target properties and calculation of molecular descriptors
In this study, three major experiments were conducted to generate molecules with extreme properties. In the first experiment, discovering molecules that could hit the multiple target properties was attempted. In the other experiments, discoveries of molecules that maximize interesting properties were attempted. Accordingly, the interesting properties could be calculated by the evaluators in the environment of the RL model. The detailed information on model accuracy can be found in ESI Note 7.†For the first experiment on materials extrapolation to hit multiple extreme target properties, seven molecular descriptors were set as the targets: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P,45 TPSA,46 QED,47 HBA, HBD, MW, and DRD2.24 Here, the DRD2 was calculated using a QSAR model for DRD2,24 while the other descriptors were calculated using RDKit.44 We selected 10 target sets of molecular properties out of known molecular data and attempted to generate the target-hitting molecules to demonstrate that our model would work well in terms of materials extrapolation. These 10 target sets of extreme properties were taken from an untrained dataset—PubChem SARS-CoV-2 clinical trials50—whose molecular properties are more widely distributed than the training data set24 (Fig. 4). Since the 10 target sets of extreme properties were taken from real molecules, they could be considered chemically feasible targets to discover.
P,45 TPSA,46 QED,47 HBA, HBD, MW, and DRD2.24 Here, the DRD2 was calculated using a QSAR model for DRD2,24 while the other descriptors were calculated using RDKit.44 We selected 10 target sets of molecular properties out of known molecular data and attempted to generate the target-hitting molecules to demonstrate that our model would work well in terms of materials extrapolation. These 10 target sets of extreme properties were taken from an untrained dataset—PubChem SARS-CoV-2 clinical trials50—whose molecular properties are more widely distributed than the training data set24 (Fig. 4). Since the 10 target sets of extreme properties were taken from real molecules, they could be considered chemically feasible targets to discover.
For the experiment to discover protein docking materials, the calculated docking score between a docking molecule and 5-HT1B protein receptor was set as the target. The docking score was calculated using QVina2,48 which calculates the docking score of a docking molecule by searching for its minimum-energy docking conformation. This program employs an empirical scoring function to predict the docking score, which includes several terms that incorporate various physical and chemical interactions between the ligand and protein. These interactions include van der Waals interactions, electrostatic interactions, hydrogen bonds, and solvation effects. Moreover, QVina2 makes use of finely tuned scoring function parameters that are derived using many experimentally-identified ligand–protein complexes. It calculates a docking score for each docking posture it produces, with the lowest value being the most energetically favorable binding conformation. The detailed calculation configuration for QVina2 is illustrated in ESI Note 4.†
For the experiment to discover HIV inhibitors, the target property was set to maximize the pIC50 score to three HIV-related targets: CCR5, INT, and RT. Each pIC50 score was calculated by the light gradient boosting machine (LGBM)62-based QSAR models2 for the three HIV-related targets.4 In addition, the QSAR model was trained to predict the pIC50 value for each target using the ChEMBL dataset.20
4.5 Training loop
To maximize the cumulative reward for sequential actions, RL trains its agent to learn which action to choose at each step. In this study, the action is a selection of a molecular fragment. The reward is the value calculated with the evaluator(s) by the experiment-specific reward function. By repeating this process, the policy that selects an action that can maximize the cumulative reward is gradually updated. After sufficient learning, the policy could then select sequential actions to generate a desired molecule that fits the given task.The episode proceeds from steps 0 to T, where T is the designated maximum fragment number of the molecule. To generate diverse molecules, the first fragment is randomly selected. When selecting the next molecular fragment to be combined with the current molecule, action masking is conducted. In the process of action masking, the molecular fragments that cannot be combined with the current molecule are masked according to the BRICS fragmentation combination rules. Subsequently, the policy selects a molecular fragment from the unmasked fragments and binds it to an unfilled binding site. If the combined molecule still has any unfilled binding sites, hydrogen atoms are attached to derive a complete molecule and evaluate its properties of the current state. When a molecule that meets the set of criteria is generated, the fragment attachment is stopped and the episode ends early before reaching step T. Otherwise, the process is repeated during step T. After the final output molecule is generated, a reward for the episode is calculated depending on how closely the targets are hit. Since the reward is given only at the end of an episode, the policy undergoes updates aimed at achieving a global solution rather than a local one. By iteratively conducting the training episodes, the agent of RL learns a policy that maximizes the given reward function. The episode training is repeated until a preset number of training iterations is reached. For each experiment, the training iteration was set to 750, 80, and 250 times.
Training for a predefined number of iterations was conducted using an Intel Xeon Gold 6226R. For each experiment, it took 12, 140, and 30 hours, respectively. The variation in training times arises from differences in the time required for property prediction and the batch size used at each training iteration. For each experiment, it takes an average of 0.35, 0.7, and 15 seconds, respectively, to predict the properties at each step. Additionally, the models' accuracy can be found in ESI Note 7 and Table S10.† For our model, retraining is required from scratch each time the target changes. Although transfer learning and other techniques for high efficiency may be considered in the future, they have not been applied as of now. In materials discovery, a fixed target is typically provided once the problem is given, enabling the training of the policy only once, and subsequent inference can be repeated at a low cost.
4.6 Rewards and terminations
In RL, it is important to have an appropriate set of termination conditions and target conditions to learn a decent policy. In all three experiments conducted in this study, there were two common termination conditions. First, molecular generation was terminated when the number of fragments that make up a compound in the current state neval exceeded the maximum number of fragments nmax, which was set to 50, 4, and 6 for each experiment. Second, the process was terminated when the number of unfilled binding sites nL was equal to zero.For the experiment on materials extrapolation to hit multiple extreme target properties, the process was terminated if the MW in the current state MWeval exceeded the maximum MW (MWmax = 3500 Da). Furthermore, it was also terminated if the error (ε) was less than the error threshold εth = 0.05. Here, ε was calculated as
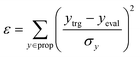 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, TPSA, QED, HBA, HBD, MW, and DRD2.
P, TPSA, QED, HBA, HBD, MW, and DRD2.
The design of the reward function is also important since RL is performed based on the reward obtained by taking an action. Moreover, a penalty can be given to avoid any undesired actions. For the experiment on materials extrapolation to hit multiple extreme target properties, the reward function r was designed as follows:
 | (6) |
For the other two experiments (discovery of protein docking materials and HIV inhibitors), the reward function r was designed as follows:
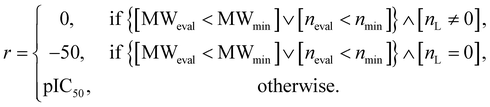 | (7) |
4.7 RL algorithm
We performed benchmark testing against the following state-of-the-art RL algorithms: IMPALA,63 APPO,64 A2C & A3C,65 and PPO.49 The detailed results of the benchmarking are summarized in ESI Note 3.† From the benchmark results, we confirmed that PPO—which is a model-free, on-policy, actor-critic, and policy-gradient algorithm—was the most suitable for our problems, with a very large discrete action space of over 2000. Moreover, PPO is known for its good performance, stability, and good sample efficiency, which makes the training process more stable by avoiding large policy updates with importance sampling and reusing learning data on the trust region. Hence, we applied PPO for all experiments conducted in this study. The objective function of PPO is defined as follows: | (8) |
4.8 Further findings
We empirically demonstrated that our methodology can discover novel molecules with extreme properties, which is impossible to accomplish with existing models that learn the probability distribution of data. However, there were two limitations with our model, which could be solved through further studies. First, the model should be re-trained if the target changes because the reward function depends on the given target. Therefore, the model must learn the policy from the start each time a new target is set. To solve this problem, a methodology such as meta-learning may be applied in future studies. With meta-learning, it is possible to predict the results of a new task or recommend hyperparameters based on the learning results from another task. Therefore, when a new task is assigned, it will be possible to learn through the experiences that have been taught in the past, requiring less additional training. For example, using methods such as MetaGenRL,66 which applies meta-learning to reinforcement learning, the model outperformed the existing reinforcement learning algorithm while exhibiting similar performance for completely different tasks. Second, there was a sparse reward problem, which occurred because the agent received little feedback or reward for the action from the environment, rendering it difficult to learn efficient policies and satisfy the desired goal. Since molecules with extreme properties are rarer than common molecules, the probability of experiencing an episode in which a rare molecule is obtained through a random combination of molecular fragments is relatively low. To solve this problem, we could adopt methods that encourage more exploration with curiosity. This would allow experiencing more episodes that could provide higher rewards. In addition, hierarchical reinforcement learning67 could be applied, which is a methodology that utilizes prior knowledge of the given problem to set sub-goals that are easier to achieve than the original goal. Accordingly, it learns a policy that can achieve the original goal through policies learned from sub-goals.Code availability
The full code used to perform the analysis is available at https://github.com/Haeyeon-Choi/RL-CC.Data availability
The curated ChEMBL datasets and MOSES data sets for training and testing cRNN24 and GCT23 are publicly available at https://github.com/MolecularAI/Deep-Drug-Coder and https://github.com/molecularsets/moses, respectively. All generated molecules in this study are available at https://github.com/Haeyeon-Choi/RL-CC/tree/main/result.Author contributions
HK proposed the concept of materials extrapolation and the scheme of RL-guided combinatorial chemistry. HK, HC, and JN designed the experiments, and they were implemented by HK, HC, and DK. All authors analyzed the results and discussed them. HK, HC, and DK wrote the manuscript, and all authors reviewed it. JN and WBL supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government through the Ministry of Science and ICT (MSIT) (NRF-2021R1C1C1012031, NRF-2021R1A4A3025742, NRF-2018M3D1A1058633, and NRF-2020M3F7A1094299).References
- Y. Pommier, A. A. Johnson and C. Marchand, Nat. Rev. Drug Discovery, 2005, 4, 236–248 CrossRef CAS PubMed.
- S. Yang, D. Hwang, S. Lee, S. Ryu and S. J. Hwang, Adv. Neural Inf. Process. Syst., 2021, 34, 7924–7936 Search PubMed.
- D. B. Kitchen, H. Decornez, J. R. Furr and J. Bajorath, Nat. Rev. Drug Discovery, 2004, 3, 935–949 CrossRef CAS PubMed.
- S. K. Gottipati, B. Sattarov, S. Niu, Y. Pathak, H. Wei, S. Liu, S. Blackburn, K. Thomas, C. Coley, J. Tang, et al., International Conference on Machine Learning, 2020, pp. 3668–3679 Search PubMed.
- A. Klein, C. Körber, A. Wachau, F. Säuberlich, Y. Gassenbauer, S. P. Harvey, D. E. Proffit and T. O. Mason, Materials, 2010, 3, 4892–4914 CrossRef CAS PubMed.
- R. L. Greenaway and K. E. Jelfs, Adv. Mater., 2021, 33, 2004831 CrossRef CAS PubMed.
- D. Sylvinson MR, H.-F. Chen, L. M. Martin, P. J. Saris and M. E. Thompson, ACS Appl. Mater. Interfaces, 2019, 11, 5276–5288 CrossRef CAS PubMed.
- K. Kim, S. Kang, J. Yoo, Y. Kwon, Y. Nam, D. Lee, I. Kim, Y.-S. Choi, Y. Jung and S. Kim, et al. , npj Comput. Mater., 2018, 4, 1–7 CrossRef.
- B. Meredig, E. Antono, C. Church, M. Hutchinson, J. Ling, S. Paradiso, B. Blaiszik, I. Foster, B. Gibbons and J. Hattrick-Simpers, et al. , Mol. Syst. Des. Eng., 2018, 3, 819–825 RSC.
- J. Ling, M. Hutchinson, E. Antono, S. Paradiso and B. Meredig, Integr. Mater. Manuf. Innov., 2017, 6, 207–217 CrossRef.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS.
- J. Liu, S. Gong, H. Li and G. Liu, Fuel, 2022, 313, 122712 CrossRef CAS.
- Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- S. S. SV, J. N. Law, C. E. Tripp, D. Duplyakin, E. Skordilis, D. Biagioni, R. S. Paton and P. C. St John, Nat. Mach. Intell., 2022, 1–11 Search PubMed.
- Y. Dong, D. Li, C. Zhang, C. Wu, H. Wang, M. Xin, J. Cheng and J. Lin, Carbon, 2020, 169, 9–16 CrossRef CAS.
- M.-Y. Lyu and T. G. Choi, Int. J. Precis. Eng. Manuf., 2015, 16, 213–220 CrossRef.
- R. Stauber, ATZ Worldwide, 2007, 109, 2–4 CrossRef.
- A. Zunger, Nat. Rev. Chem, 2018, 2, 1–16 CrossRef.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy and M. Veselov, et al. , Front. Pharmacol, 2020, 11, 1931 Search PubMed.
- D. Mendez, A. Gaulton, A. P. Bento, J. Chambers, M. De Veij, E. Félix, M. P. Magariños, J. F. Mosquera, P. Mutowo and M. Nowotka, et al. , Nucleic Acids Res., 2019, 47, D930–D940 CrossRef CAS PubMed.
- O. Méndez-Lucio, B. Baillif, D.-A. Clevert, D. Rouquié and J. Wichard, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- J. Lim, S. Ryu, J. W. Kim and W. Y. Kim, J. Cheminf., 2018, 10, 1–9 Search PubMed.
- H. Kim, J. Na and W. B. Lee, J. Chem. Inf. Model., 2021, 61, 5804–5814 CrossRef CAS PubMed.
- P.-C. Kotsias, J. Arús-Pous, H. Chen, O. Engkvist, C. Tyrchan and E. J. Bjerrum, Nat. Mach. Intell., 2020, 2, 254–265 CrossRef.
- I. Sutskever, O. Vinyals and Q. V. Le, Sequence to sequence learning with neural networks, 2014, vol. 27 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Attention is all you need, 2017, vol. 30 Search PubMed.
- M. Mirza and S. Osindero, arXiv, 2014, preprint, arXiv:1411.1784, DOI:10.48550/arXiv.1411.1784.
- K. Sohn, H. Lee and X. Yan, Learning structured output representation using deep conditional generative models, 2015, vol. 28 Search PubMed.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Generative Adversarial Networks, 2014, vol. 28 Search PubMed.
- D. P. Kingma and M. Welling, arXiv, 2013, preprint, arXiv:1312.6114, DOI:10.48550/arXiv.1312.6114.
- G. L. Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias and A. Aspuru-Guzik, arXiv, 2017, preprint, arXiv:1705.10843, DOI:10.48550/arXiv.1705.10843.
- B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, Optimizing distributions over molecular space. An Objective-Reinforced Generative Adversarial Network for Inverse-design Chemistry (ORGANIC), ChemRxiv, 2017, preprint, DOI:10.26434/chemrxiv.5309668.v3.
- T. Blaschke, M. Olivecrona, O. Engkvist, J. Bajorath and H. Chen, Mol. Inf., 2018, 37, 1700123 CrossRef PubMed.
- R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586 RSC.
- T. Long, N. M. Fortunato, I. Opahle, Y. Zhang, I. Samathrakis, C. Shen, O. Gutfleisch and H. Zhang, npj Comput. Mater., 2021, 7, 66 CrossRef CAS.
- M. Mokaya, F. Imrie, W. P. van Hoorn, A. Kalisz, A. R. Bradley and C. M. Deane, Nat. Mach. Intell., 2023, 1–9 Search PubMed.
- M. Olivecrona, T. Blaschke, O. Engkvist and H. Chen, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- A. Furka, Notarized Report (File number 36237/1982, in Hungarian), 1982 Search PubMed.
- J. Degen, C. Wegscheid-Gerlach, A. Zaliani and M. Rarey, ChemMedChem, 2008, 3, 1503–1507 CrossRef CAS PubMed.
- R. S. Bohacek, C. McMartin and W. C. Guida, Med. Res. Rev., 1996, 16, 3–50 CrossRef CAS PubMed.
- K. Klaus, Principia Cybernetica Web, 1986 Search PubMed.
- C. E. Shannon, ACM SIGMOBILE Mob. Comput. Commun. Rev., 2001, 5, 3–55 CrossRef.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- RDKit: Open-source cheminformatics, [online; accessed 02-June-2022], http://www.rdkit.org Search PubMed.
- S. A. Wildman and G. M. Crippen, J. Chem. Inf. Comput. Sci., 1999, 39, 868–873 CrossRef CAS.
- P. Ertl, B. Rohde and P. Selzer, J. Med. Chem., 2000, 43, 3714–3717 CrossRef CAS PubMed.
- G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90–98 CrossRef CAS PubMed.
- A. Alhossary, S. D. Handoko, Y. Mu and C.-K. Kwoh, Bioinformatics, 2015, 31, 2214–2216 CrossRef CAS PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, preprint, arXiv:1707.06347, DOI:10.48550/arXiv.1707.06347.
- PubChem, PubChem SARS-Cov-2 clinical trials, https://pubchem.ncbi.nlm.nih.gov/docs/covid-19 Search PubMed.
- H. Zhang, X. Gong, Y. Peng, K. M. Saravanan, H. Bian, J. Z. Zhang, Y. Wei, Y. Pan and Y. Yang, Front. Chem., 2022, 10, year Search PubMed.
- Y. Wang, J. Xiao, T. O. Suzek, J. Zhang, J. Wang, Z. Zhou, L. Han, K. Karapetyan, S. Dracheva and B. A. Shoemaker, et al. , Nucleic Acids Res., 2012, 40, D400–D412 CrossRef CAS PubMed.
- E. Hillhouse and D. Grammatopoulos, Front. Horm. Res., 2001, 27, 66–74 CAS.
- H. Kawasaki, G. M. Springett, N. Mochizuki, S. Toki, M. Nakaya, M. Matsuda, D. E. Housman and A. M. Graybiel, Science, 1998, 282, 2275–2279 CrossRef CAS PubMed.
- K.-H. Lin, G.-J. A. Wetzelaer, P. W. Blom and D. Andrienko, Front. Chem., 2021, 9, 800027 CrossRef CAS PubMed.
- C. Bevington, A. J. Williams, C. Guider, N. C. Baker, B. Meyer, M. A. Babich, S. Robinson, A. Jones and K. A. Phillips, Sci. Data, 2022, 9, 295 CrossRef.
- I. Morecroft, R. P. Heeley, H. M. Prentice, A. Kirk and M. R. MacLean, Br. J. Pharmacol., 1999, 128, 730–734 CrossRef CAS PubMed.
- K. M. Nautiyal, K. F. Tanaka, M. M. Barr, L. Tritschler, Y. Le Dantec, D. J. David, A. M. Gardier, C. Blanco, R. Hen and S. E. Ahmari, Neuron, 2015, 86, 813–826 CrossRef CAS PubMed.
- M. Clark and J. Neumaier, Psychopharmacol. Bull., 2001, 35, 170–185 CAS.
- Y. Huang, W. A. Paxton, S. M. Wolinsky, A. U. Neumann, L. Zhang, T. He, S. Kang, D. Ceradini, Z. Jin and K. Yazdanbakhsh, et al. , Nat. Med., 1996, 2, 1240–1243 CrossRef CAS PubMed.
- S. G. Sarafianos, B. Marchand, K. Das, D. M. Himmel, M. A. Parniak, S. H. Hughes and E. Arnold, J. Mol. Biol., 2009, 385, 693–713 CrossRef CAS PubMed.
- G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye and T.-Y. Liu, Adv. Neural Inf. Process. Syst., 2017, 30 Search PubMed.
- L. Espeholt, H. Soyer, R. Munos, K. Simonyan, V. Mnih, T. Ward, Y. Doron, V. Firoiu, T. Harley, I. Dunning, et al., International Conference on Machine Learning, 2018, pp. 1407–1416 Search PubMed.
- J. Schulman, F. Wolski, P. Dhariwal, A. Radford and O. Klimov, arXiv, 2017, preprint, arXiv:1707.06347, DOI:10.48550/arXiv.1707.06347.
- V. Mnih, A. P. Badia, M. Mirza, A. Graves, T. Lillicrap, T. Harley, D. Silver and K. Kavukcuoglu, International Conference on Machine Learning, 2016, pp. 1928–1937 Search PubMed.
- L. Kirsch, S. van Steenkiste and J. Schmidhuber, arXiv, 2019, preprint, arXiv:1910.04098, DOI:10.48550/arXiv.1910.04098.
- M. Riedmiller, R. Hafner, T. Lampe, M. Neunert, J. Degrave, T. Wiele, V. Mnih, N. Heess and J. T. Springenberg, International Conference on Machine Learning, 2018, pp. 4344–4353 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc05281h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |