Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Origin of dielectric polarization suppression in confined water from first principles†
T.
Dufils
ab,
C.
Schran
 cd,
J.
Chen
cd,
J.
Chen
 e,
A. K.
Geim
e,
A. K.
Geim
 ab,
L.
Fumagalli
ab,
L.
Fumagalli
 *ab and
A.
Michaelides
*ab and
A.
Michaelides
 *df
*df
aDepartment of Physics and Astronomy, University of Manchester, Manchester, M13 9PL, UK. E-mail: laura.fumagalli@manchester.ac.uk
bNational Graphene Institute, University of Manchester, Manchester, M13 9PL, UK
cCavendish Laboratory, Department of Physics, University of Cambridge, Cambridge, CB3 0HE, UK
dLennard-Jones Centre, University of Cambridge, Trinity Ln, Cambridge, CB2 1TN, UK. E-mail: am452@cam.ac.uk
eSchool of Physics, Peking University, Beijing, 100871, China
fYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, UK
First published on 4th December 2023
Abstract
It has long been known that the dielectric constant of confined water should be different from that in bulk. Recent experiments have shown that it is vanishingly small, however the origin of the phenomenon remains unclear. Here we used ab initio molecular dynamics simulations (AIMD) and AIMD-trained machine-learning potentials to understand water's structure and electronic properties underpinning this effect. For the graphene and hexagonal boron-nitride substrates considered, we find that it originates in the spontaneous anti-parallel alignment of the water dipoles in the first two water layers near the solid interface. The interfacial layers exhibit net ferroelectric ordering, resulting in an overall anti-ferroelectric arrangement of confined water. Together with constrained hydrogen-bonding orientations, this leads to much reduced out-of-plane polarization. Furthermore, we directly contrast AIMD and simple classical force-field simulations, revealing important differences. This work offers insight into a property of water that is critical in modulating surface forces, the electric-double-layer formation and molecular solvation, and shows a way to compute it.
Introduction
The reduction of the dielectric constant of interfacial and confined water has been the subject of extensive studies for many decades because of the ubiquitous presence of electrified surface/water interfaces in materials science, geology, chemistry and molecular biology as well as the development of new nanotechnologies (see e.g. ref. 1–8). However, a clear demonstration of this effect proved difficult due to challenges in both experimentally probing a dielectric response of only a few water layers near surfaces and in accurately computing it. Recently, the dielectric response of thin water layers confined in single slit-like nanochannels made of van der Waals crystals has been measured on the atomic scale.9 These measurements, which were conducted with nanoslits made of graphene and hexagonal boron nitride (hBN), revealed the presence of an electrically “dead” water layer near the slit walls with a surprisingly low dielectric constant in the direction perpendicular to the surface (ε⊥ ≈ 2) and extending around two molecular layers (∼7 Å) into the bulk.The observation of an interfacial water layer with an out-of-plane dielectric constant approximately 1/40th that of bulk water sparked renewed interest in understanding the dielectric polarization properties of nanoconfined water. In particular, there has been a surge of theory and simulation work (see e.g. ref. 10–26), including a large number of force-field molecular dynamics (FFMD) with widely used point charge models. These studies have been of tremendous value and generally predict a decrease of ε⊥ for water near surfaces, in qualitative agreement with the recent experiments. However, the intensity of the decrease, how far it extends from the surface into the bulk, and the origin of the effect are all issues under debate. In addition, the FFMD studies involve the application of water force-fields parameterised to describe bulk rather than interfacial water properties,27 and the electronic coupling between water and the confining materials is not taken into account. Indeed, previous FFMD studies have mostly focused on water confined in graphene nanoslits. This means that it remains unclear whether the dielectric properties of nanoconfined water differ (if at all) between graphene and hBN. Such considerations call for the application of a first-principles based simulation approach such as density functional theory (DFT). DFT is not without its shortcomings, particularly when dealing with water. However, when a suitable choice of exchange–correlation functional is made it can deliver the requisite accuracy for water–surface interactions28 and when combined with molecular dynamics – so-called ab initio molecular dynamics (AIMD) – has been used successfully to probe the structure and dynamics of nanoconfined water (see e.g. ref. 13 and 29–31). However, DFT has yet to be used to deliver explicit estimates of the dielectric properties of confined water, mainly because of methodological challenges in extracting an accurate dielectric constant from computationally expensive AIMD simulations.
In this study, we exploit recent developments that enable the determination of dielectric properties with AIMD32,33 to calculate water's dielectric polarization inside graphene and hBN nanoslits. We analyze the molecular origin behind water's dielectric properties by calculating the magnitude and orientational distribution of the water molecule dipole moments as well as the topology of the hydrogen bonding network near the slit surfaces. This analysis is aided by the development of AIMD-trained machine learning (ML) neural network potentials (NNP) which ensure that converged structural properties of nanoconfined water are obtained. We show that our AIMD simulations describe the experimental results with fairly good accuracy, predicting a much reduced ε⊥ that originates in the first two interfacial water layers, where the water dipoles are constrained in an antiparallel configuration with respect to the normal to the surface in a ferroelectric configuration. This in turn leads to a reduced effective polarization in the perpendicular direction, irrespective of the distance between the confining surfaces and their electronic structure. We contrast our DFT-based MD simulations with those obtained from classical force-field simulations, in particular simple point charge water models used in previous studies. They reveal significant differences in the predicted arrangement of the water dipoles near the solid interface, indicating that the electronic properties of the surface are critical for quantitatively computing properties of interfacial and confined water.
Results
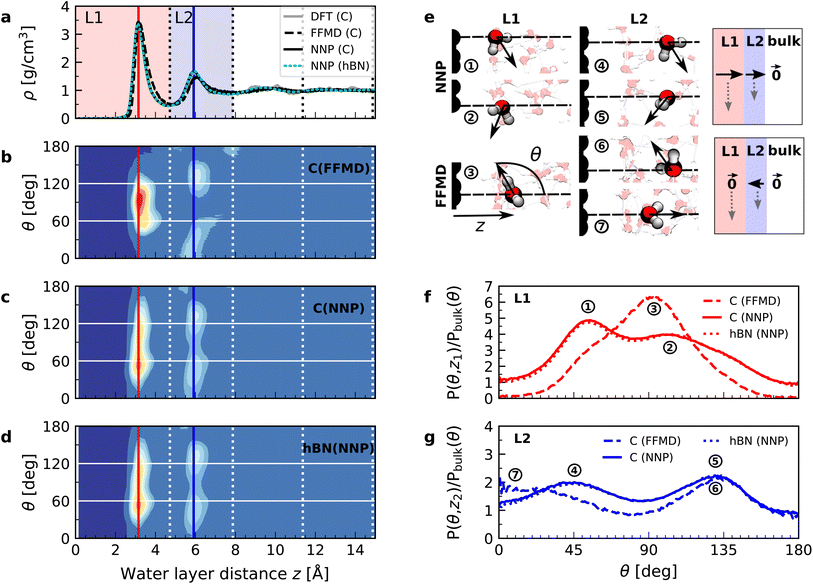
We performed simulations with AIMD, AIMD-trained ML potentials, and FFMD for water confined within graphene and hBN nanoslits, for simplicity referred to as graphene and hBN slits, as described in Materials and methods. To study the effect of extreme confinement on interfacial water, as in the experiments, we analyzed various separation distances between the confining layers: from 0.66 to 2.00 nm in AIMD simulations, and from 0.66 to 4.5 nm in FFMD simulations (labelled XS [0.66 nm], S [0.91 nm], M [1.94 nm], L [3.00 nm] and XL [4.50 nm], following the nomenclature used in ref. 13, as shown in Fig. 1b, see details in ESI Table S1†). For each distance, we took care to establish the structure of nanoconfined water films, in agreement with previous work (see e.g. ref. 29 and 34–37) that report density oscillations in the water structure perpendicular to the surface of the confining layers. An example of such a density profile obtained from the AIMD-trained ML potential is shown in Fig. 1a, from which it can be seen that at least two clear solvation layers of water can be identified at each interface.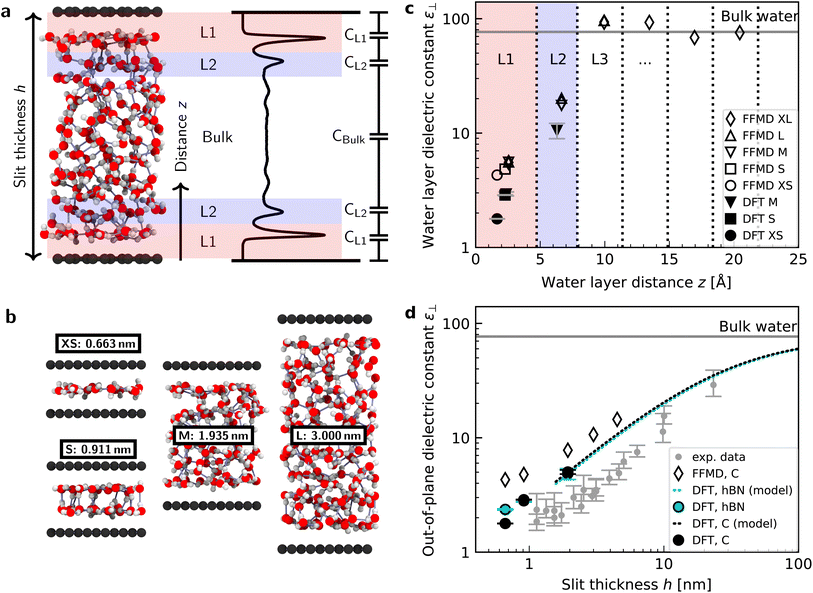 | ||
| Fig. 1 Dielectric constant of water confined between graphene and hBN. (a) Snapshot of a typical geometry for water confined within a nanoslit (left part of panel (a)) and the planar averaged water density profile (right part of panel (a)). Various terms used throughout the manuscript (h, z, L1, L2, and the capacitor model) are also indicated in this panel. (b) Snapshots for different confining distances and corresponding nomenclature (see details in ESI Table S1†). (c) Calculated ε⊥ for individual water layers as a function of the distance from graphene using ab initio (filled symbols) and force-field (open symbols) molecular dynamics calculations. Vertical dashed lines indicate the thickness of the water layers. Light red and blue colored areas highlight the first and second interfacial layer, L1 and L2, respectively. Dielectric constants obtained by FFMD calculations have been increased by 0.8 to account for the electronic polarizability. As shown by the presence of the error bars, the point for the dielectric constant of L1 for 1.935 nm [M] lies under the one for DFT and 0.911 nm [S]. (d) Effective ε⊥ as a function of the separation distance between two confining surfaces calculated using the capacitance model in eqn (7). Filled symbols are ab initio calculations for graphene (black) and hBN (cyan) slits. The dashed black (cyan) curve is the ab initio prediction using the capacitor model and the interfacial ε⊥ obtained from DFT calculations for graphene (hBN) at separation distance h = 1.935 nm [M]. Open symbols are force-field simulations for the graphene slit. Dielectric constants obtained by FFMD calculations have been increased by 0.8 to account for the electronic polarizability. Grey symbols are the experimental data from ref. 9, shifted by 3.354 Å in the x-axis direction according to the definition of h in this study (atom-to-atom distance of the slit, not water thickness). | ||
Having established the water structure, we calculated ε⊥ of water using the finite-field method.38–40 In this approach the dielectric displacement D is related to the local Maxwell field E and the local polarization P by the relation D(z) = E(z) + 4πP(z). In the slit geometry, in the absence of free charges, the dielectric displacement in the perpendicular direction, D⊥, is independent of z. Therefore it is advantageous to use it here as an independent electric variable. A variation in the local perpendicular component of the electric field, ΔE⊥, can then be obtained from the variation ΔD⊥ as
| ΔE⊥ = ∫εnl−1(z,z′)ΔD⊥(z′)dz′ | (1) |
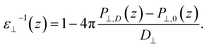 | (2) |
While in previous work14 the ratio 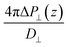 was computed from the fluctuation–dissipation relation,5 here we computed it directly from the change of polarization ΔP⊥ upon a change in the dielectric displacement D⊥ using the finite-field method.38–40 This is similar to what was done in ref. 8 (see Materials and methods), and to do so, we applied a field of magnitude −D⊥, which leads to
was computed from the fluctuation–dissipation relation,5 here we computed it directly from the change of polarization ΔP⊥ upon a change in the dielectric displacement D⊥ using the finite-field method.38–40 This is similar to what was done in ref. 8 (see Materials and methods), and to do so, we applied a field of magnitude −D⊥, which leads to
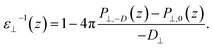 | (3) |
By combining eqn (2) and (3), we then obtained
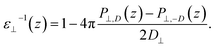 | (4) |
The advantage of this approach is that the fluctuations of P⊥,D(z) − P⊥,0(z) are of the same order of magnitude as the fluctuations of P⊥,−D(z) − P⊥,0(z). By using eqn (4), the fluctuations of the ratio of polarization variation over electric displacement is divided by 2, compared to the use of +D⊥ and 0. This allows the dielectric constant to converge faster, which is particularly important in the context of AIMD. We computed the local polarization P(z) from the charge density averaged over the parallel directions as
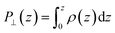 | (5) |
Fig. 1c shows the calculated interfacial water-layer ε⊥ at increasing distances from graphene using both AIMD and FFMD calculations. DFT (filled symbols) yields ε⊥,L1 ≈ 2.9 for the first layer, L1 (red colored area), which falls within the experimental error. For the second interfacial layer, L2 (blue colored area), it yields a slightly larger value, ε⊥,L2 ≈ 11, however remaining almost one order of magnitude smaller than the bulk value. We repeated our AIMD calculations of ε⊥ for water confined within hBN slits. Despite the different electronic structure of the confining material, we found no substantial differences in the computed values as compared to the graphene slits (not shown – see ESI Table S2†). This is to some extent expected, given that the structure of the water/graphene and water/hBN interfaces is extremely similar – see below and previous studies.35,41 Nonetheless, this is an important result, as it validates the assumption made in the experimental study, in which measurements were taken on asymmetric slits, that is, with graphite on one side of the slit and hBN on the other.9
We next turned to the force-field calculations (open symbols). The computed ε⊥ for the two interfacial layers is again in reasonable agreement with the experiments, yielding much reduced values relative to bulk with ε⊥,L1 ≈ 3.7 and ε⊥,L2 ≈ 16 for L1 and L2, respectively. These values are larger than the AIMD values approximately by a factor of 1.3 to 1.5, and depend little on the particular water–carbon parameterization used (see ESI Fig. S5†). Note that in the FFMD values shown in Fig. 1 we included the contribution of the electronic polarizability in order to compare them with the AIMD values. To do that, the high-frequency (electronic) dielectric constant of water, ε∞ ≈ 1.8, has been accounted for by adding 0.8 to the calculated values, as FFMD simulations with non-polarizable atoms yield high-frequency dielectric constant equal to 1, as pointed out in ref. 42. Importantly, our FFMD calculations show that water clearly recovers the bulk dielectric response beyond the first two interfacial layers. This reveals that water's dielectric response is insensitive to the presence of a surface at distances z > 7.5 Å, in agreement with the experimental findings. This is also consistent with recent theoretical calculations of another observable (the confined water function).43 Furthermore, the simulations for various thicknesses of the water slab (h = 1.935 [M], 3.0 [L] and 4.5 nm [XL]) show that the computed interfacial ε⊥ for L1 and L2 are essentially independent of the slit thickness as long as a bulk water phase exists in the system. This demonstrates that the observed polarization suppression does not arise from the confinement between the two surfaces, rather it is an intrinsic property of interfacial water molecules at each individual surface. We also ran simulations for various bulk water densities and verified that they have little effect on the predicted values (see ESI Fig. S6†).
Having calculated the dielectric constant of the interfacial water layers, we computed the effective dielectric constant over the whole water slab inside the slit as a function of the distance between the confining surfaces, h, as measured in the experiment, and directly compared it with the experimental results in Fig. 1d. To this end, we modeled the interface by three capacitors in series as in ref. 9.
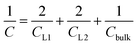 | (6) |
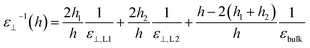 | (7) |
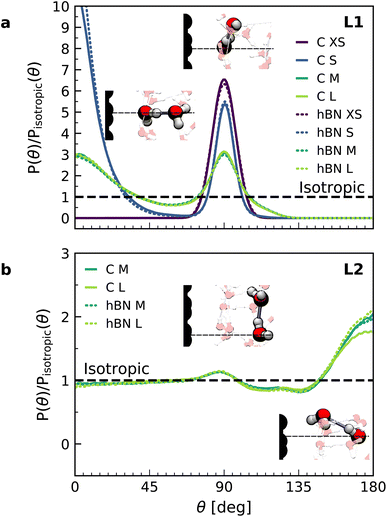
In order to understand the origin of the observed polarization behavior of the interfacial water molecules, we analyzed the structure and the electronic properties of the nanoconfined water slabs. To this end, we obtained converged structural insight from long-time simulations using neural network potentials (NNPs),45,46 which deliver DFT accuracy at zero field at substantially reduced computational cost. The NNPs for water confined by graphene and hBN were trained and validated following recent methodological developments47 and applied for extended simulations at various confinement widths (see Materials and methods). This enabled us to calculate in detail the time-averaged structural arrangement of water molecules and hydrogen-bonding network as a function of the distance from the confining surfaces. Fig. 2 shows some of these results at both graphene and hBN interfaces. As expected, we found no differences in the mass density profiles of water near graphene and hBN (Fig. 2a), which show two density maxima corresponding to the two interfacial layers (L1 and L2). Notably, the time-averaged orientational distributions obtained here reveal that water also has very similar orientations near graphene (Fig. 2c) and hBN (Fig. 2d). Indeed, there is an almost quantitative match in L1 and L2, as verified by plotting the distribution profile at the first two density maxima (Fig. 2f and g, respectively). We note that this is quite different for the in-plane alignment of the contact layer of water above these two materials, revealing distinct differences between graphene and hBN, as recently analysed in the context of water flow in nanotubes.41 Upon examining the orientation of the water molecules in the interfacial layers we find a broad distribution of orientations, falling broadly into two preferential directions in both L1 and L2. Specifically, taking θ as the angle between the surface normal and the water molecule dipole (see Fig. 2e), we find that in the first layer, the water dipole moments are oriented mainly either towards the bulk water at θ ≈ 60° or mainly towards the surface at θ ≈ 105°. These two preferential orientations are also found in the second layer, with a peak at θ ≈ 45° and the other at θ ≈ 135°. Thus, the molecules in the first two interfacial layers are loosely divided into two anti-parallel populations with respect to the dipole projection on the surface normal: either leaning towards the surface or towards the bulk.
We found that the effective dipolar polarization in the perpendicular direction that could be derived from the NNP simulations is greatly reduced compared to the water molecular dipole, in agreement with the much reduced dielectric response that was obtained here and in the experiment. This is consistent with previous simulations, indicating anticorrelated polarization of neighboring water molecules.48 It also confirms the recent suggestion of antiparallel perpendicular components of interfacial dipoles49 and the proposed Ising model, where however the perpendicular dipole moment can only take two values, positive and negative,50 at the origin of water's polarization suppression near the surface. The present study allows us to expand on this model by giving insights into which values the perpendicular moment can take in each water layer, and what constraint should be put on the total layer dipole in the absence of an external field. While an antiparallel arrangement of the interfacial dipoles is in agreement with our simulations, we observe broad distributions of dipoles with bimodular features. These distributions can be broken down into an antiparallel net orientation of the perpendicular components in the first two adsorption layers, not captured before. We also note that the force-field simulations tell a rather different story: consistent with previous force-field simulations,12,22,25,51 the dipoles in the first layer (Fig. 2b) are primarily oriented in a single dominant direction parallel to the surface. The second layer is more bimodal in nature but again different from the DFT distribution through the presence of molecules aligned precisely with the surface normal. These findings are robust with respect to the choice of the non-polarizable force field.
The dipole distribution profiles shown in Fig. 2f and g clearly show a breaking of symmetry in the two dipole orientations yielded by our NNP calculations. This translates into a residual net dipole moment in the perpendicular direction directed towards the bulk water in both the first and second interfacial layers, as sketched in Fig. 2e. This net polarization persists in the absence of an externally applied field, therefore it is ferroelectric in character and generates a local Maxwell field. We estimate the average field generated by the spontaneous polarization of the interfacial water to be around 6.5 V nm−1 in the first layer and 3.0 V nm−1 in the second layer using the relation E(z) = −4πP(z) valid in the absence of an external electric displacement. We note that the force-field calculations also predict a ferroelectric order of interfacial water, but different from the one obtained by DFT calculations, also sketched in Fig. 2e. They yield a total net dipole only in the second layer oriented towards the surface, and not the bulk, while a net zero dipole is obtained in the first layer with the water dipoles oriented parallel to the surface.
Let us now analyze the nature of the hydrogen bonding network. Fig. 3 shows the orientation distribution of the hydrogen bonds, which we calculated from NNP simulations using a common hydrogen bond criterion52 (see details in ESI†). In the first layer, the hydrogen bond orientations are split into two populations: in-plane (θ ≈ 90°) and out-of-plane pointing towards the second layer (θ ≈ 0°). As expected, the latter disappears in the case of a water monolayer confined inside the slit (Fig. 3a, blue line), as the out-of-plane hydrogen bonds are absent. Similar orientations are also observed in force-field calculations (see ESI Fig. S7†). However, our NNP simulations yield a larger proportion of out-of-plane hydrogen bonds and in a smaller angular window, indicating a more constrained hydrogen-bonding network. The second layer displays an almost bulk-like behavior, with only a slight increase in in-plane hydrogen bonds, related to the dipole orientation at θ ≈ 130°, and in out-of-plane hydrogen bonds pointing towards the first layer.
 | ||
| Fig. 3 Orientation of hydrogen bonds in the interfacial water layers. Calculated orientation distribution with respect to the normal direction of the hydrogen bonds for water on graphene (solid lines) and hBN (dashed lines) in the first (a) and second (b) interfacial layers, normalized by the isotropic distribution, obtained from the combined NNP and DFT calculations (see FFMD simulations in ESI Fig. S6†). The direction corresponds to the donor oxygen–acceptor oxygen. Inset: snapshots of the main hydrogen bonding orientations. | ||
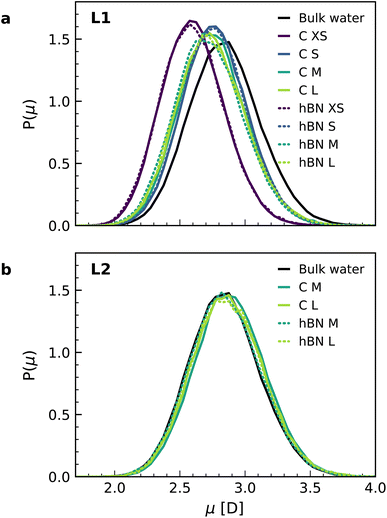
Finally, we calculated the molecular dipole moment in the first two interfacial layers using a combination of DFT and NNPs (Fig. 4) as it may also change with the change in the hydrogen-bonding network near the surface. Our results show a reduction in the dipole moment of the water molecules, but only in the first interfacial layer (Fig. 4a), not in the second one (Fig. 4b), with no appreciable dependence on the orientation of the water molecules. The decrease in the first layer (around 4%) is related to the decrease of the average number of hydrogen bonds per molecule in the first layer (2.93) as compared to the bulk (3.46), while this number remains bulk-like in the second layer (3.49). Notably, for the water monolayer confined inside the slit, it is more pronounced (around 9%) and is associated with a further decrease in the number of hydrogen bonds for each molecule down to 2.18. The observed decrease in the water molecular dipole contributes to the reduction of the dipolar polarization response and is not captured in the most commonly used force-field models, given the fixed nature of the water dipole moment. Although being a relatively minor contribution, this effect further accentuates the difference between first-principles and force-field interfacial water. As with the other properties, and despite the different electronic structures of the confining materials, we found no significant differences in the dipole moment distributions for water confined inside graphene and hBN slits.
Discussion
In this study, we performed AIMD, AIMD-trained NNP simulations, and FFMD simulations of water confined within graphene and hBN slits aimed at understanding the out-of-plane dielectric constant of confined water. Our AIMD calculations reproduce the experimental results of ref. 9 with fairly good accuracy, yielding an interfacial layer of ∼7 Å thickness with reduced ε⊥ extending the first two interfacial water layers, an effect that is seen for both graphene and hBN interfaces and is independent of the distance between the confining surfaces of the slit. While in ref. 9 this effect was attributed to the preferential in-plane orientation of the interfacial water dipoles in the in-plane direction, in accordance with previously reported51 and more recent12,22,25 force-field simulations (also confirmed here), our AIMD and NNP MD simulations reveal a different origin. They indicate that it arises from two dominant effects: the spontaneous antiparallel alignment of the out-of-plane component of water dipoles, leading to a residual ferroelectric-like polarization of these two water layers, and the relatively constrained hydrogen bonds in the first two layers. Our simulations also reveal a small reduction in the dipole moments of the individual water molecules in the first layer. Taken together, these effects are responsible for the suppression of dipolar and hydrogen bond fluctuations in the out-of-plane direction, resulting in the anomalously low dielectric constant of confined water.The value of ε⊥ obtained here from our DFT calculations quantitatively matches the experimental data within the experimental error for water layers extending 1–2 nm, that is, in the strong confinement regime. Notably, this is achieved by placing the dividing surface at the experimental position without the need of shifting it away from the water slab to match the experimental data, as discussed in the ESI.† However, for water slabs larger than 2 nm, in which bulk water molecules occupy the majority of the volume in the slits, we obtained values of ε⊥ that slightly overestimate the experimental data. This is reflected in the somewhat thicker “dead” layer reported in ref. 9, where the fitting of the experimental curve using the three-capacitor model yielded ε⊥ ≈ 2 for a layer extending ∼7 Å, that is, for both the first two interfacial layers, L1 and L2. In contrast, our simulations yield such a small ε⊥ only for L1, while for the second layer in contact with bulk water we obtained a larger value (ε⊥ ≈ 11) albeit remaining almost one order of magnitude smaller than that of bulk water. The latter confirms that the polarization suppression partially extends to the second interfacial layer far from the surface, and is not only limited to the first layer and the depletion region near the solid surface. The shift between this value and the experimental one is a relatively small difference, given the challenges of the experiment. However, it may also imply other effects not accounted for in our calculations are at play, as previously pointed out for force-field simulations.14,20 Two effects that have an impact on the quality of DFT predictions for water in general are the sensitivity of the results to the exchange–correlation functional and the importance of nuclear quantum effects (see e.g. ref. 53–58). To investigate these issues we examined our systems with a different exchange–correlation functional (PBE0-D4 as opposed to revPBED3) and with path integral molecular dynamics. As shown in the ESI† our key structural observations are not significantly changed by altering the functional or including nuclear quantum effects. Thus, the slight overestimate with respect to the experiment will require further theoretical and experimental work in the future to be fully understood.
The force-field simulations performed as part of this study also predict a reduced ε⊥ of confined water, in fairly good agreement with the experiments and previous studies.8,12,14,44 However, the extent of the reduction is underestimated compared to DFT. Partly this is down to the different interfacial water structures predicted by DFT and the force-fields, and partly because the force-field models fail to capture the small reduction in dipole moments of the interfacial (L1) water molecules. The purpose of the force-field simulations in the current study was primarily to compare these previously used methods to our DFT simulations, and so only simple point charge models were considered. Standard point charge force-field models, while being incredibly useful in deepening understanding of water in general, have been designed for bulk water and cannot be expected to deliver quantitative accuracy for interfacial water.
Finally, we note that the emergence of ferroelectricity in interfacial and confined water due to the spontaneous alignment of water dipoles near surfaces has been under debate for many years. In particular, water has been predicted to arrange in ferroelectric or antiferroelectric configurations when confined in one-dimensional channels such as nanotubes and nanopores59,60 and in 2D nanoslits in the in-plane direction,61 while experimental evidences remain scarce and are generally associated to ice phases.62–64 Our first-principles calculations provide insight into this question as they indicate that while retaining liquid-like mobility, interfacial water near hydrophobic surfaces is ferroelectric in the out-of-plane direction at room temperature, irrespective of the presence of two confining surfaces. Importantly, the electrically “dead” water layers reported in ref. 9 should arise from this effect. Note, however, that when water is under strong confinement between two hydrophobic surfaces, as in the experiment, the interfacial water at the two confining surfaces exhibits a net polarization towards the bulk water in the center of the slit (see sketch in Fig. 2e), thus ordering in opposite directions with respect to the surface normal in an overall antiferroelectric configuration in the slit. From the calculated net polarization, we estimate the coercive external field required to reorient it to be at least a few V nm−1, which is much larger than the electric field effectively applied to the water in the experiment, estimated to be around 0.05 V nm−1.9 This would explain why the interfacial water dipoles remained aligned in their spontaneous configuration near the surfaces in the experiment and did not reorient in the opposite direction with the external field. Given the general nature of confinement in our study and that much of surface chemistry and molecular biology is influenced by the dielectric properties of water at interfaces, we expect these findings to be of broader relevance, in particular for understanding water's polarization near and across biological membranes and for developing new energy storage/conversion and molecular sensing devices.
Materials and methods
Ab initio molecular dynamics calculations
AIMD simulations were performed with the CP2K65 code. We simulated boxes with a lateral size of 1.23 × 1.28 nm corresponding to 5 × 3 supercells of the orthorhombic unit cells of the two-dimensional confinement materials. These comprise 60 carbon atoms or 30 BN pairs per layer of graphene and hBN, respectively. We used the same lateral dimensions of the cell for both graphene and hBN due to their very similar lattice constants66 (see details in ESI Table S1†). The separation between the two confining surfaces, h, varied from 0.663 [XS], to 0.911 [S], to 1.935 nm [M]. A separation of 3.00 nm [L] has also been tried, but considering the slow convergence of the dielectric constant and the expensive computational cost associated with a larger number of water molecules, it was instead used to validate the NNP calculations. 2.0 nm of vacuum was introduced to prevent interactions between periodic images in the normal direction. We used the revPBE functional67 with the D3 (ref. 68) correction for dispersion interactions, given its good performance in accurately reproducing both the experimentally measured structure and dynamics of liquid water69–71 as well as the interaction energies of water on graphene and inside carbon nanotubes (CNTs) obtained using more advanced methods such as quantum Monte Carlo and coupled cluster theory.28 Despite the known weaknesses for the prediction of denser phases of ice,72 this particular choice of DFT functional provides an ideal compromise between efficiency and accuracy for the present work. Furthermore, we show in the ESI† that another reasonable choice for the DFT functional, in particular the hybrid functional PBE0 with D4 corrections, provides very similar results for the key interfacial properties of water in contact with both graphene and hBN. Goedecker–Teter–Hutter (GTH) pseudopotentials73 were used along with a DZVP basis set for carbon, boron, and nitrogen and a TZV2P basis set for oxygen and hydrogen in conjunction with a 750 Ry plane-wave cutoff. Simulations were performed in the NVT ensemble with a target temperature of 330 K using a Langevin thermostat, a timestep of 1.0 fs, and deuterium masses for the hydrogen atoms. The surface atoms were kept fixed and initial configurations were generated using the fftool and Packmol packages.74 These simulation cells were first equilibrated using FFMD calculations using the force field and simulation parameters described below. The number of water molecules was adjusted such that the mass density profiles match the ones obtained for the larger simulation cells used for the FFMD simulations described below. Each simulation was first equilibrated for 3 ps, while all shown properties were accumulated over at least 60 ps additional simulation time (see details in the ESI Fig. S3†). The dipole moment distribution of water was calculated with DFT using the same functional and set-up as described above. For this purpose we computed the position of the Wannier centers of the water molecules using uncorrelated structures obtained from the NNP trajectory (see below). Values of the dipole moments reported in Fig. 4 were obtained by averaging data obtained every 0.8 ps from the first 5 ns (0.66 nm [XS] and 0.91 nm [S]), 3 ns (1.94 nm [M]) and 2 ns (3.00 nm [L]) NNP trajectories described below.Force-field molecular dynamics calculations
We simulated boxes of lateral size of 3.76 nm with two confining layers at distance h 0.663 [XS], 0.911 [S], 1.935 [M], 3.00 [L] and 4.50 nm [XL] using the same lattice constant as in the AIMD simulations. Simulations were performed in the NVT ensemble at 300 K using a Nosé–Hoover thermostat with a time constant of 1 ps and a timestep of 2 fs. Each simulation was equilibrated for 2 ns, while data were accumulated for the following 5 ns. For simulations without an applied field, we used the LAMMPS package,75 with initial configurations generated using the fftool and Packmol packages.74 The number of water molecules was adjusted such that the density was 1 g cm−3. The density was defined as the mass of water molecules divided by the accessible volume, where the accessible volume corresponds to the region in space where the atomic number density (either oxygen or hydrogen) is non zero. For the simulations in the constant-D ensemble, we used the Metalwalls software.76 The water molecules were modeled with the SPCE model77 and three different water–carbon interaction potentials.13,78,79 All data shown in the main text were obtained with the water–carbon parameterization from.13 Data using other water–carbon models are provided in the ESI.† For the water–hBN interaction, we used the force-field of.80Dielectric constant calculations
The perpendicular dielectric constant was computed following the formalism of ref. 5 and using the finite-field method, applying an electric displacement of ±1.0 V nm−1 for DFT calculations and ±1.5 V nm−1 for FFMD calculations. The lower electric displacement value used in the DFT calculations was chosen to be safely within the linear regime, while this is estimated to be 1.5–2.0 V nm−1 for force-field calculations, showed by the emergence of non linearities at 2 V nm−1.81 Being conservative, we chose a slightly lower value for our DFT calculations. To improve the convergence, we computed the difference in polarization between positive and negative dielectric displacement, +D and −D, effectively doubling the window of the linear regime as explained in the main text. The dielectric displacement is applied only in the direction perpendicular to the confining surfaces using the same procedure as in ref. 33, implying 3D periodic boundary conditions, along with Ewald summation for the Coulomb interactions. It is based on the used of the extended Hamiltonian HD = H0 + V/(8π)[D − 4πP]2, where H0 is the Hamiltonian in the absence of external field, and V is the volume of the simulation cell. In practice, it translates into an additional force on all charged particle FD = q[D − 4πP] where q is the charge of the particle. In addition, for AIMD simulations the additional term in the Hamiltonian will affect the electron distribution. In cases of the force and electron distribution, the total polarization is computed from the Berry phase. For the AIMD calculations, we computed the local polarization from the full charge density (electrons plus nuclei), thus taking into account the multipole orders in the polarization derivation. To remove the contribution of the confining surfaces, we carried out a differential calculation, in which we subtracted the response of the confining surfaces without water to the local response of the total system (see details in the ESI Fig. S2†). As the atoms of the surface were kept fixed, only a single calculation was required to compute the former. In the case of AIMD calculations, the convergence of the dielectric profile proved to be slow (not converging after 70 ps of simulations). On the other hand, the dielectric constant converged when integrating the dielectric profile over a molecular layer, as discussed in details in the ESI (Fig. S3).† We note that the scale of the molecular layer (a slice with a width of around 0.4 nm and an infinite extension along the interface directions) is more relevant for this study, as eqn (1)–(4) have been derived in the scope of continuous media theory. Thus, we extracted the dielectric response of the first two interfacial layers, which tend to converge faster due to their small value, and the constant-D ensemble, which allowed us to directly obtain the inverse of the dielectric constant. Using the equations in the main text along with Maxwell–Gauss equation, it can be shown that working in the finite D ensemble, the averaged applied perpendicular field is equal to its local value, irrespective of the size of the simulation box. To limit the computational cost of AIMD calculations, we assumed bulk-like dielectric response for the remaining water molecules in the center of the slit, as found in the force-field calculations.Machine learning potentials
In order to access converged structural properties of water confined by graphene and hBN layers, we made use of machine learning potentials to perform long-time simulations at DFT accuracy. For that purpose, we utilized Behler–Parrinello neural network potentials (NNPs)45,46 in a committee model82 enabling the simple development47 of machine learning potentials at first-principle accuracy for the two confining materials. Using this methodology, we trained and validated the two models as described in detail in ref. 41 and applied them here for MD simulations at various surface separations, always comparing graphene and hBN confinement. As before, simulations were performed with CP2K in the NVT ensemble at 330 K using a Langevin thermostat, a timestep of 1.0 fs, deuterium masses for the hydrogen atoms and keeping the atoms of the confinement material fixed. Systems with two confining layers at distance h = 0.663 [XS], 0.911 [S], 1.935 [M], 3.00 [L] and a lateral size of 1.23 × 1.28 nm were propagated for 5 ns to converge structural properties. Furthermore, the NNPs allowed us to analyse the influence of the quantum nature of the nuclei with thermostatted ring polymer molecular dynamics simulations.83 These simulations provide access to rigorous quantum thermodynamical properties. We used a timestep of 0.25 fs and 16 ring polymer replica resulting in a converged description of structural properties.84 Simulations were performed for the 3.00 nm [L] system over a simulation length of 500 ps for both confining materials. Detailed comparison of all analysed properties of interfacial water with classical and quantum nuclei is provided in the ESI.† These results show that nuclear quantum effects have negligible impact on the key findings of this study. Two additional models trained to PBE0-D4 were used to assess the impact of the DFT functional on the interfacial properties of water in contact with both graphene and hBN. Similar to the impact of nuclear quantum effects, the choice of DFT functional does not significantly impact the properties of interfacial water, as discussed in detail in the ESI.†Data availability
The ESI† provides additional computational details. Simulation data will also be made available on the Cambridge Apollo repository prior to publication.85Author contributions
L. F., T. D., C. S. and A. M. designed the research; T. D. performed the simulations and C. S. developed the machine learning models; all authors analyzed the data; and L. F., T. D., C. S., and A. M. wrote the paper, with contributions from J. C. and A. K. G.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
The authors thank D. V. Matyushov for fruitful discussions. T. D. and L. F. were supported by the European Research Council (grant 819417) under the European Union Horizon 2020 Research and Innovation Programme. A. M. acknowledges support from the European Union under the “n-aqua” European Research Council project (grant 101071937). C. S. acknowledges partial financial support from the Alexander von Humboldt-Stiftung and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) project number 500244608. J. C. and A. M. thank Beijing Municipal Natural Science Foundation (no. JQ22001) for support. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1 and EP/T022213/1), and computational support from the UK national high performance computing service, ARCHER, for which access was obtained via the UKCP consortium, funded by EPSRC grant ref. EP/P022561/1. We are also grateful to the Research IT and the use of the High Performance Computing (HPC) Pool funded by the Research Lifecycle Programme at the University of Manchester.References
- O. Stern, Zur Theorie der elektrolytischen Doppelschicht, Z. Elektrochem. Angew. Phys. Chem., 1924, 30, 508–516 CrossRef CAS.
- B. E. Conway, J. O. Bockris and I. A. Ammar, The dielectric constant of the solution in the diffuse and Helmholtz double layers at a charged interface in aqueous solution, Trans. Faraday Soc., 1951, 47, 756–766 RSC.
- J. Hubbard and L. Onsager, Dielectric dispersion and dielectric friction in electrolyte solutions. I, J. Chem. Phys., 1977, 67, 4850–4857 CrossRef CAS.
- K. Tielrooij, D. Paparo, L. Piatkowski, H. Bakker and M. Bonn, Dielectric relaxation dynamics of water in model membranes probed by terahertz spectroscopy, Biophys. J., 2009, 97, 2484–2492 CrossRef CAS PubMed.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Dielectric profile of interfacial water and its effect on double-layer capacitance, Phys. Rev. Lett., 2011, 107, 166102 CrossRef PubMed.
- C. Zhang, F. Gygi and G. Galli, Strongly anisotropic dielectric relaxation of water at the nanoscale, J. Phys. Chem. Lett., 2013, 4, 2477–2481 CrossRef CAS.
- M. Dinpajooh and D. V. Matyushov, Dielectric constant of water in the interface, J. Chem. Phys., 2016, 145, 014504 CrossRef PubMed.
- C. Zhang, Note: On the dielectric constant of nanoconfined water, J. Chem. Phys., 2018, 148, 156101 CrossRef PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. Novoselov and A. Geim, Anomalously low dielectric constant of confined water, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- T. Sato, T. Sasaki, J. Ohnuki, K. Umezawa and M. Takano, Hydrophobic surface enhances electrostatic interaction in water, Phys. Rev. Lett., 2018, 121, 206002 CrossRef CAS PubMed.
- S. Seyedi and D. V. Matyushov, Dipolar susceptibility of protein hydration shells, Chem. Phys. Lett., 2018, 713, 210–214 CrossRef CAS.
- S. Varghese, S. Kannam, J. Hansen and S. P. Sathian, Effect of hydrogen bonds on the dielectric properties of interfacial water, Langmuir, 2019, 35, 8159–8166 CrossRef CAS PubMed.
- S. Ruiz-Barragan, D. Muñoz-Santiburcio, S. Körning and D. Marx, Quantifying anisotropic dielectric response properties of nanoconfined water within graphene slit pores, Phys. Chem. Chem. Phys., 2020, 22, 10833–10837 RSC.
- P. Loche, C. Ayaz, A. Wolde-Kidan, A. Schlaich and R. Netz, Universal and nonuniversal aspects of electrostatics in aqueous nanoconfinement, J. Phys. Chem. B, 2020, 124, 4365–4371 CrossRef CAS PubMed.
- R. Esquivel-Sirvent, Anomaly of the dielectric function of water under confinement and its role in van der waals interactions, Phys. Rev. E, 2020, 102, 042609 CrossRef CAS PubMed.
- M. H. Motevaselian and N. R. Aluru, Universal reduction in dielectric response of confined fluids, ACS Nano, 2020, 14, 12761–12770 CrossRef PubMed.
- H. Jalali, H. Ghorbanfekr, I. Hamid, M. Neek-Amal, R. Rashidi and F. Peeters, Out-of-plane permittivity of confined water, Phys. Rev. E, 2020, 102, 022803 CrossRef CAS PubMed.
- F. Deißenbeck, C. Freysoldt, M. Todorova, J. Neugebauer and S. Wippermann, Dielectric properties of nanoconfined water: A canonical thermopotentiostat approach, Phys. Rev. Lett., 2021, 126, 136803 CrossRef PubMed.
- E. Papadopoulou, J. Zavadlav, R. Podgornik, M. Praprotnik and P. Koumoutsakos, Tuning the dielectric response of water in nanoconfinement through surface wettability, ACS Nano, 2021, 15, 20311–20318 CrossRef CAS PubMed.
- D. Muñoz-Santiburcio and D. Marx, Confinement-controlled aqueous chemistry within nanometric slit pores, Chem. Rev., 2021, 121, 6293–6320 CrossRef PubMed.
- S. Mondal and B. Bagchi, Water layer at hydrophobic surface: electrically dead but dynamically alive?, Nano Lett., 2020, 20, 8959–8964 CrossRef CAS PubMed.
- I. Ahmadabadi, A. Esfandiar, A. Hassanali and M. R. Ejtehadi, Structural and dynamical fingerprints of the anomalous dielectric properties of water under confinement, Phys. Rev. Mater., 2021, 5, 024008 CrossRef CAS.
- C. Qi, Z. Zhu, C. Wang and Y. Zheng, Anomalously low dielectric constant of ordered interfacial water, J. Phys. Chem. Lett., 2021, 12, 931–937 CrossRef CAS PubMed.
- G. Monet, H. Berthoumieux, F. Bresme and A. Kornyshev, Nonlocal dielectric response of water in nanoconfinement, Phys. Rev. Lett., 2021, 126, 216001 CrossRef CAS PubMed.
- J.-F. Olivieri, J. T. Hynes and D. Laage, Confined water's dielectric constant reduction is due to the surrounding low dielectric media and not to interfacial molecular ordering, J. Phys. Chem. Lett., 2021, 12, 4319–4326 CrossRef CAS PubMed.
- S. J. Cox and P. L. Geissler, Dielectric response of thin water films: a thermodynamic perspective, Chem. Sci., 2022, 13, 9102–9111 RSC.
- J. Chen, A. Zen, J. G. Brandenburg, D. Alfe and A. Michaelides, Evidence for stable square ice from quantum monte carlo, Phys. Rev. B, 2016, 94, 220102 CrossRef.
- J. Brandenburg, A. Zen, D. Alfe and A. Michaelides, Interaction between water and carbon nanostructures: how good are current density functional approximations?, J. Chem. Phys., 2019, 151, 164702 CrossRef PubMed.
- G. Cicero, J. C. Grossman, E. Schwegler, F. Gygi and G. Galli, Water confined in nanotubes and between graphene sheets: a first principle study, J. Am. Chem. Soc., 2008, 130, 1871–1878 CrossRef CAS PubMed.
- O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen and G. Tocci, et al., Water at interfaces, Chem. Rev., 2016, 116, 7698–7726 CrossRef PubMed.
- J. Jiang, Y. Gao, W. Zhu, Y. Liu, C. Zhu, J. S. Francisco and X. C. Zeng, First-principles molecular dynamics simulations of the spontaneous freezing transition of 2D water in a nanoslit, J. Am. Chem. Soc., 2021, 143, 8177–8183 CrossRef CAS PubMed.
- T. Sayer, M. Sprik and C. Zhang, Finite electric displacement simulations of polar ionic solid-electrolyte interfaces: application to NaCl(111)/aqueous NaCl solution, J. Chem. Phys., 2019, 150, 041716 CrossRef PubMed.
- C. Zhang, J. Hutter and M. Sprik, Coupling of surface chemistry and electric double layer at TiO2 electrochemical interfaces, J. Phys. Chem. Lett., 2019, 10, 3871–3876 CrossRef CAS PubMed.
- C.-Y. Lee, J. A. McCammon and P. Rossky, The structure of liquid water at an extended hydrophobic surface, J. Chem. Phys., 1984, 80, 4448–4455 CrossRef CAS.
- G. Tocci, L. Joly and A. Michaelides, Friction of water on graphene and hexagonal boron nitride from ab initio methods: very different slippage despite very similar interface structures, Nano Lett., 2014, 14, 6872–6877 CrossRef CAS PubMed.
- Y. Zhang, H. B. de Aguiar, J. T. Hynes and D. Laage, Water structure, dynamics, and sum-frequency generation spectra at electrified graphene interfaces, J. Phys. Chem. Lett., 2020, 11, 624–631 CrossRef CAS PubMed.
- C. Calero and G. Franzese, Water under extreme confinement in graphene: oscillatory dynamics, structure, and hydration pressure explained as a function of the confinement width, J. Mol. Liq., 2020, 317, 114027 CrossRef CAS.
- C. Zhang and M. Sprik, Computing the dielectric constant of liquid water at constant dielectric displacement, Phys. Rev. B, 2016, 93, 144201 CrossRef.
- C. Zhang and M. Sprik, Finite field methods for the supercell modeling of charged insulator/electrolyte interfaces, Phys. Rev. B, 2016, 94, 245309 CrossRef.
- P. Umari and A. Pasquarello, Ab initio molecular dynamics in a finite homogeneous electric field, Phys. Rev. Lett., 2002, 89, 157602 CrossRef CAS PubMed.
- F. L. Thiemann, C. Schran, P. Rowe, E. A. Müller and A. Michaelides, Water flow in single-wall nanotubes: oxygen makes it slip, hydrogen makes it stick, ACS Nano, 2022, 16, 10775–10782 CrossRef CAS PubMed.
- S. M. Sarhangi, M. M. Waskasi, S. M. Hashemianzadeh and D. V. Matyushov, Effective dielectric constant of water at the interface with charged C60 fullerenes, J. Phys. Chem. B, 2019, 123, 3135–3143 CrossRef CAS PubMed.
- B. Coquinot, M. Becker, R. R. Netz, L. Bocquet and N. Kavokine, Collective modes and quantum effects in two-dimensional nanofluidic channels, Faraday Discuss., 2024 Search PubMed.
- H. Itoh and H. Sakuma, Dielectric constant of water as a function of separation in a slab geometry: a molecular dynamics study, J. Chem. Phys., 2015, 142, 184703 CrossRef PubMed.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- J. Behler, Four generations of high-dimensional neural network potentials, Chem. Rev., 2021, 121, 10037–10072 CrossRef CAS PubMed.
- C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Machine learning potentials for complex aqueous systems made simple, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118 CrossRef CAS PubMed.
- A. Schlaich, E. W. Knapp and R. R. Netz, Water dielectric effects in planar confinement, Phys. Rev. Lett., 2016, 117, 048001 CrossRef PubMed.
- D. V. Matyushov, Dielectric susceptibility of water in the interface, J. Phys. Chem. B, 2021, 125, 8282–8293 CrossRef CAS PubMed.
- S. Mondal and B. Bagchi, Anomalous dielectric response of nanoconfined water, J. Chem. Phys., 2021, 154, 044501 CrossRef CAS PubMed.
- C. Lee, J. A. McCammon and P. J. Rossky, The structure of liquid water at an extended hydrophobic surface, J. Chem. Phys., 1984, 80, 4448–4455 CrossRef CAS.
- J. Marti, Analysis of the hydrogen bonding and vibrational spectra of supercritical model water by molecular dynamics simulations, J. Chem. Phys., 1999, 110, 6876–6886 CrossRef CAS.
- A. Wallqvist and B. J. Berne, Path-integral simulation of pure water, Chem. Phys. Lett., 1985, 117, 214–219 CrossRef CAS.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, The nature of the hydrated excess proton in water, Nature, 1999, 397, 601–604 CrossRef CAS.
- V. Garbuio, C. Andreani, S. Imberti, A. Pietropaolo, G. Reiter, R. Senesi and M. Ricci, Proton quantum coherence observed in water confined in silica nanopores, J. Chem. Phys., 2007, 127, 154501 CrossRef CAS PubMed.
- S. Habershon, T. E. Markland and D. E. Manolopoulos, Competing quantum effects in the dynamics of a flexible water model, J. Chem. Phys., 2009, 131, 024501 CrossRef PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, Quantum nature of the hydrogen bond, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Nuclear Quantum Effects in Water and Aqueous Systems: Experiment, Theory, and Current Challenges, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- J. Köfinger, G. Hummer and C. Dellago, Macroscopically ordered water in nanopores, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13218–13222 CrossRef PubMed.
- Y. Nakamura and T. Ohno, Ferroelectric mobile water, Phys. Chem. Chem. Phys., 2011, 13, 1064–1069 RSC.
- M. S. Fernández, F. M. Peeters and M. Neek-Amal, Electric-field-induced structural changes in water confined between two graphene layers, Phys. Rev. B, 2016, 94, 045436 CrossRef.
- X. Su, L. Lianos, Y. R. Shen and G. A. Somorjai, Surface-induced ferroelectric ice on Pt(111), Phys. Rev. Lett., 1998, 80, 1533–1536 CrossRef CAS.
- M. J. Iedema, M. J. Dresser, D. L. Doering, J. B. Rowland, W. P. Hess, A. A. Tsekouras and J. P. Cowin, Ferroelectricity in water ice, J. Phys. Chem. B, 1998, 102, 9203–9214 CrossRef CAS.
- S. Bramwell, Ferroelectric ice, Nature, 1999, 397, 212–213 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: an electronic structure and molecular dynamics software package - quickstep: efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- G. Graziano, J. Klimeš, F. Fernandez-Alonso and A. Michaelides, Improved description of soft layered materials with van der Waals density functional theory, J. Phys.: Condens. Matter, 2012, 24, 424216 CrossRef PubMed.
- Y. Zhang and W. Yang, Comment on “Generalized gradient approximation made simple”, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. Morawietz, A. Singraber, C. Dellago and J. Behler, How van der Waals interactions determine the unique properties of water, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8368–8373 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfe and A. Michaelides, Perspective: how good is DFT for water?, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- O. Marsalek and T. E. Markland, Quantum dynamics and spectroscopy of ab initio liquid water: the interplay of nuclear and electronic quantum effects, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- A. Reinhardt and B. Cheng, Quantum-mechanical exploration of the phase diagram of water, Nat. Commun., 2021, 12, 1–7 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Marin-Laflèche, M. Haefele, L. Scalfi, A. Coretti, T. Dufils, G. Jeanmairet, S. K. Reed, S. Alessandra, R. Berthin and C. Bacon, et al., Metalwalls: a classical molecular dynamics software dedicated to the simulation of electrochemical systems, J. Open Source Softw., 2020, 5, 2373 CrossRef.
- H. Berendsen, J. Grigera and T. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- W. Steele, The interaction of gases with solid surfaces, Pergamon, 1974, vol. 3 Search PubMed.
- J. Brandenburg, A. Zen, M. Fitzner, B. Ramberger, G. Kresse, T. Tsatsoulis, A. Grüneis, A. Michaelides and D. Alfe, Physisorption of water on graphene: subchemical accuracy from many-body electronic structure methods, J. Phys. Chem. Lett., 2019, 10, 358–368 CrossRef CAS PubMed.
- Y. Wu, L. K. Wagner and N. R. Aluru, Hexagonal boron nitride and water interaction parameters, J. Chem. Phys., 2016, 144, 164118 CrossRef PubMed.
- D. J. Bonthuis, S. Gekle and R. R. Netz, Profile of the static permittivity tensor of water at interfaces: consequences for capacitance, hydration interaction and ion adsorption, Langmuir, 2012, 28, 7679–7694 CrossRef CAS PubMed.
- C. Schran, K. Brezina and O. Marsalek, Committee neural network potentials control generalization errors and enable active learning, J. Chem. Phys., 2020, 153, 104105 CrossRef CAS PubMed.
- M. Rossi, M. Ceriotti and D. E. Manolopoulos, How to remove the spurious resonances from ring polymer molecular dynamics, J. Chem. Phys., 2014, 140, 234116 CrossRef PubMed.
- C. Schran, F. Brieuc and D. Marx, Converged colored noise path integral molecular dynamics study of the Zundel cation down to ultralow temperatures at coupled cluster accuracy, J. Chem. Theory Comput., 2018, 14, 5068–5078 CrossRef CAS PubMed.
- T. Dufils, Research data supporting “Origin of dielectric polarization suppression in confined water from first principles”, Apollo, 2023 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04740g |
| This journal is © The Royal Society of Chemistry 2024 |