Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Systematic Raman spectroscopic study of the complexation of uranyl with fluoride†
Yating
Yang‡
 a,
Qian
Liu‡
*a,
Youshi
Lan
a,
Qianci
Zhang
a,
Liyang
Zhu
a,
Suliang
Yang
a,
Qian
Liu‡
*a,
Youshi
Lan
a,
Qianci
Zhang
a,
Liyang
Zhu
a,
Suliang
Yang
 a,
Guoxin
Tian
a,
Guoxin
Tian
 a,
Xiaoyan
Cao
a,
Xiaoyan
Cao
 *bc and
Michael
Dolg
*bc and
Michael
Dolg
 *bc
*bc
aDepartment of Radiochemistry, China Institute of Atomic Energy, Fangshan District, Beijing, 102413, China. E-mail: liuqian@cnncmail.cn
bCollege of Chemistry, Beijing Normal University, Beijing, 100875, China
cInstitute of Theoretical Chemistry, University of Cologne, Greinstr. 4, 50939 Cologne, Germany. E-mail: x.cao@uni-koeln.de; m.dolg@uni-koeln.de
First published on 14th June 2024
Abstract
A simple aqueous complexing system of UO22+ with F− is selected to systematically illustrate the application of Raman spectroscopy in exploring uranyl(VI) chemistry. Five successive complexes, UO2F+, UO2F2(aq), UO2F3−, UO2F42−, and UO2F53−, are identified, as well as the formation constants except for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 species UO2F53−, which was experimentally observed here for the first time. The standard relative molar Raman scattering intensity for each species is obtained by deconvolution of the spectra collected during titrations. The results of relativistic quantum chemical first-principles and ab initio calculations are presented for the complete set of [UO2(H2O)mFn]2−n complexes (n = 0–5), both for the gas phase as well as for aqueous solution modelling bulk water using the conductor-like screening model. Electronic structure calculations at the Møller–Plesset second-order perturbation theory level provide accurate geometrical parameters and in particular reveal that k water molecules in the second coordination sphere coordinating to the F− ligands in the resulting [UO2(H2O)mFn]2−n(H2O)k complexes need to be treated explicitly in order to obtain vibrational frequencies in very good agreement with experimental data. The thermodynamics and structural information obtained in this work and the developed methodology could be instructive for the future experimental and computational research on the complexation of the uranyl ion.
5 species UO2F53−, which was experimentally observed here for the first time. The standard relative molar Raman scattering intensity for each species is obtained by deconvolution of the spectra collected during titrations. The results of relativistic quantum chemical first-principles and ab initio calculations are presented for the complete set of [UO2(H2O)mFn]2−n complexes (n = 0–5), both for the gas phase as well as for aqueous solution modelling bulk water using the conductor-like screening model. Electronic structure calculations at the Møller–Plesset second-order perturbation theory level provide accurate geometrical parameters and in particular reveal that k water molecules in the second coordination sphere coordinating to the F− ligands in the resulting [UO2(H2O)mFn]2−n(H2O)k complexes need to be treated explicitly in order to obtain vibrational frequencies in very good agreement with experimental data. The thermodynamics and structural information obtained in this work and the developed methodology could be instructive for the future experimental and computational research on the complexation of the uranyl ion.
1. Introduction
The coordination chemistry and speciation of uranyl in aqueous solutions are of great importance in the nuclear fuel cycle and nuclear waste disposal.1,2 In the processes of fuel manufacturing and spent nuclear fuel reprocessing, the thermodynamic parameters of uranyl complexes are needed for equipment design and operation control. For the waste disposal, the speciation of uranyl under associated conditions is the base for depicting and controlling the migration of uranium. In addition, to precisely determine the thermodynamic parameters and to get structural information of uranyl complexes are not only important tasks of experimental chemistry, but also help to further develop analytical techniques and assist in selecting suitable model systems for computational calibration studies. Therefore, to develop methods and procedures for thermodynamically and structurally investigating the complexation and speciation of uranyl are essential to both fundamental research and applications.A variety of experimental methods can be applied to study the speciation of uranyl, for example, potentiometric titration,3–5 calorimetric titration,6–8 separation by ion exchange9 or solvent extraction,10,11 as well as spectral titration.12–14 Therein, among the spectroscopic methods especially Raman spectroscopy shows better adaptability since it is simple to operate, and can provide thermodynamic and structural information at the same time. Till now, a considerable amount of research has been performed to interpret the spectroscopic performances of uranyl single crystals. However, due to the difficulty in characterizing the uranyl speciation in solution caused by the dynamic ligand-solvent coordination complexity, most of the studies exist on the speciation and spectra of uranyl but very few present integrated explications. Drobot recently developed a numerical processing of single-component emission spectra to improve the signal-to-structure correlation.15,16 Additional information gained enables a cross-validation with Raman spectroscopy, but measurements of the Raman spectra of uranyl single-species were not performed. Hence, applying the nondestructive Raman spectral titration method14 to investigate the signal-to-structure correlation in uranyl single-species is necessary. In most inorganic and organic uranyl ligands, the fluoride ion (F−) has been chosen as a popular target ligand for uranyl research, since it does not show a Raman signal and will not quench the fluorescence of uranyl. Significantly, apart from the other halide ions, F− exhibits unusual coordination properties due to its high charge density and highly negative free energy of hydration, along with the formation of hydrogen bonds with water molecules in aqueous solution. Hence, complicated and changeable uranyl fluorides exhibit an extreme challenge but also offer a research prospect in structure determination through the Raman spectral titration method as well as the exact exploration of the intrinsic signal-to-structure correlation. Meanwhile, the radiotoxicity of actinides intensively motivates the associated alternative theoretical studies, which can alleviate the hazards of radioactive contamination to the environment and researchers themselves to some extent. What's more, what determines the signal-to-structure correlation is not clear, as well as how to determine the exact energy-favorable configuration in real aqueous solution and precisely describe the solvent effect for uranyl fluorides, which all need further interpretation at the atomic level. Therefore, theoretical and experimental research studies are equally important.
Modern relativistic quantum chemical methods allow a detailed investigation of molecules containing heavy elements both in the gas phase and in solution. In 1999 Schreckenbach et al. published results of gradient-corrected (BLYP)17 and hybrid (B3LYP)18 density functional theory (DFT) calculations for UO2X42− (X = F, Cl, OH) and AnF6 (An = U, Np, Pu) complexes using effective core potentials (ECP) and a quasi-relativistic (QR) all-electron (AE) approach.19 The calculated symmetric UO22+ stretching frequencies in UO2F42− of 766 cm−1 (QR AE, BLYP), 682 cm−1 (ECP, BLYP) and 771 cm−1 (ECP, B3LYP) were only in modest agreement with the experimentally observed at least 50 cm−1 higher value of 822 cm−1 for the symmetric stretching mode.20 Vallet et al. investigated in 2001 the structures of U(IV) fluoride and hydroxide complexes by extended X-ray absorption fine structure (EXAFS) spectroscopy as well as quantum chemical calculations using a relativistic U small-core ECP combined with hybrid DFT (B3LYP) and single-point Møller–Plesset second-order perturbation theory (MP2).21 Both implicit modelling and explicit modelling of hydration effects was investigated. The explicit inclusion of the second aquo solvation sphere of the investigated [UO2(H2O)5−nFn]2−n (n = 3–5) complexes was found to be essential to obtain accurate results. Mixed uranyl aquo fluoro complexes [UO2(H2O)xFy]2−y (y = 1–4, x + y = 4, 5) were investigated in the gas phase as well as in aqueous solution by Bühl et al. in 2009 using gradient-corrected DFT (BLYP) in the framework of Car–Parrinello molecular dynamics (CPMD22) simulations.23 The number of equatorial ligands on UO22+ was found to be difficult to establish. Among the fivefold coordinated complexes only [UO2(H2O)4F]+ and [UO2(H2O)3F2] were found to be stable (or metastable) for a few picoseconds in the gas phase in unconstrained CPMD simulations, whereas all other investigated complexes rearranged to species with lower coordination numbers. The CPMD results reproduced the free binding energy of fluorine in [UO2(H2O)4F]+ in aqueous solution within 1 kcal mol−1 of the published experimental value, whereas [UO2(H2O)3F2] was found to be unstable against a loss of water. Accompanying static gradient-corrected (BLYP) and hybrid (B3LYP) DFT calculations using a U small-core ECP led the authors to conclude that the affinity of [UO2F4]2− to accommodate H2O as a fifth equatorial ligand is lower than that assumed previously. Further theoretical and experimental investigations were recommended. Finally, in 2011 Odoh et al. studied the structural and electronic properties of [UO2(H2O)5−nFn]2−n (n = 0–5) in the gas phase and aqueous solution modeled using the conductor-like screening model (COSMO)24 using a U small-core ECP, the QR AE zeroth-order regular approximation (ZORA) and gradient-corrected as well as hybrid DFT (BP86, B3LYP).25 Similar to previous studies they found that the implicit modeling of hydration by COSMO, or a polarizable continuum model (PCM), is not sufficient to obtain accurate U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances, fluoride binding energies and UO22+ vibrational frequencies. Addition of five explicitly treated water molecules to the second coordination sphere of [UO2(H2O)5]2+ and [UO2F5]3−, i.e., explicitly taking into account hydrogen bonding between the first and second coordination spheres, brought the calculated symmetric stretching frequencies (878 and 799 cm−1) into good agreement with the experimental values (870 and 784 cm−1), whereas the implicit modeling only with COSMO leads to inferior values (898 and 753 cm−1). Similarly, the slope of the nearly linear variation of the U
O bond distances, fluoride binding energies and UO22+ vibrational frequencies. Addition of five explicitly treated water molecules to the second coordination sphere of [UO2(H2O)5]2+ and [UO2F5]3−, i.e., explicitly taking into account hydrogen bonding between the first and second coordination spheres, brought the calculated symmetric stretching frequencies (878 and 799 cm−1) into good agreement with the experimental values (870 and 784 cm−1), whereas the implicit modeling only with COSMO leads to inferior values (898 and 753 cm−1). Similarly, the slope of the nearly linear variation of the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances with the number n of fluoride ligands is reduced by roughly a factor of two when replacing the COSMO modeling of hydration by an explicit treatment water in the second coordination sphere combined with COSMO representing the bulk water, bringing the variation between n = 0 and n = 5 from about 0.08 Å down to 0.04 Å in good agreement with experimental evidence. However, a systematic theoretical investigation of the whole series of uranyl complexes [UO2(H2O)5−nFn]2−n (n = 0–5) in aqueous solution taking explicitly into account the second coordination sphere, especially considering the effects on the characteristic UO22+ stretching frequencies and U
O bond distances with the number n of fluoride ligands is reduced by roughly a factor of two when replacing the COSMO modeling of hydration by an explicit treatment water in the second coordination sphere combined with COSMO representing the bulk water, bringing the variation between n = 0 and n = 5 from about 0.08 Å down to 0.04 Å in good agreement with experimental evidence. However, a systematic theoretical investigation of the whole series of uranyl complexes [UO2(H2O)5−nFn]2−n (n = 0–5) in aqueous solution taking explicitly into account the second coordination sphere, especially considering the effects on the characteristic UO22+ stretching frequencies and U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances, is still missing. In particular wavefunction-based ab initio approaches have not been applied to the best of our knowledge to evaluate these characteristic quantities.
O bond distances, is still missing. In particular wavefunction-based ab initio approaches have not been applied to the best of our knowledge to evaluate these characteristic quantities.
We have therefore decided to systematically study the thermodynamic properties and structural characteristics of uranyl complexes with fluoride in aqueous solutions by combining Raman spectrometry and relativistic quantum chemical methods. First, the titrations of UO22+ with F− were conducted by monitoring the variation in Raman spectroscopy. Second, the formation constants and molar normalized intensities of single components were calculated by the deconvolution of titration spectra. Third, the vibrational bands involved in the Raman spectra were analyzed aiming at a structure-to-signal correlation. Finally, extensive electronic structure calculations for a rather complete series of [UO2(H2O)mFn]2−n(H2O)k (n = 0–5) complexes in the gas phase (k = 0) as well as in aqueous solution (k ≥ 0) modelling bulk water using the COSMO approach were performed. These studies also provided accurate data for the UO2F53− complex, which was observed here for the first time but could not be investigated in detail experimentally. To the best of our knowledge the quantum chemical study presented here is not only the most complete for the UO22+/F−/H2O system but also the first to present structures and vibrational frequencies at the ab initio level. The latter aspect as well as the explicit modeling of the second coordination sphere was found to be crucial for obtaining good agreement with the experimental results presented here.
The complexation of uranyl UO22+ with fluoride in aqueous solution was previously studied by one of the present authors using spectrophotometry.26 Four successive complexes UO2F+, UO2F2(aq), UO2F3− and UO2F42− were identified using UV/vis absorption spectroscopy in the wavelength region between 380 and 480 nm. Their stability was found to increase when the temperature was elevated in the region between 25 and 70 °C. Based on microcalometric titrations with NaF/HF the complexation of UO22+ with fluoride was analyzed to be slightly endothermic and entropy-driven. Our present study combines advanced experimental and theoretical techniques to obtain a better understanding of the UO22+/F−/H2O system.
2. Experimental
2.1. Chemicals
All chemicals except for uranium were reagent grade or higher. Deionized water from a Milli-Q system was used in the preparation of all solutions. A stock solution of UO2(NO3)2 was prepared by dissolving UO2(NO3)2·6H2O directly. For preparing a UO2(ClO4)2 stock solution, Na2U2O7 was precipitated from a UO2(NO3)2 solution by adding excess of NaOH and washed three times with deionized water, and then the precipitate was dissolved with concentrated perchloric acid (70%) under stirring and diluted with water. The concentrations of U(VI) and perchlorate were determined by Raman spectrophotometry using nitrate as internal standard and the concentration of free H+ was calculated by the law of charge conservation. A stock solution of NaF (0.9 M) was prepared by directly dissolving NaF in Milli-Q water.2.2. Spectrophotometry
The present investigation of metal-bonding equilibrium was carried out as a series of Raman spectral titrations. For a typical titration, 75 μL of UO2(ClO4)2 solutions were placed in a set of centrifuge tubes, and then different aliquots of 0.9 M NaF solutions were added into each tube and diluted to 1 mL. Furthermore, UO2(ClO4)2 and NaF were replaced by UO2(NO3)2 and (CH3)4NF to increase the F− level. All the solutions were mixed thoroughly (for 1–2 min) and maintained at 25.0 °C ± 0.1 °C through a circulating water bath before the spectra were collected.Raman spectra were acquired on a Renishaw inVia Raman micro-spectrometer at a nominal resolution of 1.4 cm−1 in the range of 800–1100 cm−1. A diode laser (532 nm line) was used as the excitation source. The excitation light with a maximum laser power of 20 mW was focused on samples by using the microscope. The exposure time was 20 s and the number of scans was 30 in all measurements.
In the titration of UO2(ClO4)2 with NaF, the same concentration of perchlorate was kept in the samples, so all the spectra were normalized to the molar intensity of perchlorate. Similarly, all the spectra were normalized to the molar intensity of nitrate during the titration of UO2(NO3)2 with (CH3)4NF.14 The formation constants and the Raman spectra of the U(VI)/F− complexes were calculated, from the normalized Raman spectral data in the range of 750–950 cm−1, with the HypSpec 2013 program.
2.3. Quantum chemistry
Quantum chemical ab initio and first principles calculations were performed with the electronic structure codes GAUSSIAN,27 MOLPRO28,29 and TURBOMOLE.30 A scalar-relativistic energy-adjusted small-core pseudopotential (ECP60MWB31) and a corresponding (14s13p10d8f6g)/[10s9p5d4f3g] basis set32 of polarized valence-quadruple-zeta quality were used for U in order to account for the leading relativistic contributions. H, O and F were described by def2-TZVPP basis sets, i.e., (11s6p2d1f)/[5s3p2d1f] for O and F, and (5s2p1d)/[3s2p1d] for H.33 Calculations including electron correlation effects were performed with the gradient-corrected B3LYP hybrid density functional25 and at the second-order level of Møller–Plesset perturbation theory (MP2). Bulk hydration effects were described by the conductor-like screening model (COSMO24) using a dielectric constant ε = 78. For the cavity generation in our calculations the following atomic radii (Å) were adopted from the default values implemented in TURBOMOLE: O (1.72), H (1.3), and U (2.223). Geometry optimizations were performed for the complexes in the gas phase as well as in aqueous solution. All minimum structures were confirmed by 3N − 6 real positive eigenvalues of the Hessian matrix (N: number of atoms), except for the [UO2(H2O)3F2](H2O)4 complex at the MP2 level in aqueous solution modeled by COSMO, where one imaginary value of 7.52i cm−1 was found in the numerical frequency evaluation (cf. ESI†). The following notation is used: ligands of UO22+ in the first coordination sphere are given inside the brackets, whereas additional explicitly treated water molecules in the second coordination sphere are listed outside the brackets, i.e., [UO22+(H2O)mFn]2−n(H2O)k. Note that for a specific first coordination sphere (a given pair n, m) an infinite number k of water molecules could be added to the second and subsequent coordination spheres, forming hydrogen bonds to the n fluoride and m water ligands as well as to the uranyl oxygens. We found in several test calculations that only those water molecules which form hydrogen bonds to the fluoride ligands in the first coordination sphere have a significant effect on the UO22+ bond distances as well as the uranyl vibrational stretching frequencies (cf. ESI†). We therefore restricted our study to such cases, thus in practice limiting, also due to steric requirements, the number k of explicitly treated additional water molecules to at most five, whereas treating bulk water with the COSMO approach. We further considered only cases where all fluoride ligands have at least one hydrogen bond to an explicitly treated water molecule. Since according to our observations each fluoride ligand forms at most two hydrogen bonds in energetically favorable arrangements, a rule of thumb n ≤ k ≤ min (2n, 5) for constructing the investigated [UO22+(H2O)mFn]2−n(H2O)k complexes results. The Cartesian coordinates of the energetically lowest complexes for given triples n, m, k found by applying these assumptions are given in the ESI.†3. Results and discussion
3.1. Raman spectra of UO22+ titrated with F−
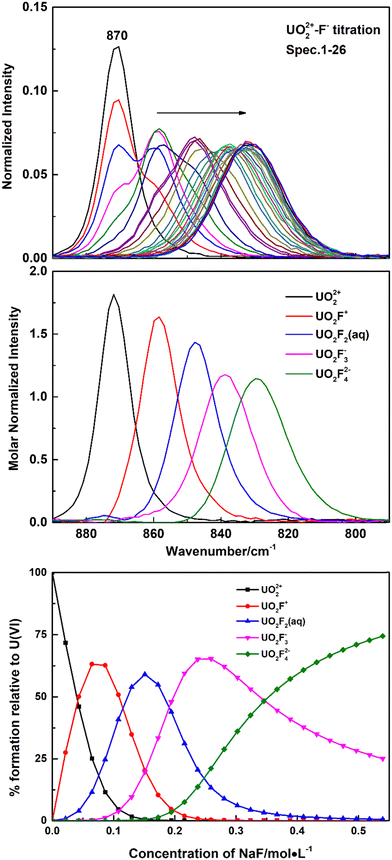
Fig. 1 shows Raman spectra of representative spectrophotometric titrations of UO2(ClO4)2 with NaF. With the addition of the NaF titrant solution, the intensities of the Raman band at 870 cm−1 that belongs to the free UO22+ cation decreased and a new band appeared at 858 cm−1, which is ascribed to the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of U(VI) with F−, UO2F+. With addition of more titrant solution, successive bands wax and wane at 858 cm−1, 848 cm−1, 837 cm−1, and 828 cm−1. The three new bands at lower frequencies were assigned to the UO2F2(aq), UO2F3−, and UO2F42− species, respectively. The band at 828 cm−1 was the last one observed in the U(VI)/NaF system of 1 M ion strength in which the highest F− concentration that could be achieved is about 0.54 M. The calculated formation constants of the 1
1 complex of U(VI) with F−, UO2F+. With addition of more titrant solution, successive bands wax and wane at 858 cm−1, 848 cm−1, 837 cm−1, and 828 cm−1. The three new bands at lower frequencies were assigned to the UO2F2(aq), UO2F3−, and UO2F42− species, respectively. The band at 828 cm−1 was the last one observed in the U(VI)/NaF system of 1 M ion strength in which the highest F− concentration that could be achieved is about 0.54 M. The calculated formation constants of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 1
2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 1
3, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 complexes (log
4 complexes (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β1, log
β1, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β2, log
β2, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β3, and log
β3, and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β4) are 4.32 ± 0.18, 7.50 ± 0.36, 9.74 ± 0.45, and 10.80 ± 0.5, respectively, which are in good agreement with the values in the literature.26
β4) are 4.32 ± 0.18, 7.50 ± 0.36, 9.74 ± 0.45, and 10.80 ± 0.5, respectively, which are in good agreement with the values in the literature.26
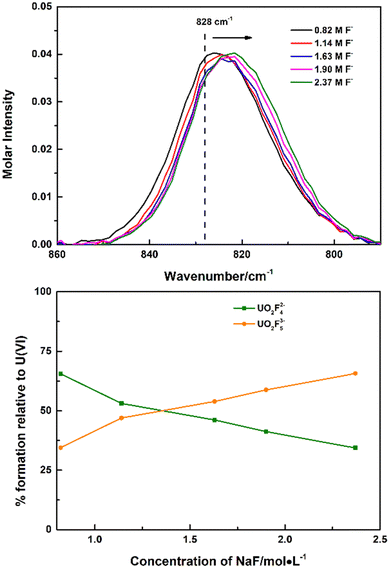
Though the UO2F53− species was not identified in UO2(ClO4)2–NaF solutions, with more soluble tetramethyl ammonium fluoride instead of NaF as the titrant, continuous shift to wavenumbers lower than 828 cm−1 was observed, which was ascribed to the formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 complex UO2F53−, Fig. 2. Every Raman spectrum of the uranyl moiety obtained in high (CH3)4NF concentrations consists of contributions from two species: UO2F42− at 828 cm−1 and UO2F53− at 817 cm−1. As the concentration of (CH3)4NF increased, intensities of the Raman band of UO2F42− decreased and the intensities of the Raman band of UO2F53− increased. The calculated stepwise formation constant of the UO2F53− complexes (K5) is 0.92, as shown in the ESI,† Table S1, and is calculated on the basis of the molar normalized intensity of the UO2F42− complex (Fig. 1) and the total concentrations of UO22+ and (CH3)4NF that were added to the solution initially.
5 complex UO2F53−, Fig. 2. Every Raman spectrum of the uranyl moiety obtained in high (CH3)4NF concentrations consists of contributions from two species: UO2F42− at 828 cm−1 and UO2F53− at 817 cm−1. As the concentration of (CH3)4NF increased, intensities of the Raman band of UO2F42− decreased and the intensities of the Raman band of UO2F53− increased. The calculated stepwise formation constant of the UO2F53− complexes (K5) is 0.92, as shown in the ESI,† Table S1, and is calculated on the basis of the molar normalized intensity of the UO2F42− complex (Fig. 1) and the total concentrations of UO22+ and (CH3)4NF that were added to the solution initially.
Nguyen-Trung et al. proposed a linear correlation between the symmetrical stretching frequency ν1 for the uranyl ion and the number of ligands coordinated in the equatorial plane of uranyl, commonly symbolized as ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , in eqn (1). Among them, the origin is UO22+, with ν1 = 870 cm−1 and
, in eqn (1). Among them, the origin is UO22+, with ν1 = 870 cm−1 and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 0.20
= 0.20
ν1 (cm−1) = −A![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + 870 cm−1 + 870 cm−1 | (1) |
In the present work, five fluoride complexes have been identified by spectral titration. A plot of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) versus the six frequencies observed in NaF and (CH3)4NF solutions is linear with slope A = 10.5 ± 1 cm−1 when the stepwise shifts in the frequency are assigned to UO22+, UO2F+, UO2F2(aq), UO2F3−, UO2F42− and UO2F53−, respectively, that is, the average difference in vibrational energies between successive complexes being 10.5 cm−1. However, there are some differences in speciation and frequencies between the present work and the literature.20 In the previous research, the UO2F53− complex was not identified in NaF and (CH3)4NF solutions, but only four new bands at 858 cm−1, 848 cm−1, 834 cm−1, and 822 cm−1, respectively, assigned to UO2F+, UO2F2(aq), UO2F3−, and UO2F42−, were reported. Besides, the average difference in vibrational energies between successive complexes is 12 cm−1. Among these bands, the first two bands around 858 cm−1 and 847 cm−1 are observed in the literature and the present work, but the frequencies corresponding to UO2F3− and UO2F42− are different. It is obvious that the frequencies of UO2F3− and UO2F42− deconvoluted from Raman spectra during titration in the present work, 837 cm−1 and 828 cm−1, by 3 cm−1 and 6 cm−1, respectively, higher than those reported in the literature (834 cm−1 and 822 cm−1). Considering that there is no observation of an old band disappearing or a new band appearing, only a continuous shift was detected at high NaF and (CH3)4NF concentrations, and it is difficult to accurately interpret slight variations of spectra and speciation of UO2F3−, UO2F42−, and UO2F53− complexes by simple curve fitting. However, with the application of Raman spectral titration, the calculated molar normalized spectrum of UO2Fn2−n can be strictly limited by formation constants of the UO2Fn2−n complex, providing a more reasonable assignment in the present work. As suggested above, it is the first time the UO2F53− complex is identified, with a symmetric vibrational stretching frequency at 817 cm−1.
versus the six frequencies observed in NaF and (CH3)4NF solutions is linear with slope A = 10.5 ± 1 cm−1 when the stepwise shifts in the frequency are assigned to UO22+, UO2F+, UO2F2(aq), UO2F3−, UO2F42− and UO2F53−, respectively, that is, the average difference in vibrational energies between successive complexes being 10.5 cm−1. However, there are some differences in speciation and frequencies between the present work and the literature.20 In the previous research, the UO2F53− complex was not identified in NaF and (CH3)4NF solutions, but only four new bands at 858 cm−1, 848 cm−1, 834 cm−1, and 822 cm−1, respectively, assigned to UO2F+, UO2F2(aq), UO2F3−, and UO2F42−, were reported. Besides, the average difference in vibrational energies between successive complexes is 12 cm−1. Among these bands, the first two bands around 858 cm−1 and 847 cm−1 are observed in the literature and the present work, but the frequencies corresponding to UO2F3− and UO2F42− are different. It is obvious that the frequencies of UO2F3− and UO2F42− deconvoluted from Raman spectra during titration in the present work, 837 cm−1 and 828 cm−1, by 3 cm−1 and 6 cm−1, respectively, higher than those reported in the literature (834 cm−1 and 822 cm−1). Considering that there is no observation of an old band disappearing or a new band appearing, only a continuous shift was detected at high NaF and (CH3)4NF concentrations, and it is difficult to accurately interpret slight variations of spectra and speciation of UO2F3−, UO2F42−, and UO2F53− complexes by simple curve fitting. However, with the application of Raman spectral titration, the calculated molar normalized spectrum of UO2Fn2−n can be strictly limited by formation constants of the UO2Fn2−n complex, providing a more reasonable assignment in the present work. As suggested above, it is the first time the UO2F53− complex is identified, with a symmetric vibrational stretching frequency at 817 cm−1.
3.2. Structures and vibrational frequencies from quantum chemistry
The Cartesian coordinates and the total energies of the optimized B3LYP and MP2 equilibrium structures of selected complexes [UO2(H2O)mFn]2−n(H2O)k in aqueous solution modeled by COSMO are provided in the ESI.† Listings with U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances and the frequencies of the symmetric UO22+ stretching vibrations are also provided for all complexes in the gas phase and in solution (COSMO), both at the B3LYP and MP2 levels of theory.
O distances and the frequencies of the symmetric UO22+ stretching vibrations are also provided for all complexes in the gas phase and in solution (COSMO), both at the B3LYP and MP2 levels of theory.
Table 1 lists U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances and UO22+ symmetric stretching frequencies for selected more stable [UO2(H2O)mFn]2−n complexes in the gas phase at the B3LYP level. The O of the H2O ligands is coordinated directly to the U center. The F− ions obviously donate more electron density to antibonding orbitals of UO22+ than H2O, so that upon replacing H2O by F− the U
O bond distances and UO22+ symmetric stretching frequencies for selected more stable [UO2(H2O)mFn]2−n complexes in the gas phase at the B3LYP level. The O of the H2O ligands is coordinated directly to the U center. The F− ions obviously donate more electron density to antibonding orbitals of UO22+ than H2O, so that upon replacing H2O by F− the U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance becomes significantly longer and the symmetric stretching frequency becomes drastically smaller, i.e., by about 0.1 Å and almost 200 cm−1 when going from [UO2(H2O)5]2+ to [UO2F5]3−. These results are in stark contrast, e.g., to the Raman data reported above, where a decrease from 870 cm−1 to 828 cm−1 was associated with the series of hydrated complexes from [UO2(H2O)5]2+ to [UO2F4]2−, i.e., a lowering of only about 10 cm−1 per H2O–F− exchange.
O bond distance becomes significantly longer and the symmetric stretching frequency becomes drastically smaller, i.e., by about 0.1 Å and almost 200 cm−1 when going from [UO2(H2O)5]2+ to [UO2F5]3−. These results are in stark contrast, e.g., to the Raman data reported above, where a decrease from 870 cm−1 to 828 cm−1 was associated with the series of hydrated complexes from [UO2(H2O)5]2+ to [UO2F4]2−, i.e., a lowering of only about 10 cm−1 per H2O–F− exchange.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances (Å) and UO22+ symmetric stretching frequencies (cm−1) from B3LYP gas phase calculations of [UO2(H2O)mFn]2−n complexes with H2O directly coordinated to U
O bond distances (Å) and UO22+ symmetric stretching frequencies (cm−1) from B3LYP gas phase calculations of [UO2(H2O)mFn]2−n complexes with H2O directly coordinated to U
| Complex |
R(U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
ω e |
|---|---|---|
| [UO2(H2O)5]2+ | 1.739 | 948 |
| [UO2(H2O)4F]+ | 1.761 | 904 |
| [UO2(H2O)3F2]meta | 1.775 | 874 |
| [UO2(H2O)2F3]ortho− | 1.790 | 838 |
| [UO2(H2O)F3]− | 1.790 | 833 |
| [UO2F4]2− | 1.819 | 794 |
| [UO2F5]3− | 1.834 | 756 |
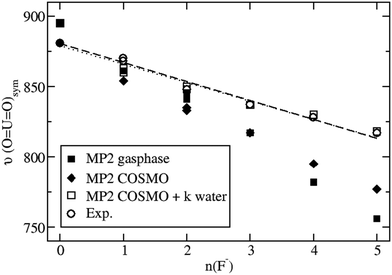
Taking bulk hydration effects into account by the COSMO approach at the B3LYP level does not improve the situation much. The symmetric stretching frequencies range from 912 cm−1 to 769 cm−1 for the series of complexes listed in Table S2 of the ESI.† When applying the ab initio approach MP2 combined with COSMO, a symmetric stretching frequency of 881 cm−1 is obtained for [UO2(H2O)5]2+ (Table S2, ESI†), in quite good agreement with the present experimental value of 870 cm−1 and an older one of 874 cm−1.34 However, the corresponding results of 795 cm−1 and 777 cm−1 for [UO2(H2O)F4]2− and [UO2F5]3− are still much too low compared to the measured and extrapolated experimental values of 828 cm−1 and 817 cm−1, respectively.
Considering [UO2(H2O)mFn]2−n(H2O)k complexes in bulk water modeled by COSMO, i.e. k additional H2O molecules in the second coordination sphere, which are not directly bonded to U, but rather form hydrogen bonds to the F− ligands, the results are improved a lot. For example, the MP2 result in COSMO for a [UO2F5]3−(H2O)5 is 818 cm−1 in excellent agreement with the extrapolated experimental value of 817 cm−1. Similarly, for [UO2F4]2−(H2O)4 a value of 819 cm−1 is calculated, compared to a measured one of 828 cm−1. Such improvements are also observed for the complexes with one to three F− ligands, although not always the number of H2O molecules building hydrogen bridges to the F− ligands can be determined unambiguously, cf.Table 2. These additional water molecules prohibit the F− ligands from donating too strong electron density to antibonding UO22+ orbitals, so that besides higher symmetric stretching frequencies also somewhat shorter U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances result. For example, at the MP2/COSMO level a U
O bond distances result. For example, at the MP2/COSMO level a U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance of 1.826 Å for [UO2F5]3− is reduced to 1.795 Å for [UO2F5]3−(H2O)5.
O bond distance of 1.826 Å for [UO2F5]3− is reduced to 1.795 Å for [UO2F5]3−(H2O)5.
Fig. 3 shows the nearly linear dependence of the symmetric UO22+ stretching frequencies on the number of fluoride ligands. It is seen that MP2 calculations neither for the gas phase nor for aqueous solution modeled solely by COSMO are in satisfactory agreement with experimental data, whereas the explicit inclusion of k water molecules in the second coordination sphere leads to an excellent agreement. Qualitatively, the behavior of the calculated B3LYP data is the same, although quantitatively the results are somewhat worse compared to that for MP2 (cf. Table S3 in the ESI†). Note that for n = 0 no water molecules in the second coordination sphere are treated explicitly in our model and only COSMO is applied. In this case the B3LYP symmetric UO22+ vibrational frequency of 912 cm−1 is significantly higher than the corresponding MP2 result of 881 cm−1 and the two experimental values of 870 and 874 cm−1. On the other hand for n = 5 five water molecules are treated explicitly in the second coordination sphere and the B3LYP and MP2 results of 817 cm−1 and 818 cm−1, respectively, virtually agree with the extrapolated experimental value of 817 cm−1. Thus the dependency of the results on the number of fluoride ligands is too strong for B3LYP and just about right for MP2.
Relativistic coupled cluster calculations (CCSD(T)) on the UO22+ cation showed that anharmonic effects decreased the vibrational frequencies, whereas spin–orbit effects increased the stretching frequencies and decreased the bending frequencies.35 Overall these two corrections led to a decrease of the vibrational frequencies, i.e., by 6 cm−1 for the asymmetric stretching mode, as well as by 3 cm−1 for the symmetric stretching and the bending modes. In view of these small corrections and the significantly more complex systems treated here we neglected both anharmonic effects as well as spin–orbit coupling in the present work. We are confident that these small corrections would not affect the general trends and main conclusions of our work.
Concerning the newly found UO2F53− complex we note that at the level of computation applied here this system is unstable in the gas phase both to the loss of an electron as well as to the loss of a fluoride ion F−, whereas it is stable in aqueous solution. In particular, based on total energies at the MP2 level using the COSMO approach [UO2F5]3− is about 21.2 kJ mol−1 more stable than its dissociation products [UO2F5]2− + F−. On the experimental side it seems to be likely that in previous studies there was a certain amount of UO2F53− in the solution as the concentration of F− has been increased to 1.0 M; however, only two bands at 834 cm−1 and 822 cm−1, which were assigned to UO2F3− and UO2F42−, respectively, have been identified by simple curve fitting, and the formation of UO2F53− was not considered. In the present work, the deconvolution of the Raman spectra for UO22+, UO2F+, UO2F2(aq), UO2F3− and UO2F42− was strictly limited by chemometrics and formation constants. As a result, it is more reasonable to assign Raman bands at 837 cm−1 and 828 cm−1, which were calculated from deconvolution, to the symmetrical stretching modes of UO2F3− and UO2F42−, respectively. Only the Raman band of UO2F53− was calculated from curve fitting at high fluoride concentration.
4. Conclusions
In this work, the thermodynamic properties and structural characteristics for five uranyl fluoride complexes in aqueous solution are investigated by combining Raman spectrometry and quantum chemical calculations. The titrations of UO22+ with F− were conducted by monitoring the variation in Raman spectroscopy. The formation constants and molar scattering intensities of single components were calculated by the deconvolution of the titration spectra. Furthermore, quantum chemical ab initio calculations at the MP2 level including relativistic contributions originating from U as well as bulk hydration effects yield frequencies in good agreement with experimental data only if water molecules in the second coordination sphere are explicitly taken into account. The formation constants, energy levels and structural information acquired as well as the developed modeling approach and quantum methodology could be beneficial to the future experimental and theoretical research on uranyl chemistry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
X. C. and M. D. are grateful for the hospitality and support during their visits at the China Institute of Atomic Energy.References
- E. Kraka, Uranium: The nuclear fuel cycle and beyond, Int. J. Mol. Sci., 2022, 23(9), 4655 CrossRef PubMed.
- A. Y. Romanchuk, I. E. Vlasova and S. N. Kalmykov, Speciation of uranium and plutonium from nuclear legacy sites to the environment: A mini review, Front. Chem., 2020, 8, 630 CrossRef CAS PubMed.
- G. Tian, S. J. Teat and L. Rao, Thermodynamic studies of U(VI) complexation with glutardiamidoxime for sequestration of uranium from seawater, Dalton Trans., 2013, 42(16), 5690–5696 RSC.
- G. Tian, S. J. Teat, Z. Zhang and L. Rao, Sequestering uranium from seawater: binding strength and modes of uranyl complexes with glutarimidedioxime, Dalton Trans., 2012, 41(38), 11579–11586 RSC.
- Z. Zhang, G. Helms, S. B. Clark, G. Tian, P. L. Zanonato and L. Rao, Complexation of uranium(VI) by gluconate in acidic solutions: a thermodynamic study with structural analysis, Inorg. Chem., 2009, 48(8), 3814–3824 CrossRef CAS PubMed.
- L. Rao and G. Tian, Thermodynamic study of the complexation of uranium(VI) with nitrate at variable temperatures, J. Chem. Thermodyn., 2008, 40(6), 1001–1006 CrossRef CAS.
- C. Xu, G. Tian, S. J. Teat and L. Rao, Complexation of U(VI) with dipicolinic acid: Thermodynamics and coordination modes, Inorg. Chem., 2013, 52(5), 2750–2756 CrossRef CAS PubMed.
- G. Tian and L. Rao, Spectrophotometric and calorimetric studies of U(VI) complexation with sulfate at (25 to 70) °C, J. Chem. Thermodyn., 2009, 41(4), 569–574 CrossRef CAS.
- R. Xie, W. Johnson, S. Spayd, G. S. Hall and B. Buckley, Arsenic speciation analysis of human urine using ion exchange chromatography coupled to inductively coupled plasma mass spectrometry, Anal. Chim. Acta, 2006, 578(2), 186–194 CrossRef CAS PubMed.
- H. Sodaye, S. Nisan, C. Poletiko, S. Prabhakar and P. K. Tewari, Extraction of uranium from the concentrated brine rejected by integrated nuclear desalination plants, Desalination, 2009, 235(1), 9–32 CrossRef CAS.
- Z. F. Wang and Z. J. Cui, Supercritical fluid extraction and gas chromatography analysis of arsenic species from solid matrices, Chin. Chem. Lett., 2016, 27(2), 241–246 CrossRef CAS.
- F. Kou, S. Yang, H. Qian, L. Zhang, C. M. Beavers, S. J. Teat and G. Tian, A fluorescence study on the complexation of Sm(III), Eu(III) and Tb(III) with tetraalkyldiglycolamides (TRDGA) in aqueous solution, in solid state, and in solvent extraction, Dalton Trans., 2016, 45(46), 18484–18493 RSC.
- F. Kou, S. Yang, L. Zhang, S. J. Teat and G. Tian, Complexation of Ho(III) with tetraalkyl-diglycolamide in aqueous solutions and a solid state compared in organic solutions of solvent extraction, Inorg. Chem. Commun., 2016, 71, 41–44 CrossRef CAS.
- Q. Liu, Q. Zhang, S. Yang, H. Zhu, Q. Liu and G. Tian, Raman spectral titration method: an informative technique for studying the complexation of uranyl with uranyl(VI)-DPA/oxalate systems as examples, Dalton Trans., 2017, 46(39), 13180–13187 RSC.
- B. Drobot, A. Bauer, R. Steudtner, S. Tsushima, F. Bok, M. Patzschke, J. Raff and V. Brendler, Speciation studies of metals in trace concentrations: The mononuclear uranyl(VI) hydroxo complexes, Anal. Chem., 2016, 88(7), 3548–3555 CrossRef CAS PubMed.
- B. Drobot, R. Steudtner, J. Raff, G. Geipel, V. Brendler and S. Tsushima, Combining luminescence spectroscopy, parallel factor analysis and quantum chemistry to reveal metal speciation-a case study of uranyl(VI) hydrolysis, Chem. Sci., 2015, 6(2), 964–972 RSC.
- A. D. Becke, Density-functional thermochemistry. I. The effect of the exchange-only gradient correction, J. Chem. Phys., 1992, 96(3), 2155–2160 CrossRef CAS.
- A. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98(7), 5648–5652 CrossRef CAS.
- G. Schreckenbach, P. J. Hay and R. L. Martin, Density functional calculations on actinide compounds: Survey of recent progress and application to [UO2X4]2- (X = F, Cl, OH) and AnF6 (An = U, Np, Pu), J. Comput. Chem., 1999, 20(1), 70–90 CrossRef CAS.
- C. Nguyen-Trung, G. M. Begun and D. A. Palmer, Aqueous uranium complexes. 2. Raman spectroscopic study of the complex formation of the dioxouranium(VI) ion with a variety of inorganic and organic ligands, Inorg. Chem., 1992, 31(25), 5280–5287 CrossRef CAS.
- V. Vallet, U. Wahlgren, B. Schimmelpfennig, H. Moll, Z. Szabo and I. Grenthe, Solvent effects on uranium(VI) fluoride and hydroxide complexes studied by EXAFS and quantum chemistry, Inorg. Chem., 2001, 40(14), 3516–3525 CrossRef CAS PubMed.
- R. Car and M. Parrinello, Unified approach for molecular dynamics and density-functional theory, Phys. Rev. Lett., 1985, 55(22), 2471 CrossRef CAS PubMed.
- M. Bühl, N. Sieffert and G. Wipff, Density functional study of aqueous uranyl(VI) fluoride complexes, Chem. Phys. Lett., 2009, 467(4–6), 287–293 CrossRef.
- A. Klamt and G. Schüürmann, COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient, J. Chem. Soc., Perkin Trans. 1, 1993, 799–805 RSC.
- S. O. Odoh, S. M. Walker, M. Meier, J. r Stetefeld and G. Schreckenbach, QM and QM/MM studies of uranyl fluorides in the gas and aqueous phases and in the hydrophobic cavities of tetrabrachion, Inorg. Chem., 2011, 50(7), 3141–3152 CrossRef CAS PubMed.
- G. Tian and L. Rao, Effect of temperature on the complexation of uranium(VI) with fluoride in aqueous solutions, Inorg. Chem., 2009, 48(14), 6748–6754 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, Gaussian 16, Wallingford, CT, 2016 Search PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152(14), 144107 CrossRef CAS PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic structure calculations on workstation computers: The program system turbomole, Chem. Phys. Lett., 1989, 162(3), 165–169 CrossRef CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, Energy-adjusted pseudopotentials for the actinides. Parameter sets and test calculations for thorium and thorium monoxide, J. Chem. Phys., 1994, 100(10), 7535–7542 CrossRef.
- X. Cao and M. Dolg, Segmented contraction scheme for small-core actinide pseudopotential basis sets, THEOCHEM, 2004, 673(1–3), 203–209 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- M. Gal, P. Goggin and J. Mink, Vibrational spectroscopic studies of uranyl complexes in aqueous and non-aqueous solutions, Spectrochim. Acta, Part A, 1992, 48(1), 121–132 CrossRef.
- V. E. Jackson, R. Craciun, D. A. Dixon, K. A. Peterson and W. A. De Jong, Prediction of vibrational frequencies of UO22+ at the CCSD(T) level, J. Phys. Chem. A, 2008, 112(17), 4095–4099 CrossRef CAS PubMed.
Footnotes |
† Electronic supplementary information (ESI) available: Calculated stepwise formation constants (K5) of the UO2F53− complex. U![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances and UO22+ symmetric stretching frequencies calculated for the gas phase/aqueous solution (COSMO) at the B3LYP/MP2 levels, as well as Cartesian coordinates and total energies of the optimized B3LYP equilibrium structures in aqueous solution (COSMO) of selected complexes [UO2(H2O)mFn]2−n(H2O)k. See DOI: https://doi.org/10.1039/d4cp01569j O bond distances and UO22+ symmetric stretching frequencies calculated for the gas phase/aqueous solution (COSMO) at the B3LYP/MP2 levels, as well as Cartesian coordinates and total energies of the optimized B3LYP equilibrium structures in aqueous solution (COSMO) of selected complexes [UO2(H2O)mFn]2−n(H2O)k. See DOI: https://doi.org/10.1039/d4cp01569j |
| ‡ Equal contributions. |
| This journal is © the Owner Societies 2024 |