Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The effect of ionic association on the electrochemistry of redox mediators for Li–O2 batteries: developing a theoretical framework†
Gabriela
Horwitz
 ab,
Vera
Kunz
a,
Samuel P.
Niblett
ab,
Vera
Kunz
a,
Samuel P.
Niblett
 a and
Clare P.
Grey
a and
Clare P.
Grey
 *ab
*ab
aYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Rd, Cambridge CB2 1EW, UK. E-mail: cpg27@cam.ac.uk
bThe Faraday Institution, Quad One, Harwell Campus, Becquerel Ave, Didcot OX11 0RA, UK
First published on 1st July 2024
Abstract
A theoretical framework to explain how interactions between redox mediators (RMs) and electrolyte components impact electron transfer kinetics, thermodynamics, and catalytic efficiency is presented. Specifically focusing on ionic association, 2,5-di-tert-butyl-1,4-benzoquinone (DBBQ) is used as a case study to demonstrate these effects. Our analytical equations reveal how the observed redox couple's potential and electron transfer rate constants evolve with Li+ concentration, resulting from different redox activity mechanisms. Experimental validation by cyclic voltammetry measurements shows that DBBQ binds to three Li+ ions in its reduced state and one Li+ ion in its neutral form, leading to a maximum in the electron transfer kinetic constant at around 0.25 M. The framework is extended to account for other phenomena that can play an important role in the redox reaction mechanisms of RMs. The effect of Li+ ion solvation and its association with the supporting salt counteranion on the redox processes is considered, and the role of “free Li+” concentration in determining the electrochemical behaviour is emphasized. The impact of Li+ concentration on oxygen reduction reaction (ORR) catalysis was then explored, again using DBBQ and modelling the effects of the Li+ concentration on electron transfer and catalytic kinetics. We show that even though the observed catalytic rate constant increases with Li+ concentration, the overall catalysis can become more sluggish depending on the electron transfer pathway. Cyclic voltammograms are presented as illustrative examples. The strength of the proposed theoretical framework lies in its adaptability to a wider range of redox mediators and their interactions with the various electrolyte components and redox active molecules such as oxygen. By understanding these effects, we open up new avenues to tune electron transfer and catalytic kinetics and thus improve the energy efficiency and rate capability of Li–O2 batteries. Although exact results may not transfer to different solvents, the predictions of our model will provide a starting point for future studies of similar systems, and the model itself is easily extensible to new chemistries.
Introduction
Lithium–air batteries (LABs) have a theoretical energy storage capacity three to five times higher than Li-ion batteries and are thus appealing candidates for high-energy density electric vehicle applications. They are composed of a lithium anode and a porous conductive matrix (usually carbon-based), at which oxygen is reduced during discharge and the discharge product, typically lithium peroxide, is oxidized during charge. One of the major issues preventing the development of LABs is the high overpotential needed to charge the battery due to the insulating nature of the solid discharge products, leading to a cascade of degradation reactions.1,2One strategy to help enable the discharge and charge reactions of the LAB, is to use soluble redox-active species (redox mediators, RMs) to increase energy efficiency and minimize electrolyte degradation. The use of these soluble species is a widespread strategy across different applications in electrochemical systems.3 Some examples include redox-flow batteries, where the dissolved electroactive species are the main source of energy storage, and hybrid solid redox flow batteries, where RMs transport the charge between an electrode and a disconnected solid active species.4 A similar concept, “redox targeting” was also introduced to overcome the insulating nature of lithium insertion materials (LiFePO4).5 Furthermore, soluble active species have been used as a liquid anode in alkali metal batteries (Na and K) coupled with different cathodes, including oxygen.6
When RMs are present in a LAB, these molecules or ions act as soluble catalysts: during the discharge, the RM is reduced at the surface of the electrode; it then diffuses through the solution where it can react with dissolved oxygen, eventually forming Li2O2 as the discharge product. As the crystallization of lithium peroxide occurs from the solution, large Li2O2 crystals can be formed while leaving free, non-passivated electrochemically active surface, leading to high discharge capacities. During charging, the RM is oxidized at the exposed, free surface of the electrode that is not blocked by discharge product, and then chemically reacts with it to release O2. Thus, RMs allow decoupling of the oxygen reduction reaction (ORR) and oxygen evolution reaction (OER) from the electron transfer (ET) reactions at the electrode, giving the charge transfer an alternative path to tunnelling through the electrically insulating Li2O2.1 Furthermore, the use of RMs can avoid reaction pathways that result in reactive oxygen species and hence improve the overall cycling stability of LABs.7–10 One of the most commonly used discharge RMs is 2,5-di-tert-butyl-1,4-benzoquinone (DBBQ), which has been shown to increase the discharge capacity of a Li–O2 battery up to 80 times under typical LAB operating conditions.11
Previous studies have mainly focused on understanding the thermodynamic aspects governing the ability of a molecule to act as a successful RM. The principal parameter analysed is usually the standard potential of the RM electrochemical couple, E0, although this quantity is usually obtained using a Li reference electrode, which is potentially complex since the electrode is reactive and not always stable and the Li/Li+ potential varies between different electrolytes.12,13 Moreover, the E0 of the RMs is also often incorrectly assumed to be independent of the solvent, Li salt identity and concentration. Some attention has been given to the effect of solvation environments on the reduction potential of iodide,14 but little has been said about other RMs.15 Since most ET reactions with RMs involve a significant change in the charge/size ratio of the molecule or ion, it is only natural that the driving force for this reaction will be dependent on the molecular environment around the species.
The kinetics of the ET and of the reaction of RM with the target species (O2 in the case of discharge RM and Li2O2 in the case of charge) are another factor that have received almost no attention, and yet they are crucial for the operation of a Li–O2 battery. The kinetics of ET directly controls the overpotential in a galvanostatic battery configuration, while the rate of catalysis needs to be fast enough to sustain the cycling. It is often assumed that the electrochemical conversion of RMs is fast, and hence Nernstian. However, most RMs exhibit quasireversible behaviour, which can limit the viable current density.16–18 In fact, significant overpotentials are seen when discharging Li–O2 batteries even when using RMs under high rates that are closer to practical values. Some effort has been made to relate the kinetics of the catalysis to the standard potential of the charge RM or the ET kinetics, but there is no consensus regarding these effects.19–23 Recently, Bawol et al. showed the importance of ionic association in the kinetics of ORR catalysis by DBBQ,15 proposing that a complex of Li-DBBQ mediates the reaction and showing that a higher association of DBBQ with a cation promotes faster catalysis.
The aim of this work is to establish relationships between chemical parameters, such as ionic association, solvation energy and parallel equilibria, and the driving force and kinetics of ET involving the RM, and hence, to understand the RM's catalytic role. These effects are directly related to the performance of a Li–O2 battery. We use DBBQ in Li+-containing dimethylsulfoxide (DMSO) solutions as a model electrolyte to illustrate the approach, because of its importance for Li–O2 batteries, however the approach presented here can be easily applied to other redox active species, or other discharge and charge RMs, in solvents where ionic pairing is expected to be significant.
DBBQ is known to undergo ionic association with up to three lithium ions, as seen from the dependence of its reduction potential on the concentration of lithium salt in DMSO electrolytes.15 The exact mechanism for this reduction has been sometimes assumed to be either concerted (eqn (1)),16,24 or stepwise (eqn (2)).15
| DBBQ + nLi + e− ⇄ DBBQ⋯Lin | (1) |
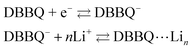 | (2) |
Inspired by the well-established behaviour of quinones in aqueous conditions, which undergo proton-coupled electron transfer, this work first develops a theoretical framework to treat RM's ionic association with Li+ ions based on the Nernst and the Butler–Volmer (BV) equations. Our framework is written in terms of a general RM, denoted as Q, which is assumed in the equations to be neutral in its initial state; however, equivalent equations can be written for the case of charged RMs.
We start by analysing how association constants and Li+ concentration impact the thermodynamics and kinetics of different possible pathways, defining an apparent rate constant and showing how it changes as a function of [Li+]. By comparing the framework predictions with experimental data obtained by cyclic voltammetry, we extract insight into the mechanism of DBBQ conversion in DMSO based electrolytes. To expand the framework's validity into systems composed of different solvents and salts, we then explore the theoretical consequences of other phenomena, namely counteranion and solvation effects. Since a typical electrolyte for Li–air batteries is composed of a lithium salt (sometimes referred to as a “supporting salt”) and a RM dissolved in much lower concentrations, we analyse the effect of competition for Li+ ions with the lithium salt counteranion, giving one more dimension to the tuning of these processes. Given further experimental data, this analysis will help determine the mechanisms by which DBBQ operates in various non-aqueous electrolytes at concentrations relevant for batteries. Furthermore, our approach opens a new route to rationally tune ET kinetics for RMs by optimizing electrolyte composition for increased electrochemical rates and hence lower overpotentials.
Once the effect of ionic association in the ET of RMs is understood, we move on to analyse the effect of ion association on the oxygen reduction reaction (ORR) catalysis. In the case of DBBQ, it has been established that the reactive intermediate is an associated monoanion-Li (DBBQ–Lin).15
The elementary steps of DBBQ's reactions have been proposed to start with the association of the reduced quinone to O2, which is expected to be reversible15,16,25
 | (3) |
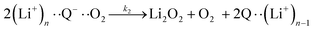 | (4) |
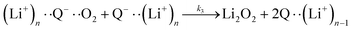 | (5) |
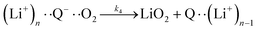 | (6a) |
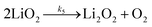 | (6b) |
It is worth noting that reaction (4) is a combination of both steps in reaction (6). To maintain consistency with previous reports,15 we have named the rate constants in eqn (3) and (6)k1, k−1, k4 and k5. Bawol et al. have found increased catalytic rates in solutions with higher ionic association of DBBQ, indicating that associated DBBQ species are the active ones during ORR.15 Here, we have considered the possibility that not only DBBQ–Li+ takes part in the reaction, but highly associated quinone species (n ≥ 1) can also be involved.
This work ends by establishing a theoretical simplified representation of how association strength affects the ORR kinetics and cyclic voltammograms. This will allow the changes in in electrochemical signatures related to association and solvation environments to be explained. Therefore, the predictions made here will serve as a guide to extract qualitative (or even quantitative) mechanistic information from the results of these types of electrochemical experiments.
Results and discussion
1. Theoretical framework: effect of ionic association on different electron transfer mechanisms under an inert atmosphere
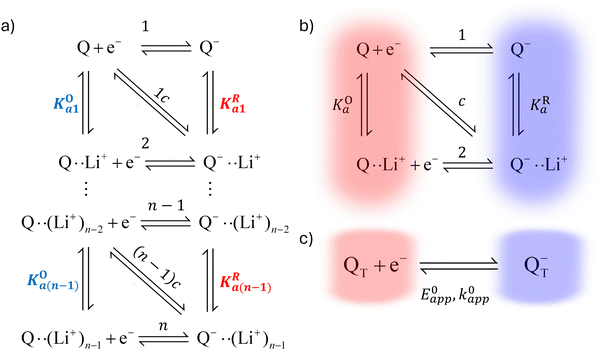
In this section, we present a general model to describe how the thermodynamic and kinetic parameters of a one-electron reaction are affected by the ionic association of the redox-active species with another ionic species using DBBQ as the model RM. For simplicity, we first assume an inert atmosphere (e.g. Ar gas) so there is no oxygen gas available to react with any component of the electrolyte. We show how this model can be used to diagnose specific pathways the redox reaction can take, helping to understand the differences observed under various experimental conditions; moreover, we show how we can use the model as a tool to tune the desired path.It is known that the DBBQ monoanion bonds to multiple lithium ions in DMSO-based electrolytes. Here, we allow for the possibility that the oxidized neutral DBBQ also bonds to Li+ ions. Taking this into account, the first reduction of DBBQ can, in principle, follow multiple pathways, depicted in Scheme 1a, where the vertical reactions represent chemical equilibria of association of quinone species with Li+ ions, the horizontal ones represent ET reactions, and the diagonal ones concerted steps where association and ET happen at the same time. To simplify the theoretical treatment, we first consider the uppermost square of the ladder, depicted in Scheme 1b, before extending to the more general case. For simplicity, and given that this treatment is general, we will call our reactive species Q.
In addition to the elemental electrochemical steps (horizontal reactions), we consider the simultaneous equilibrium of each of the associated species with its dissociated form (vertical reactions). These reactions are governed by KOa and KRa, the association constants of each of the species with the complexing ion present in solution (Li+ in this example). The RM in our work, Q, is assumed to be neutral, so the Q–Li+ coulombic interactions will be smaller than those for Q−–Li+. Therefore we assume KOa to be smaller than KRa. However, the RM could be initially charged (a reduction of Q− to Q2−, for example) and our framework would still be applicable. These reactions can be summarized in a square type diagram as represented in Scheme 1, which resembles analogous mechanisms proposed in proton-coupled redox reactions.27–29 Which reduction pathway DBBQ undergoes will depend on the key parameters: the lithium concentration, KOa, KRa, E01 and E02 the standard potentials of the elemental steps denoted as 1 and 2 in Scheme 1b.
The relations between the standard potential of the three different electrochemical reactions are defined by the strength of ionic association and can be described by eqn (7) and (8) coming simply form the relation between ΔG0, ΔE0 and Kia.
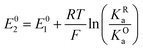 | (7) |
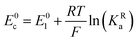 | (8) |
Taking inspiration from the proton coupled electron transfer literature and some previous ionic association studies,27,28,30–32 we define the overall apparent standard potential, E0app, as the potential in which the total oxidized and reduced species reach the half-point, i.e, [Q−] + [QLi] = [Q] + [QLi+]. Given the simultaneous association equilibria, this potential will depend on lithium concentration. The rate at which the overall reaction takes place will also depend on lithium concentration and can be described by the apparent standard heterogeneous electron transfer rate constants, k0app, which will be discussed in more detail in the next section. It is important to note that these apparent parameters are the ones that can be directly measured experimentally, for example by the use of cyclic voltammetry.
The mass balance for Q at a particular potential E can be described by eqn (9) where [i] denotes the concentration of the species i in solution and ci = [i]T the total analytical concentration dependent on the potential through the Nernst equation.
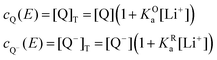 | (9) |
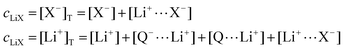 | (10) |
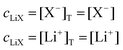 | (11) |
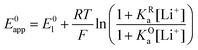 | (12) |
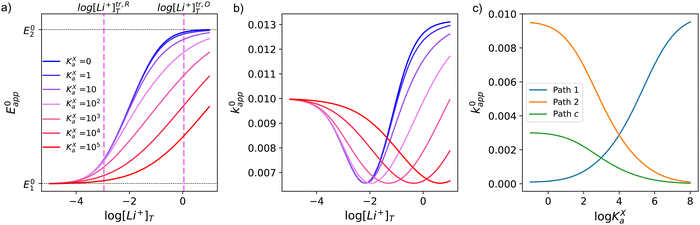
This equation describes an “S” shaped curve, analogous to a Pourbaix diagram when dealing with protonation reactions, as shown in Fig. 1. The diagram is composed of three main regions: two constant-potential regions where the lithium concentration is much higher than 1/KOa, or much lower than 1/KRa, and a close to linear evolution between those values. These regions reflect a transition from pathway 1 to pathway 2 at different lithium concentrations if KOa and KRa are non-negligible.
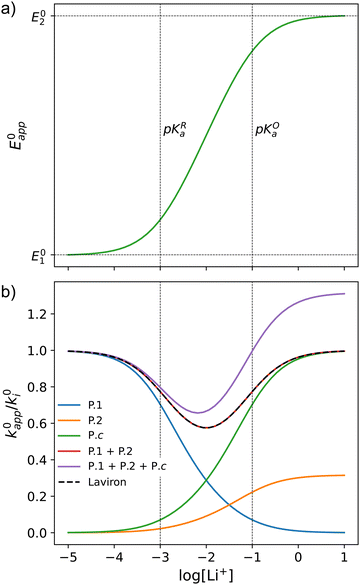 | ||
| Fig. 1 (a) Evolution of apparent potential of the system as a function of lithium concentration. (b) Evolution of individual components of the normalized rate constant and total rate constant as a function of lithium concentration. P.1, P.2, and P.c represent pathways 1, 2 and c, respectively. The black dashed line corresponds to the expression obtained by Laviron28 for the total kinetic constant, considering pathways 1 and 2, k01,app + k02,app (see text in Section 1.2 for definition), assuming α1 = α2 = 0.5. Figures were computed using KOa = 10, KRa = 1000, k01 = k02 = k03 = 0.01. | ||
It is important to note that in eqn (12), [Li+] represents the concentration of free lithium ions in solution (as opposed to their analytical concentration, which can be different in the presence of other equilibria). We assume that there are no reactions that might consume Li+, for the remainder of the current section, but later relax the assumption.
Extensive theoretical work has been performed by Laviron regarding coupled and closed sets of chemical and electrochemical reactions that can be depicted by a square, with an emphasis on protonation reactions.27,28 These systems are referred to here (and in the literature) as “square schemes”. In his seminal work, Laviron obtained expressions for the evolution of E0 and k0 as a function of the pH and pKa of weak acids in schemes analogous to Scheme 1b, where instead of Li+ he considered H+ and a concerted mechanism was not taken into account. In his calculations, an α value of 0.5 for both horizontal ET reactions was assumed, resulting in an overall k0app expression that can be interrogated to obtain reaction pathway ratios. For simplicity, and to obtain direct information about the different mechanisms, here we treat each pathway in Scheme 2 separately, before combining them to obtain the overall behaviour.
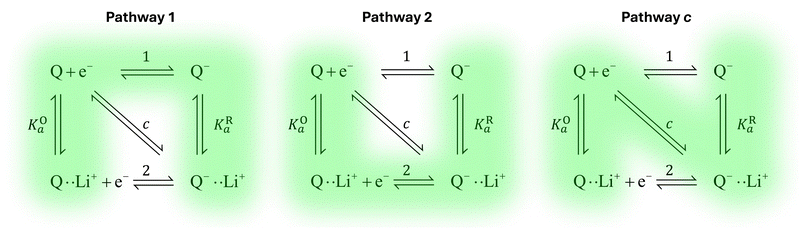 | ||
| Scheme 2 Representation of pathways 1, 2 and c, the green shading highlighting all the reactions that take part on the different pathways. For example, in pathway 1, the electron transfer reaction occurs via step 1, but the chemical equilibria involving Li+ association KO/R1 are also included in the modelling. Each of these pathways represent a subset of the ones presented in Scheme 1. | ||
By combining eqn (7)–(9), alternative expressions for E0app can be written, which will be useful in the next section when analysing each mechanistic scenario. Note that each of the eqn (12)–(14) depends on a different E0i, which means that they reflect how E0app evolves when compared to the standard reduction potential of the ET steps involved in the different pathways.
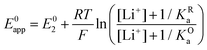 | (13) |
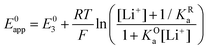 | (14) |
The rate of the reduction and oxidation processes for the elemental step 1, vred1, is described by the change in concentration of Q with time through pathway 1. Here, we only include the theoretical treatment for the reduction reaction, however, the same results can be obtained if the equations are expressed for the oxidation reaction instead.
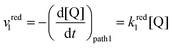 | (15) |
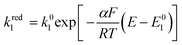 | (16) |
If we combine eqn (12), (15) and (16) so that the rate of the reduction reaction is expressed as a function of E0app, the overall rate is defined by eqn (17).
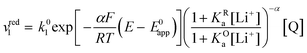 | (17) |
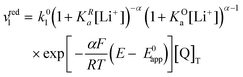 | (18) |
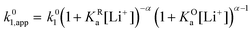 | (19) |
Now let's turn to pathway 2. In this case, only the lower electrochemical reaction in Scheme 1b is active, which is expected to be relevant at high lithium concentrations. The rate for reduction along this path is given by eqn (20). Analogously to pathway 1, if we replace E02 by its expression as a function of E0app from eqn (13), we can show that the system behaves as a single electrochemical couple with standard potential E0app, standard heterogeneous rate constant k02,app given by eqn (21), and redox active species concentration [Q]T.
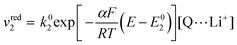 | (20) |
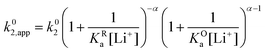 | (21) |
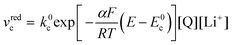 | (22) |
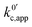 .
.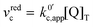 | (23) |
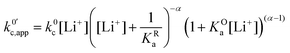 | (24) |
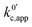 now includes the [Li+] present in the rate law described in eqn (22). This comes with the approximation that the [Li+] stays constant throughout the reaction, without the need to introduce any new assumptions (since we already stated that [Q] ≪ [Li+]). In the extreme scenario, where the intermediate species Q− and QLi+ are both highly energetic, and this is the only taken pathway, i.e. KOa is extremely small and KRa extremely large, we recover the expression obtained by Saveant for the purely concerted reaction.33
now includes the [Li+] present in the rate law described in eqn (22). This comes with the approximation that the [Li+] stays constant throughout the reaction, without the need to introduce any new assumptions (since we already stated that [Q] ≪ [Li+]). In the extreme scenario, where the intermediate species Q− and QLi+ are both highly energetic, and this is the only taken pathway, i.e. KOa is extremely small and KRa extremely large, we recover the expression obtained by Saveant for the purely concerted reaction.33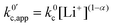 | (25) |
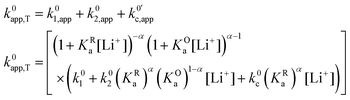 | (26) |
As expected, if we only consider pathways 1 and 2, and we assume that α1 = α2 = 0.5, then by adding up the resulting k01,app and k02,app we recover the expression obtained by Laviron for the total kinetic constant.27,28Fig. 1b nicely illustrates how the rates of pathway 1 and pathway 2 evolve with lithium concentration, and how at intermediate concentrations the reaction is more sluggish than either of the individual components at lower and higher [Li+]. If we now add the possibility of the reaction occurring partially though pathway c, we obtain the purple curve in Fig. 1b. This approach clearly represents the fraction of the reaction going through each of the pathways, proportional to the individual rate constants represented by k01,app and k02,app and 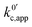 . It also depicts very clearly how, for a set value of KOa and KRa, tweaking the concentration can promote either pathway 1 or pathway 2 or c. The competition between pathways 2 and c is largely determined by whether KOa is higher or lower than 1, which reflects the relative stability of the intermediate Q⋯Li+. However, we note that the complex concerted mechanism necessary for pathway c could result in a low kinetic prefactor k0c, such that this pathway is not observed even in cases where the alternative pathways are thermodynamically disfavoured.
. It also depicts very clearly how, for a set value of KOa and KRa, tweaking the concentration can promote either pathway 1 or pathway 2 or c. The competition between pathways 2 and c is largely determined by whether KOa is higher or lower than 1, which reflects the relative stability of the intermediate Q⋯Li+. However, we note that the complex concerted mechanism necessary for pathway c could result in a low kinetic prefactor k0c, such that this pathway is not observed even in cases where the alternative pathways are thermodynamically disfavoured.
To visualize how each of the pathways will manifest themselves in the experimental cyclic voltammogram (CV) data, Fig. 2 shows CVs of the system simulated using a finite element approach by DigiElch,34 which uses a numerical solution of the electrochemical system including both kinetics and mass transport. Each of the panels represents the system when it is allowed to take only one of the three pathways shown in Scheme 2. In the simulations, each elementary step was included, and CV response was obtained. The resulting CVs showed a single peak, and the effective parameters, Eapp and k0app, of Scheme 1c were adjusted to reproduce this signal. These values were compared with the ones predicted by our framework in eqn (19), (21) and (24) and are in quantitative agreement within the limits of the approximations (i.e. [Li+] much higher than [Q]T). This confirms the validity of our framework when including mass transport effects.
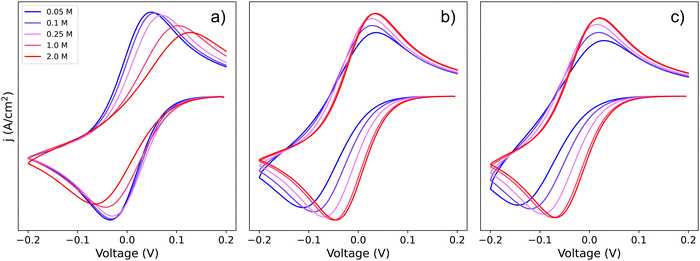 | ||
| Fig. 2 Simulated cyclic voltammograms for each of the pathways depicted in Scheme 2: pathways, (a) 1, (b) 2, and (c) c. The three plots are computed using KOa = 2, KRa = 10 and k01 = k02 = k03 = 0.01, all with a scan rate of 50 mV s−1 and [Q] = 5 mM, for [Li+] ranging from 0.05–2 M. | ||
If we focus on Fig. 2a, representing pathway 1, we can see that the peak-to-peak separation, a proxy for the rate of electron transfer,26 increases with Li+ concentration. This is in agreement with the predicted decrease in k01,app for this pathway with increasing [Li+]. For pathways 2 and c, the opposite trend appears: the peak to peak separation decreases with Li+ concentration, in agreement with the prediction seen in eqn (21) and (24) where k02,app and 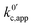 increase.
increase.
The finite element simulations also allow us to easily visualize how the individual cathodic (reduction, negative current) and anodic (oxidation, positive current) peak positions shift with changing [Li+] or reaction kinetic parameters. These positions are a proxy for the overpotentials obtained in a galvanostatic experiment, such as a Li–air battery: the higher the shift from a reversible CV shape, the higher overpotentials are expected in a battery configuration. The three different pathways show different behaviours for each of the processes as function of changing [Li+]. In the case of pathway 1, the cathodic peak undergoes a small shift towards negative potentials, while the anodic peak is more noticeably pushed towards positive potentials. Mathematically, this arises from the compounded effect of the shift in E0app (eqn (12)), that moves the average potential between the peaks, with an increase in peak-to-peak separation due to the ET becoming more sluggish. Chemically, these shifts can be rationalized in terms of the Q and Q− concentration: when the [Li+] is increased, the vertical equilibria in Scheme 1 are shifted toward the associated species (bottom). This means that the Q and Q− concentrations in the surface of the electrode are always lower than [Q]T, which delays their conversion through pathway 1.
For pathways 2 and c, the opposite trend is seen: the cathodic peak suffers a larger shift in potential than the anodic one. In this case, the displacement of the system towards higher association degrees increases the concentration of electroactive species, Q–Li+ and Q–Li, making the overall system more reversible. Interestingly, this means that for a RM following pathway 1, its reduction potential does not change drastically with lithium salt concentration, but for one following either pathway 2 or c, the reduction potential will be highly dependent on it.
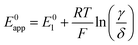 | (27) |
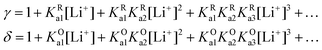 | (28) |
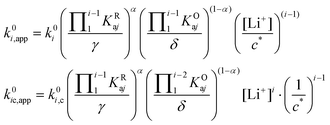 | (29) |
Fig. 3 shows the evolution of k0i,app with [Li+] for the different pathways when the maximum association steps considered correspond to n = 3 (Fig. 3a) and n = 4 (Fig. 3b), representing the association of Q with two and three Li+ ions, respectively. Interestingly, allowing for association with multiple cations makes the pathways’ apparent rate constants non-monotonic in [Li+] resulting in different concentration regions where each pathway is dominant. In particular, if KRa2 > KOa2 (which is expected based on electrostatic interactions), pathway 2 shows a maximum at intermediate [Li+]. This can be easily understood, by a shift of the equilibria governed by KOa2 and KRa2 to products at high [Li+], lowering the available [QLi+] and [QLi] to react, hence making path 2 and 1c unfavourable. Interestingly, this suggests that some of the possible pathways the reaction might take could be disentangled by examining experimental CVs as a function of [Li+]. Note that pathways 2 and 1c and 3 and 2c have the same functional dependence on [Li+], an enlargement of these curves can be seen in Fig. S2 (ESI†). This statement can be generalized to pathways i and (i + 1)c.
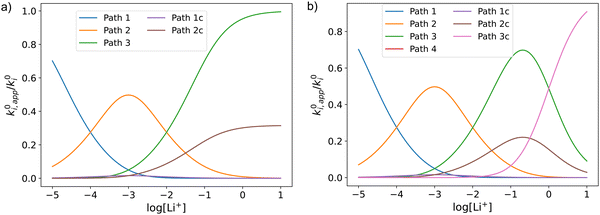 | ||
| Fig. 3 Example of behaviour of the apparent standard rate constant for each of the pathways represented in Scheme 1a with n = 2 (a) and n = 3 (b). The plots shown in the figures were computed using the parameters KRa1 = 1 × 105, KRa2 = 1 × 103, KOa1 = 1000, KOa2 = 10, and KRa3 = KOa3 = 0 for (a) and KRa3 = KOa3 = 1 for (b). The parameters were chosen so that the behaviour of the different pathways can be seen clearly. The actual positions and magnitudes of the curves’ maxima and plateaus strongly depend on these parameters, but their shapes are characteristic of the different paths. | ||
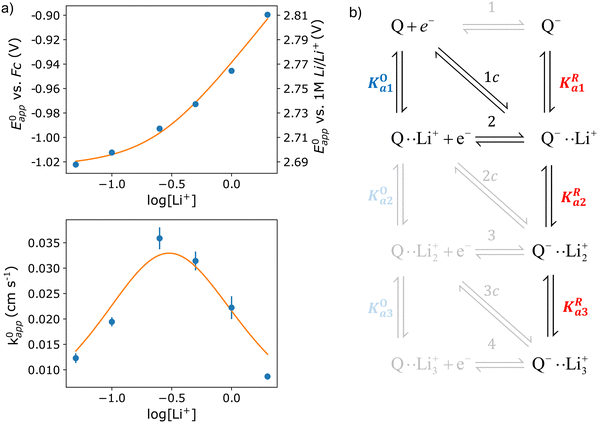 | ||
| Fig. 4 (a) Experimental standard potential, E0 (top) and kinetic constant, k0 (bottom) represented as dots compared with the fitting results when assuming the mechanism represented in panel (b). The values derived from the fits are given in Table 1. (b) Schematic of the possible pathways for redox activity of DBBQ in Li+ containing DMSO solutions. The greyed-out pathways were not needed to explain the experimental behaviour. | ||
The experimental data obtained for E0app and k0app were fitted using the mechanism shown in Fig. 4b. Multiple combinations of the possible pathways were tested, including the greyed-out reactions, with constraints placed on the association constants based on expected electrostatic interactions. Namely, the constants were set to follow the order Ka1 > Ka2 > Ka3 for both the oxidized and reduced species, and KRai > KOai for constant i, with the same number of interactions with Li+. We found that only pathways 2 and 1c were necessary to describe the experimental results, and adding more alternative pathways did not improve the fitting significantly, so they were kept inactive for the final fit. The parameters corresponding to the highlighted active pathways were varied to fit the evolution of E0app and k0appvs. the lithium-ion concentration, and the results can be found in Table 1.
| Parameter | Best fit value |
|---|---|
| E 01 | −1.0 vs. Fc/2.7 vs. Li |
| E 02 | −0.97 vs. Fc/2.73 vs. Li |
| E 0c | −0.96 vs. Fc/2.74 vs. Li |
| K Ra1 | 5.4 |
| K Ra2 | 3.2 |
| K Ra3 | 3.2 |
| K Oa1 | 1.9 |
| k 02 (KOa1)(1−α) + k01c | 0.102 cm4 mol−1 s−1 |
The first thing that becomes clear is that the quinone is highly associated in this system, binding to up to three Li+ ions in its reduced form. However, the neutral oxidized form also interacts with Li+, something that was not considered in literature before. In fact, our results indicate that, at the typical 1 M concentration, around 65% of the neutral DBBQ is bound to a Li+. Since the apparent kinetics of pathways 2 and 1c follow the same functionality with lithium concentration, it is not possible to separate the contributions from each of them with this approach. However, it is clear from the fitting results that pathway 1 and 2c are inherently much slower than 2/1c. I.e., the association of DBBQ with Li+ either prior to reduction (1) or via a concerted process (2c) result in faster reduction kinetics. Steps 2 and 1c are associated with larger free energy changes than step 1, since E01 < E02 < E0c (eqn (7) and (8) still hold). In both cases, an activated complex involving one Q molecule and 1 Li+ ion is formed. It can then be speculated that the association of the quinone with a Li+ ion modifies the electronic structure of the quinone ring in such a way that it lowers the energy of the products and activated complex, thus making these pathways kinetically predominant, i.e, they have a higher k0.
In this section, we consider the thermodynamics and kinetics of the RM reaction network discussed previously, with the addition that the Li+ ion may also interact with its counterion, X−. We limit our analysis to the case where Q binds to only 1 Li+ ion, as in Scheme 1b (i.e. n = 1) for simplicity. The extension to higher n values is trivial, and the effect on the system is analogous. In this case, mass balance eqn (11) is replaced by:
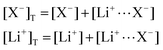 | (30) |
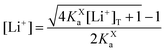 | (31) |
The dependence of ET parameters on association strength of the supporting salt is shown in Fig. 5. The apparent potential plateaux corresponding to pure pathway 1 and pure pathway 2, and the crossover region between them, now depend on KXa and are governed by eqn (12) and (31). The transition from E01 to E02 no longer follows a straight line with slope RT/F, but it slows down to a slope of RT/2F when KXa is sufficiently high. The transition between the two extreme regimes is shifted to higher [Li+], the value of this crossover concentration is stated in eqn (S4) of the ESI.†
Fig. 5 shows the effect of varying KXa on the thermodynamics and kinetics of the system. The full equations describing these phenomena can be found in eqn (S2)–(S4) (in the ESI†). As expected because of the small amount of free lithium in highly associated solutions, all changes with increasing [Li+] are delayed and happen in a less abrupt way.
Interestingly, sufficiently high competition for the lithium ions can affect the dominant pathway taken by the redox reaction. This becomes evident when we analyse how each of the contributions of k01,app, k02,app and k0c,app to the total k0app behave as a function of KXa at a given [Li+], in Fig. 5(c). We can see how higher association of the lithium salt promotes pathway 1 while slowing down pathways 2 and c. The overall mechanism is, in the end, a competition between the association of the quinone and of the supporting counteranions with lithium. We note that this effect is not important in DMSO based electrolytes due to the low ionic association of typical Li–air battery salts in this solvent, however it is expected to be relevant in glyme based electrolytes.
The “free” lithium concentration can also change due to strong interactions with solvent molecules (particularly in systems with high lithium solvation energies). For example, in the case of glymes, it has been shown that Li+ forms complexes with the solvent molecules that stabilize the Li+–glyme adducts with respect to free Li+.35,41–45 The present system can be treated analogously, with the only difference that the solvent molecules are in large excess with respect to the lithium ions. The effect of solvation strength, i.e. ΔG0 for the solvation reaction, on the standard apparent potential and rate constants is depicted in Fig. S3 in the ESI.† Qualitatively, the Li+ solvation has a similar effect to that of Li+ association with the counteranion, and experimentally a combination of both effects is likely seen. Extending the analysis of this section to n > 1 is straightforward by combining eqn (27)–(29) with eqn (31).
Overall, in this section we have shown how the strong interaction of quinone with Li+ ions affects the reduction mechanism, making the reaction rate and apparent potential depend on lithium concentration, and on solvent and supporting salt identities. We have shown that for a given RM-Li+ interaction strength (KOa and KRa), the free Li+ concentration can tune the kinetics of the system. We also discussed the effect of parallel equilibria, showing that the defining parameter is the free [Li+], which can be influenced by ionic association of Li+ with the counteranion and by its interaction with solvent molecules. Taking these results together, we conclude that to optimise electrolyte composition for minimum overpotential one must first establish the free-lithium concentration that maximises the apparent reduction rate constant in the absence of supporting salt, and then tune the supporting salt concentration to achieve that concentration. Kinetic models such as the framework presented here offer the possibility of determining these target concentrations with a reduced number of experiments, especially if some of the parameters required can ultimately be predicted computationally or else inferred from other solvent systems.
2. Effect of ionic association in catalysis of the ORR
At this point we have built a comprehensive framework to describe the electrochemical behaviour of RM systems, particularly DBBQ. We now consider whether we can we use the apparent parameters obtained in the previous section to help explain the behaviour of the Li–O2 cathode reactions, involving the catalytic processes of DBBQ reacting with O2. Since there are no systematic studies and understanding of the CV shapes of mediated ORR in Li–air electrolytes, the goal of this section is to provide a guide that can help rationalize experimental results as a step towards a unified mechanism of the DBBQ mediated ORR.We start by describing the simplest case, described with eqn (32), where O is the catalyst (in our case DBBQ) and R its reduced form, S the substrate (in our case oxygen, O2), and P the product (in our case Li2O2). It is well established in literature that homogeneous electrocatalytic processes of this type can be characterised by the shape of their cyclic voltammogram. This shape depends on the analytic concentration of O, cO, the analytic concentration of S, cS, the scan rate, υ, and the rate constant for the catalytic step in eqn (32b), kCat. The actual mechanism of DBBQ catalysis is much more complex, but qualitatively similar CV shapes are expected even for more complicated mechanisms.46–48
| O + e− ⇌ R | (32a) |
 | (32b) |
In short, 6 zones can be identified for different characteristic CV shapes, as described by Rountree et al. in their figure reproduced in Fig. 6: D (no catalysis, CV shape observed is equal to the redox couple O/R). KS (pure kinetic conditions, no substrate consumption, S shaped), K (pure kinetic conditions, substrate consumption, large catalytic reduction peak with no oxidation peak), KT (“total catalysis”, pure kinetic conditions, substrate consumption: two reduction peaks), KD (mixed kinetic-diffusion, no substrate consumption, elongated shape), KG (mixed kinetic-diffusion, with substrate consumption: asymmetric peak heights, larger reduction than oxidation peak).46–48
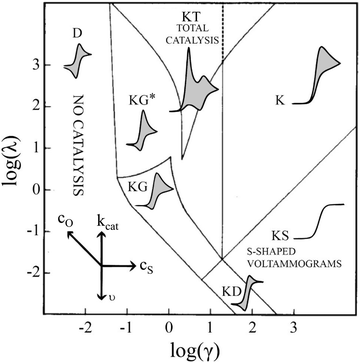 | ||
Fig. 6 Diagram of the catalytic zones for simulated CVs of one electron reduction of substrate S via a redox mediator, O. The kinetic parameter 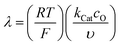 and the excess factor and the excess factor 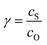 represent the competition between catalytic rate and scan rate, and the initial electrolyte composition, respectively. The CV waveforms follow the convention of negative potentials to the right and cathodic current upward. Scans are started from positive potentials. Reprinted with permission from ref. 39. Copyright 2014 American Chemical Society. represent the competition between catalytic rate and scan rate, and the initial electrolyte composition, respectively. The CV waveforms follow the convention of negative potentials to the right and cathodic current upward. Scans are started from positive potentials. Reprinted with permission from ref. 39. Copyright 2014 American Chemical Society. | ||
When we move on to DBBQ's signature CVs, even though its catalytic mechanism is more complex than this idealised case, similar shapes of CV can be identified in the literature.16 These shapes depend not only on the concentration of DBBQ and O2, but also on [Li+] and solvent choice. For example, for 10 mM DBBQ in 1 M LiTFSI TEGDME electrolyte, a KD type shape has been observed, and in 1 M LiTFSI DME electrolyte a KG type CV has been found, both at 100 mV s−1 scan rate.16 These observations suggest that DME promotes a higher observed kCat, an effect that merits further explanation.16
Since there is no clear consensus regarding the mechanism of DBBQ-mediated ORR in different electrolytes, for the purposes of this section, we model the reaction going through LiO2 intermediate, i.e.eqn (3) and (6), to exemplify the compounded effects of ET and catalytic kinetics in CVs. Further arguments supporting the selection of these reaction mechanisms can also be found in the ESI.† Qualitatively, similar effects can be expected in the case of the other mechanisms. Quantitative differences in the observed catalytic constant depending on [Li+] are described in eqn (S8)–(S10) (ESI†).
Since Li+ takes part in both the electrochemical conversion of quinone species (analysed in Section 1.1, Scheme 1) and also the catalytic reactions described in eqn (3) and (6), increasing the [Li+] results in the evolution of the shape of the CV shape via two superimposed effects. The first effect is related to the change in kinetics of the ET described in Section 1.1, which leads to a modification of the peak-to-peak separation related to the reversibility of ET. The second effect is a modification of the overall observed catalytic constant, which results in the ratio of the peak currents differing from 1 and changing with [Li+]; curves with evolving shapes correspond to different catalytic regimes. Fig. 7 shows simulated cyclic voltammograms representing the pathways 1, 2 and 1c discussed in the previous section represented in the simplified Scheme 1b, plus the catalytic reactions (3) and (6) involving O2 association and LiO2 formation, respectively, at different Li+ concentrations (with n = 1 for simplicity).
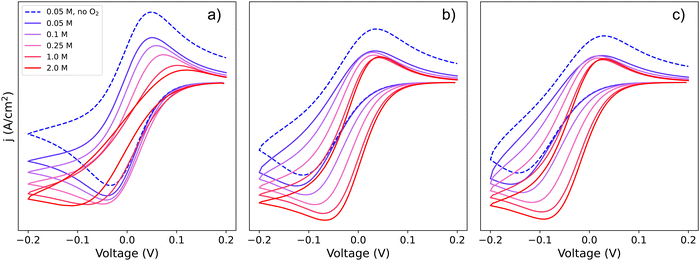 | ||
| Fig. 7 Simulated cyclic voltammograms for each of the DBBQ reduction pathways depicted in Scheme 2, pathways (a) 1, (b) 2, and (c) c, followed by reaction of DBBQ with oxygen according to eqn (3) and (6). The three plots are computed using KOa = 2, KRa = 10, k01 = k02 = k03 = 0.01 cm s−1, k4 = 50 and k5 = 1010, and a scan rate of 50 mV s−1 at different Li+ concentrations as stated in the legend. A simulated CV in the absence of O2 and 0.05 M Li+ is also shown for comparison, depicted by the blue dashed lines. | ||
Two effects can be seen in the shape of the CVs with increasing Li+ concentration: a change in overpotentials due to the dependence of k0app,i on [Li+], as discussed in Section 1, leads to an increase of peak-to-peak separation in the case of pathway 1 and a decrease for pathways 2 and c. The second effect is a noticeable increase in the catalytic activity when increasing Li+ concentration in all three cases. The latter effect leads to a change in the CV shape from region D (no catalysis), to KD (mixed kinetic-diffusion, no substrate consumption), and eventually, for pathway 1, to KG (mixed kinetic-diffusion, with substrate consumption).
The effect on the observed catalytic constant is the same regardless of the pathway for quinone reduction, and depends only on the degree of association and consequent QLin concentration (i.e., [Li+] and KRa). However, the efficiency of the overall catalytic process depends on the pathway: for pathways 2 and c, the overpotential for the catalytic process decreases with increasing [Li+], as evidenced by the shift of the reduction peak and onset potential to higher voltages. In contrast, for pathway 1, the onset and peak potentials are shifted to more negative values as [Li+] increases, which can be easily observed in the highly-distorted shape of the 2 M [Li+] curve in Fig. 7a. In other words, as Li+ concentration increases, the overpotential also increases, making the catalytic process less efficient (higher overpotentials are needed to access a the same current).
Returning to our theoretical framework, an overall positive effect is seen when both the ET k0app and the observed kcat increase: lower overpotentials and a rise in catalytic rates accompany increasing [Li+] (pathways 2 and c), but when k0app decreases, a balance between the increasing observed kcat and decreasing k0app must be achieved to get an optimized system with low overpotentials and fast catalysis, which is the case of pathway 1.
Analogous analyses can be performed for the case where the quinone associates with more than one Li+ ion, as in the example case of DMSO in this work. Previous work has shown that ionic association is important in the catalysis of ORR,15 however, it is still unclear which quinone species is the active one (i.e., what the value of n in QLin is in eqn (4)–(6)). Our framework will permit including an accurate description of DBBQ association into the kinetic interpretation of experimental results, which has the potential to narrow down the underlying active species. Future work will be devoted to a systematic exploration of the kinetics under different conditions.
Conclusions
A theoretical framework is presented to understand the effect of the interactions between redox mediators for Li–O2 batteries and other electrolyte components on the kinetics and thermodynamics of electron transfer, and subsequent effect on catalytic efficiency. We focus on the effect of Li+ ion association, and use DBBQ as an example where these effects can be observed via the CV curves.We provide analytical equations to understand how the observed reduction potential and electron transfer rate constants of an electrochemically active species evolve with Li+ concentration, and show how these predictions can be used to interpret experimental data and hence discriminate between different mechanisms of redox activity. By comparing our theoretical predictions with CV experiments, we show that DBBQ binds to up to 3 Li+ in DMSO solutions in its monoanionic reduced state and 1 Li+ ion in its neutral form. We also show that our predictions can explain the evolution of potential and electron transfer rate constant in these solutions, reproducing a maximum in the observed standard rate constant value, k0app, for DBBQ redox reactions at around 0.25 M LiTFSI. We also briefly discuss the effect of further parallel equilibria, showing that the important parameter is the free Li+ concentration, which can be affected by ionic association of Li+ with the supporting salt counteranion or its interaction with solvent molecules. This approach can also be extended to understand the effect of additives or impurities such as water, which have been previously shown to affect the redox behaviour in a similar way.
Finally, we show how the catalysis of ORR using DBBQ is affected by the Li+ concentration, considering its effect on the electron transfer and catalytic kinetics, and showing example cyclic voltammograms which are seldom analyzed in detail. We show how the shape of CVs where ORR is catalyzed by DBBQ can change significantly just by varying [Li+], shifting between different catalytic regimes, and we predict how these signature shapes will evolve depending on quinone redox pathways.
Our analysis is important in three ways: first, it gives predictive power to translate the electrochemical behaviour of associated RM from one set of conditions to another (e.g., changing the solvent or the supporting salt) based on physically meaningful parameters, such as the association constants or solvation energies. Second, it opens up new dimensions available to rationally improve the kinetics, and hence overpotentials and rate performance, of the quinone reactions in relevant electrolytes. Finally, it simplifies the system by providing apparent parameters that can be used further to understand the catalytic reaction of DBBQ with O2, as demonstrated in Section 2, providing an accurate but simple way to incorporate the complex electrochemical processes of the redox couple. The strength of our theoretical framework lies in its flexibility to be adapted to the use of different redox mediators and interactions with electrolyte components. Future work will focus on building a generalized understanding of the DBBQ behaviour in Li+ containing solutions by applying this framework to different electrolyte compositions, ultimately extending it to systems containing O2.
Experimental and simulation details
The experimental data was collected by running cyclic voltammetry of solutions containing 5 mM DBBQ at different LiTFSI concentrations in DMSO solvent, at varying scan rates between 20 mV s−1 and 10 V s−1. The solutions were prepared by weighing the corresponding amounts of DBBQ (Sigma Aldrich, 99% purity), LiTFSI (Sigma Aldrich, 99.95% purity) and anhydrous DMSO (Sigma Aldrich, 99.9% purity) in an Ar filled glovebox. Prior to use, DBBQ was further purified by recrystallization in methanol: approximately 5 g of DBBQ were recrystalized in methanol, decanted and dried under vacuum. This process was done twice and yielded yellow needle-like crystals. The solutions were prepared on the same day to the electrochemical measurements to avoid degradation of DBBQ with light, since old light-exposed solutions were observed to change colour with time. To be able to convert between different concentration units, the density of each solution was measured three times by weighing 1 ml of solution from a pipette.All electrochemical experiments were recorded inside an Ar-filled glovebox using a PalmSense 4 potentiostat. A reference electrode composed of a silver wire coated in Li1.5Mn2O4 inside a fritted compartment with 1 M LiTFSI/tetraglyme electrolyte as described elsewhere,49 a Pt wire counter electrode, and a 3 mm diameter glassy carbon working electrode were used. There were three repeats of each set of measurements including all the scan rates in each solution. Electrochemical Impedance Spectroscopy (EIS) was recorded before and after each set of measurements with a voltage amplitude of 10 mV and a frequency range of 5 to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. The obtained Nyquist plot was fitted using the PSTrace 5.8 software to a Randles circuit to obtain the resistance and capacitance of the solution.
000 Hz. The obtained Nyquist plot was fitted using the PSTrace 5.8 software to a Randles circuit to obtain the resistance and capacitance of the solution.
Prior to running any electrochemical measurement, the OCV vs. Li/Li+ couple was measured by submerging a Li strip into the electrolyte for a few seconds, and after all the CV and EIS experiments were performed, a small amount of ferrocene was added to the solution and a new CV was recorded. The average voltage between the oxidation and reduction peaks of Fc/Fc+ couple was then used as an internal reference.
The voltammograms were fitted with the commercially available software DigiElch34 to a single electron transfer event (as shown in Scheme 1c), represented by the parameters E0, k0 and α. The resistance and capacitance of the solutions obtained by EIS were provided to the simulation software to account for iR drop and capacitive currents. The diffusion coefficients of the oxidized and reduced species (DO and DR) were assumed to be equal due to the small changes expected in the size of the molecules. The value of α was kept as 0.5, since allowing for its variation didn’t present any further improvement of the fits, and E0 and k0 were systematically varied to achieve the best fit of the experimental voltammograms over the measured range of scan rates for each concentration.
The evolution of the experimentally obtained E0app and k0app were fitted to eqn (27) and (28). Each of the possible pathways was added to the simulated values one at a time, until no significant further improvement of the theoretical curve was seen. Boundary conditions were imposed for the fitting based on expected values of the constants: k0i, k0ic, KRai and KOai > 0, KRai > KOai, KRai < KRa(i+1), KOai < KOa(i+1). This ensures each uptake of a Li+ is less favourable than the previous one, and that less positive charged species have a higher tendency to bind to Li+ than more positively charged ones.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
GH acknowledges the Faraday Institution (Degradation grant no. FIRG060). CPG acknowledges the EU ERC for an Advanced Fellowship for CPG (BATNMR, grant no. 835073). SN acknowledges the H2020 Research and Innovation Program (BIG-MAP, grant no. 957189). VK acknowledges the Biotechnology and Biological Sciences Research Council. DTP2 grant number BB/M011194/1.References
- W.-J. Kwak, Rosy, D. Sharon, C. Xia, H. Kim, L. R. Johnson, P. G. Bruce, L. F. Nazar, Y.-K. Sun, A. A. Frimer, M. Noked, S. A. Freunberger and D. Aurbach, Chem. Rev., 2020, 120, 6626–6683 CrossRef CAS PubMed.
- T. Liu, J. P. Vivek, E. W. Zhao, J. Lei, N. Garcia-Araez and C. P. Grey, Chem. Rev., 2020, 120, 6558–6625 CrossRef CAS.
- X. Zhan, X. Lu, D. M. Reed, V. L. Sprenkle and G. Li, MRS Commun., 2020, 10, 215–229 CrossRef CAS.
- X. Wang, J. Chai and J. J. Jiang, Nano Mater. Sci., 2021, 3, 17–24 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, D. Wang, I. Exnar and M. Grätzel, Angew. Chem., Int. Ed., 2006, 45, 8197–8200 CrossRef CAS PubMed.
- J. Yu, Y.-S. Hu, F. Pan, Z. Zhang, Q. Wang, H. Li, X. Huang and L. Chen, Nat. Commun., 2017, 8, 14629 CrossRef PubMed.
- H. W. Lee, H. Kim, H. G. Jung, Y. K. Sun and W. J. Kwak, Adv. Funct. Mater., 2021, 31(40), 2102442 CrossRef CAS.
- H. W. Lee, J. Y. Kim, J. E. Kim, Y. J. Jo, D. Dewar, S. Yang, X. Gao, P. G. Bruce and W. J. Kwak, J. Mater. Chem. A, 2023, 11, 16003–16008 RSC.
- Z. Jiang, B. Wen, Y. Huang, Y. Guo, Y. Wang and F. Li, Angew. Chem., Int. Ed., 2024, 63(1), e202315314 CrossRef CAS PubMed.
- A. Petrongari, V. Piacentini, A. Pierini, P. Fattibene, C. De Angelis, E. Bodo and S. Brutti, ACS Appl. Mater. Interfaces, 2023, 15, 59348–59357 CrossRef CAS.
- X. Gao, Y. Chen, L. R. Johnson, Z. P. Jovanov and P. G. Bruce, Nat. Energy, 2017, 2, 1–7 Search PubMed.
- N. Mozhzhukhina and E. J. Calvo, J. Electrochem. Soc., 2017, 164, A2295–A2297 CrossRef CAS.
- E. C. Cengiz, J. Rizell, M. Sadd, A. Matic and N. Mozhzhukhina, J. Electrochem. Soc., 2021, 168, 120539 CrossRef CAS.
- E. Jónsson, J. H. J. Ellison, E. Wang, V. Kunz, T. Liu, I. Temprano and C. P. Grey, J. Electrochem. Soc., 2021, 168, 030529 CrossRef.
- P. P. Bawol, J. H. Thimm and H. Baltruschat, ChemElectroChem, 2019, 6, 6038–6049 CrossRef CAS.
- X. Gao, Y. Chen, L. Johnson and P. G. Bruce, Nat. Mater., 2016, 15, 882–888 CrossRef CAS PubMed.
- H. Wan, Y. Sun, Z. Li, W. Wang, Y. Zhu and Y. Qian, Energy Storage Mater., 2021, 40, 159–165 CrossRef.
- Y. Dou, D. Kan, Y. Su, Y. Zhang, Y. Wei, Z. Zhang and Z. Zhou, J. Phys. Chem. Lett., 2022, 13, 7081–7086 CrossRef CAS PubMed.
- Y. Chen, X. Gao, L. R. Johnson and P. G. Bruce, Nat. Commun., 2018, 9, 767 CrossRef.
- D. Cao, X. Shen, A. Wang, F. Yu, Y. Wu, S. Shi, S. A. Freunberger and Y. Chen, Nat. Catal., 2022, 5, 193–201 CrossRef CAS.
- Y. Ko, K. Kim, J. Yoo, G. Kwon, H. Park, J. Kim, B. Lee, J. H. Song, J. Kim and K. Kang, Energy Environ. Sci., 2023, 16, 5525–5533 RSC.
- B. Krueger, K. K. Rücker and G. Wittstock, ACS Appl. Energy Mater., 2022, 5, 3724–3733 CrossRef CAS.
- Y. K. Petit, E. Mourad, C. Prehal, C. Leypold, A. Windischbacher, D. Mijailovic, C. Slugovc, S. M. Borisov, E. Zojer, S. Brutti, O. Fontaine and S. A. Freunberger, Nat. Chem., 2021, 13, 465–471 CrossRef CAS PubMed.
- S. Matsuda, K. Hashimoto and S. Nakanishi, J. Phys. Chem. C, 2014, 118, 18397–18400 CrossRef CAS.
- T. Liu, J. T. Frith, G. Kim, R. N. Kerber, N. Dubouis, Y. Shao, Z. Liu, P. C. M. M. Magusin, M. T. L. Casford, N. Garcia-Araez and C. P. Grey, J. Am. Chem. Soc., 2018, 140, 1428–1437 CrossRef CAS PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley and Sons, New York, 2001 Search PubMed.
- E. Laviron, J. Electroanal. Chem., 1981, 124, 1–7 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem., 1980, 109, 57–67 CrossRef CAS.
- T. P. Silverstein and J. R. Rosé, J. Electrochem. Soc., 2022, 169, 045502 CrossRef CAS.
- S. Fukuzumi, K. Ohkubo and Y. Morimoto, Phys. Chem. Chem. Phys., 2012, 14, 8472–8484 RSC.
- J. M. Savéant, Annu. Rev. Anal. Chem., 2014, 7, 537–560 CrossRef.
- C. Costentin, Chem. Rev., 2008, 108, 2145–2179 CrossRef CAS PubMed.
- J. M. Savéant, J. Am. Chem. Soc., 2008, 130, 4732–4741 CrossRef.
- DigiElch by Gamry, https://www.gamry.com/digielch-electrochemical-simulation-software/.
- G. Horwitz, M. Factorovich, J. Rodriguez, D. Laria and H. R. Corti, ACS Omega, 2018, 3, 11205–11215 CrossRef CAS.
- G. Horwitz, C. Rodríguez, M. Factorovich and H. R. Corti, J. Phys. Chem. C, 2019, 123, 12081–12087 CrossRef CAS.
- Z. Li, R. Bouchal, T. Mendez-Morales, A.-L. Rollet, C. Rizzi, S. Le Vot, F. Favier, B. Rotenberg, O. Borodin, O. Fontaine and M. Salanne, J. Phys. Chem. B, 2019, 123, 10514–10521 CrossRef CAS.
- M. Petrowsky, R. Frech, S. N. Suarez, J. R. P. Jayakody and S. Greenbaum, J. Phys. Chem. B, 2006, 110, 23012–23021 CrossRef CAS.
- M. Petrowsky and R. Frech, J. Phys. Chem. B, 2008, 112, 8285–8290 CrossRef CAS.
- W. A. Henderson, J. Phys. Chem. B, 2006, 110, 13177–13183 CrossRef CAS.
- T. Matsui and K. Takeyama, Electrochim. Acta, 1998, 43, 1355–1360 CrossRef CAS.
- D. G. Kwabi, V. S. Bryantsev, T. P. Batcho, D. M. Itkis, C. V. Thompson and Y. Shao-Horn, Angew. Chem., Int. Ed., 2016, 55, 3129–3134 CrossRef CAS PubMed.
- M. Callsen, K. Sodeyama, Z. Futera, Y. Tateyama and I. Hamada, J. Phys. Chem. B, 2017, 121, 180–188 CrossRef CAS.
- W. Shinoda, Y. Hatanaka, M. Hirakawa, S. Okazaki, S. Tsuzuki, K. Ueno and M. Watanabe, J. Chem. Phys., 2018, 148, 193809 CrossRef PubMed.
- C. Park, M. Kanduč, R. Chudoba, A. Ronneburg, S. Risse, M. Ballauff and J. Dzubiella, J. Power Sources, 2018, 373, 70–78 CrossRef CAS.
- C. Costentin and J.-M. Savéant, ACS Catal., 2018, 8, 5286–5297 CrossRef CAS.
- E. S. Rountree, B. D. McCarthy, T. T. Eisenhart and J. L. Dempsey, Inorg. Chem., 2014, 53, 9983–10002 CrossRef CAS PubMed.
- J. M. Savéant and K. B. Su, J. Electroanal. Chem. Interfacial Electrochem., 1984, 171, 341–349 CrossRef.
- N. Mozhzhukhina, M. P. Longinotti, H. R. Corti and E. J. Calvo, Electrochim. Acta, 2015, 154, 456–461 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01488j |
| This journal is © the Owner Societies 2024 |