Open Access Article
Open Access ArticleBreaking the plane: B5H5 is a three-dimensional structure†
Gerardo
Hernández-Juárez
a,
Jorge
Barroso
 b,
Alejandro
Vásquez-Espinal
c,
Filiberto
Ortíz-Chi
b,
Alejandro
Vásquez-Espinal
c,
Filiberto
Ortíz-Chi
 d,
William
Tiznado
d,
William
Tiznado
 e,
Fernando
Murillo
*a and
Gabriel
Merino
e,
Fernando
Murillo
*a and
Gabriel
Merino
 *a
*a
aDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Unidad Mérida. Km 6 Antigua Carretera a Progreso. Apdo. Postal 73, Cordemex, 97310, Mérida, Yuc., Mexico. E-mail: gmerino@cinvestav.mx; fernando.murillo@cinvestav.mx
bDepartment of Chemistry, Clemson University, Clemson, South Carolina 29625, USA
cQuímica y Farmacia, Facultad de Ciencias de la Salud, Universidad Arturo Prat, Casilla 121, Iquique 1100000, Chile
dCONAHCYT-División Académica de Ciencias Básicas, Universidad Juárez Autónoma de Tabasco, Cunduacán 86690, Tabasco, Mexico
eDepartamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello, República 498, Santiago, Chile
First published on 16th February 2024
Abstract
In this study, we delved into the structure of B5H5 and questioned some of its accepted assumptions. By exploring the potential energy surface, we found a new three-dimensional structure as the global minimum. This finding is in contrast with the previously hypothesized planar and cage-like models. Our exploration extends to the kinetic stability of various B5H5 isomers, offering insights into the dynamic behavior of these molecules.
Introduction
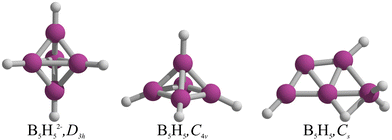
Even though B5H52− has not yet been synthetized, it is expected to assume a D3h form, a conjecture first formulated by Lipscomb and coworkers in 1961,1–3 and later rationalized through the Wade-Mingos rules.4,5 In 2000, Schleyer and coworkers explored the geometric and electronic implications of electron removal from B5H52− to elucidate the structure of the neutral B5H5.6 Upon optimization, the initial trigonal bipyramidal form with D3h symmetry transitioned to a C4v square pyramid, keeping the five B–H units intact in B5H5 (Fig. 1). This transformation from trigonal bipyramid to square pyramid was rationalized via the pairing principle of incompletely filled degenerate orbitals.6 However, McKee7 identified a Cs structure, characterized as a BH2+ and B4H3− complex, which is energetically more favorable than the C4v square pyramidal isomer by 9.8 kcal mol−1 at the B3LYP/6-31G(d) level. This preferred structure is a trapezoid with three B atoms at the base and two above, incorporating two terminal B–H bonds, a B–H–B bridge, a BH2 group, and a bare boron (see Fig. 1),7 mirroring the planar form of B5− and neutral B5.8,9In our quest to understand the structural transformations induced by the removal of two electrons from the dianions of borohydrides, denoted by the formula BnHn2−, we explored the potential energy surfaces (PESs) of all borohydrides in the series from n = 5 to 12. Our preliminary screening revealed that for nearly all these dianions, the removal of two electrons result in insignificant structural changes. Nonetheless, two exceptions were identified: B12H12 and B5H5. While the former case has been previously reported by us,10 our focus now shifts to B5H5. Contrary to prior assumptions, our results show that the global minimum structure of B5H5 is not quasi-planar but rather an asymmetrical three-dimensional form.
Computational details
The systematic exploration of the PES of B5H5 in both its singlet and triplet states was carried out through a modified genetic algorithm as implemented in GLOMOS.11 Details on GLOMOS are documented elsewhere.12 An initial screening was performed at the PBE0/def2-SVP level.13,14 Isomers within a 50 kcal mol−1 range were re-minimized and characterized at the TPSS-D3/def2-TZVP level.14,15 The stationary points were further characterized by harmonic vibrational frequency analysis at the same level. The interconversion pathways for lower-energy minima were elucidated and the corresponding transition states (TS) connecting the local minima were confirmed by intrinsic reaction coordinate (IRC) computations. Relative Gibbs free energies, including entropic and thermal corrections at 298.15 K, were computed at the CCSD(T)16/aug-cc-pVTZ//TPSS-D3/def2-TZVP level. Additionally, the stability of the wave function and the T1 diagnostic for each isomer were evaluated, indicating stable wave functions across all localized minima with T1 values below 0.02 for the singlet systems and less than 0.023 for the triplets (see Table S1, ESI†). This suggests that monodeterminantal approaches, such as DFT and CCSD(T), reliably represent the structure and energetics of these isomers. All these computations were performed using Gaussian 16.17Chemical bonding was examined using Wiberg bond indices (WBIs) and natural population analysis (NPA) via the NBO 6.018 partitioning scheme. Furthermore, the adaptive natural density partitioning (AdNDP) approach,19 as implemented in Multiwfn,20 provided further insights into the chemical bonding, describing electronic structures in terms of n-center, two-electron (nc-2e) bonds, recovering Lewis concepts such as lone pairs, 2c-2e bonds, and delocalized bonds.
The dynamic behavior was studied using Born–Oppenheimer molecular dynamics (BO–MD)21 at 900 K for 30 ps, employing a 1 fs time step and a Nosé–Hoover chain thermostat for temperature control,22–24 using deMon-2k25 at the PBE0/DZVP26 level. The chosen temperature, while is not real in the macroscopic sense, was selected to regulate the total kinetic energy of the atoms, ensuring they possess enough energy to overcome energy barriers and allow for isomer interconversions at realistic simulation times.
Results
The lowest energy structures of B5H5 in both singlet and triplet states are shown in Fig. 2. We identified two structures, 1 and 2, that are energetically more favorable than McKee's proposed structure, 3.7 The global minimum, 1, is a three-dimensional entity with C1 symmetry, characterized by four terminal B–H bonds, a B–H–B bridge, and a bare boron atom. Structure 2, which is only 0.7 kcal mol−1 higher than 1 in Gibbs free energy (computed at CCSD(T)/aug-cc-pVTZ//TPSS-D3/def2-TZVP), adopts a trapezoidal boron skeleton with three B–H units and a –BH2 group located at one vertex of the larger base, adopting a Cs symmetry. McKee's structure (3), less favorable by 1.7 kcal mol−1 compared to 1, shares a trapezoidal shape with 2 but includes a hydrogen atom bridging the central boron and the –BH2 group. Structure 4, which is 3.0 kcal mol−1 higher in energy than 3, possesses a distinctive trapezoidal shape with an out-of-plane BH unit. Structures 5, 7, 8, 13, and 14, characterized by pyramidal boron skeletons, are between 6.7 to 38.9 kcal mol−1 higher in Gibbs free energy than 1, with 7 corresponding to Schleyer's C4v structure. Three Cs-symmetry structures, 6, 9, and 10, consist of a B4 skeleton with a –BH2 unit and a bridging hydrogen on a B–B bond, ranging from 6.8 to 17.0 kcal mol−1 above 1 in Gibbs free energy. Isomers 11 and 12 adopt a cage-like structure (ΔG > 17.0 kcal mol−1), albeit with one incomplete face. Specifically, structure 12 is a trapezoid with two B–H–B bridges with an out-of-plane hydrogen atom in one bridge. The lowest-energy triplets, 13 and 14, have ΔG values more than 20 kcal mol−1 above 1. So, the putative global minimum for B5H5 is not planar but a three-dimensional structure.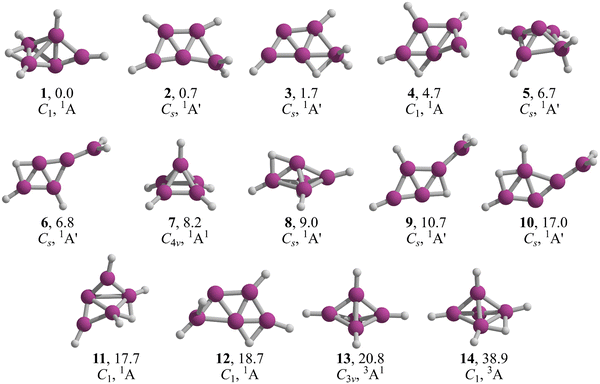 | ||
| Fig. 2 TPSS-D3/def2-TZVP low-lying energy structures of B5H5. Relative Gibbs free energies at the CCSD(T)/aug-cc-pVTZ//TPSS-D3/def2-TZVP level are in kcal mol−1. | ||
WBI analysis identifies two distinct ranges for B–H bond distances, as summarized in Table 1. Isomers 2, 5, and 7, each containing five B–H units, display high average WBIB–H of around 0.95 and show the shortest average B–H bond lengths, approximately 1.19 Å. In contrast, the presence of 3c-2e B–H–B interactions increases average B–H bond distances and lowers the average WBIB–H values. An extreme case is structure 12, which features two B–H–B bonds, leading to a WBI of 0.66. Regarding B–B bonds, planar structures 6, 9, and 10 show the highest average WBIB–B values (nearly 1.0), contrasting with Schleyer's isomer, which has the lowest (WBIB–B = 0.74). 6, 9, and 10 each contain a 2c-2e B–B bond connecting a BH2 unit to the B4H3 fragment. The formation of the BH2 unit induces electronic redistribution within the B4 rhombus, shortening several B–B distances to almost 1.55 Å. In contrast, an increase in the number of multicenter boron bonds correlates with elongated B–B bond lengths and higher WBIB–B, the C4v form being the extreme case (vide infra).
| Isomer | r B–H | r B–B | WBIBH | WBIBB |
|---|---|---|---|---|
| 1 | 1.22 | 1.67 | 0.79 | 0.85 |
| 2 | 1.19 | 1.69 | 0.94 | 0.80 |
| 3 | 1.24 | 1.67 | 0.78 | 0.89 |
| 4 | 1.23 | 1.66 | 0.78 | 0.87 |
| 5 | 1.19 | 1.72 | 0.95 | 0.77 |
| 6 | 1.24 | 1.62 | 0.79 | 1.00 |
| 7 | 1.19 | 1.71 | 0.95 | 0.74 |
| 8 | 1.23 | 1.71 | 0.79 | 0.78 |
| 9 | 1.24 | 1.63 | 0.79 | 0.99 |
| 10 | 1.24 | 1.65 | 0.78 | 1.01 |
| 11 | 1.23 | 1.71 | 0.78 | 0.84 |
| 12 | 1.28 | 1.65 | 0.66 | 0.93 |
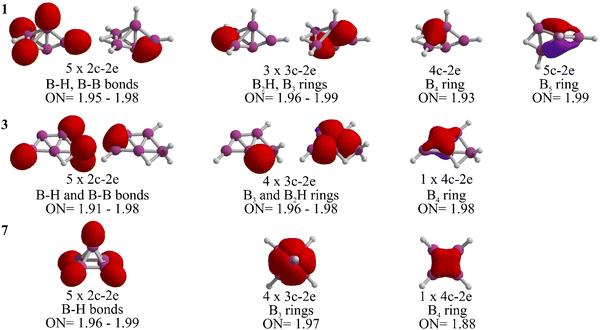
Let us analyze the bonding properties of 1, 3, and 7 (the global minimum, McKee's isomer, and Schleyer's cage-pyramidal structure, respectively). As depicted in Fig. 3, each has five 2c-2e σ-bonds. Isomers 1 and 3 are composed of four 2c-2e B–H bonds and one B–B bond, while in 7, all are B–H bonds. Isomer 1 features three 3c-2e bonds (one in a B2H ring and two in a B3 ring), in contrast to 3 and 7, which have four 3c-2e bonds. Specifically, isomer 3 includes a 3c-2e B2H bond and another in a B3 ring. In isomer 7, 3c-2e σ-bonds are found within the B3 rings of the pyramid's four triangular faces. Each isomer also contains a delocalized 4c-2e bond in a B4 unit. Distinctly, the B5 skeleton in 1 is stabilized by a 5c-2e bond, absent in 3 and 7, contributing to its enhanced stability.
The stabilization of 1 is further clarified when examining the chemical bonding in the dianion B5H52−, which has 22 electrons.27 Ten of these electrons are in the five 2c-2e B–H σ-bonds, leaving twelve for B–B bonding, including three 3c-2e and three delocalized 4c-2e σ-bonds.27 In contrast, neutral B5H5 requires different bonding configurations. 7 has five 2c-2e σ-bonds exclusively for B–H bonds, one more than isomers 1 and 3. This leaves ten electrons for B–B bonds in 7, while 1 and 3 each allocate twelve electrons to B–B bonds, similar to the dianion. Therefore, 1 and 3 are capable to maintain twelve electrons for keeping the boron skeleton in B5H5, resulting in higher relative stability.
The kinetic stability of isomers 3 and 7, in their isomerization to 1, is detailed in Fig. 4. Isomer 3 converts to 1 through a one-step pathway (Fig. 4a), with a high activation barrier (ΔG‡ = 26.3 kcal mol−1), indicating that 3 is kinetically stable. In contrast, the transformation of 7 to 1 follows a stepwise mechanism with low barriers via intermediates 4 and 2 (Fig. 4b). Initially, a hydrogen atom migrates from the pyramid's apex to its base, forming a B2–H–B3 bridge and leading to the cleavage of the B1–B2 bond. This results in the quasi-planar structure of 4, crossing a small energy barrier (TS7-4, ΔG‡ = 1.3 kcal mol−1). The subsequent conversion of 4 to 2 involves a hydrogen atom shift towards B2, forming a terminal BH2 group (TS4-2, ΔG‡ = 4.9 kcal mol−1). The final step from 2 (a quasi-planar structure) to 1 (a three-dimensional structure) implies the formation of the B2–H–B4 bridge and the B2–B5 bond, involving a barrier of 6.9 kcal mol−1 (TS2-1). Given that 7 isomerizes to 1via a stepwise mechanism with achievable energy barriers, 7 is considered kinetically unstable.
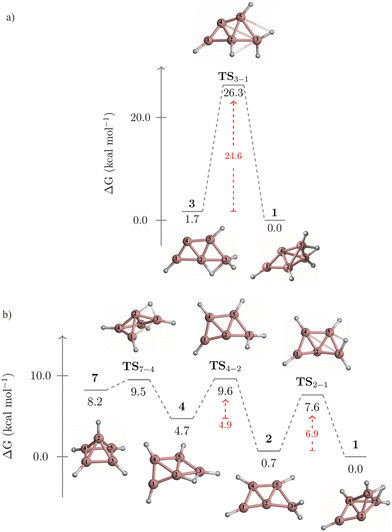 | ||
| Fig. 4 Gibbs free energy profile for the conversions of (a) 3 to 1, and (b) 7 to 1 computed at the CCSD(T)/aug-cc-pVTZ//TPSS/def2-TZVP level. | ||
Two alternative mechanisms for the isomerization of 3 to 1 were explored. Both mechanisms involve a stepwise process, with higher activation barriers than the concerted pathway (Fig. S1 and S2, ESI†). The first pathway begins with converting 3 into 2via a 1,2-H migration from B2 to B4, before transitioning to 1 (Fig. S1, ESI†). However, the initial step has a free energy barrier of 31.8 kcal mol−1 (TS3-2), which is 7.2 kcal mol−1 higher than the barrier of the concerted pathway (TS3-1, Fig. 4a).
The second pathway initiates with the cleavage of the B2–B3 bond and the formation of a B4–H–B5 bond, leading to 9 (Fig. S2, ESI†). The activation barrier for this initial step (TS3-9) is 14.9 kcal mol−1. Next, 9 is converted to 6 through a double hydrogen rearrangement viaTS9-6. This step involves breaking the B4–H–B5 bond and forming the B1–H–B2 bond with a low energy barrier (ΔG‡ = 5.6 kcal mol−1) and can be viewed as a type II-dyotropic migration.28 The conversion from 6 to 2 (TS6-2) has an activation barrier of 27.5 kcal mol−1. As in the previous stepwise pathway, this process concludes with converting 2 to 1. Note that the barrier of TS6-2, acting as the rate-determining step, is 2.9 kcal mol−1 higher than that of TS3-1, indicating that these alternative routes are energetically less favorable.
To gain deeper insight into the isomerization processes from 3 to 1 and 7 to 1, Born–Oppenheimer molecular dynamics simulations were conducted at 900 K for 30 ps, beginning with structures 3 and 7 (see the Movie S1 and S2 in the ESI†). Isomer 3 displayed minor distortions while preserving its planar structure throughout the simulation, confirming its kinetic stability in line with its high activation barrier (Fig. 4a and Movie S1, ESI†). In the case of isomer 7, a transformation occurs at 9 ps (Movie S2, ESI†), where its pyramidal cage transitions into a trapezoidal shape reminiscent of isomer 4. This stage is characterized by the heightened mobility of hydrogen atoms around the boron-based trapezoid, leading to several structural interconversions between isomers 4 and 2 until 20 ps. When structure 2 forms, it briefly shifts to 1 but reverts to 2. Around 23 ps, 2 undergoes bending and transitions into the stable structure of 1 with minimal distortions for the rest of the simulation. This series of events confirms the kinetic stability of both isomers 1 and 3, as they maintain their structural integrity throughout the simulation.
Conclusion
By exploring the B5H5 potential energy surface, we found a three-dimensional structure that challenges the previously accepted planar model as the global minimum for this neutral borohydride. The analysis of the kinetic stability of the B5H5 isomers indicates that isomer 3, suggested by Mckee, is a kinetically stable system that could potentially be experimentally detected, but it is not the global minimum. In contrast, isomer 7 (Schleyer's proposal) is likely to transform into isomer 1, making its experimental detection in the gas phase challenging, if not impossible. Through molecular dynamics simulations, we provided detailed insights into the dynamic behavior of these molecules, enhancing our understanding of their stability under various conditions.These findings open new avenues for re-examining the bonding and structure of boron hydrides, extending beyond theoretical interest, and possibly influencing future experimental endeavors and applications in related chemical areas.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. H.-J. and F. M. thank Conacyt for their PhD and postdoc fellowships, respectively. The work in Chile was supported by the National Agency for Research and Development (ANID) via the Fondecyt projects N° 1211128 (W. T.) and 1221019 (A. V.-E.).References
- W. N. Lipscomb, Extensions of the Valence Theory of Boron Compounds, Proc. Natl. Acad. Sci. U. S. A., 1961, 47(11), 1791–1795 CrossRef CAS PubMed.
- E. B. Moore, L. L. Lohr and W. N. Lipscomb, Molecular Orbitals in Some Boron Compounds, J. Chem. Phys., 1961, 35(4), 1329–1334 CrossRef CAS.
- R. Hoffmann and W. N. Lipscomb, Theory of Polyhedral Molecules. I. Physical Factorizations of the Secular Equation, J. Chem. Phys., 1962, 36(8), 2179–2189 CrossRef CAS.
- K. Wade, Structural and Bonding Patterns in Cluster Chemistry, in Advances in Inorganic Chemistry and Radiochemistry, Elsevier, 1976, pp. 1–66 Search PubMed.
- D. M. P. Mingos, A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements, Nat. Phys. Sci., 1972, 236(68), 99–102 CrossRef CAS.
- M. L. McKee, Z.-X. Wang and P. v R. Schleyer, Ab Initio Study of the Hypercloso Boron Hydrides BnHn and BnHn−. Exceptional Stability of Neutral B13H13, J. Am. Chem. Soc., 2000, 122(19), 4781–4793 CrossRef CAS.
- M. L. McKee, Ab Initio Study of BnHn and Bn(NH2)n (n = 3–6) Species. A Comparison of Classical and Nonclassical Structures, Inorg. Chem., 1999, 38(2), 321–330 CrossRef CAS.
- H.-J. Zhai, L.-S. Wang, A. N. Alexandrova and A. I. Boldyrev, Electronic Structure and Chemical Bonding of B5− and B5 by Photoelectron Spectroscopy and Ab Initio Calculations, J. Chem. Phys., 2002, 117(17), 7917–7924 CrossRef CAS.
- J. Barroso, S. Pan and G. Merino, Structural Transformations in Boron Clusters Induced by Metal Doping, Chem. Soc. Rev., 2022, 51(3), 1098–1123 RSC.
- G. Hernández-Juárez, A. Vásquez-Espinal, F. Murillo, A. Quintal, F. Ortíz-Chi, X. Zarate, J. Barroso and G. Merino, Unveiling the Electronic and Structural Consequences of Removing Two Electrons from B12H122−, Dalton Trans., 2023, 52(46), 17398–17406 RSC.
- F. Ortiz-Chi and G. Merino, GLOMOS, Mérida, México, 2020 Search PubMed.
- R. Grande-Aztatzi, P. R. Martínez-Alanis, J. L. Cabellos, E. Osorio, A. Martínez and G. Merino, Structural Evolution of Small Gold Clusters Doped by One and Two Boron Atoms, J. Comput. Chem., 2014, 35(32), 2288–2296 CrossRef CAS PubMed.
- C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401 CrossRef PubMed.
- J. D. Watts, J. Gauss and R. J. Bartlett, Coupled-Cluster Methods with Noniterative Triple Excitations for Restricted Open-Shell Hartree–Fock and Other General Single Determinant Reference Functions. Energies and Analytical Gradients, J. Chem. Phys., 1993, 98(11), 8718–8733 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 6.0: Natural Bond Orbital Analysis Program, J. Comput. Chem., 2013, 34(16), 1429–1437 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217 RSC.
- T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, Ab Initio Classical Trajectories on the Born–Oppenheimer Surface: Hessian-Based Integrators Using Fifth-Order Polynomial and Rational Function Fits, J. Chem. Phys., 1999, 111(9), 3800–3805 CrossRef CAS.
- S. Nosé, A Unified Formulation of the Constant Temperature Molecular Dynamics Methods, J. Chem. Phys., 1984, 81(1), 511–519 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover Chains: The Canonical Ensemble via Continuous Dynamics, J. Chem. Phys., 1992, 97(4), 2635–2643 CrossRef.
- W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31(3), 1695 CrossRef PubMed.
- A. M. Koster, G. Geudtner, A. Alvarez-Ibarra, P. Calaminici, M. E. Casida, J. Carmona-Espindola, V. D. Dominguez, R. Flores-Moreno, G. U. Gamboa, A. Goursot, T. Heine, A. Ipatov, A. de la Lande, F. Janetzko, J. M. del Campo, D. Mejia-Rodriguez, J. U. Reveles, J. Vasquez-Perez, A. Vela, B. Zuniga-Gutierrez and D. R. Salahub, deMon2k, Version 5, The deMon Developers, Cinvestav, Mexico City, 2018 Search PubMed.
- S. Chiodo, N. Russo and E. Sicilia, Newly Developed Basis Sets for Density Functional Calculations, J. Comput. Chem., 2005, 26(2), 175–184 CrossRef CAS PubMed.
- Y.-F. Shen, C. Xu and L.-J. Cheng, Deciphering Chemical Bonding in BnHn2− (n = 2–17): Flexible Multicenter Bonding, RSC Adv., 2017, 7(58), 36755–36764 RSC.
- I. Fernández, F. Cossío and M. A. Sierra, Dyotropic Reactions: Mechanisms and Synthetic Applications, Chem. Rev., 2009, 109, 6687–6711 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00029c |
| This journal is © the Owner Societies 2024 |