 Open Access Article
Open Access ArticleAdvancements in computational approaches for rapid metal site discovery in carbon-based materials for electrocatalysis
Somayeh
Faraji†
 ,
Zhiyu
Wang†
,
Paola
Lopez-Rivera
and
Mingjie
Liu
,
Zhiyu
Wang†
,
Paola
Lopez-Rivera
and
Mingjie
Liu
 *
*
Department of Chemistry, University of Florida, Gainesville, FL 32611, USA. E-mail: mingjieliu@ufl.edu
First published on 6th September 2023
Abstract
Heterogeneous electrocatalysts exhibit immense potential for advancing energy technologies. However, the constraints associated with noble metals have sparked a surge of interest in the exploration of single-atom catalysts and metal–carbon hybrids as alternative options. Designing metal sites in carbon-based materials has demonstrated high activity, selectivity, stability, and cost-effectiveness in various electrochemical reactions. In spite of these advantages, the intricate nature of the designed structures and the expansive design space encompassing potential metal site structures pose formidable challenges in terms of experimental characterization and optimization. To address these challenges, computational approaches have emerged as powerful tools to accelerate the discovery of new metal sites in carbon-based materials and understand the structure–catalytic property relationships for electrocatalysis. In this review paper, we provide an overview of the state-of-the-art computational approaches from reported modeled structures, theoretical foundations of computational methods in modeling electrochemical reactions, to the data-driven approaches to accelerate new catalyst design. We summarize the utilization of structure-binding energy relationships, virtual high-throughput screening methods, and machine learning techniques to explore a wide range of metal site structures and identify promising candidates for experimental validation. Furthermore, the review highlights the importance of considering the solvent effect and the impact of spin/oxidation states on extra electron transfer to enhance the accuracy of predicting binding energies. Finally, we summarize the current challenges and offer a brief perspective on future opportunities in the field of computational acceleration for carbon-based catalyst development.
1 Introduction
Electrochemical reactions are critical for sustainable energy and environment, as they form the basis of numerous essential technologies like batteries, fuel cells, and electrocatalysis.1 Heterogeneous electrocatalysts facilitate electrochemical reactions; thus, developing effective heterogeneous electrocatalysts is crucial for advancing these technologies and promoting sustainable energy and environmental practices. The bulk metals exhibit striking electrocatalytic properties for small molecule activation, for example, Pt for oxygen reduction reaction (ORR) and hydrogen evolution reaction (HER),2,3 Cu for CO2 RR,4,5 and Ru, Pd, and Ag for NRR.6–9 However, most of them are either noble metals or exhibit poor stability, selectivity, and activity. These limitations emphasize the necessity of developing new electrocatalysts to overcome these challenges.Carbon materials, such as graphene and carbon nanotubes (CNT), hold great promise for electrocatalysis due to their high surface area, excellent electric conductivity, and remarkable thermal stability. Moreover, carbon is abundant and environmentally friendly, and has a multitude of allotropes that offer a diverse range of tunable properties through structural variations. The shortcoming of chemical inertness can be addressed by introducing defects and dopants which can act as active sites while the carbon materials behave as the substrate or host materials. For example, single atom catalysts (SACs) as one of the emerging heterogeneous catalysts consist of isolated metal atoms dispersed on a support material (e.g., graphitic carbon, metals or metal oxides).10 Numerous studies have demonstrated that carbon-based SACs and other metal–carbon hybrid structures (metal clusters on graphene or CNTs) are promising as the next-generation electrocatalysts for various electrochemical reactions, for example, water splitting, CO2 RR, ORR, and NRR, with the potential to replace precious metal catalysts.11–13 Therefore, the development of metal-doped carbon-based electrocatalysts has gained significant attention in recent decades as they have the potential to meet the requirements of high activity, selectivity, stability, sustainability, and cost-effectiveness in electrocatalysis.14–21
Computational modeling based on density functional theory (DFT) has become increasingly important in catalyst design as it can offer insights into reaction mechanisms and reveal the structure–property relationship. Owing to advancements in computational power, the virtual screening of hundreds and even thousands of catalyst structures prior to experimental synthesis is now feasible. When combined with machine learning techniques that leverage large datasets, these capabilities can inform the design of new materials with superior catalytic performance.22 These approaches have revolutionized scientific research and have led to numerous breakthroughs in the development of more efficient catalytic materials.
In this review, our main focus is the application of modeling and computation to expedite the design of carbon-based materials with carefully engineered metal sites. We first overview the well-studied modeled systems and summarize the quantum simulation-based approaches to understand the properties related to the electrochemical reactions (Section 2). Although these approaches can offer detailed insights into the structure–property relationships, enabling the design of efficient catalytic sites, the main challenge lies in the extensive design space and the inherent limitations in accuracy associated with these methods. To tackle these challenges, data-driven approaches such as high-throughput screening and machine learning models are employed. In the next two sections, we review the utilization of data-driven approaches to accelerate the exploration of the extensive design space (Section 3) and the ongoing endeavors to improve the accuracy of the computational models (Section 4). At last, we envision future opportunities from the computational perspective, poised to expedite the development of metal sites in carbon-based materials (Section 5).
2 Modeled structures and computational approaches
2.1 Overview of well-explored structures
Among carbon–metal materials, the SACs are the most well-studied systems. Experimentally, most 3d and 4d metal SACs are successfully synthesized, characterized and applied in several electrochemical reactions.16–18 A recent experimental library reported 37 SACs embedded in N-doped carbon, characterized by their oxidation state, coordination number, bond length, and coordination element.23 Computationally, DFT simulations extensively investigated the single metal atom coordinated with four nitrogen atoms (M–N4) in the graphene system for CO2RR,24–28 ORR,29–31 water splitting,14,15 and nitrogen reduction reactions,32–34 as the local structure is analogous to the metal-porphyrin cofactor in enzymes.35In addition to M–N4, the general M–Nx moieties in the graphene lattice have also been explored. The number of coordinated nitrogen atoms varying from 1 to 6 can be modeled using graphene edges36,37 or defective graphene.38–42 Besides graphene as the substrate to host the M–N site, other graphitic carbon structures are also considered, such as CNTs,43–46 fullerenes,47–49 graphyne50,51 and graphdiyne.52–54 The unique properties (e.g., local curvature, sp/sp2 hybridized porous structure) provided by those allotropes can contribute to the enhancement of the catalytic reactivities. As N plays a crucial role in promoting the activity of the metal site, the CxNy systems with more N doped carbon systems are also examined (e.g., C9N4,55–57 C2N,58–61 CN,62–64 C3N465–68). Through careful examination of both computational simulations and experimental characterizations, it has been determined that the M–N4 active site may not be the most desirable option. For example, Ni coordinated with one or two N would show better reactivity compared with Ni–N4 for CO2RR;69–72 and Co–N5 exhibits better selectivity and stability compared to other Co–N sites.73 In addition, based on DFT calculations, Ni–N3 has been reported as a more favorable site for *COOH (carboxyl) formation compared to NiN4 and is active for CO2RR.74 Iqbal et al. provided a detailed review on recent advances in the design and synthesis of noble metal (Ru and Au) and non-noble metal (Mn, Fe, Co, Ni, Cu, and Mo) SACs doped with various non-metals (B, N, P, and S) for NRR.75
Investigations have also been conducted on alternative coordinated atoms, apart from nitrogen. The most common alternatives are oxygen,76 sulfur,77–80 boron,81 and phosphorus82,83 with conclusions that some of the dopants coordinated with metal can show better catalytic activity than nitrogen76,79,83 but the stability may decrease.77 Dual metals84 and metal trimers85 are also investigated on graphene and graphdiyne. However, the metal clusters beyond that are barely explored due to the ambiguous metal cluster structures. Experimentally, the dual metal catalysts have been synthesized with Cu2, CuNi,86 FeNi,87–89 and FeCo90 and the improved performance for CO2RR and ORR is explained by synergistic electronic modulation effects.89–91
2.2 Computational approaches
Computational approaches based on DFT simulations provide an atomistic understanding of catalytic reactivity and stability. In the next two subsections, we will provide a brief overview of the approaches and their application in understanding these properties.The CHE approach, pioneered by Norskov et al., is a well-established and widely utilized method for incorporating insights from ab initio calculations into electrochemistry modeling.94 The core principle of this approach involves defining a reaction pathway and considering that, at each step, the proton–electron pair was transferred together with the chemical potential as half of the gaseous hydrogen at a potential of 0 V. Then the Gibbs free energy for each step along the pathway at zero potential and zero pH is defined as ΔG = ΔE + ΔZPE − TΔS, where ΔE and ΔZPE are the reaction and zero-point energy difference of each step, respectively, and ΔS is the change in entropy. All of the values can be obtained from DFT calculations. ΔZPE is defined as 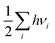 , where νi are vibrational frequencies and i goes over all vibrational modes, which can be calculated via DFT with the harmonic oscillator approximation. ΔS could be taken either from standard tables97 or by calculating translational (Strans), rotational (Srot), and vibrational (Svib) entropies as described in ref. 22. To include the influence of the electrode potential U in an electrochemical step, the CHE method sets the total energy of the electrons in the electrode to −qU, where q is the charge of the electron. Therefore, the free energy of each step is
, where νi are vibrational frequencies and i goes over all vibrational modes, which can be calculated via DFT with the harmonic oscillator approximation. ΔS could be taken either from standard tables97 or by calculating translational (Strans), rotational (Srot), and vibrational (Svib) entropies as described in ref. 22. To include the influence of the electrode potential U in an electrochemical step, the CHE method sets the total energy of the electrons in the electrode to −qU, where q is the charge of the electron. Therefore, the free energy of each step is
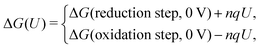 | (1) |
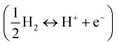 . Finally, at a pH different from 0, the free energy of H+ ions can be corrected by the concentration dependence of the entropy as ΔG(pH) = −kT
. Finally, at a pH different from 0, the free energy of H+ ions can be corrected by the concentration dependence of the entropy as ΔG(pH) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[H+].94 The CHE model therefore can be used to plot the free energy diagram, which provides an atomistic picture of the reaction computationally. The free energy diagram can be analyzed to determine the onset potential that can be compared with experimental values directly.
ln[H+].94 The CHE model therefore can be used to plot the free energy diagram, which provides an atomistic picture of the reaction computationally. The free energy diagram can be analyzed to determine the onset potential that can be compared with experimental values directly.
The CHE method could be considered as a post-processing scheme and constant charge approach in which the U-dependency of ΔG(U) comes only from nqU, assuming the reaction energy of each step is independent of the electrode potential. This simplification makes CHE a valuable tool for a quick assessment of the general thermodynamic trends but would fail to accurately describe the potential dependence in a reaction. Over the past few years, efforts have been made to connect the constant charge scheme to the constant electrode potential scheme by varying the electron in the system,98 or the size of the supercell99 so that the constant electrode potential can be extrapolated. Among those efforts, the GCDFT provides a direct simulation scheme to keep the electrode potential constant in the system by controlling the work function. This approach calculates the grand free energy (Ω = A − μN, where A is Helmholtz free energy and N is the number of atoms with chemical potential μ) by solving the Kohn–Sham equations while the number of electrons at the electrode varies to keep a constant Fermi level that corresponds to the applied potential. The details of the algorithm can be found in ref. 96.
Both methods have been applied to study the metal–carbon systems for electrocatalysis. The CHE method with the advantage of computational efficiency has been extensively applied in a wide range of metal–carbon systems for electrocatalysis to quickly screen new catalysts with the sacrificed accuracy requirement. The GCDFT method (or other constant potential approaches) which provides a more accurate description of the electrochemical process has been used specifically in certain systems to fully understand the reaction mechanisms with the potential dependence. However, due to the computational cost of GCDFT, it is challenging to apply it in high-throughput screening of catalyst design. On the one hand, when comparing the results from both models, some trends are consistent. For example, in Fe–, Co–, and Ni–N4 in graphene, the Ni–N4 site is the most effective site for CO production, while the Fe–N4 site can stabilize CO adsorption, which can potentially further reduce CO to other products such as CH3OH and CH4.27,100 On the other hand, the electrode potential-dependent processes, such as CO2 adsorption and the transition states, are critical in revealing the reaction mechanism. This indicates that the rate-determining step and catalytic selectivity predicted by GCDFT and CHE may be different101,102 (see Fig. 1 as an example). In this case, the GCDFT is expected to provide more accurate descriptions due to the nonlinear effects of the applied potential on molecular adsorption and transition states.27,72,102 In particular, in metal–carbon systems, the localized orbital would be dramatically influenced by the electrode potential due to the low density of states in 2D materials.101 Therefore, the orbital-based design principle needs to be examined carefully by taking the electrode potential into account.
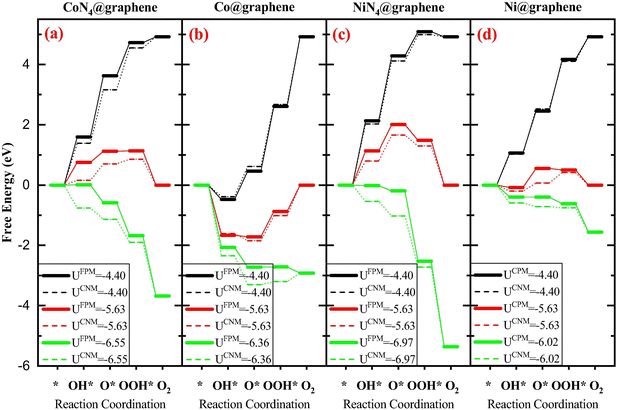 | ||
| Fig. 1 The free energy diagrams associated with the OER on four different systems: (a) CoN4@graphene, (b) Co@graphene, (c) NiN4@graphene, and (d) Ni@graphene. FPM is GCDFT and CNM is CHE. Reprinted with permission from ref. 101. Copyright 2020 Elsevier. | ||
Thermodynamic stability. To quantify the thermodynamic stability, the binding energy (Eb), formation energy (Ef), and diffusion barriers are usually calculated as criteria. The first criterion, Eb, is defined as
| Eb = EM@sub − (Esub + EM), | (2) |
The second criterion, Ef, employs a different reference energy of atoms to estimate the thermodynamics stability of the structure. For example, in the case of one metal anchored in the divacancy of N-doped graphene, the metal atom is coordinated with four atoms (i.e., M@NxC4−x), where the metal atom is bonded with x nitrogen atoms (x ≤ 4) and 4 − x carbon atoms. The value of Ef can be calculated using the following equation:
| Ef = EM@NxC4−x + (x + 2)EC − (Epsub + xEN + EM0). | (3) |
It is also important to consider the stability of the metal atoms against aggregation. This could be examined by comparing the Eb of the metal in the carbon substrate and the metal bulk cohesive energy (Ecoh) which is defined as Ecoh = EM0 − EM. Therefore, satisfying both conditions of Eb < 0 and Eb > Ecoh indicates the metal atom's propensity to aggregate. The mobility of the metal atoms in the carbon substrate has been employed as a means to assess their stability from a kinetic perspective. The diffusion barrier of the metal atom migrating in the substrate can be obtained by searching the transition states in the migration path. The lower the diffusion barrier, the easier the metal can migrate, potentially leading to favorable aggregation.
The mentioned criteria were employed in various studies. Some studies have only considered Ef for the stability.55,110 Others have employed a combination of those criteria.34,85,108 For example, the stability of Fe–N–C and Mn–N–C can be assessed based on Ef, Eb, diffusion barriers, and Ecoh.38,111
Electrochemical stability. The limitations of thermal and thermodynamic stability lies in their failure to consider the impact of electrode potential, pH, or electrolyte in actual catalytic reactions. In contrast, the evaluation of electrochemical stability specifically takes these factors into account. In the following, we will briefly discuss some attempts to address the electrochemical stability.
One way to evaluate the electrochemical stability is to consider whether the embedded metal atom will dissolve in solution. This can be examined by the dissolution potential Udiss (relative to the SHE),112 which is calculated as
| Udiss = U0diss(metal,bulk) − (Ef/nq). | (4) |
Another way to examine the electrochemical stability under operando conditions is through the Pourbaix diagram. The Pourbaix diagram depicts the thermodynamics stability regions of different chemical species in an aqueous solution as a function of electrode potential and pH.116 Examples of constructing Pourbaix plots for SACs can be found in the literature.117–120 For example, Holby et al.120 proposed an approach based on DFT-calculated properties to explore the electrochemical stability of Fe–N4 in bilayer graphene. The presented methodology can take reaction environment variables into account, such as pH, electrode potential, and reaction intermediates. Experimental observations regarding relative stability in acid vs alkaline environments, dissolution of Fe at low potential, and the possible role of O2 can be well interpreted within the presented framework. There are also some other proposed approaches to incorporate environmental conditions to make results comparable with experiments. For example, experimentally reported reversible transformation between Cu single atoms and clusters under the realistic reaction conditionss105,107 can be explained by the constant potential hybrid-solvation dynamic model.121
The computational frameworks offer a unique approach to comprehending the structure–property relationship at an atomistic scale. By combining DFT-based simulations with fundamental physical principles, these frameworks can provide valuable design principles to guide experimental synthesis. The current focus in designing metal sites with carbon materials primarily revolves around manipulating the coordination environment surrounding single or dual metal sites within graphitic carbon structures. Through a combination of experimental synthesis and characterization, the incorporation of metal atoms into carbon-based materials exhibits tremendous potential for electrocatalysis. Given the diverse methods available to engineer the molecular interactions between metals and carbon during materials design, as well as the intricacies of electrochemical processes, the development of data-driven and accuracy-driven models has emerged as a solution to address challenges and expedite catalyst design. In the subsequent sections, we will delve into the exploration of these two aspects separately, specifically in relation to the design of atomic metal sites in carbon-based materials.
We aim to provide an overview of recent successful applications of data-driven models in the field of designing metal atomic sites in carbon catalysts, encompassing high throughput screening, machine learning, and identification of key descriptors. In order to enhance the accuracy of computational modeling, we also review approaches for incorporating solvation effects, as well as electron and proton transfer mechanisms, spin states, and oxidation states into the models.
3 Structure–binding energy relationship
Catalysts are composed of various elements and combinations, which result in a high-dimensional composition space to be explored for specific catalytic reactions. In addition, catalytic reactions often involve multiple intermediates and reaction pathways which make the mechanism complex. Besides, catalyst properties depend on different factors such as surface morphology and electronic properties. Therefore, performing ab initio calculations for all possibilities becomes very challenging because of the high computational cost. The data-driven approaches to address these challenges will be discussed in this section.3.1 Linear scaling relationship and BEP relationship
The scaling relationship is a fundamental principle in catalyst design. It simplifies complex catalytic reactions which involve multiple reaction steps by finding relationships between those steps. There are two well-accepted scaling relationships for catalyst design: the linear scaling relationship and the Bell–Evans–Polanyi (BEP) relationship. The linear scaling relationship refers to the relationship between the adsorption energies of intermediates that bind to the catalyst surface through the same atom. For example, in CO2 RR, the possible intermediates are *COOH, *CO, *CHO, *COH, *CH2O, *OH, and *OCH (* denotes the adsorption site). DFT studies revealed a linear relationship between Eads[CH2O], Eads[CHO], and Eads[COOH] against Eads[CO] on transition-metal surfaces.122 Based on the scaling relationship, the complete free energy profile can be depicted by considering the adsorption energy of one (or a few) intermediate(s) on the same adsorption site. From these adsorption energies, the activity and selectivity can be inferred.123–125 The linear scaling relationship can be explained through the bond order conservation theory.126–128The BEP relationship establishes a connection between the activation energy (energy of the transition state) and reaction enthalpy (the enthalpy change in an elementary reaction). It states that these two quantities are proportional to each other. This idea was first demonstrated by Evans and Polanyi in 1937, who showed that an increase of reaction enthalpy causes a decrease in activation energy in classic molecular reactions.131 After that, Michaelides et al. found that the linear relationship between activation energy change and enthalpy change was also established well for heterogeneous catalysts for the elementary reaction.132 Since surface redox reactions usually involve multiple steps, Cheng and Hu conducted a study demonstrating that multistep surface redox reactions can be effectively simplified as one-step adsorption or desorption processes.133 As a result, the adsorption energy of the reaction species can be considered as the descriptor for catalyst screening. Based on these scaling relationships, the reactivity of catalysts (e.g., the exchange current density, or overpotential) shows a volcano relationship with the energetic descriptor.134,135
Both scaling relationships have been examined in carbon-based SACs for various reactions. For example, in SACs on N-doped graphene and C2N, the scaling relationship was established between the intermediates of ORR where ΔEads between *OH and *O exhibited a slope close to 2, and *OH and *OOH showed slopes close to 1.60,136–138 For CO2 RR, a linear relationship with a slope close to 1 was observed between the adsorption energy of *CO and *COOH or *CHO on a single metal site with C-, N-, or B-doped graphene and C2N (Fig. 2(a)).59,83,129 For NRR, a scaling relationship was established between the adsorption energy of N2H* and NH2 with a slope close to 0.8139–141 on metal (M) in single porphyrin sites and N-doped graphene (M = Cr, Mn, Fe, Co). The BEP relationship was also examined for SACs in carbon-based materials. For example, to examine the activation energy for the transition state in ORR reaction, Wang et al. investigated the BEP relationship on zigzag, armchair, and basal plane of graphene and graphene oxide. A clear linear relationship was observed between the energy of the transition state and the chemisorption energy of the O atom with different functional groups.142 Similar results were also observed in carbon-based SAC systems. Choi et al. studied 13 transition metals coordinated with N and C in graphene (denoted as M@NxCy) for C–H bond activation. The linear relationship between the activation energy and H* adsorption energy was fitted as Ea = 0.79E(H*) + 2.07 for all metal and coordination environments (Fig. 2(b)).130
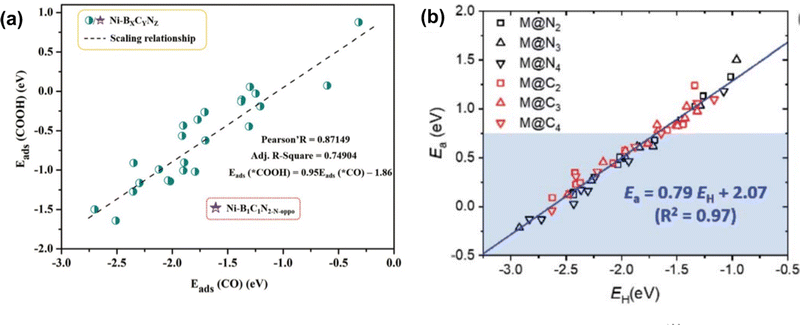 | ||
| Fig. 2 (a) Scaling relationship between the adsorption energy of *CO and *COOH. Reprinted with permission from ref. 129. Copyright 2021 Royal Society of Chemistry. (b) The scaled relationship between the activation energy and adsorption energy of H atom (BEP relationship) was examined on single-atom catalysts. Reprinted with permission from ref. 130. Copyright 2021 Royal Society of Chemistry. | ||
With the scaling relationships demonstrated for metal–carbon materials, the parameters that tune the adsorption energies of the key species can be used to screen new catalysts or catalytic sites that provide the best reactivity. However, it should be noted that the scaling relationships only apply to adsorbates that are adsorbed on the same site through the same type of atom that forms the chemical bonds with the site. Therefore, the application of linear relationships for catalyst design should be complemented by a thorough identification of active sites.143 Compared to transition metal catalysts, the active sites in metal–carbon materials exhibit greater diversity. The scaling relationship, as a consequence, can be modified if different adsorption sites are introduced.91,144,145 For example, both metal and non-metal as adsorption sites were observed in M@N4C4 moieties (M = Fe, Co, Ni) for ORR. *O and *OH were found to preferentially adsorb on the carbon site, while *OOH favored the metal site, circumventing the scaling relationship between their adsorption energies.14 Similar strategies have also been used for NRR and CO2 RR on the C3N monolayer and PC6.139,144,146
3.2 High-throughput screening of metal-centered active sites with binding energies
One of the applications of the scaling relationships is virtual high-throughput screening (VHTS). The VHTS can rapidly screen and evaluate a large number of materials and active sites, and thus the process of catalyst discovery and optimization can be accelerated. In metal–carbon materials, both metal and carbon substrates can be tuned through various strategies. For instance, optimizing the activity can be achieved by using different metals,100,136 different host materials,147 and different coordination environments.55,56,65,66,68Such flexibility in metal–carbon electrocatalysts was probed by Guo et al. They screened a total of 210 carbon-based SACs for ORR110 by exploring 30 different transition metals in combination with various coordination and substrate materials, including defective graphene, N-doped graphene, and phthalocyanine (Pc). Among them, 31 SACs have the potential to break the scaling relationship, and high activity and selectivity can be achieved towards hydroperoxide by screening the adsorption energy of O* (Fig. 3(a) and (b)). In their study, 7 SACs showed higher activity and selectivity than the benchmark PtHg4 in acidic media. Zn@Pc–N4 was recognized as the best catalyst with a small overpotential of 0.15 V, which was supported by experiments.148 In NRR, multi-step screening strategies have been used to search for the optimized catalysts.139,149,150 Ling et al. screened 540 SACs in nitrogen-doped graphene by varying metal coordinated atoms and single metal species. They found that W1C3 site exhibited the most outstanding performance with an extremely low onset potential of 0.25 V.150 In contrast, fewer VHTS have been applied for CO2RR.100,144 Guo et al. explored 72 candidates of 12 metals with 6 different coordination environments. By screening the ΔEads of *CO, *COOH and competing adsorption of *H, they found that Fe–N4, Ni–N4, Cu–N4, Pd–N4, and Pd–N4 are the most selective sites for CO2RR against HER.
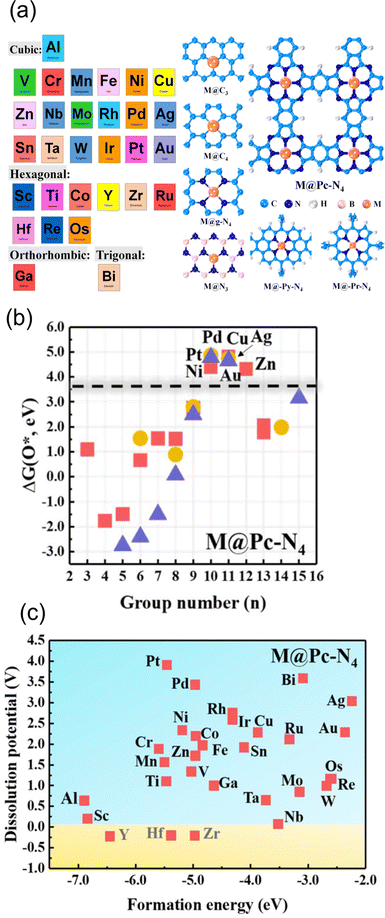 | ||
| Fig. 3 (a) Schematic illustration of screened metal atoms with their most stable bulk structure and all considered substrates. (b) The O* adsorption energy screening of metal from group 3–15 on Pc–N4 configuration. Squares, circles, and triangles represent Al, 3d transition metal, 4d transition metal, and 5d transition metal, respectively. (c) The stability screen for metal on Pc–N4 configuration. Reprinted with permission from ref. 110. Copyright 2019 American Society of Chemistry. | ||
In addition to the energetic screening for the adsorbents, stability has also been considered in the screening process.68,100,110 In a previous example,110 before screening the adsorption energy of O*, the structures were first screened regarding the thermodynamic and electrochemical stability. The criterion for stability was Udiss > 0 and ΔEf < 0 as we explained in Section 2.2.2. Based on the examination of stability, the substrates such as BN, Pc–N4, and Py–N4 are found to be good supports to host metal atoms. In terms of metal species, transition metals from group 8–12 are more likely to be stabilized under reaction conditions. In total, 146 SACs out of 210 were screened out (Fig. 3c), and Zn@Pc–N4 is verified as the best candidate for both stability and high activity for 2-electron ORR. As a support, these active moieties also have been synthesized successfully including Ni–N4–C, Fe–N4–C, and Co–N4–C.14
VHTS is a powerful tool that greatly reduces the effort required for conducting experiments. This approach enables the exploration of various tuning parameters simultaneously. However, performing a large number of DFT calculations is still computationally expensive. Machine learning-assisted high-throughput screening can be further leveraged to accelerate the VHTS.
3.3 Machine learning for adsorption energies
As discussed, the energetic descriptor such as ΔEads can be used as the property in VHST to screen new catalysts; however, calculating the energetic property from DFT to explore the vast design space is time-consuming. A surrogate model based on machine learning methods provides a faster way to predict ΔEads.151 The properties that machine learning model get trained to predict adsorption energy are known as features. By selecting key features, machine learning models can not only predict accurate ΔEads but also provide insights into the underlying mechanisms and design principles. In SACs, several machine learning models have been explored, including deep neural network (DNN),152 random forest regression (RFR),60,153 support vector machine (SVM),154 gradient boosted regression (GBR)68,155,156 and sure-independence screening and sparsifying operator (SISSO).157,158 The training data for these models range from ten to thousands. For example, Kaspe et al. combined DFT simulations and machine learning models to predict the ΔEads of *OH in carbon-based materials for ORR.154 They explored 2500 sites in 0D (graphene flakes), 1D (graphene nanoribbons), and 2D (graphene) doped with S, P, SO2 and PO2, and applied six machine learning models with 13 electronic and structural features. The SVM achieved the best performance in testing, with an R2 coefficient of determination of 0.87, followed by multiple linear regressor (R2 = 0.84), K-nearest neighbor (KNN) (R2 = 0.84), RFR (R2 = 0.83), Extreme Gradient Boosting Regressor (R2 = 0.79), and Decision Tree Regressor (R2 = 0.78). Fischer et al. studied 1700 transition metals doped in defective N-doped graphene by varying the metal species, the number of dopants, and the number of vacancies for the adsorption energies of O and H adsorbate species. The best performance was given by the RFR model with MAE = 0.31 eV for testing in predicting the ΔEads of *O compared to SVM with MAE = 0.32 eV. Umer et al. screened 364 SACs by anchoring 3d–5d single metal atoms on various substrates. A combined DFT-machine learning framework found that mono- or dual-type non-metal (B, N, and P) doping in g-C3N4, two-dimensional π-conjugated polymer, graphene and hexagonal boron nitride can substantially improve HER activity and stability. For predicting the adsorption energy for H*, Light Gradient Boosting Machine (LGBM), Histogram-based Gradient Boosting Regressor (HGBR), Extremely Randomized Trees (ERT), Gradient Boosting (GB), Bagging, XGBoost regressor (XGBR), RFR and AdaBoost regressor (ABR) are used. The top three performances are given by LGBR with RMSE = 0.20 eV, HGBR with RMSE = 0.24 eV and ERT with RMSE = 0.26 eV (Fig. 4(a)).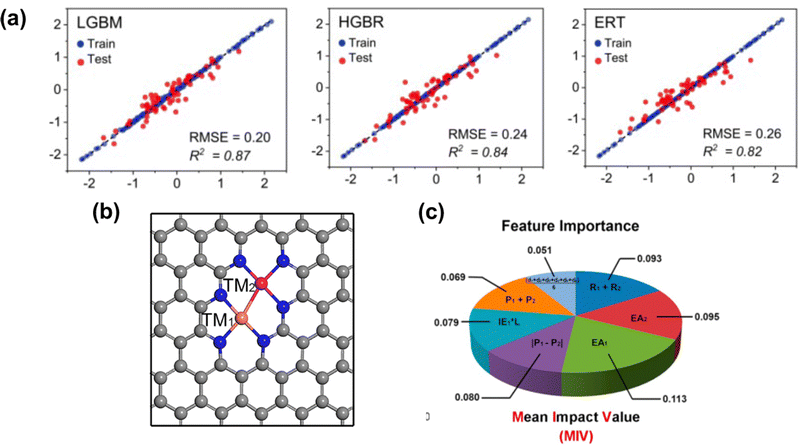 | ||
| Fig. 4 (a) Machine learning model performance for predicting the adsorption energy of H* on 2D carbon materials. (b) Schematic illustration of the bi-metal site on graphene. (c) Mean impact value (MIV) employed for considering feature importance. Reprinted with permission from ref. 159. Copyright 2022 Royal Society of Chemistry. | ||
Besides predicting ΔEads, machine learning models have also been used to reveal the structure–property–performance relationship where there are multiple properties that could influence the catalytic performance. For instance, Zhu et al.155 employed DFT and machine learning to study ORR on dual-metal site catalysts (DMSCs) in the carbon substrate and provide a comprehensive depiction of the relationship between intrinsic properties of these catalysts and their catalytic activity. They found that electron affinity, van der Waals radius, and electronegativity of two metal sites are important properties related to the adsorption energy of OH*. In another example, Deng et al. employed a DFT-machine learning study to understand the origin of the activity of bi-atom catalysts on N-doped graphene for ORR. They considered 20 electronic and geometric features in an RFR model, and the ranking of feature importance directly translated from the weight of each feature. Two dominant features, M–M (distance of two metals) and M–N (average distance between the metal and coordinated N atoms), are identified. This indicates the ineligible role of local geometry in the ORR activity.153 Zafari et al. performed high-throughput screening among B-doped graphene SACs by using machine learning methods for NRR. They employed principal component analysis (PCA) to reduce the number of features before determining the feature importance by the weight of the mean decrease in accuracy (MDA) obtained from a DNN. The results of the MDA analysis showed that the three most important features in determining the ΔEads of intermediates were metal coordination number, atomic radius of the metal, and fraction of boron among coordination atoms. It suggested that both geometric and electronic features show a significant impact on ΔEads.152
To summarize, the machine learning models have been employed to predict ΔEads to screen and discover promising catalysts, and the key properties can be identified to unravel the structure–performance relationship. Such data-driven strategies can screen out optimal catalysts that satisfy certain criteria at a large scale, greatly promoting the rational design of catalysts.
3.4 Identified descriptors
The selected features, which impact ΔEads, serve not only to comprehend the catalysts but also to predict their catalytic performance. These selected features, also known as descriptors, play a crucial role in this regard. Significant research efforts have been dedicated to identifying descriptors that exhibit a correlation with catalytic performance. In the following, we summarize the proposed descriptors for carbon-based electrocatalysts.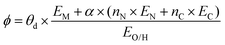 which combines the valence electrons in the occupied d orbital of the metal atom (θd) with the electronegativities of the metal (EM), nitrogen (EN), carbon (EC), oxygen (EO), and hydrogen (EH) atoms, as well as the number of nearest-neighbor nitrogen (nN) and carbon (nC) atoms. The proposed descriptor could successfully predict the activity order of previously reported experimental SACs on graphene, and it can be used to search for the optimal active centers for different reactions (guiding the synthesis of SACs that outperform precious-metal-based catalysts). It was also found that the descriptor ϕ shows a linear relationship when plotted against the ΔG of OH* and H* and fitted through linear regression: ΔG[OH*] = 0.11ϕ − 2.48, ΔG[H*] = −0.77ϕ + 1.27 when ϕ < 27 or ΔG[H*] = 0.04ϕ − 1.43 when ϕ > 27. As another example, Wang et al.114 demonstrated that descriptors combining electronic and geometric properties can effectively screen electrocatalysts for CO2 RR. The proposed descriptor takes the form
which combines the valence electrons in the occupied d orbital of the metal atom (θd) with the electronegativities of the metal (EM), nitrogen (EN), carbon (EC), oxygen (EO), and hydrogen (EH) atoms, as well as the number of nearest-neighbor nitrogen (nN) and carbon (nC) atoms. The proposed descriptor could successfully predict the activity order of previously reported experimental SACs on graphene, and it can be used to search for the optimal active centers for different reactions (guiding the synthesis of SACs that outperform precious-metal-based catalysts). It was also found that the descriptor ϕ shows a linear relationship when plotted against the ΔG of OH* and H* and fitted through linear regression: ΔG[OH*] = 0.11ϕ − 2.48, ΔG[H*] = −0.77ϕ + 1.27 when ϕ < 27 or ΔG[H*] = 0.04ϕ − 1.43 when ϕ > 27. As another example, Wang et al.114 demonstrated that descriptors combining electronic and geometric properties can effectively screen electrocatalysts for CO2 RR. The proposed descriptor takes the form 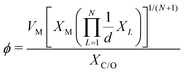 , which incorporates the number of d electrons of a metal atom (VM), the electronegativity of the metal atom (XM), its nearest atom (XL), adsorbate C (XC) or O (XO) atom connected to the metal atom, and the bond length between the metal atom and its nearest neighbor atom (d). This descriptor accurately describes the ΔEads[*CHO] for CO2 RR on M–N4–C SACs, as determined in a previous study. Additionally, a linear relationship was successfully established between ΔEads[*CHO] and ϕ with R2 = 0.70. Zhang167 studied bimetallic 2D MOFs for CO2 RR and proposed the descriptor ϕ = (4 ×VM1 × (EM1 + EN/O)/EN/O + VM2 × (EM2 + EN/O)/EN/O) × LM1–N/O, where E, V, and L represent electronegativity, the number of valence electrons, and bond length, respectively. By using this descriptor, they proposed CoPc–Zn–O and CoPc–Co–O as favorable catalysts.
, which incorporates the number of d electrons of a metal atom (VM), the electronegativity of the metal atom (XM), its nearest atom (XL), adsorbate C (XC) or O (XO) atom connected to the metal atom, and the bond length between the metal atom and its nearest neighbor atom (d). This descriptor accurately describes the ΔEads[*CHO] for CO2 RR on M–N4–C SACs, as determined in a previous study. Additionally, a linear relationship was successfully established between ΔEads[*CHO] and ϕ with R2 = 0.70. Zhang167 studied bimetallic 2D MOFs for CO2 RR and proposed the descriptor ϕ = (4 ×VM1 × (EM1 + EN/O)/EN/O + VM2 × (EM2 + EN/O)/EN/O) × LM1–N/O, where E, V, and L represent electronegativity, the number of valence electrons, and bond length, respectively. By using this descriptor, they proposed CoPc–Zn–O and CoPc–Co–O as favorable catalysts.
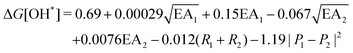 , where EA is the electron affinity of metal 1 (EA1) and metal 2 (EA2); (R1+ R2) is the summation of vDW radius of two metal centers; and (P1 − P2) is the difference of Pauling electronegativity of two metal atoms. They also show that as more features are included in the descriptor expression, the RMSE can be improved from 0.395 to 0.283 for ΔG[*OH] prediction. We summarized the descriptors for carbon-based catalysts under these three catagories in Table 1.
, where EA is the electron affinity of metal 1 (EA1) and metal 2 (EA2); (R1+ R2) is the summation of vDW radius of two metal centers; and (P1 − P2) is the difference of Pauling electronegativity of two metal atoms. They also show that as more features are included in the descriptor expression, the RMSE can be improved from 0.395 to 0.283 for ΔG[*OH] prediction. We summarized the descriptors for carbon-based catalysts under these three catagories in Table 1.
| Category | ϕ | Property | System | Reaction | Ref. |
|---|---|---|---|---|---|
| Physical-based | d-Band center | ΔEads ∝ d-band | 160 | ||
| θ d × ETM | ΔEads[OH*] | g-C3N4 | ORR | 163 | |
| k(Sv2/χβ) + b | ΔEads | Various substrates | CO2 RR, NRR, ORR | 164 | |
| θ p | ΔEads[OH*], ΔEads[OOH*] | N-Doped CNT, B-doped CNT | ORR | 165 | |
| Fitting-based |
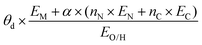
|
Activity, ΔG[OH*], ΔG[H*] | N-Doped graphene SACs | ORR, OER, HER | 166 |
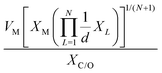
|
ΔEads[*CHO] | M–N4–C | CO2RR | 114 | |
| (4 ×VM1× (EM1 + EN/O)/EN/O + VM2× (EM2 + EN/O)/EN/O) ×LM1−N/O | Catalytic activity | Bimetallic 2D MOFs | CO2RR | 167 | |
| Machine learning-based | −1.032 × (ed/q) + 13.424 × (1/rcov) + 1.726 × (ed × EN) − 0.045 × docc2 − 9.241 | ΔG[H*] | N-Doped graphene SACs | HER | 157 |
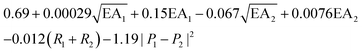
|
ΔG[OH*] | Dual-metal catalysts | ORR | 155 | |
Based on the reported descriptors, electronegativity and the number of d electrons are recognized as the top important electronic features while bond length between metal and nearest neighbor atoms is reported as the most important geometric feature. So, the mentioned approaches provide consistent results. However, it is important to remember that each approach has its own strengths and weaknesses. For instance, identifying a physics-based descriptor can be challenging for systems that are not well-understood and there is no prior knowledge of the underlying physical principles. On the other hand, machine learning-based descriptors are limited by the quality and quantity of the training data, as well as the difficulty to interpret the underlying physical relationships and mechanisms. It is worth noting that the approaches can complement each other, leading to more accurate and reliable predictions in the physical chemistry field as well as improving interpretability. On the other hand, there are some disadvantages to combining the approaches, such as creating more complex models that are harder to understand and interpret.
4 Catalytic activity beyond binding energy
Electrocatalytic processes occur in aqueous solutions; hence, there are more complex interactions and other physical parameters involved in the actual reaction that have not been fully considered. Besides, in metal–carbon systems, the spin and oxidation states are usually neglected. This section highlights the importance of accounting for both the solvent effect, which governs the interaction between the electrolyte and the electrocatalyst surface, and the spin state-induced extra electron transfer to improve the accuracy of binding energy predictions.4.1 Solvation effects
There is direct interaction of solvent molecules with substrates, catalysts, products, intermediates, and transition states. These interactions can profoundly influence electrocatalysis; the solvent not only influences the solubility and transport of reactant molecules,168 but also interacts with intermediates and catalytic sites;169,170 thus the reaction mechanisms can differ from the gas phase simulations and include the solvent effects, which further influences the reaction rate and selectivity.171–173 For example, the adsorption energy of a flat molecule on a clean Pt surface in the gas phase vs. solvent is different,169 and different solvent coverage can alter the kinetics.174 Those observations are also proved to be true in SACs. Wang et al. experimentally studied the solvent effect on N-doped graphene cobalt single-atom by altering the water/ethanol ratio.175 After adding 30% water to the ethanol solvent, the activity increased from 43.2 to 76.8 h−1, and the aniline selectivity increased from 62.8 to 99.1% for efficient hydrogenation of nitroarenes. Through further DFT study, the introducing of water weakened the binding between nitrobenzene and Co–N4 which benefits the desorption of aniline from the surface. Cao et al. studied Mn–N4/C SAC by using ab initio MD simulation and DFT calculations to investigate the influence of the solvation effect on the mechanisms of ORR by using explicit water molecules.176Fig. 5 illustrates the surface models in the gas phase and liquid phase used in this study, as well as the free-energy pathways. They found that the solvent environment promotes the charge transfer from the substrate to O2, which leads to a dissociative pathway to rupture the O–O bond before protonation. In addition, water molecules could also increase the reactivity of the protonation step for *O and *OH by elongating the Mn–O bond through a hydrogen bond.177 As the last example,178 Dub and Gordon considered metal–ligand bifunctional catalysts. They showed that when eight explicit water molecules are further added to the simulation, the first step (hydride transfer) proceeds similarly, but the relative activation barrier lowers by ∼5 kcal mol−1. They also found that in the second step of the reaction (proton transfer), the source of the proton is not C–H functionality, but the solvent. Their conclusions show that the inclusion of solvent effects changes both the reaction mechanism and the actual role of the ligand. Thus, to give an accurate reaction mechanisms, the roles of the solvent molecules must be considered in computational modeling.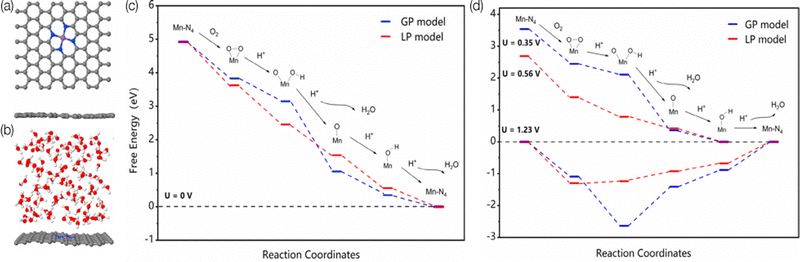 | ||
| Fig. 5 The surface models of MnN4–graphene in the (a) gas-phase (GP) and (b) liquid-phase (LP) model. The Mn, C, N, O, and H atoms are represented in purple, gray, blue, red, and white, respectively. Predicted free-energy pathways for ORR under different electrode potentials at pH = 0. (c) U = 0 V. (d) U = 1.23 V for both GP and LP models, U = 0.35 V for the GP model, and U = 0.56 V for the LP model. Reprinted with permission from ref. 176. Copyright 2020 American Chemical Society. | ||
Recent articles give an overview of various theoretical approaches that have been proposed to tackle solvation effects.179–181 These approaches include the solvation effects within implicit (or continuum), hybrid implicit/explicit (cluster/continuum) or explicit approaches. In the following, we briefly introduce these three main ways to include the solvent effects in quantum mechanical calculations.
Nowadays, most of the DFT in catalysis consider the solvent by continuum models. This methodology has proven to be highly successful in treating the solvent effects. The simplest approximation of the solvent effect is the implicit solvent models. In implicit solvent models, also known as the continuum models, the solvent is treated as a homogeneous medium, described by the dielectric constant ε. In this way, the “ad hoc” solvation correction is directly added to the Gibbs free energy of adsorption calculated in vacuum.94,182 The solvation-free energy can be calculated using various continuum solvation models, such as the polarizable continuum models (PCM)183,184 and the conductor-like screening models (COSMO).185,186 These methods are computationally efficient as they avoid sampling over solvent degree of freedom. However, it does not provide an accurate model when solvent molecules directly participate in the reaction. More examples of the success and limitations of continuum solvent models can be found in ref. 187.
The interaction between the electrolyte and the charged surface of the electrode can also be included in the implicit solvation model, for example, based on either the Poisson–Boltzmann (PB) electrostatic or generalized Born (GB) model.188–191 PB models take into account the solvent and solute charges, as well as the dielectric properties of the solvent and solute. They use the PB equation to calculate the electrostatic potential, which is then used to estimate the solvation free energy. GB models, on the other hand, approximate the model solvent as a continuous structureless medium with a uniform and certain dielectric constant to reduce the total degree of freedom of a system but ignore the potential electrostatic interaction with intermediates.188–191 They use the Born equation to calculate the solvation free energy which is based on the surface area and volume of the solute, as well as the difference in dielectric constants between the solute and solvent. Both PB and GB models are based on simplifying assumptions and approximations, which can limit their accuracy; e.g., it is highly possible to underestimate the water–adsorbate interaction. Besides, in large-scale simulations, the solution of the complex mathematical equations is computationally expensive. These methods are computationally efficient as they avoid sampling over the solvent molecules. However, since the solvent effect is averaged, it limits the model's accuracy if the solvent molecules play a direct role in the reaction. The limitation can be overcome by including a selected number of explicit solvent molecules in the atomistic calculations which is the basis of the cluster-continuum approach.192 The theoretical framework used for treating the explicit solvent molecules is the same as the rest of the catalytic system, i.e. the explicit solvent molecules are included in quantum mechanics simulations together with the catalysts. The implicit continuum solvation is then incorporated to account for long-range electrostatic effects. This combination results in hybrid implicit–explicit solvation schemes which have been discussed in detail by Pliego et al.193 Although it is a cost-effective approach, it is difficult to define the number and the location of the explicit solvent molecules.
A realistic description of the solvent in which catalytic reactions occur is the full inclusion of explicit solvent molecules in the model as individual particles. Then, the computational models can simulate the dynamics of the system which could be done for instance by ab initio MD simulations and kinetic Monte Carlo simulations, which have been developed, improved, and employed by many groups.194–197 During the simulation, each of the individual particle interacts with the solute molecule through intermolecular forces such as van der Waals and electrostatic interactions. Thus, the calculations are computationally expensive. So far, the widely accepted way to study the solvent effect on interactive interfaces is employing ab initio MD simulation to treat solvent molecules explicitly while maintaining the accuracy of interatomic force.198 This method allows for thermodynamic and dynamic equilibrium under certain temperatures, with empirically applied force fields. Quantum mechanics/molecular mechanics (QM/MM) has also been proved to be an accurate and affordable strategy for studying electrocatalytic reactions.199 The impact of the solvent effect on the energy profile can be clearly computed. However, most studies on electrolytes and catalyst surfaces have focused on metal and metal oxide surfaces, and the exploration of SACs still has not been fully understood.
4.2 Spin and charge transfer effects
In electrocatalysis, besides solvent effects, another critical issue that is often neglected in metal–carbon systems is the oxidation and spin states of the active site, which is usually the metal. In the following three paragraphs, we briefly summarize some literature searches that consider only oxidation states, spin states, and both.Some studies focus solely on the role of oxidation states. For instance, experimental and theoretical investigations on Fe–N–C SACs for CO2 RR reveal that Fe active sites maintaining +3 oxidation state during electrocatalysis exhibit superior activity for CO2-to-CO conversion.200,201 Operando X-ray absorption spectroscopy by Gu et al.201 revealed that the active sites on Fe–N–C are Fe3+ ions, coordinated to pyrrolic nitrogen atoms of the N-doped carbon support, that maintains their +3 oxidation state during electrocatalysis, probably through electronic coupling to the conductive carbon support. Electrochemical data in this study suggest that the Fe3+ sites derive their superior activity from faster CO2 adsorption and weaker CO absorption than that of conventional Fe2+ sites.
Detailed analysis of FeN4 and FeN5 in Fe–N–C reveals that the Bader charge of Fe in the FeN5 system (+1.19 e) is higher than that of Fe in FeN4 (+0.98 e), resulting in improving CO2 RR on FeN5 systems.200 A recent study considered the dynamics of the oxidation state of the Fe SAC in Nafion coated functionalized multi-wall carbon nanotubes (Fe-n-f-CNTs). According to this experimental-theory study, the dynamics of the oxidation state may occur by structural deformation of the Fe–(O)3 configuration, which modifies the coordination configuration due to the absorption of hydrogen and CO intermediates on probable active sites of Fe-n-f-CNTs.202 This study also shows that, according to the Bader charge analysis obtained from DFT calculations for different configurations of Fe in the Fe SACs in Fe-n-f-CNTs, the Bader charge state of the Fe atom is consistent with experimental results.
Some studies consider only the role of different spin states and demonstrate how these states alter the reaction pathway of catalytic reactions.104,203–206 For example, spectroscopic studies of Fe–N–C systems consider two distinct moieties, namely high-spin FeN4C12 and low/intermediate-spin FeN4C10.104 The results show that both sites initially contribute to the ORR activity but only the low/intermediate-spin moiety substantially contributes after 50 hours of operation. This experimental evidence motivated the examination of oxidation and spin states in computational catalysis. For example, DFT studies on the (salen)Mn(III)-catalyzed epoxidation reaction mechanism reveal that competing channels have different spin states.203 DFT results on M–N4–C (M = Mn, Fe, and Co) systems for ORR show that Mn–N4 and Fe–N4 centers in graphene exhibit the lowest O2 dissociation energies across three spin channels, while for Co–N4 they find two spin channels require the same dissociation energy.204 Additionally, a study on Fe–N–C systems for ORR indicates that the change of electronic spin moments of Fe and O2 due to molecular-catalyst adsorption scales with the amount of electron transfer from Fe to O2, as shown in Fig. 6, promoting the catalytic activity of C2N–Fe for driving ORR.206 Based on the relationship between catalytic activity and spin moment variation, they suggested that the electronic spin moment could be a promising catalytic descriptor for Fe SACs.
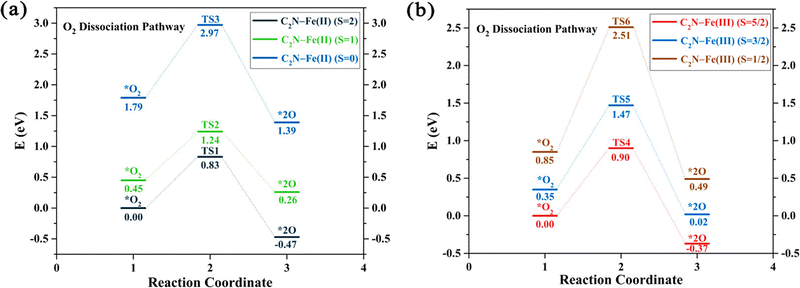 | ||
| Fig. 6 The potential energy profiles for the O2 dissociation pathway calculated for two systems: (a) C2N–Fe(II) with spin states S = 2, 1, and 0, and (b) C2N–Fe(III) with spin states S = 5/2, 3/2, and 1/2. The relative energies represented in the profiles correspond to Gibbs free energies, with the energies of the spin ground states set as a reference point at 0 eV. Reprinted with permission from ref. 206. Copyright 2021 American Chemical Society. | ||
Some studies consider the effect of both oxidation and spin states in the catalysts.207,208 For example, an experimental study on Fe–N–C for selective oxidation of C–H bonds provides evidence that among different FeNx (x = 4–6), the medium-spin Fe(III)N5 affords the highest turnover frequency (6455 h−1), and is at least 1 order of magnitude more active than the high-spin and low-spin Fe(III)N6 structures and 3 times more active than the Fe(II)N4 structure, although its relative concentration in the catalysts is much lower than that of the Fe(III)N6 structures.205 Yang et al.207 investigated dual-metal atomically dispersed Fe, Mn/N–C catalysts and found that the O2 reduction preferentially takes place on Fe(III) in the FeN4/C system with the intermediate spin state which possesses one eg electron (t2g4eg1) readily penetrating the antibonding π-orbital of oxygen. Both magnetic measurements and the theoretical calculation reveal that the adjacent atomically dispersed Mn–N moieties can effectively activate the FeIII sites by both spin-state transition and electronic modulation, rendering the excellent ORR performances of Fe,Mn/N–C in both alkaline and acidic media. Gong et al.208 developed a facile strategy to manipulate the cobalt spin state over COF-367-Co by changing the oxidation state of Co, resulting in the regulation of the photocatalytic performance for CO2RR and enhanced selectivity to HCOOH. According to their DFT calculations and experimental results, Co(II) and Co(III) are embedded in COF-367 with 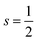 and 0 spin ground states, respectively.
and 0 spin ground states, respectively.
In electrocatalysis, the transfer of electrons and protons between the electrode, catalyst, and reactants is important. Proton transfer is often coupled with electron transfer in a process known as proton-coupled electron transfer (PCET), which can modulate the pathway that the reactants follow. Therefore, this coupled motion of electrons and protons plays a critical role in a wide range of electrochemical processes such as CO2RR, ORR, and N2RR in carbon and carbon–metal systems.134,209–214Fig. 7 provides a representative example demonstrating how electron transfer (ET), proton transfer (PT) and PCET affect the reaction mechanism during the four-electron ORR on nitridated carbon (NC) catalysts. Generally, PCET describes the mechanism of electron and proton transfer from atom to atom, which is also important for catalyst design. As described in Section 2.2, CHE predicts the thermodynamics properties of electrochemical reactions. Thus, PCET reactions can be evaluated using CHE which uses gas phase H2 formed from H+ and e− as a reference reaction. This intrinsically connects the PCET step to the standard hydrogen electrode (SHE) scale. To understand PCET at interfaces, where there are spatially inhomogeneous internal electric fields and electrostatic potentials within the active site, we need modeling strategies to explore PCET thermodynamics and further develop molecular active sites. Recent works have attempted to provide atomic-scale insight into interfacial PCET reactions, which are key steps in catalyst design. For instance, Hammes-Schiffer et al.215 provide a first-principles modeling strategy based on DFT calculations. They illustrated that investigating the interfacial PCET at graphite-conjugated catalysts (GCC) bearing organic acid moieties explains the absence of a cyclic voltammetry peak. This combined theoretical-experimental study not only demonstrates the critical role of continuous conjugation and strong electronic coupling between the GCC acid sites and the graphite in enabling PCET at acid cites, but also emphasizes the importance of understanding the connection between the atomic structure of the surfaces and the interfacial electrostatic potentials and fields that govern PCET thermochemistry. Furthermore, the study of these GCC catalysts in the presence of defects, such as heteroatom dopants in the graphitic surface, reveals that the lowest unoccupied electronic states can serve as a descriptor for changes in PCET thermodynamics.216 Such studies highlight the need to consider PCET mechanisms in the computational screening of SACs.
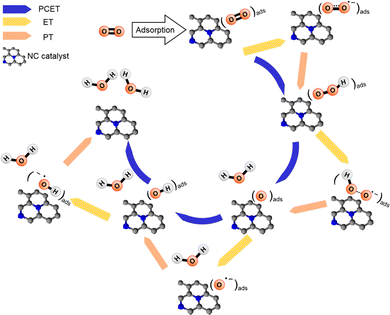 | ||
| Fig. 7 Representative possible elementary steps during four-electron ORR (O2 + 4H+ + 4e− → 2H2O) on carbon-based electrocatalysts. Black and blue balls represent carbon and nitrogen atoms, respectively. Reprinted with permission from ref. 210. Copyright 2018 American Chemical Society. | ||
The above-mentioned case studies provide evidence that oxidation states, spin states, and interfacial PCET are critical issues that cannot be ignored in catalyst design. However, providing computationally accurate results for such properties is challenging. For instance, it has been shown that the choice of DFT exchange–correlation functional can highly affect the binding energy of CO on TM atoms embedded on nitrogen-doped graphene.217 Similarly, the absolute value of the spin magnetic moment of Fe, the spin magnetic moment of *O2 (M*O2), and the d-band center gap of spin states can also be affected.218 For the (salen)Mn(III)-catalyzed epoxidation reaction mechanism, Abachkin et al. clearly showed how the choice of DFT functional and model can dramatically change the results.203 Hence, these challenges can generally be addressed for specific systems with careful treatment of each effect. Nevertheless, the solution is still computationally expensive and not feasible for widely applying in large structural space search.
5 Perspectives and future opportunities
In Section 2.1, we have summarized the computational work on single atom and multiple metal sites in carbon-based materials, covering the exploration of coordination configurations, carbon substrate structures, alternative dopants, and their influences on catalytic activity and stability. However, to find an optimal M–Xx (X = N, P, S, B, etc.) moiety that possesses high activity, selectivity and stability remains demanding and not straightforward, particularly in the exploration of moieties in different graphitic carbon structures to host M–X sites. Additionally, the curvature of the carbon substrates can also affect the properties of the electrocatalysts. Unfortunately, most modeled structures are primarily based on flat graphene substrates, with only a few studies demonstrating the importance of the curvature effects. For example, fullerenes which exhibit reactivity changes due to their curvatures219 are rarely explored. In contrast, studies on N-doped fullerenes indicate the potential of such structures as cathode catalysts for hydrogen fuel cells,220 CO oxidation,221,222 and ORR.223 In light of the challenges encountered in the exploration of optimal configurations for metal embedded in carbon-based catalysts, there are compelling opportunities to advance the field through the development of innovative computational tools and collaborative initiatives. One such opportunity lies in the creation of automated virtual high-throughput screening workflows that would be capable of swiftly exploring the huge design space. The workflows that can automatically generate diverse structures, efficiently perform DFT simulations, and subsequently conduct data-driven assessments would revolutionize the search for stable moieties that exhibit enhanced catalytic stability and selectivity.Furthermore, accurately describing the reactivity through DFT simulations presents another significant challenge. A benchmark from the comparison with experimental data to assess the accuracy of different computational models is needed. Also, modeling the catalysts under operando conditions by considering the solvent effects, electrode potential, and structural evolution during reactions increases both the complexity of the model and the computational costs dramatically. As a consequence, attaining high accuracy in virtual high-throughput screening continues to be a persistent challenge. One potential solution is to train an accurate machine learning model to replace the computationally expensive DFT simulations. The machine learning models are expected to be trained based on the database that would be obtained from simulations with high accuracy. The establishment of such database plays a pivotal role in accelerating the research in the field. The database could serve as a repository with valuable information on structural, electronic and catalytic properties regarding the metal embedded in carbon-based materials.
Overall, computational approaches such as DFT simulations and data-driven models have been extensively leveraged in discovering sustainable, cost-effective, and highly reactive electrocatalysts derived from metal–carbon materials. However, there is still a need for efficient and predictive machine learning models. Training those models requires automated virtual high-throughput screening tools as well as accessible databases, which serve as crucial components in advancing the field. In conclusion, the continued advancement and integration of computational techniques, coupled with experimental efforts, hold tremendous promise for accelerating the development and optimization of metal sites in carbon-based materials for electrocatalysis, propelling us closer to realizing efficient and scalable energy technologies.
Author contributions
Somayeh Faraji: literature curation, formal analysis, investigation, methodology, writing – original draft, writing – review and editing; Zhiyu Wang: literature curation, formal analysis, investigation, methodology, writing – original draft, writing – review and editing; Paola Lopez-Rivera: literature curation; Mingjie Liu: conceptualization, supervision, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the University of Florida's new faculty start-up funding.Notes and references
- V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57–69 CrossRef CAS PubMed.
- Y. Bing, H. Liu, L. Zhang, D. Ghosh and J. Zhang, Chem. Soc. Rev., 2010, 39, 2184–2202 RSC.
- C. Li and J.-B. Baek, ACS Omega, 2019, 5, 31–40 CrossRef PubMed.
- Y. Hori, R. Takahashi, Y. Yoshinami and A. Murata, J. Phys. Chem. B, 1997, 101, 7075–7081 CrossRef CAS.
- J. Resasco and A. T. Bell, Trends Chem., 2020, 2, 825–836 CrossRef CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- H. Tao, C. Choi, L.-X. Ding, Z. Jiang, Z. Han, M. Jia, Q. Fan, Y. Gao, H. Wang and A. W. Robertson, et al. , Chem, 2019, 5, 204–214 CAS.
- G. Deng, T. Wang, A. A. Alshehri, K. A. Alzahrani, Y. Wang, H. Ye, Y. Luo and X. Sun, J. Mater. Chem. A, 2019, 7, 21674–21677 RSC.
- H. Huang, L. Xia, X. Shi, A. M. Asiri and X. Sun, Chem. Commun., 2018, 54, 11427–11430 RSC.
- S. K. Kaiser, Z. Chen, D. Faust Akl, S. Mitchell and J. Perez-Ramirez, Chem. Rev., 2020, 120, 11703–11809 CrossRef CAS PubMed.
- Y. Wang, H. Su, Y. He, L. Li, S. Zhu, H. Shen, P. Xie, X. Fu, G. Zhou and C. Feng, et al. , Chem. Rev., 2020, 120, 12217–12314 CrossRef CAS PubMed.
- Y. Chen, L. Wang, Z. Yao, L. Hao, X. Tan, J. Masa, A. W. Robertson and Z. Sun, Acta Phys.-Chim. Sin., 2022, 38, 2206020 Search PubMed.
- D. Yu and J. Wang, Chin. J. Struct. Chem., 2022, 41, 2207002 CAS.
- H. Fei, J. Dong, Y. Feng, C. S. Allen, C. Wan, B. Volosskiy, M. Li, Z. Zhao, Y. Wang and H. Sun, et al. , Nat. Catal., 2018, 1, 63–72 CrossRef CAS.
- X. Zeng, J. Shui, X. Liu, Q. Liu, Y. Li, J. Shang, L. Zheng and R. Yu, Adv. Energy Mater., 2018, 8, 1701345 CrossRef.
- Y.-N. Chen, X. Zhang and Z. Zhou, Small Methods, 2019, 3, 1900050 CrossRef.
- Y. Yang, Y. Yang, Z. Pei, K.-H. Wu, C. Tan, H. Wang, L. Wei, A. Mahmood, C. Yan and J. Dong, et al. , Matter, 2020, 3, 1442–1476 CrossRef.
- Q. Zhang and J. Guan, Adv. Funct. Mater., 2020, 30, 2000768 CrossRef CAS.
- S. Back, J. Lim, N.-Y. Kim, Y.-H. Kim and Y. Jung, Chem. Sci., 2017, 8, 1090–1096 RSC.
- T. Liu, G. Wang and X. Bao, J. Phys. Chem. C, 2021, 125, 26013–26020 CrossRef CAS.
- K. Rossi and R. Buonsanti, Acc. Chem. Res., 2022, 55, 629–637 CrossRef CAS PubMed.
- D. R. Alfonso, D. N. Tafen and D. R. Kauffmann, Catalysts, 2018, 8, 424 CrossRef.
- L. Han, H. Cheng, W. Liu, H. Li, P. Ou, R. Lin, H.-T. Wang, C.-W. Pao, A. R. Head and C.-H. Wang, et al. , Nat. Mater., 2022, 21, 681–688 CrossRef CAS PubMed.
- K. Zhao, X. Nie, H. Wang, S. Chen, X. Quan, H. Yu, W. Choi, G. Zhang, B. Kim and J. G. Chen, Nat. Commun., 2020, 11, 1–10 CrossRef PubMed.
- X. Li, W. Bi, M. Chen, Y. Sun, H. Ju, W. Yan, J. Zhu, X. Wu, W. Chu and C. Wu, et al. , J. Am. Chem. Soc., 2017, 139, 14889–14892 CrossRef CAS PubMed.
- Y. Yang, J. Li, C. Zhang, Z. Yang, P. Sun, S. Liu and Q. Cao, J. Phys. Chem. C, 2022, 126, 4338–4346 CrossRef CAS.
- P. Brimley, H. Almajed, Y. Alsunni, A. W. Alherz, Z. J. Bare, W. A. Smith and C. B. Musgrave, ACS Catal., 2022, 12, 10161–10171 CrossRef CAS.
- W. Ju, A. Bagger, G.-P. Hao, A. S. Varela, I. Sinev, V. Bon, B. Roldan Cuenya, S. Kaskel, J. Rossmeisl and P. Strasser, Nat. Commun., 2017, 8, 1–9 CrossRef CAS PubMed.
- A. Kumar, S. Ibraheem, T. A. Nguyen, R. K. Gupta, T. Maiyalagan and G. Yasin, Coord. Chem. Rev., 2021, 446, 214122 CrossRef CAS.
- K. L. Svane, M. Reda, T. Vegge and H. A. Hansen, ChemSusChem, 2019, 12, 5133–5141 CrossRef CAS PubMed.
- C. Yin, H. Tang, K. Li, Y. Yuan and Z. Wu, New J. Chem., 2018, 42, 9620–9625 RSC.
- Z. Jiang, X. Zhang, H.-S. Chen, X. Hu and P. Yang, ChemCatChem, 2019, 11, 4558–4567 CrossRef CAS.
- W. Shan and G. Wang, J. Phys. Chem. C, 2021, 125, 16004–16012 CrossRef CAS.
- C. Choi, S. Back, N.-Y. Kim, J. Lim, Y.-H. Kim and Y. Jung, ACS Catal., 2018, 8, 7517–7525 CrossRef CAS.
- H. Yang, R. Shi, L. Shang and T. Zhang, Small Struct., 2021, 2, 2100007 CrossRef CAS.
- G. Gao, S. Bottle and A. Du, Catal. Sci. Technol., 2018, 8, 996–1001 RSC.
- Y. Zhou, G. Gao, Y. Li, W. Chu and L.-W. Wang, Phys. Chem. Chem. Phys., 2019, 21, 3024–3032 RSC.
- W. Yang, M. Zhao, X. Ding, K. Ma, C. Wu, I. D. Gates and Z. Gao, Phys. Chem. Chem. Phys., 2020, 22, 3983–3989 RSC.
- X. Rong, H.-J. Wang, X.-L. Lu, R. Si and T.-B. Lu, Angew. Chem., 2020, 132, 1977–1981 CrossRef.
- X. Wang, Z. Chen, X. Zhao, T. Yao, W. Chen, R. You, C. Zhao, G. Wu, J. Wang and W. Huang, et al. , Angew. Chem., 2018, 130, 1962–1966 CrossRef.
- X.-F. Li, Q.-K. Li, J. Cheng, L. Liu, Q. Yan, Y. Wu, X.-H. Zhang, Z.-Y. Wang, Q. Qiu and Y. Luo, J. Am. Chem. Soc., 2016, 138, 8706–8709 CrossRef CAS PubMed.
- J. Liu, X. Kong, L. Zheng, X. Guo, X. Liu and J. Shui, ACS Nano, 2020, 14, 1093–1101 CrossRef CAS PubMed.
- Y. Qin, Y. Li, W. Zhao, S. Chen, T. Wu and Y. Su, Nano Res., 2023, 16, 325–333 CrossRef CAS.
- F. Pan, B. Li, E. Sarnello, Y. Fei, Y. Gang, X. Xiang, Z. Du, P. Zhang, G. Wang and H. T. Nguyen, et al. , ACS Nano, 2020, 14, 5506–5516 CrossRef CAS PubMed.
- A. V. Kuzmin and B. A. Shainyan, Int. J. Quantum Chem., 2021, 121, e26809 CrossRef CAS.
- G. Han, X. Zhang, W. Liu, Q. Zhang, Z. Wang, J. Cheng, T. Yao, L. Gu, C. Du and Y. Gao, et al. , Nat. Commun., 2021, 12, 6335 CrossRef CAS PubMed.
- S. Yang, C. Zhao, R. Qu, Y. Cheng, H. Liu and X. Huang, RSC Adv., 2021, 11, 3174–3182 RSC.
- S. Yang, Y. Cheng, H. Liu and X. Huang, Appl. Organomet. Chem., 2022, 36, e6577 CrossRef CAS.
- A. Omidvar, Synth. Met., 2017, 234, 38–46 CrossRef CAS.
- X. Gao, Y. Zhou, Y. Tan, S. Liu, Z. Cheng and Z. Shen, Appl. Surf. Sci., 2019, 492, 8–15 CrossRef CAS.
- W. Song, K. Xie, J. Wang, Y. Guo, C. He and L. Fu, Phys. Chem. Chem. Phys., 2021, 23, 10418–10428 RSC.
- Y. Xue, B. Huang, Y. Yi, Y. Guo, Z. Zuo, Y. Li, Z. Jia, H. Liu and Y. Li, Nat. Commun., 2018, 9, 1460 CrossRef PubMed.
- Z. Feng, R. Li, Y. Ma, Y. Li, D. Wei, Y. Tang and X. Dai, Phys. Chem. Chem. Phys., 2019, 21, 19651–19659 RSC.
- T. He, S. K. Matta, G. Will and A. Du, Small Methods, 2019, 3, 1800419 CrossRef.
- Z. Xue, X. Zhang, J. Qin and R. Liu, J. Energy Chem., 2021, 55, 437–443 CrossRef CAS.
- J.-L. Chen, H.-J. Hu and S.-H. Wei, Chin. Phys. B, 2022, 31, 107306 CrossRef.
- J. Huang, C. Zhou, Z. Chu, X. Liu and X. Duan, Phys. Chem. Chem. Phys., 2021, 23, 1868–1873 RSC.
- B. He, J. Shen and Z. Tian, Phys. Chem. Chem. Phys., 2016, 18, 24261–24269 RSC.
- X. Cui, W. An, X. Liu, H. Wang, Y. Men and J. Wang, Nanoscale, 2018, 10, 15262–15272 RSC.
- Y. Ying, K. Fan, X. Luo, J. Qiao and H. Huang, J. Mater. Chem. A, 2021, 9, 16860–16867 RSC.
- S. Liu and J.-y Liu, J. Power Sources, 2022, 535, 231449 CrossRef CAS.
- H. Niu, Z. Zhang, X. Wang, X. Wan, C. Shao and Y. Guo, Adv. Funct. Mater., 2021, 31, 2008533 CrossRef CAS.
- B. Huang, Y. Wu, B. Chen, Y. Qian, N. Zhou and N. Li, Chin. J. Catal., 2021, 42, 1160–1167 CrossRef CAS.
- J.-J. Zhong, S.-P. Huang, J.-F. Gu, Y. Li, K.-N. Ding, Y.-F. Zhang, W. Lin and W.-K. Chen, Appl. Surf. Sci., 2023, 609, 155280 CrossRef CAS.
- C. Guo, T. Zhang, X. Deng, X. Liang, W. Guo, X. Lu and C.-M. L. Wu, ChemSusChem, 2019, 12, 5126–5132 CrossRef CAS PubMed.
- C. Yang, Z. Zhao and Q. Liu, Appl. Surf. Sci., 2021, 566, 150697 CrossRef CAS.
- S.-L. Li, H. Yin, X. Kan, L.-Y. Gan, U. Schwingenschlögl and Y. Zhao, Phys. Chem. Chem. Phys., 2017, 19, 30069–30077 RSC.
- H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2021, 9, 3590–3599 CrossRef CAS.
- H. Zhao, H. Cao, Z. Zhang and Y.-G. Wang, ACS Catal., 2022, 12, 11380–11390 CrossRef CAS.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777 CrossRef CAS PubMed.
- Y. Wang, L. You and K. Zhou, Chem. Sci., 2021, 12, 14065–14073 RSC.
- M. D. Hossain, Y. Huang, T. H. Yu, W. A. Goddard and Z. Luo, Nat. Commun., 2020, 11, 1–14 Search PubMed.
- Y. Pan, R. Lin, Y. Chen, S. Liu, W. Zhu, X. Cao, W. Chen, K. Wu, W.-C. Cheong and Y. Wang, et al. , J. Am. Chem. Soc., 2018, 140, 4218–4221 CrossRef CAS PubMed.
- Q. Fan, P. Hou, C. Choi, T.-S. Wu, S. Hong, F. Li, Y.-L. Soo, P. Kang, Y. Jung and Z. Sun, Adv. Energy Mater., 2020, 10, 1903068 CrossRef CAS.
- M. S. Iqbal, Z.-B. Yao, Y.-K. Ruan, R. Iftikhar, L.-D. Hao, A. W. Robertson, S. M. Imran and Z.-Y. Sun, Rare Met., 2023, 42, 1075–1097 CrossRef CAS.
- Y. Li, Z.-S. Wu, P. Lu, X. Wang, W. Liu, Z. Liu, J. Ma, W. Ren, Z. Jiang and X. Bao, Adv. Sci., 2020, 7, 1903089 CrossRef CAS PubMed.
- M. S. Ritopečki, A. S. Dobrota, N. V. Skorodumova and I. A. Pašti, Nanomaterials, 2022, 12, 4309 CrossRef PubMed.
- Y. Qin, S. Zhang, G. Gao, S. Ding and Y. Su, Mol. Catal., 2022, 517, 112048 CrossRef CAS.
- Z. Wen, H. Lv, D. Wu, W. Zhang, X. Wu and J. Yang, J. Phys. Chem. Lett., 2022, 13, 8177–8184 CrossRef CAS PubMed.
- X. Bai, L. Wang, B. Nan, T. Tang, X. Niu and J. Guan, Nano Res., 2022, 15, 6019–6025 CrossRef CAS.
- M. Guo, M. Ji and W. Cui, Appl. Surf. Sci., 2022, 592, 153237 CrossRef CAS.
- X.-Y. Xu, S. Lin, H. Xu, H. Guo and C. Zhao, Appl. Surf. Sci., 2021, 556, 149776 CrossRef CAS.
- Y. Yang, Z. Yang, C. Zhang, J. Zhou, S. Liu and Q. Cao, Inorg. Chem., 2022, 61, 12012–12022 CrossRef CAS PubMed.
- Y. Li, W. Shan, M. J. Zachman, M. Wang, S. Hwang, H. Tabassum, J. Yang, X. Yang, S. Karakalos and Z. Feng, et al. , Angew. Chem., Int. Ed., 2022, 61, e202205632 CrossRef CAS PubMed.
- X. Zheng, Y. Liu and Y. Yao, Chem. Eng. J., 2021, 426, 130745 CrossRef CAS.
- S. Li, A. Guan, C. Yang, C. Peng, X. Lv, Y. Ji, Y. Quan, Q. Wang, L. Zhang and G. Zheng, ACS Mater. Lett., 2021, 3, 1729–1737 CrossRef CAS.
- W. Wan, Y. Zhao, S. Wei, C. A. Triana, J. Li, A. Arcifa, C. S. Allen, R. Cao and G. R. Patzke, Nat. Commun., 2021, 12, 5589 CrossRef CAS PubMed.
- W. Ren, X. Tan, W. Yang, C. Jia, S. Xu, K. Wang, S. C. Smith and C. Zhao, Angew. Chem., Int. Ed., 2019, 58, 6972–6976 CrossRef CAS PubMed.
- J. Zhu, M. Xiao, D. Ren, R. Gao, X. Liu, Z. Zhang, D. Luo, W. Xing, D. Su and A. Yu, et al. , J. Am. Chem. Soc., 2022, 144, 9661–9671 CrossRef CAS PubMed.
- J. Wang, Z. Huang, W. Liu, C. Chang, H. Tang, Z. Li, W. Chen, C. Jia, T. Yao and S. Wei, et al. , J. Am. Chem. Soc., 2017, 139, 17281–17284 CrossRef CAS PubMed.
- L. Li, K. Yuan and Y. Chen, Acc. Mater. Res., 2022, 3, 584–596 CrossRef CAS.
- Z. Ao and F. Peeters, J. Phys. Chem. C, 2010, 114, 14503–14509 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477 CrossRef CAS PubMed.
- R. Sundararaman, W. A. Goddard and T. A. Arias, J. Chem. Phys., 2017, 146, 114104 CrossRef PubMed.
- P. Atkins, P. W. Atkins and J. de Paula, Atkins' physical chemistry, Oxford University Press, 2014 Search PubMed.
- E. Skúlason, V. Tripkovic, M. E. Björketun, S. Gudmundsdóttir, G. Karlberg, J. Rossmeisl, T. Bligaard, H. Jónsson and J. K. Nørskov, J. Phys. Chem. C, 2010, 114, 18182–18197 CrossRef.
- J. Rossmeisl, E. Skúlason, M. E. Björketun, V. Tripkovic and J. K. Nørskov, Chem. Phys. Lett., 2008, 466, 68–71 CrossRef CAS.
- C. Guo, T. Zhang, X. Liang, X. Deng, W. Guo, Z. Wang, X. Lu and C.-M. L. Wu, Appl. Surf. Sci., 2020, 533, 147466 CrossRef CAS.
- G. Gao and L.-W. Wang, J. Catal., 2020, 391, 530–538 CrossRef CAS.
- H. Cao, Z. Zhang, J.-W. Chen and Y.-G. Wang, ACS Catal., 2022, 12, 6606–6617 CrossRef CAS.
- B. Qiao, J.-X. Liang, A. Wang, C.-Q. Xu, J. Li, T. Zhang and J. J. Liu, Nano Res., 2015, 8, 2913–2924 CrossRef CAS.
- J. Li, M. T. Sougrati, A. Zitolo, J. M. Ablett, I. C. Oğuz, T. Mineva, I. Matanovic, P. Atanassov, Y. Huang and I. Zenyuk, et al. , Nat. Catal., 2021, 4, 10–19 CrossRef CAS.
- D. Karapinar, N. T. Huan, N. Ranjbar Sahraie, J. Li, D. Wakerley, N. Touati, S. Zanna, D. Taverna, L. H. Galvão Tizei and A. Zitolo, et al. , Angew. Chem., Int. Ed., 2019, 58, 15098–15103 CrossRef CAS PubMed.
- C. E. Creissen and M. Fontecave, Nat. Commun., 2022, 13, 2280 CrossRef CAS PubMed.
- H. Xu, D. Rebollar, H. He, L. Chong, Y. Liu, C. Liu, C.-J. Sun, T. Li, J. V. Muntean and R. E. Winans, et al. , Nat. Energy, 2020, 5, 623–632 CrossRef CAS.
- M. Chen, M. Luo, C. Liu, X. Qi, S. G. Peera and T. Liang, Comput. Theor. Chem., 2020, 1187, 112945 CrossRef CAS.
- Z. Lu, G. Xu, C. He, T. Wang, L. Yang, Z. Yang and D. Ma, Carbon, 2015, 84, 500–508 CrossRef CAS.
- X. Guo, S. Lin, J. Gu, S. Zhang, Z. Chen and S. Huang, ACS Catal., 2019, 9, 11042–11054 CrossRef CAS.
- L. Xu, L.-M. Yang and E. Ganz, Theor. Chem. Acc., 2018, 137, 1–13 Search PubMed.
- J. Greeley and J. K. Nørskov, Electrochim. Acta, 2007, 52, 5829–5836 CrossRef CAS.
- M. Ha, D. Y. Kim, M. Umer, V. Gladkikh, C. W. Myung and K. S. Kim, Energy Environ. Sci., 2021, 14, 3455–3468 RSC.
- J. Wang, M. Zheng, X. Zhao and W. Fan, ACS Catal., 2022, 12, 5441–5454 CrossRef CAS.
- Z. Huang and Q. Tang, J. Phys. Chem. C, 2022, 126, 21606–21615 CrossRef CAS.
- M. Pourbaix, Atlas of electrochemical equilibria in aqueous solutions, 1966.
- L. Yang, H. Xu, H. Liu, X. Zeng, D. Cheng, Y. Huang, L. Zheng, R. Cao and D. Cao, Research, 2020, 2020, 7593023 CAS.
- J. H. Zagal and M. T. Koper, Angew. Chem., Int. Ed., 2016, 55, 14510–14521 CrossRef CAS PubMed.
- A. S. Dobrota, N. V. Skorodumova, S. V. Mentus and I. A. Pašti, Electrochim. Acta, 2022, 412, 140155 CrossRef CAS.
- E. F. Holby, G. Wang and P. Zelenay, ACS Catal., 2020, 10, 14527–14539 CrossRef CAS.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2021, 143, 9423–9428 CrossRef CAS PubMed.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef PubMed.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804 CrossRef.
- J. Zhang, H. B. Yang, D. Zhou and B. Liu, Chem. Rev., 2022, 122, 17028–17072 CrossRef CAS PubMed.
- G. Lendvay, J. Phys. Chem., 1989, 93, 4422–4429 CrossRef CAS.
- E. Shustorovich, Surf. Sci. Rep., 1986, 6, 1–63 CrossRef CAS.
- E. Shustorovich, J. Am. Chem. Soc., 1984, 106, 6479–6481 CrossRef CAS.
- M. Ma, F. Li and Q. Tang, Nanoscale, 2021, 13, 19133–19143 RSC.
- C. Choi, S. Yoon and Y. Jung, Chem. Sci., 2021, 12, 3551–3557 RSC.
- M. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- A. Michaelides, Z.-P. Liu, C. Zhang, A. Alavi, D. A. King and P. Hu, J. Am. Chem. Soc., 2003, 125, 3704–3705 CrossRef CAS PubMed.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 1308–1311 CrossRef CAS.
- L. Zhong, L. Zhang and S. Li, ACS Mater. Lett., 2020, 3, 110–120 CrossRef.
- J. Tymoczko, F. Calle-Vallejo, W. Schuhmann and A. S. Bandarenka, Nat. Commun., 2016, 7, 1–6 Search PubMed.
- Y. Xiao and W. Zhang, Electrocatalysis, 2020, 11, 393–404 CrossRef CAS.
- L. Zhong and S. Li, ACS Catal., 2020, 10, 4313–4318 CrossRef CAS.
- S. Wang, L. Li, J. Li, C. Yuan, Y. Kang, K. S. Hui, J. Zhang, F. Bin, X. Fan and F. Chen, et al. , J. Phys. Chem. C, 2021, 125, 7155–7165 CrossRef CAS.
- J. Long, X. Fu and J. Xiao, J. Mater. Chem. A, 2020, 8, 17078–17088 RSC.
- Y. Guo, G. Wang, S. Shen, G. Wei, G. Xia and J. Zhang, Appl. Surf. Sci., 2021, 550, 149283 CrossRef CAS.
- X. Liu, Y. Jiao, Y. Zheng, M. Jaroniec and S.-Z. Qiao, J. Am. Chem. Soc., 2019, 141, 9664–9672 CrossRef CAS PubMed.
- Z. Wang, B. Yang, Y. Wang, Y. Zhao, X.-M. Cao and P. Hu, Phys. Chem. Chem. Phys., 2013, 15, 9498–9502 RSC.
- S. Vijay, G. Kastlunger, K. Chan and J. K. Nørskov, J. Chem. Phys., 2022, 156, 231102 CrossRef CAS PubMed.
- C. Li, X. Liu, F. Xu, D. Wu, H. Xu and G. Fan, Electrochim. Acta, 2022, 426, 140764 CrossRef CAS.
- P. Ma, C. Feng, Y. Kong, D. Wang, M. Zuo, S. Wang, R. Wang, L. Kuang, X. Ding and S. Zhou, et al. , Chem Catal., 2022, 2, 2764–2777 CrossRef CAS.
- R. Hu, Y. Yu, Y. Li, Y. Wang, J. Shang, Y. Nie and X. Jiang, Nano Res., 2022, 15, 8656–8664 CrossRef CAS.
- Y. Wang, R. Hu, Y. Li, F. Wang, J. Shang and J. Shui, Nano Res., 2022, 15, 1054–1060 CrossRef CAS.
- P. Sun, Z. Qiao, S. Wang, D. Li, X. Liu, Q. Zhang, L. Zheng, Z. Zhuang and D. Cao, Angew. Chem., 2023, 135, e202216041 CrossRef.
- Z. Xue, X. Zhang, J. Qin and R. Liu, Nano Energy, 2021, 80, 105527 CrossRef CAS.
- C. Ling, Y. Ouyang, Q. Li, X. Bai, X. Mao, A. Du and J. Wang, Small Methods, 2019, 3, 1800376 CrossRef.
- M. Wang, T. Wang, P. Cai and X. Chen, Small Methods, 2019, 3, 1900025 CrossRef.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC.
- C. Deng, Y. Su, F. Li, W. Shen, Z. Chen and Q. Tang, J. Mater. Chem. A, 2020, 8, 24563–24571 RSC.
- S. Kapse, N. Barman and R. Thapa, Carbon, 2023, 201, 703–711 CrossRef CAS.
- X. Zhu, J. Yan, M. Gu, T. Liu, Y. Dai, Y. Gu and Y. Li, J. Phys. Chem. Lett., 2019, 10, 7760–7766 CrossRef CAS PubMed.
- X. Wan, Z. Zhang, H. Niu, Y. Yin, C. Kuai, J. Wang, C. Shao and Y. Guo, J. Phys. Chem. Lett., 2021, 12, 6111–6118 CrossRef CAS PubMed.
- V. Fung, G. Hu, Z. Wu and D.-E. Jiang, J. Phys. Chem. C, 2020, 124, 19571–19578 CrossRef CAS.
- S. Zhang, S. Lu, P. Zhang, J. Tian, L. Shi, C. Ling, Q. Zhou and J. Wang, Energy Environ. Mater., 2023, 6, e12304 CrossRef CAS.
- M. Umer, S. Umer, M. Zafari, M. Ha, R. Anand, A. Hajibabaei, A. Abbas, G. Lee and K. S. Kim, J. Mater. Chem. A, 2022, 10, 6679–6689 RSC.
- D. Newns, Phys. Rev., 1969, 178, 1123 CrossRef CAS.
- S. Jiao, X. Fu and H. Huang, Adv. Funct. Mater., 2022, 32, 2107651 CrossRef CAS.
- G. Jones, T. Bligaard, F. Abild-Pedersen and J. K. Nørskov, J. Phys.: Condens. Matter, 2008, 20, 064239 CrossRef CAS PubMed.
- H. Niu, X. Wang, C. Shao, Y. Liu, Z. Zhang and Y. Guo, J. Mater. Chem. A, 2020, 8, 6555–6563 RSC.
- W. Gao, Y. Chen, B. Li, S.-P. Liu, X. Liu and Q. Jiang, Nat. Commun., 2020, 11, 1196 CrossRef CAS PubMed.
- K. Yang, J. Zaffran and B. Yang, Phys. Chem. Chem. Phys., 2020, 22, 890–895 RSC.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef CAS.
- Q. Zhang, P.-A. Hu, Z.-Y. Xu, B.-B. Tang, H.-R. Zhang, Y.-H. Xiao and Y.-C. Wu, Nanoscale, 2023, 15, 4991–5000 RSC.
- U. K. Singh and M. A. Vannice, Appl. Catal., A, 2001, 213, 1–24 CrossRef CAS.
- N. Singh and C. T. Campbell, ACS Catal., 2019, 9, 8116–8127 CrossRef CAS.
- S. Liu, M. G. White and P. Liu, J. Phys. Chem. C, 2016, 120, 15288–15298 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- P. Suppan, J. Chem. Soc. A, 1968, 3125–3133 RSC.
- F. Calle-Vallejo, A. Krabbe and J. M. Garca-Lastra, Chem. Sci., 2017, 8, 124–130 RSC.
- S. Mukherjee and M. A. Vannice, J. Catal., 2006, 243, 131–148 CrossRef CAS.
- H. Wang, Y. Wang, Y. Li, X. Lan, B. Ali and T. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 34021–34031 CrossRef CAS PubMed.
- H. Cao, G.-J. Xia, J.-W. Chen, H.-M. Yan, Z. Huang and Y.-G. Wang, J. Phys. Chem. C, 2020, 124, 7287–7294 CrossRef CAS.
- W. Zhang, F.-L. Sun, Q.-J. Fang, Y.-F. Yu, J.-K. Pan, J.-G. Wang and G.-L. Zhuang, J. Phys. Chem. C, 2022, 126, 2349–2364 CrossRef CAS.
- P. A. Dub and J. C. Gordon, ACS Catal., 2017, 7, 6635–6655 CrossRef CAS.
- Q. Li, Y. Ouyang, S. Lu, X. Bai, Y. Zhang, L. Shi, C. Ling and J. Wang, Chem. Commun., 2020, 56, 9937–9949 RSC.
- Y. Basdogan, A. M. Maldonado and J. A. Keith, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1446 CAS.
- J. J. Varghese and S. H. Mushrif, React. Chem. Eng., 2019, 4, 165–206 RSC.
- Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. Koper and F. Calle-Vallejo, Importance of solvation for the accurate prediction of oxygen reduction activities of Pt-based electrocatalysts, 2017 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- D. M. Chipman, Theor. Chem. Acc., 2002, 107, 80–89 Search PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- G. Norjmaa, G. Ujaque and A. Lledós, Top. Catal., 2022, 65, 118–140 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- M. Fishman, H. L. Zhuang, K. Mathew, W. Dirschka and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245402 CrossRef.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- R. B. Sunoj and M. Anand, Phys. Chem. Chem. Phys., 2012, 14, 12715–12736 RSC.
- J. R. Pliego Jr and J. M. Riveros, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1440 Search PubMed.
- J. A. Gauthier, C. F. Dickens, H. H. Heenen, S. Vijay, S. Ringe and K. Chan, J. Chem. Theory Comput., 2019, 15, 6895–6906 CrossRef CAS PubMed.
- J. Zhang, H. Zhang, T. Wu, Q. Wang and D. van der Spoel, J. Chem. Theory Comput., 2017, 13, 1034–1043 CrossRef CAS PubMed.
- M. M. Montemore, O. Andreussi and J. W. Medlin, J. Chem. Phys., 2016, 145, 074702 CrossRef PubMed.
- S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003 CrossRef.
- R. Iftimie, P. Minary and M. E. Tuckerman, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6654–6659 CrossRef CAS PubMed.
- Z. Wang and E. H. Sargent, Matter, 2021, 4, 12–14 CrossRef CAS.
- H. Zhang, J. Li, S. Xi, Y. Du, X. Hai, J. Wang, H. Xu, G. Wu, J. Zhang and J. Lu, et al. , Angew. Chem., 2019, 131, 15013–15018 CrossRef.
- J. Gu, C.-S. Hsu, L. Bai, H. M. Chen and X. Hu, Science, 2019, 364, 1091–1094 CrossRef CAS PubMed.
- K. Lakshmanan, W.-H. Huang, S. A. Chala, B. W. Taklu, E. A. Moges, J.-F. Lee, P.-Y. Huang, Y.-C. Lee, M.-C. Tsai and W.-N. Su, et al. , Adv. Funct. Mater., 2022, 32, 2109310 CrossRef CAS.
- Y. G. Abashkin, J. R. Collins and S. K. Burt, Inorg. Chem., 2001, 40, 4040–4048 CrossRef CAS PubMed.
- W. Orellana, J. Phys. Chem. C, 2013, 117, 9812–9818 CrossRef CAS.
- W. Liu, L. Zhang, X. Liu, X. Liu, X. Yang, S. Miao, W. Wang, A. Wang and T. Zhang, J. Am. Chem. Soc., 2017, 139, 10790–10798 CrossRef CAS PubMed.
- W. Zhong, Y. Qiu, H. Shen, X. Wang, J. Yuan, C. Jia, S. Bi and J. Jiang, J. Am. Chem. Soc., 2021, 143, 4405–4413 CrossRef CAS PubMed.
- G. Yang, J. Zhu, P. Yuan, Y. Hu, G. Qu, B.-A. Lu, X. Xue, H. Yin, W. Cheng and J. Cheng, et al. , Nat. Commun., 2021, 12, 1734 CrossRef CAS PubMed.
- Y.-N. Gong, W. Zhong, Y. Li, Y. Qiu, L. Zheng, J. Jiang and H.-L. Jiang, J. Am. Chem. Soc., 2020, 142, 16723–16731 CrossRef CAS PubMed.
- A. M. Verma, K. Honkala and M. M. Melander, Front. Energy Res., 2021, 388, 606742 CrossRef.
- K. Sakaushi, M. Eckardt, A. Lyalin, T. Taketsugu, R. J. Behm and K. Uosaki, ACS Catal., 2018, 8, 8162–8176 CrossRef CAS.
- Y. Li, Z. Qiao, Y. Cao, H. Wang, H. Liang, H. Yu and F. Peng, ChemSusChem, 2019, 12, 1133–1138 CrossRef CAS PubMed.
- K. Sun, W. Xu, X. Lin, S. Tian, W.-F. Lin, D. Zhou and X. Sun, Adv. Mater. Interfaces, 2021, 8, 2001360 CrossRef CAS.
- Y. Li, S. Zhang, J. Yu, Q. Wang, Q. Sun and P. Jena, Nano Res., 2015, 8, 2901–2912 CrossRef CAS.
- J. C. Peters, Faraday Discuss., 2023, 243, 450–472 RSC.
- R. E. Warburton, P. Hutchison, M. N. Jackson, M. L. Pegis, Y. Surendranath and S. Hammes-Schiffer, J. Am. Chem. Soc., 2020, 142, 20855–20864 CrossRef CAS PubMed.
- P. Hutchison, R. E. Warburton, Y. Surendranath and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2022, 13, 11216–11222 CrossRef CAS PubMed.
- Q. Wu, G. Wang and M. Liu, ChemPhysChem, 2022, 23, e202100787 CrossRef CAS PubMed.
- K. Liu, J. Fu, Y. Lin, T. Luo, G. Ni, H. Li, Z. Lin and M. Liu, Nat. Commun., 2022, 13, 2075 CrossRef CAS PubMed.
- T. Lin, W.-D. Zhang, J. Huang and C. He, J. Phys. Chem. B, 2005, 109, 13755–13760 CrossRef CAS PubMed.
- F. Gao, G.-L. Zhao, S. Yang and J. J. Spivey, J. Am. Chem. Soc., 2013, 135, 3315–3318 CrossRef CAS PubMed.
- I.-H. Lin, Y.-H. Lu and H.-T. Chen, J. Comput. Chem., 2017, 38, 2041–2046 CrossRef CAS PubMed.
- E. Shakerzadeh, H. Hamadi and M. D. Esrafili, Inorg. Chem. Commun., 2019, 106, 190–196 CrossRef CAS.
- B. Modak, K. Srinivasu and S. K. Ghosh, Int. J. Hydrogen Energy, 2017, 42, 2278–2287 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |
