Fusing a machine learning strategy with density functional theory to hasten the discovery of 2D MXene-based catalysts for hydrogen generation†
B. Moses
Abraham‡
 a,
Priyanka
Sinha‡
a,
Prosun
Halder
a and
Jayant K.
Singh
a,
Priyanka
Sinha‡
a,
Prosun
Halder
a and
Jayant K.
Singh
 *ab
*ab
aDepartment of Chemical Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India. E-mail: jayantks@iitk.ac.in
bPrescience Insilico Private Limited, Bangalore 560049, India
First published on 14th March 2023
Abstract
The complexity of the topological and combinatorial configuration space of MXenes can give rise to gigantic design challenges that cannot be addressed through traditional experimental or routine theoretical methods. To this end, we establish a robust and more broadly applicable multistep workflow using supervised machine learning (ML) algorithms to construct well-trained data-driven models for predicting the hydrogen evolution reaction (HER) activity of 4500 MM′XT2-type MXenes, where 25% of the materials space (1125 systems) is randomly selected to evaluate the HER performance using density functional theory (DFT) calculations. As the most desirable ML model, the gradient boosting regressor (GBR) processed with recursive feature elimination (RFE), hyperparameter optimization (HO) and the leave-one-out (LOO) approach accurately and rapidly predicts the Gibbs free energy of hydrogen adsorption (ΔGH) with a low predictive mean absolute error (MAE) of 0.358 eV. Based on these observations, the H atoms adsorbed directly on top of the outermost metal-atom layer of the MM′XT2-type MXenes (site 1) with Nb, Mo and Cr metals with O functionalization are discovered to be highly stable and active for catalysis, surpassing commercially available platinum-based counterparts. Overall, the physically meaningful predictions and insights of the developed ML/DFT-based multistep workflow will open new avenues for accelerated screening, rational design and discovery of potential HER catalysts.
1 Introduction
Growing concerns about environmental problems and the energy crisis demand the urgent development of affordable and clean renewable energy sources as a viable replacement for fossil fuels. In this regard, electrochemical water splitting is an effective and sustainable approach to generate a massive impact in clean-energy technologies.1–3 However, the currently-used platinum group metals (PGMs) are expensive, which limits their large-scale applications, thereby promoting continuous research attempts toward highly active non-noble metal electrocatalysts. Several promising candidates with zero or reduced content of PGMs are being considered, such as transition metals4 and their dichalcogenides,5–8 phosphides,9 nitrides,10 borides11 and carbides,12 and metal-free carbon nitrides.13,14 Although extensive experimental and theoretical studies have demonstrated the usage of such catalysts in the hydrogen evolution reaction (HER), the overall catalytic activity for large-scale hydrogen production is still limited by their few active sites and poor electrical transport.15 Therefore, it is of paramount significance to develop a broad range of catalytic materials with more active sites and higher conductivity, for which a fundamental understanding from an atomic-scale point of view is highly essential.MXenes, unique accordion-like structures exfoliated from MAX phases (M = transition metal; A = p-block element; X = C and/or N), have recently attracted significant attention for electronic device,16–19 electromagnetic shielding,20 electrocatalysis,21–24 and energy storage and conversion25–30 applications. In particular, the long-term structural stability in acidic electrolytes,31 large active surface area (21 m2 g−1)32 and high electrical conductivity (4600 ± 1100 S cm−1)33 make them suitable candidates for HER catalysis. In MXenes (Mn+1XnTx; n = 1, 2, 3), tuning of M (transition metal), X (C and/or N) and T (surface functionalization) is found to improve the hydrogen evolution activity.34 For instance, variation of the transition metal atoms in Mn+1XnTx (Mn+1XnO2, M2M′X2O2, and M2M′2X3O2) led to the identification of 110 unexplored candidates with better HER performance.35 Sun et al.36 screened 271 different configurations of Mn+1Xn by tuning X from C to B and found that Mn/Co2B2, Os/Co2B2, Co2B2, Pt/Ni2B2 and Co/Ni2B2 candidates surpass the HER activity of PGMs. Doping of P-group elements (surface functionalization) modulates the in-plane surface atom activity and improves the HER performance, thereby leading to an optimal HER Gibbs free energy.37 MXenes can also be used as substrates in HER applications because of their adjustable surface structures as well as promising physicochemical properties.38,39 In such cases, the performance of Ti2CO2 at various hydrogen coverages is found to improve with doping of S atoms to substitute the surface O atoms.40 NiS2@VMXene exhibits long-term durability and low HER overpotential.35 The aforementioned configurational space offered by the broad range of MXenes and their active sites makes using traditional approaches for optimization of catalysts via experimental and theoretical screening particularly challenging, time-consuming and expensive. Thus, finding suitable advanced methods has become an essential task for accelerating the rational design of efficient catalysts.
The screening of potential MXene-based catalysts from their tremendous combinatorial and structural space requires a huge amount of computational resources.41 In traditional routine simulations, the H-adsorption energy is typically the most important parameter in evaluating the HER activity.42 According to the Sabatier principle, the binding of hydrogen should be neither too strong nor too weak to obtain the best catalytic activity.43 However, direct simulations of this might not provide complete information regarding HER performance since the descriptors of various reaction processes are equally important. In this regard, the incorporation of physical interaction through scientific knowledge into models trained by data-driven approaches has gradually emerged as a powerful and reliable tool for hastening the identification of catalysts.44–46 In particular , random forest regression, support vector regression (SVR), kernel ridge regression and Elman artificial neural network (Elman ANN) algorithms are typically employed to predict Gibbs free energy, which is a widely accepted descriptor of HER activity. For instance, the regularized random forest learning method reveals the Ni–Ni bond length to be the primary feature in determining the binding strength of hydrogen on the Ni2P (0001) plane.47 Sun et al.48 predicted the HER performance of graphdyine-based atomic catalysts using the bag-tree learning model. These results demonstrate that machine learning (ML) models not only allow discovery of novel catalyst materials, but also provide an in-depth understanding of the fundamental correlation between the catalytic structures and their properties. This is highly essential to modify the strategies for developing new design principles in improving the electrocatalytic efficiency.
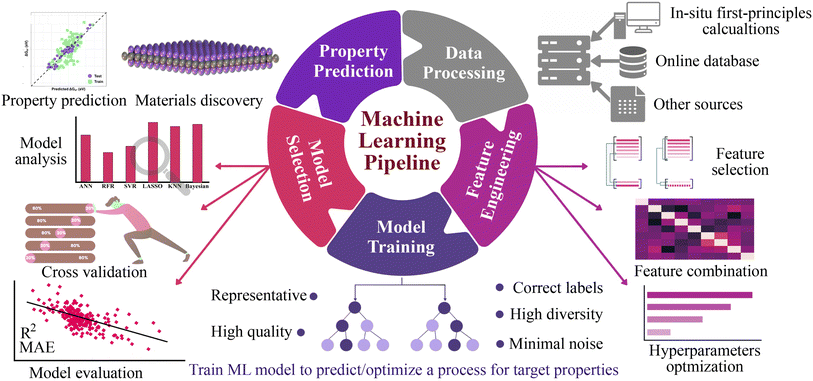
Here, we explore a robust and more broadly applicable multistep workflow, as shown in Fig. 1, where the ab initio adsorption properties are combined with supervised machine learning algorithms for the source, verification and predictions. For this purpose, a data set of 4500 MM′XT2-type MXenes was constructed and their HER performance was systematically investigated. Among them, 1125 systems (25% of the materials space) were randomly selected for evaluation of their HER activity using density functional theory (DFT) calculations as well as to train the ML model. Predominating indicators were then employed to build an interpretable ML model that predicts the HER performance of the remaining 85% of the materials space. Overall, the ML model achieves better prediction activity, on par with first-principles calculations. It deciphers the underlying factors that govern the HER performance and provides a coherent path to investigate a large number of MXene configurations.
2 Methods
2.1 Density functional theory
Ab initio simulations were performed using plane-wave-based Vienna ab initio simulation package (VASP) code within the framework of density functional theory. The exchange correlation effects and ion–electron interactions were incorporated through the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA) functional and projected augmented wave (PAW) method, respectively. For structural relaxation, the convergence thresholds of 10−2 eV Å−1 force and 10−5 eV energy, with a cutoff energy and Monkhorst–Pack method k-point grid of 450 eV and 7 × 7 × 1, respectively, were employed to expand the electron wave functions and sample the Brillouin zone. A vacuum space of 15 Å was adopted along the z-direction to prevent spurious interaction between the periodic units. Grimme’s empirical correction scheme (DFT + D3) was adopted to describe the van der Waals interactions.The hydrogen adsorption Gibbs free energy (ΔGH) was defined based on the computational hydrogen electrode (CHE) model54 as follows:
| ΔGH = ΔEH + ΔEZPE − TΔS | (1) |
 | (2) |
The cohesive energy (Ecoh), which is a measure of the total energy of the system extracted from the sum of the individual constituent atom energies, can be used to determine the structural stability by understanding the strength of the forces that bind the atoms together in a system and is defined as follows:
| Ecoh = Etotal − NEM − NEM′ − NEX − NET | (3) |
 .
.
2.2 Feature space construction
To establish accurate ML models or to evaluate the main contributions controlling the hydrogen evolution reaction, it is important to map the material-to-attribute connection. In view of this, a group of features (materials variables) that represent a system in a computationally friendly manner is highly required. Typically, an ideal feature set reveals the structure–activity relationships of a system and specifically describes each materials input data set. However, materials representations are an area of complex and intense development, where their explicit interpretation is a significant challenge when compared with the success recently attained for molecular representations.55,56 Thus, it is very important to generate suitable and comprehensive features during the construction of ML models. For easy training of an efficient and fast ML model, every selected feature has to independently represent the physicochemical properties. For this purpose, we have considered atomistic, structural and electronic indicators as an initial pool of descriptors, leading to a total of 60 primary features, as shown in Table S1.† Nevertheless, the selected primary features were unable to capture the HER performance due to different numbers of constituent atoms that have different feature space sizes. To this end, statistical measures of some selected primary features were considered, including average, weighted average, maximum, minimum, standard deviation, variance, and squared values (see Table S2†). Feature addition using statistical functions increased the features to 125. These features are categorized into Set 1 (atomistic features), Set 2 (surface features) and Set 3 (statistical features) and their corresponding subset combinations are employed to identify the key descriptors. The considered descriptors may not provide complete information about the fundamental physicochemical principles. However, from a pragmatic outlook, their predictions can be used as an indicator to understand the importance of variables that influence the property of interest, thereby establishing a potential practical model to solve this complicated problem.2.3 Machine learning
Our ML approach is designed for establishing a regression relationship between the HER catalytic activity and predominating indicators, based on the results from DFT calculations. Nine ML algorithms, namely the AdaBoost regressor (ABR), elastic net regressor (ENR), gradient boosting regressor (GBR), K neighbors regressor (KNR), kernel ridge regressor (KRR), lasso (LAS), partial least squares (PLS), random forest regressor (RFR) and ridge regression (RDG) were employed to predict the HER performance. An open-source Python distribution platform was used to train the models via scikit-learn libraries. 25% of the materials space (1125 systems) was randomly selected to evaluate the HER performance using DFT calculations, while the activity of the remaining 75% of the materials space was predicted through the well-trained ML model. To ensure the accuracy and generalization of the supervised ML models, the H binding energy data obtained from DFT-calculations were randomly partitioned into training and test sets in an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio. The stability and accuracy of all models were evaluated through the coefficient of determination (R2) and mean absolute error (MAE), with standard deviations indicated, and the formulae are:
20 ratio. The stability and accuracy of all models were evaluated through the coefficient of determination (R2) and mean absolute error (MAE), with standard deviations indicated, and the formulae are: | (4) |
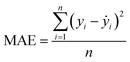 | (5) |
2.4 General workflow
The general workflow of the DFT-ML hybrid scheme for the prediction of potential HER catalysis by MXenes is depicted in Fig. 1. The first step involves data preprocessing to construct a data set of 4500 MM′XT2-type MXenes. The DFT calculations were then performed to predict the target property of hydrogen adsorption Gibbs free energy (ΔGH) for the 1125 configurations that were randomly selected from the data set. Subsequently, the data underwent feature engineering to produce a unique collection of machine learning descriptors that cover the entire materials design space, which includes atomistic, structural and electronic indicators. Various ML algorithms were then trained and the best two models were selected based on the cross-validation (train/test) score. The accuracy of the developed ML model was further improved by recursive feature elimination (RFE), hyperparameter optimization (HO), and the leave-one-out (LOO) approach. Using the best-performing model, we predicted the catalytic properties of the remaining configurations (3375 MM′XT2-type MXenes) that were not included in the training data. Finally, analysing these results helped identify the key descriptors that govern the HER activity of MXenes.3 Results and discussion
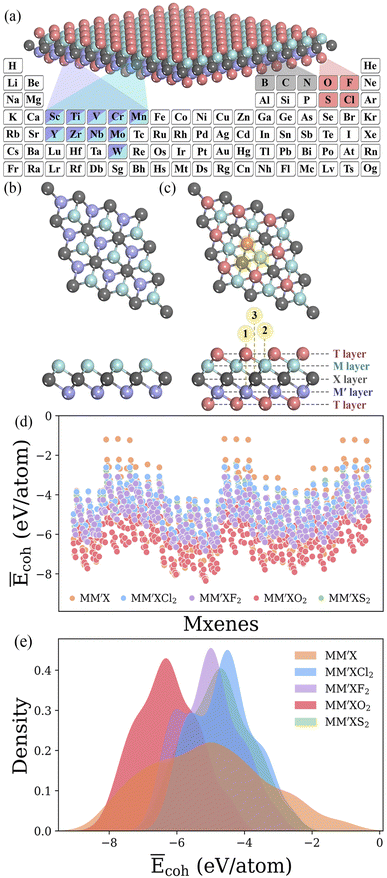
MM′XT2-type (M/M′ = Sc, Ti, V, Cr, Mn, Y, Zr, Nb, Mo or W; X = B, C or N; T = O, F, Cl or S) MXenes were constructed with quintuple atomic layers of T–M–X–M′–T, where the X layers are alternately sandwiched between different metal layers (M/M′) and the surfaces are terminated with functional groups (T), as shown in Fig. 2a–c. Possible combinations of metal layers were then considered to generate 1500 MM′XT2-type MXenes. Initially, we evaluated the cohesive energies to understand the stability trends of these configurations. The computed normalized cohesive energies Ēcoh (eV per atom) and corresponding distributions of the various functionalized MXenes are shown in Fig. 2d and e. From the viewpoint of functionalization, the lowest Ēcoh is obtained for –O terminated MXenes when compared with the other terminations, –F, –Cl and –S, which indicates that –O is more likely to be synthesized during experimentation. Moreover, the structural stability of the terminated MXenes increases in the order of MM′X < MM′XCl2 < MM′XS2 < MM′XF2 < MM′XO2, showing better stability for fully functionalized MXenes with respect to their pristine counterpart. This observed behavior also confirms why MXenes are usually terminated with functional groups during experimental synthesis.49 In addition, the Ēcoh values of MM′CT2 are lower than those of MM′BT2 and MM′NT2, suggesting that carbon-based MXenes are more stable than boride- and nitride-based MXenes (see Fig S1a and b†). This also provides an alternative explanation for the poor stability of boride- and nitride-based MXenes during etching in their synthesis process.50,513.1 Adsorption energy distribution
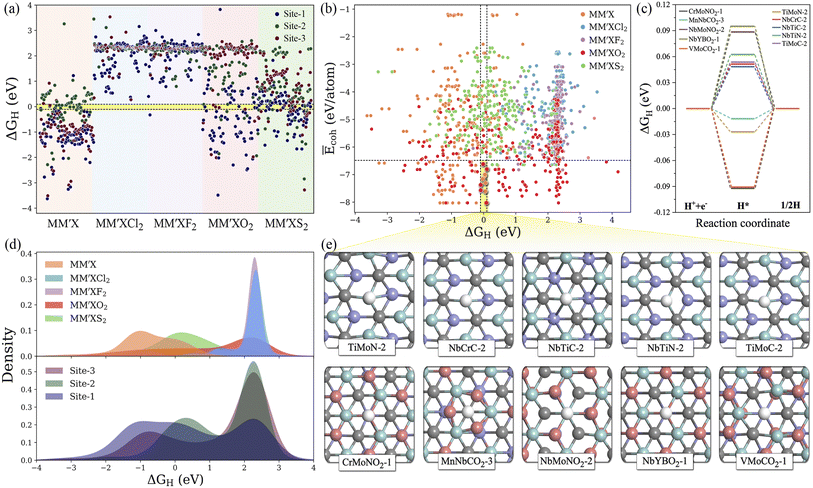
Typically, the availability of active catalytic sites on the surface of MXenes is highly required to carry out the HER: the larger the number of active sites on the surface, the stronger the catalytic performance will be. There are three possible adsorption sites available on MXene surfaces for hydrogen adsorption. Site 1 has the H atom adsorbed directly on the innermost metal-atom layer of the MXene, site 2 has the H atom adsorbed on top of the outermost M atom of the MXene and site 3 has the H atom adsorbed directly above the X atom of the MXene structure. Overall, the adsorption of the H atom on the three available active sites of the 1500 MM′XT2-type MXenes leads to 4500 configurations. Among them, 1125 systems (25% of the materials space) were randomly selected to evaluate the HER activity using DFT calculations as well as to train the ML models, while the catalytic performance of the rest of the materials was predicted using the well-trained ML model. Based on the computational hydrogen electrode (CHE) model,52 the Gibbs free energy of the adsorbed hydrogen (ΔGH) is a universal indicator to evaluate the HER performance. Accordingly, a |ΔGH| close to zero signifies prominent HER activity of the catalyst, while a negative or positive ΔGH, indicating too strong or too weak adsorption, will tend to reduce the overall reaction rate. The HER performance is highly dependent on functionalization (see Fig. 3a–e and S2†); for instance, most of the F- and Cl-terminated MXenes exhibit poor HER activity due to their highly positive ΔGH, indicating a weak interaction between the adsorbed H and F- and Cl-groups on the MXene surfaces. There is even a significant difference in HER activity when varying the X layers, where the carbon-based MXenes with |ΔGH| smaller than 0.1 eV show better HER performance when compared to boride- and nitride-based MXenes. Overall, 48 systems show optimal ΔGH values in the range of −0.1 to 0.1 eV. Among them, CrMoNO2-1, MnNbCO2-3, NbMoNO2-3, NbYBO2-1, VMoCO2-1, TiMoN-2, NbCrC-2, NbTiC-2, NbTiN-2 and TiMoC-2 have better stability and superior HER activities when compared with the noble metal Pt53 and thus can be considered as promising HER catalysts. These results reveal that the HER activity also depends on the active site where the H is adsorbed. It is found that the H adsorbed directly on the outermost metal-atom layer of the MXene structure (site 2) has better HER catalytic performance when compared with that on other sites.3.2 ML model optimization
The precision of a well-trained ML model mainly depends on the materials descriptor as well as the choice of algorithm. Historically, several aspects have been considered to be connected with the chemical reactivity of catalytic materials, such as the d-band characteristics, coordination number and bulk or atomic properties. Correlating such physical aspects with the adsorption energies using highly non-linear regression algorithms requires features from the fully optimized geometries of the pristine adsorption sites. With the selected subset of atomistic, surface and statistical features, we establish nine different ML models as shown in Table S3,† namely the ABR, ENR, GBR, KNR, KRR, LAS, PLS, RFR and RDG, using the dataset containing 1125 H-adsorption energies obtained from DFT calculations. To ensure the accuracy and generalization of the supervised ML models, we partitioned the data into training and test sets in an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
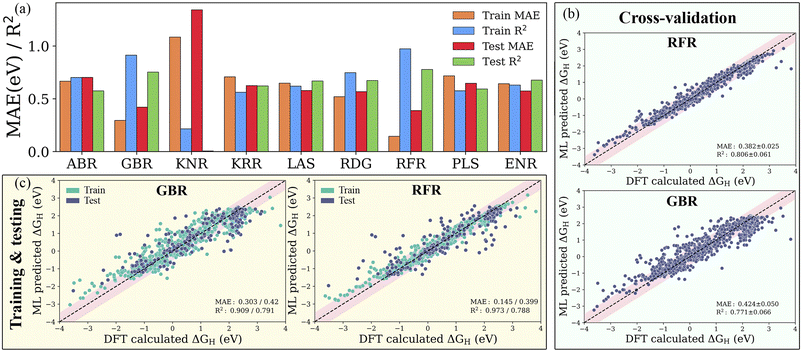
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ratio (see Fig. S3†). For controlling and assessing against overfitting, the coefficient of determination value (R2 score) and mean absolute error (MAE) were estimated with and without using the 10-fold cross-validation technique. As shown in Fig. S4 and Table S4,† the subset of features with representative physical indicators anisotropically captures the H adsorption energy on the studied MXenes. Among all the subsets of features, the combination of primary features with the indicators processed through statistical functions provides the best predictive performance. The predicted MAE and R2 of the ABR, ENR, GBR, KNR, KRR, LAS, PLS, RFR and RDG algorithms using primary and statistical function-processed features are presented in Fig. 4a. The use of the RFR model results in convergence to a low MAE with the highest R2 score, irrespective of the feature subset, thereby demonstrating its good generalization ability. Predictions by the best-performing RFR and GBR models with and without cross-validation using the DFT dataset of the hydrogen adsorption Gibbs free energies (ΔGH) are shown in Fig. 4b and c, respectively. The GBR model shows better performance with an R2 score of 0.909 (0.791) and MAE of 0.303 (0.420) eV in the model training (testing), indicating inferior accuracy prediction to the RFR model. It should be noted that these tree-based RFR and GBR ensemble models are robust for high-dimensional data sets due to the good ability to fit nonlinear data. On the other hand, the ABR, ENR, KNR, KRR, LAS, PLS and RDG methods have unsatisfactory prediction performance, which is reflected by their considerable MAEs of 0.702, 0.573, 1.342, 0.625, 0.578, 0.647 and 0.568 eV (see Table S5†), respectively, due to the poor extrapolation capabilities of the models. Using 10-fold cross-validation, the studied models exhibit similar prediction performance for the training/testing sets, as shown in Fig. S5.† These results demonstrate that the materials descriptors are crucial to reproduce the adsorption energies on MM′XT2-type MXenes, thereby validating the suitability of our feature pool. The combination of primary and statistical features achieved satisfactory prediction accuracy. Nevertheless, the presence of a large number of input features makes it difficult to readily derive physical insights, thereby increasing the complexity and time consumption in the ML model. Thus, it is important to look for a fine balance between accuracy and the number of features for obtaining efficient results.
20 ratio (see Fig. S3†). For controlling and assessing against overfitting, the coefficient of determination value (R2 score) and mean absolute error (MAE) were estimated with and without using the 10-fold cross-validation technique. As shown in Fig. S4 and Table S4,† the subset of features with representative physical indicators anisotropically captures the H adsorption energy on the studied MXenes. Among all the subsets of features, the combination of primary features with the indicators processed through statistical functions provides the best predictive performance. The predicted MAE and R2 of the ABR, ENR, GBR, KNR, KRR, LAS, PLS, RFR and RDG algorithms using primary and statistical function-processed features are presented in Fig. 4a. The use of the RFR model results in convergence to a low MAE with the highest R2 score, irrespective of the feature subset, thereby demonstrating its good generalization ability. Predictions by the best-performing RFR and GBR models with and without cross-validation using the DFT dataset of the hydrogen adsorption Gibbs free energies (ΔGH) are shown in Fig. 4b and c, respectively. The GBR model shows better performance with an R2 score of 0.909 (0.791) and MAE of 0.303 (0.420) eV in the model training (testing), indicating inferior accuracy prediction to the RFR model. It should be noted that these tree-based RFR and GBR ensemble models are robust for high-dimensional data sets due to the good ability to fit nonlinear data. On the other hand, the ABR, ENR, KNR, KRR, LAS, PLS and RDG methods have unsatisfactory prediction performance, which is reflected by their considerable MAEs of 0.702, 0.573, 1.342, 0.625, 0.578, 0.647 and 0.568 eV (see Table S5†), respectively, due to the poor extrapolation capabilities of the models. Using 10-fold cross-validation, the studied models exhibit similar prediction performance for the training/testing sets, as shown in Fig. S5.† These results demonstrate that the materials descriptors are crucial to reproduce the adsorption energies on MM′XT2-type MXenes, thereby validating the suitability of our feature pool. The combination of primary and statistical features achieved satisfactory prediction accuracy. Nevertheless, the presence of a large number of input features makes it difficult to readily derive physical insights, thereby increasing the complexity and time consumption in the ML model. Thus, it is important to look for a fine balance between accuracy and the number of features for obtaining efficient results.
3.3 Feature elimination and hyperparameter optimization
Identifying the most representative descriptors is an extremely critical step for feature engineering to minimize prediction biasing and increase the efficiency of the ML model. For this purpose, recursive feature elimination (RFE) is used to filter the descriptors with extreme asymmetry (skewness) and with low/zero variance for recognizing a more suitable and smaller subset of features. In addition, hyperparameter optimization (HO) was performed on the RFR and GBR models by varying the range of parameters using 10-fold cross-validation; the best combinations of hyperparameters are presented in Table S6.† RFE decreased the number of features from 125 to 24 and 30 for the RFR and GBR, respectively. Subsequently, a leave-one-out (LOO)57 approach with 20-fold cross-validation was utilized to further reduce the number of features. The leave-one-out approach decreased the 24 features obtained from RFE to 15 descriptors for the RFR model with a low predictive mean absolute error of 0.367 eV. Using the same approach for the GBR model, the descriptors were reduced from 30 to 19 and the MAE was further improved to 0.358 eV (see Fig. 5a, S6–S8 and Table S7†). This demonstrates that the GBR model is slightly more suitable and the best algorithm in our multistep ML workflow. However, by splitting the data into smaller subsets with similar configurations, we found that the MAE decreased significantly, for instance, to 0.195 eV (0.193 eV) for MXenes functionalized with Cl and F for the final RFR (GBR) model. This indicates that the MAE for a smaller subset of MXenes with particular functionalization is very low. Additionally, it has been determined that the reduced set of features is sufficient for capturing the complex interactions influencing the Gibbs free energies, where the further removal of any feature leads to a relative decrease in the efficacy of the model. The Pearson correlation coefficient (PCC) heat map, which measures the linear relationship between two variables, is shown in Fig. 5b. Here, a positive correlation indicates that the two features tend to decrease or increase together, while a negative correlation means that one feature tends to decrease while the other increases. In addition, a high ranking of a descriptor indicates a vital role in governing the HER activity of MXenes; for example, the number of valence electrons of the terminating groups (VT) predominately affects the adsorption ability of H atom. As the typical descriptor sets generated from the RFE–HO–LOO process vary with the RFR and GBR models, we particularly identified common potential descriptors that precisely relate to the physicochemical properties of MXenes. Subsequently, the number of valence electrons (VT) and electron affinity (EAT) of the terminating groups and d-band center variance with respect to the average (dbcσ2) were identified as the strong key predictors of the Gibbs free energy (see Fig. 5c, S9 and Tables S8 and S9†). Overall, the feature importance based on the mean decrease in impurity indicates that features with a high score could have more importance in making accurate predictions.3.4 Performance prediction of the unknown space
After developing the well-trained model, the best-performing GBR and RFR strategies with RFE–HO–LOO were further applied to the remaining 3375 MM′XT2-type MXenes to predict the HER activity. As mentioned, the well-trained GBR model with RFE–HO–LOO through cross-validation has an MAE of 0.358 for the randomly selected 25% of the materials space (1125 systems). Thus, the optimal ΔGH values for the remaining ML-predicted materials’ space were set as −0.458 eV (−0.1 − 0.358) to 0.458 eV (0.1 + 0.358). Fig. 5d presents the ΔGH for the complete list of MM′XT2-type MXenes using the well-trained ML methodology. Clearly, the ΔGH is anisotropically distributed over a large energy scale ranging from 2.75 to −2.94 eV, indicating the substantial heterogeneity of the active sites. Out of the 4500 MM′XT2-type MXenes, 30 candidates show an optimal ΔGH, which signifies excellent HER catalyst activity (see Table S10†). Similar to the DFT-computed results, the thermodynamic increase in the proton adsorption energies on F- and Cl-functionalized MXenes suppresses the hydrogen production activity, while O termination gives more optimal ΔGH values. These results reveal that the HER activity mainly depends on the type of functionalization. In addition, the type of active site also influences the catalytic activity, where site 1 (site 2) is found to exhibit efficient HER performance for O-terminated (pure) MXenes (see Fig. S10a–c†). In a broader context, our calculation results indicate that the H adsorbed on site 1 with O functionalization can make MM′XT2-type MXenes suitable for enhancing HER activity.4 Conclusion
In the present work, we have developed a multistep workflow for rapid and accurate ΔGH predictions of 4500 MM′XT2-type MXenes, from which 1125 systems were randomly selected as the training samples to evaluate the HER performance using DFT calculations. These MXenes show high structural stability; in particular, O-terminated structures are highly preferable and more likely to be synthesized during experimentation. The DFT results demonstrate that hydrogen adsorbed directly on the outermost metal-atom layer of the MXene structures (site 2) is beneficial to enhancing the HER performance. Predominating indicators were then employed to build interpretable ML models, where the Gradient Boosting Regressor (GBR) algorithm with RFE–HO–LOO parameterization showed the best predictive performance towards ΔGH with a low MAE and high R2 of 0.358 eV and 0.826, respectively. These results demonstrate that the materials descriptors are crucial to reproducing the adsorption energies on MM′XT2-type MXenes, thereby validating the suitability of our feature pool. The feature importance analysis revealed the number of valence electrons (VT) and electron affinity (EAT) of the terminating groups, and the d-band center variance with respect to the average (dbcσ2) to be key descriptors that govern the HER performance. The well-trained GBR model was then used to predict the HER activity of the remaining materials space and we found that the metal layers of MM′XT2-type MXenes with O-terminated Nb, Mo and Cr show high stability and better HER activity. Overall, the present work not only establishes a robust and more broadly applicable ML–DFT-based multistep workflow for efficient and accurate screening of HER activity but also provides potential factors that govern the efficiency of the catalysts, thereby accelerating the design and development of novel catalysts with high performance.Code availability
The code can be retrieved from our GitHub repository (https://github.com/cnislab/MXenes4HER). Several python libraries are employed in the current work: pandas to analyse the dataset, scikit-learn to build the regression models, Joblib to save the best models, and Matplotlib together with Seaborn to visualize the plots.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work is supported by the Department of Science and Technology, Government of India, under grant number SPO/DST/CHE/2021535. BMA would like to thank the SERB for the financial support under grant number PDF/2021/000487. We acknowledge the National Supercomputing Mission (NSM) for providing computing resources via PARAM Sanganak at IIT Kanpur.References
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 0003 CrossRef CAS.
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473 CrossRef CAS PubMed.
- J. R. McKone, B. F. Sadtler, C. A. Werlang, N. S. Lewis and H. B. Gray, ACS Catal., 2013, 3, 166–169 CrossRef CAS.
- J. Yang, D. Voiry, S. J. Ahn, D. Kang, A. Y. Kim, M. Chhowalla and H. S. Shin, Angew. Chem., Int. Ed., 2013, 52, 13751–13754 CrossRef CAS PubMed.
- D. Voiry, H. Yamaguchi, J. Li, R. Silva, D. C. B. Alves, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nat. Mater., 2013, 12, 850–855 CrossRef CAS PubMed.
- Z. Chen, D. Cummins, B. N. Reinecke, E. Clark, M. K. Sunkara and T. F. Jaramillo, Nano Lett., 2011, 11, 4168–4175 CrossRef CAS PubMed.
- J. Xie, H. Zhang, S. Li, R. Wang, X. Sun, M. Zhou, J. Zhou, X. W. D. Lou and Y. Xie, Adv. Mater., 2013, 25, 5807–5813 CrossRef CAS PubMed.
- Y. Feng, X. Y. Yu and U. Paik, Chem. Commun., 2016, 52, 1633–1636 RSC.
- B. F. Cao, G. M. Veith, J. C. Neuefeind, R. R. Adzic and P. G. Khalifah, J. Am. Chem. Soc., 2013, 135, 19186–19192 CrossRef CAS PubMed.
- H. Vrubel and X. Hu, Angew. Chem., Int. Ed., 2012, 51, 12703–12706 CrossRef CAS PubMed.
- W.-H. Chen, C. H. Wang, K. Sasaki, N. Marinkovic, W. Xu, J. T. Muckerman, Y. Zhu and R. R. Adzic, Energy Environ. Sci., 2013, 6, 943–951 RSC.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- S. Meng, B. Li, S. Li and S. Yang, Mater. Res. Express, 2017, 4, 055602 CrossRef.
- Q. Tang and D. E. Jiang, ACS Catal., 2016, 6, 4953–4961 CrossRef CAS.
- A. Chandrasekaran, A. Mishra and A. K. Singh, Nano Lett., 2017, 17, 3290–3296 CrossRef CAS PubMed.
- M. Khazaei, A. Ranjbar, M. Arai and S. Yunoki, Phys. Rev. B, 2016, 94, 125152 CrossRef.
- C. Si, K. Jin, J. Zhou, Z. Sun and F. Liu, Nano Lett., 2016, 16, 6584–6591 CrossRef CAS PubMed.
- M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192 CrossRef CAS.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. M. Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137–1140 CrossRef CAS PubMed.
- J. Ran, G. Gao, F.-T. Li, T.-Y. Ma, A. Du and S.-Z. Qiao, Nat. Commun., 2017, 8, 1–10 CrossRef PubMed.
- Z. Li, Z. Qi, S. Wang, T. Ma, L. Zhou, Z. Wu, X. Luan, F.-Y. Lin, M. Chen, J. T. Miller, H. Xin, W. Huang and Y. Wu, Nano Lett., 2019, 19, 5102–5108 CrossRef CAS PubMed.
- Z. W. Seh, K. D. Fredrickson, B. Anasori, J. Kibsgaard, A. L. Strickler, M. R. Lukatskaya, Y. Gogotsi, T. F. Jaramillo and A. Vojvodic, ACS Energy Lett., 2016, 1, 589–594 CrossRef CAS.
- J. Zhang, Y. Zhao, X. Guo, C. Chen, C.-L. Dong, R.-S. Liu, C.-P. Han, Y. Li, Y. Gogotsi and G. Wang, Nat. Catal., 2018, 1, 985–992 CrossRef CAS.
- X. Tang, X. Guo, W. Wu and G. Wang, Adv. Energy Mater., 2018, 8, 1801897 CrossRef.
- M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall′Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Science, 2013, 341, 1502–1505 CrossRef CAS PubMed.
- M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, J. Am. Chem. Soc., 2013, 135, 15966–15969 CrossRef CAS PubMed.
- J. Zhou, X. Zha, X. Zhou, F. Chen, G. Gao, S. Wang, C. Shen, T. Chen, C. Zhi, P. Eklund, S. Du, J. Xue, W. Shi, Z. Chai and Q. Huang, ACS Nano, 2017, 11, 3841–3850 CrossRef CAS PubMed.
- V. Parey, B. M. Abraham, S. H. Mir and J. K. Singh, ACS Appl. Mater. Interfaces, 2021, 13, 35585–35594 CrossRef CAS PubMed.
- V. Parey, B. M. Abraham, M. V. Jyothirmai and J. K. Singh, Catal. Sci. Technol., 2022, 12, 2223–2231 RSC.
- P. Li, J. Zhu, A. D. Handoko, R. Zhang, H. Wang, D. Legut, X. Wen, Z. Fu, Z. W. Seh and Q. Zhang, J. Mater. Chem. A, 2018, 6, 4271–4278 RSC.
- B. Wang, A. Zhou, F. Liu, J. Cao, L. Wang and Q. Hu, J. Adv. Ceram., 2018, 7, 237–245 CrossRef CAS.
- A. Lipatov and A. Sinitskii, 2D Metal Carbides and Nitrides (MXenes), Springer International Publishing, Cham, 2019, pp. 301–325 Search PubMed.
- X. Hui, X. Ge, R. Zhao, Z. Li and L. Yin, Adv. Funct. Mater., 2020, 30, 2005190 CrossRef CAS.
- P. Kuang, M. He, B. Zhu, J. Yu, K. Fan and M. Jaroniec, J. Catal., 2019, 375, 8–20 CrossRef CAS.
- X. Sun, J. Zheng, Y. Gao, C. Qiu, Y. Yan, S. Deng and J. Wang, Appl. Surf. Sci., 2020, 526, 146522 CrossRef CAS.
- Y. Yoon, A. P. Tiwari, M. Choi, T. G. Novak, W. Song, H. Chang, T. Zyung, S. S. Lee, S. Jeon and K.-S. An, Adv. Funct. Mater., 2019, 29, 1903443 CrossRef.
- G. Gao, A. P. O′Mullane and A. Du, ACS Catal., 2017, 7, 494–500 CrossRef CAS.
- Y. Cheng, Y. Zhang, Y. Li, J. Dai and Y. Song, J. Mater. Chem. A, 2019, 7, 9324–9334 RSC.
- S. Wang, L. Chen, Y. Wu and Q. Zhang, ChemPhysChem, 2018, 19, 3380–3387 CrossRef CAS PubMed.
- B. M. Abraham, V. Parey and J. K. Singh, J. Mater. Chem. C, 2022, 10, 4096 RSC.
- M. Lopez, A. M. Garcia, F. Vines and F. Illas, ACS Catal., 2021, 11, 12850–12857 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Norskov, Nat. Mater., 2006, 5, 909 CrossRef CAS PubMed.
- O. Pique, I. Z. Koleva, A. Bruix, F. Vines, H. A. Aleksandrov, G. N. Vayssilov and F. Illas, ACS Catal., 2022, 12, 9256–9269 CrossRef CAS PubMed.
- A. Mazheika, Y.-G. Wang, R. Valero, F. Vines, F. Illas, L. M. Ghiringhelli, S. V. Levchenko and M. Scheffler, Nat. Commun., 2022, 13, 419 CrossRef CAS PubMed.
- E. Vignola, S. N. Steinmann, B. D. Vandegehuchte, D. Curulla, M. Stamatakis and P. Sautet, J. Chem. Phys., 2017, 147, 054106 CrossRef PubMed.
- R. B. Wexler, J. M. P. Martirez and A. M. Rappe, J. Am. Chem. Soc., 2018, 140, 4678–4683 CrossRef CAS PubMed.
- M. Sun, A. M. Dougherty, B. Huang, Y. Li and C.-H. Yan, Adv. Energy Mater., 2020, 10, 1903949 CrossRef CAS.
- M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331 CrossRef CAS PubMed.
- B. Soundiraraju and B. K. George, ACS Nano, 2017, 11, 8892–8900 CrossRef CAS PubMed.
- V. M. H. Ng, H. Huang, K. Zhou, P. S. Lee, W. Que, J. Z. Xu and L. B. Kong, J. Mater. Chem. A, 2017, 5, 3039–3068 RSC.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Norskov, Nat. Mater., 2006, 5, 909 CrossRef CAS PubMed.
- K. O. Obodo, C. N. M. Ouma, J. T. Obodo, M. Braun and D. Bessarabov, Comput. Condens. Matter, 2019, 21, e00419 CrossRef.
- J. K. Norskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef CAS.
- W. Pronobis, A. Tkatchenko and K. R. Muller, J. Chem. Theory Comput., 2018, 14, 2991–3003 CrossRef CAS PubMed.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed.
- O. Pique, I. Z. Koleva, A. Bruix, F. Vines, H. A. Aleksandrov, G. N. Vayssilov and F. Illas, ACS Catal., 2022, 12(15), 9256–9269 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta00344b |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2023 |