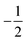Open Access Article
Open Access ArticleHierarchical defect-induced condensation in active nematics†
Timo
Krüger‡
a,
Ivan
Maryshev‡
 a and
Erwin
Frey
a and
Erwin
Frey
 *ab
*ab
aArnold Sommerfeld Center for Theoretical Physics (ASC) and Center for NanoScience (CeNS), Department of Physics, Ludwig-Maximilians-Universität München, Theresienstrasse 37, 80333 Munich, Germany. E-mail: frey@lmu.de
bMax Planck School Matter to Life, Hofgartenstraße 8, 80539 Munich, Germany
First published on 16th November 2023
Abstract
Topological defects play a central role in the formation and organization of various biological systems. Historically, such nonequilibrium defects have been mainly studied in the context of homogeneous active nematics. Phase-separated systems, in turn, are known to form dense and dynamic nematic bands, but typically lack topological defects. In this paper, we use agent-based simulations of weakly aligning, self-propelled polymers and demonstrate that contrary to the existing paradigm phase-separated active nematics form −1/2 defects. Moreover, these defects, emerging due to interactions among dense nematic bands, constitute a novel second-order collective state. We investigate the morphology of defects in detail and find that their cores correspond to a strong increase in density, associated with a condensation of nematic fluxes. Unlike their analogs in homogeneous systems, such condensed defects form and decay in a different way and do not involve positively charged partners. We additionally observe and characterize lateral arc-like structures that separate from a band's bulk and move in transverse direction. We show that the key control parameters defining the route from stable bands to the coexistence of dynamic lanes and defects are the total density of particles and their path persistence length. We introduce a hydrodynamic theory that qualitatively recapitulates all the main features of the agent-based model, and use it to show that the emergence of both defects and arcs can be attributed to the same anisotropic active fluxes. Finally, we present a way to artificially engineer and position defects, and speculate about experimental verification of the provided model.
1 Introduction
The characteristic features of a nematic liquid crystal are the emergence of long-range orientational order and the occurrence of half-integer topological defects, which, however, are annealed at thermodynamic equilibrium.1 The dynamics of its nonequilibrium counterpart, an active nematic,2–4 is in contrast governed by the persistent creation and annihilation of pairs of topological defects with opposite charges, leading to a dynamic steady state commonly referred to as active turbulence.5 Dense gel-like mixtures of microtubules (cytoskeletal filaments) and kinesins (molecular motors) that cause relative sliding between microtubules have become experimental platforms for studying the formation, dynamics, and annihilation of these toplogical defects.6,7 The observed complex defect dynamics have been investigated using hydrodynamic theories.8,9 The basic insight derived from such studies is that topological defects constantly generate active flow in momentum-conserving systems10,11 or active flux in momentum non-conserving systems.12,13Another experimental model system for active nematics is the actomyosin motility assay, in which actin filaments actively glide over a lawn of myosin motor proteins, performing a persistent random walk with constant speed.14,15 These systems exhibit phase separation into dense polar-ordered regions and dilute disordered regions, which is further corroborated by numerical analyses of corresponding theoretical models.16–18 Tuning the interaction between actin filaments by the addition of polyethylene glycol led to the emergence of a dynamic coexistence of ordered states with fluctuating nematic and polar symmetry,19 which has been explained by pattern-induced symmetry breaking.20 Systems exhibiting dense, purely nematic lanes have been thoroughly investigated by both simulations and hydrodynamic theories.13,21–28
As for half-integer topological defects, the common paradigm states that they are absent in dilute self-propelled active nematics,29 but fundamental exclusion criteria for their existence have not been given. In fact, no steady-state topological defects have yet been found in this subclass of strongly phase-separated active matter. So far, it has only been observed that transient defects can occur in models with weak density inhomogeneity during the coarsening process.30 Moreover, toy models inspired by dilute nematic systems without self-propulsion can exhibit defect formation.25 However, the authors attest that the connection of their phenomenological theory to existing experimental systems is tenuous.
Here we investigate dilute active nematics for the presence of defects using an agent-based model of “weakly-aligning self-propelled polymers” (WASP) which has been shown to faithfully reproduce the behavior of real actomyosin motility assays on all relevant length and timescales including pattern formation processes and the topology of the phase diagram.18,19 This allows us to leverage these agent-based simulations as an in silico experimental system with which to discover new phenomena. We show that the two hitherto seemingly incompatible phenomena—phase separation and topological defects—are actually closely linked in weakly interacting active nematics.
In particular, we characterize a subclass of topological defects associated with the compression of nematic fluxes, which are similar to phenomena predicted in conceptual models,25,30 albeit in a different context. These defects appear as characteristic collective excitations in a novel nonequilibrium steady state. They are in dynamic equilibrium with nematic lanes from which they emerge and into which they disassemble. Additionally, we find another type of topologically charged structure, filamentous arc ejections (FAEs)—elongated arc-shaped polymer bundles that detach from nematic bands—remotely resembling +1/2 defects. To elucidate the mechanisms underlying these phenomena, we also introduce a hydrodynamic theory, building on previously published models.13,25 Exploiting the respective strengths of these two complementary theoretical approaches, we uncover a close relationship between the dynamics of phase-separated nematic bands, formation of topologically charged structures, and the associated condensation phenomena.
2 Results
2.1 Simulation setup
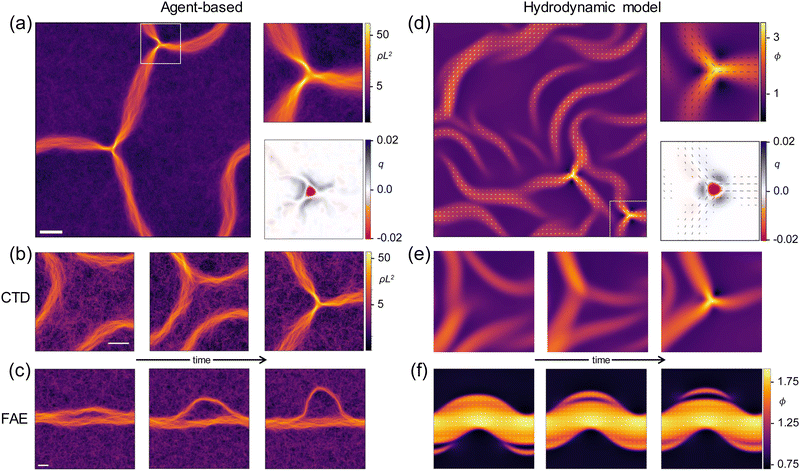
We use agent-based simulations that emulate the dynamics of weakly interacting self-propelled polymers (WASP) of fixed length L on two-dimensional surfaces building on earlier work;18,19 refer to the ESI† for further details on the algorithm. Each polymer consists of a tail pulled by a tip that follows a trajectory corresponding to a persistent random walk with persistence length Lp. Upon collision of a polymer tip with the contour of another polymer, a weak alignment torque is assumed to act that changes its direction of motion [Fig. 1(a)]. Here we use a purely nematic alignment interaction [Fig. 1(b)] whose strength is set by the parameter αn. Additionally, a small repulsion force F acts on polymer tips that overlap with other polymers.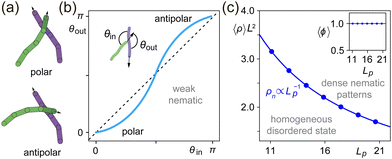 | ||
Fig. 1 Nematic interaction between polymers and onset of order. (a) Schematic depiction of two interacting polymers. Depending on whether or not the impact angle is smaller or larger 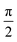 , polymer directions are either aligned (upper panel) or anti-aligned (lower panel). (b) Illustration of the binary collision statistics corresponding to a weak nematic interaction between polymers, which is symmetric with respect to the point , polymer directions are either aligned (upper panel) or anti-aligned (lower panel). (b) Illustration of the binary collision statistics corresponding to a weak nematic interaction between polymers, which is symmetric with respect to the point 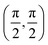 . (c) Phase diagram of active nematics with collision statistics shown in panel (b). The blue line shows the density corresponding to isotropic–nematic transition ρn, which is inversely proportional to the persistence length ρn ∝ Lp−1. Please refer to the ESI† for details. Inset: The same graph plotted as a function of 〈ϕ〉 = 〈ρ〉/ρn and Lp. . (c) Phase diagram of active nematics with collision statistics shown in panel (b). The blue line shows the density corresponding to isotropic–nematic transition ρn, which is inversely proportional to the persistence length ρn ∝ Lp−1. Please refer to the ESI† for details. Inset: The same graph plotted as a function of 〈ϕ〉 = 〈ρ〉/ρn and Lp. | ||
Here we are interested in systems that have a collision statistics with purely nematic symmetry [Fig. 1(b)]. Fig. 1(c) shows the phase diagram of such a weak nematic as a function of the average polymer density 〈ρ〉L2 and path persistence length Lp; hereafter 〈…〉 denotes spatial averaging. It exhibits an isotropic–nematic transition from a disordered homogeneous phase to a nematically ordered phase.
The phase boundary ρn(Lp) approximately scales as Lp−1; refer to the ESI† for details. Thus, when the phase diagram is redrawn as a function of Lp and the spatially averaged normalized density 〈ϕ〉 = 〈ρ〉/ρn, the phase boundary essentially becomes a horizontal line [inset of Fig. 1(c)].
2.2 Dense topologically charged structures
As expected for nematically interacting systems, our simulations show isolated nematic lanes that exhibit strong bending fluctuations on large length and time scales (cf. Movie S1, ESI†) caused by lateral instabilities.21,31In our simulations, in addition to these typical nematic lanes, we also discover distinct types of topologically charged structures. One class of these are three-armed filamentous structures containing a topological defect with charge −1/2 at their center [Fig. 2(a)]. They are typically formed when three curved nematic lanes—with their convex sides facing each other—meet and condense into a topological defect with a high-density core region [Fig. 2(b)]; we do not observe “collisions” of four lanes. Unlike defects in non phase-separated active nematics, these condensed topological defects (CTDs) do not have a directly corresponding positively charged partner. Instead, they are surrounded by an extended topologically charged region with a dispersed positive charge, as can be seen in Fig. 2(a) (lower right panel), which depicts the topological charge density as defined in ref. 25,32. Moreover, our simulations show that the active nematic flux is gradually compressed as the triple junction of the nematic lanes (defect core) is approached [Fig. 2(a), top right panel]. This leads to a reduction in lane width and a corresponding increase in density, which reaches a maximum in proximity of the core. These three-armed topological defects are dynamic structures that are constantly being dissolved and reassembled. A second class of structures we observe are lateral filamentous arcs that separate from the bulk of a straight nematic band and eventually move in transverse direction. A time trace of such a filamentous arc ejection (FAE) is shown in Fig. 2(c). These structures distantly resemble +1/2 defects: they are “curved” and they always emanate in the direction of their convex side. However, it is crucial to acknowledge that the observed arced structures possess a characteristic “hollow core”' and, naturally, cannot be regarded as defects. Somewhat similar observations have been made in continuum models constructed for nematic particles with velocity reversals.23 However, the authors did not address the properties of these structures or the reasons underlying their formation. While there are certainly similarities on a superficial phenomenological level between FAEs and these structures, the underlying mechanisms and nature of these structures may be quite different.
Having discovered these collective topological structures in our in silico experiments, we sought to explore how their emergence is affected by a change of parameters. However, since the lateral instabilities of nematic bands required for the formation of CTDs (cf. section “From CTDs to FAEs and bands” below) occur only on very long time scales, a systematic investigation of a phase diagram in agent-based simulation is numerically prohibitively demanding. Therefore, we sought an alternative way to explore the spatiotemporal dynamics of the systems that would enable us to dissect the processes underlying the formation of CTDs and FAEs. As explained next, we achieved this through constructing a hydrodynamic approach that captures all the main features of our agent-based simulation setup.
2.3 Hydrodynamic model provides access to the phase diagram
To this end we used the standard Boltzmann-like approach (see ESI†). However, as discussed below, this model was insufficient to explain the emergence of half-integer defects and was therefore generalized to include density-dependent corrections.By analogy with passive model C in the Hohenberg–Halperin classification scheme33 we formulate a hydrodynamic model in terms of a density and an order parameter field. For an active nematic, these are the (normalized) polymer density 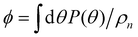 , and the traceless and symmetric tensor
, and the traceless and symmetric tensor 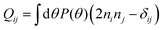 (nematic order parameter), where the unit vector n = (nx,ny) = (cos
(nematic order parameter), where the unit vector n = (nx,ny) = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,sin
θ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) defines the the local polymer orientation vector and P(θ) denotes the probability density for the polymer orientation θ. The eigenvector associated with the larger of the two eigenvalues of the Q-tensor can be viewed as depicting the average orientation of the polymers.
θ) defines the the local polymer orientation vector and P(θ) denotes the probability density for the polymer orientation θ. The eigenvector associated with the larger of the two eigenvalues of the Q-tensor can be viewed as depicting the average orientation of the polymers.
Unlike classical model C, however, a hydrodynamic model for active nematics must be intrinsically nonequilibrium in character and its dynamics can not be determined by the gradient descent in a single free-energy landscape. Nevertheless, using the analogy to the dynamics near thermal equilibrium, some intuition can be gained for the design of the model. As we discuss in more detail below, part of the system's dynamics can be understood in terms of two separate effective free-energy functionals for the non-conservative Q-tensor (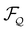 ) and the conservative density field (
) and the conservative density field (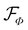 ), similar to related nonequilibrium models discussed recently.34
), similar to related nonequilibrium models discussed recently.34
Mass-conservation requires that the density obeys a continuity equation ∂tϕ = −∂iJi. In general, for symmetry reasons, the current must be the gradient of a scalar quantity and a tensorial quantity containing the Q-tensor. Similar to model B, the scalar component is of the form Jisoi = −∂iμ(ϕ) with chemical potential μ(ϕ) = ν(ϕ)ϕ. Here, the first and second terms of ν(ϕ) = λ2 + νϕϕ account for motility-induced effective diffusion with the diffusion constant λ2 ∝ Lp2,35 and for steric repulsion due to excluded–volume interactions,36–38 respectively. The latter contribution represents the density-dependent correction.
For the tensorial part, we write Janisoi = −∂j[χ(ϕ)Qij], which again is assumed to contain motility- and interaction-induced parts: χ(ϕ) = λ2 + χϕϕ. Similar as above, the latter term represents the density-dependent correction motivated by theories for active nematics,13,26 and it is controlled by the phenomenological parameter χϕ. It will turn out that this anisotropic term leads to phase separation, since it causes compression in the direction perpendicular to the axis of the local orientational order. Taken together, one gets
| ∂tϕ = ∂i∂j[ν(ϕ)ϕδij + χ(ϕ)Qij]. | (1) |
The isotropic flux (first term) can be written in terms of an effective free-energy functional 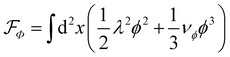 . In contrast, however, the anisotropic flux (second term in eqn (1)) violates time-reversal symmetry.4,39
. In contrast, however, the anisotropic flux (second term in eqn (1)) violates time-reversal symmetry.4,39
We assume the time evolution of the nematic tensor to be of the form
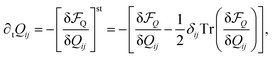 | (2) |
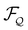 ; here and in the following […]st denotes the traceless and symmetric part of a tensor. We have chosen the timescale such that the friction coefficient in the gradient dynamics is set to 1.
; here and in the following […]st denotes the traceless and symmetric part of a tensor. We have chosen the timescale such that the friction coefficient in the gradient dynamics is set to 1.
The effective free-energy functional has a standard Landau-deGennes (LdG) part1 responsible for an isotropic to nematic transition, but also includes a coupling between density gradients and the orientation of polymers as in inhomogeneous active nematics,13,26
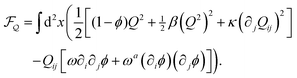 | (3) |
The LdG free-energy density in terms of the order parameter Q2 = QklQkl describes a nematic ordering transition at the critical density ϕc = 1 with the gradient term playing the role of a generalised elasticity. The stiffness coefficient (or Frank constant) κ also contains two contributions, one from the motility of the polymers,21,23 and the other due to interactions:13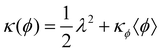 . Note that the last term—the density-dependent correction to elasticity—is linearised around the mean value of density 〈ϕ〉 (see ESI†). The second line in eqn (3) takes into account the coupling between density gradients and nematic order, and can be derived solely on the basis of symmetry considerations. The functional derivatives of
. Note that the last term—the density-dependent correction to elasticity—is linearised around the mean value of density 〈ϕ〉 (see ESI†). The second line in eqn (3) takes into account the coupling between density gradients and nematic order, and can be derived solely on the basis of symmetry considerations. The functional derivatives of 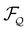 with respect to the nematic tensor correspond to “interfacial torques”13 in the equation of motion for the nematic tensor. They rotate the director at the interface between high- and low-density domains, where the gradients of ϕ are the strongest.
with respect to the nematic tensor correspond to “interfacial torques”13 in the equation of motion for the nematic tensor. They rotate the director at the interface between high- and low-density domains, where the gradients of ϕ are the strongest.
The lowest-order coupling—and the associated “aligning torque”2ω[∂i∂jϕ]st—is iconic for active nematics.2,29,35,39 It is responsible for the destabilization of straight nematic lanes, eventually resulting in lane undulations (or other types of chaotic behavior associated with “dry active turbulence'”5,13,23). In our case, this term is due to self-advection (ω = λ2, see ESI†) but it can be considered as “diffusive” since anisotropic diffusion of particles leads to an analogous contribution.
Interaction between the polymers yields the next-order couplings in eqn (3). On symmetry grounds there are two different terms quadratic in ϕ: [ϕ∂i∂jϕ]st and [(∂iϕ)(∂jϕ)]st; both can also be obtained by explicitly coarse-graining microscopic models for interacting active polymers.13 The former recalls the diffusive ω-term (especially after the linearization around 〈ϕ〉) and therefore is ignored here. The latter is associated with torque, which is bilinear in the density gradients ωa[(∂iϕ)(∂jϕ)]st, providing an effective liquid-crystalline “anchoring”'25,40,41 (or preferred orientation) of the nematic director field with respect to the density gradients. The parameter ωa is taken to be negative to ensure tangential anchoring, implying that polymers tend to orient perpendicular to the density gradients (or parallel to the boundary of dense lanes).
For simplicity, we ignore additional non-linearities in the equation of motion for the Q-tensor. Such contributions are considered elsewhere13,42,43 where they are typically regarded as a modification to the elasticity terms.
Taken together eqn (1) and (2) are a generalization of the active model C,13,25 which was originally introduced for non self-propelled biofilaments in the presence of molecular motors. The major difference is that the model now explicitly includes self-propulsion. Moreover, by including density-dependent terms, it shows the same results as the agent-based simulations (see discussion below) and is therefore quantitatively linked to the actomyosin motility assay. Finally, it possesses less degrees of freedom, since most of the terms are rigorously derived and are controlled by the same parameter (λ).
We consider νϕ,χϕ,κϕ,ω and ωa as phenomenological parameters and solve the equations of motion numerically. This model robustly reproduces the results obtained in the agent-based simulation to a very high degree of fidelity and for a large range of parameters. It exhibits CTDs and FAEs whose structure, topological charge, and formation process are very similar to the ones observed in WASP; cf.Fig. 2(d)–(f). Therefore, in the following we use this hydrodynamic approach to analyse and underpin the main mechanisms of formation of CTDs and FAEs.
In summary, our model (and the active model C13,25) differs significantly from the standard theory of active nematics,23 since it contains density-dependent corrections and higher order terms. Without such modifications the standard active nematic model is unable to reproduce CTDs.
2.4 From CTDs to FAEs and bands
Encouraged by the promising initial results shown by our hydrodynamic theory, we took advantage of the relative ease with which it can be used to determine the long-term behavior, and generated a (λ, 〈ϕ〉) phase diagram [Fig. 3(a)]. As can be seen, at low values of λ and 〈ϕ〉, CTD formation dominates, while in areas of large λ and 〈ϕ〉 stable nematic lanes emerge. Between these regions lies a band of parameters where the system mainly exhibits FAEs. To test whether these findings obtained with the hydrodynamic model also hold for our agent-based simulations, we determined the average number of CTDs present at a given time in the agent-based simulation along one-dimensional lines of the (Lp, 〈ϕ〉) phase space—one along a constant value of 〈ϕ〉 and one along a constant value of Lp. Reassuringly, the results for the agent-based simulations and hydrodynamic model are in good agreement [Fig. 3(c) and (d)]. We further checked the mean number of FAEs present in the agent-based simulations as a function of Lp [Fig. 3(e)]; see ESI† for details. The observed decline in FAE frequency with increasing Lp is consistent with the observations in the hydrodynamic model, where at high λ no FAEs occur [cf.Fig. 3(a)]. Taken together, these results demonstrate that not only do the agent-based and hydrodynamic models share the same collective states, the frequency of these states also shows the same dependence on parameter changes.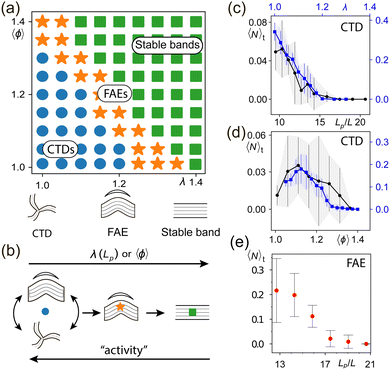 | ||
| Fig. 3 Quantification of the occurrence of condensed defects and filamentous arc ejections in the agent-based simulations and the hydrodynamic model, plotted as a function of the indicated parameters. As the density and/or the persistence length (agent-based model) or λ (hydrodynamic model) is increased, the most frequently observed type of collective state changes from CTDs to FAEs to straight lanes. (a) Phase diagram obtained from the numerical solution of the hydrodynamic model, which depicts the parameter regimes in which CTDs (blue dots), FAEs (orange stars), and straight nematic lanes (green squares) are the dominant structures. (For further details, see ESI†). (b) Illustration of the three qualitatively different system behaviors as a function of the indicated parameters (upper arrow) or the strength of bending undulation (lower arrow). (c) Mean number of CTDs observed in the agent-based (hydrodynamic) model, plotted as a function of Lp (λ). (d) Mean number of CTDs observed in the agent-based (hydrodynamic) model as a function of 〈ϕ〉. (e) Mean number of FAEs observed in the agent-based model as a function of Lp. | ||
The above relationships between model parameters and the occurrence of CTDs or FAEs can be related to the overall dynamic behavior (in short, “activity”) of the system. For both hydrodynamic and agent-based approaches, three distinct, qualitatively different dynamic states can be distinguished [Fig. 3(b)].
The first of these is associated with very strong bending undulations of nematic lanes. It occurs at low values of Lp/λ or 〈ϕ〉 and is characterized by constant rearrangement of lanes [Movies S2, S3, S7, ESI† and Fig. 2(a), (b), (d), (e)]: Lanes frequently collide leading to the formation of CTDs. In addition, system-spanning configurations of straight (or only slightly curved) lanes [cf.Fig. 2(c) and (f)], which may form randomly, are disrupted by undulations within a fairly short time. This is consistent with the observation that CTDs are the predominant phenomenon at low values of Lp/λ and 〈ϕ〉, respectively [Fig. 3(c) and (d)]. Notably, FAEs can also be formed in this parameter regime following the emergence of short-lived system-spanning nematic lanes.
The second dynamic state can be found at intermediate values of Lp/λ or 〈ϕ〉. In this regime, bending undulations are fewer and less pronounced, resulting in straight (or only slightly curved) and system-wide lanes that are stable over long periods of time: Elongated openings often appear in the lateral areas of the lanes, which develop into filamentous arcs [Movies S4, S8, ESI† and Fig. 2(c), (f) and middle panel of Fig. 3(b)]. This is in accordance with the observation that FAEs are the predominant phenomenon observed at intermediate values of Lp/λ or 〈ϕ〉 [Fig. 3(a) and (c)–(e)].
The third dynamic state is associated with vanishing bending undulations at high values of Lp/λ or 〈ϕ〉. Here, straight and system-spanning configurations are stable and no openings develop in their lateral regions [Movies S5, S9, ESI† and right panel of Fig. 3(b)]. Consequently, neither FAEs nor CTDs are observed [Fig. 3(a) and (c)–(e)].
The tendency just discussed for the bending undulations to become weaker as the values of Lp/λ or 〈ϕ〉 are increased from low to high values can be rationalized by the following heuristic arguments. With increasing Lp/λ the Frank constant44 grows, and the effective elasticity (or collective stiffness of the polymers) yields stronger penalties for orientational distortions. As a result, the bending instability weakens, as described above. The hydrodynamic model has allowed us to verify this hypothesis: upon varying the elastic constant κ (independently from other parameters), we observe that weak elasticity favors the formation of CTDs, while a strong one yields stable bands. As the density 〈ϕ〉 is increased (for a given and constant system size), a further effect contributing to higher stability of lanes is that a system-spanning nematic band occupies a growing fraction of space, i.e., the bands become wider while the bulk density remains largely the same [cf. ESI†]. Since broader bands are less susceptible to a bending instability, an increase of 〈ϕ〉, as discussed above, leads to the decay of defect formation.
An interesting aside can be mentioned here in the context of varying values of 〈ϕ〉: for very small densities, close to the onset of order, both models show a drop in the observed CTD number [Fig. 3(d)], which is likely due to the fact that there is less mass within the ordered phase, and therefore not enough mass to form multiple curved bands necessary for lanes to collide and CTDs to be created.
Overall, the formation of condensed defects and filamentous arc ejections are both strongly linked to the stability of the nematic lanes, i.e., to their propensity to exhibit a bending instability,13,21,24–26 which, in turn, can be externally controlled by tuning either Lp/λ or 〈ϕ〉.
2.5 Detailed structure of CTDs and FAEs
To better understand the structure of the CTDs forming in agent-based simulations, we studied the polymer flows through them in detail. To this end, we tracked the motion of each polymer as it passed through a condensed defect. This enables us to distinguish the polymer flows from one to another arm of a defect and investigate whether there is a relationship between the lateral position of individual polymers and their eventual direction of turning.Fig. 4(a) illustrates the flux from one arm of a defect (arm 1) into the two other arms (arms 2 and 3) [see Movie S6, ESI† for a representative flux recorded in an agent-based simulation]. The flux in each defect arm gets strongly compressed laterally in the vicinity of a defect core and then splits almost exactly at the centerline of the lane, while undergoing a sharp change in direction [Fig. 4(a)]. Symmetrically the same flux enters the defect from arms 2 and 3, resulting in the nematic flow structure depicted in Fig. 4(a) and (c). This also shows that the flows begin to mix again only at a greater distance from the center of the defect [cf. color mixing in Fig. 4(b) and (c)]. Hence, the overall topology often present at the birth of the defect [Fig. 2(b) and (e)] is preserved in the flow structure of the fully formed CTD as three barely intermingling nematic flows.
In addition, we investigated whether the velocity of the polymers is affected as they move through a CTD. As can be seen from Fig. 4(e), their speed remains almost unchanged and only a slowdown in the per mil range is observed. One can see two insignificant velocity drops corresponding to regions with the maximal density of polymers. Interestingly, in the immediate vicinity of the core of the defect, the particle velocity briefly returns to the average value, corresponding to particles inside the nematic band.
We also studied the temporal evolution of FAEs and their occurrence over time. To this end, we periodically projected the density of a system in a configuration that allows the formation of FAEs onto one-dimensional slides and stacked them to obtain kymographs (see Fig. S5, ESI†). These reveal that the detachment of arcs accelerate over time. Further, they show that in the hydrodynamic model, due to no noise being present, FAE events occur at regular intervals, whereas in the agent-based simulations they form stochastically.
Having established the existence of CTDs and FAEs, and characterized them in our agent-based in silico experimental system, and having successfully introduced a hydrodynamic theory that faithfully reproduces the results of the simulations as well as providing access to the phase space of the observed pattern, we asked: why are these phenomena observed? What are the underlying mechanisms responsible for their formation?
To answer these questions, we leveraged the ability of the hydrodynamic model to provide access to single terms of its defining equations [eqn (1) and (2)]. This analysis reveals that both the formation of dense defects and the movement of arcs have the same root cause, namely the anisotropic (“curvature-induced”) density flux,2,45–47 described by −∂j(χQij) in eqn (1) in the hydrodynamic model. This can be understood by plotting −∂j(χQij) in the region of an FAE or a CTD; see the left and right panels of Fig. 4(d), respectively. As can be seen, on opposite sides of the arcs the amplitudes of the fluxes are distinct. An effective “active force”' acting on the concave side is greater than that on the opposite side, which leads to the movement of the bent band (or arc) in the corresponding direction [Fig. 4(d), left panel].
When three lanes meet, the same curvature-dependent fluxes concentrate polymers in the core of the resulting defect [Fig. 4(d), right panel]. This condensation is eventually balanced by the isotropic part of eqn (1) and particularly by steric repulsion of polymers. To test this hypothesis, we set the excluded volume force F (see ESI†) to zero in our agent-based simulations. Observations in this case indicate that the formation of CTDs is reduced and that, when they form, they decay faster. Thus, we conclude that formation of the dense defects is predominantly determined by the interplay between two counteracting processes: isotropic and anisotropic density fluxes.
In addition to the “emergent” way of obtaining CTDs just studied, in which spontaneously formed bands interact randomly and spontaneously condense into defects at stochastically distributed positions, we have sought a way to overcome this limitation by artificially generating and positioning CTDs. In contrast to non-phase-separated systems—where such an endeavor would involve the forced separation of a defect pair—the way CTDs form spontaneously [Fig. 2(b) and (e)] suggests that finding a way to position and form nematic lanes in suitable configurations could trigger the creation of a CTD. In combination with the observation of polymer fluxes near a defect [Fig. 4(h)], we hypothesized that placing active polymer sources in a three-strand configuration should trigger the formation of three lanes that immediately condensate into CTDs. To test this prediction, we implemented the possibility to add such “active particle throwers” into our agent-based simulations and positioned them as described. Indeed, we found that this way a CTD can be formed at a predetermined location where it persists for an arbitrary amount of time, cf.Fig. 4(h) and Movie S10, ESI.† This may be of potential application in cases where topological defects and/or high-density regions (in a low density background) need to be created and controlled with high accuracy.
3 Discussion
In summary, we have used a combination of agent-based simulations and hydrodynamic theory to study pattern formation in phase-separated nematic active matter. Our analysis shows that topological defects and nematic lanes, previously considered as two distinct and separate collective states, coexist and are tightly coupled.We investigated the structure, formation and decomposition of CTDs in phase-separated systems. We observed that CTDs appear as characteristic collective excitations in a novel nonequilibrium steady state. Moreover, the formation process of CTDs constitutes a new hierarchical condensation phenomenon. Given the previously demonstrated and close connection of our agent-based algorithm to the actin motility-assay, a paradigmatic experimental model system, it is plausible to expect that CTDs will be observed in experimental active matter systems. Below we discuss these observations step by step.
First of all, we characterized topologically charged structures, such as CTDs and FAEs, for the first time observed in a phase-separated nematic system with self-propulsion. It is apparent that CTDs differ markedly from defects observed in homogeneous active matter, particularly in the dynamics of their formation and decay and in their spatial structure as well.
To begin with, CTDs upconcentrate density nearby their cores and condensate nematic fluxes. This condensation phenomena is interesting by itself, since the majority of experimental active matter systems show a depletion of particles in −1/2 disclinations, e.g., bacteria embedded in liquid crystals48 and cultures of neural progenitors.49 Weak density accumulation around the defects has been discussed in slightly inhomogeneous nematic;30 however, in such systems, the −1/2 defects occur only during the transient and eventually disappear via annihilation with their +1/2 counterparts.
Similar CTDs, among other structures, were observed in parameter sweeps of the phenomenological toy model for mixtures of non-self-propelled microtubules and kinesin motors.25 However, they were either transient or formed only under very special conditions (elasticity almost zero). In the latter case, the shape and the mechanism of formation of the defects were clearly different from the CTDs observed here.
In our case CTDs are typically formed by the collision of three curved nematic lanes that condense into a high-density three-armed structure, trapping the previously spatially distributed negative charge [Fig. 2(a) and (d)].
One might think of comparing condensation to CTDs with the process of motility-induced phase separation (MIPS).50 However, the fundamental difference between the two is that CTDs are not associated with particle slowdown or prolonged residence of agents in high-density regions. In addition, the formation of condensed defects provides a condensation mechanism for anisotropically shaped particles, which is not possible with MIPS.51 We may also argue that in MIPS the agents themselves condense into high-density clusters, while we observe the condensation of dynamical collective states (nematic lanes) into topological defects.
The mutual orientation of defects is also non-typical: we observe that two CTDs can be connected by a single nematic streamline (a filamentous bundle of polymers) [Fig. 2(a) and 4(f)], whereas in non-phase-separated active matter negative half-integer disclinations usually point towards a corresponding defect with the opposite charge +1/2 [Fig. 4(g)].52
The dynamic processes of defect decay in phase-separated and homogeneous active nematics are also clearly distinct. In homogeneous systems, pairs of defects with opposite charges annihilate each other.8,53 In contrast, we find that CTDs do not annihilate with other defects, but disintegrate due to the undulating dynamics of the lanes that connect to the defect arms (Fig. 4(g) and Movie S3, ESI†). This means that the destruction of a negatively charged defect does not depend on the mobility or dynamics of a positively charged pair, rendering this process potentially easier to control. In cases where all three lanes that connect to the respective arms have the same bending orientation (curvature of all either clockwise or anti-clockwise with respect to center), this decay takes place via an interesting process in which defects rotate before they dissolve [Fig. 4(g)].
Thus, CTDs not only emerge from “collisions” of nematic lanes, but also are connected by, and disassemble into them. Taken together, this leads to one of the main conclusions of our work, namely that the presence of CTDs constitutes a novel nonequilibrium steady state which corresponds to a dynamic equilibrium between dense nematic lanes and condensed topological defects coexisting in a diluted background of disordered filaments. This is reminiscent of other recent findings in active matter, in which a dynamical coexistence between patterns of different symmetry (nematic and polar) was observed.19,20,27 During the persistent formation and subsequent decay of CTDs, those defects act as temporal capacitors of negative topological charge (i.e., the curvature on the boundaries of lanes gets temporarily trapped in a very small region of space) which eventually gets released again. It is well worth reiterating that this is a continuous cyclic phenomenon, not a transient one (unlike the defect formation observed in ref. 30).
The most important factors that allow this nonequilibrium steady state to occur are probably the following. First, since CTDs emerge from interaction of curved nematic lanes, a lateral undulation instability of nematic lanes—as exhibited by our agent-based model—is a basic prerequisite for their formation. Another factor that is likely to favor the formation of CTDs is the nature of the interaction between the polymers (agents), which exhibit only weak mutual alignment and weak steric exclusion. The latter, in particular, is likely to be a critical factor necessary for the high compression of polymer density during CTD formation.
Starting from a rigorously derived hydrodynamic model for self-propelled particles, we have generalized it to include higher-order phenomenological corrections. The resulting equations are reminiscent of a conceptual active model C,25 but they include all terms arising from particle self-propulsion, which is an important additional feature here. In particular, the hydrodynamic model presented here has many fewer degrees of freedom than the toy model presented in ref. 25, since the coefficients in front of all “standard” terms have a fixed relation among them.
This hydrodynamic theory provides additional insight into the physics of CTDs. For example, it shows that density gradients play a crucial role through their coupling with the orientation field. In particular, we consider density-dependent corrections of these coupling terms (controlled by the parameters χϕ and ωa), which typically disappear due to the linearization of terms around the mean value of density in the majority of hydrodynamic theories. We want to stress again that these additional terms, which are missing in standard theories of active nematics, are crucial for a proper description of the system, because without them CTDs are no longer observed. We argue that strong phase separation (and the resulting large density gradients) inevitably amplifies the effect of higher-order coupling terms between the density and the orientation field on the dynamics. For example, the bilinear anchoring ωa(∂iϕ)(∂jϕ) causes the nematic lines to closely follow the contour of the density field constituting a defect (Fig. S7, ESI†) and therefore can stabilize defects. This is in line with the observation that a decrease in ωa leads to a decrease in the number of defects (similar conclusion can be referred from25). However, in our model CTDs still can be formed even if ωa = 0, χϕ ≠ 0, κϕ ≠ 0.
We firmly believe that the phenomena we found can also be observed in experiments, even though our study is purely theoretical. The weakly aligning, self-propelled polymers simulation approach we base our study on, has previously shown not only excellent agreement with experiments, but was also able to predict then novel states that were later found in experiments;19 thus it can be viewed, as elaborated in the introduction, as a computational version of an experimental system. In light of this, we expect that the most promising experimental model system that could allow observation of the new topological defects we predict is most likely the actomyosin motility assay.14,15,54,55 This paradigmatic system not only satisfies the requirement of weakly interacting agents,19,56 but also offers the advantage of high particle numbers. Previously, not only polar waves14 but also nematic lanes19 have been observed. This has been achieved by adding depletion agents that enable one to tune the strength as well as the symmetry of the interaction between the actin filaments. It is conceivable that similar and other changes in the design of the actin motility assay could be used to produce a weak and purely nematic interaction as used in our agent-based simulations. For example, other depletion agents could be used and/or the properties of the surface to which the driving molecular motors are attached could be changed. Recently, the latter was indeed shown to have a direct impact on polymer interactions.57 Alternatively, CTDs could potentially be observed in other types of motility assays,58,59 biofilms formed by chaining bacterial such as Bacillus subtilis60 or in reticulate patterns exhibited by filamentous cyanobacteria.61 Another intriguing possibility for observing the predicted CTDs is to directly produce a configuration of nematic lanes favoring the formation of CTDs by suitably structuring the surface used in the motility assay.62,63
The deep understanding we gained about the formation of CTDs owing to the combination of agent-based simulation and hydrodynamic approach allowed us to find a way to generate them artificially (Fig. 4(h) and Movie S10, ESI†). Given the availability of directed particle sources in an experimental system, the position of defects (and therefore the location of a domain of extremely high density) could be controlled with pin-point accuracy. This provides a new tool for cases where −1/2 defects and/or small regions of high particle density (in an overall dilute system) are needed at specific positions. Given the strong and controlled nature of the focusing of the fluxes in nematic lanes, this method could be termed “active matter optics”.
Another important insight from the broader perspective of the active matter field is that phase-separated active matter exhibits a hierarchy of emergent collective states. Interaction between dense nematic lanes, considered as “first-order” collective states in active nematics, can lead to the formation of “second-order” collective states, here half-integer topological defects with an even higher density. A phenomenon which one can call “hierarchical, alignment-induced phase-separation”. It is reasonable to assume that similar effects may lead to new phenomena in other active systems with different symmetry, e.g., polar symmetry with polar waves as first-order collective states.18,29 Another class of systems in which higher-order collective states might emerge are active systems that are subject to external gradients64 or signalling interactions between the agents.65,66
A promising extension of our present investigations are active foams. In this state of active matter, which has recently received increasing attention,25,67–69 dense ordered bands assemble into actively reforming cellular networks. Indeed, in preliminary simulations of the hydrodynamic theory, we have identified parameter regimes in our model where we observe active foams: CTDs are more frequent, interconnected, and persist for longer times. Thus, the formation of active foams in active nematics seems very plausible, but a thorough investigation of the entire phase space in the agent-based model is computationally demanding and will be reserved for a future study.
Author contributions
T. K., I. M., and E. F. designed the research, performed research, analyzed data, and wrote the paper.Conflicts of interest
There are no conflicts to declare.Appendix
Agent-based simulation method
We now describe our agent-based simulation model. Please also refer to the ESI† and the ESI† of ref.18 and 19 for more details.In our systems we simulate M polymers, each of length L. Orientational diffusion causes the tip of each polymer to perform a persistent random walk. Upon collision with another polymer, local interaction causes the tip to gradually align with its direction. Attached to the polymer tips are tails that just follows the path that is outlined by the tip.
This dynamics mimics the behavior of actin filaments in actomyosin motility assays,18,19 in which polymers move in a snake-like fashion over a lawn of motor proteins and motion orthogonal to the contour is suppressed.14,56 Here we use purely nematic interactions between polymers which are primarily tuned by the nematic alignment amplitude αn that allows for a continuous variation of the rate of alignment.
Parameters
If not stated otherwise, we used the following model parameters: discretization N = 5, polymer aspect ratio L/d = 21, nematic alignment strength αn = 0.126 ≈ 7.2° and a periodic simulation box of length Lbox = 162.5L. The velocity v(n) of each polymer is randomly drawn from the interval [0.75,1.]v0. We started simulations with random initial conditions, i.e. randomly oriented polymers were placed at random positions in the simulation box. Time is measured in units of L/v0, where v0 is the maximal velocity of a free polymer. Density in Fig. 2(a)–(c) and 4(g)–(h) is time-averaged for better visibility, with averaging times of 159 for Fig. 2(a) and 16 for Fig. 2(b), (c) and 4(g)–(h). Note that the system shown in Fig. 4(h) does not have the usual periodic boundary conditions. Rather, the particles crossing the boundaries are moved either to a random position along a boundary with random orientation or to one of the particle sources. The ratio of these two possibilities is chosen so that the particle flux from the sources is kept constant.Continuous theory
We numerically investigate eqn (1) and (2) under periodic boundary conditions by using finite differences of second order70 on a 300 × 300 grid with the spatial resolution δx = 0.5. The time integration was performed via a second-order predictor-corrector scheme with time step dt = 10−2. We use the parameter values β = 0.05, κϕ = 0.2, ωa = −0.5, χϕ = 0.4, νϕ = 1. Unless explicitly stated, we initialize simulations from an isotropic uniform state with a small amount of noise. To make time and space dimensionless we rescale them by setting the rotational diffusion coefficient and μρ equal to unity.Acknowledgements
We acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the Excellence Cluster ORIGINS under Germany's Excellence Strategy (EXC-2094-390783311) and through Project-ID 201269156 – Collaborative Research Center (SFB) 1032 – Project B2. IM acknowledges European Union's Framework Programme for Research and Innovation Horizon 2020 (2014-2020) under the Marie Skłodowska-Curie grant agreement no. 754388 (LMU Research Fellows) and from LMUexcellent, funded by the Federal Ministry of Education and Research (BMBF) and the Free State of Bavaria under the Excellence Strategy of the German Federal Government and the Länder.References
- P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford university press, 1993 Search PubMed.
- M. C. Marchetti, J.-F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- A. Doostmohammadi, J. Ignés-Mullol, J. M. Yeomans and F. Sagués, Nat. Commun., 2018, 9, 3246 CrossRef PubMed.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- R. Alert, J. Casademunt and J.-F. Joanny, Annu. Rev. Condens. Matter Phys., 2022, 13, 143–170 CrossRef.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- S. J. DeCamp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110–1115 CrossRef CAS PubMed.
- L. Giomi, M. J. Bowick, X. Ma and M. C. Marchetti, Phys. Rev. Lett., 2013, 110, 228101 CrossRef PubMed.
- S. Shankar, S. Ramaswamy, M. C. Marchetti and M. J. Bowick, Phys. Rev. Lett., 2018, 121, 108002 CrossRef CAS PubMed.
- S. P. Thampi, R. Golestanian and J. M. Yeomans, Europhys. Lett., 2014, 105, 18001 CrossRef.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. Cristina Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
- E. Putzig, G. S. Redner, A. Baskaran and A. Baskaran, Soft Matter, 2016, 12, 3854–3859 RSC.
- I. Maryshev, A. B. Goryachev, D. Marenduzzo and A. Morozov, Soft Matter, 2019, 15, 6038–6043 RSC.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- T. Butt, T. Mufti, A. Humayun, P. B. Rosenthal, S. Khan, S. Khan and J. E. Molloy, J. Biol. Chem., 2010, 285, 4964–4974 CrossRef CAS PubMed.
- G. Grégoire and H. Chaté, Phys. Rev. Lett., 2004, 92, 025702 CrossRef PubMed.
- A. P. Solon, H. Chaté and J. Tailleur, Phys. Rev. Lett., 2015, 114, 068101 CrossRef PubMed.
- L. Huber, T. Krüger and E. Frey, Phys. Rev. Res., 2021, 3, 013280 CrossRef CAS.
- L. Huber, R. Suzuki, T. Krüger, E. Frey and A. Bausch, Science, 2018, 361, 255–258 CrossRef CAS PubMed.
- J. Denk and E. Frey, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 31623–31630 CrossRef CAS PubMed.
- F. Ginelli, F. Peruani, M. Bär and H. Chaté, Phys. Rev. Lett., 2010, 104, 184502 CrossRef PubMed.
- A. Peshkov, I. S. Aranson, E. Bertin, H. Chaté and F. Ginelli, Phys. Rev. Lett., 2012, 109, 268701 CrossRef PubMed.
- S. Ngo, A. Peshkov, I. S. Aranson, E. Bertin, F. Ginelli and H. Chaté, Phys. Rev. Lett., 2014, 113, 038302 CrossRef PubMed.
- R. Großmann, F. Peruani and M. Bär, Phys. Rev. E, 2016, 94, 050602 CrossRef PubMed.
- I. Maryshev, A. Morozov, A. B. Goryachev and D. Marenduzzo, Soft Matter, 2020, 16, 8775–8781 RSC.
- L.-B. Cai, H. Chaté, Y.-Q. Ma and X.-Q. Shi, Phys. Rev. E, 2019, 99, 010601 CrossRef CAS PubMed.
- R. Großmann, I. S. Aranson and F. Peruani, Nat. Commun., 2020, 11, 5365 CrossRef PubMed.
- T. Kozhukhov and T. N. Shendruk, Sci. Adv., 2022, 8, eabo5788 CrossRef PubMed.
- H. Chaté, Annu. Rev. Condens. Matter Phys., 2020, 11, 189–212 CrossRef.
- S. Mishra, S. Puri and S. Ramaswamy, Philos. Trans. R. Soc., A, 2014, 372, 20130364 CrossRef PubMed.
- E. Bertin, H. Chaté, F. Ginelli, S. Mishra, A. Peshkov and S. Ramaswamy, New J. Phys., 2013, 15, 085032 CrossRef.
- M. L. Blow, S. P. Thampi and J. M. Yeomans, Phys. Rev. Lett., 2014, 113, 248303 CrossRef PubMed.
- P. C. Hohenberg and B. I. Halperin, Rev. Mod. Phys., 1977, 49, 435 CrossRef CAS.
- Y. I. Li and M. E. Cates, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 119 CrossRef CAS PubMed.
- A. Baskaran and M. C. Marchetti, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–8 CrossRef PubMed.
- A. Ahmadi, M. C. Marchetti and T. B. Liverpool, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 061913 CrossRef PubMed.
- A. Baskaran and M. C. Marchetti, J. Stat. Mech.: Theory Exp., 2010, 2010, P04019 Search PubMed.
- I. Maryshev, D. Marenduzzo, A. B. Goryachev and A. Morozov, Phys. Rev. E, 2018, 97, 22412 CrossRef CAS PubMed.
- M. E. Cates, arXiv, 2019, preprint.
- N. Sulaiman, D. Marenduzzo and J. Yeomans, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041708 CrossRef CAS PubMed.
- T. Araki and H. Tanaka, Phys. Rev. Lett., 2004, 93, 015702 CrossRef.
- S. Mishra, R. A. Simha and S. Ramaswamy, J. Stat. Mech.: Theory Exp., 2010, 2010, P02003 Search PubMed.
- E. Putzig and A. Baskaran, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042304 CrossRef PubMed.
- T. Sato and A. Teramoto, Macromolecules, 1996, 29, 4107–4114 CrossRef CAS.
- S. Ramaswamy, R. A. Simha and J. Toner, Europhys. Lett., 2003, 62, 196–202 CrossRef CAS.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- M. M. Genkin, A. Sokolov, O. D. Lavrentovich and I. S. Aranson, Phys. Rev. X, 2017, 7, 011029 Search PubMed.
- K. Kawaguchi, R. Kageyama and M. Sano, Nature, 2017, 545, 327–331 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- M. N. Van Der Linden, L. C. Alexander, D. G. Aarts and O. Dauchot, Phys. Rev. Lett., 2019, 123, 098001 CrossRef CAS PubMed.
- S. Shankar and M. C. Marchetti, Phys. Rev. X, 2019, 9, 041047 CAS.
- D. Cortese, J. Eggers and T. B. Liverpool, Phys. Rev. E, 2018, 97, 022704 CrossRef CAS PubMed.
- S. Hussain, J. E. Molloy and S. M. Khan, Biophys. J., 2013, 105, 1456–1465 CrossRef CAS PubMed.
- R. Suzuki and A. R. Bausch, Nat. Commun., 2017, 8, 41 CrossRef PubMed.
- R. Suzuki, C. A. Weber, E. Frey and A. R. Bausch, Nat. Phys., 2015, 11, 839–843 Search PubMed.
- A. Sciortino and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2017047118 CrossRef CAS PubMed.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- F. L. Memarian, J. D. Lopes, F. J. Schwarzendahl, M. G. Athani, N. Sarpangala, A. Gopinathan, D. A. Beller, K. Dasbiswas and L. S. Hirst, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2117107118 CrossRef CAS PubMed.
- Y. I. Yaman, E. Demir, R. Vetter and A. Kocabas, Nat. Commun., 2019, 10, 2285 CrossRef PubMed.
- M. K. Faluweki, J. Cammann, M. G. Mazza and L. Goehring, arXiv, 2023, preprint.
- T. Turiv, R. Koizumi, K. Thijssen, M. M. Genkin, H. Yu, C. Peng, Q.-H. Wei, J. M. Yeomans, I. S. Aranson, A. Doostmohammadi and O. D. Lavrentovich, Nat. Phys., 2020, 16, 481–487 Search PubMed.
- A. Sciortino, L. J. Neumann, T. Krüger, I. Maryshev, T. F. Teshima, B. Wolfrum, E. Frey and A. R. Bausch, Nat. Mater., 2022, 260–268 Search PubMed.
- M. N. Popescu, W. E. Uspal, C. Bechinger and P. Fischer, Nano Lett., 2018, 18, 5345–5349 CrossRef CAS PubMed.
- F. A. Lavergne, H. Wendehenne, T. Bäuerle and C. Bechinger, Science, 2019, 364, 70–74 CrossRef CAS PubMed.
- A. Ziepke, I. Maryshev, I. S. Aranson and E. Frey, Nat. Commun., 2022, 13, 6727 CrossRef CAS PubMed.
- K. H. Nagai, Y. Sumino, R. Montagne, I. S. Aranson and H. Chaté, Phys. Rev. Lett., 2015, 114, 168001 CrossRef PubMed.
- B. Ventejou, H. Chaté, R. Montagne and X.-Q. Shi, Phys. Rev. Lett., 2021, 127, 238001 CrossRef CAS PubMed.
- B. Lemma, N. P. Mitchell, R. Subramanian, D. J. Needleman and Z. Dogic, Phys. Rev. X, 2022, 12, 031006 CAS.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, New York, 1964 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00895a |
| ‡ T. K. and I. M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |