Open Access Article
Open Access ArticleGenuine quadruple bonds between two main-group atoms. Chemical bonding in AeF− (Ae = Be–Ba) and isoelectronic EF (E = B–Tl) and the particular role of d orbitals in covalent interactions of heavier alkaline-earth atoms†‡
Ruiqin
Liu
a,
Lei
Qin
a,
Zhaoyin
Zhang
a,
Lili
Zhao
 *a,
Filip
Sagan
b,
Mariusz
Mitoraj
*a,
Filip
Sagan
b,
Mariusz
Mitoraj
 *b and
Gernot
Frenking
*b and
Gernot
Frenking
 *ac
*ac
aInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, State Key Laboratory of Materials-Oriented Chemical Engineering, Nanjing Tech University, Nanjing 211816, China
bDepartment of Theoretical Chemistry, Faculty of Chemistry, Jagiellonian University, R. Gronostajowa 2, 30-387 Cracow, Poland
cFachbereich Chemie, Philipps-Universität Marburg, Hans-Meerwein-Strasse 4, D-35043 Marburg, Germany. E-mail: ias_llzhao@njtech.edu.cn; mitoraj@chemia.uj.edu.pl; frenking@chemie.uni-marburg.de
First published on 4th April 2023
Abstract
Quantum chemical calculations of anions AeF− (Ae = Be–Ba) and isoelectronic group-13 molecules EF (E = B–Tl) have been carried out using ab initio methods at the CCSD(T)/def2-TZVPP level and density functional theory employing BP86 various basis sets. The equilibrium distances, bond dissociation energies and vibrational frequencies are reported. The alkali earth fluoride anions AeF− exhibit strong bonds between the closed-shell species Ae and F− with bond dissociation energies between 68.8 kcal mol−1 for MgF− and 87.5 kcal mol−1 for BeF− and they show an unusual increasing trend MgF− < CaF− < SrF− < BaF−. This is in contrast to the isoelectronic group-13 fluorides EF where the BDE continuously decreases from BF to TlF. The calculated dipole moments of AeF− are very large between 5.97 D for BeF− and 1.78 D for BaF− with the negative end always at the Ae atom (Ae→F−). This is explained by the location of the electronic charge of the lone pair at Ae, which is rather distant from the nucleus. The analysis of the electronic structure of AeF− suggests significant charge donation Ae←F− into the vacant valence orbitals of Ae. A bonding analysis with the EDA-NOCV method suggests that the molecules are mainly covalently bonded. The strongest orbital interaction in the anions comes from the inductive polarization of the 2pσ electrons of F−, which leads to a hybridization of the (n)s and (n)pσ AOs at Ae. There are two degenerate π donor interactions Ae←F− in all anions AeF−, which provide 25–30% to the covalent bonding. There is another σ orbital interaction in the anions, which is very weak in BeF− and MgF−. In contrast, the second stabilizing σ orbital interaction in CaF−, SrF− and BaF− yields a strongly stabilizing σ orbital, because the Ae atoms use their (n − 1)dσ AOs for bonding. The energy lowering of the second σ interaction in the latter anions is even stronger than the π bonding. The EDA-NOCV results suggest that BeF− and MgF− have three strongly polarized bonds, whereas CaF−, SrF− and BaF− have four bonding orbitals. The quadruple bonds in the heavier alkaline earth species are made possible because they use s/d valence orbitals like transition metals for covalent bonding. The EDA-NOCV analysis of the group-13 fluorides EF gives a conventional picture with one very strong σ bond and two rather weak π interactions.
1 Introduction
In recent years, great progress has been made in the field of multiple bonds of atoms of groups 2 and 13 of the periodic table in a variety of compounds.1 Experimental and theoretical studies have shown that there are stable molecules that have homoatomic or heteroatomic double or even triple bonds between alkaline earth or group 13 atoms and other elements of the periodic table. Prominent examples are compounds with a boron–boron triple bond L→B![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) B←L with various donor ligands L such as CO2 or N-heterocyclic carbenes.3 A gallium–gallium triple bond was suggested for the compound Na2{GaC6H3-2,6-Trip2}2 (Trip = C6H2-2,4,6-iPr3), which has a trans-bent geometry,4 but the bond order was disputed by other researchers.5 Numerous compounds with homo- and hetero-atomic double bonds of the heavier group-13 atoms Al–In have been prepared,6 and the first stable molecule with a classical Al
B←L with various donor ligands L such as CO2 or N-heterocyclic carbenes.3 A gallium–gallium triple bond was suggested for the compound Na2{GaC6H3-2,6-Trip2}2 (Trip = C6H2-2,4,6-iPr3), which has a trans-bent geometry,4 but the bond order was disputed by other researchers.5 Numerous compounds with homo- and hetero-atomic double bonds of the heavier group-13 atoms Al–In have been prepared,6 and the first stable molecule with a classical Al![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Al double bond is clearly a milestone in synthetic main group chemistry following an earlier synthesis of a dialuminium complex with a formal triple bond.7a,b A compound with a triple bond between Al and N has lately been prepared and structurally characterized by X-ray crystallography.7c
Al double bond is clearly a milestone in synthetic main group chemistry following an earlier synthesis of a dialuminium complex with a formal triple bond.7a,b A compound with a triple bond between Al and N has lately been prepared and structurally characterized by X-ray crystallography.7c
Very recently, the compound HN BeCO featuring a triple bond between beryllium and nitrogen has been reported, where one bonding component is a dative bond.8 This is related to the triple bond in carbon monoxide |C
BeCO featuring a triple bond between beryllium and nitrogen has been reported, where one bonding component is a dative bond.8 This is related to the triple bond in carbon monoxide |C O|, which is also best described with two electron-sharing π bonds and one σ dative bond.9 The relevance of dative bonds in main-group compounds, which goes back to original work by Lewis10 and Sidgwick,11 has been pointed out in several review articles.12 It became prominent with the discovery of carbones13 L→C←L and related species L→En←L (E = B–Tl, Si–Pb, and N–Bi; n = 1–3), where L is a donor ligand.14 The first compound with a beryllium–nitrogen double bond (CAAC)N
O|, which is also best described with two electron-sharing π bonds and one σ dative bond.9 The relevance of dative bonds in main-group compounds, which goes back to original work by Lewis10 and Sidgwick,11 has been pointed out in several review articles.12 It became prominent with the discovery of carbones13 L→C←L and related species L→En←L (E = B–Tl, Si–Pb, and N–Bi; n = 1–3), where L is a donor ligand.14 The first compound with a beryllium–nitrogen double bond (CAAC)N BeR (CAAC = cyclic alkylaminocarbene; R = imino group) that is stable at ambient temperatures was recently synthesized by Gilliard.15 This came shortly after the isolation of the first stable compound with a beryllium–carbon bond featuring a double donation L2C
BeR (CAAC = cyclic alkylaminocarbene; R = imino group) that is stable at ambient temperatures was recently synthesized by Gilliard.15 This came shortly after the isolation of the first stable compound with a beryllium–carbon bond featuring a double donation L2C Be, which takes advantage of the appearance of two lone-pair orbitals at the C(0) atom of a carbone L2.16
Be, which takes advantage of the appearance of two lone-pair orbitals at the C(0) atom of a carbone L2.16
The examples show that the main group atoms of groups 2 and 13 can form molecules with double and triple bonds just like carbon, where alkene and alkyne compounds are ubiquitous. Molecules with multiple bonds between the heavier homologues of carbon are more difficult to synthesize, but even the heavy-atom group-14 homologues of alkynes REER (E = Si–Pb) could be isolated and were found to have trans-bent geometries.17–19 Triple bonds between two main group atoms appear to be the maximum bond order that can be achieved between two atoms, which have a valence shell with (n)s and (n)p orbitals. A few years ago, it was suggested that C2 has a quadruple bond that is stronger than the triple bond of acetylene,20 which was rejected by other authors.21 The controversy was most recently settled by an experimental study using a high-resolution photoelectron imaging spectrometer, which revealed that the dominant contribution to dicarbon bonding in C2 is a double-bonded configuration with two π-bonds and no accompanying σ-bond.22
Higher bond orders than 3 may be achieved by transition metals, which have a valence shell with (n)s, (n)p and (n − 1)d orbitals where the latter usually dominate in covalent bonds.23 There are numerous transition metal compounds known with the formal bond order 4 or even higher, because the (n − 1)d-AOs form additional bonding MOs in covalent bonds.24 Very recently it was shown that a quadruple bond between two atoms may even be achieved when only one of the atoms is a transition metal. The diatomic anion RhB− was experimentally detected and the transition to neutral RhB was studied by photoelectron spectroscopy.25 The analysis of the spectra and quantum chemical calculations suggest that the neutral molecule in its 1Σ+ electronic ground state possesses a quadruple bond Rh![[quadruple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e003.gif) B, which consists of two σ and two π bonds. The conclusion is that a quadruple bond between two atoms is possible when only one of the atoms is a transition metal.
B, which consists of two σ and two π bonds. The conclusion is that a quadruple bond between two atoms is possible when only one of the atoms is a transition metal.
Very recently it was shown that the heavier alkaline earth atoms Ae = Ca, Sr and Ba, which are main-group metals belonging to the s-shell elements of group 2, use mainly their (n − 1)d AOs for covalent bonding and that they exhibit the full scenario of transition-metal compounds. The octa-coordinated carbonyls Ae(CO)8 (ref. 26) and the isoelectronic dinitrogen adducts Ae(N2)8 (ref. 27) as well as the tris–benzene complexes Ae(Bz)3,28 which fulfill the 18-electron rule for transition metals, could be prepared in the gas phase and in low-temperature matrices. A systematic study of the valence orbitals of the alkaline earth atoms in a variety of compounds showed that the lighter atoms Be and Mg use their (n)s and (n)p orbitals in polar covalent bonds, whereas the valence orbitals of the heavier atoms Ca, Sr and Ba comprise (n)s and (n − 1)d orbitals.29 It was concluded that the alkaline earth metals beryllium and magnesium form covalent bonds like typical main-group elements, whereas calcium, strontium and barium covalently bind like transition metals.30 The finding lead to a theoretical study of the diatomic anions AeB− and the isoelectronic neutral species AeC (Ae = Ca, Sr, Ba), which have an electron triplet (3Σ−) ground state.31 The analysis of the bonding situation has shown that the six valence electrons occupy two bonding σ-orbitals with two electrons each and a degenerate π-orbital, in which each component has one electron. Accordingly, there are four occupied bond orbitals, but since there are only six valence electrons, the formal bond order is only three.31
In order to find a main-group molecule with a genuine quadruple bond where four bonding orbitals are doubly occupied, we searched for analogous systems with a larger number of valence electrons. A previous study of AeO showed that heavier molecules with Ae = Ca, Sr, Ba have only three doubly occupied MOs, because the oxygen atom is too electronegative for Ae←O σ-backdonation into a vacant dσ AO of the Ae atom. Here we report about the anions AeF− (Ae = Be–Ba), where the alkaline earth atoms are bonded to the electropositive fluorine anion. Since F− has a completely filled valence shell, it can only serve as a donor. In contrast to the isoelectronic Ne, the fluorine anion should be a somewhat stronger donor. Our work was stimulated by the recent joint experimental and theoretical study of BeF− by Heaven and co-workers,32 which showed that there is a strong dative bond between the closed-shell atoms Be and F−. The bond energy of BeF− has been estimated with a lower bound of 81.9 kcal mol−1, which shows that a dative bond between main-group atoms can be very strong.32 The nature of the bond in BeF− was analysed with a valence bond (VB) model by Kalemos, who reported a similar bond energy of ∼83 kcal mol−1 using high-level ab initio methods.33 Very recently, the results of laser cooling and quantum chemical calculation of the beryllium anions BeX− (X = F–I) were reported by Madi et al.34 There are no studies of the heavier fluorides AeF− (Ae = Mg–Ba) known to us. Here we report about the equilibrium geometries and bond dissociation energies (BDEs) of the full set of alkaline earth anions AeF− and we present a thorough analysis of the bonding situation. We also calculated the neutral compounds of the group-13 atoms EF (E = B–Tl) in order to compare the chemical bonds between the isoelectronic molecules.
2 Methods
The bond lengths, vibrational frequencies and BDEs of AeF− (Ae = Be–Ba) and EF (E = B–Tl) in the electronic singlet ground state were calculated at the CCSD(T)35 and BP86 (ref. 36) levels in conjunction with the basis sets def2-TZVPP and def2-QZVPP.37 The calculations were carried out with the program Gaussian 16.38 The NBO calculations were carried out using the program NBO 7.0.39 The QTAIM (Quantum Theory of Atoms in Molecules)40 calculations of the Laplacian distribution ∇2ρ(r) were performed with the Multiwfn program.41The bonding situation in the diatomic molecules was further analyzed by means of an energy decomposition analysis (EDA), which was introduced by Morokuma42 and by Ziegler and Rauk43 in conjunction with the natural orbitals for chemical valence (NOCV)44 method. The EDA-NOCV45 calculations were carried out with the ADF 2018.105 program package46 at the BP86-D3(BJ)47 level with the Slater-type basis function of DZP quality48 using the BP86/def2-QZVPP optimized geometries. DZP is a double-ζ quality basis set augmented by two sets of polarization functions. In this analysis, the intrinsic interaction energy (ΔEint) between two fragments can be divided into four energy components as follows:
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp. | (1) |
The electrostatic ΔEelstat term represents the quasiclassical electrostatic interaction between the unperturbed charge distributions of the prepared fragments, and the Pauli repulsion ΔEPauli corresponds to the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction, which properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the production wavefunction. Since we used D3(BJ), this method also gives dispersion contribution (ΔEdisp). The orbital term ΔEorb comprises the mixing of orbitals, charge transfer and polarization between the isolated fragments. The energy change involved in the latter step, which is the main difference between the Morokuma42 and Ziegler/Rauk43 approaches, is calculated with an extension of Slater's transition state method49 for energy differences. It is often referred to as the ETS method. The orbital term ΔEorb can be further decomposed into contributions from each irreducible representation of the point group of the interacting system as follows:
 | (2) |
The combination of the EDA with NOCV enables the partition of the total orbital interactions into pairwise contributions of the orbital interactions, which is very vital to get a complete picture of the bonding. The charge deformation Δρk(r), resulting from the mixing of the orbital pairs ψk(r) and ψ−k(r) of the interacting fragments, presents the amount and the shape of the charge flow due to the orbital interactions (eqn (3)), and the associated energy term ΔEorb provides the size of stabilizing orbital energy originated from such interaction (eqn (4)).
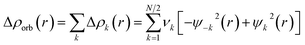 | (3) |
 | (4) |
More details about the EDA-NOCV method and its application are given in recent review articles.50
3 Bond lengths, vibrational frequencies and bond dissociation energies
Table 1 shows the calculated bond lengths and vibrational frequencies along with previous theoretical and experimental data. The bond distances at CCSD(T)/def2-TZVPP of BeF− and EF (E = B–Tl) agree quite well with experimental results and previous calculations.51 The BP86/def2-QZVPP values show slightly larger deviations but the agreement with the ab initio values and the experimental data is sufficient to use DFT calculations for the bonding analysis, which is discussed below. It is interesting that the BP86/def2-QZVPP bond lengths of AeF− (Ae = Ca, Sr, Ba) are slightly too short, whereas the interatomic distances for the isoelectronic molecules EF (E = Ga, In, Tl) are a bit too long, which might be due to the fact that spin–orbit coupling is neglected.| Atom Ae or E | Bond length | Frequencies | ||||||
|---|---|---|---|---|---|---|---|---|
| BP86a | CCSD(T)b | Exper. | Previous | BP86a | CCSD(T)b | Exper. | Previous | |
| a Using a def2-QZVPP basis set. b Using a def2-TZVPP basis set. c Ref. 51a. d Ref. 51b. e Ref. 51c. f Ref. 51d. g Ref. 32. h Ref. 33. i Ref. 51e. | ||||||||
| AeF − | ||||||||
| Be | 1.428 | 1.429 | — | 1.414g | 1019.7 | 1028.0 | 1059 ± 6g | 1073h |
| Mg | 1.847 | 1.840 | — | — | 548.3 | 577.7 | — | — |
| Ca | 1.992 | 2.104 | — | — | 517.3 | 485.6 | — | — |
| Sr | 2.134 | 2.237 | — | — | 432.8 | 410.6 | — | — |
| Ba | 2.234 | 2.399 | — | — | 411.7 | 408.3 | — | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| EF | ||||||||
| B | 1.274 | 1.273 | 1.267d | 1.264e | 1346.4 | 1396.5 | 1402d | 1394e |
| Al | 1.683 | 1.665 | 1.654d | 1.663c | 752.1 | 796.8 | 802d | 800c |
| Ga | 1.805 | 1.780 | 1.774d | — | 586.8 | 633.9 | 622d | — |
| In | 2.018 | 1.988 | 1.985d | 2.01f | 501.5 | 545.0 | 535d | 555f |
| Tl | 2.122 | 2.096 | 2.084d | 2.101i | 449.3 | 482.6 | 477d | — |
A related conclusion concerns the calculated vibrational frequencies, which will be helpful to identify the yet unknown anions AeF− (Ae = Mg–Ba). The agreement with experimental results and previous calculations is quite good and the BP86/def2-QZVPP values deviate only slightly from the CCSD(T)/def2-TZVPP data.
Table 2 shows the calculated BDEs of the molecules along with experimental results and previous calculations.51,52 The data for the alkaline earth anions AeF− suggest that the dative interactions between closed-shell atoms are very strong not only in BeF− but also in the heavier homologues. The trend of the BDEs for AeF− is very interesting, because it does not show the regular decrease in bond strength normally observed from the top to the bottom of the periodic table. The CCSD(T)/def2-TZVPP values show that the BDE of AeF− first decreases from Be to Mg, but then increases again and rises continuously with the unusual trend Ca < Sr < Ba. This is in striking contrast to the trend of the isoelectronic neutral species EF, where the BDE strongly decreases in the expected order B > Al > Ga > In > Tl. The BDE of TlF is only slightly stronger than one half of the BDE of BF, but the BDE of BaF− is not much less than the BDE of BeF−. The BP86/def2-QZVPP values for AeF− are very similar to the CCSD(T)/def2-TZVPP data. The BDEs for EF at BP86/def2-QZVPP are slightly higher than the more reliable CCSD(T)/def2-TZVPP values but the deviation is not substantial.
| Atom Ae or E | D e(Do) | |||
|---|---|---|---|---|
| BP86a | CCSD(T)b | Exper. | Previous calc. | |
| a Using a def2-QZVPP basis set. b Using a def2-TZVPP basis set. c Ref. 51b. d Ref. 51d. e Ref. 51c. i Ref. 52. g Ref. 32. h Ref. 33. | ||||
| AeF − | ||||
| Be | 88.7 (87.3) | 87.5 (86.0) | (≥81.4g) | 82.9h |
| Mg | 61.9 (61.1) | 68.8 (68.0) | — | — |
| Ca | 82.1 (81.4) | 73.7 (73.0) | — | — |
| Sr | 76.8 (76.2) | 77.5 (76.9) | — | — |
| Ba | 83.0 (82.4) | 80.5 (79.9) | — | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| EF | ||||
| B | 185.6 (183.7) | 177.5 (175.5) | 182.1c (180.1c) | 182.7e |
| Al | 163.1 (162.0) | 157.4 (156.3) | 160.0c (158.9c) | 162.1i |
| Ga | 144.8 (144.0) | 137.8 (136.9) | 138.8c (137.9c) | — |
| In | 133.5 (132.8) | 124.7 (123.9) | 121.9c (121.1c) | 122.0d |
| Tl | 125.8 (125.2) | 115.4 (114.7) | 106.2c (105.4c) | — |
The size and the trend of the BDEs of AeF− are surprising and they contradict common wisdom that chemical bonding between closed-shell atoms is weak.53 The analysis of the interatomic interactions is discussed in the next section.
4 Bonding analysis
A pivotal piece of information about the chemical bonding in the diatomic molecules AeF− and EF is given by the atomic partial charges, which indicates the electronic charge distribution. Table 3 shows the calculated atomic charges of the four different methods used, namely the NBO, Hirshfeld, Voronoi and CM5 partitioning. The NBO results for the anions AeF− suggest that there is very little charge donation from F− to Ae. The magnesium species MgF− is a particularly interesting system, because it exhibits according to the NBO results no charge migration Mg←F− at all although it has a BDE of De = 68.8 kcal mol−1. In contrast to NBO, the Hirshfeld, Voronoi and CM5 methods indicate that there is a substantial donation of Ae←F− for all systems, with the CM5 method giving smaller partial charges.| q | P(A–B) | ||||||
|---|---|---|---|---|---|---|---|
| Atom | NBO | Hirshfeld | Voronoi | CM5 | Bond | Wiberg | Mayer |
| Be | −0.02 | −0.65 | −0.59 | −0.49 | Be–F | 0.25 | 1.13 |
| Mg | 0.00 | −0.51 | −0.43 | −0.41 | Mg–F | 0.14 | 0.58 |
| Ca | −0.08 | −0.55 | −0.51 | −0.40 | Ca–F | 0.30 | 0.70 |
| Sr | −0.06 | −0.52 | −0.49 | −0.36 | Sr–F | 0.25 | 0.66 |
| Ba | −0.07 | −0.54 | −0.54 | −0.37 | Ba–F | 0.28 | 0.66 |
| B | 0.54 | 0.05 | 0.03 | 0.00 | B–F | 0.85 | 1.41 |
| Al | 0.83 | 0.30 | 0.26 | 0.29 | Al–F | 0.34 | 1.05 |
| Ga | 0.80 | 0.33 | 0.32 | 0.34 | Ga–F | 0.39 | 0.93 |
| In | 0.83 | 0.38 | 0.36 | 0.41 | In–F | 0.34 | 0.83 |
| Tl | 0.82 | 0.41 | 0.40 | 0.44 | Tl–F | 0.35 | 0.78 |
The negligible charge donation by the NBO method can be explained by its dubious way of division between valence and Rydberg orbitals and the bias in favour of the valence AOs in the algorithm. The NBO procedure considers only those AOs as valence orbitals, which are occupied in the electronic ground state of the atom, while vacant AOs are considered as Rydberg orbitals. It means that only the (n)s AOs of Be–Ba are treated as valence orbitals by the NBO method but not the (n)p and (n − 1)d AOs. The contributions of the latter AOs are neglected in the NBO calculation of bonding MOs and thus, the occupation of the (n)p and (n − 1)d AOs of Be–Ba due to Ae←F− is mistreated. A related problem was recently reported for the systems ENi(CO)3− (E = Li–Cs),54 where the covalent bond between Ni and the alkaline earth atoms E–Ni is neglected by the NBO method, because the (n)p AOs of Ni and E atoms are not considered as valence orbitals.55
The NBO method calculates, in contrast to the anions AeF−, a much larger charge migration in the neutral systems EF (E = B–Tl) E→F than the Hirshfeld, Voronoi and CM5 methods. The difference is not due to the division of the AOs in valence and Rydberg orbitals, because the (n)s and (n)p AOs of B–Tl are both considered as valence AOs in the NBO method since both are occupied in the atomic ground states. The very small partial charges calculated for BF by the Hirshfeld, Voronoi and CM5 methods appear to contradict chemical intuition, because fluorine has a much higher electronegativity than boron. But the migration of the σ charge B→F is partly compensated for by the backdonation of the π charge from the two degenerate π orbitals of fluorine B F. It has been shown before that π donation from fluorine is not negligible.56
F. It has been shown before that π donation from fluorine is not negligible.56
Table 3 gives also the calculated bond orders PAB using the Wiberg57 and Mayer58 approaches. The Wiberg bond order (WBO) method is based on the semiempirical CNDO method and it neglects the overlap of the AOs. The Mayer bond order (MBO) considers the overlap and it is better suited for polar bonds.59 The MBO values in Table 3 are significantly larger than the WBO data and they are always bigger for neutral EF than for the isoelectronic anion AeF−. The numerical values appear to contradict the existence of multiple bonds particularly for AeF−. However, the bonds are very polar, which gives low values for the bond order.60
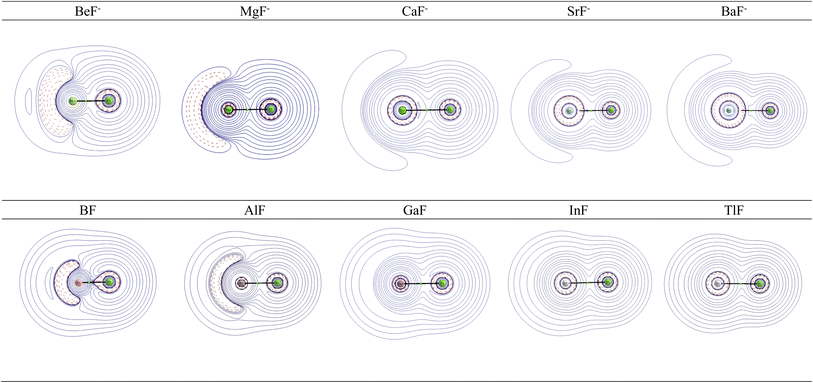
Further information about the charge distribution in the molecules is provided by the shape of relevant molecular orbitals and by the Laplacian ∇2ρ(r). The atomic charges are only scalar quantities, which do not give any insight into the local charge concentration, which is of central importance for the physical and chemical properties of a molecule. Fig. 1 shows the shape of the highest occupied MOs (HOMO) of the molecules, which provides a first hint about the interatomic interactions. The HOMO of AeF− has σ symmetry, which is essentially a lone-pair orbital at the Ae atom that is composed of the (n)s and (n)pσ AOs of Be and Mg and the (n)s and (n − 1)dσ AOs of Ca, Sr, and Ba. There is a small bonding contribution from the 2s and 2pσ AOs of fluorine. The HOMO of EF has a similar shape, but the contribution of the 2s and 2pσ AOs of F is larger and therefore the polarity of the orbital is smaller. Moreover, the AO part of the E atom is always a hybrid of the (n)s and (n)pσ AOs with negligible (n − 1)d contribution, which emphasizes the peculiar covalent bonding of the heavier alkaline earth atoms.
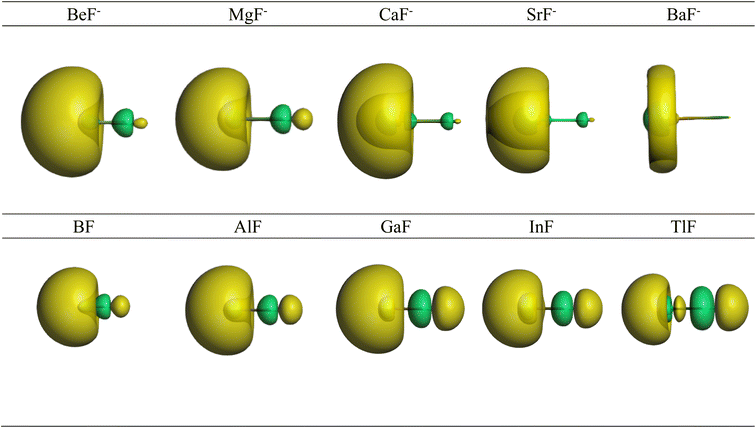 | ||
| Fig. 1 Shape of the HOMO of AeF− (Ae = Be–Ba) and EF (E = B–Tl). The Ae/E atoms are on the left side and the fluorine atom on the right. | ||
Fig. 2 shows the shape of the Laplacian distribution ∇2ρ(r) of the molecules. There is a local area of charge concentration ∇2ρ(r) < 0 in AeF− in the lone-pair region of the Ae atom, which becomes more diffuse for the heavier atoms. In contrast, the charge concentration in AeF− at F exhibits a very spherical shape with only a very weak droplet-like appendix in BeF−. The Laplacian distribution ∇2ρ(r) of EF shows a similar anisotropic charge distribution to that in AeF−, but the area of charge concentration ∇2ρ(r) < 0 at B and Al is more condensed and closer to the nucleus than at Be and Mg in the isoelectronic anions BeF− and MgF−. Visual inspection of the Laplacian distribution of GaF, InF and TlF suggests that the local area of charge concentration is obscured and it becomes indistinguishable with the in-plane π charge distribution.
Table 4 shows the calculated electric dipole moments of the molecules in comparison with previous work.61 The agreement between the calculated and experimental values is quite good. The experimental value for BF has a rather large uncertainty, because the experimental setup is difficult and it has been suggested that the experimental value is underestimated.62 Our values agree reasonably well with the most recent theoretical data. It is noteworthy that the BP86/def2-QZVPP values are in good agreement with the CCSD(T)/def2-TZVPP data.
| CCSD(T)/def2-TZVPP | BP86/def2-QZVPP | Previous | Experim. | |
|---|---|---|---|---|
| a Ref. 61c. b Ref. 61b. c Ref. 61a. d Ref. 61d. e Ref. 61e. f Ref. 61f. g Ref. 61g. h Ref. 61h. | ||||
| BeF− (Be→F) | −5.97 | −5.78 | — | — |
| MgF− (Mg→F) | −2.80 | −2.90 | — | — |
| CaF− (Ca→F) | −3.27 | −3.32 | — | — |
| SrF− (Sr→F) | −1.90 | −1.86 | — | — |
| BaF− (Ba→F) | −1.78 | −2.04 | — | — |
| BF (B→F) | −0.82 | −1.03 | −0.877c | −0.5 ± 0.2g |
| AlF (Al←F) | 1.37 | 1.49 | 1.407a; 1.54f | 1.515b |
| GaF (Ga←F) | 2.25 | 2.27 | 2.22h | 2.45d |
| InF (In←F) | 3.24 | 3.24 | 2.86h | 3.40d |
| TlF (Tl←F) | 4.39 | 4.04 | 3.21h | 4.23e |
The electric dipole moment of charged molecules depends on the origin of the coordinate system.63 The values of AeF− have been calculated with respect to the mass center of the nuclear charge, which is the conventional choice. The theoretically predicted dipole moments of AeF− at the CCSD(T)/def2-TZVPP level range from an amazing value of 5.97 Debye for BeF− to 1.78 Debye for BaF− with the negative end always at the Ae atom. The highly anisotropic charge distribution in AeF− represented by the Laplacian distribution (Fig. 2) explains the surprising size and orientation of the dipole moments, which are vector quantities reflecting the spherical distribution of the electronic charge. There is a local region of charge concentration in the lone pair region of Ae that is quite distant from the nucleus. In contrast, the negative charge on the fluorine in AeF− is spherical around the nucleus, resulting in a comparatively small atomic contribution to the dipole moment. The interatomic distance in AeF− increases, which leads to smaller absolute values of the dipole moment, because the bonding component to the dipole moment, which is dominated by the bond polarity toward fluorine, cancels part of the very large atomic component of Ae due to its anisotropic charge distribution. The increase of the dipole moment from MgF− to CaF− is likely caused by the change from sp hybridization at Mg to sd hybridization at Ca, which is discussed below.
Table 4 shows that the dipole moment at BF also has the negative pole at the less electronegative atom B, but the absolute value of 0.82 Debye is much smaller than that for isoelectronic BeF−. Moreover, the polarity of the dipole moment reverses and the absolute values increase with atomic size for the heavier systems AlF–TlF. The dipole moment of BF has been calculated before and the inverse polarity B→F has been discussed using VB and MO methods.61a,i,k The studies underline the particular role of the lone pair MO at beryllium, which yields a large atomic contribution to the dipole moment. This becomes obvious from the shape of the Laplacian distribution of BF in Fig. 2, which displays a clear region of charge accumulation ∇2ρ(r) < 0 at boron. A comparison with the Laplacian of BeF− shows that the charge accumulation at B in BF is more concentrated and closer to the nucleus than the charge accumulation at Be in BeF−. This explains why BF has a much smaller dipole moment than BeF−. The inverse polarity in AlF with respect to BF has been noted before61c,f and was explained by the longer bond in the former molecule. Klein and Rosmus64 showed that the dipole moments of BF and AlF have a similar slope as a function of the interatomic distance and that the dipole moment function of AlF also has a region with a polarity Al→F, but due to the larger equilibrium bond length the polarity in the vibrational ground state is Al←F. The contribution of the electronic charge in the bonding region of AlF, which is polarized towards F, overcompensates the atomic component of the anisotropic charge distribution at Al and yields a dipole moment with the polarity Al←F. This effect increases further when the bonds become longer and when the atoms E in EF become more electropositive. The decrease of the dipole moments of AeF− and the increase of the dipole moments of EF can thus straightforwardly be explained when the spatial charge distribution of the electronic charge is considered. The atomic partial charges are not sufficient to explain the dipole moments, because they are scalar values whereas dipole moments are vector quantities.
We investigated the nature of the bonds in the AeF−/EF systems using the EDA-NOCV method, which gives a detailed description of the interatomic interactions in terms of electrostatic attraction, Pauli repulsion and pairwise orbital interactions. The goal was to provide a physically meaningful explanation for the surprisingly strong BDEs and the unusual trend of the bond strength in terms of a bonding model using a method, which has been proven to be very useful in a large variety of molecules.50,65Table 5 gives the numerical results for BeF− and MgF− using the neutral atoms Ae and F− as interacting moieties. The results for the heavier homologues CaF−, SrF− and BaF− show significant differences and are discussed separately.
| Energy term | Orbital interaction | Be (1S) + F− (1S) | Mg (1S) + F− (1S) |
|---|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | |||
| ΔEint | −93.45 | −72.64 | |
| ΔEPauli | 186.70 | 93.03 | |
| ΔEdispa | −0.4 (0.1%) | −0.5 (0.3%) | |
| ΔEelstata | −165.8 (59.2%) | −96.3 (58.1%) | |
| ΔEorba | −114.0 (40.7%) | −68.8 (41.6%) | |
| ΔEorb1b | Ae←F− σ polarization/induction | −77.8 (68.3%) | −47.7 (69.2%) |
| ΔEorb2b | Ae←F− π donation | −14.6 (12.8%) | −8.9 (13.0%) |
| ΔEorb3b | Ae←F− π donation | −14.6 (12.8%) | −8.9 (13.0%) |
| ΔEorb4b | Ae←F− σ polarization/induction | −6.3 (5.5%) | −2.7 (4.0%) |
| ΔErestb | −0.6 (0.6%) | −0.6 (0.8%) | |
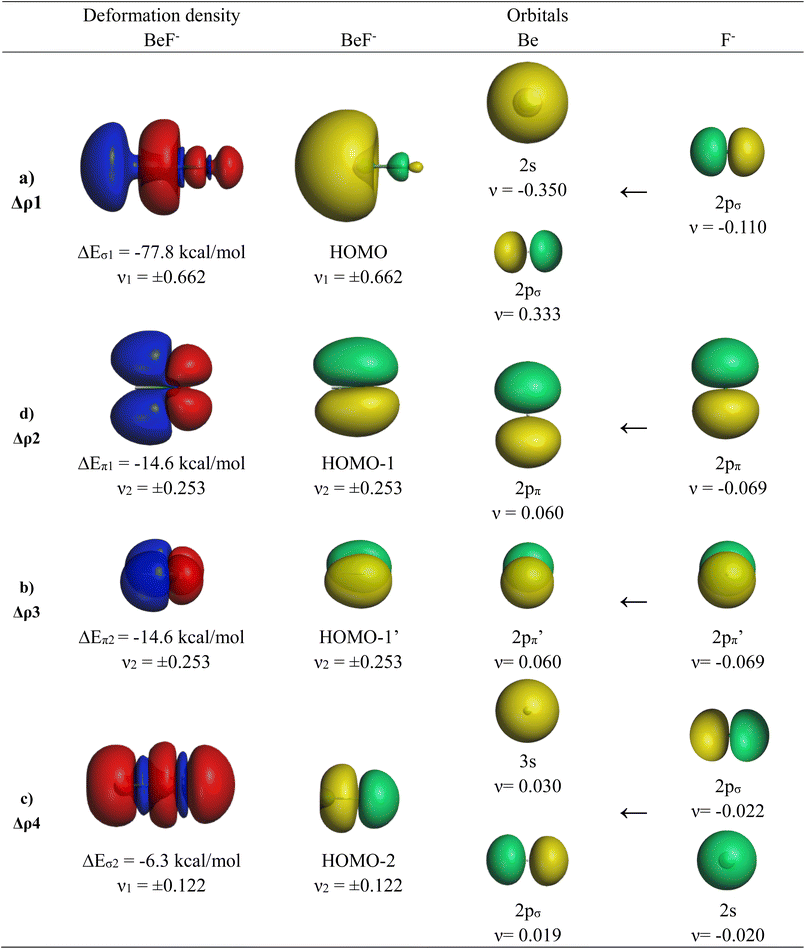
The calculations suggest that the attractive interactions between Ae and F− have ∼60% electrostatic character, whereas ∼40% comes from orbital (covalent) interactions ΔEorb. It is noteworthy that the trend of the orbital interaction closely follows the trend of the total interaction energy ΔEint. The breakdown of the total orbital term into pairwise interactions gives four major contributions ΔEorb1–ΔEorb4, which can be identified by inspecting the associated deformation densities and the connected orbitals. They are shown for BeF− in Fig. 3. The deformation densities and orbitals of MgF− are very similar and they are shown in Fig. S1 of the ESI.‡
The strongest orbital contribution ΔEorb1 in AeF− (Ae = Be, Mg) comes from a polarization of the (n)s AO of Ae through the inductive charge interaction of the 2pσ AO of F−, which leads to a (n)s/(n)pσ hybridization at Ae. The deformation density in Fig. 3 shows that there is mainly charge migration to the terminal end of Be, but also a small charge accumulation in the bonding region leading to energy lowering due to the donation of the 2pσ AO of F− into the vacant (n)pσ AO of Ae. The HOMO of AeF− is mainly a lone-pair orbital at Ae but it has an energetically significant Ae–F− bonding contribution. The weaker orbital terms ΔEorb2 and ΔEorb3 come from the degenerate π bonding orbitals HOMO−1 and HOMO−1′, which are due to the dative π interaction (n)pπ(Ae)←2pπ(F−). The nature of the fourth orbital interaction ΔEorb4 is interesting. The orbital HOMO−2 in AeF− (Ae = Be, Mg) suggests that it is also a σ bonding orbital. The nature of this orbital in isoelectronic CO has been discussed in great detail and it was shown that the bonding character depends on the different electronegativities of the atoms.66 The shape of the deformation density of Δρ4 suggests some charge accumulation in the (n)pσ AOs of the atoms originating from the corresponding depletion from F− 2s/2pσ, which yields a small energy lowering. The mixing of the vacant 3s AO of Be comes from the diffuse negative charge of the anion. But the stabilization of ΔEorb4 in BeF− and particularly in MgF− is very small and it is too small to declare the molecules as quadruply bonded species. The analysis of the orbital interaction by the EDA-NOCV method agrees with the suggestion of dative bonding as originally suggested by Heaven et al.32
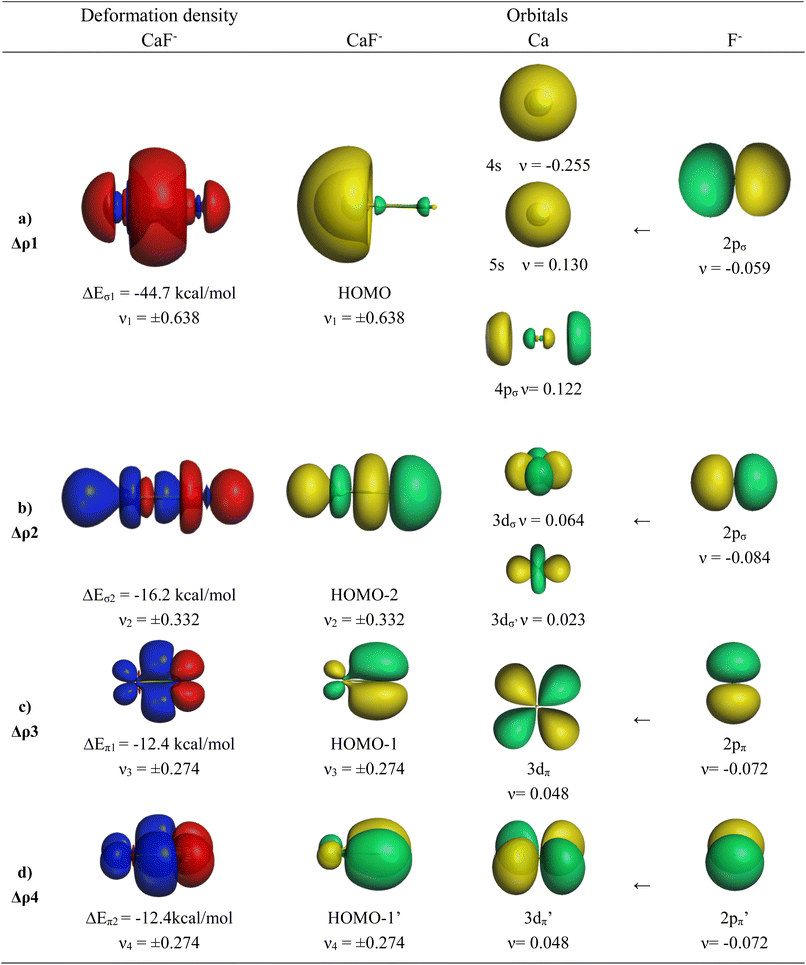
The EDA-NOCV results for the heavier homologues CaF−/SrF−/BaF− exhibit significant differences to the lighter systems BeF−/MgF− and they show some peculiar features. The numerical data are shown in Table 6. The deformation densities Δρ and the connected fragment orbitals of CaF− are shown in Fig. 4. The plots of the heavier systems SrF− and BaF− look very similar and are shown in Fig. S2 and S3 of the ESI.‡ The percentage contributions of covalent (orbital) interactions and coulombic forces are very similar in all five anions AeF−, but the pairwise orbital interactions in CaF−/SrF−/BaF− differ from the lighter systems BeF−/MgF−. The strongest orbital term ΔEorb1 in the heavier systems has a similar feature to that in the lighter homologues coming from the induction/polarization interaction between the occupied 2pσ AO of F− and the occupied and vacant AOs of Ae. In contrast to the lighter systems BeF−/MgF−, the second σ interaction ΔEorb2 in the heavier systems (which is ΔEorb4 in BeF−/MgF−) is quite strong and even stronger than the degenerate π bonding terms ΔEorb3/4 (Table 6). The inspection of the σ AOs of the atomic fragments in the ΔEorb2 of the heavier systems shows that the stabilizing interaction is due to Ae←F− donation from the occupied 2pσ AO of F− into the vacant (n)dσ AOs of Ae, which leads to the bonding orbital HOMO-2 (Fig. 4 and S2, S3‡). This is a profound difference from the lighter systems BeF−/MgF−, where the second σ-interaction provides only minor energy stabilization. Another difference concerns the AOs of the Ae atoms in the π bonding interactions. Fig. 4 and S2, S3‡ show that the degenerate π bonding terms ΔEorb3/4 of the heavier atoms Ca, Sr, and Ba involve the (n)dπ AOs of the metals, whereas the π bonding terms ΔEorb2/3 of BeF−/MgF− comprise the (n)pπ AOs. These are further examples for the finding that the valence orbitals of the heavier alkaline earth atoms Ca, Sr, and Ba are the (n)s and (n)d AOs.26–30 However, the most important conclusion is that the diatomic anions AeF− (Ae = Ca, Sr, Ba) have four polarized bonding orbitals due to the presence of d-valence AOs and therefore can be considered as quadruply bonded molecules.
| Energy term | Orbital interaction | Ca (1S) + F− (1S) (1S) | Sr (1S) + F− (1S) | Ba (1S) + F− (1S) |
|---|---|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | ||||
| ΔEint | −92.94 | −90.66 | −101.47 | |
| ΔEPauli | 108.59 | 97.57 | 104.78 | |
| ΔEdispa | −0.7 (0.4%) | −0.8 (0.4%) | −0.9 (0.4%) | |
| ΔEelstata | −113.8 (56.5%) | −104.0 (55.2%) | −110.5 (53.5%) | |
| ΔEorba | −87.0 (43.2%) | −83.5 (44.3%) | −94.9 (46.0%) | |
| ΔEorb1b | Ae←F− σ polarization/induction | −44.7 (51.4%) | −40.6 (48.7%) | −39.0 (41.1%) |
| ΔEorb2b | Ae←F− σ donation | −16.2 (18.6%) | −17.5 (21.0%) | −25.5 (26.9%) |
| ΔEorb3b | Ae←F− π donation | −12.4 (14.3%) | −11.9 (14.3%) | −14.1 (14.8%) |
| ΔEorb4b | Ae←F− π donation | −12.4 (14.3%) | −11.9 (14.3%) | −14.1 (14.8%) |
| ΔErestb | −1.3 (1.5%) | −1.4 (1.7%) | −2.2 (2.3%) | |
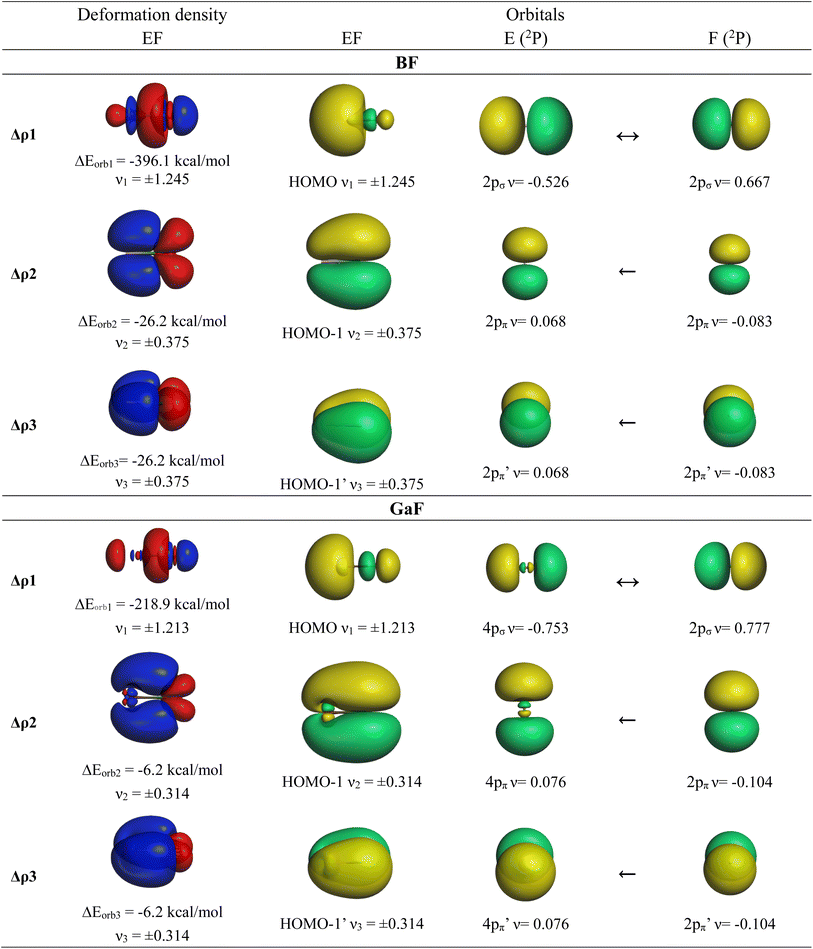
We also analyzed the chemical bonds in the group-13 fluorides EF (E = B–Tl) with the EDA-NOCV method. Table 7 gives the numerical results of the calculations. The deformation densities Δρ and the connected fragment orbitals of BF and GaF− are shown in Fig. 5. The plots of the other systems AlF, InF and TlF look very similar and are shown in Fig. S4 of the ESI.‡ The stabilizing contributions of the orbital (covalent) term ΔEorb are for all molecules ∼70% of the total attraction, which is a little higher than in the anions AeF−. As for the anions AeF−, the trend of the orbital interaction ΔEorb of EF is the same as that for the total interaction energy ΔEint. This is remarkable particularly for the heavier species showing the order GaF > InF > Tl, whereas the values of ΔEorb and ΔEint for BaF− are higher than those for CaF− (Tables 6 and 7). The breakdown of the total orbital interactions ΔEorb of EF into pairwise interactions agrees with chemical intuition. The covalent bonding comes mainly from the electron-sharing σ interaction ΔEorb1 due to pairing of the unpaired electrons, which provides > 85% of ΔEorb. The contribution of the degenerate E←F π donation ΔEorb2/3 is 10% in BF and it continuously decreases up to TlF, where it provides only 3% of ΔEorb. The shape of the deformation densities Δρ and the connected fragment orbitals of EF− show a conventional picture (Fig. 5, and S1–S3‡). The group-13 fluorides EF have strong σ single bonds reinforced by weak π bonds. All five occupied MOs of AeF− and EF are provided in Fig. S5–S12.‡
| Orbital interaction | B (2P) + F (2P) | Al (2P) + F (2P) | Ga (2P) + F (2P) | In (2P) + F (2P) | Tl (2P) + F (2P) |
|---|---|---|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb + ΔEdisp. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | |||||
| ΔEint | −183.42 | −160.45 | −141.71 | −130.85 | −123.37 |
| ΔEPauli | 486.98 | 246.13 | 197.47 | 151.46 | 125.83 |
| ΔEdispa | −0.3 (0.0%) | −0.6 (0.1%) | −0.5 (0.2%) | −0.6 (0.2%) | −0.7 (0.3%) |
| ΔEelstata | −210.8 (31.4%) | −120.9 (29.7%) | −103.8 (30.6%) | −79.9 (28.3%) | −67.4 (27.0%) |
| ΔEorba | −459.3 (68.5%) | −285.1 (70.1%) | −234.9 (69.2%) | −201.7 (71.5%) | −181.1 (72.7%) |
| ΔEorb1b | −396.1 (86.2%) | −261.7 (91.8%) | −218.9 (93.2%) | −191.1 (94.7%) | −173.3 (95.6%) |
| ΔEorb2b | −26.2 (5.7%) | −9.4 (3.3%) | −6.2 (2.7%) | −4.0 (2.0%) | −2.8 (1.5%) |
| ΔEorb3b | −26.2 (5.7%) | −9.4 (3.3%) | −6.2 (2.7%) | −4.0 (2.0%) | −2.8 (1.5%) |
| ΔErestb | −10.7 (2.3%) | −4.7 (1.6%) | −3.5 (1.5%) | −2.7 (1.3%) | −2.3 (1.3%) |
The peculiar orbital interaction in the anions AeF− and the unusual trend of the surprisingly large BDEs suggest that the polarizabilities of the Ae atoms might play a role in the calculated data. Table 8 shows the static dipole polarizabilities aD of Be–Ba, which have been recommended through evaluation of experimental and calculated data.67 The polarizability increases sharply as the atom becomes heavier, with a particularly large increase from Mg to Ca. This contributes to the interatomic attraction, which explains the unusual increase of the BDE of AeF− from Mg to Ba. One reviewer pointed out that the calculated dissociation energies correlate nicely with a charge induced dipole model (α/r4) except for Sr. This supports the conclusion that the chemical bonds and the peculiar bond strength of the latter systems are largely due to the charge induced interactions.
Summary
The results of this work can be summarized as follows:• The alkali earth fluoride anions AeF− (Ae = Be–Ba) have very strong bonds between the closed-shell species Ae and F−. The theoretically predicted bond dissociation energies De at CCSD(T)/def2-TZVPP are between 68.8 kcal mol−1 for MgF− and 87.5 kcal mol−1 for BeF− and they exhibit an unusual increasing trend MgF− < CaF− (73.7 kcal mol−1) < SrF− (77.5 kcal mol−1) < BaF− (80.5 kcal mol−1). This is in contrast to the isoelectronic group-13 fluorides EF (E = B–Tl), where the BDE continuously decreases from BF (177.5 kcal mol−1) to TlF (115.4 kcal mol−1).
• The calculated dipole moments of AeF− are very large between 5.97 D for BeF− and 1.78 D for BaF− with the negative end always located at the Ae atom (Ae→F−). This can be explained by the location of the electronic charge of a lone pair at Ae, which is rather distant from the nucleus.
• The analysis of the electronic structure of AeF− with different methods suggests a significant charge donation Ae←F− into the vacant valence orbitals of Ae. In contrast, calculations with the NBO method give negligible charge transfer, because the (n)p AOs of the alkaline earth atoms are not considered as valence orbitals.
• The EDA-NOCV calculations suggest that ∼60% of the attractive forces in AeF− come from the orbital interactions ΔEorb, which have the same trend as the total interactions ΔEint. The largest contribution ΔEorb1 is in all anions due to the inductive polarization of the 2pσ electrons of F−, which leads to a hybridization of the (n)s and (n)pσ AOs at Ae. There are two degenerate π donor interactions Ae←F− in all anions AeF−, which provide 25–30% to the covalent bonding. There is another σ orbital interaction ΔEorb4 in the anions, which is very weak in BeF− and MgF−. In contrast, the second stabilizing σ orbital interaction ΔEorb2 in CaF−, SrF− and BaF− yields a bonding orbital, because the Ae atoms use their (n − 1)dσ AOs for bonding. The energy lowering ΔEorb2 in the latter anions is even stronger than the π bonding of ΔEorb3/4. The EDA-NOCV results suggest that BeF− and MgF− have three strongly polarized bonds, whereas CaF−, SrF− and BaF− have four bonding orbitals. The quadruple bonds in the heavier alkaline earth species are made possible, because they use s d valence orbitals like transition metals for covalent bonding.
• The EDA-NOCV analysis of the group-13 fluorides EF gives a conventional picture with one very strong σ bond and two rather weak π interactions.
Data availability
Additional information is found in the ESI.‡Author contributions
R. Liu, L. Qin, Z. Zhang and F. Sagan carried out the calculations and analyzed the results. L. Zhao supervised the work at Nanjing and M. Mitoraj supervised the work at Cracow. G. Frenking was responsible for the conceptual framework of the project, analyzed the results and wrote the first draft of the manuscript. L. Zhao, M. Mitoraj and G. Frenking prepared the final version of the work.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
LZ and GF acknowledge the financial support from Nanjing Tech University (No. 39837123 and 39837132), the National Natural Science Foundation of China (No. 21973044), and the Natural Science Foundation of the Jiangsu province (BK20211587), and the International Cooperation Project at Nanjing Tech University. We appreciate the high performance center of Nanjing Tech University for supporting the computational resources. We thank the PL-Grid Infrastructure and the Academic Computational Centre Cyfronet of the University of Science and Technology in Krakow for providing additional computational resources.References
- (a) R. C. Fischer and P. P. Power, π-Bonding and the Lone Pair Effect in Multiple Bonds Involving Heavier Main Group Elements: Developments in the New Millennium, Chem. Rev., 2010, 110, 3877 CrossRef CAS PubMed; (b) A. Sekiguchi, Disilyne with a silicon-silicon triple bond: a new entry to multiple bond chemistry, Pure Appl. Chem., 2008, 80, 447 CrossRef CAS; (c) P. P. Power, Bonding and Reactivity of Heavier Group 14 Element Alkyne Analogues, Organometallics, 2007, 26, 4362 CrossRef CAS; (d) E. Rivard and P. P. Power, Multiple Bonding in Heavier Element Compounds Stabilized by Bulky Terphenyl Ligands, Inorg. Chem., 2007, 46, 10047 CrossRef CAS PubMed; (e) M. Weidenbruch, Triple Bonds of the Heavy Main-Group Elements: Acetylene and Alkylidyne Analogues of Group 14, Angew. Chem., Int. Ed., 2003, 42, 2222 CrossRef CAS PubMed; (f) M. Weidenbruch, From a Cyclotrisilane to a Cyclotriplumbane: Low Coordination and Multiple Bonding in Group 14 Chemistry, J. Organomet. Chem., 2002, 646, 39 CrossRef CAS.
- (a) M. Zhou, N. Tsumori, Z. Li, K. Fan, L. Andrews and Q. Xu, OCBBCO: A Neutral Molecule with Some Boron−Boron Triple Bond Character, J. Am. Chem. Soc., 2002, 124, 12936–12937 CrossRef CAS PubMed; (b) L. C. Ducati, N. Takagi and G. Frenking, Molecules with All Triple Bonds: OCBBCO, N2BBN2, and [OBBBBO]2−, J. Phys. Chem. A, 2009, 113, 11693–11698 CrossRef CAS PubMed.
- (a) H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Ambient-Temperature Isolation of a Compound with a Boron-Boron Triple Bond, Science, 2012, 336, 1420–1422 CrossRef CAS PubMed; (b) G. Frenking and N. Holzmann, A Boron-Boron Triple Bond, Science, 2012, 336, 1394–1395 CrossRef CAS PubMed; (c) R. Köppe and H. Schnöckel, The Boron–Boron Triple Bond? A Thermodynamic and Force Field based Interpretation of the N-heterocyclic Carbene (NHC) Stabilization Procedure, Chem. Sci., 2015, 6, 1199–1205 RSC; (d) N. Holzmann, M. Hermann and G. Frenking, The Boron–Boron Triple Bond in NHC→B≡B←NHC, Chem. Sci., 2015, 6, 4089–4094 RSC.
- J. Su, X.-W. Li, R. C. Crittendon and G. H. Robinson, J. Am. Chem. Soc., 1997, 119, 5471 CrossRef CAS.
- (a) F. A. Cotton, A. H. Cowley and X. Feng, J. Am. Chem. Soc., 1998, 120, 1795 CrossRef CAS; (b) T. L. Allen, W. H. Fink and P. P. Power, Theoretical studies of multiple bonds in gallium–gallium and germanium–germanium compounds, J. Chem. Soc., Dalton Trans., 2000, 407–412 RSC.
- V. Nesterov, D. Reiter, P. Bag, P. Frisch, R. Holzner, A. Porzelt and S. Inoue, NHCs in Main Group Chemistry, Chem. Rev., 2018, 118, 9678–9842 CrossRef CAS PubMed.
- (a) P. Bag, A. Porzelt, P. J. Altmann and S. Inoue, A Stable Neutral Compound with an Aluminum−Aluminum Double Bond, J. Am. Chem. Soc., 2017, 139, 14384–14387 CrossRef CAS PubMed; (b) R. J. Wright, A. D. Phillips and P. P. Power, The [2 + 4] Diels-Alder Cycloaddition Product of a Probable Dialuminene, Ar′AlAlAr′ (Ar′ = C6H3 – 2,6-Dipp2; Dipp = C6 H3–2,6-Pri2), with Toluene, J. Am. Chem. Soc., 2003, 125, 10784 CrossRef CAS PubMed; (c) J. D. Queen, S. Irvankoski, J. C. Fettinger, H. M. Tuononen and P. P. Power, A Monomeric Aluminum Imide (Iminoalane) with Al–N Triple-Bonding: Bonding Analysis and Dispersion Energy Stabilization, J. Am. Chem. Soc., 2021, 143(17), 6351–6356 CrossRef CAS PubMed.
- L. Wang, S. Pan, G. Wang, X. Zeng, M. Zhou and G. Frenking, Triple Bonding Between Beryllium and Nitrogen in HNBeCO, Chem. Commun., 2022, 58, 8532 RSC.
- G. Frenking, C. Loschen, A. Krapp, S. Fau and S. H. Strauss, Electronic Structure of CO–An Exercise in Modern Chemical Bonding Theory, J. Comput. Chem., 2006, 28, 117 CrossRef PubMed.
- (a) G. N. Lewis, Acids and bases, J. Franklin Inst., 1938, 226, 293–313 CrossRef; (b) M. Hermann and G. Frenking, Gilbert Lewis and the Model of Dative Bonding, Struct. Bond, 2016, 169, 131 CrossRef.
- (a) N. V. Sidgwick, Co-ordination Compounds and the Bohr Atom, J. Chem. Soc., 1923, 123, 725–730 RSC; (b) N. V. Sidgwick, The Electronic Theory of Valency, Clarendon Press, Oxford, 1927 Search PubMed; (c) N. V. Sidgwick, Structure of Divalent Carbon Compounds, Chem. Rev., 1931, 9, 77–88 CrossRef CAS.
- (a) A. Haaland, Covalent versus Dative Bonds to Main Group Metals, a Useful Distinction, Angew. Chem., Int. Ed., 1989, 28, 992–1007 CrossRef; (b) L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Dative Bonding in Main Group Compounds, Coord. Chem. Rev., 2017, 344, 163 CrossRef CAS; (c) L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 8781–8845 CrossRef CAS PubMed.
- (a) R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Angew. Chem., Int. Ed., 2006, 45, 8038 CrossRef CAS PubMed; (b) R. Tonner and G. Frenking, Angew. Chem., Int. Ed., 2007, 46, 8695 CrossRef CAS PubMed; (c) R. Tonner and G. Frenking, Chem.–Eur. J., 2008, 14, 3260 CrossRef CAS PubMed; (d) R. Tonner and G. Frenking, Chem.–Eur. J., 2008, 14, 3273 CrossRef CAS PubMed.
- Reviews: (a) G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, New Bonding Modes of Carbon and Heavier Group 14 Atoms Si–Pb, Chem. Soc. Rev., 2014, 43, 5106–5139 RSC; (b) G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Donor–Acceptor Bonding in Novel Low-Coordinated Compounds of Boron and Group-14 Atoms C–Sn, Chem. Soc. Rev., 2016, 45, 1129–1144 RSC; (c) W. Petz and G. Frenking, Neutral and Charged Group 13–16 Homologues of Carbones EL2 (E = B-–In-; Si–Pb; N+–Bi+, O2+–Te2+), Prog. Inorg. Chem., 2022, 79, 243 Search PubMed.
- G. Wang, J. E. Walley, D. A. Dickie, A. Molino, D. J. D. Wilson and R. J. Gilliard Jr, s-Block Multiple Bonds: Isolation of a Beryllium Imido Complex, Angew. Chem., Int. Ed., 2021, 60, 9407 CrossRef CAS PubMed.
- M. R. Buchner, S. Pan, C. Poggel, N. Spang, M. Müller, G. Frenking and J. Sundermeyer, Di-ortho-beryllated carbodiphosphorane: A Compound with a Metal−Carbon Double Bond to an Element of the s-Block, Organometallics, 2020, 39, 3224 CrossRef CAS.
- (a) A. Sekiguchi, R. Kinjo and M. Ichinohe, A Stable Compound Containing a Silicon-Silicon Triple Bond, Science, 2004, 305, 1755–1757 CrossRef CAS PubMed; (b) M. Stender, A. D. Phillips, R. J. Wright and P. P. Power, Synthesis and Characterization of a Digermanium Analogue of an Alkyne, Angew. Chem., Int. Ed., 2002, 41, 1785–1787 CrossRef CAS; (c) A. D. Phillips, R. J. Wright, M. M. Olmstead and P. P. Power, Synthesis and Characterization of 2,6-Dipp2-H3C6SnSnC6H3-2,6-Dipp2 (Dipp = C6H3-2,6-iPr2): A Tin Analogue of an Alkyne, J. Am. Chem. Soc., 2002, 124, 5930–5931 CrossRef CAS PubMed; (d) L. Pu, B. Twamley and P. P. Power, Synthesis and Characterization of 2,6-Trip2H3C6PbPbC6H3-2,6-Trip2 (Trip = C6H2-2,4,6-iPr3): A Stable Heavier Group 14 Element Analogue of an Alkyne, J. Am. Chem. Soc., 2000, 122, 3524–3525 CrossRef CAS.
- For the earlier syntheses of the parent systems HEEH in low-temperature matrices see: (a) M. Bogey, H. Bolvin, C. Demuyneck and J. L. Destombes, Nonclassical Double-Bridged Structure in Silicon-Containing Molecules: Experimental Evidence in Si2H2 from its Submillimeter-Wave Spectrum, Phys. Rev. Lett., 1991, 66, 413 CrossRef CAS PubMed; (b) M. Cordonnier, M. Bogey, C. Demuynck and J.-L. Destombes, Nonclassical Structures in Silicon-Containing Molecules: The Monobridged Isomer of Si2H2, J. Chem. Phys., 1992, 97, 7984 CrossRef CAS; (c) X. Wang, L. Andrews and G. Kushto, Infrared Spectra of the Novel Ge2H2 and Ge2H4 Species and the Reactive GeH1,2,3 Intermediates in Solid Neon, Deuterium and Argon, J. Phys. Chem. A, 2002, 106, 5809–5816 CrossRef CAS; (d) X. Wang, L. Andrews, G. V. Chertihin and P. F. Souer, Infrared Spectra of the Novel Sn2H2 Species and the Reactive SnH1,2,3 and PbH1,2,3 Intermediates in Solid Neon, Deuterium, and Argon, J. Phys. Chem. A, 2002, 106, 6302–6308 CrossRef CAS; (e) X. Wang and L. Andrews, Infrared Spectra of Group 14 Hydrides in Solid Hydrogen: Experimental Observation of PbH4, Pb2H2 and Pb2H4, J. Am. Chem. Soc., 2003, 125, 6581–6587 CrossRef CAS PubMed.
- For an explanation of the trans-bent geometries in the heavier molecules HEEH (E = Si–Pb) see: M. Lein, A. Krapp and G. Frenking, Why Do the Heavy-Atom Analogues of Acetylene E2H2 (E = Si−Pb) Exhibit Unusual Structures?, J. Am. Chem. Soc., 2005, 127, 6290–6299 CrossRef CAS PubMed.
- (a) S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Quadruple Bonding in C2 and Analogous Eight-Valence Electron Species, Nat. Chem., 2012, 4, 195–200 CrossRef CAS PubMed; (b) S. Shaik, H. S. Rzepa and R. Hoffmann, One Molecule, Two Atoms, Three Views, Four Bonds?, Angew. Chem., Int. Ed., 2013, 52, 3020–3033 CrossRef CAS PubMed; (c) D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, The Nature of the Fourth Bond in the Ground State of C2: The Quadruple Bond Conundrum, Chem.–Eur. J., 2014, 20, 6220–6232 CrossRef CAS PubMed; (d) S. Shaik, D. Danovich, B. Braida and P. C. Hiberty, The Quadruple Bonding in C2 Reproduces the Properties of the Molecule, Chem.–Eur. J., 2016, 22, 4116–4128 CrossRef CAS PubMed.
- (a) M. Hermann and G. Frenking, The Chemical Bond in C2, Chem.–Eur. J., 2016, 22, 4100–4108 CrossRef CAS PubMed; (b) W. Zou and D. Cremer, C2 in a Box: Determining Its Intrinsic Bond Strength for the X1Σg+ Ground State, Chem.–Eur. J., 2016, 22, 4087–4099 CrossRef CAS PubMed; (c) M. Piris, X. Lopez and J. M. Ugalde, The Bond Order of C2 from a Strictly N-Representable Natural Orbital Energy Functional Perspective, Chem.–Eur. J., 2016, 22, 4109–4115 CrossRef CAS PubMed; (d) D. L. Cooper, R. Ponec and M. Kohout, New insights from domain-averaged Fermi holes and bond order analysis into the bonding conundrum in C2, Mol. Phys., 2016, 114, 1270–1284 CrossRef CAS; (e) L. T. Xu Jr and T. H. Dunning, Insights into the Perplexing Nature of the Bonding in C2 from Generalized Valence Bond Calculations, J. Chem. Theory Comput., 2014, 10, 195–201 CrossRef PubMed; (f) D. W. O. de Sousa and M. A. C. Nascimento, Is There a Quadruple Bond in C2?, J. Chem. Theory Comput., 2016, 12, 2234–2241 CrossRef CAS PubMed.
- B. A. Laws, S. T. Gibson, B. R. Lewis and R. W. Field, The dicarbon bonding puzzle viewed with photoelectron imaging, Nat. Commun., 2019, 10, 5199 CrossRef CAS PubMed.
- G. Frenking and N. Fröhlich, The Nature of the Bonding in Transition-Metal Compounds, Chem. Rev., 2000, 100, 717–774 CrossRef CAS PubMed.
- F. A. Cotton, L. A. Murillo and R. A. Walton, Multiple Bonds Between Metal Atoms, Springer, Berlin, 3rd edn, 2005 Search PubMed.
- L. F. Cheung, T.-T. Chen, G. S. Kocheril, W.-J. Chen, J. Czekner and L.-S. Wang, Observation of Four-Fold Boron–Metal Bonds in RhB(BO–) and RhB, J. Phys. Chem. Lett., 2020, 11(3), 659–663 CrossRef CAS PubMed.
- X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Observation of Alkaline Earth Complexes M(CO)8 (M = Ca, Sr, Ba) that Mimic Transition Metals, Science, 2018, 361, 912 CrossRef CAS PubMed.
- Q. Wang, S. Pan, S. Lei, J. Jin, G. Deng, G. Wang, L. Zhao, M. Zhou and G. Frenking, Dinitrogen Activation with Alkaline Earth Metals: Octa-Coordinated Complexes M(N2)8 (M = Ca, Sr, Ba), Nat. Commun., 2019, 10, 3375 CrossRef PubMed.
- Q. Wang, S. Pan, Y. Wu, G. Deng, J.-H. Bian, G. Wang, L. Zhao, M. Zhou and G. Frenking, Transition-Metal Chemistry of Alkaline-Earth Elements: The Trisbenzene Complexes M(Bz)3 (M = Sr, Ba), Angew. Chem., Int. Ed., 2019, 58, 17365 CrossRef CAS PubMed.
- I. Fernandez, N. Holzmann and G. Frenking, The Valence Orbitals of the Alkaline Earth Atoms, Chem.–Eur. J., 2020, 26, 14194 CrossRef CAS PubMed.
- G. Frenking and M. Zhou, The Transition Metal Chemistry of the Heavier Alkaline Earth Atoms Ca, Sr, Ba, Acc. Chem. Res., 2021, 54, 3071 CrossRef PubMed.
- Y.-q. Liu, M.-h. Wang, B. Yan, L. Li, S. Pan, Z.-h. Cui and G. Frenking, Quest of Quadruple Bonding Between Two Main-Group Atoms in AeB- and AeC (Ae = Ca, Sr, Ba) and the Role of d Orbitals of Heavier Alkaline-Earth Atoms in Covalent Interactions, CCS Chem., 2023, e202300446 Search PubMed , submitted for publ..
- M. L. Green, P. Jean and M. C. Heaven, Dative Bonding between Closed-Shell Atoms: The BeF- Anion, J. Phys. Chem. Lett., 2018, 9, 1999–2002 CrossRef CAS PubMed.
- A. Kalemos, The Nature of the Chemical Bond in BeF− and Related Species, J. Phys. Chem. A, 2018, 122, 8882–8885 CrossRef CAS PubMed.
- A. Madi, N. El-Kork, I. Zeid and M. Korek, Laser cooling and electronic structure of Be halide anions BeX− (X = Cl, Br, F, and I), J. Chem. Phys., 2022, 157, 024104 CrossRef CAS PubMed.
- G. D. Purvis and R. J. Bartlett, A full coupled-cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- (a) A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed; (b) J. P. Perdew, Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: New Vistas in Localized and Delocalized Chemical Bonding Theory, J. Comput. Chem., 2019, 40, 2234–2241 CrossRef CAS PubMed.
- (a) R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994 Search PubMed; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. Morokuma, Molecular Orbital Studies of Hydrogen Bonds. III. C=O···H–O Hydrogen Bond in H2CO···H2O and H2CO···2H2O, J. Chem. Phys., 1971, 55, 1236 CrossRef CAS.
- T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- (a) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576 CrossRef CAS; (b) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681 CrossRef CAS PubMed.
- (a) A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933 CrossRef CAS PubMed; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theor. Comput., 2009, 5, 962 CrossRef CAS PubMed.
- (a) ADF2018, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed; (b) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- J. C. Slater, Statistical Exchange-Correlation in the Self-Consistent Field, Adv. Quant. Chem., 1972, 6, 1 CrossRef CAS.
- (a) L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed; (b) G. Frenking and F. M. Bickelhaupt, The Chemical Bond. Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 121–158 CrossRef; (c) G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, New bonding modes of carbon and heavier group 14 atoms Si–Pb, Chem. Soc. Rev., 2014, 43, 5106 RSC; (d) L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Dative bonding in main group compounds, Coord. Chem. Rev., 2017, 344, 163 CrossRef CAS; (e) G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Donor–acceptor bonding in novel low-coordinated compounds of boron and group-14 atoms C–Sn, Chem. Soc. Rev., 2016, 45, 1129 RSC; (f) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: modern energy decomposition analysis, Nat. Rev. Chem., 2019, 3, 48 CrossRef CAS; (g) L. Zhao, S. Pan and G. Frenking, Energy Decomposition Analysis of the Chemical Bond: Scope and Limitation, Chem. Mol. Sci. Chem. Eng., 2022 DOI:10.1016/B978-0-12-821978-2.00021-0.
- (a) J. Zhao, H. Zeng and Z. Zhu, A theoretical study of the accurate analytic potential energy curve and spectroscopic properties for AlF (X1Σ+), Comput. Theor. Chem., 2011, 963, 130 CrossRef CAS; (b) K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV, Constants of Diatomic Molecules, Springer US, New York, 1979 CrossRef; (c) I. Magoulas, A. Kalemos and A. Mavridis, An ab initio study of the electronic structure of BF and BF+, J. Chem. Phys., 2013, 138, 104312 CrossRef PubMed; (d) A. Banerjee, A. Pramanik and K. K. Das, Ab initio configuration interaction study of the low-lying electronic states of InF, Chem. Phys. Lett., 2006, 429, 62–67 CrossRef CAS; (e) L. V. Skripnikov, A. N. Petrov, N. S. Mosyagin, V. F. Ezhov and A. V. Titov, Ab initio calculation of the spectroscopic properties of TlF−, Opt. Spectrosc., 2009, 106, 790–792 CrossRef CAS.
- J. Zhao, H. Zeng and Z. Zhu, A theoretical study of the accurate analytic potential energy curve and spectroscopic properties for AlF (X1Σ+), Comput. Theor. Chem., 2011, 963, 130 CrossRef CAS.
- R. Wesendrup and P. Schwerdtfeger, Extremely Strong s2–s2 Closed-Shell Interactions, Angew. Chem., Int. Ed., 2000, 39, 907 CrossRef CAS PubMed.
- C. Chi, S. Pan, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Alkali Metal Covalent Bonding in Nickel Carbonyl Complexes ENi(CO)3−, Angew. Chem., Int. Ed., 2019, 58, 1732 CrossRef CAS PubMed.
- There is an old NBO 3.1 version available in Gaussian 16, which has a larger AO valence space for transition metals.
- G. Frenking, S. Fau, C. M. Marchand and H. Grützmacher, The π-Donor Ability of the Halogens in Cations and Neutral Molecules. A Theoretical Study of AX3+, AH2X+, YX3, and YH2X (A = C, Si, Ge, Sn, Pb; Y = B, Al, Ga, In, Tl; X = F, Cl, Br, I), J. Am. Chem. Soc., 1997, 119, 6648 CrossRef CAS.
- K. Wiberg, Application of the Pople-Santry-Segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083 CrossRef CAS.
- (a) I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270 CrossRef CAS; (b) I. Mayer, Bond order and valence: Relations to Mulliken's population analysis, Int. J. Quantum Chem., 1984, 26, 151 CrossRef CAS.
- For an insightful discussion of the WBO and MBO approaches see: (a) A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, The Mayer bond order as a tool in inorganic chemistry, J. Chem. Soc. Dalton Trans., 2001, 2095–2108 RSC; (b) I. Mayer, Bond order and valence indices: a personal account, J. Comput. Chem., 2006, 28, 204 CrossRef PubMed.
- L. Zhao, S. Pan and G. Frenking, The nature of the polar covalent bond, J. Chem. Phys., 2022, 157, 034105 CrossRef CAS PubMed.
- (a) D. W. O. de Sousa and M. A. C. Nascimento, Quantum Interference Contribution to the Dipole Moment of Diatomic Molecules, J. Phys. Chem. A, 2018, 122, 1406 CrossRef PubMed; (b) S. Truppe, S. Marx, S. Kray, M. Doppelbauer, S. Hofsäss, H. C. Schewe, N. Walter, J. Pérez-Ríos, B. G. Sartakov and G. Meijer, Spectroscopic characterization of aluminum monofluoride with relevance to laser cooling and trapping, Phys. Rev. A, 2019, 100, 052513 CrossRef CAS; (c) M. Yousefi and P. F. Bernath, Line Lists for AlF and AlCl in the X1Σ+ Ground State, Astrophys. J. Suppl., 2018, 237, 8 CrossRef; (d) J. Hoeft, F. J. Lovas, E. Tiemann and T. Törring, Microwave Absorption Spectra of AlF, GaF, InF, and TIF, Z. Naturforsch., 1970, 25, 1029 CrossRef CAS; (e) R. v. Boeckh, G. Gräff and R. Ley, Die Abhängigkeit innerer und äußerer Wechselwirkungen des TlF-Moleküls von der Schwingung, Rotation und Isotopie, Z. Phys., 1964, 179, 285–313 CrossRef CAS; (f) D. E. Woon and E. Herbst, Quantum Chemical Predictions of the Properties of Known and Postulated Neutral Interstellar Molecules, Astrophys. J. Suppl., 2009, 185, 273 CrossRef CAS; (g) F. J. Lovas and D. R. Johnson, Microwave Spectrum of BF, J. Chem. Phys., 1971, 55, 41–43 CrossRef CAS; (h) J. Kobus, D. Moncrieff and S. Wilson, Calculated at the Hartree-Fock level, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 062503 CrossRef; (i) F. Fantuzzi, T. M. Cardozo and M. A. C. Nascimento, Nature of the chemical bond and origin of the inverted dipole moment in boron fluoride: a generalized valence bond approach, J. Phys. Chem. A, 2015, 119, 5335 CrossRef CAS PubMed; (j) S. Al Shawa, N. El-Kork, G. Younes and M. Korek, Theoretical study with dipole moment calculation of new electronic states of the molecule BF, Nanotechnol. Rev., 2016, 5, 363–368 CAS; (k) S. Huzinaga, E. Miyoshi and M. Sekiya, Electric dipole polarity of diatomic molecules, J. Comput. Chem., 1993, 14, 1440 CrossRef CAS , and further references therein..
- K. Q. Zhang, B. Guo, V. Braun, M. Dulick and P. F. Bernath, Infrared emission spectroscopy of BF and AlF, J. Mol. Spectrosc., 1995, 170, 82 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, The classical theory of fields, Course of theoretical physics No. 2, Elsevier Butterworth Heinemann, Amsterdam Heidelberg, 4th edn, 2010 Search PubMed.
- R. Klein and P. Rosmus, Ab initio calculations of infrared transition probabilities in the electronic ground states of AlF and AlF+, Theor. Chim. Acta., 1984, 66, 21 CrossRef CAS.
- (a) C. Chi, S. Pan, J. Jin, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Octacarbonyl Ion Complexes of Actinides [An(CO)8]+/− (An=Th, U) and the Role of f Orbitals in Metal–Ligand Bonding, Chem.–Eur. J., 2019, 25, 11772–11784 CrossRef CAS PubMed; (b) J. Jin, S. Pan, X. Jin, S. Lei, L. Zhao, G. Frenking and M. Zhou, Octacarbonyl Anion Complexes of the Late Lanthanides Ln(CO)8− (Ln=Tm, Yb, Lu) and the 32-Electron Rule, Chem.–Eur. J., 2019, 25, 3229–3234 CrossRef CAS PubMed; (c) C. Poggel and G. Frenking, Relativistic Effects on Donor–Acceptor Interactions in Coinage Metal Carbonyl Complexes [TM(CO)n]+ (TM=Cu, Ag, Au; n=1, 2), Chem.–Eur. J., 2018, 24, 11675–11782 CrossRef CAS PubMed; (d) S. Pan, L. Zhao, H. V. R. Dias and G. Frenking, Bonding in Binuclear Carbonyl Complexes M2(CO)9 (M = Fe, Ru, Os), Inorg. Chem., 2018, 57, 7780–7791 CrossRef CAS PubMed; (e) X. Wu, L. Zhao, D. Jiang, I. Fernández, R. Berger, M. Zhou and G. Frenking, Barium as Honorary Transition Metal in Action: Experimental and Theoretical Study of Ba(CO)+ and Ba(CO)−, Angew. Chem., Int. Ed., 2018, 57, 3974–3980 CrossRef CAS PubMed; (f) M. Chen, Q. Zhang, M. Zhou, D. M. Andrada and G. Frenking, Carbon Monoxide Bonding With BeO and BeCO3: Surprisingly High CO Stretching Frequency of OCBeCO3, Angew. Chem., Int. Ed., 2015, 54, 124–128 CrossRef CAS PubMed; (g) W. Fang, S. Pan, W. Su, S. Wang, L. Zhao, G. Frenking and C. Zhu, Complex Featuring Two Double Dative Bonds Between Carbon(0) and Uranium, CCS Chem., 2021, 4, 1921–1929 CrossRef; (h) W. Su, Y. Ma, L. Xiang, J. Wang, S. Wang, L. Zhao, G. Frenking and Q. Ye, Isolation of a Uranium (III)-Carbon Multiple Bond Complex, Chem.–Eur. J., 2021, 27, 10006 CrossRef CAS PubMed and further references cited therein..
- T. A. Albright, J. K. Burdett and M. H. Whangbo, Orbital Interactions in Chemistry, Wiley, New York, 1985, The HOMO−2 of CO was sketched in this first edition as a σ bonding orbital (Figure 6.4, page 81). In the second edition it was sketched as slightly antibonding: T. A. Albright, J. K. Burdett, M. H. Whangbo, “Orbital Interactions in Chemistry”, Figure 6.7, page 108, 2nd edn, Wiley, New York, 2013 Search PubMed.
- P. Schwerdtfeger and J. K. Nagle, Table of static dipole polarizabilities of the neutral elements in the periodic table, Mol. Phys., 2019, 117, 1200 CrossRef CAS.
Footnotes |
| † This paper is dedicated to Prof. Bernd Engels on the occasion of his 65th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc00830d |
| This journal is © The Royal Society of Chemistry 2023 |