Open Access Article
Open Access ArticleAn exchange coupled meso–meso linked vanadyl porphyrin dimer for quantum information processing†
Davide
Ranieri‡
 a,
Fabio
Santanni‡
a,
Fabio
Santanni‡
 a,
Alberto
Privitera
a,
Alberto
Privitera
 a,
Andrea
Albino
a,
Andrea
Albino
 a,
Enrico
Salvadori
a,
Enrico
Salvadori
 b,
Mario
Chiesa
b,
Mario
Chiesa
 b,
Federico
Totti
b,
Federico
Totti
 a,
Lorenzo
Sorace
a,
Lorenzo
Sorace
 *a and
Roberta
Sessoli
*a and
Roberta
Sessoli
 a
a
aDepartment of Chemistry “Ugo Schiff” & INSTM RU, University of Florence, Via della Lastruccia 3, 50019 Sesto Fiorentino, Italy. E-mail: lorenzo.sorace@unifi.it
bDepartment of Chemistry, NIS, University of Turin, Via P. Giuria 7, I10125 Torino, Italy
First published on 14th November 2022
Abstract
We report here the synthesis of a new meso–meso (m–m) singly linked vanadyl–porphyrin dimer that crystallizes in two different pseudo-polymorphs. The single crystal continuous-wave electron paramagnetic resonance investigation evidences a small but crucial isotropic exchange interaction, J, between the two tilted, and thus distinguishable, spin centers of the order of 10−2 cm−1. The experimental and DFT studies evidence a correlation between J values and porphyrin plane tilting angle and distortion. Pulsed EPR analysis shows that the two vanadyl dimers maintain the coherence time of the monomer. With the obtained spin Hamiltonian parameters, we identify suitable transitions that could be used as computational basis states. Our results, coupled with the evaporability of porphyrin systems, establish this class of dimers as extremely promising for quantum information processing applications.
Introduction
A qubit is a quantum object suitable to define a superposition state in which the information is encoded.1 For a physical system to act as a qubit, its coherence time Tm (i.e., the lifetime of its superposition state) must be long enough to allow manipulability.2 For this reason, electron or nuclear spins, either as solid-state systems3 or quantum dots,4 are appealing platforms for encoding qubits.3,5 More recently, electron spin-based molecular qubits gained interest in this field because of the chemical tunability of their properties.6,7 In these systems, magnetic exchange interaction between spin centers, either dipolar or isotropic, is crucial to establish the entanglement condition needed for implementing quantum logic gates. However, for this aim, the interqubit interaction should be finely tuned to avoid a strong-exchange regime6,8 thus maintaining the individual addressability of each qubit.Various molecular systems have been investigated and proposed as multi-qubit platforms.9–13 Here, addressability has been achieved through two different molecular design strategies: (i) inclusion of paramagnetic centers with different electronic and magnetic properties (e.g., two different Landé factors, g);9,10,13,14 (ii) inclusion of the same paramagnetic moiety characterized by significant magnetic anisotropy and different orientation in space.11 Most of these systems were also designed to minimize the hyperfine interactions detrimental to Tm.
In the quest for molecular systems acting as potential qubits, our groups mainly focused on VIVO metal complexes, which show good coherence times and can be operated as a nuclear qubit with an electronic spin ancilla.15,16 More recently, dinuclear VIVO-based complexes with weakly coupled electron spins were proposed as an electron-mediated nuclear quantum simulator.17,18 However, these complexes were of no use as quantum logic gates since the two VIVO ions were iso-oriented and thus not singly addressable. To harness the potential of VIVO dimers as potential quantum gates, it is crucial to introduce a tilting angle between two interacting spins.
Singly-linked porphyrin dimers are appealing candidates to solve this issue since the two macrocycle units adopt a tilted geometry imparting different orientations to the two spin centers.19,20 Furthermore, their marked thermal stability and excellent deposition properties on various metal and semi-conducting surfaces21–23 make them interesting for engineering prototypical devices. However, little is still known about the magnetic interactions in paramagnetic porphyrin dimers.24,25 Osuka and coworkers investigated the isotropic exchange interaction in meso–meso (m–m) singly linked, m-β β-m doubly linked, and β–β m–m β–β triply linked CuII and AgII porphyrin dimers.24 They found that the magnitude of the antiferromagnetic superexchange interaction between the spins increases by three orders of magnitude for β–β linked systems, compared to m–m linked systems, because of the larger conjugation between the two quasi coplanar porphyrin rings. In agreement with this, an ELDOR-detected NMR study revealed very weak exchange interactions compatible with a dipolar origin in m–m singly linked CuII complexes vs. a significant exchange interaction for the triply linked analog.25 A very recent report on triply linked vanadyl dimers26 suggests two orders of magnitude reduction of the exchange interaction compared to CuII dimers,25 as expected for the different symmetry of the magnetic orbital.
Following these results, we decided to synthesize and investigate a novel m–m linked bis vanadyl 5,10,15-triphenylporphyrin ([VO(TrPP)]2) to combine the interesting magnetic properties of porphyrins with the good coherence times characteristic of their vanadyl complexes.15,16 Since porphyrin units in m–m linked porphyrin dimers are tilted to each other, they might also be singly addressable by exploiting the large anisotropy of hyperfine coupling in vanadyl complexes. Angular-dependent continuous-wave electron paramagnetic resonance (CW EPR) measurements were performed on oriented single crystals along with CW and pulsed X- (ca. 9 GHz) and Q-band (ca. 34 GHz) EPR experiments on frozen solutions. Our experimental investigation indicates that [VO(TrPP)]2 maintains a coherence time comparable to its monomer building block while showing an exchange interaction comparable to that of triply linked species.26 The presence of a non-negligible magnetic exchange is a counterintuitive result that we rationalized by DFT calculations. The latter suggest that optimal coupling between distinguishable vanadyl qubits can be achieved. Combined with the evaporability of porphyrin systems, these results establish this class of dimers as extremely promising for quantum information processing applications.
Results and discussion
Synthesis
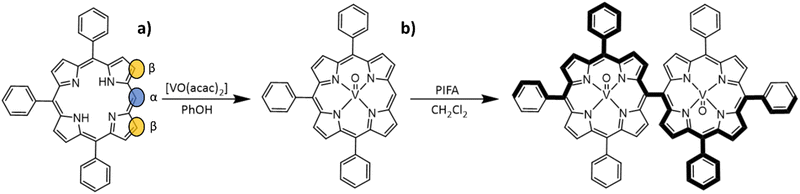
Compound [VO(TrPP)] was synthesized by a slight modification of a previously reported procedure.15 The reaction of the free H2TrPP ligand with the vanadyl precursor [VO(acac)2] (acac = acetylacetonate) was conducted in phenol (PhOH) as reported in Scheme 1a. The dimer [VO(TrPP)]2 was then obtained by performing an oxidative coupling reaction on [VO(TrPP)], in analogy to literature reports for other metal derivatives.27 Among the different strategies reported in the literature to obtain m–m linked metal porphyrin complexes,24,28 the use of (bis(trifluoroacetoxy)iodo)benzene (PIFA) as an oxidative coupling reagent recently turned out to be a good alternative to commonly used AgI hexafluorophosphate (AgPF6),29 ScIII triflate (Sc(OTf)3),30 and AuIII chloride/AgI triflate (AuCl3/AgOTf) mixtures.31 Indeed, the PIFA reactant is cheaper and, being metal-free, it does not interfere in the magnetic characterization of the final product. Previous studies showed that PIFA leads to highly selective reactions characterized by almost quantitative yields in the case of the reaction of ZnII and NiII porphyrin dimers.27 The reaction reported in Scheme 1b was then conducted in dry CH2Cl2 under an inert atmosphere by adding PIFA. The exact stoichiometric amount of PIFA added during the reaction turned out to be crucial for the efficiency and overall yield of the reaction. The use of 2 eq. of PIFA and 40′ reaction time at room temperature gave the desired porphyrin dimer in almost quantitative yields.Structural characterization
Details of the X-ray diffractometry characterization on single crystals of [VO(TrPP)] and [VO(TrPP)]2 are reported in the ESI.† Needle-shaped X-ray quality crystals of the monomeric unit [VO(TrPP)] (Fig. S1†) were grown by slow evaporation of a CH2Cl2/CH3CN (98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) solution. This system crystallizes in the P21/c space group (no. 14) with two pairs of centrosymmetrically related molecules per unit cell (Fig. S1 and Table S1†). The asymmetric unit is a single [VO(TrPP)] molecular complex, in which VIV presents a square pyramidal coordination geometry comprising the four porphyrin N atoms and the apical O atom of the V
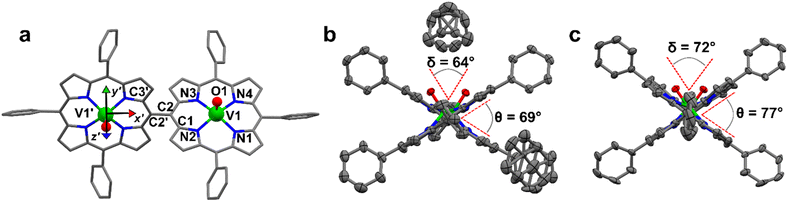
2) solution. This system crystallizes in the P21/c space group (no. 14) with two pairs of centrosymmetrically related molecules per unit cell (Fig. S1 and Table S1†). The asymmetric unit is a single [VO(TrPP)] molecular complex, in which VIV presents a square pyramidal coordination geometry comprising the four porphyrin N atoms and the apical O atom of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. To better characterize the porphyrin plane distortion modes, the normal-coordinate structure decomposition (NSD) tool was used.32,33 As evidenced in Fig. S1,† the porphyrin ring assumes a distorted ruffle shape,32,34B1u. This ruffle shape distortion differs from the planar structure of some m- and β substituted vanadyl–porphyrin complexes.15,35–37 On the other hand, the distance of the V atom from the plane individuated by the four N atoms, 0.51 Å, is the same as that observed in tetraphenyl derivatives.28 The mean V–N and V–O distances of 2.06 Å and 1.58 Å are comparable with those observed in similar vanadyl complexes, while the shortest intermolecular VO–VO distance is 9.42 Å. This is about 1.2 Å shorter than in the tetraphenyl analogous, as expected for the reduced hindering. The dimeric compound [VO(TrPP)]2 is highly soluble in various solvents, including acetonitrile, ethers, and toluene. Single crystals of [VO(TrPP)]2 suitable for X-ray measurements were obtained using two strategies involving toluene as crystallization solvent. Prism-shaped red to violet crystals were grown by very slow evaporation (∼1 month) of a toluene solution dispersed in Sephadex® gel. In this case, the dimer (hereafter, m-[VO(TrPP)]2, Fig. 1b) crystallizes in the monoclinic C2/c space group (no. 15), with three crystallization toluene molecules per dimer molecule. The molecular structure is composed by two [VO(TrPP)] units, symmetry-related by the C2 axis (Fig. 1a). The asymmetric unit is thus composed of half a dimer unit, one disordered toluene molecule, and half of a disordered toluene molecule lying in a special position (Fig. 1b and S3†). The dihedral angle θ, formed by the planes passing through C1–C2–C2′ and C2–C2′–C3′ (see Fig. 1a) at the porphyrin ring, is about 69° (Fig. 1b). The molecular structure presents an intrinsic disorder of the vanadyl moieties below and above the porphyrin planes, not observed for [VO(TrPP)], with occupancy factors of 85
O moiety. To better characterize the porphyrin plane distortion modes, the normal-coordinate structure decomposition (NSD) tool was used.32,33 As evidenced in Fig. S1,† the porphyrin ring assumes a distorted ruffle shape,32,34B1u. This ruffle shape distortion differs from the planar structure of some m- and β substituted vanadyl–porphyrin complexes.15,35–37 On the other hand, the distance of the V atom from the plane individuated by the four N atoms, 0.51 Å, is the same as that observed in tetraphenyl derivatives.28 The mean V–N and V–O distances of 2.06 Å and 1.58 Å are comparable with those observed in similar vanadyl complexes, while the shortest intermolecular VO–VO distance is 9.42 Å. This is about 1.2 Å shorter than in the tetraphenyl analogous, as expected for the reduced hindering. The dimeric compound [VO(TrPP)]2 is highly soluble in various solvents, including acetonitrile, ethers, and toluene. Single crystals of [VO(TrPP)]2 suitable for X-ray measurements were obtained using two strategies involving toluene as crystallization solvent. Prism-shaped red to violet crystals were grown by very slow evaporation (∼1 month) of a toluene solution dispersed in Sephadex® gel. In this case, the dimer (hereafter, m-[VO(TrPP)]2, Fig. 1b) crystallizes in the monoclinic C2/c space group (no. 15), with three crystallization toluene molecules per dimer molecule. The molecular structure is composed by two [VO(TrPP)] units, symmetry-related by the C2 axis (Fig. 1a). The asymmetric unit is thus composed of half a dimer unit, one disordered toluene molecule, and half of a disordered toluene molecule lying in a special position (Fig. 1b and S3†). The dihedral angle θ, formed by the planes passing through C1–C2–C2′ and C2–C2′–C3′ (see Fig. 1a) at the porphyrin ring, is about 69° (Fig. 1b). The molecular structure presents an intrinsic disorder of the vanadyl moieties below and above the porphyrin planes, not observed for [VO(TrPP)], with occupancy factors of 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 (Fig. S2†). The O1–V1–V1′–O1′ tilting angle, δ, is ca. 64° (red dashed line in Fig. 1b). The intramolecular VO–VO distance is of 8.37 Å, while the minimum intermolecular VO–VO distance of 9.70 Å is found between parallel molecules on adjacent layers (Fig. S3 left, ESI†). The porphyrin molecules in m-[VO(TrPP)]2 are not aligned to any crystallographic axes.
15 (Fig. S2†). The O1–V1–V1′–O1′ tilting angle, δ, is ca. 64° (red dashed line in Fig. 1b). The intramolecular VO–VO distance is of 8.37 Å, while the minimum intermolecular VO–VO distance of 9.70 Å is found between parallel molecules on adjacent layers (Fig. S3 left, ESI†). The porphyrin molecules in m-[VO(TrPP)]2 are not aligned to any crystallographic axes.
As a second crystallization strategy, X-ray quality crystals of [VO(TrPP)]2 were grown by very slow evaporation of a toluene/acetone (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) solution. These crystals were similar in shape, size, and color to those grown in toluene, but the system crystallized in the acentric orthorhombic Ccc2 (no. 37) space group without cocrystallized solvent molecules (hereafter o-[VO(TrPP)]2, Fig. 1c and S4†). Even in this case, the asymmetric unit is composed of one vanadyl–porphyrin unit, and the dimer is generated by the C2 axis parallel to c and perpendicular to the C2–C2′ meso-bridging bond. The structure presents solvent-accessible voids of about 302 Å3 along the c crystallographic direction (Fig. S5, ESI†). The absence of significative residual electron density suggests an intrinsic porous nature of the material. The molecules are oriented with the C2–C2′ bridging bond direction along the crystallographic b axis (Fig. S4, ESI†). An intrinsic disorder in the VO center is also observed in this case, with estimated occupancy factors of 75
5) solution. These crystals were similar in shape, size, and color to those grown in toluene, but the system crystallized in the acentric orthorhombic Ccc2 (no. 37) space group without cocrystallized solvent molecules (hereafter o-[VO(TrPP)]2, Fig. 1c and S4†). Even in this case, the asymmetric unit is composed of one vanadyl–porphyrin unit, and the dimer is generated by the C2 axis parallel to c and perpendicular to the C2–C2′ meso-bridging bond. The structure presents solvent-accessible voids of about 302 Å3 along the c crystallographic direction (Fig. S5, ESI†). The absence of significative residual electron density suggests an intrinsic porous nature of the material. The molecules are oriented with the C2–C2′ bridging bond direction along the crystallographic b axis (Fig. S4, ESI†). An intrinsic disorder in the VO center is also observed in this case, with estimated occupancy factors of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25. The tilting of the two porphyrin moieties is higher in o-[VO(TrPP)]2, as indicated by both θ and δ angles, of about 77° and 72°, respectively. On the other hand, the first coordination sphere does not present any major difference with respect to m-[VO(TrPP)]2, and the intramolecular VO–VO distance (8.37 Å) is also comparable. The closest intermolecular contact for the o-[VO(TrPP)]2 is instead shorter than in the previous case, with an average distance of 7.78 Å considering the VO disorder (Fig. S3, right, ESI†). The shorter distance can be related to the absence of crystallization solvent molecules in o-[VO(TrPP)]2.
25. The tilting of the two porphyrin moieties is higher in o-[VO(TrPP)]2, as indicated by both θ and δ angles, of about 77° and 72°, respectively. On the other hand, the first coordination sphere does not present any major difference with respect to m-[VO(TrPP)]2, and the intramolecular VO–VO distance (8.37 Å) is also comparable. The closest intermolecular contact for the o-[VO(TrPP)]2 is instead shorter than in the previous case, with an average distance of 7.78 Å considering the VO disorder (Fig. S3, right, ESI†). The shorter distance can be related to the absence of crystallization solvent molecules in o-[VO(TrPP)]2.
The dominant distortion mode in both porphyrin dimers is the saddle distortion B2u, also found in other A3B type porphyrins.38–40 The average dihedral angle among the pyrrole planes is 7.41° for o-[VO(TrPP)]2, while it is 4.36° for m-[VO(TrPP)]2, indicating a larger deviation from planarity and a higher degree of distortion in the solvent-free crystal structure o-[VO(TrPP)]2 than in m-[VO(TrPP)]2.
The observation of tilting angles significantly different from 90° is not unprecedented in linked porphyrins. At least two reported structures of pentacoordinated ZnII–porphyrin dimers, including bulky t-Bu groups on peripheral positions, are characterized by a dihedral angle of about 72°.41,42 The dihedral angle, however, cannot be directly correlated to the coordination number of the central ion since at least one previous result reports a pentacoordinated ZnII system showing a dihedral angle of about 90°.43
EPR experiments
We investigated the electronic structure and magnetic interactions in both [VO(TrPP)] and [VO(TrPP)]2 compounds by using EPR spectroscopy. The low temperature (T = 30 K) CW-EPR X-band spectrum of a frozen 1 mM solution of the monomer [VO(TrPP)] is shown in Fig. 2a (black trace), while the Q-band (ν = 33.8 GHz) Electron Spin Echo (ESE) detected EPR spectrum, corresponding to the absorption spectrum, is shown in Fig. 2b (black trace). Both spectra show the characteristic EPR powder pattern due to the anisotropic hyperfine coupling of the electron spin to the I = 7/2 nuclear spin of 51V. Spectral simulations, shown in Fig. 2a and b, were performed based on the following Hamiltonian:44Ĥ[VO(TrPP)] = μB![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ·g·Ŝ + Ŝ·A·Î ·g·Ŝ + Ŝ·A·Î | (1) |
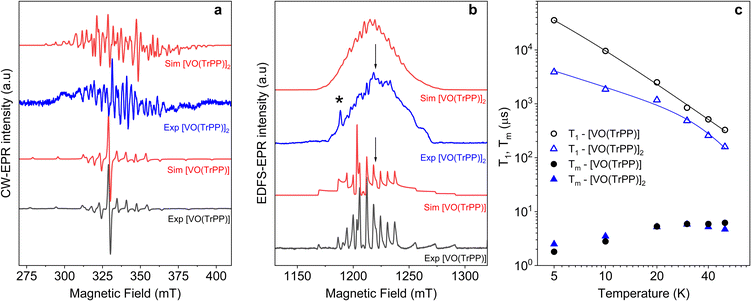 | ||
Fig. 2 (a) X-band (ν = 9.40 GHz) CW-EPR spectra of [VO(TrPP)] and [VO(TrPP)]2 in frozen toluene solution (T = 30 K) together with their best simulations obtained using spin Hamiltonian parameters reported in Table 1. (b) Q-band (ν = 33.8 GHz) ESE-EPR spectra of [VO(TrPP)] and [VO(TrPP)]2 in frozen – toluene/CH2Cl2 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution (T = 5 K). The arrows indicate the magnetic field settings at which pulse EPR experiments were performed. The asterisk indicates the signal of background impurities. (c) Temperature dependence of T1 (open symbols) and Tm (full symbols) for [VO(TrPP)] (circles) and [VO(TrPP)]2 (triangles) measured at 1214 mT at Q-band frequency in a 0.5 mM frozen d8-toluene solution. Error bars are within the size of the symbols. The continuous lines represent the best fit curves obtained using model and parameters reported in the text and ESI.† 1 solution (T = 5 K). The arrows indicate the magnetic field settings at which pulse EPR experiments were performed. The asterisk indicates the signal of background impurities. (c) Temperature dependence of T1 (open symbols) and Tm (full symbols) for [VO(TrPP)] (circles) and [VO(TrPP)]2 (triangles) measured at 1214 mT at Q-band frequency in a 0.5 mM frozen d8-toluene solution. Error bars are within the size of the symbols. The continuous lines represent the best fit curves obtained using model and parameters reported in the text and ESI.† | ||
| Simulation parameters | [VO(TrPP)] | Single crystal [VO(TrPP)]2 | Frozen solution [VO(TrPP)]2 |
|---|---|---|---|
| g z | 1.985 (1) | 1.985 | 1.985 |
| g x,y | 1.962 (1) | 1.962 | 1.962 |
| A z (MHz) | 168 (2) | 168 | 168 |
| A x,y (MHz) | 480 (2) | 480 | 480 |
| |J| (cm−1) | 1.0(5) × 10−2 (m-) | >1.0 × 10−2 | |
| 5(1) × 10−2 (o-) | |||
| D (cm−1) | [2.8, –5.6, 2.8] 10−3 |
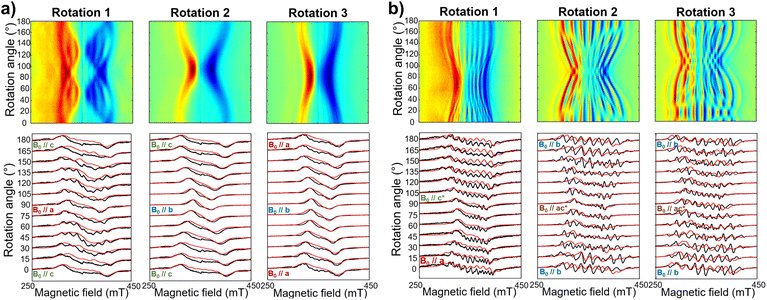
The same complex spectral profile is observed in Q-band ESE-EPR experiments (blue trace in Fig. 2b) and suggests that the two vanadyl units in [VO(TrPP)]2 are coupled through an exchange interaction smaller than the microwave quantum of energy (hν ≈ 0.3 cm−1 for X-band). Under these circumstances, magnetic coupling of the two S = 1/2 electron spins results in four states, which are neither pure “triplet” nor pure “singlet”, leading to 4(2I1 + 1)(2I2 + 1) = 256 ΔMs = 1 allowed EPR transitions, where I1 = I2 = 7/2 are the nuclear spin quantum numbers of the two coupled 51V nuclei.45 In the case of a randomly oriented sample (frozen solution), the spectrum will contain overlapping peaks from those orientations corresponding to ∂B/∂θ = 0 or ∂B/∂φ = 0. Such conditions occur along principal directions, although extra peaks may occur at other orientations (off-axis turning points),46 leading to the intricate spectral pattern reported in Fig. 2a and b. Single crystal CW-EPR experiments were performed to simplify the problem and determine the spin-Hamiltonian parameters for the coupled dimers. Studies on oriented single crystals of coupled porphyrins were never reported before, despite their capability to characterize weak magnetic interactions. The angular dependence of the EPR spectra on both the m-[VO(TrPP)]2 and o-[VO(TrPP)]2 crystals was studied by performing crystal rotations along three orthogonal directions (Fig. 3). For the monoclinic case, the rotations were performed along the crystallographic b axis (Rotation 1) and two orthogonal axes (Rotations 2 and 3) in the ac* plane, clockwise tilted by 14° with respect to the a and c* axes (Fig. S7†). For the orthorhombic crystal, the rotations were performed along directions collinear to the crystallographic a (Rotation 2), b (Rotation 1), and c (Rotation 3) axes.
The experimental EPR spectra of the two forms are characterized by a different linewidth, most likely attributable to different intermolecular through-space dipolar coupling in the two crystals. The spectra were simulated based on the spin Hamiltonian shown in eqn (2):
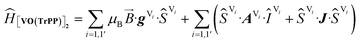 | (2) |
This includes the Zeeman and hyperfine interaction terms for both VO porphyrin units (first and second term) and an interaction term described by a general matrix J,47 which comprises the isotropic component J of the exchange interaction and a through-space dipolar coupling D (eqn (3)):
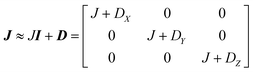 | (3) |
Intramolecular dipolar interaction was fixed at the value calculated by point-dipole approximation (see Table 1). The antisymmetric and the anisotropic exchange contribution to the J matrix were neglected since both are expected to be negligible due to the small orbital contribution of vanadyl ions.47
Based on the results of the crystallographic study, two different tilting angles between the magnetic tensors of the two VO units were considered for m-[VO(TrPP)]2 and o-[VO(TrPP)]2, of 64° and 72° respectively. The molecular reference framework that we adopted for the simulation has the Z-axis parallel to the C2 axis of the molecule, the Y-axis parallel to the m–m bond direction, and the X-axis perpendicular to these two directions. The principal values of the g and A tensors of the two vanadyl centers were kept fixed to the values obtained by the best simulation of the [VO(TrPP)] monomer, with their local z direction oriented along the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Intermolecular through-space dipolar interactions were included as a broadening of the linewidth. Specifically, we used a peak-to-peak Lorentzian linewidth of 8 mT for m-[VO(TrPP)]2 and 13 mT for o-[VO(TrPP)]2, which highlights a stronger dipolar interaction in the latter, consistent with the shorter intermolecular distance. In Fig. S8 and S9,† we survey simulated EPR spectra for the two crystals to assess the effect of |J| magnitudes ranging from 1.0 × 10−5 to 1 cm−1. Our analysis shows that for m-[VO(TrPP)]2, the |J| value that best simulates the angular dependence of the EPR spectra is about 0.01 (0.005) cm−1 while for o-[VO(TrPP)]2 |J| is about 0.05 (0.01) cm−1. The simulated spectra are shown in Fig. 3a and b (red traces), while the extracted spin-Hamiltonian parameters are listed in Table 1.
O bond. Intermolecular through-space dipolar interactions were included as a broadening of the linewidth. Specifically, we used a peak-to-peak Lorentzian linewidth of 8 mT for m-[VO(TrPP)]2 and 13 mT for o-[VO(TrPP)]2, which highlights a stronger dipolar interaction in the latter, consistent with the shorter intermolecular distance. In Fig. S8 and S9,† we survey simulated EPR spectra for the two crystals to assess the effect of |J| magnitudes ranging from 1.0 × 10−5 to 1 cm−1. Our analysis shows that for m-[VO(TrPP)]2, the |J| value that best simulates the angular dependence of the EPR spectra is about 0.01 (0.005) cm−1 while for o-[VO(TrPP)]2 |J| is about 0.05 (0.01) cm−1. The simulated spectra are shown in Fig. 3a and b (red traces), while the extracted spin-Hamiltonian parameters are listed in Table 1.
The same parameters provide a convincing simulation of the frozen solution spectra at both X- and Q-band frequencies (Fig. 2a and b, S10†, and Table 1), confirming the consistency of the determined values. A survey of the simulation parameters allows defining a lower limit of |J| = 10−2 cm−1 to simulate the spectra, consistent with the spanned range in the crystalline phases.
Inversion recovery and echo decay experiments at Q-band frequency were performed to get insight into the temperature dependence (T = 5–50 K) of the spin-lattice relaxation time T1 and the coherence time Tm, respectively. In Fig. 2c and Table S2,† we report the T1 and Tm values for both [VO(TrPP)] and [VO(TrPP)]2 in 0.5 mM deuterated d8-toluene obtained from the fit of the inversion recovery and echo decay traces. The temperature dependence of T1 shows a slight divergence between the monomer and the dimer below 20 K but is in essential agreement with previous reports of T1 in vanadyl porphyrins. The temperature dependent data for T1 were fitted by assuming a combination of direct and Raman process:
| T1−1 = aT + bTn | (4) |
The best fit parameters (Table S3†) suggest that the direct process is more efficient in the dimer than in the monomer, and that the two Raman processes show low values of the exponent n (2.2 for [VO(TrPP)] and 4.2 for [VO(TrPP)]2), in the range reported for vanadyl complexes.48–51 We note however that due to the limited temperature range in which the investigation is possible, the number of experimental points is small compared to the number of parameters of eqn (4). The numerical values of the obtained best-fit parameters should then be considered with caution. The experimental coherence times Tm are very similar for the two samples and of the order of few μs in the 5–50 K range; the small decrease in Tm observed on decreasing temperature has already been reported for other S = 1/2 molecular species.49 The decoherence times reported here are comparable to or even higher than those reported for weakly interacting vanadyl moieties16,25 or molecular dimers based on either Cr7Ni rings52 or lanthanide complexes.9
DFT calculations
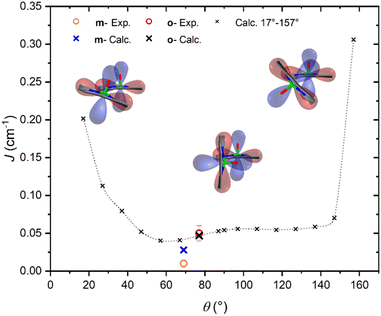
It is interesting to highlight two counterintuitive results of our investigation. First, the exchange interaction is larger in vanadyl than in copper m–m dimers,25 despite the weaker overlap (π vs. σ interaction) of the magnetic orbital with the ligand scaffold. Notably, for triply linked dimers, the exchange is stronger in the copper derivative, as expected.24,25 Second, the exchange interaction increases with the VO tilting angle, which is also counterintuitive when considering the extent of conjugation between the two porphyrin units.To elucidate the nature of the observed exchange interaction and establish magneto-structural correlations, we performed DFT Broken-Symmetry (BS) calculations (technical details can be found in ESI†).53 First, we focus on the crystallographic structures: the computed J values for m- and o-[VO(TrPP)]2 are both antiferromagnetic and in striking agreement with their experimental estimated magnitude: 1.4 × 10−2 and 4.7 × 10−2 cm−1, respectively. The computed magnetic orbitals (labeled according to the standard reference system for vanadyls) for both derivatives are localized on the VIV centers (dxy) with in-plane π contributions from the N–C2,5 sp components for each of the four pyrrole subunits (see Fig. S11†). Next, we investigated the J variation as a function of the dihedral angle θ, keeping the other structural parameters fixed to those of the orthorhombic structure. Calculated J values for θ angles in the 17–157° range are reported in Table S4.† The results (see Fig. 4) show an asymmetric double-well behavior with the absolute minimum for θ ∼ 60° and a less pronounced one for θ ∼ 125°. The double-well asymmetry originates from the non-planarity of each vanadyl–porphyrin moiety, which alters the overlap between their π–π systems for the clock- and the anti-clockwise rotation around θ = 90°.
The highest J values were computed for the smallest and largest accessible θ values (θ = 17° and 157°), i.e., close to coplanarity where the largest overlap between two out-of-plane π porphyrins systems is expected. The relative maximum for θ ∼ 90° is achieved when the overlap between the sp system of one porphyrin and the out-of-plane π system of the other is largest. The computed angular dependence is, however, not sufficient to justify the different J magnitude in the two derivatives, otherwise well reproduced when using the real structures. This observation points to the key role of the saddle distortion of the single porphyrin unit that alters the mixing of the local sp (in-plane) and delocalized π (out-of-plane) contributions: indeed, the average dihedral angle between pyrrole planes is larger for the o- than the m- derivative (7.4° vs. 4.4°, see structural characterization).
As discussed in other works,54–56 the distortion of the porphyrin plane indeed alters their chemical and physical properties. The change in electronic properties of the porphyrins is reflected by the red-shift of the Q and B-bands in the UV/vis spectrum and their respective broadening, which is also visible in our spectra (see Fig. S12†). Although the red-shift in the UV/vis spectrum can be exclusively attributed to the plane distortion, in porphyrin dimers, the conjugation between two porphyrin rings might be the dominant cause.56,57 Discrimination between these two hypotheses would require more detailed calculations which are beyond the scope of this study.
The DFT analysis confirmed the magnitude of the interaction and allowed us to disclose its antiferromagnetic nature and explain the reason for the larger coupling in the orthorhombic form. Both the deviation from the planarity of the single porphyrin units and the vanadyl magnetic orbital lying slightly above/below the porphyrin plane are responsible for the not negligible J value. These geometrical features contribute to the involvement of the out-of-plane π systems providing a more efficient superexchange interaction. These considerations also explain the negligible exchange coupling recently observed for the similar m–m linked Cu–porphyrin dimer.25
That system is indeed characterized by high planarity of the porphyrins and an in-plane nature of the magnetic orbitals. Moreover, in [VO(TrPP)]2, access to the out-of-plane π system can occur via spin polarization processes through the oxygen atom in the VO group, as witnessed by a non-negligible spin density on it (see Fig. S11†). Therefore, the VO systems present intrinsic properties that make them more appealing than the copper ones for their exploitation as multi-qubit systems in m–m porphyrin systems.
Computational states
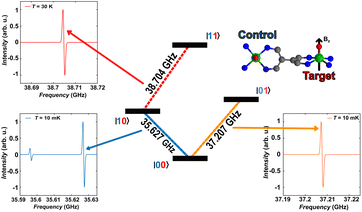
As a final step, we illustrate in the following that [VO(TrPP)]2 fulfils the conditions that allow individual addressing of the spins. The presence of a sizeable exchange interaction and the small homogeneous linewidths estimated by the measured Tm indicate that selective excitation is possible, i.e., at a given field the frequency difference between spin transitions on the two electronic sites is larger than the decoherence rate.To analyse this issue in more detail we performed simulations of frequency-swept EPR spectra on an oriented crystal of o-[VO(TrPP)]2. We assumed a static magnetic field of 1.3 T applied along the local z direction of A and g tensors of one of the vanadyl moieties (Fig. 5) and swept the frequency in the Q-band region (see Fig. S13 and S14†). This configuration has been chosen to maximise the difference between the resonant frequencies of the two sites. However, the operative conditions in two-frequency experiments implementing logic gates can be easily matched by aligning the field closer to the two-fold symmetry axis of the dimer. To better reproduce the initialization process of our system we performed our simulation at 10 mK.
The direction of the field establishes the so-called “target” (T) qubit, while the other unit, tilted by 72°, is defined as the “control” one (C). Under these conditions the ground state of the system is given by 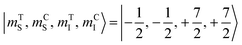 (with minor contributions from states with different mI), and the system is initialized as |00〉. We selected spin transitions among almost completely factorized states following the selection rules Δms = ±1 and ΔmI = 0, so that the computational basis can be roughly defined by the electronic spin states of the two moieties (i.e.,
(with minor contributions from states with different mI), and the system is initialized as |00〉. We selected spin transitions among almost completely factorized states following the selection rules Δms = ±1 and ΔmI = 0, so that the computational basis can be roughly defined by the electronic spin states of the two moieties (i.e., 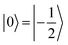 and
and 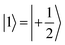 ). This option guarantees a unique computational basis for the two-qubit architecture given by the four states |00〉, |10〉, |01〉 and |11〉, where the first label indicates C and the second T.
). This option guarantees a unique computational basis for the two-qubit architecture given by the four states |00〉, |10〉, |01〉 and |11〉, where the first label indicates C and the second T.
A scheme of the transitions involved in the quantum computing process, together with the zoom on spectral region of interest, are visible in Fig. 5. By using the spin Hamiltonian parameters reported in Table 1, the transition |00〉 → |10〉 and |00〉 → |01〉 are separated by an energy of 1.575 GHz, far exceeding the decoherence rate. Furthermore, no other transitions are visible close to the |00〉 → |01〉 (Fig. 5, bottom right corner), while a much less intense peak is observed in proximity of |00〉 → |10〉. However, this minor transition involves a higher lying initial state, with different nuclear spin projection compared to those of |00〉; thus, this would not interfere with the quantum computational process. This means that it is possible to excite selectively either C or T moiety once the system is properly initialized in the |00〉 state.
The computational process requires that the spin state of T must be selectively changed only when C is set to |1〉, i.e., the spin transition |10〉 → |11〉 must be selectively probed. This implies to first excite our system from |00〉 → |10〉 and only then to invert the target spin by promoting the transition |10〉 → |11〉. Our simulation, performed at 30 K to obtain a reasonable population of the excited |10〉 state, indicates that the transition occurs at 38.704 GHz (red dashed lines in Fig. 5). This is the only allowed transition in the probed frequency range, and it can be selectively excited without involving sides transitions.
We notice here that, on increasing temperature from 10 mK, further nuclear transitions would appear because of the 16 × 16 dimension of the electronuclear spin space. While this might be seen as detrimental for quantum information applications, the possibility to exploit the nuclear spin degrees of freedom has been highlighted as a further advantage of vanadyl over other systems.16,58
Conclusions
In summary, we obtained [VO(TrPP)]2 by an oxidative coupling reaction in almost quantitative yields. Its high solubility made it possible to obtain two pseudo polymorph single crystals (monoclinic m-[VO(TrPP)2] and orthorhombic o-[VO(TrPP)]2). These two compounds showed significant intramolecular exchange interactions, generally not observed for paramagnetic singly linked m–m porphyrin dimers. The possibility to perform single crystal magnetic studies of two polymorphs slightly differing in the molecular structure also allowed us to investigate the dependence of the exchange coupling constant on the molecular geometry. Indeed, DFT calculations showed that the dependence of the antiferromagnetic exchange interaction on the dihedral angle between porphyrin planes, is mainly determined by the saddle-like distortion of the porphyrin plane. These new magneto-structural correlations open the possibility of chemically tuning the magnetic interaction in this platform, which presents unique and appealing features for quantum technology applications. Indeed, we showed here that, thanks to the anisotropic hyperfine interaction, the two tilted but exchange coupled vanadyl units are individually addressable as requested for quantum logic gate implementation. Furthermore, the coherence time of the dimer turned out to be comparable to that of monomeric vanadyl porphyrins. Since the latter have a relatively long coherence time up to room temperature when diluted in a diamagnetic host,15,16,59 we foresee that coherent properties in the dimer can be improved by working on single crystals of diamagnetic hosts, which are currently under investigation. Multi-porphyrin structures are also synthetically accessible28,60–63 to extend the number of coupled spins, thus offering a solution to the crucial issue of scalability in quantum architectures. Additionally, deposition on a surface to perform single qubit addressing via scanning tunnel microscopy combined with microwaves64–66 appears also within reach.Data availability
All data associated with this article have been included in the main text and ESI.†Author contributions
D. R.: investigation, formal analysis, writing – original draft, writing review and editing. F. S.: investigation, formal analysis, writing – original draft, writing review and editing. A. P.: investigation, formal analysis, writing – original draft. A. A.: investigation. E. S.: investigation, formal analysis, writing – original draft. M. C.: supervision, writing review and editing. F. T.: investigation, formal analysis, writing – original draft. L. S.: supervision, project administration, writing review and editing. R. S.: conceptualization, supervision, fund acquisition, writing review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The support of EC through EU Commission through the FETOPEN project FATMOLS (GA 862893) and Italian MIUR for Progetto Dipartimenti di Eccellenza 2018–2022 (ref. B96C1700020008) is acknowledged. National Recovery and Resilience Plan, Mission 4 Component 2 – Investment 1.4 – National Center for HPC, Big Data and Quantum Computing – funded by the European Union – NextGenerationEU – CUP (B83C22002830001) is acknowledged. We acknowledge the support of Dr S. Ciattini, Dr L. Chelazzi and Dr E. Fantechi (CRIST – University of Florence), for the crystallographic data analysis and Prof. S. Carretta and Dr A. Chiesa (Univ. of Parma) for fruitful discussion.Notes and references
- J. P. Dowling and G. J. Milburn, Philos. Trans. R. Soc., A, 2003, 361, 1655–1674 CrossRef PubMed.
- D. P. Di Vincenzo, Fortschr. Phys., 2000, 48, 771–783 CrossRef.
- M. H. Abobeih, Y. Wang, J. Randall, S. J. H. Loenen, C. E. Bradley, M. Markham, D. J. Twitchen, B. M. Terhal and T. H. Taminiau, Nature, 2022, 606, 884–889 CrossRef CAS.
- A. Morello, J. J. Pla, P. Bertet and D. N. Jamieson, Adv. Quantum Technol., 2020, 3, 2000005 CrossRef CAS.
- A. Barenco, C. H. Bennett, R. Cleve, D. P. Di Vincenzo, N. Margolus, P. W. Shor, T. Sleator, J. A. Smolin and H. Weinfurter, Phys. Rev. A, 1995, 52, 3457–3467 CrossRef CAS PubMed.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119–3129 RSC.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Science, 2020, 370, 1309–1312 CrossRef CAS.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef.
- S. Von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2021, 143, 8069–8077 CrossRef CAS.
- S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 51, 9860–9864 CrossRef CAS.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, Npj Quantum Inf., 2015, 1, 15012 CrossRef.
- D. Maniaki, D. Garay-Ruiz, L. A. Barrios, D. O. T. A. Martins, D. Aguilà, F. Tuna, D. Reta, O. Roubeau, C. Bo and G. Aromi, Chem. Sci., 2022, 13, 21–25 RSC.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed.
- T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 12090–12101 CrossRef CAS.
- S. Chicco, A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi, R. Sessoli and S. Carretta, Chem. Sci., 2021, 12, 12046–12055 RSC.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183–6192 RSC.
- I. Borilovic, P. J. Alonso, O. Roubeau and G. Aromí, Chem. Commun., 2020, 56, 3139–3142 RSC.
- A. A. Ryan and M. O. Senge, Eur. J. Org. Chem., 2013, 2013, 3700–3711 CrossRef CAS.
- S. Hiroto, Y. Miyake and H. Shinokubo, Chem. Rev., 2017, 117, 2910–3043 CrossRef CAS PubMed.
- K. Eguchi, T. Nakagawa, Y. Takagi and T. Yokoyama, J. Phys. Chem. C, 2015, 119, 9805–9815 CrossRef CAS.
- A. Urtizberea, E. Natividad, P. J. Alonso, L. Pérez-Martínez, M. A. Andrés, I. Gascón, I. Gimeno, F. Luis and O. Roubeau, Mater. Horiz., 2020, 7, 885–897 RSC.
- Q. Sun, L. M. Mateo, R. Robles, P. Ruffieux, N. Lorente, G. Bottari, T. Torres and R. Fasel, J. Am. Chem. Soc., 2020, 142, 18109–18117 CrossRef CAS.
- T. Ikeue, K. Furukawa, H. Hata, N. Aratani, H. Shinokubo, T. Kato and A. Osuka, Angew. Chem., Int. Ed., 2005, 44, 6899–6901 CrossRef CAS PubMed.
- N. Wili, S. Richert, B. Limburg, S. J. Clarke, H. L. Anderson, R. Timmel and G. Jeschke, Phys. Chem. Chem. Phys., 2019, 21, 11676–11688 RSC.
- I. Pozo F. Lombardi D. Alexandropoulos F. Kong J.-R. Deng P. Horton S. Coles W. Myers L. Bogani H. Anderson, ChemRxiv 2022, preprint DOI:10.26434/chemrxiv-2022-1v5b4.
- Q. Ouyang, Y.-Z. Zhu, C.-H. Zhang, K.-Q. Yan, Y.-C. Li and J.-Y. Zheng, Org. Lett., 2009, 11, 5266–5269 CrossRef CAS.
- T. Tanaka and A. Osuka, Chem. Soc. Rev., 2015, 44, 943–969 RSC.
- A. Osuka and H. Shimidzu, Angew. Chem., Int. Ed. Engl., 1997, 36, 135–137 CrossRef CAS.
- M. Kamo, A. Tsuda, Y. Nakamura, N. Aratani, K. Furukawa, T. Kato and A. Osuka, Org. Lett., 2003, 5, 2079–2082 CrossRef CAS.
- S. Hiroto and A. Osuka, J. Org. Chem., 2005, 70, 4054–4058 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- C. J. Kingsbury and M. O. Senge, Coord. Chem. Rev., 2021, 431, 213760 CrossRef CAS.
- R. Harada, H. Ōkawa and T. Kojima, Inorg. Chim. Acta, 2005, 358, 489–496 CrossRef CAS.
- S.-Y. Wong, R. Wai-Yin Sun, N. P.-Y. Chung, C.-L. Lin and C.-M. Che, Chem. Commun., 2005, 3544 RSC.
- W.-T. Chen, Y. Yamada, G.-N. Liu, A. Kubota, T. Ichikawa, Y. Kojima, G.-C. Guo and S. Fukuzumi, Dalton Trans., 2011, 40, 12826 RSC.
- G. Nandi, H. M. Titi and I. Goldberg, Cryst. Growth Des., 2014, 14, 3557–3566 CrossRef CAS.
- M. Gouterman, J. Mol. Spectrosc., 1961, 6, 138–163 CrossRef CAS.
- W. Jentzen, X. Z. Song and J. A. Shelnutt, J. Phys. Chem. B, 1997, 101, 1684–1699 CrossRef CAS.
- A. Stone and B. Everly, J. Am. Chem. Soc., 1968, 90, 2735–2748 CrossRef CAS.
- Y. Jun-i, N. Fukui, K. Furukawa and A. Osuka, Chem.–Eur. J., 2018, 24, 1528–1532 CrossRef CAS.
- A. K. D. Dime, C. H. Devillers, H. Cattey, B. Habermeyer and D. Lucas, Dalton Trans., 2012, 41, 929–936 RSC.
- Y. Inokuma, N. Ono, H. Uno, D. Y. Kim, S. B. Noh, D. Kim and A. Osuka, Chem. Commun., 2005, 3782 RSC.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS.
- T. D. Smith and J. R. Pilbrow, Coord. Chem. Rev., 1974, 13, 173–278 CrossRef CAS.
- I. V. Ovchinnikov and V. N. Konstantinov, J. Magn. Reson., 1978, 32, 179–190 CAS.
- A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer Berlin Heidelberg, 1st edn, 1990 Search PubMed.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed.
- J. L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1995, 115, 236–240 CrossRef CAS.
- J. L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1996, 119, 240–246 CrossRef CAS.
- J. Ferrando-Soria, E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS.
- L. Noodleman and J. G. Norman, J. Chem. Phys., 1979, 70, 4903–4906 CrossRef CAS.
- B. Röder, M. Büchner, I. Rückmann and M. O. Senge, Photochem. Photobiol. Sci., 2010, 9, 1152–1158 CrossRef PubMed.
- M. O. Senge, Chem. Commun., 2006, 243–256 RSC.
- C. J. Kingsbury, K. J. Flanagan, H. G. Eckhardt, M. Kielmann and M. O. Senge, Molecules, 2020, 25, 3195 CrossRef CAS PubMed.
- A. Osuka, S. Nakajami, T. Nagata, K. Maruyama and K. Torium, Angew. Chem., Int. Ed. Engl., 1991, 30, 582–584 CrossRef.
- I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Chem. Sci., 2021, 12, 5621–5630 RSC.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS.
- N. Aratani and A. Osuka, Org. Lett., 2001, 3, 4213–4216 CrossRef CAS.
- C. Schissler, E. K. Schneider, B. Felker, P. Weis, M. Nieger, M. M. Kappes and S. Bräse, Chem.–Eur. J., 2021, 27, 3047–3054 CrossRef CAS PubMed.
- M. Rickhaus, A. Vargas Jentzsch, L. Tejerina, I. Grübner, M. Jirasek, T. D. W. Claridge and H. L. Anderson, J. Am. Chem. Soc., 2017, 139, 16502–16505 CrossRef CAS.
- A. K. Sahoo, Y. Nakamura, N. Aratani, K. S. Kim, S. B. Noh, H. Shinokubo, D. Kim and A. Osuka, Org. Lett., 2006, 8, 4141–4144 CrossRef CAS.
- D. Serrate, P. Ferriani, Y. Yoshida, S. W. Hla, M. Menzel, K. Von Bergmann, S. Heinze, A. Kubetzka and R. Wiesendanger, Nat. Nanotechnol., 2010, 5, 350–353 CrossRef CAS PubMed.
- K. Yang, W. Paul, S. H. Phark, P. Willke, Y. Bae, T. Choi, T. Esat, A. Ardavan, A. J. Heinrich and C. P. Lutz, Science, 2019, 366, 509–512 CrossRef CAS.
- W. Ko, C. Ma, G. D. Nguyen, M. Kolmer and A. P. Li, Adv. Funct. Mater., 2019, 29, 1903770 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic procedures, experimental details, additional crystallographic and EPR characterization, DFT computational details. CCDC 2202805 ([VO(TrPP)]), 2203175 (m-[VO(TrPP)]2), and 2203176 (o-[VO(TrPP)]2). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc04969d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |