C–H functionalization of quinoline N-oxides catalyzed by Pd(II) complexes: a computational study

Abstract

Pd(II) catalysts, particularly the acetate salt in acetic acid, tended to favor regioselective C–H activation of quinoline N-oxides (QOs) at the C2 position. However, Pd(II)Cl₂ was shown to catalyze their C–H activation at C8 and, in the presence of water, C8–H activation was accompanied by the formation of 2-quinolinones. The aim of the DFT study described in this work was to shed light on the complete mechanism of these competing catalytic reactions, when PdCl₂ reacts with QO and benzaldehyde in dichloroethane. C–H activation of QO was the first step of the reaction and involved either a metallacycle, with a C_QO–Pd(II) σ-bond and a C(8)–H–Pd(II) agostic bond, or an η³-QO complex, with three carbon atoms of the heteroring of QO binding PdCl₂. The first situation led to the unusual C8 activation and the second to C2 activation. The σ-metallacycle undergoes C8–H activation and the energy of the TOF determining the transition state to form the product is ∼17 kcal mol⁻¹, while for the reaction through the π-metallacycle (C2–H activation) the corresponding energy is higher (∼29 kcal mol⁻¹) and thus is not competitive under the same conditions. The reaction proceeding through the σ-complex, activating the C8 position, is preferred, in agreement with experimental results. Both reactions involve oxidation of Pd(II) to Pd(IV) and the catalyst is regenerated. When small amounts of water are added to the reaction mixture, C8–H activation (acylation) results from the same σ-metallacycle with the same barrier, but the simultaneous formation of 2-quinolinones is more complicated. It starts with OH⁻ attack at the C2 position, and is followed by the migration of two hydrogen atoms, and the final reductive elimination step ends with Pd(0). The higher barriers for the migration and reoxidation of Pd(0) are associated with the more demanding reaction conditions. The different reactivity of Pd(II)(OAc)₂ under analogous conditions is clarified, as it is only capable of forming the above mentioned π-complex and thus of activating the C2 position of QO. This catalyst can preferentially activate the C8–H bond under rather different conditions, including in particular acetic acid medium, as shown by other authors.

---

Introduction

Quinoline is a versatile and important heterocyclic system found in many natural products, and used in pharmaceuticals, agrochemicals, functional materials, and ligands in transition metal catalysts.¹ To increase the range of available quinoline derivatives, regioselective C–H functionalization catalyzed by transition metals had all the qualifications to overcome the challenge of modifying quinolines through atom- and step-saving processes with high functional group compatibility.² While most of the known C–H activation processes of quinolines enabled their functionalization with poor regioselectivity,³ the N-oxide group present in quinoline-N-oxides (QOs), on the other hand, is an excellent directing group to reach higher regioselectivity.⁴ Fagnou and co-workers were the first to develop C–H cross-coupling reactions of pyridine N-oxides, in which the N-oxide group is a key element for introducing functional groups at the carbon position ortho to the nitrogen atom (C2).⁵ Later, some of us first achieved the palladium-catalyzed C-2 dehydrogenative Heck reaction of QOs without external oxidants.⁶ Here, the N–O group played a dual role, both as an internal oxidant and a directing group. Inspired by this progress, a variety of C2–H bond functionalization reactions of QOs were developed by several groups using Pd, Cu, Ru or Rh catalysts.⁷ Meanwhile, the C8–H bond functionalization of QOs has successfully been explored using appropriate substrates. After the activation of the C8–H bond, the N-oxide moiety acted as a directing group to form five-membered metallacyclic intermediates, which subsequently reacted with suitable reagents in the presence of Ru, Rh, or Ir catalysts to give C8-substituted quinolines or quinoline N-oxides.⁸ However, C-8 functionalization reactions of quinoline N-oxides catalyzed by Pd are still rare.⁹ Recently, some of us managed to promote the Pd-catalyzed C8–C coupling of the QOs with several substrates.¹⁰ In the presence of PdCl₂, QOs reacted with benzaldehyde at the C8 position (Scheme 1) to form P1.^10b Addition of water leads to the formation of P2.^10a C8–H activation of quinoline N-oxides reflects a reactivity different from the one previously reported for Pd(II) catalysts, whose standard behavior involves functionalizing the C2 position. For instance, Pd(OAc)₂ is a poor catalyst for the previous C8–H activation, but it easily activates the C2–H bond,¹¹ under analogous conditions, to yield P3, albeit with a different substrate. A table with some experimental results¹⁰ is shown in the ESI† (Table S1).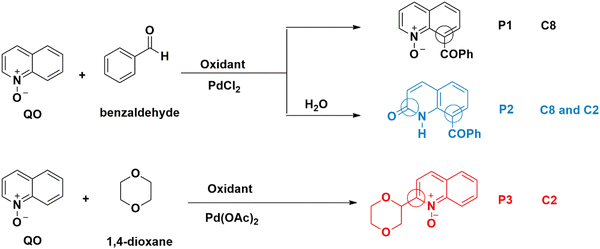

Scheme 1 Experimentally observed reaction paths for Pd(II)-catalyzed quinoline N-oxide C–H activation.

Many aspects of the former reactions remained unexplained, ranging from the nature of the intermediate formed after the reaction with the QO substrate (monomer or dimer?), to the C2 vs. C8 preferences. The initial metalation step addressed in a previous attempt at comparing C2 and C8 arylation of QOs is one of the first examples where C8-functionalization with Pd was observed.⁹ The catalysts, however, were Pd(II) complexes bearing acetate and acetic acid ligands, with acetic acid as the solvent, and an Ag(I) salt as the oxidant. The authors only studied the first step of the reaction between Pd(II) and QO.⁹ These reaction conditions are very different from those of the present work, where tert-butyl hydroperoxide (TBHP) as an oxidant led to the highest conversions, and different intermediates and mechanisms are expected.

Therefore, we performed DFT calculations (Gibbs energies from PBE0(D3)/def2-tzvpp calculations, see the Computational details section for more information) to determine the mechanism of C2–H and C8–H activation by the PdCl₂ catalyst and to understand the reasons underlying the origin of the regioselectivity as sketched in Scheme 1.

Results and discussion

The C8 mechanisms

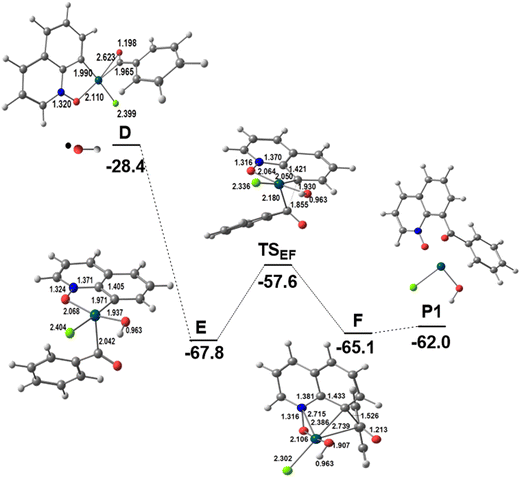
Quinoline N-oxides react with aldehydes in the presence of Pd(II) catalysts and an oxidant, giving rise to products (P1 and P2) where the C8 position of the quinoline ring is functionalized (Scheme 1, top reaction). The model reaction consisted of PdCl₂, since this reaction affords better yields when using this species as the catalyst, and QO and benzaldehyde as substrates, with dichloroethane as the solvent. According to experimental results, the reaction starts with the activation of the QO molecule by the catalyst. The energy profile for the initial transformations describing the coordination of the two substrates and related reactions is shown in Fig. 1. The reagents, transition states and products are shown in a 3D view. A complementary presentation with sketches is shown in Fig. S1 of the ESI.† This pathway ends at an intermediate that was found to be common to the formation of P1 and P2 (D).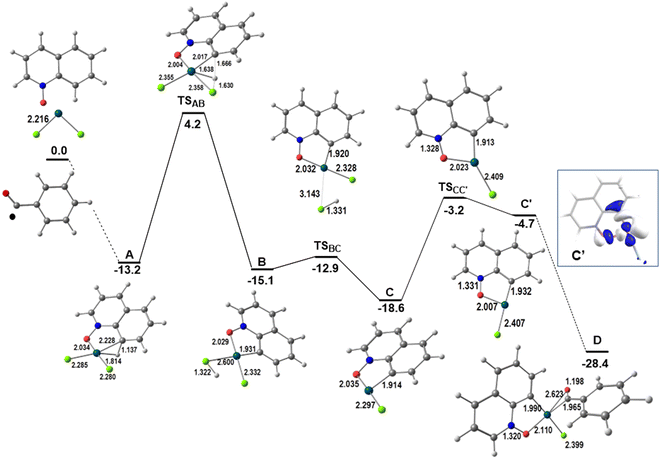

Fig. 1 Energy profile for the initiating steps of the functionalization at C8 of QO and LUMO of C′ (relative Gibbs energies in kcal mol⁻¹ in dichloroethane; distances in Å).

QO binds palladium(II) by the oxygen and the C(8)–H bond, forming a more stable metallacycle (A). The Pd–Cl bonds become slightly longer, from ∼2.22 to ∼2.28 Å, while the Pd–C and Pd–H distances of 2.285 and 1.814 Å, respectively, together with the elongated C(8)–H bond of 1.137 Å, characterize an agostic bond. The C–H activation proceeds easily from A. In this process, the hydrogen atom is transferred to one of the chlorine atoms in transition state TS_AB, with a barrier of 17.4 kcal mol⁻¹. In the transition state, the hydrogen is moving from C to Cl, with C–H and Cl–H distances of 1.666 and 1.630 Å, respectively. The new intermediate (B) has only one Pd–C bond (1.931 Å) and the Pd–ClH bond is much longer than the Pd–Cl one (2.600 and 2.332 Å). Although this species is more stable than A, it loses HCl (ΔG^# = 2.2 kcal mol⁻¹) to yield an even more stable three-coordinate intermediate C. The empty position may be occupied by a ˙COPh radical, which will likely be present in the media owing to the reaction conditions.

Indeed, TBHP generates radicals as depicted in Scheme 2.^12–14 Although the cleavage of the O–O bond is endergonic, the reaction of tBuO˙ with benzaldehyde producing tBuOH and the benzaldehyde radical is exergonic. These radicals will participate in the catalytic reaction at different stages.

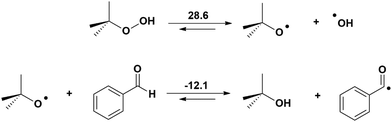Scheme 2 Mechanism for the generation of the benzaldehyde and hydroxyl radicals (Gibbs energy, kcal mol⁻¹).

The reaction of ˙COPh with intermediate C, where Cl is trans to the oxygen, yields a high energy product (not shown). However, the isomer with Cl trans to the carbon (C′) can be obtained with a barrier of 15.4 kcal mol⁻¹, and reacts with ˙COPh giving rise to the stable intermediate D. This behavior can be explained by the nature of the LUMO of C′, the accepting orbital needed to form the new Pd–C bond to the benzaldehyde radical, which is an M-Cl/C/O antibonding orbital, hybridized along the direction of the incoming ligand (Fig. 1, right side). Intermediate C does not have such a LUMO, being a worse acceptor.

The ˙COPh radical binds in a η²-CO mode, not surprisingly, since the spin density is localized in the C=O group (see Scheme S1 in the ESI†), but the Pd–O bond is longer (0.658 Å) than the Pd–C one. The formation of a C₂ dimer is not competitive and the reaction continues through the mononuclear species. It should be added as further proof that intermediate C′ has been experimentally trapped and structurally characterized as the complex with PPh₃,^10b which is shown in Fig. S2 (ESI†). The Pd–Cl and Pd–O distances are very similar to those calculated for C′.

Intermediate D formally containing Pd(III)¹² is a key intermediate, with the OCPh ligand binding the metal in a η²-CO mode and the spin density mostly localized at the metal and partly at the C=O group (Scheme S1 in the ESI†). At this stage, the two substrates are bound to the catalyst and the outcome of the reaction depends on the experimental conditions, namely the presence or absence of water. Product P1 is formed in the absence of water (Scheme 1 and Fig. 2; a complementary presentation with sketches is available in Fig. S3, ESI†) and product P2 is formed in the presence of water (see below).

Fig. 2 Energy profile for the second part of the functionalization of QO at C8 in the absence of water (relative Gibbs energies in kcal mol⁻¹ in dichloroethane; distances in Å).

Under these conditions, the metal in intermediate D is attacked by the second radical, ˙OH, also present under the reaction conditions (Scheme 2), which converts D to the Pd(IV) intermediate E and the OCPh ligand changes its coordination mode from η² to η¹. The Pd–O_COPh distance has become quite large (2.796 Å). A reductive elimination reaction allows the formation of the new C–C bond between the two fragments derived from the substrates and affords F with a barrier of 10.2 kcal mol⁻¹. The product P1 is weakly bound to Pd(II) in this intermediate and its release is slightly endergonic, forming the Pd(OH)Cl intermediate, which may undergo exchange of OH by Cl to reinitiate the catalytic cycle. This may also proceed from Pd(OH)Cl (Fig. 2). Notice that in this pathway, the TOF-determining transition state¹⁵ is TS_AB and corresponds to the C–H activation step. Indeed, a strong kinetic isotope effect (k_H/k_D = 3.4) was observed experimentally,^10a whereas the calculated value was k_H/k_D = 3.2 (see the Computational details section), thus further confirming the proposed mechanism. Stephens et al.⁹ studied possible mechanisms of C8–H activation of QO catalyzed by Pd(OAc)₂ in acetic acid, assuming the initial formation of [Pd(HOAc)₃QO]²⁺, [Pd(OAc)(HOAc)QO]⁺, and [Pd(OAc)₂] complexes with QO, and compared it with C2–H activation. The three mechanisms showed a clear preference for C8–H activation (see below), with the barrier for cleaving the C–H bond being 24.7, 20.1, and 22.2 kcal mol⁻¹, all higher than our calculated value corresponding to TS_AB (17.4 kcal mol⁻¹). These results suggest that PdCl₂ may indeed favor C8–H activation compared to Pd(OAc)₂.

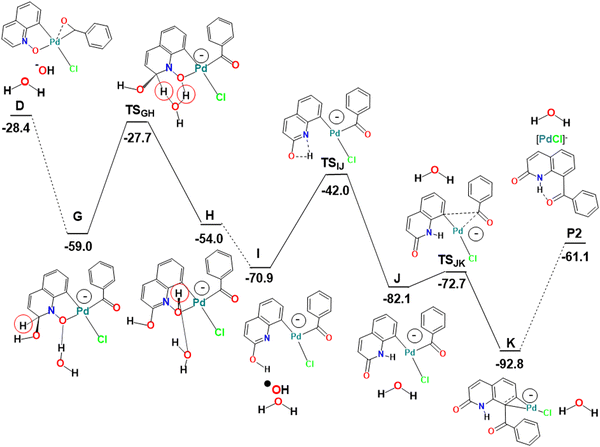
When the experimental conditions are modified by the controlled addition of water to the dichloroethane reaction solution containing the PdCl₂ catalyst and the substrates, a new reactivity has been described, featuring both C8–H activation as described above and a different type of C2–H activation leading to the formation of 2-quinolinones (product P2, Scheme 1 and Fig. 3). Labelling experiments using H₂¹⁸O revealed that the labelled oxygen atom was transferred to the ketone in product P2, confirming the role of water in the mechanism. The yield of P2 also increased with the amount of added water (Table S1 in the ESI†).^10a

Fig. 3 Energy profile for the second part of the alternative functionalization at C8 and functionalization at C2 of QO in the presence of water (relative Gibbs energies in kcal mol⁻¹ in dichloroethane; the negative charge represents the charge of the complex and the red circle highlights the hydrogen migrating in the G to H transformation).

The first part of the mechanism consists of the C8–H activation, as described above until the formation of the intermediate D (Fig. 1). The second part involves many intermediates and transition states, as shown in the energy profile of Fig. 3, where all species are represented with sketches to make interpretation easier. Key intermediates and transition states are represented in a 3D view with distances in Fig. 4. A complementary energy profile, with 3D pictures, similar to Fig. 1 and 2, is also available as Fig. S4 in the ESI.†

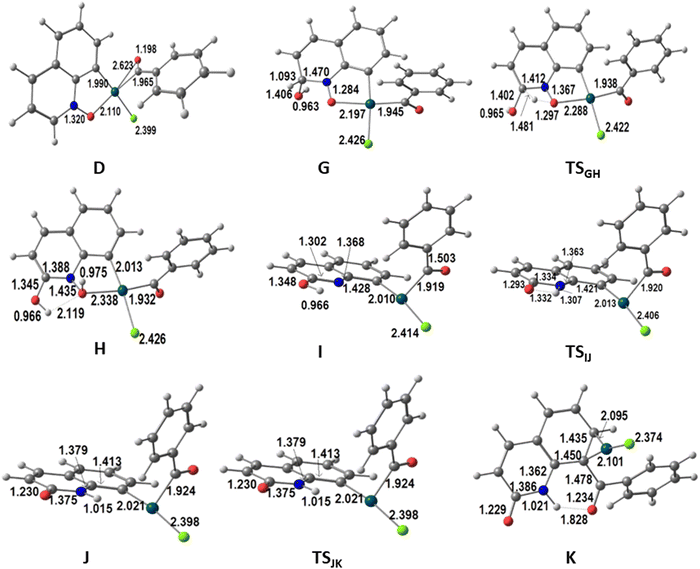Fig. 4 Structures of the intermediates and transition states in the energy profile for the second part of the alternative functionalization at C8 of QO in the presence of water (distances in Å).

The Pd(III) complex D could be attacked by OH⁻ (H₂O is too weak a nucleophile) at the QO ring or at the metal. The C2 position has a high positive charge of 0.232, only overcome by the charge at C9 (0.472), but attack at this position would prevent any aromaticity of the ring. Attack at C2, on the other hand, leaves the C₆H₃ ring of QO unchanged, being thus favored. The new negatively charged intermediate G maintains a square planar geometry and is very stable (−59.0 kcal mol⁻¹). Its stoichiometry is very similar to that of E, but it has a negative charge, while E was a radical. In order to form the product P2, it is easy to see how G can undergo a reductive elimination reaction leading to the formation of the new C–C bond involving C8 of the QO derived fragment. It is more difficult, however, to envisage how the CH(OH) group in G will transform into C=O, as observed in the C2 reactivity, since the two hydrogen atoms must migrate to different atoms and in different orders. No paths could be obtained in most of these possibilities.

The proposed pathway starts with the migration of the hydrogen from the CH(OH) group at C2 (highlighted with a red circle in Fig. 3) to the O(N), which is completed in intermediate H, but is already taking place in TS_GH. The calculated barrier was initially too high. Since it has been shown¹⁶ that proton and hydroxide mobility are highly facilitated by water molecules, and experiments indicated that the formation of P2 requires the presence of water, it was possible that the real barriers for steps involving proton transfers were lower. Therefore, the energy profile showing the conversion of D into P2 was also calculated in the presence of one explicit water molecule. In these conditions, the barrier to transform G into H was 31.3 kcal mol⁻¹, as shown in Fig. 3. This barrier seems reasonable, considering that the formation of P2 requires high temperatures and long reaction times. It is expectable that an even more realistic model, with more water molecules, would lead to an even lower barrier, nonetheless, it is outside the scope of this work to extend this search. The assistance of the water molecule as a hydrogen shuttle is explicit in intermediates G and H, as well as in TS_GH, the migrating hydrogen being highlighted (red circle). Its presence affects essentially the energy of the transition state, which has been stabilized by 21.0 kcal mol⁻¹, and that of intermediate G (−5.3 kcal mol⁻¹). The energy of the other species remains the same. A comparison of the conversion of G into H without and with the explicit water molecule is shown in Scheme S2 (ESI†).

In H, the oxygen atom of the new N–O–H group is coordinated to Pd (Pd–O 2.338 Å) and is involved as an acceptor in a O–H⋯O hydrogen bond with the water molecule, which acts as a donor to the adjacent OH group at C2 in another hydrogen bond. The Pd(III) metal center keeps the square planar environment. Complex H loses ˙OH easily to afford I. The metal is reduced to Pd(II) in this process and becomes three-coordinated, with the nitrogen atom 2.967 Å away from the metal in H and I. Proton migration from oxygen (OH) to nitrogen in I is another down-hill process, as the energy of intermediate J is 11.2 kcal mol⁻¹ lower, despite a relatively high barrier (TS_IJ 28.9 kcal mol⁻¹). The hydrogen is almost at the same distance from the nitrogen (1.332 Å) and the oxygen (1.307 Å) in the TS_IJ transition state. In J, the proton binds to N (1.015 Å), and remains far from bonding distance to Pd (2.636 Å). J is still a three coordinate Pd(II) complex with a T-shaped coordination sphere. Its low energy is due to the restored planarity of the QO ring. Complex J undergoes reductive elimination to form the C–C bond between the two ligands derived from the substrates, which is needed to yield the product P2, going through the TS_JK transition state with an energy 9.4 kcal mol⁻¹ higher than that of J. In TS_JK, the C–C distance is 1.912 Å, having started as 2.760 Å in J. P2 is weakly bound to Pd(0) in intermediate K, through a η²-coordination of the C6 ring, with Pd–C distances of 2.095 and 2.101 Å. Release of P2 leaves behind a Pd(0) species, [PdCl]⁻ or Pd(0) and Cl⁻, which must be reoxidized to Pd(II) to complete the catalytic cycle. This reaction has been studied by several authors in acetic acid/acetate medium. The barrier was calculated to be 24.6 kcal mol⁻¹ using a simplified ligand (1,2-bis(methylsulfonyl)ethane),¹⁷ but it was claimed to be similar when the full 1,2-bis(phenylsulfonyl)ethane ligand was considered. Later calculations using a variety of computational conditions led to ∼32 kcal mol⁻¹ for the reoxidation of Pd(0) in the same system.¹⁸ These values suggest that the reoxidation step has a barrier similar to that of the migration step highlighted above (31.3 kcal mol⁻¹ to transform G into H, in Fig. 3).

The two paths depicted above in Fig. 2 and 3 are characterized by the C8–H activation of the QO ring and start with the formation of intermediate D where the two substrates bind the metal. Considering the full mechanisms describing the formation of P1 and P2, it is clear that C–H activation (Fig. 1) corresponds to the TOF-determining transition state (4.2 kcal mol⁻¹), defined as the transition state with the highest energy in the full pathways from A to F (P1) or A to K (P2), in agreement with experiments.^10a

In the absence of water, ˙OH radicals attack the metal (E, −67.8 kcal mol⁻¹), and the metal undergoes reductive elimination from the Pd(IV) complex E forming product P1 and regenerating the Pd(II) catalyst. When water is present, the C2 position of bound QO is attacked by OH⁻ (G, −59.0 kcal mol⁻¹), while the final reductive elimination step takes place from Pd(II) after several other steps associated with functionalization of the C2 position, where the CH bond is transformed into a C=O bond (formation of the 2-quinolinenone). Although the product P2 is formed, the catalyst must be reoxidized, which is in agreement with experimental findings.

The TOF-determining intermediates are E (−67.8 kcal mol⁻¹) and K (−92.8 kcal mol⁻¹), so that the reaction energy span is higher for P2 than for P1, respectively.¹⁵ These energies reflect the reaction temperatures for each reaction, namely 80 °C for P1 and 140 °C for P2.

We also analyzed the possibility of direct conversion of P1 into P2, even though it was not found experimentally (Fig. S5, ESI†).^10a The two products differ by the presence of the ketone at C2 and the conversion of the NO group into NH. In a reaction similar to the conversion of complex D in G (Fig. 3) product P1 undergoes nucleophilic attack of OH⁻ at the C2 position yielding intermediate a (Fig. S5 in the ESI†). The next step is the migration of the hydrogen at the C2 position to the oxygen of the NO group, over TS_ab, with the highest barrier of the process (42.9 kcal mol⁻¹). The water molecule formed remains hydrogen bonded to the new C=O group. Protonation of b leads to product P2. The activation energy for the migration step is similar to that of the catalyst in the absence of an explicit water molecule to assist proton migration (Scheme S2 in the ESI†). However, the endergonic protonation of the nitrogen atom contributes to make this reaction very unlikely.

The C2 mechanism

As shown in Scheme 1 and discussed in the Introduction section, the activation of the QO ring in the presence of the Pd(OAc)₂ catalyst and several substrates, and in the absence of external oxidants leads to the reaction at the C2 position and then to product P3. This reaction is not observed when the catalyst is PdCl₂. Therefore the C2–H activation will be studied for PdCl₂ in order to understand why it does not compete with the C8–H activation described above when the reaction conditions are the same. Although P3 has only been obtained for another substrate (1,4-dioxane) the same model will be used for comparison.^7h

The possibility of activating a different position of QO required a different precursor. Another coordination mode of QO, which would direct the reactivity, was explored. This can be achieved by the formation of a π-complex. Indeed, a likely mechanism could be determined, as can be seen in the energy profile of Fig. 5, with QO binding in an allylic η³ mode through the three C(H) carbon atoms C2, C3, and C4, in the C₅N cycle (L), with Pd–C distances of 2.290, 2.107, and 2.205 Å, respectively. A complementary view of this pathway with sketches is shown in Fig. S6 of the ESI.†

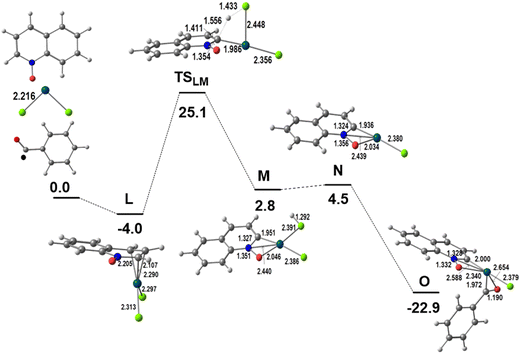Fig. 5 Energy profile for the first part of the functionalization of QO at C2 (relative Gibbs energies in kcal mol⁻¹ in dichloroethane; distances in Å).

The asymmetry introduced by the NO group in the ring is small in the two Pd–Cl bonds of L (2.295 and 2.313 Å). The C–H activation takes place at the C2–H bond, with a hydrogen migration to one of the Cl atoms occurring over TS_LM (ΔG^≠ = 25.1 kcal mol⁻¹) and producing the intermediate M. The transition state TS_LM is a σ-complex with one Pd–C bond (1.986 Å) and two Pd–Cl bonds of similar length (Pd–Cl 2.386 and Pd–ClH 2.391 Å), while the hydrogen is being transferred from the C2 to the Cl atom. The coordination sphere of M is increased by coordinating also to the oxygen, but the Pd–Cl distance is long (2.440 Å). M loses HCl to afford N, with a T-shaped environment. This intermediate is stabilized by the reaction with the ˙COPh radical to form O. The Pd(III) species (O) is a radical species equivalent to D in the C8 activation reaction (Fig. 1 and 2) and its energy is 5.5 kcal mol⁻¹ higher. The spin density is more localized in Pd (0.63) in intermediate O than in D (0.44). Notice that the barrier for C–H activation from the initial [Pd(QO)Cl₂] is now 29.1 kcal mol⁻¹, much higher than the corresponding barrier from the σ-complex described in Fig. 1 (17.4 kcal mol⁻¹).

The remaining steps to form the product P3, shown in Fig. 6, are very similar to those described in Fig. 2 to obtain P1. Intermediate O reacts with the ˙OH radical to yield the Pd(IV) intermediate P. Besides the increase in coordination number, an OH⋯Cl hydrogen bond stabilizes this arrangement. During the last two reactions, the metal was formally oxidized stepwise from Pd(II) (L, M, N) to Pd(III) (O) and then to Pd(IV) (P). Reductive elimination of the two Pd–C bonded fragments, derived from the two substrates, in P is a low energy process (barrier 7.7 kcal mol⁻¹), which affords the product (P3) bound to Pd (Q), with Pd–O bond distances of 2.072 and 2.075 Å. Release of P3 leaves Pd(II) as Pd(OH)Cl, to continue the catalytic cycle as it is or regenerate the PdCl₂ catalyst. This result again shows that the PdCl₂ catalyst will promote the lower energy reaction starting with C8–H activation, as discussed above.

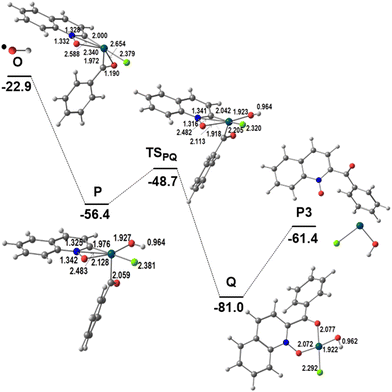Fig. 6 Energy profile for the second part of the functionalization of QO at C2 (relative Gibbs energies in kcal mol⁻¹ in dichloroethane; distances in Å).

The two pathways leading to the activation of C2 or C8 differ by the coordination mode of QO and therefore influence the position of the CH activation step. Interestingly, reductive elimination is easier from P (Fig. 6) than from E (Fig. 2), however, this is a low energy step and therefore not determining.

In the calculations of Stephens et al.⁹ addressing the Pd(OAc)₂ catalyst, it was mentioned that all mechanistic routes studied favored C8–H activation. Indeed, it required a change in the catalyst to Pd(PMe₃)Ph for them to find a mechanism depicting C2–H activation.⁹ The authors did not, however, explore the possibility of a π-QO complex of Pd(II) as an intermediate.

Comparison between the C8 and the C2 mechanisms and substrates

Both TOF determining transition states in C8 and C2 activation, TS_AB and TS_LM, respectively, are associated with CH activation. These energy profiles are independently presented in Fig. 1 and 5, and, for an easier comparison they are shown simultaneously in Scheme 3.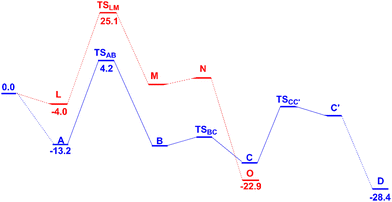

Scheme 3 The two energy profiles for the first steps in the C8 (blue) and C2 (red) activation reactions in dichloroethane with relevant Gibbs energies (kcal mol⁻¹).

The energy difference between the initial complexes A and L and the respective transition states, TS_AB and TS_LM, is higher for the C2 activation (29.1 kcal mol⁻¹) than for the C8 one (17.4 kcal mol⁻¹). These values reflect the reactivity experimentally observed, namely, the PdCl₂ catalyst activates preferentially the C8 position. These barriers parallel the relative energy of the initial complexes containing QO coordinated to the catalyst (−13.2 and −4.0 kcal mol⁻¹, for A and L, respectively) and reflect the different coordination modes of QO, as shown in Scheme 4.

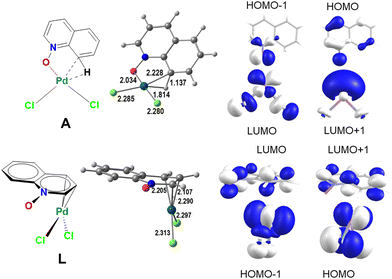Scheme 4 The geometries of intermediates A and L (distances in Å) and the frontier molecular orbitals of QO and PdCl₂ relevant for their bond: A (top) and L (bottom).

In A (Scheme 4, top), QO binds as a bidentate ligand through O and CH, the latter forming an agostic bond to Pd(II), with Pd–C and Pd–H bonds of 2.228 and 1.814 Å, while the C–H bond is stretched to 1.137 Å. The complex has a square planar geometry, as expected for a d⁸ metal center. The HOMO and HOMO−1 of undistorted QO are located in the oxygen atom and have the right symmetry to combine with the two acceptor orbitals, LUMO and LUMO+1, of PdCl₂, forming a strong σ Pd–O bond with donation of electrons from the ligand to the metal. At the same time, the C8–H bond approaches Pd, distorting the geometry of the QO ligand and leading to the formation of the Pd–CH agostic bond, which weakens the CH bond and facilitates C–H cleavage. The ligand forms two σ bonds and the complex may be considered a σ-QO complex.

On the other hand, in L (Scheme 4, bottom), QO binds the metal center by means of a π-QO allylic complex, where there are three Pd–C bonds (2.205, 2.107, and 2.290 Å) and two Pd–Cl bonds, also in a pseudo-square planar arrangement. These are only very slightly longer than in A. The LUMO and LUMO+1 of QO have adequate symmetry to combine with the HOMO and HOMO−1 of PdCl₂. This will be a π back donation component from the metal to the QO ligand.

The different stabilities of the Pd-QO complexes can therefore be understood by the metal–ligand interaction (Scheme 4, bottom). The lower energy of A is assigned to the stronger metal–ligand interaction (σ in A, π in L). The presence of the agostic bond in A may explain the lower activation barrier for CH activation, since the C–H bond is already weakened.

We also performed an energy decomposition analysis (EDA)¹⁹ using the ADF program²⁰ (see the Computational details section and Table S2 in the ESI†). The binding energy (BE) of QO to the PdCl₂ fragment is −36.7 and −28.4 kcal mol⁻¹ in A and L, respectively. The interaction energies, ΔE_int (−51.6 (A) and −38.7 (L) kcal mol⁻¹), differ from the BE by the preparation energy of the fragments, due to the change in geometry when the optimized fragment is in the molecule (ΔE_prep). These energies differ by 4.6 kcal mol⁻¹ and are larger (more destabilizing) for A. Among the other terms, the preference for σ coordination (A) can be assigned to a much larger electrostatic interaction (−126.9 and −91.2 kcal mol⁻¹, respectively for A and L), which is not compensated by the smaller Pauli repulsion term and more attractive orbital interaction in L. Solvent effects are negligible.

Comparison between different catalysts

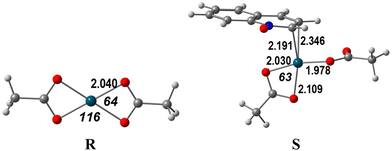
Another remaining question addresses the reactivity of the Pd(OAc)₂ catalyst compared to that of PdCl₂. Complex Pd(OAc)₂ appears to be less active in these reactions, compared to other studies where acetic acid is present. In order to find an answer, we focused on the first step, the C–H activation.

As described above, PdCl₂ is an unsaturated and very reactive species. QO coordinates Pd(II) to form stable complexes, namely σ-complex A (energy −13.2 kcal mol⁻¹, Fig. 1) and π-complex L (energy −4.0 kcal mol⁻¹, Fig. 5). On the other hand, Pd(OAc)₂ (henceforth denoted as R) is a very stable square planar d⁸ Pd(II) complex, as depicted in Scheme 5, despite the distortion (O–Pd–O angles of 64° and 116° instead of 90°). The approach of the QO reagent does not lead easily to a complex similar to A (C8 activation) but can afford the high energy complex S (12.7 kcal mol⁻¹, Scheme 5) similar to L (C2 activation). Because acetate is a bidentate ligand, the QO binds Pd in an η² mode in S, while it binds in an η³ coordination in L (Fig. 5 and Scheme 4) contributing to larger stability. It can be added that the C–H activation of QO and elimination of acetic acid require almost 35 kcal mol⁻¹. It is thus not surprising that PdCl₂ will be a much better catalyst to activate QO, favoring, as discussed, the activation at C8. The species R considered as the precursor is different from those considered in a similar study already mentioned,⁹ where C8 activation took place in the acetic acid medium. These authors only addressed the CH activation step of the reaction. Their initial species, containing coordinated acetic acid molecules are not likely to be relevant under the conditions of the reactions studied in the present work (solvent dichloroethane). The barrier for the C–H activation step studied was larger than 20 kcal mol⁻¹, the value depending on the model, as was discussed above.

Scheme 5 The geometries of Pd(OAc)₂ (left panel) and [Pd(OAc)₂(η²-QO)] (right panel).

It is known, however, that the formation of P3 type products, not competitive with benzaldehyde, is sometimes observed but for rather different ether substrates, namely 1,4-dioxane.^7h The bonding capabilities of this substrate are very different from those of benzaldehyde and different outcomes are likely, but their study is outside the scope of this work. Just as an example, the relative energies of several relevant intermediates in the PdCl₂ pathways leading to P1 and P3 with 1,4-dioxane were higher than those with benzaldehyde, making them less likely to occur.

Conclusions

The regioselectivity of the QO C–H activation (C8 vs. C2) was explained by the different nature of the first intermediate (A or L), resulting from the reaction between the PdCl₂ catalyst and QO (Fig. 7, bottom left). The formation of the σ-metallacycle A, with a Pd–O bond and a Pd–CH agostic bond, led to C8 activation, with a 17.4 kcal mol⁻¹ energy barrier, while the η³-QO complex L with three carbon atoms of the hetero-ring ended in C2 activation, with a barrier of 29.1 kcal mol⁻¹. The benzaldehyde ˙COPh and the ˙OH radicals attack the metal successively affording Pd(III) intermediates D or O and Pd(IV) intermediates E or P, as reported in other experimental studies. After reductive elimination, products P1 and P3, respectively, are obtained, regenerating the Pd(II) catalyst. P1 is favored as observed experimentally, explaining the preference for C8 activation shown by PdCl₂.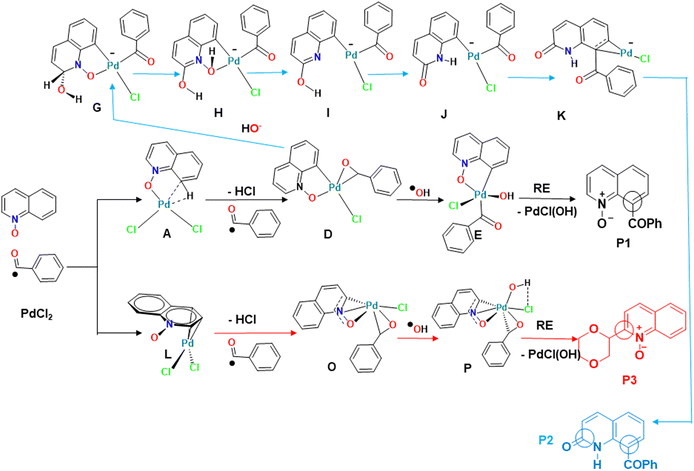

Fig. 7 Comparison between the three pathways leading to P1, P2 and P3, emphasizing the most relevant intermediates and the similarities between them.

In the presence of water, the same intermediate D obtained from the σ-Pd-QO complex (Fig. 7, top) undergoes nucleophilic attack of OH⁻ at the C2 position, initiating the formation of the C=O function (2-quinolinenone) and conversion of NO into NH to afford the P2 product. This pathway has a high energy step with a barrier of 29.1 kcal mol⁻¹, consistent with the higher temperatures and reaction times experimentally required. The Pd(II)(OAc)₂ catalyst is much less active under these experimental conditions (dichloroethane as the solvent) without acetic acid. The QO substrate can also easily bind as a π-complex, promoting C2 activation, but the energies are higher and not competitive when benzaldehyde is the substrate.

Computational details

Density functional theory (DFT) calculations²¹ were performed using the Gaussian09 package.²² The PBE0 functional, with the def2-tzvpp basis set and associated effective core potential, downloaded from the EMSL Basis Set Library,^23–25 for Pd, as well as a standard 6-311G** basis set for the other atoms, was used in the geometry optimizations. The PBE0 combines the generalized gradient functional of Perdew, Burke and Ernzerhof (PBE)²⁶ with 25% exchange and 75% correlation weighting defined by Adamo and Barone.²⁷ The geometries of all intermediates and transition states were optimized without symmetry constraints. Possible isomers and coordination modes of the QO ligand were tested. Frequency calculations were performed for all species in order to characterize the nature of the stationary points. For transition state structures (the negative frequencies are given in the coordinates file), intrinsic reaction coordinate (IRC) calculations were carried out to confirm the nature of the transition state and the connecting minima. All calculations were performed in a dichloroethane Polarizable Continuum Model (PCM) using the integral equation formalism variant (IEFPCM) implemented in Gaussian.²⁸

In order to check the reliability of several functionals and basis sets, single point calculations on the initially optimized PBE0/6-311G** geometries were run and compared with CCSD(T)^29–31 calculations with a def2-tzvpp basis set for all atoms for the first step of the C8 activation mode (TS_AB in Fig. 1). Herein we tested: (1) the M06-2X(D3) functional with the def2-tzvpp basis set (Pd) and a standard 6-311G** for the remaining atoms (M06-2X(D3)/6-311G**), or with def2-tzvpp for all atoms (M06-2X(D3)/def2-tzvpp); (2) the PBE0 functional with the def2 tzvpp basis set (Pd) and a standard 6-311G** for the remaining atoms (PBE0/6-311G**), with the D3 version of Grimme's dispersion with Becke–Johnson damping,^32,33 the def2-tzvpp basis set (Pd) and a standard 6-311G** for the remaining atoms (PBE0(D3)/6-311G**), and with def2-tzvpp for all atoms (PBE0(D3)/def2-tzvpp). The results are summarized in Table S3 (ESI†). Notice that although the def2-tzvpp and 6-311g(d,p) basis sets are commonly considered triple-ζ quality, they are substantially different. Indeed, def2-tzvpp is often considered acceptably-accurate for most DFT calculations,³⁴ whereas owing to a weakness in the construction of the 6-311G basis set, this basis is not of triple-ζ quality.³⁵ Using as reference value for the 16.5 kcal mol⁻¹TS_AB barrier obtained at the CCSD(T)/def2-tzvpp level, it is clear that the M06-2X functional overestimates the barrier, while the PBE0 functional yields better results (MAEs < 2.6 kcal mol⁻¹). The best approach is PBE0 with Grimme's D3 dispersion correction along with the def2-tzvpp basis for all atoms (Table S3, ESI†). Therefore, the Gibbs energy values in the manuscript correspond to PBE0(D3)/def2-tzvpp single point calculations on PBE0/6-311G** geometries.

All free energies values were calculated at 300 K using GoodVibes v3.2,³⁶ which computes thermochemical data allowing corrections for the low lying imaginary frequencies. Herein, the vibrational contribution to entropy was calculated using a quasi-rigid-rotor-harmonic-oscillator (quasi-RRHO) approximation³⁷ with a frequency cut-off value of 100.0 cm⁻¹. A standard concentration correction to solvent media was also applied as implemented in the software package. Kinetic isotope effects were computed at 413.15 K (the temperature used in the experimental KIE determination),^10a using Kinisot.py version 2.0.1, freely available at https://github.com/patonlab/Kinisot.

The EDA¹⁹ analysis (DFT²¹ calculations) was performed with the ADF program²⁰ for the optimized geometries of intermediates A and L. The Local Density Approximation (LDA) of the correlation energy (Vosko–Wilk–Nusair³⁸) and the Generalized Gradient Approximation (Becke's³⁹ exchange and Perdew's⁴⁰ correlation functionals) with gradient correction, solvent correction (COSMO model implemented in ADF) and relativistic effect (ZORA approximation⁴¹) were used. The basis set consisted, for all electrons of all atoms, of triple-ζ Slater-type orbitals (STOs) with a set of two polarization functions (TZ2P in ADF).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank the Fundação para a Ciência e a Tecnologia, Portugal, for financial support (Projects UIDB/04046/2020 and UIDP/04046/2020), and Cooperação Científica e Tecnológica FCT/CHINA-BILATERAL-2017/2019. PJC acknowledges FCT for the CEEC 2021 Initiative (2021.00381.CEECIND). XC and CP acknowledge the Ministry of Science and Technology of China (2016YFE0132600). FFM thanks Prof Cui and her group for the warm welcome in Zhengzhou during the short-term scientific mission in which this paper started.

References

1. (a) T. Eicher, S. Hauptmann and A. Speicher, The Chemistry of Heterocycles, Wiley-VCH, Weinheim, 2nd edn, 2003, vol. 6, pp. 316–336; (b) C. H. McAteer, M. Balasubramanian and R. Murugan, 7.06 - Pyridines and their Benzo Derivatives: Applications, in Comprehensive Heterocyclic Chemistry III, ed. A. R. Katritzky, C. A. Ramsden, E. F. V. Scriven and R. J. K. Taylor, Elsevier, Oxford, 2008, vol. 7, pp. 309–336; (c) C. H. Chen and J. Shi, Metal chelates as emitting materials for organic electroluminescence, Coord. Chem. Rev., 1998, 171, 161–174.
2. For selected examples, see: (a) R. H. Crabtree and A. Lei, Introduction: CH Activation, Chem. Rev., 2017, 117, 8481–8482; (b) R. Sharma and U. Sharma, Remote C–H bond activation/transformations: A continuous growing synthetic tool; Part II, Catal. Rev., 2018, 60, 497–565; (c) R. Sharma, K. Thakur, R. Kumar, I. Kumar and U. Sharma, Remote C–H Bond Functionalizations: Methods and Strategies in Organic Synthesis, Catal. Rev., 2015, 57, 345–405; (d) T. Iwai and M. Sawamura, Transition-Metal-Catalyzed Site-Selective C–H Functionalization of Quinolines beyond C2 Selectivity, ACS Catal., 2015, 5, 5031–5040; (e) P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, 3d Transition Metals for C–H Activation, Chem. Rev., 2019, 119, 2192–2452.
3. For selected examples, see: (a) Y. Nakao, K. S. Kanyiva and T. Hiyama, A strategy for C–H activation of pyridines: direct C-2 selective alkenylation of pyridines by nickel/Lewis acid catalysis, J. Am. Chem. Soc., 2008, 130, 2448–2449; (b) B.-T. Guan and Z. Hou, Rare-Earth-Catalyzed C–H Bond Addition of Pyridines to Olefins, J. Am. Chem. Soc., 2011, 133, 18086–18089; (c) J. Roger, A. L. Gottumukkala and H. Doucet, Palladium-Catalyzed C3 or C4 Direct Arylation of Heteroaromatic Compounds with Aryl Halides by C–H Bond Activation, ChemCatChem, 2010, 2, 20–40; (d) Y. Nakao, Transition-Metal-Catalyzed C–H Functionalization for the Synthesis of Substituted Pyridines, Synthesis, 2011, 3209–3219.
4. (a) D.-Y. Li, Z.-L. Huang and P.-N. Liu, Heterobicyclic Core Retained Hydroarylations through C−H Activation: Synthesis of Epibatidine Analogues, Org. Lett., 2018, 20, 2028–2032; (b) X. Chen, X. Cui and Y. Wu, C8-Selective Acylation of Quinoline N-Oxides with α-Oxocarboxylic Acids via Palladium-Catalyzed Regioselective C–H Bond Activation, Org. Lett., 2016, 18, 3722–3725; (c) J. Jeong, P. Patel, H. Hwang and S. Chang, Rhodium(III)-Catalyzed C–C Bond Formation of Quinoline N-Oxides at the C-8 Position under Mild Conditions, Org. Lett., 2014, 16, 4598–4601; (d) J. Kwak, Y. Ohk, Y. Jung and S. Chang, Rollover Cyclometalation Pathway in Rhodium Catalysis: Dramatic NHC Effects in the C–H Bond Functionalization, J. Am. Chem. Soc., 2012, 134, 17778–17788; (e) Y. Shang, X. Jie, H. Zhao, P. Hu and W. Su, Rh(III)-Catalyzed Amide-Directed Cross-Dehydrogenative Heteroarylation of Pyridines, Org. Lett., 2014, 16, 416–419.
5. L. C. Campeau, S. Rousseaux and K. Fagnou, A Solution to the 2-Pyridyl Organometallic Cross-Coupling Problem:  Regioselective Catalytic Direct Arylation of Pyridine N-Oxides, J. Am. Chem. Soc., 2005, 127, 18020–18021.
6. J. Wu, X. Cui, L. Chen, G. Jiang and Y. Wu, Palladium-Catalyzed Alkenylation of Quinoline-N-oxides via C−H Activation under External-Oxidant-Free Conditions, J. Am. Chem. Soc., 2009, 131, 13888–13889.
7. (a) X. Chen, F. Yang, X. Cui and Y. Wu, Potassium Hydroxide-Catalyzed Alkynylation of Heteroaromatic N-Oxides with Terminal Alkynes, Adv. Synth. Catal., 2017, 359, 3922–3926; (b) Z. Zhang, C. Pi, H. Tong, X. Cui and Y. Wu, Iodine-Catalyzed Direct C–H Alkenylation of Azaheterocycle N-Oxides with Alkenes, Org. Lett., 2017, 19, 440–443; (c) X. Chen, X. Cui, F. Yang and Y. Wu, Base-Promoted Cross-Dehydrogenative Coupling of Quinoline N-Oxides with 1,3-Azoles, Org. Lett., 2015, 17, 1445–1448; (d) C. Zhu, M. Yi, D. Wei, X. Chen, Y. Wu and X. Cui, Copper-Catalyzed Direct Amination of Quinoline N-Oxides via C–H Bond Activation under Mild Conditions, Org. Lett., 2014, 16, 1840–1843; (e) H. Wang, X. Cui, Y. Pei, Q. Zhang, D. Wei, J. Bai and Y. Wu, Direct regioselective phosphonation of heteroaryl N-oxides with H-phosphonates under metal and external oxidant free conditions, Chem. Commun., 2014, 50, 14409–14411; (f) H. Wang, Y. Pei, J. Bai, J. Zhang, Y. Wu and X. Cui, Dimerization of heteroaromatic N-oxides under metal-free conditions, RSC Adv., 2014, 4, 26244–26246; (g) Z. Wu, H. Song, X. Cui, C. Pi, W. Du and Y. Wu, Sulfonylation of Quinoline N-Oxides with Aryl Sulfonyl Chlorides via Copper-Catalyzed C–H Bonds Activation, Org. Lett., 2013, 15, 1270–1273; (h) Z. Wu, C. Pi, X. Cui, J. Bai and Y. Wu, Direct C-2 Alkylation of Quinoline N-Oxides with Ethers via Palladium-Catalyzed Dehydrogenative Cross-Coupling Reaction, Adv. Synth. Catal., 2013, 355, 1971–1976; (i) L.-Y. Xie, T.-G. Fang, J.-X. Tan, B. Zhang, Z. Cao, L.-H. Yang and W.-M. He, Visible-light-induced deoxygenative C2-sulfonylation of quinoline N-oxides with sulfinic acids, Green Chem., 2019, 21, 3858–3863; (j) S. Han, X. Gao, Q. Wu, J. Li, D. Zou and Y. Wu, Nickel-promoted C(2)–H amidation of quinoline N-oxides with N-fluorobenzenesulfonimide, Org. Chem. Front., 2019, 6, 830–834; (k) G.-H. Li, D.-Q. Dong, Y. Yang, X.-Y. Yu and Z.-L. Wang, Direct Carbamoylation of Quinoline N-oxides with Hydrazinecarboxamides via C−H Bond Activation Catalyzed by Copper Catalyst, Adv. Synth. Catal., 2019, 361, 832–835; (l) Y. Zhang, S. Zhang, G. Xu, M. Li, C. Tang and W. Fan, Cu-Catalyzed carbamoylation versus amination of quinoline N-oxide with formamides, Org. Biomol. Chem., 2019, 17, 309–314.
8. (a) T. Shibata and Y. Matsuo, Directed C–H Alkenylation of Quinoline N-Oxides at the C-8 Position Using a Cationic Rhodium(I) Catalyst, Adv. Synth. Catal., 2014, 356, 1516–1520; (b) H. Hwang, J. Kim, J. Jeong and S. Chang, Regioselective Introduction of Heteroatoms at the C-8 Position of Quinoline N-Oxides: Remote C–H Activation Using N-Oxide as a Stepping Stone, J. Am. Chem. Soc., 2014, 136, 10770–10776; (c) K. Shin, S.-W. Park and S. Chang, Cp*Ir(III)-Catalyzed Mild and Broad C−H Arylation of Arenes and Alkenes with Aryldiazonium Salts Leading to the External Oxidant-Free Approach, J. Am. Chem. Soc., 2015, 137, 8584–8592; (d) D. Kalsi, R. A. Laskar, N. Barsu, J. R. Premkumar and B. Sundararaju, C-8-Selective Allylation of Quinoline: A Case Study of β-Hydride vs. β-Hydroxy Elimination, Org. Lett., 2016, 18, 4198–4201; (e) N. Barsu, M. Sen, J. R. Premkumar and B. Sundararaju, Cobalt(III) catalyzed C-8 selective C–H and C–O coupling of quinoline N-oxide with internal alkynes via C–H activation and oxygen atom transfer, Chem. Commun., 2016, 52, 1338–1341; (f) B. Wang, C. Li and H. Liu, Cp*Rh(III)-Catalyzed Directed C–H Methylation and Arylation of Quinoline N-Oxides at the C-8 Position, Adv. Synth. Catal., 2017, 359, 3029–3034; (g) J. Kim, S. Kim, D. Kim and S. Chang, Ru-Catalyzed Deoxygenative Regioselective C8–H Arylation of Quinoline N-Oxides, J. Org. Chem., 2019, 84, 13150–13158; (h) A. K. Dhiman, S. S. Gupta, R. Sharma, R. Kumar and U. Sharma, Rh(III)-Catalyzed C(8)–H Activation of Quinoline N-Oxides: Regioselective C–Br and C–N Bond Formation, J. Org. Chem., 2019, 84, 12871–12880; (i) C. You, T. Yuan, Y. Huang, C. Pi, Y. Wu and X. Cui, Rhodium-catalyzed regioselective C8–H amination of quinoline N-oxides with trifluoroacetamide at room temperature, Org. Biomol. Chem., 2018, 16, 4728–4733; (j) C. You, C. Pi, Y. Wu and X. Cui, Rh(III)-Catalyzed Selective C8–H Acylmethylation of Quinoline N-Oxides, Adv. Synth. Catal., 2018, 360, 4068–4072.
9. D. E. Stephens, J. Lakey-Beitia, A. C. Atesin, T. A. Atesin, G. Chavez, H. D. Arman and O. V. Larionov, Palladium-Catalyzed C8-Selective C–H Arylation of Quinoline N-Oxides: Insights into the Electronic, Steric, and Solvation Effects on the Site Selectivity by Mechanistic and DFT Computational Studies, ACS Catal., 2015, 5, 167–175.
10. (a) X. Chen, X. Cui and Y. Wu, “One-Pot” Approach to 8-Acylated 2-Quinolinones via Palladium-Catalyzed Regioselective Acylation of Quinoline N-Oxides, Org. Lett., 2016, 18, 2411–2414; (b) X. Chen, X. Cui and Y. Wu, C8-Selective Acylation of Quinoline N-Oxides with α-Oxocarboxylic Acids via Palladium-Catalyzed Regioselective C–H Bond Activation, Org. Lett., 2016, 18, 3722–3725.
11. J. Wu, X. Cui, L. Chen, G. Jiang and Y. Wu, Palladium-catalyzed alkenylation of quinoline-N-oxides via C–H activation under external-oxidant-free conditions, J. Am. Chem. Soc., 2009, 131, 13888–13889.
12. M. Sun, L.-K. Hou, X.-X. Chen, X.-J. Yang, W. Sun and Y. Zang, Palladium-Catalyzed Regioselective ortho-Acylation of Azoxybenzenes with Aldehyde Derivatives, Adv. Synth. Catal., 2014, 356, 3789–3793.
13. X. Chen, C. Zhu, X. Cui and Y. Wu, Direct 2-acetoxylation of quinoline N-oxides via copper catalyzed C–H bond activation, Chem. Commun., 2013, 49, 6900–6902.
14. C.-S. Wang, T. Roisnel, P. H. Dixneuf and J.-F. Soule, Synthesis of 2-Pyridinemethyl Ester Derivatives from Aldehydes and 2-Alkylheterocycle N-Oxides via Copper-Catalyzed Tandem Oxidative Coupling–Rearrangement, Org. Lett., 2017, 19, 6720–6723.
15. (a) S. Kozuch, A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815; (b) S. Kozuch and S. Shaik, How to Conceptualize Catalytic Cycles? The Energetic Span Model, Acc. Chem. Res., 2011, 44, 101–110; (c) A. Uhe, S. Kozuch and S. Shaik, Automatic analysis of computed catalytic cycles, J. Comput. Chem., 2011, 32, 978–985; (d) S. Kozuch and J. M. L. Martin, The Rate-Determining Step is Dead. Long Live the Rate- Determining State, ChemPhysChem, 2011, 12, 1413–1418.
16. N. Agmon, Mechanism of hydroxide mobility, Chem. Phys. Lett., 2000, 319, 247–252.
17. F. Nahra, F. Liron, G. Prestat, C. Mealli, A. Messaoudi and G. Poli, Striking AcOH Acceleration in Direct Intramolecular Allylic Amination Reactions, Chem. – Eur. J., 2009, 15, 11078–11082.
18. F. J. S. Duarte, G. Poli and M. J. Calhorda, Mechanistic Study of the Direct Intramolecular Allylic Amination Reaction Catalyzed by Palladium(II), ACS Catal., 2016, 6, 1772–1784.
19. (a) T. Ziegler and A. Rauk, Carbon monoxide, carbon monosulfide, molecular nitrogen, phosphorus trifluoride, and methyl isocyanide as.Sigma. donors and.pi. acceptors. A theoretical study by the Hartree-Fock-Slater transition-state method, Inorg. Chem., 1979, 18, 1755–1759; (b) T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10.
20. (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Towards an Order-N DFT Method, Theor. Chem. Acc., 1998, 99, 391–403; (c) Theoretical Chemistry, Vrije Universiteit, Amsterdam, ADF2013 SCM http://www.scm.com (accessed July 28th, 2023).
21. R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1989.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, J. A. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2009.
23. D. Feller, The role of databases in support of computational chemistry calculations, J. Comput. Chem., 1996, 17, 1571–1586.
24. F. Weigend and R. Ahldrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
25. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community, J. Chem. Inf. Model., 2019, 59, 4814–4820.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169.
28. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3093.
29. R. J. Bartlett and G. D. Purvis, Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem, Int. J. Quantum Chem., 1978, 14, 561–581.
30. G. D. Purvis and R. J. Bartlett, A full coupled-cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918.
31. J. A. Pople, M. Head-Gordon and K. Raghavachari, Quadratic configuration interaction. A general technique for determining electron correlation energies, J. Chem. Phys., 1987, 87, 5968–5975.
32. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
33. S. Grimme, J. Antony, S. Ehrlic and H. Krieg, A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
34. N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115, 2315–2372.
35. R. S. Grev and H. F. Schaefer, III, 6-311G is not of valence triple-zeta quality, J. Chem. Phys., 1989, 91, 7305–7306.
36. G. Luchini, J. V. Alegre-Requena, I. Funes-Ardoiz and R. S. Paton, GoodVibes: automated thermochemistry for heterogeneous computational chemistry data, F1000Research, 2020, 9, 291.
37. S. Grimme, Supramolecular Binding Thermodynamics by Dispersion-Corrected Density Functional Theory, Chem. – Eur. J., 2012, 18, 9955–9964.
38. S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58, 1200–1211.
39. A. D. Becke, A new inhomogeneity parameter in density-functional theory, J. Chem. Phys., 1998, 109, 2092–2098.
40. (a) J. P. Perdew, Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824; (b) J. P. Perdew, Erratum: Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406.
41. E. van Lenthe, A. Ehlers and E. J. Baerends, Geometry Optimizations in the Zero Order Regular Approximation for Relativistic Effects, J. Chem. Phys., 1999, 110, 8943–8953.

---

Footnote

† Electronic supplementary information (ESI) available: Summary of experimental results (Table S1), EDA analysis (Table S2), benchmarking of the DFT methods (Table S3), energy profiles with alternative representation of the molecules (Fig. S1 and S3–S6, Scheme S2), spin densities (Scheme S1), the single crystal X-ray structure of [PdCl(QO)(PPh₃)] (Fig. S2), and the coordinates of all optimized species with the negative frequencies of the transition states. See DOI: https://doi.org/10.1039/d3cp02445h

---