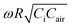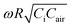Effects of AC frequency on the capacitance measurement of hybrid response pressure sensors†
Zhengjie
Li
 a,
Kyoung-Ho
Ha
b,
Zheliang
Wang
a,
Sangjun
Kim
b,
Ben
Davis
b,
Ruojun
Lu
b,
Jayant
Sirohi
a,
Kyoung-Ho
Ha
b,
Zheliang
Wang
a,
Sangjun
Kim
b,
Ben
Davis
b,
Ruojun
Lu
b,
Jayant
Sirohi
 a and
Nanshu
Lu
*abcd
a and
Nanshu
Lu
*abcd
aDepartment of Aerospace Engineering and Engineering Mechanics, the University of Texas at Austin, TX 78712, USA. E-mail: nanshulu@utexas.edu
bDepartment of Mechanical Engineering, the University of Texas at Austin, TX 78712, USA
cDepartment of Biomedical Engineering, the University of Texas at Austin, TX 78712, USA
dDepartment of Electrical and Computer Engineering, the University of Texas at Austin, TX 78712, USA
First published on 14th October 2022
Abstract
E-skins consisting of soft pressure sensors are enabling technology for soft robots, bio-integrated devices, and deformable touch panels. A well-known bottleneck of capacitive pressure sensors (CPS) is the drastic decay in sensitivity with increasing pressure. To overcome this challenge, we have invented a hybrid-response pressure sensor (HRPS) that exhibits both the piezoresistive and piezocapacitive effects intrinsic to a highly porous nanocomposite (PNC) with carbon nanotube (CNT) dopants. The HRPS is constructed with two conductive electrodes sandwiching a laminated PNC and a stiff dielectric layer. We have simplified the hybrid response into a parallel resistor–capacitor circuit, whose output depends on the AC (alternating current) frequency used for the capacitance measurement. Herein, through theoretical analysis, we discover a dimensionless parameter that governs the frequency responses of the HRPS. The master curve is validated through experiments on the HRPS with various doping ratios, subject to different compressive strains, under diverse AC frequencies. In addition, the relative contribution of piezoresistive and piezocapacitive mechanisms are also found to vary with the three parameters. Based on this experimentally validated theory, we establish a very practical guideline for selecting the optimal AC frequency for the capacitance measurement of HRPSs.
1 Introduction
E-skins refer to soft electronics that can imitate certain characteristics of human skin. Specifically, e-skins with soft pressure sensors that can mimic the human sensation of touch are best poised for soft robotic applications.1–7 Pressure-sensing e-skins are also useful in flexible touch panels8,9 or wearable sensors for detecting surface pulse waves.10,11 Various pressure-sensing mechanisms, including piezoresistive,12–16 piezoelectric,17,18 capacitive,3,19–24 optical,25–27 and iontronic responses to applied pressure,28,29 have been explored. Among them, the capacitive pressure sensor (CPS) stands out by virtue of its combined high sensitivity, large sensing range, good repeatability, temperature independence, low power consumption, and simple implementation.30–33 However, even after intensified research, there remains a longstanding bottleneck of CPS – a large trade-off between sensitivity and applied pressure.34Our recent invention of hybrid response pressure sensors (HRPSs) has broken the limit set by conventional CPSs.24 As shown in Fig. 1a, we constructed a CPS by sandwiching a laminated barely conductive porous nanocomposite (PNC) and an ultrathin dielectric layer between two parallel electrodes. The PNC is a highly porous open cell structure with tubular ligaments composed of carbon nanotube (CNT) doped Ecoflex. When the CNT doping ratio is around the percolation threshold,35 the PNC ligaments become piezoresistive and the air pores surrounded by such ligaments exhibit parasitic capacitance. As a result, the overall PNC is endowed with hybrid piezoresistivity and piezocapacitivity. The insertion of an ultrathin poly(methyl methacrylate) (PMMA) layer between the PNC and the bottom electrode tries to keep the overall sensor assembly capacitive. The experimentally measured relative capacitance change vs. applied pressure in Fig. 1b proved that the sensitivity of the HRPS outperforms all types of conventional CPSs with common dielectric materials such as Ecoflex, porous Ecoflex, and CNT doped solid or porous Ecoflex before reaching the percolation threshold. To reveal the HRPS sensing mechanism, we built an equivalent circuit as shown in Fig. 1c, where the PNC is represented by a parallel piezoresistor–piezocapacitor circuit, which is connected in series with a fixed capacitor that acts for the PMMA layer. An analytical model based on this simplified circuit was established to calculate the change of HRPS capacitance upon applied pressure.24 This model has found reasonable agreement with the experimental measurements up to a CNT doping ratio of 0.75 wt%. It offers a fundamental explanation to why the hybrid response pressure sensors afford much higher sensitivity than conventional dielectric-based CPSs. It is also able to predict the optimal CNT doping ratio that yields the best pressure sensitivity. We have demonstrated the application of a HRPS to human pulse wave detection at the surfaces of radial, carotid, and even the temporal arteries.24 We have an ongoing project to fabricate a stretchable HRPS (SHRPS) and apply it on soft inflatable grippers.
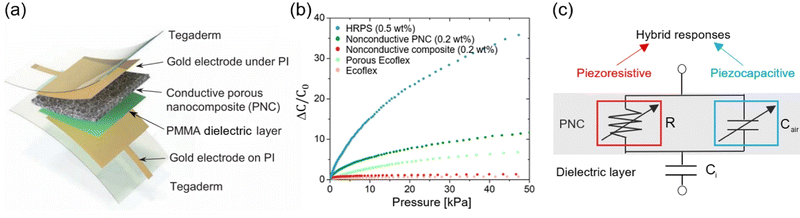 | ||
| Fig. 1 (a) A schematic showing the layers of the HRPS.24 (b) The HRPS is much more sensitive than the conventional CPS.24 (c) A simplified circuit model to represent the hybrid piezoresistive and piezocapacitive responses of the HRPS. (a and b) Reproduced from ref. 24 with the permission of Wiley. | ||
Although the effects of CNT doping ratio have been well characterized both experimentally and theoretically, we have always used the same AC (alternating current) frequency to measure HRPS capacitance – 1 kHz,24 following the convention of a traditional CPS.3,36,37 However, while the AC frequency does not matter for the capacitance measurement of dielectric-based pure capacitors, it should play a role in the HRPS because the current division between the resistive and the capacitive branch (Fig. 1b) is tunable by the AC frequency applied. In addition to its effects on the equivalent circuit of a HRPS, the AC frequency could also affect the electrical material properties of the CNT-doped composite, such as the resistivity and the dielectric constants. According to existing experimental findings, CNT-dopped-polymer composites exhibited frequency-dependent electrical conductivity.38–41 When the AC frequency was changed over a wide range, the assumption of constant dielectric constants could also breakdown.41
These considerations prompted us to perform a systematic investigation on the effects of the AC frequency on both the HRPS and the PNC. We first carried out experiments to characterize the frequency responses of the HRPS and the PNC separately. The discovery of frequency-dependent resistance and capacitance of the PNC echoes other studies on composites in the literature. We then treated the AC frequency as a variable and reanalyzed the equivalent circuit in Fig. 1c. Our derivation yielded a master curve controlled by a single dimensionless parameter. This dimensionless parameter contains three variables—the AC frequency, the resistance of the PNC, and the capacitance of air pores. The latter two are functions of both the AC frequency and the compressive strain. Experimental validations of the master curve are provided, for various CNT doping ratios, AC frequencies, and compressive strains. Our theoretical framework has fully uncovered the interplay between the three variables as well as distinctively quantified the relative contributions of the piesoresistive and piesocapacitive mechanisms in the HRPS. Ultimately, it offers a simple guideline for selecting the optimal AC frequency to measure the capacitance of the HRPS.
2 Experiments
2.1 PNC and HRPS fabrication
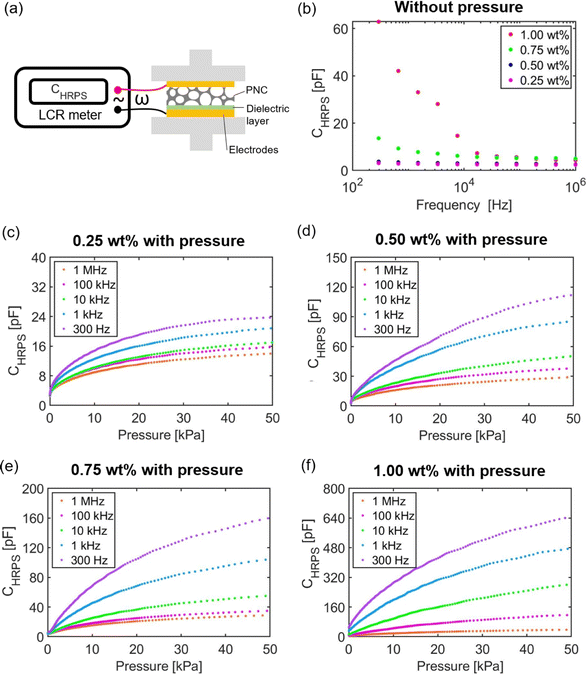
We fabricated the PNC and the HRPS following the exact recipe offered in our previous paper.24 Very briefly, the PNC was fabricated by dip-coating a commercially available nickel foam with a CNT-Ecoflex solution, curing the CNT-Ecoflex composite, and etching away the nickel foam using hydrochloric acid. The HRPS was then prepared by sandwiching the PNC by two gold electrodes with a PMMA dielectric layer inserted between the PNC and one of the electrodes.2.2 Measurement of HRPS capacitance
The experimental setup of HRPS capacitance measurement is illustrated in Fig. 2a, where the LCR meter we used was Hioki 3532-50 and the AC frequency is denoted by ω. Using this setup, we performed the following two types of experiments.Frequency sweep tests: Without applying any pressure, the capacitance of the HRPS (CHRPS) with CNT doping ratios of 0.25 wt%, 0.5 wt%, 0.75 wt%, and 1 wt% was measured using the Hioki 3532-50 with a frequency sweep from 300 Hz to 1 MHz. The applied voltage was set to be 2 V and the measurement mode was chosen to be the parallel mode. Although both resistance and capacitance readings were offered by Hioki 3532-50, only the capacitance readings are plotted in Fig. 2b. It is clear that the capacitance of the specimens with a CNT doping ratio of 0.25 wt% and 0.5 wt% is almost independent of the applied AC frequency whereas the capacitance of 0.75 wt% and 1 wt% HRPS first decreases and then reaches a plateau as the frequency increases. Specifically, the frequency where 1.00 wt% HRPS steps into a plateau is larger than that of the 0.75 wt% HRPS. In addition, at any given frequency, the capacitance increases as the doping ratio increases.
Compression tests: A dynamic mechanical analyzer (DMA, RSA-G2, TA Instruments) was used to compress the HRPS in its thickness direction. Both the compressive force and the displacement were recorded by the DMA, which can be readily converted to pressure and compressive strain. In situ capacitance measurement was performed by Hioki 3532-50. The tests were performed on four types of HRPS each under 5 different frequencies (300 Hz, 1 kHz, 10 kHz, 100 kHz, and 1 MHz) and the results are plotted in Fig. 2c–f. For all doping ratios, CHRPS increases with decreasing AC frequency. When the AC frequency went below 300 Hz, CHRPS was out of the measurement range of Hioki 3532-50. When the doping ratio increases, both the initial capacitance and the capacitance at 50 kPa increase. In addition, it is obvious that the HRPS with a greater CNT doping ratio yields a larger absolute capacitance change. These experimental results will be further explained in the Results and discussion section.
2.3 Measurements on PNC
As the PNC is much more compliant than PMMA, when subjected to the same pressure, the PMMA deformation is negligible compared with the PNC. Therefore, the PNC is the only pressure sensing layer within the HRPS. To fully understand the frequency-dependence of CHRPS, the frequency-dependent PNC properties need to be characterized. To do this, we sandwiched the PNC between two gold electrodes without a PMMA layer and performed frequency sweep tests without any applied pressure, as illustrated in Fig. 3a. The PNC specimens of different CNT doping ratios (0.25 wt%, 0.5 wt%, 0.75 wt%, and 1.00 wt%) were prepared. We used a different LCR meter, Keysight E4980AL, for the PNC measurements, because its impedance is out of the measurement range of Hoiki 3532-50. The AC frequency range was between 100 Hz and 100 kHz and the AC voltage was set to be 2 V. The resistance and capacitance results measured in the parallel mode (Rp and Cp) are displayed as markers in the log–log plots given by Fig. 3b and c, respectively. As the PNC was measured in the parallel mode, essentially Rp = R0 and Cp = Cair0, which refer to the initial undeformed resistance and capacitance of the PNC. A few important observations can be made by examining Fig. 3b and c. First, it is reasonable to have lower resistance with higher CNT doping ratios (Fig. 3b). Second, as the CNT fillers enhance the dielectric constants of the nanocomposites,41 the increases in the amount of CNTs also yields higher PNC capacitance (Fig. 3c). Third, it is clear that in general, both R0 and Cair0 have frequency dependence except that the frequency dependence is weak in the R0 of the 1 wt% PNC and in the Cair0 of the 0.25 wt% PNC. Lastly, linear segments in both log–log charts indicate that there exist some power-law relationships with the frequency.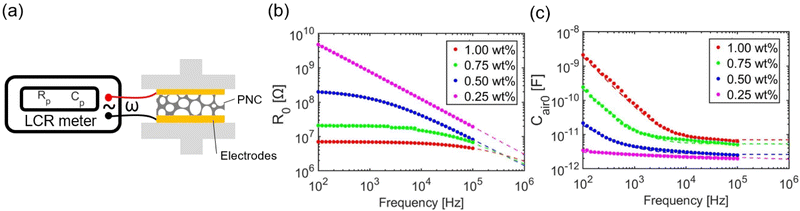 | ||
| Fig. 3 (a) A schematic of the experimental setup for measuring the frequency response of PNC without and with applied pressure. Rp and Cp represent the resistance and capacitance measured by the LCR meter in the parallel mode. Frequency response of the (b) resistance and (c) capacitance of the PNC with different CNT doping ratios. R0 = Rp and Cair = Cp. Dashed curves are fitted based on eqn (2) and (3). | ||
The experimental measurements in Fig. 3b and c can be analytically fitted. Previous studies on universal dielectric responses42 suggested a power-law scaling relationship between the conductivity and the dielectric properties of conductive filler doped polymer composites and the applied AC frequency.38,40–42 This can be understood as follows.43 The conductive fillers in a composite could be viewed as many small elements containing resistors and capacitors in parallel. A higher AC frequency will lead to a lower impedance of the micro-capacitors, effectively resulting in an increase of the overall conductivity of composites. Therefore, the conductivity-frequency relationship of these composites can be approximated by the following empirical equation:38
| σ(ω) =σdc + σac(ω) =σdc + αωs | (1) |
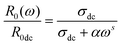 | (2) |
Eqn (2) suggests that at low AC frequency, R0(ω) is dominated by σdc, hence it has weak dependence on frequency, which explains the plateaus at small frequencies in Fig. 3b except that for 0.25 wt%, there is no plateau in the given AC frequency range. Moreover, the DC resistance of 0.25 wt% is too large to be measured by our Keysight E4980AL LCR meter. We therefore had to obtain R0dc by extrapolating the resistance to ω = 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s−1, as inspired by the literature.38 As our Keysight E4980AL LCR meter has an upper limit of AC frequency of 100 kHz, we further extrapolated R0(ω) to 1 MHz as dashed curves in Fig. 3b based on eqn (1) and (2).
s−1, as inspired by the literature.38 As our Keysight E4980AL LCR meter has an upper limit of AC frequency of 100 kHz, we further extrapolated R0(ω) to 1 MHz as dashed curves in Fig. 3b based on eqn (1) and (2).
Fig. 3c can be fitted in a similar manner provided that we know the kair0 ∼ ω dependence where kair0 is the dielectric constant of the undeformed PNC that appears in Cair0 = kair0ε0A/t, where ε0 is the vacuum permittivity. Theoretically speaking, the capacitance of air should be independent of frequency. However, apart from the capacitance of air, PNC also has parasitic capacitance within the composite which is dependent on the CNT doping ratios and the AC frequency. According to the universal dielectric response, the dielectric constants of the conductive filler doped composites follows the power law:41,45
| kair0(ω) ∼ ω−p, kair0(ω) = kair0dc + βω−p | (3) |
3 Analytical model for HRPS
In our previous work,24 a simplified equivalent circuit model illustrated by Fig. 1b was established under the following four assumptions: (1) the electrical field is uniform and perpendicular to the parallel electrodes; (2) the PNC has a uniform initial porosity, φ0, and all the applied compression is accommodated by the reduction of the porosity; (3) there is no lateral deformation when HRPS is subjected to pressure; (4) the frequency and pressure effects are fully decoupled. These assumptions allow us to establish a simple analytical expression for Cair as a function of both the applied compressive strain e and the AC frequency ω: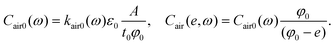 | (4) |
We follow the fitted resistance ∼ strain relation in our previous work24 to express R as a function of both e and ω (not shown in this paper):
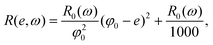 | (5) |
During compression, both R and Cair vary with the compressive strain, while the capacitance of the dielectric layer Ci remains a constant which equals 7.08 nF in all of our specimens.
The impedance of all three components in Fig. 1c can be expressed as:
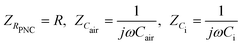 | (6) |
Because ZRPNC and ZCair are first connected in parallel and then connected in series with ZCi, the impedance of the whole HRPS can be expressed as:
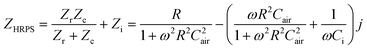 | (7) |
Whose capacitance component is:
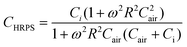 | (8) |
If we introduce two dimensionless parameters 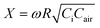 , Y = ωRCair, we can rewrite CHRPS (after normalizing by Ci):
, Y = ωRCair, we can rewrite CHRPS (after normalizing by Ci):
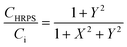 | (9) |
Note that X2 and Y2 are correlated because they share the same variables Cair and R. The range of Cair in the parameter space we explored in our experiments was ∼300 pF before compression (1.00 wt%, 300 Hz) and 2 nF after compression. Since Ci is 7.08 nF, Ci ≫ Cair, hence X2 ≫ Y2 is always true in our problem.
Next, let's evaluate the relative magnitudes of X2, Y2 and 1.
Case I: if Y2 ≪ 1, Y2 is negligible in both the numerator and the denominator of eqn (9) such that CHRPS can be approximated as:
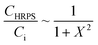 | (10) |
Therefore, in Case I, CHRPS is only governed by a single dimensionless parameter, X. This approximate solution is plotted in Fig. 4a. In addition, if X2 ≪ 1, then:
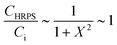 | (11) |
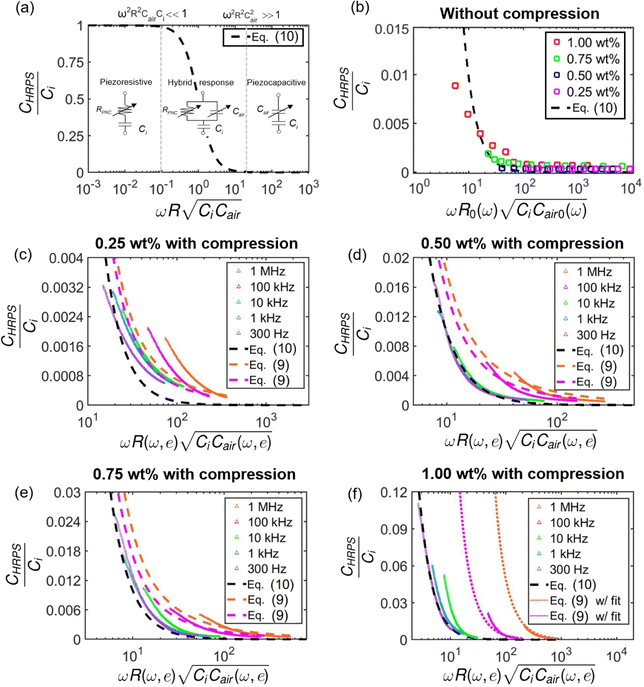 | ||
Fig. 4 (a) A master curve based on eqn (10) that can capture all three regimes – piezoresistive, hybrid, and piezocapacitive responses. (b) Frequency-only validation of the master curve. (c–f) Frequency and pressure validation of the master curve (black dashed curve). The colored dashed and dotted curves are based on eqn (9). Note that as the compressive strain increases, the x axis 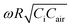 goes left. goes left. | ||
In this case, most of the current will flow through the piezoresistor and the piezocapacitor no longer plays a role. It corresponds to the far left limit in Fig. 4a, which is no longer a functional CPS because CHRPS is not responsive to pressure.
Case II: if Y2 ≫ 1, CHRPS could be approximated as:
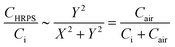 | (12) |
After rearrangement,
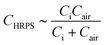 | (13) |
This expression indicates that the HRPS degenerates into two capacitors connected in series, meaning that the resistive branch is negligible. It corresponds to the far right limit in Fig. 4a, which loses the hybrid response and also becomes an insensitive CPS.
With the analyses of the limiting cases, we can readily divide Fig. 4a into three regimes, each with an equivalent circuit illustrated. The two dividers are therefore X2 = ω2R2CiCair ≪ 1 between the piezoresistive and the hybrid response regimes, and Y2 = ω2R2C2air ≫ 1 between the hybrid and the piezocapacitive regimes. Thus far, we have derived a simple analytical expression for CHRPS (eqn (10)) which can be plotted into a master curve (Fig. 4a) that reveals the fundamental interplay among the resistive, capacitive, and frequency factors – in the form of a single dimensionless parameter 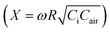 . In addition to capturing the three equivalent circuits through the analysis of the limiting cases, the master curve offers quantitative estimations for the condition of the hybrid response of HRPS:
. In addition to capturing the three equivalent circuits through the analysis of the limiting cases, the master curve offers quantitative estimations for the condition of the hybrid response of HRPS: 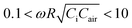 . While the other dimensionless parameter (Y = ωRCair) is not included in the master curve, Y has a clear physical meaning which will be discussed in Section 4.3.
. While the other dimensionless parameter (Y = ωRCair) is not included in the master curve, Y has a clear physical meaning which will be discussed in Section 4.3.
Because R and Cair are functions of the CNT doping ratio and the compressive strain, the experimental validation of the master curve will involve many different scenarios and it is very interesting to see how well the master curve can capture those diverse situations and where the limits of the master curve are.
4 Results and discussions
4.1 Experimental validations
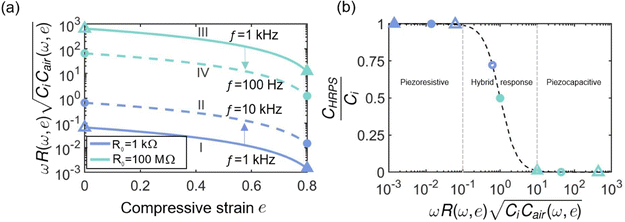
To validate our theory, in this section, we replot the experimental results for CHRPS in Section 2 by normalizing it by Ci and changing the horizontal axis to be the dimensionless parameter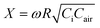 , which is a function of both ω and e. X essentially increases with increasing ω but decreases with increasing e (because R ∼ (φ0 − e)2 in eqn (5) whereas Cair ∼ (φ0 − e)−1 in eqn (4)). Fig. 4b is replotted from Fig. 2b, which are frequency sweep tests without any applied pressure. Therefore, the horizontal axis of Fig. 4b only varies with ω, and R = R0(ω) (eqn (2)) and Cair = Cair0(ω) (eqn (3) and (4)) have been plugged in. The different marker colors represent the experimental results of HRPS with different CNT doping ratios. Note that the CHRPS of the as-fabricated specimens (without compression) varies more with ω at lower ω in specimens with higher CNT doping ratios. The black dashed curve is the master curve given in eqn (10). It is encouraging to see that all the experimental results collapse after replotting and the measured trends are well captured by the master curve without any fitting for CHRPS. It is a strong indicator that our theoretical framework has uncovered all the essential physics of the frequency effects – (1) tuning the current flow through the resistive vs. the capacitive branches and (2) tuning the resistivity and the permittivity of the PNC.
, which is a function of both ω and e. X essentially increases with increasing ω but decreases with increasing e (because R ∼ (φ0 − e)2 in eqn (5) whereas Cair ∼ (φ0 − e)−1 in eqn (4)). Fig. 4b is replotted from Fig. 2b, which are frequency sweep tests without any applied pressure. Therefore, the horizontal axis of Fig. 4b only varies with ω, and R = R0(ω) (eqn (2)) and Cair = Cair0(ω) (eqn (3) and (4)) have been plugged in. The different marker colors represent the experimental results of HRPS with different CNT doping ratios. Note that the CHRPS of the as-fabricated specimens (without compression) varies more with ω at lower ω in specimens with higher CNT doping ratios. The black dashed curve is the master curve given in eqn (10). It is encouraging to see that all the experimental results collapse after replotting and the measured trends are well captured by the master curve without any fitting for CHRPS. It is a strong indicator that our theoretical framework has uncovered all the essential physics of the frequency effects – (1) tuning the current flow through the resistive vs. the capacitive branches and (2) tuning the resistivity and the permittivity of the PNC.
When pressure is applied, another variable, e, which is obtained as the ratio of the compressive displacement to the initial thickness of HRPS, comes into play. To best display the results of three variables, CNT doping ratio, ω, and e, we plot CHRPS/Civs.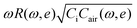 in four different charts, each with a fixed CNT doping ratio and variable ω in different colors (Fig. 4c–f). Each colored curve in Fig. 4c–f therefore represents a compression experiment on a HRPS with a fixed CNT doping ratio under a fixed ω. And when e (i.e., applied pressure) increases, the x axis goes left. Note that the y axes of Fig. 4c–f have different scales. A few important observations can be made by comparing the experimental results with the master curve. (1) The master curve agrees well with the low frequency experiments on 0.5 wt%, 0.75 wt%, and 1 wt% HRPS. This is because the master curve given by eqn (10) has a prerequisite that Y = ωRCair ≪ 1, which can be met when ω is small. (2) When ω is too large for Y = ωRCair ≪ 1 to hold, we plot the exact solution eqn (9) as the colored dashed curves in Fig. 4c–e and find them to have good agreement with the experimental results measured under high frequencies. (3) When the CNT doping ratio is 1 wt%, eqn (4) no longer captures the experimental relationship between Cair and e. We therefore assume a power law given by ESI† eqn (S2) to fit the experimentally measured Cair with the fitted exponents given in the ESI† Table S2 and the fitted curves plotted as dashed curves in the ESI† Fig. S2d. Replacing eqn (4) by ESI† eqn (S2), eqn (9) is replotted as the colored dotted curves in Fig. 4f, which are in excellent agreement with the experimental curves, indicating that our overall theoretical framework still holds. (4) In general, neither the master curve nor the exact solution can well predict the experimental results of the 0.25 wt% HRPS, which may be due to the inaccurate R0 that was extrapolated following ref. 38 because it was too large to be measurable by our LCR meter. (5) All of our experiments only operated in the regimes of piezocapacitive and hybrid responses. (6) Fig. 4c–f are not the most straightforward plots for HRPS sensitivity discussions because they are plotting CHRPS instead of ΔCHRPS. When it comes to sensitivity evaluation, we have to examine ΔC/C0, in which C0 plays a big role. As a result, although the absolute change of CHRPS appears to be the largest in 1 wt% specimens, the most sensitive specimens were actually the 0.5 wt% ones (see the ESI† Fig. S3b).24 With this point in mind, at given doping ratios of 0.5 wt% (Fig. 4d) and 0.75 wt% (Fig. 4e), it is still obvious in those figures that ω = 300 Hz offers the best sensitivity, which happens to be the cases that are best traced by the master curve.
in four different charts, each with a fixed CNT doping ratio and variable ω in different colors (Fig. 4c–f). Each colored curve in Fig. 4c–f therefore represents a compression experiment on a HRPS with a fixed CNT doping ratio under a fixed ω. And when e (i.e., applied pressure) increases, the x axis goes left. Note that the y axes of Fig. 4c–f have different scales. A few important observations can be made by comparing the experimental results with the master curve. (1) The master curve agrees well with the low frequency experiments on 0.5 wt%, 0.75 wt%, and 1 wt% HRPS. This is because the master curve given by eqn (10) has a prerequisite that Y = ωRCair ≪ 1, which can be met when ω is small. (2) When ω is too large for Y = ωRCair ≪ 1 to hold, we plot the exact solution eqn (9) as the colored dashed curves in Fig. 4c–e and find them to have good agreement with the experimental results measured under high frequencies. (3) When the CNT doping ratio is 1 wt%, eqn (4) no longer captures the experimental relationship between Cair and e. We therefore assume a power law given by ESI† eqn (S2) to fit the experimentally measured Cair with the fitted exponents given in the ESI† Table S2 and the fitted curves plotted as dashed curves in the ESI† Fig. S2d. Replacing eqn (4) by ESI† eqn (S2), eqn (9) is replotted as the colored dotted curves in Fig. 4f, which are in excellent agreement with the experimental curves, indicating that our overall theoretical framework still holds. (4) In general, neither the master curve nor the exact solution can well predict the experimental results of the 0.25 wt% HRPS, which may be due to the inaccurate R0 that was extrapolated following ref. 38 because it was too large to be measurable by our LCR meter. (5) All of our experiments only operated in the regimes of piezocapacitive and hybrid responses. (6) Fig. 4c–f are not the most straightforward plots for HRPS sensitivity discussions because they are plotting CHRPS instead of ΔCHRPS. When it comes to sensitivity evaluation, we have to examine ΔC/C0, in which C0 plays a big role. As a result, although the absolute change of CHRPS appears to be the largest in 1 wt% specimens, the most sensitive specimens were actually the 0.5 wt% ones (see the ESI† Fig. S3b).24 With this point in mind, at given doping ratios of 0.5 wt% (Fig. 4d) and 0.75 wt% (Fig. 4e), it is still obvious in those figures that ω = 300 Hz offers the best sensitivity, which happens to be the cases that are best traced by the master curve.
4.2 Indications of the master curve
The existence of a master curve offers a guideline for choosing the optimal AC frequency for a given doping ratio and sensing range. Fig. 5a first reveals how the X variable (plotted as the y axis in the log scale) varies with e at different hypothetical R0 (equivalent to different doping ratios, dark blue indicates a higher doping ratio) and different ω (equivalent to f). The four different scenarios are labeled in Fig. 5a. This figure confirms that a higher CNT doping ratio and larger compression reduce X. The open markers indicate before compression and the solid markers denote after compression. These markers are replotted on the master curve in Fig. 5b to best illustrate how much CHRPS can be changed through compression under different scenarios. It should be reminded that the X variable (plotted as the x axis in Fig. 5b) reduces upon compression and enlarges with increasing ω. In Scenario I indicated by the dark blue solid curve and triangular markers, a large CNT doping ratio makes the open triangular marker to fall in the piezoresistive regime before compression and compression further moves the marker toward the left, yielding little change in CHRPS. Without changing the CNT doping ratio, the master curve offers a new remedy for improving the HPRS sensitivity—increasing ω such that the triangular markers are shifted to the circular markers, which corresponds to Scenario II in Fig. 5a and leverages the hybrid responses. Conversely, in Scenario III, when the CNT doping ratio is low, both the light blue open and solid triangular markers fall in the piezocapacitive regime. But simply reducing ω could shift the light blue triangular markers to the circular markers, which corresponds to Scenario IV in Fig. 5a, which is also able to leverage the hybrid responses. Therefore, the master curve has a very effective indication for tuning the sensitivity of HRPS—modifying the CNT doping ratio and the AC frequency to make X fall in the hybrid response regime within the range of compression (or pressure), roughly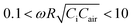 .
.
4.3 Piezoresistive vs. piezocapacitive contributions
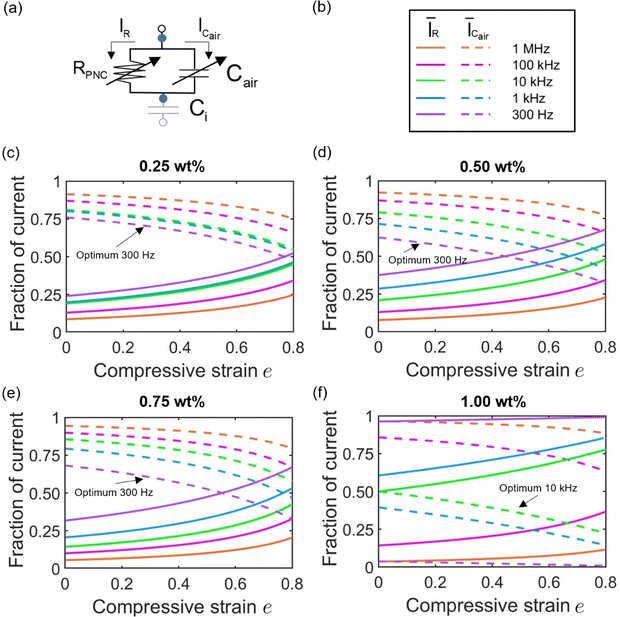
There remains one more unanswered question for the hybrid response—how much is the relative contributions of the piezoresistive vs. piezocapacitive responses. Our theory is also able to provide an answer to this curiosity. Fig. 6a illustrates the current flowing through the resistive branch (IR) and the capacitive branch (ICair). The higher relative current flow indicates more contribution to the overall response. We therefore define the fractions of the current flow to be| ĪR = IR/(IR + ICair), ĪCair = ICair/(IR + ICair) | (14) |
Due to the parallel connection, there is an intrinsic trade-off between them:
| ĪR + ĪCair = 1 | (15) |
Furthermore,
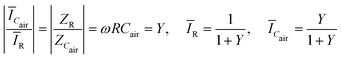 | (16) |
Therefore, the physical meaning of Y is actually the ratio of the current flowing through the capacitive branch to that of the resistive branch. This explains why (Y2 ≫ 1) represents the piezocapacitive regime and (Y2 ≪ X2 ≪ 1) represents the piezoresistive regime in Fig. 4a. With the legends given in Fig. 4b, the two fractions of current are plotted in Fig. 6c–f, and each represents a CNT doping ratio. It is clear that a higher AC frequency leads to a larger current flow through the capacitive branch. Moreover, in Fig. 6c–e, ĪCair starts higher than ĪR but the former decreases whereas the latter increases with compression. A cross-over between the two indicates that there is a swap of the dominating mechanism as the compression progresses – from piezocapacitivity to piezoresistivity. This can be easily understood as follows: before the compression, there are large air pores and the deformation of those air pores mainly drives the change of CHRPS at small pressure; when the pressure is large, the air pores are compressed and the conductive ligaments start to make contacts such that the piezoresistivity becomes dominant. Among the five frequencies examined, the optimal frequency observed from Fig. 4c–e is the one that keeps the two current fractions closest to 0.5, suggesting that the scenario with the most balanced hybrid response has the best sensitivity. For 1.00 wt%, the optimal frequency also shares this characteristic (Fig. 6f). Detailed explanations are provided in the ESI.†
5 Conclusions
Although AC frequency does not matter for conventional CPSs with dielectric pressure sensing layers, it plays a significant role in the HRPS where the pressure sensing layer is a PNC with a CNT doping ratio near the percolation threshold. In this paper, we have analyzed the equivalent circuit of the HRPS to extract a dimensionless controlling parameter,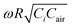 , and a corresponding master curve that can govern both the frequency and the pressure responses of the HRPS. The master curve is validated through experiments on the HRPS with various CNT doping ratios, compressive strains, and AC frequencies. The relative contributions of piezoresistive and piezocapacitive effects are found to vary with the three variables. Based on this theory, we have established a guideline for selecting the optimal frequency at a given CNT doping ratio. Essentially, with a given CNT doping ratio, we should choose a frequency which enables the pressure induced changes of CHRPS/Ci to move along the steep section of the master curve as indicated in Fig. 5b. This is the first formal investigation of the frequency effects on the HRPS. The fundamental understanding we have achieved is valuable because it offers predictable tunability for a post-fabricated HRPS to adapt to different working conditions.
, and a corresponding master curve that can govern both the frequency and the pressure responses of the HRPS. The master curve is validated through experiments on the HRPS with various CNT doping ratios, compressive strains, and AC frequencies. The relative contributions of piezoresistive and piezocapacitive effects are found to vary with the three variables. Based on this theory, we have established a guideline for selecting the optimal frequency at a given CNT doping ratio. Essentially, with a given CNT doping ratio, we should choose a frequency which enables the pressure induced changes of CHRPS/Ci to move along the steep section of the master curve as indicated in Fig. 5b. This is the first formal investigation of the frequency effects on the HRPS. The fundamental understanding we have achieved is valuable because it offers predictable tunability for a post-fabricated HRPS to adapt to different working conditions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was sponsored partially by the US Office of Naval Research (ONR) under Grant No. N00014-20-1-2112 and partially by the US National Science Foundation (NSF) ASCENT program under Grant No. 2133106. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the US Office of Naval Research, the US National Science Foundation, or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. Z. L. acknowledges the Warren A. and Alice L. Meyer Endowed Scholarship in Engineering.References
- S.-H. Sunwoo, K.-H. Ha, S. Lee, N. Lu and D.-H. Kim, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 359–391 CrossRef CAS PubMed
.
- C. M. Boutry, M. Negre, M. Jorda, O. Vardoulis, A. Chortos, O. Khatib and Z. Bao, Sci. Rob., 2018, 3, eaau6914 CrossRef
.
- S. C. B. Mannsfeld, B. C. K. Tee, R. M. Stoltenberg, C. V. Chen, S. Barman, B. V. O. Muir, A. N. Sokolov, C. Reese and Z. Bao, Nat. Mater., 2010, 9, 859–864 CrossRef CAS
.
- W. W. Lee, Y. J. Tan, H. Yao, S. Li, H. H. See, M. Hon, K. A. Ng, B. Xiong, J. S. Ho and B. C. K. Tee, Sci. Rob., 2019, 4, eaax2198 CrossRef PubMed
.
- R. F. Shepherd, F. Ilievski, W. Choi, S. A. Morin, A. A. Stokes, A. D. Mazzeo, X. Chen, M. Wang and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20400–20403 CrossRef CAS PubMed
.
- S. S. Robinson, K. W. OBrien, H. Zhao, B. N. Peele, C. M. Larson, B. C. Mac Murray, I. M. Van Meerbeek, S. N. Dunham and R. F. Shepherd, Extreme Mech. Lett., 2015, 5, 47–53 CrossRef
.
- M. L. Hammock, A. Chortos, B. C.-K. Tee, J. B.-H. Tok and Z. Bao, Adv. Mater., 2013, 25, 5997–6038 CrossRef CAS PubMed
.
- U. Khan, T.-H. Kim, H. Ryu, W. Seung and S.-W. Kim, Adv. Mater., 2017, 29, 1603544 CrossRef PubMed
.
- C. Yan, J. Wang, W. Kang, M. Cui, X. Wang, C. Y. Foo, K. J. Chee and P. S. Lee, Adv. Mater., 2014, 26, 2022–2027 CrossRef CAS
.
- C. M. Boutry, A. Nguyen, Q. O. Lawal, A. Chortos, S. Rondeau-Gagné and Z. Bao, Adv. Mater., 2015, 27, 6954–6961 CrossRef CAS
.
- Y. Cheng, R. Wang, J. Sun and L. Gao, Adv. Mater., 2015, 27, 7365–7371 CrossRef CAS PubMed
.
- L. Zhao, F. Qiang, S.-W. Dai, S.-C. Shen, Y.-Z. Huang, N.-J. Huang, G.-D. Zhang, L.-Z. Guan, J.-F. Gao and Y.-H. Song, Nanoscale, 2019, 11, 10229–10238 RSC
.
- S. Lee, A. Reuveny, J. Reeder, S. Lee, H. Jin, Q. Liu, T. Yokota, T. Sekitani, T. Isoyama and Y. Abe, Nat. Nanotechnol., 2016, 11, 472–478 CrossRef CAS
.
- Y. Lee, J. Park, S. Cho, Y.-E. Shin, H. Lee, J. Kim, J. Myoung, S. Cho, S. Kang and C. Baig, ACS Nano, 2018, 12, 4045–4054 CrossRef CAS PubMed
.
- K. He, Y. Hou, C. Yi, N. Li, F. Sui, B. Yang, G. Gu, W. Li, Z. Wang and Y. Li, Nano Energy, 2020, 73, 104743 CrossRef CAS
.
- M. Liu, X. Pu, C. Jiang, T. Liu, X. Huang, L. Chen, C. Du, J. Sun, W. Hu and Z. L. Wang, Adv. Mater., 2017, 29, 1703700 CrossRef PubMed
.
- M. T. Chorsi, E. J. Curry, H. T. Chorsi, R. Das, J. Baroody, P. K. Purohit, H. Ilies and T. D. Nguyen, Adv. Mater., 2019, 31, 1802084 CrossRef
.
- J. Chun, K. Y. Lee, C. Kang, M. W. Kim, S. Kim and J. M. Baik, Adv. Funct. Mater., 2014, 24, 2038–2043 CrossRef CAS
.
- Y. Wan, Z. Qiu, J. Huang, J. Yang, Q. Wang, P. Lu, J. Yang, J. Zhang, S. Huang and Z. Wu, Small, 2018, 14, 1801657 CrossRef
.
- S. R. A. Ruth, L. Beker, H. Tran, V. R. Feig, N. Matsuhisa and Z. Bao, Adv. Funct. Mater., 2020, 30, 1903100 CrossRef CAS
.
- H. Shi, M. AlRubaiai, C. M. Holbrook, J. Miao, T. Pinto, C. Wang and X. Tan, Adv. Funct. Mater., 2019, 29, 1809116 CrossRef
.
- S. Park, H. Kim, M. Vosgueritchian, S. Cheon, H. Kim, J. H. Koo, T. R. Kim, S. Lee, G. Schwartz and H. Chang, Adv. Mater., 2014, 26, 7324–7332 CrossRef CAS
.
- C. G. Núñez, W. T. Navaraj, E. O. Polat and R. Dahiya, Adv. Funct. Mater., 2017, 27, 1606287 CrossRef
.
- K. Ha, W. Zhang, H. Jang, S. Kang, L. Wang, P. Tan, H. Hwang and N. Lu, Adv. Mater., 2021, 33, 2103320 CrossRef CAS PubMed
.
- Y. Yamada, T. Morizono, Y. Umetani and H. Takahashi, IEEE Trans. Ind. Electron., 2005, 52, 960–968 CrossRef
.
- S. K. Ravi, N. Paul, L. Suresh, A. T. Salim, T. Wu, Z. Wu, M. R. Jones and S. C. Tan, Mater. Horiz., 2020, 7, 866–876 RSC
.
- N. Bai, L. Wang, Y. Xue, Y. Wang, X. Hou, G. Li, Y. Zhang, M. Cai, L. Zhao, F. Guan, X. Wei and C. F. Guo, ACS Nano, 2022, 16, 4338–4347 CrossRef CAS PubMed
.
- Y. Chang, L. Wang, R. Li, Z. Zhang, Q. Wang, J. Yang, C. F. Guo and T. Pan, Adv. Mater., 2021, 33, 2003464 CrossRef CAS
.
- V. Amoli, J. S. Kim, S. Y. Kim, J. Koo, Y. S. Chung, H. Choi and D. H. Kim, Adv. Funct. Mater., 2020, 30, 1904532 CrossRef CAS
.
- A. Chortos, J. Liu and Z. Bao, Nat. Mater., 2016, 15, 937–950 CrossRef CAS
.
- M. Ramuz, B. C. Tee, J. B. Tok and Z. Bao, Adv. Mater., 2012, 24, 3223–3227 CrossRef CAS
.
- J. Li, R. Bao, J. Tao, Y. Peng and C. Pan, J. Mater. Chem. C, 2018, 6, 11878–11892 RSC
.
- H. Yousef, M. Boukallel and K. Althoefer, Sens. Actuators, A, 2011, 167, 171–187 CrossRef CAS
.
- K.-H. Ha, H. Huh, Z. Li and N. Lu, ACS Nano, 2022, 16, 3442–3448 CrossRef CAS PubMed
.
- J. W. Essam, Rep. Prog. Phys., 1980, 43, 833 CrossRef CAS
.
- Y. Joo, J. Yoon, J. Ha, T. Kim, S. Lee, B. Lee, C. Pang and Y. Hong, Adv. Electron. Mater., 2017, 3, 1600455 CrossRef
.
- A. Chhetry, S. Sharma, H. Yoon, S. Ko and J. Y. Park, Adv. Funct. Mater., 2020, 30, 1910020 CrossRef CAS
.
- S. Barrau, P. Demont, A. Peigney, C. Laurent and C. Lacabanne, Macromolecules, 2003, 36, 5187–5194 CrossRef CAS
.
- H. Bizhani, A. A. Katbab, E. Lopez-Hernandez, J. M. Miranda and R. Verdejo, Polymers, 2020, 12, 853 CrossRef
.
- Y. J. Kim, T. S. Shin, H. D. Choi, J. H. Kwon, Y.-C. Chung and H. G. Yoon, Carbon, 2005, 43, 23–30 CrossRef CAS
.
- Y. Song, T. W. Noh, S. I. Lee and J. R. Gaines, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 904–908 CrossRef CAS
.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CrossRef CAS
.
- J. C. Dyre and T. B. Schrøder, Rev. Mod. Phys., 2000, 72, 873–892 CrossRef
.
- R. Rizvi, J.-K. Kim and H. Naguib, Smart Mater. Struct., 2009, 18, 104002 CrossRef
.
- L. Zhang, Z. Liu, X. Lu, G. Yang, X. Zhang and Z.-Y. Cheng, Nano Energy, 2016, 26, 550–557 CrossRef CAS
.
- C. Ang and Z. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 174109 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01250b |
| This journal is © The Royal Society of Chemistry 2022 |