DOI:
10.1039/D2MA00131D
(Paper)
Mater. Adv., 2022,
3, 5344-5349
Light induced quasi-Fermi level splitting in molecular semiconductor alloys†
Received
6th February 2022
, Accepted 27th April 2022
First published on 29th April 2022
Abstract
Quasi-Fermi-level (QFL) splitting is a direct measure of the open-circuit voltage (VOC) in an optically illuminated semiconductor solar cell (SC). The evolution of QFL splitting under 1 sun illumination in ternary blends of Gaussian disordered (GD) excitonic molecular semiconductors (MSs) is a complex process. The experimental diagonal band-gap (ECT) fitted with Vegard's law provided a bowing parameter as low as 0.05 for the used ternary alloys as a function of the mixing of two n-type semiconductors, which is a hallmark of good mixing without much alloying disorder. An analytical model based on population occupancy in GD systems is used to determine the change in QFLs as a function of the alloy composition in ternary (two n-type and one p-type) MS blends under 1 sun light illumination. The model predicts a remarkable quantitative change in the QFL due to light-induced charge carriers in such alloys to fit the experimental VOC value. This analytical model, combined with temperature-dependent mobility studies on unipolar devices with various MS alloy compositions, also reveals an interesting observation that a suitable change in QFL is due to the formation of an effective density of states (DOS) between the two n-type MSs. Further, a simpler routinely used double-diode model is also used for comparison with the Gaussian disorder model to fit the VOC values of ternary-alloy-based organic solar cells (OSCs). We show that, overall, the model is more generalized for use with any binary and ternary MS heterojunction systems being used for photovoltaic applications to determine the QFL splitting.
Introduction
Excitonic molecular semiconductors (MSs) with Gaussian disorder are unconventional compared to commonly used crystalline inorganic semiconductors; hence different mechanisms are required to explain the charge-transport and photo-physical properties of such materials.1,2 In particular, for the case of photovoltaic devices—where great progress has been made recently with single-junction efficiencies going beyond 18%3—an elaborate fundamental-level physical model needs to be developed to explain their operation. The photo-physics of voltage losses is a heavily discussed topic in the solar cell community,4 and is particularly crucial when excitonic materials are employed.5,6 MSs require solar cell physics which includes the excitonic state as the intermediate state for the generation of free carriers, as it imposes a revised fundamental Shockley–Queisser limit7 and a revised ideal-diode equation to get a clear physical picture.8 Excitonic MS solar cells generally utilize a mixture of two (or three) materials in the form of a bulk heterojunction (BHJ): at least one with a high ionization potential (called the donor) and the other with a high electron affinity (called the acceptor). Exciton dissociation is facilitated by photo-induced charge transfer at the donor (D)/acceptor(A) interfaces, with a high interfacial area overcoming the limited diffusion length of optically generated excitons.9 Intriguingly, recent studies have suggested that ternary mixtures of these materials might create optimal devices.10 Understanding such ternary BHJ systems is extremely challenging, with each individual system having its own energetic disorder (σ), electronic band-gap, charge-transport properties, compositional disorder, and interfacial states.11,12
Significant efforts have been made to design single-junction BHJ solar cells by adding a third component for improved solar cell performance.13,14 Certain criteria have been put forward regarding the selection of the material for the third component (donor or acceptor) in these ternary blend systems, including: (i) complementary absorption,15–17 (ii) favorable solid state packing10,18,19 to suppress recombination, and (iii) appropriate energy levels to reduce voltage losses20–22 and the complementary photovoltaic parameters for two binary extreme solar cells.23–25 The tunable VOC in a ternary solar cell are in general fitted using a parallel-diode-type model. This model is based on the assumption (D:A1:A2) that the two acceptor systems do not interact electrically at all and behave as separate donor–acceptor systems within the bulk heterojunction despite the mixing.26 Such a model also excludes the possibility of cascade transfer of charge carriers.27 This is hence an unrealistic picture, since it ignores the significant interactions between both the acceptors and between the acceptors and the donor on account of the mixing, which can introduce significant compositional disorder, a revised effective joint DOS, and energetic disorder of individual components.28 These are the basic ingredients which are required to understand QFL splitting in any semiconductor material being used as an absorber in a photovoltaic device. It is pretty evident that a tunable VOC can be realized by choosing either systems of two donors with one acceptor or systems of one donor with two acceptors. Mollinger et al., for example, reported the tuning of VOC for a system with one donor and two acceptors,29 while Felekidis et al. demonstrated a tunable VOC by using two donors with one acceptor, explaining this observation with a state-filling model using Gaussian disorder.30 Considering the growing interest in ternary systems,13,31 detailed experimental studies combined with an analytical understanding of solar cell device physics in such systems are essential for better insight into and further development of this field.
In this report, we have chosen a system with one p-type, referred to as a donor in the MS (PTB7-Th; D) and two n-type, referred to as acceptors in MS (PC71BM, long-range ordered MS;32 A1 as acceptor-1 and IC61BA, amorphous MS;33 A2 as acceptor-2), D:A1:A2, to study the light-induced quasi-Fermi-level (QFL) splitting as a function of acceptor composition. Both n-type MSs (A1 & A2) form type II heterojunctions with D, and it could be expected that the observed VOC would be dictated by the minimum diagonal band-gap of the D:A1 system; however, a monotonic change in VOC with a change in the A1vs. A2 ratio has been observed (Fig. 1) by us and by others.24,25 An analytical model based on the population occupancy of light-induced fermions in a Gaussian disordered broadened joint DOS for an MS alloy is utilized with most parameters experimentally determined to gain insights into the MS semiconductor physics of these ternary alloys.30,34,35 A quantitative change in the light-induced QFL of holes and electrons was determined using our analytical model with experimentally determined semiconductor parameters. We believe the framework of this study to be applicable beyond VOC fitting and to be capable of providing useful insights into the photo-physics and charge transport physics of MSs.36
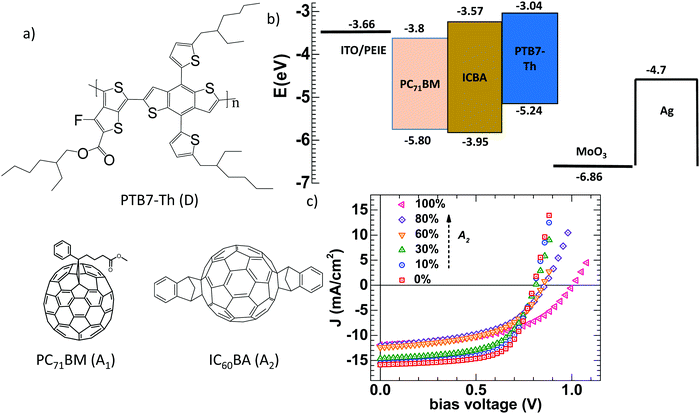 |
| | Fig. 1 (a) The molecular structures of D, A1, and A2; (b) the device structure with the HOMO and LUMO energy levels (A1 and A2,35 D33) and work functions of various layers; and (c) illuminated J–V characteristics for different A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios in D polymer based solar cells under AM1.5 illumination. A2 ratios in D polymer based solar cells under AM1.5 illumination. | |
Results
Fig. 1a presents the molecular structures of PTB7-Th (D), PC71BM (A1) and ICBA (A2). The work functions of the electrodes and energy levels corresponding to the organic semiconductors (highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO)) and interlayers are depicted in Fig. 1b.37–41 The illuminated J–V characteristics of D:A1:A2 solar cells with different ratios of A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 (100
A2 (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 90
0, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 70
10, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 40
30, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 20
60, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 0
80, 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) are shown in Fig. 1c. Parameters such as short circuit current JSC, VOC, fill factor (FF) and power conversion efficiency (PCE) are extracted from the illuminated J–V characteristics (Table S1, ESI†). VOC is found to vary from 0.80 V (0% A2) to 0.81 V (10% A2), 0.82 V (30% A2), 0.86 V (60% A2), 0.89 V (80% A2) and to 1.01 V for 100% A2. Clearly, VOC is monotonically tuned towards higher values with increasing A2 concentration and reaches its maximum when there is no A1 present.42,43 The total change in VOC is found to be 210 mV in going from 0% A2 to 100% A2 in this ternary BHJ system. JSC and FF are also found to vary from 16.1 mA cm−2 (0% A2) to 12.0 mA cm−2 (100% A2), and from 66% (0% A2) to 51% (100% A2). The corresponding PCE for the 0% A2 and 100% A2 cells are 8.5% and 6.2% respectively, consistent with previous reports.18
100) are shown in Fig. 1c. Parameters such as short circuit current JSC, VOC, fill factor (FF) and power conversion efficiency (PCE) are extracted from the illuminated J–V characteristics (Table S1, ESI†). VOC is found to vary from 0.80 V (0% A2) to 0.81 V (10% A2), 0.82 V (30% A2), 0.86 V (60% A2), 0.89 V (80% A2) and to 1.01 V for 100% A2. Clearly, VOC is monotonically tuned towards higher values with increasing A2 concentration and reaches its maximum when there is no A1 present.42,43 The total change in VOC is found to be 210 mV in going from 0% A2 to 100% A2 in this ternary BHJ system. JSC and FF are also found to vary from 16.1 mA cm−2 (0% A2) to 12.0 mA cm−2 (100% A2), and from 66% (0% A2) to 51% (100% A2). The corresponding PCE for the 0% A2 and 100% A2 cells are 8.5% and 6.2% respectively, consistent with previous reports.18
V
OC in OPVs is dictated by the diagonal band-gap of the system and disorder at the D:A interface; hence the broadening of charge transfer (CT) states in the corresponding ternary blend systems will play a crucial role in determining the voltage losses for a given diagonal band-gap.44 The BHJ ternary solar cell could be modelled as having 2 diodes in parallel,26 with each making an opposite contribution to the total current flowing through the device.
| | | Jtotal = J1(V) + J2(V) | (1) |
| | 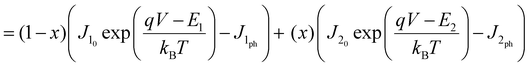 | (2) |
Here,
Jtotal is the total current density.
J1 and
J2 are the current densities of the A
1 and A
2 sub-cells, respectively.
J10 and
J20 are the maximum possible recombination current densities of the A
1 and A
2 sub-cells.
J1ph and
J2ph are the photocurrent densities for each respective sub-cell, and are taken as 16.1 mA cm
−2 for a D:A
1 based OSC and 12 mA cm
−2 for a D:A
2 based OSC, from experimental measurements of the short circuit currents under 1 sun illumination.
E1 and
E2 are the diagonal band-gaps (HOMO
D − LUMO
A) of A
1 and A
2 with D, respectively.
x is the fraction of A
2 in the mixed devices,
q is the electronic charge,
V is the applied voltage,
kB is the Boltzmann constant and
T is the temperature, assumed to be 300 K. The
VOC can then be calculated by numerically finding the value of
V at which the total current density (
Jtotal) is 0, with appropriate parameter values.
Fig. 2a shows the fit according to a parallel-diode model. The model could fit the
VOC. However, due to the several assumptions pointed out in the introduction, it is not justifiable to use this model in disordered semiconductors.
27 So, we employ an analytical model based on population occupancy in Gaussian disordered semiconductors. The model assumes good mixing between A
1 and A
2. To confirm this, we performed the atomic force microscopy measurements shown in Fig. S1 (ESI
†). We did not observe much difference in the roughness for a ternary system compared with two binary systems. To verify this, we calculated the diagonal band-gap experimentally using Marcus charge transfer (MCT) theory for different A
1:A
2 concentrations (Fig. S2, ESI
†).
45 Then Vegard's law was used to fit the diagonal band-gap (
ECT) for different A
1:A
2 concentrations to calculate the bowing parameter.
46| | | ECT(x) = (1−x)ECT−1 + xECT−2 − Bx(1−x) | (3) |
where
x is the fraction of A
2 in the mixture and
B is the bowing parameter.
ECT−1 and
ECT−2 are the diagonal band-gaps of A
1 and A
2, respectively. The fitting of the experimentally calculated
ECT with the above equation is shown in
Fig. 2b. The best fit is observed for a bowing parameter as low as 0.05. We note that this low value of the bowing parameter supports the good mixing assumption with least compositional disorder due to the alloying of different MSs
28,46 to be used in the population occupancy in the Gaussian disordered model for these ternary alloy systems.
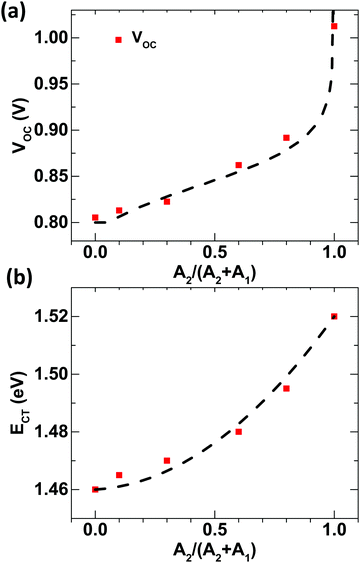 |
| | Fig. 2 Alloy composition vs. (a) changes in VOC using the double-diode model (the dotted line represents the fitting of experimental VOC values with eqn (2)) and (b) changes in the ECT value of the BHJ alloy composition determined from sensitive EQE studies (the dotted line represents the fitting of experimental ECT values with eqn (3). | |
It should be noted that VOC is equal to the QFL spitting of hole and electron populations:
Thus, in order to determine the QFL splitting (and hence, VOC) for different ratios of A1vs. A2, the population occupancy in the Gaussian disordered semiconductor system is estimated with the following equation:47
| | 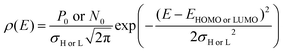 | (5) |
where
σH (
σL) is the broadening (disorder) of the DOS for the HOMO (LUMO),
P0 (
N0) is the total site density of holes (electrons), and
EHOMO (
ELUMO) is the energy level of the donor (acceptor) material. The total site density in the MS is considered to be 10
26 m
−3.
48 The value of
σH(
σL) for D:A
1 and D:A
2 is calculated from temperature-dependent mobility (Fig. S5, ESI
†) using a disorder-controlled transport mechanism. The details of this procedure are explained in ESI.
† By using the temperature-dependent mobility, we found that the
σH values are 69 meV and 63 meV for D:A
1 and D:A
2, respectively. Similarly, we found that
σL varies from 72 meV to 78 meV for D:A
1 and D:A
2, respectively. Hence, it should be noted that there is no significant change in the energetic disorder with D:A
1vs. D:A
2. Since this study focuses on devices with different acceptor concentrations, an effective DOS (
ρe) for the electrons can be defined as:
| | 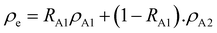 | (6) |
where
RA1 (
RA2) is the ratio of acceptor A
1 (A
2) concentration to the total acceptor concentration, and
ρA1 and
ρA2 are the Gaussian density of states for A
1 and A
2, respectively. The effective DOS is then plotted for different A
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
A
2 ratios, as shown in
Fig. 3a. It is interesting to see a monotonic change in the effective LUMO with the different A
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
A
2 ratios. It is observed that while A
1 and A
2 show a single Gaussian, the mixture of A
1:A
2 comprises both Gaussians, as can be clearly seen in
Fig. 3a. It has previously been reported that A
1 and A
2 mix well
29,49 and do not alter the packing of the D MS, which suggests that the HOMO of D is not changed as a function of ternary composition. This is consistent with our observation of a low bowing parameter value for the ternary series of alloys used in this study. Hence, using the simulated effective HOMO/LUMO for alloys using
eqn (5) and (6), the QFL of holes (
Efh) and electrons (
Efe) can be extracted from
eqn (7) and (8):
| | 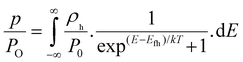 | (7) |
| | 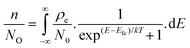 | (8) |
where
p/
P0 is the hole occupation density,
n/
N0 is the electron occupation density,
ρh and
ρe =
ρ(E) with e defined above (
eqn (6)). The free hole carrier concentration (
p) depends upon the absorption profile (Fig. S4, ESI
†), internal quantum efficiency, illumination source (solar spectrum, AM1.5G), device thickness and carrier lifetime. These quantities are used to calculate
p/
P0, as described in SI. The standard technique of minimum standard deviation (between experimentally and computationally obtained
VOC) was then used to obtain the value of
n/
N0. This optimized value was further used for calculating
Efe and, thus,
VOC as a function of relative acceptor concentration. Further details of the methodology and parameter values (Table S4, ESI
†) are provided in the ESI.
†Fig. 3b shows that
VOC obtained from the Gaussian disordered state-filling model evidently reproduces the relative-acceptor-concentration-tuned experimental
VOC pretty well with respect to other models. Furthermore, the extracted values of QFL for holes and electrons are presented in
Fig. 3c. It should be noted that while
Efh remains almost same for all concentrations,
Efe changes continuously.
Efe gets shallower as it moves from D:A
1 to D:A
2, as expected.
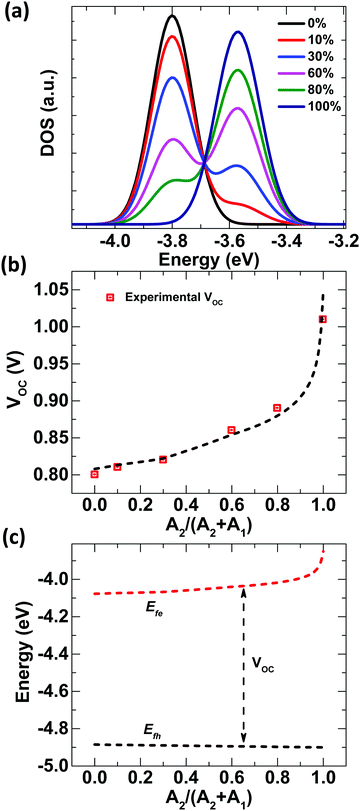 |
| | Fig. 3 Changes in DOSs for different A1:A2 concentrations plotted against energy using eqn (2) and eqn (3); (b) experimental VOC values (red squares) fitted with a population occupancy DOS model (dashed line); and (c) QFL splitting for different A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios in D ternary blend solar cells, obtained from population occupancy in a Gaussian disorder model. A2 ratios in D ternary blend solar cells, obtained from population occupancy in a Gaussian disorder model. | |
Discussion
V
OC depends directly upon the diagonal band-gap and the nature of the D:A interface. In these alloys we noted a continuous change in experimental VOC. This experimental finding suggested that while alloying two acceptors, a new joint density of states is developed which is filled by light-induced carriers based on Fermi–Dirac statistics. The joint DOS for MSs is modeled using Bässler's Gaussian disordered model (eqn (5)). Using this model, we could determine the QFL splitting for these alloys under 1 sun illumination conditions as a function of alloy composition, which suggested that energetic disorder is least influenced by alloying. To further understand the effect of molecular packing, we performed grazing incidence wide-angle X-ray scattering (GIWAXS) studies on D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1, D
A1, D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 (1
A2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5) and D:A2 systems (Fig. S9, ESI†). GIWAXS studies indicate that there are only relatively minor changes in the molecular packing of the polymer donor, with the lamellar stacking peak (100) and π–π stacking peak (010) showing similar spacing. There is a slightly larger coherence length of these peaks for the case of D:A1 compared to D:A2 and D:A1:A2 (Table S4, ESI†), indicating slightly increased microstructural disorder for D in D:A2 and D:A1:A2 thin-films with respect to D:A1 blended films. However, in general, the influence of changes in molecular packing is expected to be insignificant and not to play a significant role in the observed monotonic change in VOC. The formation of the joint DOS between A1 and A2 is the reason for the change in electron QFL with different concentrations of A1:A2. If we look at Fig. 3a closely, it is clearly observable that the LUMO of A1 dominates up to 30% of A2 with the presence of a small A2 Gaussian on the shallower side. This is the reason even after adding 30% A2, when the change in VOC is dominated by the PCBM and very minor changes are obtained in VOC. However, after 30% of A2, the LUMO of A2 starts to dominate with a small A1 Gaussian on the deeper side and the change in VOC is higher with 30% to 60% compared to 0% to 30%. Interestingly, the VOC is still not dominated by A2, because the light-induced charges have to fill the lower energy bands first, which are dominated by A1. The prominent change in the from 80% to 100% A2 concentration is because of the removal of the A2 band on the lower energy side. At 100% A2 concentration, light-induced charges will be directly filled within the Gaussian DOS of A2 and hence a dramatic shift is observed in the electron QFL (or VOC) from 80% to 100% of A2 concentration. Hence, this detailed framework to analyze the BHJ OSCs not only allowed us to fit the experimental VOC for the used compositions, but it also allows us to determine many useful parameters like charge transport physics (μ vs. T, Fig. S8, ESI†) and generation/recombination physics (TPV Fig. S3 and Table S2, ESI† used for the model) of OSCs correlated with effective energy levels along with the associated energetic disorder values.
0.5) and D:A2 systems (Fig. S9, ESI†). GIWAXS studies indicate that there are only relatively minor changes in the molecular packing of the polymer donor, with the lamellar stacking peak (100) and π–π stacking peak (010) showing similar spacing. There is a slightly larger coherence length of these peaks for the case of D:A1 compared to D:A2 and D:A1:A2 (Table S4, ESI†), indicating slightly increased microstructural disorder for D in D:A2 and D:A1:A2 thin-films with respect to D:A1 blended films. However, in general, the influence of changes in molecular packing is expected to be insignificant and not to play a significant role in the observed monotonic change in VOC. The formation of the joint DOS between A1 and A2 is the reason for the change in electron QFL with different concentrations of A1:A2. If we look at Fig. 3a closely, it is clearly observable that the LUMO of A1 dominates up to 30% of A2 with the presence of a small A2 Gaussian on the shallower side. This is the reason even after adding 30% A2, when the change in VOC is dominated by the PCBM and very minor changes are obtained in VOC. However, after 30% of A2, the LUMO of A2 starts to dominate with a small A1 Gaussian on the deeper side and the change in VOC is higher with 30% to 60% compared to 0% to 30%. Interestingly, the VOC is still not dominated by A2, because the light-induced charges have to fill the lower energy bands first, which are dominated by A1. The prominent change in the from 80% to 100% A2 concentration is because of the removal of the A2 band on the lower energy side. At 100% A2 concentration, light-induced charges will be directly filled within the Gaussian DOS of A2 and hence a dramatic shift is observed in the electron QFL (or VOC) from 80% to 100% of A2 concentration. Hence, this detailed framework to analyze the BHJ OSCs not only allowed us to fit the experimental VOC for the used compositions, but it also allows us to determine many useful parameters like charge transport physics (μ vs. T, Fig. S8, ESI†) and generation/recombination physics (TPV Fig. S3 and Table S2, ESI† used for the model) of OSCs correlated with effective energy levels along with the associated energetic disorder values.
Conclusions
In conclusion, QFL splitting as a function of the ternary alloy composition was studied for MSs, where a BHJ blend was prepared using one p-type and two n-type MSs. An analytical model based on the population occupancy of photoinduced fermions in a Gaussian disordered broadened joint DOS for an MS alloy is employed, with most of the parameters experimentally determined. A simple double-diode model or effective LUMO (i.e., Vegard's law) model can explain the monotonic change in VOC qualitatively, but these models can avoid good fitting and miss insights into the MSs physics. A monotonic change in VOC is due to a monotonic change in Efe while Efh remains almost the same. Interestingly, a detailed Gaussian disorder with joint DOS based model fits the experimental VOC values excellently and explains quantitatively that the deeper lying LUMO of A1 dominates when determining VOC in this ternary system, even at a relatively smaller concentration of D compared to A2, since electrons start to fill from the lower energy state. These results were found to be consistent with the almost similar estimated energetic disorder (σ) values and negligible bowing parameter. Our model and transport studies can provide essential insights into light-induced QFL splitting for any general excitonic MS alloy system.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We acknowledge Department of Science &Technology DST-AISRF and Global Challenges Research Fund (GCRF), SUNRISE for funding. DK acknowledges the Indo-Swedish joint project funded by DST-India (DST/INT/SWD/VR/P-20/2019) for funding support. We would like to acknowledge NCPRE IITB for providing the device fabrication and characterization facilities. This work was performed in part at the SAXS/WAXS beamline at the Australian Synchrotron, part of ANSTO.43 We acknowledge Urvashi Bothra for preparing the sample for GIWAXS studies and Prof. Sir Richard H. Friend (Cambridge University, UK) for useful discussion and feedback. NJ acknowledges the Council of Scientific and Industrial Research (CSIR), India for the provision of a research fellowship.
References
-
M. Pope and C. E. Swenberg, Electronic processes in organic crystals and polymers, Oxford University Press on Demand, 1999 Search PubMed
 .
.
- T. Kirchartz, J. Nelson and U. Rau, Phys. Rev. Appl., 2016, 5, 054003 CrossRef
 .
.
- Q. Liu, Y. Jiang, K. Jin, J. Qin, J. Xu, W. Li, J. Xiong, J. Liu, Z. Xiao and K. Sun, Sci. Bull., 2020, 65(4), 272–275 CrossRef CAS
 .
.
- J. Yao, T. Kirchartz, M. S. Vezie, M. A. Faist, W. Gong, Z. He, H. Wu, J. Troughton, T. Watson, D. Bryant and J. Nelson, Phys. Rev. Appl., 2015, 4, 014020 CrossRef
 .
.
- M. Azzouzi, J. Yan, T. Kirchartz, K. Liu, J. Wang, H. Wu and J. Nelson, Phys. Rev. X, 2018, 8, 031055 CAS
 .
.
- F. Gao, W. Tress, J. Wang and O. Inganäs, Phys. Rev. Lett., 2015, 114, 128701 CrossRef PubMed
 .
.
- N. C. Giebink, G. P. Wiederrecht, M. R. Wasielewski and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195326 CrossRef
 .
.
- N. C. Giebink, G. P. Wiederrecht, M. R. Wasielewski and S. R. Forrest, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155305 CrossRef
 .
.
- A. D. Chepelianskii, J. Wang and R. H. Friend, Phys. Rev. Lett., 2014, 112, 126802 CrossRef CAS PubMed
 .
.
- N. Gasparini, X. Jiao, T. Heumueller, D. Baran, G. J. Matt, S. Fladischer, E. Spiecker, H. Ade, C. J. Brabec and T. Ameri, Nat. Energy, 2016, 1, 16118 CrossRef CAS
 .
.
- S. Albert-Seifried, J. M. Hodgkiss, F. Laquai, H. A. Bronstein, C. K. Williams and R. H. Friend, Phys. Rev. Lett., 2010, 105, 195501 CrossRef PubMed
 .
.
- I. Lange, J. C. Blakesley, J. Frisch, A. Vollmer, N. Koch and D. Neher, Phys. Rev. Lett., 2011, 106, 216402 CrossRef PubMed
 .
.
-
Z. Xiao, X. Jia and L. Ding, Ternary organic solar cells offer 14% power conversion efficiency, 2017.
-
H. Li, Z. Xiao, L. Ding and J. Wang, Thermostable single-junction organic solar cells with a power conversion efficiency of 14.62%, 2018.
- N. Gasparini, L. Lucera, M. Salvador, M. Prosa, G. D. Spyropoulos, P. Kubis, H.-J. Egelhaaf, C. J. Brabec and T. Ameri, Energy Environ. Sci., 2017, 10, 885–892 RSC
 .
.
- P. Xue, Y. Xiao, T. Li, S. Dai, B. Jia, K. Liu, J. Wang, X. Lu, R. P.-S. Han and X. Zhan, J. Mater. Chem. A, 2018, 6, 24210–24215 RSC
 .
.
- R. Sharma, S. Bhalerao and D. Gupta, Org. Electron., 2016, 33, 274–280 CrossRef CAS
 .
.
- W. Huang, E. Gann, N. Chandrasekaran, S. K.-K. Prasad, S.-Y. Chang, L. Thomsen, D. Kabra, J. M. Hodgkiss, Y.-B. Cheng, Y. Yang and C. R. McNeill, Adv. Energy Mater., 2017, 7(11), 1602197 CrossRef
 .
.
- R. Sharma, H. Lee, M. Seifrid, V. Gupta, G. C. Bazan and S. Yoo, Sol. Energy, 2020, 201, 499–507 CrossRef CAS
 .
.
- C. Wang, X. Xu, W. Zhang, S. B. Dkhil, X. Meng, X. Liu, O. Margeat, A. Yartsev, W. Ma, J. Ackermann, E. Wang and M. Fahlman, Nano Energy, 2017, 37, 24–31 CrossRef CAS
 .
.
- D. Baran, R. S. Ashraf, D. A. Hanifi, M. Abdelsamie, N. Gasparini, J. A. Röhr, S. Holliday, A. Wadsworth, S. Lockett, M. Neophytou, C. J.-M. Emmott, J. Nelson, C. J. Brabec, A. Amassian, A. Salleo, T. Kirchartz, J. R. Durrant and I. McCulloch, Nat. Mater., 2016, 16, 363 CrossRef PubMed
 .
.
- R. Sharma, H. Lee, V. Gupta, H. Kim, M. Kumar, C. Sharma, S. Chand, S. Yoo and D. Gupta, Org. Electron., 2016, 34, 111–117 CrossRef CAS
 .
.
- X. Ma, A. Zeng, J. Gao, Z. Hu, C. Xu, J. H. Son, S. Y. Jeong, C. Zhang, M. Li, K. Wang, H. Yan, Z. Ma, Y. Wang, H. Y. Woo and F. Zhang, Natl. Sci. Rev., 2020, 8 CAS
 .
.
- W. J. Xu, X. L. Ma, J. H. Son, S. Y. Jeong, L. B. Niu, C. Y. Xu, S. P. Zhang, Z. J. Zhou, J. H. Gao, H. Y. Woo, J. Zhang, J. Wang and F. J. Zhang, Small, 2022, 18 CAS
 .
.
- Z. H. Hu, J. Wang, Z. Wang, W. Gao, Q. S. An, M. Zhang, X. L. Ma, J. X. Wang, J. L. Miao, C. L. Yang and F. J. Zhang, Nano Energy, 2019, 55, 424–432 CrossRef CAS
 .
.
- L. Yang, H. Zhou, S. C. Price and W. You, J. Am. Chem. Soc., 2012, 134, 5432–5435 CrossRef CAS PubMed
 .
.
- T. Ameri, P. Khoram, J. Min and C. J. Brabec, Adv. Mater., 2013, 25, 4245–4266 CrossRef CAS PubMed
 .
.
- M. Schwarze, W. Tress, B. Beyer, F. Gao, R. Scholz, C. Poelking, K. Ortstein, A. A. Günther, D. Kasemann, D. Andrienko and K. Leo, Science, 2016, 352, 1446 CrossRef CAS PubMed
 .
.
- S. A. Mollinger, K. Vandewal and A. Salleo, Adv. Energy Mater., 2015, 5, 1501335 CrossRef
 .
.
- N. Felekidis, E. Wang and M. Kemerink, Energy Environ. Sci., 2016, 9, 257–266 RSC
 .
.
- Y. Cui, H. Yao, L. Hong, T. Zhang, Y. Xu, K. Xian, B. Gao, J. Qin, J. Zhang, Z. Wei and J. Hou, Adv. Mater., 2019, 31 Search PubMed
 .
.
- T. T. To and S. Adams, Phys. Chem. Chem. Phys., 2014, 16, 4653–4663 RSC
 .
.
- Y. Xie, F. Yang, Y. Li, M. A. Uddin, P. Bi, B. Fan, Y. Cai, X. Hao, H. Y. Woo, W. Li, F. Liu and Y. Sun, Adv. Mater., 2018, 30 Search PubMed
 .
.
- H. Bässler, Phys. Status Solidi B, 1981, 107, 9–54 CrossRef
 .
.
-
S. M. Sze and K. K. Ng, Physics of semiconductor devices, Wiley-Interscience, Hoboken, N.J., 2007 Search PubMed
 .
.
- Q. S. An, J. Wang, W. Gao, X. L. Ma, Z. H. Hu, J. H. Gao, C. Y. Xu, M. H. Hao, X. L. Zhang, C. L. Yang and F. J. Zhang, Sci. Bull., 2020, 65, 538–545 CrossRef CAS
 .
.
- M. Kröger, S. Hamwi, J. Meyer, T. Riedl, W. Kowalsky and A. Kahn, Appl. Phys. Lett., 2009, 95, 123301 CrossRef
 .
.
- Y. Zhou, C. Fuentes-Hernandez, J. Shim, J. Meyer, A. J. Giordano, H. Li, P. Winget, T. Papadopoulos, H. Cheun, J. Kim, M. Fenoll, A. Dindar, W. Haske, E. Najafabadi, T. M. Khan, H. Sojoudi, S. Barlow, S. Graham, J.-L. Brédas, S. R. Marder, A. Kahn and B. Kippelen, Science, 2012, 336, 327–332 CrossRef CAS PubMed
 .
.
- S. Zhang, L. Ye, W. Zhao, D. Liu, H. Yao and J. Hou, Macromolecules, 2014, 47, 4653–4659 CrossRef CAS
 .
.
- S. Park, J. Jeong, G. Hyun, M. Kim, H. Lee and Y. Yi, Sci. Rep., 2016, 6, 35262 CrossRef CAS PubMed
 .
.
- Z.-L. Guan, J. Bok Kim, Y.-L. Loo and A. Kahn, J. Appl. Phys., 2011, 110, 043719 CrossRef
 .
.
- P. Cheng, Y. Li and X. Zhan, Energy Environ. Sci., 2014, 7, 2005–2011 RSC
 .
.
- P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2011, 133, 14534–14537 CrossRef CAS PubMed
 .
.
- N. Jain, U. Bothra, D. Moghe, A. Sadhanala, R. H. Friend, C. R. McNeill and D. Kabra, ACS Appl. Mater. Interfaces, 2018, 10, 44576–44582 CrossRef CAS PubMed
 .
.
- N. Jain, R. Sharma, S. Mahesh, D. Moghe, H. J. Snaith, S. Yoo and D. Kabra, ACS Appl. Mater. Interfaces, 2021, 13, 60279–60287 CrossRef CAS PubMed
 .
.
- R. A. Street, D. Davies, P. P. Khlyabich, B. Burkhart and B. C. Thompson, J. Am. Chem. Soc., 2013, 135, 986–989 CrossRef CAS PubMed
 .
.
- G. Paasch and S. Scheinert, J. Appl. Phys., 2010, 107, 104501 CrossRef
 .
.
- P. K. Nayak, G. Garcia-Belmonte, A. Kahn, J. Bisquert and D. Cahen, Energy Environ. Sci., 2012, 5, 6022–6039 RSC
 .
.
- P. P. Khlyabich, B. Burkhart, A. E. Rudenko and B. C. Thompson, Polymer, 2013, 54, 5267–5298 CrossRef CAS
 .
.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Rishabh
Saxena
a,
Rishabh
Saxena
 a,
Sumukh
Vaidya
a,
Wenchao
Huang
b,
Adam
Welford
b,
Christopher R
McNeill
a,
Sumukh
Vaidya
a,
Wenchao
Huang
b,
Adam
Welford
b,
Christopher R
McNeill
 b and
Dinesh
Kabra
b and
Dinesh
Kabra
 *a
*a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios in D polymer based solar cells under AM1.5 illumination.
A2 ratios in D polymer based solar cells under AM1.5 illumination.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 (100
A2 (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 90
0, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 70
10, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, 40
30, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 20
60, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80, 0
80, 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100) are shown in Fig. 1c. Parameters such as short circuit current JSC, VOC, fill factor (FF) and power conversion efficiency (PCE) are extracted from the illuminated J–V characteristics (Table S1, ESI†). VOC is found to vary from 0.80 V (0% A2) to 0.81 V (10% A2), 0.82 V (30% A2), 0.86 V (60% A2), 0.89 V (80% A2) and to 1.01 V for 100% A2. Clearly, VOC is monotonically tuned towards higher values with increasing A2 concentration and reaches its maximum when there is no A1 present.42,43 The total change in VOC is found to be 210 mV in going from 0% A2 to 100% A2 in this ternary BHJ system. JSC and FF are also found to vary from 16.1 mA cm−2 (0% A2) to 12.0 mA cm−2 (100% A2), and from 66% (0% A2) to 51% (100% A2). The corresponding PCE for the 0% A2 and 100% A2 cells are 8.5% and 6.2% respectively, consistent with previous reports.18
100) are shown in Fig. 1c. Parameters such as short circuit current JSC, VOC, fill factor (FF) and power conversion efficiency (PCE) are extracted from the illuminated J–V characteristics (Table S1, ESI†). VOC is found to vary from 0.80 V (0% A2) to 0.81 V (10% A2), 0.82 V (30% A2), 0.86 V (60% A2), 0.89 V (80% A2) and to 1.01 V for 100% A2. Clearly, VOC is monotonically tuned towards higher values with increasing A2 concentration and reaches its maximum when there is no A1 present.42,43 The total change in VOC is found to be 210 mV in going from 0% A2 to 100% A2 in this ternary BHJ system. JSC and FF are also found to vary from 16.1 mA cm−2 (0% A2) to 12.0 mA cm−2 (100% A2), and from 66% (0% A2) to 51% (100% A2). The corresponding PCE for the 0% A2 and 100% A2 cells are 8.5% and 6.2% respectively, consistent with previous reports.18
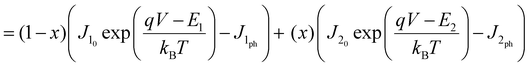

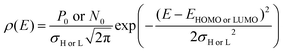
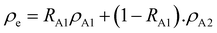
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios, as shown in Fig. 3a. It is interesting to see a monotonic change in the effective LUMO with the different A1
A2 ratios, as shown in Fig. 3a. It is interesting to see a monotonic change in the effective LUMO with the different A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios. It is observed that while A1 and A2 show a single Gaussian, the mixture of A1:A2 comprises both Gaussians, as can be clearly seen in Fig. 3a. It has previously been reported that A1 and A2 mix well29,49 and do not alter the packing of the D MS, which suggests that the HOMO of D is not changed as a function of ternary composition. This is consistent with our observation of a low bowing parameter value for the ternary series of alloys used in this study. Hence, using the simulated effective HOMO/LUMO for alloys using eqn (5) and (6), the QFL of holes (Efh) and electrons (Efe) can be extracted from eqn (7) and (8):
A2 ratios. It is observed that while A1 and A2 show a single Gaussian, the mixture of A1:A2 comprises both Gaussians, as can be clearly seen in Fig. 3a. It has previously been reported that A1 and A2 mix well29,49 and do not alter the packing of the D MS, which suggests that the HOMO of D is not changed as a function of ternary composition. This is consistent with our observation of a low bowing parameter value for the ternary series of alloys used in this study. Hence, using the simulated effective HOMO/LUMO for alloys using eqn (5) and (6), the QFL of holes (Efh) and electrons (Efe) can be extracted from eqn (7) and (8):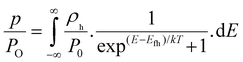
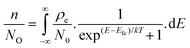

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 ratios in D ternary blend solar cells, obtained from population occupancy in a Gaussian disorder model.
A2 ratios in D ternary blend solar cells, obtained from population occupancy in a Gaussian disorder model.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1, D
A1, D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A1
A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A2 (1
A2 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5
0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5) and D:A2 systems (Fig. S9, ESI†). GIWAXS studies indicate that there are only relatively minor changes in the molecular packing of the polymer donor, with the lamellar stacking peak (100) and π–π stacking peak (010) showing similar spacing. There is a slightly larger coherence length of these peaks for the case of D:A1 compared to D:A2 and D:A1:A2 (Table S4, ESI†), indicating slightly increased microstructural disorder for D in D:A2 and D:A1:A2 thin-films with respect to D:A1 blended films. However, in general, the influence of changes in molecular packing is expected to be insignificant and not to play a significant role in the observed monotonic change in VOC. The formation of the joint DOS between A1 and A2 is the reason for the change in electron QFL with different concentrations of A1:A2. If we look at Fig. 3a closely, it is clearly observable that the LUMO of A1 dominates up to 30% of A2 with the presence of a small A2 Gaussian on the shallower side. This is the reason even after adding 30% A2, when the change in VOC is dominated by the PCBM and very minor changes are obtained in VOC. However, after 30% of A2, the LUMO of A2 starts to dominate with a small A1 Gaussian on the deeper side and the change in VOC is higher with 30% to 60% compared to 0% to 30%. Interestingly, the VOC is still not dominated by A2, because the light-induced charges have to fill the lower energy bands first, which are dominated by A1. The prominent change in the from 80% to 100% A2 concentration is because of the removal of the A2 band on the lower energy side. At 100% A2 concentration, light-induced charges will be directly filled within the Gaussian DOS of A2 and hence a dramatic shift is observed in the electron QFL (or VOC) from 80% to 100% of A2 concentration. Hence, this detailed framework to analyze the BHJ OSCs not only allowed us to fit the experimental VOC for the used compositions, but it also allows us to determine many useful parameters like charge transport physics (μ vs. T, Fig. S8, ESI†) and generation/recombination physics (TPV Fig. S3 and Table S2, ESI† used for the model) of OSCs correlated with effective energy levels along with the associated energetic disorder values.
0.5) and D:A2 systems (Fig. S9, ESI†). GIWAXS studies indicate that there are only relatively minor changes in the molecular packing of the polymer donor, with the lamellar stacking peak (100) and π–π stacking peak (010) showing similar spacing. There is a slightly larger coherence length of these peaks for the case of D:A1 compared to D:A2 and D:A1:A2 (Table S4, ESI†), indicating slightly increased microstructural disorder for D in D:A2 and D:A1:A2 thin-films with respect to D:A1 blended films. However, in general, the influence of changes in molecular packing is expected to be insignificant and not to play a significant role in the observed monotonic change in VOC. The formation of the joint DOS between A1 and A2 is the reason for the change in electron QFL with different concentrations of A1:A2. If we look at Fig. 3a closely, it is clearly observable that the LUMO of A1 dominates up to 30% of A2 with the presence of a small A2 Gaussian on the shallower side. This is the reason even after adding 30% A2, when the change in VOC is dominated by the PCBM and very minor changes are obtained in VOC. However, after 30% of A2, the LUMO of A2 starts to dominate with a small A1 Gaussian on the deeper side and the change in VOC is higher with 30% to 60% compared to 0% to 30%. Interestingly, the VOC is still not dominated by A2, because the light-induced charges have to fill the lower energy bands first, which are dominated by A1. The prominent change in the from 80% to 100% A2 concentration is because of the removal of the A2 band on the lower energy side. At 100% A2 concentration, light-induced charges will be directly filled within the Gaussian DOS of A2 and hence a dramatic shift is observed in the electron QFL (or VOC) from 80% to 100% of A2 concentration. Hence, this detailed framework to analyze the BHJ OSCs not only allowed us to fit the experimental VOC for the used compositions, but it also allows us to determine many useful parameters like charge transport physics (μ vs. T, Fig. S8, ESI†) and generation/recombination physics (TPV Fig. S3 and Table S2, ESI† used for the model) of OSCs correlated with effective energy levels along with the associated energetic disorder values.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
