Open Access Article
Open Access ArticleSensitivity of ice nucleation parameterizations to the variability in underlying ice nucleation rate coefficients
Isabelle
Steinke
 * and
Susannah M.
Burrows
* and
Susannah M.
Burrows

Atmospheric Sciences & Global Change Division, Pacific Northwest National Laboratory, Richland, Washington, USA. E-mail: isabelle.steinke@pnnl.gov
First published on 2nd August 2022
Abstract
Deriving aerosol-type-dependent parameterizations for ice nucleation processes remains challenging due to large uncertainties associated with laboratory studies and field measurements. One source of uncertainty is a lack of knowledge about the magnitude of particle-to-particle differences in freezing efficiency associated with particles' chemical composition and surface features. In most experimental setups, it is challenging to disentangle the contributions of inherent experimental uncertainties, variability in aerosol surface area and the particle-to-particle differences in freezing efficiency. Therefore, in this study, we use a Monte Carlo approach to simulate synthetic ice nucleation experiments to better understand the impact of variability in heterogeneous ice nucleation propensities on simulated frozen fractions. We represent this variability by differently-shaped distributions of the heterogeneous ice nucleation rate coefficients Jhet. Distributions spanning one order of magnitude result in simulated median frozen fractions that are up to a factor of two higher compared to simulations with narrow Gaussian distributions, in the case of small frozen fractions. For the assumed range of variability in Jhet, impacts on cloud variables (e.g., ice water path based on Hawker et al. (2021)) calculated from hypothetical parameterizations based on our simulated frozen fractions seem to be relatively small, with only up to 25% difference between lognormal and constant Jhet distributions. One of the major unknowns, however, is the interparticle variability in Jhet, which depends on particle composition and surface features. Resolving this uncertainty requires a combination of laboratory studies and field experiments relating physicochemical particle features and ice nucleation propensity in a size-resolved manner.
Environmental significanceThe representation of cloud ice formation remains one of the largest uncertainties in climate models, with ice nucleation parameterizations representing primary ice formation in clouds being a major contributor to this uncertainty. As of now, these parameterizations do not account for the particle-to-particle variability of ice nucleation propensities in a systematic manner. Based on our simulations of freezing droplet ensembles, the variability in ice nucleation propensities is mostly relevant at small frozen fractions and for polydisperse aerosol populations. Estimates of cloud impacts based on our simulations indicate only a minor influence of the particle-to-particle variability of ice nucleation propensities. However, these effects could be significantly larger for mixtures of particle types with dramatically different ice nucleation propensities. |
1 Introduction
The cloud ice phase has a defining impact on the formation of precipitation and the atmospheric radiation budget.1,2 However, the representation of cloud ice formation processes in weather prediction and climate models is challenging, limiting our ability to predict cloud phase and climate feedbacks.3,4 Representing cloud formation processes and associated climate impacts in Earth system models requires the development of parameterizations that reliably predict ice crystal concentrations for complex ambient particle populations present at cloud altitude. Ambient particles are characterized by a wide range of particle sizes, compositions, and surface properties, and their ice nucleation propensities may therefore vary by several orders of magnitude.5Additional challenges for predicting cloud phase include representing particle emissions and other processes that control the atmospheric population of particles participating in ice nucleation.6 Further complexity is introduced by processes controlling the cloud response to ice-nucleating particles (INPs), including secondary ice formation processes,7 and the multiscale interactions between cloud microphysical and dynamical processes.8 Improved prediction of the cloud phase and its response to Earth system processes will ultimately require improvements to the predictability of both INPs and cloud responses.9
In this study, we focus our discussion on parameterizations describing immersion freezing (i.e., the formation of ice crystals in cloud droplets), which is the primary pathway for heterogeneous ice nucleation in mixed-phase clouds.10 Recently, aerosol-type-dependent ice nucleation propensities have been characterized by either ice nucleation active surface site (INAS) densities or heterogeneous nucleation rate coefficients. These approaches differ in their treatment of the observed time dependence, describing the frozen fraction fice by
| fice = 1 − exp(−Jhet(T)At) | (1) |
| fice = 1 − exp(−ns(T)A) | (2) |
Several approaches have been used to expand the applicability of eqn (1) and (2) by accounting for the variability in A and Jhet/ns. Instead of using a single value to represent aerosol-type-dependent ice nucleation propensities (Jhet, ns), distributions of values have been found to better represent ice nucleation propensities observed for certain particle types, e.g., mineral dust.12–15 This heterogeneity in ice nucleation propensities is caused by variations in particle composition and morphology, which are highly variable across aerosol particle classes and even within populations of a similar particle type.5,16,17 Note that in some cases, ice nucleation propensities and their variabilities are also expressed as more indirectly derived metrics, e.g., as contact angles.14,18,19 Most approaches accounting for the heterogeneity of ice nucleation propensities implicitly assume that the relevant quantity describing the observed ice nucleation efficiency (e.g., contact angle θ) follows a Gaussian distribution.18,20,21 However, it is not clear a priori which distribution shapes are most suitable for representing the ice nucleation behavior of complex ambient particles. Also, most studies implicitly assume that the ensemble of freezing droplets or aliquots is large11 and therefore neglect stochastic uncertainties.22 For the aerosol surface area (A), which is an important quantity in ice nucleation studies, observed size distributions are commonly approximated by lognormal distributions.23,24
In this study, we use Monte Carlo simulations to conduct synthetic ice nucleation experiments, with the goal to better understand the interplay between aerosol size distributions, Jhet distribution shapes, and droplet ensemble sizes in determining the range of observable frozen fractions in ice nucleation experiments.
2 Methods
Synthetic experimental data are commonly used to better understand the causes of features observed in laboratory and field experiments, e.g., to analyze orographic effects on precipitation (Bae and Oh25), to better understand the performance of cloud probes,26 or to evaluate methane emissions.27 Here, we use synthetic experiments to test the impact of different particle characteristics (size distributions, temperature-dependent ice nucleation efficiencies) on simulated frozen fractions while using these simulations to mimic the characteristics of real-world experimental setups (e.g., droplet ensemble sizes).2.1 General setup of Monte Carlo simulations
We simulate two different types of droplet ensembles: ensembles with relatively few freezing droplets (Ndrop = 100) and ensembles with many freezing droplets (Ndrop = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). Smaller droplet ensembles (Ndrop < 100) can be found for droplet freezing assays that investigate the freezing of suspension droplets, whereas the latter ensemble type is more representative of continuous flow diffusion chamber (CFDC) experiments.28 In the context of ambient INP measurements, droplet freezing experiments are commonly used to analyze previously collected samples for ice nucleation activity at warmer temperatures (e.g., >−25 °C), while CFDC experiments produce real-time measurements of INP concentrations (typically at T < −20 °C).5,17
000). Smaller droplet ensembles (Ndrop < 100) can be found for droplet freezing assays that investigate the freezing of suspension droplets, whereas the latter ensemble type is more representative of continuous flow diffusion chamber (CFDC) experiments.28 In the context of ambient INP measurements, droplet freezing experiments are commonly used to analyze previously collected samples for ice nucleation activity at warmer temperatures (e.g., >−25 °C), while CFDC experiments produce real-time measurements of INP concentrations (typically at T < −20 °C).5,17
For an ensemble of droplets, we describe the freezing behavior of an individual freezing droplet (j) containing a particle with surface Aj by
| Pj,frz = 1 − exp(−Jhet,j·Aj·δt). | (3) |
We introduce the element of stochasticity by evaluating freezing probabilities against a random number between 0 and 1, and simulate a freezing event when that random number exceeds Pj,frz, following the procedure described in Alpert and Knopf (2016).22 All values for Jhet,j and Aj are sampled from distributions described in the following sections. For simplicity, we evaluate frozen fractions after δt = 10 s, assuming that the temperature remains constant during the simulated time interval. The value chosen for time scale δt corresponds to the order-of-magnitude residence time within most current CFDC-style experiments.28 For each droplet freezing ensemble, we conduct 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulation runs.
000 simulation runs.
2.2 Simulated ice nucleation rate coefficient distributions
Through our synthetic experiments, we analyze the range of possible outcomes (i.e., the stochastic uncertainty associated with simulated frozen fractions), depending on the shape and width of the underlying Jhet distributions.In this study, we test the impact of four different hypothetical distribution types (Fig. 1).
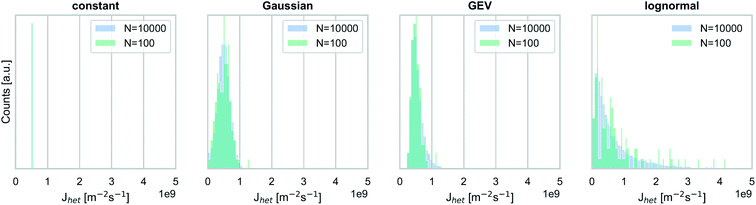 | ||
| Fig. 1 Nucleation rate coefficient distribution types (median: Jhet = 5 × 108 m−2 s−1) used for synthetic experiments shown in Fig. 3 and 4. | ||
Ice nucleation propensities observed for individual particle types (e.g., mineral dust) may vary by up to one or two orders of magnitude at a fixed temperature,5,17 and we represent this behavior by a generalized extreme value (GEV) distribution (w = 0.3, ξ = −0.1) and a lognormal distribution (σ = 1.2). GEV distributions are used to evaluate the impact of tails within a Jhet distribution (i.e., rare, highly ice-active particles).29 We also employ a broad lognormal distribution to analyze the impact of highly ice-active particles in a population where most individual particles have a low ice nucleation propensity. Note, however, that even our very broad lognormal distribution may still be an underestimate of variability observed for ambient particles with complex mixing states and a wide range of ice nucleation propensities. For example, INP populations consisting of internal and external mixtures of dust, sea spray, and biological particles, each with dramatically different ice nucleation propensities, have been observed at locations around the world. Also, while there is some indication from observations that ice nucleation propensities vary widely across different particle types (e.g., primary biological particles and mineral dust), there are currently no direct measurements of this variability of Jhet across the same particle class.
As a contrast to these broad distributions, we also include a relatively narrow Gaussian (σ = 0.4, with σ normalized to the median) and a constant Jhet value in our analysis. We hypothesize that the skewness of the Jhet distribution as well as the distribution width are key factors in determining not only the median of simulated fice values but also the range of possible outcomes.
In addition to analyzing the role of different Jhet distribution types, we also investigate the impact of ice nucleation efficiencies by analyzing two different median values for each distribution type, namely Jhet = 5 × 108 m−2 s−1 and Jhet = 5 × 1010 m−2 s−1. These two Jhet values can also be interpreted as proxies for the ice nucleation propensities of mineral dust particles at two different temperatures (248 K, and 238 K, respectively).16
2.3 Simulated aerosol surface distributions
To account for the variability in aerosol surface area, we use two lognormal aerosol size distributions with the same median value (A = 10−12 m2) but with a variable width. As represented in Fig. 2, we specifically analyze a distribution with a width σ = 3.0, which is more representative of a realistic aerosol distribution in experiments, and a quasi-monodisperse distribution with σ = 1.1, which is more representative of size-selected experiments.28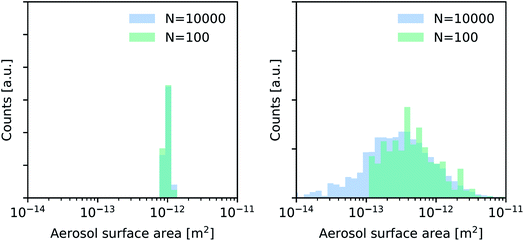 | ||
| Fig. 2 Exemplary aerosol surface area distributions used for synthetic experiments shown in Fig. 3 and 4—quasi-monodisperse (left) and broad lognormal distribution (right). | ||
3 Results and discussion
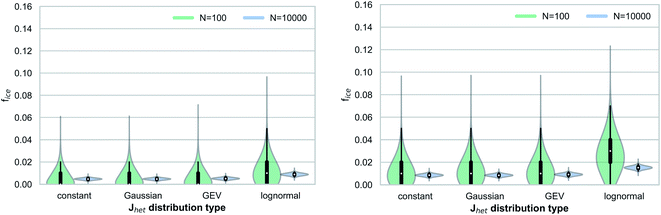
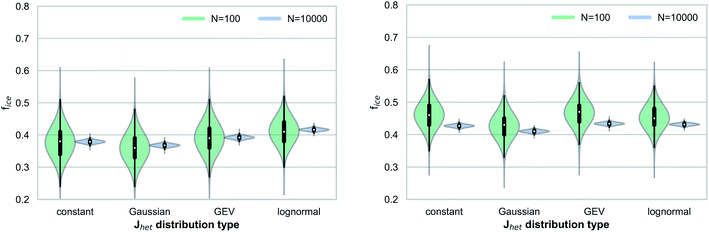
Fig. 3 shows the range of simulated frozen fractions (fice) for our Monte Carlo simulations investigating the interplay between Jhet and aerosol surface area variability. The results shown in Fig. 3 assume a median ice nucleation rate coefficient of Jhet = 5 × 108 m−2 s−1, which can be interpreted as a representation of freezing for mineral dusts at 248 K.17Fig. 3 shows that the number of droplets or droplet equivalents, e.g., water-filled wells in droplet assays, has a significant impact on the range of possible outcomes and therefore the stochastic uncertainties. Additionally, the larger widths of the underlying Jhet distributions broaden the range of possible outcomes by up to a factor of two for the small droplet ensemble (Ndrop = 100) if all outliers are taken into consideration. This behavior is more pronounced for the quasi-monodisperse aerosol surface area distribution.In addition to affecting the range of possible outcomes, the variability in Jhet (i.e., the distribution type) also affects the median value of fice, particularly for the case of a lognormal distribution. For both aerosol surface area distributions, the median fice value is shifted by approximately a factor of up to three when comparing between results for the constant Jhet value and the lognormal Jhet distribution. This finding demonstrates that the underlying shape of Jhet distributions may contribute to systematic uncertainties if a narrow Gaussian distribution is implicitly assumed when evaluating observed frozen fractions. Relative measurement uncertainties Δns/ns of up to 40% across different measurement techniques28 translate into similar uncertainties for ΔJhet/Jhet if eqn (1) and (2) are used. Therefore, for our simulated cases these measurement uncertainties would be smaller than the systematic uncertainties potentially introduced by the variability in Jhet. Note that all results presented in this study are within the context of a timescale of δt = 10 s after which the frozen fractions are evaluated in our simulations.
Fig. 4 shows results analogous to Fig. 3 but for a higher median Jhet value (Jhet = 5 × 1010 m−2 s−1), which can be interpreted as a proxy for immersion freezing of mineral dust particles at temperatures around 238 K.17 We observe a similar interplay between Jhet variability and the aerosol surface area distributions, as in Fig. 3 for the quasi-monodisperse surface area. However, the overall sensitivity to the shape of the Jhet distribution is less pronounced at higher Jhet values due to the sublinear relationship between frozen fractions fice and Jhet.
The relative shift of the median fice values when comparing between a constant Jhet value and lognormal Jhet distribution is slightly smaller, but still in the same range as typical measurement uncertainties. For the broader surface area distribution, we do not observe a consistent relationship between different Jhet distributions and frozen fractions (i.e., a shift of median fice values). In both cases (Fig. 3 and 4), we find that the range of possible outcomes (within a confidence interval CI 95%, i.e., the 2.5th and 97.5th percentiles) is similar to estimates using an approximation based on a normal distribution of errors,30 with more significant deviations in the case of smaller droplet ensembles and for constant Jhet values (Table 1). This approximation is commonly used to evaluate confidence ranges associated with droplet freezing experiments.31 Another method of approximation relies on Poisson distributions, implicitly assuming large droplet ensembles and thus not fully resolving statistical uncertainties as a function of sample size.32
| Experiment type | Constant Jhet value | Lognormal Jhet distribution | ||
|---|---|---|---|---|
| f ice | f ice | f ice | f ice | |
| 2.5th perc./CI 95% | 97.5th perc./CI 95% | 2.5th perc./CI 95% | 97.5th perc./CI 95% | |
| Quasi-monodisperse aerosol + low Jhet (N = 100) | 0.000/0.001 | 0.020/0.046 | 0.000/0.002 | 0.030/0.053 |
| Polydisperse aerosol + low Jhet (N = 100) | 0.000/0.002 | 0.030/0.054 | 0.000/0.005 | 0.050/0.067 |
| Quasi-monodisperse aerosol + high Jhet (N = 100) | 0.290/0.297 | 0.480/0.485 | 0.330/0.321 | 0.500/0.511 |
| Polydisperse aerosol + high Jhet (N = 100) | 0.380/0.365 | 0.540/0.557 | 0.390/0.369 | 0.540/0.561 |
Quasi-monodisperse aerosol + low Jhet (N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.003/0.004 | 0.007/0.007 | 0.006/0.007 | 0.010/0.010 |
Polydisperse aerosol + low Jhet (N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.007/0.007 | 0.010/0.011 | 0.012/0.012 | 0.016/0.017 |
Quasi-monodisperse aerosol + high Jhet (N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.370/0.369 | 0.388/0.389 | 0.407/0.406 | 0.423/0.425 |
Polydisperse aerosol + high Jhet (N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) 000) |
0.424/0.423 | 0.440/0.442 | 0.429/0.427 | 0.444/0.446 |
In conclusion, our simulations demonstrate that the variability in Jhet may introduce differences in observed frozen fractions, which could lead to systematic uncertainties for parameterizations that are derived from these measurements if the variability in Jhet is not well known. However, it is unclear how grave consequent errors would be if these parameterizations were used in climate models. To illustrate these effects, we quantify the cloud impacts associated with different Jhet distributions, and consequently hypothetical INP parameterizations that can be derived from our simulated frozen fractions. Hawker et al. showed that choosing a weaker/stronger temperature dependence of INP parameterizations produced increases/decreases in outgoing radiation, the average cloud fraction and the ice water path (IWP) for deep convective clouds simulated by a cloud resolving model.33 We combine our frozen fraction simulations with the relationships reported by Hawker et al.33 to estimate the impact on modeled clouds.
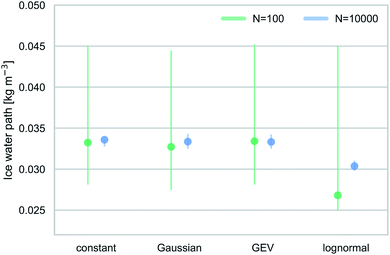
Fig. 5 shows estimated IWP values, based on frozen fractions simulated for different Jhet distributions and applying the relationship between dlog10(INP)/dT and IWP given in Hawker et al.33 for a system of tropical convective clouds. The ranges in Fig. 5 indicate the 5th and 95th percentile of simulated frozen fractions. For the small droplet ensembles, we assume the lower limit to be q5(fice) = 0.001, except in the case of the lognormal Jhet distribution where q5(fice) > 0.001. We use A = 10−12 m2 to convert frozen fractions into ns values, and then use the same aerosol surface area concentration as in Hawker et al.,33Aamb = 5 × 10−5 m2 m−3, to calculate INP concentrations.
Median IWP values are similar for small and large droplet ensembles. The IWPs for the lognormal Jhet distribution are roughly 25% lower compared to the other three cases. Despite these differences, the estimated IWP values agree within their respective uncertainties, and the impact from assuming different Jhet distributions or errors in Jhet within the uncertainties are small.
4 Conclusions
Our synthetic experiments demonstrate that Jhet distributions may have an impact on observed frozen fractions but only for distributions spanning at least one order of magnitude, and that this impact is more significant at low frozen fractions (i.e., warmer temperatures and less efficient INPs). Very broad aerosol surface area distributions may contribute to a shift in observed frozen fractions by up to a factor of two in our simulation setup, particularly for low frozen fractions. At higher frozen fractions and with a broad aerosol surface area distribution, simulations with different underlying Jhet distributions cannot be clearly distinguished from each other in our synthetic freezing experiments.We also infer potential cloud impacts associated with hypothetical ice nucleation parameterizations based on our simulations. The temperature dependence of different ice nucleation parameterizations—which is determined by ice nucleation propensities particularly at warm temperatures and by our ability to measure them—may have an impact on simulated cloud properties, e.g., the IWP in tropical convective cloud systems.33 For the cases that we considered in this study, these differences appear to be negligible in comparison to order-of-magnitude changes in ambient INP number concentrations.34 However, for a more comprehensive understanding of these effects, more detailed studies taking into account different cloud types and detailed cloud microphysics are needed.
Our synthetic experiments have shown that the number of freezing droplets has a significant impact on our ability to measure ice nucleation efficiencies with small uncertainty ranges, which agrees with findings by Alpert and Knopf.22 Note, however, that our synthetic experiments only consider the statistical uncertainties, without taking into consideration other factors that introduce additional uncertainties in real experiments, e.g., the counting efficiency of optical particle counters used to quantify the number of ice crystals or differences in sample handling impacting the comparability of observed frozen fractions across experimental setups.
Our analysis highlights the importance of studies with large droplet ensemble sizes to enhance our ability to precisely measure (median) ice nucleation propensities. These conditions may not be achievable for field measurements seeking to characterize ambient ice nucleating particles because of low number concentrations and highly complex compositions (i.e., numerous ice nucleating components) but can be more easily achieved in laboratory experiments and offline ice nucleation analyses. Also, even for the INP types that have been studied extensively, e.g., mineral dusts, the particle-to-particle variability of Jhet remains virtually unknown. Finally, we note that effects are expected to be larger in particle populations containing particle types with dramatically different ice nucleation propensities, e.g., internal and external mixtures of sea spray and dust.
Author contributions
IS and SMB designed the study and wrote the paper. IS developed the numerical Monte Carlo tools, with contributions from SMB. IS conducted all analyses.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the U.S. Department of Energy (DOE), Office of Science, Biological and Environmental Research program through the Early Career Research Program. Pacific Northwest National Laboratory is operated for DOE by Battelle Memorial Institute under contract DE-AC05-76RL01830. We also thank D. Knopf for valuable conversations.References
- O. Boucher, D. Randall, P. Artaxo, C. Bretherton, G. Feingold, P. Forster, V.-M. Kerminen, Y. Kondo, H. Liao and U. Lohmann, et al., in Climate Change 2013: the Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, ed. T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. M. Midgley, Cambridge University Press, 2013, pp. 571–657 Search PubMed.
- J. Mülmenstädt, M. Salzmann, J. E. Kay, M. D. Zelinka, P.-L. Ma, C. Nam, J. Kretzschmar, S. Hörnig and J. Quaas, Nat. Clim. Change, 2021, 11, 508–513 CrossRef.
- G. Cesana and T. Storelvmo, J. Geophys. Res., D: Atmos., 2017, 122, 4594–4599 CrossRef.
- I. Tan, T. Storelvmo and M. D. Zelinka, Science, 2016, 352, 224–227 CrossRef CAS PubMed.
- Z. A. Kanji, L. A. Ladino, H. Wex, Y. Boose, M. Burkert-Kohn, D. J. Cziczo and M. Krämer, Meteorol. Monogr., 2017, 58, 1.1–1.33 CrossRef.
- B. J. Murray, K. S. Carslaw and P. R. Field, Atmos. Chem. Phys., 2021, 21, 665–679 CrossRef CAS.
- A. Korolev and T. Leisner, Atmos. Chem. Phys., 2020, 20, 11767–11797 CrossRef CAS.
- J. Fan, Y. Wang, D. Rosenfeld and X. Liu, J. Atmos. Sci., 2016, 73, 4221–4252 CrossRef.
- S. M. Burrows, C. S. McCluskey, G. Cornwell, I. Steinke, K. Zhang, B. Zhao, M. Zawadowicz, A. Raman, G. Kulkarni, S. China, A. Zelenyuk and P. J. DeMott, Rev. Geophys., 2022, 60, e2021RG000745 CrossRef.
- L. B. Hande and C. Hoose, Atmos. Chem. Phys., 2017, 17, 14105–14118 CrossRef CAS.
- D. Barahona, Geophys. Res. Lett., 2020, 47, e2019GL086033 CrossRef.
- J. Savre and A. M. L. Ekman, J. Geophys. Res., 2015, 120, 4937–4961 CrossRef.
- S. L. Broadley, B. J. Murray, R. J. Herbert, J. D. Atkinson, S. Dobbie, T. L. Malkin, E. Condliffe and L. Neve, Atmos. Chem. Phys., 2012, 12, 287–307 CrossRef CAS.
- C. Marcolli, S. Gedamke, T. Peter and B. Zobrist, Atmos. Chem. Phys., 2007, 5081–5091 CrossRef CAS.
- I. Steinke, C. Hoose, O. Möhler, P. Connolly and T. Leisner, Atmos. Chem. Phys., 2015, 15, 3703–3717 CrossRef CAS.
- B. J. Murray, D. O'Sullivan, J. D. Atkinson and M. E. Webb, Chem. Soc. Rev., 2012, 41, 6519–6554 RSC.
- C. Hoose and O. Möhler, Atmos. Chem. Phys., 2012, 12, 9817–9854 CrossRef CAS.
- D. Niedermeier, R. A. Shaw, S. Hartmann, H. Wex, T. Clauss, J. Voigtländer and F. Stratmann, Atmos. Chem. Phys., 2011, 11, 8767–8775 CrossRef CAS.
- L. Ickes, A. Welti and U. Lohmann, Atmos. Chem. Phys., 2017, 17, 1713–1739 CrossRef CAS.
- R. J. Herbert, B. J. Murray, T. F. Whale, S. J. Dobbie and J. D. Atkinson, Atmos. Chem. Phys., 2014, 14, 8501–8520 CrossRef CAS.
- T. P. Wright and M. D. Petters, J. Geophys. Res., 2013, 118, 3731–3743 CrossRef.
- P. A. Alpert and D. A. Knopf, Atmos. Chem. Phys., 2016, 16, 2083–2107 CrossRef CAS.
- H. R. Pruppacher and J. D. Klett, Microphysics of Clouds and Precipitation, Springer, Dordrecht, 2010 Search PubMed.
- J. Heintzenberg, Aerosol Sci. Technol., 1994, 21, 46–48 CrossRef.
- H. J. Bae and J. H. Oh, Asia-Pacific J. Atmos. Sci., 2017, 53, 403–410 CrossRef.
- S. J. O'Shea, J. Crosier, J. Dorsey, W. Schledewitz, I. Crawford, S. Borrmann, R. Cotton and A. Bansemer, Atmos. Meas. Tech., 2019, 12, 3067–3079 CrossRef.
- S. M. Miller, R. Commane, J. R. Melton, A. E. Andrews, J. Benmergui, E. J. Dlugokencky, G. Janssens-Maenhout, A. M. Michalak, C. Sweeney and D. E. J. Worthy, Biogeosciences, 2016, 13, 1329–1339 CrossRef CAS.
- N. Hiranuma, S. Augustin-Bauditz, H. Bingemer, C. Budke, J. Curtius, A. Danielczok, K. Diehl, K. Dreischmeier, M. Ebert, F. Frank, N. Hoffmann, K. Kandler, A. Kiselev, T. Koop, T. Leisner, O. Möhler, B. Nillius, A. Peckhaus, D. Rose, S. Weinbruch, H. Wex, Y. Boose, P. J. DeMott, J. D. Hader, T. C. J. Hill, Z. A. Kanji, G. Kulkarni, E. J. T. Levin, C. S. McCluskey, M. Murakami, B. J. Murray, D. Niedermeier, M. D. Petters, D. O'Sullivan, A. Saito, G. P. Schill, T. Tajiri, M. A. Tolbert, A. Welti, T. F. Whale, T. P. Wright and K. Yamashita, Atmos. Chem. Phys., 2015, 15, 2489–2518 CrossRef CAS.
- R. P. Sear, Atmos. Chem. Phys., 2013, 13, 7215–7223 CrossRef CAS.
- A. Agresti and B. A. Coull, Am. Stat., 1998, 52, 119–126 Search PubMed.
- T. C. J. Hill, P. J. DeMott, Y. Tobo, J. Fröhlich-Nowoisky, B. F. Moffett, G. D. Franc and S. M. Kreidenweis, Atmos. Chem. Phys., 2016, 16, 7195–7211 CrossRef CAS.
- G. Vali, Atmos. Meas. Tech., 2019, 12, 1219–1231 CrossRef CAS.
- R. E. Hawker, A. K. Miltenberger, J. M. Wilkinson, A. A. Hill, B. J. Shipway, Z. Cui, R. J. Cotton, K. S. Carslaw, P. R. Field and B. J. Murray, Atmos. Chem. Phys., 2021, 21, 5439–5461 CrossRef CAS.
- J. Fan, L. R. Leung, D. Rosenfeld and P. J. DeMott, Atmos. Chem. Phys., 2017, 17, 1017–1035 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |