Ultrafast molecular dynamics in ionized 1- and 2-propanol: from simple fragmentation to complex isomerization and roaming mechanisms

Abstract

Upon photoexcitation, molecules can undergo numerous complex processes, such as isomerization and roaming, leading to changes in the molecular and electronic structure. Here, we report on the time-resolved ultrafast nuclear dynamics, initiated by laser ionization, in the two structural isomers, 1- and 2-propanol, using a combination of pump–probe spectroscopy and coincident Coulomb explosion imaging. Our measurements, paired with quantum chemistry calculations, identify the mechanisms for the observed two- and three-body dissociation channels for both isomers. In particular, the fragmentation channel of 2-propanol associated with the loss of CH₃ shows possible evidence of methyl roaming. Moreover, the electronic structure of this roaming methyl fragment could be responsible for the enhanced ionization also observed for this channel. Finally, comparison with similar studies done on ethanol and acetonitrile helps establish a correlation between the length of the alkyl chain and the likelihood of hydrogen migration.

---

1 Introduction

Laser-induced ionization of molecules can lead to changes in their molecular structures and, by extension, their chemical properties via different types of characteristic isomerization processes such as single and double hydrogen migration,^1,2 rotation about a bond³ and tautomerization.⁴ In general, isomerization is a universal phenomenon which is important to the fields of biochemistry and pharmacology, and has a wide variety of technological applications, specifically in the context of molecular motors and re-writable optical memories.⁵ In particular, hydrogen migration involves the ultrafast motion of one or more hydrogen atoms accompanied by a chemical bond rearrangement and is often observed in numerous systems, ranging from small hydrocarbons⁶ and organic molecules² to large biomolecules like proteins and peptides.⁷ The reported timescale for such fast nuclear dynamics varies from a few femtoseconds in acetylene⁶ to several hundred femtoseconds in acetonitrile¹ and ethanol.² More generally, migration of other groups such as hydroxyl has been observed in ionized amino acids.⁸

Additionally, some molecules upon photoexcitation may undergo dissociation through alternate pathways which involve roaming fragments.^9,10 In such cases, instead of completely dissociating from the parent molecule along the minimum energy path, a nearly dissociated fragment may remain weakly bound and participate in long-range interactions with the remaining moiety. Subsequently, this roaming fragment may additionally extract other atoms from the remaining moiety, as has been observed in the case of formaldehyde^11,12 and alcohols of varying primary carbon chain lengths.^13,14 Since the ‘roaming hydrogen atom’ mechanism was proposed to explain the abnormal rotational and vibrational energy of the dissociation photoproducts of formaldehyde, not only have roaming signatures been observed in many carbonyl compounds like acetone and acetaldehyde,^15–17 but different types of roaming reactions involving excited electronic states^18,19 and isomerization reactions^20–22 have also been proposed and observed.

In order to understand the underlying molecular dynamics that govern such light-induced ultrafast processes, a systematic study is necessary. This can ideally be achieved by using coincident momentum imaging,²³ which allows for a kinematically complete measurement of the fragments produced in ionized molecules. In combination with Coulomb explosion imaging (CEI),²⁴ this scheme has been used as a tool to identify isomers,³ to study the geometry of molecules²⁵ and even to map the presence of conical intersections.²⁶ In order to study the time-resolved CEI of the molecules in real time, a laser pump–probe scheme is implemented. The pump pulse initiates a molecular wave packet onto an excited electronic state whose propagation is interrogated by the probe pulse arriving at variable time delays. This intense probe pulse further ionizes the molecule to a highly charged state and thereby, induces a violent Coulomb explosion. The measured correlated momenta of the photoions provides information on the fragmentation and isomerization dynamics of the molecule on the excited electronic state. Pump–probe experiments have been successfully used to study rotational, vibrational, and electronic dynamics in a wide variety of systems ranging from simple molecules to complex nanosystems and bulk solids.²⁷

In this work, we study the time-resolved, photo-induced fragmentation dynamics including hydrogen migration in the two- and three-body breakup channels of the two structural isomers, 1- and 2-propanol. Additionally, we compare the isomerization dynamics previously studied in ethanol² and acetonitrile¹ with that of the propanol isomers to understand the effect of increasing carbon chain length on hydrogen migration. We also observe experimental indications of methyl roaming^17,28 in the fragmentation channel of 2-propanol, which is supported by state-of-the-art molecular dynamics simulations. The simulations show that the roaming CH₃ remains trapped in the electrostatic potential of the remaining moiety before complete fragmentation.

2 Methods

2.1 Experiment

The experimental setup is identical to the one described in a previous publication.² Briefly, the 790 nm, 35 fs pulses generated from a Ti:sapphire laser, with a repetition rate of 10 kHz, were focused into a hollow core fibre filled with Ar to generate 9 fs pulses with a central wavelength of 730 nm. These pulses were then split into pump and probe arms, where the probe arm is time-delayed with respect to the pump. Subsequently, the pulses were spatially overlapped and focused to a peak intensity of 2.29 × 10¹⁵ W cm⁻² and a spot size ∼11 μm inside the COLTRIMS,²⁹ onto an orthogonally propagating molecular jet of the gas phase sample (1-propanol, 2-propanol). Upon ionization of the sample, the ionic fragments were directed to a position-sensitive detector using a static, homogeneous electric field. The three-dimensional momentum distributions of the charged fragments were then reconstructed using their time of arrival at the detector and their two-dimensional position information.

2.2 Theory

Ionization induced by a strong IR pump pulse as is used in the current experiment proceeds through both multi-photon absorption and tunneling and cannot be described with the existing theoretical tools. Hence, there is no way to know the amount of excitation energy in the remaining molecular cation or the populations of its ground and excited electronic states. Therefore, following previous work,^2,8,30–33 we will assume that, irrespective of the electronic excited states of the cation that are populated, their decay into the nuclear degrees of freedom associated with the ground electronic state (e.g., through conical intersections) occurs within the first few tens of fs. This is indeed the case for most molecular cations with a size comparable to propanol that have similar floppy structures. Hence, this theoretical description will only be appropriate to describe the fragmentation dynamics occurring beyond 100 fs.

Under these assumptions, ab initio molecular dynamics (AIMD) simulations were performed starting with the Frank-Condon geometry (optimized ground-state geometry of the neutral molecule) with a certain amount of internal energy randomly distributed among the nuclear degrees of freedom. The internal energies used here are 10 and 15 eV. These energy values were chosen because (i) they are comparable to those found or estimated in other molecules ionized by strong IR fields with similar pulse energies, (ii) they were successfully used to describe a similar experiment with ethanol,² and (iii) they represent the minimum amount of energy that the system must have for all fragmentation channels to appear within 1 ps (our propagation time). For the case of singly ionized 2-propanol, calculations were also performed with an internal energy of 5 eV.

Quantum chemistry calculations were carried out using the density functional theory (DFT), in particular the B3LYP functional^34,35 in combination with the 6-31++G(d,p) basis set. This method was employed both in the exploration of the potential energy surface (PES) and in the AIMD simulations. In the PES exploration, critical points in the relevant pathways were located, thus allowing computation of the ionization potentials and dissociation energies for the relevant channels. Further exploration of the potential energy surface has been carried out by scanning bond distances allowing the rest of the variables to be optimized (relaxed scan). Using the geometry of each point in the scan, the energy of the electronic excited states have been computed using the Time-Dependent DFT formalism (TDDFT).^36–38 AIMD simulations were carried out using the Atom-centered Density Matrix Propagation method (ADMP),^39–42 imposing a timestep of 0.1 fs and up to 1 ps. The dynamics are run in the electronic ground state for both cationic and dicationic states with 600 trajectories for each energy value and charge state. All the simulations have been carried out with the Gaussian16 program.⁴³ The combination of AIMD with PES exploration has been used with success in the past to study the fragmentation dynamics of ionized molecules of different nature.^{2,8,30,31,44,45}

3 Results

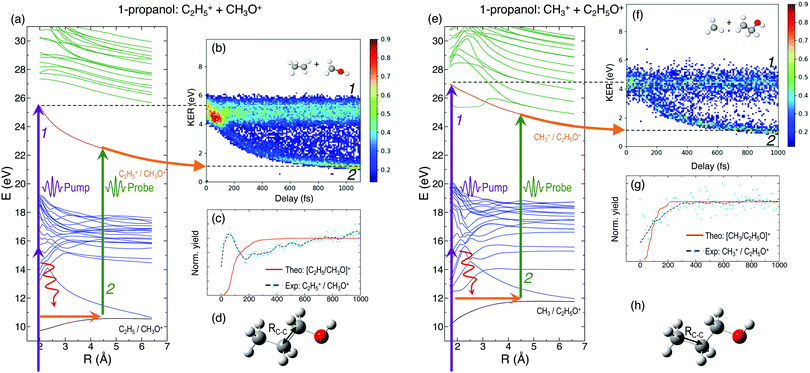
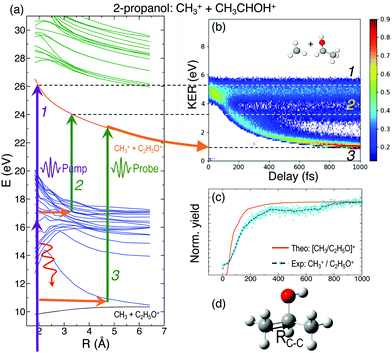
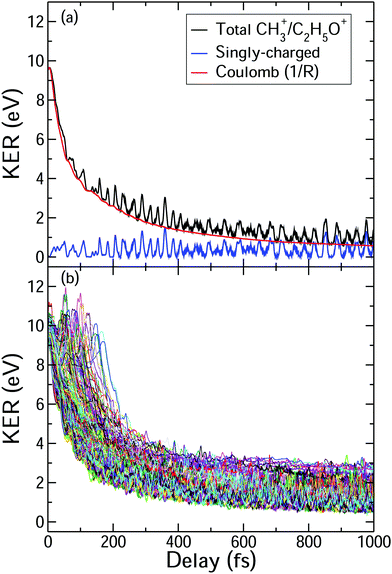
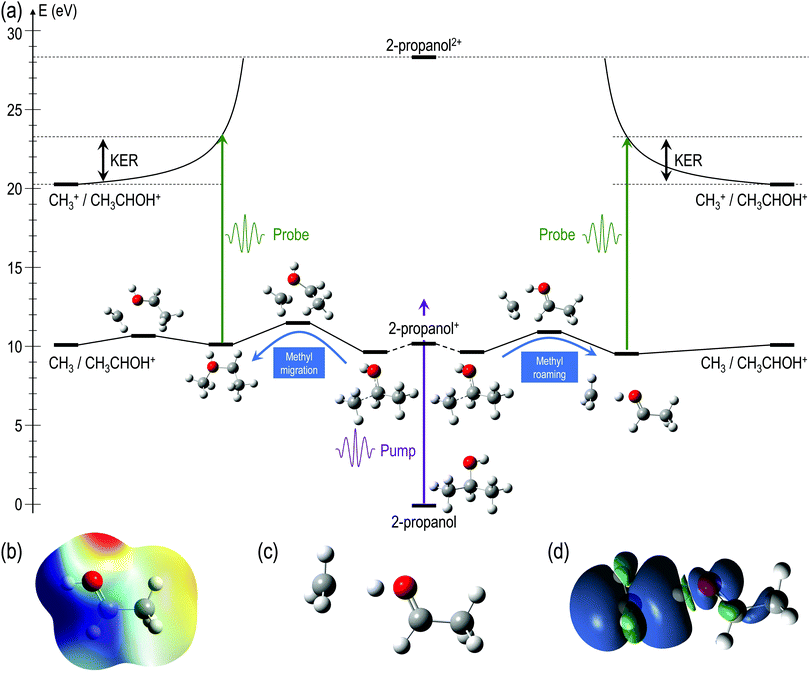
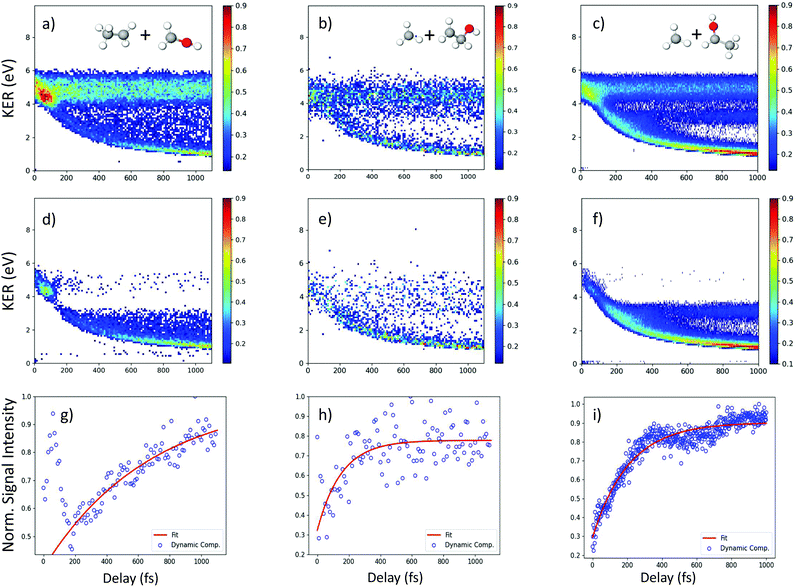
In general, the laser pump pulse can initiate various types of dynamics in a molecule which can result in the formation of different ionic fragments depending on the molecular geometry and its potential energy surfaces. Due to the position of the –OH group on one of the terminal carbon atoms in 1-propanol (see Fig. 1(d)), cleavage of either of the two C–C bonds gives rise to two unique double-ion coincidence channels: C₂H₅⁺ + CH₂OH⁺ or CH₃⁺ + C₂H₄OH⁺. The experimentally obtained delay-dependent kinetic energy release (KER) of these two fragmentation channels are shown in Fig. 1(b) and (f) and the corresponding potential energy diagrams, along the C–C bonds highlighted in (d) and (h), are shown in (a) and (e), respectively. The black and orange curves are the ground cationic and dicationic states, while the blue and green curves are the excited cationic and excited dicationic states, respectively. The potential energy curves explain the two types of distributions seen in the KER plots. The time-independent (static) distribution, indicated as 1, centered around ∼5 eV in both Fig. 1(b) and (f) is observed due to the direct promotion of the molecule to the dication state by the pump pulse. The time-dependent (dynamic) band, indicated by 2, shows a decrease in the KER as a function of pump–probe time delay. This band, which originates at 5 eV and reaches its asymptotic limit at ∼1 eV, shows the dynamics that the molecule undergoes upon excitation to the ground or excited cationic states by the pump pulse. The probe pulse subsequently excites the molecule to the ground dicationic state which results in the typical Coulomb explosion (CE) behavior as the ionic fragments repel each other along the 1/R Coulomb potential curve. Fig. 1(c) and (g) show the projection (cyan dots) of the dynamic band from the respective KER signal intensities (Fig. 1(b) and (f)) onto the time delay axis. Additionally, the black dashed line shows the moving average of the projection signal. The fitting procedure for the extraction of solely the dynamic band from the KER plot is discussed in detail in the Discussion section. The theoretically obtained delay-dependent yield (red line) for the corresponding channels are plotted in the same figure. As can be seen, in general, there is qualitative agreement between theory and experiment, although, in some cases, theory predicts slightly faster fragmentation times compared to experiment. A possible explanation is that the excitation energy used in these calculations (10–15 eV) may be somewhat overestimated.

In contrast to 1-propanol, the central location of the –OH group in 2-propanol results in the same photo-products upon cleavage of either of the two C–C bonds. Strictly speaking, for neutral 2-propanol, the C–H bond (on the central carbon) breaks the symmetry and points towards one of the methyl groups. However, the energy required to move the central H atom from one side of the molecule to the other is much smaller than the amount of energy available in the system. Therefore, the effect on the dynamics is expected to be negligible. Similar to Fig. 1, Fig. 2(a) and (b) show the potential energy diagram and the delay-dependent KER for the fragmentation channel CH₃⁺ + C₂H₄OH⁺ of 2-propanol. Here, three distinct features are observed in the the KER plot for this channel, marked as distributions 1, 2 and 3 in Fig. 2(b). 1 and 3 are similar to the time-independent and -dependent features observed for 1-propanol (Fig. 1) and can be explained using the same mechanisms. 2 is indistinguishable from 3 up to 200 fs, after which it appears as a separate time-independent distribution centered around 3 eV. This KER distribution is unique to the fragmentation of 2-propanol and will be discussed in more detail in the next section. Additionally, for completeness, Table 1 shows a comparison between the calculated and measured relative yields for the two-body fragmentation channels shown in Fig. 1 and 2. These channels have been unambiguously identified in the coincidence maps and in the calculations. As can be seen, the agreement for the relative yields is reasonable for all initial internal energies considered in the calculations.

Fig. 1 (a) and (e) Potential energy curves showing the ground and excited cationic and dicationic states of 1-propanol along the C–C bonds indicated in the ball-and-stick models shown in (d) and (h), respectively. Purple arrows, representing multiphoton absorption induced by the pump pulse, indicate population transfer to electronically excited states. Red curly arrows indicate relaxation to the ground state of the cation, with energy transfer to vibrational modes. Kinetic energy release as a function of the time delay between the pump and probe pulses for the double coincidence fragmentation channels (b) C₂H₅⁺ + CH₂OH⁺ and (f) CH₃⁺ + C₂H₄OH⁺ of 1-propanol. (c) and (g) Comparison between the projection of experimentally obtained dynamic KER signal intensities and theoretical yields using E_exc = 10 eV for the corresponding channels.

Fig. 2 (a) Potential energy curves of the ground and excited cationic and dicationic states of 2-propanol along the C–C bond shown in (d). Purple arrows, representing multiphoton absorption induced by the pump pulse, indicate population transfer to electronically excited states. Red curly arrows indicate relaxation to the ground state of the cation, with energy transfer to vibrational modes. (b) Delay-dependent KER for the fragmentation channel CH₃⁺ + CHOHCH₃⁺. (c) Comparison between the projection of experimentally obtained dynamic KER signal intensity and theoretical yield using E_exc = 10 eV for the fragmentation channel.

Table 1 Comparison between the calculated and measured relative branching ratios for channels leading to the breakup of the singly ionized molecule into two fragments, which are detected as double ion coincidences

1-Propanol	Experimental yield	5 eV	10 eV	15 eV
C2H5^+ + CH3O^+	93.77		82.68	80.69
CH3^+ + C2H4OH^+	6.23		17.32	19.31

---

2-Propanol	Experimental yield	5 eV	10 eV	15 eV
CH3^+ + C2H5O^+	99.91	98.2	86.12	67.39
H^+ + C3H7O^+	0.09	1.7	13.88	32.61

---

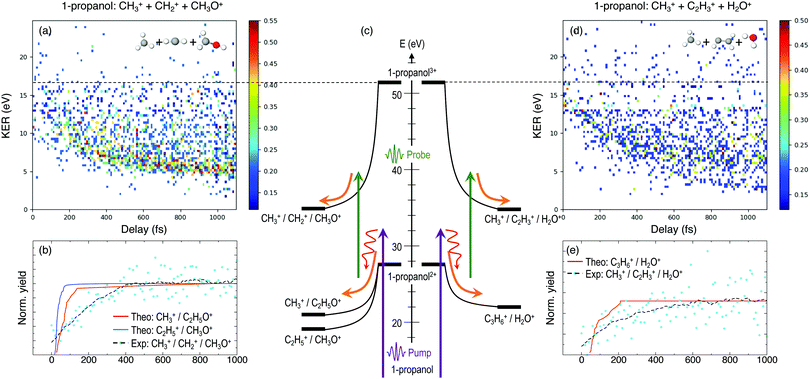
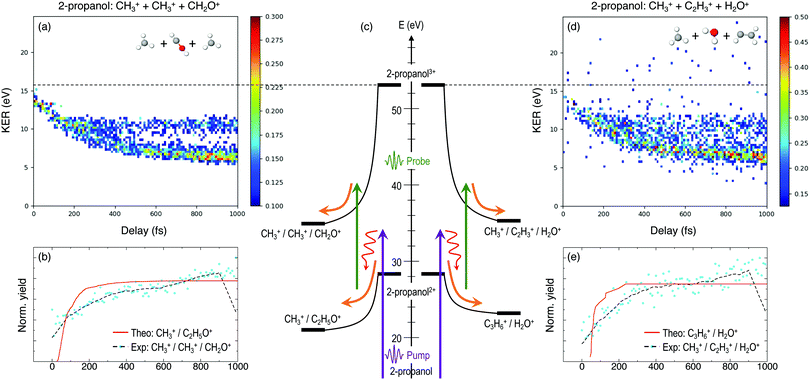
Furthermore, triple ionization of the molecule by the pump and probe pulses can result in three-body breakup channels which may reveal new fragmentation mechanisms induced in the molecule or may shed more light on subsequent fragmentation of the previously observed two-body channels. Fig. 3 and 4 show the delay-dependent KER plots for the observed triple coincidence channels for 1- and 2-propanol along with their potential energy diagrams. In this case, both isomers show similar dynamics, each undergoing either fragmentation or hydrogen migration. Direct breakup of both C–C bonds in 1-propanol gives rise to the fragmentation channel CH₂⁺ + CH₃⁺ + CH₃O⁺. Similarly, in 2-propanol, both C–C bonds fragment giving rise to CH₃⁺ + CH₃⁺ + CH₂O⁺. Besides fragmentation, there is evidence of single hydrogen migration (SHM) in the three body channels. H₂O⁺ is detected in coincidence with the CH₃⁺ and C₂H₃⁺ ions, thereby forming kinematically complete channels in both 1- and 2-propanol. However, the low yield of the SHM channels compared to the three-body fragmentations indicates that hydrogen migration is not very probable in both propanol isomers.

Fig. 3 KER as a function of the time delay between the pump and probe pulses for the triple coincidence channels showing direct fragmentation, (a) CH₂⁺ + CH₃⁺ + CH₂OH⁺, and single hydrogen migration (d) CH₃⁺ + H₂O⁺ + C₂H₃⁺ in 1-propanol, respectively. (c) Schematic of the fragmentation and hydrogen migration dynamics evolving from doubly ionized 1-propanol. (b) and (e) Comparison between the experimentally obtained dynamic KER signal intensity along with the theoretical yields using E_exc = 10 eV for the two triple coincidence channels.

Fig. 4 KER as a function of the time delay between the pump and probe pulses for the triple coincidence channels showing direct fragmentation, (a) CH₃⁺ + CH₃⁺ + CHOH⁺, and single hydrogen migration (d) CH₃⁺ + H₂O⁺ + C₂H₃⁺ in 2-propanol, respectively. (c) Schematic of the fragmentation and hydrogen migration dynamics evolving from doubly ionized 2-propanol. (b) and (e) Comparison between the experimentally obtained dynamic KER signal intensity along with the theoretical yields using E_exc = 10 eV for the two triple coincidence channels.

4 Discussion

To understand the time dependence of the measured KER spectra, we will focus on the double-coincidence spectrum shown in Fig. 2. The experimentally measured KER results from two contributions: (i) the nuclear dynamics occurring in the singly-charged molecule in between the pump and the probe steps, and (ii) the nuclear dynamics occurring in the doubly-charged molecule after the probe step. Our AIMD simulations only give access to the dynamics associated with (i). In order to make a full comparison to the experimental KER, one should, in principle, include the effect of the probe pulse, which is not possible due to the computational demand. One can, however, estimate the KER associated with (ii) by using a sudden approximation, i.e., by assuming a perfect projection of the molecular geometry on the potential energy surface of the doubly charged molecule. In this approximation, the KER acquired after the probing step is approximately given by 1/R, where R is the C–C distance between the two separating fragments at a given time. Fig. 5(b) shows the calculated KER as a function of the pump–probe delay for some of the trajectories associated with the CH₃⁺ + C₂H₅O⁺ channel resulting from the fragmentation and subsequent probing of singly-ionized 2-propanol. As the estimations of both components of the measured KER are only meaningful when the C–C bond distance stretches significantly, the figure does not include the results of those trajectories associated with roaming or other dissociation mechanisms. The temporal evolution of the KER for all trajectories is quantitatively very similar to that obtained in the experiment (see Fig. 2(b)). Furthermore, Fig. 5(a) shows a typical trajectory in which Coulomb explosion of the doubly-charged molecule makes the dominant contribution to the KER. KER contributions from before and after the interaction with the probe pulse (Coulomb explosion) become comparable only at about 1 ps (of the order of 0.5 eV).

Fig. 5 (a) Decomposition of the measured CH₃⁺ + C₂H₅O⁺ KER (black line) into the KER gained by the two fragments in the singly-charged 2-propanol molecule, i.e., before the probe step (blue line), and the KER resulting from Coulomb explosion after the probe step (red line). (b) Calculated KER as a function of the pump–probe delay for some trajectories associated with the CH₃⁺ + C₂H₅O⁺ channel of 2-propanol.

In Fig. 2(b), distribution 2 is a unique feature since it neither follows the asymptotic behavior of distribution 3 (Coulomb repulsion) nor the time-independent nature of distribution 1. A possible explanation is that this distribution is the result of the pump-excited molecular wave packet evolving along the excited cationic states which have very strong bonding character below 3 Å (Fig. 2(a)). Consequently, for small time delays, there is a decrease in the KER as the C–C bond elongates but at larger delays, this bond cannot get stretched beyond 3 Å. Due to this, the probe pulse populates the same point in the dicationic surface resulting in no change in the KER value after ∼200 fs. Despite the potential energy curves for both 1- and 2-propanol cations being identical along the H₃C–C₂H₅O bond distance, distribution 2 is not observed in the KER spectrum associated with double coincidences in 1-propanol. This could be due to the lower statistics available for 1-propanol, but the difference in atomic configurations of the two isomers is a more likely explanation.

For a better understanding of the KER distribution 2, one must go beyond the present AIMD simulations and perform explicit calculations of the critical points of the multi-dimensional potential energy surface, i.e., the local minima and saddle points that determine the fate of the calculated trajectories. After the pump pulse, cationic 2-propanol can undergo relaxation via a significant elongation of one of the C–C bonds. As discussed earlier, the methyl group can not only be directly ejected by the probe pulse but can also change its position relative to the remaining molecular fragment. Two isomerization pathways involving one of the methyl groups are shown in the Fig. 6(a): (i) methyl migration: this leads to the formation of a new C–O bond, and CH₃ is subsequently released from the new structure and (ii) methyl roaming: the methyl fragment moves around forming a hydrogen-bonded structure before undergoing probe-induced fragmentation. Both mechanisms shown in Fig. 6(a) indicate that the CH₃ group does not immediately escape; instead it remains temporally trapped in the potential generated by the larger CH₃CHOH⁺ fragment. Fig. 6(b) shows the electrostatic potential generated by the remaining cationic fragment (CH₃CHOH⁺) after cleavage of neutral CH₃ in singly-charged 2-propanol. The dark blue color indicates the region of attractive potential which is favorable for CH₃ roaming and facilitates the formation of hydrogen bonded structure shown in Fig. 6(c). Since neutral CH₃ is a radical, with one unpaired electron in a p_z orbital perpendicular to the molecular plane, it can be easily polarized by the electrostatic potential. As a result, the methyl group is electrostatically trapped before getting ejected by the probe pulse.

Fig. 6 (a) Critical points in the potential energy surface of singly ionized 2-propanol showing isomerization of the methyl group. Pathway to the left involves cleavage of the C–C bond and formation of a new C–O bond. Methyl migration is stable in the new structure. Pathway to the right shows methyl roaming leading to the formation of a hydrogen bonded structure. CH₃ is subsequently released in both the pathways. Relative energies are given in eV and are relative to the ground state of neutral 2-propanol. (b) Electrostatic potential projected on the electron density; isovalue of the electron density: 0.0004 a.u., limits of the potential: 0.15 a.u. (red) 0.22 a.u. (blue). (c) Hydrogen bonded structure, minimum in the PES of the cationic 2-propanol after CH₃ roaming (d) Spin density difference: δρ_spin = ρ_α–ρ_β in the singly-charged hydrogen bonded structure.

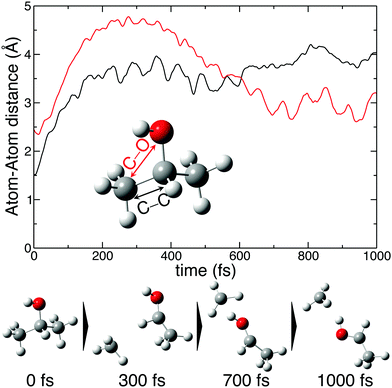
The molecular dynamics simulations confirm our hypothesis of methyl roaming in 2-propanol. As an illustration, Fig. 7 shows the results for a typical trajectory demonstrating methyl roaming, where the methyl group evolves, approaching the –OH group to form the hydrogen bonded structure. C–C bond cleavage is observed after approximately 200 fs while the methyl group remains at a distance of 3–4 Å during the propagation time of 1000 fs. We note from Fig. 2(a) that a C–C distance of ∼3 Å leads to ∼3 eV KER of the fragments when projected onto the dicationic state after the probe pulse. The appearance of methyl roaming strongly depends on the energy available in the system; at 10 eV and 15 eV internal energy, it is very rare, but at 5 eV, methyl roaming is seen in about 7.5% of the trajectories. A similar roaming mechanism is not possible in 1-propanol due to its different atomic configuration. In summary, distribution 2 in 2-propanol indicates a possible methyl roaming mechanism, wherein the trapping of CH₃ in the electrostatic potential leads to an unchanging distance between the fragments with time, thereby giving rise to a constant KER. However, further experimental and theoretical work is needed to explicitly assign this feature to methyl roaming. For instance, previous experiments have observed similar methyl roaming mechanisms in the photodissociation of acetaldehyde, which was inferred from the formation of vibrationally hot CH₄ due to a hydrogen atom abstraction by the roaming CH₃.^17,28 These results were then confirmed by ab initio calculations⁴⁶ as well as quasi-classical trajectory calculations using a global potential energy surface for acetaldehyde.⁴⁷

Fig. 7 A typical trajectory of the molecular dynamics simulations showing methyl roaming. The upper plot shows C–O and C–C bond distances as a function of time. The lower part shows snapshots of methyl roaming at different propagation time.

An important aspect of studying these molecular dynamics is to resolve the ultrafast timescales on which such processes occur. In order to obtain quantitative temporal information from the time-dependent KER band of different channels, a 2D global fitting method is used.¹ The KER vs time delay spectra for all the reported channels is fit using two independent Gaussian functions at each recorded delay step. One Gaussian is used to fit the static band centered around 4.8 eV for the two-body coincidence channels (around 14 eV for the three-body coincidence channels). The mean position, amplitude and width of this Gaussian are constrained in order to model the relatively constant position and intensity of the static KER bands. The second Gaussian is used to model the dynamic KER distribution. Subtraction of the time-independent Gaussian fit from the KER vs. time delay spectrum isolates the time-dependent distribution which is then projected onto the delay axis. Afterwards, the data is fit to a saturating exponential of the form 1 − e^{−(Δt−t₀)/τ} in order to obtain the exponential time constant τ and time offset t₀. Fig. 8(a)–(c) show the experimental delay-dependent KER for the two-body fragmentation channels of 1- and 2-propanol. Fig. 8(d)–(f) show the isolated time-dependent distributions obtained from subtraction of the static Gaussian fit from the experimental data, and (g)–(i) show the projections of the dynamic distributions and their fits to a saturating exponential. The values of τ and t₀ for all the channels of 1- and 2-propanol are given in Tables 2 and 3 respectively. Interestingly, of all the coincidence channels analyzed, only the two-body fragmentation channel C₂H₅⁺ + CH₃O⁺ of 1-propanol shows a strong enhancement in intensity at small delays, with the peak occurring at around 50 fs. For comparison, the temporal resolution of our experiment is ∼13 fs. We do not have a complete understanding of what causes this enhancement effect but it can possibly be attributed to some kind of enhanced ionization (EI) for this particular channel at small time delays.

Fig. 8 Fitting and projection of the delay-dependent KER for three different fragmentation channels of 1- and 2-propanol. Experimentally obtained KER vs time delay spectra for (a) CH₃⁺ + CH₃O⁺ and (b) CH₃⁺ + C₂H₅O⁺ of 1-propanol and (c) CH₃⁺ + C₂H₅O⁺ of 2-propanol, respectively. (d)–(f) the time-dependent KER spectra obtained from the subtraction of the Gaussian fit of the static KER band from the experimental data. (g)–(i) the projection of the time-dependent KER onto the delay axis (blue circles) along with their fits to a saturating exponential function (red line).

Table 2 Time constant and time shift of double and triple coincidence channels observed for 1-propanol

Channel	τ (fs)	t 0 (fs)
CH3^+ + C2H4OH^+ (Fragmentation)	152 ± 64	37 ± 30
C2H5^+ + CH2OH^+ (Fragmentation)	671 ± 338	73 ± 70
CH2^+ + CH3^+ + CH2OH^+ (Fragmentation)	219 ± 73	33 ± 29
CH3^+ + H2O^+ + C2H3^+ (SHM)	289 ± 187	56 ± 58

---

Table 3 Time constant and time shift of double and triple coincidence channels observed for 2-propanol

Channel	τ (fs)	t 0 (fs)
CH3^+ + C2H4OH^+ (Fragmentation)	210 ± 13	8 ± 6
CH3^+ + CH3^+ + CHOH^+ (Fragmentation)	728 ± 310	35 ± 33
CH3^+ + H2O^+ + C2H3^+ (SHM)	321 ± 94	29 ± 28

---

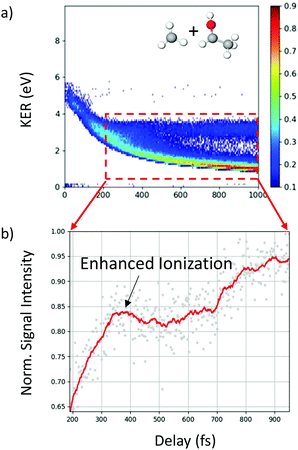
In addition to the unique distribution 2 indicating possible methyl roaming in the fragmentation channel CH₃⁺ + C₂H₅O⁺ of 2-propanol, evidence of EI identified by an increase in the ionization yield is also observed. To better quantify the EI, Fig. 9(b) shows the projection of the dynamic part of the KER signal inside the red dashed box from Fig. 9(a) onto the pump–probe delay axis. The dashed box spans from 200 fs to 1000 fs on the delay axis and from 0.5 eV to 4.0 eV on the KER axis. The experimental data points (grey dots) in Fig. 9(b) are used to generate a moving average (red line) which shows an increase in the signal intensity between 200 fs and 450 fs, indicating EI. This phenomenon has been observed in various hydrocarbons like ethylene, acetylene and 1,3-butadiene^48,49 where unexpectedly high molecular charge states are observed when the internuclear distance reaches a critical value. As the bond gets stretched in the presence of an external laser field, there may exist regions in the molecular potential where the tunneling barriers become lower and/or narrower than at equilibrium geometry. This can result in a more efficient ionization pathway for the electrons to tunnel out. In the case of 2-propanol, it is possible that at some critical internuclear separation between the two carbon atoms and in the presence of the electric field of the probe pulse, electrons are more readily ejected leading to an increase in the yield of this double coincidence channel. More precisely, from a plot of the spin density difference (ρ_α–ρ_β, see Fig. 6(d)) for the geometry corresponding to the hydrogen bonded structure (the more favorable one in methyl roaming), one can observe that the unpaired electron of the methyl group appears quite delocalized with one lobe pointing outwards in the direction perpendicular to the molecular plane. This electronic distribution of the unpaired electron of the roaming CH₃ fragment could also be responsible for the enhanced ionization observed in 2-propanol.

Fig. 9 (a) Delay-dependent KER for the fragmentation channel CH₃⁺ + CHOHCH₃⁺ of 2-propanol. (b) Projection of KER signal inside the red-dashed box, shown in (a), onto the delay axis shows increase in ionization yield indicating enhanced ionization. See text for more details.

Single and double hydrogen migration, though ubiquitous, are complicated molecular processes that are not completely understood. Similar experiments to study hydrogen migration conducted on ethanol² and acetonitrile¹ reveal stark differences in the molecular dynamics initiated by laser ionization. Comparison with the propanol isomers shows that factors such as the length of the carbon chain have a strong impact on the likelihood of hydrogen migration. Reported yields for double ion coincidences in ethanol² show that the double hydrogen migration (DHM) channel has the highest yield, followed by SHM and direct fragmentation of the C–C bond. Similarly, in acetonitrile,¹ hydrogen migration leads to formation of very stable linear and ring isomers upon laser excitation, most of which are more stable than its canonical cationic structure. This results in SHM being the most likely process, closely followed by DHM. However, in the propanol isomers, no hydrogen migration is observed in the two-body fragmentation channels, and only weakly observed in the three-body channels. These findings indicate, surprisingly, that the viability of intramolecular hydrogen migration decreases as the carbon chain length increases, even though the number of hydrogen atoms available for migration increases. Our results show similar trends to a recent study of primary alcohols in a strong laser field, where it was observed that the probability of H₃⁺ formation, via a roaming neutral H₂, decreases as the carbon chain length increases from methanol to the propanol isomers.¹³ The authors indicate that molecular structural features such as the prevalence of α-hydrogen atoms affect the pathways and thus the probability of H₃⁺ formation.

5 Conclusion

Using a combination of coincident Coulomb explosion imaging and pump–probe spectroscopy, we have investigated the ultrafast molecular dynamics in ionized 1- and 2-propanol induced by photoexcitation. Ab initio molecular dynamics calculations and exploration of several potential energy surfaces, employing density functional theory, have been used to provide deeper insights into the underlying mechanisms. The major channels identified in the double and triple ion-coincidences for both isomers indicate that a direct C–C bond fragmentation is the most dominant channel. Additionally, we see a clear indication of enhanced ionization for the double coincidence channel of 2-propanol, but see no sign of such a process occurring in 1-propanol. Similarly, methyl roaming is observed in 2-propanol, but not in 1-propanol. Although roaming of radicals has been reported in the past, the role of ionization and excitation of the parent molecule is not fully understood. Excited state dynamics play a major role in determining the outcome of an ionization process; however, it is difficult to computationally access such states. On the experimental side, highly differential measurements involving detection of photoelectrons and multiple ions in coincidence using COLTRIMS allows for a more quantitative determination of the excited states involved in the different fragmentation channels, including channels that show roaming dynamics. Therefore, further experimental and theoretical work in other molecular systems where methyl radicals are likely to be produced is desirable.

For both isomers, hydrogen migration is found to occur only in the case of triple ionization and with very low yield. Our work, in combination with previous work on ethanol² and acetonitrile,¹ sheds light on the strong effect of an increase in carbon chain length on the likelihood of hydrogen migration. The results indicate that as the alkyl chain length increases along with the overall number of hydrogen atoms in the molecule, the hydrogen migration process becomes less likely. In particular, while double hydrogen migration is the most dominant channel observed in ethanol, this process is absent in both the propanol isomers.

Author contributions

D. M. and R. O. performed analysis of the experimental data which was collected by R. O. J. R. G., S. D. T. and F. M. analyzed the theoretical results. Everyone was involved in the interpretation of the data. D. M. wrote the paper with contributions from everyone. S. D. T., F. M. and N. B. supervised the project.

Conflicts of interest

The authors declare no conflicting interests.

Acknowledgements

The experimental work was funded by the National Science Foundation under award No. 1700551. The calculation was funded by the MICINN (MCIN/AEI/10.13039/501100011033) projects PID2019-105458RB-I00 and PID2019-110091GB-I00, ‘Severo Ochoa’ Programme for Centres of Excellence in R & D (SEV-2016-0686) and ‘María de Maeztu’ Programme for Units of Excellence in R & D (CEX2018-000805-M). We acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). Debadarshini Mishra acknowledges Sachin Vaidya for helpful discussions on the topic.

Notes and references

1. M. McDonnell, A. C. LaForge, J. Reino-González, M. Disla, N. G. Kling, D. Mishra, R. Obaid, M. Sundberg, V. Svoboda and S. Daz-Tendero, et al. , J. Phys. Chem. Lett., 2020, 11, 6724–6729.
2. N. G. Kling, S. Daz-Tendero, R. Obaid, M. Disla, H. Xiong, M. Sundberg, S. Khosravi, M. Davino, P. Drach and A. Carroll, et al. , Nat. Commun., 2019, 10, 2813.
3. S. Pathak, R. Obaid, S. Bhattacharyya, J. Bürger, X. Li, J. Tross, T. Severt, B. Davis, R. C. Bilodeau and C. A. Trallero-Herrero, et al. , J. Phys. Chem. Lett., 2020, 11, 10205–10211.
4. M. F. Shaw, B. Sztáray, L. K. Whalley, D. E. Heard, D. B. Millet, M. J. Jordan, D. L. Osborn and S. H. Kable, Nat. Commun., 2018, 9, 2584.
5. C. Dugave and L. Demange, Chem. Rev., 2003, 103, 2475–2532.
6. C. Burger, N. G. Kling, R. Siemering, A. S. Alnaser, B. Bergues, A. M. Azzeer, R. Moshammer, R. de Vivie-Riedle, M. Kübel and M. F. Kling, Faraday Discuss., 2016, 194, 495–508.
7. F. Turecek and E. A. Syrstad, J. Am. Chem. Soc., 2003, 125, 3353–3369.
8. D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martn, M. Alcam, B. A. Huber, P. Rousseau, A. Domaracka and S. Daz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767–16778.
9. A. G. Suits, Acc. Chem. Res., 2008, 41, 873–881.
10. A. G. Suits, Annu. Rev. Phys. Chem., 2020, 71, 77–100.
11. T. Endo, S. P. Neville, V. Wanie, S. Beaulieu, C. Qu, J. Deschamps, P. Lassonde, B. E. Schmidt, H. Fujise and M. Fushitani, et al. , Science, 2020, 370, 1072–1077.
12. F. A. Mauguiére, P. Collins, Z. C. Kramer, B. K. Carpenter, G. S. Ezra, S. C. Farantos and S. Wiggins, J. Phys. Chem. Lett., 2015, 6, 4123–4128.
13. N. Ekanayake, T. Severt, M. Nairat, N. P. Weingartz, B. M. Farris, B. Kaderiya, P. Feizollah, B. Jochim, F. Ziaee and K. Borne, et al. , Nat. Commun., 2018, 9, 5186.
14. E. Livshits, I. Luzon, K. Gope, R. Baer and D. Strasser, Chem. Commun., 2020, 3, 49.
15. K.-C. Lin, P.-Y. Tsai, M.-H. Chao, M. Nakamura, T. Kasai, A. Lombardi, F. Palazzetti and V. Aquilanti, Int. Rev. Phys. Chem., 2018, 37, 217–258.
16. C.-J. Tso, T. Kasai and K.-C. Lin, Sci. Rep., 2020, 10, 4769.
17. L. Rubio-Lago, G. Amaral, A. Arregui, J. Izquierdo, F. Wang, D. Zaouris, T. Kitsopoulos and L. Banares, Phys. Chem. Chem. Phys., 2007, 9, 6123–6127.
18. H. Xiao, S. Maeda and K. Morokuma, J. Phys. Chem. Lett., 2011, 2, 934–938.
19. M. P. Grubb, M. L. Warter, H. Xiao, S. Maeda, K. Morokuma and S. W. North, Science, 2012, 335, 1075–1078.
20. M. L. Hause, N. Herath, R. Zhu, M.-C. Lin and A. G. Suits, Nat. Chem., 2011, 3, 932–937.
21. A. S. Mereshchenko, E. V. Butaeva, V. A. Borin, A. Eyzips and A. N. Tarnovsky, Nat. Chem., 2015, 7, 562–568.
22. Z. Homayoon and J. M. Bowman, J. Phys. Chem. A, 2013, 117, 11665–11672.
23. J. Gagnon, K. F. Lee, D. Rayner, P. Corkum and V. Bhardwaj, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 215104.
24. B. Feuerstein, T. Ergler, A. Rudenko, K. Zrost, C. Schröter, R. Moshammer, J. Ullrich, T. Niederhausen and U. Thumm, Phys. Rev. Lett., 2007, 99, 153002.
25. Z. Vager, R. Naaman and E. Kanter, Science, 1989, 244, 426–431.
26. M. E. Corrales, J. González-Vázquez, R. de Nalda and L. Bañares, J. Phys. Chem. Lett., 2018, 10, 138–143.
27. M. Fushitani, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem, 2008, 104, 272–297.
28. P. Houston and S. Kable, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16079–16082.
29. J. Ullrich, R. Moshammer, R. Dörner, O. Jagutzki, V. Mergel, H. Schmidt-Böcking and L. Spielberger, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 2917.
30. S. Maclot, D. G. Piekarski, A. Domaracka, A. Méry, V. Vizcaino, L. Adoui, F. Martn, M. Alcam, B. A. Huber and P. Rousseau, et al. , J. Phys. Chem. Lett., 2013, 4, 3903–3909.
31. S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. Huber, L. Adoui, F. Martn, M. Alcam, L. Avaldi and P. Bolognesi, et al. , Phys. Rev. Lett., 2016, 117, 073201.
32. D. G. Piekarski, R. Delaunay, A. Mika, S. Maclot, L. Adoui, F. Martn, M. Alcam, B. A. Huber, P. Rousseau and S. Daz-Tendero, et al. , Phys. Chem. Chem. Phys., 2017, 19, 19609–19618.
33. P. Rousseau, D. G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martin, M. Alcam, S. Daz-Tendero and B. A. Huber, Nat. Commun., 2020, 11, 3818.
34. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
37. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
38. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
39. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
40. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
41. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
42. S. S. Iyengar, H. B. Schlegel and G. A. Voth, J. Phys. Chem. A, 2003, 107, 7269–7277.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, 2016, Gaussian Inc., Wallingford CT.
44. M. Capron, S. Daz-Tendero, S. Maclot, A. Domaracka, E. Lattouf, A. aawicki, R. Maisonny, J.-Y. Chesnel, A. Méry and J.-C. Poully, et al. , Chem. – Eur. J., 2012, 18, 9321–9332.
45. E. Kukk, D. Ha, Y. Wang, D. G. Piekarski, S. Daz-Tendero, K. Kooser, E. Itälä, H. Levola, M. Alcam, E. Rachlew and F. Martín, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 043417.
46. L. B. Harding, S. J. Klippenstein and A. W. Jasper, Phys. Chem. Chem. Phys., 2007, 9, 4055–4070.
47. B. C. Shepler, B. J. Braams and J. M. Bowman, J. Phys. Chem. A, 2007, 111, 8282–8285.
48. X. Xie, S. Roither, M. Schöffler, H. Xu, S. Bubin, E. Lötstedt, S. Erattuphuza, A. Iwasaki, D. Kartashov and K. Varga, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 023429.
49. S. Roither, X. Xie, D. Kartashov, L. Zhang, M. Schöffler, H. Xu, A. Iwasaki, T. Okino, K. Yamanouchi and A. Baltuska, et al. , Phys. Rev. Lett., 2011, 106, 163001.

---