Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cooperative and synchronized rotation in motorized porous frameworks: impact on local and global transport properties of confined fluids†
Jack D.
Evans
 *a,
Simon
Krause
*a,
Simon
Krause
 b and
Ben L.
Feringa
b and
Ben L.
Feringa
 b
b
aDepartment of Inorganic Chemistry, Technische Universität Dresden, Bergstraße 66, 01062 Dresden, Germany. E-mail: jack.evans@tu-dresden.de
bCentre for Systems Chemistry, Stratingh Institute for Chemistry, University of Groningen, Groningen, The Netherlands
First published on 9th March 2020
Abstract
Molecules in gas and liquid states, as well as in solution, exhibit significant and random Brownian motion. Molecules in the solid-state, although strongly immobilized, can still exhibit significant intramolecular dynamics. However, in most framework materials, these intramolecular dynamics are driven by temperature, and therefore are neither controlled nor spatially or temporarily aligned. In recent years, several examples of molecular machines that allow for a stimuli-responsive control of dynamical motion, such as rotation, have been reported. In this contribution, we investigate the local and global properties of a Lennard-Jones (LJ) fluid surrounding a molecular motor and consider the influence of cooperative and non-directional rotation for a molecular motor-containing pore system. This study uses classical molecular dynamics simulations to describe a minimal model, which was developed to resemble known molecular motors. The properties of an LJ liquid surrounding an isolated molecular motor remain mostly unaffected by the introduced rotation. We then considered an arrangement of motors within a one-dimensional pore. Changes in diffusivity for pore sizes approaching the length of the rotor were observed, resulting from rotation of the motors. We also considered the influence of cooperative motor directionality on the directional transport properties of this confined fluid. Importantly, we discovered that specific unidirectional rotation of altitudinal motors can produce directed diffusion. This study provides an essential insight into molecular machine-containing frameworks, highlighting the specific structural arrangements that can produce directional mass transport.
Introduction
Transport properties of fluids in confinement are essential for both biological and artificial systems. Enhancement of diffusion with the preservation of selectivity is essential for the improvement of separation technologies,1 particularly for membrane-based systems.2,3 In biological systems, diffusion enhancement is primarily facilitated by pore shape agitation of the channels embedded in soft matter.4–8 However, similar effects can also be found in artificial porous media such as carbon nanotubes in which phonon-induced oscillating friction is found to enhance diffusion of fluids.9–11 In both cases the nanoscopic oscillation of pore contraction and expansion propagates cooperatively through the lattice allowing for accelerated transport properties on a larger length scale.Recently, Marbach et al. established a general model to describe the “transport and dispersion across wiggling nanopores”, which is primarily activated by thermal processes and occurs in a variety of different materials, with differing effects on diffusion properties.12 Although this global vibration-induced diffusion enhancement in nanochannels might in principle also allow for separation of solutes as a function of their own Peclet number,13 diffusion enhancement dictated by local stimuli-responsive dynamic molecular species in artificial systems remains largely unexplored. In fact, biological systems frequently manipulate transport properties by local dynamic mechanisms beyond the activated processes of pore shape agitation.14–16 Transmembrane diffusion is often facilitated by enzymatic molecular machines (MMs) that allow transport against a concentration gradient with unprecedented efficiency and selectivity.17,18
The combination of local and global dynamic mechanisms to impact transport properties, as employed in biological systems, is expected to drastically enhance properties of artificial nanomaterials.19 Inspired by natural systems, chemists have successfully produced artificial MMs that can act as artificial muscles20 and also be bound to and open membranes for diffusion of guest species.21,22 However, only a few examples show that these dynamic molecular systems can enhance diffusion in solution23,24 and the actual effects, as well as their origin, are currently controversially discussed.25 Similarly, for the dynamics of nanoscopic swimmers.26 Instead, controlled rotational motion by MMs in porous systems is expected to enhance diffusion due to confinement effects.27,28 Recently, Danowski et al. reported on the incorporation of 2nd generation light-driven MMs in the backbone of a porous metal–organic framework.29 They demonstrated that the unidirectionality of rotation is maintained and that the immobilized motors exhibit rotational frequencies similar to the motors in solution. This is one of the few examples of artificial MMs employed in ordered porous solids30 and the only example that illustrates regular spatial organization of unidirectionally rotating molecules in a porous crystal. Although rotational intramolecular motion is well known31 also in crystalline solids,32 stimuli-driven unidirectional rotation in light driven molecular motors represents the ability to control the frequency and directionality by molecular design.33 Using E–Z photoisomerization of an overcrowded alkene, the rotor can be switched into a metastable state. A subsequent thermal relaxation step produces 180° rotation, where the stereocenter adjacent to the double bond dictates the directionality. Successive photoisomerisation and thermal relaxation steps lead to unidirectional 360° rotation of the rotor around the double bond axis (Fig. 1).34 A broad variety of artificial light driven molecular motors with different structures, properties and functionalities were established by changing the molecular design.35
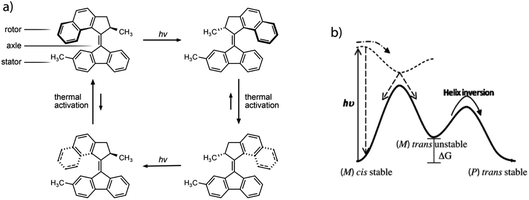 | ||
| Fig. 1 The prototypical light driven molecular motor, highlighting the steps that provide rotation (a). The underlying potential energy surface for the molecule (solid line) and the excited state potential energy surface (dashed line), which induces the motion (b). Portions of this figure are reprinted from ref. 36. | ||
In this contribution, we demonstrate the interactions and transport properties of fluids in motorized porous frameworks and investigate the influence of cooperative synchronized and non-cooperative rotation of molecular motors. This study is performed by molecular dynamics simulations using a minimal toy-model, which resembles known molecular rotors. The molecular machine design incorporates elements of existing molecular motors including their geometry and hypothetical orientations in a one-dimensional pore, in an effort to establish a close representation of a real-world system. Initially, the result of an isolated motor surrounded by fluid was considered. Subsequently, different pore sizes were investigated so that the effects of confinement on the transport properties of the fluid can be captured. We also probed the influence of cooperativity on the transport properties of the confined fluid by computing systems where the rotation of two rotors are either correlated, in direction, or uncorrelated. This allows us to investigate fundamental scenarios present in materials currently known in literature29 and compare this to proposed cooperatively working motorized frameworks.
This study provides a physical blueprint for molecular machine-containing frameworks poised as new devices by which external stimuli can act to provide activated diffusion for directional mass transport or nanoscale microfluidic devices, mimicking biological systems. The introduction of MMs into the backbone of periodic framework materials has yielded stimuli-responsive assemblies of controlled dynamics in the solid-state.29 Although this specially defined arrangement of MMs in the solid-state represents dynamic heterogeneous interfaces, the collective synchronized work of MMs in the solid-state is unprecedented and molecular simulations, like that presented here, provide essential insight for experimental endeavours.
Methodology
MM-systems were investigated using molecular dynamics (MD) simulations, employed by the lammps code.37 We simulate the motor as Lennard-Jones (LJ) particles, which interact with surrounding LJ particles by interatomic interactions described by the classic LJ potential (eqn (1))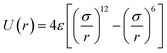 | (1) |
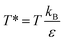 and kB represents the Boltzmann constant. Importantly, time is defined as τ = (ε/mσ2)1/2t. We have employed these units here for simplicity, as the aim of this study is a qualitative assessment of molecular motor systems in confined fluids. The timestep for simulations was set to 0.005τ. The MMs were modelled by six particles with additional bond, angle and dihedral interactions computed by harmonic potentials (eqn (2)–(4)).
and kB represents the Boltzmann constant. Importantly, time is defined as τ = (ε/mσ2)1/2t. We have employed these units here for simplicity, as the aim of this study is a qualitative assessment of molecular motor systems in confined fluids. The timestep for simulations was set to 0.005τ. The MMs were modelled by six particles with additional bond, angle and dihedral interactions computed by harmonic potentials (eqn (2)–(4)).| E(r) = Kbond(r − r0)2 | (2) |
| E(r) = Kangle(θ − θ0)2 | (3) |
E(r) = Kdihedral[1 + d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(nϕ)] cos(nϕ)] | (4) |
The energy coefficients Kbond, Kangle and Kdihedral were set to 500ε, 300ε and 100ε, respectively. The specified geometry and thus equilibrium values of these potentials are discussed in detail later. This provides a robust and customizable framework for modelling molecular motifs.
The dynamics of the fluid, and dynamics of the MMs, were simulated using a Langevin thermostat38 in the NVE ensemble, which effectively performs Brownian dynamics.39 The temperature of the fluid was controlled to 1.0T* using a damping parameter of 1.0τ. Confinement was achieved using wall potentials that interact with fluid particles using only the repulsive part of the LJ potential (eqn (1)).
Representative input files for the simulation reported in this study are available online in our data repository at https://github.com/jackevansadl/supp-data.
Results
Minimal representation of a molecular rotor
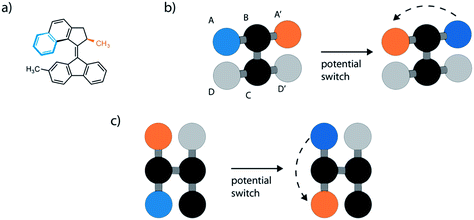
Our model drew inspiration from the prototypical 2nd generation molecular motor with a rotor that reassembles the structure embedded in the previously discussed motorized framework29 (Fig. 2a). However, we sought to simplify this molecular motif using the fewest number of particles, bonds and angles and symmetrize the rotor. This led us to our first and generic model displayed in Fig. 2b and c. This model uses six particles arranged such that two particles act as the rotor (A and A′), two as the axle (B and C) and two as the stator (D and D′). Only the particles of the rotor and axle (A, A′, B and C) were chosen to noncovalently interact with surrounding LJ fluid particles with the same strength and particle size parameters as the surrounding LJ fluid, σ = 1 and ε = 1. These values were chosen as, generally, molecular rotors do not interact strongly with solvents and are of similar relative size. Particles D and D′ have no interactions as they are employed to define the necessary dihedral potential. Moreover, the forces and velocities of B, C, D and D′ particles were set to 0, fixing their position throughout the simulation. The key bond parameter that dictates the size of the rotor, r0 between particles A–B and A′–B, was set to 1.5σ. Notably, this arrangement can be rotated so that both azimuthal40 and altitudinal41 motion can be modelled (Fig. 2c).Simulations of the prototypical 2nd generation molecular motor have used excited-state MD simulations, where the mechanism for light-driven unidirectional rotation was investigated.42 These simulations use expensive atomistic descriptions of the MM, which indeed are useful to provide accurate details about the free energy landscape. However, these simulations are difficult to extend in understanding long timescale dynamics. To our knowledge the consistent rotational motion of these systems using classical molecular dynamics has not been described and this is an important development for the investigation of molecular motors.43 In the literature, the motion of other important stimuli-responsive molecular machines and switches, such as azobenzene, is typical treated by a two potential system.44 This straightforward approach describes the two long lived states, which these molecules exhibit. Depending on the molecular structure, rotary motion of MMs might involve multiple steps, however for simplicity we will consider a bistable scenario in this work.
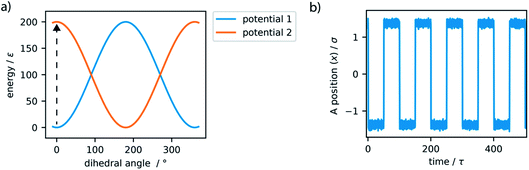
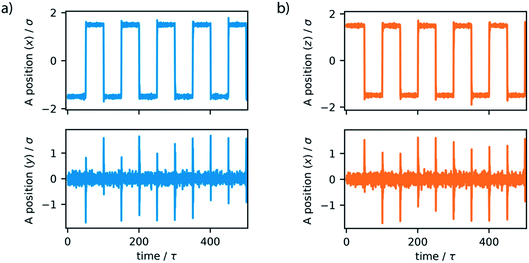
To dictate the photoactive motion displayed by this MM we define two potential states of the system. This uses the dihedral potential between the particles A–B–C–D and A′–B–C–D′ noted in eqn (4). This potential has the parameter d, which is set as 1 or −1. This can be changed during the simulation to produce two distinct potential states as demonstrated in Fig. 3. These potential states have a minimum at either 0° or 180°, which effectively switches the stable configuration of particles A and A′ to opposite sides of the molecule. Sequentially switching the potential parameter d during the simulation, after a set number of time steps, a stepwise periodic rotation is achieved. This stepwise rotation is comparable to the type of motion observed in the experimental system. The motion between the two states occurs over a few simulation steps, which is comparable to the ultrafast dynamics reported for the excited-state photoisomerization rotation found in the experimental system.45 Throughout this study, the switching period, between the two potentials, was chosen as 50τ. Currently, molecular rotary motors exhibit MHz-scale rotational frequencies.46,47 If we consider the particles in this study to have similar size and characteristics to argon, the rotation rate is approximately 4.6 GHz. This is currently faster than is observed for MMs but represents the potential for such systems, as with specific functionalisation these systems could in principle function in the GHz regime.48
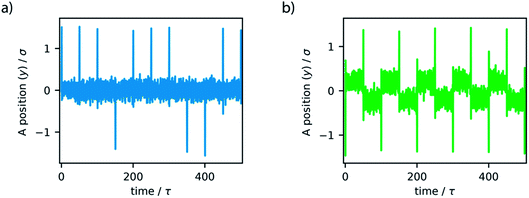
The simple switching of the dihedral potentials can effectively produce a rotation about the axes of the molecule. However, because the potential switch sets this structural configuration atop the symmetric maximum of the dihedral potential energy surface the system can equally relax (by rotation) in either direction. This results in the non-directional rotation of the motor as demonstrated in Fig. 4a. Unidirectional motion is a sought-after characteristic of molecular rotors known to work in porous frameworks.29 However, as with biological motor systems, directionality is essential to perform mechanical tasks.49 Synthetically this is achieved by photo-responsive sterically overcrowded alkenes, which results in four distinct steps as outlined in Fig. 1.50 To achieve unidirectional rotation in our simulations we employ a torsional bias force, orientated in the direction of the axle, thus mimicking the influence of sterically crowded functionalisation. This use of applied torque avoids increasing complex descriptions of the dihedral potential energy surface. While large bias forces result in continued and uncontrolled rotation, subsequent to the potential switch event, a bias force of 30σ/ε results in singular and unidirectional rotation (Fig. 4b). Notably, the sign of this bias torque dictates the direction of rotation, either clockwise or counter clockwise allowing the control of directionality, similar to the experimental MM for which rotational directionality is dictated by the nature of the stereocentre adjacent to the double bond.50
As detailed here, we have demonstrated that a six-particle system can produce a minimal description of a molecular motor for classical molecular dynamics simulations. Our model switches between two distinct dihedral potentials and when combined with a bias torque this results in unidirectional rotation. Importantly, the motion we observe is comparable to the ratchet-like rotation designed in many synthetic molecular motors.51
Dynamics of rotor surrounded by fluid
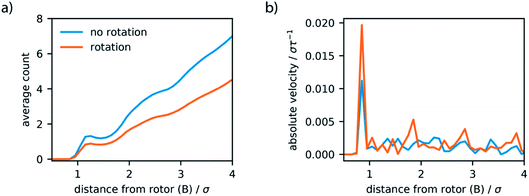
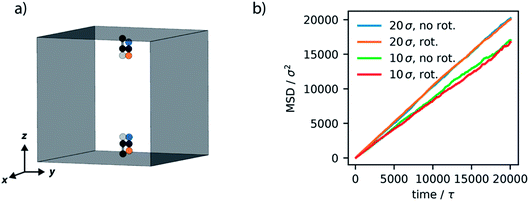
Initially, we investigated the results obtained by surrounding the model motor with LJ particles, which act like a fluid. The motor model, described in the previous section, was placed in a simulation box of 20σ × 20σ × 20σ, with periodic boundary conditions. LJ particles were included in this simulation box with a density of 0.34ρ, which at 1.0T* behave as a liquid.52 Simulations where the motor remains fixed, by virtue of a consistent dihedral potential, and where the motor rotates unidirectionally were performed and system properties sampled over 4 million steps (equivalent to 20 × 103τ). The trajectories show constant temperatures but when the potential is switched there is a spike in total energy, associated with the drastic increase in potential energy of the system. This high energy state quickly subsides as the motor rotates to the new stable configuration.These simulations demonstrate that the global dynamics of the fluid show no changes resulting from rotation of the motor. In particular, the structure of the fluid, determined by the radial distribution function, and the dynamics of the fluid, revealed by mean-squared displacement, remain unaffected (Fig. S2, ESI†). Given the size of the molecular rotor is equivalent to the size of the fluid particles this is perhaps not surprising. To completely understand the effect of artificial molecular rotation in this system the local properties of the rotor and fluid were investigated. As displayed in Fig. 5a, the rotation produces a lower density of fluid in a spherical area directly surrounding the centre of the rotor (particle B). This local defect in the structure is attributed to the constant reorganisation of the fluid due to rotation. Moreover, the dynamics in this region also appear to be influenced by the motion. The average velocity of spherical slices surrounding the rotor (Fig. 5b) show an increase in absolute velocity. This increase is apparent in the locations where the rotor particles (A and A′) are located, suggesting that the movement of the rotor produces this increase in local velocity of the fluid.
Clearly the relatively small size of the molecular rotor limits its influence on the properties of a surrounding medium, which is known to influence the rotational speed of light driven motors52,53 and rotors.53–55 The effects of the motor rotation and its frequency are neglected in this model but are expected to play an important role in a real world system. By increasing the rotor size the interactions with surrounding fluid could be enhanced, allowing in principle for molecular stirring.23
Azimuthal rotor in a one-dimensional pore
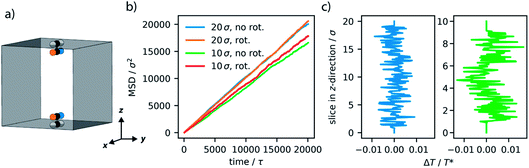
One appealing method to increase the effectiveness of molecular machines is their positions within materials.56 Especially confining a reaction media in close proximity to the motion of rotors is expected to enhance dynamic effects.27 We consider the effect of this by arranging our motor system on the walls of a one-dimensional pore (Fig. 6a). The pore is constructed using repulsive wall potentials that interact with only fluid particles. This confinement arrangement is analogous to simulations of nanoconfined water, and these repulsive walls are suggested to act like hydrophobic walls.57 Two azimuthal rotors were positioned on opposite walls and arranged such that the stable configuration of the rotor is aligned with the one-dimensional pore. Unidirectional rotation is directed with the bias torque in the same direction for each rotor. The LJ fluid was added to this system at a density of 0.09ρ. A lower density, compared to the non-confined example, was employed to avoid overcrowding the rotors. Importantly, two distinct pore sizes were investigated, a larger pore of 20σ × 20σ and a smaller pore of 10σ × 10σ. The axis of the one-dimensional pore was 20σ and includes periodic boundary conditions, only in this dimension. Simulation results are presented as averaged observations from 10 unique samples, each included 4 million steps, as described in the previous section.We find that for the large pore system the global and local properties of the confined fluid (Fig. 6b and c) show little influence from rotation. The transport of the fluid is observed as the slope of the mean-squared displacement, also referred to as diffusivity (Fig. 6b). There appears to be little influence on the transport of the fluid for this larger pore structure. Similarly, there are no local increases in the average motion (temperature) observed (Fig. 6c).
In contrast to the larger pore, the smaller pore structure of 10σ × 10σ, which approaches the length of the rotor (3σ), demonstrated a considerable effect from the set motion of the molecular motor. As a result of the increased confinement the diffusivity of the fluid decreases by approximately 15%, in agreement with our understanding of diffusion in porous media.58 However, if the motors rotate there is an evident increase in diffusivity where the smaller pores now only result in a 10% decrease in diffusivity. The greater confinement provided by the smaller pore size greatly enhances the effect of the motor’s rotation on the LJ fluid. Particularly, the analysis of the average local properties of the fluid demonstrates an increase in local temperature at the location of the rotors. This enhanced temperature in the area directly surrounding the rotor is representative of the convection-like processes that have been experimentally observed to produce enhanced diffusion in molecular catalysts.25
Altitudinal rotor in a one-dimensional pore
The synthetic design of molecular motors can hypothetically produce rotors that rotate in distinctive directions. When immobilized on a surface these motors can exhibit different orientations.59 As a result, we also investigated the effects of rotation arranged in an altitudinal fashion,60 as illustrated in Fig. 2c. This arrangement can localize the specified motion towards the centre of a porous structure where it may have a greater influence on the transport properties. An equivalent one-dimensional pore system was constructed for investigating the use of altitudinal rotors (Fig. 7a) which includes two motors orientated perpendicular to the pore direction, such that the rotation is orientated in the direction of diffusion. The unidirectional rotation for this case is also arranged with the bias torque in the same direction for each rotor. The sampling and simulation details are analogous to that discussed for the azimuthal case.Similar to the system containing azimuthal motors, we observe no discernible influence from the motor rotation in the large pore structures. Moreover, for the small pore structures, where the positions of the rotor particles are in close proximity there is also the same relative decrease in diffusion.
When the motors rotate, however, we observe no significant change in diffusivity, in direct contrast to that observed for the azimuthal rotor system. This result suggests that only specific orientations of rotation by molecular motors aligned in pore channels may lead to an increase in transport properties.
Non-directional rotation in a one-dimensional pore
The unidirectional motion of molecular rotors is considered imperative for directing movement at the molecular level. Thus, we sought to consider how non-directional motion manifests and effects diffusion in small pore systems, for both the azimuthal and altitudinal rotors. In fact, such a case resembles the scenario of rotors frequently incorporated in the backbone of porous frameworks but not governed by a stimulus, such as light.28 To investigate this, we conducted similar simulations as described in the previous two sections, but with the absence of the bias torque. This resulted in non-directional motion of the rotors (Fig. 8).Without the application of bias force, the rotation is observed to consecutively oscillate in random directions, clockwise or anti-clockwise. The presence and dynamics of the confined LJ liquid is not observed to produce unidirectional or preferred directional rotation of the rotors. Non-directional motion of the azimuthal rotor resulted in equivalent diffusivity as the unidirectional motion previously described. Contrastingly, the altitudinal rotor showed enhanced diffusivity, greater than both the considered unidirectional and fixed rotor dynamics (6% greater than the fixed rotor case). This non-directional motion can provide the altitudinal system with the same diffusivity as the azimuthal system.
The altitudinal rotor system, as it extends into the pore, demonstrates the profound influence of the directionality of the motor. The motion of each rotor can interact like that of a turnstile, where rotation in a cooperative manner, if not directed favourably, can hinder diffusion.
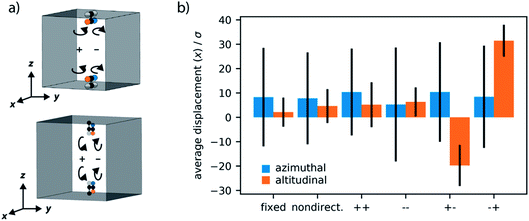
Directional and cooperative rotation
As the directionality, and hence cooperativity, of the motors in this small pore structure can affect the transport properties of the confined fluid we examined different combinations of rotation and their effect on the directionality of the diffusion in the small pore, for both orientations of the motor. Please note the rotation of the motors are synchronous, here we only investigate the direction. We considered six different cases: fixed rotors, non-directional rotors and the four combinations of clockwise or anti-clockwise rotation. We label the direction of rotation by the sign of the bias torque (Fig. 9a).The alignment of azimuthal motors with the pore walls shows no distinct direction of diffusivity, with the average displacement close to centre, around 0σ. This indicates equal diffusion in either direction of the one-dimensional pore. Notably, this is not affected by different combinations of rotation by the motors. The altitudinal motors, however, exhibit important dependence on the set rotation of the motors. If the rotors have no rotation (fixed), non-directional rotation or aligned rotation the LJ fluid is observed to show no directional preference. The cooperative, and opposite, rotation of each motor, labelled here as “+−” and “−+” can induce a preferential direction to the diffusion of confined fluid. This turnstile-like system can produce a flow of fluid in either direction in the pore dependent on the combination of rotations used.
Although the magnitude of diffusion is only marginally affected by the arrangement of motors, for example we have not demonstrated on/off switchable diffusion, the induction of a preferential diffusion direction is certainly promising. Notably, the rotors used here are of relative size to the diffusing LJ particles and of equal interaction strength. It is the effect of cooperativity and confinement that is responsible for this significant outcome on the global transport properties. Amplification of these effects are expected to occur if the average rotor–fluid interactions as well as the confinement effects are optimized. An increase in motor density per void volume is certainly also expected to enhance the observed diffusion effects.
Discussion
The molecular simulations, described in this study, represents a minimalistic and qualitative picture of molecular motors, and the possible consequence of arranging them in confined solid-state. Many approximations are made to describe the motion of rotors in this study. For example, the rotation mechanism is significantly reduced to a two-state motion. Notably, the rotation between the two-states occurs almost instantaneously, when the dihedral potential is switched. In reality molecular motors show complex rotational dynamics with slow and fast movements to produce a full rotation.49 In future studies, it is possible to use more complex potential energy surfaces and gradual potential changes to more realistically reflect the intricate dynamics of real-world motors. Nevertheless, the potential switching mechanism should provide the foundation to build new atomistic models of molecular machines.A key observation from considering the combined dynamics of the rotor surrounded by fluid is the impervious nature of the fluid bulk. The small rotor system is a drop in the ocean compared to the stable dynamics of a fluid. This is clear from the global properties remaining unaffected by rotational dynamics, while only the very local properties, for example the particles in the arc of rotation, show some evidence of change. This observation is in line with recent scepticism about diffusion enhancement by dynamic species in diluted solutions.25 In turn, this demonstrates the importance of regular, defined arrangement with a maximal high motor density of these machines in confinement. It was only when the fluid was confined in a pore of comparable size to the molecular rotor where the applied rotation began to affect the global transport properties of the fluid. Still, in our initial model we find relatively modest changes to diffusivity. However, by considering the orientation of the motor and the effect of different rotations of rotors we find the greatest change. By combination of altitudinal rotors aligned into the pore and synchronization of the rotational directionality we could produce a turnstile-like system able to direct the diffusion in a specified direction of the pore. This illustrates that random orientation and non-directional rotation of molecular motors in the solid-state are unlikely to produce diffusion enhancement on a larger length scale let alone directed diffusion. Cooperative rotation and specific arrangement of unidirectional rotation are required to produce designed transport phenomena.
Summary and outlook
In this work, we have outlined the influence of rotating molecular species and the importance of their orientation, cooperativity and directionality on the transport properties of confined fluids. Our findings help to understand the influence of local dynamics of molecular motors and rotors on the surrounding fluid. This includes, the nature of pore space functionalized with dynamic groups and potential strategies to manipulate transport properties of confined fluids by this dynamic pore space. Although the applied model drastically simplifies real-world molecular motors, it captures the most important aspects being unidirectional rotation and orientation of the rotor. Our results, however, provide helpful indications about the need for high rotational frequencies in addition to the detection of minor changes in diffusivity locally and globally. We envision the guidelines, presented here, to be crucial for the design of stimuli-responsive dynamic materials, capable of manipulating guest transport properties by dynamic molecular machines. However, the currently reported porous materials that include molecular machines30 or rotors28 do not meet the specified criteria defined by this investigation.As discussed in the introduction, many transport phenomena are supported by activated vibrations of the pore walls,12 a property neglected in the present work. The combination and alignment of local dynamics from a functional surface, by anchored groups, and global vibrational dynamics of the framework backbone, towards cooperative pore agitation on different length scales, represents an interesting avenue for novel transport phenomena in porous solids and should be further explored.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. D. E. and S. K. acknowledge the support of the Alexander von Humboldt foundation and HPC platforms provided by a GENCI grant (A0070807069) and the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. We thank Michael Kathan for critical reading and comments on a draft of this paper.References
- D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437 CrossRef.
- M. S. Denny, J. C. Moreton, L. Benz and S. M. Cohen, Nat. Rev. Mater., 2016, 1, 16078 CrossRef CAS.
- S. Yuan, X. Li, J. Zhu, G. Zhang, P. Van Puyvelde and B. Van der Bruggen, Chem. Soc. Rev., 2019, 48, 2665–2681 RSC.
- A. J. Wand, Nat. Struct. Biol., 2001, 8, 926–931 CrossRef CAS.
- S. Y. Noskov, S. Bernèche and B. Roux, Nature, 2004, 431, 830–834 CrossRef CAS.
- G. Bhabha, J. Lee, D. C. Ekiert, J. Gam, I. A. Wilson, H. J. Dyson, S. J. Benkovic and P. E. Wright, Science, 2011, 332, 234–238 CrossRef CAS.
- T. W. Allen, S. Kuyucak and S.-H. Chung, Biophys. J., 1999, 77, 2502–2516 CrossRef CAS.
- G. Wei, W. Xi, R. Nussinov and B. Ma, Chem. Rev., 2016, 116, 6516–6551 CrossRef CAS.
- M. Ma, G. Tocci, A. Michaelides and G. Aeppli, Nat. Mater., 2016, 15, 66–71 CrossRef CAS.
- E. R. Cruz-Chú, E. Papadopoulou, J. H. Walther, A. Popadić, G. Li, M. Praprotnik and P. Koumoutsakos, Nat. Nanotechnol., 2017, 12, 1106–1108 CrossRef.
- M. Ma, F. Grey, L. Shen, M. Urbakh, S. Wu, J. Z. Liu, Y. Liu and Q. Zheng, Nat. Nanotechnol., 2015, 10, 692–695 CrossRef CAS.
- S. Marbach, D. S. Dean and L. Bocquet, Nat. Phys., 2018, 14, 1108–1113 Search PubMed.
- S. Marbach and L. Bocquet, J. Chem. Phys., 2017, 147, 154701 CrossRef.
- N. Gamper and M. S. Shapiro, Nat. Rev. Neurosci., 2007, 8, 921–934 CrossRef CAS.
- S. G. Dahl, I. Sylte and A. W. Ravna, J. Pharmacol. Exp. Ther., 2004, 309, 853–860 CrossRef CAS.
- H. F. Lodish, Molecular cell biology, W. H. Freeman and Co., New York, 2013 Search PubMed.
- C. R. Sanders and J. M. Hutchison, Curr. Opin. Struct. Biol., 2018, 51, 80–91 CrossRef CAS.
- F. M. Goñi, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 1467–1476 CrossRef.
- B. A. Grzybowski and W. T. S. Huck, Nat. Nanotechnol., 2016, 11, 585–592 CrossRef CAS.
- J. Chen, F. K.-C. Leung, M. C. A. Stuart, T. Kajitani, T. Fukushima, E. van der Giessen and B. L. Feringa, Nat. Chem., 2018, 10, 132–138 CrossRef CAS.
- V. García-López, F. Chen, L. G. Nilewski, G. Duret, A. Aliyan, A. B. Kolomeisky, J. T. Robinson, G. Wang, R. Pal and J. M. Tour, Nature, 2017, 548, 567–572 CrossRef.
- M. A. Watson and S. L. Cockroft, Chem. Soc. Rev., 2016, 45, 6118–6129 RSC.
- J. Chen, J. C. M. Kistemaker, J. Robertus and B. L. Feringa, J. Am. Chem. Soc., 2014, 136, 14924–14932 CrossRef CAS.
- K. K. Dey, F. Y. Pong, J. Breffke, R. Pavlick, E. Hatzakis, C. Pacheco and A. Sen, Angew. Chem., Int. Ed., 2016, 55, 1113–1117 CrossRef CAS.
- T. S. C. MacDonald, W. S. Price, R. D. Astumian and J. E. Beves, Angew. Chem., Int. Ed., 2019, 58, 18864–18867 CrossRef CAS.
- K. K. Dey, Angew. Chem., Int. Ed., 2019, 58, 2208–2228 CrossRef CAS.
- H. Huang and T. Aida, Nat. Nanotechnol., 2019, 14, 407 CrossRef CAS.
- A. Gonzalez-Nelson, F.-X. Coudert and M. A. van der Veen, Nanomaterials, 2019, 9, 330 CrossRef CAS.
- W. Danowski, T. van Leeuwen, S. Abdolahzadeh, D. Roke, W. R. Browne, S. J. Wezenberg and B. L. Feringa, Nat. Nanotechnol., 2019, 14, 488–494 CrossRef CAS.
- P. Martinez-Bulit, A. J. Stirk and S. J. Loeb, Trends in Chemistry, 2019, 1, 588–600 CrossRef.
- G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Chem. Rev., 2005, 105, 1281–1376 CrossRef CAS.
- C. S. Vogelsberg and M. A. Garcia-Garibay, Chem. Soc. Rev., 2012, 41, 1892–1910 RSC.
- N. Koumura, R. W. J. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Nature, 1999, 401, 152–155 CrossRef CAS.
- T. van Leeuwen, A. S. Lubbe, P. Štacko, S. J. Wezenberg and B. L. Feringa, Nat. Rev. Chem., 2017, 1, 0096 CrossRef CAS.
- S. Kassem, T. van Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- R. D. Astumian, Chem. Sci., 2017, 8, 840–845 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302–1322 CrossRef CAS.
- M. P. Allen, D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, 1989 Search PubMed.
- R. A. van Delden, M. K. J. ter Wiel, M. M. Pollard, J. Vicario, N. Koumura and B. L. Feringa, Nature, 2005, 437, 1337–1340 CrossRef CAS.
- G. T. Carroll, G. London, T. F. Landaluce, P. Rudolf and B. L. Feringa, ACS Nano, 2011, 5, 622–630 CrossRef CAS.
- S. Grimm, C. Bräuchle and I. Frank, ChemPhysChem, 2005, 6, 1943–1947 CrossRef CAS.
- A. Singharoy and C. Chipot, J. Phys. Chem. B, 2017, 121, 3502–3514 CrossRef CAS.
- C. Pezzato, C. Cheng, J. F. Stoddart and R. D. Astumian, Chem. Soc. Rev., 2017, 46, 5491–5507 RSC.
- J. Conyard, K. Addison, I. A. Heisler, A. Cnossen, W. R. Browne, B. L. Feringa and S. R. Meech, Nat. Chem., 2012, 4, 547–551 CrossRef CAS.
- M. Klok, N. Boyle, M. T. Pryce, A. Meetsma, W. R. Browne and B. L. Feringa, J. Am. Chem. Soc., 2008, 130, 10484–10485 CrossRef CAS.
- M. M. Pollard, M. Klok, D. Pijper and B. L. Feringa, Adv. Funct. Mater., 2007, 17, 718–729 CrossRef CAS.
- B. Oruganti, C. Fang and B. Durbeej, Phys. Chem. Chem. Phys., 2015, 17, 21740–21751 RSC.
- V. García-López, D. Liu and J. M. Tour, Chem. Rev., 2020, 120, 79–124 CrossRef.
- D. Roke, S. J. Wezenberg and B. L. Feringa, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9423–9431 CrossRef CAS.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS.
- B. Smit, J. Chem. Phys., 1992, 96, 8639–8640 CrossRef CAS.
- J. C. M. Kistemaker, A. S. Lubbe, E. A. Bloemsma and B. L. Feringa, ChemPhysChem, 2016, 17, 1819–1822 CrossRef CAS.
- M. Klok, L. P. B. M. Janssen, W. R. Browne and B. L. Feringa, Faraday Discuss., 2009, 143, 319–334 RSC.
- A. Vyšniauskas and M. K. Kuimova, Int. Rev. Phys. Chem., 2018, 37, 259–285 Search PubMed.
- E. Moulin, L. Faour, C. C. Carmona-Vargas and N. Giuseppone, Adv. Mater., 2020, 1906036 CrossRef CAS.
- P. Kumar, F. W. Starr, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011202 CrossRef.
- K. Malek and M.-O. Coppens, J. Chem. Phys., 2003, 119, 2801–2811 CrossRef CAS.
- V. Balzani, A. Credi and M. Venturi, ChemPhysChem, 2008, 9, 202–220 CrossRef CAS.
- G. London, G. T. Carroll, T. Fernández Landaluce, M. M. Pollard, P. Rudolf and B. L. Feringa, Chem. Commun., 2009, 1712–1714, 10.1039/b821755f.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0fd00016g |
| This journal is © The Royal Society of Chemistry 2021 |